Peter Tucker and Duncan Smith (1999)
Journal of Artificial Societies and Social Simulation vol. 2, no. 3, <https://www.jasss.org/2/3/3.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 30-Aug-99 Accepted: 25-Sep-99 Published: 31-Oct-99
![]()
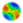 Abstract
AbstractThe model is aimed at providing decision support for local and regional waste management planning.
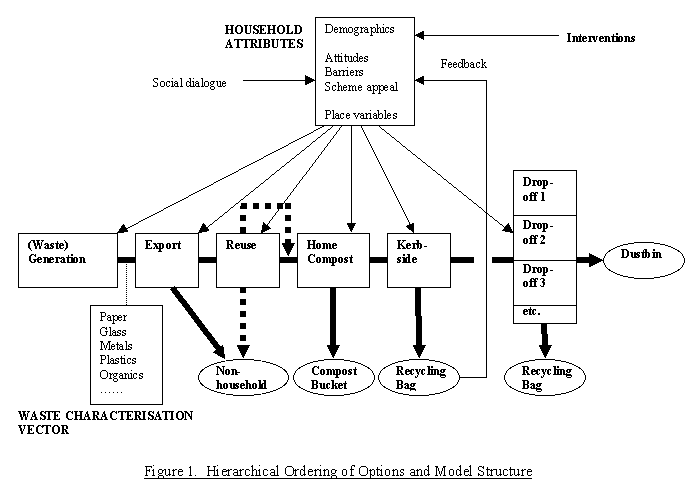
|
|
| Table 1: Material Flux Classification | |
| Prime Category | Sub-categories |
| Paper | Newspaper, magazines, junk mail, catalogues, other paper, card |
| Glass | Green bottles, amber bottles, clear bottles, jars, other glass |
| Plastic | Beverage bottles, other dense plastic, carrier bags, other film |
| Metal | Ferrous cans, other ferrous, aluminium cans, aluminium foil, other |
| Organics | Kitchen veg., other kitchen, garden soft, garden woody, other* |
| Textiles | Second hand clothes/bedding, clean rags, other |
| Combustibles | n/a |
| Non-combustibles | n/a |
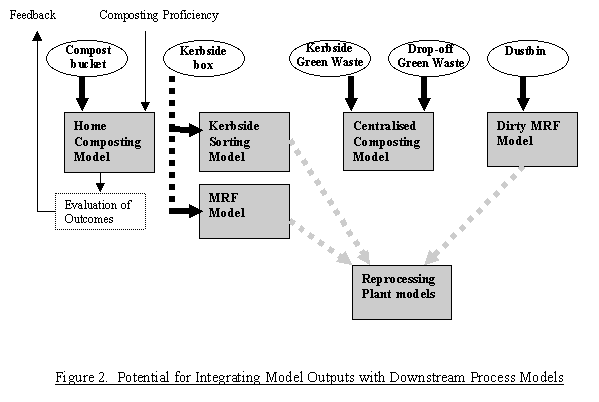
|
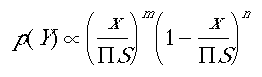
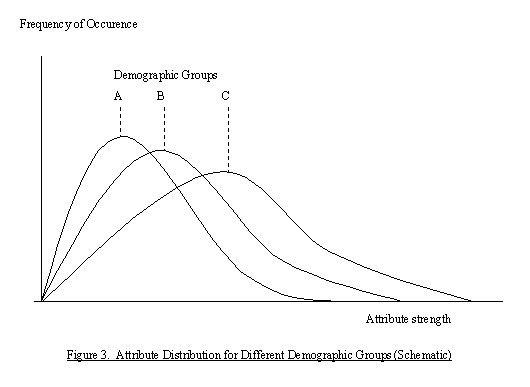
where S are the socio-demographic descriptors and x represents the scale unit (Kg. or strength of attitude etc.). m and n are fixed model parameters, estimated from observational or survey data (Tucker et al., 1998c, 1998d, 1999a), or set through empirical adjustment.
| Table 2: Household Attribute Set | ||
| Attribute | Description | |
| Demographics | ||
| Housing type | ||
| Family Life Cycle | ||
| Family Size | ||
| Car Ownership | ||
| Attitudes/Barriers | ||
| Pro-recycling attitude | A | Strength of pro-recycling attitudes |
| General recycling barriers | C | Strength of general recycling barriers faced or perceived |
| Norms | N | Susceptibility to normative pressures |
| Threshold weight | W0(j) | Minimum perceived weight worthwhile recycling |
| Threshold weight | W1 | Storage capacity of household |
| Save decision 1 | D1 | To accumulate material until W0 is reached - or to discard |
| Save decision 2 | D2 | With adverse PD: to save for favourable PD - or to discard |
| Awareness | AS(j) | Knowledge that the scheme exists |
| Lifestyle | LF | Frequency of lifestyle events negating intention to recycle |
| Ignorance | I(k) | Misperceptions of types of material accepted by scheme |
| Forgetfulness | F(k) | Frequency of forgetting to recycle individual items |
| Distaste | DT(k) | Deliberate choice not to divert some items |
| Resilience to setback | R | Susceptibility to change behaviour with adverse experience |
| Intervention susceptibility | X | Susceptibility to respond to external stimuli |
| Pro-composting attitude | A' | Strength of pro-composting attitudes |
| Composting barriers | C' | Strength of general composting barriers faced or perceived |
| Composting proficiency | P | Expertise in producing home compost |
| Behavioural Control | ||
| Scheme appeal | SA(j) | Scheme specific appeal or scheme specific barriers |
| Personal difficulty | PD | Frequency of events stopping intended participation |
| Have bin | HB | Ownership of a compost bin |
| Place Variables | ||
| Neighbourhood | ||
| Street | ||
| Waste Generation | ||
| Waste arisings | W'(k) | Average weekly arisings of waste material k |
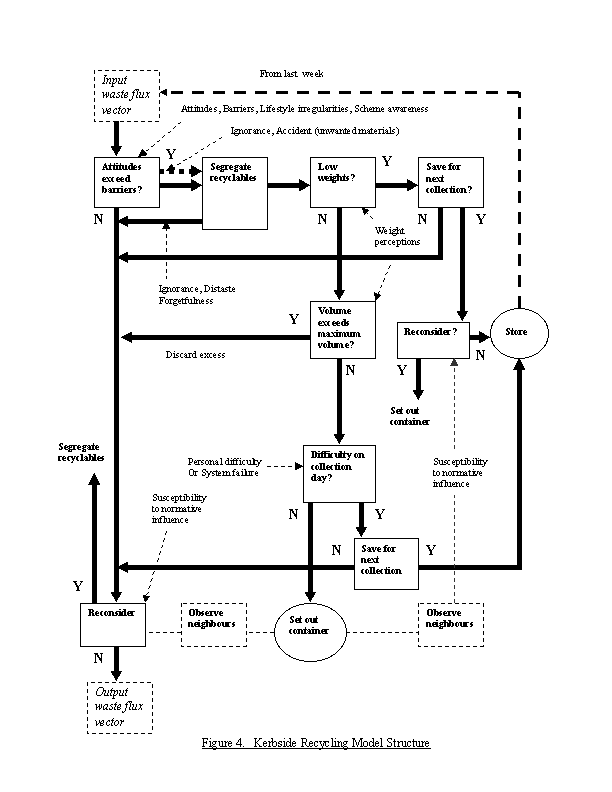
|
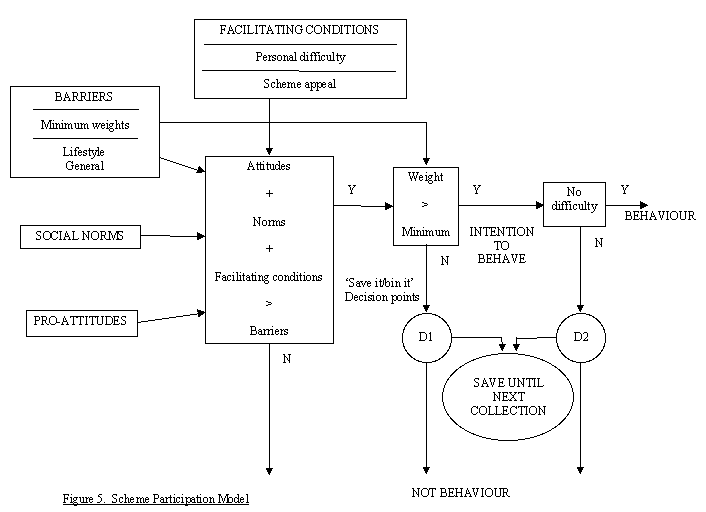
|
SA (i,j) = GA(j) + c1(i) * MM(j) + c2(i) * D(i,j) + c3(i) * V(i,j)
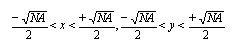
![]()
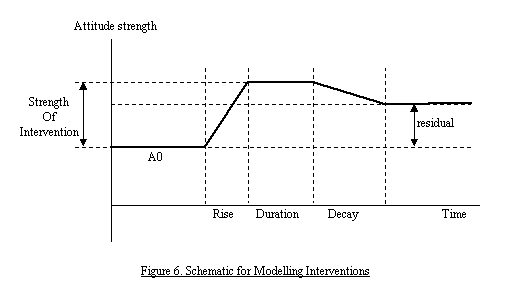
|
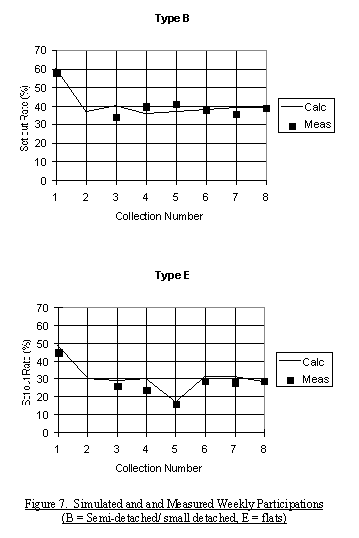
|
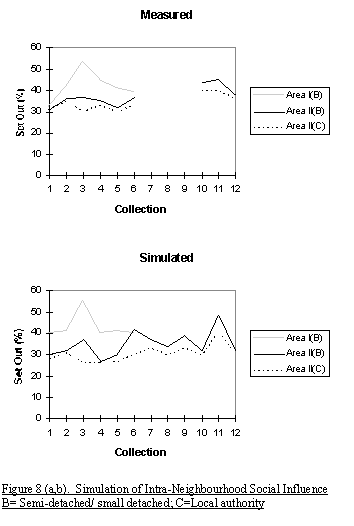
|
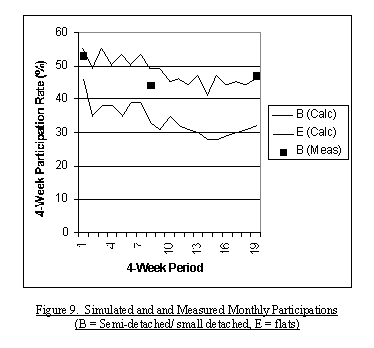
|
| Table 3: Simulation of Collection Frequency Change | ||||
| SCENARIO | 2 Week | 4 Week | ||
| Measured | Simulated | Measured | Simulated | |
| Set-out rate (%) | 35.0 | 35.3 | 44.8 | 44.1 |
| Participation rate (%) | 48.5 | 48.4 | 44.8 | 44.1 |
| 8-week participation (%) | Not measured | 55.7 | 54.0 | 55.8 |
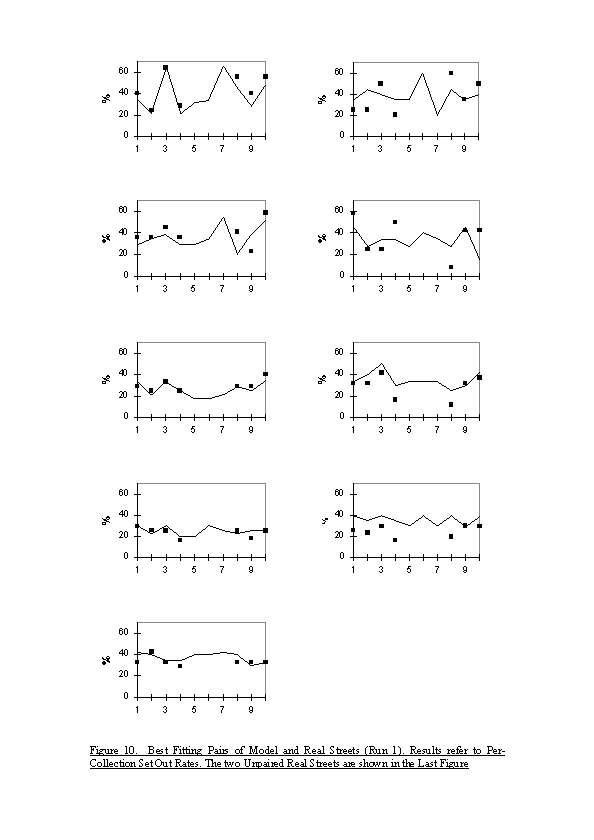
|

|
| Table 4: Mean Per-Collection Set Out Rate (%) | ||||
| House Type | Measured | Run 1 | Run 2 | Run 3 |
| B (Semi and small detached) | 29.9 | 32.0 | 28.4 | 30.3 |
| C (Local authority) | 18.9 | 22.1 | 21.1 | 21.7 |
| D (Terraced) | 12.5 | 13.5 | 14.2 | 15.1 |
| All | 19.7 | 21.7 | 21.3 | 21.6 |
| Table 5: Standard Deviation in Per-Collection Set Out Rate (%) | ||||
| House Type | Measured | Run 1 | Run 2 | Run 3 |
| B (Semi and small detached) | 5.4 | 2.6 | 2.6 | 3.1 |
| C (Local authority) | 3.6 | 1.3 | 1.1 | 1.8 |
| D (Terraced) | 1.9 | 0.8 | 1.0 | 1.1 |
| All | 3.1 | 1.0 | 0.8 | 1.4 |
 Acknowledgements
AcknowledgementsAZJEN, I. (1985), From Intentions to Actions: A Theory of Planned Behaviour. In Action Control: From Cognition to Behaviour, (Kuhl and Beckmann, eds.), Springer Verlag: New York.
BOLDERO, J. (1995), The Prediction of Household Recycling of Newspapers: The Role of Attitudes, Intentions and Situational Factors. Journal of Applied Social Psychology, 25(5), pp. 440-462.
COGGINS, P.C. (1994), Who is the Recycler? Journal of Waste Management and Resource Recovery, 1(2), pp. 69-75.
DOE. National Household Waste Analysis Programme, Phase 2, Vol 1. Report No. CWM O82/94. Department of the Environment:London, 1994.
ELLEN, P.S. (1994), Do We Know What We Need To Know? Objective and Subjective Knowledge Effects on Pro-Ecological Behaviours. Journal of Business Research, 30, pp. 43-52.
EVERETT, J.W. AND PEIRCE, J.J. (1992) Social Networks, Socio-Economic Status and Environmental Collective Action: Residential Curbside Block Leader Recycling. J. Env. Systems, 1992, 21(1), pp 65-84.
FIENBERG, S.E., (1970), An Iterative Process for Estimation in Contingency Tables. Annals of Mathematical Statistics, 41, pp. 907-917.
GOLDENHAR, L.M. and Connell, C.M. (1993), Understanding and Predicting Recycling Behavior: An Application of the Theory of Reasoned Action. Journal of Environmental Systems, 22(1), pp. 9-103.
GUAGNANO, G.A., Stern, P.C., Dietz, T. (1995), Influences on Attitude-Behavior Relationships. A Natural Experiment with Curbside Recycling. Environment and Behaviour, 27(5), pp. 699-718.
JACKSON, A.L., Olsen, J.E., Granzin, K.L., Burns, A.C. (1993). An Investigation of the Determinants of Recycling Consumer Behavior. Advances in Consumer Behavior, 20, pp. 481-487.
JONES, R.E. (1990), Understanding Paper Recycling in an Institutionally Supportive Setting: An Application of the Theory of Reasoned Action. Journal of Environmental Systems, 19(4), pp. 307-321.
JONES, A., Nesaratnam, S., Porteous, (1998a), Regional Variations in Household Waste Arisings in the UK. Environmental and Waste Management, 1(2), pp. 97-106.
JONES, A., Nesaratnam, S., Porteous, A. (1998b), Enumerating the Sources of Variation in Household Refuse Arisings Rates. Environmental and Waste Management, 1(4), pp 235-241.
JONES, A.E. and Porteous, A. (1996), Modelling Public Use of Bring Recycling Sites. IWM Proceedings, March, pp. 3-4.
LAKE, I.R., Bateman, I.J., Parfitt, J.P. (1996), Assessing a Kerbside Recycling Scheme: A Quantitative and Willingness to Pay Study. Journal of Environmental Management, 46, pp. 239-254.
LEACH, S. (1995), Kerbside Weighing of Household Waste. Journal of Waste Management and Resource Recovery, 2(3), pp. 111-117.
LEACH, M.A., Bauen, A., Lucas, N.J.D. (1997), A Systems Approach to Materials Flow in Sustainable Cities. Journal of Environmental Planning and Management, 40(6), pp. 705-723.
MCCARTY, J.A. and Shrum, L.J. (1994), The Recycling of Solid Wastes: Personal Values, Value Orientations, and Attitudes about Recycling as Antecedents of Recycling Behavior. Journal of Business Research, 30, pp. 53-62.
MEL. Multi-material recycling in Birmingham, MEL Wastes Research Report 89/06, MEL:Birmingham, 1989.
MEL. Analysing Household Waste. MEL Research, Aston Science Park: Birmingham,1996.
PIETERS, R.G.M. (1989), Attitudes and Behavior in a Source Separation Program. A Garbology Approach, Eurobon: Delft, The Netherlands.
PORTER, B.E., Leeming, F.C., Dwyer, W.O. (1995), Solid Waste Recovery: A Review of Behavioural Programs to Increase Recycling. Environment and Behavior, 2, pp.122-152.
POWELL, J.C., Craghill, A.L., Parfitt, J.P., Turner, K. (1996), A Life-cycle Assessment and Economic Valuation of Recycling. Journal of Environmental Planning and Management. 39(1), pp. 97-112.
RESCHOVSKY, J.D. and Stone, S.E. (1994), Market Incentives to Encourage Household Waste Recycling: Paying for what you Throw Away. Journal of Policy Analysis and Management, 13(1), pp. 120-139.
RUFFORD, N.M. (1984), The Analysis and Prediction of the Quantity and Composition of Household Refuse. Unpublished PhD Thesis, The University of Aston, UK.
SALIMANDO, J. (1987) Camden County sets the Recycling Pace. Waste Age, 1987, 18(7), pp 48-53.
SALTZMAN, C., Duggal, V.G., Williams, M.L. (1993), Income and the Recycling Effort: A Maximization Problem. Energy Economics, 15(1), pp. 33-38.
SCHULTZ, P.W., Oskamp, S. Mainieri, T. (1995), Who Recycles and When? A Review of Personal and Situational Factors. Journal of Environmental Psychology, 1995, 15, pp. 105-121.
SCHWARTZ, S.H. (1977), Normative Influences on Altruism. Advances in Experimental Social Psychology, (Berkowitz, L. ed.), 1977, 10, Academic Press: New York.
SPIERS, D., Tucker, P., Taylor, I. (1999), Research into the Environmental Impact of Recycling in South-West Scotland. University of Paisley Environmental Technology Group Research Report 022, 1999, University of Paisley: Paisley, PA1 2BE, Scotland
TAYLOR, S. and Todd, P. (1995), An Integrated Model of Waste Management Behavior: A Test of Household Recycling and Composting Intentions. Environment and Behaviour, 27(5), pp. 603-30.
TUCKER P., Lewis K.A. (1993), Process Simulation For Waste Management. Proceedings Of Seminar Waste Handling, Processing And Recycling. I.Mech.E:London (1993) pp. 47-54.
TUCKER, P., Murney, G., Lamont, J. (1997), Participation in Recycling: A Comparative Study of Four Kerbside Collection Schemes. Journal of Waste Management and Resource Recovery, 4(1), 1997, pp. 11-26.
TUCKER, P., LAMONT, J., MURNEY, G., SMITH, D., SMITH P. (1997b) Statistics on Household Recycling Behaviour in South Ayrshire: Material Capture Rates. University of Paisley Environmental Technology Group Research Report 014, University of Paisley: Paisley, PA1 2BE, Scotland.
TUCKER, P., Murney, G., Lamont, J. (1998a), Predicting Recycling Scheme Performance: A Process Simulation Approach. Journal of Environmental Management, 52, pp. 31-48.
TUCKER, P. Murney, G., Lamont, J. (1998), A Decision Support Model for the Management of Recycling Schemes. Journal of Environmental Planning and Management, 41(4), pp. 445-462.
TUCKER, P., Murney, G., Lamont, J. (1998c), What Newspaper Recyclers Recycle and What they do not Recycle. Environmental and Waste Management, 1(1), pp. 33-56.
TUCKER, P., Lamont, J., Murney, G., Smith, D. (1998), Material Capture Rates in Household Waste Recycling Schemes. Environmental and Waste Management, 1(3), pp. 169-181.
TUCKER, P. (1999a), A Survey of Attitudes and Barriers to Kerbside Recycling. Environmental and Waste Management, 2(1), pp. 55-63.
TUCKER, P. (1999b), Normative Influences in Household Waste Recycling. Journal of Environmental Planning & Management, 42(1), pp. 63-82.
WANG, F.S. Richardson, A.J., Rodderick, F.A. (1997), Relationships between Set-out Rate, Participation Rate and Set out Quantity in Recycling Programs. Resources, Conservation and Recycling, 1997, 20(1), pp. 1-17.
WERNER, C.M., TURNER, J., SHIPMAN, K., TWITCHELL, S., DICKSON, B.R., BRUSHKE, G.V., VON BISMARCK, W.B. (1995), Commitment, Behavior and Attitude Change: An Analysis of Voluntary Recycling. J. Env. Psychology, 1995, 15, 197-208.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999