 Abstract
Abstract
- We present a study of the spreading of trends in artificial social influence networks using agent based models. We concentrate on basic properties of the agents which describe their individual attitudes towards a trend, as well as the influence which they exert in their social neighbourhood. Using a simple random network, we investigate the impact of network dynamicity, situations of opposing trends, and the disappearance of trends. A 'community' network is used to study the impact of group cohesiveness and connectors for the spreading of trends in social communities.
- Keywords:
- ABM, Norms, Social Influence
 Introduction
Introduction
- 1.1
- Observing and imitating others help us to ensure that our social interactions run smoothly in situations where no identifiable legal or moral rules are at hand. When we decide how to behave as social beings in such a situation, different aspects play a role, namely what we would prefer to do if the decision depended only on ourselves, what other people are doing, and how strong our desire for identification with these other people is. Someone who acts according to alleged expectations in such circumstances is influenced by the behaviour of other people. If this influence is strong enough it might lead to situations where we subordinate our possibly deviating personal preferences. These situations guide a large domain of our social life, and studying them is therefore a relevant way to a more profound understanding of human behaviour.
- 1.2
- Some of these interdependent social interactions may lead to the development of certain rules or norms which are not legal or moral in nature, but rather behavioural. A large class of these rules is known as social norms. In this work, however, we want to focus on a type of behavioural rule which is not unambiguously counted among social norms but rather among so-called descriptive norms (Section Trends as Descriptive Norms).[1] The norms we are interested in are connective behavioural patterns which vary on short timescales, i.e. on timescales that are short as compared to one's lifetime. To get an idea of how such a short-lived, variable behavioural pattern might manifest itself, one might for example think of a fashion trend. We will use the term 'trend' to refer to these patterns for the remainder of this paper.
- 1.3
- Although trends individually are not able to explain our societal life, their superabundance in all areas of our every-day life is striking. So, while the single trend is irrelevant for our understanding of human behaviour from a philosophical point of view, trends as a whole have an enthralling impact on society. They are characterised by their emergence and their sinking into (temporal) obscurity, they are like manners of behaviour which wave through a population or social group. Trends are very interesting phenomena as they are simultaneously characterised on the one hand by uniformity of behaviour and by change of behaviour on the other hand. Every trend implies a societal transition, a shift from some currently established behaviour to some alternative behaviour in the absence of any compelling reasons for this to happen. Even so, a trend does not have to come up with something completely new. Fashion trends, for instance, are very cyclical in their nature. Although trends are passing and highly momentary phenomena, one should not be fooled into believing that they are not important. When a trend is current it usually has great influence on those who come in touch with it. It then seems important to each of us to position ourselves with respect to the trend, to either follow it or oppose it.[2] How we react to a trend is relevant for our self-conception and positioning in our socio-environment.[3]
- 1.4
- The literature on the explicit modelling of descriptive norms is limited. A recent example is Muldoon et al. (2014), where they study the structure and emergence of a standing ovation. In their model, however, the authors use a lattice environment which allows only for a restricted neighbourhood of an agent and thus confines the straightforward transferability of the model to real-life situations (see also Section The Basic Model). Network effects on the spreading of two social norms, of which one of them might be associated with what we call trends (their 'opinion'), are studied by Nakamaru and Levin (2004) and found to be important. But also these authors consider only fixed social networks. Dynamically changing network topologies in a general context of norm emergence have been studied, for instance, by Savarimuthu et al. (2009) (see also the references cited therein). In their model, however, agents are only allowed to increase the number of their links. Rewiring of links is taken into account e.g. by Villatoro et al. (2011), although in the context of convention emergence.
- 1.5
- In this work, we present a study of the spreading of descriptive norms in (fixed and dynamically changing) artificial social networks using agent based models. The aim of this work is to formulate simple models for the evolution of trends, and to test if processes described by empirical studies of highly complex real-life situations can be captured by them. We concentrate on basic, simplified properties of the agents which describe their individual attitude towards a trend, as well as the influence which they exert in their social neighbourhood. Our systems evolve in time using a discretised decision rule for the agents. Apart from the spreading of a trend itself, we also study situations of opposing trends, and of the abatement of trends. We note that we are not aware of any previous work which has studied the disappearance of trends systematically. Through the analysis of our model results, we are able not only to draw conclusions regarding the conditions for a trend to spread or vanish, but also to classify certain equilibrium situations for a trend to exist for a certain period in a social network. Besides, we focus on dynamical aspects of networks as well as on the role of network structure. Although our models are simplistic and do not represent real-world social networks and conditions, we can nevertheless infer general results from them which help us to understand the dynamics of trends in social networks.
- 1.6
- This paper is organised as follows: In Section Trends as Descriptive Norms we introduce the relevant theoretical background for our characterization of trends as descriptive norms. We give a short overview of our models at the beginning of Section Modelling Trends. In Sections The Basic Model, The Equilibrium Model, and The Stability Model we present results based on simple, dynamically changing random networks which are designed for the study of certain situations and effects that might be associated with the spreading and the disappearance of trends. A model inspired by theoretical and empirical findings related to network structure is presented in Section The Community Model. Our main findings are discussed in Section Discussion and Outlook, where we also give an outlook on possible future work.
 Trends
as Descriptive Norms
Trends
as Descriptive Norms
- 2.1
- Trends as introduced in Section Introduction and as they should be understood in the context of this work can be characterised as descriptive norms. The term 'descriptive norm' was first introduced for 'norms that characterize the perception of what most people do' (Cialdini et al. 1990). Due to societal and cultural diversity, however, descriptive norms are not 'right' or 'wrong', and they are not 'better' than some alternative norms. In our understanding, someone decides to follow a descriptive norm – whilst taking into account his personal preferences – because he believes[4] that a relevant subset of the social group in consideration conforms to the respective behavioural pattern. We want to stress that, although there is no explicit exertion of peer pressure present in our models, we yet would classify the sort of influence that is wielded onto the individual members of the group as a slight form of group pressure, as soon as it results in someone changing his behaviour regardless of his own deviant attitude.[5] People conform to descriptive norms for many reasons, e.g. because of the desire to be part of a certain group of people, or just to adapt oneself to a social situation. People will look for descriptive norms when entering hitherto unfamiliar social situations, or if they have reason to believe that the appropriate behavioural rule is different from what they assumed so far. By following descriptive norms, we are driven to act according to the information we infer from other people's behaviour. Therefore, the apparent social approval of a practice can be sufficient for us to engage in it. Descriptive norms can be highly specific to the social environment, even if it is only represented by a small group of people. One or few individuals can be sufficient to trigger the spreading of a descriptive norm,[6] as it will be the case in the situations we are going to investigate in this work.
- 2.2
- When adopting a descriptive norm, one acts as a consequence of social influence, which can be differentiated in normative and informational influence (Deutsch & Gerard 1955). Normative influence usually comes into play if someone is afraid of embarrassing himself or wishes 'to be like the others' and therefore to be accepted within a social context. Changes in someone's behaviour due to normative influence are regarded as to be strongly correlated with the actual situation of influence. That means that the changes are merely temporary and might be reverted after leaving the situation of wielded influence. We will see this effect in some of our models which we investigate later on, when someone with a rather deprecating private attitude regarding a certain trend is influenced by a trendsetter to follow the trend, and then again stops following the trend after the social tie to the trendsetter is removed (cf. the 'basic model', the 'equilibrium model' without conversion, and the 'stability model'). Informational influence, on the other hand, is likely to have more serious impact on the individual. It normally occurs when people are insecure about how to behave correctly in a certain situation and therefore observe other group members for guidance. A person reacting to informational influence accredits his group members a higher degree of information about the respective situation, assuming that they know better what to do or how to behave. Although informational influence is primarily related to situations of decision-making or to social circumstances which are genuinely new to the affected person, we will study a model with similar consequences for the individual regarding the permanent and irreversible change in the subject's beliefs (cf. the 'equilibrium model with conversion').
- 2.3
- In our understanding, the emergence and the spreading of a trend takes place as follows: In a social group one or a few people begin to do something new (with regard to their social environment) or in a different way, e.g. they start to wear flared pants. These are the people to set the trend. To be considered a trend, the new behaviour necessarily has to be adopted by a sufficient number of other members of the social group. In the most general sense, the conditions for the spreading of the new behaviour are a combination of positionality and influenceability of the individuals in the group.[7] However, from an observer's point of view a trend occurs (i) if the behaviour is new (for the social group considered) and (ii) if a sufficiently large fraction of the social group begins to adjust to the behaviour after its emergence. One could add a third point which is related to the novelty value of the trend, namely the fact that a trend is short-lived. This is often due to the behaviour of the original trendsetters which after some time lose interest in the subject and come up with something new which then possibly replaces the old trend. These three points outline the defining feature of a trend as it is understood in this work: it's dynamicity. Concisely, a trend is a short-lived descriptive norm which spans from its emergence over its diffusion to its disappearance. It is often triggered by individuals which have a tendency to do something new and it spreads through a social group governed by individual attitudes in a network of social influence.[8]
 Modelling
Trends
Modelling
Trends
- 3.1
- In what follows, we give a short outline of the four models studied in this paper, and of the purpose of these models. The first three models are based on simple random networks, whilst the fourth model is based on a group structure.[9]
- 3.2
- The basic model consists of a trendsetter and a certain number of initially unconcerned agents. Individual agents decide if to follow the trend or not depending on their personal attitude towards the trend and on the behaviour of their neighbours. Unconcerned agents as well as trendsetters are asked to rewire themselves during the simulation, i.e. to drop existing links and to establish new ones. Agents may reconsider their decision to follow the trend depending on changes in the physical structure of the network. Using this model, we want to investigate the underlying dynamics of our networks.
- 3.3
- In the equilibrium model we introduce an agent who sets an anti-trend and has influence within the social group comparable to that of the original trendsetter. Using this model, we want to investigate possible equilibria of two opposing norms within a social group. In this model agents may also be 'converted', meaning that they do not only act in accordance with a trend but actually start to modify their personal attitudes towards the trend. This might convert a trend to a convention.
- 3.4
- In the stability model the trendsetter loses his interest in supporting the trend if too many group members start to follow it. Using this model, we want to investigate the stability of an existing trend after loosing its initial support. The model is relevant for the understanding of the nature of trends, because it realistically models how trends come and go.
- 3.5
- Finally, we use the community model as a simplified, but more realistic, representation of an actual social group. We study the role of close-knit agent communities with similar attitudes towards the subject of interest, the impact of bridge ties between these communities, and the role of the associated agents, the connectors. This model is motivated by empirical and theoretical findings regarding social influence networks.
- 3.6
- The individual models are built upon common assumptions about the two parameters we think primarily relevant for the emergence and spreading of trends, namely the internal propensity \(f\) of an agent to follow the trend, and a measure for the social influence \(i\) of individual agents within the social group. This approach follows basic ideas outlined in Muldoon et al. (2014). However, we significantly differ from this study in the choice of the influential social environment of the agents which we model as a network structure. This ansatz allows us to detach the agents from any influences unrelated to the trend in question, and it represents an environment which is more suitable to compare to many real-life situations which are not restricted to a fixed geometry. Also, in contrast to Muldoon et al. (2014), we do not fix the internal propensity of the agents to a single value: The internal propensity \(f\) can attain values between zero and two, \(f \in [0; 2]\), where a value of zero means that the agent does by no means want to follow the trend, and a value of two means that the agent definitely wants to follow the trend. Therefore, this parameter represents the individual attitude of an agent regarding the trend. We choose \(f = 2\) as initial value for the trendsetter. If not stated otherwise, the distribution of the internal propensity f of the unconcerned agents is described by a truncated normal distribution with a mean of \(f = 1\) and a standard deviation of \(0.35\), i.e. \(f \sim \mathcal{N}(1, 0.35)\) with \(f \in [0; 2]\),[10] thus making sure that most agents are not particularly inclined to follow the trend at the beginning of the simulation, nor to not do so. We choose a normal distribution assuming that the internal propensities of the agents are initially independent from one another. The influence parameter i is determined by the social environment of the agent as it is measured by the degree of the agent, i.e. by his number of links. Although the influence values are set initially, they may change as agents are allowed to rewire themselves during the simulation. There is a third parameter \(T \in \{0; 1\}\) which observes if the agent follows the trend (\(T = 1\)) or not (\(T = 0\)). At the beginning of the simulation only the trendsetter follows the trend whereas all unconcerned agents do not do so.
- 3.7
- In general, the decision of agents to follow the trend or not is dependent on their own internal propensity and on what all of their neighbours are doing. This latter point basically implies a certain social threshold for an agent to join the trend, which is also unique for every agent due to his internal propensity and the number of his neighbours. We choose this model of social influence to simulate the spreading of trends as it corresponds to a conformity behaviour.[11]
- 3.8
- The time evolution of our systems is discretised and starts
with the setup of the simulation at time step \(t = 0\). Now, at every
time step each unconcerned agent (\(T = 0\)) decides if to follow the
trend or not. To do so, an agent compares the social influence of his
neighbours who follow the trend, weighted by his own internal
propensity, and the influence of his neighbours who do not follow the
trend. Let \(\mathcal{A}\) be the set of all agents in the setup. The
decision process of agent \(j \in \{\mathcal{A}|T = 0\}\) at time step
\(t = n\) is then described by a step function for the parameter \(T\),
$$ T_j^{(n)} = \left\{\begin{array}{ll} 1 & \quad\mbox{if } f_j \cdot \sum_{k=0}^{N_{f,j}^{(n)}} i_k^{(n-1)} > \sum_{l=0}^{N_{u,j}^{(n)}} i_l^{(n-1)},\\ 0 & \quad\mbox{otherwise,}\\ \end{array}\right. $$ (1) where \(N_{f,j}^{(n)}\) is the number of neighbours of agent \(j\) at time step \(t = n\) who follow the trend at time step \(t = n-1\), and \(N_{u,j}^{(n)}\) is the number of neighbours of agent \(j\) at time step \(t = n\) who do not follow the trend at time step \(t = n-1\). Therefore, \(i_k\) sums up the influence i of all neighbours of agent j who follow the trend (\(T = 1\)) at the time step \(t = n-1\), and \(i_l\) sums up the influence of all neighbours of agent j who do not follow the trend (\(T = 0\)) at the time step \(t = n-1\).
- 3.9
- If this were the only ingredients in the model, i.e. if
agents were not allowed to rewire themselves, then a model described by
Equation (1) would be purely
deterministic, and a simulation time step would always be reached when
no more changes in the social network could be observed. In such a
static model, the eventual fraction of followers drops rapidly with
increasing network size, because the influence of the trendsetter can
reach only a limited number of agents.
The Basic Model
- 3.10
- A common characteristic of many kinds of social groups is that they are not static. Because socializing is the natural phenomenon which leads to the creation of social groups as well as to their existence, its impact should not be ignored in the modelling of social groups and interactions as well. One side effect of socializing is the modification of a social network with time. This means that new relationships can come into existence and already existing ones can die out.[12] To take such events into account in our model, we modify the network structure over time by asking agents to rewire their links. The trendsetter is asked once per time step to drop one of his links and to create a new trend link with a random agent. Similarly, one agent per time step is asked to drop one of his links and to create a new agent link with a random agent.[13]
- 3.11
- As the network is dynamic and thus the respective
neighbourhoods of the agents change over time, the agents are not only
asked if they want to follow the trend, but also if they want to
reconsider their decision to follow the trend if they already do so
(\(T = 1\)). This is implemented according to the decision rule as
$$ T_m^{(n)}= \left\{ \begin{array}{ll} 1 & \quad\mbox{if } f_m \cdot \sum_{k=0}^{N_{f,m}^{(n)}} i_k^{(n-1)}< \sum_{l=0}^{N_{u,m}^{(n)}} i_l^{(n-1)},\\ 0 & \quad\mbox{otherwise,}\\ \end{array}\right. $$ (2) with \(m \in\{\mathcal{A}|T = 1\}\). Using this rule together with Equation (1) in principle allows the agents to change their decision if to follow the trend or not several times during the simulation. Agents who stop following the trend are referred to as 'turncoats'.
- 3.12
- For the basic model, we investigate network sizes ranging
from an initial number of 50 up to 1000 unconcerned agents and setups
with 1/20/2 and 1/20/3, where the labelling is 'number of trendsetters'
/ 'number of links of a trendsetter' ('trend links') / 'average number
of links of regular agents (\(N_{al}\))'.[14]
Simulations are terminated at time step t = 1000, or before if every
agent follows the trend.[15]
Each simulation was repeated a 100 times, it not stated otherwise, to
collect sufficient statistics.
Main Results
- The fraction of followers is highly affected by the dynamism of the model inasmuch as it is always higher as compared to a static model. The rewiring of agents and especially of the trendsetter has such a huge effect because it is the only non-deterministic element in a population with fixed attitudes. The trendsetter can influence, directly or indirectly, every other group member, as a matter of principle. Even if he might not be able to do so until the end of a simulation, the rewiring process enables him to spread his attitude all over the place.
- Increasing the connectivity of the initially unconcerned agents favours the spreading of the trend only for small network sizes and high numbers of trend links, but impedes it in all remaining cases. This is exemplarily shown for the fraction of followers in Fig. 1. The important difference in the two setups for networks larger than 500 agents lies in the evolution of the fraction of followers in the individual runs: For 1/20/2, the trendsetter would be able to convince all agents to follow the trend if he only had more time, whereas in the 1/20/3 run he would never be able to convince more than a few percent of the group (cf. Fig. 2). This underlines the importance of group cohesiveness.[16]
- The number of time steps until all agents follow the trend are highly dependent on the network size, as shown in Fig. 3. No saturation level was found within the limiting factors of the basic model, namely the network size limit (1000) and the time step limit (1000), although it can already be anticipated for larger networks with a higher time limit.
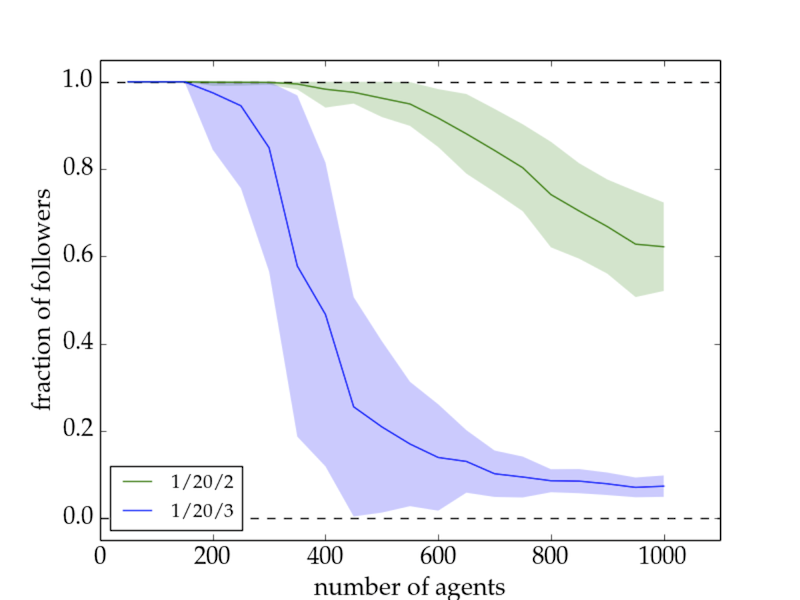
Figure 1. Fraction of followers as a function of network size for the basic model with a 1/20/2 setup (green), and a 1/20/3 setup (blue). \(1\sigma\) confidence intervals are shown as the shaded areas. The fraction of followers drops much more rapidly with increasing network size for the runs with higher \(N_{al}\). 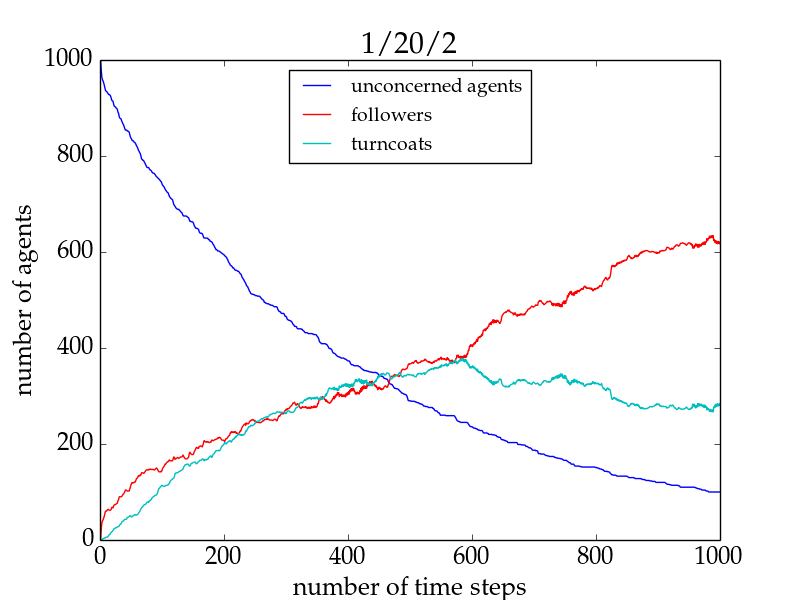
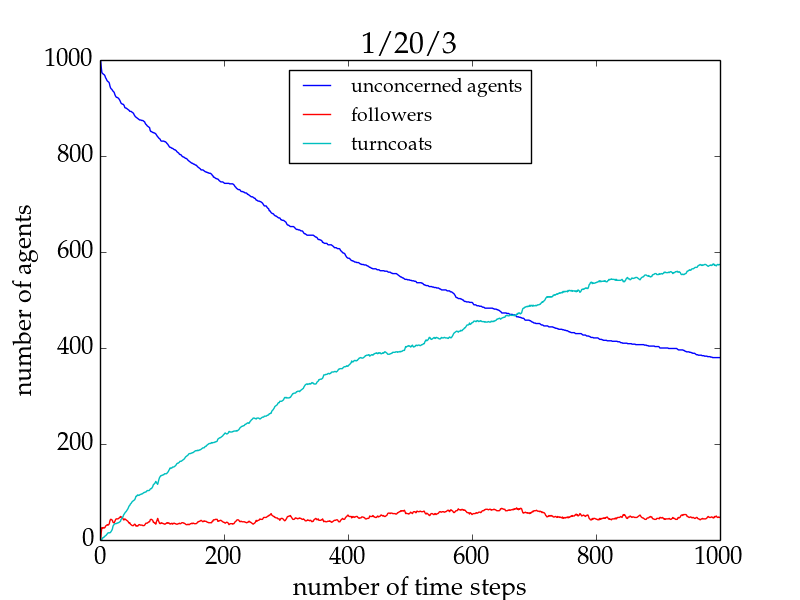
Figure 2. Number of agents of different agent types as a function of time for a typical run with 1/20/2 (left panel) and one with 1/20/3 (right panel) for a network size of 1000 for the basic model. Followers are shown in red, turncoats in turquoise, and unconcerned agents in blue. Both simulations are terminated at \(t = 1000\). See the main text for a discussion. 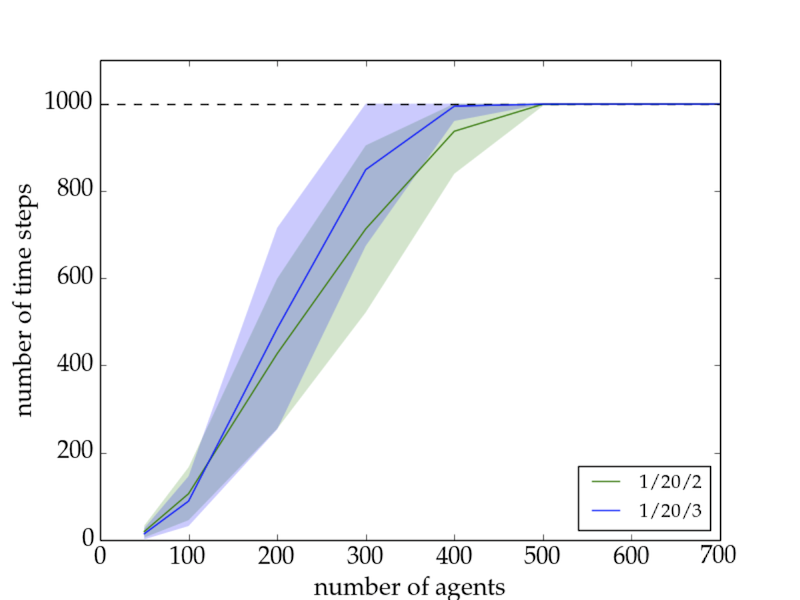
Figure 3. Number of time steps until all agents follow the trend as a function of network size for the basic model with a 1/20/2 setup (green), and a 1/20/3 setup (blue). \(1\sigma\) confidence intervals are shown as the shaded areas. Runs with lower \(N_{al}\) converge in general faster to a state where all agents follow the trend, except for small networks. For network sizes of \(> 500\) the trendsetter is no longer able to convince all agents within the given time. The Equilibrium Model
- 3.13
- In the basic model we considered situations where only a single trend was at stake against the background of an otherwise unconcerned social group. We now extend this model by introducing an additional, opposing trend in the equilibrium model. Here, we want to investigate if people tend to favour one of the trends, or if all trends on average have comparable numbers of followers. We also include the possibility of conversion in this model, meaning that the agents become positive about following the trends after some time, which we discussed as a potential reaction to informational influence in Section Trends as Descriptive Norms. Conversion is taken into consideration in this specific model because we assume that the need for people to feel convinced and reassured of their attitude is higher in situations where one has to position himself not only in favour of some behaviour but also against another behaviour. In this context it is important to understand that a true establishment of any kind of coexistence of different behavioural patterns, as it can be achieved through the conversion of agents, does convert a trend to a convention.[17]
- 3.14
- To implement the opposing trend, we introduce a so-called
'oppositionist', who tries to establish an anti-trend. The value of the
internal propensity of an oppositionist is set to \(f = 0\), and the
parameter \(T\) is set to \(T = -1\), meaning that the agent opposes
the trend. Unconcerned agents who decide to follow the anti-trend are
referred to as 'boycotters'. In this model, both boycotters and
followers who stop following the (anti-)trend are referred to as
'turncoats'. To account for the new agent types we have to modify the
time evolution of the system accordingly. Now, at every time step each
unconcerned agent decides if to follow the trend, to boycott the trend,
or none of the two, i.e. to stay or to turn unconcerned. The decision
process is again guided by comparing the behaviour and the respective
social influence of one's neighbours and by weighting these with one's
own internal propensity regarding the (anti-)trend. The decision
process of agent \(j\in\{\mathcal{A}|T = 0\}\) at time step \(t = n\)
is therefore described by a step function for the parameter \(T\) of
the following form:
$$ T_j^{(n)}= \left\{ \begin{array}{ll} 1 & \quad \mbox{if } f_j\cdot \sum_{k=0}^{N_{f,j}^{(n)}} i_k^{(n-1)} > \sum_{l=0}^{N_{u,j}^{(n)}} i_l^{(n-1)} \wedge f_j \cdot \sum_{k=0}^{N_{f,j}^{(n)}} i_k^{(n-1)} > \sum_{m=0}^{N_{b,j}^{(n)}} i_m^{(n-1)},\\ -1 & \quad\mbox{if }(2-f_j) \sum_{m=0}^{N_{b,j}^{(n)}} i_m^{(n-1)} > \sum_{l=0}^{N_{u,j}^{(n)}} i_l^{(n-1)} \wedge (2-f_j) \sum_{m=0}^{N_{b,j}^{(n)}} i_m^{(n-1)} > \sum_{k=0}^{N_{f,j}^{(n)}} i_k^{(n-1)},\\ 0 & \quad \mbox{otherwise.}\\ \end{array} \right. $$ (3) Here, \(N_{b,j}^{(n)}\) is the number of neighbours of agent \(j\) at time step \(t = n\) who boycott the trend (i.e. follow the anti-trend) at time step \(t = n- 1\). The factor \((2-f_j)\) is caused by the highest possible value for the internal propensity of an agent, \(f = 2\) in our models.
- 3.15
- The rule which describes the reconsideration of an agent's
decision has to be modified likewise. For an agent who follows the
trend at \(t = n-1\) this is implemented as
$$ T_p^{(n)}= \left\{\begin{array}{ll} 0 & \quad \mbox{if } f_p\cdot \sum_{k=0}^{N_{f,p}^{(n)}} i_k^{(n-1)} < \left( \sum_{l=0}^{N_{u,p}^{(n)}} i_l^{(n-1)} + \sum_{m=0}^{N_{b,p}^{(n)}} i_m^{(n-1)} \right),\\ 1 & \quad\mbox{otherwise},\\ \end{array}\right. $$ (4) and for an agent who boycotts the trend at \(t = n-1\) this is implemented as
$$ T_q^{(n)}= \left\{\begin{array}{ll} 0 & \quad \mbox{if } (2-f_q) \cdot \sum_{m=0}^{N_{b,q}^{(n)}} i_m^{(n-1)} < \left( \sum_{l=0}^{N_{u,q}^{(n)}} i_l^{n-1} + \sum_{k=0}^{N_{f,q}^{(n)}} i_k^{(n-1)} \right),\\ -1 & \quad\mbox{otherwise},\\ \end{array}\right. $$ (5) with \(p \in\{\mathcal{A}|T = 1\}\) and \(q \in\{\mathcal{A}|T = -1\}\).
- 3.16
- In this model, as already mentioned, we also want to study in more detail what happens if an agent does not only climb on the bandwagon for reasons of peer pressure, but if he starts to believe that he himself actually wants to follow the trend/anti-trend - i.e. if he is converted. We assume that agents, after deciding to follow or boycott a trend, start to adjust their individual attitude to their outwardly projected behaviour after some time. In the framework of our model this can be realised through a continuative adjustment of the agents' internal propensity with time. To do so, we count the time steps during which an agent is already following/boycotting the trend for every individual agent. For every ten successive time steps during which an agent follows the trend, his internal propensity is increased by \(0.05\) until it reaches \(2\). Analogously, it is reduced by \(0.05\) until it reaches \(0\) for every ten successive time steps during which an agent boycotts the trend.[18] If the internal propensity of an agent reaches \(2\) or \(0\), we classify him as 'fully converted' and he is removed from the decision making and reconsidering processes.[19] Using this model, we can study the conditions under which an equilibrium of two opposing behaviours in a social group can be established.[20] We find that the conditions for reaching an equilibrium depend on network size as well as on making the conversion of the agents possible. Surprisingly, the fractions of followers/boycotters within the reached equilibria are highly different, even for models with equal total numbers of trend/opposition links.
- 3.17
- For the equilibrium model, we investigate network sizes
ranging from \(50\) up to \(1000\) regular agents. Simulations are
terminated if all agents are converted, or at \(t = 1000\). In the
equilibrium model, we concentrate on setups with one trendsetter and
one oppositionist, both owing \(20\) links each \((1/20/1/20)\), and
\(N_{al} = 2\).
Main Results
- Although the fraction of followers/boycotters is on an average the same for setups with as many trend links as opposition links (cf. Fig. 4), the outcomes of individual simulations are generally strongly dominated by one of the two groups (cf. Fig. 5). This is true for network sizes up to \(\sim 750\) agents for the model without conversion and up to \(\sim 950\) agents for the model with conversion. The determining factor is the actual physical structure of the network which is less uniform for smaller network sizes and therefore more inclined to allow bandwagon effects (in both directions). For models with conversion, the initial conditions (i.e. the random network structure) determine the outcome of the simulation.
- For all network sizes the fraction of agents who either support or oppose a trend is higher in the model with conversion as compared to the model without conversion (cf. Fig. 4). In the model with conversion (right panel), almost all agents (\(> 90\)%) are converted at the end of a simulation run.
- Equilibrium situations for the two opposing behaviours can be reached in the model with as well as without conversion of agents, but they are by construction less stable in the model without conversion. If a significant group of agents is fully converted in the equilibrium model with conversion, then the original trend has evolved into a convention. This usually occurs within a simulation run.
The Stability Model
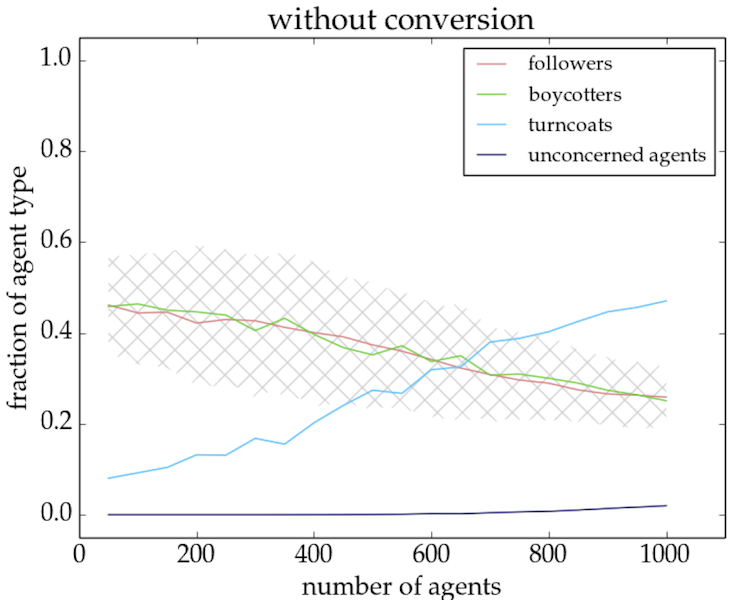
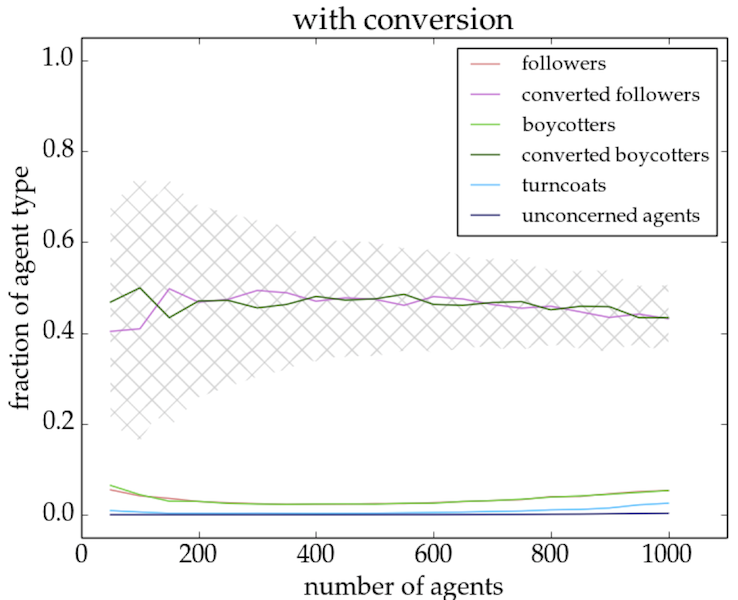
Figure 4. Fraction of agent type as a function of network size for a 1/20/1/20 setup of the equilibrium model without (left panel) and with (right panel) conversion. The crossed grey areas indicate combined \(1\sigma\) confidence levels for followers and boycotters (left panel) and for converted agents (right panel). In general, the followers/boycotters make up for almost a 100 percent in the runs with conversion. 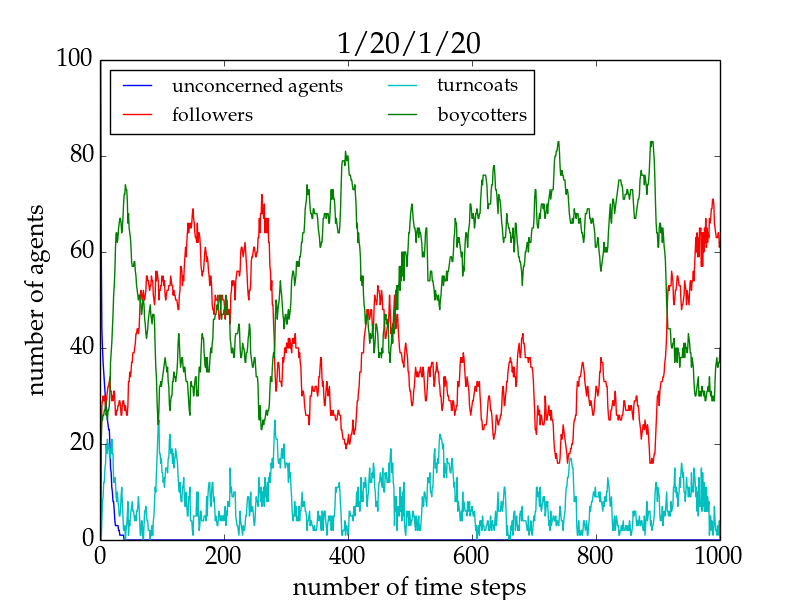
Figure 5. Number of agents of different agent types as a function of time for a 1/20/1/20 run of the equilibrium model without conversion and a network size of 100. Although the trendsetter and the oppositionist have the same number of links, the number of followers are not comparable but one group dominates the field for a certain time span. In many cases, however, no group is able to dominate for long times but eventually the other group will take over, and so forth. - 3.18
- In the stability model we focus again on only one trend within the social group. So far, we investigated situations of trend emergence and spreading only. Now we want to study what happens if a trend loses its initial support after some time, i.e. if the trendsetter's support for the trend vanishes as more and more agents join the trend. The idea behind this is that a trendsetter as understood in this work is someone who, on the one hand, wants to perceive his influence within the social group, but, on the other hand, has an eagerness to be characterised by a unique 'selling point', e.g. the setting or leading of a trend. However, if the fraction of followers of the trend increases within the social group of interest, it seems plausible that the trendsetter loses interest in supporting the trend and rather devotes himself to another cause. To study if, and, if so, under which conditions a trend can live on within a social group without further support from its initiator, we investigate the following situation: The support of the trendsetter for the trend is described by a decay function which depends on the fraction of trend followers. After exceeding a certain fraction of followers, the trendsetter's support will vanish as the number of followers increases further. This means that his internal propensity will decrease until it reaches \(f = 1\), i.e. until the trendsetter can be described as unconcerned regarding the trend. The decision process of agents is described by Equation (1).
- 3.19
- For the stability model, we investigate network sizes ranging from an initial number of \(50\) up to \(1000\) unconcerned agents. Simulations are terminated at time step \(t = 1000\), or before if either every agent follows the trend, or if the number of followers goes down to zero after the trendsetter stops supporting the trend.
- 3.20
- We fix the threshold of the fraction of followers from
which on, if it is ever reached, the trendsetter starts losing interest
in spreading the trend at \(\phi_{th} = 0.25\). We relate the
first-time eventuation of this event with the respective time step \(t
= t_{th}\). We further fix the fraction of followers from which on, if
it is ever reached, the trendsetter is eventually indifferent to
spreading the trend (i.e., \(f_{ts} = 1\)) to \(\phi_{ins} = 0.5\).
Again, we relate the first-time eventuation of this event with the
respective time step \(t = t_{ins}\). The latter is our boundary
condition. In the style of a solution to a differential equation which
describes an exponential decay we arrive at the following general
equation describing the trendsetter's internal propensity:
$$ f_{\rm ts} (t, \phi) = f_{\phi=0} \cdot e^{-\lambda \cdot \phi}\quad\mbox{for}\quad t\in[t_{th}; t_{ins}[ . $$ (6) - 3.21
- If we insert the boundary conditions, we get a value of
\(\lambda\approx 1.39\). This leads to the following description of
\(f_{\rm ts}\):
$$ f_{\rm ts} (t,\phi) = \left\{ \begin{array}{ll} 2 & \quad\mbox{if}\quad t< t_{th} \quad \mbox{and}\quad \phi<\phi_{th},\\ 2\cdot e^{-1.39\cdot\phi} & \quad\mbox{if}\quad t_{th} \leq t < t_{ins}\quad \mbox{and}\quad \phi_{th} \leq \phi < \phi_{ins},\\ 1 & \quad \mbox{if}\quad t \geq t_{ins}.\\ \end{array}\right. $$ (7) - 3.22
- If the trendsetter continues to be an agent with
above-average influence but who is now unconcerned with respect to the
trend, then he strongly influences other agents into behaving
indifferently regarding the trend and thus convinces already following
agents to now stop following the trend. Consequently, the number of
followers decreases again. An equilibrium might be reached after the
trendsetter stops supporting the trend if he is afterwards treated like
a common agent, i.e. if he is not asked, as before, to rewire himself
at every time step. In this case, the fraction of followers usually
decreases a few percent as soon as the trendsetter stops supporting the
trend but stays more or less constant afterwards. This shows that after
the loss of the initial support the determining factor in the decay
model for the trend is not just the influence of the (former)
trendsetter, but his ability to reach out to so many individuals in the
social group.
Main Results
- The fraction of followers decreases inexorably as soon
as the trendsetter's internal propensity reaches \(f = 1\) if the
trendsetters keeps on rewiring himself, as a matter of principle. This
is exemplarily shown in the left panel of Fig. 6.
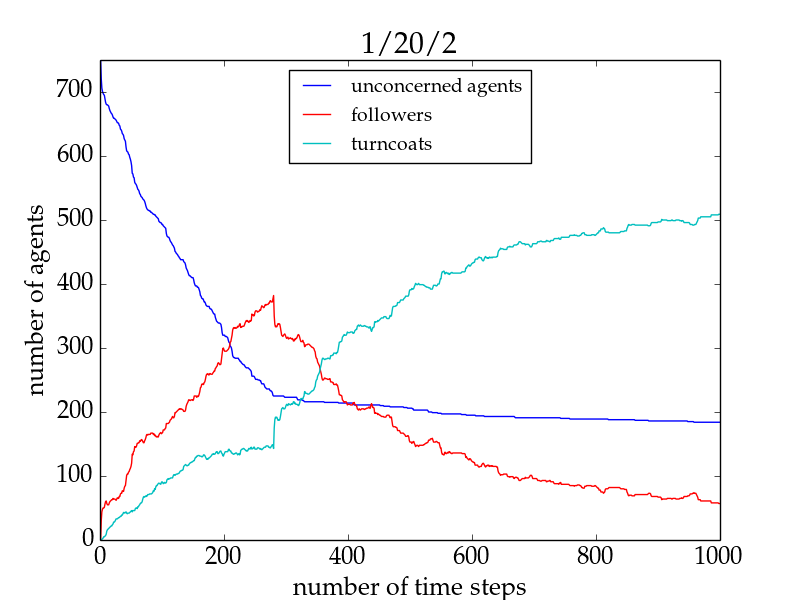
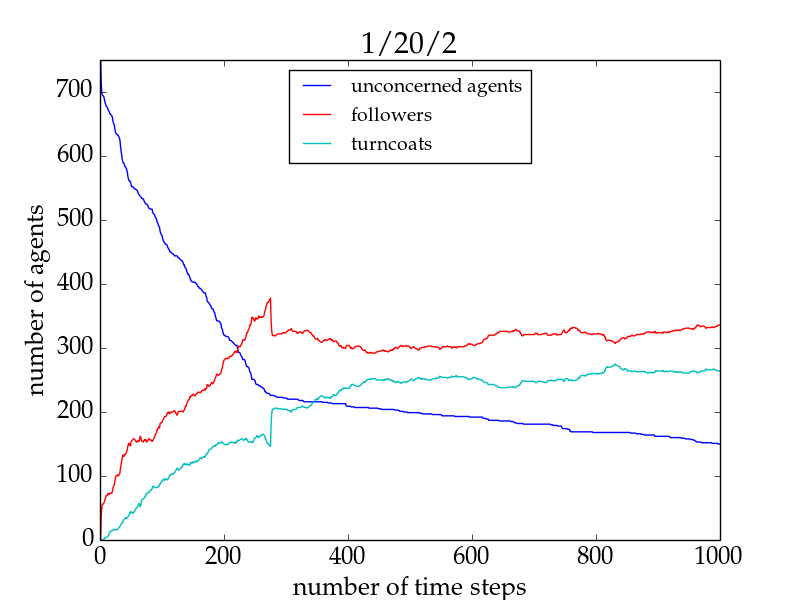
Figure 6. Number of agents of different agent types as a function of time for a 1/20/2 run and a network size of 750 for the stability model. Left panel: Stop of support - the internal propensity of the trendsetter decays from \(f = 2\) to \(f = 1\) within the time range of \(t_{th} = 114\) and \(t_{ins} = 279\). The fraction of followers decreases inexorably as soon as the trendsetter stops supporting the trend. Right panel: Stop of support and forfeiture of the trendsetter's ability to reach out to the group - the internal propensity of the trendsetter decays from \(f = 2\) to \(f = 1\) within the time range of \(t_{th} = 102\) and \(t_{ins} = 274\). The fraction of followers decreases a few percent as soon as the trendsetter stops supporting the trend but stays more or less constant afterwards, as the trendsetter is not longer asked to rewire himself at every time step. - A more or less stable equilibrium of the followers and the unconcerned agents might be reached if the trendsetter is treated as a regular agent regarding the rewiring of his links after he stopped supporting the trend. This is exemplarily shown in the right panel of Fig. 6.
- The determining factor for the spread and the disappearance of a trend with regard to the trendsetter is not just his influence, but his ability to reach out to so many individuals in the social group. This ability allows him to exercise his influence in large social groups in the first place.
The Community Model
Empirical and Theoretical Studies
- The fraction of followers decreases inexorably as soon
as the trendsetter's internal propensity reaches \(f = 1\) if the
trendsetters keeps on rewiring himself, as a matter of principle. This
is exemplarily shown in the left panel of Fig. 6.
- 3.23
- After getting a well-founded impression of several different network dynamics and their interaction with the time evolution of our systems in the previous sections, we now investigate a different type of model, the community model. This model is motivated by some insights from theoretical and empirical studies regarding social influence networks.
- 3.24
- Our treatment of trendsetters as presented in the previous models has support from early work regarding 'opinion leaders' (e.g. Lazarsfeld et al. 1968). Several studies on the diffusion of innovation, however, found that 'pioneers', who are by tendency not opinion leaders, are important for the widespread adoption of innovations.[21] We explicitly allow for the emergence of autonomous trend followers in one version of the community model. We will also be able to confirm with our model claims from recent work that large-scale changes in public opinion, as realised through a trend, are more likely to be driven by the existence of easily influenced people as compared to influentials (Watts & Dodds 2007).
- 3.25
- Instead of modelling the spreading of a trend in a single homogenous group we now use a so-called 'community structure', which is assumed to be common among social networks. A network exhibits a community structure if it consists of several close-knit groups, which then are connected through comparably fewer links on the larger scale.[22] The community structure of networks is also hold liable for the unique characteristics of real-world social networks, such as assortative mixing (e.g. Newman & Park 2003). Our community model supports homophily through our choice of group-dependent distributions of the internal propensity (see below).
- 3.26
- In completion to the community structure we pay heed to
empirical findings which emphasise the role of the connecting agents
and links between different close-knit social groups (e.g. Granovetter 1973; Burt 1992). Not only are these
links more crucial for the structure of a network as compared to
connections between agents of one group, but also more effective in any
kind of information processing. We take this into account through a
modified computation of an agent's influence which is now also
dependent on the agent's betweenness centrality[23].
Model Description
- 3.27
- Due to the higher complexity and the more sophisticated implementation of the parameters which describe the individual agents we do not consider the dynamic effects in the community model which we already have presented in the previous models. This means that the network remains static in time (i.e. the influence distribution is fixed), neither the agents change their private attitude towards the trend, nor the trendsetter (i.e. the internal propensity is fixed), and no opposing norms are included.
- 3.28
- The community model includes the agent types 'trendsetter' and 'unconcerned agent'. As before, agents who decide to follow the trend are referred to as 'followers'. The network generally consists of several subgroups which are somehow connected among each other. The time evolution is discretised and described through Equation (1). However, the implementation of the internal propensity and the influence of the agents differ from what we had in the previous models.
- 3.29
- As for the random model, the distribution of the internal propensity \(f\) is generally described by a normal distribution with parameters \(\mathcal{N}(1, 0.35)\). However, we now distribute the internal propensity adjusted to the subgroups in the model.[24] To do so, we proceed as follows: Firstly, we draw distinct values \(f\) for each group in the network from a \(\mathcal{N}(1, 0.35)\) distribution. Secondly, we draw values for the individual group members from a \(\mathcal{N}(f, 0.15)\) distribution. As the single mean values of the distributions can get close to \(0\) or \(2\), we set values below \(0\) to \(0\) and values above \(2\) to \(2\). The resulting individual distributions for the internal propensity may look quite differently. Naturally, the distribution of \(f\) based on the community structure of the network has a huge impact on the outcome of individual simulation runs, as a trend can possibly spread much faster in a group with an above-average value of \(f\), or not at all in a group with a very low \(f\). From a statistical point of view, however, the differences between simulations with a group-based distribution of \(f\) and simulations with a simple normal distribution of \(f\) for all agents are not very large, but still observable.[25] We also modify the influence of an agent: it is now given by an agent's degree divided by the maximal degree present in the network times the agent's betweenness centrality divided by the maximal betweenness centrality present in the network. This means that the influence of an agent is no longer solely determined by his number of connections to other members of the social group, but also by his strategic location within the network: The more important an agent is in connecting other agents, the higher is his influence.
- 3.30
- In the simulation runs which are analysed in the following we choose as trendsetter (or initiator) the agent with the maximal betweenness centrality in the network. In the majority of cases this agent owes a bridge link, i.e. he embodies a connector role between his own community and some other community.
- 3.31
- In some of our runs we implemented another new feature, namely the emergence of agents who decide on their own to follow the trend, so-called 'autonomous agents'. Agents who are qualified for becoming such a follower and possible trendsetter have to have an internal propensity towards the trend of \(f \geq 1.8\), i.e. they have to be strongly inclined to follow the trend. At each time step, the probability for these agents to openly pursue the trend is \(p_{em} = 0.5\). It is clear that not in every run where the emergence of autonomous followers is in principle possible they do in fact emerge. The probability for them to actually arise increases with network size and decreases with group size, as the probability to get a group with a well above average mean internal propensity increases with increasing number of groups. The fraction of runs where autonomous followers emerge, if this possibility is activated, is lower than 20 percent for the smallest network sizes and all group sizes. For a network of 500 agents, however, we found fractions of about 60 percent (group size 50), above 80 percent (group size 25), and about 95 percent (group size 10) of runs where autonomous followers actually came into existence. Even in the latter case, though, their share of all following agents is under 20 percent, which accounts for seven autonomous followers on an average for a network of 500 agents in groups of 10 agents.
- 3.32
- For the community model, we investigate network sizes
ranging from 50 up to 500 agents. The size of the communities, \(N_g\)
varies between 10, 25, and 50 agents. Each simulation is repeated 200
times for reasons of statistics.
Main Results
- The fraction of followers decreases with increasing network size, but increases with increasing group size, as shown in Fig. 7.
- The number of followers as well as the timespan until the simulation stops are relatively independent of network size. However, if the emergence of autonomous followers is possible, both quantities increase with increasing network size.
- Even if a group as a majority does not adopt the trend, a single agent can be sufficient to pass the trend on to another group, as shown exemplarily in Fig. 8. This underlines the importance of connectors and weakens the role of the original trendsetter.
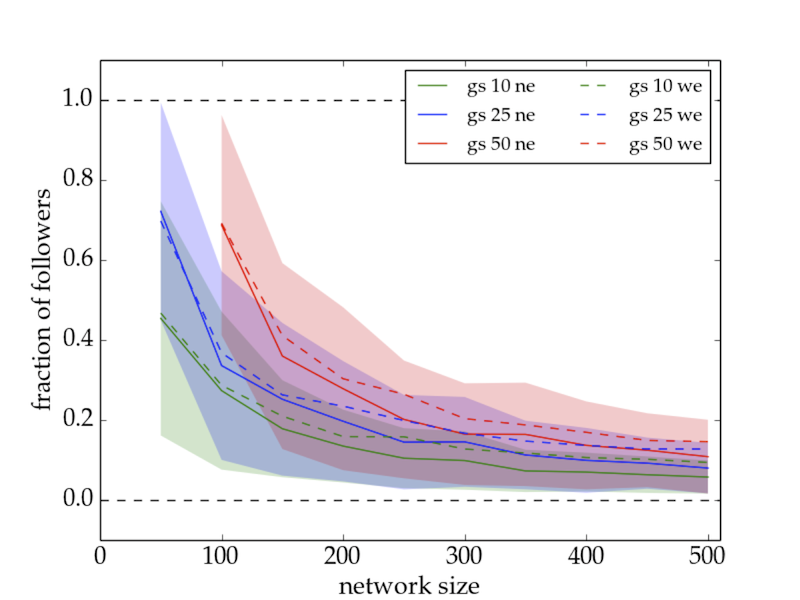
Figure 7. Fraction of followers as a function of network size for group sizes (gs) of 10 (green), 25 (blue), and 50 agents (red), and runs without (ne; solid lines) and with (we; dashed lines) the emergence of autonomous followers in the community model. Shaded regions indicate a standard deviation of \(1\sigma\) for runs without emergence. The fraction of followers decreases with increasing network size and increases with increasing group size. 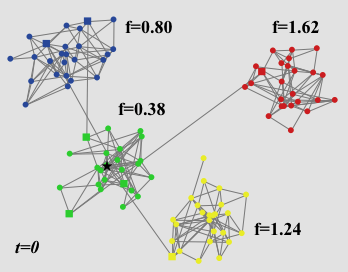
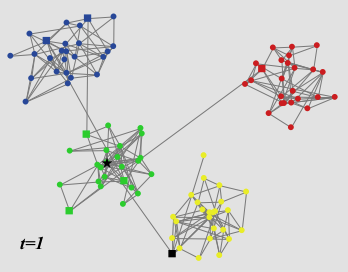
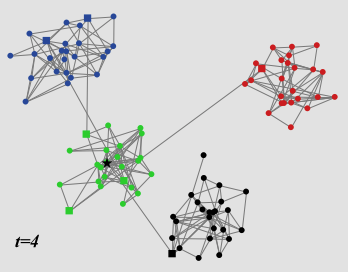
Figure 8. A community network of size 100 with four groups of 25 agents each at the simulation setup (left panel), at \(t = 1\) (middle panel), and at the final time step \(t = 4\) (right panel). The average internal propensities of the groups are \(f = 0.80\) (blue), \(f = 0.38\) (green), \(f = 1.24\) (yellow), \(f = 1.62\) (red). Agents who own bridge links to other groups are indicated as squares, except for the trendsetter which is indicated as a black star (green group). He is located in a group with low internal propensity towards the trend where he is not able to spread the trend. In spite of that, the trend passes over to another group (yellow) with above average internal propensity where it spreads out.
 Discussion
and Outlook
Discussion
and Outlook
- 4.1
- We have proposed a family of models of private attitude and social influence concerning the spreading of a 'trend', that is, in this context, a temporary, behavioural pattern within a social group. Our models allow for situations where bandwagon effects occur, as well as situations where a new behaviour is not able to manifest itself as a trend. To study the emergence and the spreading of trends in social groups, we have used two different types of artificial networks, namely the dynamic random model with three subtypes, and the community model. While we have kept up the terminology of trends throughout the analysis of our models, it is safe to say that the models do not only apply to situations involving trends, but to situations where social influence comes to play in general. These are exactly the situations described in Section Trends as Descriptive Norms, with people behaving according to descriptive norms, be it or not because they actually experience social influence or even some form of pressure. We have built our models on well-founded theoretical work regarding social influence and common reactions to it, as well as, for the community model, on a number of insights from theoretical and empirical studies which deal with trends and influence structures in society. While we do not claim for our models to be able to explain every facet of a trend or to even comprehensively reflect the complexities of human behaviour in situations of engagement with social movements, we do nevertheless think that they successfully reproduce key aspects of trend evolution in general. Although both our models and their variations are but simplified representations of the highly complex real-world situations in which trends occur, we believe that we have been able to capture typical patterns of the flow of influence in the absence of coercion in social networks.
- 4.2
- Using the random model, we have been able to study the general concepts of different dynamical effects which can be associated with behavioural change triggered by some source of influence. Although the network under consideration is biased regarding the spreading of a trend by the explicit implementation of a trendsetter who has considerably more influence than a regular agent in the network (i.e. about a factor 3-10), the model is very useful for studying the time evolution of the system. We investigated three variations of the random model in this paper, i.e. the basic model, the equilibrium model, and the stability model.
- 4.3
- With the basic model we have studied dynamic networks which are a common form of social networks due to the making and dropping of social contacts. This kind of dynamicity usually leads to a far-reaching spreading of the trend in the network. One feature we have been able to identify is the evolution of a trend if it indeed succeeds in carrying along a significant fraction of the population: This happens only if the trendsetter has been able to trigger a cascade. Otherwise, the fraction of followers stays comparably low (at the order of 10 percent).
- 4.4
- The equilibrium model has been used to study situations where two opposing trends are at stake. We have found that, although in a statistical sense both trends have comparable numbers of followers, the individual social situation is always dominated by one of these trends. This indicates that a permanent equilibrium situation is more likely to occur if the majority favours one of the trends. In this model we have also included the conversion of the agents, meaning that they become positive about following the trends after some time, thus converting the trend to a convention. Naturally, we have found higher fractions of followers (about twice as high) and an increased number of equilibrium situations if the conversion of agents is possible.
- 4.5
- Our third random model, the stability model, deals with the loss of the initial support of the trend which is a process common to the nature of trends. The evolution of individual simulations after the removal of a trendsetter is very sensitive to the particular situations in the network, and to the treatment of the trendsetter. The trend might decline if the trendsetter continues to socialize with his fellow group members. This can be related to the establishment of a new trend or the re-establishment of an old one. By contrast, the trend might live on or even keep on spreading throughout the network if the trendsetter ceases his social activities. The stability model is relevant for the study of trends because it describes realistically how trends come and go.
- 4.6
- The second type of network we are using, the community model, is inspired by the empirical results which we have presented at the beginning of Section . The two most influential factors on the development of this model are (i) the community structure of social networks and (ii) the importance of connectors and weak ties in influence networks. Community structure was found to be a feature of many different social networks. While not all types of communities necessarily imply a solidarity of interest, commonality of some kind usually plays a crucial role in their formation. The idea that connectors or weak ties are vital in spreading information between otherwise distinct social groups is easily understandable: Whereas in a close-knit group an individual receives a piece of information several times from different sources, a connector can pass information to another group where it is still 'new'. The importance of weak ties becomes even clearer if one thinks about the effects of removing such links in a network. We have taken these ideas into account by measuring the influence of agents in the network not only by their number of social contacts but also by their betweenness score which quantifies how important an agent is in connecting the other agents. Using the community model we have also been able to reproduce other empirical findings presented at the beginning of Section The Community Model. We have been able to catch two observations regarding how information or influence flow in a community network, and what kind of persons the initiators of such flows are. Many studies have found that such occurrences as trends or innovations are not necessarily triggered by influential people or so-called opinion leaders, but are often driven by people which are easily influenced, or alternatively by so-called innovators. Both situations are captured in our model: If a trendsetter passes the trend to a relatively isolated group, it might be able to spread because the easily influenced people pass it along to other easily influenced people. If, simultaneously, the trend does not spread in the trendsetter's own group, then it is safe to say that the cascade itself is not driven by the trendsetter. Comparable is a situation where individual agents 'emerge' as followers and convince their neighbours to join the trend. To sum up, we believe that the community model, regardless of its simplifications and flaws, constitutes a good enough representation of a real-world social influence network to study and capture intrinsic features of the flow of influence in such networks, as well as to simulate more specific situations regarding the spreading of trends.
- 4.7
- Trends are a fascinating phenomenon in human society. People are often influenced by what others are doing, and the phenomenon of trends provides a unique and excellent opportunity to investigate this important aspect of human nature. Many empirical studies have concentrated on the conditions of the emergence of trend behaviour. Recent work specifically addresses the regime of online social communities which goes beyond the scope of our models. However, there is a big domain of social life where trends might occur, e.g. friendship circles, schools, working places, or simply the social environment of the place one lives at. Although empirical work in this field is usually dedicated to one specific trend and not to the phenomenon of trends in general, it is possible to deduce certain general characteristics. All the same, if a new behaviour will be successful in spreading through a considerably large part of a population or social group, thereby becoming a trend, is difficult or even impossible to predict. The situations of the emergence of trends are highly unique, and the social relations of people are too changeable to pin down a 'standard situation' of trend emergence. However, some general remarks can be made: (i) a trend is more likely to spread if influential persons engage in joining it, and (ii) people are prone to subordinate their personal attitudes if they recognize a trend through its support in their social neighbourhood. We have tried to capture these features in our models. Precisely because of the uniqueness of social situations in empirical studies, the method of using simulations allows us to purposefully study the general mechanisms of trend emergence, spreading, and disappearance in a statistically comprehensive way. Another characteristic feature of trends is that they appear to be relatively independent of their content. Our models take this important aspect into account through their general formulation of agents' internal propensities and through their emphasis on the role of social influence on human behaviour.
- 4.8
- We hope that we have succeeded in motivating why the study of trends takes us one step further in the understanding of human behaviour and its complex peculiarities, and that we have been able to illuminate some of the key features of trends in this work.
- 4.9
- There is room for exploration and improvement. Although we believe that our model of social influence captures many important aspects of how influence is experienced and exerted in real life, certainly there are modifications one could think of. One obvious modification would be, for instance, to abandon purely equivalent bidirectional influence relations and to allow for asymmetric relations where one person has higher influence on someone than the other way around. However, it does not seem to be an easy task to define and model such circumstances. Another point would be to explicitly model possible expense factors related to a trend which we only subsumed into the personal attitudes of the agents. A more detailed modelling of the agents' cognitive processes and their effects on the acceptance of trends would constitute an enthralling continuation of our present efforts.
- 4.10
- Besides improvements regarding the model itself, there are still open questions regarding trends one might want to answer. For instance, how high is the significance we ascribe to our private attitudes as compared to public opinion, and to what extent are we aware of the society's influence on our behaviour? There are other aspects which have been left out in our proposed model and related models of norm emergence, namely the different stages of life or the social background of agents and their impact on their estimation of private attitude, public opinion, and behaviour. It would be an interesting task to address these questions. Further comparison of possibly improved models with empirical data extending beyond the presented discussion would certainly represent an important contribution.
- 4.11
- Much progress can be expected in this field in the upcoming years. With the extended abilities to conduct surveys or to monitor social behaviour due to the increasing networking activities of people and due to the enormous amount of data which is provided by the internet, there is a potential for major advance regarding the evaluation of social influence and related behaviour. The study of trends is a promising field for future research in philosophy and in the social sciences, thereby linking up-to-date technology to the very foundations of our human nature.
 Acknowledgements
Acknowledgements
- We thank the anonymous referees for valuable comments on the draft which helped to improve the paper. Also, we would like to thank Malte Döhne, Chiara Lisciandra, and Conor Mayo-Wilson for helpful comments, and the participants of the conference on Agent-Based Modeling in Philosophy at the Center for Advanced Studies at the LMU Munich in December 2014 for useful feedback.
 Notes
Notes
-
1 There are varying
conceptions in the literature of how a social rule or norm is defined,
many of them emphasizing the role of expected or existing sanctions.
For a recent review of social norms, see e.g. Bicchieri and Muldoon (2014). For surveys on the
modelling of (social) norms, see e.g. Savarimuthu and Cranefield (2011), Andrighetto et al. (2013), and Elsenbroich and
Gilbert (2014). The
latter point out the distinction between social norms and descriptive
norms which is elucidated in Bicchieri (2006).
2 It is assumed that a trend might be opposed in two different ways: either by ignoring it, i.e. by just not following it, or by actively bucking the trend.
3 We note that the concept of a trend by itself may suffice to serve miscellaneous personality traits. Opposing a trend is generally some sort of social protest. But whilst following a trend satisfies our need to fit in, the (possibly unintentional) initiating of a trend might as well be a form of alienation or separation from the crowd.
4 For experimental evidence on the discrepancy between how people perceive norms, and what the norms actually are, see e.g. Borsari and Carey (2003).
5 We note that there is literature stating a descriptive norm exists if people prefer to conform to the norm without assuming that the other group members share any common position regarding how oneself should act (Bicchieri 2006).
6 Especially cases where a descriptive norm is triggered by one person or very few people might lead to the kick off of a `bandwagon effect' or an `informational cascade' (Bikhchandani et al. 1992). These terms describe a situation where a large group of people aligns its behaviour to that of other people, independently of the personal attitude of the individuals towards this behaviour, and where this alignment proceeds the faster the more people are joining.
7 Of course, one could think of various other aspects which might play a role, e.g. the cost of the new behaviour. For reasons of simplicity we only consider the personal attitude and the influence of the group in our models. Positive and negative expense factors of any kind are assumed to be subsumed under the positionality of a person, e.g. resulting in a more indifferent or negative attitude towards the trend if following it requires noticeable financial involvement.
8 A social influence network represents the influential relations among members of a social group. A theoretical approach can be found in, for instance, Friedkin and Johnsen (2014).
9 The models presented in this work are written in NetLogo. We use the NW Extension for network analysis to generate and utilise the networks used in our models. The simulation code can be obtained from the first author upon request.
10 We note that the truncated normal distribution contains 99.6 percent of the volume of the full normal distribution.
11 We believe that a social threshold model for the adoption of trends is realistic because people usually consult several other people before engaging in a new behaviour. This might be due to possible expense factors or to reasons of conformity. The threshold level itself could be argued about.
12 Another kind of modification would be the strengthening or weakening of existing social ties. Although this might be an important mechanism regarding changes in social influence, it is not clear how its effects could be tested in a controlled manner in our models. Therefore, these processes are not incorporated in our models for reasons of simplicity.
13 The choice of `one agent per time step' is arbitrary. An alternative option would be to ask a certain fraction of agents per time step to rewire themselves. In the manner presented here, the impact of the rewiring process on the network structure is higher for smaller networks as compared to larger ones. This can also be observed in real life social networks, e.g. the impact of a broken friendship in a school class vs. a new contact in a much larger, computer mediated social network.
14 We also tested different numbers of links for the trendsetter. Unsurprisingly, the trend spreads faster, the higher the number of trend links. Likewise, the trend spreads faster if more trendsetters are incorporated.
15 For all our models, the time interval represented by one time step may be variable for different social settings, depending on the nature of the trend. A trend coming up in a school class, for instance, might spread within a few days or weeks, whereas the spreading of a fashion trend in a whole society might go on for months. Regarding the duration of our simulations, we found the number of 1000 (500, cf. Section "The Community Model") time steps to be sufficient to identify the effects studied in our models.
16 This confirms a similar result by Villatoro et al. (2011) regarding the higher resistance of highly clustered networks to rewiring in a context of convention emergence. They also investigate different rewiring mechanisms and network topologies.
17 Conventions are brought into existence if a descriptive rule is actually followed, and if it is stable over a certain timespan long enough (cf. Bicchieri 2006).
18 Of course, these values could be chosen in a different way. For our simulations, however, we want to mimic the process of conversion on timescales comparable to a typical simulation run. Increasing or decreasing the parameters would only affect the timescales on which agents are converted, except for a high number of required successive time steps which might prevent the conversion of agents in general. With our choice of parameters, there are, on average, still a few percent of agents left who are not fully converted at the end of a simulation run with conversion (cf. right panel in Fig. 4).
19 We note that there is literature on conversion which states that the process of conversion occurs only as long as the influential social group is a minority, as otherwise people would just start to conform without rethinking their behaviour (e.g. Moscovici 1985).
20 A related issue is a setup with a minority group which is immune to influence from the remaining, influenceable population. This setup allows to address the question how high the minimum fraction of this minority has to be to successfully convince the rest of the group to adopt their behavioural pattern (see e.g. Xie et al. 2011, for a respective study considering complete and random graphs, as well as scale-free networks, and references therein).
21 See Rogers (2003) for an overview of related research.
22 There are several studies of social networks where a distinctive community structure was revealed. They address e.g. networks of communication (e.g. Guimerà et al. 2003), collaboration and citation networks (e.g. Ravasz & Barabáasi 2003), friendship networks (e.g. Moody 2001), or online social communities (e.g. Porter et al. 2009). See also Scott (2000), and references therein.
23 The betweenness centrality of an agent in a network is determined by the number of all shortest paths between two other agents in the network of which the agent is a part of.
24 A different approach to model the influential relations of agents with similar attitudes is the so-called bounded confidence model where agents adjust their `opinion' based on similar opinions of other agents only (e.g. Hegselmann & Krause 2002).
25 The latter specifically applies to simulation runs where the emergence of additional trendsetters during the simulation is possible. In general, it holds that the larger the network and the individual groups, the more similar the distribution of \(f\) will be to \(\mathcal{N}(1, 0.35)\).
 References
References
- ANDRIGHETTO, G.,
Castelfranchi, C., Mayor, E., McBreen, J., Lopez-Sanchez, M. &
Parsons, S. (2013). (Social) norm dynamics. In: Normative
Multi-Agent Systems (Andrighetto, G., Governatori, G.,
Noriega, P. & van der Torre, L., eds., vol. 4 of Dagstuhl
Follow-Ups, pp. 1–26). Dagstuhl Publishing.
BICCHIERI, C. (2006). The Grammar of Society: The Nature and Dynamics of Social Norms. Cambridge University Press.
BICCHIERI, C. & Muldoon, R. (2014). Social norms. In: The Stanford Encyclopedia of Philosophy (Zalta, E. N., ed., Spring 2014 edition).
BIKHCHANDANI, S., Hirshleifer, D. & Welch, I. (1992). A theory of fads, fashion, custom, and cultural change as informational cascades. Journal of Political Economy 100(5), 992–1026. [doi:10.1086/261849]
BORSARI, B. & Carey, K. B. (2003). Descriptive and injunctive norms in college drinking: A meta-analytic integration. Journal of Studies on Alcohol 6, 331–341. [doi:10.15288/jsa.2003.64.331]
BURT, R. S. (1992). Structural Holes: The Social Structure of Competition. Harvard University Press.
CIALDINI, R. B., Kallgren, C. A. & Reno, R. R. (1990). A focus on normative conduct: A theoretical refinement and reevaluation of the role of norms in human behavior. Advances in Experimental Social Psychology 24, 201–234. [doi:10.1016/S0065-2601(08)60330-5]
DEUTSCH, M. & Gerard, H. B. (1955). A study of normative and informational social influences upon individual judgement. Journal of Abnormal and Social Psychology 51(3), 629–636. [doi:10.1037/h0046408]
ELSENBROICH, C. & Gilbert, N. (2014). Modelling Norms. Dordrecht: Springer. [doi:10.1007/978-94-007-7052-2]
FRIEDKIN, N. E. & Johnsen, E. C. (2014). Social Influence Network Theory: A Sociological Examination of Small Group Dynamics. Structural Analysis in the Social Sciences. Cambridge University Press.
GRANOVETTER, M. S. (1973). The strength of weak ties. American Journal of Sociology 78(6), 1360–1380. [doi:10.1086/225469]
GUIMERÀ, R., Danon, L., Díaz-Guilera, A., Giralt, F. & Arenas, A. (2003). Self-similar community structure in a network of human interactions. Physical Review E 68(6), 065103. [doi:10.1103/PhysRevE.68.065103]
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation 5(3), https://www.jasss.org/5/3/2.html
LAZARSFELD, P. F., Berelson, B. R. & Gaudet, H. (1968). The People's Choice: How the Voter Makes up his Mind in a Presidential Campaign (3rd edition). Columbia University Press.
MOODY, J. (2001). Race, school integration, and friendship segregation in america. American Journal of Sociology 107(3), 679–716. [doi:10.1086/338954]
MOSCOVICI, S. (1985). Social influence and conformity. In: Handbook of Social Psychology (Lindzey, G. & Aronson, E., eds., vol. 2, chap. 20, pp. 347–412). Random House.
MULDOON, R., Lisciandra, C., Bicchieri, C., Hartmann, S. & Sprenger, J. (2014). On the Emergence of Descriptive Norms. Politics, Philosophy & Economics 13(1), 3–22. [doi:10.1177/1470594X12447791]
NAKAMARU, M. & Levin, S. A. (2004). Spread of two linked social norms on complex interaction networks. Journal of Theroretical Biology 230(1), 57–64. [doi:10.1016/j.jtbi.2004.04.028]
NEWMAN, M. E. J. & Park, J. (2003). Why social networks are different from other types of networks. Physical Review E 68(3), 036122. [doi:10.1103/PhysRevE.68.036122]
PORTER, M. A., Onnela, J. & Mucha, P. J. (2009). Communities in networks. Notices of the AMS 56(9), 1082–1097.
RAVASZ, E. & Barábási, A. (2003). Hierarchical organization in complex networks. Physical Review E 67(2), 026112. [doi:10.1103/PhysRevE.67.026112]
ROGERS, E. M. (2003). Diffusion of Innovations (5th edition). Free Press.
SAVARIMUTHU, B. T. R. & Cranefield, S. (2011). Norm creation, spreading and emergence: A survey of simulation models of norms in multi-agent systems. Multiagent and Grid Systems - An International Journal 7, 21–54.
SAVARIMUTHU, B. T. R., Cranefield, S., Purvis, M. K. & Purvis, M. A. (2009). Norm emergence in agent societies formed by dynamically changing networks. Web Intelligence and Agent Systems 7(3), 223–232.
SCOTT, J. (2000). Social Network Analysis: A Handbook (2nd edition). Sage Publications.
VILLATORO, D., Sabater-Mir, J. & Sen, S. (2011). Social instruments for robust convention emergence. In: Twenty-Second International Joint Conference on Artificial Intelligence (Walsh, T., ed.). IJCAI/AAAI.
WATTS, D. J. & Dodds, P. S. (2007). Influentials, networks, and public opinion formation. Journal of Consumer Research 34(4), 441–458. [doi:10.1086/518527]
XIE, J., Sreenivasan, S., Korniss, G., Zhang, W., Lim, C. & Szymanski, B. K. (2011). Social consensus through the influence of committed minorities. Physical Review E 84(1), 011130. [doi:10.1103/PhysRevE.84.011130]