Gérard Weisbuch and Guillemette Duchateau-Nguyen (1998)
Journal of Artificial Societies and Social Simulation vol. 1, no. 2, <https://www.jasss.org/1/2/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 17-Jan-1998 Accepted: 11-Feb-1998 Published: 31-Mar-1998
 Abstract
AbstractConcerning the second motivation, the role of cultural, social and political factors in economic and technical choices concerning the environment is now well established (Descola, 1996). Most schemes describing the loops of interactions among climatic, natural and economic variables include control terms due to these factors, see for instance figure 1. Economic models consider these factors as exogenous and treat them as constant parameters of a choice function; this is the case for instance when economic agents are supposed to maximize a given utility function. Another view from the integrated assessment literature is that the scientist's task ends when choices of possible measures, including the analysis of their potential costs and benefits, are presented to the political authority which requested the assessment to be performed. The authority then chooses one of the proposed actions according to how it weights cultural, political and social factors. Within this framework, human factors are made even more exogenous to the modeling effort and are, supposedly, entirely taken into account by the political authority. This is the view of a number of scientists who are very much in favor of the neutrality of science; for them, the political level should be entirely responsible for the decision process.
Figure 1: The three layer scheme: agents' representations depend
upon resource level and economic variables and they control resource usage
via economics.
where P, the production function, has decreasing returns in terms of the labour force, L, and the invested capital, K. This simple Cobb-Douglas expression, with half powers on K and L and a unitary power on N, was chosen to allow simple algebraic computations rather than to be realistic. We further distinguish between Pk, the size of the harvest in monetary units, and Pn, the size in number of fish, by multiplying P by coefficients ak and an respectively. ak/an can be thought of as a price. The labour force is assumed to be constant in time2.
Capital K is decreased at the capital depreciation rate µ, (representing, for instance, the inverse mean life time of the boats and fishing gear). It is also increased by some investment proportional to the harvest. Capital then obeys equation:
f(t) is the fraction of production in value that the agents choose to consume; the rest of the production is reinvested in capital. Fraction f(t) is chosen by the agents according to their internal representation of the environment and according to their economic interest.
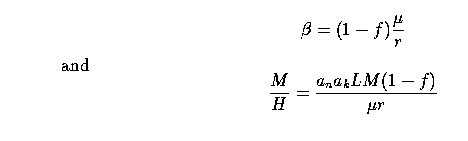 (5)
(5)
H, defined by the above equation, is called the harvest limited
resource (in the limit of large M, the environment's carrying capacity, the resource N goes to
H).
An important result of the formal analysis is that attraction toward equilibrium
is slow with large oscillations when ![]() is small, which is true for most fisheries (except whales for which lifetime is
larger than inverse capital depreciation rate), and when M>>H,
i.e. when the fishery is exploited well below its carrying capacity. In
other words, these are the conditions when we can expect difficulties in controlling
the fishery, and this is indeed what is observed in simulations.
is small, which is true for most fisheries (except whales for which lifetime is
larger than inverse capital depreciation rate), and when M>>H,
i.e. when the fishery is exploited well below its carrying capacity. In
other words, these are the conditions when we can expect difficulties in controlling
the fishery, and this is indeed what is observed in simulations.
Vector X is the vector of linear predictors.
![]()
![]()
![]()
where![]() is
a constant small decay factor along the gradient of the error function
is
a constant small decay factor along the gradient of the error function
![]() with respect
to the predictor vector X
with respect
to the predictor vector X
where the nf
consumption fractions f(t + i)
are chosen to maximize the sum of consumptions discounted with discount
rate ![]() during
the nf future
time periods following time t. We will use the notation
during
the nf future
time periods following time t. We will use the notation ![]() to present simulation results.
to present simulation results.
The dot stands for the scalar product of the two representations. If the two successive representations are the same, the overlap is 1. This measure is often used to compare attractors in configuration space in the statistical mechanics of spin glasses or neural nets (Mezard et al 1987). Monitoring Q shows whether the agents keep stable representations that are simply updated by new information or whether they experience strong changes in opinion.
| Parameter | Value |
|---|---|
|
initial value of resource N |
5 |
|
initial value of capital K |
0.1 |
|
capital decrease rate |
0.2 |
|
reproduction rate r |
0.5 |
|
carrying capacity M |
5.0 |
|
production coefficient in capital |
0.5 |
|
production coefficient in fish units |
0.2 |
|
discount rate for the future |
0.7 |
|
learning parameter |
0.05 |
| Variable | Value at optimum consumption |
|---|---|
|
consumption fraction |
0.86 |
|
resource |
2.92 |
|
capital |
1.08 |
Figure 3: Simulated performance of agents using predictors linear in capital. Time plots of capital, actual and agents' predicted production, consumption, fraction of consumed production and overlap. The overlap between consecutive agents' representations is an indication of the stability of representations when it stays close to one. After 70 initial time steps, agents use knowledge about previous performance to adjust consumption and investment. Although performance fluctuates as seen on the time plot, average consumption remains only a few percent lower than maximal sustainable consumption.
Figure 4: Time plot of predicted and actual production, consumption and overlap of representations, when agents use predictors linear in the square root of capital, thus using some knowledge about the form of the production function. The amplitudes of the oscillations are strongly reduced, and the intermittent dynamics with a quasi-period of 70 steps is more clearly visible.
Figure 5: "Widrow-Hoff updating": Time plot of predicted and actual production, consumption and overlap of representations, when agents use Widrow-Hoff incremental updating of the linear predictors. The amplitude of the oscillations is strongly reduced.
Figure 6: "El Niño effect": the system is able to readjust to a new resource dynamics after the carrying capacity decreases by a factor of 2.
Figure 7: Variation of equilibrium resource, capital and consumptions in the case of two populations of agents with different discount rates for the future. Population 1 has a constant discount factorwhile the other population discount factor
varies along the x axis between 0.5 and 0.9. Thinner lines are the performance of the short-sighted population 1, thicker lines those of population 2. The dotted line represents the ratio of equilibrium resource to optimal equilibrium resource.
Let us now come to the question of comparing the model predictions with empirical data. In fact, we have in real life a number of examples of fisheries in situations which do not seem to be (perfectly) rationally managed: consider fish depletion in Newfoundland, Iceland, the Northern Pacific or the Peruvian coast. A number of explanations have been proposed based on biological, climatic or economical mechanisms, all based on full rationality of the actors. But no single mechanism is unanimously accepted as the explanation for the depletion of a specific fishery. What we have discussed here is how the lack of information about fish stock and dynamics can also play a role in observed fish dynamics. Trying to work out which mechanisms are most relevant for a given fishery is outside the scope of this paper.
Supplementary material Computer programs and supplementary materials, with more simulation results and references to halieutics, can be retrieved in a tar format file.
1 Because we are using such a minimal model of a fishery, we cannot pretend to represent a real fishery to the point where we could compare numerical predictions with empirical data. By contrast, the nature of the attractors of the dynamics is a robust property which is independent of modeling details. This level of description is then relevant to the minimal model that we are using.
2 Maintaining a constant labour force is only an approximation done in order to keep the model simple. An economist might be tempted to suppose that agents enter or leave fishing activity according to available profits. A constant labour force is reasonable for artisanal and traditional fisheries when other economic activities are not readily available. But this assumption is not crucial to the model which can be easily generalised by supposing the existence of a competitive labour market with minimal profit.
3 In fact, we have no formal proof that a constant f regime is optimal in term of consumption. It is possible than some oscillatory regime gives higher average consumption. But for all the simulations that we have done, the constant f optimal consumption appeared as an upper limit of observed average consumptions, and we therefore took it as the reference for comparison of the agents' performance.
4 Linear predictors can be "learnt" using algorithms that are closer to human cognition than the matrix inversion algorithms we use in the present paper, for instance the Rescorla Wagner algorithm inspired from classical conditioning in behavioural psychology. We use here the most classical inversion algorithm for the sake of simplicity and availability, since anyway the resulting linear predictors are equivalent after learning. To be more specific, the linear predictors are directly computed by inverting the matrices in previous P K and f by the singular value decomposition method and multiplying the pseudo-inverse matrix by the previous production vector according to the algorithms given in Numerical recipes (routines svdcmp and svbksb).This does not mean that we imagine that fishermen would invert matrices using singular value decomposition as we do here! We only imply that the best they can do with the limited information that they posess corresponds to the algorithm we use.
5 There are many modelling options for the way agents choose f. Consumption optimisation, equivalent in the present case to profit optimisation, was chosen here in order to depart from economics modelling only on the issue of available information. Such a way of adjustment would make more sense in the case of industrial than artisanal fishery. In the numerical computations, rather than optimising on the series of consumptions, we supposed that the fraction of consumption evolves in the future according to:
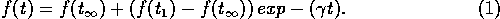
This smooth adjustment of f(t) has two advantages:
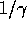 , the range of the agent's interest in the future.
, the range of the agent's interest in the future.
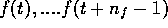 we only have to do it for the three variables
we only have to do it for the three variables 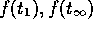 and
and 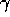 .
.
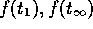 and
and 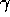 at each time step. During the iteration procedure of the simplex
the algorithm might go too far from the finally selected values
of f(t), generating negative K values which would stop execution. We therefore used in the numerical simulations a "pseudo square root" production function given by:
at each time step. During the iteration procedure of the simplex
the algorithm might go too far from the finally selected values
of f(t), generating negative K values which would stop execution. We therefore used in the numerical simulations a "pseudo square root" production function given by:
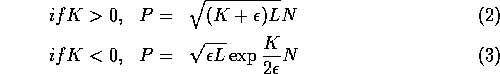
which is continuous and has a continuous derivative at the origin.  was taken as 0.001.
was taken as 0.001.
6 A constant f = 0.5 is used during steps 0 and 1. Linear extrapolation from the two previous steps are then used to adjust f during the first ten steps of the simulation. The linear predictors model with an increasing number of predictors and memory size is used thereafter. np is increased by 1 and memory size increased by 10 whenever time is a multiple of 10, until np = 6 and memory size = 70.
7 The equality between memory size and intermittency period was checked by using different memory sizes such as 40 and 50.
8 Most standard models of cultural evolution draw from epidemiology, and represent cultural evolution by the change of one attribute through an "infection" mechanism. Such models then suppose that the most appropriate value of the attribute is known a priori and fixed, and that cultural traits are independent. Models based on mutation mechanisms such as genetic algorithms might look promising, but they are certainly further from human cognition than the neural net approach to learning described here.
BERGÉ, P., Dubois, M., Manneville, P., and Pomeau, Y. 1979. Intermittency in Raleigh-Bénard convection. J. Physique Lettres, 40:L--505.
BOUSQUET, F., Cambier, C., Mullon, C., Morand, P., Quensiere, J., and Pave, A. 1993. Simulating the interaction between a society and a renewable resource. Journal of biological systems, 1:199--214.
CAVALLI-SFORZA, L. and Feldman, M. 1981. Cultural Transmission and Evolution: A Quantitative Approach. (Princeton University Press).
CHARLES, A. T. 1989. Bio-socio-economic fishery models: labour dynamics and multiobjective management. Canadian journal of fisheries and aquatic sciences, 46:1313--1322.
CLARK, C. W. 1990. Mathematical bioeconomics: The optimal management of renewable resources (2nd edition). (Wiley-Intersciences, New-York).
DESCOLA, P. and Gisli, P. eds. 1996. Nature and Society: Anthropological Perspectives. European Association of Social Anthropologists. (Routledge, New York).
HARDIN, G. 1968. The tragedy of the commons. Science, 162: 1243-1247.
IDYLL, C. P. 1973. The anchovy crisis. Scientific American, 228:22--29.
KOHONEN, T. 1988. Self-organization and associative memory. (Springer-Verlag, Heidelberg).
MARSH, J. 1991. Exploration and exploitation in organizational learning. Organization Science, 2(1):71--87.
MÉZARD, M., Parisi, G., and Virasoro, M. 1987. Spin glass theory and beyond. (World scientific, Singapore).
PRESS, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T. 1989. Numerical recipes. The art of scientific computing. (Cambridge University Press, Cambridge).
RESCORLA, R. and Wagner, A., 1972. A Theory of Pavlovian Conditioning: The Effect of Reinforcement and Nonreinforcement, In Classical Conditioning II: Current Research and Theory. Eds. Black A. and Prakasy W., 64--69, Appleton-Century- Crofts, New York.
WEISBUCH, G. 1991. Complex systems dynamics. (Addison-Wesley, Redwood City).
WEISBUCH, G., Stanley, E. A., Duchateau-Nguyen, G., Antona, M., and Clément-Pitiot, H. 1997. Influence of capital inertia on renewable resource depletion. Theory Bioscienc., 97--117.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1998