Introduction and Literature Overview
The seminal paper by Nordhaus et al. (1992) applied a general equilibrium model to analyse the trade-off between economic growth and climate change; this approach has been extended to incorporate technological progress, heterogeneity and uncertainty. However, to assess the trade-off between these two potentially conflicting objectives (economic growth and climate change prevention), a family of Integrated Assessment models (IAMs) has been proposed, such as AIM (Kainuma et al. 1999), DEMETER (Gerlagh & Van Der Zwaan 2004), DICE (Nordhaus et al. 1992), ENTICE (Popp 2004), FUND (Tol 1997), IMAGE (Rotmans 2012), MERGE (Manne et al. 1995), MIND (Edenhofer et al. 2005), PAGE (Hope 2006), REMIND (Leimbach et al. 2010), RICE (Nordhaus & Yang 1996), and WITCH (Bosetti et al. 2006). For surveys, see Dowlatabadi (1995) on policy motivated integrated assessments of climate change, Kelly & Kolstad (1999) on methodologies applied, Stanton et al. (2009) on climate-economy models and Weyant (2017) on key challenges and areas for improvement. Moreover, Weyant (2017) (page 116) defines an
IAM of global climate change to be any model that encompasses the whole world and, at a minimum, includes some key elements of climate change mitigation and climate impacts systems at some level of aggregation.
For example, MIND[1], the Model of INvestment and endogenous technological Development, makes use of a macroeconomic approach and operates on aggregated economic values; technological progress and invest-ments are considered by funding the sectors (i) labour, (ii) fossil energy, (iii) fossil resource extraction, (iv) renew-able energy, (v) research and development, and (vi) carbon capturing and sequestration technologies. MIND admits dynamic optimisation of investments after a calibration of the productivity and sensitivity parameters, supported by empirical and theoretical parameter (interval) values. Extensions of MIND are, for instance, addressing uncertainty over selected parameters by chance constraint programming (Held et al. 2009), heterogeneous regions (Leimbach et al. 2010), value of learning (Lorenz et al. 2012), and cost-risk analysis (Neubersch et al. 2014). In the latter approach, the goal function includes a weighted sum of the welfare measure and the risk of exceeding the climate (temperature) target over the optimisation horizon. Furthermore, the trade-off parameter between social welfare and risk is calibrated within the cost-risk analysis. The IAM by Scheffran (2008) considers energy production technologies causing low or high carbon emissions within an adaptive optimisation process. Such a modelling approach can provide decision support to negotiate admissible emission trajectories and to better understand the choices of climate politics, including multiple agents and their interdependencies. Within the regional DICE model (RICE, Nordhaus & Boyer 2000), heterogeneity of regional impacts and income inequalities are investigated by Dennig et al. (2015), presenting estimates on the per capita consumption of the poorest agents (the lowest quantile) and showing the poorest in all regions can participate in economic growth when carbon pricing is optimal in a world with inversely proportional damage. Stern (2016), however, points out that the IAM class of models does not take all the relations among economics, social and environmental factors into account and fails to consider all of the consequences (e.g. potential conflicts, migrations as a result of sea level rise) in the decision evaluation, thus underestimating the uncertainty. Agent-Based Models (ABMs), by contrast, “seek to provide more realistic representations of socio-economics by simulating the economy through the interactions of a large number of different agents, on the basis of specific rules” (Stern 2016).
Balint et al. (2017) provide a survey of agent-based literature on the economics of climate change. In particular, they identify four areas in the relevant literature: (i) coalition formation and climate negotiations, (ii) macro-economic impacts of climate-related events, (iii) energy markets, and (iv) diffusion of climate-friendly technologies. In all of these areas, the impact of heterogeneity is one of the major research problems. For example, McGinty (2007) investigates the stability of coalitions of nations under heterogeneity. Lessmann et al. (2015) find that the heterogeneity of regions improves incentives to participate in climate agreements. Dosi et al. (2010) investigate the impact of public policies on heterogenous companies. In the family of LAGOM models (Haas & Jaeger 2005), heterogeneous households and producers facing climate-related risk are considered. Weber et al. (2005) develops a Multi-Actor Dynamic Integrated Assessment Model (MADIAM) which couples a climate change model (nonlinear impulse response model of a climate sub-system — NICCS) to an economic growth model (multi-actor dynamic economic model — MADEM). The adoption paths of climate-friendly technologies and the impact of heterogeneity in individual behaviours and preferences are studied in Windrum et al. (2009). In this context, Vona & Patriarca (2011) show that agent heterogeneity can hinder the diffusion of energy efficient technologies. The problem of the impact of heterogeneity on the diffusion of new technologies is also considered by Janssen & Jager (2002), Schwoon (2006), and Tran et al. (2013).
An agent-based approach provides the framework to consider the interplay of economic and climate-related problems. In this spirit, Lamperti et al. (2018) extend an agent-based macroeconomic model to include the climate-related aspects of economic growth at the global level and so provides the first agent-based integrated assessment model. The authors find that “climate damages from uncontrolled emissions are substantial and much more severe than predicted by many cost-benefit driven integrated assessment models” (Lamperti et al. 2018, 329). The modelling approach presented in this paper differs from theirs with respect to the specific agent types’ characteristic and behaviour. In general, the model presented in (Lamperti et al. 2018) focuses on technological growth and the financial sector, whereas our model is focused on the power generation and fuel extraction sectors. Our model is also limited to the real economy. Moreover, our model is calibrated based on real-world data and takes into account regional differences by considering ten different regions. Safarzyńska & van den Bergh (2017) analyse the interactions between technological, financial and energy systems. They consider heterogeneous agents: consumers, producers, power plants and banks. Ponta et al. (2018) investigate energy system transitions in the context of sustainable growth paths by using an extended version of the Eurace model. Geisendorf & Klippert (2017) investigates the effects of green investments within an agent-based climate-economy model and finds that IAMs cannot deal with the changing preferences or decision heuristics of the relevant agents.
The economic impact of climate change is estimated using damage functions. These damage functions relate climatological quantities, such as temperature, sea level height and CO2 concentration, to economic damages in monetary terms (Diaz & Moore 2017). These damage functions are therefore a crucial component of IAMs. Covington & Thamotheram (2015) compares three widely used damage functions from Nordhaus (2013), Weitzman (2012) and Dietz & Stern (2015). As Figure 1 of Covington & Thamotheram (2015) demonstrates, the damage function produces a similar level of damage up to a 2 degree warming but differs widely for greater warming. An extensive discussion of damage functions is provided by National Academies of Sciences & Medicine (2017).
In our model we consider three types of damage. Damage to the agricultural sector, a decrease in labour productivity (Burke et al. 2015), and damage related to natural hazards related (see Coronese et al. (2019); Franzke (2017); Franzke & Czupryna (2019), for a more detailed discussion of this type of economic damage). The main contribution of this paper is to provide a bottom-up estimation of the shape of the relevant damage functions. The intermediate results are the GDP growth forecasts, with particular focus on energy sector development, for different scenarios with respect to the quantity of remaining fuel reserves and the dynamics of growth rates in renewable energy resources (primarily solar and wind). We also show that heterogeneity may play a significant role in such scenarios.
In the section entitled Model Overview, we introduce and provide the general description of the model. Implementation details are provided in the Model Details section. The simulation results, with an accompanying econometric analysis, are provided in the Results section. The findings and implications of our paper are summarised in the Conclusions section. The calibration methodology and the macroeconomic data used for the calibration are discussed in the dedicated Appendix.
Model Overview
With our model, we would like to address the following two research questions. Firstly: what is the relation between climate change, as measured by CO2 concentrations, and different economic growth scenarios? Secondly, what is the difference in the observed economic growth when we consider heterogeneous agents instead of homogeneous agents. Similarly, what is the difference when we consider the heterogeneous impact of dam-age upon agents, instead of the homogeneous impact? To answer these research questions, we construct an agent-based model (ABM) that focuses on the energy sectors and relevant climate facts in a detailed way, while combining it with consumer and capital goods, labour and capital markets modelled in a basic way. Fagiolo et al. (2007) lists four main characteristics of ABM models: a bottom-up perspective, heterogeneity, bounded rationality, and networked direct interactions. In our model, we first focus on autonomous decisions made by agents in the form of private households and companies, expressed in terms of planned activities relating to consumption and production respectively. Secondly, we consider different regions with a fixed number of agents in each region, but whose quantity may differ between regions. The agents cannot change their assigned region. In the first analysis which we present, all of the agents in a given region are homogeneous at the simulation start, but agents across two different regions may differ from each other. Additionally, agents in the same region may become different from each other (i.e. heterogenous) in subsequent rounds of the simulation. In the additional sensitivity analysis we also consider simulations with heterogeneous agents in the same region, right from the beginning of the simulation. Thirdly, all of the agents use simple heuristics for complex decisions having high levels of uncertainty, such as households planning the budget or companies deciding upon production levels. Finally, for consumer goods and capital goods, we consider local markets with customers directly linked to a subgroup of producers.
General framework
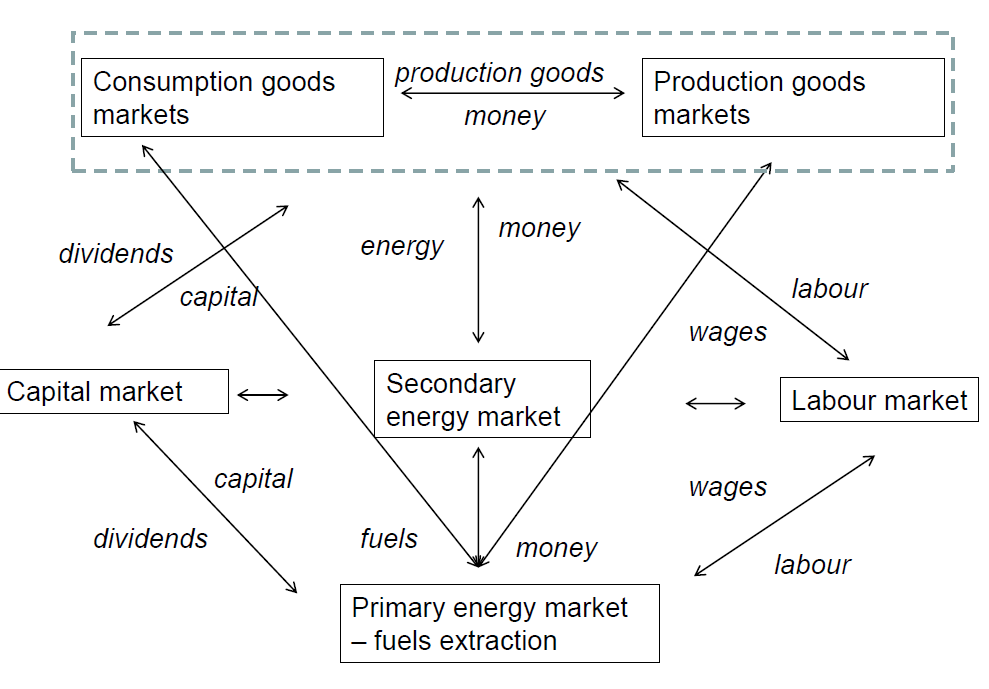
We consider the following agent types in our model, see 1:
- Citizens (private households)
- Energy sector companies
- Consumer goods companies
- Capital goods companies.
Consumer goods companies are further divided with respect to the goods produced within the following sectors: agriculture, textiles, chemicals, other manufacturing, transport and other services. We model the capital goods sector in a simplified manner as only one homogeneous capital good is considered in the model. The energy sector is subdivided into fuel extraction companies (with coal, gas and crude oil considered separately) and the electricity sector (power plants). As climate change influences different industry sectors in different ways (e.g. agriculture is the most sensitive sector to climate change) such subdivision enables us to consider the climate change effect for each sector individually.
Agents
Generally, we assume that agents optimise their behaviour when faced with relatively straightforward problems (the result depends mostly on the agent). However, when faced with more complex problems they use simple heuristics for the decision rules. A complex problem is taken to be a problem wherein the result depends on interactions with other agents or where a high degree of uncertainty prevails. Moreover, we assume that agents’ behaviour is subdivided into three phases. In the first phase, the agents update their state variables with the results of the market interactions with other agents. In the second phase, agents make forecasts of relevant market parameters, such as prices of goods, and plan their market behaviour accordingly. In the third and final phase, agents visit the relevant markets in the following order: capital, labour, fuel, electricity, capital goods and consumer goods, in order to buy or sell goods traded in these markets.
Agents use their next period (year) forecast of the gross domestic product (further abbreviated as GDP) growth rate to update their plans. Such forecasts are constructed under the assumption that real GDP growth rates can be described by the mean reverting process (Equation 1). This equation represents a discrete version of the Vasicek model, (Vasicek 1977) additionally limited from below by at the \(\textrm{min}_{\textrm{gdp}}\).
| $$f_{\textrm{gdp}} = max(\mu_{\textrm{gdp}} + \alpha_{\textrm{gdp}} \left(c_{\textrm{gdp}} - \mu_{\textrm{gdp}}\right) + \sigma_{\textrm{gdp}} \times \epsilon,\textrm{min}_{\textrm{gdp}})$$ | (1) |
We now briefly describe the agents used in the simulation, more details of which are provided in the next section.
Citizens
We first assume that private household preferences are represented by a Stone-Geary utility function (Stone 1954) with \(n\) consumer goods. The goal of citizens is to maximise their preferences, taking into account budgetary constraints. The budget available for consumption results firstly from a citizen’s income — labour wages and capital dividends — and secondly from his or her propensity to consume. The latter specifies how the total budget is divided between consumption and the purchase of new investments. The consumption budget is further divided according to the planned consumption of goods of different types, depending on agents’ preferences and the forecasted prices.
Energy sector companies - fuel extraction companies
We first assume that there is only one extraction company per geographical region and fuel type. We also assume that the marginal fuel extraction costs (and consequently the fuel prices also) depend on the cumulative extraction. This relation may be expressed as a Rogner curve (Nordhaus & Boyer 2000). The fuel extraction depends on the marginal cost of extraction and the physical capital available for a company. Due to the long investment period in this particular sector, we assumed that the fuel extraction company plans the necessary capital investments one period ahead. The company wants to increase the amount of physical capital available if the actual demand is higher than what was initially planned and decrease otherwise. Each company also has a production reserve.
Energy sector companies – power plants
We consider the following power plant (electricity producer) types: coal, gas, oil, nuclear, hydro, wind, and so-lar. Each power plant is characterised by total capacity , a lifetime that depends on power plant type, a capacity factor which gives the average percent of time a given power plant is available, operations and management cost factor (refers to the total electricity produced before transmission losses and depends on the power plant type), electricity transmission loss factor and a conversion efficiency – the percentage of primary energy in fuel converted to electricity. Solar and wind power plants are additionally characterised by the storage capacity. A lifetime parameter is used for explicit modelling of the ageing of the installed capacities. The power plants adjust their capacities based on electricity demand and forecast GDP growth rates. We take the stochastic char-acter of electricity production (especially prominent in the case of renewable energy power plants) by using the parameterised Beta distribution.
Consumer goods companies
The technology of a consumer goods company is represented by a constant elasticity of substitution (CES) pro-duction function. The company uses capital, labour and energy as production factors. The goal of the company is to maximise its profit, calculated as the difference between revenue and the variable production costs (labour and energy costs). In the next simulation period, the planned production quantity and prices are set using sim-ple heuristics. The company adapts to changing demand and production costs. The necessary quantities of production factors are optimised so as to minimise the production cost yet still produce the planned production quantity. Profits are paid out in the form of a dividend to the owners (analogously, loss is covered by the owners) in return for the invested capital, which is primarily used for the purchase of the physical capital necessary for sustaining production.
Capital goods companies
Markets
We also consider the following markets:
- Capital markets
- Labour markets
- Fuel markets
- Electricity markets
- Capital goods markets
- Consumer goods markets
Capital markets
The capital market is demand driven. There is a separate market for each region. Private households invest in companies providing them with new capital. If the value of the new capital is higher than the capital goods demand (planned new investment and replacement investment), the surplus is redistributed among the owners. Otherwise, the planned capital goods demand is proportionally lowered. Although there is no debt market in our model, we allow for a negative cash reserve in the case of companies (similar to the case of private households).
Labour markets
The labour market is also modelled in a simplified way. Private households looking for employment are randomly matched with companies looking for employees. Companies fire employees if the planned labour requirements exceed the current labour force by more than one. We consider separate labour markets for different regions.
Fuel markets
fuel markets are modelled as centrally cleared markets, individually for each type of fuel considered in the model: coal, crude oil and gas. The fuel extraction companies offer the fuel at their marginal extraction cost with regular and maximal quantities (the difference is the production reserve)[2]. The fuel consuming agents (citizens, consumption and capital goods companies, power plants) bid the quantities and accept the market price (we assume that the demand for fuel is inelastic in the short term). The price results from the intersection of the supply curve and the vertical demand curve. The vertical shape of a demand curve represents the fact that the demand is inelastic in the short term.
Electricity markets
Electricity markets function in a similar way to the fuel markets but only on a regional level, rather than the global level that applies to fuel markets. Moreover, we consider a certain number of different electricity market clearing periods in a single simulation step. In this manner, we take into account the randomness in power generation, as power output from wind and solar plants may be different in each clearing period. To model the periodicity of electricity demand. we have introduced alternately changing periods of high and low electricity demand (we model the day and night demand regimes with peaks during daytime and lows at nighttime). We do not model seasonality of demand for reasons of simplicity.
Capital goods markets
The capital goods market is a global market but with local interactions. The demand side of the market con-sists of fuel extraction, electricity generation, capital goods companies and consumer goods companies. The demand for capital goods for a company equals the planned capital increase. The supply side consists of capital goods companies. The market is modelled in a simplified way, namely, we allow for capital goods companies to first produce the necessary capital increase for their own use. Furthermore, this portion of capital is available from the beginning of the simulation step. To model the local market — market fragmentation — we implement an adaptive approach with local interactions (Assenza et al. 2015). Each customer is connected to a certain number of producers (companies). A customer first buys from the connected producer that offers the lowest price. When the total demand exceeds the total supply of a company, the demand is only partly satisfied (in the same proportion for each customer). A customer with unsatisfied demand turns to the next connected company with the second lowest price, and so on.
Consumer goods markets
The consumer goods markets are modelled in an analogous way to capital goods markets. We have global markets for all sectors other than transportation and ‘other services’, which we consider as regional markets. The demand side of the market consists of citizens.
Damages
We consider the following types of damage related to global temperature increases: diminished productivity in an agricultural sector, diminished labour supply and efficiency, and natural disasters.
Time and space
We consider \(100\) discrete simulation steps, with each step representing one year. Moreover, we consider 10 geographical regions: Africa, Japan, China, India, Rest of Asia (including Australia and New Zealand), Europe, North America, Central and South America, Commonwealth of Independent States (CIS) and the Middle East. We have used the division of the World Trade Organisation, though China, India and Japan are treated separately to en-able comparability with the following models: RICE (Nordhaus & Boyer 2000) and REMIND (Leimbach et al. 2010). Each agent is assigned to only one of the regions considered in the model, so geographical factors are only implicitly, and in a simplified way, considered in our model.
Model Details
Model implementation details are provided in this section. We assume that the simulation step \(t\) is completed (agents planned their actions and visited all relevant markets where they interacted) and we discuss the next simulation step \(t+1\).
Citizens (private households)
In each step, a citizen first updates their state with the consequences of their market interactions with other agents (in the simulation step \(t\)). Then they plan their actions in the next period (in simulation step t+1). In particular, the agent collects a dividend, which is calculated as the sum of companies’ financial results in the simulation period \(t\) multiplied by the share of capital the agent holds in these companies, see Equation 2, where \(h_j^t\) is capital share in a company \(j\) and \(\pi_j^t\) its profit in period \(t\).
| $$\pi^t = \sum_{j=1}^{J} h_j^t \pi_j^t$$ | (2) |
Moreover, an agent similarly calculates the total expenditure for consumer goods as a sum of quantities of goods purchased and eventually consumed in the period \(t\) multiplied by their purchase prices, see Equation 3, where \(x_i\) is a quantity of good \(i\) consumed in period \(t\), and \(p_i^t\) its price.
| $$c^t = \sum_{i=1}^{n} x_i^t p_i^t$$ | (3) |
Then the savings from the previous period \(s_{t-1}\) are updated with the dividends and wages received, and the money spent on consumption in the simulation period \(t\), see Equation, where \(w^t\) is the wage earned over a period \(t\):
| $$s^t = s^{t-1} + w^t + \pi^t - c^t$$ | (4) |
In the planning phase, the agent first plans the prices. This is done in a simplified way by setting the planned price for the period \(t+1\) equal to the actual price observed in a period \(t\), namely setting \(\widetilde{p}^{t+1}_i= p^t_i\) for all goods other than electricity[3]. In the case of electricity, the planned price is calculated as an exponentially weighted moving average, with a parameterized weight \(w_{\textrm{el}}\).
| $$\widetilde{p}^{t+1}_{\textrm{el}} = w_{\textrm{el}} p^{t}_{\textrm{el}} + (1-w_{\textrm{el}}) \widetilde{p}^{t}_{\textrm{el}}$$ | (5) |
The agent then plans a total income during the period \(t+1\). Forecasts of both wage income and dividend payments are based on the current period values, increased in line with the forecasted GDP growth rate. Planned dividend income is calculated according to Equation 6.
| $$\widetilde{\pi}^{t+1} = \pi^t \times (1+ f_{\textrm{gdp}})$$ | (6) |
Additionally, the next period wage forecast also takes the regional unemployment rate into consideration. Namely, we assume that an unemployment rate value higher than \(s_{\textrm{unemp}}\), which is a simulation parameter, reduces the next period wage forecast to the value of the current period. For an unemployment rate equal to 0%, the next period wage forecast is calculated similarly to that of dividend income (planned wage growth rate is equal to planned GDP growth rate). For intermediate values of the unemployment rate — between 0% and \(s_{\textrm{unemp}}\), the planned wage growth rate is proportionally (linearly) decreased. Here we capture the stylized fact that the oversupply of the labour force reduces the increase in the price of labour (wage). We also assume that citizens always plan for a non-negative GDP growth rate in the susbequent period.
| $$\widetilde{w}^{t+1} = w^t \times (1+ f_{\textrm{unemp}} \times f_{\textrm{gdp}})$$ | (7) |
Eventually, the wage value will be increased using the nominal GDP growth rate \(r_{\textrm{gdp}}\) in the simulation period \(t+1\). As this variable can take on negative values (actual growth can be negative), some modifications are necessary. In particular, the factor \(f_{\textrm{unemp}}\) is modified for actual negative GDP growth rates in such a way that an unemployment rate higher than \(s_{\textrm{unemp}}\), which a simulation parameter, leads to a current period wage decrease equal to \(r_{\textrm{gdp}}\); an unemployment rate of 0% leads to no changes in the current wage and for intermediate (between 0% and \(s_{\textrm{unemp}}\)) values of the unemployment rate, the current wage reduction is determined by linear interpolation.
The agent also calculates planned total minimum consumption expenditure, see Equation 8.
| $$\widetilde{c}^{t+1}_{\textrm{min}} = \sum_{i=1}^{n} x_i^{\textrm{min}} \widetilde{p}_i^{t+1}$$ | (8) |
Accordingly, the total minimum income available (such an income that enables just a minimum consumption for a given propensity to consume value, modelled using a propensity to consume parameter – \(a\)) is planned, see Equation 9:
| $$\widetilde{i}^{t+1}_{\textrm{min}} = \left(\widetilde{c}^{t+1}_{\textrm{min}}\right)^{1/a}$$ | (9) |
A household \(l\) plans total available income \(\widetilde{i}^{t+1}\) as the sum of planned wage income and planned dividend payments, see Equation 10.
| $$\widetilde{i}^{t+1} = max(\widetilde{w}^{t+1} + \widetilde{\pi}^{t+1},\widetilde{i}^{t+1}_{\textrm{min}} )$$ | (10) |
Then a citizen \(l\) decides on the next period’s planned total consumption level, depending on the propensity to consume \(a \in [0,1]\), in two steps, see Equations 11 and 12. In the first step, planned consumption for period \(t+1\) is calculated as a certain proportion of the planned income for period \(t+1\).
| $$\widetilde{c}^{t+1}_0 = \left(\widetilde{i}^{t+1}\right)^{a}$$ | (11) |
In the second step, the overall consumption level is corrected by the savings component (cash at hand) by adding:
| $$\widetilde{c}^{t+1} = max(\widetilde{c}^{t+1}_0 + \alpha_{\textrm{savings}} \times \left(s^{t} - s^{0} \right), \widetilde{c}^{t+1}_{\textrm{min}})$$ | (12) |
Equation 12 represents the behaviour of households that plan to spend part of their accumulated cash by gradually increasing their planned consumption level or, conversely, plan to increase cash holdings (in the case where it is decreased) by gradually reducing planned consumption. We use a parameter \(\alpha_{\textrm{savings}}\) to model this behaviour. Note that usage of the terms ’savings’ and ’investments’ deviate from the standard economic approach: private households use savings to transfer money to the next time period, without any kind of interest accruing. The investments by private households to companies generate a dividend payment in the future. The difference between planned income and planned consumption gives the values of planned total investments, see Equation 13.
| $$\widetilde{o}^{t+1} = \widetilde{i}^{t+1} - \widetilde{c}^{t+1}$$ | (13) |
In the next step, total planned consumption is decomposed into different types of goods. As noted in the introduction, we model seven consumer goods sectors, such that \(n = 7\). For this purpose we assume that private household preferences are represented by a Stone-Geary utility function (Stone 1954) with \(n\) consumer goods:
| $$U_{l}(x_{1},\dots, x_{n})=\prod_{i=1}^{n}(x_i-x_i^{min}) ^{\alpha_i}\\$$ | (14) |
| $$\widetilde{x}^{t+1}_k = x_k^{min} + \alpha_k/ \widetilde{p}^{t+1}_k \times (\widetilde{c}^{t+1} - \sum_{i=1}^{n} x_i^{min} \widetilde{p}^{t+1}_i ), \forall k\in \{1,\dots, n\} \\$$ | (15) |
Hence, given that all basic needs \(x_{k}^{min}\) are fulfilled, the remaining amount for consumption, \(\widetilde{c}^{t+1} - \sum x_i^{min} \widetilde{p}^{t+1}_i\), is spent according to the ratio of the preference weighting \(\alpha_k\) and the planned price \(\widetilde{p}^{t+1}_k\).
The planned total energy consumption \(\widetilde{x}^{t+1}_7 = x_{ec}\) is first decomposed into electricity and energy from fuels, and then the energy obtained directly from fuels is further decomposed into energy from coal (solid fuel), gas (gaseous fuel) and crude oil (liquid fuel), using the nested Constant Elasticity of Substitution (CES) functions (we further skip indexation by period \(t+1\) for the sake of clarity ):
| $$x_{e} = ((\eta_{el} x_{el})^{\rho_{e}} + (\eta_f x_f)^{\rho_{e}})^{1/\rho_{e}} \\$$ | (16) |
| $$x_f = ((\eta_{coal} x_{coal})^{\rho_f} +(\eta_{gas} x_{gas})^{\rho_f}+(\eta_{oil} x_{oil})^{\rho_f} )^{1/\rho_f} \\$$ | (17) |
| $$x_{el} = \frac{x_e}{\eta_{el}} \times \frac{{\left(\frac{p_{el}}{\eta_{el}}\right)}^{\frac{1}{\rho_{e}-1}}} {{\left({\left(\frac{p_{el}}{\eta_{el}}\right)}^{\frac{\rho_{e}}{\rho_{e}-1}} + {\left(\frac{p_{f}}{\eta_{f}}\right)}^{\frac{\rho_{e}}{\rho_{e}-1}} \right)}^\frac{1}{\rho_{e}}}$$ | (18) |
Capital decisions are modelled in the following simplified way. The planned capital investments \(\widetilde{o}^{t+1}\) are divided by a citizen into separate companies \(j\) based on the current portfolio of shares in different companies and the values of the companies’ planned capital increase, according to Equation 19.
| $$\widetilde{o}^{t+1}_j=\frac{h_j^t \widetilde{\Delta k}^{t+1}_j}{\sum_{i=1}^{J} h_i^t \widetilde{\Delta k}^{t+1}_i} \times \widetilde{o}^{t+1}$$ | (19) |
\(\widetilde{o}^{t+1}_j\) stands for the total value of new capital that is planned for investment in company \(j\) in the next period \(t+1\) by a private household. \(h_j^t\) is the current share of the total capital invested in company \(j\) that is owned by a particular citizen. In general, a company may be owned by many citizens. \(\widetilde{\Delta k}^{t+1}_j\) is the total (physical) capital increase planned by company \(j\) in the period \(t=1\). Its value is calculated by multiplying with \(\bar{p}_{pg}^t\), which is the average price of the capital goods in period \(t\) in the simulation. The symbol \(\widetilde{o}^{t+1}\) denotes total planned investments in the period \(t+1\). This mechanism represents a simplification and captures the fact that the planned investments in company \(j\) is proportional to the company’s capital requirements and the value of current capital already invested in the company (ownership 'bias').
Consumer goods company
In each step, a consumer goods company first updates its state with the consequences of the market interactions with other agents (in the already completed simulation step \(t\)). Then it plans its actions for the next period (in simulation step \(t+1\) which just began, all agents first plan their actions). Firstly, the financial result based on cash flow is calculated by deducting variable production costs from revenues, as shown in Equation 20, where \(d^t\) is the total demand in period t, \(y^t\) is the total production in the same period, \(\textrm{st}^{t-1}\) represents stocks at the end of the given period \(t-1\), \(p^t\) is the unit price, \(\bar{w}^t\) the average wage offered, \(l^t\) the number of employees, \(e^t\) the total energy used in period \(t\) and \(p_e^t\) the mean price of this energy.
| $$\pi^t_0 = p^t min\left(d^t,y^t - (\textrm{st}^{t} - \textrm{st}^{t-1})\right) - \bar{w}^tl^t - p_e^t e^t$$ | (20) |
Moreover, the cash surplus is calculated as the difference between money for investments collected from citizens in period \(t\) and the value of the actual investments — the difference between capital value after depreciation at the end of period \(t-1\) and the capital value before depreciation at the end of period \(t\) — in this period \(\Delta \textrm{kv}^t = \textrm{kv}^t - \textrm{kv}_d^{t-1}\), as shown in Equation 21, where \(\widetilde{o}^{t}_{ji}\) is the money planned for investment in company \(j\) by citizen \(i\) in period \(t\).
| $$\pi^t_1 = \sum_{i=1}^{i=m} \widetilde{o}^{t}_{ji} - \Delta \textrm{kv}^t$$ | (21) |
The total dividend to be distributed among owners in period \(t\) is calculated as the sum of \(\pi^t = \pi^t_0 + \pi^t_1\).
A company also calculates the average production cost as Equation 22
| $$\bar{c}_p^t = \frac{\bar{w}^tl^t + p_e^t e^t}{y^t}$$ | (22) |
Depending on the relation of the current price \(p^t\) to the average market price \(\bar{p}^t\) and of demand \(d^t\) to production \(y^t\) and the average production cost \(\bar{c}_p^t\), the planned price and production in the next period \(t+1\) are adjusted in the following way, see (Assenza et al. 2015):
- if \(p^t \le \bar{p}^t\) and \(d^t < y^t\) then production is decreased
- if \(p^t \le \bar{p}^t\) and \(d^t \ge y^t\) then price is increased
- if \(p^t > \bar{p}^t\) and \(d^t < y^t\) then price is decreased
- if \(p^t > \bar{p}^t\) and \(d^t \ge y^t\) then production is increased
As an example, the necessary adjustments are shown in Equation 23 for the first case and Equation 24 for the second case, where \(\nu\) is a uniformly distributed random variable. \(f_{\textrm{price}}\) and \(f_{\textrm{prod}}\) are the simulation parameters. Additionally, \(f_{\textrm{price}}\) limits the maximum price increase. This additional restriction limits excessive price fluctuations resulting from changes in the prices of production prices (it expresses a certain level of conservatism in the price-setting mechanism by companies).
| $$\begin{split} \widetilde{p}^{t+1} = \textrm{min}(\textrm{max}(p^t,\bar{c}^t ),p^t(1+f_{\textrm{price}})) \\ \widetilde{y}^{t+1} = y^t (1+f_{\textrm{gdp}}) (1+f_{\textrm{prod}} \nu) \end{split}$$ | (23) |
| $$\begin{split} \widetilde{p}^{t+1} = \textrm{min}(\textrm{max}(p^t (1+f_{\textrm{price}}\nu),\bar{c}^t ),p^t(1+f_{\textrm{price}})) \\ \widetilde{y}^{t+1} = y^t (1+f_{\textrm{gdp}}) \end{split}$$ | (24) |
Other prices are planned similarly to the case of households, see Equations 7 and 5. The cost of capital is set to the value of the depreciation rate \(f_{\textrm{depr}}\). At the end of each period, capital is depreciated according to the formula in Equation 25.
| $$k_d^t = k^t \times (1-f_{\textrm{depr}})$$ | (25) |
The production function is a CES function with the following production factors: capital \(k\), labour \(l\) and energy, denoted by symbol \(e\):
| $$y_j = ((\eta_{k} k)^{\rho_y} +(\eta_{l} l)^{\rho_y}+(\eta_{e} e)^{\rho_y} )^{1/\rho_y} \\$$ | (26) |
The company minimises its production cost given the planned production in the next period \(\widetilde{y}^{t+1}\) and the assumed values of the CES production function. The quantities of the necessary production factors — capital, labour and energy — are shown in Equation 27.
| $$\begin{split} d={\left({\left(\frac{f_{\textrm{depr}}}{\eta_{k}}\right)}^{\frac{\rho_{y}}{\rho_{y}-1}} + {\left(\frac{\widetilde{w}^{t+1}}{\eta_{l}}\right)}^{\frac{\rho_{y}}{\rho_{y}-1}} + {\left(\frac{\widetilde{p}_e^{t+1}}{\eta_{e}}\right)}^{\frac{\rho_{y}}{\rho_{y}-1}} \right)}^\frac{1}{\rho_{y}} \\ \widetilde{k}^{t+1}= \frac{\widetilde{y}^{t+1}}{\eta_{k}} \times \frac{{\left(\frac{f_{\textrm{depr}}}{\eta_{k}}\right)}^{\frac{1}{\rho_{y}-1}}}{d} \\ \widetilde{l}^{t+1}= \frac{\widetilde{y}^{t+1}}{\eta_{l}} \times \frac{{\left(\frac{\widetilde{w}^{t+1}}{\eta_{l}}\right)}^{\frac{1}{\rho_{y}-1}}}{d} \\ \widetilde{e}^{t+1}= \frac{\widetilde{y}^{t+1}}{\eta_{e}} \times \frac{{\left(\frac{\widetilde{p}_e^{t+1}}{\eta_{e}}\right)}^{\frac{1}{\rho_{y}-1}}}{d} \\ \end{split}$$ | (27) |
Energy demand for electricity and energy from solids (coal, gas and oil) is modelled by the nested CES function in a similar way to that of private households. The company minimises its production and energy cost, providing the required level of planned production.
A consumer goods company goes bankrupt if it is not able to continue production. This may result from lack of demand or lack of necessary production factors. In this case, the owners cover possible losses.
Capital goods company
Capital goods companies are subject to similar mechanisms as consumer goods companies. The major difference is that the company may produce the physical capital (production factor) for its own use.
Fuel extraction company
The fuel extraction company in our model is fundamentally subject to similar mechanisms as the consumer goods company. Therefore, we will limit the description here to the specific differences relative to consumer goods companies. Since the fuel extraction sector is generally considered to be strategic by governments, and it is typically either heavily regulated or state-owned, we model the fuel extraction company in a simplified way. First, we assume that there is only one extraction company per geographical region and fuel type. Second, we assume that the marginal fuel extraction costs (and thus the fuel price also) depend on the cumulative extrac-tion. This relation may be expressed as a Rogner curve (Nordhaus & Boyer 2000). We model extraction company production using the calibrated Rogner curve, as done in the MIND model, (Edenhofer et al. 2005). To be more precise, the marginal fuel extraction costs are given by Equation 28, where \(\chi_1\), \(\chi_2\), \(\chi_3\) and \(\chi_4\) are the parameters of the calibrated Rogner curve. The parameters \(\chi_1\) and \(\chi_3\) both have a straightforward economic interpretation. Namely, \(\chi_1\) is the initial (at the beginning of the simulation) price of the fuel and \(\chi_3\) equals the total regional fuel reserves remaining. \(Y\) is the accumulated fuel resource extraction since the simulation began.
| $$c_m =\chi_1 + \chi_2 \left({\frac{Y}{\chi_3}}\right)^{\chi_4}$$ | (28) |
Third, we assume that the fuel extraction company holds more capital than required to extract the planned amount of fuel, and maintains production reserves. For example, similar behaviour can be observed for OPEC countries, where the production potential is higher than current production.
The financial result — based on cash flow — is calculated as shown in Equation 29, where \(d^t\) represents total demand in period t, \(y^t\) is total production in the same period, \(\textrm{st}^{t-1}\) represents the stocks available at the end of the given period \(t-1\), \(p^t\) is the unit price, \(\bar{w}^t\) the average wage offered, \(l^t\) denotes number of employees, and \(\textrm{sub}^t\) is the sum of the subsidy granted to the local power plant fired with this particular type of fuel.
| $$\pi^t_0 = p^t \textrm{min}\left(d^t,y^t-(\textrm{st}^{t} - \textrm{st}^{t-1})\right) - \bar{w}^t l^t - \textrm{sub}^t$$ | (29) |
In the Middle East and Asia regions the observed electricity prices are at such a low level that they do not even cover the costs of fossil fuels used for their production. Local power plants can buy the fuels (gas and crude oil) below the world market price. We model this observation by moving part of the earnings from fuel extraction companies to the regional electricity companies in the form of subsidies.
Due to the long investment period applicable to this particular sector, we assumed that the fuel extraction company plans the necessary capital allocation one period ahead[4] depending on actual demand in period \(t\), denoted \(d^t\), initially planned demand for period \(t\), denoted \(\widetilde{d}^t\), and a forecast GDP growth rate for the second consecutive period, denoted \(f^1_{\textrm{gdp}}\). Additionally, \(\nu\) is a uniformly distributed random variable and \(f_{\textrm{prod}}\) is the simulation parameter. The company wants to increase the amount of physical capital available if the actual demand is higher than what was initially planned or decrease it otherwise. The prolonged investment period enables the fuel markets to clear before capital goods markets during the simulation.
| $$\begin{split} d^t<\widetilde{d}^t: \widetilde{k}^{t+1} =k^t (1+f^1_{\textrm{gdp}}) (1- \nu f_{\textrm{prod}} ) \\ d^t=\widetilde{d}^t: \widetilde{k}^{t+1} =k^t (1+f^1_{\textrm{gdp}}) \\ d^t>\widetilde{d}^t: \widetilde{k}^{t+1} =k^t (1+f^1_{\textrm{gdp}}) (1+ \nu f_{\textrm{prod}}) \\ \end{split}$$ | (30) |
Then the production supply and demand prices for period \(t+1\) are planned in five steps.
- The current value of the marginal extraction cost \(c_m^t\) is calculated according to Equation 28. Second, the planned production for period t+1 is calculated as given in Equation 31
| $$\widetilde{y}^{t+1}_j = \frac{\chi_1}{c_m^t} \times k^{t} \times \textrm{kp} \times (1-\textrm{rr})$$ | (31) |
- We initially considered the individual and independent fuel extraction for each region. However different regional values for the ratio: total accumulated fuel extraction to initial (at simulation start) total fuel reserves remaining (fuel reserve depletion rates) observed in the different regions led to different planned prices between regions. Generally, we can expect that more easily accessible fuel deposits will be extracted first. As the fuel markets are global, we can also expect that fuel extraction will have an additional tendency to move from regions with higher depletion rates to those with lower depletion rates. We model this observation by additionally multiplying planned production by the factor defined by Equation 32, where \(j\) denotes a region, \(J\) is the number of fuel extraction companies, \(y_j\) denotes for planned fuel extraction, \(Y_j^t/\chi_{3,j}\) is the regional exhaustion rate and \(\textrm{con}_{\textrm{fuel}}\) the extraction convergence factor, which is used as a simulation parameter. At the end of the process, the planned production values are proportionally adjusted so that global planned production, before and after scaling with the factor defined in Equation 32, remains the same.
| $$1 + \left(\frac{\sum_{j=1}^{J} \widetilde{y}^{t+1}_j \times \frac{Y_j^t}{\chi_{3,j}}}{\sum_{j=1}^{J}\widetilde{y}^{t+1}_j} - \frac{Y_j^t}{\chi_{3,j}} \right) \times \textrm{con}_{\textrm{fuel}}$$ | (32) |
- The maximum production in period \(t+1\) is calculated as in Equation 33.
| $$\widetilde{y}_{\textrm{max}}^{t+1} = \frac{\widetilde{y}^{t+1}}{1-\textrm{rr}}$$ | (33) |
- The planned price is set to the current value of the marginal extraction cost \(\widetilde{p}^{t+1}=c_m^t\).
- Planned demand is set to the value of planned production \(\widetilde{d}^{t+1} = \widetilde{y}^{t+1}\).
The number of employees remains constant until all available resources are exhausted. This is a simplifying assumption, since labour is not explicitly used as a production factor but is only assigned, based on the empirical values for each individual company. The fuel extraction company goes bankrupt if all the resources are exhausted. In this case, the owners cover possible losses.
Electricity company
We consider the following power plant (electricity producer) types: coal, gas, oil, nuclear, hydro, wind, and solar. Each power plant is characterised by a total capacity \(c_p^t\), an additional term for storage capacity \(c_s^t\) in the case of solar and wind power plants, a lifetime that is dependent on power plant type \(T\), a capacity factor \(f_{\textrm{capacity}}\) giving the average percentage of time a given power plant is available, an operations and management cost factor \(f_\textrm{om}\) (refers to the total electricity produced before transmission losses and depends on the power plant type), electricity transmission loss factor \(f_{\textrm{eloss}}\) and the conversion efficiency \(f_\textrm{conveff}\) — the percentage of primary energy in fuel converted to electricity. A lifetime \(T\) is used for explicit modelling of the ageing of the installed capacities — each part of the installed power plant capacity is characterised by age and is removed (depreciated) at the age of \(T\).
For each simulation step, we consider \(N_e\) electricity market sub-steps with separate clearing. We use finer time gradations for electricity markets in order to model the stochastic power generation profiles for different power plant types. First, at the beginning of the simulation step, a power plant updates the total electricity produced (corrected for electricity transmission losses) in step \(t\), denoted \(y^t\), see Equation 34 and the average price, denoted \(\bar{p}^t\).
| $$\begin{split} y^t=\sum_{i=1}^{N_e} y_i^t \\ y^t_{\textrm{max}}=max(y_1^t,y_2^t,...,y_{N_e}^t) \\ \end{split}$$ | (34) |
| $$\begin{split} y_t>0: \bar{p}^t=\frac{\sum_{i=1}^{N_e} y_i^t p_i^t}{\sum_{i=1}^{N_e} y_i^t} \\ y_t = 0: \bar{p}^t=\frac{\sum_{i=1}^{N_e} p_i^t}{N_e} \\ \end{split}$$ | (35) |
The financial result — based on cash flow — is calculated as the difference between income and production cost, details are presented in Equation 36, where \(f_{\textrm{om}}\) is operations and management cost factor, \(x_f^t\) the fuel used for electricity production, and \(p_f^t\) its price. \(x_s^t\) denotes settlement cost, which is discussed later in greater detail. We assumed that in such regions as the Middle East and Asia, gas and crude oil prices used for electricity production are subsidised, with \(f_{\textrm{sub}}\) being the subsidy rate.
| $$\pi^t_0 = y^t \bar{p}^t - \frac{y^t}{1-f_{\textrm{eloss}}} f_{\textrm{om}} - p_f^t (1-f_{\textrm{sub}}) + x_s^t$$ | (36) |
There are more power plants (the number of power plants in the simulation was decided according to typical power plant capacity) than citizens[5] working in the electricity sector in the simulation model. In order to avoid the partial allocation of employees to specific power plants, citizens are only allocated to the electricity sector as a whole but not to a particular power plant. Such a partial allocation of employers would represent the possibility of a citizen working in many power plants simultaneously, which we avoided for reasons of simplicity. As a consequence, the operations and management (O&M) cost at the power plant level are calculated in a different way than for the sector as a whole — as the product of O&M factors and energy produced in the former case, and as a sum of the wages of all citizens employed in the sector in the latter. Therefore, these two values may be different. The consideration of settlement cost eliminates this difference (details are given below). For a given company \(k\), \(x_{s,k}^t\) denotes a cost settlement in period \(t\), which gives the difference between the total O&M cost and the total labour cost for the entire power sector, in a given region, allocated based on the O&M cost of company \(k\), see Equation 37.
| $$\begin{split} \textrm{om}_j = \frac{y^t_j}{1-f_{\textrm{eloss},j}} f_{\textrm{om,j}}\\ x_{s,k}^t= \left(\sum_{j=1}^{J} \textrm{om}_j - \bar{w}^t l^t \right) \frac{\textrm{om}_k}{\sum_{j=1}^{J} \textrm{om}_j} \end{split}$$ | (37) |
Additionally, we define for each region the ratio of total labour cost in the electricity sector to total O&M cost, denoted \(r_{\textrm{om}}^t\), see Equation 38.
| $$r_{\textrm{om}}^t= \frac{\bar{w}^t l^t }{\sum_{j=1}^{J} \textrm{om}_j}$$ | (38) |
If the ratio \(r_{\textrm{om}}^t > 1\), the total labour cost in electricity sector is higher than the total O&M cost, and values of the factors \(f_{\textrm{om,j}}\) are adjusted for the next simulation step, in the manner defined in Equation 39, where the adjustment factor \(f_{\textrm{omadj}}\) is a simulation parameter. The factor \(f_{\textrm{om,j}}\) enables a smoother adjustment process.
| $$f_{\textrm{om,j}}^{t+1} = f_{\textrm{om,j}} \left(1 + f_{\textrm{omadj}} (r_{\textrm{om}}^t -1) \right)$$ | (39) |
Each power plant type is characterised by an overnight investment cost (USD/1kW). Additionally, for solar and wind energy we allow for a learning process that is modelled by a learning rate and the floor overnight investment cost. Thus for these plant types, the current overnight investment cost, \(\textrm{OIC}_\textrm{t}\), is defined in Equation 40 (as in the MIND model (Edenhofer et al. 2005)).
| $$\textrm{OIC}_\textrm{t} = \textrm{OIC}_\textrm{floor} + (\textrm{OIC}_\textrm{initial} - \textrm{OIC}_\textrm{floor}) \times \left(\frac{\textrm{TIC}_\textrm{t}}{\textrm{TIC}_\textrm{initial}}\right)^\textrm{lr}$$ | (40) |
\(\textrm{OIC}_\textrm{floor}\) represents the floor overnight investment cost, \(\textrm{TIC}\) stands for the total installed capacity of solar or wind. Variable \(\textrm{lr}\) represents the learning rate, as it is assumed that for new technologies (solar and wind) that the more units produced the more efficient the production becomes, \(\textrm{lr}<0\). For the storage capacity, we use a simplified version, see Equation 41. Furthermore, electricity storage technology (e.g. batteries) develops independently from the storage capacity actually installed and operating in electricity grids. This is due to, for example, the rapid development of electric cars. The value of the parameter \(\textrm{lr}\) is set to \(0.99\).
| $$\textrm{OIC}_\textrm{t} = \textrm{OIC}_\textrm{floor} + (\textrm{OIC}_\textrm{t-1} - \textrm{OIC}_\textrm{floor}) \times \textrm{lr}$$ | (41) |
To be able to take into account both changing capital goods prices and changing overnight investment cost, we model physical capital as the product of capacity and the overnight investment cost, whereas capital value remains a product of physical capital and the capital goods price (actual capital expenditures). The total capital value \(\textrm{kv}^t\) and total capacity \(c_p^t\) are allocated to individual years over the power plant lifetime \(T\), see Equation 42, with \(i=1\) the oldest and \(i=T\) the newest part.
| $$\begin{split} \textrm{kv}^t=\sum_{i=1}^{T} \textrm{kv}_i^t \\ c_p^t=\sum_{i=1}^{T} c_{p,i}^t \\ \end{split}$$ | (42) |
At the end of the simulation period \(t\), capital is depreciated by liquidating the oldest part of capacity, according to the formula in Equation 43[6].
| $$\begin{split} \textrm{kv}_d^t = \textrm{kv}^t - \textrm{kv}_1^t \\ c_{pd}^t = c_p^t - c_{p,1}^t \\ \end{split}$$ | (43) |
Additionally, for solar and wind power plants a storage capacity $c_s^t$ is depreciated in a simplified standard way, Equation 44.
| $$c_{sd}^t = c_{s}^t * (1-f_{\textrm{depr}})$$ | (44) |
The planned electricity price for period \(t+1\) is set to the marginal production cost, which consists of the O&M cost in period \(t\) and the fuel price in period \(t\) (a power plant does not forecast changes in fuel prices), if relevant for the power plant type, and is given by Equation 45.
| $$\widetilde{p}^{t+1}_j = \frac{f_{\textrm{om,j}}^{t+1} + \frac{p_f^t}{f_\textrm{conveff}} (1-f_{\textrm{sub}})}{1-f_{\textrm{eloss},j}}$$ | (45) |
The planned electricity available over a given time period \(\widetilde{y}^{t+1}_j\) is calculated in different ways for different power plant types. For nuclear power plants, which are characterised by a stable operation mode, we use the deterministic approach and calculate the planned electricity produced as the product of installed capacity and the capacity availability factor, see Equation 46.
| $$\begin{split} \widetilde{y}^{t+1}_j = c_{p,j}^t f_{\textrm{capacity}} (1-f_{\textrm{eloss},j}) \Delta t \end{split}$$ | (46) |
For all the other types of power plants, the energy available in the current period is modelled with a beta distribution (Gupta & Nadarajah 2004) with parameters \(\alpha\) and \(\beta\). This expresses the fact that for solar and wind energy power plants the actual energy produced is stochastic and depends on the weather conditions, whereas for other power plant types the stochasticity is related to necessary downtime related to maintenance. The parameter values are given in Equation 47. The parameters are set in such a way that the mean availability equals the capacity factor — \(f_{\textrm{capacity}}\).
| $$\begin{split} \alpha = 2 \\ \beta = \alpha \times \frac{1 - f_{\textrm{capacity}}}{ f_{\textrm{capacity}}} \\ \end{split}$$ | (47) |
Then for all other types of power plants, with the exception of solar power plants, electricity available in a given time period \(\widetilde{y}^{t+1}_j\) is then calculated according to Equation 48. \(F^{-1}_{\alpha,\beta}\) is an inverse cumulative probability distribution function having a Beta distribution with the parameters \(\alpha\) and \(\beta\), and \(\nu\) is a uniformly distributed random variable.
| $$\begin{split} \widetilde{y}^{t+1}_j = c_{p,j}^t F^{-1}_{\alpha,\beta}(\nu) (1-f_{\textrm{eloss},j}) \Delta t \end{split}$$ | (48) |
For solar power plants, electricity available in a given time period \(\widetilde{y}^{t+1}_j\) is calculated according to Equation 49, in order to take into account the fact that solar energy is only available during daylight.
| $$\begin{split} \textrm{day}: \widetilde{y}^{t+1}_j = 2 c_{p,j}^t F^{-1}_{\alpha,\beta}(\nu) (1-f_{\textrm{eloss},j}) \Delta t \\ \textrm{night}: \widetilde{y}^{t+1}_j = 0 \\ \end{split}$$ | (49) |
Additionally, for solar and wind energy power plants the amount of available energy is increased by the amount of stored energy multiplied by \((1-f_{\textrm{eloss},j})\). The maximum electricity available in a given time period is calculated according to Equation 50 for coal, gas, oil, and nuclear power plants, thus allowing for an additional capacity reserve, calculated using the reserve rate \(r_{\textrm{spin}}\).
| $$\begin{split} \widetilde{y}^{t+1}_{\textrm{max},j} = \widetilde{y}^{t+1}_j (1+r_{\textrm{spin}}) \end{split}$$ | (50) |
In each period a certain share of capacity, which is as old as the power plant lifetime[7], is replaced with planned investments. The decision depends on whether the power plant capacity after depreciation would be able (on average) to cover the maximum demand in the next simulation step. For the condition to be verified (Equation 51), the following parameters need to be taken into account for this decision: the required capacity reserve (\(r_{\textrm{cap}}\)), the spinning reserve for fuels power plants (\(r_{\textrm{spin}}\)), and a time slice (\(\Delta t\)).
| $$c_{pd}^t (1-f_{\textrm{eloss}}) \times \Delta t \times f_{\textrm{capacity}} > y^t_{\textrm{max}} (1+f^1_{\textrm{gdp}}) (1 + r_{\textrm{cap}}) (1+r_{\textrm{spin}})$$ | (51) |
Let us assume that the condition, given in Equation 51 is satisfied. In this case, the total installed capacity will be gradually decreased. The planned partial replacement \(\Delta c_{p}^t\) is given by Equation 52, where \(e_{\textrm{down}}\) and \(e_{\textrm{freeze}}\) are simulation parameters, and \(\nu\) is a uniformly distributed random variable.
| $$c_{pd}^t (1-f_{\textrm{eloss}}) \times \Delta t \times f_{\textrm{capacity}} > y^t_{\textrm{max}} (1+f^1_{\textrm{gdp}}) (1 + r_{\textrm{cap}}) (1+r_{\textrm{spin}})$$ | (52) |
The parameter \(e_{\textrm{freeze}}\) is calculated according to Equation 53, based on the simulation parameter values \(\textrm{red}\) and \(\textrm{period}\).
| $$e_{\textrm{freeze}} = e_{\textrm{red}}^{\lfloor{\frac{\textrm{step}}{\textrm{period}}}\rfloor}$$ | (53) |
This limits the magnitude of the changes in the electricity market structure occurring over a fixed number of periods (denoted by \(\textrm{period}\)) by using the reduction rate value \(e_{\textrm{red}}\) (without this factor, one would obtain geometric growth rates of capacities and potential overinvestment in later simulation steps). Let us now assume that the condition given in Equation 51 is not satisfied.In this case, the total installed capacity will be gradually increased, and the planned replacement \(\Delta c_{p}^t\) is calculated according to Equation 54.
| $$\left(c_{p}^t-c_{pd}^t \right) \left(1 + \textrm{max}(1,e_{\textrm{up}} e_{\textrm{freeze}}) f_{\textrm{prod}} \nu\right)$$ | (54) |
\(e_{\textrm{up}}^{\textrm{w}}\), nuclear and hydro \(e_{\textrm{up}}^{\textrm{nh}}\). This allows us to capture differences in constraints for different power plants (e.g. natural, as in the case of hydro, or political, as in case of nuclear). In the case of the following regions (Africa, Commonwealth of Independent States, and Middle East), the initial wind and solar power plant capacities are negligibly low, so for these regions the replacement rate for wind and solar power plants is defined by a constant \(e_{\textrm{up}}^{\textrm{af}}\). Finally, total planned capacity is adjusted by the planned GDP growth rate for the second consecutive period, see Equation 55.
| $$\widetilde{c}_{p}^{t+1} = \left(c_{p}^t+ \Delta c_{p}^t \right)(1+f^1_{\textrm{gdp}})$$ | (55) |
Additionally, solar and wind energy companies may also invest in storage capacity (apart from investments in power capacity). We assume that a company will invest in storage capacity if storing the energy is more profitable than additional potential energy production. This means that instead of selling the energy to the market when electricity prices are relatively low, the solar (wind) power plant could store the energy and sell it when electricity prices are relatively high. We capture this idea by assuming that the company invests in storage capacity based on the distribution of historical market electricity prices. This applies when the ratio of the interquartile range of electricity prices to the current overnight investment cost of storage capacity is higher than twice the ratio of the average electricity price to the current overnight investment cost of power capacity, see Equation 56. We assumed that energy can be stored in one period and used in the subsequent period.
| $$\frac{2\bar{p}^t}{\textrm{OIC}_p} < \frac{p^t_{\textrm{Q3}}-p^t_{\textrm{Q1}}} {\textrm{OIC}_s}$$ | (56) |
The total planned storage capacity is then calculated according to Equation 57.
| $$\widetilde{c}_s^{t+1} = max\left(c_s^t (1+f_{\textrm{prod}}\nu), \frac{c_p^t}{T}\right)\left(1+f^1_{\textrm{gdp}}\right)$$ | (57) |
Otherwise, it is calculated according to Equation 58.
| $$\widetilde{c}_s^{t+1} = \left(c_s^t (1-f_{\textrm{prod}}\nu)\right)\left(1+f^1_{\textrm{gdp}}\right)$$ | (58) |
The power plant plans the required fuel stocks for the next period \(t+1\) in a simplified way. The planned amount is, based on the previous period production, forecasted GDP growth rate and necessary stock rate \(r_{\textrm{cap}}\), see Equation 59. \(s_f^t\) are the stocks left from the previous period.
| $$\widetilde{s}_f^{t+1} = \textrm{max}\left(\frac{y^t}{f_{\textrm{conveff}}}(1 + r_{\textrm{cap}}) (1+f_{\textrm{gdp}}),s_f^t\right)$$ | (59) |
For fuel-fired (coal, gas, oil) power plants, we also take into consideration limitations due to the fuel stocks currently available for electricity production in a given simulation step.
Market Clearing Mechanisms
This section provides a detailed discussion of market clearing mechanisms, which are examined in the following order:
- Capital markets
- Labour markets
- Fuel markets
- Electricity markets
- Capital goods markets
- Consumer goods markets
Capital markets
As mentioned earlier, a capital market is demand driven and is modelled in a simplified way. Let us consider a simulation period \(t+1\) and a given region. We consider all \(I\) citizens living in this region, indexed by \(i\), and all \(J\) companies from this region, indexed by \(j\). First, the capital raised by company \(j\) is calculated as the sum of new capital that is planned for investment in company \(j\) in the next period \(t+1\) by citizens (denoted \(\widetilde{o}^{t+1}_{i,j}\) for citizen i, see also Equation 19, see Equation 60.
| $$\widehat{\Delta \textrm{kv}}^{t+1}_j = \sum_{i=1}^{I} \widetilde{o}^{t+1}_{i,j}$$ | (60) |
Second, citizens' shares in companies are updated. According to Equation 61, the new capital ratio \(r^{t+1}_{\textrm{ni},j}\) is calculated, where \(\textrm{kv}^t_j\) is the current capital value and \(s^t_j\) the current cash at hand value.
| $$r^{t+1}_{\textrm{n},j} = min\left(\frac{\widehat{\Delta \textrm{kv}}^{t+1}_j}{\widehat{\Delta \textrm{kv}}^{t+1}_j +\textrm{kv}^t_j + s^t_j},1\right)$$ | (61) |
Then, citizens’ shares in a company (\(h_{i,j}^{t+1}\) denotes a capital share of a citizen \(i\) in a company \(j\) in a simulation period \(t\)) are updated as a weighted mean of new capital and existing capital owned by company \(j\), as presented in Equation 62.
| $$h_{i,j}^{t+1} = r^{t+1}_{\textrm{n},j} \frac{\widetilde{o}^{t+1}_{i,j}}{\widehat{\Delta \textrm{kv}}^{t+1}_j} + (1-r^{t+1}_{\textrm{n},j}) h_{i,j}^{t}$$ | (62) |
The planned capital value increase in period \(t+1\), denoted as \(\widetilde{\Delta \textrm{kv}}^{t+1}_j\) is limited from above by the value of the capital raised \(\widehat{\Delta \textrm{kv}}^{t+1}_j\). \(\widetilde{\Delta \textrm{kv}}^{t+1}_j\) is calculated for a company as the difference between planned physical capital, necessary for production in the period \(t+1\), and the available physical capital at the beginning of simulation period \(t+1\), multiplied by the expected price of the production goods. The difference between collected capital \(\widehat{\Delta \textrm{kv}}^{t+1}_j\) and the increase in actual total capital in period \(t+1\) is subsequently distributed among owners in proportion to the number of shares held in a given company.
Labour markets
The labour market is also modelled in a simplified way. Private households looking for a job are randomly matched with companies looking for employees. In a more detailed way. First, a company for which the current labour in step \(t\) exceeds the planned labour for step \(t+1\) by at least one employee \(k^t-\widetilde{k}^{t+1}\ge1\) and having at least one employee \(k^t>1\) lays off unnecessary employees. Second, only the companies for which the planned labour[8] for step \(t+1\) exceeds the current labour[9] in step \(t\) by at least half \(\widetilde{k}^{t+1}- k^t\ge 0.5\) are considered as looking for employees. Third, unemployed citizens are randomly matched with companies looking for employees in a stepwise manner. At each single step. one unemployed citizen and one company looking for employees are selected and matched. A citizen will receive the average wage at the company. If \(\widetilde{k}^{t+1}- k^t< 0.5\), a company is no longer interested in looking for employees. The process stops if there are either no more companies looking for employees or no more unemployed citizens. In the final step, regional unemployment rates \(r_{\textrm{unemp}}^{t+1}\) are calculated and then unemployment factors, as given in Equation 63. \(s_{\textrm{unemp}}\) is a simulation parameter.
| $$f_{\textrm{unemp}}^{t+1} = 1 - \textrm{min}\left(1, \frac{r_{\textrm{unemp}}^{t+1}}{s_{\textrm{unemp}}}\right)$$ | (63) |
Moreover, as discussed earlier, since the number of power plants reflects technical considerations and not the number of citizens employed in this sector, the number of power plants is much higher than the number of employed citizens. Therefore, citizens are not directly assigned to a power plant but the labour cost is proportionally (to production) distributed among power plants. The number of electricity sector employees is kept constant during the simulation for simplicity.
Fuel markets
Fuel markets are modelled as centrally cleared markets, separately for each type of fuel \(f\): coal, crude oil and gas. The \(J\) fuel extraction companies offer the fuel at their marginal extraction cost with regular and maximum quantities. The \(I\) fuel consuming agents (citizens, consumer goods and capital goods companies, power plants) bid the quantities and accept the market price (we assume that the demand for fuels is inelastic in the short term). Total fuel demand is calculated as the sum of individual planned consumption for the fuel consuming agents (citizens as a result of utility, and consumer/capital goods companies as a result of profit maximisation) according to Equation 64. Additionally, planned fuel demand for power plants is calculated as the difference between planned fuel stocks and current fuel stocks, see Equation 65.
| $$d_f^{t+1} = \sum_{i=1}^{I} \widetilde{x}_{f,i}^{t+1}$$ | (64) |
| $$\widetilde{x}_{f,i}^{t+1} = \widetilde{s}_{f,i}^{t+1} - {s}_{f,i}^{t}$$ | (65) |
Total fuel supply is calculated as the sum of planned production (fuel extraction) of all fuel extraction companies, according to Equation 66.
| $$s_f^{t+1} = \sum_{j=1}^{J} \widetilde{y}_{f,j}^{t+1}$$ | (66) |
Total maximum fuel supply is calculated analogously by summing the planned maximum production, according to Equation 67.
| $$s_{f,max}^{t+1} = \sum_{j=1}^{J} \widetilde{y}_{f,max,j}^{t+1}$$ | (67) |
In the next step, total demand is compared with both total supply and total maximum fuel supply. We consider three separate cases. In the first case, total demand is lower or equal to the total supply; in the second case, total demand is higher than total supply but lower or equal to the maximum supply; and in the third case, total demand is higher than maximum supply.
- \(d_f^{t+1} \le s_f^{t+1}\)
- \(s_f^{t+1} < d_f^{t+1} \le s_{f,max}^{t+1}\)
- \(d_f^{t+1} > s_{f,max}^{t+1}\)
We also order the suppliers according to the offer price (marginal extraction cost), from lowest to highest, then calculate the market price \(p_f^{t+1}\) and clear transactions.
In the first of the three cases considered, the market price is calculated as the intersection point of the demand and supply curves, see Equation 68 for calculation details.
| $$\begin{split} k: \sum_{j=1}^{k-1} \widetilde{y}_{f,j}^{t+1} < d_f^{t+1} \wedge \sum_{j=1}^{k} \widetilde{y}_{f,j}^{t+1} \ge d_f^{t+1} \\ p_f^{t+1} = \widetilde{p}_{f,k}^{t+1} \\ \end{split}$$ | (68) |
Then for each fuel consuming agent, current demand in step \(t + 1\) is set to the value of planned demand \(x_{f,i}^{t+1} = \widetilde{x}_{f,i}^{t+1}\). For all producers whose planned price is lower than the market price, current production equals planned production \(y_{f,j}^{t+1} = \widetilde{y}_{f,j}^{t+1}\). For all producers with planned price equal to the market price, current production equals planned production multiplied by the factor (assures proportional reduction) defined in Equation 69, where \(k_\textrm{min} = \textrm{min}(j: \widetilde{p}_{f,j}^{t+1} = p_f^{t+1})\) and \(k_\textrm{max} = \textrm{max}(j: \widetilde{p}_{f,j}^{t+1} = p_f^{t+1})\).
| $$f_{\textrm{supply1}} = \frac{d_f^{t+1} -\sum_{j=1}^{k_{\textrm{min}}-1} \widetilde{y}_{f,j}^{t+1} }{\sum_{j=k_{\textrm{min}}}^{k_{\textrm{max}}} \widetilde{y}_{f,j}^{t+1}}$$ | (69) |
For producers having a planned price higher than the market price, the current production equals \(0\).
In the second case, the market price equals the planned price of the producer having the highest planned price. Additionally, it might have been increased by multiplication with the first stress factor \(f_\textrm{fuelStress1}\), see Equation 70. However, we set the values of both fuel stress factors: \(f_\textrm{fuelStress1}\) and \(f_\textrm{fuelStress2}\) (introduced later) to 1, in order to have exactly the same fuel price dynamics as given by the Rogner curve.
| $$p_f^{t+1} = \widetilde{p}_{f,J}^{t+1} \times f_\textrm{fuelStress1}\\$$ | (70) |
Then for each fuel consuming agent, current demand in step \(t + 1\) equals planned demand \(x_{f,i}^{t+1} = \widetilde{x}_{f,i}^{t+1}\). The excess demand is distributed among producers proportionally, see Equation 71.
| $$\begin{split} f_{\textrm{supply2}} = \frac{d_f^{t+1}-s_{f}^{t+1}}{s_{f,max}^{t+1}-s_{f}^{t+1}} \\ y_{f,j}^{t+1} = \widetilde{y}_{f,j}^{t+1} + f_{\textrm{supply2}} \left(\widetilde{y}_{f,max,j}^{t+1} - \widetilde{y}_{f,j}^{t+1}\right) \\ \end{split}$$ | (71) |
Finally, in the third case, the market price equals the planned price of the producer having the highest planned price. It might have been additionally increased by multiplication with the second stress factor \(f_\textrm{fuelStress2}\), see Equation 72.
| $$p_f^{t+1} = \widetilde{p}_{f,J}^{t+1} \times f_\textrm{fuelStress2}\\$$ | (72) |
Then for each fuel consuming agent, current demand in step \(t + 1\) equals planned demand reduced proportionally, see Equation 73.
| $$\begin{split} f_{\textrm{demand3}} = \frac{s_{f,max}^{t+1}}{d_f^{t+1}} \\ x_{f,i}^{t+1} = \widetilde{x}_{f,i}^{t+1} \times f_{\textrm{demand3}} \\ \end{split}$$ | (73) |
For each fuel producer, current production in step \(t + 1\) equals maximum production \({y}_{f,j}^{t+1} = \widetilde{y}_{f,max,j}^{t+1}\). For all the three cases considered above, and for each fuel extraction company, the current demand is set to the value of current production \(y_{f,j}^{t+1}\) = \(y_{f,j}^{t+1}\). As a result, a fuel extraction company will try to increase fuel extraction (in line with forecast GDP growth) by increasing the amount of physical capital if the actual production was higher than planned production, and will decrease production otherwise, as described in Equation 30.
Electricity markets
Electricity markets function in a similar way to the fuel markets, but only on the regional level and not on a global level as is the case for fuel markets. Moreover, we consider \(N_e\) different electricity market clearing periods in a single simulation step. In this way, we can take into account randomness in power generation, since power output from wind and solar installations may be different in each of the clearing periods. To model the periodicity of the electricity demand, we have introduced alternately changing periods of high and low electricity demand (we model the day and night demand regimes with peaks in daytime and lows at nighttime). We do not model the seasonality for reasons of simplicity. However, it must be mentioned that demand partially levels off at the regional level (compared to the national level or the even finer levels observed in practice) and the increased winter electricity demand (for heating purposes) may be balanced to some extent by the increased summer demand for cooling purposes. Total electricity demand is calculated as the sum of individual demand, according to Equation 74.
| $$d_e^{t+1} = \sum_{i=1}^{I} \widetilde{x}_{e,i}^{t+1}$$ | (74) |
Total electricity supply is calculated as the sum of individual electricity that can be supplied by the power plants, according to Equation 75.
| $$s_e^{t+1} = \sum_{j=1}^{J} \widetilde{y}_{e,j}^{t+1}$$ | (75) |
Total maximum electricity supply is calculated analogously by summing the maximum amount of electricity that can be supplied by power plants, according to Equation 76.
| $$s_{e,max}^{t+1} = \sum_{j=1}^{J} \widetilde{y}_{e,max,j}^{t+1}$$ | (76) |
Next, total demand is compared with total supply and total maximum electricity supply. We consider three cases. In the first case, total demand is lower or equal to total supply; in the second case, total demand is higher than total supply but lower or equal to the maximum supply; in the third case, total demand is higher than maximum supply:
- \(d_e^{t+1} \le s_e^{t+1}\)
- \(s_e^{t+1} < d_e^{t+1} \le s_{e,max}^{t+1}\)
- \(d_e^{t+1} > s_{e,max}^{t+1}\)
The subsequent steps and calculations are almost identical to the case of fuel markets. We consider different values of stress factors in the case of electricity markets (price increases are observed in case of the market stress), however.
Initially, we observed a relatively low share of electricity produced by peak load power plants (gas and oil fired) in the simulation results, when compared to the empirical data. This might be caused by the aggregation of the many national electricity markets into one market for each region (diversification of electricity production may reduce the need for expensive peak load sources). Such aggregation is limited in reality, not only due to administrative reasons (borders or separate grids for countries) but also due to network constraints (limited capacity of the power grid). In order to also take this mechanism into account, a certain percentage of coal power plant electricity production is replaced with gas and crude oil power plant electricity production (the coal power percentage being calibrated so that the simulated and empirical energy mix agree for each region in the first initial simulation step). The introduced constraint is relaxed with each simulation step (by multiplying the electricity production to be shifted to the peak power plant by a constant equal to 99%, to allow for gradual relaxation of the introduced network constraint; this may represent a gradual extension of the electricity network). In particular, the amount of additionally produced electricity by oil power plants \(\Delta_{e,\textrm{oil}}^{t+1}\) is shown in Equation 77. \(f_{\textrm{min,oil}}\) is a simulation factor (giving the percentage of electricity supply to be satisfied by oil power plants during peak load), \(s_{e,\textrm{oil}}^{t+1}\) is the unconstrained electricity supply by oil power plants.
| $$\Delta_{e,\textrm{oil}}^{t+1} = \textrm{max}\left(f_{\textrm{min,oil}} \times s_e^{t+1}- s_{e,\textrm{oil}}^{t+1},0\right)$$ | (77) |
The amount of additionally produced electricity by oil power plants \(\Delta_{e,\textrm{gas}}^{t+1}\) is calculated in an analogous way. Both values can be scaled down by the factor defined in Equation 78, which takes into consideration the actual supply by coal power plants (the electricity generation increase of oil and gas power plants is limited by the potential decrease of such generation by coal power plants).
| $$\textrm{min}\left(\frac{s_{e,\textrm{coal}}^{t+1}}{\Delta_{e,\textrm{oil}}^{t+1} + \Delta_{e,\textrm{gas}}^{t+1}},1\right) $$ | (78) |
The market clearing price is also finally recalculated as a weighted mean and adjusted in the manner defined in Equation 79. It is assumed that all electricity consumers cover the cost of the network constraints.
| $$p_e^{t+1} = \frac{d_e^{t+1} - \Delta_{e,\textrm{oil}}^{t+1} - \Delta_{e,\textrm{gas}}^{t+1}}{d_e^{t+1}} \times p_e^{t+1} + \frac{\Delta_{e,\textrm{gas}}^{t+1}}{d_e^{t+1}} \times \textrm{max}(p_e^{t+1}, \widetilde{p}_{\textrm{gas}}^{t+1}) + \frac{\Delta_{e,\textrm{oil}}^{t+1}}{d_e^{t+1}} \times \textrm{max}(p_e^{t+1}, \widetilde{p}_{\textrm{oil}}^{t+1}) $$ | (79) |
For the Middle East, electricity produced by gas power plants may be shifted to electricity produced by oil power plants in an analogous way. If the electricity storage capacity is available, produced but unconsumed electricity is stored.
Capital goods market
The capital goods market is a global market but with local interactions. The demand side of the market consists of fuel extraction, electricity, capital goods companies and consumer goods companies. The demand for capital goods for company \(i\) equals the minimum of the planned physical capital increase, \(\widetilde{\Delta k}_i^{t+1}\), and the planned monetary value of the capital increase \(\widetilde{\Delta kv}_i^{t+1}\), divided by the capital goods price. In this way, a capital goods price increase may lower the demand for these goods. The supply side consists of capital goods companies, with the supply for company \(j\) being \(y_j^{j+1}\). The market is modelled in a simplified way. Namely, we allow for capital goods companies to produce the necessary capital increase for their own use beforehand. Furthermore, this part of capital is also available from the beginning of the simulation step.
We know that, in the general case, the increase in planned physical capital — and consequently its value — is bounded by the equation — \(\widetilde{\Delta \textrm{kv}}_j^{t+1} = \widetilde{\Delta \textrm{k}}_j^{t+1} \times \bar{p}_{pg}^t\). In the case of the power plants, the planned physical capital increase is calculated as the product of the planned capacity increase \(\widetilde{\Delta c_p}_j^{t+1}\) and the current value of the overnight investment cost \(\textrm{OIC}_\textrm{t+1}\), according to the formula specified in Equation 80. As a result, we can model decreasing OIC due to increased efficiency for different types of power plants.
| $$\widetilde{\Delta \textrm{k}}_j^{t+1} = \widetilde{\Delta c_p}_j^{t+1} \times \textrm{OIC}_\textrm{t+1}$$ | (80) |
For solar and wind power plants, acquired capital goods are divided between electricity production and storage capacities, based on the proportion of existing capacities.
To model the local market — market fragmentation — we implement an adaptive approach with local interactions (Assenza et al. 2015). Each customer is connected to a certain number of producers (companies). A customer first buys from the connected producer that offers the lowest price. When the total demand exceeds the total supply of a company, the demand is only partly satisfied (in the same proportion for each customer). A customer with unsatisfied demand turns to the next connected company with the second lowest price, and so on.
The production function of a capital goods company \(j\) is a CES function with the following production factors: capital \(k_j^t+\widetilde{\Delta k}_j^{t+1}\), labour \(l_j^{t+1}\) and energy \(e_j^{t+1}\), see Equation 81.
| $$y_j^{t+1} = \left(\left(\eta_{k} (k_j^t+\widetilde{\Delta k}_j^{t+1})\right)^{\rho_y} +(\eta_{l} l_j^{t+1})^{\rho_y}+(\eta_{e} e_j^{t+1})^{\rho_y}\right)^{1/\rho_y} \\$$ | (81) |
We assume that capital goods companies can produce capital goods for their own use. Therefore, the capital goods available for companies in other sectors is specified in Equation 82. \(s_j^t\) denotes the previous state of stocks. We use the minimum function in this formula to consider the hypothetical case when stocks and current production are lower than the planned increase of capital goods for own use. However, for the value of parameters \(\eta_{k}\) used in the simulation, such a situation does not generally occur.
| $$y_j^{t+1} + s_j^t - \textrm{min}\left(\textrm{min}\left(\frac{\widetilde{\Delta \textrm{kv}}_j^{t+1}}{p_j^{t+1}},\widetilde{\Delta k}_j^{t+1} \right) , y_j^{t+1} + s_j^t \right)$$ | (82) |
The offer price equals the planned price for a producer, \(p_j^{t+1} = \widetilde{p}_j^{t+1}\).
Let us first assume that each capital goods company is connected to \(I\) customers. Let us also assume that each customer is connected to \(J\) capital goods companies. In the first step, each customer orders the capital goods companies it is connected to by price, with a preference for the producer that has a lower offer price (ties are dealt with using randomised selection). We also implemented an additional mechanism, depending on the export or import surplus in a given region. Through this mechanism, the ordering of capital goods producers is additionally changed, depending on their region of origin. This mechanism is implemented as a (partial) bubble sort algorithm, where in each iteration the original ordering based on production price is changed by swapping the order of the two categories of producers. The first category consists of producers from the same region as the consumer, whereas the second category consists of producers from a different region. To illustrate this, let us consider the situation of an export surplus in a given region. In this case, the companies in this region try to increase imports by giving preference to capital goods companies from other regions. For example, let us consider an ordered pair of producers. The first producer with the lower price has the same region as the customer and the second producer with a higher price has a different region than the customer. In this case, the ordering of these two producers is swapped. Such mechanisms enable balancing of the trade deficit. In the second step, customers with unsatisfied demand visit a producer that is placed first on the list of connected producers. If there are no more connected producers (the connected producers list is empty), a customer randomly selects one of the producers with remaining supply. In the third step, the total demand \(d_j^{t+1}\) (see Equation 83) is compared with the remaining supply \(s_j^{t+1}\).
| $$d_j^{t+1} = \sum_{i=1}^{I} \textrm{min}\left(\frac{\widetilde{\Delta \textrm{kv}}_j^{t+1}}{p_j^{t+1}},\widetilde{\Delta k}_j^{t+1} \right)$$ | (83) |
We consider three cases, see Equation 84.
| $$\begin{split} d_j^{t+1} > y_j^{t+1} \\ d_j^{t+1} = y_j^{t+1} \\ d_j^{t+1} < y_j^{t+1} \\ \end{split}$$ | (84) |
In the first case, demand is higher than supply. In this event, demand is satisfied only proportionally, according to the factor \(y_j^{t+1}/d_j^{t+1}\), and the remaining demand is reduced by multiplication by the factor \(1-y_j^{t+1}/d_j^{t+1}\) for each customer. The remaining supply will be equal to zero, so the producer leaves the market. In the second case, when demand equals the remaining supply, the customer demand is fully satisfied (all customers leave the market) and the producer’s remaining supply equals zero. The producers also leave the market in this case. In the third case, when demand is lower than remaining supply, then customer demand is fully satisfied (all customers leave the market) and the remaining supply is decreased by the demand \(y_j^{t+1} - d_j^{t+1}\). In the fourth and final step, the list of customers that had just visited a producer is cleared for each producer remaining in the market. Steps two to four are repeated until there are either no more producers or no more customers in the market. The unsold products increase the value of stocks. Finally, the average price of the capital goods \(\bar{p}_{pg}^{t+1}\) is calculated for each region considered in the simulation, based on the individual transaction data: price and quantity.
Consumer goods market
The consumer goods markets are modelled in an analogous way to capital goods markets. We have global markets for all sectors apart from transportation and other services, which we consider as regional markets. The demand side of the market consists of citizens. The current demand for consumer goods by citizen i is defined in Equation 85.
| $$\widetilde{x}_{i,k}^{t+1} \left(1 + \frac{p_{j,k}^{t+1}-\widetilde{p}_{i,k}^{t+1}}{\widetilde{p}_{i,k}^{t+1}} \eta_p\right)$$ | (85) |
\(widetilde{x}_{i,k}^{t+1}\) is the current unsatisfied portion of demand for the good \(k\) (initially equal to planned consumption, as defined in Equation 15 and is gradually updated during market clearing by the amount of already acquired consumer goods), \(p_{j,k}^{t+1}\) is the offer price of producer \(j\), \(\widetilde{p}_{i,k}^{t+1}\) is the currently planned price (initially equal to the planned price, as defined in Equation 15, and is always substituted during market clearing by the last transaction price), and \(\eta_p\) is price elasticity, a simulation parameter. In this manner, we allow a citizen to adjust his/her demand to current price changes. Furthermore, we also assume that a citizen is always willing to buy at least the required minimum consumption of goods, \(x_{i,k}^{\textrm{min}}\), regardless of the offer price in a given simulation round \(t+1\).
The supply side consists of consumer goods companies, with the supply for companies \(j\) being \(y_j^{j+1}\). The following additional details are given in order to highlight the differences between this market and the capital goods market. The production function of consumption goods company \(j\) is a CES function with the following production factors: capital \(k_j^{t+1}\), labour \(l_j^{t+1}\) and energy \(e_j^{t+1}\), Equation 86.
| $$y_j^{t+1} = \left((\eta_{k} k_j^{t+1})^{\rho_y} +(\eta_{l} l_j^{t+1})^{\rho_y}+(\eta_{e} e_j^{t+1})^{\rho_y}\right)^{1/\rho_y} \\$$ | (86) |
Consumer goods available for citizens are specified in Equation 87. \(s_j^t\) denotes the previous state of stocks.
| $$y_j^{t+1} + s_j^t$$ | (87) |
The offer price equals the planned price for a producer, \(p_j^{t+1} = \widetilde{p}_j^{t+1}\).
Climate module
We use the discrete form of the climate system (Petschel-Held et al. 1999):
| $$F(t_{n+1})-F(t_n) \, = \, E(\Delta t) \\$$ | (88) |
| $$C(t_{n+1}) - C(t_n)\, =\, B \times F(t_n) + \beta \times E(\Delta t) - \sigma \times \left(C(t_n) - C_1\right) \\$$ | (89) |
| $$T(t_{n+1}) - T(t_n)\, = \,\mu \times \log \left( \frac{C(t_{n+1})}{C_1} \right) + \alpha \times \left( T(t_n) - T_1 \right)$$ | (90) |
Types of damage
We consider the following mechanisms associated with damage related to global temperature increases: diminished productivity in an agricultural sector, diminished labour supply and efficiency, and natural disasters.
Agricultural damages
We implemented an agricultural sector related damage function \(d^s(T_t-T_0)\), where \(T_t\) denotes the global temperature in simulation step \(t\), and \(T_0\) is the initial global temperature, following the estimations by Ciscar et al. (2011) for Europe, IPCC's Fifth Assessment Report for Africa, see e.g. (Barros 2014), and the magnitude applied to other continents is half of that in Africa. Namely, we have assumed that, depending on the global temperature increase \(T_t-T_0\), the following changes in production will occur (assuming constant production factors), see Table 1. Intermediate values are obtained by linear interpolation. These values are further adjusted by adding the simulation parameter, factor \(f_\textrm{agriculture}^\textrm{damages}\) in the parameter sensitivity analysis.
The agricultural damages are implemented as temporary shocks, such that labour, capital, and energy production factors efficiency (\(\eta_l, \eta_k, \eta_e\)) are gradually modified, as defined in Equation 91, for all companies in the agricultural sector. This modification takes place before a company produces its goods but after it decides on the necessary (optimal) quantities of the production factors in simulation period \(t\). New values for the production factors efficiency are however used for deciding on the necessary (optimal) quantities of the production factors in the next simulation period \(t+1\). This allows for gradual adaptation to temperature changes by relatively increasing the demand for production factors in consecutive periods.
| \(\Delta t\) | Europe | Africa | Rest |
| 0 | 0% | 0% | 0% |
| 1 | 1% | -10% | -5% |
| 2 | 2% | -15% | -7.5% |
| 3 | 3% | -20% | -10% |
| 4 | -5% | -25% | -12.5% |
| 5 | -10% | -30% | -15% |
| 6 | -20% | -40% | -20% |
| $$\eta_{l,t}^d = \eta_{l,t} \times \frac{1+d^a(T_t-T_0)}{1+d^a(T_{t-1}-T_0)} \\ \eta_{k,t}^d = \eta_{k,t} \times \frac{1+d^a(T_t-T_0)}{1+d^a(T_{t-1}-T_0)} \\ \eta_{e,t}^d = \eta_{e,t} \times \frac{1+d^a(T_t-T_0)}{1+d^a(T_{t-1}-T_0)} \\$$ | (91) |
Labour damages
The labour damage function \(d^l(T^r_t)\) represents the diminished labour supply and efficiency due to global temperature increase and is inspired by Burke et al. (2015). The symbol \(T^r_t\) denotes the temperature in the region \(r\) in simulation step \(t\). The function is presented in Equation 92. The slope of the quadratic part is set in such a way that regional temperature increases from 13º to 33º lead to 45%. This base value is further adjusted by the simulation parameter, \(f_\textrm{labour}^\textrm{damages}\) in the parameter sensitivity analysis.
| $$T^r_t\le13: d^l_t = 0\\ T^r_t>13: d^l_t = - 0.001125 \times \left(T^r_t-13\right)^2 \\$$ | (92) |
The regional temperature increase is set to the same value as the global temperature increase, see Equation 93.
| $$T^r_t = T^r_{t-1} + \left(T_t-T_{t-1}\right)$$ | (93) |
The initial values are calculated as a weighted mean (by population size), according to 2015 World Bank data on country-specific annual mean temperature, see Table 2.
| region | \(t^r_0\) |
| AF | 24.871 |
| AS | 24.163 |
| CHN | 7.483 |
| CIS | 2.882 |
| EU | 10.912 |
| IND | 24.620 |
| JPY | 11.805 |
| ME | 22.373 |
| NAM | 10.816 |
| SCA | 23.749 |
Just as we did for agricultural damage, labour damage is implemented in terms of temporary shocks, i.e. the labour efficiency factor is modified as defined in Equation 94. This is done for all the production and consumer goods companies before a company produces its goods but after it has decided on the necessary (optimal) quantities of the production factors in simulation period \(t\).
| $$\eta_{l,t}^d = \eta_{l,t} \times \frac{1+d^l(T_t)}{1+d^l(T_{t-1})}$$ | (94) |
Natural disasters damages
EM-DAT (the international disaster database) data on damage due to natural disasters, the global mean surface temperature HadCRUT 4.6.0.0 annual means, and GDP estimates from the World Bank (adjusted to 2017 USD) were used in order to initially estimate the damage function parameters for natural disasters. In particular, we regressed disaster damage values on mean temperature and controlled for differences in GDP. The time period 1960-2017 was considered in the regression analysis. Regression analysis was done separately for geographical continents, listed in Table 3. Estimated values of the regression coefficients, together with corresponding standard errors, are also presented in the same table. The value of the coefficient represents the estimated values of additional disaster-related damage due to a temperature increase of 1°C, expressed in billions USD.
| region | value | est. error |
| Africa | 0.04062 | 0.65187 |
| Asia | 20.706 | 11.527 |
| Europe | 7.483 | 8.471 |
| North America | 50.069 | 35.631 |
| Central America | 2.7683 | 2.2186 |
To calculate the damage coefficients that were finally used in the simulation, the initially estimated values were broken down into the geographical regions used in the simulation (in proportion to the 2016 GDP values). Conservatively, we added one standard deviation of the estimation error to the initially estimated values, to take into account the fact that not all damage may be included in the database (especially true for older data but partially missing data problems may also concern most recent data). This value of this conservative correction factor (one standard deviation) is further adjusted by the simulation parameter, \(f_\textrm{disaster}^\textrm{damages}\) in the parameter sensitivity analysis. Moreover, the values were adjusted to the present values by multiplication by the factor defined in Equation 95, which uses global GDP values from 1960 and 2017 respectively (the beginning and end of the estimation period). GDP data was used as a proxy for scaling, to take into account the different values of total capital that could potentially be affected by the same disaster in different years.
| $$f_\textrm{disasters} =(2\times80076)/(11359+80076)$$ | (95) |
In the final step, the damage values were divided by the initial total capital value for each region, to obtain the following regional coefficients \(d_{dcr}\). The values are presented in Table 4. In each simulation step, the physical capital value for each company is decreased, according to the formula in Equation 97.
| region | \(t^r_0\) |
| AF | 0.028% |
| AS | 0.048% |
| CHN | 0.035% |
| CIS | 0.054% |
| EU | 0.065% |
| IND | 0.064% |
| JPY | 0.117% |
| ME | 0.061% |
| NAM | 0.726% |
| SCA | 0.062% |
| $$k_t^{dis} = k_t \left(1 - d^{dc}_r \times (T_t-T_0) \right)$$ | (96) |
The database contains information on the amount of direct physical damage to property, crops, and livestock but not indirect ones, namely on lost revenues due to production outages caused by natural disasters. We have assumed that such indirect damage is equal to the direct kind. Thus, as in the last step, the damage values were divided by the initial GDP value for each region to get the following regional coefficients \(d^{dp}_r\). The values are presented in Table 5.
| region | \(t^r_0\) |
| AF | 0.023% |
| AS | 0.115% |
| CHN | 0.115% |
| CIS | 0.100% |
| EU | 0.100% |
| IND | 0.115% |
| JPY | 0.115% |
| ME | 0.115% |
| NAM | 0.686% |
| SCA | 0.0120% |
In each simulation step, the production output for each consumer goods and capital goods company is decreased according to the formula in Equation 97. The decrease of physical capital value in the case of power plants and fuel extraction companies directly leads to a proportional production decrease, as this is considered as the only production factor in these sectors (both sectors are capital intensive and may produce energy for production purposes by themselves).
| $$y_t^{dis} = y_t \left(1 - d^{dp}_r \times (T_t-T_0) \right)$$ | (97) |
Technology growth
We additionally model the effects of technology growth. Firstly, the increase of production factors: labour, capital and energy efficiency for consumption and capital goods companies. Secondly, for power plants the technology growth is modelled implicitly by the assumed learning process that leads to gradually decreasing prices for the new installed capacities for renewable power plants. Thirdly, for the fuel extraction companies, capital efficiency increase is overweighted with a more capital intensive accessibility of remaining fuel resources. Therefore, technology growth in this sector is not modelled additionally. Conservatively, we also do not con-sider technology growth for private households. It is to be expected that energy demand reduction due to improved energy efficiency of existing appliances will somehow be balanced by energy demand increase due to introduction of new appliances (for instance, though we now have more efficient washing machines, laundry dryers are also gaining in popularity).
The increase of production factors efficiency is implemented in a similar fashion to agricultural damage, i.e. as temporary shocks, with labour, capital, and energy efficiency factors being modified as defined in Equation 98. For all the consumer goods and capital goods companies, this takes place before starting production but after having decided on the necessary (optimal) quantities of the production factors in simulation period \(t\). New values are however used for deciding on the necessary (optimal) quantities of the production factors in the next simulation period \(t+1\). We use as the simulation parameters, the factor \(f_{\eta}\), which gives the expected growth rate, the factor \(f_{\eta}^{\sigma}\), which gives the range of random deviations from the expected values, i.e. \(\left(-f_{\eta}^{\sigma},f_{\eta}^{\sigma}\right)\), and \(\nu\) is a uniformly distributed random variable.
| $$\eta_{l,t}^n = \eta_{l,t} \times (1 + f_{\eta} + f_{\eta}^{\sigma} \times (2 \nu-1)) \\ \eta_{k,t}^n = \eta_{k,t} \times (1 + f_{\eta} + f_{\eta}^{\sigma} \times (2 \nu-1)) \\ \eta_{e,t}^n = \eta_{e,t} \times (1 + f_{\eta} + f_{\eta}^{\sigma} \times (2 \nu-1)) \\$$ | (98) |
The technological possibility of substitution of fuel energy by electricity may also be increased due to technological progress. To model this effect, we first define the parameter \(\Delta_\rho\), which expresses the increased ease of substitution and is defined in Equation 99. Symbol \(N\) is the number of simulation steps. \(\rho_e\) is used as a simulation parameter in the manner previously defined in Equation 16, and specifies how easy it is to substitute electricity with fuel energy, \(\rho_f\) is used as a parameter in Equation 17 and indicates how easy it is to substitute energy production of different types of fuel. Finally, the factor \(f_{\rho}\) is a simulation parameter. The general idea is that the value of the substitution coefficient of energy from fuel by electricity gradually increases towards that of the substitution coefficients of energy from one kind of the fuel by energy from another kind of fuel, and may reach a fraction \(f_{\rho}) of this value at the end of the simulation.
| $$\Delta_\rho = \frac{\rho_f - \rho_e}{N} \times f_{\rho} $$ | (99) |
Analogously we define \(\Delta_\rho^\sigma\) using the factor \(f_{\rho}^\sigma\).
| $$Delta_\rho^\sigma = \frac{\rho_f - \rho_e}{N} \times f_{\rho}^\sigma$$ | (100) |
Finally, the actual change of the e parameter in each simulation round is calculated as follows in Equation 101. \(\nu\) is a uniformly distributed random variable.
| $$Delta_\rho^\sigma = \frac{\rho_f - \rho_e}{N} \times f_{\rho}^\sigma$$ | (101) |
Heterogeneity
In our simulation we consider three different variants of heterogeneity (\(h_0\) is a homogeneous scenario, \(h_1\) is a moderately heterogeneous scenario and \(h_2\) is a strongly heterogeneous scenario) with respect to the following aspects:
- minimum consumption parameter together with minimum consumption dispersion
- initial wealth distribution among citizens
- heterogeneity of consumer/capital goods companies
- heterogeneity of technology growth
- heterogeneity of temperature-related damage
Scenario h0: In this scenario, the minimum required consumption parameters are set to fixed values and equal 40% of initial consumption for the agriculture and energy sectors and 30% for other sectors. Each individual minimum required consumption parameter is not further transformed. The individual shares in a company’s capital were initially equally distributed among citizens. In this variant, companies are homogeneous. Technology growth and damage are also homogeneous.
Scenario h1: In this scenario, the minimum required consumption parameters are also initially set to fixed values. Each individual minimum required consumption parameter is further transformed by adding a random variable, having a normal distribution with mean \(0\) and standard deviation \(0.05\). The individual shares in the company’s capital were distributed in such a way that the wealth distribution in the population of the given region reflects the real wealth distribution in the selected range between the \(0.4\) and \(0.6\) percentiles. Empirical wealth distribution was first approximated by the log normal distribution, with parameters estimated based on real data. The initial number of employees is randomly redistributed between pairs of the same industry sector companies, in such a way that the minimum number of employees in the smaller (of the pair) company was \(5\). In a more detailed way, companies are first grouped into pairs and then for each company a randomly selected number of employees (from zero to the number defined as the excess over the minimum required employees) is taken and allocated from the first company in a pair to the second company in a pair. All other initial company parameters are proportionally adjusted, including the number of customers, capital value and energy usage. Technology growth is heterogeneous on the regional level. The values of the changes in both parameters: \(\eta\), the production factors efficiency parameters, and \(\rho_e\), the electricity and fuel substitutability, are further randomised on a regional level by adding a uniformly distributed noise factor with mean value \(0\) and a parameterised range, using the parameter \(f_{\eta}^{\sigma, \textrm{region}}\) as described in Equation 98, and \(\Delta_\rho^{\sigma,\textrm{region}}\) as described in Equation 101 (values may be different for different regions but remain the same for all agents in the same region). Similarly, the damage due to temperature increase is randomised on a regional level by adding normally distributed random variables with mean value \(0\) and parameterised (using a simulation parameter) standard deviation.
Scenario h2: In this scenario, the minimum required consumption parameters are also initially set to fixed values. Each individual minimum required consumption parameter is further transformed by adding a random variable, having a normal distribution with mean \(0\) and standard deviation \(0.1\). The individual shares are distributed in such a way that wealth distribution in the population of the given region reflects the real wealth distribution in the selected range between the \(0.2\) and \(0.8\) percentiles. Empirical wealth distribution was also approximated by the log normal distribution, with parameters estimated based on real data. The initial num-ber of employees is randomly redistributed between pairs of the same industry sector companies, in such a way that the minimum number of employees in the smaller (of the pair) company was \(3\). All other initial parameters are proportionally adjusted, including the number of customers, capital value and energy usage. Technology growth is heterogeneous on both the regional and individual levels. In the first step, the values of the change in \(\eta\), the production factors efficiency parameters, and \(\rho_e\), the electricity and fuel substitutability, are further randomised on the regional level by adding a uniformly distributed noise factor with mean value \(0\) and parameterised range, using the parameter \(f_{\eta}^{\sigma, \textrm{individual}}\), as described in Equation 101, and \(\Delta_\rho^{\sigma,\textrm{individual}}\). In the second step, the regional values of the parameters are further randomised on the individual level by adding a uniformly distributed noise factor with mean value \(0\) and a parameterised range (values may be different for different regions and also may be different for all agents in the same region). Similarly, the damage due to temperature increase is randomised on a regional level by adding normally distributed random variables with mean value \(0\) and parameterised standard deviation, and then on the individual level also by adding normally distributed random variables with mean value \(0\) and parameterised standard deviation.
Stylised Facts
The role of stylised facts in macroeconomic agent-based models is widely discussed, see (Fagiolo et al. 2019; Fagiolo & Roventini 2017), for instance. Although we do not use stylised facts for indirect calibration, the model satisfies the following stylised facts, listed in Table 6. One should also take into account that present empirical macroeconomic data may be different from the macroeconomic data generated by an economy in distress due to running out of energy resources.
| 1 | (Endogenous) self-sustained growth with persistent fluctuations | Kuznets & Murphy (1966) |
| 2 | Le skewed GDP growth-rate distribution | empirical analysis |
| 3 | Fat-tailed GDP growth-rate distribution | Fagiolo et al. (2008) and empirical analysis |
| 4 | Recession duration exponentially distributed | Ausloos et al. (2004) |
| 5 | Cross-correlations of macro-variables | Stock & Watson (1998) |
| 6 | Pro-cyclical energy demand | Moosa (2000) |
| 7 | Negative relation between wages and unemployment rate | Snowdon et al. (1994) |
| 8 | Trade deficits tends to correct themselves over time | Snowdon et al. (1994) |
| 9 | The scarcity effects for fossil fuels | Nordhaus & Boyer (2000) |
| 10 | The learning by doing effects for renewable resources power plants | Edenhofer et al. (2005) |
| 11 | Production factor can be substituted | Edenhofer et al. (2005) |
We have analysed the World Development Indicators historical time series on the annual percentage growth rate of GDP per capita (based on local currency). Aggregated values are based on constant 2010 U.S. dollars, (The World Bank 2019) for the time period 1960-2017. We obtained the statistical results, which are shown in the second column of Table 7. In the third column of the same table we present the same statistical measures, calculated as an average over all \(1056\) (\(4 \times 256\)) simulation runs of the later presented scenarios (without considering damage for reasons of comparability).
| statistic | historical | simulation |
| mean value | 1.861% | 0.843% |
| standard deviation | 1.460% | 0.252% |
| skewness | -0.635 | -0.355 |
| excess kurtosis | 0.718 | 1.196 |
| pacf[1][10] | 0.365 | 0.047 |
| pacf[2] | -0.125 | 0.348 |
| pacf[3] | 0.170 | -0.091 |
The growth is partially endogenous, caused by an increase in energy used and capital, and partially exogenous, in a strict sense, by means of technology shocks in the case of consumer/capital goods companies and learning by doing in the case of solar power , wind power and energy storage facilities. In our simulation, we have obtained lower mean annual GDP growth rates than those observed historically. This may be explained by considering only moderate technology growth being applied in all four simulation scenarios, but also due to situations of distress arising from the depletion of fuel reserves, as considered in the simulation. Moreover, although the partial auto-correlation coefficients (abbreviated as pacf) are of a similar magnitude (in an absolute sense), i.e. lower than 0.4, their signs and value differ. This may be a result of the time that the simulated economy needs to adapt to the technology shocks, and the one-period prolonged investments of power plant and fuel extraction companies (in reality, we also observe long investment periods for these two sectors but not as synchronised as it is in the simulation model). We obtained a negative skewness and positive excess kurtosis in the simulation. Recession periods (measured on a regional level) are exponentially distributed. The stylised facts 6–11 results from the direct implementation of the relevant mechanisms in the model.
Parametrisation
The model is implemented in Java, using the MASON 19 framework. For the initial parameterisation, we use data from the World Bank (GDP, population data), World Trade Organisation (trade statistics), ILOSTAT (for labour data) and the United Nations for gross fixed assets classification. The parameters in citizen utility functions and company production functions are calibrated so that the simulated initial 2015 results equal the observed empirical data. For the energy sector, we use the BP Statistical Review of World Energy (BP 2016) and the Enerdata Global Statistical YearBook (Yearbook 2016). Some parameters (overnight investment cost, learning rate, capacity factors) are taken from the initial MIND and REMIND model parameterisation (Edenhofer et al. 2005). The parameterisation process and initial parameter values are described in Appendix in more detailed way.
Results
We present the results of three different analyses in this section:
- selected scenario analysis without damages
- selected scenarios analysis with damages
- parameter sensitivity analysis
In the first analysis, we consider four selected scenarios that are a combination of optimistic and pessimistic with respect to two criteria, remaining fuel resources and the growth rate of renewable energy sources. In the second analysis, we additionally consider damage related temperature increases. In the third analysis, we perform a systematic parameter space search. We consider the heterogeneity of the agents: citizens with respect to their ownership share in companies and minimum required consumption parameters, and companies with respect to their size and the rate of technology growth. We also allow the agents to be a ected by damage in different ways.
Scenario analysis
We ran four different scenarios that differ with respect to the remaining fuel reserves and growth dynamics of renewable energy sources, as these are the key factors in the transition from traditional to renewable resources based energy sector. In particular we considered the following scenarios:
- renewable energy production growth pessimistic, remaining fuel reserves pessimistic
- renewable energy production growth pessimistic, remaining fuel reserves optimistic
- renewable energy production growth optimistic, remaining fuel reserves pessimistic
- renewable energy production growth optimistic, remaining fuel reserves optimistic
The parameter sets used for these scenarios are presented in Table 8.
The meaning of specified parameter groups is reminded below.
- \(f_\textrm{elStress1}\) and \(f_\textrm{elStress2}\) — electricity market stress factors
- \(w_{\textrm{ep}}\) — current electricity price weight in the planned electricity price
- \(r_\textrm{cap}\) — power plant capacity reserve, factors
- \(e_{\textrm{down}}\), \(e_{\textrm{up}}\), \(e_{\textrm{up}}^{\textrm{w}}\),
- \(e_{\textrm{up}}^{\textrm{s}}\), \(e_{\textrm{up}}^{\textrm{nh}}\), \(e_{\textrm{red}}\), \(e_{\textrm{inj}}^{\textrm{sw}}\), and \(\textrm{period}\) — determine the electricity market energy mix dynamics, see Equation 51, 52, and 54 for more details.
- \(f_\textrm{fuelReserves}\) — fuel reserves factor
- \(\mu_{\textrm{gdp}}\), \(\alpha_{\textrm{gdp}}\), \(\sigma_{\textrm{gdp}}\), and \(\textrm{min}_{\textrm{gdp}}\) — determine planning of next period GDP growth rates, see Equation 1 for more details.
| Parameter | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
| \(f_\textrm{elStress1}\) | 1.2 | 1.2 | 1.2 | 1.2 |
| \(f_\textrm{elStress2}\) | 1.4 | 1.4 | 1.4 | 1.4 |
| \(w_{\textrm{ep}}\) | 0.15 | 0.15 | 0.15 | 0.15 |
| \(r_\textrm{cap}\) | 1.2 | 1.2 | 1.2 | 1.2 |
| \(e_{\textrm{down}}\) | 25 | 25 | 25 | 25 |
| \(e_{\textrm{up}}\) | 7.5 | 7.5 | 7.5 | 7.5 |
| \(e_{\textrm{up}}^{\textrm{w}}\) | 10 | 10 | 200 | 200 |
| \(e_{\textrm{up}}^{\textrm{s}}\) | 30 | 30 | 600 | 600 |
| \(e_{\textrm{up}}^{\textrm{nh}}\) | 5 | 5 | 25 | 25 |
| \(e_{\textrm{red}}\) | 0.5 | 0.5 | 0.5 | 0.5 |
| \(\textrm{period}\) | 37 | 37 | 37 | 37 |
| \(e_{\textrm{inj}}^{\textrm{sw}}\) | 25 | 25 | 75 | 75 |
| \(f_\textrm{fuelReserves}\) | 0.75 | 1.25 | 0.75 | 1.25 |
| \(\mu_{\textrm{gdp}}\) | 0.02 | 0.02 | 0.02 | 0.02 |
| \(\alpha_{\textrm{gdp}}\) | 0.625 | 0.625 | 0.625 | 0.625 |
| \(\sigma_{\textrm{gdp}}\) | 0.01 | 0.01 | 0.01 | 0.01 |
| \(\textrm{min}_{\textrm{gdp}}\) | 0.003 | 0.003 | 0.003 | 0.003 |
| \(f_{\eta}\) | 0.0075 | 0.0075 | 0.00755 | 0.0075 |
We also set parameter \(f_{\eta}\), which represents the annual rate of increase of production factors efficiency, to 0.75%. This corresponds to moderate technological growth. Conservatively, we do not consider the possibility of easier substitution of fuel energy by electricity due to technological advances. This will, however, be considered in the parameter sensitivity analysis. The base value of the remaining fuel reserves is additionally multiplied by the factor \(f_\textrm{fuelReserves}\) in each scenario. This led to the pessimistic (only 75% of base value of re-maining fuel reserves are available) and optimistic (125% of base value remaining fuel reserves are available) scenarios.
Each scenario was run 216 times using different random (seed) values. The aggregated results (mean \(\mu\) and standard deviation \(\sigma\)) are presented in Table 9 for GDP growth rates \(\textrm{gdp}_\textrm{gr}\) over the next \(100\) years. We use constant prices and we directly compare GDP values in the initial and final (100th) simulation step. The analogous results for global temperature growth \(t_g\) are presented in Table 11, which has the same structure as Table 9. Additionally, in both tables in columns four and five we show aggregated results that are calculated for the first half of the simulation steps only. Respectively, in columns six and seven we show the results for the second half.
| Scenario | \(\mu\) | \(\sigma\) | \(\mu_{(1-50)}\) | \(\sigma_{(1-50)}\) | \(\mu_{(51-100)}\) | \(\sigma_{(51-100)}\) |
| 1 | 1.213 | 0.075 | 0.564 | 0.021 | 0.415 | 0.049 |
| 2 | 1.391 | 0.049 | 0.594 | 0.021 | 0.500 | 0.022 |
| 3 | 1.283 | 0.056 | 0.562 | 0.020 | 0.462 | 0.031 |
| 4 | 1.377 | 0.069 | 0.594 | 0.022 | 0.491 | 0.031 |
We can observe significant differences among the scenarios, resulting from the different growth rates observed in both the first fifty and the second fifty simulation steps. Moreover, the aggregated GDP growth rates observed in scenarios \(2\) and \(4\) are similar, and higher than the GDP growth rates observed in the remaining scenarios. This suggests that fuel reserves may have the most significance for the GDP growth rate. The GDP growth rate observed in scenario \(3\) is significantly higher than in scenario \(1\). This implies that the intensive long-term growth of renewable energy resources could, at least partially, compensate for lower fuel reserves.
The aggregated results (mean \(\mu(i)\) and standard deviation \(\sigma(i)\), where \(i\) is the number of the scenario considered) for GDP growth rates \(\textrm{gdp}_\textrm{gr}\) over the next 100 years in the regions considered in the simulation are presented in Table \ref{tab: scenarios production regions}. Similarly, we use constant prices. One can see that growth rates are relatively higher for regions rich in fossil fuels.
| region | \(\mu(1)\) | \(\sigma(1)\) | \(\mu(2)\) | \(\sigma(2)\) | \(\mu(3)\) | \(\sigma(3)\) | \(\mu(4)\) | \(\sigma(4)\) | |
| 1 | AF | 1.291 | 0.051 | 1.362 | 0.043 | 1.472 | 0.046 | 1.498 | 0.053 |
| 2 | AS | 1.344 | 0.063 | 1.472 | 0.043 | 1.475 | 0.049 | 1.492 | 0.055 |
| 3 | CHN | 1.138 | 0.224 | 1.594 | 0.088 | 1.506 | 0.145 | 1.612 | 0.099 |
| 4 | CIS | 1.131 | 0.238 | 1.455 | 0.081 | 1.349 | 0.165 | 1.451 | 0.097 |
| 5 | EU | 1.251 | 0.043 | 1.318 | 0.046 | 0.925 | 0.116 | 1.141 | 0.159 |
| 6 | IND | 1.348 | 0.136 | 1.559 | 0.049 | 1.548 | 0.140 | 1.611 | 0.050 |
| 7 | JPY | 1.150 | 0.084 | 1.250 | 0.041 | 1.273 | 0.068 | 1.290 | 0.058 |
| 8 | ME | 1.370 | 0.139 | 1.657 | 0.072 | 1.483 | 0.060 | 1.657 | 0.072 |
| 9 | NAM | 1.071 | 0.102 | 1.173 | 0.058 | 1.106 | 0.102 | 1.176 | 0.078 |
| 10 | SCA | 1.319 | 0.097 | 1.336 | 0.102 | 1.435 | 0.102 | 1.399 | 0.133 |
| Scenario | \(\mu\) | \(\sigma\) | \(\mu_{(1-50)}\) | \(\sigma_{(1-50)}\) | \(\mu_{(51-100)}\) | \(\sigma_{(51-100)}\) |
| 1 | 2.477 | 0.030 | 1.424 | 0.008 | 1.052 | 0.025 |
| 2 | 2.808 | 0.031 | 1.486 | 0.004 | 1.321 | 0.030 |
| 3 | 2.301 | 0.044 | 1.384 | 0.009 | 0.917 | 0.038 |
| 4 | 2.606 | 0.051 | 1.448 | 0.005 | 1.157 | 0.049 |
The observed values for temperature growth depend on both the remaining fuel reserves (the higher it is, the higher the temperature growth) and the renewable energy resources growth rate (the higher it is, the lower the temperature growth).
The observed growth dynamics of production in different industry sectors are also highly dependent on which scenario applies. Mean values are presented in Figure 2.
Only in the case of pessimistic scenario 1 (limited remaining fuel reserves, combined with moderate increase in renewable energy resources) can we observe a significant production decline in the final simulation steps. Moreover, we can see that economic growth problems (due to restricted energy production) will appear in the second half of this century.
The observed growth dynamics of the electricity produced by the different types of power plants is highly dependent on which scenario applies. Mean values are presented in Figure 3.
The observed dynamics of electricity prices produced by different regions depends on the scenario. Mean values are presented in Figures 4 and 5. We can observe increased price volatility but also regional differences in price increases. The price increase is dramatic for scenarios 1 and 3 with limited fuel reserves. This is also magnified due to the assumed limited growth rate of the solar and wind power plants, see Equation 53 and is especially evident for Europe. Europe has the highest share of electricity produced from renewable resources: wind and solar have a share of (17:095%) at the beginning of the simulation. Therefore, in this region one can observe the highest dependence on these power plant types.
The observed growth rate of fuel extraction also depends on the scenario, see Figure 6. For an optimistic scenario with respect to available fuel reserves, the annual extraction increases in the first fifty years and only then starts to decline. For the pessimistic scenario, the annual extraction starts to decline almost from the very beginning.
The observed growth rate of fuel prices also depends on the scenario, see Figure 7. For an optimistic scenario with respect to available fuel reserves, prices rise only moderately in the first fifty years and only start to increase significantly from that point on. For the pessimistic scenario, prices rise in a similar fashion to the optimistic scenario, although the rates of increase are relatively higher.
Damage
We have also considered temperature-related damage in the scenario analysis described in the previous paragraph. We use basic parameterisation to quantify the damage, as described in Section 4.15, by setting the value are of the factors \(f_\textrm{agriculture}^\textrm{damages}\), \(f_\textrm{labour}^\textrm{damages}\) and \(f_\textrm{disaster}^\textrm{damages}\) to \(0\). The aggregated results (mean \(\mu\) and standard deviation \(\sigma\)) are presented in Table 12 for GDP growth rates \(\textrm{gdp}_\textrm{gr}\) over the next \(100\) years. We use constant prices and we directly compare GDP values in the initial and final (100th) simulation step. Additionally, in columns four and five we show aggregated results that are calculated for the first half of the simulation steps only. Respectively, in columns six and seven we show the results for the second half.
| Scenario | \(\mu\) | \(\sigma\) | \(\mu_{(1-50)}\) | \(\sigma_{(1-50)}\) | \(\mu_{(51-100)}\) | \(\sigma_{(51-100)}\) |
| 1 | 1.163 | 0.063 | 0.520 | 0.018 | 0.423 | 0.042 |
| 2 | 1.291 | 0.055 | 0.560 | 0.019 | 0.469 | 0.027 |
| 3 | 1.214 | 0.056 | 0.518 | 0.019 | 0.459 | 0.030 |
| 4 | 1.315 | 0.083 | 0.558 | 0.020 | 0.485 | 0.044 |
The aggregated results (mean \(\mu\) and standard deviation \(\sigma\)) for GDP growth rates \(\textrm{gdp}_\textrm{gr}\) over the next 100 years in the regions considered in the simulation are presented in Table 13. We use constant prices, as in the previous analyses. The differences between cumulative growth rates for simulations with damages and without are shown in the Table 14. We can observe a relatively high regional variability of damage, with regions such as Africa having high damage rates, whereas in Europe the damage is minimal or may even lead to GDP increase (due to more productive agriculture and production transfer from other regions).
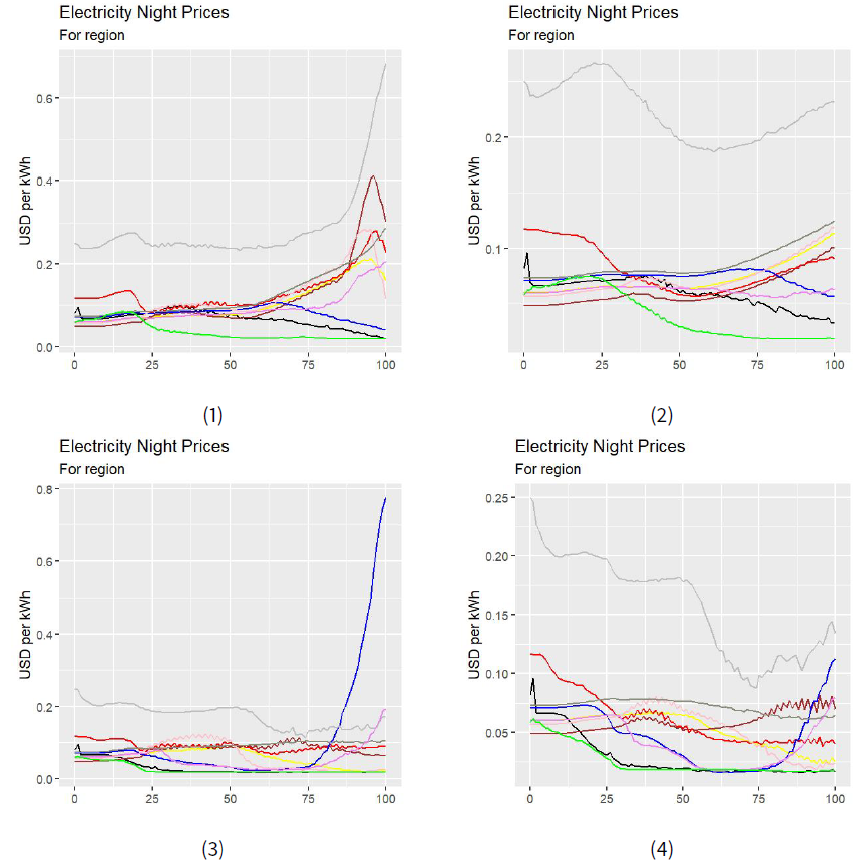
| region | \(\mu(1)\) | \(\sigma(1)\) | \(\mu(2)\) | \(\sigma(2)\) | \(\mu(3)\) | \(\sigma(3)\) | \(\mu(4)\) | \(\sigma(4)\) | |
| 1 | AF | 1.013 | 0.045 | 1.041 | 0.034 | 1.193 | 0.038 | 1.158 | 0.051 |
| 2 | AS | 1.169 | 0.046 | 1.212 | 0.055 | 1.285 | 0.042 | 1.282 | 0.061 |
| 3 | CHN | 1.201 | 0.165 | 1.562 | 0.086 | 1.479 | 0.124 | 1.583 | 0.092 |
| 4 | CIS | 1.257 | 0.099 | 1.406 | 0.060 | 1.365 | 0.090 | 1.432 | 0.090 |
| 5 | EU | 1.283 | 0.041 | 1.332 | 0.042 | 0.944 | 0.139 | 1.291 | 0.192 |
| 6 | IND | 1.170 | 0.084 | 1.284 | 0.047 | 1.379 | 0.083 | 1.330 | 0.055 |
| 7 | JPY | 1.182 | 0.051 | 1.242 | 0.045 | 1.283 | 0.083 | 1.306 | 0.057 |
| 8 | ME | 1.242 | 0.076 | 1.383 | 0.060 | 1.336 | 0.055 | 1.464 | 0.059 |
| 9 | NAM | 0.992 | 0.127 | 1.092 | 0.097 | 1.088 | 0.099 | 1.104 | 0.107 |
| 10 | SCA | 1.159 | 0.073 | 1.236 | 0.056 | 1.217 | 0.106 | 1.279 | 0.121 |
The damage functions are presented in Figure 8. On the \(x\)-axis we display the temperature increase due to greenhouse gas emissions in the damage scenario and on the \(y\)-axis the relative difference between the mean GDPs of the simulations, with and without damages. For representation, we smoothed the results using Generalized Linear Models (GLM) by assuming a polynomial up to the third order. A model selection exercise (Burnham & Anderson 2003) using the Bayesian Information Criterion shows that for scenarios 1, 3 and 4 a quadratic fit is best, whereas for scenario 2 a cubic polynomial is best. We find an almost linear relationship between temperature increase and the percentage of GDP lost due to damage, across a range of temperature increases up to roughly 1.5 °C. In scenarios \(1\) and \(3\) (with restricted fuel reserves) the damage functions’ growth rates decrease for temperatures above 2 °C. The observed shape of the damage functions is the result of two opposing tendencies. On the one hand, the damage increase is both linear (agricultural damage and damage related to natural disasters) and also non-linear (due to diminishing labour efficiency with gradually increasing diminution rates at higher temperatures) in relation to the global temperature increase. On the other hand, there is at least some partial adaptation to temperature increase: i.e. a tendency to substitute labour with capital and energy, a higher amount of production factors involved in the agricultural sector, tendency to at least partially rebuild the capital goods destroyed by temperature-related damage[11], and transferring global production to regions that are less affected by the damage. The adverse consequences prevail but the overall effect is roughly linear. However, we do not consider all potential consequences of a temperature increase, such as migration, civil conflicts, greater incidence of new diseases, and stranded assets. The main reason is that the consequences of these are currently unknown. Moreover, we have also assumed a linear relationship between the severity of natural disasters (as measured by the percentage of capital or production affected) as it was the simplest function to model. Such simplification allowed for the most robust parameter estimation, in the case where the damage data is available only for a moderate range of temperature increase. Developing a more complete damage function remains an objective for our future research.


Parameter sensitivity
In order to estimate the sensitivity of the results, both to changes in parameter values and heterogeneity of the agents, simulations were run for a total 1200 combinations of heterogeneity scenarios and parameter values. In particular, we considered 400 separate parameter sets applied to each heterogeneity scenario considered. Each single parameter set is selected, using the Sobol numbers sequence (Christophe & Petr 2018), from the entire parameter space, which is defined as the Cartesian product of permissible parameter values for each of the parameters, as defined in Table 15. The meaning of the symbols used is reiterated below for ease of reference.
- \(f_\textrm{elStress1}\) and \(f_\textrm{elStress2}\) — electricity market stress factors
- \(w_{\textrm{ep}}\) — current electricity price weight in the planned electricity price
- \(r_\textrm{cap}\) —power plants capacity reserve
- \(e_{\textrm{down}}\), \(e_{\textrm{up}}\), \(e_{\textrm{up}}^{\textrm{w}}\), \(e_{\textrm{up}}^{\textrm{s}}\), \(e_{\textrm{up}}^{\textrm{nh}}\), \(e_{\textrm{red}}\), \(\textrm{period}\), \(e_{\textrm{inj}}^{\textrm{sw}}\) — determine the change rates of the energy mix, see Equation 51, 52, 54 for more details.
- \(f_\textrm{fuelReserves}\) — fuel reserves factor
- \(\mu_{\textrm{gdp}}\), \(\alpha_{\textrm{gdp}}\), \(\sigma_{\textrm{gdp}}\), and \(\textrm{min}_{\textrm{gdp}}\) — determine planning of the next period GDP growth rates, see Equation 1 for more details.
- \(f_\textrm{agriculture}^\textrm{damages}\) — agricultural damage related factor, see Paragraph 4.16
- \(f_\textrm{labour}^\textrm{damages}\) — labour damage related factor, see Paragraph 4.18
- and \(f_\textrm{disaster}^\textrm{damages}\) — natural disaster damage related factor, see Paragraph 4.20
- \(f_\eta\), \(f_\eta^{\sigma}\), \(\Delta_\rho\), \(\Delta_\rho^\sigma\) — technology growth related parameters, introduced in Paragraph 4.23.
- \(f_\eta^{\sigma,region}\), \(f_\eta^{\sigma,individual}\), \(\Delta_\rho^{\sigma,region}\) and \(\Delta_\rho^{\sigma,individual}\) — technology growth related parameters, introduced in Paragraph 4.26.
- \(h_i\) — different variants of heterogeneity considered in the simulation. Described in Paragraph 4.26.
| region | 1 | 2 | 3 | 4 | |
| 1 | AF | -0.278 | -0.322 | -0.279 | -0.340 |
| 2 | AS | -0.175 | -0.260 | -0.190 | -0.209 |
| 3 | CHN | 0.063 | -0.032 | -0.028 | -0.029 |
| 4 | CIS | 0.126 | -0.049 | 0.016 | -0.019 |
| 5 | EU | 0.032 | 0.015 | 0.018 | 0.149 |
| 6 | IND | -0.178 | -0.274 | -0.169 | -0.281 |
| 7 | JPY | 0.032 | -0.008 | 0.010 | 0.016 |
| 8 | ME | -0.129 | -0.274 | -0.147 | -0.192 |
| 9 | NAM | -0.079 | -0.081 | -0.018 | -0.071 |
| 10 | SCA | -0.159 | -0.101 | -0.219 | -0.120 |
| 11 | WORLD | -0.050 | -0.101 | -0.069 | -0.062 |
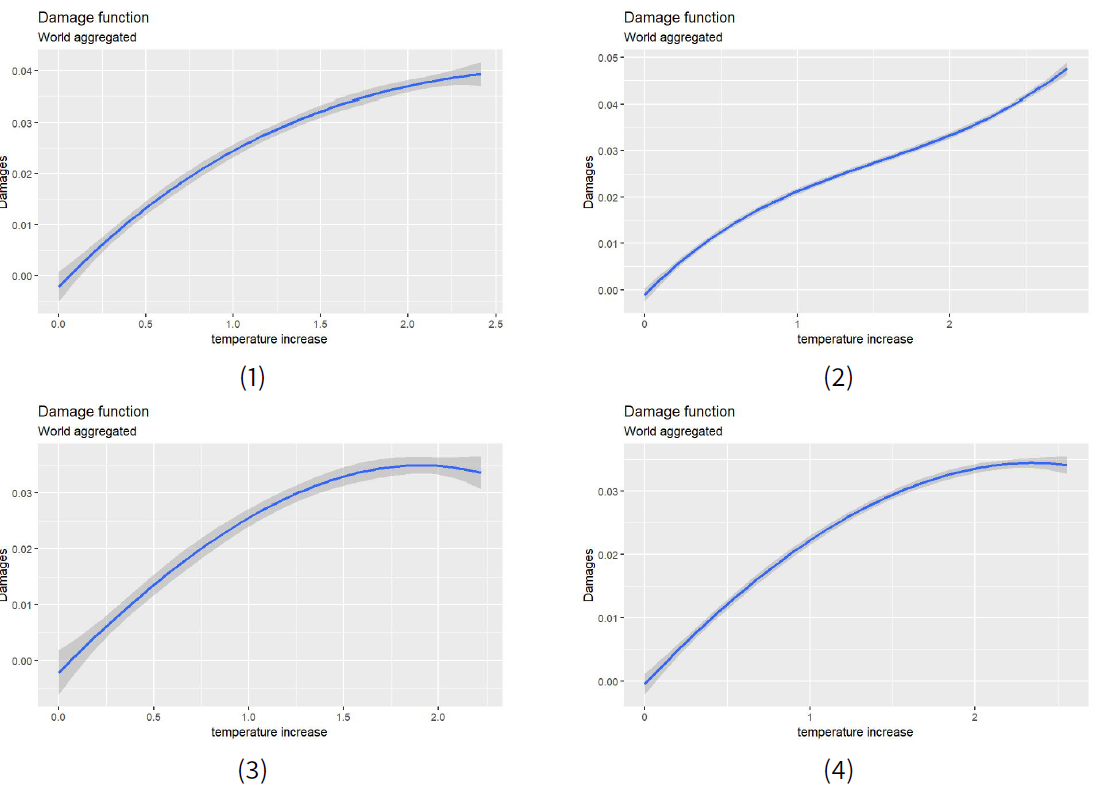
| Parameter | Lower value | Upper value |
| \(f_\textrm{elStress1}\) | 1.1 | 1.3 |
| \(f_\textrm{elStress2}\) | 1.2 | 1.6 |
| \(w_{\textrm{ep}}\) | 0.1 | 0.2 |
| \(r_\textrm{cap}\) | 1.1 | 1.3 |
| \(e_{\textrm{down}}\) | 20 | 30 |
| \(e_{\textrm{up}}\) | 5 | 10 |
| \(e_{\textrm{up}}^{\textrm{w}}\) | 10 | 200 |
| \(e_{\textrm{up}}^{\textrm{s}}\) | 30 | 600 |
| \(e_{\textrm{up}}^{\textrm{nh}}\) | 5 | 25 |
| \(e_{\textrm{red}}\) | 0.4 | 0.6 |
| \(\textrm{period}\) | 25 | 50 |
| \(e_{\textrm{inj}}^{\textrm{sw}}\) | 25 | 75 |
| \(f_\textrm{fuelReserves}\) | 0.75 | 1.25 |
| \(\mu_{\textrm{gdp}}\) | 0.01 | 0.03 |
| \(\alpha_{\textrm{gdp}}\) | 0.5 | 0.75 |
| \(\sigma_{\textrm{gdp}}\) | 0.005 | 0.015 |
| \(\textrm{min}_{\textrm{gdp}}\) | 0.001 | 0.005 |
| \(f_\textrm{agriculture}^\textrm{damages}\) | -0.05 | 0.05 |
| \(f_\textrm{labour}^\textrm{damages}\) | -0.15 | 0.15 |
| \(f_\textrm{disaster}^\textrm{damages}\) | -1 | 1 |
| \(f_\eta\) | 0.005 | 0.01 |
| \(f_\eta^{\sigma}\) | 0 | 0.0025 |
| \(f_\eta^{\sigma,region}\) | 0 | 0.0025 |
| \(f_\eta^{\sigma,individual}\) | 0 | 0.0025 |
| \(\Delta_\rho\) | 0 | 0.04359 |
| \(\Delta_\rho^\sigma\) | 0 | 0.0087 |
| \(\Delta_\rho^{\sigma,region}\) | 0 | 0.0087 |
| \(\Delta_\rho^{\sigma,individual}\) | 0 | 0.0087 |
Linear regression results of the world's total GDP (constant prices) growth rate (expressed as a number for readability) in the entire simulation on the selected parameters are presented in Table 16. We additionally took the heterogeneity scenarios into account with factors \(h_1\) and \(h_2\), and also included the interaction terms between damage-related parameters and heterogeneity scenarios. As the electricity market stress factors \(SF_E^1\) and \(SF_E^2\) are linearly dependent, we replaced both by their mean value \(SF_E\). The adjusted \(R^2\) is equal to \(0.9785\).
We can observe that higher expectations, particularly the long-term mean expected GDP growth rate (\(\mu_{\textrm{gdp}}\)), the minimum expected GDP growth rate (\(\textrm{min}_{\textrm{gdp}}\)) parameters, and available fuel reserves (\(f_\textrm{fuelReserves}\)) contribute to more rapid economic growth. In addition, GDP growth is supported by technology growth, leading to easier substitution of different types of energy (\(\Delta_\rho\)), and by higher production factors efficiency (\(f_\eta\)). Similarly, but to a lesser extent, sustained intensive growth in the installed capacity for solar and wind power plants (\(e_{\textrm{red}}\), \(\textrm{period}\)), and greater consideration of current electricity price changes in planning (\(w_{\textrm{ep}}\)), contribute to the faster economy growth. Higher rates of labour damage (\(f_\textrm{labour}^\textrm{damages}\)), as well as higher rates of damage from natural disasters (\(f_\textrm{disaster}^\textrm{damages}\)), lead to a fall in GDP growth rates. Counterintuitively, greater amounts of agricultural damage (\(f_\textrm{agriculture}^\textrm{damages}\)) lead to higher GDP growth rates. This results from the fact that decreased agricultural productivity can be substituted with more capital and energy use (the agricultural sector constitutes a relatively small part of total GDP). However, this effect disappears when taking into account heterogeneity on both the regional and individual levels. Heterogeneity generally decreases the GDP growth rate, although this effect is only statistically significant where there is heterogeneity on both the regional and individual levels, (\(h_2\)).
Linear regression results of absolute temperature growth in the entire simulation for the selected parameters (as used in the previous regression) are presented in Table 17. The adjusted \(R^2\) equals \(0.903\).
We can observe that those parameters which lead to higher GDP growth rates will also lead to increased global temperature. One might expect that more intensive growth of renewable resources (\(e_{\textrm{up}}^{\textrm{w}}\), \(e_{\textrm{up}}^{\textrm{s}}\), \(e_{\textrm{up}}^{\textrm{nh}}\)) lead to lower temperature increases.
As a final result, we show the distribution of temperature increases for all 4800 simulations in Figure 9. The chart on the left represents an empirical histogram and the chart on the right a smoothed density function. The mean increase was 2.476 °C and the standard deviation 0.125 °C.
| Parameter | Estimate | Std. Error | t value | Pr(>jtj) |
| (Intercept) | -0.832 | 0.028 | -30.012 | 0.000 |
| \(h_1\) | -0.004 | 0.002 | -1.900 | 0.058 |
| \(h_2\) | -0.123 | 0.002 | -64.309 | 0.000 |
| \(f_\textrm{elStressI}\) | -0.026 | 0.009 | -2.821 | 0.005 |
| \(w_{\textrm{ep}}\) | 0.167 | 0.027 | 6.099 | 0.000 |
| \(r_\textrm{cap}\) | -0.009 | 0.014 | -0.691 | 0.489 |
| \(e_{\textrm{down}}\) | 0.000 | 0.000 | 0.866 | 0.386 |
| \(e_{\textrm{up}}\) | -0.000 | 0.001 | -0.483 | 0.629 |
| \(e_{\textrm{up}}^{\textrm{w}}\) | 0.000 | 0.000 | 0.131 | 0.896 |
| \(e_{\textrm{up}}^{\textrm{s}}\) | 0.000 | 0.000 | 2.909 | 0.004 |
| \(e_{\textrm{up}}^{\textrm{nh}}\) | -0.000 | 0.000 | -0.029 | 0.977 |
| \(e_{\textrm{red}}\) | 0.065 | 0.014 | 4.742 | 0.000 |
| \(\textrm{period}\) | 0.001 | 0.000 | 5.821 | 0.000 |
| \(e_{\textrm{inj}}^{\textrm{sw}}\) | 0.000 | 0.000 | 0.468 | 0.640 |
| \(f_\textrm{fuelReserves}\) | 0.164 | 0.005 | 30.029 | 0.000 |
| \(\mu_{\textrm{gdp}}\) | 3.716 | 0.136 | 27.267 | 0.000 |
| \(\alpha_{\textrm{gdp}}\) | -0.077 | 0.011 | -7.034 | 0.000 |
| \(\sigma_{\textrm{gdp}}\) | 2.661 | 0.273 | 9.752 | 0.000 |
| \(\textrm{min}_{\textrm{gdp}}\) | 2.495 | 0.462 | 5.402 | 0.000 |
| \(f_\textrm{agriculture}^\textrm{damages}\) | 0.527 | 0.047 | 11.183 | 0.000 |
| \(f_\textrm{labour}^\textrm{damages}\) | -0.190 | 0.016 | -12.083 | 0.000 |
| \(f_\textrm{disaster}^\textrm{damages}\) | -0.022 | 0.002 | -9.343 | 0.000 |
| \(\Delta_\rho\) | 0.881 | 0.063 | 14.063 | 0.000 |
| \(\Delta_\rho^\sigma\) | -0.237 | 0.313 | -0.757 | 0.449 |
| \(\Delta_\rho^{\sigma,region}\) | 0.460 | 0.313 | 1.472 | 0.141 |
| \(\Delta_\rho^{\sigma,individual}\) | -0.699 | 0.318 | -2.199 | 0.028 |
| \(f_\eta\) | 249.321 | 0.548 | 455.349 | 0.000 |
| \(f_\eta^{\sigma}\) | -6.713 | 1.089 | -6.165 | 0.000 |
| \(f_\eta^{\sigma,region}\) | -2.170 | 1.091 | -1.989 | 0.047 |
| \(f_\eta^{\sigma,individual}\) | -21.798 | 1.091 | -19.977 | 0.000 |
| \(h_1 \times f_\textrm{agriculture}^\textrm{damages}\) | -0.163 | 0.067 | -2.440 | 0.015 |
| \(h_2 \times f_\textrm{agriculture}^\textrm{damages}\) | -0.721 | 0.067 | -10.813 | 0.000 |
| \(h_1 \times f_\textrm{labour}^\textrm{damages}\) | 0.003 | 0.022 | 0.141 | 0.888 |
| \(h_2 \times f_\textrm{labour}^\textrm{damages}\) | -0.061 | 0.022 | -2.734 | 0.006 |
| \(h_1 \times f_\textrm{disaster}^\textrm{damages}\) | 0.003 | 0.003 | 0.868 | 0.386 |
| \(h_2 \times f_\textrm{disaster}^\textrm{damages}\) | 0.003 | 0.003 | 0.876 | 0.381 |
| Parameter | Estimate | Std. Error | t value | Pr(>jtj) |
| (Intercept) | 1.714 | 0.020 | 85.966 | 0.000 |
| \(h_1\) | -0.006 | 0.001 | -4.131 | 0.000 |
| \(h_2\) | -0.039 | 0.001 | -28.182 | 0.000 |
| \(f_\textrm{elStressI}\) | 0.010 | 0.007 | 1.606 | 0.108 |
| \(w_{\textrm{ep}}\) | 0.303 | 0.020 | 15.358 | 0.000 |
| \(r_\textrm{cap}\) | 0.000 | 0.010 | 0.022 | 0.982 |
| \(e_{\textrm{down}}\) | 0.000 | 0.000 | 0.452 | 0.651 |
| \(e_{\textrm{up}}\) | 0.000 | 0.000 | 0.944 | 0.345 |
| \(e_{\textrm{up}}^{\textrm{w}}\) | -0.001 | 0.000 | -63.709 | 0.000 |
| \(e_{\textrm{up}}^{\textrm{s}}\) | -0.000 | 0.000 | -22.748 | 0.000 |
| \(e_{\textrm{up}}^{\textrm{nh}}\) | -0.001 | 0.000 | -10.169 | 0.000 |
| \(e_{\textrm{red}}\) | -0.023 | 0.010 | -2.349 | 0.019 |
| \(\textrm{period}\) | -0.002 | 0.000 | -19.110 | 0.000 |
| \(e_{\textrm{inj}}^{\textrm{sw}}\) | -0.001 | 0.000 | -13.565 | 0.000 |
| \(f_\textrm{fuelReserves}\) | 0.641 | 0.004 | 163.574 | 0.000 |
| \(\mu_{\textrm{gdp}}\) | 1.271 | 0.098 | 12.962 | 0.000 |
| \(\alpha_{\textrm{gdp}}\) | -0.021 | 0.008 | -2.610 | 0.009 |
| \(\sigma_{\textrm{gdp}}\) | 1.598 | 0.196 | 8.139 | 0.000 |
| \(\textrm{min}_{\textrm{gdp}}\) | 1.273 | 0.332 | 3.830 | 0.000 |
| \(f_\textrm{agriculture}^\textrm{damages}\) | -0.540 | 0.034 | -15.913 | 0.000 |
| \(f_\textrm{labour}^\textrm{damages}\) | -0.028 | 0.011 | -2.468 | 0.014 |
| \(f_\textrm{disaster}^\textrm{damages}\) | -0.022 | 0.002 | -12.800 | 0.000 |
| \(\Delta_\rho\) | -0.953 | 0.045 | -21.143 | 0.000 |
| \(\Delta_\rho^\sigma\) | -0.358 | 0.225 | -1.592 | 0.111 |
| \(\Delta_\rho^{\sigma,region}\) | -0.254 | 0.225 | -1.127 | 0.260 |
| \(\Delta_\rho^{\sigma,individual}\) | -0.045 | 0.229 | -0.196 | 0.844 |
| \(f_\eta\) | 37.869 | 0.394 | 96.103 | 0.000 |
| \(f_\eta^{\sigma}\) | -2.068 | 0.784 | -2.639 | 0.008 |
| \(f_\eta^{\sigma,region}\) | 0.232 | 0.785 | 0.296 | 0.767 |
| \(f_\eta^{\sigma,individual}\) | -14.573 | 0.785 | -18.558 | 0.000 |
| \(h_1 \times f_\textrm{agriculture}^\textrm{damages}\) | 0.044 | 0.048 | 0.910 | 0.363 |
| \(h_2 \times f_\textrm{agriculture}^\textrm{damages}\) | 0.375 | 0.048 | 7.818 | 0.000 |
| \(h_1 \times f_\textrm{labour}^\textrm{damages}\) | -0.003 | 0.016 | -0.196 | 0.844 |
| \(h_2 \times f_\textrm{labour}^\textrm{damages}\) | 0.024 | 0.016 | 1.513 | 0.130 |
| \(h_1 \times f_\textrm{disaster}^\textrm{damages}\) | 0.001 | 0.002 | 0.500 | 0.617 |
| \(h_2 \times f_\textrm{disaster}^\textrm{damages}\) | -0.000 | 0.002 | -0.165 | 0.869 |

Conclusions and Further Research
The baseline scenario results (for homogeneous agents and a linear, sector-independent damage function) enable a benchmarking with current existing CGE and IAM models. The results we obtained show that future GDP trends are very sensitive to factors that influence the transition from fuel-based energy production to energy production from renewable resources. The advantage of using the agent-based approach is that the optimisation process is distributed among the agents (individual agents act in their own interest) and the observed variables result from market interactions. This is less abstract and more realistic than global macroeconomic aggregated optimisation. Moreover, it enabled us to investigate the effect of heterogeneity (which is also closer to reality): heterogeneous private households with respect to wealth, heterogeneous companies with respect to size, and heterogeneous technology growth and damage.
Using our model, the estimated damage function has the following properties. It assumes values in the range 3% – 4% for a 2 °C temperature increase and has a linear (or slightly concave) shape. Nevertheless, we only used damage related to labour efficiency, the agricultural sector and natural disasters, as there are enough data to reliably estimate the impact of other damage types in a quantitative and not just qualitative way. In future research, our objective is to develop probabilistic damage functions which are similar to Franzke & Czupryna (2019) for the regions considered in our study. Some policies could be carried out, based on the results obtained from our model. Especially the ones that influence the growth rates of the installed capacities of different types of power plants. However, with further research, standard policies may be proposed that include taxes, subsidies, different mechanisms e.g. additional mechanisms for electricity markets or supporting mechanisms to incentivise the development of energy storage capacity.
Model Documentation
The code and the parameter files are available on the OPEN ABM platform, see https://www.comses.net/codebases/ff93e3f3-6181-46b6-9b39-738600ba27f9/releases/1.0.0/.Acknowledgements
The Work was supported through the Cluster of Excellence, Integrated Climate System Analysis and Prediction, 'CliSAP' (DFG EXC177), Universität Hamburg, funded through the Deutsche Forschungsgemeinschaft. Marcin Czupryna thanks CliSAP for financial support of his research stay in Hamburg and Cracow University of Economics for supporting further work on this paper. We would like to thank Hermann Held, Chao Li and attendees of SSC 2017, GENED 2017 and ABM Workshops in Hamburg (March 2017), Berlin (May 2017) and Münster (July 2017) for helpful suggestions and fruitful discussions. Sascha Hokamp owes special thanks to Alexander Yanke. However, all errors and opinions are ours. We would also like to thank Timothy Harrell for his advice concerning matters of English usage.Notes
- However, a climate-related objective is also indirectly included in the model as a restriction on the global mean temperature change.
- A company can produce a maximal quantity but this requires an additional extraordinary e ort as for example overtime in case of labour force.
- We will further use the tilde symbol to distinguish next \(t+1\) period values estimated and planned by an agent at the beginning of this period, from the actual values that are observed at the end of the period. These results from the market interaction among agents
- More precisely, the physical capital amount, which is first planned at the beginning of simulation period \(t+1\) and denoted \(\widetilde{k}^{t+1}\), then updated after the capital goods market has cleared — \(k^{t+1}\) will be subsequently used for production in the simulation period \(t+2\).
- Having more than one citizen for a power plant is not in general realistic. It results from the fact that the electricity sector is modelled in a more detailed way than we model other components and has no impact on the validity of the results.
- Depreciation at the end of the period is due to the fact that, as in the case of fuel extraction companies, power plants are characterised by a prolonged investment period. Therefore, we assumed that the entire phys-ical capacity purchased up to simulation step t, and not depreciated thus far, will be available for electricity generation in the period \(t + 1\).
- Initially at the simulation start the capacities are uniformly distributed over the whole power plant lifetime.
- The planned labour is a continuous variable in the model.
- The current labour is a discrete variable in a model.
- pacf[k] represents \(k\) lagged coefficient of the partial autocorrelation function (PACF).
- Such a phenomenon may be seen in Japan. Natural disasters do not necessarily lead to a decrease in GDP; they may even have demand stimulating effects (Hallegatte & Ghil 2008).
Appendix: Parametrisation
In the following appendix we discuss the parameterisation process in a more detailed way.
GDP and production
The basis for GDP parameterisation was the World Bank data, see World Bank (2016) on GDP expressed in international USD, taking into account purchasing power parity. Then the total GDP was hierarchically disaggregated into industry sectors, using the same data source and time series on industry sectors: Agriculture, Chemicals, Food and beverages, Industry, Machinery, Manufacturing, Other manufacturing, Services, and Textiles, complemented by information on Mining and quarrying, Electricity, Gas and Water supply, Construction, and Transport, Storage and Communication from United Nations (2017), see Table 18. The data for the category Mining, electricity, and construction was calculated as the difference between the original categories: Industry and Manufacturing.
| Level 0 | Level 1 | Level 2 | |
| GDP | Agriculture | Agriculture | |
| Food and beverages | |||
| Textiles | |||
| Manufacturing | Other manufacturing | ||
| Chemicals | |||
| Machinery | |||
| Mining and quarrying | |||
| Mining, electricity, and construction | Electricity and Gas | ||
| Construction | |||
| Services | Services without transport | ||
| Transport | |||
For China, we have directly used information from the Chinese Statistical Office (Chinese Statistical Office 2015).
In the second step, Agriculture and Food and Beverages were aggregated into one category. Similarly, Machinery, Mining and Construction were aggregated into one Production Goods sector.
In the final step, energy sector usage was added to GDP. This allowed us to obtain the data on total production per industry sector, see Table 19.
| region | Agriculture | Textiles | Chemicals | Other manufacturing | Transport | Other Services | Production Goods |
| AF | 1215603.4 | 50908.0 | 85472.4 | 323257.7 | 463242.4 | 2577313.7 | 300526.3 |
| AS | 1850817.7 | 177132.9 | 283900.2 | 784657.8 | 1145809.5 | 5856196.2 | 1860446.0 |
| CHN | 2521281.0 | 470318.6 | 1295076.1 | 1825100.0 | 990107.4 | 8633349.9 | 4020099.7 |
| CIS | 457091.6 | 17133.4 | 101727.2 | 461553.8 | 575304.4 | 2623878.4 | 515506.3 |
| EU | 1039843.9 | 170877.6 | 558179.5 | 1517193.2 | 1825938.2 | 14753915.1 | 2709000.0 |
| IND | 1588671.7 | 123950.7 | 245043.8 | 639793.2 | 665352.7 | 3492902.2 | 1027855.9 |
| JPY | 184052.7 | 16638.5 | 133701.8 | 343539.1 | 361013.9 | 3589645.5 | 666847.7 |
| ME | 302718.9 | 20346.7 | 225826.2 | 325581.3 | 456635.3 | 2216310.7 | 420795.7 |
| NAM | 950634.5 | 96561.8 | 380334.1 | 1288947.7 | 1641604.3 | 15367281.1 | 1970657.4 |
| SCA | 768049.8 | 55831.6 | 135839.7 | 431720.7 | 643008.9 | 4258900.4 | 881206.8 |
To get the consumption data, international trade statistics data on exports and imports (cross-tabulated for each region in the simulation) was used, World Trade Organisation (2014) complemented by Royal Bank of India (August 2014).
Labour markets
The basis for the labour force data was the World Bank data on the total population and percentage share of employed and unemployed, see World Bank (2016). This information allowed us to calculate the total labour force per region (as a product of the total population and the percentage sum of employees and unemployed). Using the information on the proportion of employees in the following broad industry sectors — agriculture, industry, and services (International Labour Office (ILO) 2015), together with GDP per sector, we allocated employees to the industry sectors considered in the simulation.
Information regarding remuneration share in GDP International Labour Office (ILO) () can be used to calculate the average remuneration per region.
The results are presented in Tables 20 and 21.
| region | Agriculture | Textiles | Chemicals | Other manuf. | Transport | Services | Prod. goods | Energy | Fuel Extraction |
| AF | 393 | 3 | 5 | 20 | 48 | 277 | 18 | 6 | 45 |
| AS | 300 | 7 | 10 | 31 | 54 | 297 | 71 | 16 | 12 |
| CHN | 303 | 15 | 39 | 59 | 39 | 381 | 125 | 16 | 14 |
| CIS | 27 | 1 | 2 | 11 | 19 | 97 | 12 | 5 | 14 |
| EU | 31 | 3 | 6 | 23 | 27 | 236 | 40 | 8 | 3 |
| IND | 380 | 8 | 14 | 40 | 29 | 163 | 64 | 13 | 15 |
| JPY | 4 | 1 | 2 | 5 | 5 | 49 | 9 | 2 | 0 |
| ME | 19 | 1 | 2 | 4 | 12 | 64 | 5 | 1 | 22 |
| NAM | 21 | 1 | 4 | 16 | 20 | 214 | 24 | 6 | 6 |
| SCA | 81 | 2 | 3 | 12 | 25 | 182 | 24 | 7 | 9 |
| region | renum |
| AF | 1833.9 |
| AS | 6726.3 |
| CHN | 7805.1 |
| CIS | 10187.5 |
| EU | 31816.0 |
| IND | 3565.6 |
| JPY | 38856.4 |
| ME | 9900.9 |
| NAM | 38573.6 |
| SCA | 8513.7 |
Subsequently, we made two further adjustments, one for Japan’s textiles industry sector (divided by two) and the other for the Asian energy sector (subtracted 1000 USD), since the initial parameterisation led to a financial loss (due to rounding in the case of Japan). The remuneration figures in other sectors were adjusted accordingly.
Capital
Despite initially planning to use real data on capital per sector and region, it transpired that such data for this degree of detail is only available for Europe and North America. Therefore, we have applied a simplified ap-proach. In the first step, we calculated the capital based on the production to capital ratio, derived from the values in Europe and North America (see Table 22), and production per sector. We have also taken into account regional differences by scaling the capital values down for less developed regions, see Table 23.
In the second step, we scaled the capital values in such a way that savings equal the capital demand for each region (we have assumed a depreciation of 7%). The reason for the second step is data consistency.
Capital values per sector and region are presented in Table 24.
Energy markets
For electricity markets, we have used the parameters presented in Table 25.
| Sector | Ratio |
| Agriculture | 0.7 |
| Textiles | 0.8 |
| Chemicals | 0.8 |
| Other manufacturing | 0.8 |
| Transport | 1.2 |
| Services | 0.4 |
| Production Goods | 0.8 |
| Mining | 0.35 |
| Electricity | 0.25 |
| Regions | Ratio |
| EU, JPY, NAM | 1 |
| CHN, CIS, AS | 0.9 |
| SCA, IND | 0.8 |
| AF | 0.7 |
| region | Agriculture | Textiles | Chemicals | Other manuf. | Transport | Other Services | Production |
| AF | 623365.7 | 22842.6 | 38351.7 | 145046.7 | 138572.2 | 2312897.1 | 134847.0 |
| AS | 3297090.3 | 276105.2 | 442528.2 | 1223081.9 | 1190683.7 | 18256640.5 | 2899962.1 |
| CHN | 6227199.1 | 1016416.5 | 2798819.1 | 3944266.3 | 1426496.2 | 37315468.3 | 8687931.4 |
| CIS | 520757.8 | 17079.9 | 101409.2 | 460111.3 | 382337.6 | 5231356.1 | 513895.2 |
| EU | 1018636.9 | 146468.5 | 478446.3 | 1300469.6 | 1043407.9 | 25292781.4 | 2322032.6 |
| IND | 2204487.6 | 150497.9 | 297526.2 | 776821.4 | 538570.1 | 8481994.4 | 1247997.7 |
| JPY | 118510.8 | 9374.3 | 75328.8 | 193553.1 | 135599.0 | 4044878.2 | 375708.1 |
| ME | 334731.0 | 19686.0 | 218493.6 | 315009.7 | 294538.8 | 4288693.6 | 407132.4 |
| NAM | 507793.8 | 45132.3 | 177765.3 | 602444.7 | 511515.9 | 14365108.9 | 921070.8 |
| SCA | 969487.2 | 61665.3 | 150033.2 | 476830.1 | 473463.5 | 9407803.7 | 973281.8 |
| Source | Cost | Floor cost | Learning rate | Capacity factor | Efficiency | Avg. Power |
| coal | 750 | 40 | 0.7000 | 10 | ||
| gas | 600 | 35 | 0.5000 | 2 | ||
| nuclear | 3100 | 40 | 0.8000 | 10 | ||
| oil | 600 | 35 | 0.3000 | 1 | ||
| hydro | 2300 | 70 | 0.4000 | 2 | ||
| wind | 1500 | 900 | -0.1844 | 25 | 0.2500 | 2 |
| solar | 5000 | 500 | -0.3219 | 30 | 0.1500 | 1 |
| storage | 4000 | 340 |
| Region | Coal | Gas | Oil | Nuclear | Hydro | Wind | Solar |
| AF | 0,03 | 0,07 | 0,07 | 0,035 | 0,015 | 0,01 | 0,01 |
| AS | 0,03 | 0,06 | 0,06 | 0,035 | 0,015 | 0,01 | 0,01 |
| CHN | 0,02 | 0,03 | 0,03 | 0,035 | 0,015 | 0,01 | 0,01 |
| CIS | 0,02 | 0,03 | 0,03 | 0,035 | 0,015 | 0,01 | 0,01 |
| EU | 0,04 | 0,12 | 0,12 | 0,045 | 0,015 | 0,01 | 0,01 |
| IND | 0,02 | 0,03 | 0,03 | 0,035 | 0,015 | 0,01 | 0,01 |
| JPY | 0,14 | 0,18 | 0,18 | 0,145 | 0,015 | 0,01 | 0,01 |
| ME | 0,02 | 0,03 | 0,03 | 0,035 | 0,015 | 0,01 | 0,01 |
| NAM | 0,03 | 0,07 | 0,07 | 0,035 | 0,015 | 0,01 | 0,01 |
| SCA | 0,02 | 0,03 | 0,03 | 0,035 | 0,015 | 0,01 | 0,01 |
The following time series were also used. Combining electric power consumption (kWh per capita) with the total population gives us the total power consumption. Using the information on electric power transmission and distribution losses, we were able to calculate the total power production. Using the data on electricity production from coal, hydroelectric, natural gas, nuclear, oil, and renewable (excluding hydroelectric) sources (% of total), we allocate the total power production to different electric energy sources. The category renewable, excluding hydroelectric sources, is then broken down into wind and solar (SPV and CSP) using the world share of wind energy in total energy production in the renewable category (91.667 %). Using the capacity factors (percentage of time the source was generating electricity) presented in Table 25, we calculated the total installed capacities for each region, see Table 27.
| region | coal | gas | oil | nuclear | hydro | wind | solar |
| AF | 0.0436 | 0.0656 | 0.0248 | 0.0020 | 0.0337 | 0.0056 | 0.0005 |
| AS | 0.1216 | 0.1480 | 0.0446 | 0.0246 | 0.0611 | 0.0316 | 0.0029 |
| CHN | 0.6747 | 0.0263 | 0.0036 | 0.0190 | 0.3016 | 0.1000 | 0.0092 |
| CIS | 0.0496 | 0.1585 | 0.0048 | 0.0380 | 0.0695 | 0.0011 | 0.0001 |
| EU | 0.1525 | 0.1464 | 0.0247 | 0.1189 | 0.1766 | 0.2789 | 0.0256 |
| IND | 0.1603 | 0.0146 | 0.0088 | 0.0052 | 0.0382 | 0.0294 | 0.0027 |
| JPY | 0.0576 | 0.0930 | 0.0356 | 0.0014 | 0.0250 | 0.0355 | 0.0033 |
| ME | 0.0043 | 0.1493 | 0.1440 | 0.0006 | 0.0060 | 0.0008 | 0.0001 |
| NAM | 0.2623 | 0.3768 | 0.0294 | 0.1384 | 0.1881 | 0.1591 | 0.0146 |
| SCA | 0.0117 | 0.0582 | 0.0538 | 0.0033 | 0.1969 | 0.0402 | 0.0037 |
Based on the total installed capacities, and the average assumed capacity of the power plant (or group of power plants as in the case of wind farms), see Table 25, the numbers of power plants of each type and for each region were calculated. Additionally, these numbers were divided by 10 and rounded to reduce the simulation running time.
We also assumed the following electricity prices for the regions (see Table 28), based on Birol et al. (2016).
| Region | cnts/kWh | Region | cnts/kWh |
| AF | 0.1400 | IND | 0.0800 |
| AS | 0.0800 | JPY | 0.2600 |
| CHN | 0.0800 | ME | 0.0800 |
| CIS | 0.1100 | NAM | 0.1200 |
| EU | 0.2500 | SCA | 0.1400 |
We also used 2015 data on fuel consumption (coal, crude oil and gas), fuel extraction, and prices (BP London 2016). The original units of tonne, barrel, and million btu (British thermal units) used in the report were trans-formed to toE (tonne of oil equivalent) and the prices respectively recalculated. In order to use both data sources BP London (2016) and World Bank (2016) in a coherent way, we have used the following approach. Based on the electricity production data and efficiency factors, we calculated the quantity of fuel used for electricity production. We then subtracted these values from the total consumption data and obtained the fuel quantities used directly for energy generation. Then the global total consumption values were distributed among regions, based on their respective share of total world production (the assumption that total world fuel consumption equals total world production is a simplification, which we make on the basis that the differences are small and due to missing data on regional fuel stocks). BP Statistical Review publishes world reserve values using a conservative approach, e.g. reserves reported in 2015 are 50.73% higher for crude oil, 55.88% higher for gas and 13.58% lower for coal than the same values reported in 1995, despite continuous extraction. Therefore, we assumed that for both crude oil and gas, new reserves amounting to 10% of current reserves will be discovered each decade, whereas for coal the same proportion of new reserves would take 100 years. The values used in the simulation are presented in Table 1 Tables 29, Table 1 30, and Table 1 31.
The energy sources (electricity and fuel not used for electricity production) were broken down into the industry sectors considered in the simulation. As the data is very limited, we have used a hierarchical approach (consecutively using data from (Government Publications Office 2016)) and some approximations whenever necessary.
In the first step, we used the data on crude oil and related products, natural gas, coal, and electricity use in residential, commercial, industrial, and transportation sectors, to first calculate the shares of these sectors in total energy usage per region and then break down the total energy usage. In the second step, industrial energy usage was broken down according to the simulation-relevant industry sectors using their energy intensity factors and the value of the gross domestic product. The energy intensity factors (representing energy usage per product) were approximated using the 2012 data (see Government Publications Office (2016)) on energy-intensive sectors for the following categories: Basic chemicals, Food, Iron and steel, Non-ferrous metals, Non-metallic minerals, Paper, Refining, and a ‘Remaining’ category, with figures presented separately for OECD and non-OECD countries. The category Remaining was additionally distributed according to the industry sector. The factors are presented in Table 32.
| Fuel | Price |
| crude oil | 378.7961 |
| gas | 262.1038 |
| coal | 107.1429 |
| region | coal | gas | oil |
| AF | 183.7556 | 177.6806 | 385.4379 |
| AS | 706.4734 | 318.9744 | 136.9703 |
| CHN | 2497.0506 | 123.1939 | 207.8462 |
| CIS | 353.2338 | 786.3530 | 650.3617 |
| EU | 442.0734 | 234.2506 | 166.2632 |
| IND | 539.2401 | 28.9834 | 41.1664 |
| JPY | 0.0000 | 2.5324 | 0.4305 |
| ME | 0.7763 | 533.5892 | 1291.5848 |
| NAM | 622.6246 | 838.7811 | 738.3602 |
| SCA | 79.0822 | 197.1512 | 510.1115 |
| region | coal | gas | oil |
| AF | 64.1553 | 82.4030 | 20.2616 |
| AS | 178.9946 | 185.7604 | 36.3947 |
| CHN | 993.1812 | 32.9971 | 2.9711 |
| CIS | 72.9348 | 198.9908 | 3.9289 |
| EU | 224.4746 | 183.8010 | 20.1638 |
| IND | 235.9599 | 18.3440 | 7.1673 |
| JPY | 84.7652 | 116.7073 | 29.0531 |
| ME | 6.2829 | 187.4435 | 117.4866 |
| NAM | 386.0364 | 473.0257 | 24.0158 |
| SCA | 17.2483 | 73.0311 | 43.9235 |
| OECD | NON OECD | ||
| Sector | Value | Sector | Value |
| Agriculture | 7.9510 | Agriculture | 5.9603 |
| Textiles | 4.4684 | Textiles | 4.7795 |
| Other manufacturings | 6.4259 | Other manufacturings | 5.0713 |
| Chemicals | 39.0114 | Chemicals | 14.5624 |
| Machinery mining | 11.7900 | Machinery mining | 11.6536 |
| Construction | 4.4684 | Construction | 4.7795 |
Climate module
We have used the original values of the Petschel-Held model (with the exception of the \(T_1\) parameter, which is the 2015 global temperature value), see Table 33.
| parameter | value | X |
| \(B\) | 0.002 | ppm/GtC*yr |
| \(\beta\) | 0.470 | ppm/GtC |
| \(\sigma\) | 0.021 | /yr |
| \(\mu\) | 0.087 | C/yr |
| \(C_1\) | 290.000 | ppm |
| \(\alpha\) | 0.017 | /yr |
| \(T_1\) | 14.600 | °C |
| F | 545.000 | GtC |
| C | 400.000 | ppm |
| E | 7.900 | GtC/yr |
| T | 14.800 | °C |
References
ASSENZA, T., Gatti, D. D. & Grazzini, J. (2015). Emergent dynamics of a macroeconomic agent based model with capital and credit. Journal of Economic Dynamics and Control, 50, 5–28.
AUSLOOS, M., Miśkiewicz, J. & Sanglier, M. (2004). The durations of recession and prosperity: does their distri-bution follow a power or an exponential law? Physica A: Statistical Mechanics and its Applications, 339(3-4), 548–558.
BALINT, T., Lamperti, F., Mandel, A., Napoletano, M., Roventini, A. & Sapio, A. (2017). Complexity and the economics of climate change: a survey and a look forward. Ecological Economics, 138, 252–265.
BARROS, V. R. (2014). Climate Change 2014–Impacts, Adaptation and Vulnerability: Global and Sectoral Aspects. Cambridge, MA: Cambridge University Press.
BIROL, F. et al. (2016). World energy outlook 2016. International Energy Agency, 1(3).
BOSETTI, V., Carraro, C., Galeotti, M., Massetti, E. & Tavoni, M. (2006). Witch a world induced technical change hybrid model. The Energy Journal, 13–37
BP LONDON (2016). BP Statistical Review of World Energy June 2016.
BURKE, M., Hsiang, S. M. & Miguel, E. (2015). Global non-linear effect of temperature on economic production. Nature, 527(7577), 235.
BURNHAM, K. P. & Anderson, D. R. (2003). Model Selection and Multimodel Inference: A Practical Iinformation-Theoretic Approach. Berlin/Heidelberg: Springer.
CHINESE Statistical Office (2015). Chinese statistical Office database: http://www.stats.gov.cn/tjsj/ndsj/2016/indexeh.htm.
CHRISTOPHE, D. & Petr, S. (2018). randtoolbox: Generating and Testing Random Numbers. R package version 1.17.1.
CISCAR, J.-C., Iglesias, A., Feyen, L., Szabó, L., Van Regemorter, D., Amelung, B., Nicholls, R., Watkiss, P., Chris-tensen, O. B., Dankers, R. et al. (2011). Physical and economic consequences of climate change in Europe. Proceedings of the National Academy of Sciences, 108(7), 2678–2683.
CORONESE, M., Lamperti, F., Keller, K., Chiaromonte, F. & Roventini, A. (2019). Evidence for sharp increase in the economic damages of extreme natural disasters. Proceedings of the National Academy of Sciences of the United States of America, 116(43), 21450–21455.
COVINGTON, H. & Thamotheram, R. (2015). The case for forceful stewardship (part 1): The financial risk from global warming. Tech. rep., SSRN. Last accessed: 29.04.2017.
DENNIG, F., Budolfson, M. B., Fleurbaey, M., Siebert, A. & Socolow, R. H. (2015). Inequality, climate impacts on the future poor, and carbon prices. Proceedings of the National Academy of Sciences, 112(52), 15827–15832.
DIAZ, D. D. & Moore, F. (2017). Quantifying the economic risks of climate change. Nature Climate Change, 7, 774–782.
DIETZ, S. & Stern, N. (2015). Endogenous growth, convexity of damage and climate risk: how Nordhaus’ framework supports deep cuts in carbon emissions. The Economic Journal, 125(583), 574–620.
DOSI, G., Fagiolo, G. & Roventini, A. (2010). Schumpeter meeting Keynes: A policy-friendly model of endogenous growth and business cycles. Journal of Economic Dynamics and Control, 34(9), 1748–1767.
DOWLATABADI, H. (1995). Integrated assessment models of climate change: An incomplete overview. Energy Policy, 23(4-5), 289–296.
EDENHOFER, O., Bauer, N. & Kriegler, E. (2005). The impact of technological change on climate protection and welfare: Insights from the model mind. Ecological Economics, 54(2-3), 277–292.
FAGIOLO, G., Guerini, M., Lamperti, F., Moneta, A. & Roventini, A. (2019). ‘Validation of agent-based models in economics and finance.’ In C. Beisbart & N. J. Saam (Eds.), Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives,, (pp. 763–787). Berlin/Heidelberg: Springer.
FAGIOLO, G., Moneta, A. & Windrum, P. (2007). A critical guide to empirical validation of agent-based models in economics: Methodologies, procedures, and open problems. Computational Economics, 30(3), 195–226.
FAGIOLO, G., Napoletano, M. & Roventini, A. (2008). Are output growth-rate distributions fat-tailed? some evidence from OECD countries. Journal of Applied Econometrics, 23(5), 639–669.
FAGIOLO, G. & Roventini, A. (2017). Macroeconomic policy in DSGE and agent-based models redux: New developments and challenges ahead. Journal of Artificial Societies and Social Simulation, 20 (1) 1: https://www.jasss.org/20/1/1.html.
FRANZKE, C. L. (2017). Impacts of a changing climate on economic damages and insurance. Economics of Disaster and Climate Change, 1(1), 95–110.
FRANZKE, C. L. & Czupryna, M. (2019). Probabilistic assessment and projections of us weather and climate risks and economic damages. Climatic Change, (pp. 1–13)
GEISENDORF, S. & Klippert, C. (2017). The effect of green investments in an agent-based climate-economic model. Environmental Modeling & Assessment, 22(4), 323–343.
GERLAGH, R. & Van Der Zwaan, B. (2004). A sensitivity analysis of timing and costs of greenhouse gas emission reductions. Climatic Change, 65(1-2), 39–71.
GOVERNMENT Publications Office (2016). International Energy Outlook 2016: With Projections to 2040. Government Printing Office.
GUPTA, A. K. & Nadarajah, S. (2004). Handbook of Beta Distribution and its Applications. Boca Raton, FL: CRC Press.
HAAS, A. & Jaeger, C. (2005). Agents, bayes, and climatic risks-a modular modelling approach. Advances in Geosciences, 4, 3–7.
HALLEGATTE, S. & Ghil, M. (2008). Natural disasters impacting a macroeconomic model with endogenous dynamics. Ecological Economics, 68(1), 582–592.
HELD, H., Kriegler, E., Lessmann, K. & Edenhofer, O. (2009). Efficient climate policies under technology and climate uncertainty. Energy Economics, 31, S50–S61.
HOPE, C. (2006). The marginal impact of co2 from page2002: An integrated assessment model incorporating the IPCC’s five reasons for concern. Integrated Assessment, 6(1).
INTERNATIONAL LABOUR OFFICE (ILO) (2015). ILOSTAT database: https://www.ilo.org/ilostat.
JANSSEN, M. A. & Jager, W. (2002). Stimulating diffusion of green products. Journal of Evolutionary Economics, 12(3), 283–306.
KAINUMA, M., Matsuoka, Y., Morita, T. & Morita, T. (1999). Analysis of Post-Kyoto scenarios: The Asian-Pacific integrated model. The Energy Journal, 207–220.
KELLY, D. L. & Kolstad, C. D. (1999). ‘Integrated assessment models for climate change control.’ In H. Folmer & T. Tietenberg (Eds.), International Yearbook of Environmental and Resource Economics, 2000, 171–197. Cheltenham: Elgar.
KUZNETS, S. & Murphy, J. T. (1966). Modern Economic Growth: Rate, Structure, and Spread, Vol. 2. New Haven, CT: Yale University Press.
LAMPERTI, F., Dosi, G., Napoletano, M., Roventini, A. & Sapio, A. (2018). Faraway, so close: coupled climate and economic dynamics in an agent-based integrated assessment model. Ecological Economics, 150, 315–339.
LEIMBACH, M., Bauer, N., Baumstark, L., Lüken, M. & Edenhofer, O. (2010). Technological change and international trade–insights from remind-r. The Energy Journal, 109–136.
LESSMANN, K., Kornek, U., Bosetti, V., Dellink, R., Emmerling, J., Eyckmans, J., Nagashima, M., Weikard, H.-P. & Yang, Z. (2015). The stability and effectiveness of climate coalitions. Environmental and Resource Economics, 62(4), 811–836.
LORENZ, A., Schmidt, M. G., Kriegler, E. & Held, H. (2012). Anticipating climate threshold damages. Environmental Modeling & Assessment, 17(1-2), 163–175.
LUCAS, R. E. & Sargent, T. J. (1981). Rational Expectations and Econometric Practice, Minneapolis, MN: University of Minnesota Press.
MANNE, A., Mendelsohn, R. & Richels, R. (1995). Merge: A model for evaluating regional and global effects of GHG reduction policies. Energy Policy, 23(1), 17–34.
MCGINTY, M. (2007). International environmental agreements among asymmetric nations. Oxford Economic Papers, 59(1), 45–62.
MOOSA, I. A. (2000). Cyclical asymmetry in energy consumption and intensity: the Japanese experience. Opec Review, 24(1), 53–59.
NATIONAL ACADEMIES OF SCIENCES, E. & MEDICINE (2017). Valuing Climate Damages: Updating Estimation of the Social Cost of Carbon Dioxide. National Academies Press: https://www.nap.edu/catalog/24651/valuing-climate-damages-updating-estimation-of-the-social-cos.
NEUBERSCH, D., Held, H. & Otto, A. (2014). Operationalizing climate targets under learning: An application of cost-risk analysis. Climatic change, 126(3-4), 305–318.
NORDHAUS, W. D. (1992). The ‘dice’ model: Background and structure of a dynamic integrated climate-economy model of the economics of global warming. Tech. rep., Cowles Foundation for Research in Eco-nomics, Yale University.
NORDHAUS, W. D. (2013). The Climate Casino: Risk, Uncertainty, and Economics for a Warming World. New Haven, CT: Yale University Press.
NORDHAUS, W. D. & Boyer, J. (2000). Warming the World: Economic Models of Global Warming. Cambridge, MA: MIT Press.
NORDHAUS, W. D. & Yang, Z. (1996). A regional dynamic general-equilibrium model of alternative climate-change strategies. The American Economic Review, 741–765.
PETSCHEL-HELD, G., Schellnhuber, H.-J., Bruckner, T., Toth, F. L. & Hasselmann, K. (1999). The tolerable windows approach: theoretical and methodological foundations. Climatic Change, 41(3-4), 303–331.
PONTA, L., Raberto, M., Teglio, A. & Cincotti, S. (2018). An agent-based stock-flow consistent model of the sustainable transition in the energy sector. Ecological Economics, 145, 274–300.
POPP, D. (2004). Entice: endogenous technological change in the dice model of global warming. Journal of Environmental Economics and management, 48(1), 742–768.
ROTMANS, J. (2012). IMAGE: An integrated model to assess the greenhouse effect, vol. 1. Springer Science & Business Media.
SAFARZYŃSKA, K. & van den Bergh, J. C. (2017). Integrated crisis-energy policy: Macro-evolutionary modelling of technology, finance and energy interactions. Technological Forecasting and Social Change, 114, 119–137.
SCHEFFRAN, J. (2008). Adaptive management of energy transitions in long-term climate change. Computational Management Science, 5(3), 259–286.
SCHWOON, M. (2006). Simulating the adoption of fuel cell vehicles. Journal of Evolutionary Economics, 16(4), 435–472.
SNOWDON, B., Vane, H. R., & Wynarczyk, P. (1994). A Modern Guide to Macroeconomics. Cheltenham: Elgar.
STANTON, E. A., Ackerman, F. & Kartha, S. (2009). Inside the integrated assessment models: Four issues in climate economics. Climate and Development, 1(2), 166–184.
STERN, N. (2016). Current climate models are grossly misleading. Nature, 530.
STOCK, J. H. & Watson, M. W. (1998). Business cycle fluctuations in us macroeconomic time series.
STONE, R. (1954). Linear expenditure systems and demand analysis: an application to the pattern of British demand. The Economic Journal, 64(255), 511–527.
TOL, R. S. (1997). On the optimal control of carbon dioxide emissions: an application of fund. Environmental Modeling & Assessment, 2(3), 151–163.
TRAN, M., Banister, D., Bishop, J. D. & McCulloch, M. D. (2013). Simulating early adoption of alternative fuel vehicles for sustainability. Technological Forecasting and Social Change, 80(5), 865–875.
UNITED Nations (2017). United Nations Database: http://www.un.org/en/databases/index.html.
VASICEK, O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics, 5(2), 177–188.
VONA, F. & Patriarca, F. (2011). Income inequality and the development of environmental technologies. Ecological Economics, 70(11), 2201–2213.
WEBER, M., Barth, V. & Hasselmann, K. (2005). A multi-actor dynamic integrated assessment model (MADIAM) of induced technological change and sustainable economic growth. Ecological Economics, 54(2-3), 306–327.
WEITZMAN, M. L. (2012). GHG targets as insurance against catastrophic climate damages. Journal of Public Economic Theory, 14(2), 221–244.
WEYANT, J. (2017). Some contributions of integrated assessment models of global climate change. Review of Environmental Economics and Policy, 11(1), 115–137.
WINDRUM, P., Ciarli, T. & Birchenhall, C. (2009). Consumer heterogeneity and the development of environmentallyfriendly technologies. Technological Forecasting and Social Change, 76(4), 533–551.
WORLD BANK (2016). World development indicators: https://datacatalog.worldbank.org/dataset/world-development-indicators.
WORLD BANK (2019). World Development Indicators: https://databank.worldbank.org/home.aspx.
WORLD TRADE ORGANISATION (2014). International trade statistics 2014 database: https://www.wto.org/english/res_e/statis_e/its2014_e/its2014_e.pdf.
YEARBOOK, G. E. S. (2016). Enerdata. Google Scholar .


