Introduction
In this paper we present a model of democratic discussion and decision-making about norms of behavior in a context where the decisions are delegated to a share of the groups. Our model was inspired by a long field work (see Appendix A for the chronology and details of the field work) about french NPOs that developed an alternative food network (Lamine 2005), and who try to implement their theoretical ideas about “good food” in shared behavioral norms. Our model is meant to reproduce elements of a dynamics of decision-making that has actually taken place. The coordination of groups at national level of the NPOs did not always result in consensual decision and occasioned some splits, but they can be taken as an example of democratic decision-making – where all agents are considered to be equals in the process, discussion are regular, and there exists trans-parency in the decision-making that lead to the establishment of norms.
Our model is based on a long field work during which we observed the self-organized structuration of a large group of numerous NPOs. Each of them was organizing a short food chains called AMAP, inspired by Community Supported Agriculture in the US (Amemiya 2011; Lamine & Rouchier 2016). The idea is that people belonging to the NPO (AMAP) pay in advance for a weekly “basket” at fair price. This can secure the farmer revenue who, in exchange, works so that to provide food that is of “good” quality (Lamine 2005). The exact content of the basket (quantity and goods provided) is not defined in advance because it depends on the actual production of the farmer. The NPO itself is not buying but is the place to gather people and establish the rules. Main questions are: what should the price be? What is the approximate quantity in a basket? Should the farmer possess a label for organic food or just have a reasonable use of chemical additives? etc. In that sense the NPO is a negotiation space were the practices of production and exchange are defined (Mundler 2009). All groups have to sign a charter, so as to be allowed to be called AMAP, but this charter is based on “principles” and not clear practices, which have to be renegotiated regularly. We already studied the way these right practices were defined through multiple negotiations (Lamine & Rouchier 2016) and represent some relevant aspects in this model.
Several stylized facts have indeed emerged from our field work (see Appendix A for more details on the field work):
- The multidimensionality of the discussion, and thus the necessary multidimensionality of opinion.
- Participants do not easily get involved in the discussion about norms, which is time consuming and thus they accept not to be part of norm formation.
- Not many people want to be delegates to decide on norms, and thus there is no need to vote, delegates are self-designated (which we model as randomness)
- The fact that we start simulation with one large group that splits in time into subgroups.
The central issue we deal with, communication, is at the center of many discussions within the national group of AMAPs, as their role is to make sure that the norms that are chosen are eventually implemented. In the basic situation, delegates come back to their local NPO and share the information with others, but it is also necessary to inform the NPO who have no delegates, who do not necessarily look for information. Different means of communication are thus thought about and developed, which we describe later.
With this whole field work we realized how difficult it is to find an equilibrium in this democratic organization, following a representative democratic setting, where enough agents feel happy to follow chosen norms to keep the organization coherent. It is even more interesting that the discussion is multi-dimensional, and thus rather complex, and that some agents can accept to disagree on some dimensions if they agree on others. This is why we observe the dynamics following two main indicators: stability (that there is not too many splits along the simulation and the organizations are at some point stable) and representativeness (that each agent can belong to a group, which values are not at odd with his).
The paper is built on an original model that has already been described and tested more thoroughly, and which sensitivity analysis can be found in Appendix G and in Barbet et al. 2019, and its basic idea can be summarized in: Agents hold multidimensional opinions about the best practices to implement in their organization. They can influence each others’ opinions through interpersonal influence. They can leave or join an organization. Agents that are designated as delegates can split their organization in case of disagreement. The setting being fixed, we discuss different types of “vertical communication”. Contrary to interpersonal communication, it does not inform on opinions but of the decisions taken by the board, and is perceived by all Agents at once. We particularly investigate the effect of this vertical communication in the context of multidimensionality.
We show the following three main results:
- vertical communication has more positive impact when discussions deal with more dimensions on which to establish norms
- no miracle: the effect of vertical communication remains limited
- vertical communication should be well designed: only broad and non agressive communication is able to improve both stability and representativeness at the same time.
The paper is articulated in four parts. The first part describes the stylized facts we kept from our field work (with more details in Appendix B) and we relate to the main literature we can refer to for the dynamics of our model: inter-individual influence and opinion dynamics models. In the second part we describe the model, made of three sub-models, and the simulation protocol. Then the results are described in the third part: we will explain how results are extracted, the macro-behaviors and micro-mechanisms of the model without vertical communication and the results with vertical communication. In the fourth part, we conclude on the interest of the model, showing some counterintuitive elements, others that are in line with expected dynamics and the potential re-usability of the model.
Motivation and Method
Questions of values and practices
As said earlier, the exchanges defined by AMAPs are not usual market exchanges, they promote different values that are not so usual in the liberal world, such as risk-sharing between producer and consumer. It thus relies on strong values but also on strong links among people. However, as it can be often witnessed, the translation of “values” (often abstract, such as “fairness”) into “good practices” (how to practically establish the price of a basket so that everyone is happy) is subject to subjective interpretation, and thus to negotiation within groups that have to share the same practices. As said in the introduction, the history of AMAPs has been made of groups getting together to share ideas and knowledge, trying to establish norms of behaviors for all, and splitting as a consequence of disagreements.
Since the creation of AMAPs in 2001 we have identified 6 important conflicting topics (Lamine & Rouchier 2016):
- Organic: Should the farmers have the organic label or not? To which extent farmer can use chemical treatment? etc.
- 0 intermediary: To what extent can the farmers be helped by other farmers to complete their baskets?
- Flexibility: If a farmer has large quantities of products, should he share all of it with his consumers or may he sell part of it to the general public for complementary income? For consumers: are consumers compelled to take one basket every week or is it possible to have a more adaptive system? Should there be different basket sizes for different numbers of family members?
- Fairness in price: What is a fair price for the farmer? What are the criteria? How is the price of a basket computed?
- Quality evaluation: How can consumers monitor the “good practices” of their farmer?
- Group dynamics: Should the NPO gathering AMAPs be prescriptive for the definition of good practices or should there be freedom for each AMAP to decide on their own rules about the 5 preceding elements.
This variety of interpretation on multiple dimensions leads to many different practical implementations of the principles: AMAPs can function with different rules, and tensions can arise within or between AMAPs when in-teractions repeat over time. This is why we can witness several creations and splittings of groups. These groups are called “réseaux”, which means “networks”: which shows that horizontal relations are the central concept put forward by the actors, and not hierarchy. Another word used is “mouvement” to designate the spreading of the AMAP principle, which is a clear reference to political activity, which is confirmed by the strong interest on democratic processes. More details on the history we could reconstruct from our field work are presented in Appendix B, where we describe the dynamics of participation to the functioning of the groups, and the different reasons why groups appeared and disappeared.
In particular one important parameter of the model is the number of active members since it is of interest for discussions about the values of representative democracy vs direct democracy. Indeed, some AMAPs are leaders in the construction of the movement. They delegate one member to belong to the board of regional or national groups. Other AMAPs are not very active and are just following the direction of a charter that they did not contribute to write. This difference of implication can also be found inside each AMAP, but we will not detail this here. Without leading a serious quantitative study we estimated to 5% the proportion of active AMAPs. The influence of this parameter is tested in the robustness check and fixed to 5% in the core paper.
Another element in the history of the emergence and structuring of AMAPs was the reasons for quitting the group, which are of two kinds. One is the gap between these good practices identified by the board and imposed to the most passive members and the habits that these members had before: this gap can lead them to quit the group in order to keep their own “good practices”. The second is the impossibility to reach agreement within the board, which can imply that the delegates that disagree split the group by creating a new group. Both of these features are implemented in our model.
As it can now be clear, this model was created with a very precise context in mind, but we will discuss its dynamics as providing information in a wider context in the conclusion.
An agent-based opinion model
In this paper, we address the following question: what is the impact of communicating about voted norms on the stability and representativeness of a democratic organization of agents?. We approach this question as and influence and opinion dynamics issue. For this we constructed a specific model of democratic discussion and decision-making based on the field work described above and in Appendix A. While discussing, agents influence each other’s opinion. Moreover, vertical communication also impacts the opinions of agents.
A large part of ABM opinion dynamics models study the emergence of opinion clusters among a closed set of agents, who repeatedly influence each other opinions, most of the time sequentially and through random paired interactions. Opinions are, mainly, modeled in two ways. The first is to consider discrete opinions, expressed as a vector of integers, whose length is the number of dimensions on which opinions are expressed – each integer being an opinion taken from a finite set (Epstein 2001; Holyst et al. 2002; Axelrod 1997; Stauffer 2001; Nowak et al. 2005; Rouchier & Tanimura 2012; March 1991). The second way is to consider a continuous opinion about one dimension, taken in \([0; 1]\), \([ 1; 1]\) or even in \(\mathbb{R}\) (Hegselmann & Krause 2002; Weisbuch et al. 2001; Deffuant et al. 2002; Jager & Amblard 2005; Amblard & Deffuant 2004; Flache & Mäs 2008; Abrica-Jacinto et al. 2017). Papers explore the impact of different parameters or initial condition on the final outcome and the dynamics: initial distribution of opinions, heterogeneity of agents, networks of communication, spatial repartition of agents, and introduction of bias. We chose to deal at the same time with multi-dimensionality (which seemed to be very important to explain the dynamics of organizations in our field work) and the continuous opinion model for each dimension (because this model is the simplest to define a measure of satisfaction for our agents).
The major part of continuous opinion dynamics models (and some of the discrete ones) relies on what is called the uncertainty or the confidence interval which is a characteristic of agents. It represents how much agents are convinced about their opinion and takes the form of a distance. The basic idea is the following: if the opinions of an other agent is more distant from mine than my confidence threshold, then she can not manage to influence me. Depending on the model, this uncertainty/confidence threshold, can be heterogeneous among agents and allowed to vary through interactions (Hegselmann & Krause 2002; Deffuant et al. 2002; Weisbuch et al. 2002). The influence model we have chosen here for our model is the translation of the Social Judgement Theory (SJT exposed in Sherif & Hovland 1961) of Jager & Amblard 2005, it is defined by an uncertainty/confidence threshold, and also a rejection threshold, both being fixed over time and interactions. The rejection threshold works as follow: if the opinions of other agent is more distant from mine than this threshold then we will enter in conflict and our opinions will negatively influence each other (repellent opinions).
Few papers tackle the multidimensionality in the continuous case. Indeed multi-dimensionality rises two is-sues: the distance measurement between opinions and the way to apply the influence process depending on this distance. For example in Li & Xiao 2017 agents compute the euclidian distance between their vectors of opinions and depending on this aggregate distance they attract or repel all their opinions in all the dimensions at once. In Huet et al. 2008 the type of influence will depend on diverse particular configuration of opinions on the two dimensions. In this paper we adopt a point of view closer to the second article. The influence on each dimension will depend on the particular configuration on this dimension. Then agents can attract each others opinions on one dimension while repelling it on an other dimension.
The idea of mixing interpersonal influence and vertical communication has already been used in innovation diffusion models as Deffuant et al. (2005) or Delre et al. (2007). In both case the vertical communication is modeled as an exogenous information: agents become aware of the existence of an innovation, triggering the process of choice and their opinions are not influenced by this information. On this point, the originality of the present work is to propose an endogenous vertical communication where norms are obtain through opinions and norms can also influence opinions through the vertical communication. In the spirit of Delre et al. 2007 where authors control for different design of this vertical communication (to whom the vertical communication is addressed and its timing), we will also control for its design: to whom the vertical communication is addressed and how it influences agents opinions).
In our model, opinions[1] are the points of view agents hold about the good practices to implement in their organization, that is the behavioral rule they want to apply. Active agents are those who decide for the behavioral rules and negotiate with other active agents for this. Once the rule has been chosen, it is imposed to passive agents who check if it is consistent with their opinion about good practice. One dimension of the vectors of opinions can be considered as a topic and the dimension that is discussed by actors at a point in time as the hot topic of the moment. In the paper, we will use the term “topic” when referring to the field work and the real world and use the term “dimension” when referring to the model.
To conclude on opinion dynamics models we can highlight that they are regularly successfully used in more applied model on different field. For example, in Deffuant et al. (2005), the bounded confidence model of relative agreement (Deffuant et al. 2002) is used in an innovation diffusion model, where social utility matters. In Rouchier et al. (2014) the relative agreement is used again to study the transmission of opinions and norms to newcomers in an institution. Rouchier & Tanimura (2012) have studied the effect of over confident agent in the learning process of a group using a multidimensional binary model of opinions. In Casilli et al. (2014), the Social Judgement Theory is used to study the evolution of norms in eating disorder internet forum.
Model
Our model is based on collective norms construction and on organizations which are articulated around these norms. In this section we will describe the model. The underlying assumptions made are justified with respect to our AMAP case study in Appendix C. The model code and its ODD can be found following this link to the CoMSES website: https://www.comses.net/codebases/6cc6a99b-cde1-4e49-bef8-e6fd4f997259/releases/1.0.0/.
The different agents and their interactions
The model is constituted of two main types of agents:
“Basic” agents
Simply called Agents in the rest of the paper, they are characterized by their vectors of opinions (\(\overrightarrow{a}\) uniformly distributed in \([-1,1]^{d}\) where \(d\) is the number of dimensions) and their uncertainty (\(U\)) and rejection (\(T \)) thresholds. Each dimension of the vector of opinions corresponds to a specific topic and represents the opinion an agent holds on the norm to apply on this topic. Agents’ actions are articulated around three submodels, Agents can:
- influence each other opinions during interpersonal interaction through an opinion dynamic model.
- negotiate norms from their opinions through a negotiation model.
- take decisions (leave, split, stay or join an Organization) depending on their degree of agreement with the negotiated norms through a decision model composed of:
- utility function which computes the utility derived by an Agent to belong to some Organizations
- decision rules which define actions taken by an Agent depending on her utility
“Structure” agents
They are called Organizations and are constituted of “basic” agents (their members). They are characterized by their boards (\(\cal{B}\) a set of motivated Agents randomly chosen among the Organization’s members) and their vector of norms (\(\overrightarrow{b}\)) of dimension \(d\) resulting from the negotiation between representatives (the members of the board). Organizations do not make decisions, their evolution only depends on decisions taken by their Agents. An Agent can belong to only one Organization at a time.
Splitting and leaving organizations
Agents in the board impose norms (modify the vector of norms of the Organization). Each turn, one dimension is selected, Agents in the board discuss/debate[2] and compute a negotiated norm based on their opinions. If they all retrieve a positive utility by applying this new norm, then the norm is settled and imposed to all Agents related to this Organization. The rest of the members of the Organization have to choose whether to stay or leave it[3]. If some members of the board retrieve a negative utility by applying the new norm, then the Organization is split into two, along with the former board. Each board computes a new negotiated norm on the disrupting topics, these norms are automatically adopted by the two new Organizations. Finally the members of the former Organization choose to join one or the other new Organizations or to leave[4].
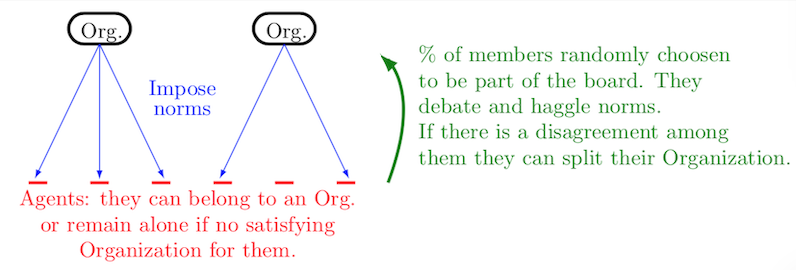
Joining organizations
At the beginning, all Agents are gathered in one Organization with an empty vector of norms. Turn after turn new dimensions are normed or revised and Organizations keep on splitting or losing members, but can also be joined by isolated Agents. They join the Organization that gives them the maximum positive utility, if none they remain in isolation. A general scheme of the model is given in Figure 1.
At this point we have not presented vertical communication in Organizations. The only communication is through interpersonal influence inside boards. The model without vertical communication will be our touchstone to discuss the effect of the different vertical communication. Before exposing vertical communications we will explicit the three submodels describing the behavior of Agents and the scheduling of the model without vertical communication.
Agents’ submodels
In this subsection we will explicit the three submodels describing the behavior of Agents: the opinion dynamic model, the negotiation model and the decision model.
The Social Judgement Theory
We will use the Social Judgement Theory of Jager & Amblard (2005) to model the interpersonal influence between Agents (the reasons behind this choice can be found in Appendix C on assumptions). Influence occurs between pairs of Agents, who hold vectors of opinions of dimension \(d\) (\(\overrightarrow{a} = (a^{1},a^{2}, ... , a^{d})\) with \(a^{k} \in [-1;1], \forall k \in \{1,2, ... ,d\} \)). They also have their own characteristics an uncertainty/confidence (\(U\)) and a rejection (\(T\)) thresholds. We first assume that \(U\) and \(T\) are the same for all Agents and for all dimensions. When two Agents i and i0 influence each others they modified their opinions as follow:
Influence of Agent \(i'\) on Agent \(i\) on the dimension \(k\):
| $$\left\{ \begin{array}{l c c l} \text{if} & |a^{k}_{i}-a^{k}_{i'}| < U & \text{then} & a^{k}_{i} = a^{k}_{i} + \mu(a^{k}_{i'} - a^{k}_{i})\\ \text{if} & U \leqslant |a^{k}_{i}-a^{k}_{i'}| \leqslant T & \text{then} & \text{no influence}\\ \text{if} & T < |a^{k}_{i}-a^{k}_{i'}| & \text{then} & a^{k}_{i} = a^{k}_{i} + \mu(a^{k}_{i} - a^{k}_{i'}) \end{array} \right.$$ | (1) |
At the same time, Agent \(i\) influences Agent \(i'\) in a symmetric way:
| $$\left\{ \begin{array}{l c c l} \text{if} & |a^{k}_{i}-a^{k}_{i'}| < U & \text{then} & a^{k}_{i'} = a^{k}_{i'} + \mu(a^{k}_{i} - a^{k}_{i'})\\ \text{if} & U \leqslant |a^{k}_{i}-a^{k}_{i'}| \leqslant T & \text{then} & \text{no influence} \\ \text{if} & T < |a^{k}_{i}-a^{k}_{i'}| & \text{then} & a^{k}_{i'} = a^{k}_{i'} + \mu(a^{k}_{i'} - a^{k}_{i}) \end{array} \right. $$ | (2) |
If opinions are less distant than \(U\), they attract each other. If opinions are more distant than \(T\), then they repel each other. If the distance between the opinions is between \(U\) and \(T\), no influence occurs, Agents are indifferent. \(\mu\) denotes the strength of influence, it is the same for all Agents and is settled to \(0.10\) as in Jager & Amblard (2005). Figure 10 in Appendix D shows the amplitude of the influence of agent \(i'\) on \(i\) depending on the position of Agent \(i'\)’s opinion with respect to Agent \(i'\) opinion.

In a board of \(n\) Agents the influence takes place asynchronously. A first pair of Agents is randomly taken and influence each other, then a second pair is randomly taken. The influence process stops after \(n=2\) pairs have interacted[5]. In this process, some Agent will perhaps not interact at all when others can be chosen several times. In a group of 2 Agents, they automatically interact and only once. This process of interaction is exactly the one used in Jager & Amblard 2005. Inside a given board every Agent of this board can interact with any other Agent, as if they are in a fully-connected network (this assumption is justified in Appendix C).
The negotiation submodel
In our model when Agents in boards negotiate, they simply compute the arithmetic mean of their opinions. They are only able to negotiate norm on one dimension at a time. For a board \({\cal{B}}\) (composed by \(n\) Agents) which negotiates a norm on the \(k\)th dimension (\(b\)k) the formula is given by:
| $$b^{k}_{{}_{}} = \frac{\underset{i \in {\cal{B}}_{}}{\sum} a_{i}^{k}}{n}$$ | (3) |
The decision submodel
Agents are able to influence each other and negotiate norms for their Organizations, they only need now to be able to position themselves with respect to these norms and take the adequate actions.
First an Agent needs to compute her utility thanks to her opinions (\(\overrightarrow{a} = (a^{1},a^{2}, ... , a^{d})\)) and the norms of her Organization (\(\overrightarrow{b} = (b^{1},b^{2}, ... , b^{d})\)). Let \(U\) be the uncertainty and \(T\) the rejection thresholds of the Agent, the utility retrieved by this Agent in her Organizations is denoted \(W\) and is computed as follows
| $$W(\overrightarrow{a},\overrightarrow{b}) = \sum_{k=1}^{d} w^{k}(\overrightarrow{a},\overrightarrow{b})$$ | (4) |
| $$\text{ with } w^{k}(\overrightarrow{a},\overrightarrow{b}) = \left\{ \begin{array}{l c l} U^{}_{} - |a_{}^{k} - b_{}^{k}| \geqslant 0 & \text{if} & 0 \leqslant |a_{}^{k} - b_{}^{k}| \leqslant U^{}_{} \\ 0 & \text{if} & U^{}_{} \leqslant |a_{}^{k} - b_{}^{k}| \leqslant T^{}_{} \\ T^{}_{} - |a_{}^{k} - b_{}^{k}| \leqslant 0 & \text{if} & T^{}_{} \leqslant |a_{}^{k} - b_{}^{k}| \end{array} \right.$$ | (5) |
\(w^{k}_{} \) is the utility obtained on the \(k^{th}\) dimension. It is positive if the norm on dimension \(k\) is close enough to Agent’s opinion: the Agent is quite comfortable with the norm imposed by her Organization. If the norm is far enough but not too far (between \(U^{}_{}\) and \(T^{}_{}\)), the Agent is indifferent. Finally, if the norm imposed is too far the utility becomes negative, modeling disagreement of the Agent. Then \(w^{k}_{}\) decreases with the distance between the norm and the current Agent’s opinion. Figure 2 shows the principle of \(w^{k}_{}\) computation.
The global utility is the sum of the utility derived on each dimension. This is an important point, because negative utilities on some dimensions (local disagreements) can be compensated by an high positive utility on one or more other dimensions. An Agent can agree (retrieve a positive utility) with the negotiated norms of her Organization even if she disagrees locally on some dimensions. The agreement with norms is then a global notion.
The utility is maximal if \(\overrightarrow{a} = \overrightarrow{b}\) and \(W(\overrightarrow{a},\overrightarrow{b}) = W(\overrightarrow{a},\overrightarrow{a}) = dU\). It is the case if the Organization apply norms exactly equal to the opinions of an Agent or if the Organization imposes no norms to its members (i.e each member is free to follow their own rules). The second case is true when the Organization have not yet negotiated any norms.
Second, depending on its utility, an Agent needs to decide which action to take:
Scheduling
We will now give the precise scheduling of the model and present in the next subsection the vertical communication.[6]
- Initialization: creation of Agents and creation of the primary Organization gathering all the Agents. A fraction of Agents are randomly chosen to be the representatives constituting the board of this primary Organization.
- For each Organization, a specific dimension of the vector of opinions is randomly picked-up:
- Influence: If allowed by the user (parameter \(influence\)? turned TRUE), the Agents of the board of the Organization influence each other on this specific dimension of their vectors of opinions.
- negotiation: Agents of the board negotiate a new norm for the specific dimension.* This new norm replaces the old one in the Organization vector of norms:
- If the board agrees[7] with this new vector of norms, then it is imposed to all the Agents of the Organization. If some other Agents (not in the board) disagree,[8] they leave the Organization.
- If at least one Agent of the board disagrees, then the board is split in two parts by affinity on the specific dimension giving birth to the two new Organizations.* Then all the Agents of the previous Organization have to join one or the other new Organizations or leave[9]. The new Organizations inherit the vector of norms of the old one except for the component of the disrupting dimension.
- Isolated agents get in: isolated Agents join the existing Organization that gives them the highest positive utility.**
- Communication campaign (vertical communication) if selected by the user: adopted norms of each Organization are advocated to all the members
- Organization dissolution: Organizations with only one member are dissolved, the Agent member becomes isolated and is able to join an Organization next turn.
- Completion of boards: boards of Organizations for which the fraction of representatives is less than parameter %-in-board are completed.
- Next time step: back to point 1.
The pseudocode of the model for steps 1 to 5 can be found in Appendix E.
Details
The primary Organization: the vector of norms of the primary Organization is initialized to \(\text{NA}^{d}\). In the case \(d=6\), we have \(\overrightarrow{b} = (\text{NA},\text{NA},\text{NA},\text{NA},\text{NA})\). When a dimension is turned to \(\text{NA}\), no norm is imposed by the Organization, and each Agent applies its own rule on this dimension, that is its own opinion. The utility of Agents belonging to the primary Organization at initialization is then the maximum possible utility ie \(W(\overrightarrow{a},\text{NA}^{6}) = W(\overrightarrow{a},\overrightarrow{a}) =\sum_{k=1}^{6} w^{k}(\overrightarrow{a},\overrightarrow{a}) = 6 U\). Indeed in this case Agents have all the advantages of belonging to an Organization without having any constraint (no norms to comply with).
Splitting of the board by affinity: if the board \({\cal{B}}\) disagrees with the new vector of norms after having negotiated a new norm on the specific dimension \(k\) (\(b^{k}_{{\cal{B}}}\)), then representatives which have opinions on the left side of \(b_{{\cal{B}}}^{k}\) constitute the board \({\cal{B}}_{l}\) (\({\cal{B}}_{l} = \{i \in \mathcal{B},\text{ st } a_{i}^{k} \leq b_{{\cal{B}}}^{k}\}\)) and the others constitute the board \({\cal{B}}_{r}\). Each board computes a new negotiated norm on the \(k\)th dimension (\(b^{k}_{{\cal{B}}_{l}}\) and \(b^{k}_{{\cal{B}}_{r}}\) ) giving birth to two new Organizations which inherit the norms of the old one except on the dimension \(k\).

Vertical communication
As exposed above, without vertical communication, norms are computed through the opinions held by the Agents of the boards whose opinions are only influenced through interpersonal interactions during the discussion/debate step. With vertical communication, we allow the vectors of norms to influence the vector of opinions of the Agents inside an Organization: norms can be advocated in order to influence the opinions of Agents. The general relationship between opinions and norms is illustrated in Figure 3.
We will control for different levels of communication (who is reached by the communication and when) inspired from our field work and associated with different theoretical type of communications (how norms are advocated / how it influences opinions of Agents reached). The vertical communication is then modeled as a couple: a level of vertical communication and a type.
Three levels of communication
Incarnation: communication only for members of the board and on a specific dimension of the vectors each turn. It takes place after a new norm is negotiated on a specific dimension and before members of the board have to say if they agree or not with it (see the first * in step 1b of the scheduling). It also happens when a board splits, after each side of the board has negotiated their own new norm (see the second * in step 1b of the scheduling). In the AMAP network case, Agents can be interpreted as a group itself, in that case a group sends some delegates to participate in the debate and negotiate in the board of the Organization. Before deciding to adopt or not a new norm, these delegates can come back in their group and advocate for the new norm. Indeed, even if they, a priori, disagree with the negotiated norm, they can still be willing to value the huge amount of time/work spent during the debate and negotiation process by at least trying to defend it.
Special Training: communication that takes place once and only for newcomers (see ** in step 2 of the scheduling) but simultaneously influences all the dimensions of the vector of opinions. The studied AMAP network (Les AMAP De Provence) has a training program on their practices for new AMAPs joining the network.
Communication Campaign: after a new norm on a specific dimension has been imposed and newcomers have arrived, Organizations can decide to make a broad communication campaign on this new norm (see step 3 in the scheduling). This communication reaches every members of the Organization and is only on a specific dimension each turn. In our AMAP network case, the network often tries to communicate the decisions that are made and the reasons why they have been made to all of its members. This type of communication can occur through different means: newsletters, flyers, meetings.
Four types of communication
We have few evidences from our field work and literature on how precisely vertical communication can influence opinions. Thus, we control for different types of communication that influence differently the opinion of the receiver. Each is expressed as a variation of the SJT model. In the field work, we have observed that communication does not always have the intended effect on receivers and can also create more polarization if too intrusive or stigmatizing. Therefore we have modeled four types of communication, 3 of which do not generate more polarization (non-aggressive ones) and one which can generate negative reactions for some receivers (the aggressive one).
Three non-aggressive communication types:Advertising: communication that is designed to influence every agent reached: always makes opinions move toward the norms. We model it the following way: whatever is the opinion of the agent it gets closer to the norm with a strength of influence of \(\mu = 0.10\). The absolute shift of the opinion toward the norm is then equal to \(\mu|norm - opinion|\). Influence on agent \(i\) on the dimension of \(k\) of the norm:
| $$\forall a^{k}_{i} \in [-1;1] \text{ and } \forall b^{k} \in [-1;1] \text{ we have } a^{k}_{i} = a^{k}_{i} + 0.10 \times (b^{k} - a^{k}_{i})$$ | (6) |
Targeted: communication that is designed to influence few people but to be very convincing. We model it the following way: if the norm is inside the uncertainty threshold the agent adopts the norms (her opinion become almost equal to the norm, \(\mu = 0.99\)[10]), if the norm is outside the uncertainty threshold the communication has no effect. Influence on agent \(i\) on the dimension \(k\) of the norm:
| $$\left\{ \begin{array}{l c c l r} \text{if} & |a^{k}_{i}-b^{k}| < U & \text{then} & a^{k}_{i} = a^{k}_{i} + 0.99 \times (b^{k} - a^{k}_{i}) & \text{(opinion becomes the norm)}\\ & & \text{else} & \text{no influence} \\ \end{array} \right.$$ | (7) |
Descriptive: type of communication that do not generate negative reactions but not very convincing. We model it by cutting the rejection of the SJT, only members for whom the norm is inside their uncertainty threshold are influenced and with a strength of influence of \(\mu = 0.10\). Influence on agent \(i\) on the dimension \(k\) of the norm:
| $$\left\{ \begin{array}{l c c l r} \text{if} & |a^{k}_{i}-b^{k}| < U & \text{then} & a^{k}_{i} = a^{k}_{i} + 0.10 \times (b^{k} - a^{k}_{i}) & \text{(opinion moves toward the norm)}\\ & & \text{else} & \text{no influence} \\ \end{array} \right.$$ | (8) |
Aggressive: type of communication that can generate rejection from the receiver whose opinion is too far from the norm: making her opinion to move away from the advocated norm. We simply model it with the SJT. As in Jager & Amblard (2005) and in the present paper for interpersonal influence we take a strength of influence of \(\mu = 0.10\), making no specific assumption whether the vertical communication can have a stronger or a weaker effect on opinion than interpersonal influence[11]. Influence on agent \(i\) on the dimension \(k\) of the norm:
| $$\left\{ \begin{array}{l c c l r} \text{if} & |a^{k}_{i}-b^{k}| < U & \text{then} & a^{k}_{i} = a^{k}_{i} + 0.10 \times (b^{k} - a^{k}_{i}) & \text{(opinion moves toward the norm)}\\ \text{if} & U \leqslant |a^{k}_{i}-b^{k}| \leqslant T & \text{then} & \text{no influence} & \\ \text{if} & T < |a^{k}_{i}-b^{k}| & \text{then} & a^{k}_{i} = a^{k}_{i} + 0.10 \times (a^{k}_{i} - b^{k}) & \text{(opinion moves away from the norm)} \\ \end{array} \right.$$ | (9) |
In the rest of the paper we will extract the effect of each couple of vertical communication by comparing them to the case without vertical communication. Having the effects of each couple allows us to compare them and discuss the mechanisms at stake behind each couple.
Simulation protocol
The parameters of the model are the following:
- \(nb.Agents\): number of Agents created for the simulation.
- \(nb.dimensions\): number of topics, ie dimension of vectors of opinions and norms.
- \(U\): Uncertainty threshold of the SJT, homogeneous among Agents.
- \(T\): Rejection threshold of the SJT, homogeneous among Agents.
- \(strength.of.influence\): denotes the speed of attraction or rejection of opinions in the SJT.
- \(%.in.board\): define the size of the board of an Organization as a percentage of its number of members.
- \(influence?\): allows the user to cut o the influence process among the Agents of the board (step 1a of the scheduling): Agents are no longer allowed to influence each others opinions.[12]
- \(Vertical-communication-level\): allows the user to activate the vertical communication and to choose the level at which it will take place.
- \(Vertical-communication-type\): allows the user to choose the way vertical communication influence opinions of Agents.
| Behavior space of the model | |
| \(nb.Agents^{*} = \{100,\mathbf{200},400\}\) | \(U \in \mathbf{\{0.1,0.2,...,1,1.1\}}\) |
| \(\%.in.board \in \{\mathbf{5},10,20,50,100\}\) | \(T \in \mathbf{\{0.1,0.2,...,1,1.1\}}\) |
| \(nb.dimensions \in \mathbf{\{1,2,6\}}\) | \(strength.of.influence = 0.10\) |
| \(influence? \in \{\mathbf{true},false\}\) | |
| \(Vert-communication-level = \mathbf{\{no, incarnation, spec\text{-}training, com\text{-}campaign\}}\) | |
| \(Vert-communication-type = \mathbf{\{aggressive, descriptive, targeted, advertising\}}\) | |
| *: \(nb.Agents = 100\) and \(400\) were only run with \(influence\) = \(true\) | |
In the core of the paper we will not explore the whole behaviour space but focus on the one around the vertical communication. The rest of the exploration is le in the robustness check section (Appendix G). The explored behaviour space is shown in Table 1 .
A simulation for a given set of parameters is made of \(d \times 100\) time steps. With 1 dimension a simulation will last \(100\) time steps whereas \(600\) time steps with 6 dimensions. This time allows opinions of agents to fully converge in clusters which means the system is stable: no more splits or Agents leaving[13]. This choice is consistent with Jager & Amblard ( 2005) and our own observations with a replication of the SJT and with our model. We do not aim for a realistic calibration of time steps for several reasons. The first is that in opinion dynamic models, as the one used here, time steps are theoretical. The literature does not aim to strongly interpret it: a time step can refer to a single encounter between two agents or a set of encounters between pairs of agents, moreover an encounter can be interpreted as a single discussion or several discussions during a period of time. The second reason is that in our case influence between agents can take place at different occasions (formal and informal -- see paragraph 3 of Appendix C for more details) and deal with several dimensions at a time. It is then difficult to collect complete data on interactions to make a direct interpretation with the model. Moreover, the form of interaction can play a role in the influence: in debates, one individual speaks to a crowd which is quite different from one to one discussion or informal group discussion and so on. Tackling this issue is a subject of research in itself like in Butler et al. (2019).
Indicators
We will look at two specific dimensions in the model:
- the stability of Organizations. As there is only one Organization at the beginning gathering all the Agents inside so each new Organization comes from a split, then the number of Organizations alive at the end of the simulation (\(nb.Orgs\)) is a good proxy for measuring the stability of the system.[14] An Organization is considered as alive when it is composed of at least 2 Agents.
- the representativeness of Organizations: do Agents decide to stay isolated or to belong to an Organization? The fraction of all Agents engaged in an alive Organization at the end of the simulation. \(fraction.Agents.in.Orgs\) is then a good proxy for measuring the representativeness.
Our indicators are measured at the end of each simulation when the steady state is reached. For our results we compute and draw for each set of parameters the mean of each indicator on the 100 runs.
Results
The section will be divided in three part. We will first present how we extract results from our indicators, then expose the basic mechanisms linking our parameters to the indicators in the absence of vertical communication. In a third part, we will give the main results specific to vertical communication
Observation
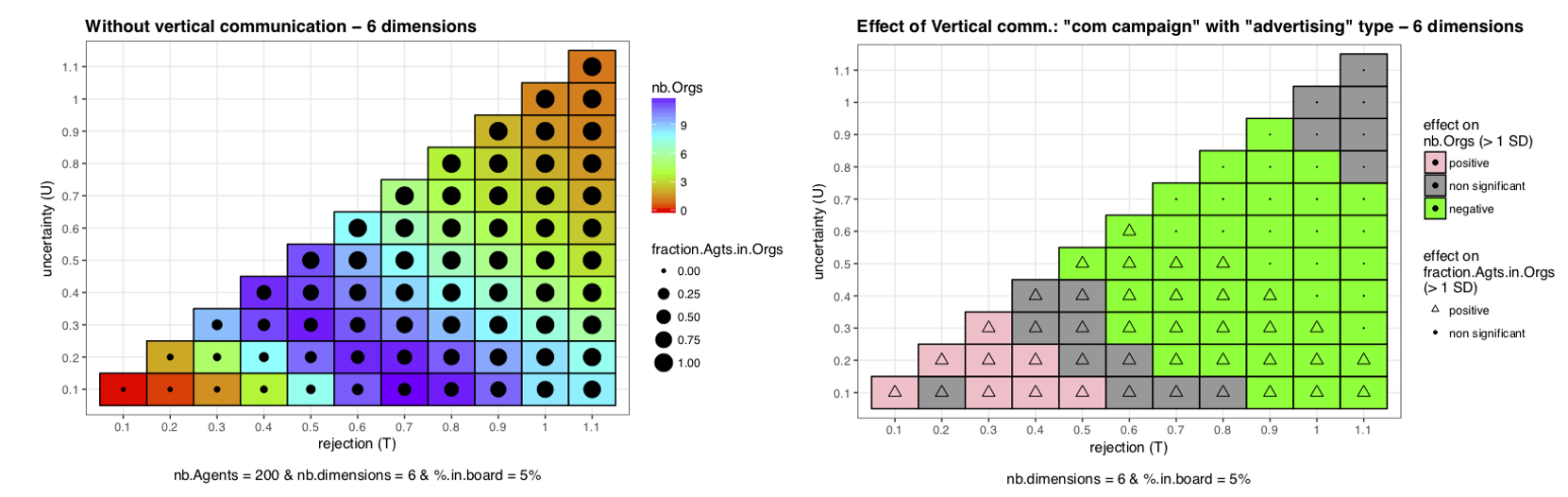
To obtain our results, we plotted our two indicators on a graph that represents a mapping of the characteristics of agents. The horizontal axis represents the rejection threshold (\(T\)) and the vertical axis the uncertainty threshold \(U\). Each square of the mapping corresponds to a unique couple (\(U,T\)) and the mapping is triangular because by definition \(U \leq T\). The colour of a square represents the mean on the 100 runs for a given couple (\((U,T)\)) of \(nb.Orgs\). Similarly the size of points in the middle of each square represents the mean of the representativeness obtained for the given couple on the 100 runs. An example is given in Figure 4, left panel.
Alone, a graph only gives information on the effect of \(U\) and \(T\) on indicators for a given set of parameters. To see the effect of other parameters, we need to compare graphs two by two. Nevertheless comparisons between graphs are not always easy and do not tell us more about whether the effect is significant or not. That is why we have chosen to plot a second mapping, which summarizes the differences between two graphs and gives an idea of whether they are significant or not. The right panel of Figure 4 is an example, which shows the effect of introducing a particular vertical communication compared to a situation without vertical communication. Again the colors of square indicates the effect of this introduction on the stability, and the shape of the dots indicates the effect on representativeness.
To obtain this second graph we compute for each couple (\(U,T\)) (each square of the graph) the difference with and without the vertical communication in the number of organizations (stability - color of the square) or in the fraction of agents in organizations (representativeness - size of dots). Then this difference is divided by the standard deviation on \(nb.Orgs\) (resp. \(fraction.Agents.in.Orgs\)) without communication. The result gives us a measure in terms of standard deviation of the effect on stability (resp. representativeness) of introducing this specific vertical communication. The definition of a significant result is when the effect of communication is superior to one standard deviation. If it is inferior to one standard deviation then the result is considered as not significant. In the rest of the paper, the set of parameters used as reference to obtain the results correspond to a baseline scenario without vertical communication inspired by observations in our field work: 200 agents, 5% become representatives, there are 6 dimensions to norms and representatives can influence each other’s opinions through interpersonal interactions. Mathematical details can be found in Appendix F.
Behavior of the model without vertical communication and qualitative mechanisms
Personality of agents: \(U\) and \(T\)
To understand the mechanism behind the model, we pay attention to the determinants of the utility function since all decisions taken by Agents are made with respect to the sign of the utility function. For a given vector of opinions and a given vector of norms the sign of the utility function depends on the characteristics of the Agent (\(U\) and \(T\) thresholds). The chance for the utility to be positive (respectively negative) increase with an increase (resp. a decrease) in \(U\) and \(T\). Thus for a given vector of norms open-minded Agents (large \(U\) and \(T\)) have more chance to retrieve a positive utility: they agree more easily with negotiated norms. This local mechanism actually results in less splits (improving stability) and less departures (improving representativeness). It is also easier for open-minded isolated Agents to find a corresponding Organization (also improving representativeness). The opposite effect occurs with narrow-minded Agents (small \(U\) and \(T\)).
Multidimensionality
Based on this first mechanism we can discuss the micro-mechanism behind the addition of dimensions to vectors of norms and opinions. For \(U\) and \(T\) large enough, the chance for an Agent to retrieve a positive utility from a negotiated norm on a new dimension becomes superior to 50%. Then the chances of the overall utility to be positive will increase with the number of dimensions. On the opposite, for less open-minded Agents the probability to have a negative utility on a new dimension becomes superior to 50%. Then increasing the number of dimensions will lead to more disagreement, that is to more splits and departures (decreasing stability and representativeness). It will also be harder for isolated Agents to find an Organization giving them positive utility (decreasing representativeness).
To better understand, we can draw a partial analogy with Axelrod’s culture dissemination model (Axelrod 1997). Axelrod’s number of features correspond here to the number of dimensions. Axelrod’s number of traits per feature (parameter \(q\)) corresponds to an interplay between \(U\), \(T\) and the width of possible opinions (set to \([-1,1]\) in our model): openminded Agents are analogical to small \(q\) and narrow-minded Agents to large \(q\). In our model the culture of an Agent can be reflected by the vector of norms of his Organization. As shown in Axelrod (1997) and Lanchier (2012) when the number of features exceed the number of traits there is constitution of an unique culture in the population and when \(q\) is higher than the number of features, several stable cultures can emerge. In the same way with open minded agents (small \(q\)) adding dimensions have a tendency to stabilize Organizations and increase representativeness: there are few Organizations (cultures) and lot of Agents belong to these Organizations. Still in the same way with narrow-minded agents (lot of traits per features) stability and representativeness decreases: there are more Organizations (\(\neq\) cultures) and few Agents recognizing themselves in these Organizations. But in Axelrod’s model, increasing the number of dimensions with narrow minded agents (making the number of features higher than the number of traits) does not stabilize Organizations(culture). This different behaviour is basically due to the computation of the cultural similarity which corresponds to the utility function in our analogy. In Axelrod’s model only identical traits are taken into account and positively, whereas in our model the distance between the traits matter and can give large negative utility on some dimensions for narrow minded agents.
Trade off between stability and representativeness: The effect of democratic settings
Another important mechanism to understand is the one linking stability and representativeness. For a given Agents’ personality and a given dimension of vectors, more instability during a simulation means more Organizations. Then isolated Agents have more potential Organizations to join, the offer of Organizations is larger, increasing their chances of finding an Organization that gives them a positive utility. Therefore, the number of isolated Agents decreases, increasing the representativeness.
This last mechanism explains the behavior of the model when introducing more democracy. By more “more democracy” we mean playing on different parameters: allowing more people to be part of the board, introducing a turnover in the board to regularly renew it, cutting or allowing debate in the board. All these parameters have the same effect: decreasing stability while improving representativeness. By different means they make boards less cohesive creating more splits (decreasing stability) but, on the other hand, with more Organization to join for given \(U\), \(T\) and \(d\) the representativeness increases.
| Form. | Incarn. | Com. Camp. | |
| Advertising | Stab. \(\sim\) Rep. \(\nearrow\) | Stab. \(\nearrow\) Rep. \(\searrow\) | Stab. \(\nearrow\) Rep. \(\nearrow\) |
| Targeted | Stab. \(\sim\) Rep. \(\sim\) | Stab. \(\nearrow\) Rep. \(\searrow\) | Stab. \(\nearrow\) Rep. \(\nearrow\) |
| Descriptive | Stab. \(\sim\) Rep. \(\sim\) | Stab. \(\nearrow\) Rep. \(\searrow\) | Stab. \(\nearrow\) Rep. \(\nearrow\) |
| Agressive | Stab. \(\sim\) Rep. \(\searrow\) | Stab. \(\sim\) Rep. \(\sim\) | Stab. \(\nearrow\) Rep. \(\searrow\) |
The instability induced by democracy comes from the distribution of opinions inside the board. With higher %.in.board the distribution is more likely to be wide, increasing the chances of activating the rejection features of the SJT during debates thus generating polarization and splits. With turnover, new Agents arriving in the board will change the distribution of opinions, generating rejection and change in the negotiated norms creating disagreement and splits. With debates influence? = true, the distribution of opinions in board will change through interpersonal influence and if rejection occurs during influence there will be polarization leading to splits in Organizations.
Vertical communication with six dimensions
In this subsection we discuss the effect of vertical communication in 6 dimensions, to fit our observations on the topics of discussion. Table 2 summarizes our results.
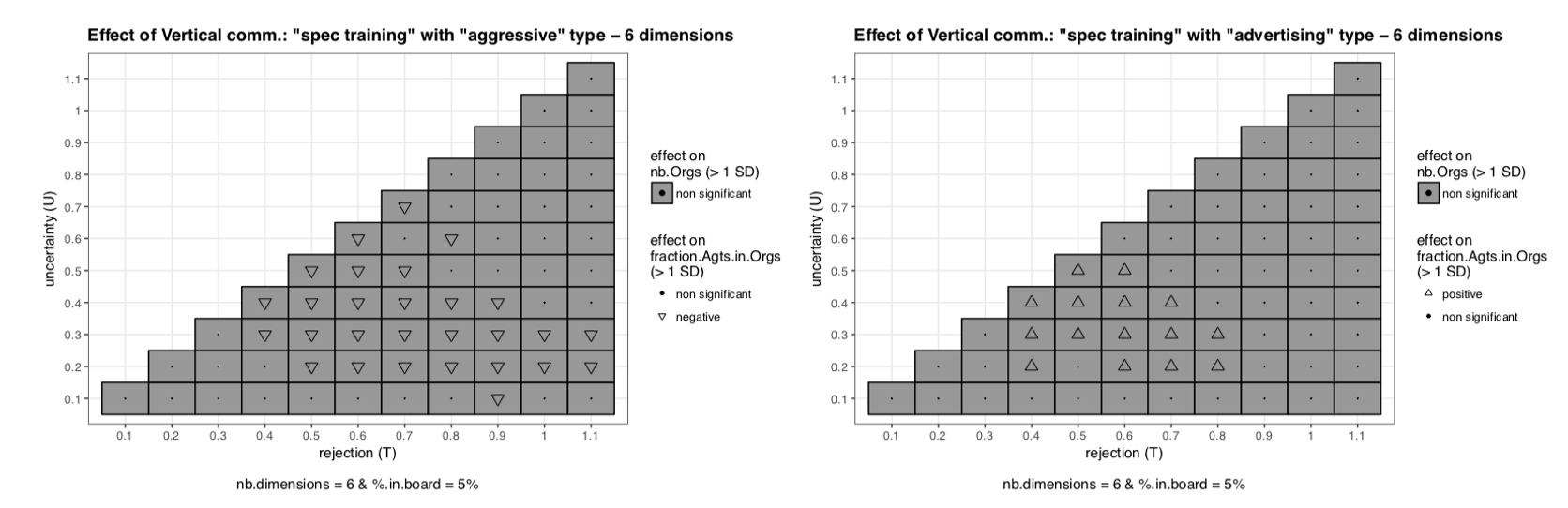
Special training
Special training has a limited effect, as it does not affect stability but only representativeness. Aggressive communication and advertising have opposite impacts (see Figure 5). The fact that it has no effect on stability is because it is not addressed at all to the members of the boards (who play the major role for stability by splitting Organizations). With advertising representativeness improves because advertising makes the vector of opinions of newcomers closer to the vector of norms of the Organization on all the dimensions, then new-comers are more likely to agree with the future transformation of the vector of norms and thus to stay in the Organization, improving the fraction on Agents in Organizations (representativeness). Aggressive communication creates the opposite mechanism: in some cases the vector of opinions diverges which can make diverge from the vector of norms.
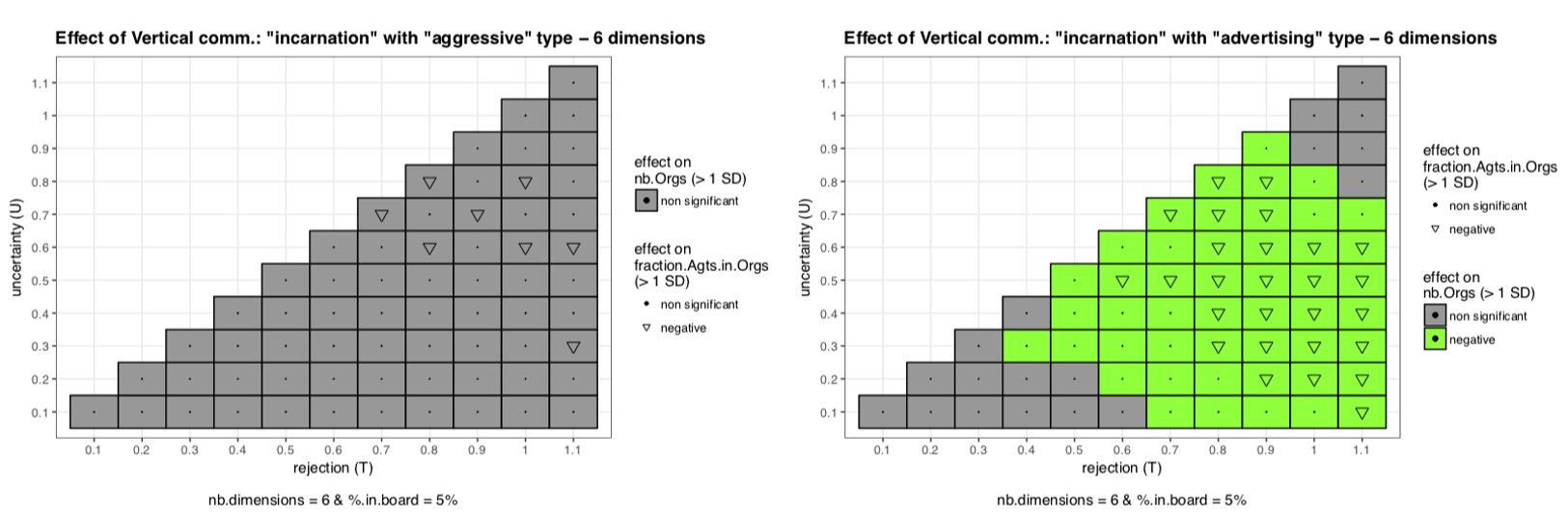
Incarnation
With non agressive communication (descriptive, targeted, advertising) incarnation improves stability (see the right panel on Figure 6 for advertising type). Indeed these types of communication tend to create a more cohesive board by making the vectors of opinions of the representatives get more or less close to the vector of norms of the Organization. Again, this gain in stability is at the price of representativeness due to the same mechanism exposed in the subsection on the model without communication.
Aggressive type of communication with incarnation has no significant effect neither on stability nor representativeness (see the le panel on Figure 6). As it occurs only in board, the effect of incarnation with aggressive communication (standard SJT) is very similar to the effect of the debates in the board on the opinions of the representatives, then it does not change the results, it only accelerates splits that would have eventually occurred (in few time steps).
Communication campaign
With non agressive communication, communication campaigns are able to improve both stability and representativeness (see Figure 7). The improvement in stability comes from the same mechanism exposed for incarnation with non-aggressive communication which creates cohesive boards. The large non-aggressive communication makes the vector of opinions of the non-motivated members converge in some (with targeted) or in all the dimensions (with advertising) to the vector of norms of their Organizations. Then members will agree more with their Organizations and will not leave easily, improving representativeness.
With aggressive vertical communication (SJT) the representativeness decrease because the rejection leads the members of Organizations who barely agree with the vector of norms to leave it. On the other side, the improvement of the stability observed has to be discussed carefully because it comes from the following assumption: if a representative disagrees with the new vector of norms after the aggressive communication campaign (due to the rejection), it is too late, she will not be able to split the Organization at this step and will simply leave it. This assumption is not realistic, but if we do not make it, the representative will split the Organization next turn after negotiating on another dimension even if this dimension is consensual among the representatives, leading to an incoherent split on the wrong dimension (to be coherent the split should have occurred on the former dimension discussed).
Impacts of the vertical communication
Increasing the number of dimensions increases the number of significant effects (\(>1SD\)) we can observe on the mapping \(U\) and \(T\) for incarnation and communication campaign (see Figure 8 for communication campaign). The mechanism behind is the following: with fewer dimensions, debates are quite straightforward and splits happen quicker and then the final steady state is reached quicker and with fewer splits. In this context, vertical communication is important less far in time and then have more limited effect than with a larger number of dimensions. Moreover with lot of dimensions the system is very constrained (Organizations are more sensitive to little variations of norms on one dimension) then even a limited help from the vertical communication to ease these tensions can have a great impact on the system.
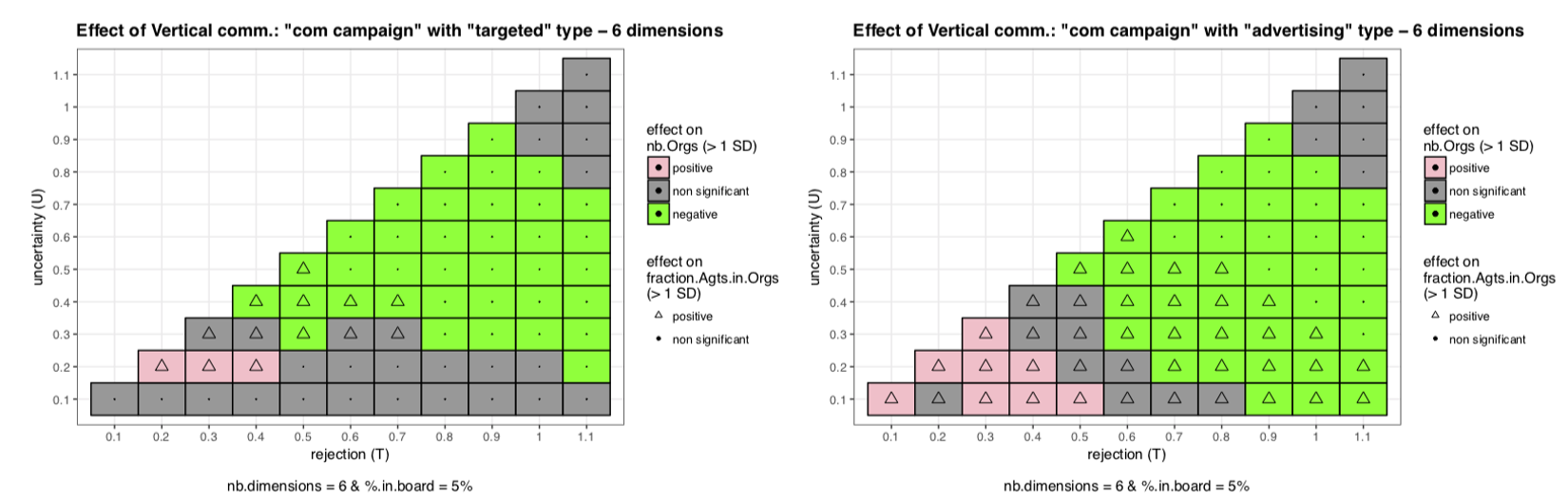
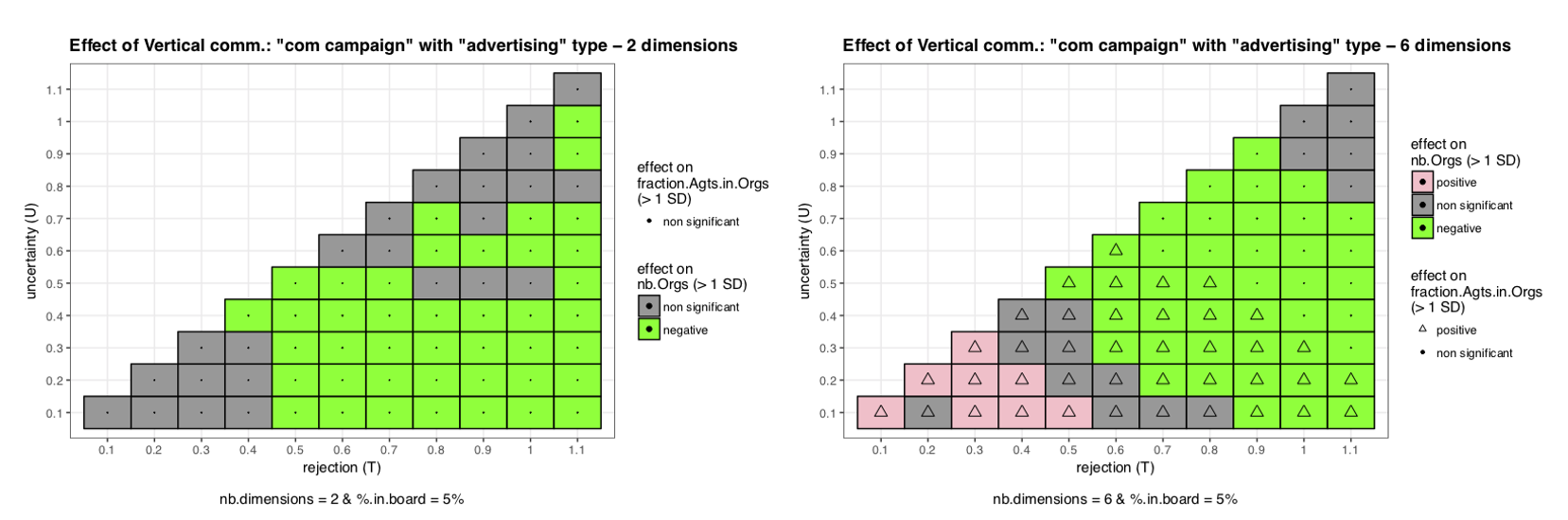
We can also observe that the impact of the vertical communication is quite limited, indeed we almost observed no effect superior to \(1SD\) where we are able to observe effects usually superior to \(2SD\) by playing on other parameters of interest (see Appendix G - Robustness check - where we use a threshold at \(2SD\) to detect significant effects).
Discussion and Interpretation
We built an ABM to study the sensitivity of representative democracy to some aspects confluent to it that we parametrized and tested (the multi-dimensionality of values, the form of communication, etc.). The model we introduce in this article derives from the evolution of an NPO organization (AMAP and its regional association called Alliance Provence/LADP) we observed during our field work in which, collectively, people decided to apply very dense democratic proceedings to choose the norms they would follow.
The model we present here is rather robust in that it gives us relevant and logical results concerning the dynamics of norm creation within an organization in which agents share the same values and try to agree on what norms to implement. Our basic model shows that there is tension between representativeness and stability — when changing the values of our parameters in the attempt to increase stability, we lose representativeness and vice versa. It seems that we can get a slight simultaneous increase of both characteristics only by adding vertical communication. This is what we studied here. Even though the effect observed is not huge, certain forms of vertical communication improve the quality of the democratic process we describe: it is possible to improve, at the same time, representativeness and stability. To attain satisfactory levels of representativeness and stability in organizations, it seems more grounded and more straightforward to use vertical communication than increasing the open-mindedness of agents, which is the only solution, if the latter communication did not exist.
For real-life actors who are interested in improving democratic participation and who already have the intuition of its importance, this is a useful tool to implement. Our model also shows that the way information is handled in terms of how it is communicated has a huge impact on representativeness and stability, subtle result that stakeholders could take into account more seriously. Some elements of our model can help extricate which type of communication is or may be the most appropriate for the dynamics of NPO organizations. Of course, our model is too generic to be applied directly to a case study but can be used to guide or provide guidelines to the analysis of vertical communication, and consider with more precision the questions of when, who, how to do this in specific settings.
For example, in our model, the best way to make norms evolve without causing the organizations to dissolve is to communicate broadly and not just among members of the board, who then have to disseminate the information to others in their own AMAP. This last option is used very frequently in real-life for practical reasons, but it tends to disconnect the board from the other members of the organization as time passes. It is possible for us to show the limits of this practice and possibly open the discussion on this topic with the people we met in our field work. From an economic point of view, actors can also be interested in playing with our model, since they also have to consider the costs of communication, which can be high (it takes skills, materials (papers, goodies, computers...) and benevolent or payed hours). Furthermore, our model shows that it is important to deliver quality communication which cannot be easily interpreted as aggressive so that it has the expected or desired effect, and that the simple descriptive type of communication (which corresponds to the newsletter, certainly the cheapest type) can generate positive effects on stability; whereas special training (particularly expensive) has no positive effect on stability in our model, and slight positive effect on representativeness.
The evolution of the number of dimensions also implies a different evolution of the network than without communication. Indeed introducing communication, especially broad and non-aggressive vertical communication, is able to counterbalance the negative effect of the number of dimensions on both stability and representativeness with respect to the cases where there is no communication. The efficiency of vertical communication increases in organization that are engaged in complex discussions, with many dimensions to norms. Investing in communication can then be a good idea for networks who already know that they will have multidimensional interests.
The model proposed here derives from AMAP organization, in particular because we use this model to communicate with them. Nevertheless, the model can be seen as more generic, and it should be possible to fit in it other organizations who are interested in implementing stable and representative decision-making mechanisms.
Further research can strive to improve different mechanisms of the model — and in particular the scission mechanism of the Organization: here we allow isolated representatives who disagree with the board to split the network. This assumption makes our model very sensitive to disagreements, and thus helps us discuss more easily the theoretical impacts of our parameters of interest. Reality is more complex: splits are costly depending on the role the network attempts to fulfill, the act of splitting should require a sufficient number of motivated agents to do so in its boards, and it is unlikely that an isolated representative is able to split the whole network alone at once. Moreover, this constraint on the number of representatives can cut or decrease some of the effect observed here. Indeed, It should increase stability but at the price of a negative impact on representativeness. It may also create situations in which there exist boards where nobody agrees on the norms but nobody splits, to allow the network to fulfill its role anyway (they might consider the existence of the network as more important than their own satisfaction). Now that we have a first stable version of the model, we will try to test its sensitivity to this new sub-model. We are also thinking of a yet simpler model to address the issue of democratic processes in small groups.
Acknowledgements
This work was funded by the Conseil Régional Provence-Alpes-Côte d’Azur (France) through two PhD programs. We want to specially thank George Butler for his kind grammar and spell check of the paper.Notes
- The general term of “opinion” dynamics cover all the above ABM literature but inside papers terms used and theirs definitions may vary depending on the object studied and the aims of authors. For example in Axelrod (1997), each dimensions is called a trait, the possible values each trait can take are called features and when agent of a same area shared the same feature on a trait (due to influence) this feature is then called a culture or a cultural feature. Epstein (2001) deals with norms (not opinions), agents can choose to behave with respect to two different norms. In Deffuant et al. (2002), opinions are called the points of view of the agents, and clusters of opinions are called norms, it is the same in Jager & Amblard (2005), but opinions there, are identified to individual attitudes of agents.
- Influence each other opinions on this specific dimension through inter-personal interaction. Details about inter-personal interaction are provided in the Social Judgment Theory section.
- If they still retrieve a positive utility they stay else they leave.
- They join the one giving them the maximum positive utility, if none they become an isolated Agent.
- The time scale used in the SJT and the Relative Agreement (Deffuant et al. 2002) models is the average number of interactions per agents. An increase of one unit on this scale correspond to \(n/2\) pairs formed: 2 interactions by pairs.
- The * and ** show some moments when vertical communication occurs depending on their levels if allowed by the user. * stands for the incarnation which reaches only members of the board. ** stands for the special training which reaches only newcomers. The communication campaign reaching everyone in an Organization is the entire step 3. For more information see the next subsection on vertical communication.
- By “agree”, we mean that Agents still retrieve a positive utility with this new vector of norms.
- By “disagree”, we mean that the Agent now retrieve a negative utility with this new vector of norms
- Each Agent joins the new Organization which gives to it the highest positive utility, if both utilities are negative the Agent stays in isolation.
- We use here 0.99 instead of 1 because using 1 can generate issues when splitting boards during a split. Indeed, if on the disruptive dimension \(k\) all the members of the board have an opinion inferior or equal to the norm they all will be in the le board and the right board will be empty. Using 0.99 ensures us to have members in both boards and to manage the split of the Organization.
- When used with the communication campaign aggressive communication can generates members of the board who have previously agreed with the negotiated norm during debates to now disagree with it due to rejection during the vertical communication. We make the assumption here that these representatives who disagree a posteriori choose to leave the Organization without trying to split it. This assumption is important because it has an important impact on the effect of aggressive communication campaign on stability.
- Purely theoretical case to test the behaviour of the model.
- For \(T \leq 1.1\) and \(n \leq 200\), \(100\) time steps is sufficient with the SJT for opinions on one dimension to completely converge in clusters. As we have here several dimensions and that at each times step only one dimension is discussed, we need \(d \times 100\) for opinions to converge to clusters on each dimension. With introduction of the vertical communication, stability of opinions in board cannot always be reached but this does not imply significant changes on our indicators after \(d \times 100\) time steps.
- There exists an exception: narrow-minded agents (small \(U\) and \(T\)). They split their Organizations so often that they end up alone in their own Organization and this Organization is dissolved. Then for narrow-minded agents few Organizations does not mean more stability, it is the opposite. We should then be careful when interpreting the increase (respectively the decrease) of Organizations when agents have small \(U\) and \(T\).
Appendix
A: A field work on AMAP and AMAP networks
What we call in this paper a field work is a collection of interactions and studies realized since 2006 on AMAP short food chain. Researchers of this field work lead by Juliette Rouchier have interacted with several actors on both side: the associative sector of AMAP (LADP, PAMA, MIRAMAP, see below) and the public sector at a regional level (ORCC, see below). It is import to note that the field work and the different studies was not designed to feed and validate the present model. We had not hold a field strategy of data collection specifically addressing the conception and validation of the model. It was main and side observations and conclusions made along the fieldwork which have made relevant for us to model democratic discussion in organisations. Then we have used available observations and data to construct and validate the model, in particular to design our hypothesis about the splitting of networks (See Appendix B and C).
Organizations studied
For the associative sector of AMAP short food chain, 3 main organizations has been followed:
- Les AMAP De Provence (LADP): PACA regional AMAP Network created in 2002 and first owner of the AMAP trademark aiming to protect the AMAP system. They have created the first AMAP charter associated to the trademark. Disagreement inside the organization gave birth to other AMAP networks (Créamap in 2004 and PAMA in 2007, see below). Until 2014 LADP was known as Alliance Provence. Most of the interactions and work done on LADP was made by Juliette Rouchier through regular participation to the organization meetings like local assembly and other periodic meeting (concerning specially the monitoring of quality and application of the charter in the AMAPs of the network). Noé Guiraud worked with LADP to do the first and third AMAP inventory in 2010 and 2015 (see Figure 9). He has also realized an interview with the coordinator of the network (coordinating network’s activities with AMAPs members of the network)/li>
- Les Paniers Marseillais (PAMA): Local AMAP network localised around the city of Marseille. Created in 2007 due to disagreement in LADP: see Section 1 and Appendix B for more details. Most of the interaction and work done on PAMA was made by Noé Guiraud through regular participation to the organization meetings like general assembly or other periodic meeting. He realized one interview of the president of the network and one with its coordinator.
- Le Mouvement Inter-Régional des AMAP (MIRAMAP): The only AMAP network at the national level in France. It was created in 2009 and lead the revision of the AMAPs charter in 2013 and 2014 at a national level this time. Juliette Rouchier followed and participated to this revision along with Claire Lamine from the French national institute of agricultural research (INRA) who was leading her own study on AMAP (Lamine & Rouchier 2016). Juliette Rouchier is still part of the scientific council (“comité d’orientation”) of MI-RAMAP.
For the public sector one organization has been studied through the participation of Noé Guiraud to it:
- l’Observatoire Régional des Circuit Courts de PACA (ORCC): Organization originally created by the PACA regional council to facilitate coordination between sort food chain actors and to improve the use of public founds. Noé Guiraud has participated to the ORCC and has collected data during his own participation to the ORCC (Guiraud 2016; Guiraud & Rouchier 2016a, b). He has realized 4 interviews, one of the regional council coordinator and 3 of delegates of their structures to the ORCC.
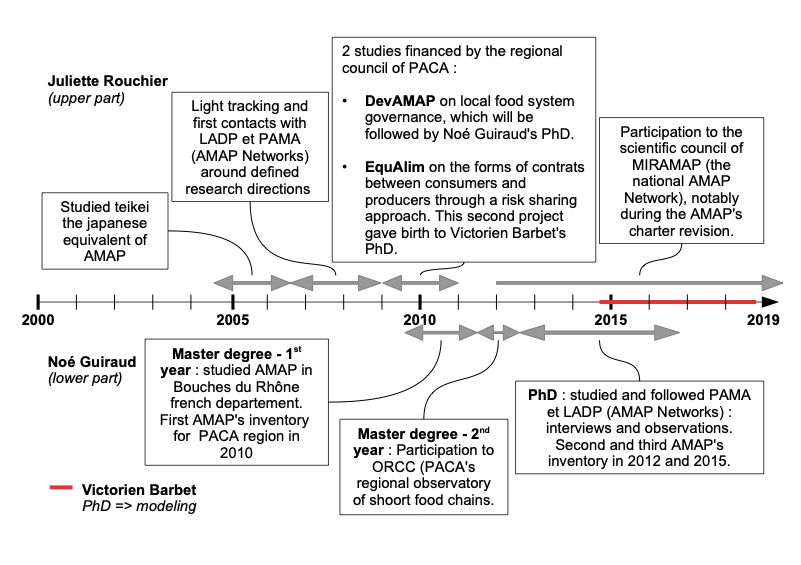
Overview and chronology
The modeling process presented in this article started in November 2014 at the beginning of Victorien Barbet’s PhD. Figure 9 summarizes the general chronology of the field work, showing how research projects from the beginning lead to the further investigations made Juliette Rouchier trough her own work on the revision of the charter and two PhD projects.
Associated publications
This field work lead to several output in terms of publications, some are linked with other researchers working on the same field: Guiraud et al. 2014; Lamine & Rouchier 2016; Guiraud & Rouchier 2016a, b; Guiraud 2016; Barbet 2018; Guiraud 2020.
B: AMAP networks
Soon after the first AMAP were created they gathered into NPO of AMAP called AMAP networks. Motivations behind were to develop the economic model of AMAP through a trial-and-error process, with frequent communication to share information and to spread and define the values that AMAPs want to promote. Networks are highly democratic structures where decisions are taken collectively through negotiation and voting. We can distinguish in this democratic process between two main types of members in networks:
- the “passive” members who belong to the network but are not implicated in its daily life, and do not come to the general assembly. They rarely participate to the democratic process. They are then not really concerned by the interpersonal communication on opinions but only subject to the vertical communication settled by their network.
- the “active” members who are invested actors. They participate in the daily life and to the decision of the network. They constitute the representatives and they constitute the board of the network. Our observations shows that active members are a fraction of approximatively 5% of all the members of a network. They are subject to both interpersonal interactions on opinions among themselves and to the network vertical communication.
Of course, “passive” members can decide to invest more time and participate more becoming “active” members and “active” members can also decide to quit the board because of a lack of time or interest becoming “passive” agents. Divergences of point of view often arise among the “active” members who take decisions. These divergences sometimes lead to the split of the network. Indeed Alliance Provence the first AMAP network, created in 2002, quickly split in two because of disagreement in its board on the function of the network. The split gave birth in 2004 to Creamap France which concentrated its task on the first function of the network (development of the economic model) and Alliance Provence kept on going bearing the second function of diffusion and definition of the principles of AMAP. Nevertheless, this effort of definition was achieved a year before, in 2003 by the edition of the charter of AMAPs which was rewritten in 2014 and saying that AMAPs are based on 5 principles: small farming, ecological agricultural practices, products of quality financially accessible, popular education and solidarity.
However, inside the network of Alliance Provence beside the consensus found on the principles of AMAP, tensions appeared around the local interpretations of the charter into norms. These tensions leaded the network to split again, giving birth to Les PAniers MArseillais (PAMA) in 2007. This split occurred around three disagreements. The first one is a structural disagreement on the organisation of the decision process in the network, and the two others are on organic labelling and quality evaluation topics previously exposed in the part on AMAP.
Here we can see that the conflicting topics identified at the AMAP level also hold at the network level. Then for an AMAP being part of a network is not only a question of following the principles defined in the charter but also following the specific norms collectively decided by the board of the network, even if these norms differ from the local consensual behaviors already implemented in the AMAP.
Nowadays in France AMAP networks are very diverse and numerous, we have counted at least 27 of them orga-nized on 6 different geographic levels (from the city level to the international level). On a same geographical level, each network is mainly independent from the other but they can depend on a network from a higher geographical level. For example, a regional network can possess departmental networks and itself belong to a national network. Moreover networks also often differ in the function they fulfill like in the previous example of Creamap France and Alliance Provence.
The splitting of networks are thus rather frequent, and three main factors can explain this:
- A geographic factor. It is when for example regional network splits into departmental one
- A disagreement inside the network whether on its function, or on the norms to impose in the network.
- This factor is a case of network disappearance, it is when the network does not make sense any more for its AMAP members, who just leave it. For this third factor we have identified three main cases:
- When the functions of two linked network at different geographic levels overlap, the upper network seems not needed any more by its members.
- When the network does not communicate enough on its actions and “passive” members then do not see the point any more of belonging to the network.
- When the norms imposed by the network enter too strongly in competition with the locally pre-existing behaviours of its “passive” members pushing them to quit.
To conclude on AMAP networks, we can say that they are highly democratic structures which evolve through time because of influence and disagreements on opinions and norms. Disrupting topics in networks are the same as the one inside an AMAP (5 topics) plus one on the network’s function.
All these observations came from the field work exposed in Appendix A. The field work has followed mainly the evolution of two AMAP networks: PAMA and Alliance Provence/Les AMAP De Provence (LADP), two of the three networks we have spoken about above. In the paper, we used this empirical work along with to construct and justify our primary model without vertical communication:
- to identify the stylized facts we want to replicate (in bold in this section)
- to identify the parameters of interest in the replication of our stylized facts
- to justify the assumptions we make to build the model
- to fix the values of some of our parameters
- to establish the robustness of our model.
C: Assumptions of the model justified with respect to our field work
There is no cost for agents to enter, quit, split or destroy an Organization. This is definitely not completely true, but here we are interested in the mechanism of norms creation which leads organizations to split so we put aside other economic considerations which are not as important for actors engaged in AMAPs than norms considerations.
For null utility Agents always prefer to be involved in an Organization rather than remaining isolated. As we can observe in the introduction AMAP Networks seems to be a natural and wanted way of collective organisation of AMAPs, then for a null utility an Agent will prefer to belong to an Organization rather than remaining isolated.
Agents opinions can be influenced through the Social Judgement Theory Model of Jager & Amblard(2005). influence take place everywhere between representatives in AMAP networks: phone call, mailing, regular meeting for the daily life of the network, general assembly. We have chosen the SJT for three main reasons:
- The rejection grasps the tensions described in the empirical observations, and well replicates the conflicts that arise in AMAPs and Network on hot topics due to repeated interactions on disruptive subjects.
- The existence of two thresholds allows us to model a larger set of personalities for our agents. If the two thresholds are close together, then there is an hight ego involvement (Jager & Amblard 2005), giving birth to segregative agents, not open to discussion: either you are with me or against me. A larger gap between confidence and rejection allows us to model agent more open to discussion and consensus: agent who can be really confident in her position (little uncertainty) but who will not easily enter in conflict with others (large rejection) and who are able to seek for and find consensus. Modelling these types of personalities makes sense because we have encountered these two types of behaviours among the representatives of AMAP networks during the field observations.
- The fact that rejection and confidence are fixed thresholds eases the definition of a simple utility function on norms for agents, based on this two parameters.
Inside a given board every Agent of this board can interact with any other Agent, as if they are in a fully-connected network. As representatives are strongly involved in the daily life of their network, the communication among them is essential for its survival. Thus, representatives cannot avoid to interact with one and other.
Agents members of the board are randomly chosen, and stay in the board unless they leave the Organization during a split. In the specific case of AMAP, members willing to be part of the board do not show off specific shape of opinions and are not so numerous. Then every motivated AMAP can be part of the board without restriction. Indeed as there is often less applicants than places offered in board the elections are most of the time a simple formality. That is why we can take randomly the members of the board among the members of the Organization. Moreover, still in the specific case of AMAP we can observe that there is almost no turn-over in board, and most of its members are involved since the beginning.
At each turn Agents in boards can influence each others opinions and negotiate new norms only around one specific dimension randomly picked-up. We have observed in our field work on AMAP that some dimensions become hot topics through time and began the core of the discussions in the network. Moreover all the topics are rarely discussed at the same time.
Organization can split. Splits occurs only when members of the boards disagree on a newly negotiated norm on one specific dimension. The two new Organizations resulting from a split inherit the norms of the old one except on the disrupting dimension.
Representatives of the split Organization are automatically representatives of the new Organizations they have chosen to belong to. As said before members of board are motivated members and are few in our case. We observe in spite of the successive splits that representatives of the new networks are often the representatives of the former one and many of them are here since the creation of the first network.
Agents which are not involved in an Organization join the existing Organization which gives them the maximum positive utility. It’s the same during a split, Agents of the former Organization join the new one which gives them the maximum positive utility. We assume it’s quite easy and not much time consuming for AMAPs to gather data on the norms of networks (you can find them on their websites), and then to join the best for them.
D: Social Judgment Theory influence profile
Figure 10 shows the amplitude of the influence of agent \(i'\) on \(i\) depending on the position of agent \(i'\)’s opinion with respect to agent \(i\)’s opinion.
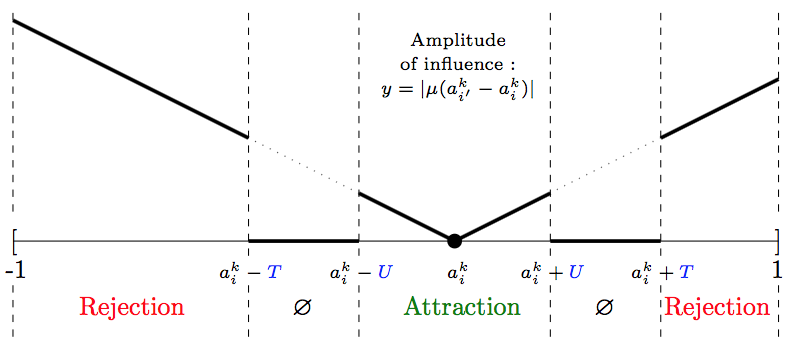
E: Pseudocode
The pseudocode of the model for steps 1 to 5 of the scheduling (subsection 3.22). Moreover, the model code and its ODD can be found following this link to the CoMSES website: https://www.comses.net/codebases/6cc6a99b-cde1-4e49-bef8-e6fd4f997259/releases/1.0.0/.
Step 1: Debate/negotiation/splitting
Step 2: Isolated agents inscription
Step 3: Communication campaign
Step 4: Organizations dissolution
Step 5: Completion of boards
F: Constructing observations
To plot the effect on stability and representativeness of introducing communication or changing a parameter like the number of dimensions discussed, we need to compare for each couple \((U,T)\) our indicators nb.Orgs and fraction.Agents.in.Orgs before and after the change in parameters.
Mathematically we have for each couple \((U, T)\) and a given indicator \(I\) nb.Orgs or fraction.Agents.in.Orgs series of \(100\) observations of \(I\) for every possible sets of parameters. To test the effect on the indicator \(I\) of switching from a set of parameters \(s\) (without communication for example) to a set \(s'\) (with communication for example), we compute for each couple \((U,T)\) and both sets of parameters the mean of \(I\) over the \(100\) observations: \(\overline{I^{s}_{(U,T)}}\) and \(\overline{I^{s'}_{(U,T)}}\). Then we make the difference between these two means (absolute effect) and divide it by the standard deviation on \(I\) for the set \(s\) (denoted \(SD(I^{s}_{(U,T)})\)). We obtain the following relative effect:
| $$\Delta^{s \rightarrow s'}_{(U,T)} = \frac{\overline{I^{s'}_{(U,T)}}-\overline{I^{s}_{(U,T)}}}{SD(I^{s}_{(U,T)})}$$ | (10) |
G: Robustness check
In this section we will explore more deeply the model without vertical communication. We will describe the effects of most of the parameters of interests along with the mechanisms behind and in a second step we will interpret and validate the results to the light of our field work.
We have used here the same methodology as the one exposed in the results section of the core paper, except that now we take, by convention, an effect for significant if superior to two standard deviation (instead of one when studying the effects of communication). The complete behavior space for the robustness check can be found in Table 1: except that vertical communication is switch to “no” for the robustness check.
A simulation for a given set of parameters of the model is made of 100 time steps, time for the system to reach a steady state where all Organizations are stable and isolated Agents are not able to find a corresponding Organization any more. Each set of parameters is run 100 times.
From the data we have observed in the field, we define what we call our baseline scenario:
- \(nb.Agents = 200\)
- \(nb.dimensions = 6\)
- \(\%.in.board = 5\)
- \(influence? = true\)
We will use it most of the time as a reference in this robustness check section. The results are summarized in the Table 3 and will be exposed more widely just after.
Effect of the number of agents
Increasing the number of Agents in the primary Organization decreases stability but improves representativeness (see Figure 11).
The mechanism behind is the same as the one exposed in the core paper for increasing the participation to boards, indeed if the number of Agents increase for a constant %.in.board the size of boards increases too, making the distribution of opinions among representatives wider leading to more conflicts and then more splits. These splits increase the offer in Organization to join for isolated Agents improving the representativeness.
| Stability | Representativeness | ||
| \(\nearrow\) nb of Agents | \(\searrow\) | \(\nearrow\) | |
| characteristics of agents | open-minded (large \(U\) and \(T\)) | \(\nearrow\) | \(\nearrow\) |
| narrow-minded (small \(U\) and \(T\)) | \(\searrow\) | \(\searrow\) | |
| topics discussed | \(\nearrow\) nb of topics | \(\searrow\) | \(\searrow\) |
| preference for the first topic | \(\nearrow\) | \(\nearrow\) | |
| organisation of the board | \(\nearrow\) \(\%.in.board\) | \(\searrow\) | \(\nearrow\) |
| \(\nearrow\) turn-over in board | \(\searrow\) | \(\nearrow\) | |
| no debate | \(\nearrow\) | \(\searrow\) | |
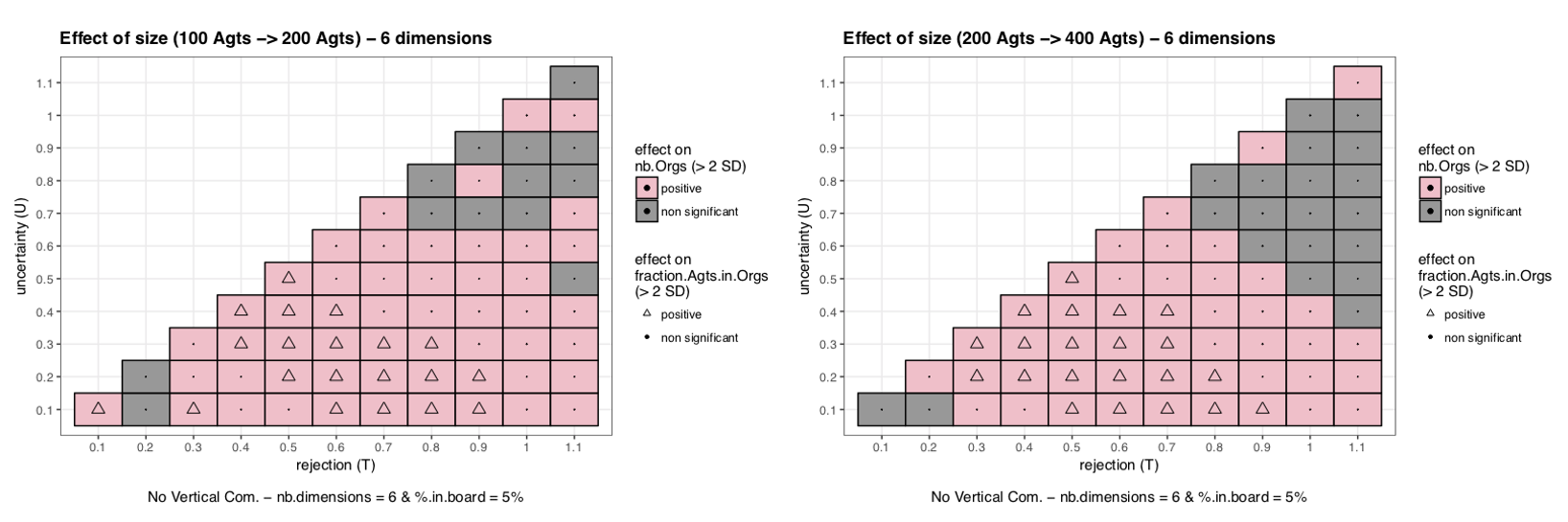
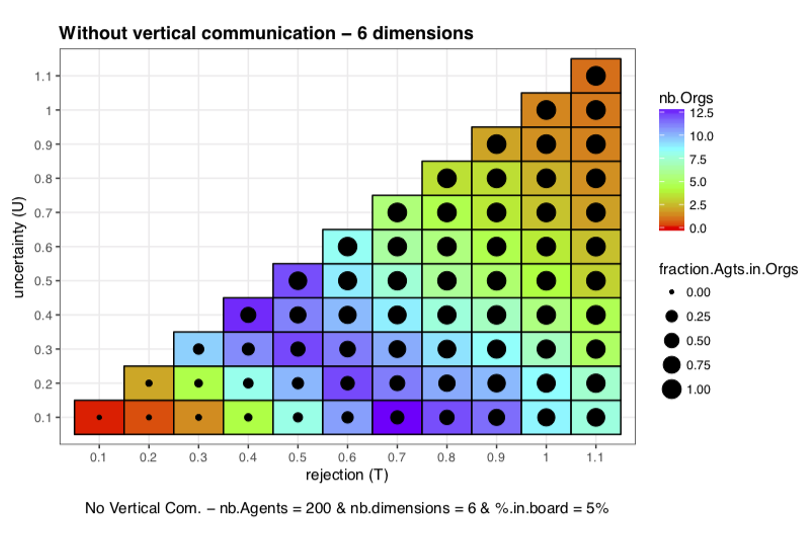
Characteristics of agents
Effect of the open-mindedness (\(U\) and \(T\))
Increasing \(U\) and \(T\) increases the stability (few Organizations at the end) and the representativeness (Organizations gather lots of Agents). Decreasing \(U\) and \(T\) implies less stability (lots of Organizations) and less representativeness. Continuing decreasing \(U\) and \(T\), representativeness keeps on shrinking and the number of Organizations begins to decrease too (see Figure 12).
The mechanism behind is quite straight forward as agents are open-minded (large \(U\) and \(T\) ) they more easily retrieve positive utility of a negotiated norms and often agree with it. But, as they are narrow-minded, they retrieve less positive utility on negotiated norms and the rejection tends to move away their opinions decreasing again their utility. In this second context Organizations split more often (decreasing stability) and isolated Agents are more exigent when it comes to join an Organization, decreasing the representativeness. When agents are extremely narrow-minded, Organizations splits a lot and lose their members until they are dissolved, then at the end there is few Organizations alive gathering few Agents. Here the small number of Organizations does not imply high stability, it is exactly the opposite.
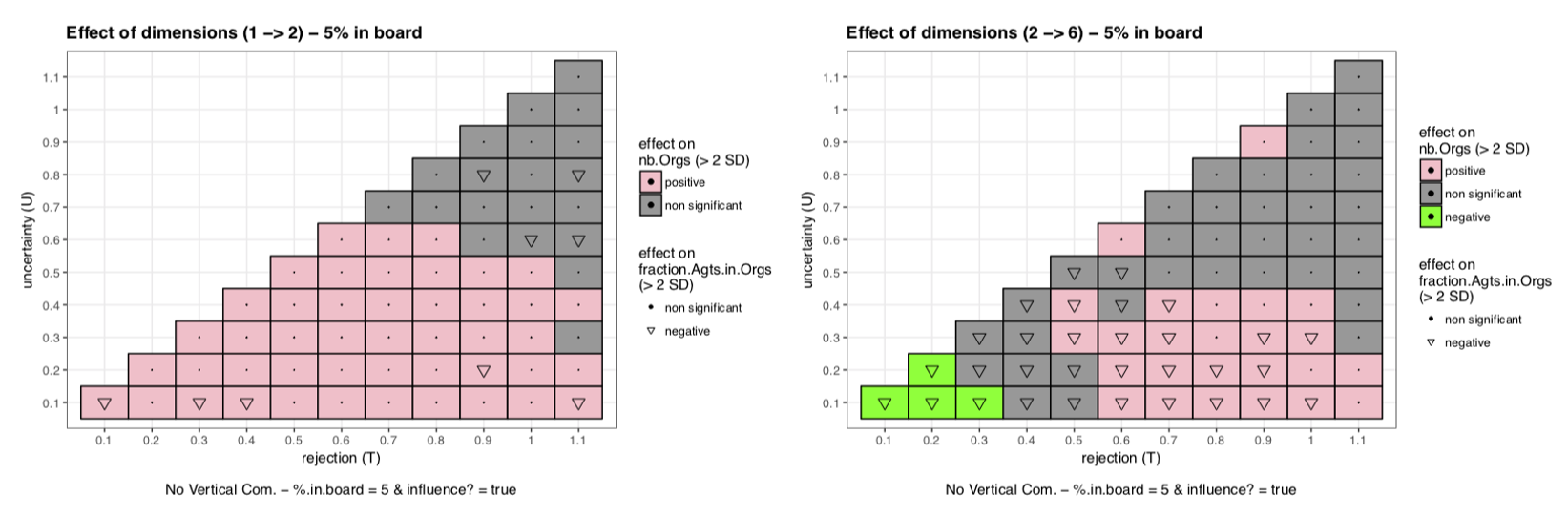
We have stopped the exploration of the behaviour space of \(U\) and \(T\) at \(1.1\) because for \(T > 1.1\) the model ends up generally with the following pattern: one big Organization gathering a large majority of Agents.
Dimensions
Effect of the number of dimensions
The effect of the number of dimensions depends on the mapping \(U\) and \(T\). If they are large enough, nothing really significant seems to happens. If they are not too large, increasing the number of dimensions have a negative effect on the representativeness and stability. Again here for \(U\) and \(T\) very small the diminishing number of Organizations does not mean more stability but more dissolution of Organizations (see Figure 13 and Endnote 14).
The mechanism is the one exposed in the core paper in the subsection on the behaviour of the model without vertical communication.
Effect of preference for the first dimension
Here we want to introduce a preference on one common dimension for all agents. The idea behind comes from our field work: some topics are often considered by the majority of actors as more important than others. To model this fact we have introduced a preference for the first dimensions. Which means here that agents weight more the utility retrieved on the first dimension than on others. For \(n>2\) dimensions, the utility on the first dimension is weighted \((n-1)\) and utilities on other dimensions are weighted only 1. The first dimension is now as important as all the others together.
The introduction of such a preference improves stability. The representativeness is improved too for small U and T. The effect observed is significant for only one standard deviation (see Figure 14).
Here adding preference for one common dimensions counter the negative effect of adding new dimensions. In the example, even if there are 6 dimensions, thanks to the preference, at the utility function level it is almost like there is only 2 of same weight. Then the situation obtained at the end is in between the case of 2 and 6 dimensions without preferences (see Figure 15).
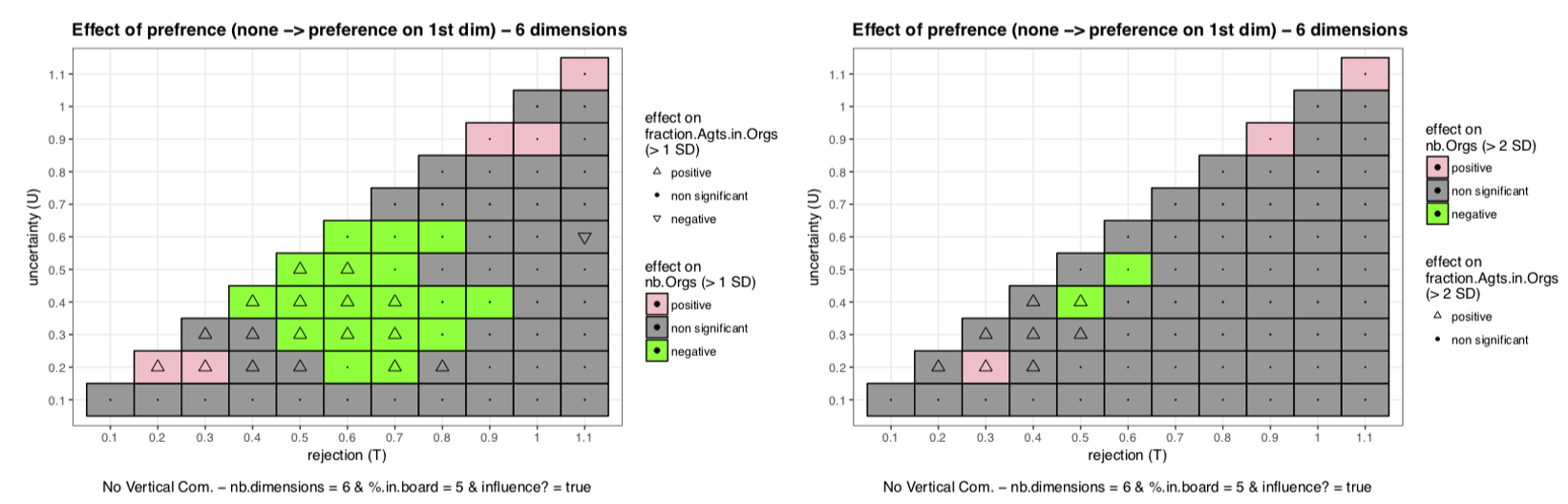
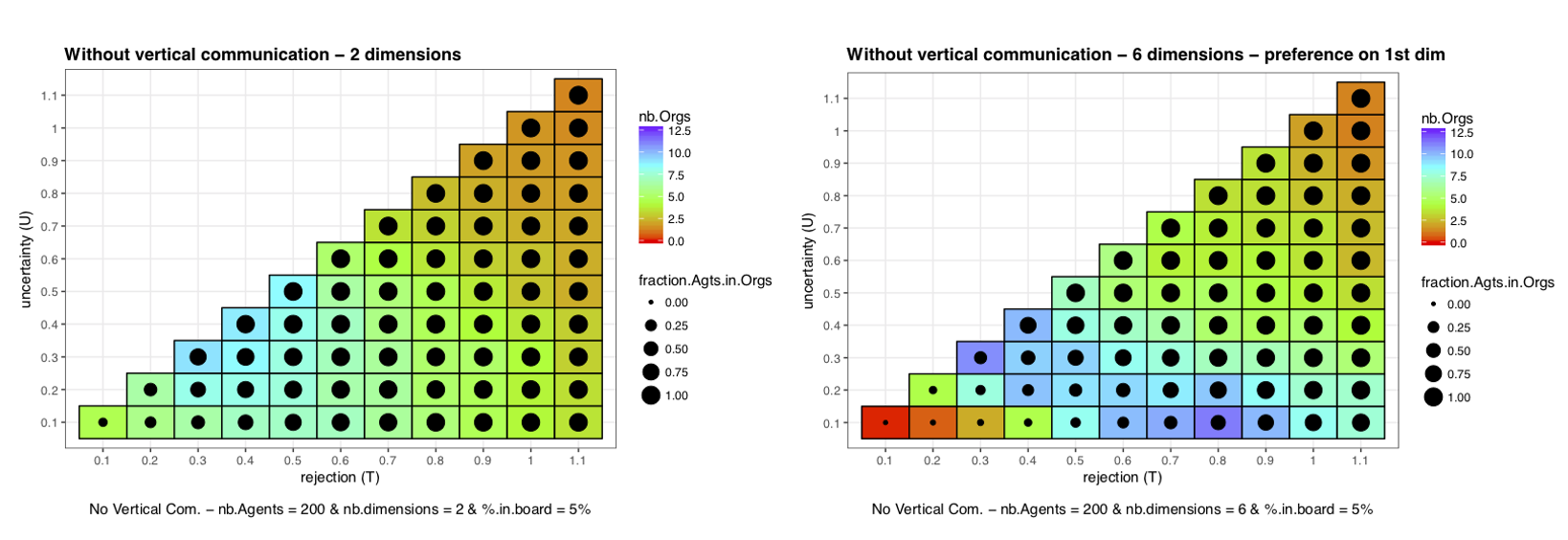
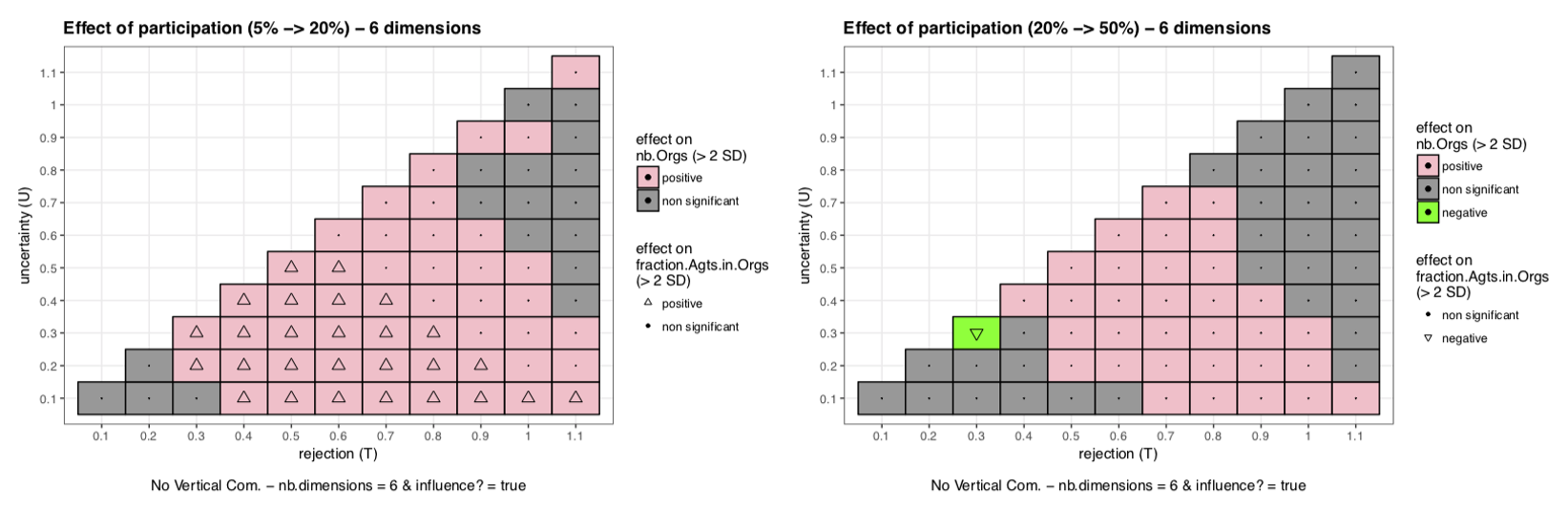
Organization of the board
Effect of the size of board
Increasing the percentage of members chosen to be representatives decreases the stability but enhances the representativeness (see Figure 16).
Indeed as the number of representatives increases, the distribution of opinions in the board is wider and a wider distribution increases the chance of disagreement and then of splits. But then as the number of Organizations is higher the choice for isolated Agents is larger and it is easier for them to find a corresponding Organization to join, improving representativeness.
Effect of the turnover in board
In our model we have a structural turnover in our boards only due to the mechanism of splitting and board completion, but without splits, no turnover. Nevertheless in the real world we have observed a small turnover, most of the time due to active members who have no more time or energy for the network. Then they quit the board but keep on belonging to the network. To model this fact we have added a probabilistic turnover in boards. Each turn Agents of board have a percentage of chances to quit the board and remain in the network as passive members. After this if the number of Agents in the board is lower than the minimum authorized by \(%.in.board\) then new members are randomly picked up among the passive members to become representatives.
The results for the introduction of turnover are the following. Increasing the turnover in board decreases the stability but enhances the representativeness. The effect of the turnover is sharp when we switch from none to some turnover, but then seems to quickly fade away for representativeness.

The mechanism behind results are the following. The turnover threatened the stability of boards leading to more splits, but in exchange these splits gave birth to new Organizations improving the offer of Organization for isolated Agents, increasing the representativeness (as in the case of the effect of participation).
Effect of the influence
Cutting the influence (debate) in board improves stability but decreases representativeness (see Figure 18).
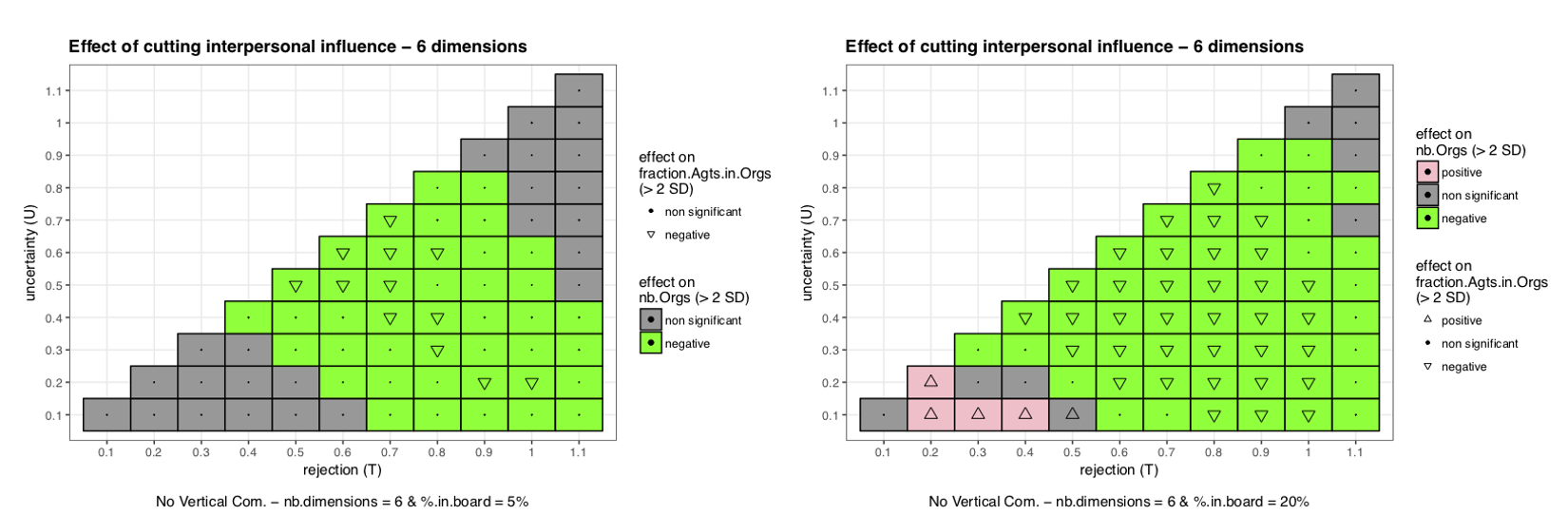
As there is no more influence among representatives, there is no more rejection, decreasing the probability of disagreement and then improving stability. But as the number of Organizations is lower ceteris paribus there is a smaller offer for isolated Agents decreasing their chances to find a corresponding Organization and then diminishing the representativeness.
Validations and interpretations
In this section we propose a validation of our model by showing how the effect we have observed hold in the reality. When we have no data to validate or invalidate our model, ie when the model tells more than our observations we propose an interpretation of these results.
Negative effect of the number of dimensions on the stability and representativeness of organization, and the counter effect of preference
According to our model the number of normed dimensions is really important, because this is the main factor which is able to decrease both in the same time stability and representativeness. On the field representatives are al-ready well aware of its negative effect and take some counter measures. First representatives can play on the level of application (more or less strictly) of their norms to relax tensions in the network. Actually for example their is no direct penalty taken against an AMAP which is not respecting the rules but corrective actions are col-lectively decided with this AMAP and time scheduled in the long run. Second counter measure: representatives can takes the decision of imposing no norm on a too disrupting topic which threaten their unity. In fact, this decision is linked with the importance representatives gives to the topic. There are mainly two cases:
- If the topics is really important, which means they acknowledge that this dimension has to be normed, they can simply buy some time by post-pounding the decision in order to discuss a little bit more. In this case our model due to the rejection will predict that a second round of deliberation (influence) will produce even more disagreement leading the network to split for sure. Then post-pounding the decision, according to our model do not save the network but only buy time to prepare a well organised split.
- If the topic discussed is considered by the representative as not much important, they can simply decide not to norm it. They consider there is no need to threat the network unity for such a “weak” topic.
Even if its mechanism is not descriptive our modeling of preferences introduced in the model tries to grasp these two points by saying: their is topics which are considered consensually as more important than others, what is the impact of modelling such preferences in the utility function? The results obtained are quite realistic, indeed the introduction of a common hierarchy in dimensions improves the stability of the networks compared to the case where all dimensions have the same importance: it well replicates the effect of the second points exposed.
Negative effect of the size of the board on organization stability
Our model tells us that the percentage of members chosen to be part of the board of a network has a negative effect on its stability, leading networks to split more often. This point is particularly interesting because during our field observations, representatives of networks often complained about the low rate of participation of passive members in the network’s daily life and decision process. But according to our model this low percentage of participation helps the constitution of a strong group of representatives sharing common vision on norms to implement, stabilizing the network. Nevertheless the results of our model need to be lowered: in reality whereas in our model, all disagreement in the board do not lead to the systematic split of the network. Indeed a representative alone who disagree rarely causes the network to split, it depends on her personality and on her opportunity to find other representatives who share her opinions and agree to split. These factors are not taken into account in our model where split occurs as soon as at least one representative disagrees. All this said, we can always conclude that an increase of the percentage of participants creates a favorable playground for disagreements threatening the stability.
Negative effect of the influence on the stability of organizations
We have seen that the less representatives can influence each other’s the more stable the network. Indeed, in our model as in the reality, influence is a double edge knife, on one side if opinions of representatives are already close, influence will tightened the board and then the network. On the other side, if the distribution of their opinions is wide the influence process is more likely to create two cohesive groups of opposite opinions (polarization observed in the SJT) leading the network to split. Nevertheless cutting all influence in the real world is impossible and preventing debates in the board does not fit with the strong democratic will of actors. That is why through years networks have developed animation skills in order to allow everyone to express their points of view while preventing violent clashes (rejection feature of the Social Judgement Theory) which conduct to the polarization of opinions and to splits.
The negatively correlated impact on stability and representativeness
Instability is not necessarily a negative aspect for networks. For instance, increasing the size of board or allowing the influence in board does increase the instability but in return the number of different networks in-creases, giving more chances to isolated Agents to find a corresponding network, enhancing representativeness of networks as a whole. On the one hand, the relative weights of networks decreases, but on the other hand less Agents are le in isolation. The paradox is that the instability of networks helps them to be more e icient at the global level because they reach more Agents, but less efficient at their individual level assuming that larger networks are able to mobilise more means to help their Agents.
Moreover, this negatively correlated impact occurs when playing on parameters which imply “more democracy”:
- the number of Agents: Organizations have to conceal peacefully opinions of more and more members (\(nb.Agents\)).
- the participation rate to boards: More people are motivated to participate together to the daily life of Organizations (\(%.in.board\)).
- the organisation of debates: Organisation of democratic debates in board where every representative can express her own point of view to others (\(influence?\)).
- turnover in boards: The members of the boards are regularly renewed.
References
ABRICA-JACINTO, N. L., Kurmyshev, E. & Juárez, H. A. (2017). Effects of the interaction between ideological affinity and psychological reaction of agents on the opinion dynamics in a relative agreement model. Journal of Artificial Societies and Social Simulation, 20(3), 3: https://www.jasss.org/20/3/3.html. [doi:10.18564/jasss.3377]
AMBLARD, F. & Deffuant, G. (2004). The role of network topology on extremism propagation with the relative agreement opinion dynamics. Physica A: Statistical Mechanics and its Applications, 343, 725–738. [doi:10.1016/s0378-4371(04)00858-1]
AMEMIYA, H. (2011). Du teikei aux AMAP: le renouveau de la vente directe de produits fermiers locaux. Rennes: Presses Universitaires de Rennes.
AXELROD, R. (1997). The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]
BARBET, V. (2018). Pluralisme et stabilité des organisations: modéliser la dynamique d’organisations démocratiques où plusieurs dimensions sont discutées: le cas des AMAP de Provence. Ph.D. thesis.
BARBET, V., Guiraud, N., Laperrière, V. & Rouchier, J. (2019). or trouble. Working paper AMSE 2019-09. Available at: https://halshs.archives-ourvertes.fr/halshs-02066846/file/WP%202019%20-%20Nr%2009.pdf.
BUTLER, G., Pigozzi, G. & Rouchier, J. (2019). Mixing dyadic and deliberative opinion dynamics in an agent-based context of group decision-making. Unpublished. [doi:10.1155/2019/3758159]
CASILLI, A., Rouchier, J. & Tubaro, P. (2014). How to build consensus in a health-oriented online community: Modeling a “Pro-Ana” forum. Revue Française de Sociologie, 55(4), 731–764. [doi:10.3917/rfs.554.0731]
DEFFUANT, G., Amblard, F. & Weisbuch, G. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), 1: https://www.jasss.org/5/4/1.html.
DEFFUANT, G., Huet, S. & Amblard, F. (2005). An individual-based model of innovation diffusion mixing social value and individual benefit. American Journal of Sociology, 110(4), 1041–1069. [doi:10.1086/430220]
DELRE, S., Jager, W., Bijmolt, T. & Janssen, M. (2007). Targeting and timing promotional activities: An agent-based model for the takeoff of new products. Journal of Business Research, 60(8), 826-835. [doi:10.1016/j.jbusres.2007.02.002]
EPSTEIN, J. M. (2001). Learning to be thoughtless: Social norms and individual computation. Computational Economics, 18(1), 9–24.
FLACHE, A. & Mäs, M. (2008). Why do faultlines matter? A computational model of how strong demographic faultlines undermine team cohesion. Simulation Modelling Practice and Theory, 16(2), 175–191. [doi:10.1016/j.simpat.2007.11.020]
GUIRAUD, N. (2016). La relocalisation agricole et alimentaire en région Provence-Alpes-Côte d’Azur: Une étude multi approche des circuits courts (2000-2015). Ph.D. thesis. [doi:10.3917/eg.434.0356]
GUIRAUD, N. (2020). Le retour des ceintures maraîchères? Une étude de la proximité géographique des amap en bouches-du-rhône (2006-2015). Géocarrefour, forthcoming. [doi:10.4000/geocarrefour.13873]
GUIRAUD, N., Laperrière, V. & Rouchier, J. (2014). A geography of short supply chains in Provence-Alpes-Côte d’Azur. L’Espace Géographique, 43(4), 356–373. [doi:10.3917/eg.434.0356]
GUIRAUD, N. & Rouchier, J. (2016a). La visibilité comme ressource dans la gouvernance des circuits courts: Une approche institutionnaliste de l’évaluation pour l’observatoire des circuits courts de PACA. Working paper. Available at: https://halshs.archives-ouvertes.fr/halshs-01366242. [doi:10.3917/eg.434.0356]
GUIRAUD, N. & Rouchier, J. (2016b). L’observatoire régional des circuits courts à l’aune de la proximité organisée: vers une évaluation du dispositif. In P. Mundler & J. Rouchier (Eds.), Alimentation et proximités. Jeux d’acteurs et territoires, (pp. 103–127). Paris: Educagri.
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.
HOLYST, J. A., Kacperski, K. & Schweitzer, F. (2002). Social impact models of opinion dynamics. Annual Reviews of Computational Physics, 9, 253–273.
HUET, S., Deffuant, G. & Jager, W. (2008). A rejection mechanism in 2d bounded confidence provides more conformity. Advances in Complex Systems, 11(04), 529–549. [doi:10.1142/s0219525908001799]
JAGER, W. & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behav-ior with an agent-based simulation model of attitude change. Computational & Mathematical Organization Theory, 10(4), 295–303. [doi:10.1007/s10588-005-6282-2]
LAMINE, C. & Rouchier, J. (2016). D’une charte l’autre: le processus de révision de la charte des AMAP comme indicateur d’une institution qui se renforce. Revue de la Régulation, 2e semestre/ Autumn (20). [doi:10.4000/regulation.11966]
LAMINE, C. B. A. (2005). Settling shared uncertainties: Local partnerships between producers and consumers (english). Sociologia Ruralis, 45(4), 324–345. [doi:10.1111/j.1467-9523.2005.00308.x]
LANCHIER, N. (2012). The Axelrod model for the dissemination of culture revisited. Annals of Applied Probability, 22(2), 860–880. [doi:10.1214/11-aap790]
LI, J. & Xiao, R. (2017). Agent-based modelling approach for multidimensional opinion polarization in collective behaviour. Journal of Artificial Societies and Social Simulation, 20(2), 4: https://www.jasss.org/20/2/4.html. [doi:10.18564/jasss.3385]
MARCH, J. G. (1991). Exploration and exploitation in organizational learning. Organization Science, 2(1), 71–87.
MUNDLER, P. (2009). Les associations pour le maintien de l’agriculture paysanne: solidarité, circuits courts et relocalisation de l’agriculture. Pour, (2), 155. [doi:10.3917/pour.201.0155]
NOWAK, A., Vallacher, R. R., Kus, M. & Urbaniak, J. (2005). The dynamics of societal transition: Modeling nonlinear change in the polish economic system. International Journal of Sociology, 35(1), 65–88. [doi:10.1080/00207659.2005.11043141]
ROUCHIER, J. & Tanimura, E. (2012). When overconfident agents slow down collective learning. Simulation, 88(1), 33–49. [doi:10.1177/0037549711428948]
ROUCHIER, J., Tubaro, P. & Emery, C. (2014). Opinion transmission in organizations: An agent-based modeling approach. Computational and Mathematical Organization Theory, 20(3), 252. [doi:10.1007/s10588-013-9161-2]
SHERIF, M. & Hovland, C. I. (1961). Social Judgment: Assimilation and Contrast Effects in Communication and Attitude Change. New Haven, CT: Yale University Press.
STAUFFER, D. (2001). Monte Carlo simulations of Sznajd models. Journal of Artificial Societies and Social Simulation, 5(1), 4: https://www.jasss.org/5/1/4.html.
WEISBUCH, G., Deffuant, G., Amblard, F. & Nadal, J. (2002). Meet, discuss, and segregate! Complexity, 7(3), 55–63. [doi:10.1002/cplx.10031]
WEISBUCH, G., Deffuant, G., Amblard, F. & Nadal, J. P. (2001), N. J. P. (2001). Interacting agents and continuous opinion dynamics. ArXiv Preprint: http://arXiv.org/pdf/cond-mat/0111494v1.

