Introduction
Knowledge management including the creation, sharing, absorption and the transmission of knowledge is becoming ever more essential for the development of society and the economy today, i.e., the so-called knowledge economy era (Herie & Martin 2002; Phelps et al 2012). Knowledge is diffused through knowledge networks including personnel, innovative organizations and companies that have socio-economic relevance (Hansen 2002; Molm et al. 2012). Therefore, problems related to knowledge diffusion in knowledge networks, which become a very important part of knowledge management, can be classified into two main categories; the modelling of knowledge diffusion and the evolution of knowledge networks. In order to solve such problems, co-evolutionary dynamics combining the knowledge diffusion of agents with the topological evolution of network structure is urgently needed and is a recent research trend in the field of complex network (Gross & Blasius 2008; Vazquez 2013; Luo et al 2015).
Research on the co-evolutionary dynamics of knowledge diffusion and network structure have been purposed to improve the spread of knowledge indicated as average knowledge stock and knowledge growth rate etc.. Thus, previous work has mainly focused on the modeling of knowledge diffusion process based on agent-based approach and the evolution of network structure based on probabilistic methodology (Paruchuri 2010; Boone & Ganeshan 2008). Cowan & Jonard (2004) considered the knowledge diffusion process as a barter process and used an agent-based approach to study knowledge diffusion in the network structure with a rewiring probability.
Simulation results show that the average knowledge stock is highest at the equilibrium state in the case of a small world network. These results were also reported by Kim & Park (2009), who investigated the influence of network structure on knowledge diffusion in the research cooperation network. Mueller et al. (2017) modelled the knowledge diffusion process as a barter process and used an agent-based model to explore the influence of overall degree distribution on knowledge diffusion performance in informal networks.
They additionally exploited four well-known network topology algorithms based on probabilistic methods to analyze their effects on knowledge diffusion and verify the model’s validity through policy experiments. Sun (2017) proposed a knowledge diffusion model introducing the concept of network distance to study the influence of inter-organizational network distance on knowledge diffusion and reported that the close connection between innovative organizations formed by changing the network rewiring mode is an important factor to improve organizatonal knowledge growth rate. Zhuang et al. (2011) further followed a multi-agent-based approach to design a knowledge diffusion model in which knowledge stock and update are considered together, and also proposed four policies to update network structures. Their simulation results showed that it is more effective to absorb knowledge globally from the whole range of networks than locally from the neighbor with a high knowledge level.
Luo et al. (2015) studied the co-evolutionary dynamics of knowledge diffusion and network structure by combining the KT (Knowledge Transfer) rule with the NA (Neighborhood Adjustment) rule. Their simulations indicated that the co-evolution of knowledge diffusion and network structure changes the topological structure from random to small world networks. Xuan et al. (2011) also developed an agent-based model adjusting the "knowledge - connection" structure of network to evaluate knowledge diffusion performance and reported that the bidirectional knowledge diffusion (BKD: Bidirectional knowledge diffusion model; see Xuan et al. 2011) model interferes with the long-term effect of knowledge diffusion compared to the unidirectional knowledge diffusion (UKD) model (Xuan et al. 2011). This can be overcome through the periodical adaptation of re-adjustment mechanism. Additionally, Wang (2013) conducted a theoretical research to analyze the formation and structural evolution of knowledge network and reported that the diffusion of knowledge between agents in the organization with a weak connection and a low reliance is based on social exchange mechanism, and the reciprocal mechanism plays a leading role as the cooperation and reliance between agents are enhanced. Finally, Liu et al. (2017) proposed the social knowledge diffusion model (SKD) in which the interaction frequency between agents is considered. They found that their proposed model is more beneficial for knowledge diffusion, compared to Null (defined by the random selection mechanism) and TKD (Traditional Knowledge Diffusion via knowledge distance) models.
With the exception of this latter research, several other studies on the co-evolution of agents’ opinion forming and network structure have been conducted (Gil & Zanette 2006; Vazquez 2013; Hegselmann & Krause 2002; Su et al. 2014; Luo et al. 2014). All of these used the probabilistic methodology to change the connection between agents and update the network structure. From the previous studies, the following summary can be drawn. Firstly, the studies on the co-evolutionary dynamics of knowledge diffusion and network structure, in which mainly adopted agent-based approach, focused on making the knowledge diffusion models as close as to the real world on the basis of knowledge network’s formation mechanism. Secondly, in the evolution of network structure, researchers simply tried to exploit the probabilistic methodology to implement the rewiring between agents and update the network structure based on the knowledge diffusion model.
Since the actual mechanism of the co-evolution of knowledge diffusion and network structure is generally difficult to explore, it is reasonable to a certain extent to study the co-evolutionary dynamics by using various probabilistic methods that has however certain limits, too. The fact that the evolution of network structure depends on random factors, makes it impossible to accurately evaluate and improve the knowledge diffusion performance of a co-evolution model. The knowledge diffusion performance of a co-evolution model obviously depends on the initial knowledge distribution and the topological evolution mechanism of networks. That is, this mechanism determines whether the knowledge stock and growth rate of the whole network converges into the target maximum value rapidly or not. It is therefore necessary to develop the topological evolution mechanism of a knowledge network, which can maximize the knowledge stock and growth rate of the whole network during the process of co-evolution.
In this study, we have developed a genetic algorithm-agent based model (GA-ABM) combining genetic algorithms (GA) with agent-based modelling (ABM) and evaluated its knowledge diffusion performance compared to several other models. The genetic algorithm, which mimics biological evolution, was introduced into the evolution of a network structure to develop the topological evolution mechanism, which is combined with an agent-based model of knowledge diffusion. From simulation, the proposed model was proven to improve the average knowledge stock and knowledge growth rate of the whole network, compared with other models. In addition, the topological structure of the optimal network obtained by GA-ABM has the property of random network, and the clustering coefficients of agents are not significant in improving knowledge diffusion performance[1].
The rest of this paper is organized as follows: In Section 2, we proposed a GA-ABM to investigate the co-evolutionary dynamics of knowledge diffusion and network structure. In Section 3, the simulation of GA-ABM is performed, and the results are discussed. Finally, this paper is concluded in Section 4.
The Model
Here, the knowledge diffusion process is modeled by using an agent-based model, and the evolution of network structure is performed by using a genetic algorithm. This section provides a detailed description of the proposed model.
General description of the knowledge diffusion model
The knowledge network consists of \(N\) agents with different knowledge levels. A group of these agents is represented as \(E = \{1, 2, \dots, N\}\). Each agent can share, spread and absorb information and knowledge through edges. A group of these edges is indicated as \(L\). Thus, the knowledge network can be defined as \(KN = \{E, L\}\). For any agents \(i\), \(j \in E(i \neq j)\), if there is a connection between \(i\) and \(j\), \(e_{ij} = 1\), otherwise \(e_{ij} = 0\).
Here, we referred to the KT (Knowledge transfer) rule of Luo et al (2015) for modeling the knowledge diffusion process in an agent-based model. We followed this rule because it is the most effective when the knowledge distance between two interacting agents is neither too large nor too small. When the knowledge distance is greater than the given threshold, it is predicted that the lack of knowledge inhibits learning and there is no gain from the interaction. The knowledge distance is in essence, the knowledge difference between two agents. The knowledge distance between two agents (i and j) that are connected to each other is expressed as follows.
| $$k_{d_{ij}} = \sum_l \max (k_{j,l} - k_{i,l}, 0)$$ | (1) |
The real gains in knowledge list l for two agents are as follows:
| $$g_l = \begin{cases} \min \bigl\{ \max \{ k_{j,l} - k_{i,l}, 0 \}, k_u \bigr\}\text{,} & k_{d_{ij}} < k_d \\ 0\text{,} & k_{d_{ij}} \geq k_d \end{cases} $$ | (2) |
In Equation 2, when \(k_{d_{ij}}\) is less than the threshold \(k_d\), agent \(i\) obtains a limited amount of knowledge (less than the given upper limit, \(k_u\) shown in Equation 2) from agent \(j\). When the knowledge distance is smaller than \(k_u\), the larger the knowledge distance, the more knowledge the agent receives from its neighboring agents. In contrast, when \(k_{dj}\) exceeds \(k_d\), there is no any knowledge passed from the neighboring agents. The updated values of knowledge in agent \(i\) after interaction and knowledge exchange are as follows.
| $$k_{i,l} (t + 1) = k_{i,l} (t) + g_l \quad l = 1, 2, \dots, n$$ | (3) |
Genetic operator
Here, a genetic algorithm is applied to the structural evolution of the knowledge network, and genetic operators are developed to reflect our research assumptions. In general, genetic operators used in GA include selection, crossover, mutation and fitness tests. The process in which they are applied to the evolution of network structure is as follows:
Selection
The selection operator selects excellent individuals in the current population, and the selected excellent individuals are included in the next generation of population. The first step in the selection process is to form a population of individuals. Here, the population consisting of knowledge networks with different topological structures is represented by \(A = \{ KN_1, KN_2, \dots, KN_M \}\). Here, the size of \(E\) and \(L\) are the same for any networks \(KN_i, KN_j \in A\). From the viewpoint of genetic algorithm, each knowledge network in a population can be regarded as one individual, and in a matrix that mathematically represents a network, each element is defined as a gene. That is, gene and agent are different concepts.
Next, the selection operation is performed by using the Roulette wheel selection, which Holland proposed (Gen et al. 1997). The Roulette wheel selection is a well-known selection type. The basic idea is to determine the selection probability or survival probability of each individual in proportion to its fitness value. The Roulette wheel selection can be formulated as:
| $$P(F_i) = \frac{F_i}{\sum_j F_j} $$ | (4) |
Crossover
The crossover operator randomly selects two individuals (parents) in the current population and subsequently some genes included in each individual and then creates new individuals (children) by exchanging (= crossing) those genes with each other. Since the knowledge network has the symmetric matrix structure in which the diagonal elements are zero, multi-dimensional crossover ( Gen 1997) is used in accordance with the characteristics of network structure to perform crossover operation and defined as follows:
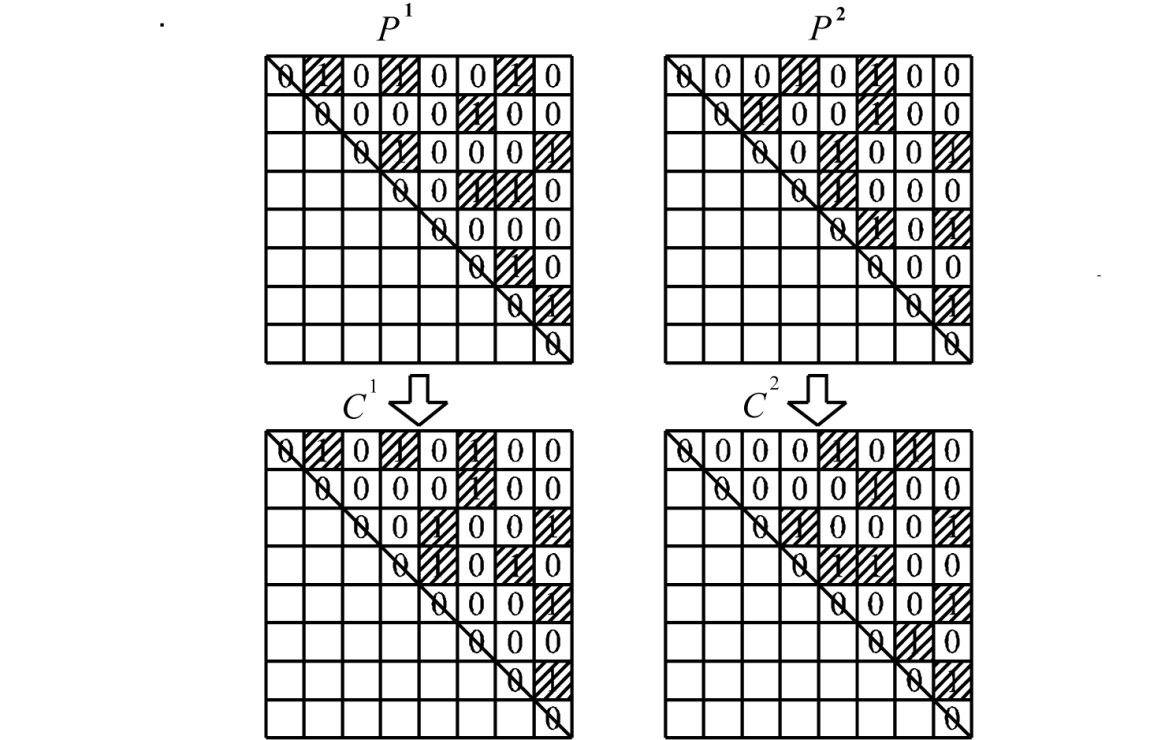
Definition: when \(p^1\) and \(p^2\) are the randomly selected parents (two individuals) in the population, the new individuals generated by Algorithm*, \(C^1\) and \(C^2\), are called the children (two individuals) of the parents \(p^1\) and \(p^2\) in the viewpoint of the genetic algorithm.
In this algorithm, \(P_{ij}\) and \(C_{ij}\) are the arbitrarily selected genes from parents and children, respectively. This algorithm stochastically preserves the number of the genes that the child inherits from the parents. The generating process of children from parents is shown in Figure 1. In Figure 1, \(p^1\) and \(p^2\) are any pair of parents selected from the population, and \(C^1\) and \(C^2\) are the children generated from the parents. In order to preserve the number of individuals in a population, two children are created from a pair of parents. All individuals are symmetric matrices, where diagonal elements are all zero and other elements are only 0 and 1, as shown in the figure. In other words, since the upper triangular matrix and the lower triangular matrix coincide with each other around the diagonal elements, only the change of the upper triangular matrix is considered.
The crossover operation is as follows: If the genes (\(P_{ij}^1\) and \(P_{ij}^2\)) of the parents (\(p_{ij}^1\) and \(p_{ij}^2\)) are equal to each other, the genes (\(C_{ij}^1\) and \(C_{ij}^2\)) of the children (\(p_{ij}^1\) and \(p_{ij}^2\)) receive the same value as the parents. If the genes of the parents are different, the genes of the children resemble the parents with a probability of 0.5. At this point, the numbers 0 and 1 in the parents and children are preserved.
Mutation
The mutation operator arbitrarily selects one individual and then changes certain genes of the selected individual. The probability of mutation is defined as the proportion of the number of mutated genes to the total number of genes in a population. Here, the mutation operation is performed referring to the rewiring rule of Liu et al. (2017). These rules are as follows.
- The target agent \(i\) is rewired to the neighbors of its original neighbors with a probability of \(\omega\); otherwise, it is rewired to one of the randomly selected agents among all agents except its nearest neighbors with a probability of \(1 - \omega\).
- If the target agent is successfully rewired to a new agent, one of the original edges is removed.
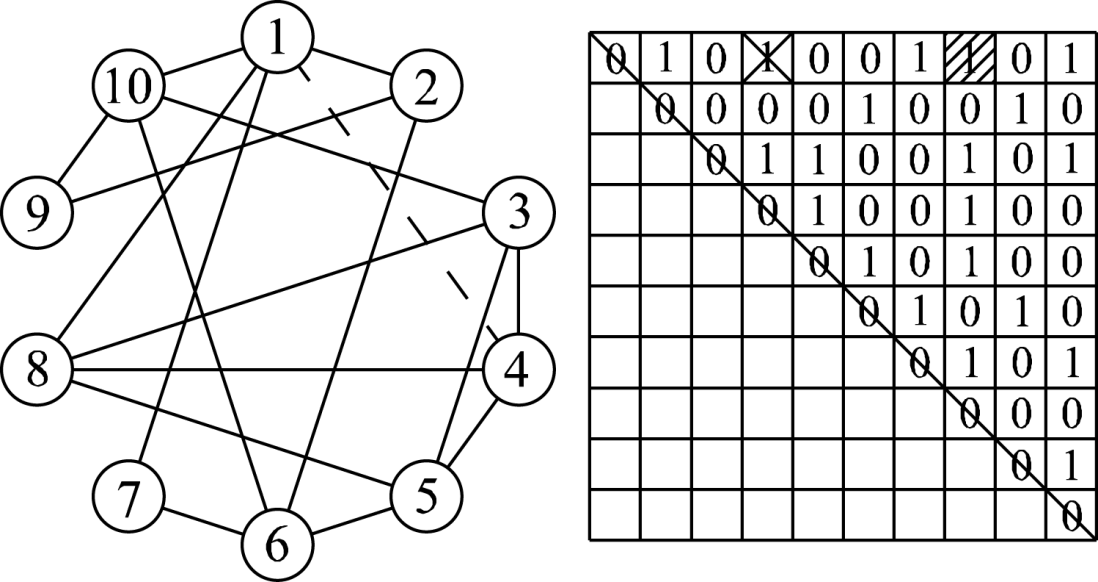
Figure 2 illustrates the mutation process by citing the rewiring with a probability of \(\omega\) as an example. If agent 1 is the target agent, its connected neighbors are the agents 2, 4, 7 and 10. Among these neighbors, if agent 4 is randomly selected, its neighbor, agent 8, is rewired to agent 1. Then, the existing edge (marked with the dotted line) of agents 1 and 4 is cut off. Likewise, it is not difficult to implement the rewiring with a probability of \(1 - \omega\).
Fitness test
A fitness test is a process of evaluating the fitness of the newly created population after crossover and mutation. In essence, the co-evolutionary dynamics of knowledge diffusion and network structure is to determine the optimum network to improve knowledge diffusion performance. Thus, the fitness of each individual in the population is calculated by applying Equation 2.
The topological evolution mechanism of the network structure is constituted of the genetic operators developed in Section 2.6-2.8 (selection, crossover, mutation, fitness test).
Overall execution procedure of GA-ABM
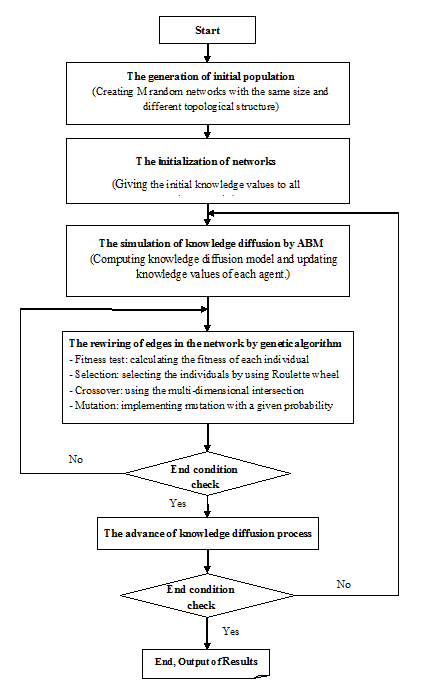
The co-evolutionary dynamics model combining the agent-based model with the genetic algorithm is briefly called GA-ABM. Figure 3 shows the flowchart of the simulation process of co-evolutionary dynamics by GA-ABM. The overall execution procedure of GA-ABM is as follows:
- Step 1: The generation of the initial population Randomly generate \(M\) networks. Here, all the network equally has \(N\) agents and \(K\) edges. (That is, the sizes of all the network are the same, but the topological structures are different.)
- Step 2: The initialization of networks (i.e., the initialization of individuals) Give the initial knowledge values to all networks. Here, the corresponding agents between networks have the same initial knowledge value.
- Step 3: The simulation of knowledge diffusion by ABM Compute the agent-based model of knowledge diffusion described in Sections 2.2-2.5 and update the knowledge value of each agent.
- Step 4: The rewiring of edges in the network by genetic algorithm Rewire the edges in the network by using the genetic operators mentioned in Sections 2.6-2.8.
- Step 5: The check on the end condition of the genetic algorithm Once the number of iterations reaches the predefined value, exit the step, return the updated population and the optimal network and go to Step 6. If not, go to Step 4.
- Step 6: The advance of knowledge diffusion process Advance the time step and go back to Step 3.
- Step 7: The check on the end condition of knowledge diffusion process Once the number of iterations reaches the predefined value, end the procedure and output the results.
Simulation Results and Discussion
Firstly, we used the WS small world model proposed by Watts & Strogatz (1998) to form populations by generating \(M\) random networks with \(N\) agents and \(K\) edges. At this point, the rewiring probability of the network was \(P = 0.2\). In the process of co-evolution, the size of the population and the number of the agents and the edges in each individual remains constant. That is, \(N= 100\), \(K= 800\), and \(M= 100\). Where \(K\) is the product of the mean degree and the number of agents in the network, i.e., \(K=m \times N\), where \(m\) is the mean degree of the network and \(m= 8\).
We introduced the following assumptions in the simulation process.
Firstly, all the agents have only a single kind of knowledge. That is, the homogeneity of knowledge is guaranteed. Secondly, agents can have multiple levels of expertise.
In addition, we examine the average knowledge stock and the knowledge growth rate, which are two macro - statistical values, to measure the knowledge diffusion performance. If the knowledge network consists of \(N\) agents, the average knowledge stock of network by knowledge accumulation at each agent can be written as
| $$\bar{k}(t) = \frac{1}{N} \sum_{i = 1}^N k_i (t) $$ | (5) |
At time \(t\), the knowledge growth rate of the whole network can be written as follows.
| $$k = \frac{\bar{k} (t) - \bar{k} (t - \Delta t)}{\bar{k} (t - \Delta t)} $$ | (6) |
\(\bar{k}\) is a basic parameter for evaluating knowledge diffusion performance of knowledge network. In the knowledge network, agents have the following initial knowledge values, \(k_{i,1} (0) = U [0,1]\).
However, if all agents have similar knowledge values, it becomes difficult to spread knowledge. Therefore, we introduced 10 experts with a highly specialized knowledge (Cowan and Jonard 2004). Each expert's initial knowledge value ranged from 1 to 10. The upper limit of the knowledge amount to be exchanged per iteration was \(k_u = 0.3\) and the threshold was \(k_d = 3\). The calculation simulation was performed by using MATLAB R2016b.
The comparison of GA-ABM with the models in which the co-evolutionary dynamics is not considered
Here, we evaluated the knowledge diffusion performance of GA-ABM by comparing the proposed model with the models in which the co-evolutionary dynamics was not considered. In case of not considering the co-evolutionary dynamics, in essence, there was only knowledge diffusion and no topological evolution of the network structure. Therefore, for convenience, this model is simply called the agent-based model (ABM). We compared GA-ABM with ABM in terms of knowledge distribution of agents, average knowledge stock and knowledge growth rate of network. Figure 4 shows the knowledge distribution in the initial and final states of the knowledge network by ABM. The initial and final states indicated the initial and last calculation time, respectively.
In Figure 4, the dotted line shows the knowledge distribution of the network at the final state and the solid line shows the knowledge distribution at the initial state. On the solid line, we can see a few sharp peaks, which represent the knowledge values of a few experts in the network in the initial state. The value is close to 10 at its maximum. Most agents have small knowledge values between 0 and 1. The state of the dotted line shows that most agents reached some equilibrium values (approximately 4.1). However, there are still several peaks and the large difference between its maximum and equilibrium values indicates that most agents did not fully absorbed the experts’ knowledge. This meant that the knowledge stock of agents in a given network structure cannot be maximized.
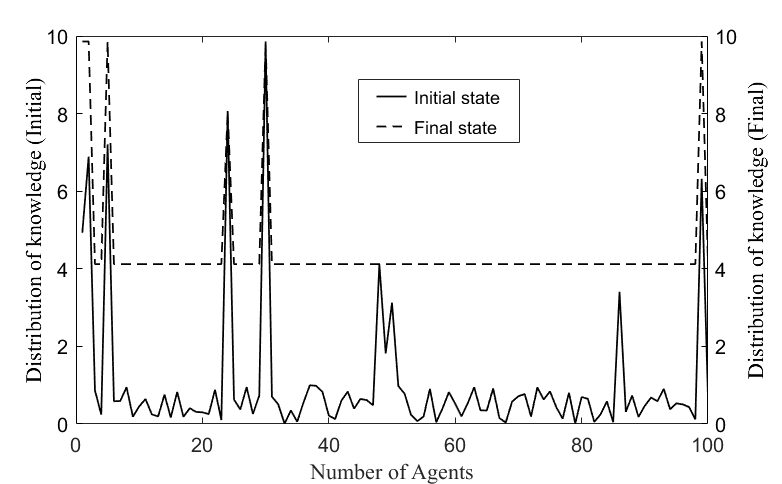
Figure 5 shows the knowledge distributions in the initial and final states of the knowledge network by GA-ABM. The initial knowledge distribution and parameters of the network were the same as the former. The state of the dotted line showed that all agents reached an equilibrium value (approximately 9.8). This equilibrium value is consistent with the maximum value of the expert's knowledge in the initial distribution of knowledge. This means that all agents in the knowledge network fully absorbed the knowledge of experts through the co-evolution of the knowledge diffusion and topological structure.
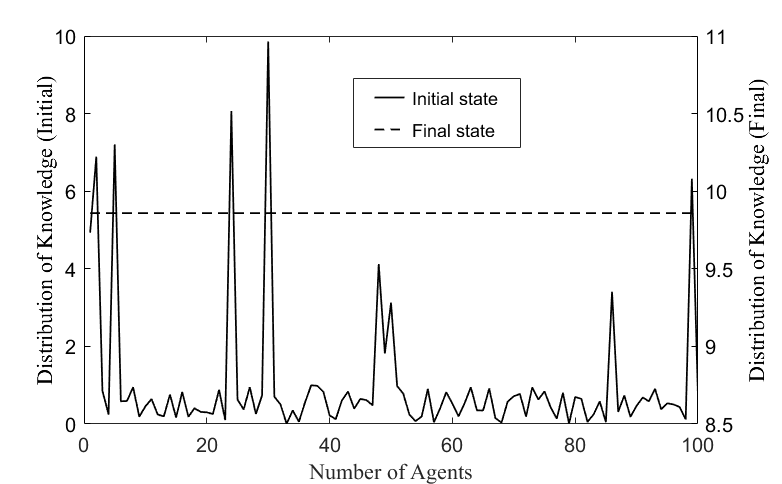

Figure 6 shows the average knowledge stocks of ABM and GA-ABM with time. The results of both models linearly increase with time and reach an equilibrium value at a certain time step. The ABM reached an equilibrium value at about 45s and its value is about 4.4. The GA-ABM reached an equilibrium value at about 55s and its value is about 9.8. In other words, the GA-ABM had a time delay of about 10 seconds to reach the equilibrium value compared to ABM, but the average knowledge stock was more than twice higher than ABM. This is because GA-ABM uses the genetic algorithm optimal for the topological evolution of the network structure. Thanks to the genetic algorithm, the network structure was evolved to the optimization of the knowledge level of agents at each time step; as a result, the knowledge level of each agent converged to its maximum value.
Figure 7 shows the change of knowledge growth rate with time in the ABM (solid line) and GA-ABM (dotted line). The knowledge growth rate of the ABM decreased slowly at the beginning according to time, but decreased sharply in the vicinity of 33s and converged to 0 at around 45s.
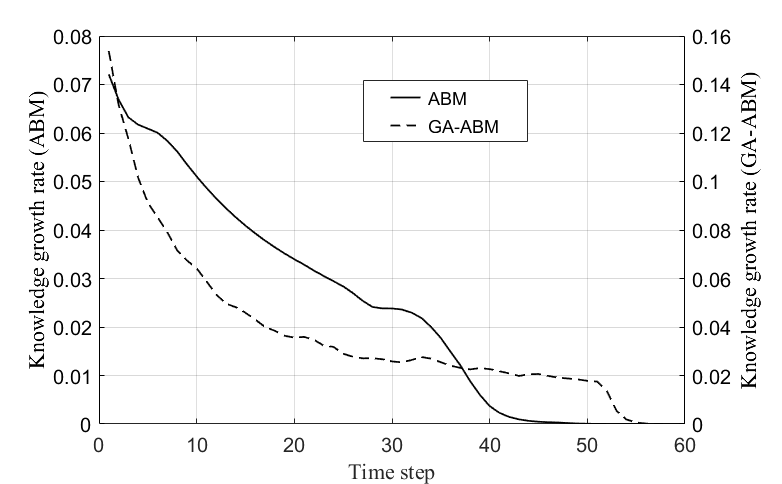
The knowledge growth rate of the GA-ABM decreased sharply at the beginning according to time, but gradually decreased at about 20s, and sharply decreased again at about 51s, converging to 0 at around 55s. The knowledge growth rate of the GA-ABM was more than about twice the ABM, and the time to converge to zero was about 10 seconds later. These results are also consistent with the analytical results shown in Figure 5 on time and quantitative level. These results suggest that GA-ABM has superior knowledge diffusion performance than the ABM.
When not considering co-evolution, knowledge diffusion is clearly related to the initial knowledge distribution and the network structure. Whether all agents in the network can have a high knowledge stock or not depends on the topological structure of the network under the condition that networks have the same value in the initial distribution of knowledge and the parameters.
As shown in the calculation results, in the ABM, not all agents in the network had the maximum value of knowledge stock. This was entirely due to the topological structure of the network. This is because the original topological structure of network is not the ideal structure to maximize the knowledge stock and knowledge growth rate of agents. However, GA-ABM showed twice as more knowledge stock and knowledge growth rate as ABM, i.e., its knowledge diffusion performance was higher. This is due to the co-evolutionary dynamics of the knowledge diffusion and the network structure, particularly to the use of genetic algorithm, which is an optimization method for the evolution of network structure.
The comparison of GA-ABM with the models in which the co-evolutionary dynamics is considered
Here, we selected the model of Luo et al (2015), which is the most typical co-evolutionary dynamics model, as a comparison. In this model, an agent obtains new knowledge from its neighbor by using the KT rule with a probability of p or uses the NA (Neighborhood Adjustment) rule with a probability of 1-p to conduct the network adjustment for rewiring the existing edges between the target and another agent. Therefore, the knowledge diffusion performance of the knowledge network depends on the probability p. For convenience, we will call this model a KT-NA (Co-evolutionary dynamics model of knowledge diffusion and social network structure; see Luo et al. 2015) model. Here, we compared the KT-NA model (according to various p values) with a GA-ABM under the condition that the networks had the same value in the initial knowledge distribution and the parameter values. The initial knowledge distribution differs from that of Section 3.1. The results are shown in the Figures below.
Figure 8 shows the knowledge distribution of agents in the initial and final states of the knowledge network by the KT-NA model and the GA-ABM. The dotted line shows the knowledge distribution of the network in its final state, and the solid line shows the knowledge distribution in the initial state. As shown in the figure, the KT-NA model and the GA-ABM have the same knowledge distribution characteristics in their final state. In other words, this shows that the knowledge value of the agents in the final state by both models was the same and reached an equilibrium value (about 7.95). This equilibrium value is consistent with the maximum value of the expert-possessing knowledge in the initial knowledge distribution. This means that all agents in the knowledge network fully absorbed the experts’ knowledge through the co-evolutionary dynamics of the knowledge diffusion and topological structure by both models.
Figure 9 shows the average knowledge stock with time of the KT-NA and GA-ABMs.
Here, the KT-NA model is calculated with various p values. The average knowledge stock of both models increased linearly with time and reached an equilibrium value (about 7.95). Although the average knowledge stock of both models reached the same equilibrium value, the time to reach the equilibrium state was significantly different. The convergence time of the GA-ABM, which is indicated by the solid line, was about 50s and reachds the equilibrium state earlier. In the KT-NA model, the time for reaching the equilibrium state was shortened in order to increase probability p values. The values were approximately 130s, 180s, and 350s, respectively. As described above, since the frequency of knowledge diffusion and network rewiring are determined according to the p value, it is obvious that the arrival time to the equilibrium state would differ with this value.

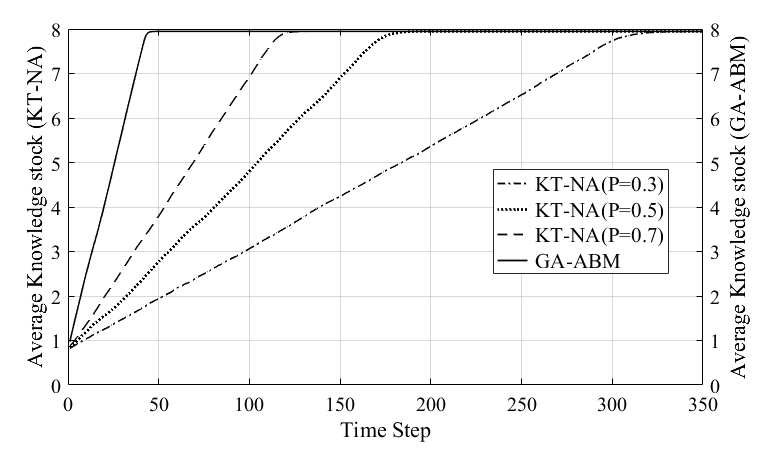
Figure 10 shows the change of knowledge growth rate with time for KT-NA model and GA-ABM. The knowledge growth rate of the GA-ABM (solid line) decreased sharply with time, converging to zero at around 50s. The knowledge growth rate of the KT-NA model with each P value sharply decreased exponentially while vibrating, and the time to converge to zero differed depending on the magnitude of the p value. That is, the larger the P value, the shorter the time to converge to zero, the values of 130s, 180s, and 350s, were respectively, in decreasing order of P value. In addition, the knowledge growth rate of the GA-ABM was about twice that of the KT-NA model. In other words, the average knowledge stock of the two models was the same, but the knowledge growth rate of the GA-ABM was faster than the KT-NA model. From these results, although both models were co-evolutionary dynamics models, we can see that GA-ABM had superior knowledge diffusion performance than the KT-NA model.
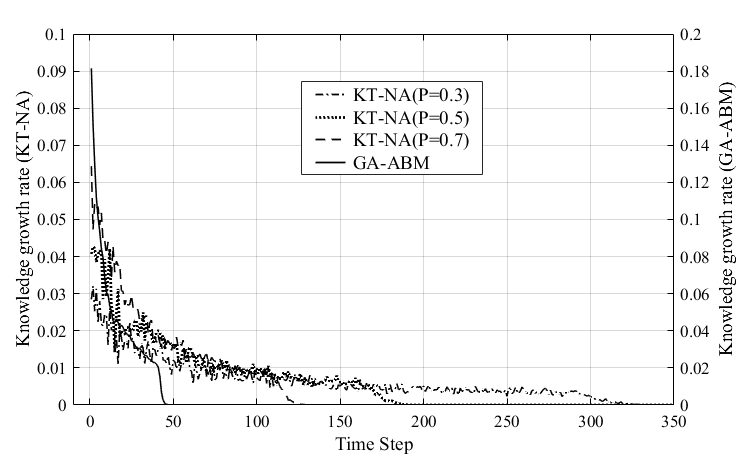
When considering co-evolution, knowledge diffusion is clearly related to the topological evolution mechanism of the knowledge network. By this mechanism, the knowledge stock of the whole network may or not rapidly converge to its maximum value over time. As the results showed, the average knowledge accumulations of the KT-NA model and GA-ABM were the same in the final state, but the knowledge growth rate of the GA-ABM was faster than one of KT-NA model. This was entirely due to the topological evolution mechanism of the network. This is also because the topological evolution mechanism of the KT-NA model is not an ideal mechanism to maximize the knowledge growth rate of agents. However, the GA-ABM had a twice as high knowledge growth rate as that of the KT-NA model. That is, its knowledge diffusion performance was higher. This is because the GA-ABM generates an optimal network structure that maximizes the knowledge stock of agents at each time step of co-evolution through a topological evolution mechanism by using genetic algorithm.
Analysis of optimal network structure
As described above, we can use the GA-ABM to obtain the network structure and knowledge distribution that can maximize knowledge diffusion at each time step. Then, there is a question of what structural characteristics this optimal network has and what kind of rule it can derive from its analysis. Therefore, it is necessary to analyze the optimal network structure. The process of exploring and analyzing the optimal network structure by using the GA-ABM can be summarized as follows:
First, we searched for an individual (here, one knowledge network) whose fitness function value (knowledge diffusion) is maximized at the execution stage of the genetic algorithm executed at each time step of knowledge diffusion. This individual is the optimal network that maximizes the amount of knowledge diffusion at this time. We grouped the optimal networks that are searched at each time step to obtain a single time series.
Next, we analyzed the topological structure of these optimal networks. The basic statistical values that characterize the topological structure of the network are the average path length and the clustering coefficient (Morone & Taylor 2004). The average path length of the network can better describe the connectivity of the network.
The distance \(A_{d_{i,j}}\) between two agents \(i\) and \(j\) in the network is defined as the number of edges on the shortest path connecting the two agents. The average path length \(APL\) of the network is defined as the average of the shortest path between any two agents, i.e
.| $$ APL = \frac{1}{\frac{1}{2} N (N - 1)} \sum_{i > j} A_{d_{i, j}} $$ |
The clustering coefficient characterizes the clustering characteristics of the network, that is, the community characteristics. It is generally assumed that agent \(i\) in the network are associated with \(_ik\) edges, that is, connected to other \(k_i\) agents. Obviously, there may be up to \(k_i (k_i - 1) / 2\) edges between the \(k_i\) agents. The number of edges actually present between the \(k_i\) agents is \(e_i\). Then the ratio of \(e_i\) the number of edges actually existing between the \(k_i\) agents and the total possible number of edges \(k_i (k_i - 1) / 2\) is defined as the clustering coefficient \(C_i\) of the agent i, i.e.,
| $$ C_i = \frac{2e_i}{k_i (k_i - 1)}$$ |
The average of the clustering coefficients of all agents in the network is the clustering coefficient CC of the entire network, i.e.,
| $$ CC = \frac{1}{N} \sum_{i = 1}^N C_i $$ |
We analyzed the change characteristics of these two statistical values with time.
Finally, the topological structure of the network was discriminated on the basis of the average path length and the clustering coefficient of the optimal network obtained. Its crucial equation is as follows (Neal 2017):
| $$ SWI = \frac{APL - APL_l}{APL_r - APL_l} \times \frac{CC - CC_r}{CC_l - CC_r}$$ |
\(SWI\) is an abbreviation for small-world index. Where \(CC_l\) and \(APL_l\) are the clustering coefficient and average path length of the regular reference network, respectively, and \(CC_r\) and \(APL_r\) are the clustering coefficient and average path length of the random reference network, respectively. These reference networks should have the same size, density and mean degree as the observed network (the optimal network in our study). In our case, the initial network and the optimal network had the same size and since the number of edges in the whole network was preserved during the evolution process, it matched the preconditions as mentioned above. These values were calculated as follows:
| $$ CC_l = \frac{3 (m - 2)}{4 (m - 1)}\text{,} \quad APL_l = \frac{N}{2m}\text{,} \quad CC_r = \frac{m}{N}\text{,} \quad APL_r = \frac{\ln N}{\ln m} $$ |
The results are shown in Figure 11, 12, and Table 1 . Figure 11 shows the variation of average path length and clustering coefficient with time. As can be seen from the figure, the average path length over time decreases slowly while vibrating, and the clustering coefficient causes only vibration in the range of minimum value 0.081 and maximum value 0.11, and there is almost no change in the inclination.
Through several simulations, we found that this phenomenon is maintained even at the rewiring probability \(P \in [0.1, 0.6]\) of the initial network.
The average path length of the optimal network obtained by the GA-ABM in our study is gradually decreasing over time. The average path length of the network is a measure of the network level and is a value that averages the shortest path lengths of all agent’s pair belonging to the network. The shorter the average path length, the shorter the distance between agents, which makes it easier to transfer knowledge and absorb knowledge from other agents. Therefore, knowledge diffusion performance such as the average knowledge stock and knowledge growth rate of the knowledge network will be higher (Watts & Strogatz 1998). Our results showed that the average shortest path length of the network had a significant effect on knowledge diffusion performance.
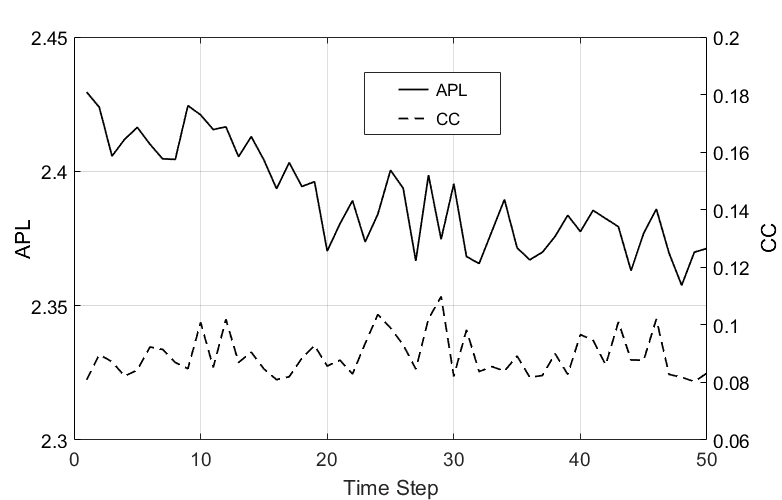
Next, in our study, the clustering coefficient of the optimal network obtained by the GA-ABM did not change slope over time. That is, it only caused vibrations in a certain range of values, and did not show any tendency to increase or decrease. The clustering coefficient is a measure of the agent level, meaning that agents with large values had many neighbors connected to each other. The larger the clustering coefficient was, the more neighbors were connected and can be accessed with shorter distances, making it easier to acquire knowledge. On the other hand, it may not be possible to acquire higher knowledge because the knowledge level of neighbors can easily become similar. Therefore, the relationship between the clustering coefficient and knowledge diffusion performance of the network is difficult to predict clearly (Cowan & Jonard 2004; Park 2015). Our results confirm these findings from previous work.
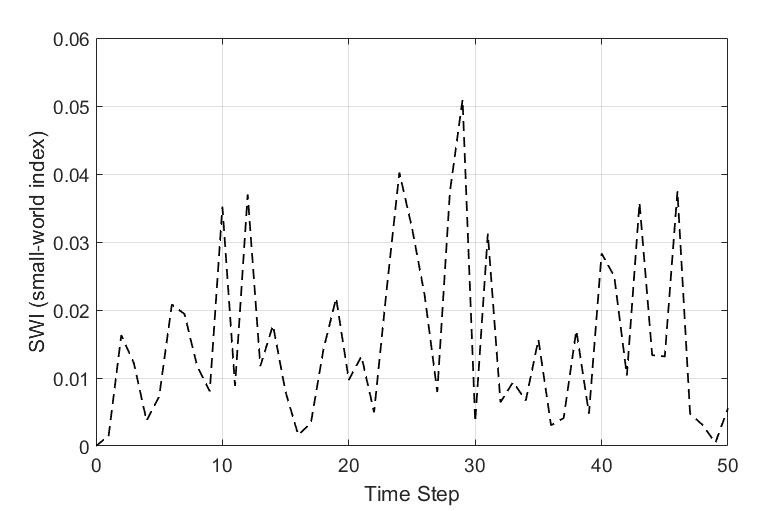
Figure 12 shows the SWI (small-world index) of the optimal network over time, and Table 1 shows the average path length and clustering coefficients of the rule and random networks. As shown in Figure 12, the SWI oscillates with a value close to zero over time.
| \(APL_l\) | \(CC_l\) | \(APL_r\) | \(CC_r\) |
| 6.250 | 0.643 | 2.215 | 0.080 |
This means that the optimal network does not exhibit "small world" characteristics in the evolutionary process. In this case, the question is then whether this optimal network is a rule network or a random network. As shown in Figure 11, the average path length of the optimal network oscillates between a maximum of 2.43 and a minimum of 2.36, and the clustering coefficient oscillates between a maximum of 0.11 and a minimum of 0.081. As shown in Table 1, the average path length and clustering coefficients of the optimal network were much smaller than the values of the rule reference network and slightly larger than those of the random reference network. This means that the optimal network had random network characteristics in the co-evolution process.
Luo et al. (2015) reported that small world networks are created and destroyed in succession, and pointed out that the co-evolution of knowledge diffusion and network structures is a key factor in the formation of a "small world" network. It is also known that a small world network has a relatively small average path length and a relatively large clustering coefficient, and its knowledge diffusion performance is higher than other networks (Cowan & Jonard 2004; Kim & Park 2009).
However, in our proposed model, the optimal network in the process of co-evolution did not show any "small world" characteristic and maintained the same random property as the initial network, but its knowledge diffusion performance was very high. This implies that the small world network is not necessarily associated with a high knowledge diffusion and that there is room for the improvement of knowledge diffusion performance during co-evolution process, even in case of the random network which average path length is short and clustering coefficient is small. In future work, we will discuss this issue in more depth.
Conclusions
Summary and conclusions on the simulation results
In this paper, we studied the co-evolutionary dynamics of knowledge diffusion and network structure in the knowledge network including agents such as personel, corporations and innovative organizations by developing a GA-ABM. We found first that the GA-ABM is superior to other models in knowledge diffusion performance. As shown in our simulation results, our GA-ABM is able to maximize the average knowledge stock and knowledge growth rate of the knowledge network. In most previous work, the probabilistic rules or methods have been applied to the network’s topological evolution mechanism. The purpose of this study was to overcome certain defects of such stochastic approaches and explore the optimal network structure that can maximize the knowledge diffusion performance of knowledge network by using a deterministic method. We therefore developed a topology evolution mechanism of network by using genetic operators and proposed the GA-ABM with an excellent knowledge diffusion performance by combining the genetic algorithm with an agent-based knowledge diffusion model. Through the comparative simulation study, the GA-ABM was proven to have a higher knowledge diffusion performance compared to several other models.
Secondly, the analysis on the time series data of the opimal network structure obtained by GA-ABM shows that this model produced an interesting phenomenon different from previous studies. At first, the evolution of network structure in the co-evolution process does not necessarily represent small world characteristics. Cowan & Jonard (2004) and Kim & Park (2009) found that a small world network is the most effective topology structure for knowledge diffusion. The KT-NA model of Luo et al. (2015) showed that the topological structure is sequentially constructed and destroyed from random to small-world networks in the co-evolution process. Xuan et al. (2011) considered that the higher the adjustment rate, the farther the adjusted network deviates from the 'small world' region, and as a result, the improvement of knowledge diffusion performance gets unclear. However, here, the optimal network maintained the same random characteristics as the initial network in the co-evolution process, but its knowledge diffusion performance was very high. This also shows that the proposed topological evolution mechanism makes it possible to obtain a high knowledge diffusion performance even in a random network. This is attributed to the superior optimization capability of the topological evolution mechanism proposed on the basis of a genetic algorithm. Next, the clustering coefficients of agents are not significant in the improvement of knowledge diffusion performance. In other words, the larger the clustering coefficients, the larger the possibility that the knowledge levels between neighbors get similar and knowledge is not well absorbed. Note that such a result was also reported in Cowan & Jonard (2004) and Park (2015).
Managerial implications
In knowledge networks consisting of agents such as personnel, companies and innovation organizations, the knowledge diffusion is influenced by the network structure. Therefore, the formation and rewiring of the network structure are very important in knowledge management for the creation, retention, diffusion and dissemination of knowledge. From this point of view, the information obtained here could offer a management implication that can promote knowledge diffusion. In other words, regardless of the initial structure of knowledge network and the knowledge level of each agent, GA-ABM provides the optimal network structure that can maximize the knowledge diffusion performance and allow the knowledge management to follow such a structure.
Let us consider an innovation organization as an example. It is assumed that each member of an innovational organization has the same qualifications. In other words, they can freely exchange information with each other according to their capabilities. Of course, their knowledge levels are different from each other, and the linking structure between them is random. In case of the purpose to shorten the knowledge update cycle in the innovation organization and raise the knowledge levels of total members in the organization within the shortest period, the GA-ABM can be applied.
The process is as follows: At first, quantitatively evaluate the initial knowledge holding of each member in the innovation organization and properly select various parameters (threshold, knowledge limit, etc.). Next, determine the time steps and the goal (the desired maximum value of knowledge) according to the property of organization and the level of each member. Then, implement the first calculation step in the co-evolution of knowledge diffusion and network structure. As a result of this calculation, the knowledge update of members corresponding to this step and the topological evolution of the network structure is completed and the optimum network structure is obtained. The knowledge manager (or the network manager, in this case, the head of the innovation organization) rewires the members within the organization according to the optimal network structure. In this way, continue to advance the time steps, update the knowledge values of all the members and implement the rewiring of the network structure. As a result, all members of the organization have the maximum knowledge value at the final time step, and the knowledge update cycle is fast.
This type of managerial implication belongs to macroscopic and approximate forecasting. In order to complete this model, many studies on agent and knowledge attributes should be conducted. In spite of these limitations, this study provides the possibility to enhance knowledge diffusion performance and shorten the knowledge update cycle in knowledge network composeds of such agents on the basis of a new co-evolutionary dynamics model.
Limitations and future work
The evolution of knowledge network can be regarded as an evolution process of complex system and has non-linear self-organization characteristics. In this study, the genetic algorithm that finds an optimal solution by mimicking the evolution of living organisms was used to study the co-evolutionary dynamics of knowledge diffusion and network structure. Genetic algorithm is a powerful adaptive search method that can be used to solve multiple objects and multiple shape problems as well as the optimization problems of large and complex functions. In this study, we could not fully address the problem of the nonlinear self-organization characteristics of the knowledge network in combination with the principle of genetic algorithms. Moreover, more research on agent and network attributes should be performed to improve our understanding of the knowledge diffusion model.
In future, we will focus on overcoming these limitations by further completing the knowledge diffusion model for agent and knowledge attributes and elucidating their effects on the topological evolution of network structure.
Acknowledgements
This research is supported by the National Science Foundation of China (No. 71531003). Thanks also to the editor and reviewers who have contributed to our paper.Notes
- A brief explanation of the relationship between genetic algorithm and network. From the viewpoint of genetic algorithm, it is important to precisely grasp the concepts of population, individual, chromosomes, genes and genetic operators, A population consists of individuals, usually of one or several chromosomes. The genetic operator (selection, crossover, mutation) is an operator who transforms chromosomes. If an individual has a single chromosome, an individual and chromosome have the same meaning. A chromosome (or individual) consists of several genes. In our study, an individual and a group of networks correspond to a network and a population, respectively. The network consists of agents and edges which connect them with each other. However, genes do not correspond to agents. In other words, a gene entails an element in the matrix that mathematically represents a network.
References
BOONE, T., & Ganeshan, R. (2008). Knowledge acquisition and transfer among engineers: Effects of network structure. Managerial and Decision Economics, 29(5), 459–468. [doi:10.1002/mde.1401]
COWAN, R., & Jonard, N. (2004). Network structure and the diffusion of knowledge. Journal of Economic Dynamics and Control, 28(8), 1557–1575. [doi:10.1016/j.jedc.2003.04.002]
GEN, M., Cheng, R., & Lin, L. (1997) Network Models and Optimization: Multiobjective Genetic Algorithm Approach. Berlin/Heidelberg: Springer.
GIL, S., & Zanette, D.H. (2006). Coevolution of agents and networks: Opinion spreading and community disconnection. Physics Letters A, 365(2), 89–94. [doi:10.1016/j.physleta.2006.03.037]
GROSS, T., & Blasius, B. (2008). Adaptive coevolutionary networks: A review. Journal of the Royal Society Interface, 5(20), 259–271. [doi:10.1098/rsif.2007.1229]
HANSEN, MT. (2002). Knowledge Networks: Explaining Effective Knowledge Sharing in Multiunit Companies. Organization Science, 13(3), 232-248. [doi:10.1287/orsc.13.3.232.2771]
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence:models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.
HERIE, M., & Martin, G. (2002). Knowledge diffusion in social work: A new approach to bridging the gap. Social Work, 47(1), 85–95. [doi:10.1093/sw/47.1.85]
KIM, H., & Park, Y. (2009). Structural effects of R&D collaboration network on knowledge diffusion performance. Expert Systems with Applications, 36(5), 8986-8992. [doi:10.1016/j.eswa.2008.11.039]
LIU, J., Zhou, Q., Guo, Q., Yang, Z., Xie, F., & Han, J. (2017). Knowledge diffusion of dynamical network in terms of interaction frequency. Scientific Reports, 7(1), 10755. [doi:10.1038/s41598-017-11057-8]
LUO, S., Xia, H., & Yin, B. (2014). Continuous opinion dynamics on an adaptive coupled random network. Advances in Complex Systems, 17(03n04), 1450012. [doi:10.1142/s021952591450012x]
LUO, S., Du, Y., Liu, P., Xuan, Z., & Wang, Y. (2015). A study on coevolutionary dynamics of knowledge diffusion and social network structure. Expert Systems Applications, 42(7), 3619–3633. [doi:10.1016/j.eswa.2014.12.038]
MOLM, L.D., Whitham, M.M., & Melamed, D. (2012). Forms of Exchange and Integrative Bonds: Effects of History and Embeddedness. American Sociological Review, 77(1), 141-165. [doi:10.1177/0003122411434610]
MORONE, P., & Taylor, R. (2004). Knowledge diffusion dynamics and network properties of face-to-face interactions. Journal of Evolutionary Economics, 14(3), 327-351. [doi:10.1007/s00191-004-0211-2]
MUELLER, M., Bogner, K., Buchmann, & Kudic, M. (2017). The effect of structural disparities on knowledge diffusion in networks: an agent-based simulation model. Journal of Economic Interaction and Coordination, 12(3), 613-634. [doi:10.1007/s11403-016-0178-8]
NEAL, Z. P. (2017). How small is it? Comparing indices of small worldliness. Network Science, 5(1), 30-44. [doi:10.1017/nws.2017.5]
PARK, C. (2015). Interaction Effect of Network Structure and Knowledge Search on Knowledge Diffusion. Korean Management Science Review, 32(4), 81-96. [doi:10.7737/kmsr.2015.32.4.081]
PARUCHURI, S. (2010). Intraorganizational networks, interorganizational networks, and the impact of central inventors: A longitudinal study of pharmaceutical firms. Organization Science, 21(1), 63–80. [doi:10.1287/orsc.1080.0414]
PHELPS, C., Heidl, R., & Wadhwa, A. (2012). Knowledge, networks, and knowledge networks: A review and research agenda. Journal of Management, 38(4), 1115–1166. [doi:10.1177/0149206311432640]
SU, J., Liu, B., Li, Q., & Ma, H. (2014). Coevolution of opinions and directed adaptive networks in a social group. Journal of Artificial Societies and Social Simulation, 17(2), 4.https://www.jasss.org/17/2/4.html. [doi:10.18564/jasss.2424]
SUN, M. (2017). The Relation between Organizational Network Distance and Knowledge Transfer Based on Social Network Analysis Method. International Journal of Emerging Technologies in Learning (iJET), 12(06), 171-177. [doi:10.3991/ijet.v12i06.7094]
VAZQUEZ, F. (2013). Opinion dynamics on coevolving networks. In A. Mukherjee, M. Choudhury, F. Peruani, N. Ganguly & B. Mitra (Eds.),Dynamics On and Of Complex Networks, Volume 2. Applications to Time-Varying Dynamical System. Berlin Heidelberg: Springer, pp. 89-107.
WANG, X. (2013). Forming mechanisms and structures of a knowledge transfer network: theoretical and simulation research. Journal of Knowledge Management, 17(2), 278-289. [doi:10.1108/13673271311315213]
WATTS, D.J., & Strogatz, S.H. (1998). Collective Dynamics of‘Small-World’ Networks. Nature, 393(6684), 440. [doi:10.1038/30918]
XUAN, Z., Xia, H., & Du, Y. (2011). Adjustment of knowledge-connection structure affects the performance of knowledge transfer. Expert Systems with Applications, 38(12), 14935-14944. [doi:10.1016/j.eswa.2011.05.054]
ZHUANG, E., Chen, G., & Feng, G. (2011). A network model of knowledge accumulation through diffusion and upgrade. Physica A: Statistical Mechanics and its Applications, 390(13), 2582-2592. [doi:10.1016/j.physa.2011.02.043]
