Introduction
In today’s rapidly changing environment, knowledge is a dominant source of organisation sustainable competitive advantage (Chen 2004; Lyles & Salk 1996; Tsai 2001), thus, the ability to acquire information the knowledge creation is a large organisations force (Nonaka 1994; Zander & Kogut 1995). Moreover, Nonaka & Takeuchi (1995) postulate that knowledge is no longer one of the traditional elements of production, but it becomes the only factor of production, which determines the company’s competitiveness. Therefore, the knowledge transfer is one of the most important elements in the management process, especially, for the organisational change (Martinez et al. 2016), the project management (Spałek 2014), and widely understood development. Organisations which manage changes and adaptations effectively will not only survive, but thrive (Brown 2003). Organisational change is a complex process and includes alterations in technology, structures and/or systems. It may be defined as alterations of existing work routines and strategies that affect an entire organisation (Herold et al. 2008).
Both the organisational change and the development require the transfer of knowledge, which allows people to acquire knowledge, while the organisations distribute it and properly use it. However, there are substantial barriers which make that the transfer of knowledge within the firm difficult and complicated (Szulanski 1996). The efforts to share knowledge are often impeded by employees’ tendencies to guard and selectively share information (Gilmour 2003). Moreover, knowledge transfer needs to span different knowledge holders and requires a collaborative effort of both, the knowledge recipients and senders. A very important element for an efficient knowledge transfer is thus a senders’ disseminative capacity and a receivers’ absorptive capacity (Tang 2011). The disseminative capacity can be defined as the network member’s ability to effectively and efficiently communicate and transmit knowledge to other network members, whereas the absorptive capacity is the ability of the recipient to receive knowledge. Knowledge can be either explicit or tacit (Nonaka & Takeuchi 1995). The explicit knowledge is an information that is stored in the form of documents or other media, while the tacit knowledge is an information that results from a person’s experience and it consists partly of technical skills (Novianto & Puspasari 2012). Particularly, the study of transfer of tacit knowledge seems to be interesting, because this kind of knowledge is difficult to spread among members within an organisation (Tang 2011; Teece 2000; Tsai 2002).
Many studies highlight also the importance of social interaction among organisational members in knowledge exchange (Chen & Huang 2007; Ibarra 1993; Tsai 2002). They suggested that organisational units can leverage knowledge resources through interacting among them. Furthermore, interactions among organisation members are mainly informal, but such informal relations play an increasing role and they are the main source of influence in organisations in the context of organisation learning, innovation and adaptation processes (Ibarra 1993). Such a point of view indicates the emergence and ‘bottom-up’ approach to knowledge transfer, because this approach is also postulated in the change process (Butcher & Atkinson 2000; Higgs & Rowland 2005; Kempster et al. 2014). Moreover, in organisation, knowledge more often moves in a horizontal direction and it is an informal process (Girdauskiene & Savaneviciene 2012) whereas formal sharing of knowledge can reach much broader populations but may stifle some of spontaneous and creative aspects of the informal sharing modes (O‘Deal et al. 1999). This informal sharing of knowledge is carried out by informal communication between members of the organisation, and its most important role is to fulfil the employees’ informational needs (Kraut et al. 1993). Information is exchanged spontaneously and interactively, through meetings and conversations. This type of communication with other members of the group is more often used when the work groups are engaged in more complex tasks (Van de Ven et al. 1976), and this is the case, when knowledge is transferred about important matters for organisations such as organisation change, project management or widely understood organisation development. This type of communication between members of the organisation therefore helps them in learning about each other and their work, it supports both production work and the social relations that underlie it (Kraut et al. 1993). In this article, knowledge transfer is thus understood as a common process in a creative organisation, which is mostly implemented informally by sharing knowledge ‘face to face’ (Girdauskiene & Savaneviciene 2012).
Knowledge in the organisation as mentioned earlier is very important for the progress and development of a competitive organisation/enterprise. In the process of acquiring knowledge by organisations, the ability to transfer knowledge plays a significant role Boone & Ganeshan (2008). Organisations can facilitate knowledge transfer by facilitating learning in organisations, converting tacit knowledge to explicit knowledge, generating new knowledge, relevant knowledge management and creating appropriate knowledge Alipour et al. (2011). An important element for knowledge transfer is also modifying members’ knowledge through training Argote & Fahrenkopf (2016).
Despite burgeoning literature on knowledge transfer, relatively little is known about how strategic knowledge is created and exchanged. As behaviours that come from interactions of individuals and groups are characterised by complexity, dynamics, adaptation and non-linearity, they are very difficult for empirical studies. This means, than virtual simulation can be a useful tool to explore knowledge transfer dynamics. As emphasised by Carley (1995), one of the important contributions of computational models is that they can be used to demonstrate gaps in extant verbal theories. Additionally, they enable the researcher to think through how assumptions of models of agents influence their collective behaviour. The agent-based modelling approach for the study of knowledge transfer was used for example by Morone & Taylor (2004), Xuan et al. (2011), Hirshman et al. (2011), Giacchi et al. (2016). These studies concerned mainly the impact of the network properties on the transfer of knowledge within the network (organisation). In particular Morone & Taylor (2004) using cellular automata model examined how knowledge spreads in a network in which agents interact by word of mouth communication. Their results show the influence of network structure upon the knowledge diffusion process. Xuan et al. (2011), investigated the effect of the ‘knowledge-connection’ structure on knowledge transfer within that network. They showed that the knowledge diversity in the small world network fosters knowledge transfer. Hirshman et al. (2011) used agent-based simulation based on the homophily mechanism to examine the tiering effects of social ties. They have posited a society in which agents interact with those who are similar to them. Their studies suggest, that simulation of the emergence of multi-tiered social ties using a homophily model is possible, and the simulation results correspond to patterns observed in real-world human networks. In the model proposed by Giacchi et al. (2016) agents (nodes) transfer knowledge based on two criteria: knowledge distance and confidence. They results show that in a more distributed network configuration the dynamics of knowledge diffusion and of the confidence level are observable much more than a centralised structure.
The above models concern the impact of agent network properties on the knowledge transfer. Our goal is to build a knowledge transfer model based on the above and to investigate: what is the role of the initial level and distribution of knowledge of organisation’s members (knowledge acquired during training, courses etc.)? Initial knowledge is acquired in a formal way, while it is spread among members of the organisation through informal communication. This topic is very interesting because—as mentioned earlier—facilitating learning in organisations and thereby creating appropriate knowledge is one way of facilitating the acquisition of knowledge by the organisation. Although in many models of knowledge transfer, the population of individuals was often ‘endowed with different levels of initial knowledge’—as pointed out by Morone & Taylor (2004) when describing the model of Cowan & Jonard (1999) —the influence of initial knowledge distribution in the organisation on knowledge propagation and its exchange among members of organisation was earlier not specifically discussed.
We propose a model of knowledge transfer based on cellular automaton (CA) (Wolfram 2002; Ilachinski 2001). In the CA technique the model system is represented as a regular grid of cells. For each site \(i\) a scalar variable \(s^i\) is assigned from finite set of possible states \(s^i\in\mathcal{S}1\). The rule \(\mathcal{F}\) maps the state of \(i\)-th cell in time \(t\) into state of this cell \(i\) in the next time step \(t+1\) basing on states of sites in \(i\)-th site neighbourhood \(\mathcal{N}^i\)
| $$s^i(t+1)=\mathcal{F}(\mathcal{N}^i(t))$$ |
The rule \(\mathcal{F}\) is applied synchronously to all sites in the system.
In our approach we extend a classical definition of CA scalar variable \(s^i\) to the vector one \(\mathbf{C}^i\). Formally our set of states \(\mathcal{S}\) has \(2^K\) elements in \(\{ 0,1,\cdots,2^K-1\}\), however, we prefer to think about a binary representation of these numbers, i.e. on \(K\)-elements long Boolean vectors \(s^i=[c_1^i,c_2^i,\cdots,c_K^i]_{\text{bin}}=\mathbf{C}^i\). Such representation yields comfortable interpretation of \(c_k^i\) in terms of our conceptual model described below, however, the rigorous mathematical and formal definition of the transition function \(\mathcal{F}\) become a little bit cumbersome—thus we will provide its definition in a narrative manner.
The rest of this paper is organised as follows: The next section presents the model of knowledge transfer (concept of the model, formal model and design of virtual experiments). Subsequently, the results of our simulations are analysed. Then, discussion and conclusions are presented. Finally, we propose future research.
Model Concept
To allow for analysis of the dynamics of the transfer of knowledge in the perspective of complex systems, in this paper, a CA model has been proposed. Such an approach was used by Morone & Taylor (2004) to study the informal process of knowledge diffusion. In this paper, similarly to the cited authors, people exchange knowledge by means of personal interactions, and as was mentioned earlier, such relationships between the members of the organisation play a significant role in the transfer of knowledge.
Knowledge
In knowledge transfer models, knowledge has been represented in several ways: as a stock (each agent has an initial level of knowledge, which is an integer chosen at random from a given range) (Morone & Taylor 2004), as a vector (Cowan & Jonard 2004; Xuan et al. 2011; Giacchi et al. 2016), as a tree, where each node corresponds to a bit of potential knowledge (Morone & Taylor 2003) or as a set of facts and agent-to-knowledge matrix (Hirshman et al. 2011).
The basic assumption of the our model is a division of transferred knowledge into a certain amount of chunks. This concept was inspired by the empirical studies of Reagans & McEvily (2003), who proposed the division of knowledge in the firm into areas (pieces) of expertise knowledge and the model of Hirshman et al. (2011), where the transferred knowledge consisted of certain facts (elements, pieces of knowledge). Thus, knowledge in this model is presented as a vector consisting of knowledge chunks. The chunks of knowledge proposed here can be understood in many ways. For example, in the perspective of knowledge management, they may be elements of tacit knowledge in the organisational model of knowledge creation, proposed by Nonaka & Takeuchi (1995). In the approach of cited authors, knowledge (and thus also its chunks) applies to both information, beliefs and expectations. We also assume that, the pieces of knowledge are not related to each other but all together are needed by the organisation to change the organisational culture, improve organisational performance etc.
Agent network
Static regression models of the network parameters impact on the easiness of knowledge transfer as shown by Reagans & McEvily (2003) in empirical studies. They suggest first of all that strong ties and a dense network facilitate the transfer. Therefore, the adoption of CA model with lattice fully populated by agents as a model organisation, allows for reflecting a dense network of social interaction, whereas, the von Neumann neighbourhood of four neighbours reflects the network, which takes account only strong ties among agents (as in the model of Morone & Taylor 2004). Moreover, the number of strong ties, declared by the Reagans & McEvily (2003) is on average less than six. Hirshman et al. (2011) point out, that for most people, ‘core discussion groups’ consist of three to five people. The von Neumann neighbourhood, proposed by this work, seems to well approximate the strong ties between agents.
Rules
The rules in the adopted model are a compromise of different perspectives of the knowledge transfer mechanism. First of all, it is assumed that the agents are members of the organisation/community and they have (at the beginning of the simulation). A certain amount of the common knowledge (chunks of knowledge). This common knowledge is the result of the organisation’s activities, for example, in the framework of the knowledge management policy. The model assumes that each agent with equal probability can absorb each portion of knowledge ‘offered’ by the organisation. The level of probability reflects the quality of the activities of the formal ‘knowledge leadership’ (e.g., this is the result of investment in the area of knowledge management).
Secondly, each agent can be a leader of knowledge or a follower. The agent role in the step of interaction depends on the quantity and quality of owned chunks of knowledge. In a single interaction, an agent who has more knowledge (more chunks) is the leader of knowledge.
Thirdly, in accordance with empirical findings of Reagans & McEvily (2003) the transfer of knowledge is effective, if the distance of common knowledge between the source and recipient is small. Also simulations driven by the homophily principle (‘birds of a feather flock together’) assume that ‘agents are likely to exhibit strong preferences towards agents to whom they are similar’ (Hirshman et al. 2011). The model simplification introduces blocking the transfer of knowledge between agents (the leader and follower) if a distance of their knowledge (measured by the difference in the number of chunks of knowledge) is larger than one. This approach is not significantly different from the opinion exchange model of Deffuant et al. (2000) when interaction among agents is possible only when the distance between agents opinions in one- (Hegselmann & Krause 2002; Malarz 2006; Zhao et al. 2016; Dong et al. 2016) or two-dimensional (Kułakowski 2009; Malarz & Kułakowski 2014; Malarz et al. 2011) space of opinions is smaller than the assumed confidence level.
In addition, as in the studies of Morone & Taylor (2004); Xuan et al. (2011) agents give away information for free (‘gift economy’).
Computerised model
The model organisation is an \(L\times L\) large square lattice with helical boundary conditions with von Neumann neighbourhoods, i.e. the nearest neighbours of \(i\)-th agent (\(i=1,\cdots,L^2\)) are agents occupying nodes at \(i\pm 1\) and \(i\pm L\). The agents occupying virtual positions \(i=-L+1,\cdots,0\) and \(i=L^2+1,\cdots,L^2+L\) mirror opposite edges of the system, i.e. they are doppelgangers of agents from sites \(i=L^2-L+1,\cdots,L^2\) and \(i=1,\cdots,L\), respectively.
Each agent may possess some of the \(K\) chunks of knowledge \(\mathbf{C}^i=[c_1^i,c_2^i,\cdots,c_K^i]\) and \(c_k^i\in\{0,1\}\), where \(c_k^i=0\) (\(c_k^i=1\)) indicates that this particular \(k\)-th chunks of knowledge is absent (present) in the \(i\)-th agent’s knowledge. Initially (at \(t=0\)), each agent \(i\) has each of these knowledge chunks \(c^i_{k=1,\cdots,K}(t=0)=1\) with probability \(p\).
Every time step agent \(i\) may inherit single chunk of information from one of his/her neighbours. The knowledge transfer is possible if in time \(t\) the neighbour \(n\) has exactly one more chunks of knowledge than agent \(i\):
| $$c^i_k(t+1)=1 \iff c^i_k(t)=0, \quad c^n_k(t)=1, \quad \nu^n(t)=\nu^i(t)+1,$$ |
The design of experiment
Simulation experiments must be designed to answer a question: how does the level and distribution of initial knowledge in an organisation influence the acquisition of the required knowledge by their members? This knowledge acquisition takes place through the transfer of knowledge between the organisational members. To answer the research question both the effectiveness and efficiency of knowledge transfer are examined. Daft (1998, p. 663) defines effectiveness as ‘the degree to which goals are attained’ and efficiency as ‘amount of resources used to produce a unit of output’. In addition, according to Pérez-Nordtvedt et al. (2008), the comprehension and usefulness can be construed as reflecting knowledge transfer ‘effectiveness’, while the speed and economy can be understood as reflecting ’efficiency’ in the knowledge transfer process. It should also be noted that, the level of adoption of each initiative by the recipient units, is one of the measure of the knowledge transfer effectiveness (Jensen & Szulanski 2007), and the speed at which the receiver acquires the new insights and skills, can be understood as reflecting ‘efficiency’ in the knowledge transfer process (Pérez-Nordtvedt et al. 2008).
In connection with the above definitions, to examine the effectiveness and efficiency of knowledge transfer, we determine:
- how the initial level (initial concentration of chunks of knowledge) and distribution of knowledge through transfer of knowledge will affect the final level of knowledge in the organisation?
- and how long does this process take?
We also take into account the amount of knowledge that is ultimately needed in an organisation (to change the organisational culture, launch a new product, etc.). As it is known, different organisational processes, organisational changes require knowledge resources of different sizes. Therefore, studies were conducted for different sizes of knowledge resources (different number of knowledge chunks). In addition, to check whether the size of the organisation affects the simulated process run, the studies concerns organisations of different sizes.
In view of the above, as the dependent variable describing an effectiveness of knowledge transfer the following parameters were adopted:
- \(n(k)\) — the fraction of agents having \(k\) chunks of knowledge,
- \(n(K)\) — the fraction of agents having all chunks of knowledge,
- \(f(k)\) — the fraction of agents having \(k\)-th chunk of knowledge \(c_k\),
- \(\langle f\rangle\)— the coverage of any chunks of knowledge \(c_k\) in agents’ knowledge, i.e. the fraction of knowledge chunks held by typical member of the organisation.
Additionally, as the dependent variable describing an efficiency of knowledge transfer, the time \(\tau\) necessary for reaching a stationary state was adopted.
On the other hand, the following independent variables were chosen in the designed experiments:
- maximal number of chunks of knowledge \(K\),
- lattice size (\(L\)),
- initial concentration of chunks of knowledge (\(p\)).
The following levels of parameters were assumed in the first study:
- \(K=4\) (transfer of smaller amount of knowledge is required) and \(K=8\) (transfer of greater amount of knowledge is required),
- \(L=5\) (the equivalent of a small organisation), \(L = 20\) (the equivalent of an average organisation)
- \(p\in\{0.2, 0.5, 0.8\}\).
We also performed additional experiments (second-fourth experiments) to find the threshold values of the parameters described in the first study.
Results
The results presented in Figures 1-3 and Figures 5-8 are obtained as a result of procedure of data aggregation from \(M\) independent simulation with different initial distributions of chunks of knowledge \(\mathbf{C}^i\) for all agents (\(i=1,\cdots,L^2\)). The program allowing for reproduction of these results is attached in Appendix B as Listing 3. The only exception are the results presented in Figure 4 which were obtained using program listed in Listing 4. If the number of independent simulations \(M\) is not explicit specified then \(M=100\).
Model verification
The model verification for computer models ‘is defined as checking the adequacy among conceptual models and computerised models’ (David 2013, p. 138).
In Listings 1 and 21 the values of \(\mathbf{C}^i\) for small organisation \(L=5\) in several subsequent times steps \( t<5\) are presented. The vectors \(\mathbf{C}^i\) between pairs of dashed lines correspond to \(i=1,\cdots,5\) (in the first row), \(i=6,\cdots,10\) (in the second row), etc. The chunks of knowledge inherited in step \(t\) are indicated by a red cross (x). Eleventh lines of the listings contain information on global presence/absence of chunks of knowledge in organisation. In both examples (Listings 1 and 2) each chunk of knowledge is known at least by one of the agents. The lines 50–54 show time evolution of the aggregated number \(F(k)\equiv\sum_{r=1}^M F_r(k)\) of agents having \(k\)-th chunk of knowledge \(c_k\) and aggregated number \(N(k)\equiv\sum_{r=1}^M N_r(k)\) of agents having exactly \(k\) chunks of knowledge, where \(F_r(k)\) [\(N_r(k)\)] are numbers of agents having \(k\)-th chunk of knowledge \(c_k\) and aggregated number \(N(k)\equiv\sum_{r=1}^M N_r(k)\) of agents having exactly \(k\) chunks of knowledge, where \(F_r(k)\) [\(N_r(k)\)] are numbers of agents having \(k\)-th chunk of knowledge \(c_k\) [numbers of agents having exactly \(k\) chunks of knowledge] in \(r\)-th simulation. These values (normalised to the system size \(L^2\) and the number of simulations \(M\)) will be presented in Figure 1.
| $$f(k)\equiv\dfrac{F(k)}{L^2}=\dfrac{\sum_{r=1}^M F_r(k)}{ML^2}$$ |
| $$n(k)\equiv\dfrac{N(k)}{L^2}=\dfrac{\sum_{r=1}^M N_r(k)}{ML^2}$$ |
In Listing 1 the system evolution for \(K=4\) and \(p=0.2\) are presented. During the first time step the agents (followers 3, 10, 11, 13, 14, 16, 18, 19, 20, 21 and 23) acquire new chunks of knowledge (\(c_3\), \(c_3\), \(c_1\), \(c_3\), \(c_2\), \(c_3\), \(c_3\), \(c_2\), \(c_2\), \(c_3\) and \(c_4\), respectively). These transfers come from local leaders (agents 23, 5, 6, 14, 9, 11, 19, 24, 25, 1, 22). Please note that some agents (11, 14, 19) play both roles and simultaneously send and receive chunks of knowledge. The transfer of \(c_3\) to agent 18 is possible from agents 19 and 23 as \(c_3^{18}(t=0)=0\) and \(\nu^{18}(t=0)=0\) and simultaneously \(c_3^{19}(t=0)=1, \nu^{19}(t=0)=1\) and \(c_3^{23}(t=0)=1, \nu^{23}(t=0)=1\). Agent 18 chooses an agent from whom he/she randomly inherit \(c_3\).
In Listing 2 the system evolution for the same set of parameters as in Listing 1 is presented. The only exception is that the value of \(p\) is four times larger (\(p=0.8\) instead of 0.2). The larger value of \(p\) results in higher coverage of chunks of knowledge \(\{F(c_1),\cdots,F(c_4)\}=\{23,24,24,24\}\) (\(p=0.8\)) instead of \(\{ 6,14,20,10\}\) for \(p=0.2\). Also qualitative difference in the number of agents \(N(k)\) possessing \(k\) chunks of knowledge is observed as for \(p=0.2\) agents with \(k=K=4\) chunks of knowledge are absent while they are dominant (23/25) fraction of \(N(k)\) distribution for \(p=0.8\)
Please note that although in both cases all chunks of knowledge are available in the system the evolution stops before transfer of all chunks of knowledge to all agents.
As both, the initial distributions of chunks of knowledge \(c_k\) among agents and the missing chunks of knowledge which will be inherited are selected randomly we do not expect any difference in \(f(k)\) time evolution. And indeed, curves of \(f(k)\) vs. \(t\) for various \(k\) collapse into single curve for fixed values of \(L\), \(K\) and \(p\) as presented in Figure 1.
Main results
First experiment: \(n(k)\)
Initially, the evolution of agents fraction \(n(k)\) who have \(k\) required knowledge chunks depending on the simulation time \(t\) was examined. The study was conducted according to the experiment design for \(K=4\) (when organisation change requires less knowledge, Figure 2) and for \(K = 8\) (when organisation change requires more knowledge, Figure 3).
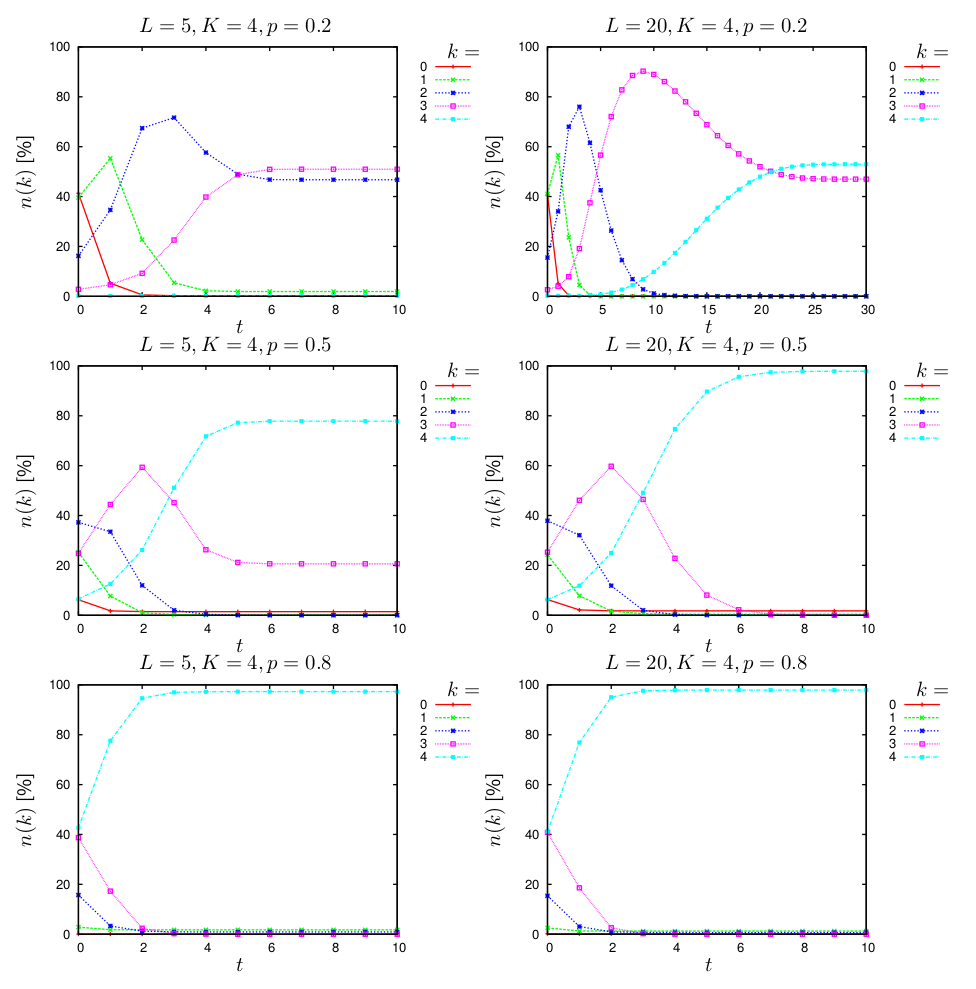
In both cases, the simulations were conducted for both a small organisation (\(L=5\)), and an average organisation (\(L=20\)) with three levels of initial concentration chunks of knowledge \(p=0.2\), \(0.5\) and \(0.8\). As shown in Figure 2 and 3 the effectiveness of the knowledge transfer as measured by \(n(k)\) depends on \(L\) and \(p\). The greater \(p\) the greater the percentage of agents having a greater number of \(k\) portions of all the required chunks of knowledge. For example, let us look at Figure 22 (left panel, for \(L=5\) and \(K=4\)): for \(p=0.2\) the lack of agents having all four required knowledge chunks is observed, whereas for \(p = 0.5\), nearly 80% of agents have four knowledge chunks and for \(p=0.8\) almost 100% of the agents have all required knowledge chunks. In addition, to obtain a high enough percentage of the agents having \(K\) portions of knowledge, the value of p must be much greater for \(K=8\) (Figure 3) than it is for \(K=4\) (Figure 2). For an average organisation (\(L=20\)), the level of \(p=0.2\) is high enough to make agents with all required chunks of knowledge the dominant fraction of agents in the organisation (for \(p=0.2\), more than 50% of agents have \(k=4\) of the knowledge chunks, while agents with \(k\le 2\) chunks of knowledge are absent). A similar relationship is observed in Figure 3, that is, in larger organisations, a smaller value of p is needed to obtain a greater percentage of agents having the \(k\) knowledge chunks.
The efficiency of the knowledge transfer may be quantitatively described as a time \(\tau_r\) necessary for reaching the stationary state of the system during the \(r\)-th running. The value of \(\tau_r\) indicates the number of simulation time steps necessary for reaching the time point after which neither \(F_r(k)\) (\(k=1,\cdots,K\) nor \(N_r(k)\) undergo any changes. The dependence of the average time \(\tau=M^{-1}\sum_{r=1}^M\tau_r\) for small (\(L = 5\)) and average (\(L=20\)) organisation sizes are dependent on the initial fraction of chunks of knowledge \(p\) for \(K=4\) and \(K=8\) as presented in Figure 4. The results are averaged over \(M=10^3\) independent simulations. The values obtained for the uncertainties of \(\tau\), are:
| $$u(\tau)=\sqrt{\dfrac{\sum_{r=1}^M (\tau_r-\tau)^2}{M(M-1)}}$$ | (1) |
Second experiment: \(n(K)\)
In Figure 5 the results of the second experiment are presented. Identical levels of \(L\) (5 and 20) as in the first experiment have been adopted, whereas levels of \(K\) (2, 3, 4, 8) and \(p\) (from 0.1 to 0.9 in steps of 0.1) have been expanded. The basic result of the conducted simulation confirmed, that the dependencies obtained in the first study are valid. For a larger lattice a relatively lower value of \(p\) is sufficient to achieve desired fraction \(n(K)\) of agents having a complete knowledge. Furthermore, as can be seen in Figure 5, the greater the number of knowledge chunks \(K\) needed in an organisation, the greater must be initial fraction \(p\) of knowledge chunks in order to make almost all the organisation members fully comprehensive, i.e. having all \(K\) desired chunks of knowledge. Please note however, that for some sets of parameters the full coverage of chunks of knowledge by all agents becomes impossible. For small organisation (\(L=5\)), \(K=8\) and \(p\ge 0.8\) the fraction of agents with total knowledge reaches \(90\%\)\(\le n(K)\le\)\(100\%\). For an average size organisation \((L=20)\) such level of agents knowledge is reached for \(p\ge 0.6\). On the other hand for \(K=8\) and \(p\le 0.5\) (small organisation) and for \(p\le 0.3\) (average organisation) less than 10% of agents possess all chunks of knowledge.
As can be seen in Figure 5, the efficiency of knowledge transfer is greater for smaller organisations, i.e. the stationary state is reached earlier for \(L=5\) than for \(L=20\).
Third experiment: \(n(K)\) vs. \(L\) and \(p\)
The third experiment was designed to precisely analyse the impact of the lattice size \(L\) on the investigated dependent variables. The experiments were conducted for \(K=4\) and \(K=8\) (small and medium-sized organisations) and for the \(p\) levels—as in the second experiment. The size of the lattice (organisation) was changed to the levels \(L=5, 10, 20, 50, 100, 200, 500\) and \(1000\). The results of average values of \(n(K)\) (independent replicates obtained for the simulation from 50 to 1000 runs) is shown in Figure 6. The results are averaged over \(M\) independent simulations as indicated in the picture inset. The system reached the stationary state in \(t<200\) (\(t<1000\)) steps for \(L<400\) (\(L>400\)). The bottom part of the figure shows enlarged fragments of the top figure part. Dependencies shown in the figures, generally confirm the model behaviour obtained in the previous two studies. First of all, the large size \(L^2\) of modelled organisations require a smaller value of probability \(p\) for a full (or nearly full, \(n(K)\ge90\%\)) knowledge into the system.
Let \(p_C\) be an initial fraction \(p\) of chunks of knowledge which guarantee that half of agents will acquire the total knowledge. The quantity \(p_C\) may be treated as characteristic of efficiency of knowledge transfer complementary to time \(\tau\). In Figure 7(a) the critical values of initial concentration of chunks of knowledge \(p_C\) as dependent on linear system size \(L\) are presented. These dependencies become roughly linear in logarithmic scale which indicate that \(p_C(L)\propto L^{-\gamma}\). The least square method fit results in the exponent \(\gamma=0.4718\ldots\) and \(\gamma=0.1895\ldots\) for \(K=4\) and \(K=8\), respectively. Of course, for \(K=8\) threshold \(p_C\) is greater than that for \(K=4\), that is, if the organisational change requires more knowledge, more individual portions of knowledge at the beginning of the knowledge transfer (measured by \(p\)) must be available in the organisation.
Consider the bottom panel of Figure 6. As can be seen, for all tested lattice sizes \(L\), after reaching the maximum value of \(n(K)\) (which takes place at \(p=p_O\)), a decrease of the fraction \(n(K)\) for each test, is observed. This decrease takes place until a certain value of \(p\) and then \(n(K)\) again increases with \(p\). This phenomenon takes place both for \(K=4\) and \(K=8\) and it is a consequence of the assumptions of our model. Agents can acquire knowledge only from neighbours, who have exactly one more of knowledge chunk from them. This shows, that at some point agents can no longer acquire more knowledge since neighbouring agents are much smarter than they are.
The optimal value of initial concentration of chunks of knowledge \(p_O\) which guarantee the most efficient transfer of knowledge[1], as dependent on a linear system size \(L\), is presented in Figure 7(b). For \(p=p_O\) the dependencies \(n(K)\) presented in Figure 6 have local maximum. In both cases (\(K=4\), 8) the dependencies \(p_O(L)\) do not grow with \(L\). Please note, that for \(K=8\) and small- or average-sized organisations (\(L\le 20\)) the dependencies \(n(K)\) vs. \(p\) (see Figure 6) grow monotonically with \(p\) and \(p_O=1\).
Fourth experiment: \(\langle f\rangle\)
Subsequently, in the fourth experiment, the effectiveness of knowledge transfer expressed by average coverage of knowledge chunks of agents having any chunk of knowledge \(c_k\):
| $$\langle f\rangle=\frac{1}{K} \sum_{k=1}^K f(k),$$ |
In Figure 8 for \(K=2\), 3 and 4 the dependencies \(\langle f\rangle\) on \(p\) increases to a certain threshold value of \(p\) (the threshold value of \(p\) is different for various \(K\)), then it decreases, and it increases again. These complex behaviours are more visible in the larger lattice (\(L=20\)) than in the smaller (\(L=5\)). We see again, that for \(L=20\) and \(K\ge 7\) a drop in \(\langle f\rangle\) is absent.
Discussion and Conclusions
We have investigated a CA model to study the transfer of knowledge within an organisation. The transfer of existing knowledge is studied since the acquisition of such knowledge is the key to build competitive advantage of companies (Szulanski 1996). Moreover, the knowledge is in the organisation, as emphasised by Grant (1996). Our goal was to answer the research question: how does the level of initial knowledge in an organisation influence the acquisition of the required knowledge by their members? To answer this question, we performed simulations
- for various initial knowledge (\(p\)), which is in the organisation,
- for different sizes of knowledge resources (\(K\)),
- for model organisations of different sizes (\(L\)).
As we have shown previously, the larger size of the organisation \(L\), the smaller initial fraction \(p\) of knowledge chunks among members of the organisation is necessary for reaching (in series of knowledge transfers) the required level of knowledge by almost all members of the organisation. The value \(L^2p^K\) is also an average number of agents \(i\) who initially have all chunks of knowledge (i.e. \(\nu^i(0)=K\)). In other words, to obtain finally a similar level of knowledge saturation among agents for larger organisations we need fewer agents with all portions of knowledge before the transfer of knowledge will start when compared to the smaller organisations. In addition, in the larger organisation it is more likely that the required knowledge will be acquired by almost all the members of the organisation. This phenomenon results from the assumptions of the model, as explained above. The condition for the effective transfer in our model, is having all knowledge chunks by at least one individual. If the organisation is small and the initial concentration \(p\) of chunks of knowledge is low, it is possible that no person has all of the knowledge chunks. Furthermore, in our model, we assumed that agents (organisation members) can acquire knowledge only from neighbours, who have exactly one more knowledge chunk than they have. As it was shown at some point they can no longer acquire knowledge, since all agents in the neighbourhood are much smarter than them. The adoption of such a way of knowledge transfer is sometimes not fully effective. This is particularly visible in the graphs of Figure 6(c-d) and Figure 8. The radical model assumption that the transfer takes place only between agents, who differ in a single chunk of knowledge, may result in the inability to achieve the full knowledge of the organisation. This phenomenon suggests taking action in the organisation to shorten the distance (social distance) between people with different levels of knowledge (educational attainment), or working out incentives to share knowledge.
The simulation results shown in Figure 8 suggest a decrease in the effectiveness of knowledge transfer with rising probabilities \(p\) for the initial individual portions of knowledge. However, this surprising phenomenon can be explained on the basis of the assumed rules of transfer and assignment of ‘knowledge’ by agents. Undoubtedly, the dynamics of the knowledge transfer depends on the initial parameters adopted in the model. The probabilities of initial appearance of agents with \(k\) chunks of knowledge are given by the Bernoulli distribution:
| $$\mathcal{B}_K(k)={K \choose k}p^k(1-p)^{K-k} $$ | (2) |
For \(p\ge 0.5\) we can observe the strong increase of the possibility of the transfer of useful information from agents with two chunks of knowledge to those who have just one. Although the number of pairs blocking the knowledge transfer decreases, the drastic decrease of the possibility of obtaining knowledge by agents without any chunks of knowledge from those who have single chunk of knowledge is simultaneously observed. Hence, in further steps, the increase of the number of pairs potentially blocking the knowledge transfer may occur and consequently the system does not reach the state of ‘full knowledge’. It seems that this reasoning justifies the results shown in Figure 8 for \(K = 2\). Please note however, that our reasoning has a rather ‘mean field’ character and it neglects totally the spatial correlations among agents. The latter are crucial in a CA technique and thus our interpretation remains only qualitative.
Efficiency is understood here as the time \(\tau\) needed to achieve a stable state of the system. The larger the organisation, the longer the time \(\tau\) of knowledge transfer. This time depends also on the number of knowledge chunks \(K\). The more knowledge is needed to be transfer, the time of this process is longer.
As it was postulated by Reagans & McEvily (2003), effective knowledge transfer is a very important part of the knowledge management. Without knowledge of the critical factors related to the effective transfer of knowledge, managers may have a problem with supporting the exchange of knowledge (Levin et al. 2004). Our findings provide practical guidance for managers in the context of knowledge transfer within an organisation, where the knowledge of all its members is needed to change organisation, organisational culture, etc. Our simulation shows that, the state of knowledge at the beginning of the transfer is very important.
The higher the initial level of knowledge in the organisation, the greater the chance that almost all members will have the requisite knowledge they need to make the changes. As we have shown, this takes place in particular with our assumption that the knowledge transfer takes place in the manner described in this article, i.e. when a small distance of knowledge between the recipient and the sender is established. Therefore, managers should conduct courses and training for their employees to increase the level of knowledge in the organisation.
Further, if agents transfer knowledge when others have one more knowledge chunk than them, the transfer of knowledge is more effective when knowledge is spread more evenly between members of the organisation, i.e. when there are few agents with a large distance of knowledge from others. Although in our description the correlations between knowledge of neighbouring agents are neglected, it is clear that an organisational structure should allow agents of small differences of knowledge to work together. The more people will possess the required knowledge (which is needed to change organisation, organisational culture, etc.) the more effective and efficient transfer of knowledge will be.
Knowledge transfer is also influenced by the size of the organisation and the knowledge resources. The greater size of the organization and greater the necessity for more chunks of knowledge increase time of the knowledge transfer. It is also related to the assumed model of knowledge transfer and the probability of the initial appearance of agents with \(K\) chunks of knowledge (as explained in paragraph 4.3, see Figure 9). In a larger organization there are more agents with a smaller distance of knowledge between them, which means that agents more often (and therefore longer) exchange knowledge among themselves. A similar situation occurs when the larger number of chunks of knowledge should be transferred in the organization. A larger number of chunks of knowledge \(K\) results in more knowledge exchange processes among agents (members of the organization). Moreover, the more chunks of knowledge are required for organizational change, the larger the initial level \(p\) of knowledge in organisation is necessary to make almost all members of organisation fully comprehensive i.e. having all desired chunks of knowledge.
As Harari et al. (2014) point out, the knowledge transfer consists of two dimensions: seeking out knowledge from others and sharing one’s knowledge with others. On the one hand, employees strive to enhancing their own knowledge, on the other hand, they should share knowledge with those who need it. Inside the organisation, knowledge transfer involves therefore, actively communicating to others and actively consulting others to learn what they know.
In the model presented, we assume that employees are willing to share knowledge with their closest neighbours, if the knowledge distance between them is small. These can be teams of employees—formal groups and informal groups when employees meet for example on breaks, dinner, etc., but communication between them is informal. This assumption results in quite effective knowledge transfer (as shown in the previous section). Additionally, Alipour et al. (2011) postulate, that the manager should design a structure, in which organisational members can share their information, experience, and their knowledge. The structure based on close formal or informal contacts between employees seems to be a good solution. Close relationships between employees (they know each other well) have a positive effect on their openness and trust, and this leads to positive behaviours such as sharing knowledge (Krylova et al. 2016). Managers should, therefore, support the creation of informal groups between employees as well as ensure good cooperation in formal staff teams to develop informal communication.
Further research
This is a preliminary study on the transfer of knowledge within the organisation. The results suggest further development of the model that will contain more variables describing the transfer of knowledge within an organisation.
Firstly, we were going to describe the way of knowledge transfer by another or modified rules. For example, it seems interesting to investigate the transfer of knowledge consisting in acquiring knowledge from individuals who have other pieces of knowledge (not necessarily have more knowledge than a learning agent) and/or acquiring knowledge from the wisest individuals in the neighbourhood (knowledge leaders). This will allow the comparison of different variants of the model and examine how a different knowledge transfer rules influence effectiveness and efficiency of this process (Kowalska-Styczeń et al. 2018).
Secondly, because our research shows a significant role of an initial knowledge level and distribution in the organisation, it seems to be interesting to study the company’s policy involving the different training strategies for their employees. Undoubtedly managers could be interested in an identification of relationships between the range and scope of training and on quality of knowledge transfer. For example, the knowledge whether do training for a wider range of employees, or for a smaller number of units; whether to train comprehensively a few people, or teach different skills of a larger group of employees, it may prove to be very valuable.
Thirdly, studying the effects of strong and weak ties to the transfer of knowledge, is very interesting (Uzzi 1997, 1999; Hansen 1999). It is related to the introduction of social distance and the different neighbourhood size in our model—here restricted to the smallest possible, i.e. von Neumann neighbourhood where interactions only with the nearest neighbours are considered (Paradowski et al. 2017).
Acknowledgements
AKS and KM are grateful to Krzysztof Kułakowski for fruitful discussion on cellular automaton rules and critical comments on the manuscript. KM is grateful to Naven Chetty for linguistic revision of the manuscript. This research was supported by National Science Centre (NCN) in Poland (grant no. UMO-2014/15/B/HS4/04433), in part by PL-Grid Infrastructure and partially by AGH-UST statutory tasks (grant no. 11.11.220.01/2) within subsidy of Ministry of Science and Higher Education.Appendix
To access "Appendix A: Java applet presenting system evolution" and "Appendix B: Program code listings", please see the appendix section of the pdf version of the article here.Notes
- I.e., giving the largest fraction of agents with \(K\) chunks of knowledge.
References
ALIPOUR, F., Idris, K. & Karimi, R. (2011). Knowledge creation and transfer: role of learning organization. International Journal of Business Administration, 2(3), 61–67. [doi:10.5430/ijba.v2n3p61]
ARGOTE, L. & Fahrenkopf, E. (2016). Knowledge transfer in organizations: The roles of members, tasks, tools, and networks. Organizational Behavior and Human Decision Processes, 136, 146–159.
BOONE, T. & Ganeshan, R. (2008). Knowledge acquisition and transfer among engineers: Effects of network structure. Managerial and Decision Economics, 29(5), 459–468. [doi:10.1002/mde.1401]
BROWN, D. C. (2003). Leading complex change: A five-stage process to promote employee buy-in. Behavioral Health Management. Butcher, D. & Atkinson, S. (2000). The bottom-up principle. Management Review, 89(1), 48–53.
CARLEY, K. M. (1995). Computational and mathematical organization theory: perspective and directions. Computational and Mathematical Organization Theory, 1(1), 39–56. [doi:10.1007/BF01307827]
CHEN, C. (2004). The effects of knowledge attribute, alliance characteristics, and absorptive capacity on knowledge transfer performance. R&D Management, 34(3), 311–321.
CHEN, C. & Huang, J. (2007). How organizational climate and structure affect knowledge management—the social interaction perspective. International Journal of Information Management, 27(2), 104–118. [doi:10.1016/j.ijinfomgt.2006.11.001]
COWAN, R. & Jonard, N. (1999). Network structure and the diffusion of knowledge. MERITWorking Papers, (pp. 99–028).
COWAN, R. & Jonard, N. (2004). Network structure and the diffusion of knowledge. Journal of Economic Dynamics and Control, 28(8), 1557–1575. [doi:10.1016/j.jedc.2003.04.002]
DAFT, R. L. (1998). Organization Theory and Design. Cincinnati, OH: South-Western College Publishing.
DAVID, N. (2013). Validating simulations. In B. Edmonds & R. Meyer (Eds.), Simulating Social Complexity, (pp. 135–171). Berlin/Heidelberg: Springer-Verlag. [doi:10.1007/978-3-540-93813-2_8]
DEFFUANT, G., Neau, D., Amblard, F. & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(1-4), 87.
DONG, Y., Chen, X., Liang, H. & Li, C.-C. (2016). Dynamics of linguistic opinion formation in bounded confidence model. Information Fusion, 32(A), 52–61. [doi:10.1016/j.inffus.2016.03.001]
GIACCHI, E., La Corte, A. & Di Pietro, E. (2016). A dynamic and context-aware model of knowledge transfer and learning using a decision making perspective. In V. M. Muñoz, O. Gusikhin & V. Chang (Eds.), Proceedings of the 1st International Conference on Complex Information Systems, (pp. 66–73). Setúbal: Science and Technology Publications.
GILMOUR, D. (2003). How to fix knowledge management. Harvard Business Review, 81, 16–17 https://hbr.org/2003/10/how-to-fix-knowledge-management.
GIRDAUSKIENE, L. & Savaneviciene, A. (2012). Leadership role implementing knowledge transfer in creative organization: how does it work? Procedia—Social and Behavioral Sciences, 41, 15–22.
GRANT, R. M. (1996). Prospering in dynamically-competitive environments: organizational capability as knowledge integration. Organization Science, 7(4), 375–387. [doi:10.1287/orsc.7.4.375]
HANSEN, M. T. (1999). The search-transfer problem: The role of weak ties in sharing knowledge across organization subunits. Administrative Science Quarterly, 4(4), 82–111. [doi:10.2307/2667032]
HARARI, M. B., Jain, N. K. & Joseph, T. (2014). The five-factor model of personality and knowledge transfer in the United Arab Emirates. International Journal of Selection and Assessment, 22(4), 399–410.
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence: models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.
HEROLD, D. M., Fedor, D. B., Caldwell, S. D. & Liu, Y. (2008). The effects of transformational and change leadership on employees’ commitment to a change: A multilevel study. Journal of Applied Psychology, 93, 346–357.
HIGGS, M. & Rowland, D. (2005). All changes great and small: exploring approaches to changes and its leadership. Journal of Change Management, 5(2), 121–151. [doi:10.1080/14697010500082902]
HIRSHMAN, B. R., Charles, J. S. & Carley, K. M. (2011). Leaving us in tiers: can homophily be used to generate tiering effects? Computational and Mathematical Organization Theory, 17, 318–343.
IBARRA, H. (1993). Network centrality, power, and innovation involvement: Determinants of technical and administrative roles. Academy of Management Journal, 36(3), 471–501. [doi:10.2307/256589]
ILACHINSKI, A. (2001). Cellular automata: A discrete Universe. Singapore: World Scientific.
JENSEN, R. J. & Szulanski, G. (2007). Template use and the effectiveness of knowledge transfer. Management Science, 53(11), 1716–173. [doi:10.1287/mnsc.1070.0740]
KEMPSTER, S., Higgs, M. & Wuerz, T. (2014). Pilots for change: exploring organisational change hrough distributed leadership. Leadership and Organization Development Journal, 35(2), 152–167.
KOWALSKA-STYCZEŃ, A., Malarz, K. & Paradowski, K. (2018). Searching for effective and efficient way of knowledge transfer within an organization. In A. P. Rocha & J. van den Herik (Eds.), Proceedings of the 10th International Conference on Agents and Artificial Intelligence, (pp. 151–158). Rome: SciTePress. [doi:10.5220/0006546701510158]
KRAUT, R. E., Fish, R. S., Root, R. W. & Chalfonte, B. L. (1993). Information communication in organizations: form, function, and technology. In R. M. Baecker (Ed.), Readings in Groupware and Computer-Supported Cooperative Work, (pp. 287–314). San Mateo, CA: Morgan Kaufmann Publishers.
KRYLOVA, K. O., Vera, D. & Crossan, M. (2016). Knowledge transfer in knowledge intensive organizations: the crucial role of improvisation in transferring and protecting knowledge. Journal of Knowledge Management, 20(5), 1045–1064. [doi:10.1108/JKM-10-2015-0385]
KUŁAKOWSKI, K. (2009). Opinion polarization in the receipt–accept–sample model. Physica A: Statistical Mechanics and its Applications, 388(4), 469–476.
LEVIN, D. Z., Cross, R., Abrams, L. C. & Lesser, E. L. (2004). Trust and knowledge sharing: A critical combination. In E. Lesser & L. Prusak (Eds.), Creating Value with Knowledge, (pp. 36–41). Oxford: Oxford University Press. [doi:10.1093/0195165128.003.0003]
LYLES, M. & Salk, J. (1996). Knowledge acquisition from foreign parents in international joint venture: An empirical examination in the Hungarian context. Journal of International Business Studies, 27(5), 877–903.
MALARZ, K. (2006). Truth seekers in opinion dynamics models. International Journal of Modern Physics C, 17(10), 1521–1524. [doi:10.1142/S0129183106009850]
MALARZ, K., Gronek, P. & Kułakowski, K. (2011). Zaller–Deffuant model of mass opinion. Journal of Artificial Societies and Social Simulation, 14(1), 2: https://www.jasss.org/14/1/2.html.
MALARZ, K. & Kułakowski, K. (2014). Mental ability and common sense in an artificial society. Europhysics News, 45(4), 21–23. [doi:10.1051/epn/2014402]
MARTINEZ, L. F., Ferreira, A. I. & Can, A. B. (2016). Consultant-client relationship and knowledge transfer in small-and medium-sized enterprises change processes. Psychological Reports, 118(2), 608–625.
MORONE, P. & Taylor, R. (2003). Small world dynamics and the process of knowledge diffusion: The case of the metropolitan area of greater Santiago de Chile. Journal of Artificial Societies and Social Simulation, 7(2), 5: https://www.jasss.org/7/2/5.html.
MORONE, P. & Taylor, R. (2004). Knowledge diffusion dynamics and network properties of face-to-face interactions. Journal of Evolutionary Economics, 14(3), 327–351.
NONAKA, I. (1994). A dynamic theory of organizational knowledge creation. Organization Science, 5(1), 14–37. [doi:10.1287/orsc.5.1.14]
NONAKA, I. & Takeuchi, H. (1995). The knowledge Creating Company. How Japanese Companies Create the Dynamic of Innovation. New York: Oxford University Press.
NOVIANTO, O. & Puspasari, D. (2012). Knowledge management system’s implementation in a company with different generations: A case study. Procedia—Social and Behavioral Sciences, 65, 942–947. [doi:10.1016/j.sbspro.2012.11.224]
O‘DEAL, C., Wiig, K. & Odem, P. (1999). Benchmarking unveils emerging knowledge strategies. Benchmarking: An International Journal, 6(3), 202–211.
PARADOWSKI, K., Malarz, K. & Kowalska-Styczeń, A. (2017). Influence of a range of interaction among agents on efficiency of knowledge transfer within an organization. https://arxiv.org/abs/1711.05065.
PÉREZ-NORDTVEDT, L., Kedia, B. L., Datta, D. K. & Rasheed, A. A. (2008). Effectiveness and efficiency of cross-border knowledge transfer: an empirical examination. Journal of Management Studies, 45(4), 714–744.
REAGANS, R. & McEvily, B. (2003). Network structure and knowledge transfer: the effects of cohesion and range. Administrative Science Quarterly, 48(2), 240–267. [doi:10.2307/3556658]
SPAŁEK, S. (2014). Does investment in project management pay off? Industrial Management & Data Systems, 114(5), 832–856.
SZULANSKI, G. (1996). Exploring internal stickness: Impediments to the transfer of best practice within the firm. Strategic Management Journal, 17(S2), 27–43. [doi:10.1002/smj.4250171105]
TANG, F. (2011). Knowledge transfer in intra-organization networks. Systems Research and Behavioral Science, 28(3), 270–282.
TEECE, D. J. (2000). Strategies for managing knowledge assets: The role of firm structure and industrial context. Long Range Planning, 33(1), 35–54. [doi:10.1016/S0024-6301(99)00117-X]
TSAI, W. (2001). Knowledge transfer in intraorganizational networks: Effects of network position and absorptive capacity on business unit innovation and performance. Academy of Management Journal, 44(5), 996–1004.
TSAI, W. (2002). Social structure of ‘coopetition’ within a multiunit organization: Coordination, competition, and intra-organizational knowledge sharing. Organization Science, 13(2), 179–190. [doi:10.1287/orsc.13.2.179.536]
UZZI, B. (1997). Social structure and competition in interfirm networks: The paradox of embeddedness. Administrative Science Quarterly, 4(2), 35–67.
UZZI, B. (1999). Social relations and networks in the making of financial capital. American Sociological Review, 64, 481–505. [doi:10.2307/2657252]
VAN DE VEN, A. H., Delbecq, A. L. & Koenig Jr., R. (1976). Determinants of coordination modes within organizations. American Sociological Review, 41, 322–338. [doi:10.2307/2094477]
WOLFRAM, S. (2002). A New Kind of Science. Champaign, IL: Wolfram Media.
XUAN, Z., Xia, H. & Du, Y. (2011). Adjustment of knowledge-connection structure affects the performance of knowledge transfer. Expert Systems with Applications, 38(12), 14935–14944. [doi:10.1016/j.eswa.2011.05.054]
ZANDER, U. & Kogut, B. (1995). Knowledge and the speed of the transfer and imitation of organizational capabilities: An empirical test. Organization Science, 6(1), 76–92.
ZHAO, Y., Zhang, L., Tang, M. & Kou, G. (2016). Bounded confidence opinion dynamics with opinion leaders and environmental noises. Computers & Operations Research, 74, 205–213. [doi:10.1016/j.cor.2015.07.022]
