Introduction
Cooperative behaviour is prevalent in a public goods setting. Why cooperation occurs, despite theoretical justification for non-cooperative behaviour, has preoccupied experimentalists across many disciplines (Kurzban & Houser 2005; Ledyard 1995). The main objectives of many of these experiments was to identify factors influencing contribution rates as well as to explain dynamic contribution patterns (see survey articles by Chaudhuri 2011; Ledyard 1995). The decay phenomenon, in particular, has received much attention. Subjects initially contribute a substantial amount of their endowment, between 40% and 60%. Contributions decline significantly with repetition, though never reach the free-riding level predicted by rational choice theory (Dawes 1980; Ledyard 1995).
While various explanations for declining contributions have been proposed, for example learning or strategic considerations (Andreoni 1988), the most prominent explanation relates to intrinsic traits and motivations that shape an individual’s social preferences.
Public goods experiments designed to identify social preferences classify subjects into a few distinct groups, mainly free-riders (subjects who never contribute to the public good) and conditional cooperators who reciprocate the contribution of other group members (see for example Fischbacher, Gächter, & Fehr 2001). It is argued that the existence of imperfect conditional cooperators, those who tend to contribute a value that is less than the average of their group, and free-riders, are the main cause of declining contributions over time. Contributions remain above the free-riding level mainly due to above-average conditional cooperators (whose contributions are above the average contribution) and unconditional cooperators (Fischbacher et al. 2001; Herrmann & Thöni 2009; Keser & Winden 2000; Kocher et al. 2015).
Experiments typically consist of a few decision periods (usually ten decision periods) which might be insufficient to determine whether declining contributions eventually reach the free-riding level. Furthermore, experiments provide observations for one specific composition of social preference types of subjects present at a particular experimental session. Thus, though experiments are very effective in providing a highly abstract and controlled environment to test specific hypotheses, they can become costly and are sometimes difficult to extend beyond a certain parameter space.
In response, an agent-based model (ABM) could compensate for such shortcomings and enable the adjustment of conditions of the system under study observing outcomes for different compositions of agent preferences and different sets of parameter values over extended decision periods (Abdou, Hamill, & Gilbert 2012; Helbing & Balietti 2011).
Furthermore there are incentives to combine simulation modeling with empirical methods. Human-subject experiments (especially experimental economics) and agent-based modeling share the same basis. Both reject the assumption of the homo-economicus individual, and instead endorse heterogeneity and bounded-rationality of subjects/agents. Together, they form a powerful technique to understand and disentangle the complexities underlying social behaviors and phenomena (Dal Forno & Melone 2004; Duffy 2006; Janssen & Ahn 2006).
The methodology of agent-based modeling can enhance experimental studies involving human-subjects in a number of ways. In agent-based modeling we can replace human-subjects with artificial agents; thus, allowing for greater control over behaviors and information-processing capabilities of agents than in the case of lab experiments (Dal Forno & Melone 2004; Duffy 2006). Agent-based modeling is also used to explain results and findings of human-subject experiments (Boero, Bravo, Castellani & Squazzoni 2010; Wendel & Oppenheimer 2010). Finally, data collected from experimental studies provide the needed empirical regularities for evaluating the validity of an ABM.
In this study the approach of combining experiments and simulation models is used to enhance analysis on the public goods problem. While the importance of heterogeneous agents in explaining the dynamics of voluntary contributions to public goods is evident in numerous experimental studies, there are dimensions to analysis of the public goods problem that would be difficult to conduct or infeasible using human subject experiments. Our ABM overcomes the shortcomings of experimental studies and extends the investigation of the effect of heterogeneous social preferences on the dynamics of voluntary contributions in a public goods setting.
Relatively few studies have considered the effect of social preferences and conditional cooperation on contributions to public goods using an integrated experimental-social simulation approach. The ABM in Lucas, de Oliveira and Banuri (2014) studies the effect of group compositions, which vary from completely homogeneous to completely heterogeneous agents, on contributions. The contribution of each social preference type is based on experimental data from Fischbacher and Gächter (2010). Social preference heterogeneity is found to have a negative impact on contributions. However, the dynamics of voluntary contributions, though an important dimension of the public goods problem, is not dealt with in the research conducted by Lucas et al. (2014).
Arifovic and Ledyard (2012) formulate a model in which social preference types can evolve in a learning process. Though their model replicates the decay phenomenon, as well as other observations in public goods experiments, their assumption concerning the stability of preferences is not corroborated by experimental evidence. Many experiments have demonstrated that social preferences are stable: agents’ intrinsic motivations do not change (Burlando & Guala 2005; Chaudri 2010; Kurzban & Houser 2005).
We began our research by conducting an experiment designed to elicit cooperative behavior. The data observed was then used to determine each subject’s social preference type. The experiment, based on a linear public goods game, replicates Fischbacher and Gächter (2010). Description of the public goods game, as well as the design and implementation of the experiment are presented in Section 2 of the paper. The procedure for classifying social preferences of experimental subjects is presented in Section 3.
In the simulation study, the ABM is intended to simulate the decisions of human subjects with different social preferences in a repeated public goods setting. It incorporates agents programmed to act according to social preference types observed in our experiment. Section 4 presents a description of the ABM and a comparison of experimental observations with simulations.
As stated above, the objectives of this paper is to extend and augment previous theoretical and experimental results on the public goods game. First, we examine steady state contributions in Section 5.1. A frequency distribution of simulated contribution levels is generated and a statistical analysis conducted to determine the likelihood of observing free-riding.
In a public goods setting, group composition influences long-run contribution levels. We consider how each agent type (representing a social preference type) influences contributions by varying its proportion in the population. Our simulations are meant to address questions related to critical proportions of each agent that drive the population towards free-riding. For example, we ask whether a small proportion of free-riders can drive the population to a state where contributions cease. These simulations and implications of the results are presented in sections 5.2 and 5.3.
A summary and implications of the results are presented in Section 6, which also includes suggestions for future research.
Experimental Procedure and Implementation
The experiment described in this section is based on the linear public goods game, using the voluntary contribution mechanism (VCM) (Ledyard 1995). In the public goods game, an individual, \(i\), is given an endowment, \(I\), and decides on its allocation between a private account and public account. The contribution to the public account, \(y_i\), \(i\) is made to maximize payoff. The payoff for individual \(i\) is: \(\pi_i=(I-y_i)+(\frac{a}{N})y\). In the equation \(y_i\) is the allocated amount to the public account; \(x_i=I-y_i\) is the amount allocated to the private account; and \(y=\sum_{i=1}^N y_i\) is the total contribution to the public account made by the \(N\) members in the group. The public account yields a return \(a\), and (\(a/N\)) represents the marginal per capita return (\(mpcr\)). When the marginal per capita return \(mpcr<1\) the individual has an incentive to keep all contributions in the private account.
In the experiment, the endowment is fixed for all participants and all decision periods at \(I=10\) tokens; group size is set at \(N = 4\); marginal per capita return is set at a fixed value of \(mpcr = 0.5.\)
The experiment, following Fischbacher and Gächter (2010), is divided into two phases. The first phase of the experiment (replicating Fischbacher et al. 2001) is dedicated to eliciting initial cooperative behaviors of subjects and consists of two stages: a one-shot VCM public goods game (the unconditional contribution round) and a contribution schedule or table (the contribution table stage). The aim of the unconditional contribution round is to determine initial contributions of subjects without subjects being given any information about their group. In the contribution table stage, subjects were asked to fill in a schedule of the amount they are willing to contribute to the provision of a public good given different hypothetical levels of average group contributions. The aim of this stage is to determine the conditional cooperative tendencies of subjects.
The second phase of the experiment is a standard repeated VCM public goods game. The subjects are randomly assigned to groups of size \(N=4\). The partners’ condition, in which subjects interact with the same group through all the decision periods, was used. This allows individuals to form strategies in a repeated public goods game and allows the experimenter to monitor such strategic moves. The repeated public goods game lasted for ten decision periods. Subjects were informed of the number in their group and marginal per capita return, but were not informed about the number of decision periods to observe the formation of strategies of participants independent of the end of termination effect. No communication was allowed during the experiment.
In each decision period, subjects were asked to report the amount he/she wants to contribute to the public account and their belief concerning the average contribution their group members are going to provide, which is assumed to be an important influence of subjects’ contributions. Subjects were left to decide, learn and form strategies throughout the ten decision periods until the experimenter announced the end of the decision rounds. At the end of each decision period, each participant was provided with information on the average contribution of the other three group members.
The repeated public goods game was followed by a questionnaire. In the questionnaire, participants provided standard socio-economic information such as gender, age and major field of study.
Seventy-two students from the Faculty of Economics and Political Science, Cairo University, were recruited for the experiment. Undergraduate students from all departments were invited to participate. Announcement for the experiment was made by e-mail. Registration for the experiment was through an online form. The experiment was conducted in six sessions and a pilot study session during a two-week period, from May 4th 2014 to May 15th 2014 at the Faculty of Economics and Political Science Research lab. The experimental software z-Tree (Zurich Toolbox for Ready-made Economic Experiments) was used for the experiment (see Fischbacher 2007). The control questions were presented in a separate program developed using Visual Basic.NET. Instructions were given in Arabic. Each session included twelve subjects divided into three groups of four. The sessions lasted around an hour and a half, and the average earnings for each participant was fifty Egyptian pounds including the show-up payment. To the best of our knowledge, students did not encounter any similar decision problems in their undergraduate studies and have no prior knowledge about the public goods game.
The majority of the participants (85%) were females. According to Ledyard (1995), gender does not yield any significant effect on the rates of contribution. In addition data analysis showed that the contribution behavior of males and females do not differ significantly. The age of participants ranged from 18 years to 22 years, with an average of 20 years.
Beliefs were found to be highly dependent on the previous period contribution of the other group members. There is a strong positive correlation between the average contributions and average belief of all subjects at each decision period (Spearman’s correlation coefficient = 0.9). Due to this high correlation, the choice to use one indicator (i.e. previous decision period average contribution) was made.
Classifying Social Preference Types
The objective in this section of the paper is to analyze the experimental data. The main purpose of this analysis is to determine the social preference type of each subject, which is a challenging task. The procedure we follow first classifies the social preference type from data observed in the contribution schedule (phase one of the experiment), then tests its consistency with data observed in the repeated experiment.
A subject is classified as a free-rider if the subject contributes 0 tokens at all or most levels of other group members’ average contribution, or contributes at most 1 token at some given levels of other group members’ average contribution. This definition is different from the strict definition of free-riding used by Fischbacher et al. (2001). However, this alternative definition is used for two reasons: there is an insignificant number of strict free-riders in the experiment and increasing the scale of free-riding makes it easier to observe the unraveling and decay of contributions. This alternative definition is used in experimental studies: Isaac and Walker (1988) define an individual as a free-rider if his/her contribution to the public good is less than one third of the endowment.
A subject is classified as a conditional cooperator if the subject’s contribution increases monotonically with the average contribution of other group members (Fischbacher et al. 2001). A subject is classified as a triangular or hump-shaped contributor if there is an increasing monotonic trend of contributions up to a certain level, then a decreasing monotonic trend of contributions (Fischbacher et al. 2001). Lastly, a subject whose contribution pattern does not follow any of the previously mentioned behaviors is classified as type “other”. Since “other” subjects show no particular contribution pattern, their contributions are considered random and hence are called random contributors in the model.
In our experiment, we report four types of conditional cooperators. Conditional cooperators who contribute the exact value of the average contribution of other group members are ‘perfect conditional cooperators’. Those who contribute an amount greater than, or equal to, average contributions are ‘above-diagonal conditional cooperators’. Conditional cooperators whose contribution is lower than, or equal to, average contribution are ‘below-diagonal conditional cooperators’. Finally, ‘alternating-diagonal conditional cooperators’ are conditional cooperators who contribute a value greater than the average contribution when the average contribution is less than half the endowment; and contribute a value less than the average contribution, when the average contribution exceeds half the endowment. It is worth noting that contributions of alternating-diagonal conditional cooperators are significantly different from triangular contributors, as their contribution still has a monotonically increasing relationship with the contribution of their group members[2]. Fischbacher et al. (2001) only report the first three types of conditional cooperators. Alternating-diagonal conditional cooperators have not been reported in any similar experimental studies.
Initial classification, using data from the contribution schedule (phase one), suggests that 8.3% of subjects are free-riders. This is remarkably less than that reported in Fischbacher et al. (2001), in which free-riders constitute approximately 30% of the subject pool. Herrmann and Thöni ( 2009) replicating the same experiment with Russian subjects report 6.3% free-riders, which is relatively close to the percentage found in our experiment. Conditional cooperators are the vast majority of the subjects (75%), while 5.6% are classified as triangular contributors. The remaining 11.1% are subjects with peculiar contribution patterns classified as others[3].
It is expected that actual contributions in the repeated public goods game for a subject will never be exactly the same as the expressed contribution in the contribution schedule. The individual’s response is inconsistent if his/her contribution pattern in the repeated game is different from the expressed contribution pattern in the contribution schedule at all levels. The second condition is that the values of actual contribution in the repeated game deviates by more than two tokens \(\pm 2\) at more than half of the levels of a given belief of others contribution.
Ten subjects displayed inconsistent contribution patterns (approximately 14% of the subjects). Those who displayed inconsistencies were free-riders, below-diagonal conditional cooperators and alternating-diagonal conditional cooperators. Inconsistent conditional cooperator subjects are found to fit better as another type of conditional cooperator. Table 1 shows the classification of subjects according to their initial cooperative preferences (i.e. phase one) as expressed in the contribution schedule and according the repeated public goods game (i.e. phase two) after reclassification of inconsistent subjects[4].
| Subject Type | Number of Subjects in Phase 1 | Number of Subjects in Phase 2 |
| Free-Riders | 6 | 5 |
| Conditional Cooperators | 54 | 55 |
| Perfect Conditional Cooperators | 3 | 3 |
| Above-diagonal Conditional Cooperators | 5 | 11 |
| Below-diagonal Conditional Cooperators | 25 | 24 |
| Alternating-diagonal Conditional Cooperators | 21 | 17 |
| Triangular Contributors | 4 | 4 |
| Other | 8 | 8 |
| Total | 72 | 72 |
The Agent-Based Simulation Model (ABM)
The agent-based model is designed to simulate the response of different social preference types observed in the repeated linear public goods game. The initial endowment, number of decision periods, profit return on one token invested in the public good and return on one token invested in the private good are set as the basic parameters in the model. The main assumption underlying this ABM is that strategies used by agents are the main determinant of the overall level of contribution to the public good. The ABM incorporates these different types of players by a set of programmed strategies based on the experimental data in the repeated experiment (phase two of the experiment)[5].
The model starts by creating an artificial society with a number of agents for each preference type as specified by the user. Agents are assumed to have stable social preferences, so the strategy of each agent remains unchanged throughout the simulations. Agents’ actions depend on their pre-programmed preference type and the average contribution of other group members in the previous decision period. Parameters used to simulate agent type are obtained from our experiment. The initial contribution level is set at the average contribution in the first decision period in the repeated public goods game. After an agent places its contribution in a given time period, it is informed about the average contribution of its group, and adjusts its contribution behavior accordingly for the following period. The total contribution and average contribution in each decision period are calculated and reported. The model is programmed using Netlogo 5.1.0. The pseudo code and functional forms of each strategy are presented in the (Appendix[6].
The programming of the model is followed by a thorough verification procedure to make sure that agents are programmed to accurately simulate real-life players and that there are no technical problems with the model (Sargent 2013). After verification of the model, validation of the model was conducted using the stylized facts of the public goods problem from experimental studies and the results of our experiment. Simulations show that the model is valid and capable of simulating real-life behavior.
A comparison between experimental and simulated average contribution levels over 10 decision periods is depicted in Figure 1. The simulated standard deviation at each period is also plotted. In the simulation, 72 agents are created using the classification of preference types of subjects in phase two of the experiment. Each agent receives an endowment of \(I = 10\) tokens at the beginning of every time period and the marginal per capita return is fixed at \(mpcr\) = 0.5. The simulation is run 1000 times.
Figure 1 shows that simulated contributions are comparable to the experimental values. The overall average contributions reported in the experiment and that generated by the simulation model are almost identical (2.25 tokens in the simulation compared to 2.27 tokens in the experiment). The ABM is able to adequately replicate our experimental results.

The Effect of Social Preference Types on Contributions
In this section of the paper, our focus is to determine the proportions of different preference types that cause the emergence of cooperation in a public goods dilemma. In Sections 5.3 - 5.8, we explore the discrepancy between the theoretical stipulation that voluntary contributions will reach free-riding with repetition in the public goods setting, and the experimental observations that report contributions do in fact decline with repetition but do not reach free-riding. In Sections 5.9 - 5.14, we analyze the effect of different proportions of one preference type in heterogeneous populations. Finally, in Sections 5.15 - 5.24, we examine the mutual interaction between two types of agents.
In the reported simulations, we choose populations of size \(N=100\) to ensure a fair representation of the different agent preference types and marginal per capita return \(mpcr = 0.5\). The endowment is fixed at \(I=10\) in each time period. We also choose to report results of 100 decision periods to ensure that populations have reached their steady state contribution level[7]. Each simulation with a given setting is run 1000 times and the average of the values is reported. This is done to ensure that the results reported are reliable and not affected by the random elements embedded in the behavior of our agents (Gilbert & Troitzsch 2005).
Predicting steady state contribution levels
One of the benefits of agent-based modeling is the ability to extend the analysis to longer runs. In Figure 2, we extend the previous simulation (depicted in Figure 1Figure 1) to 100 decision periods to investigate steady state contributions for a group with agent preference composition corresponding to our experiment. The average contribution level reaches a steady state of 2 tokens (for groups without random contributors) and 2.5 tokens (for groups with random contributors): this represents 10% and 15% above free-riding levels (the free-riding level is set at 10% of the endowment). It is worth mentioning that most of the fluctuations in contributions occur in the first 10 decision periods, after which the population settles onto the steady state.

An important issue from a theoretical perspective is whether decaying contributions converge to the Nash equilibrium (i.e. the free-riding level). Experimental results indicate that decay in contributions is greatest in the first few decision periods, but contributions do not reach the free-riding level (Ledyard 1995). Determining the range of final period contributions is a difficult task. From the experiments reviewed in Ledyard, final period contributions may be as low as 4% and as high as 37% of the endowment. Although the design of our experiment differs from experiments surveyed in Ledyard (1995), we refer to this literature due to the substantial number of initial experiments conducted on public goods. Experiments based on conditional cooperation with repetition are relatively few (Burlando & Guala 2005; Fischbacher & Gächter 2010). Fischbacher and Gächter (2010) report final period contributions, in their experiment, that range from 10% to 15% of the endowment[8].
To further explore the degree of corroboration between experiments and simulations, ten thousand simulations with randomly selected agent types were conducted (random contributors excluded). Each simulation encompasses 100 agents, each receiving an endowment of \(I = 10\) at the beginning of each period for 100 decision periods. The marginal per capita return is fixed at \(mpcr = 0.5\).
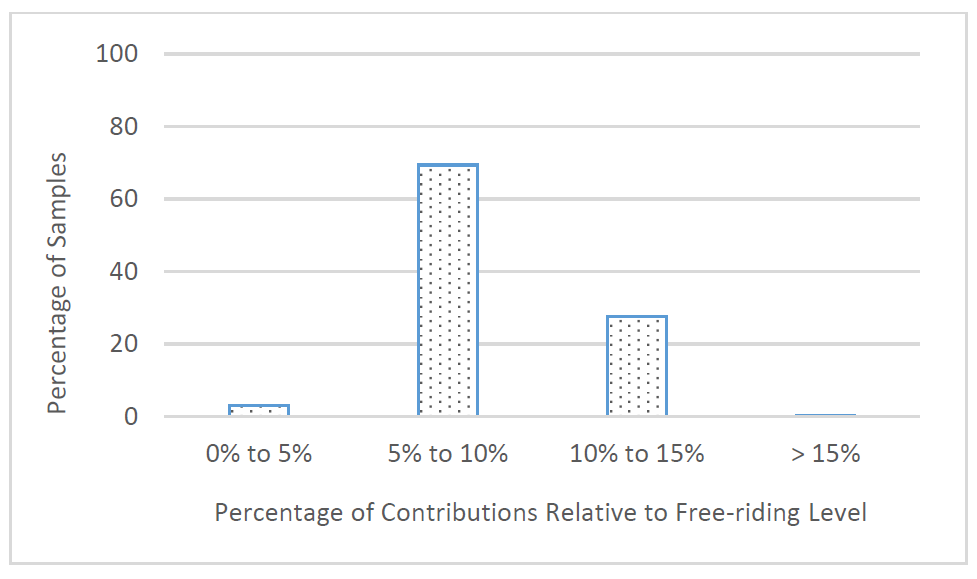
Figure 3 shows the probability distribution of steady state contributions (average of the final 5 periods) for the 10,000 populations. Approximately 3% of the populations have contributions 5% or less above the free-riding level. Almost 69.4% of the populations have steady state contributions between 5% and 10% above free-riding levels, 27.5% of the populations have contributions at 10% to 15% above free-riding levels and the small remaining percentage of populations reach a steady state that is more than 15% above the free-riding level.
To test whether the steady state contributions of our populations are significantly greater than the free-riding level, we conduct a one-sided t-test ((\H_0\): Steady state contribution \(~\leq~1\), (\H_a\): Steady state contribution \(~>~1\). The t-test confirms that the steady states of our simulations are statistically greater than the free-riding level (t-test, reject \(H_0\), p-value (\~<~\) 0.05). Our simulation results indicate that contributions do not reach the free-riding level and almost all populations have contributions between 5% and 15% above free-riding level.
Sensitivity analysis is an integral part of any simulation-based research. It concerns analyzing the robustness of the results to changes in its parameters (Gilbert & Troitzsch 2005). As expected marginal per capita return does not influence contributions in the simulations, since agents are responsive to each other’s contributions not their own payoff[9]. Simulations were conducted for groups of size of \(N=4\) and \(N=100\) agents. The marginal per capita return is fixed at a level of \(mpcr = 0.5\) for all group sizes. Small groups of size \(N = 4\) contribute more than groups of size \(N = 100\)[10]. In our simulations we set \(N=100\) to ensure a fair representation of each agent type. We expect that for any given group composition higher contribution levels would be observed for a small size group (\(N=4\)).
The effect of one type of agent on contributions levels
Having corroborated experimental results that steady state contributions rarely reach the free-riding level, we now study how different preference types contribute to this observation. For this purpose, we classify our agents into two categories based on their effect on contributions in a dynamic setting. Cooperation enhancing agents, whose actions increase contributions in a dynamic setting, are perfect conditional cooperators, above-diagonal conditional cooperators and alternating-diagonal conditional cooperators. Cooperation inhibiting agents, whose actions cause contributions to decline in a dynamic setting, are free-riders, below-diagonal conditional cooperators and triangular contributors. Random contributors are excluded from this classification and from the subsequent simulations.
In this section, we focus on the interaction of one type of agent in a heterogeneous population of randomly selected agent types. In particular, the aim is to investigate the minimal percentage in the population of cooperation inhibiting agents that leads to contributions decaying to the free-riding level. Likewise, we examine the effect of each of the cooperation enhancing agents in a heterogeneous population that keeps contributions above free-riding levels and that allow high cooperation levels to be sustained.
We use populations of size \(N = 100\) and fix the marginal per capita return at \(mpcr=0.5\). The initial endowment is fixed at \(I=10\) tokens for each decision period. We vary the percentage of each type of agent from 0% to 100%. The average contribution of the last five periods, when the population has reached a steady state, is plotted. Each simulation, with a single specified percentage of an agent type, is run a thousand times and the contributions reported are the average of these runs. The program determines the composition of the remaining population (excluding the agent type under examination) randomly.
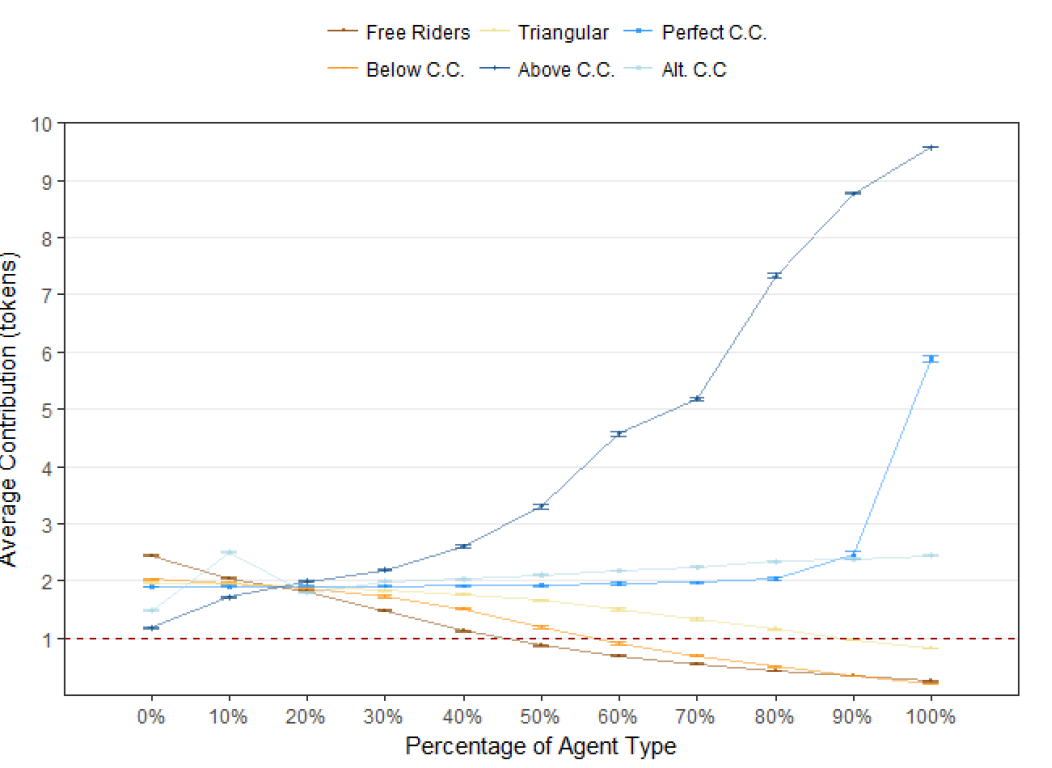
These simulations give us an indication of critical points when a specific agent type dominates contribution dynamics; in particular critical values at which contributions unravel towards the free-riding level. Figure 4 shows that contributions reach a free-riding level (average contribution less than one token) only when there is a high proportion of free-riders: more than 40%. A population where at least 60% of the agents are below-diagonal conditional cooperators will reach the free-riding zone. Triangular contributors also have a negative effect on contributions. A higher proportion, approximately 85% of triangular contributors pull contributions to the free-riding zone.
On the other hand, Figure 4 also shows that perfect conditional cooperators tend to retain contributions at a level near the initial contribution and increases contribution when they constitute more than 80% of the population. A small proportion, 5%, of above-diagonal conditional cooperators is sufficient to keep contributions above the free-riding level. Finally, only 10% of alternating-diagonal conditional cooperators can keep contributions above the free-riding level.
Our simulations provide insights to critical levels of each agent type required for contributions to reach free-riding levels. Experiments to determine the minimal percentage of each agent type in a heterogeneous population that lead to convergence to the free-riding level have not been conducted. This may be due to the extensive number of trials that would be required.
The effect of interaction between agent types on contribution levels
In the previous section, we managed to pinpoint the percentage of a specific agent type required to direct a heterogeneous population’s contribution to free-riding or to divert the population’s contribution from free-riding.
In this section, we consider a population consisting only of two agent types, and examine the effect of changing the proportion of each agent type on the contribution level. This exploration will help us understand how different agent types interact with each other and the critical points at which one type prevails and changes the course of contributions. We use a group size of \(N = 100\) agents and fix the marginal per capita return at \(mpcr = 0.5\). Initial endowment is fixed at \(I=10\) for each decision period. We vary the percentages of two types of agents from 0% to 100%. Each simulation run lasts for 100 time periods. The simulation is run 1000 times and the results reported are the average contribution of the one thousand simulation runs.
First, interaction between cooperation enhancing and cooperation inhibiting agents. Figure 5 shows the dynamic interaction between populations consisting of one cooperation enhancing agent type and each of the cooperation inhibiting agent types.
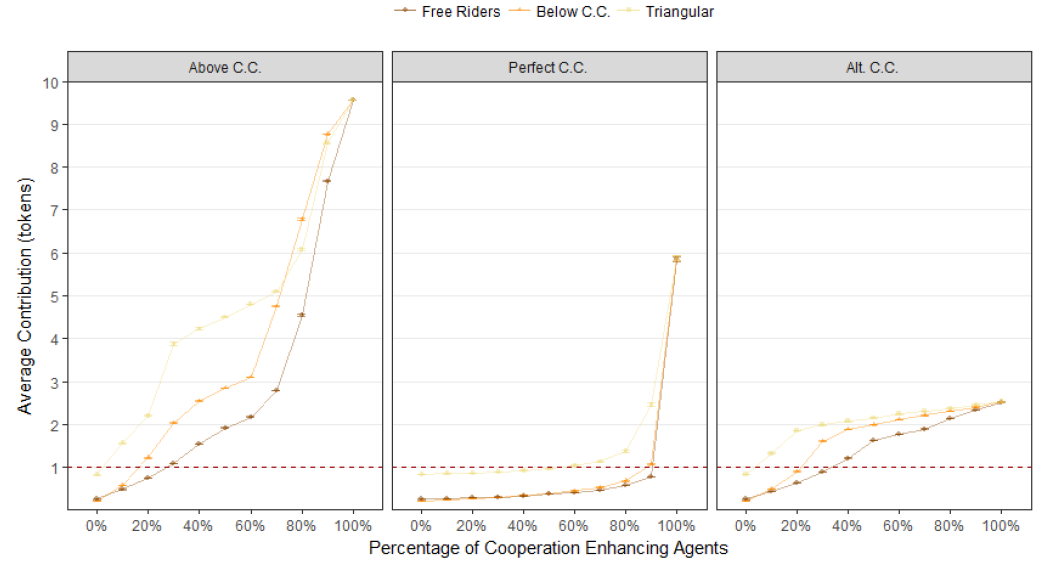
Above-diagonal conditional cooperators are the most cooperative agents and require a large percentage of cooperation inhibiting agents for free-riding to occur. Approximately 30% of above-diagonal conditional cooperators can keep a population of 70% free-riders above the free-riding level. Only 20% of above-diagonal conditional cooperators are required to keep a population with a majority of below-diagonal conditional cooperators above the free-riding level. Ten percent of above-diagonal conditional cooperators are required to rescue contributions in a population with a majority of triangular contributors from the free-riding zone.
Prefect conditional cooperators reciprocate uncooperative behaviour immediately A population with only 10% of free-riders or below-diagonal conditional cooperators (in a population with 90% perfect conditional cooperators) will bring contributions to a free-riding level. The unraveling of contributions towards free-riding is observed in populations with 30% or more of triangular contributors (i.e. equivalent to 70% or less of perfect conditional cooperators).
Alternating-diagonal conditional cooperators are the kind of cooperators who are helpful when contributions are low and opportunistic when contributions are high. A population with 30% or more alternating-diagonal conditional cooperators will keep contribution levels above free-riding when placed with free-riders or below-diagonal conditional cooperators. Only 10% of alternating-diagonal conditional cooperators in a population with triangular contributors will prevent contributions from unraveling towards free-riding.
Second, interaction within cooperation enhancing populations and within cooperation inhibiting populations. Figure 6 depicts the dynamic interaction within populations consisting of either two cooperation enhancing agent types or two cooperation inhibiting agent types.
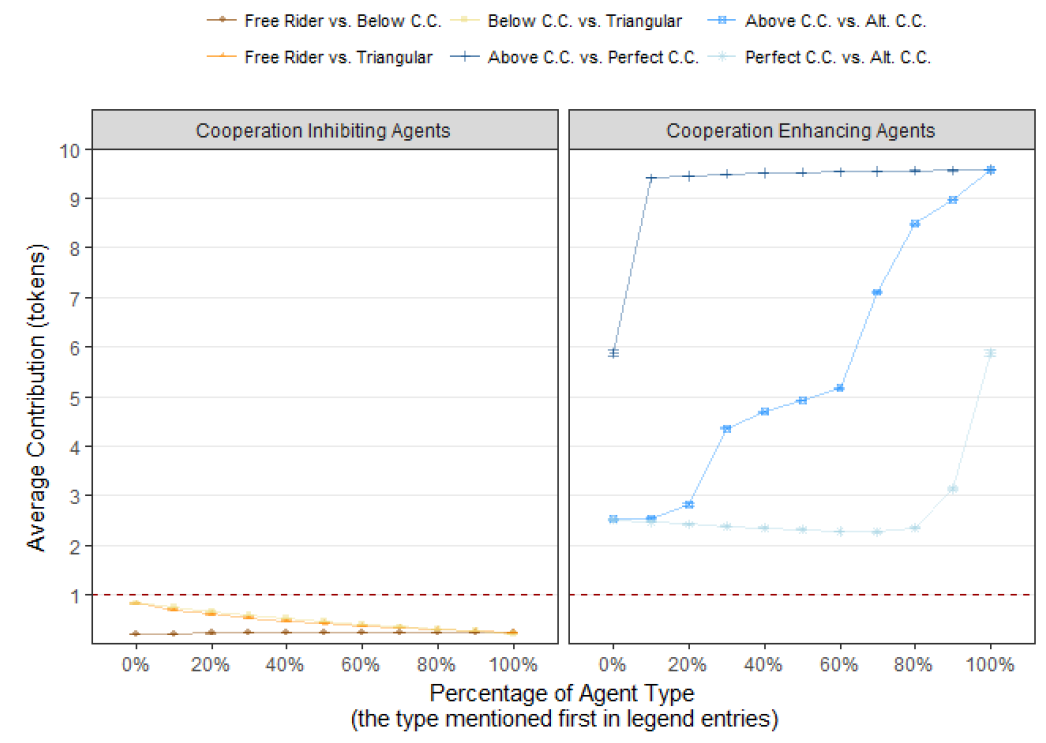
Steady state contributions are never above free-riding levels for any composition of a population consisting only of cooperation inhibiting agents.
In a population of perfect and above-diagonal conditional cooperators, altruism is observed as total contributions reach near the maximum level. For populations of above-diagonal and alternating-diagonal conditional cooperators high contribution levels are achieved in most cases. Finally, in a population of perfect and alternating-diagonal conditional cooperators, contribution stabilizes at 10% to 20% above the free-riding level.
In our simulations, we see that it is possible for populations of cooperation inhibiting agents to reach absolute free-riding levels and for populations with above-diagonal conditional cooperators to achieve altruism. These results confirm experimental observations. Burlando and Guala (2005) conducted an experiment to directly test the role of each preference type in decaying contributions in a public goods game. After subjects participate in a repeated public goods game within a heterogeneous group they are classified according to preference types. Subsequently, subjects were divided into homogeneous groups consisting only of their own preference type. In the free-rider group, convergence to the Nash equilibrium of zero contribution is observed. Groups of cooperators have much higher contribution levels than the heterogeneous population, reaching maximum possible contribution. Experiments to determine the interaction between two agent types have not been conducted. We need to consider, in future research, how to experimentally test the effect of various frequencies of each agent type on contribution patterns.
Conclusions
In this study the approach of combining experiments and agent-based models was used to enhance analysis on the public goods problem. Our research focused on the role of heterogeneous agents in explaining the dynamics of voluntary contributions to public goods. The aim of this research is to extend the scope of analysis on public goods not addressed by studies in the experimental literature. The main results of our study are mentioned in the following.
Our simulation results corroborate experimental observations. Simulation results demonstrate that contributions do not reach the free-riding level and are expected to be between 5% and 15% of income as suggested by experimental studies (Ledyard 1995). Our experiment replicates Fischbacher and Gächter (2010). Their analysis deals with determining the main factor responsible for the decay in contributions using econometric models which best fit their experimental data (see Fischbacher and Gächter 2010). Their results demonstrate that below-average conditional cooperators do indeed result in the decay phenomenon. However, their study does not deal with determining steady state contribution levels.
Simulations also demonstrate that the decay to free-riding occurs only in populations with a high proportion of cooperation inhibiting agents (more than 40% free-riders; almost 60% below diagonal conditional cooperators; and 90% triangular contributors). Free-riding is certain to occur only when all the population are cooperation inhibiting agents. These results contrast to Fehr and Schmidt's (1999) theoretical analysis. They show that only one free-rider can cause a large number of inequity-averse conditional cooperators to behave selfishly, and therefore, cause the emergence of free-riding behavior.
According to Fischbacher et al. (2001) the decay in contributions is the result of interaction between free-riders and below-diagonal conditional cooperators. The proportion of these different social preference types that ultimately lead to convergence to free-riding in the population was not considered. Our simulations investigated critical proportions of each social preference type agent that drive the population towards free-riding.
The simulation results suggest that conditions for the evolution of cooperation (denoted by positive contribution levels) are not stringent. A small proportion of contribution enhancing agents (for example 5% of above-diagonal conditional cooperators in a population) may be sufficient for the provision of public goods. Related research on social dilemmas also seems to support this observation. Using a different approach, Axelrod (1984) demonstrates that only a small proportion of cooperators, when interacting in clusters, is required for cooperation to emerge in a population of defectors in the prisoner’s dilemma game.
Our results are based on the assumption that artificial agents do not change their strategies. This assumption is based on experimental observations concerning the stability of social preference types. Previous studies have considered how contributions change when learning and evolutionary dynamics is included. When learning based on evolutionary principles is incorporated in the public goods model convergence to zero contribution levels is observed (Miller & Andreoni 1991). Other mechanisms such as punishment are required in an evolutionary model for positive contributions to public goods (Ye et al. 2011). Social structure has also been shown to have significant effects on cooperation among heterogeneous agents (Bravo, Squazzoni & Boero 2012). In future research we need to consider conditions that cause agents to change strategies and how contributions would change when learning, social structure and evolutionary dynamics are included.
Our analysis relied on social simulation and experiments, but we could also consider other approaches that integrate methodologies. Research on social dilemmas have integrated different methodologies to examine the problem of cooperation. In the analysis of the prisoner’s dilemma simulations of a replicator dynamic model used strategies that were submitted to participate in computer tournaments (Axelrod 1984).
The ultimate aim of our research is to understand factors that promote cooperation. Our ABM can be used as a building block of a more inclusive platform for studying different scopes of the public goods problem. Agents can be programmed to be responsive to factors such as social information and marginal per capita return. In addition, the model can be expanded to include other mechanisms in addition to the voluntary contribution mechanism, such as incorporating a provision point or including the possibility of punishment and communication.
Acknowledgments
We would like to express our gratitude and appreciation to the anonymous referees for their valuable and insightful comments and suggestions which considerably helped in improving the manuscript.Notes
- Non-parametric statistical tests are used to determine whether there is a statistically significant difference between the subcategories of conditional cooperators. Non-parametric tests do not assume the data is normally distributed. At a 95% confidence level, there is a significant difference between the four subcategories of conditional cooperators at each and every level of hypothetical average contribution of other group members (Kruskal Wallis H tests, p < 0.05). Tests are also conducted between pairs of subcategories. There is at least one value of hypothetical group average where the pairs of subcategories are significantly different from each other (Mann-Whitney tests, p < 0.05). These results confirm the validity of separate subcategories of conditional cooperators.
- There is a significant difference between the number of free-riders reported in Fischbacher et al. (2001) and other experiments (Fisher exact tests, p < 0.05). However, the percentage of free-riders in our experiment is not significantly different from that reported in Herrmann and Thoni’s (2009) (Fisher exact test, p = 0.58). The percentages of triangular contributors across different experiments are similar (Fisher exact tests, p > 0.05).
- McNemar tests are conducted to test if there are significant differences in the proportions of different preference types in phase one and after classification in phase two. The tests showed that there is a significant difference in the proportion of above-diagonal conditional cooperators in phase one and phase two (McNemar test, p < 0.05).
- Another model was developed using experimental data from the first phase of the experiment (unconditional contribution round and contribution schedule) and results of the simulations were generally similar. We choose to report the results of the model based on the second phase of the experiment (repeated public goods game).
- The model description, code, and experimental instructions can be found at https://www.openabm.org/model/5168/version/3.
- Simulations through 1000 and 2000 decision periods were conducted to determine if contribution pattern changes through extended decision periods. No change in the contribution pattern was detected, so we terminate our simulations at decision period number 100.
- Burlando and Guala (2005) do not indicate the value of contribution for heterogeneous groups in the repeated experiment.
- Since our artificial agents do not process payoffs, marginal per capita return should not have an effect on their decisions. Simulations conducted with different values of marginal per capita return (\(mpcr\) = 0.25, \(mpcr\) = 0.5, \(mpcr\) = 0.75) and different preference types, confirm that marginal per capita return, as expected, does not systematically affect contributions.
- The differences in contribution between different group sizes are found to be statistically significant (Kruskal Wallis, p-value < 0.05). Average contributions for group size \(N = 100\) is 1.9 tokens and for group size \(N = 4\) is 2.1 tokens which corresponds to 9% and 11% above the free-riding level (which in our case is 10%).
Appendix
Pseudo code of the dynamics of the simulation model.
Agents’ behaviours functional form
Let the average contribution of other group members in a previous time period be \(v_{t-1}\); the initial endowment granted to each agent at each time period be \(I\) tokens (\(I=10\) in the experimental study).
Free riders
The probability of not contributing to the public good at any given time period be \(l\), where \(l\) follows a continuous uniform distribution from 0 to 1. Then the contribution function at time period \(t\) will be:
| $$Contribution_t= \begin{cases} 0 & \text{when}\,\, l\leq 0.75\,\forall\, v_{t-1}\\ 1 & \text{when}\,\, l> 0.75\,\forall\, v_{t-1}\\ \end{cases}$$ | (1) |
Perfect conditional cooperators
| $$Contribution_{t=1}=\biggl\{uniform\biggl(0,\frac{1}{2}\biggr)\biggr\}$$ | (2) |
| $$Contribution_{t>1}=\{v_{t-1}+Normal(0.04,0.4)\,\,\text{when}\,\,0\leq v_{t-1}\leq I\}$$ | (3) |
Above-diagonal conditional cooperator
| $$Contribution_{t=1}=\{Normal(3.8,4.2)\} $$ | (4) |
| $$Contribution_{t>1}= \begin{cases} v_{t-1}+Normal(1.9,4.84) & \text{when}\,\, 0\leq v_{t-1}\leq 0.2I\\ v_{t-1}+Normal(1.09,3.24) & \text{when}\,\, 0.2T < v_{t-1}\leq I\\ \end{cases} $$ | (5) |
Alternating-diagonal conditional cooperator
| $$Contribution_{t=1}=\{Normal(3.2,3.61)\}$$ | (6) |
| $$Contribution_{t>1}= \begin{cases} v_{t-1}+Normal(1.25,5.07) & \text{when}\,\, 0\leq v_{t-1}\leq 0.2I\\ v_{t-1}+Normal(-0.4,4) & \text{when}\,\, 0.2T < v_{t-1}\leq 0.5I\\ v_{t-1}+Normal(-2.2,6.76) & \text{when}\,\, 0.5T < v_{t-1}\leq 0.9I\\ v_{t-1}+Normal(-3.7,14.44) & \text{when}\,\, v_{t-1}=I\\ \end{cases} $$ | (7) |
Below-diagonal conditional cooperator
| $$Contribution_{t=1}=\{Normal(2.7,4.84)\} $$ | (8) |
| $$Contribution_{t>1}= \begin{cases} v_{t-1}+Normal(-0.7,1.15) & \text{when}\,\, 0 \leq v_{t-1}\leq 0.3I\\ v_{t-1}+Normal(-2.3,1.96) & \text{when}\,\, 0.3T < v_{t-1}\leq 0.5I\\ v_{t-1}+Normal(-4.07,5.29) & \text{when}\,\, 0.5T < v_{t-1}\leq I\\ \end{cases} $$ | (9) |
Triangular contributors
| $$Contribution_{t=1}=\{Normal(2.4,3.61)\}$$ | (10) |
| $$Contribution_{t}= \begin{cases} v_{t-1}+Normal(-0.4,2.25) & \text{when}\,\, 0 < v_{t-1}\leq 0.5I\\ v_{t-1}+Normal(-5.2,12.96) & \text{when}\,\, 0.5T < v_{t-1}\leq I\\ \end{cases} $$ | (11) |
Random contributors
| $$Contribution_t=Uniform(0,10)\,\,\text{when}\,\,0\leq v_{t-1}\leq I $$ | (12) |
References
ABDOU, M., Hamill, L., & Gilbert, N. (2012). 'Designing and Building an Agent-Based Model.' In A. J. Heppenstall, A. T. Crooks, L. M. See, & M. Batty (Eds.), Agent-Based Models of Geographical Systems. Heidelberg: Springer Netherlands,141–165. [doi:10.1007/978-90-481-8927-4_8]
ANDREONI, J. (1988). Why Free Ride? Strategies and Learning in Public Goods Experiments. Journal of Public Economics, 37, 291–304.
ARIFOVIC, J., & Ledyard, J. (2012). Individual evolutionary learning, other-regarding preferences, and the voluntary contributions mechanism. Journal of Public Economics, 96(9-10), 808–823. [doi:10.1016/j.jpubeco.2012.05.013]
AXELROD, R. (1984). The Evolution of Cooperation. Basic Books, New York.
BOERO, R., Bravo, G., Castellani, M., & Squazzoni, F. (2010). Why Bother with What Others Tell You? An Experimental Data-Driven Agent-Based Model. Journal of Artificial Societies and Social Simulation, 13 (3), 6: https://www.jasss.org/13/3/6.html. [doi:10.18564/jasss.1620]
BRAVO, G., Squazzoni, F., & Boero, R. (2012). Trust and partner selection in social networks: An experimentally grounded model. Social Networks, 34(4), 481–492. [doi:10.1016/j.socnet.2012.03.001]
BURLANDO, R. M., & Guala, F. (2005). Heterogeneous Agents in Public Goods Experiments. Experimental Economics, 8(1), 35–54. [doi:10.1007/s10683-005-0436-4]
CHAUDHURI, A. (2011). Sustaining Cooperation in Laboratory Public Goods Experiments: A Selective Survey of the Literature. Experimental Economics, 14(1), 47–83.
DAL FORNO, A., & Merlone, U. (2004). From classroom experiments to computer code. Journal of Artificial Societies and Social Simulation,7(3), 2: https://www.jasss.org/7/3/2.html.
DAWES, R. M. (1980). Social Dilemmas. Annual Review of Psychology, 31(1), 169–193.
DUFFY, J. (2006). 'Agent-based Models and Human Subject Experiments.' In L. Testfatsion & K. L. Judd (Eds.), Handbook of Computational Economics, Volume II. Amsterdam: North Holland, pp, 949–1011. [doi:10.1016/S1574-0021(05)02019-8]
FEHR, E., & Schmidt, K. (1999). A theory of fairness, competition, and cooperation. The Quarterly Journal of Economics, 114(3), 817–868.
FISCHBACHER, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178. [doi:10.1007/s10683-006-9159-4]
FISCHBACHER, U., & Gächter, S. (2010). Social Preferences, Beliefs, and the Dynamics of Free Riding in Public Goods Experiments. American Economic Review, 100(1), 541–556.
FISCHBACHER, U., Gachter, S., & Fehr, E. (2001). Are People Conditionally Cooperative ? Evidence from a Public Goods Experiment. Economics Letters, 71, 397–404. [doi:10.1016/S0165-1765(01)00394-9]
GILBERT, N., & Troitzsch, K. G. (2005). Simulation for the Social Scientist (Second Ed). London: Open University Press.
HELBING, D., & Balietti, S. (2011). How to Do Agent-Based Simulations in the Future: From Modeling Social Mechanisms to Emergent Phenomena and Interactive Systems Design, Santa Fe Institute Working Paper No. 2011-06-024, Santa Fe Institute.
HERRMANN, B., & Thöni, C. (2009). Measuring conditional cooperation: a replication study in Russia. Experimental Economics, 12(1), 87–92.
ISAAC, R., & Walker, J. (1988). Group size effects in public goods provision: The voluntary contributions mechanism. The Quarterly Journal of Economics, 103(1), 179–199. [doi:10.2307/1882648]
JANSSEN, M A & Ahn, T K (2006). Learning, signaling, and social preferences in public-good games. Ecology and Society, 11(2) 21: https://www.ecologyandsociety.org/vol11/iss2/art21/.
KESER, C., & Winden, F. Van. (2000). Conditional Cooperation and Voluntary Contributions to Public Goods. The Scandinavian Journal of Economics, 102(1), 23–39. [doi:10.1111/1467-9442.00182]
KOCHER, M. G., Martinsson, P., Matzat, D., & Wollbrant, C. (2015). The role of beliefs, trust, and risk in contributions to a public good. Journal of Economic Psychology, 51, 236–244.
KURZBAN, R., & Houser, D. (2005). Experiments investigating cooperative types in humans: a complement to evolutionary theory and simulations. Proceedings of the National Academy of Sciences of the United States of America, 102(5), 1803–7. [doi:10.1073/pnas.0408759102]
LEDYARD, J. O. (1995). 'Public Goods: A Survey of Experimental Research.' In A. E. Roth & J. Kagel (Eds.), Handbook of Experimental Economics. Princeton, NJ: Princeton University Press.
LUCAS, P., de Oliveira, A. C. . M., & Banuri, S. (2014). The Effects of Group Composition and Fractionalization in a Public Goods Game An Agent-Based Simulation. Journal of Artificial Societies and Social Simulation, 17(3), 5: https://www.jasss.org/17/3/5.html.
MILLER, J. H., & Andreoni, J. (1991). Can evolutionary dynamics explain free riding in experiments?. Economics Letters, 36(1), 9-15.
SARGENT, R. G. (2013). Verification and validation of simulation models. Journal of Simulation, 7(1), 12-24. [doi:10.1057/jos.2012.20]
WENDEL, S., & Oppenheimer, J. (2010). An agent-based analysis of context-dependent preferences. Journal of Economic Psychology, 31(3), 269–284.
YE, H., Tan, F., Ding, M., Jia, Y., & Chen, Y. (2011). Sympathy and Punishment: Evolution of Cooperation in Public Goods Game. Journal of Artificial Societies and Social Simulation, 14(4), 20: https://www.jasss.org/14/4/20.html. [doi:10.18564/jasss.1805]
