This article is in memoriam of Rosaria Conte (1954-2016).
Introduction
Social influence is a pervasive force in human social interaction. In many social encounters, individuals modify their opinions, attitudes, beliefs, or behavior towards resembling more those of others they interact with. Individuals are socially influenced because they are persuaded by convincing arguments (Myers 1982), because they seek to be similar to others (Akers et al. 1979), because they are uncertain about a decision and follow the lead of others (Bikhchandani, Hirshleifer and Welch 1992), or because they feel social pressure to conform with social norms (Festinger, Schachter and Back 1950; Homans 1950; Wood 2000).
Despite much research, social influence remains one of the most puzzling social phenomena. On the one hand, empirical studies across a variety of areas have documented how social influence reduces differences between people, as has been found in experiments on conformity (Asch 1956), research on small group behavior (Sherif and Sherif 1979), persuasion (Myers 1982), innovation diffusion (Rogers 1995), the influence of mass media (Katz and Lazarsfeld 1955) or online social networks (Bond et al. 2012). On the other hand, there is a long-lasting debate about the complex dynamics that social influence in interpersonal interactions generates on the collective level (Mason, Conrey and Smith 2007). For one thing, while assimilation seems to be the predominant pattern in interpersonal interactions, people may not only influence each other to become more alike, but also sometimes reject attitudes or behavior of those they interact with, and even seek to become more different from them (Hovland, Harvey and Sherif 1957). However, there is much uncertainty about the exact conditions and mechanisms that elicit assimilation or differentiation in interpersonal influence (Takács, Flache and Mäs 2016), and about how these processes recombine in generating opinion dynamics at the macro-level of groups, organizations, or societies at large.
The complex relationship between social influence as a micro-level process and its macro-consequences for consensus or divisions in society resonates in classic as well as highly contemporary debates in the social sciences. A first example is Durkheim’s classical analysis of social integration in the face of increasing societal differentiation as society moves into modernity (Elias 1978; Durkheim 1982 [1895]; Mäs, Flache and Helbing 2010; Turner 1995). Durkheim argued that consensus in individuals’ opinions and values depends on a cohesive society that exposes its members to highly similar social influences. However, as a society modernizes, Durkheim believed, it may also become less cohesive, for example because economic differentiation and division of labor makes people’s social roles and living situations increasingly different from each other. What then are the conditions and mechanisms that prevent increasing disagreement on fundamental norms and values between members of a society?
A second example is the question why there is cultural differentiation, which is essentially Axelrod’s question. Theorists of cultural differentiation (Bourdieu 1984 [1979]) aimed to understand how cultural differences and boundaries between societal groups, like between an upperclass "high-brow" culture and a lower class "low brow" culture, emerge and are maintained although there is interaction between members of different classes in which social influence could reduce these differences. A third, highly contemporary, debate is whether and under what conditions societies polarize, falling apart into a small number of deeply antagonistic factions, with ever increasing differences between them, as some observers note for the current political landscape of the U.S. (Abramowitz and Saunders 2008; DiMaggio, Evans and Bryson 1996; Evans 2003; Fiorina and Abrams 2008; Gentzkow 2016) and many other Western societies. Based on extensive empirical studies of opinion formation at the community level in the U.S., Abelson (1964) noted already five decades ago the prevalence of polarization but failed to reconcile this pattern with models in which social influence was described as reducing rather than amplifying opinion differences. Abelson famously wondered "what on earth one must assume in order to generate the bimodal outcome of community cleavage studies" (p. 153). Echoing this question, Bonacich and Lu (2012) recently included explaining "how groups become polarized or how two groups can become more and more different" (p. 216) in their list of important unsolved problems of sociology.
Such questions cannot be answered by empirical studies alone, but require theoretical modelling. The evolution of a distribution of political opinions observed in a society results from numerous simultaneous interactions between individuals, typically connected by heterogeneous social networks and embedded in diverse local and socio-demographic contexts. Most importantly, social influence dynamics can give rise to complex micro-macro links in which the societal outcome of individual interactions can be unexpected and unintended from individuals’ point of view. Identifying the conditions and mechanisms of consensus, diversity and polarization in large-scale social-influence dynamics is therefore a major scientific issue with a long tradition of vivid debate (Mason et al. 2007).
The earliest formal models of the dynamics of opinion formation in a group were inspired by conformity experiments (Abelson 1964; French 1956; Harary 1959). They took as basic building block the assumption that if two members of a group interact "each member of the group changes his attitude position towards the other by some constant fraction of the ‘distance’ between them" (Abelson 1964). It could then be shown analytically for a broad class of models of this type that repeated social influence always leads to consensus of all group members unless the network of interactions consists of perfectly disconnected subgraphs (Abelson 1964; Berger 1981; DeGroot 1974; Harary 1959; Lehrer 1975). This can explain why many groups often have consensus on a lot of issues - a fact that is often overlooked because these issues are not matter of contention anymore. But the result also seems to be in striking contrast to many empirical cases social scientists have studied in the field.
Neither small groups, organizations, neighborhoods, nor society at large exhibit an inevitable tendency towards perfect consensus on all issues, as examples from group discussion experiments as well as studies of political, social, and cultural views demonstrate (Glaeser and Ward 2006; Liu and Srivastava 2015; Mark 2003). Studies of college dormitories (Feldman and Newcomb 1969), international work teams (Earley and Mosakowski 2000), representative opinion surveys on controversial issues in the public debate (Abramowitz and Saunders 2008; Evans 2003; Levendusky 2009) and experiments even suggest that influence dynamics sometimes result in gradually increasing dissimilarity and polarization (Mäs and Flache 2013; Moscovici and Doise 1994). This contrast between results from early formal models of social influence dynamics and empirical evidence led Axelrod to formulate the question why not all differences eventually disappear if social influence reducing differences between people is such a pervasive force in social interaction (Axelrod 1997)?
Neither Axelrod, nor any of his predecessors, did of course believe that real social-influence dynamics consist of nothing else but of repeated encounters in which any two individuals become more alike every time they interact. In the real world, networks are not always connected, social influence is sometimes rejected, individuals’ views may be deeply entrenched on some issues and open to influence on others, and at the societal level mass media, divisive political propaganda or dividing lines between different group identities may curb the assimilating forces of interpersonal social influence. Agent-based modelling is a method that has the potential to rigorously explore the complex dynamics that may result from the interplay of all these factors with different fundamental influence mechanisms in interpersonal interactions.
As Chattoe-Brown (2014) points out, such models have the ability to separate calibration (empirically justifying, for example, assumptions about individual behavior) from validation (empirical testing of model implications, establishing how well simulated data match corresponding real data). Models can thus be built "representing social actors directly [...] as they interact with each other and with their environment" (p. 2). In this way, agent-based modelling holds the promise to provide models that are not only descriptive of interpersonal influence dynamics as they occur in real-world settings at the micro-level, but also can "grow" from these assumptions patterns of opinion diversity and their association with context variables (e.g. group size or initial diversity) observed at the macro-level of a group, organization, or society that the model targets. Agent-based models of empirically observed social-influence dynamics could thus move beyond the correlational explanations conventional empirical research can offer and meet instead the necessary criterion for a complete scientific explanation that Epstein famously formulated in his "bumper sticker reduction of the agent-based computational model", "If you didn’t grow it, you didn’t explain it" (Epstein 1999).
For this promise to be fruitfully realized, however, agent-based modelers need to have a solid understanding of how each of the many factors and mechanisms that could affect the outcomes of social influence in the real world interact separately and simultaneously with simple "first principles" (Mark 1998) of interpersonal social interaction. As Macy and Flache (2009) put it, rephrasing Epstein, "If you don’t know how you grew it, you didn’t explain it." (p. 63). We thus believe that in order to understand how and why empirically calibrated models may or may not succeed in reproducing social influence dynamics in real life, agent-based modelers should have a good overview over the main approaches to modelling social influence in the literature and how they relate to the more specific models that have been proposed. In this paper, we start from an overview over the main approaches trying to answer Axelrod’s question building on "first principles". We show that extensions of the early formal models of social influence developed in recent decades cannot only generate the emergence of persistent opinion diversity, but also patterns of collective extremization, stable diversity in form of clustering of opinions, or polarization of a population into two or more antagonistic factions with large and possibly increasing opinion differences between them alongside strong internal consensus.
In what follows, we discuss the main theoretical ingredients that have been added to the early models, and show why they generate different outcomes. Notwithstanding some exceptions (e.g. Brousmiche et al. 2016, 2017; Deffuant, Huet and Skerratt 2008); most of the work in the literature pursues the theoretical goal of identifying conditions for consensus, clustering or polarization that emerge from fundamental micro-processes of social influence. However, this does not mean that these models have not been calibrated to empirical data whatsoever, or that their outcomes have not been compared to empirical evidence. In many contributions authors derive the theoretical assumptions they make both from fundamental psychological theories about social influence and from empirical evidence, thus ‘calibrating’ models in a broad sense. Similarly, in many papers outcomes of social influence dynamics observed in experiments or field data are used to assess at least qualitatively the plausibility of model predictions, thus aiming at ‘validation’ of models in a loose sense. To show this, we discuss for each the classes of models the theoretical and empirical foundations on which they draw, which qualitatively distinct outcomes in opinion distributions they aim to generate, and how they have served as basis for follow-up work including further factors such as media influence, heterogeneous networks or different forms of social influence co-occurring at the micro level.
Yet, despite all advances, we conclude from our overview that the agent-based modelling literature still cannot offer reliable explanations and predictions for concrete real-life influence dynamics a researcher may be interested to study, a situation that has not much changed since nearly a decade ago an earlier review of the field came to a similar conclusion (Sobkowicz 2009). One reason for this is that, as we discuss in Section 3, the field needs to move forward towards calibration and validation of models in a more precise sense, linking models and data on a more detailed level. Another, related problem is that the literature provides many explanations for many possible collective dynamics of opinions, beliefs, or behavior. Despite efforts to gradually extend models, much remains unclear about which model ingredient or which combination of them might be the most useful one to ‘grow’ a given empirical phenomenon observed in a particular context with a particular type of data available, like for example the increasing polarization observed in surveys on political issues in recent years in the U.S. (Gentzkow 2016), the increasing acceptance of homosexual relations found in U.K. surveys since the early 2000’s (Chattoe-Brown 2014), or the dynamics of opinions subjects express in a small-scale group discussion experiment (e.g. Moussaïd et al. 2013).
A central challenge for the development of social-influence models is that a model that in one setting accurately describes opinion shifts resulting from influence may fail to capture social influence in another setting. For instance, empirical research suggests that individuals are more open to voicing their opinions in computer-mediated than in face-to-face interaction (Ho and McLeod 2008) and that social influence is stronger in face-to-face interaction (Sassenberg, Boos and Rabung 2005). This implies that a model that was not empirically supported in a given setting may still accurately describe empirical patterns found in another one. We believe researchers should follow a "middle-range approach" (Hedström and Ylikoski 2010; Merton 1957), in which the choice of assumptions about social influence is guided by theoretical and empirical arguments specifying why a particular assumption is considered plausible in a given setting. Furthermore, both the assumptions made in a model and empirical predictions a model generates should be confronted with data available for the specific social setting a modeler wants to address.
Next to a need for more empirical grounding, another challenge the field faces in our view is insufficient theoretical integration and comparison of a multitude of different modelling approaches. Still very little is known about the dynamics resulting from two or multiple model ingredients acting in tandem. These gaps in the understanding of influence dynamics leave the modeler of a given real-life setting with a long list of alternative model assumptions and qualitatively different sets of parameter values that can be included in her model. As even very subtle and seemingly innocent changes in the assumptions in social-influence models can have profound and unexpected effects on model predictions, the modeler’s ability to derive precise and reliable predictions is highly limited. This leads us, finally, to propose frontiers for future research on models of social influence dynamics. Future work should move towards these frontiers with theoretical as well as empirical research, and with addressing new practical applications of social influence models.
Ideal Typical Models and Outcomes
Here, we review the literature on social influence models. Given the huge number of modelling studies in the literature, it is impossible to do justice to every contribution. Nevertheless, we argue that large parts of the literature can be categorized into three classes of models
Models were grouped into the same class if their theoretical assumptions about social influence were formally implemented in a similar way and, therefore, lead to similar answers to Axelrod’s question. Models within the same category may represent different social contexts and may be based on different theories about social influence, but the formal implementation of these theories gives rise to similar fundamental dynamics and conditions for different forms of opinion diversity.
Our review covers influence models with continuous as well as nominal traits representing opinions. In the early influence models developed in the 1950 and 60s (Abelson 1964; Berger 1981; DeGroot 1974; French 1956; Harary 1959; Lehrer 1975), actors are socially influenced in the position they take on a continuous spectrum representing their "opinion" on some issue, for example their stance on what the appropriate speed on a highway should be. In what follows, we likewise use the term "opinion" for the agent’s property that is affected by social influence in a model. However, opinion should be seen as a generic concept that can also represent a belief (e.g. What is the average speed of all cars driving in a highway?) or a behavior (e.g. How fast does the actor actually drive on highways?), or an attitude (e.g. How good or bad is it to drive at a given average speed on highways?). To paraphrase Axelrod (1997), an opinion "is taken to be what social influence influences" (p. 207). A later generation of modelers assumed instead that opinions do not vary on a continuous scale, but model the choice between distinct options, like a person's favorite political party, music band, or movie genre (Axelrod 1997; Latané 1996; Liggett 1985; Sznajd-Weron and Sznajd 2000). Some modelers see such ‘nominal traits’ as a simplified representation of underlying continuous dimensions (Nowak, Szamrej and Latané 1990). While the assumed scale of the influence dimension can alter model predictions decisively in some cases (e.g. Flache, Macy and Takács 2006), often fundamental results for models belonging to the same class generalize, as we show below.
Our review does not cover so-called diffusion or contagion models (e.g. Valente 1996). These models describe processes in which some entity, like a virus, or a piece of information spreads in a network through ‘contagion’, a process that is unidirectional. In models of virus diffusion in networks, for instance, an actor carrying a virus can infect her network contacts, but these contacts cannot heal their infected contact. Likewise, a person who is unaware of the existence of a new product can be informed about the product but the person cannot erase the memory of others. In contrast, the models that we review assume bi-directional influence, in that they do not assume that influence acts only in one direction. Note that the information or virus diffusion models should not be confused with innovation diffusion models. Indeed, the diffusion of innovations is a more complicated process than the diffusion of information or viruses and its models generally include attitude or opinion dynamics such as the ones described below (e.g. Deffuant, Huet and Amblard 2005; Deffuant, Huet and Skerratt 2008; Valente 1995).
Social influence on the micro-level can result in various macro-structures and dynamics of opinion distributions, as documented by empirical research across various contexts, such as work teams (Earley and Mosakowski 2000), groups of college students (Feldman and Newcomb 1969), school classes (Pearson, Steglich and Snijders 2006), society at large (Abramowitz and Saunders 2008; DiMaggio et al. 1996; Fiorina and Abrams 2008) and in the laboratory (Mäs and Flache 2013). Figure 1 illustrates three distinct ideal-typical opinion dynamics for continuous opinions that received much attention in the modeling literature. Some other patterns will be discussed elsewhere in this paper. To generate the figure we used the illustrative models that we formally define in the remainder of this section (Equations 1-5).
First, reflecting Durkheim’s concern with societal integration, models can describe the formation of a collective consensus from initial disagreement. Figure 1a shows how such a consensus emerges on a ‘moderate’ position close to the mean initial opinion in the population. However, sometimes a pattern called "group polarization" (Myers and Lamm 1976) in social psychology occurs, when a group moves towards a consensus that is more extreme than most or even all of the views individuals held prior to being exposed to social influence (Moscovici and Zavalloni 1969; Myers 1978). Below we discuss how this emergence of an extreme consensus was likewise addressed with formal models. Second, as a potential answer to Bourdieu’s (and Axelrod’s) question how social differentiation can persist, models were developed that can generate opinion clustering. Figure 1b shows such a process in which a population with initially uniformly randomly distributed opinions divides into multiple internally homogenous but mutually distinct clusters in the opinion spectrum. Third, while opinion clustering does not necessarily imply sharp differences between subgroups, modelers also addressed Abelson’s question of how processes of polarization could be understood (called bi-polarization hereafter to distinguish this from the concept of "group polarization" which describes the formation of an extreme consensus). Figure 1c illustrates such a dynamic. It shows how bi-polarization is distinct from opinion clustering in that from a random start the population increasingly falls apart into two factions with disagreement between them eventually growing towards the theoretical maximum
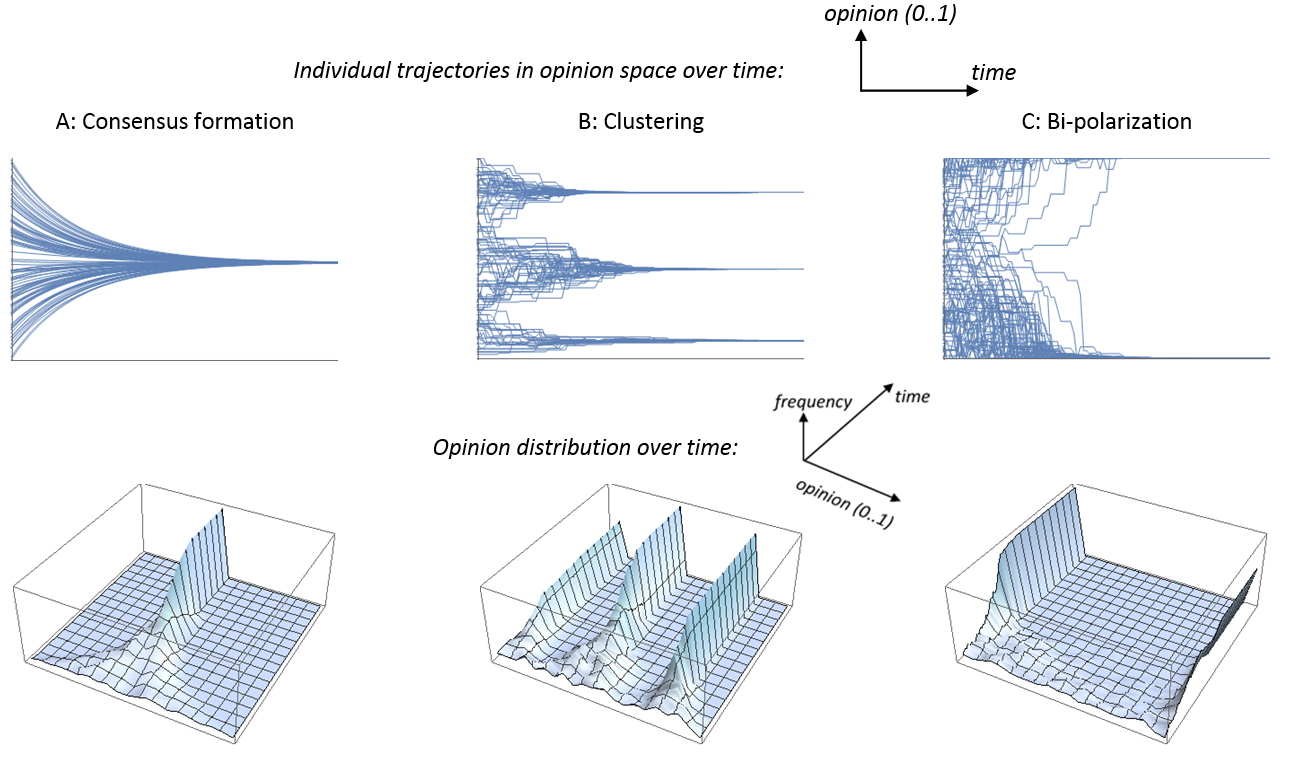
Table 1 provides an overview over the three classes of models that we distinguish. In the following subsections, we illustrate for each class the main idea with a simple illustrative model, discuss alternative theoretical and empirical arguments underlying the models assigned to each class, and main results as well as different versions and extensions implementing the same core principles. Drawing on the classical models of the 1950s and 60s, we use continuous opinions for the illustrative models that we present.
While our three ideal-types of models capture a large part of the literature, they are not exhaustive. For instance, many contributions to the literature combine assumptions from multiple ideal types. Yet, we believe that a good understanding of the characteristic behaviors of each type of model is indispensable for understanding the dynamics of combined models, too. Furthermore, our synthesis of the literature identifies critical assumptions and central predictions of existing models and, therefore, proposes perspectives for future empirical and theoretical research on social-influence dynamics that we discuss in Section 3 of this paper.
| Model class | Core assumption | Core result |
| Models of assimilative social influence | Individuals connected by a structural relationship always influence each other towards reducing opinion differences. | If relationships form a connected network, influence dynamics (with continuous opinions) inevitably generate consensus in the long run. |
| Models with similarity biased influence | Only sufficiently similar individuals can influence each other towards reducing opinion differences. How much similarity is sufficient depends on additional psychological mechanisms (e.g. social identity, confidence in others). | Consensus can be avoided. If the similarity bias is sufficiently strong, then multiple homogenous but mutually different clusters emerge (fragmentation). Opinions, however, never leave the initial range. |
| Models with repulsive influence | When individuals are too dissimilar (in some models on a specific opinion dimension) they can also influence each other towards increasing mutual opinion differences (repulsive influence). How much dissimilarity is needed to trigger repulsive influence depends on additional psychological mechanisms (e.g. social identity, "ego-involvement"). | Consensus can be avoided. Clusters form and may even adopt maximally opposing views (bi-polarization). Opinions can leave the initial range. |
Models of assimilative social influence
Main idea
The central building block of models in this class is the assumption that if two individuals are connected by an influence relationship, they will always exert influence on each other towards reducing their opinion differences (assimilation). Note, however, that while the network of influence relationships is assumed to be structurally given and fixed in these models, it is not excluded that social influence can be ineffective. Influence does not result in opinion adjustments, for instance, when an actor is exposed to influences from multiple sources that cancel each other out, or when the influence exerted by an actor is superseded by more influential parties. However, models of assimilative influence share the assumption that actors connected by an influence relationship would always grow more similar if there were no such third-party effects.
Theoretical and empirical justifications
Models of assimilative influence have been developed based on various theoretical and empirical lines of research. Cognitive theories emphasized that when interaction partners discuss an issue they persuade each other (Myers 1982; Vinokur and Burnstein 1978), other approaches highlighted the role of imitation or social learning among peers (Akers et al. 1979), or of social pressure to conform with group norms (Allport 1924; Asch 1955; Homans 1950; Sherif 1935). Likewise, cognitive consistency theories and social balance theory posit that individuals seek to be similar to people they like or respect (Festinger 1957; Heider 1967). In order to resolve the dissonance resulting from disagreement with other actors, individuals try to convince those actors to adopt similar opinions or may change their own opinions to conform to theirs (for a formal derivation how this entails assimilative influence see Groeber, Lorenz and Schweitzer 2014). It has also been argued that social influence is deeply rooted in humans’ nervous system, forming a natural and unconscious propensity to imitate or echo the gestures and postures of observed others (Rizzolatti and Craighero 2004). Evolutionary game theory and empirical research on social learning suggest furthermore that our tendency to imitate and follow group pressures may have evolved as a successful decision making strategy in the human evolutionary past (Richerson and Boyd 2005).
Formal implementations with continuous opinions
Prominent representatives of models with assimilative social influence are the averaging-models that were developed in the 1950ies and 60ies (Abelson 1964; DeGroot 1974; French 1956; Harary 1959; Lehrer 1975). These models treat individuals as nodes in a network. Nodes are connected by a network link if they, in one way or the other, exert influence on each other. Network links are assumed to remain unchanged over time, but they are weighted. Weights scale the strength of social influence one actor exerts upon another and can be seen as capturing structural differences in, for example, persuasiveness, social status, frequency of interaction, or power between actors. The defining feature of this type of models is that influence weights are fixed. Following Hegselmann and Krause (2002) models of assimilative influence, with continuous opinions and fixed influence weights, are also often called "classical" models in the literature.
Classical averaging models assume that opinions vary on a continuous scale and implement social influence as averaging (Friedkin and Johnsen 1990, 2011). That is, when an actor’s opinion is updated, her new opinion moves towards the weighted average of her previous opinion and the opinions of her network neighbors. Equation 1 illustrates how under social influence actor i shifts her opinion oi,t at time point t. The weights wi,j represent the impact that agent j has on i's opinion. To simplify the exposition, we assume 0 ≤ oi, t ≤ 1 throughout, but this is not an essential model feature.
| $$o_{i,t+1}=o_{it}+\Delta o_{it}=o_{it}+\mu \sum_j w_{ij} (o_{jt}-o_{it})$$ | (1) |
The parameter μ (0 < μ ≤ 1) defines the rate of opinion convergence and can be used to smoothen opinion dynamics. Often, in these models the constraint is imposed that the weights represent the influence of a particular other actor on i relative to the total amount of influence imposed on a target, i.e. \(\forall i\): \(\sum_j(w_{ij})=1\). Most classical implementations also assume that all agents update their opinions simultaneously in one discrete time step, based on the state of the population that resulted after updating at the previous time point. Figure 1a shows model behavior under these assumptions for a smooth rate of change (μ=0.1)[1].
Typical macro behavior
Already early contributions demonstrated that the classical averaging models imply the emergence of perfect opinion consensus in the long run, as long as the social network is connected. In a connected network, every actor is influenced directly or indirectly via intermediate links by every other actor. Whenever there is influence, overall opinion differences in the network decline such that eventually all actors align with the emergent consensus. Figure 1a illustrates this dynamic.
Formal implementations with nominal opinions
Deviating from the classical averaging models, several formal theories assume that the opinion scale is nominal, i.e. an opinion represents a choice from a set of distinct options, like a choice between political parties or different music styles, rather than a position on a continuous scale. This makes it impossible to define gradual distances between different opinions, two actors can only agree or disagree in one dimension of the opinion space. Depending on how social influence is implemented in these models, this seemingly innocent assumption can alter model implications profoundly, even when there is always assimilative social influence between connected actors.
An important implication of assuming nominal opinions is that social influence cannot be implemented as averaging. The voter model assumed, for instance, that actors can adopt an opinion of either +1 or -1, and copy the opinion of one of their contacts (Holley and Liggett 1975). Similar to the macro-implications of the classical averaging models, this imitation dynamics typically entails eventual consensus in connected networks. Extensive studies of this model by socio-physicists also revealed that the dynamic can provide very rich patterns including metastable states with co-existing regions with opposite opinions in a network, when networks have special structures or are infinitely large (Castellano, Fortunato and Loreto 2009).
An alternative implementation of unconditional social influence in models with discrete opinions assumes that actors adopt the most frequent opinion amongst their network contacts, like in models implementing a local majority rule intended to describe dynamics of public debate (Galam 2002). Sometimes influence of network neighbors is weighted by their individual "social impact" (Latané and L’Herrou 1996; Liggett 1985; Nowak et al. 1990; Parisi, Cecconi and Natale 2003). When opinions adopt either a value of -1 or +1, Equation 2 describes this model.
| $$ o_{i,t+1}=Sign\Bigl( \sum_j w_{ij} o_{jt} \Bigr) $$ | (2) |
This model generates consensus when all pairs of agents in a population are connected by influence relationships. However, when all actors are only exposed to a small local subset of the population in their network, configurations can arise in which everyone holds an opinion that is locally a majority view, but is different in different regions of the network.
Critical conditions and limitations
Models of assimilative influence are prone to generate consensus, in particular when they assume opinions with a continuous scale. Across different model versions, the most important critical condition for whether diversity can be maintained is the structure of networks. Segmented networks can preserve diversity if they entirely isolate subgroups from outside influence or at least restrict interactions to small local neighborhoods (in models with local majority rules).
Some diversity may also be maintained in continuous models despite connected networks, if agents are assumed to be stubborn to some extent (Friedkin 1990; Friedkin and Johnsen 2011). These models assume that opinion adjustments are always a tradeoff between social influence and actors’ initial view that represents individual interests, or entrenched beliefs differing between individuals. With stubbornness, models can reach equilibria where actors still disagree but refuse to change opinions any further, because they do not want to deviate even more from their initial convictions. However, even then social influence greatly reduces opinion diversity over time. In particular, the averaging assumption implies that opinions will never move outside of the range of initial opinions (Friedkin and Johnsen 2011). Models that assume assimilative social influence thus fall short of explaining how diversity could increase over time (Abelson’s question) or how opinion clustering can persist in dense highly connected networks (Axelrod’s question) without individuals’ fixation on their initial opinions.
Models with similarity bias
Main idea
Models with similarity bias abandon the assumption that there is always influence as long as there is a structural connection between agents. Instead, whether social influence occurs between connected individuals and how strongly they influence each other, is now linked to individuals’ similarity.
Agent-based modelers used this assumption to explain why under certain conditions influence may stop altogether reducing opinion differences (Axelrod 1997; Carley 1991; Deffuant et al. 2000; Hegselmann and Krause 2002; Mark 1998). The key assumption in these models is that if an agent disagrees too much with the opinion of a source of influence, the source can no longer influence the agent’s opinion. How much disagreement is "too much" before an agent loses "confidence" in a source, that is – at what point exactly the disagreement exceeds the critical level and an agent is no longer open to influence – can be further elaborated, modelling psychological processes that were studied in research on "attitude strength" in social psychology (e.g. Eagly and Chaiken 1993a, 1993b; Festinger 1957). Confidence in the opinion of a source may be related to things like whether two actors belong to the same social category or not, or whether the issue at stake is very salient or central for an agent’s identity ("ego-involvement"), etc.
With these assumptions a similarity bias can generate a self-reinforcing dynamic in which agreement strengthens influence and influence leads to greater agreement with those who already have a similar opinion. Multiple modelling studies demonstrated how this feedback loop can result in the emergence of persistent opinion clusters (Axelrod 1997; Deffuant et al. 2000; Hegselmann and Krause 2002; Mark 1998).
Models with similarity bias were first proposed for opinion dynamics in nominal opinion spaces (Axelrod 1997; Carley 1991). For sake of illustration we present here a slightly modified version of the continuous model of Deffuant et al (2000). Unlike in the model of assimilative influence formalized by Equation 1, the weights wij are in this model not exogenously given, but depend on the current disagreement in opinions between the two agents, wij = fw(oi, oj).
In our illustrative model, the influence dynamic consists of a sequence of events in which at every time point exactly one randomly chosen population member i can update her opinion and does so by selecting at random one other agent j to interact with. If i and j interact, then i modifies her opinion to move closer towards the opinion of j, but only if their opinions were sufficiently similar before. Equations 3 and 4 below describe the rules for opinion change in our illustrative model
| $$o_{i,t+1}=o_{it}+\Delta o_{it}=o_{it}+f_w(o_{it},o_{jt})(o_{jt}-o_{it})$$ | (3) |
| $$f_w(o_i,o_j)= \begin{cases} \mu\text{,} & \text{if } |o_i-o_j|\leq \epsilon\\ 0\text{,} & \text{otherwise} \end{cases}$$ | (4) |
The parameter ε in Equation 4 defines what Hegselmann and Krause (2002) called a confidence level (also called confidence threshold). Influence from another actor j can only affect i’s opinion if their disagreement |oi-oj| does not exceed this threshold. The parameter μ defines the rate of opinion convergence and is typically constrained to 0 < μ 0.5 (e.g. Deffuant et al. 2000). The core principle of influence in this model has been implemented with different assumptions about the exact "communication regime" (Urbig, Lorenz, and Herzberg 2008). The two basic versions of the model consider on the one hand agents meeting in pairs and possibly influencing each other, and on the other hand agents meeting everyone else at once while only being influenced by those in sufficient agreement with them. Indeed, in Deffuant et al (2000) and many follow-up papers both i and j change opinions simultaneously, while in another seminal model of bounded confidence, Hegselmann and Krause (2002) assumed instead that all agents in the population influence each other simultaneously. In their model, every agent i adopts in one time step the average opinion of all those whose disagreement with i did not exceed ε before the interaction. Urbig et al (2008) integrated these different versions, varying the number of agents meeting at once, and showed that while there are some differences in model behavior, core model implications remain the same. In our illustrative model used for generating Figure 1b we thus slightly modified the model of Deffuant et al (2000) in assuming that only one of two agents "meeting" modifies her opinion. This modification does not change the basic properties of the dynamics.
Theoretical and empirical foundations
Models that introduce a similarity bias draw on theoretical sources similar to those of unconditional social influence. Yet, an important difference is that these theories are not only applied to the way how individuals modify their opinions, but also to the change of the social or cognitive interpersonal relations through which influence occurs. Broadly, two perspectives can be distinguished. One line of work draws on cognitive theories and emphasizes the similarity between the attitude conveyed in a message of social influence and the attitude of the recipient. Another line of work focuses more on the social relation between a source of influence and the recipient, highlighting that social influence is stronger or more likely between more similar people.
Assumptions of "bounded confidence" (Deffuant et al. 2000; Hegselmann and Krause 2002) emphasize the similarity between message and attitude of the recipient, drawing on the theory of "confirmation bias" (Nickerson 1998), the tendency to take into account preferentially information that confirms one’s preconceptions and avoids contradictions with prior beliefs. Social judgement theory (Sherif and Hovland 1961) links this more specifically to attitude change in interactions. In this view, individuals are most influenced by a source if the source expresses an opinion that falls within a zone of non-commitment where it is neither too similar nor too different from the receiver’s opinion. If the opinion of the source is very similar, it falls within a zone of acceptance for the receiver but induces only little further change, while source opinions that are too different fall in a rejection zone where they do not influence the individual. Differences between individuals and contexts in the width of these zones can be further derived from psychological theories and experiments about the extent of ego-involvement and attitude strength (Eagly and Chaiken 1993, for a review), suggesting that more confident individuals are more resistant to influence from discrepant sources (Moussaïd et al. 2013) and thus have a smaller zone of non-commitment and a wider zone of rejection.
Other modelers highlight more the similarity between source and recipient to justify the assumption of similarity-biased influence. One foundation of this view is that individuals are cognitively more receptive to influence if the source of influence is more similar to them. Mark (1998) bases this idea on symbolic interactionism (Stryker 1980), a theory positing that in situations where new information is needed, people seek input preferably from sources with whom they have more similarity in terms of shared ideas about the world. Others (e.g. Axelrod 1997) take a different approach and derive the assumption of a similarity bias from one of the most prevalent regularities of social life, known as the principle of "homophily" (Lazarsfeld and Merton 1954; McPherson, Smith-Lovin and Cook 2001; Wimmer and Lewis 2010), according to which people more likely interact and communicate with similar others. It should be noted that despite similar formalizations, the underlying idea is different. Homophily may be caused by structural patterns of social interaction that systematically sort similar people into similar "foci" (Feld 1982) where they meet and interact, like schools, neighborhoods, or workplaces. But a similarity bias in selecting interaction partners can also be cognitive or emotional. Psychological research underpinning Byrne’s (Byrne 1971) "attraction paradigm" showed that more similar people like each other more and therefore seek each other more as partners of interaction and are more open to influence from each other, a pattern supported by research on social networks (Pearson et al. 2006; Stark and Flache 2012; Wimmer and Lewis 2010).
Typical macro behavior
Models using dynamics like those described by Equations 3 and 4 have been used to study the convergence process of opinions from initial diversity (Deffuant et al. 2000; Hegselmann and Krause 2002). A key insight is that if the confidence level ε is sufficiently small, the population ends up fragmented in separate opinion clusters, while otherwise convergence towards consensus occurs just as in classic continuous models. The smaller the confidence level, the smaller and more numerous are the opinion clusters in which the population fragments.
Figure 1b illustrates a typical dynamic for an intermediate confidence level of ε=0.15, using the model of Equations 3 and 4 with 100 agents with initially uniformly randomly distributed opinions. Agents who initially have relatively similar opinions are pulled towards the mean opinion in an emergent cluster close to their initial position. As clusters crystallize out, the differences between them increase until differences exceed the confidence level ε and influence between different clusters ceases to "pull" agents towards the opinions of other clusters than their own.
It is noteworthy that typical macro-behaviors of bounded-confidence type models also include extremization of most or all members of a population, both in the form of bi-polarization and of a pattern resembling "group polarization". Figure 2 below shows two examples of convergence of a large majority of the population to one extreme from an initially uniform opinion distribution. This pattern can arise from bounded confidence dynamics, when the initial population of agents comprises both extremist agents, having an opinion close to the extremes and a very small confidence level ε, and moderate agents with a larger openness to outside influences (larger confidence level) and an initially randomly distributed opinion. With these assumptions, the extremist agents are very influential and are hardly influenced by moderates.
Depending on the exact initial distributions of opinions and uncertainty levels, social influence in populations with heterogeneity in uncertainty levels may result in bi-polarization – where extreme agents on both sides of the spectrum pull large numbers of moderates to their extreme position -, or a pattern more resembling "group polarization". In this outcome most or all initially moderate agents move to the same position more extreme than their initial opinion. Figure 2a shows group polarization with a small minority of moderates taking the extreme position opposite to the emergent mainstream, while 2B shows "single extreme convergence" in which everyone except the initial extremists at o=0 ends up in the extreme group with o=1. Also a mix of those patterns with some moderate groups surviving the influence from extremists is possible.

As Figure 2B demonstrates, bounded confidence dynamics can in particular also imply that a whole population of initial moderates can be driven to one extreme, despite an equal initial distribution of extremists at both extremes of the opinion spectrum. This pattern, and the others, have been systematically studied for different variants of the bounded confidence model, particularly ones in which the tolerances are also modified during the interactions, different types of networks and different values of the model parameters (Amblard and Deffuant 2004; Deffuant 2006; Deffuant et al. 2002; Lorenz 2008,Lorenz 2010). As shown in Deffuant and Weisbuch (2008) the single extreme convergence happens if moderates first concentrate in the center of the opinion spectrum where they can get outside of the range of influence of one of the extremes because of random fluctuations. Then the moderates drift to the other extreme. This pattern is more likely to take place when the extremists are not too numerous, because when they are, they attract the moderates to both extremes. Morever, under the original bounded confidence model (with constant tolerances), a pattern in which, the opinions of the moderate agents keep fluctuating all the time also can take place (Mathias, Huet and Deffuant 2016). This is because moderate agents with large tolerances keep strong interactions with opinions of opposed "stubborn" extremists and this prevents them from creating stabilized clusters. This does not occur in the variants of the model with changing tolerances, because the tolerances of the moderates decrease with interactions with extremists which leads finally extremist agents to stop interacting with one or both extremes.
Recent work by Hegselmann and Krause (2015) used a combination of simulations and analytical tools to derive many of these phenomena from a general model in which a population following bounded confidence dynamics is exposed to an external signal as additional source of influence, sent for example by charismatic leaders, radical groups or – in a scientific discourse – by empirical evidence of the "truth" about a real-world phenomenon under discussion by scientists. They showed that the exact effects of the intensity of signals on the degree of extremization in a population interact sensitively and in sometimes counterintuitive ways with the distribution of confidence levels and initial opinions in the population. Resonating earlier results discussed above, they find for example that more intensive signals may decrease rather than increase convergence on extreme positions advocated by the signal. This happens if those agents moving towards the position of the signal move too quickly, so that they drop out of the confidence range of a majority of population members who do not "hear" the signal. This majority is then "left behind" and stays at moderate positions, because it can no longer be influenced by those who hear the signal.
Bounded confidence models have become a hugely influential modelling class implementing similarity biased social influence with continuous opinions. A large literature has evolved on extensions, modifications and analytical treatments of these models, often using tools of statistical physics. It is impossible to give a complete overview here. Comprehensive reviews can be found in Lorenz (2007) or Castellano et al. (2009).
Alternative implementations of similarity-biased influence
Like for models of assimilative influence, an important distinction is between models assuming a continuous opinion space (Bounded Confidence-models) and models assuming distinct nominal opinion categories. Models with nominal opinion spaces combine social influence with homophily, implemented as a lack of interaction if dissimilarity exceeds a critical threshold. In these models the agents have a vector including several discrete opinions (or cultural traits) and the similarity is computed between such vectors. Drawing on Carley (1991), Axelrod (1997) modelled spatially local interaction with a regular bounded lattice. The likelihood for an agent to select a particular neighbor for interaction is equal to the proportion of opinion dimensions (called features by Axelrod) in which they have the same trait (modelling homophily). If an agent interacts with a neighbor, then on a feature in which they still disagree, the trait of the neighbor is copied (modelling influence) so that the agents become more alike as a result. Most importantly for model behavior, interaction and thus influence becomes impossible if two neighbors have nothing in common.
Axelrod’s (1997) computational studies showed how local convergence can lead to stable spatial opinion clustering from initial randomness. In areas of the spatial network where agents locally happen to be relatively similar to each other, they influence each other more and thus agree on an increasing number of opinion dimensions while differentiating from neighbors at the same time. Eventually spatially connected "cultural regions" emerge and stabilize with maximal consensus within and disagreement on all features between neighboring regions.
Modelling symbolic interactionism, Mark (1998) proposed a model with essentially similar behavior, but representing opinions as a set of "facts" actors can learn from each other when interacting. The more facts two actors share in their knowledge base, the more likely they interact with each other and thus communicate more facts to each other. Again, interaction is impossible if agents have no facts in common. Mark’s model can generate in particular social differentiation from initial homogeneity. This is possible because in an interaction, actors cannot only share known facts, but also create with some probability new unique facts. This models the assumption of symbolic interactionism that individuals can create in social interactions new symbols with unique meaning for them, like "cool" new words members of a youth-clique invent to distinguish themselves. New unique facts further spread through social influence primarily to those who are similar to their initial creators and so further differentiate the recipients from other agents in the system.
Like the bounded confidence models, Axelrod’s model of "cultural dissemination" has sparked a massive follow-up literature addressing a wide range of extensions, modifications and analytical treatments (for reviews see e.g. Castellano et al. 2009). Studies addressed the role of mass media (González-Avella et al. 2007; Shibanai, Yasuno and Ishiguro 2001), globalization modelled as increasing spatial range of interaction (Greig 2002), or geographical boundaries (Parisi et al. 2003). One problem that received particular attention is the sensitivity of cultural differentiation to noise. Axelrod’s model assumes that interaction and thus influence is impossible if agents disagree on all features. However, in the real-world agents may occasionally be exposed to other sources of influence than their network neighbors, or may make errors in perceiving each other’s traits or similarity, even when distinct cultural regions have crystallized out. Addressing these sources of error, Klemm et al. (2003a, 2003b) and De Sanctis and Galla (2009) allowed a small probability of random perturbation of cultural traits in Axelrod’s model and found that this small change made cultural diversity far more fragile than Axelrod had suggested. Random changes of traits can generate new cultural overlap between otherwise dissimilar neighbors, thereby breaching through emergent cultural boundaries. Further studies explored mechanisms explaining opinion clustering despite noise. One is that homophily extends to "network homophily" (Centola et al. 2007) in that agents choose to structurally disconnect from dissimilar neighbors (similar to moving into a different neighborhood). Flache and Macy (2011a) showed how cultural diversity could become even more robust when the bilateral interpersonal interaction Axelrod’s model assumed is replaced with "social interaction", reflecting local conformity pressure. Recently, Ulloa et al. (2016) further extended their model to include conformity pressures exerted by social institutions, like a family to which one belongs that discourages deviation from the family’s cultural identity.
Other authors have moved towards integrating and comparing continuous and nominal models of similarity-biased social influence. The bounded confidence model has been adapted to a vector of binary opinions, by defining the threshold ε on the sum of the different opinions in two vectors (Deffuant et al. 2000). The study of this model in the case of completely connected populations showed a frequent convergence to a large majority opinion cluster and several minority opinion clusters. This skewed distribution of cluster sizes is very similar to the opinion clustering the model of Axelrod generates if multiple traits are possible per opinion dimension, whereas Axelrod’s model can lead at most to two clusters in a totally connected network with the same setting (2 possible traits per opinion dimension). Other authors approximated continuous opinions in Axelrod’s framework with features on which discrete traits have a defined distance from each other, such that the only way how interaction between i and j is impossible is that they maximally disagree on all features (Flache, Macy and Takács 2006; De Sanctis and Galla 2009). These studies further highlighted the similarity of conclusions arising from different modelling frameworks. Like in bounded confidence models, sufficiently restrictive interaction thresholds based on opinion distance were needed to sustain levels of diversity similar to those of Axelrod’s original model.
Critical conditions and limitations
Across different models of similarity-biased influence, several similar critical conditions for opinion clustering emerge. Most importantly, the more similarity is needed to make social influence possible between structurally connected agents, the smaller and more numerous are emergent opinion clusters. In bounded confidence models, this condition is governed by the width of confidence intervals. For models based on Axelrod’s (Axelrod 1997), the number of cultural features and traits affects the likelihood of interaction. The more features, the more likely it is that neighboring agents agree by random chance on at least one feature and thus can interact, while more different possible traits per feature make it less likely to agree by random chance and thus have the opposite effect on the likelihood of interaction (Axelrod 1997; Klemm et al. 2005). Generally, confidence levels and the number of features on which individuals are open to influence can be seen as representation of societal level characteristics, like the degree of tolerance, "broad-mindedness" or generalized trust in a society, but also as representation of individual trust, openness to discrepant views or connectedness with dissimilar people.
Network density overall fosters the emergence of consensus in models with nominal opinions, mirroring some of the results obtained when network structures where integrated in bounded confidence models. Amblard & Deffuant (2004) for example found that "single-extreme convergence" rather than opinion fragmentation became more likely with higher connectivity (number of ties per agent in the influence graph - see also Fortunato 2005; Stauffer and Meyer-Ortmanns 2004). In Mark’s (1998) model, network density depends on the likelihood of interaction between agents, which in turn depends on the size of the memory of agents. The more facts agents can memorize, the more likely two agents can have at least one fact in common and thus interact with a positive probability. Correspondingly, Mark finds that distinct subgroups become larger and less numerous if memory size increases.
Noise is a second condition with similar effects across different models. A small amount of random noise greatly reduces opinion diversity in Axelrod’s model (cf. Flache & Macy 2011) and similar effects of noise occur under bounded confidence dynamics (Kurahashi-Nakamura, Mäs and Lorenz 2016; Mäs et al. 2010). The mechanism through which noise reduces diversity is essentially the same. In the study of Mäs et al. (Mäs et al. 2010), small random changes of opinions eventually lead actors to shift their opinions into each other’s bound of confidence even when separated opinion clusters have emerged. Like in Axelrod’s model, this re-opens the possibility for new social influence across previously established subgroup boundaries, eventually eliminating opinion differences between opinion clusters. Other implementations of noise under bounded confidence (Pineda, Toral and Hernández-García 2009) show how noise also can help preserve opinion clustering. In their models, agents adopt with a small probability any possible opinion on the opinion scale, while they otherwise follow a bounded confidence rule. Agents adopting random positions in between emergent clusters can trigger influence cascades towards merging those clusters, because they fall into the confidence ranges of both of them. However, agents adopting random positions close to only one cluster join that cluster and thus stabilize its existence as a separate group in the opinion space. When noise rates are such that both dynamics are in balance, this form of noise can preserve diversity rather than destroy it.
This result resembles findings obtained in the Axelrod framework (Klemm et al. 2003a, b), where noise can help sustain diversity if the noise rate is in an intermediate range such that opinion clusters cannot merge faster with their neighboring regions than spontaneous changes create new diversity within clusters. This process, finally, is similar to how the random creation of new facts drives the emergence of differentiation in Mark’s (1998) model.
Similarity-biased social influence offers a preliminary answer to Axelrod’s question. At the same time, for many models in this class the opinion clustering generated by models with similarity-biased influence can be fragile against noise, and is limited to particular slices of the parameters space (sufficiently restrictive confidence bounds, low numbers of features, etc.). Models with similarity-biased influence can explain why there is no influence between some agents and they thus fail to converge. Especially if they assume a nominal opinion space, they cannot readily offer an explanation why interaction may sometimes cause actors to even increase and accentuate their mutual differences in one opinion dimension, as suggested by Abelson’s question. The reason is that in nominal opinion spaces differences within one feature do not have a magnitude. Bounded Confidence models instead can show how a whole population can become extremist and possibly bi-polarized by adopting the opinions of its initially most extreme members. Yet, in these models a population cannot become more extreme than its initial extremists. This cannot account for results from some experiments on group polarization (Moscovici and Doise 1994; Myers 1982) and has thus motivated the search for further answers to Abelson’s question.
Models with repulsive influence
Main idea
Some model builders tackled Abelson’s question by relaxing the assumption that if influence occurs between individuals, it always implies assimilation (Jager and Amblard 2005; Macy et al. 2003; Mark 2003; Salzarulo 2006). In these models of repulsive influence, assimilation was combined with its counterpart, differentiation – the assumption that some interactions lead individuals to adjust their opinions in such a way as to become more dissimilar to others they disagree with. Different terms have been used in the literature to denote repulsive influence, like rejection, negative influence, differentiation or reactance. Hunter et al. (1984) referred to repulsive influence as the "boomerang" effect occurring if an attempt to attract someone through social influence can have the opposite effect.
We illustrate the implementation of this mechanism with a modification of our basic model of similarity-biased continuous opinion dynamics given in Equations 3 and 4, similar to the formalization given by Jager and Amblard (2005). Compared to similarity-biased influence, the only change concerns the way how influence weights are implemented. Equation 5 describes that influence weights can become either positive or negative, depending on the opinion differences.
| $$ f_w(o_i,o_j)=\mu (1-2|o_{jt}-o_{it}|)$$ | (5) |
Equations 3 and 5 jointly show how the direction of influence switches from a "pull" towards the opinion of the source towards a "push" away from it, as soon as the disagreement |ojt-oit| shifts above a critical level. This critical level is here set to 0.5, half of the theoretically maximal disagreement of one unit (0≤ oit ≤1). In this basic form, Equations 2 and 5 allow interactions to push the opinion outside of the opinion interval [0,1]. In some models this is prevented by a smoothening (Flache and Macy 2011b) or truncating function (Feliciani, Flache and Tolsma 2017); in some others the opinion space is self-contained by the specification of the interaction dynamics (Huet and Deffuant 2010). For the simulations shown in Figure 1c we used a simple truncation rule.
Different implementations of the weight function f have been proposed for models with repulsive influence on continuous opinions (e.g. Jager and Amblard 2005; Mäs et al. 2014), including non-linear and non-continuous versions, but they all share the assumption that weights are positive for small distances and negative for large ones (hence the names "positive influence" and "negative influence" some authors also use, e.g. Takács et al. 2016).
Theoretical and empirical motivations
A number of model builders (Baldassarri and Bearman 2007; Flache and Macy 2011b; Macy et al. 2003; Mark 2003) motivated the assumption of repulsive social influence by theories that also were used to justify similarity-biased influence, Heider’s balance theory (1946) and Festinger’s theory of cognitive dissonance (1957). But this time these theories were interpreted as to not only imply that individuals want to be similar to people they like, or to accept the opinion of others when these are similar, but also that individuals strive to be dissimilar to people they dislike, and accentuate disagreement with others if these are too dissimilar. Additionally, several authors assume that social influence relations between individuals are not only modified by homophily, but also by xenophobia (Baldassarri and Bearman 2007; Flache and Macy 2011b; Macy et al. 2003; Mark 2003). Xenophobia is the counterpart of the assumption that people are more open to influence from similar others: the larger the dissimilarity between two interacting individuals, the more they evaluate each other negatively (Rosenbaum 1986), triggering differentiation from the source. Other modelers (Huet and Deffuant 2010; Huet, Deffuant, and Jager 2008) derived repulsive influence from a different psychological process. In line with the social judgement theory (Sherif and Hovland 1961) they assume that the degree of ego-involvement and self-relevance play a crucial role in social influence processes. In case of strong disagreement on a highly ego-involved issue (represented as an opinion dimension), individuals may increase their opinion difference on a less ego-involved issue (represented as another opinion dimension). This can occur in particular when issues are at stake that are central to the social identity of an individual. Building on research on intergroup dynamics (Brewer 1991; Tajfel 1978), further models (Salzarulo 2006; Dykstra et al. 2015) assume that individuals may change their opinion to adopt a position prototypical for their ingroup or to distance themselves from an opinion perceived as prototypical for an outgroup.
Typical macro behavior
Figure 1c describes a typical dynamic that has been generated with the model presented above. Starting from an opinion that is initially randomly uniformly distributed in the population, soon two clusters start to form at the opposite extremes of the spectrum, until eventually all agents have joined one of the two emergent factions. Due to their large distance from other members of the population, initial extremists "push" even moderate agents to differentiate from their extreme views and to thus shift towards the opposite pole. The assimilation pressures of positive influence then "pulls" their "moderate friends" with them in the process, adjusting their opinions towards increasingly extreme positions on the opinion scale. This class of models offers a possible explanation of how bi-polarization can arise despite the presence of simultaneous assimilative influence, as well as how agents can adopt opinions that are more extreme than any of the initial opinions present in the population.
Alternative ways of modelling repulsive social influence
Like unconditional and similarity-biased influence, also repulsive influence has been implemented for both continuous as well as nominal opinion spaces.
Different implementations of the same principle were proposed for continuous opinions. For instance, some models (Jager and Amblard 2005) introduce threshold levels for the difference between opinions that determine whether an interaction triggers assimilation (small differences), differentiation (large differences), or has no effect (intermediate range). These models exhibit opinion clustering, moderate and extreme consensus as well as bi-polarization.
Other models allow for smooth non-linear weight functions that approximate such threshold models (Mäs et al. 2014). Yet other modelers assume that the weight measures similarity across several opinion dimensions, including static attributes that represent demographic characteristics like gender or race (Feliciani et al. 2017; Flache and Mäs 2008a, 2008b; Grow and Flache 2011; Macy et al. 2003). Depending on the parametrization and exact distribution of static attributes across the population, these models have been shown to generate opinion consensus on moderate opinions or bi-polarization or, sometimes, also fragmentation.
Among models that differentiate between multiple opinion dimensions, some distinguish between an opinion dimension concerning a primary topic (representing an important topic, associated with strong ego-involvement), and secondary opinion dimensions (Baldassarri and Bearman 2007; Huet and Deffuant 2010; Huet et al. 2008). In such models, disagreement on the primary opinion dimension can trigger repulsive influence on the second dimension. These models display opinion clustering and polarization on at least one opinion dimension. This perspective draws on experimental research testing combined implications of social identity theory and cognitive dissonance theory (Wood et al. 1996), reflecting the view that "attitude shifts reflect normative pressures to align with valued groups and to differentiate from derogated groups" (Huet and Deffuant 2010, p. 2).
Historically, differentiation from dissimilar others was first included in models with nominal opinion spaces (Macy et al. 2003; Mark 2003). In these models, the similarity between two interacting agents determines the probability that they either copy a trait from an individual they interact with, or adopt a trait dissimilar from that of their interaction partner in order to increase difference. Like continuous models, nominal models show how repulsive influence can promote the self-organization of antagonistic factions in which opinion differences between groups align across multiple dimensions of an opinion space, maximizing intergroup differences.
Another variation of the idea of repulsive influence is that differentiation from a source of influence does not need to be caused by large dissimilarity, but could also result from high similarity. This idea was first implemented in models of majority influence in nominal opinion spaces (Galam 2004; Wio, de la Lama, and Lopez 2006). Here, "contrarian" agents are introduced who after group discussion always deviate from the local majority that was adopted by other agents. These models show how the presence of contrarians can prevent the formation of a clear majority despite conformity pressure at the local level. Motivated by psychological research on nonconformity and uniqueness (Imhoff and Erb 2009; Snyder and Fromkin 1980), optimal distinctiveness theory (Brewer 1991) and Durkheim’s discussion of societal differentiation (Durkheim 1982 [1895]), some authors applied a similar idea for continuous opinion spaces (Mäs et al. 2010). They assumed that agents are simultaneously exposed to assimilative social influence and strive for uniqueness, trying to shift away from the majority opinion in their social environment when too many others adopt an opinion too similar to their own. Similar to the nominal models, they find that the combination of assimilation and strive for uniqueness can generate dynamically changing opinion clusters through a process of fusion (assimilation) and fission (splitting away of individuals from clusters if they become too big). Arguably, the combination of assimilative influence and differentiation from similar others offers a tentative answer to Durkheim’s and Bourdieu’s questions how some level of (local) consensus and global differentiation can co-exist in society despite tendencies towards both assimilation and individualization. The stronger social influence is relative to individualization in these models, the larger are the clusters that form and the less different are individuals’ opinions on average (Mäs et al. 2010, 2014).
Critical conditions and limitations
A core condition for bi-polarization identified by various models of repulsive influence is that in interpersonal interaction both assimilation and differentiation can occur. Assimilation occurs if agents are not too dissimilar and differentiation happens if agents are not too similar. If this is the case, assimilative influence can lead to the emergence of factions with high levels of internal consensus among initially more similar agents, while differentiation can push these emergent factions to increasingly disagree with each other. In models with continuous opinion spaces, this can be related to the position of the threshold level of dissimilarity, above which influence turns repulsive (Huet et al. 2008; Jager and Amblard 2005; Mäs et al. 2014) - or to the likelihood with which in an interaction between dissimilar agents differentiation occurs (Chattoe-Brown 2014) - compared to the threshold dissimilarity below which influence is assimilative. Broadly, if there is enough room for both assimilation and differentiation, bi-polarization is likely to occur, while consensus is likely to occur if interpersonal interactions result primarily in assimilation and not in differentiation. In a similar vein, repulsive influence models with nominal opinions identify "openness" to social pressures to both assimilate or differentiate (Macy et al. 2003) as condition fostering bi-polarization.
The extent to which repulsive influence occurs in individual interactions also depends on macro-structural properties of the population that define how dissimilar are two interacting agents on average. One important condition here is the shape of the initial distribution of opinions. Broadly, more variance in agents’ opinions in the initial condition increases the chances that bi-polarization arises (Mäs et al. 2014), because it increases the chances that agents interact who are dissimilar enough to influence each other negatively. Another, related, condition is the dimensionality of the opinion space. In models with multi-dimensional opinion spaces, the dissimilarity between agents is often modelled as aggregated dissimilarity across all dimensions (e.g. Flache and Macy 2011b; Huet et al. 2008; Macy et al. 2003). If this is the case, more dimensions can decrease the likelihood that from a random start two agents who happen to interact will strongly disagree on most dimensions, which in turn makes bi-polarization a less likely outcome at the macro-level. However, more complicated relationships between the number of opinion dimensions and bi-polarization arise when models differentiate between a primary and secondary opinion dimension, where the primary dimension mainly defines whether influence is assimilative or repulsive on both dimensions (Huet and Deffuant 2010).
In addition, repulsive influence models appear to be sensitive to the network structure: networks with strong local clustering and small average distances between nodes (caveman graphs) display a strong polarizing tendency originating from long-range ties. These ties potentially connect highly dissimilar local regions in a network and thus can trigger repulsive influence (Flache and Macy 2011b). Building on this finding, Feliciani et al (2017) showed how under local interaction, spatial segregation between dissimilar groups can reduce bi-polarization dynamics, because segregation minimizes potentially repulsive influence encounters. Similarly, they found that interactions between random dyads in otherwise fixed, non-complete networks may exacerbate the polarizing tendency under certain conditions (Feliciani et al. 2017), because they increase the likelihood that demographically dissimilar actors interact.
Further research has investigated the effects of assuming multiple opinion dimensions (Flache and Macy 2011b) and a combination of opinion dimensions and fixed demographic attributes (Flache and Mäs 2008a, 2008b; Macy et al. 2003). On the one hand, fixed attributes allow to investigate the effects of demographic faultlines and of different distributions of influence thresholds across a population (Grow and Flache 2011). On the other hand, they allow to model spatial segregation as exogenous condition (Feliciani et al. 2017). Both aspects have been shown to affect the system dynamics. Broadly, reflecting research on "demographic faultlines" in work teams (Lau and Murnighan 1998), these studies found that the more the distribution of demographic attributes segregates a population into distinct subgroups, the more likely bi-polarization will be. An important further aspect in modelling the role of social categories is that different categories can have different relevance for the direction and magnitude of social influence. Drawing on self-categorization theory and social identity theory, some models assume that those categories central to a social identity can affect the direction of influence between individuals depending on their group membership (Huet and Deffuant 2010), while similarity or dissimilarity on other categories may be of less relevance.
Models with repulsive influence provide a tentative answer to both Axelrod’s and Abelson’s questions. However, whether consensus, opinion clustering or bipolarization arises from their dynamics depends on a number of critical conditions including variance in the initial opinion distribution, the number of distinct dimensions of an opinion space, distribution of demographic attributes in a population and – importantly, whether agents differentiate from similar others (striving for uniqueness) or dissimilar others.
The main limitation we see at this moment for this class of models, however, is the lack of empirical work that convincingly demonstrates the micro process of repulsive social influence that is critical for the model’s behavior. While early social influence experiments (e.g. Hovland et al. 1957) suggest a systematic tendency of individuals to differentiate from dissimilar or disliked sources of influence, many of these studies have been criticized for methodological weaknesses (Mäs and Flache 2013). More recent experiments that aim to avoid such weaknesses failed instead to find evidence that disliking or dissimilarity consistently triggers differentiation (Takács et al. 2016). While these results do not refute repulsive social influence, they highlight that conditions under which it occurs at the individual level may be more specific, requiring for example strong emotional content (Gargiulo and Huet 2012; Sobkowicz 2012, 2015), high ego-involvement, or strong antagonistic group identities (Huet and Deffuant 2010).
Hybrid models and alternative models
The three classes we have described each cover a broad range of models proposed and analyzed in literatures about mathematical, socio-physical and agent-based models of social influence dynamics. Nonetheless, many other models remain that cannot be readily assigned to any of these classes and that offer yet other possible answers to Axelrod’s and Abelson’s questions. It is impossible to do justice to all of this work in one overview paper. As a very coarse-grained categorization, one can distinguish hybrid models, combining assimilative influence, similarity biased influence and repulsive influence within one model, and models implementing alternative approaches to fundamental principles of social influence that do not fall into any of our three classes.
Many hybrid models have been proposed. Generally, it can be said that behavior of these models often can be well understood from combining the main conditions and mechanisms we identified for consensus, opinion clustering and bi-polarization in the three model classes. Examples can be found in models that combine bounded-confidence principles of similarity-biased influence with both assimilative and repulsive influence. For instance, the model proposed by Huet and Deffuant (2010) that we discussed above combines bounded confidence dynamics driven by agreement on the main opinion dimension with positive or repulsive influence on the secondary dimension. Further hybrid models similarly combining similarity-biased influence and repulsive influence have been proposed for example by Grow and Flache (2011), Del Vicario et al (2017) or Duggins (2017). In a similar vein, Allahverdyan and Galstyan (2014) elaborated a model of opinion dynamics based on non-Bayesian probabilistic opinion revision in the evaluation of new information. Their model could reproduce empirically observed phenomena like confirmation bias, primacy-recency effect, boomerang effect or cognitive dissonance.
Next to hybrid models, a variety of models were proposed that draw on principles of social influence not covered by the three classes we discussed. One line of work are models drawing on persuasive argument theory (Myers 1982; Vinokur and Burnstein 1978), which assume that influence occurs through communication of arguments (Mäs et al. 2013; Mäs and Flache 2013). These models assume similarity biased influence in the sense that agents who are more similar interact more likely. But more similar agents also hold more likely arguments supporting the same opinion, such that the interaction between them strengthens their convictions and thus fosters extremization of their opinions towards the same pole of an opinion spectrum, a process that those models implementing social influence as averaging cannot generate (Mäs and Flache 2013). Interaction between dissimilar agents has the opposite effect, because arguments opposing the current tendency of an agent are learned in such an interaction and differences are thus reduced. The conditions under which these models generate consensus and bi-polarization overlap only partially with those known from similarity-biased or repulsive influence. In particular, bi-polarization becomes more likely when more similar agents interact in separate groups (see also Feliciani et al. 2017), a condition opposite to what models of repulsive influence suggest. Similar mechanisms with similar dynamics have also been proposed by models of selective exposure to different opinions in a multidimensional opinion space (Urbig and Malitz 2007) and models of "biased assimilation" (Dandekar, Goel, and Lee 2013), and information accumulation systems (Shin and Lorenz 2010).
Frontiers
Since Axelrod and Abelson formulated their research questions, a huge literature has emerged containing mathematical as well as computational agent-based models of social influence dynamics. Multiple possible answers to their questions can be derived from these models. However, we contend that the field faces at least two important challenges before formal models of social influence can be used to inform researchers aiming to understand and predict outcomes and processes as they can be observed in specific societal realms. Here, we discuss in turn the interrelated challenges of 1) theoretical integration and structuring of alternative models, and 2) empirical calibration and testing of model implications. More generally, we believe that for assessing the progress achieved in an ABM study of social influence, it is important to specify in advance whether the goal pursued is a theoretical one (e.g. comparison of implications of different models, exploring implications of a psychological process hitherto not addressed in social influence models) or whether the aim is to generate outcomes that match empirical data observed in a specific realm. This defines how the researcher can assess whether and to what extent the aim of the modelling study has been achieved.
Frontier 1: Theoretical questions
A central problem of the literature on social-influence dynamics is that there are many models but little is known about their relation to each other. Many contributions fail to identify how they add to insights of earlier work. As a consequence, many publications contribute more to the accumulation of social-influence models than of scientific insight into social-influence processes.
In order to reduce the number of plausible models for a given setting and to allow the development of decisive empirical tests, modelers need to identify the critical assumptions and predictions of their models, and need to compare these assumptions as well as their formal implementation to existing models. Ironically, however, there seems to be too little influence between social-influence modelers to create the dynamic necessary to develop scholarly consensus on what are core model ingredients, in which implications models really differ and where they don’t, and how models can be compared. In this section, we propose four directions for future theoretical work we believe is needed.
Work that compares alternative technical implementations of the "same" theoretical assumption
In Section 2, we argued that large parts of the literature can be categorized into three model classes, proposing that all models belonging to the same class share critical assumptions and key results. However, this does not imply that modelers can freely choose between models to generate whatever opinion dynamic one would like to have. Instead, modeling choices need to be made explicit, defended with theoretical and empirical arguments, and backed up with sensitivity analyses. For example, we argued that Axelrod’s model of cultural dissemination and bounded-confidence models implement – albeit in different ways - the theoretical principle of similarity-biased influence, with many similar answers emerging from seemingly very different models. While hundreds of papers work with these models, authors rarely discuss why they chose one of the two models and virtually never explore whether their conclusion might differ if they had chosen the alternative model. As a consequence, it remains unexplored whether findings hinge upon the technical differences, for example between continuous and nominal scaling of opinions, or generalize to the whole class of models and thus represent potentially more general insights. Thus, more work is needed to understand to what extent models belonging to the same class make the same predictions and whether (technical) differences between models also entail substantively different implications.
Identifying competing predictions of models that belong to the same category will also help reduce the number of models or at least their scope. If it turns out that two implementations of the same theoretical mechanism lead to different predictions, empirical research testing these predictions against each other can identify conditions under which each of the models makes more accurate predictions. We will discuss possibilities of empirically testing implications derived from models of social influence further below.
Work that compares models with different theoretical approaches
Our review of the literature demonstrates that models belonging to different classes employ critically different assumptions. Modelers should, therefore, provide convincing arguments for their choice of model ingredients, making explicit why or why not they assumed assimilative influence, similarity-biased or repulsive influence and why they chose a specific implementation. What is more, as similarity bias and repulsive influence can be critical assumptions, modelers should explore whether the results of their analysis hinge on their choice of assumptions. To be sure, similarity bias and repulsive influence do not always entail different model predictions. For instance, the conditions of bi-polarization proposed by some models from both classes are relatively similar. Especially for those models that link the possibility and direction of influence mainly to opinion disagreement, the higher are confidence thresholds or thresholds triggering repulsive influence, the more likely an opinion dynamics generates consensus. However, we emphasize that the fact that a given model assumption has critical impact on a theory’s prediction is not a weakness of the model. In contrast, testable hypotheses about the conditions under which similarity bias and repulsive influence lead to different predictions can guide empirical research and, thus, help identify the appropriate model for a given setting.
This also requires moving towards shared standards of how to make comparable the conditions (like thresholds triggering rejection of influence or repulsive influence) that are manipulated in computational experiments and the model outcomes that should be compared (like bi-polarization), for example by drawing on recent advances in measuring and disentangling different aspects of bi-polarization in an opinion distribution (Bramson et al. 2016).
Work that explores how different micro-level mechanisms can be derived from the same more fundamental principles under different conditions
Often it is very important and leads to new insight if we open the "black box" of a model assumption and explicate in a "deeper" model the process that supposedly leads to the assumption. For example, if we just assume that more similar people influence each other more because they want to reduce cognitive dissonance, we may end up with different results than a model would generate in which we actually make the dissonance reduction mechanism explicit and then study under what conditions it produces our initial assumption (e.g.Groeber et al. 2014).
A more general question is which processes of social influence follow under which conditions from fundamental principles of human cognition. Rosaria Conte and her co-authors have repeatedly and forcefully argued for the importance of this question. They call for an integrated approach in ABM that links the social structure in which an individual is embedded to a model of its cognitive, "symbolic representations and the operations performed upon them, involved in mental activities including understanding, problem-solving, (social) reasoning and planning, communicating, interacting and […] learning" (Conte and Castelfranchi 1995, p. 1). This approach has been applied to dynamics akin to social influence, like the spreading of gossip or the formation of opinions about actors’ reputation in a population (e.g. Conte and Paolucci 2002). Recently, first steps have been taken to link this approach to models of social influence with the development of "a cognitively grounded computational model of opinions in which they are described as mental representations and defined in terms of distinctive mental features" (Giardini, Vilone and Conte 2015).
Frontier 2: Empirical questions
The question which of the many available models of social influence is the best choice for studying a given empirical phenomenon is eventually an empirical one, given that the researcher can narrow down the empirical scope that a model addresses. Thus, while answers to the described theoretical research questions are vital to develop informative empirical studies, the assumptions and predictions of theoretical models need to be put to the empirical test. This also requires that researchers specify the empirical scope their model addresses, that is: under which empirical conditions the assumptions used in a model are expected to be valid and which empirical phenomena at macro-level the model should be able to "grow".
Unfortunately, the assumptions of social-influence models, the dynamics that they generate, and also many of their predictions are notoriously difficult to put to the test. In the following, we outline 4 approaches to testing models of social influence that we deem promising.
Validation and calibration of micro assumptions with experiments
Our review of the literature has illustrated that micro-level assumptions in models of social influence dynamics often have been derived from theories based on social-psychological research, many based on experiments into social influence, conformity or small group decision making conducted in the 1950s and 1960s, notwithstanding some more recent work (e.g. Bohner and Dickel 2011). While these studies have revealed much insights into determinants of assimilative influence, similarity-bias or repulsive influence in social interactions, basic empirical questions about how to underpin model assumptions remain unanswered. For instance, while social influence has been documented many times, little is known about the conditions under which influence is stronger or weaker. Are individuals equally open to influence on their beliefs, opinion, and behavior? How flexibly do individuals adjust their opinions in a given time frame and do opinion adjustments after social influence remain effective also in the long run? Modelers’ decisions to either adopt or reject certain assumptions can have decisive effects on model behavior, but the empirical literature on social influence is still too limited to validate social-influence models at the level of precision needed for empirically informed choices between model alternatives.
Furthermore, even some of the most important assumptions of existing models have hardly been tested. For instance, the predictions of bounded-confidence models depend critically on the position of the confidence thresholds beyond which individuals are not influenced. Likewise, whether repulsive influence alters opinion dynamics depends on how much opinion divergence between two individuals is required to trigger repulsive influence. To our knowledge, however, there is no research quantifying these thresholds and their distributions in a population. There is also relatively little research yet directly testing the psychological and structural conditions under which confidence thresholds or repulsive-influence thresholds shift (for some exceptions see Chacoma and Zanette 2015; Mavrodiev, Tessone and Schweitzer 2013; Moussaïd et al. 2013). Furthermore, modeling work has demonstrated that the predictions of bounded-confidence models can change when actors sometimes deviate from the bounded-confidence assumption, even when deviations are rare and random (Kurahashi-Nakamura et al. 2016; Mäs et al. 2010; Pineda et al. 2009). There is, however, no empirical research on the frequency and nature of these deviations. While it is not necessarily the task of agent-based modellers to conduct themselves experimental studies that allow better testing and calibration of micro-level assumptions, it is important that model-builders carefully scrutinize available evidence and seek collaboration with empirical researchers where possible, in order to improve the match of empirical evidence with model assumptions.
Assessing model assumptions at the level of precision needed to inform agent-based models requires experiments that systematically vary the degree of dissimilarity between opinions and source, experimentally or statistically controlling for many other potential sources of opinion change such as learning effects, or individual differences in attractiveness, persuasiveness or salience for an issue. In the tradition of Friedkin and Johnsen’s seminal work (Friedkin and Johnsen 2011), recently laboratory experiments have become available that are designed with the goal of testing assumptions of social-influence models (Chacoma and Zanette 2015; Kerckhove et al. 2016; Mavrodiev et al. 2013; Moussaïd et al. 2013). While results of some of these experiments lend some support to assumptions of bounded confidence models, other studies (Takács et al. 2016) find support only for assimilative influence and not for similarity-biased or repulsive influence. Clearly, more experimental research is needed that tests social influence mechanisms in the way they are quantitatively formalized in models of social influence dynamics.
Indirect tests of micro-models with experiments
A fundamental problem of the empirical approach discussed in the previous section is that the assumptions of social-influence models are often hard to put to the test. A key bottleneck is that opinions are latent constructs and, thus, difficult to quantify with the precision assumed in the formal models. Standard opinion measures apply survey methods that provide measures on ordinal scales, making it impossible to directly test key model assumptions, such as the width of confidence intervals for BC models or the opinion distance between two individuals that sparks repulsive influence.
A powerful approach to indirectly test model assumptions is to create laboratory settings for which alternative models of social influence make clearly distinct predictions about the collective outcomes of social-influence dynamics. For instance, Flache and Mäs (Flache and Mäs 2008a; Mäs and Flache 2013) demonstrated that models make opposite predictions about the effects of the timing of contacts. According to models of assimilative social influence, the outcome of influence dynamics hardly depend on who is when interacting with whom. In a model with repulsive influence, in contrast, opinion bi-polarization is likely to obtain when individuals are first exposed to social influence from dissimilar sources and only later experience influence from similar actors, because repulsive influence will intensify opinion differences in the first phase. In the reversed scenario, however, influence between similar actors in the first phase will decrease opinion differences in the population and, thus, decrease chances that actors will influence each other negatively when they interact with others who held divergent views at the outset. Finding empirical support for the prediction that the timing of contacts matters in the described way, would provide indirect support for the repulsive influence assumption. Furthermore, the timing-of-contacts prediction also allows the exploration of the conditions of repulsive influence. One could test, for instance, whether the timing-of-contacts effect is stronger when the issue at stake is highly emotional or when influence dynamics act in tandem with processes of group identification.
Testing micro-models with survey data
Surveys are the workhorse of much social-scientific research on beliefs, opinions, and behavior. While survey studies have been conducted to test assumptions about opinion changes in public debate over time (e.g. Krosnick, Holbrook and Visser 2000), it remains challenging to link such results to the micro-assumptions about social influence in agent-based models. A central disadvantage of many survey studies is that they are based on random or quasi-random sampling, a method designed to test hypotheses about the distribution of individual characteristics and the statistical relationships between them. The challenge to using this data for the study of social influence is that influence processes can amplify relationships between individual characteristics. For instance, a causal relationship between individuals’ educational level and their political opinions is intensified when individuals with similar educational levels tend to interact more (homophily), and therefore tend to be socially influenced by others with similar education. As a consequence, relatively small statistical relationships resulting from a causal relation between educational level and political opinion can be largely exaggerated in survey data (DellaPosta, Shi and Macy 2015). This may mislead research into attributing strong observed associations to causal effects of individual attributes, while actually the main driving force is social influence.
Uncovering the impact of social influence on statistical relationships with random samples is challenging because the statistical analysis of random samples requires the assumption that observations are independent, which contradicts the assumption of social influence. To be sure, it is not impossible to study social influence with random samples. For instance, Opp and Gern found that during the revolution in East Germany survey respondents who reported that their friends and family were politically active participated more in the protests (Opp and Gern 1993). However, in order to put to the test the critical assumptions of similarity biased or repulsive influence, survey respondents would need to be able to reliably quantify the opinions of their potentially influential contacts, which appears impossible with existing survey methods.
A promising development for empirically testing micro-assumptions of social influence models in field settings is the increasing availability of longitudinal datasets that combine the dynamics of social networks as well as of opinions in complete social networks, like in school classes (Stark and Flache 2012) or workplaces (Ellwardt, Steglich and Wittek 2012). Rather than drawing random samples in big populations, these studies assess complete social networks in relatively small populations. Recent developments in statistical methodologies have made it possible to utilize such data. Stochastic actor oriented models developed by Snijders and others (Snijders 2011; Snijders and Steglich 2015; Steglich, Snijders and Pearson 2010) combine agent-based modeling of such longitudinal data with statistical estimation and testing of the mechanisms assumed by the modeler. Broadly, the statistical method selects the parameters for the effects (e.g. ethnic homophily and assimilative opinion influence) specified by the modeler by simulating the distribution of the networks and actor attributes for a range of selected parameter values. The program then selects the set of parameters for which the simulation yields the best match with the observed dynamics of network and behavior, allowing statistical inference to estimate parameter values from the data. Applications of this approach allow to disentangle mechanisms of social selection, like homophily based on opinions or ethnicity (Stark and Flache 2012), from processes of social influence. Yet, while many studies using this paradigm have documented social influence, future research is needed to test more specific assumptions about social influence that allow assessing and distinguishing assimilative, similarity-biased or repulsive influence, and how the degree to which such processes occur in microlevel interactions relates to macro-structural properties of emergent network structures (Snijders and Steglich 2015) and opinion distributions.
Testing macro-predictions
A key question is whether and to what extent the structural conditions predicted by the models can explain differences in diversity or polarization at the macro-level (e.g. between countries). Large scale social surveys as the European Social Survey, the World/European Values Survey and others provide a source of validation and further improvement of social influence models (e.g. Brousmiche et al. 2016; Chattoe-Brown 2014). Such surveys repeatedly (e.g. every couple of years) ask a representative sample of the populations in several countries to report opinions and attitudes to the same or similar standard questions which are often measured on a relatively fine-grained "quasi-continuous" scale (e.g. 0 → 10). This does not provide us with data of opinion change on the individual level, but it shows macroscopic opinion landscapes as demonstrated in Figure 3 for the political left-right self-placement (and opinion about European integration) in France (and other countries) from the European Social Survey 2012.
All these opinion landscapes do neither look exactly as stylized outcomes of the simple versions from our core model, nor do they show a simple shape like a normal or Beta-distribution. Yet, these data can be seen as some evidence for the main characteristics of all the three core mechanisms of social influence dynamics discussed above:
- A strong dominant central peak in all landscapes suggests some assimilation towards the moderate or central opinion in a population.
- A tendency for off-central but non-extreme clusters - usually on both sides of the central cluster – is consistent with the clustering generated by social influence processes with similarity bias.
- Extremal peaks, typically on both extreme ends of the spectrum, resemble the bi-polarization generated by a mix of assimilative and repulsive processes. However, such peaks might also be explained by an attraction of extreme positions per se or by overshooting as Lorenz (2009) found in histograms of movie ratings.
The fact that clusters are not perfectly separated can be explained relatively well by noise in the form of a small influx of fresh opinions through turnover or reconsideration of opinions through processes independent from social influence as modeled by random draws as the initial distribution (see Pineda et al. 2009). Nevertheless, it is not possible to model such landscapes with the bounded confidence model and noise alone (Lorenz 2017).
Analysis and characterization of such opinion landscapes can be a route to data-driven modeling of more realistic and more predictive models of social influence using the knowledge gained by a deeper understanding of the mechanisms presented here. Calibrating models to resemble patterns observed in opinion surveys will be most fruitful if agent-based modelers at the same time assess to what extent those models that best fit macro-level patterns also contain assumptions that are compatible with empirical evidence available about micro-level processes of social influences and meso-structural conditions (e.g. structures of social networks). As we argued above, micro level evidence that can narrow down the set of models suitable to match opinion distributions observed in surveys can be obtained from experimental studies or studies of the co-evolution of networks and opinions in longitudinal data. Further empirical sources can be used to calibrate assumptions models make about meso-level structures. For example, structural features of social networks in a population at large can be assessed from increasingly available data sets of online networks (Eagle, Macy and Claxton 2010) or global network indicators measured in surveys (DiPrete et al. 2011).
Conclusion
While scholars agree that social influence is a strong force in social interaction, our review of the literature documented considerable variation across approaches on how to formally capture social influence on the micro-level, as well as about the macro-consequences arising from repeated social influence in networks. Nevertheless, we argued that a large part of the literature can be categorized into three classes of formal models, each of which is described by certain crucial assumptions about social influence on the micro level and characteristic predictions about emergent macro-dynamics.
Our review could not do justice to every contribution to the literature, but we believe our classification can serve as a general guideline for the development and communication of social-influence models. As important predictions generated by models belonging to each of the three classes are well understood, contributions based on a model falling into one of the three categories should make explicit the commonalities with existing models. Readers should also be provided with theoretical and empirical arguments for the choice of a given model class. Furthermore, contributions to the literature that do not belong to one of the three classes should discuss where the proposed model deviates from the assumptions defining the three classes and why this deviation was included. Ideally, it would also be tested whether and under what conditions the deviation from the three classes is responsible for new predictions about macro outcomes.
In the second part of the present paper, we identified two main frontiers in the literature on social-influence models. We argued that the field of social-influence modeling profits from a rich arsenal of theoretical models, but also suffers from a lack of systematic comparison of competing models. Likewise, resonating earlier calls for closer interaction between social scientists and model-builders (Sobkowicz 2009), we conclude that there is a need for more empirical research testing micro-level assumptions as well as macro-level predictions, and for a better link of both to model results.
Progress on both frontiers is urgently needed if modelers want to make use of the potential of social-influence models to inform public debate, and decision-making about policies. Various promising developments in the literature highlight this potential. For instance, models extending the approaches discussed here have been calibrated and validated to study dynamics of citizens’ opinions about the conflicting forces in the Afghan civil war (Brousmiche et al. 2016, 2017). Similarly, an increasing number of agent-based social influence models aim to explain changes in the distribution of political opinions in western societies based on partially calibrated micromodels of social influence (Chattoe-Brown 2014; Duggins 2017). Similar efforts address effects of agri-environmental policies on the spreading of environmentally friendly measures among farmers (Deffuant, Huet and Skerratt 2008). As a last example, models that incorporate social-influence dynamics as one part of the process of strategic decision-making in political contexts have been calibrated to detailed data about specific policy-domains and were successfully applied in modelling outcomes in areas such as climate-treaty negotiations (Stokman, Van der Knoop and Van Oosten 2013).
These examples of efforts to link agent-based models of social influence to concrete societal realms are encouraging, but too often the literature on social-influence dynamics leaves us with great uncertainty about the causes and consequences of important societal dynamics. For instance, while there is no doubt that globalization and technological advances such as the Internet have changed how and with whom people communicate, agent-based modelers have only just begun to use models of social influence to address the question how this will affect societal processes of collective decision making and opinion polarization (e.g. Del Vicario et al. 2017). Based on models of social-influence, some warn that the personalization of Internet services can contribute to processes of opinion polarization (Dandekar et al. 2013; Mäs and Bischofberger 2015). Personalization algorithms tailor online services to the preferences and interests of each individual user, increasingly exposing them to other users advocating views and ideas that support their opinions. Being socially influenced, it has been argued, Internet users’ opinions are reinforced, a process that can aggregate to polarized opinion distributions. While this prediction has been demonstrated to be in line with some models of social influence, it is also in clear contrast to the predictions of other models – in particular models with repulsive influence. Repulsive influence fosters opinion polarization when actors with opposing opinions interact. Such encounters, however, are rare if the web is personalized, which would lead to less rather than more opinion polarization (Mäs and Bischofberger 2015) according to these models.
Effects of the Internet on public debate is but one area in which different social influence models entail radically different predictions. This illustrates that based on the current state-of-the-art in the field, it remains difficult to explain and predict outcomes of social influence processes shaping concrete societal dynamics. This highlights the need to move further ahead in integrating, calibrating and testing models. The tools in the toolbox of agent-based modelers on the one hand and of empirical social scientists on the other hand, offer perspectives to successfully address these problems. A marriage between their approaches is not only possible, but also urgently needed. We are convinced that this marriage will lead to deeper insights than each of the partners could obtain without the other one.
Acknowledgements
AF, MM and TF acknowledge that their contribution to this work has benefited from stimulating discussions with the members of the "Norms and Networks" research group at the Department of Sociology / ICS, University of Groningen. JL acknowledges funding from the German Research Foundation (DFG LO2024/2-1 "Opinion Dynamics and Collective Decision"). SH and GD acknowledge funding from the Auvergne Region (Emergent themes 2015, project Associatione). All authors wish to thank Flaminio Squazzoni for his great patience in waiting for us to finish the manuscript.Notes
- In addition we assumed for Figure 1a a population of N=100 agents, initial opinions were drawn randomly from a uniform distribution and weights were homogenous with wij = 1/n for all i,j.
References
ABELSON, R. P. (1964). "Mathematical Models of the Distribution of Attitudes Under Controversy." Pp. 142–60 in Contributions to Mathematical Psychology, edited by N. Frederiksen and H. Gulliksen. New York: Rinehart Winston.
ABRAMOWITZ, A. I. and K. L. Saunders, K. L. (2008). Is Polarization a Myth?. Journal of Politics 70(2): 542–55. [doi:10.1017/S0022381608080493]
AKERS, R. L., Krohn, M. D., Lanza-Kaduce, L. and Radosevich, M. (1979). Social Learning and Deviant Behavior: a Specific Test of a General Theory. American Sociological Review 44(4): 636–55. [doi:10.2307/2094592]
ALLAHVERDYAN, A. and Galstyan, A. (2014). Opinion dynamics with confirmation bias. PLoS ONE, 9(7): e99557.
ALLPORT, G. W. (1924). Social Psychology. Boston: Houghton Mifflin.
AMBLARD, F. and Deffuant, G. (2004). The Role of Network Topology on Extremism Propagation with the Relative Agreement Opinion Dynamics. Physica A: Statistical Mechanics and its Applications 343: 725–38. [doi:10.1016/j.physa.2004.06.102]
ASCH, S. E. (1955). Opinions and Social Pressure. Readings about the social animal 193: 17–26.
ASCH, S. E. (1956). Studies of Independence and Conformity: I. A Minority of One against a Unanimous Majority. Psychological Monographs: General and Applied 70(9): 1–70. [doi:10.1037/h0093718]
AXELROD, R. (1997). The Dissemination of Culture - A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution 41(2): 203–26. [doi:10.1177/0022002797041002001]
BALDASSARRI, D. and Bearman, P. (2007). Dynamics of Political Polarization. American Sociological Review 72(5): 784–811. [doi:10.1177/000312240707200507]
BERGER, R. L. (1981). A Necessary and Sufficient Condition for Reaching a Consensus Using DeGroot’s Method. Journal of the American Statistical Association 76: 415–18. [doi:10.1080/01621459.1981.10477662]
BIKHCHANDANI, S., Hirshleifer, D. and Welch, I. (1992). A Theory of Fads, Fashion, Custom, and Cultural-Change as Informational Cascades. Journal of Political Economy 100(5): 992–1026. [doi:10.1086/261849]
BOHNER, G. and Dickel, N. (2011). Attitudes and Attitude Change. Annual Review of Psychology 62(1): 391–417. [doi:10.1146/annurev.psych.121208.131609]
BONACICH, P. and Lu, P. (2012). Introduction to Mathematical Sociology. Princeton and Oxford: Princeton University Press.
BOND, R. M., Fariss, C. J., Jones, J. J., Kramer, A. D., Marlow, C., Settle, J. E., & Fowler, J. H. (2012). A 61-Million-Person Experiment in Social Influence and Political Mobilization. Nature 489(7415): 295–98. [doi:10.1038/nature11421]
BOURDIEU, P. (1984) [1979]. Distinction: A Social Critique of the Judgment of Taste. Cambridge, MA: Harvard University Press.
BRAMSON, A., Grim, P., Singer, D.J., Fisher, S., Berger, W., Sack, G. and Flocken, C., (2016). Disambiguation of social polarization concepts and measures. The Journal of Mathematical Sociology, 40(2): 80-111. [doi:10.1080/0022250X.2016.1147443]
BREWER, M. B. (1991). The Social Self: On Being the Same and Different at the Same Time. Personality and Social Psychology Bulletin 17(5): 475–82. [doi:10.1177/0146167291175001]
BROUSMICHE, K.-L., Kant, J.-D., Sabouret, N. and Prenot-Guinard, F. (2016). From Beliefs to Attitudes: Polias, a Model of Attitude Dynamics Based on Cognitive Modeling and Field Data. Journal of Artificial Societies and Social Simulation 19(4), 2: https://www.jasss.org/19/4/2.html. [doi:10.18564/jasss.3161]
BROUSMICHE, K., Kant, J.-D., Sabouret, N. and Prenot-Guinard, F. (2017). From Field Data to Attitude Formation. in Advances in Social Simulation 2015, edited by W. Jager et al. Cham, Switzerland: Springer International Publishing. [doi:10.1007/978-3-319-47253-9_1]
BYRNE, D. (1971). The Attraction Paradigm. New York, London: Academic Press.
CARLEY, K. (1991). A Theory of Group Stability. American Sociological Review 56(3): 331–54. [doi:10.2307/2096108]
CASTELLANO, C., S. Fortunato, and V. Loreto. (2009). Statistical Physics of Social Dynamics. Reviews of Modern Physics 81(2): 591–646. [doi:10.1103/RevModPhys.81.591]
CENTOLA, D., González-Avella, J. C., Eguíluz, V. M. and San Miguel, M. (2007). Homophily, Cultural Drift, and the Co-Evolution of Cultural Groups. Journal of Conflict Resolution 51(6): 905–29. [doi:10.1177/0022002707307632]
CHACOMA, A. and Zanette, D. H. (2015). Opinion Formation by Social Influence: From Experiments to Modeling. PLoS ONE 10(10): e0140406. [doi:10.1371/journal.pone.0140406]
CHATTOE-BROWN, E. (2014). Using Agent Based Modelling to Integrate Data on Attitude Change. Sociological Research Online 19(1), 16: http://www.socresonline.org.uk/19/1/16.html. [doi:10.5153/sro.3315]
CONTE, R., Castelfranchi, C. (1995). Cognitive and Social Action. London: UCL Press.
CONTE, R. and Paolucci, M. (2002). Reputation in Artificial Societies: Social Beliefs for Social Order. Kluwer Academic Publishers. Boston (Ma.): Kluwer. [doi:10.1007/978-1-4615-1159-5]
DANDEKAR, P., Goel, A. and Lee, D. T.. (2013). Biased Assimilation, Homophily, and the Dynamics of Polarization. Proceedings of the National Academy of Sciences of the United States of America, 110(15): 5791–96. [doi:10.1073/pnas.1217220110]
DEFFUANT, G. (2006). Comparing Extremism Propagation Patterns in Continuous Opinion Models. Journal of Artificial Societies and Social Simulation 9(3), 8: https://www.jasss.org/9/3/8.html.
DEFFUANT, G., Amblard, F., Weisbuch, G. and Faure, T. (2002). How Can Extremism Prevail? A Study Based on the Relative Agreement Interaction Model. Journal of Artificial Societies and Social Simulation 5(4), 1: https://www.jasss.org/5/4/1.html.
DEFFUANT, G., Huet, S. and Amblard, F. (2005). An Individual-Based Model of Innovation Diffusion Mixing Social Value and Individual Benefit. American Journal of Sociology 110(4): 1041–69. [doi:10.1086/430220]
DEFFUANT, G., Huet, S. and Skerratt, S. (2008). 'An Agent Based Model of Agri-Environmental Measure Diffusion: What For?' Pp. 55–73 in Agent Based Modelling in Natural Resource Management, edited by A. Lopez Paredes and C. Hernandez Iglesias. Valladolid: INSISOC.
DEFFUANT, G., Neau, D., Amblard, F. and Weisbuch, G. (2000). Mixing Beliefs among Interacting Agents. Advances in Complex Systems 3(01n04): 87–98.
DEFFUANT, G. and Weisbuch, G. (2008). 'Probability Distribution Dynamics Explaining Agent Model Convergence to Extremism'. In Edmonds, B., Troitzsch, K. G., & Hernández Iglesias, C. (Eds.), Social Simulation: Technologies, Advances and New Discoveries, Hershey, PA: IGI Global, pp. 43-60. [doi:10.4018/978-1-59904-522-1.ch004]
DEGROOT, M. H. (1974). Reaching a Consensus. Journal of the American Statistical Association 69:118–21. [doi:10.1080/01621459.1974.10480137]
DELLAPOSTA, D., Shi, Y. and Macy, M. (2015). Why Do Liberals Drink Lattes?. American Journal of Sociology 120(5): 1473–1511. [doi:10.1086/681254]
DE SANCTIS, L. and Galla, T. (2009). Effects of noise and confidence thresholds in nominal and metric Axelrod dynamics of social influence. Physical Review E, 79(4): 046108. [doi:10.1103/PhysRevE.79.046108]
DIMAGGIO, P., Evans, J. and Bryson, B. (1996). Have American’s Social Attitudes Become More Polarized?. American Journal of Sociology 102(3):690. [doi:10.1086/230995]
DIPRETE, T. A., Gelman, A., McCormick, T., Teitler, J. and Zheng, T. (2011). Segregation in Social Networks Based on Acquaintanceship and Trust. American Journal of Sociology 116(4): 1234–83. [doi:10.1086/659100]
DUGGINS, P. (2017). A Psychologically-Motivated Model of Opinion Change with Applications to American Politics. Journal of Artificial Societies and Social Simulation 20(1), 13: https://www.jasss.org/20/1/13.html. [doi:10.18564/jasss.3316]
DURKHEIM, E. (1982) [1895]. The Rules of Sociological Method. edited by S. Lukes. New York: The Free Press. [doi:10.1007/978-1-349-16939-9]
DYKSTRA, P., Jager, W., Elsenbroich, C., Verbrugge, R. and de Lavalette G.R. (2015). An Agent-Based Dialogical Model with Fuzzy Attitudes. Journal of Artificial Societies and Social Simulation 18(3), 3: https://www.jasss.org/18/3/3.html. [doi: 10.18564/jasss.2813]
EAGLE, N., Macy, M. and Claxton, R. (2010). Network Diversity and Economic Development. Science 328(5981): 1029–31. [doi:10.1126/science.1186605]
EAGLY, A. H. and Chaiken, S. (1993a). 'Process Theories of Attitude Formation and Change: Attribution Approaches and Social Judgment Theory.' Pp. 351–88 in The Psychology of Attitudes, edited by A. H. Eagly and S. Chaiken. Worth, TX: Thomson/Wadsworth.
EAGLY, A. H. and Chaiken, S. (1993b). The Nature of Attitudes. The Psychology of Attitudes 1–21.
EARLEY, P. C. and Mosakowski, E. (2000). Creating Hybrid Team Cultures: An Empirical Test of Transnational Team Functioning. Academy of Management Journal 43(1): 26–49. [doi:10.2307/1556384]
ELIAS, N. (1978). The Civilizing Process: The History of Manners. Oxford: Blackwell.
ELLWARDT, L., Steglich, C. and R. Wittek, R. (2012). The Co-Evolution of Gossip and Friendship in Workplace Social Networks. Social Networks 34(4): 623–33. [doi:10.1016/j.socnet.2012.07.002]
EPSTEIN, J. M. (1999). Agent-Based Computational Models and Generative Social Science. Complexity 4(5): 41–60. [doi:10.1002/(SICI)1099-0526(199905/06)4:5<41::AID-CPLX9>3.0.CO;2-F]
EVANS, J. H. (2003). Have Americans’ Attitudes Become More Polarized? An Update. Social Science Quarterly 84(1): 71–90. [doi:10.1111/1540-6237.8401005]
FELD, S. L. (1982). Social Structural Determinants of Similarity among Associates. American Sociological Review 47(6): 797–801. [doi:10.2307/2095216]
FELDMAN, K. A. and Newcomb, T. M. (1969). The Impact of College on Students. San Francisco: Jossey-Bass.
FELICIANI, T., Flache, A. and Tolsma, J. (2017). How, When and Where Can Spatial Segregation Induce Opinion Polarization? Two Competing Models. Journal of Artificial Societies and Social Simulation, 20(2), 6: https://www.jasss.org/20/2/6.html. [doi:10.18564/jasss.3419]
FESTINGER, L. (1957). A Theory of Cognitive Dissonance. Stanford: Stanford University Press.
FESTINGER, L., Schachter, S. and Back, K. (1950). Social Pressures in Informal Groups. Stanford, CA: Stanford University Press.
FIORINA, M. P. and S. J. Abrams. (2008). Political Polarization in the American Public. Annual Review of Political Science 11: 563–88. [doi:10.1146/annurev.polisci.11.053106.153836]
FLACHE, A., Macy, M., & Takács, K. (2006). 'What sustains cultural diversity and what undermines it? Axelrod and beyond'. P. 9 – 16. In S. Takahashi (Ed.), Advancing Social Simulation: Proceedings of the First World Congress on Social Simulation (pp. 9 - 16). Kyoto, Japan: Springer.
FLACHE, A. and Macy, M. W. (2011a). Local Convergence and Global Diversity: From Interpersonal to Social Influence. Journal of Conflict Resolution 55(6): 970–95. [doi:10.1177/0022002711414371]
FLACHE, A. and Macy, M. W. (2011b). Small Worlds and Cultural Polarization. The Journal of Mathematical Sociology 35(1–3): 146–76. [doi:10.1080/0022250X.2010.532261]
FLACHE, A. and Mäs, M. (2008a). How to Get the Timing Right. A Computational Model of the Effects of the Timing of Contacts on Team Cohesion in Demographically Diverse Teams. Computational and Mathematical Organization Theory 14(1): 23–51. [doi:10.1007/s10588-008-9019-1]
FLACHE, A. and Mäs, M. (2008b). Why Do Faultlines Matter? A Computational Model of How Strong Demographic Faultlines Undermine Team Cohesion. Simulation Modelling Practice and Theory 16(2): 175–91. [doi:10.1016/j.simpat.2007.11.020]
FORTUNATO, S. (2005). On The Consensus Threshold for the Opinion Dynamics of Krause-Hegselmann. International Journal of Modern Physics C 16(2): 259–70. [doi:10.1142/S0129183105007078]
FRENCH, J. R. (1956). A Formal Theory of Social Power. Psychological Review 63(3): 181–94. [doi:10.1037/h0046123]
FRIEDKIN, N. E. (1990). Social Networks in Structural Equation Models. Social Psychology Quarterly 53(4): 316–28. [doi:10.2307/2786737]
FRIEDKIN, N. E. and Johnsen, E. C. (1990). Social Influence and Opinions. The Journal of Mathematical Sociology 15(3–4): 193–206. [doi:10.1080/0022250X.1990.9990069]
FRIEDKIN, N. E. and Johnsen, E. C. (2011). Social Influence Network Theory. New York: Cambridge University Press. [doi:10.1017/CBO9780511976735]
GALAM, S. (2002). Minority Opinion Spreading in Random Geometry. The European Physical Journal B 25(4): 403–6. [doi:10.1140/epjb/e20020045]
GALAM, S. (2004). Contrarian Deterministic Effects on Opinion Dynamics: the "Hung Elections Scenario". Physica A: Statistical Mechanics and its Applications 333: 453–60. [doi:10.1016/j.physa.2003.10.041]
GARGIULO, F. and Huet, S. (2012). New Discussions Challenge the Organization of Societies. Advances in Complex Systems 15(7): 1250033. [doi:10.1142/S0219525912500336]
GENTZKOW, M. (2016). Polarization in 2016. Toulouse Network of Information Technology white paper.
GIARDINI, F., Vilone, D., Conte, R. (2015). Consensus emerging from the bottom-up: the role of cognitive variables in opinion dynamics. Frontiers in Physics 3: 64: http://journal.frontiersin.org/article/10.3389/fphy.2015.00064. [doi:10.3389/fphy.2015.00064]
GLAESER, E. L. and Ward, B. A. (2006). Myths and Realities of American Political Geography. Journal of Economic Perspectives 20(2): 119–44. [doi:10.1257/jep.20.2.119]
GONZÁLEZ-AVELLA, J. C., Cosenza, M. G., Klemm, K., Eguíluz, V. M. and San Miguel, M. (2007). Information Feedback and Mass Media Effects in Cultural Dynamics. Journal of Artificial Societies and Social Simulation 10(3), 9: https://www.jasss.org/10/3/9.html.
GREIG, M. J. (2002). The End of Geography? Globalization, Communication and Culture in the International System. Journal of Conflict Resolution 46(2): 225–43. [doi:10.1177/0022002702046002003]
GROEBER, P., Lorenz, J. and Schweitzer, F. (2014). Dissonance Minimization as a Microfoundation of Social Influence in Models of Opinion Formation. The Journal of Mathematical Sociology 38(3): 147–74. [doi:10.1080/0022250X.2012.724486]
GROW, A. and Flache, A. (2011). How Attitude Certainty Tempers the Effects of Faultlines in Demographically Diverse Teams. Computational and Mathematical Organization Theory 17(2): 196–224. [doi:10.1007/s10588-011-9087-5]
HARARY, F. (1959). 'A Criterion for Unanimity in French’s Theory of Social Power.' Pp. 168–82 in Studies in social power, edited by D. Cartwright. Ann Arbor: Institute for Social Research.
HEDSTRÖM, P. and P. Ylikoski. (2010). Causal Mechanisms in the Social Sciences. Annual Review of Sociology 36(1): 49–67. [doi:10.1146/annurev.soc.012809.102632]
HEGSELMANN, R. and Krause, U. (2002). Opinion Dynamics and Bounded Confidence: Models, Analysis and Simulation. Journal of Artificial Societies and Social Simulation 5(3), 2: https://www.jasss.org/5/3/2.html.
HEGSELMANN, R. and Krause, U. (2015). Opinion Dynamics under the Influence of Radical Groups, Charismatic Leaders, and Other Constant Signals: A Simple Unifying Model. Networks and Heterogeneous Media 10(3): 477–509. [doi:10.3934/nhm.2015.10.477]
HEIDER, F. (1946). Attitudes and Cognitive Organization. The Journal of Psychology 21: 107–12. [doi:10.1080/00223980.1946.9917275]
HEIDER, F. (1967). 'Attitudes and Cognitive Organization.' Pp. 39–41 in Readings in Attitude Theory and Measurement, edited by M. Fishbein. New York, London, Sydney: John Wiley and Sons, Inc.
HO, S. S. and McLeod, D. M. (2008). Social-Psychological Influences on Opinion Expression in Face-to-Face and Computer-Mediated Communication. Communication Research 35(2): 190–207. [doi:10.1177/0093650207313159]
HOLLEY, R. A. and T. M. Liggett. (1975). Ergodic Theorems for Weakly Interacting Infinite Systems and the Voter Model. Annals of Probability 2(5): 347–70. [doi:10.1214/aop/1176996306]
HOMANS, G. C. (1950). The Human Group. New York: Harcourt, Brace, & World.
HOVLAND, C. I., Harvey, O. J. and Sherif, M. (1957). Assimilation and Contrast Effects in Reactions to Communication and Attitude Change. The Journal of Abnormal and Social Psychology 55(2): 244–52. [doi:10.1037/h0048480]
HUET, S. and Deffuant, G. (2010). Openness Leads to Opinion Stability and Narrowness to Volatility. Advances in Complex Systems 13(3): 405–23. [doi:10.1142/S0219525910002633]
HUET, S., Deffuant, G. and Jager, W. (2008). A Rejection Mechanism in 2D Bounded Confidence Provides More Conformity. Advances in Complex Systems 11(4): 529–49. [doi:10.1142/S0219525908001799]
HUNTER, J. E., Danes, J. E. and Cohen, S. H. (1984). Mathematical Models of Attitude Change. edited by P. R. Monge. Academic Press.
IMHOFF, R. and Erb, H.-P. (2009). What Motivates Nonconformity? Uniqueness Seeking Blocks Majority Influence. Personality & social psychology bulletin 35(3): 309–20. [doi:10.1177/0146167208328166]
JAGER, W. and Amblard, F. (2005). Uniformity, Bipolarization and Pluriformity Captured as Generic Stylized Behavior with an Agent-Based Simulation Model of Attitude Change. Computational & Mathematical Organization Theory 10(4): 295–303. [doi:10.1007/s10588-005-6282-2]
KATZ, E. and Lazarsfeld, P. F. (1955). Personal Influence. Glencoe, IL: Free Press.
KLEMM, K., Eguiluz, V. M., Toral, R. and Miguel, M. S. (2003). Global Culture: A Noise-Induced Transition in Finite Systems. Physical Review E 67(4): 045101(R). [doi:10.1103/PhysRevE.67.045101]
KLEMM, K., Eguiluz, V. M., Toral, R. and Miguel, M. S. (2003). Nonequilibrium Transitions in Complex Networks: A Model of Social Interaction. Physical Review E 67(2): 026120 (R). [doi:10.1103/PhysRevE.67.026120]
KLEMM, K., Eguiluz, V. M., Toral, R. and Miguel, M. S. (2005). Globalization, Polarization and Cultural Drift. Journal of Economic Dynamics & Control 29(1–2): 321–34. [doi:10.1016/j.jedc.2003.08.005]
KROSNICK, J. A., Holbrook, A. L. and Visser, P. S. (2000). The Impact of the Fall 1997 Debate about Global Warming on American Public Opinion. Public Understanding of Science 9(3): 239–60. [doi:10.1088/0963-6625/9/3/303]
KURAHASHI-NAKAMURA, T., Mäs, M. and Lorenz, J. (2016). Robust Clustering in Generalized Bounded Confidence Models. Journal of Artificial Societies and Social Simulation 19 (4), 7: https://www.jasss.org/19/4/7.htm [doi:10.18564/jasss.3220]
LATANÉ, B. (1996). Dynamic Social Impact: The Creation of Culture by Communication. Journal of Communication 46(4): 13–25. [doi:10.1111/j.1460-2466.1996.tb01501.x]
LATANÉ, B. and L’Herrou, T. (1996). Spatial Clustering in the Conformity Game: Dynamic Social Impact in Electronic Groups. Journal of Personality and Social Psychology 70(6): 1218–30. [doi:10.1037/0022-3514.70.6.1218]
LAU, D. C. and Murnighan, J. K.. (1998). Demographic Diversity and Faultlines: The Compositional Dynamics of Organizational Groups. Academy of Management Review 23(2): 325–40.
LAZARSFELD, P. F. and Merton, R. K. (1954). 'Friendship and Social Process: A Substantive and Methodological Analysis'. Pp. 18–66 in Freedom and Control in Modern Society, edited by M. Berger, T. Abel, and C. H. Page. New York, Toronto, London: Van Nostrand.
LEHRER, K. (1975). Social Consensus and Rational Agnoiology. Synthese 31: 141–60. [doi:10.1007/BF00869475]
LEVENDUSKY, M. S. (2009). The Microfoundations of Mass Polarization. Political Analysis 17(2): 162–76. [doi:10.1093/pan/mpp003]
LIGGETT, T. M. (1985). Interacting Particle Systems. New York: Springer. [doi:10.1007/978-1-4613-8542-4]
LIU, C. C. and Srivastava, S. B. (2015). Pulling Closer and Moving Apart: Interaction, Identity, and Influence in the U.S. Senate, 1973 to 2009. American Sociological Review 80(1): 192–217. [doi:10.1177/0003122414564182]
LORENZ, J. (2007). Continuous Opinion Dynamics under Bounded Confidence: A Survey. International Journal of Modern Physics C 18(12): 1819–38. [doi:10.1142/S0129183107011789]
LORENZ, J. (2008). 'Fostering Consensus in Multidimensional Continuous Opinion Dynamics under Bounded Confidence'. Pp. 321–34 in Managing Complexity: Insights, Concepts, Applications, vol. 2008. Berlin, Heidelberg: Springer Berlin Heidelberg. [doi:10.1007/978-3-540-75261-5_15]
LORENZ, J. (2009). Universality in Movie Rating Distributions. The European Physical Journal B 71(2): 251–58. [doi:10.1140/epjb/e2009-00283-3]
LORENZ, J. (2010). Heterogeneous Bounds of Confidence: Meet, Discuss and Find Consensus! Complexity 15(4): 43–52. [doi:10.1002/cplx.20295]
LORENZ, J. (2017). 'Modeling the Evolution of Ideological Landscapes Through Opinion Dynamics'. Pp. 255–66 in Advances in Social Simulation 2015, edited by W. Jager et al. Cham, Switzerland: Springer International Publishing. [doi:10.1007/978-3-319-47253-9_22]
MACY, M. and Flache, A. (2009). 'Social Dynamics from the Bottom Up: Agent-Based Models of Social Interaction'. Pp. 245–68 in The Oxford Handbook of Analytical Sociology, vol. 1, edited by P. Bearman and P. Hedström. Oxford University Press.
MACY, M. W., Kitts, J. A.,Flache, A. and Benard, S. (2003). 'Polarization in Dynamic Networks: A Hopfield Model of Emergent Structure'. Pp. 162–73 in Dynamic Social Network Modeling and Analysis: Workshop Summary and Papers, edited by R. Breiger, K. Carley, and P. Pattison. Washington: The National Academies Press.
MARK, N. P. (1998). Beyond Individual Differences: Social Differentiation from First Principles. American Sociological Review 63(3): 309–30. [doi:10.2307/2657552]
MARK, N. P. (2003). Culture and Competition: Homophily and Distancing Explanations for Cultural Niches. American Sociological Review 68(3): 319–45. [doi:10.2307/1519727]
MÄS, M. and Bischofberger, L. (2015). Will the Personalization of Online Social Networks Foster Opinion Polarization? Paper presented at Lorenz Workshop on Socio-Economic Complexity, Lorenz Center Leiden, The Netherlands. Available at SSRN: https://ssrn.com/abstract=2553436. [doi:10.2139/ssrn.2553436]
MÄS, M. and Flache, A. (2013). Differentiation without Distancing. Explaining Opinion Bi-Polarization without Assuming Negative Influence. PLoS ONE 8(11). [doi:10.1371/journal.pone.0074516]
MÄS, M., Flache, A. and Helbing, D. (2010). Individualization as Driving Force of Clustering Phenomena in Humans. PLoS Computational Biology 6(10): e1000959. [doi:10.1371/journal.pcbi.1000959]
MÄS, M., Flache, A. and Kitts, J. A. (2014). 'Cultural Integration and Differentiation in Groups and Organizations'. Pp. 71–90 in Perspectives on Culture and Agent-based Simulations, edited by V. Dignum and F. Dignum. Cham: Springer International Publishing. [doi:10.1007/978-3-319-01952-9_5]
MÄS, M., Flache, A. Takács, K. and Jehn, K. (2013). In the Short Term We Divide, in the Long Term We Unite: Demographic Crisscrossing and the Effects of Faultlines on Subgroup Polarization. Organization Science 24(3): 716–36. [doi:10.1287/orsc.1120.0767]
MASON, W. A., Conrey, F. R. and Smith, .E. R. (2007). Situating Social Influence Processes: Dynamic, Multidirectional Flows of Influence within Social Networks. Personality and Social Psychology Review 11(3): 279–300. [doi:10.1177/1088868307301032]
MATHIAS, J.-D., Huet, S. and Deffuant, G. (2016). Bounded Confidence Model with Fixed Uncertainties and Extremists: The Opinions Can Keep Fluctuating Indefinitely. Journal of Artificial Societies and Social Simulation 19(1), 6: https://www.jasss.org/19/1/6.html. [doi:10.18564/jasss.2967]
MAVRODIEV, P., Tessone, C. J. and F. Schweitzer, F. (2013). Quantifying the Effects of Social Influence. Scientific Reports 3: 1360. [doi:10.1038/srep01360]
MCPHERSON, M., Smith-Lovin, L. and Cook, J. M. (2001). Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology 27(1): 415–44. [doi:10.1146/annurev.soc.27.1.415]
MERTON, R. K. (1957). Social Theory and Social Structure. New York, NY: The Free Press.
MOSCOVICI, S. and Doise, W. (1994). Conflict and Consensus: A General Theory of Collective Decisions. London: Sage.
MOSCOVICI, S. and Zavalloni, M. (1969). The Group as a Polarizer of Attitudes. Journal of Personality and Social Psychology 12(2): 125–35. [doi:10.1037/h0027568]
MOUSSAÏD M., Kämmer, J. E., Analytis, P. P. and Neth, H. (2013). Social Influence and the Collective Dynamics of Opinion Formation. PLoS ONE 8(11): e78433. [doi:10.1371/journal.pone.0078433]
MYERS, D. G. (1978). Polarizing Effects of Social-Comparison. Journal of Experimental Social Psychology 14(6): 554–63. [doi:10.1016/0022-1031(78)90049-5]
MYERS, D. G. (1982). 'Polarizing Effects of Social Interaction'. Pp. 125–61 in Group Decision Making, edited by H. Brandstätter, J. H. Davis, and G. Stocker-Kreichgauer. London: Academic Press.
MYERS, D. G. and Lamm, H. (1976). The Group Polarization Phenomenon. Psychological Bulletin 83(4): 602–27. [doi:10.1037/0033-2909.83.4.602]
NICKERSON, R. S. (1998). Confirmation Bias: A Ubiquitous Phenomenon in Many Guises. Review of General Psychology 2(2): 175–220. [doi:10.1037/1089-2680.2.2.175]
NOWAK, A., Szamrej, J. and Latané, B. (1990). From Private Attitude to Public Opinion: A Dynamic Theory of Social Impact. Psychological Review 97(3): 362–76. [doi:10.1037/0033-295X.97.3.362]
OPP, K.-D. and Gern, C. (1993). Dissident Groups, Personal Networks, and Spontaneous Cooperation: The East German Revolution of 1989. American Sociological Review 58(5): 659–80. [doi:10.2307/2096280]
PARISI, D., Cecconi, F. and F. Natale, F. (2003). Cultural Change in Spatial Environments: The Role of Cultural Assimilation and Internal Changes in Cultures. The Journal of Conflict Resolution 47(2): 163–79. [doi:10.1177/0022002702251025]
PEARSON, M., Steglich, C. E G. and Snijders, T. A. B. (2006). Homophily and Assimilation among Sportactive Adolescent Substance Users. Connections 27(1): 47–63.
PINEDA, M., Toral, R. and Hernández-García, E. (2009). Noisy Continuous-Opinion Dynamics. Journal of Statistical Mechanics: Theory and Experiment 2009(8): P08001. [doi:10.1088/1742-5468/2009/08/P08001]
RICHERSON, P. J. and Boyd, R. (2005). Not by Genes Alone: How Culture Transformed Human Evolution. Chicago: University of Chicago Press.
RIZZOLATTI, G. and Craighero, L. (2004). The Mirror-Neuron System. Annual Review of Neuroscience 27: 169–92. [doi:10.1146/annurev.neuro.27.070203.144230]
ROGERS, E. M. (1995). Diffusion of Innovations. New York: Free Press.
ROSENBAUM, M. E. (1986). The Repulsion Hypothesis: On the Nondevelopment of Relationships. Journal of Personality and Social Psychology 51(6): 1156–66. [doi:10.1037/0022-3514.51.6.1156]
SALZARULO, L. (2006). A Continuous Opinion Dynamics Model Based on the Principle of Meta-Contrast. Journal of Artificial Societies and Social Simulation 9(1), 13: https://www.jasss.org/9/1/13.html.
SASSENBERG, K., Boos, M. and Rabung, S. (2005). Attitude Change in Face-to-Face and Computer-Mediated Communication: Private Self-Awareness as Mediator and Moderator. European Journal of Social Psychology 35(3): 361–74. [doi:10.1002/ejsp.254]
SHERIF, M. (1935). A Study of Some Social Factors in Perception. Archives of Psychology 27, 187: 23- 46.
SHERIF, M. and Hovland, C. I. (1961). Social Judgment. New Haven, CT: Yale University Press.
SHERIF, M. and Sherif, C. W. (1979). 'Research on Intergroup Relations'. Pp. 7–18 in The Social Psychology of Intergroup Relations, edited by W. G. Austin and S. Worchel. Monterey, California: Brooks/Cole Publishing Company.
SHIBANAI, Y., Yasuno, S. and Ishiguro, I. (2001). Effects of Global Information Feedback on Diversity. Journal of Conflict Resolution 45(1): 80–96. [doi:10.1177/0022002701045001004]
SHIN, J. K. and Lorenz, J. (2010). Tipping Diffusivity in Information Accumulation Systems: More Links, Less Consensus. Journal of Statistical Mechanics: Theory and Experiment 2010(6): P06005. [doi:10.1088/1742-5468/2010/06/P06005]
SNIJDERS, T. A. B. (2011). Statistical Models for Social Networks. Annual Review of Sociology 37(1): 131–53. [doi:10.1146/annurev.soc.012809.102709]
SNIJDERS, T. A. B. and Steglich, C. E. G.. (2015). Representing Micro–Macro Linkages by Actor-Based Dynamic Network Models. Sociological Methods & Research 44(2): 222–71. [doi:10.1177/0049124113494573]
SNYDER, C. R. R. and Fromkin, H. L.. (1980). Uniqueness: The Human Pursuit of Difference. edited by S. S. & B. Media. Boston, MA: Springer US. [doi:10.1007/978-1-4684-3659-4]
SOBKOWICZ, P. (2009). Modelling Opinion Formation with Physics Tools: Call for Closer Link with Reality. Journal of Artificial Societies and Social Simulation 12(1), 11: https://www.jasss.org/12/1/11.html.
SOBKOWICZ P. (2012). Discrete Model of Opinion Changes Using Knowledge and Emotions as Control Variables. PLoS ONE 7(9): e44489. [doi:10.1371/journal.pone.0044489]
SOBKOWICZ, P. (2015). Extremism without Extremists: Deffuant Model with Emotions. Frontiers in Physics 3: 17. [doi:10.3389/fphy.2015.00017]
STARK, T. H. and Flache, A. (2012). The Double Edge of Common Interest: Ethnic Segregation as an Unintended Byproduct of Opinion Homophily. Sociology of Education 85(2): 179–99. [doi:10.1177/0038040711427314]
STAUFFER, D. and Meyer-Ortmanns, H. (2004). Simulation of Consensus Model of Deffuant et Al. on a Barabási- Albert Network. International Journal of Modern Physics C 15(2): 241–46. [doi:10.1142/S0129183104005644]
STEGLICH, C. E. G., Snijders, T. A. B. and Pearson, M. (2010). Dynamic Networks and Behavior: Separating Selection from Influence. Sociological Methodology 40(1): 329–93. [doi:10.1111/j.1467-9531.2010.01225.x]
STOKMAN, F. N., Van der Knoop, J. and Van Oosten, R. C. H. (2013). 'Modeling Collective Decision Making'. Pp. 151–82 in Handbook of Rational Choice Social Research, edited by V. Nee, R. Wittek, and T. A. B. Snijders. Stanford CA: Stanford University Press.
STRYKER, S. (1980). Symbolic Interactionism: A Social Structural Version. Benjamin-Cummings Publishing Company.
SZNAJD-WERON, K. and Sznajd, J. (2000). Opinion Evolution in Closed Community. International Journal of Modern Physics C 11(6):1157–65. [doi:10.1142/S0129183100000936]
TAJFEL, H. (1978). Social Categorization, Social Identity and Social Comparison. Differentiation between social groups: Studies in the Social Psychology of Intergroup Relations. London: Academic Press, pp. 61-76.
TAKÁCS, K., Flache, A. and Mäs, M. (2016). Discrepancy and Disliking Do Not Induce Negative Opinion Shifts. PloS ONE 11(6): e0157948. [doi:10.1371/journal.pone.0157948]
TURNER, J. H. (1995). Macrodynamics. Toward a Theory on the Organization of Human Populations. New Brunswick, N.J: Rutgers University Press.
ULLOA, R., Kacperski, C. and Sancho, F. (2016). Institutions and Cultural Diversity: Effects of Democratic and Propaganda Processes on Local Convergence and Global Diversity. PLoS ONE 11(4): e0153334. [doi:10.1371/journal.pone.0153334]
URBIG, D., Lorenz, J. and Herzberg, H. (2008). Opinion Dynamics: The Effect of the Number of Peers Met at Once. Journal of Artificial Societies and Social Simulation, 11(2), 4: https://www.jasss.org/11/2/4.html.
URBIG, D. and Malitz, R. (2007). Drifting to More Extreme but Balanced Attitudes: Multidimensional Attitudes and Selective Exposure. Paper presented at Fourth Conference of the European Social Simulation Association, Toulouse.
VALENTE, T. (1995). Network Models of the Diffusion of Innovations. Cresskill, N.J.: Hampton Press.
VALENTE, T. W. (1996). Social Network Thresholds in the Diffusion of Innovations. Social Networks 18(1): 69–89. [doi:10.1016/0378-8733(95)00256-1]
VANDE KERCKHOVE, C., Martin, S., Gend, P., Rentfrow, P. J., Hendrickx, J. M. and Blondel, V. D. (2016). Modelling Influence and Opinion Evolution in Online Collective Behaviour. PLoS ONE 11(6): e0157685. [doi:10.1371/journal.pone.0157685]
DEL VICARIO, M., Scala, A., Caldarelli, G., Stanley, H. E. and Quattrociocchi, W. (2017). Modeling Confirmation Bias and Polarization. Scientific Reports 7: 40391 [doi:10.1038/srep40391]
VINOKUR, A. and Burnstein, E. (1978). Depolarization of Attitudes in Groups. Journal of Personality and Social Psychology 36(8): 872–85. [doi:10.1037/0022-3514.36.8.872]
WIMMER, A. and Lewis, K. (2010). Beyond and Below Racial Homophily: ERG Models of a Friendship Network Documented on Facebook. American Journal of Sociology 116(2): 583–642. [doi:10.1086/653658]
WIO, H. S., de la Lama, M. S. and Lopez, J. M. (2006). Contrarian-like Behavior and System Size Stochastic Resonance in an Opinion Spreading Model. Physica A: Statistical Mechanics and its Applications 371(1): 108–11. [doi:10.1016/j.physa.2006.04.103]
WOOD, W. (2000). Attitude Change: Persuasion and Social Influence. Annual Review of Psychology 51: 539–70. [doi:10.1146/annurev.psych.51.1.539]
WOOD, W., Pool, G. J., Leck, K. and Purvis, D. (1996). Self-Definition, Defensive Processing, and Influence: The Normative Impact of Majority and Minority Groups. Journal of Personality and Social Psychology 71(6): 1181–93. [doi:10.1037/0022-3514.71.6.1181]

