Introduction
The iterated prisoner’s dilemma is a game that allows to understand various basic truths about social behaviour and how cooperation between entities is established and evolves sharing same space: living organisms sharing an ecological niche, companies competitors fighting over a market, people with questions about the value of conducting a joint work, etc (Axelrod 2006; Beaufils & Mathieu 2006; Kendall et al. 2007; Mathieu et al. 1999; Mittal & Deb 2009; Poundstone 1992; Rapoport & Chammah 1965; Sigmund 2010). Although based on an extreme simplification of the interactions between entities, the mathematical study of the iterated prisoner’s dilemma remains difficult, and often, only computer simulations are able to solve classical questions or identify ways of building efficient behaviours (Beaufils et al. 1996; Kendall et al. 2007; Li et al. 2011; Mathieu et al. 1999; Tzafestas 2000).
A series of works (Beaufils et al. 1996; Delahaye et al. 2000; Li & Kendall 2013; Li et al. 2011; O’Riordan 2000; Press & Dyson 2012; Tzafestas 2000;Wedekind & Milinski 1996) have introduced other efficient strategies than the famous tit_for_tat. Each time, discovered strategies have been justified by mathematical or experimental arguments trying to establish that we are dealing with better strategies than tit_for_tat. These arguments are often convincing, but however, they do not help to highlight a strategy that can be unanimously considered better than the others. It is not even possible today to know what are among the best fifteen strategies identified, those actually in the top, and what are the right elements for structuring efficient and robust behaviour. We have begun to study the actual situation with the desire to reach clear and as unbiased as possible conclusions.
Our method is based on three main ideas, each converging toward robust results and objectives aims.
- Confronting the candidate strategies on a \(\texttt{tournament}\) (mainly for information) and the method of \(\texttt{evolutionary competition}\) which leads to results partially independent from initial conditions.
- Using sets of strategies coming from a particular class (eg using the last move of past of each player) are in competition. This method of \(\texttt{complete classes}\) (Beaufils et al. 1998) avoids the subjective choice usually done when one tries to build his own set of strategies. We use these classes in two ways. First, we use them alone (thus without any added strategy), thereby objectively identify efficient strategies, and secondly we complement with sets of the most successful strategies that we want to compete and rank. This allows us to identify the most robust and resilient strategies.
- Taking an incremental approach , combining the results of several progressive series of massive confrontation experiments in order to be able to formulate, as closely as possible, robust conclusions.
Our aim in this paper is to identify new systematic, reproducible and objective experiments, suggesting several ways to design robust and efficient new strategies and more than that, a general scheme to identify new ones.
This experimental method has no known theoretical equivalent. Indeed, for iterated games in general, but especially for the iterated prisoner’s dilemma, notions of Nash equilibrium, Pareto optimality or evolutionarily stable strategies Lorberbaum (1994); Lorberbaum et al. (2002) do not suggest new and efficient strategies and have never led to discover any new interesting strategy. One will find in Wellman (2006) other paths to follow that would lead to strengthen our results or add new ones. This field is quite difficult to study theoretically.
One of the obvious reasons is that it is impossible to make the optimal score against all strategies. This is a consequence of the first move: to play optimally against all_d it is necessary to defect at the first round, to play optimally against spiteful it is necessary to cooperate. Another reason comes from the infinite set of possible strategies, not endowed with a natural topology. The approach by evolutionary algorithms do not seem to work and never reveal any new robust strategy. The incremental method described in this paper allows to discover new behaviours and unexpected simple strategies.
In Section 2 we recall the rules of the iterated prisoner’s dilemma and specially tournaments and evolutionary competitions used to evaluate strategies. In Section 3 we define precisely well known classical deterministic strategies and several probabilistic ones coming from the state of the art, and evaluate them both in tournaments and evolutionary competitions. In Section 4 we present the complete classes principal which is an objective frame to find and compare strategies: the main idea is to build a set of all the possible strategies using the same size of memory. In Section 5 we show all the results we can identify with these complete classes alone. Using these results we identify four promising new strategies. In Section 6 we confront all the strategies defined during the previous sections all together mainly to test robustness of the best ones.
This paper is a completed and extended version of the two page paper (Mathieu & Delahaye 2015). All the strategies, experiments and mainly the whole package allowing to replicate reported simulation experiments can be downloaded on our web site http://www.lifl.fr/IPD/ipd.html.
Rules of the Game
The prisoner’s dilemma is that accorded to two entities with a choice between cooperation \(\texttt{c}\) and defection (\texttt{d}\) and are remunerated by \(\texttt{R}\) points each if each plays \(\texttt{c}\), \(\texttt{P}\) points if each plays \(\texttt{d}\) and receiving \(\texttt{T}\) respectively \(\texttt{S}\) points if one plays \(\(\texttt{d}\) and the other \(\texttt{c}\). We describe these rules by writing:
\(\verb|[c, c] -> R + R| , \verb|[d, d] -> P + P| , \verb|[d, c] -> T + S|\).
We require that \(T>R>P>S\) and \(T+S<2R\) The classical chosen values are \(\texttt{T = 5, R = 3, P = 1, S = 0}\), which gives: \(\verb|[c, c] -> 3 + 3|, \verb|[d, d] -> 1 + 1| , \verb|[d, c] -> 5 + 0|\).
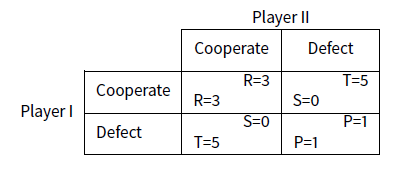
It is a dilemma situation because both entities can collectively win 6 points playing \(\texttt{[c, c]}\), whereas they win less playing \(\texttt{[c, d]}\) and even less playing \(\texttt{[d, d]}\). The collective interest is that everyone play \(\texttt{c}\), but a single logical analysis leads inevitably to \(\texttt{[d, d]}\) which is collectively the worst case!
The dilemma is iterated when we imagine that the situation of choice between \(\texttt{c}\) and \(\texttt{d}\) is presented periodically to the same two entities. The game consists in choosing a strategy that, informed about the past (hence the previous behaviour of the opponent), shows how to play the next move. We recall that in this game, we can-not play well against everyone. Playing well against all_d need to always betray (and in particular for the first move), and playing well against all_c need to always cooperate. But moves being simultaneous, one cannot play optimally against these two strategies.
In this game, since winning against everyone is trivial (all_d does), it is obvious that “playing well” corresponds to earning a maximum of points, which in evolutionary competitions is equivalent to ending with the greatest population possible.
When a set A of strategies is given, we can evaluate it in two ways to get a ranking.
- Tournaments: each strategy meets each other (including itself) during a series of n moves (we take n = 1,000 in the experiments below). Accumulated points earned by a strategy give its score (which thus depends on A). The ranking is in respect with the scores.
- Evolutionary competition (Axelrod 2006): take a number K of strategies of each kind in A (eg K = 100), which is what is known as Generation 1, \(\texttt{G1}\). A tournament between the strategies \(\texttt{G1}\) determines the scores of each strategy. Each strategy will have in generation 2, \(\texttt{G2}\), a number of descendants proportional to its score and only those descendants constitute generation 2, \(\texttt{G2}\). It is assumed that the total number of strategies remains constant from one generation to the next (Cardinal (G1) = Cardinal (G2) = ...). Generation 3, \(\texttt{G3}\), is calculated from the same 2nd generation etc. In an evolutionary competition, strategies that are playing poorly are quickly eliminated. Therefore, those exploiting some strategies playing poorly (which can be numerous especially in complete classes) soon stop to take benefit of them. Finally one can note that only survive the strategies playing efficiently against strategies playing efficiently too.
The Basic Strategies
We make a distinction between deterministic strategies and probabilistic strategies, where choices can depend on chance.
The study of literature about the dilemma led us to define a set of 17 basic deterministic strategies (including the simplest imaginable strategies). We have added 13 probabilistic strategies mainly taking into account the recent discoveries of Press and Dyson on extortion (Press & Dyson 2012).
Let us present the set of 17 basic strategies
all_c always cooperates
all_d always defects
tit_for_tat cooperates on the first move then plays what its opponent played the previous move (Rapoport & Chammah 1965).
spiteful cooperates until the opponent defects and thereafter always defects (Axelrod 2006). Sometimes also called \(\textit{grim}\).
soft_majo begins by cooperating and cooperates as long as the number of times the opponent has cooperated is greater that or equal to the number of times it has defected. Otherwise she defects (Axelrod 2006).
hard_majo defects on the first move and defects if the number of defections of the opponent is greater than or equal to the number of times she has cooperated. Else she cooperates (Axelrod 2006).
per_ddc plays ddc periodically
per_ccd plays ccd periodically
mistrust defects on the first move then play what my opponent played the previous move (Axelrod 2006). Sometimes also called suspicious_tft.
per_cd plays cd periodically
pavlov cooperates on the first move and defects only if both the players did not agree on the previous move (Wedekind & Milinski 1996). Also called \(\textit{win-stay-lose-shift}\).
tf2t cooperates the two first moves, then defects only if the opponent has defected during the two previous moves (Some authors call it sometimes erroneously hard_tft. These is often a confusion between these two).
hard_tft cooperates the two first moves, then defects only if the opponent has defected one of the two previous moves
slow_tft cooperates the two first moves, then begin to defect after two consecutive defections of its opponent.
Returns to cooperation after two consecutive cooperations of its opponent.
gradual Cooperates on the first move, then defect \(n\) times after \(n^{th}\) defections of its opponent, and calms down with 2 cooperations (Beaufils et al. 1996).
prober plays the sequence \(\texttt{d,c,c}\) then always defects if its opponent has cooperated in the moves 2 and 3.
Plays as tit_for_tat in other cases (Mathieu et al. 1999).
mem2 behaves like tit_for_tat: in the first two moves, and then shi s among three strategies all_d, tit_for_tat, tf2t according to the interaction with the opponent on last two moves:
- if the payoff in the two moves is \(\texttt{2R}\) \(\texttt{[c,c]}\) and \(\texttt{[c,c]}\) then tit_for_tat in the following two moves
- if the payoff in the last move is \(\texttt{T+S}\) (\(\texttt{[c,d]}\) or \(\texttt{[d,c]}\) then tf2t in the following 2 moves
- in all other cases she plays all_d in the following two moves
- if all_d has been chosen twice, she always plays all_d. (Li & Kendall 2013)
Let us present now a set of 12 probabilistic strategies. These strategies start with c, then play c with probability
- \(p_1\) if the last move is \(\texttt{[c,c]}\)
- \(p_2\) if the last move is \(\texttt{[c,d]}\)
- \(p_3\) if the last move is \(\texttt{[d,c]}\)
- \(p_4\) if the last move is \(\texttt{[d,d]}\)

These 12 strategies have been chosen randomly among the infinity of possible choices, for no reason other than to obtain a sample as diverse as possible. \(\textit{Equalizers}\) and \(\textit{Extortions}\) have been introduced in Press & Dyson (2012) and are among strategies called \(\textit{Zero-Determinant}\) (ZD) strategies. A \(\textit{ZD}\) strategy can enforce a fixed linear relationship between expected payoff between two players. Extortion strategies ensure that an increase in one’s own payoff exceeds the increase in the other player’s payoff by a fixed percentage. Extortion is therefore able to dominate any opponent in a one-to-one meeting. Equalizer strategies ensure to the other player any payoff between P and R.
We conclude this set with the random strategy , playing 50% \(\texttt{c}\), 50% \(\texttt{d}\)
Evaluation of the 17 basic strategies
The experiment \(\texttt{Exp1}\), is done using the 17 basic strategies and leads to the following results:
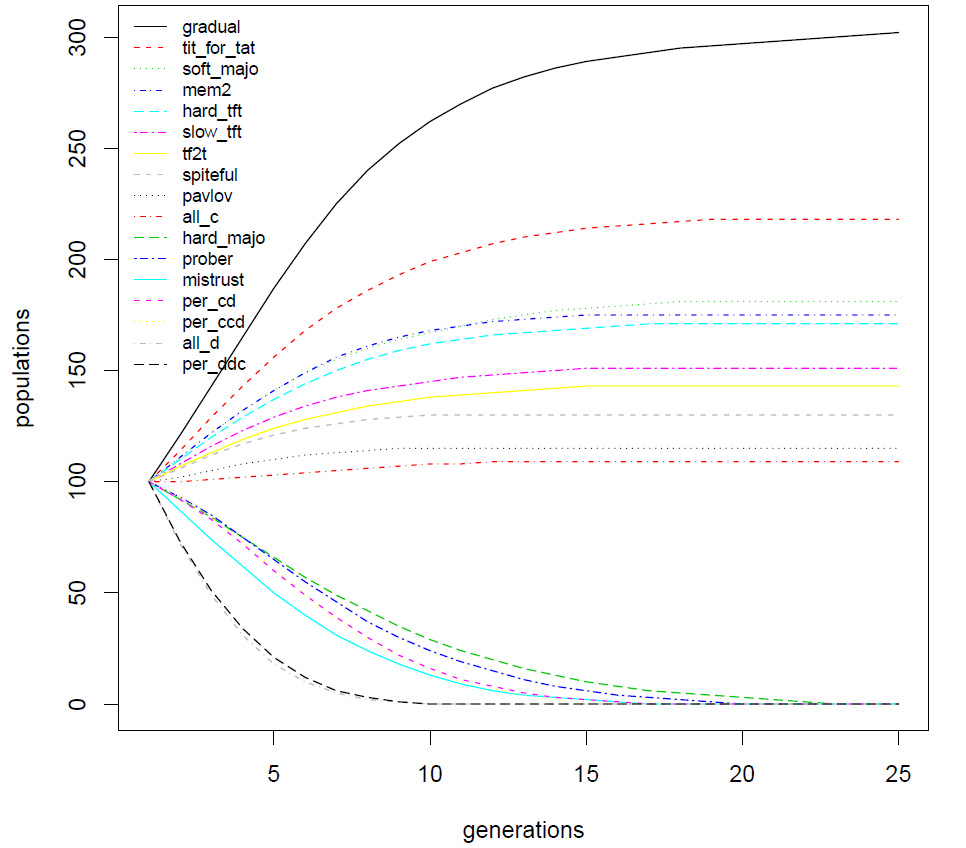
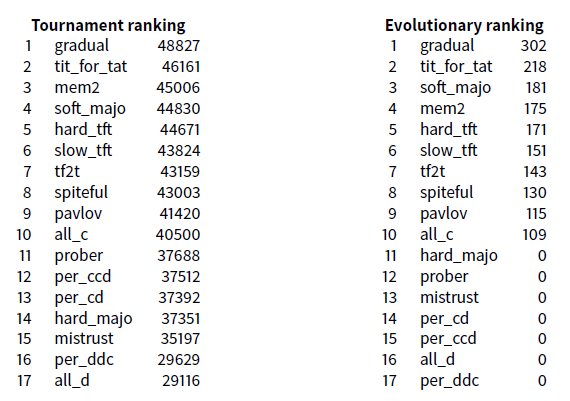
Note that in all the evolutionary rankings presented in this papers the order of the strategies is determined by the survival population, and if not, by the time of death.
The result of the meetings (Tournament and Evolutionary competition) of this set of 17 classic deterministic strategies is a really good validity test of any IPD simulator.
Evaluation of the 30 (17+13) strategies
Experiment \(\texttt{Exp2}\) uses the 30 deterministic and probabilistic strategies and leads to the following results (Only the 10 first strategies are given):
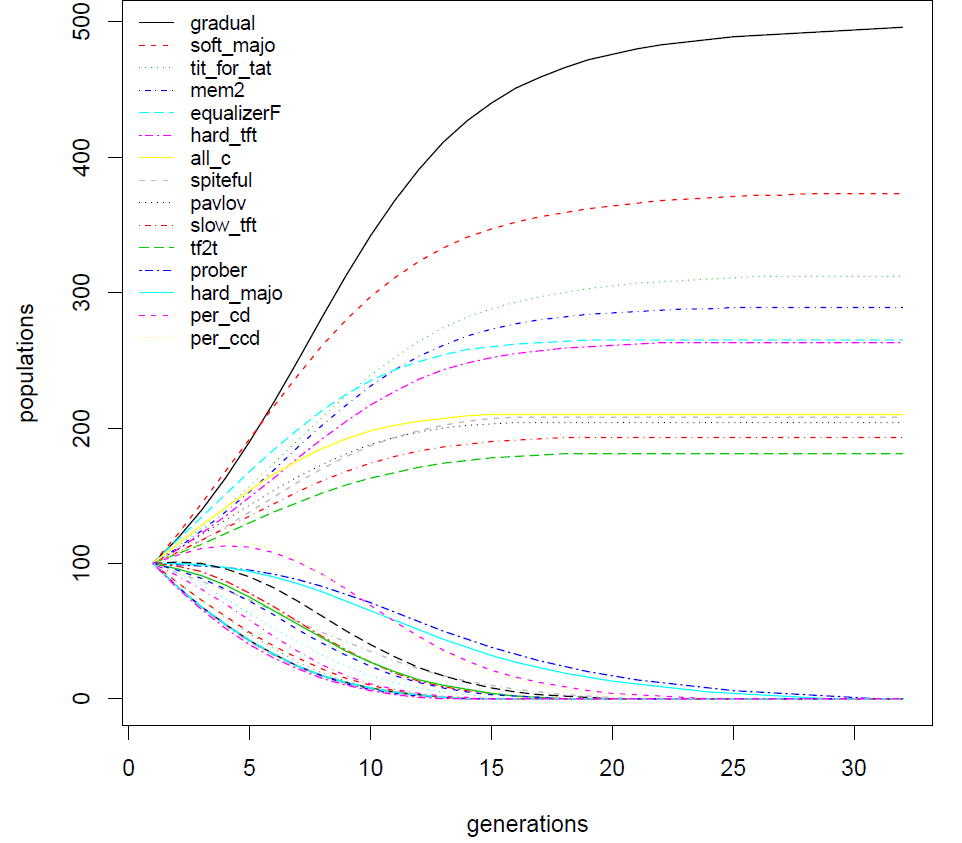
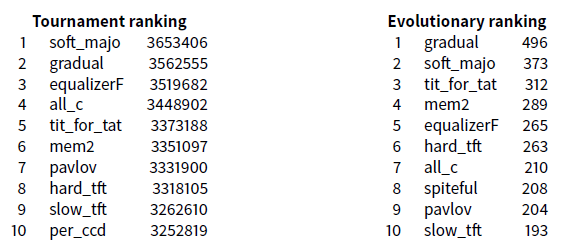
We emphasize that for each tournament including a probabilistic strategy, the tournament is always repeated 50 times.
We note that the only strategy that appears coming from Press and Dyson ideas is the \(\textit{equalizerF}\) strategy, that we will encounter often further. It reveals itself the fi h of the 30 strategies here on a competitive basis.
The Complete Classes Principle
We define the \(\textit{memory(X,Y)}\) complete class which is the class of all deterministic strategies using my \(\textit{X}\) last moves and the \(\textit{Y}\) last moves of my opponent.
In each \(\textit{memory(X,Y)}\) complete class, all deterministic strategies can be completely described by their “genotype” i.e. a chain of C/D choices that begin with the \(max(X,Y)\) first moves (not depending on the past). These starting choices are written in lower case. The list of cases of the past is sorted by lexicographic order on my \(\textit{X}\) last moves (from the older to the newer) followed by my opponent’s \(\textit{Y}\) last moves (from the older to the newer). Here is the genotype of a memory(1,2) strategy noted \(\textit{mem12_ccCDCDDCDD}\) also called below winner12.
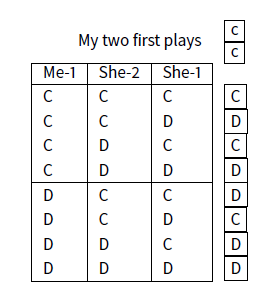
We indicate the number of strategies we can define in each memory class. Each \(\textit{memory(X,Y)}\) class contains a large number of memXY_… strategies. The general formula for the number of elements of a \(\textit{memory(X,Y)}\) complete class is \(2^{max(X,Y)}.2^{2^{X+Y}}\).

Many well known strategies can be defined with this kind of genotype:

Let \(X,X',Y,Y'\) be four integers with \(X \leq X'\) and \(Y~\leq~Y'\),
If \(max(X,Y)=max(X',Y')\) then
\(memory(X,Y) \subseteq memory(X',Y')\).
Take care that if \(max(X,Y) \neq max(X',Y')\) then there is no inclusion because of the beginning.
That means that if one increases the \(min(X,Y)\) of a memory class, not more than the max, then all the \(\textit{memory(X,Y)}\) are always in the increased class. For example \(\textit{memory(0,3)}\) \(\subset\) \(\textit{memory (1,3)}\) \(\subset\) \(\textit{memory (2,3)}\) \(\subset\) \(\textit{memory (3,3)}\) but not in \(\textit{memory(0,4)}\).
We can note that several different genotypes can describe finally the same behaviour. For example, the all_d strategy appears four times in the memory(1,1) complete class:mem11_dCCDD, mem11_dCDDD, mem11_dDCDD, mem11_dDDDD.
Our theoretical hypothesis is that the better you are in a complete class, and the larger the class is, the more chances you have of being robust. Indeed the extent of the complete class guarantees a high degree of behavioral variability without the slightest subjective bias to which one could not escape if one chooses one by one the strategies that one puts in competition.
17 Deterministic and memory(1,1)
If we consider only deterministic strategies making their decision using the last move of each player, we can define a set of 32 strategies, each determined by a 5-choice genotype \(C_1 C_2 C_3 C_4 C_5\).
\(C_1\) = move chosen at first when no information is available.
\(C_2\) = move chosen when last move was \(\texttt{[c,c]}\)
\(C_3\) = move chosen when last move was \(\texttt{[c,d]}\)
\(C_4\) = move chosen when last move was \(\texttt{[d,c]}\)
\(C_5\) = move chosen when last move was \(\texttt{[d,d]}\)
Some strategies for this complete class are already among the 30 basic strategies that we have adopted. Some strategies with different genotypes yet still behave identically. We have not sought to remove these duplicates because it makes very small difference to the results, and when we consider larger complete classes it becomes almost impossible.
\(\texttt{Exp3}\) experiment uses the 17 basic deterministic strategies and the 32 strategies coming from the complete class memory(1,1). This leads to a set of 49 strategies.

The all_d strategy that goes well ranked during the tournament, disappears from the top ten of the evolutionary competition. It’s easy to find an explanation: all_d exploits strategies playing poorly (nonreactive for example); when they are gone, all_d is not able to win enough points to survive.
All Basics and memory(1,1)
Now in \(\texttt{Exp4}\) we take all the basic strategies (deterministic and probabilistic) with the 32 of the complete class memory(1,1). This builds a set of 62 (= 17 + 13 + 32) strategies.

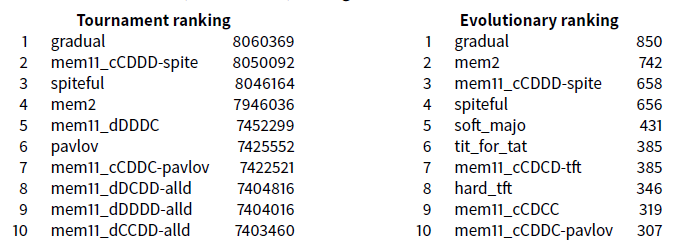
This ranking confirms that the strategies we have adopted are effectively efficient strategies. The strategies gradual, spiteful and mem2 are the three winners: they are good, stable and robust strategies. The strategy equalizerF is the fourteens of the evolutionary competition, and does not confirm its success during the \(\texttt{Exp3}\) experimentation. It does not seem as robust as the 3 winners.
As with all the experiments of this paper, containing a probabilistic strategy, this \(\texttt{Exp4}\) experience is based on a tournament repeated 50 times between the involved strategies. For example, to check the stability of this result, here is the ranking obtained by the first five strategies after the first ten executions.
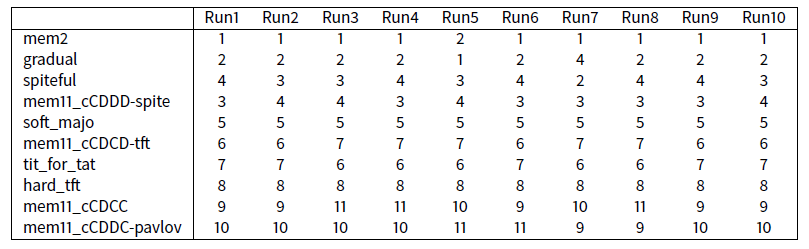
This experiment shows that probabilistic strategies introduced by Press and Dyson are not good competitors (except forequalizerF, which is relatively efficient). This had already been noted in several papers (Hilbe et al. 2014, 2013; Stewart & Plotkin 2013; Adami & Hintze 2013,2014; Dong et al. 2014; Szolnoki & Perc 2014). Press and Dyson strategies are designed to equal or beat each strategy encountered in a one-to-one game. The all_d strategy itself also is never beaten by another strategy, and is known to be catastrophic because she gets angry with everyone (except stupid non-reactive strategies) and therefore does not earn nearly point, especially in evolutionary competitions where only survive efficient strategies after a few generations. To win against any opponent is pretty easy, scoring points is more difficult! The right strategies in the prisoner’s dilemma are not those who try to earn as many points than the opponent (such as equalizers) or require to earn more points than any other (as extortioners), these are the ones that encourage cooperation, know how to maintain it and even restore it if necessary after a sequence of unfortunate moves.
Complete classes alone
So as objectively confirm the results of the first experiments and also to identify other strategies that need to be added to our selection, we began to conduct competitions among all strategies coming from as large as possible complete classes. Our platform has allowed us to compete in tournament and evolutionary competitions families of 1,000 and even 6,000 strategies (our limit today). The results found are full of lessons.
memory(1,1)
The experiment Exp5 starts with the results of the complete class of the 32 memory(1,1) strategies. It objectively shows that spiteful, tit_for_tat and pavlov are efficient strategies. We can see that the victory of all_d in the tournament cannot resist to the evolutionary competition.
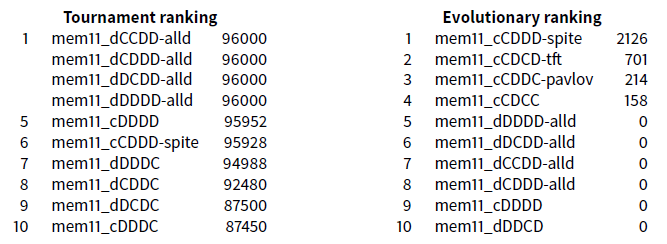
When we consider complete classes we note the first plays (which do not depend on the past) in lowercases, and the other plays in uppercases.
memory(1,2)
The experiment \(\texttt{Exp6}\) concerns the memory(1,2) class (a move of my past, and two moves of the opponent’s past) which contains 1024 strategies. To define a strategy for this class, we must choose what she plays in the first two moves (placed at the head of the genotype) and what she plays when the past was: \(\texttt{[c ; (c c)]}\) \(\texttt{[c ; (c d)]}\) \(\texttt{[c ; (d c)]}\) \(\texttt{[c ; (d d)]}\) \(\texttt{[d ; (c c)]}\) \(\texttt{[d ; (c d)]}\) \(\texttt{[d ; (d c)]}\) \(\texttt{[d ; (d d)]}\).

The winner is a strategy that plays pavlov except at the beginning where she plays \(\texttt{c,c}\) and, when she was betrayed twice, she betrays (unlike pavlov). We will name it winner12.
This winner12 makes us think to a mixture as simple as possible of tit_for_tat and spiteful: She plays tit_for_tat unless she has been betrayed two times consecutively, in which case she always betrays (plays all_d). We will call this new strategy t _spiteful which to our knowledge has never been previously identified in any paper, despite its simplicity.

memory(2,1)
\(\texttt{Exp7}\) experiment concerns the memory(2,1) complete class which contains 1024 strategies. The genotype is defined with the same principle as memory(1,2).
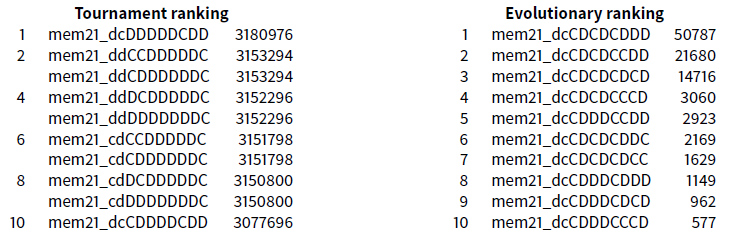
The winner is a strategy that plays tit_for_tat except that it starts with \(\texttt{d,c}\), and, when she betrayed twice and the other has nevertheless cooperated she reacts by a \(\texttt{d}\) (this is the only round that differentiates it from tit_for_tat). She exploits the kindness of the opponent. We will name it winner21.
The following slightly simpler and less provocative strategy (which is usually a quality) seemed interesting to us: she plays \(\texttt{cc}\) at the beginning and then plays spiteful. We call it spiteful_cc It is a kind of softened spiteful.
memory(1,2) + memory(2,1)
The \(\texttt{Exp8}\) experiment shows a confrontation including the two complete classes: memory(1,2) and memory(2,1). This leads to a set of 2,048 strategies.
Computing these results requires a 2,048* 2,048 matrix to fill, so roughly 4 million meetings, and for each of them, 1,000 rounds. It also need for the evolutionary competition a population of 2,048 * 100 agents operating a thousand times.
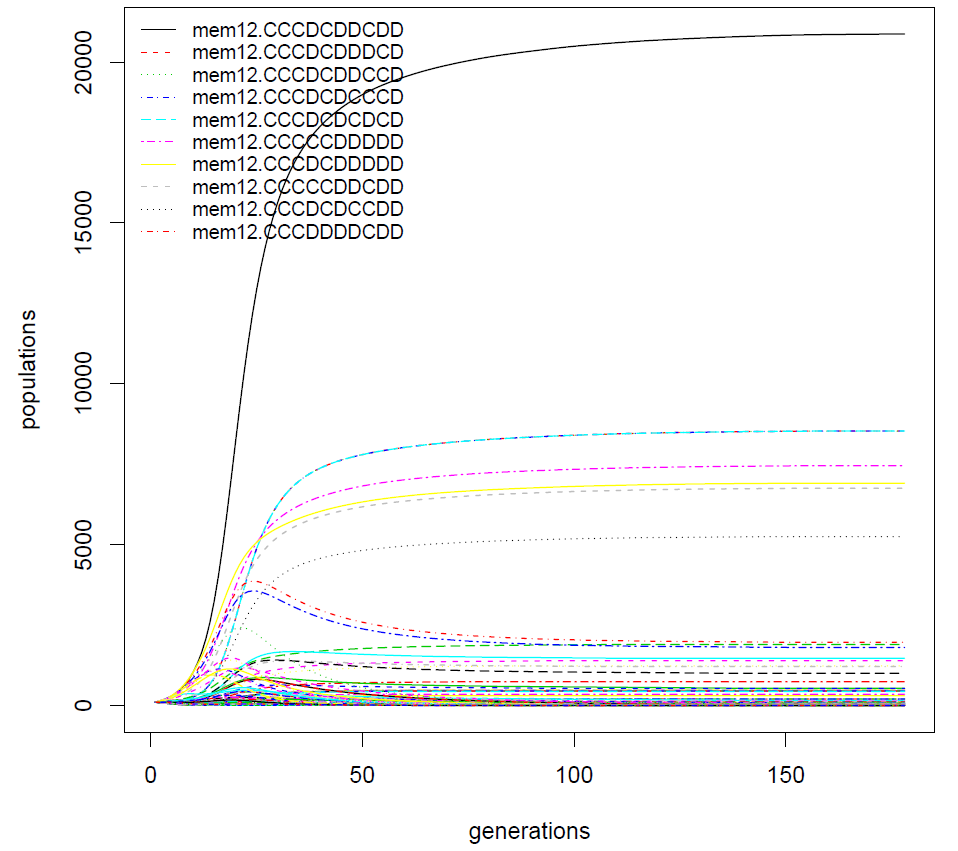
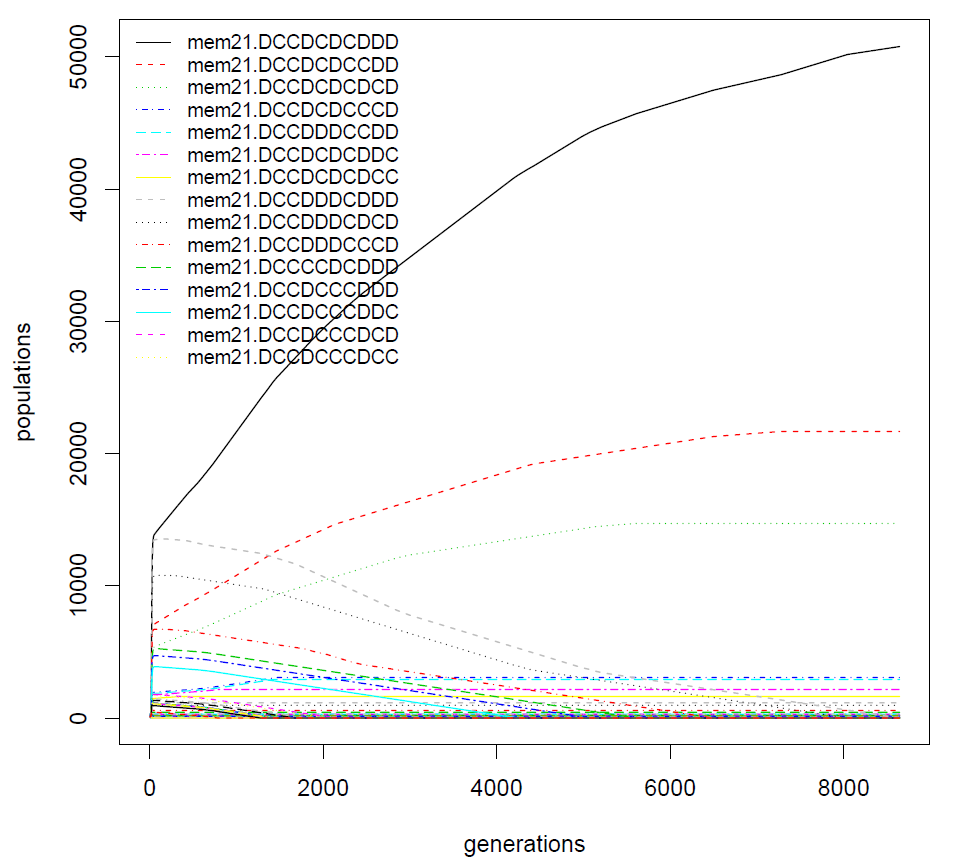
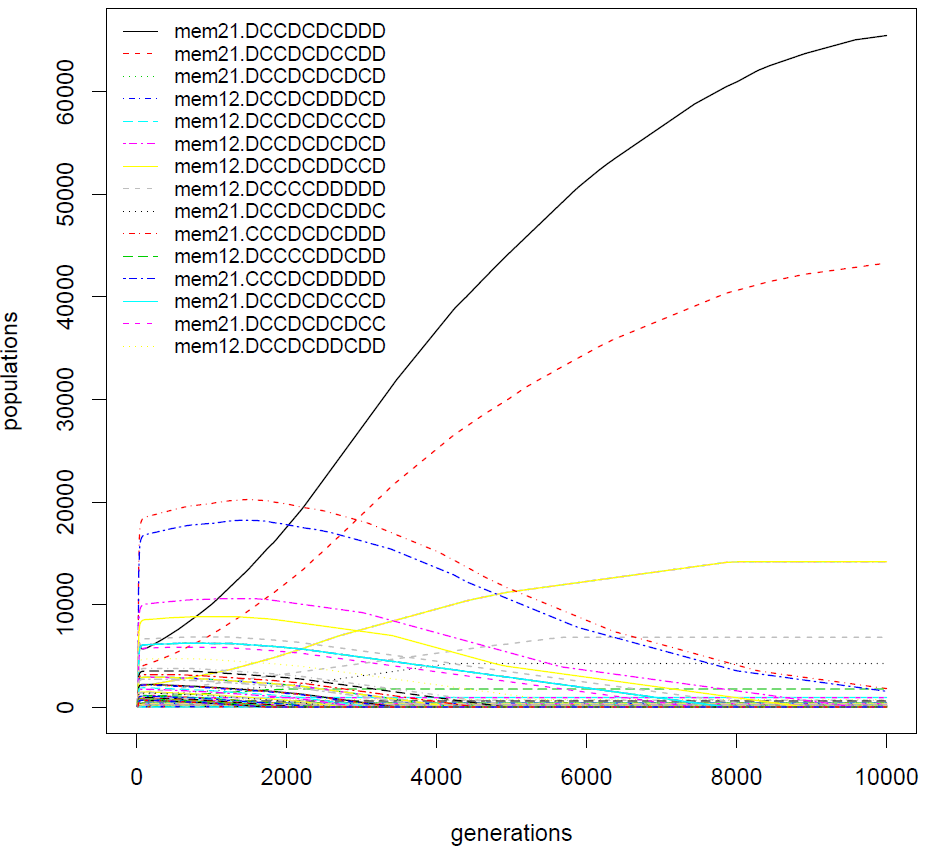
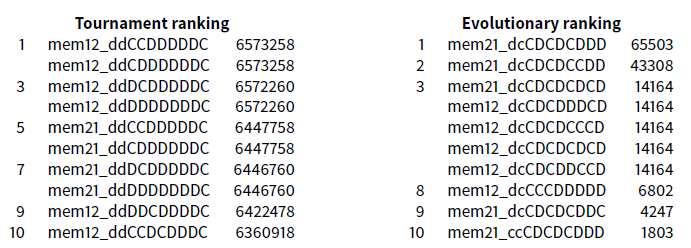
It is remarkable that the winner is winner21. It remains to be seen whether the 4 new strategies we have just introduced are really robust, and how they are ranked when confronted to the best previously identified strategies.
Same experiments with the 4 new strategies
We take once again the first 4 experiments done in Sections 3 and 4, each time adding our four new strategies, which allows us to evaluate both the robustness of former winners and put them in competition with the new four.
17 basic + 4 new strategies
The experiment \(\texttt{Exp9}\) involves the 17 basic strategies like in \(\texttt{Exp1}\) (Section 3.7) with the four new strategies dis covered thanks to the complete classes experiments (Section 5.4 and Section 5.7).
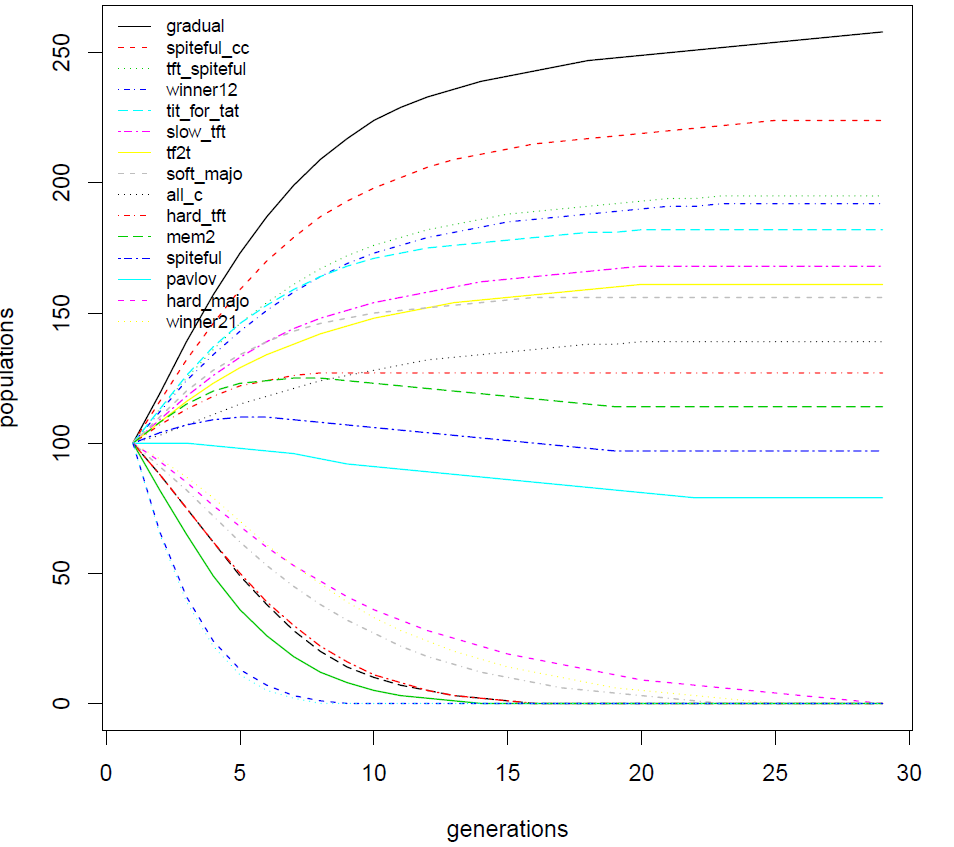
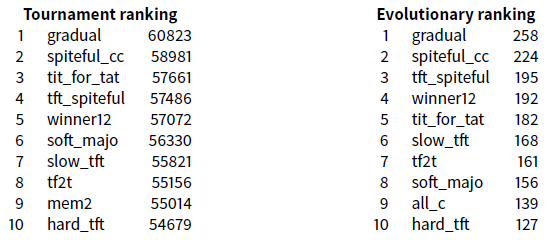
It is remarkable that three among the four new introduced strategies are in the four first evolutionary ranking.
It appears here that mem2 is not a robust strategy. She is the 9\(^{th}\) in tournament and is not even in the top 10 in the ecological competition.
30 + 4 new strategies
\(\texttt{Exp10}\) studies the 30 deterministic and probabilistic basic strategies like in \(\texttt{Exp2}\) ( Section 3.10) with the four new strategies discovered thanks to the complete classes experiments (Section 5.4 and 5.7). This leads to a set of 34 strategies.
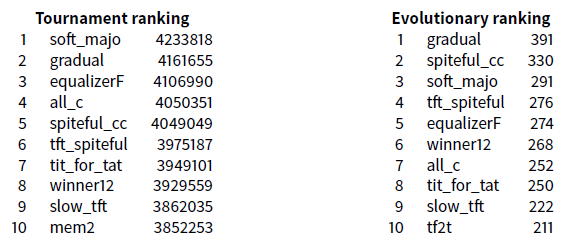
The strategy gradual wins, and strangely, all_c is the seventh, but the three new introduced strategies (spiteful_cc, winner12, t _spiteful) are among the 10 best.
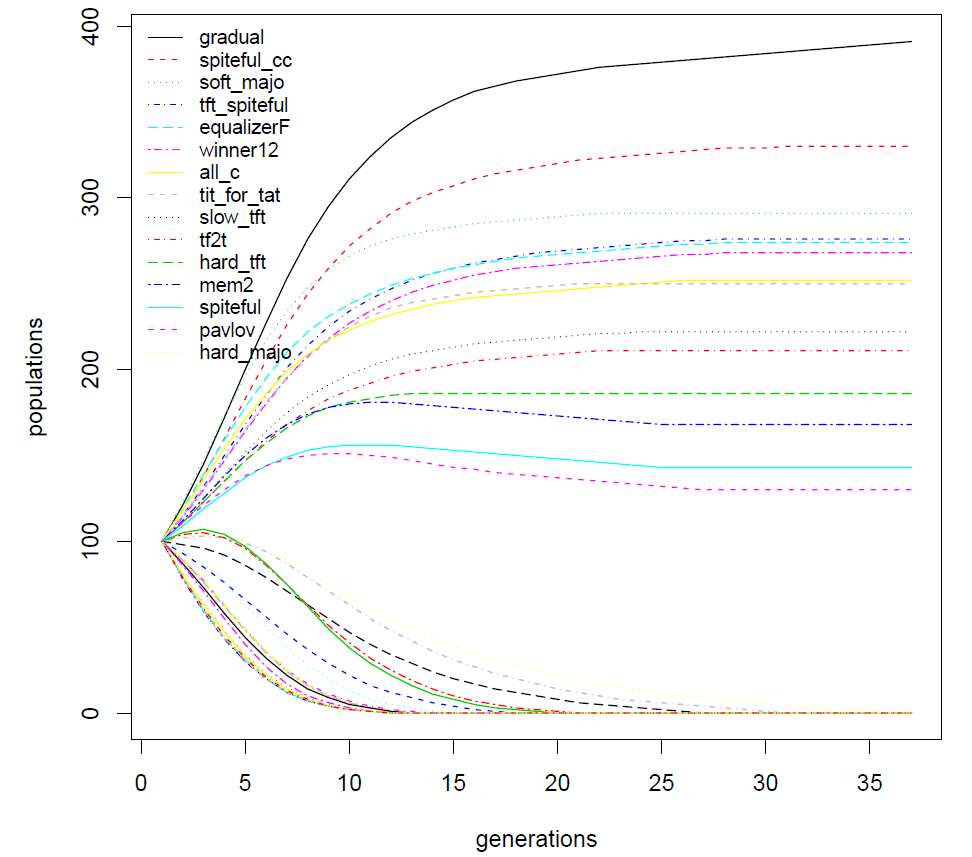
For example, to check the stability of the \(\texttt{Exp10}\) result, here is the ranking obtained by the first five strategies after the first ten executions.
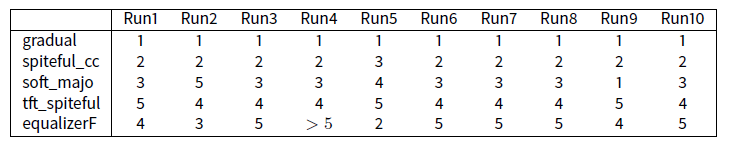
Note that in this table the extreme stability of the beginning of ranking. Except from the run4, the first five strategies are always the same. Of course, lower one goes in these rankings, more there are permutations, but the first five remain the same.
All deterministic + 4 new strategies
For the \(\texttt{Exp11}\) take all the deterministic strategies obtained with the 17 initial basic strategies and the memory(1,1) complete classes, thus \(17+32\) like in \(\texttt{Exp3}\) (Section 4.10) with the four new strategies discovered thanks to the complete classes experiments (Section 5.4 and 5.7). This leads to a set of 53 strategies.
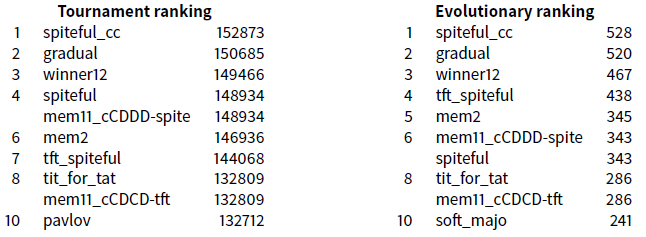
This time, the four winners are exactly the same as in \(\texttt{Exp9}\) but not exactly in the same order. This result shows the robustness of these four strategies.
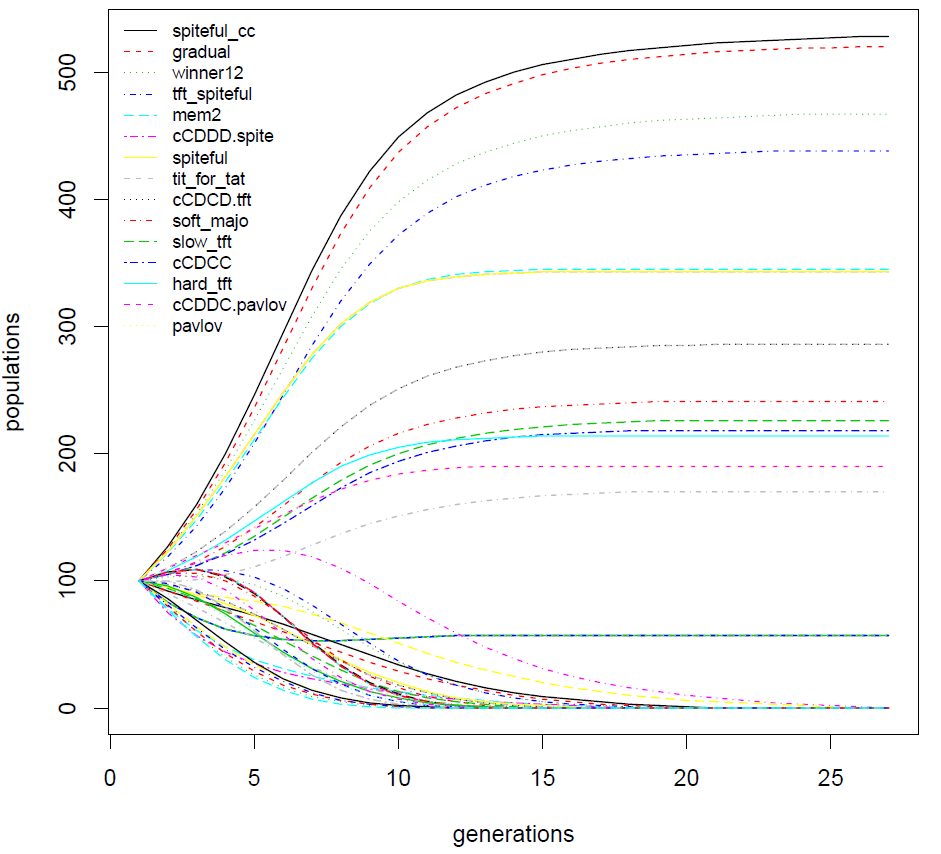
All deterministic and probabilistic
\(\texttt{Exp12}\) is built with all the basic deterministic strategies obtained with the 17 initial basic strategies and the memory(1,1) complete class added with the 13 probabilistic strategies like in \(\texttt{Exp4}\) (Section 4.14) with the four new strategies discovered thanks to the complete classes experiments (Section 5.4 and Section 5.7). This leads to a set of 66 strategies.
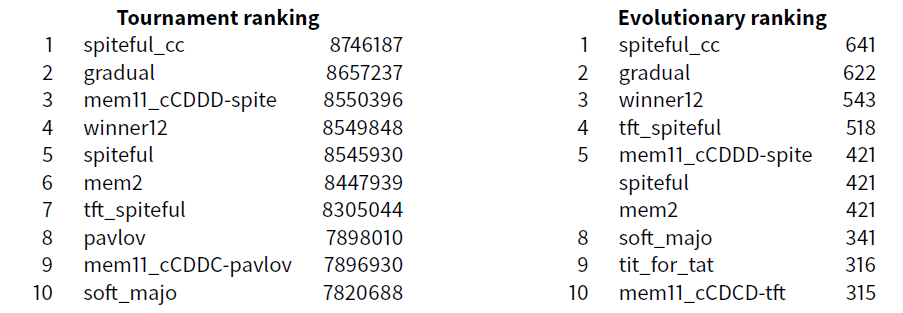
Once again, the same four strategies win this competition. This confirms the results obtained during \(\texttt{Exp1}\) to \(\texttt{Exp8}\) experiments. winner21 is only 16th in this ranking.
Stability and Robustness of the Results
To test the stability of these results, we have built a set of five experiments. The first one test if probabilistic strategies makes the ranking unstable. The second test measures the effects of the length of the meetings. The third test verifies that the changes of coefficients in the payoff matrix have any effect. The last test ensures that even when taking strategies that have a longer memory and using diversified strategies, the results are always stable.
Test with respect to probabilistic strategies
In previous experience \(\texttt{Exp12}\), scores are obtained by averaging over 50 rounds to ensure stability. To see in detail the influence of probabilistic strategies we point out, 10 classifications obtained without making any average.
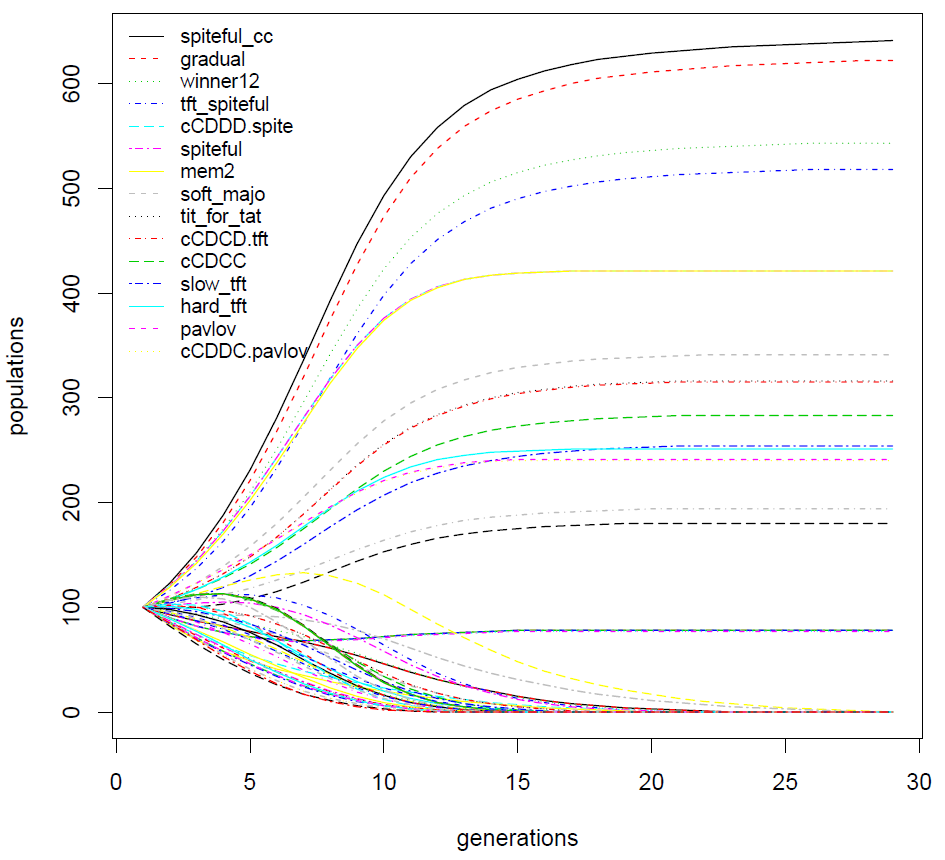
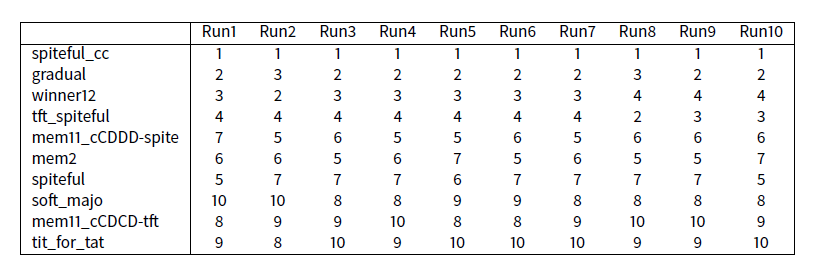
We can see that the first ten strategies are always the same. Only their ranking changes.
Test with respect to meetings lengths
Previous experiences were made with 1,000 rounds by meeting. We are now testing whether the length of the meetings influences many rankings.
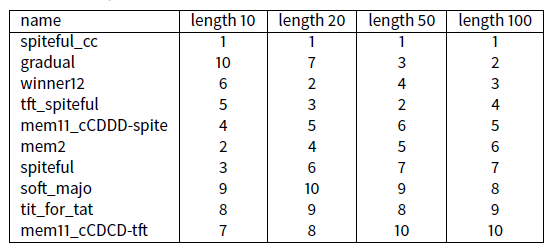
One can see that, when the length of the meeting is greater than 10 rounds, then the first 10 strategies stay the same. Just their ranking changes. From a length of 60, nothing changes in the ranking of the first 10. We note that shorter the meetings are, more \(\texttt{mem2}\) is favoured and less gradual is disadvantaged. This results shows clearly that the qualities of \(\texttt{gradual}\) require a certain length of meeting.
Test with respect to the payoff matrix
In this section we change the coefficients of the experience \(\texttt{Exp12}\) (Section 6.11) by transforming (5, 3, 1, 0) to (2, 1, 0, 0) in the matrix of gains, to test the stability relative to earnings, while remaining under the classic dilemma of inequality. These coefficients corresponds to the British TV show on ITV Networks called “Golden Balls, Split or Steal”. This experiment have been repeated fifty times with 1000 rounds meetings.

These results have to be compared with those of Exp12 (see Section 6.11) which are quite the same.
Test of independence
To test if the four new strategies are individually efficient, that is their good results do not depend from the others, we make compete each of the 17 + 4 strategies one of one, with the set of 1024 memory(1,2). In each of these 21 experiments involving 1025 strategies, we measure this time the rank of the added strategy.
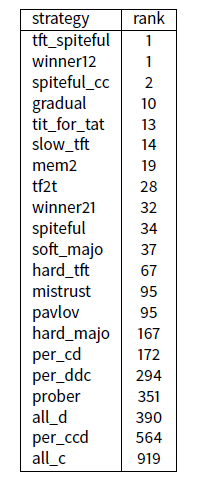
One can see on these results that if we just add t_spiteful to the set of 1024 memory(1,2) strategies, it finishes first. This is also the case obviously for winner12. In the same way, spiteful_cc finishes second. On the other hand tit_for_tat finishes only 13th. Again, we find that among the 4 added strategies, 3 of them are really excellent.
Test with a rich soup
As it is impossible to run large complete classes (memory(2,2) contains for example 262,144 strategies), one example have been obtained by taking randomly 1,250 strategies from memory(2,2) + 1,250 strategies from memory(3,3) + 1,250 strategies from memory(4,4) + 1,250 strategies from memory(5,5) with the now famous 17+4.
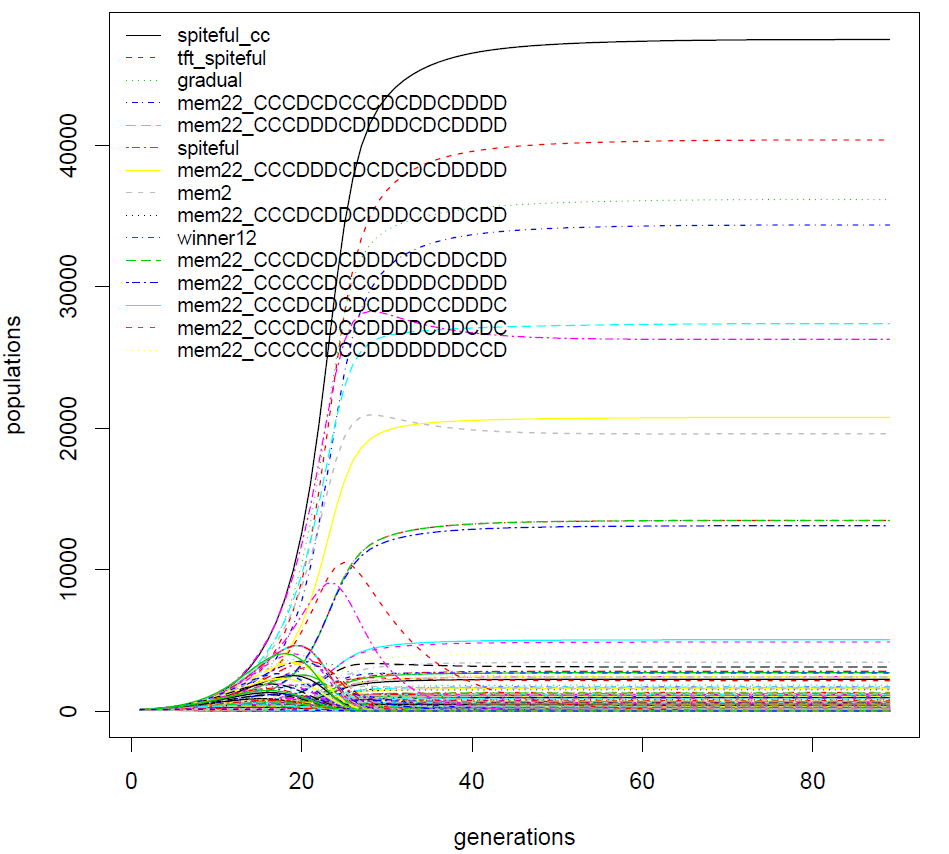
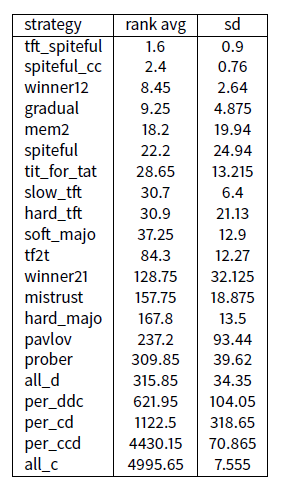
This set contains then 5,021 strategies. This experiment is run twenty times to be able to compute relevant rank average and standard deviation.
This test illustrates once again that three of the four (spiteful_cc, t _spiteful and winner12) new introduced strategies are in the top (1,2 and 3). One can note also the great robustness of gradual who finished fourth of this huge experiment.
Test of evolutionary stability
In order to add a robustness test to the strategies identified, we conducted a series of experiments to test their stability against invasions of different types.
We are interested in the following 10 strategies which are the best knows strategies resulting from our experiments: t_spiteful, spiteful_cc, winner12, gradual, mem2, spiteful, tit_for_tat, slow_tft, hard_tft, soft_majo.
In turn, we take 10,000 copies of all_d and 10,000 copies of one of the 10 previously mentioned strategies that come together in an evolutionary competition. In each case, all_d is quickly and totally eliminated.
We then changed the proportion (10,000 vs 10,000) by gradually decreasing the numbers of each of the strategies studied. all_ is always eliminated, except when the number of the strategy added is less than 75 copies. For example, 10,000 all_d are eliminated by 100 winner12, but are not eliminated by 60.
The same experiment has been performed by replacing all_d by the random strategy. This time the soft_majo strategy proves to be weaker: the switching is done at approximately 500 while for the others the switching is at approximately 200 which confirms the robustness to the invasion of our 10 selected strategies.
Not only do these 10 strategies not let themselves be invaded by others, they invade the others, even when their starting population are much lower.
More in-depth methods for studying evolutionary stability can be envisaged using methods described in Ficici & Pollack (2003); Ficici et al. (2005).
Conclusion
According to the state of the art, in the first part of this paper we have collected the most well-known interesting strategies. Then we have used the systematic and objective complete classes method to evaluate them. These experiments led us to identify new efficient and robust strategies, and more than that, a general scheme to find new ones. The four new strategies are actually successful strategies, even if winner21 seems less robust. Al-though detected by calculating in special environments the three new robust strategies (spiteful_cc, winner12, t_spiteful) remain excellent even in other environments unrelated to that of their "birth". The method of complete classes is clearly an efficient method to identify robust winners.
At this time, we consider, according with the final ranking in Section 7.10 that the best actual strategies in the IPD are in order
tft_spiteful, spiteful_cc, winner12, gradual mem2, spiteful, tit_for_tat, slow_tft, hard_tft, soft_majo
The two best strategies come from this paper. We encourage the community to take systematically into account these new strategies in their future studies.
We note that these are almost all mixtures of two basic strategies: tit_for_tat and spiteful. This suggests that tit_for_tat is not severe enough, that spiteful is a little too much severe and that finding ways to build hybrids of these two strategies is certainly what gives the best and most robust results.
We also note that using information about the past beyond the last move is helpful. Among the eight strategies that our tests put in the head of ranking some of them use the past from the beginning (gradual and soft_majo) and all the others use (except equalizer-F) two moves of the past or a little more. The memory also seems useful to play well (confirming the results of Li & Kendall 2013; Moreira et al. 2013).
A promising way to find other efficient strategies is probably to carefully study larger complete classes, to identify the best and check their robustness. The lessons learned from these experiments generally concern many multiagent systems where strategies and behaviours are needed.
References
ADAMI, C. & Hintze, A. (2013). Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything. Nature Communications, 4(2193). [doi:10.1038/ncomms3193]
ADAMI, C. & Hintze, A. (2014). Corrigendum: Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything. Nature Communications, 4, 2193. [doi:10.1038/ncomms4764]
AXELROD, R. M. (2006). The Evolution of Cooperation. New York, NY: Basic Books.
BEAUFILS, B., Delahaye, J.-P. & Mathieu, P. (1996). Our meeting with gradual, a good strategy for the iterated prisoner’s dilemma. In Proceedings of the Fi h International Workshop on the Synthesis and Simulation of Living Systems (ALIFE’5), (pp. 202–209). Boston, MA: The MIT Press/Bradford Books.
BEAUFILS, B., Delahaye, J.-P. & Mathieu, P. (1998). Complete classes of strategies for the classical iterated pris-oner’s dilemma. In Evolutionary Programming VII (EP’7), vol. 1447 of Lecture Notes in Computer Science, (pp. 33–41). Berlin/Heidelberg: Springer.
BEAUFILS, B. & Mathieu, P. (2006). Cheating is not playing: Methodological issues of computational game theory. In Proceedings of the 17th European Conference on Artificial Intelligence (ECAI’06), (pp. 185–189). Amsterdam: IOS Press.
DELAHAYE, J.-P., Mathieu, P. & Beaufils, B. (2000). The iterated lift dilemma. In Computational Conflicts : Conflict Modeling for Distributed Intelligent Systems, (pp. 203–223). Berlin/Heidelberg: Springer. [doi:10.1007/978-3-642-56980-7_11]
DONG, H., Zhi-Hai, R. & Tao, Z. (2014). Zero-determinant strategy: An underway revolution in game theory. Chinese Physics B, 23(7), 078905. [doi:10.1088/1674-1056/23/7/078905]
FICICI, S. & Pollack, J. (2003). A game-theoretic memory mechanism for coevolution. In Genetic and Evolutionary Computation – GECCO 2003, (pp. 203–203). Berlin/Heidelberg: Springer. [doi:10.1007/3-540-45105-6_35]
FICICI, S. G., Melnik, O. & Pollack, J. B. (2005). A game-theoretic and dynamical-systems analysis of selection methods in coevolution. IEEE Transactions on Evolutionary Computation, 9(6), 580–602. [doi:10.1109/TEVC.2005.856203]
HILBE, C., Nowak, M. A. & Sigmund, K. (2013). Evolution of extortion in Iterated Prisoner’s Dilemma games. Proceedings of the National Academy of Sciences, 110(17), 6913–6918. [doi:10.1073/pnas.1214834110]
HILBE, C., Röhl, T. & Milinski, M. (2014). Extortion subdues human players but is finally punished in the Prisoner’s Dilemma. Nature Communications, 5, 3976. [doi:10.1038/ncomms4976]
KENDALL, G., Yao, X. & Chong, S. Y. (2007). The Iterated Prisoners’ Dilemma: 20 Years on. Singapore: World Scientific Publishing Co. [doi:10.1142/6461]
LI, J., Hingston, P. & Kendall, G. (2011). Engineering design of strategies for winning iterated prisoner’s dilemma competitions. Computational Intelligence and AI in Games, IEEE Transactions on, 3(4), 348–360. [doi:10.1109/TCIAIG.2011.2166268]
LI, J. & Kendall, G. (2013). The effect of memory size on the evolutionary stability of strategies in iterated pris-oner’s dilemma. Evolutionary Computation, IEEE Transactions on, PP(99), 1–8.
LORBERBAUM, J. (1994). No strategy is evolutionarily stable in the repeated prisoner’s dilemma. Journal of Theoretical Biology, 168(2), 117–130. [doi:10.1006/jtbi.1994.1092]
LORBERBAUM, J. P., Bohning, D. E., Shastri, A. & Sine, L. E. (2002). Are there really no evolutionarily stable strategies in the iterated prisoner’s dilemma? Journal of Theoretical Biology, 214(2), 155–169. [doi:10.1006/jtbi.2001.2455]
MATHIEU, P., Beaufils, B. & Delahaye, J.-P. (1999). Studies on dynamics in the classical iterated prisoner’s dilemma with few strategies: Is there any chaos in the pure dilemma ? In Proceedings of the 4th european conference on Artificial Evolution (AE’99), vol. 1829 of Lecture Notes in Computer Science, (pp. 177–190). Berlin/Heidelberg: Springer.
MATHIEU, P. & Delahaye, J.-P. (2015). New winning strategies for the iterated prisoner’s dilemma. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems (AAMAS), (pp. 1665–1666).International Foundation for Autonomous Agents and Multiagent Systems.
MITTAL, S. & Deb, K. (2009). Optimal strategies of the iterated prisoner’s dilemma problem for multiple conflicting objectives. Evolutionary Computation, IEEE Transactions on, 13(3), 554–565. [doi:10.1109/TEVC.2008.2009459]
MOREIRA, J., Vukov, J., Sousa, C., Santos, F. C., d’Almeida, A. F., Santos, M. D. & M., P. J. (2013). Individual memory and the emergence of cooperation. Animal Behaviour, 85(1), 233 – 239. [doi:10.1016/j.anbehav.2012.10.030]
O’RIORDAN, C. (2000). A forgiving strategy for the iterated prisoner’s dilemma. Journal of Artificial Societies and Social Simulation, 3(4), 3: https://www.jasss.org/3/4/3.html.
POUNDSTONE, W. (1992). Prisoner’s Dilemma: John von Neuman, Game Theory, and the Puzzle of the Bomb. New York, NY: Doubleday.
PRESS, W. H. & Dyson, F. J. (2012). Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent. Proceedings of the National Academy of Sciences, 109(26), 10409–10413. [doi:10.1073/pnas.1206569109]
RAPOPORT, A. & Chammah, A. (1965). Prisoner’s Dilemma: A Study in Conflict and Cooperation. Ann Arbor, MI: University of Michigan Press. [doi:10.3998/mpub.20269]
SIGMUND, K. (2010). The Calculus of Selfishness. Princeton, NJ: Princeton University Press. [doi:10.1515/9781400832255]
STEWART, A. J. & Plotkin, J. B. (2013). From extortion to generosity, evolution in the iterated prisoner’s dilemma. Proceedings of the National Academy of Sciences, 110(38), 15348–15353. [doi:10.1073/pnas.1306246110]
SZOLNOKI, A. & Perc, M. (2014). Defection and extortion as unexpected catalysts of unconditional cooperation in structured populations. Scientific Reports, 4, 5496. [doi:10.1038/srep05496]
TZAFESTAS, E. (2000). Toward adaptive cooperative behavior. In Proceedings of the Simulation of Adaptive Behavior Conference. Paris.
WEDEKIND, C. & Milinski, M. (1996). Human cooperation in the simultaneous and the alternating prisoner’s dilemma: Pavlov versus generous tit-for-tat. Proceedings of the National Academy of Sciences, 93(7), 2686– 2689. [doi:10.1073/pnas.93.7.2686]
WELLMAN, M. P. (2006). Methods for empirical game-theoretic analysis. In Proceedings of the National Conference on Artificial Intelligence, vol. 21, (p. 1552). Cambridge, MA: MIT Press.
