Introduction
This paper studies the emergence of conventions in a variant of the Hawk-Dove game that we call Ali Baba and the Thief. Conventions are a special type of norms related to coordination problems. According to Ulmann-Margalit (1977), conventions are “those regularities of behaviour which owe either their origin or their durability to their being solutions to recurrent (or continuous) coordination problems, and which, with time, turn normative”. Conventions are used to guide the behaviour of humans in societies. Conformity to conventions reduces social frictions and facilitates cooperation. Conventions have also been extensively studied as a mechanism for coordinating interactions within multi-agent systems.
Conventions are defined using different terms in the literature, e.g. social laws, social conventions, social norms. Those terms have been used as synonyms, often without clearly distinguishing between them (Sen & Sen 2010; Villatoro et al. 2011). A distinction between conventions and social law is made in (Shoham & Tennenholtz 1997), where a social law is a restriction on the set of actions available to agents. A social law that restricts the agents’ behaviour to one particular action is called a convention. In Bicchieri (2006), convention is a notion weaker than social norm in the sense that:
- A convention is pattern of behaviour such that individuals prefer to conform to it on condition that they believe that most people in their relevant network conform to it;
- A social norm is a pattern of behaviour such that individuals prefer to conform to it on condition that:
- they believe that most people in their relevant network conform to it;
- most people in their relevant network believe they ought to conform to it.
Although it is not the objective of this paper to study the subtle difference between conventions and other notions of norms, we prefer to use convention to term the pattern of behaviour emerged in Ali Baba and the Thief because we do not address the issue of oughtness in Ali Baba and the Thief, while norms are often defined as concepts involving oughtness.
In the normative multi-agent system (NorMAS) community, Shoham & Tennenholtz (1996, 1997) distinguish two general approaches to the generation of conventions: online approaches and offline approaches. Online approaches (Shoham & Tennenholtz 1997; Sen & Airiau 2007; Morales et al. 2011; Morales et al. 2015) aim at establishing agents with the ability to dynamically coordinate their activities, for example by reasoning explicitly about coordination at run-time or learning from the interaction with other agents. Online approaches may also be termed as the convention emergence approaches because conventions in these approaches are not designed by any legislator but come to exist by themselves in the process of agents’ repeated interactions. The evolutionary game theoretical study of convention emergence in Alexander (2007) and Skyrms (2014), which are well-known in the philosopher’s community, fall into this category. In contrast, offline approaches (Shoham & Tennenholtz 1996; van der Hoek et al. 2007; Ågotnes & Wooldridge 2010; Ågotnes et al. 2012) aim at developing a coordination device at design-time, and build this regulation into a system for use at run-time. Offline approaches can be termed as the convention creation approaches because conventions in these approaches are created by system designers. The classical game theoretical study of conventions developed by social scientists (Vanderschraaf 1995; Gintis 2010), in which conventions are viewed as correlated equilibrium and can be created by computing correlated equilibria, can be classified into this category.
There are arguments in favour of both approaches: online approaches are potentially more flexible, and may be more robust against unanticipated events, while offline approaches benefit from offline reasoning about coordination, thereby reducing the run-time decision-making burden on agents. This paper belongs to online approaches.
In Alexander (2007) and Skyrms (2014), two features of convention emergence are emphasized: relatively simple learning processes and networked interactions. Both Alexander and Skyrms explore a variety of games such as the prisoner’s dilemma and the stag hunt to illustrate the emergence of conventions in different situations. Though Skyrms uses the replicator dynamics occasionally, both of them tend to adopt simple learning rules like “imitate-the-best” because such rules are less cognitively demanding. Alexander justifies the use of these simple rules on the grounds that they are extremely simple to follow for agents of bounded rationality. The general methodology for studying the emergence of conventions in Alexander (2007) is the following:
- Identify a convention with a particular strategy in a two-player game.
- Use multi-agent learning to test whether a convention emerges as a result of the repeated play of the two-player game.
- Test convention emerge with different social networks.
Two-player games studied in Alexander (2007) include prisoner’s dilemma, stag hunt, cake cutting and ultimatum game. Alexander uses these games to analyze the emergence of conventions of cooperation, trust, fairness and retaliation respectively. In this paper we study the emergence of conventions of peace. We follow Alexander’s general methodology but we study a game called Ali Baba and the Thief, which is not explored in Alexander (2007). We believe the study of different games is helpful in explaining different conventions.
We propose Ali Baba and the Thief as a variant of the famous Hawk-Dove game[1]. In this 2-player game, each agent has two strategies: Ali Baba and Thief. Each agent has initial utility x. If both agents choose Ali Baba, then their utility does not change. If they both choose Thief, then there will be a fight between them and they are both injured. The resulting utility is 0. If one chooses Ali Baba and the other chooses Thief, then Thief robs Ali Baba and the utility of the one who chooses Thief increases by d and the other one decreases by d, where 0 < d < x. We call d the amount of robbery. The payoff matrix of this game is shown in Table 1. Using standard techniques of game theory we know that there are two pure Nash equilibria in this game: (Thief, Ali Baba) and (Ali Baba, Thief). However, we will show later in this paper that repeated play of this game will sometimes drive the players to (Ali Baba, Ali Baba) as a stable outcome.
| Ali Baba | Thief | |
| Ali Baba | x, x | x d, x + d |
| Thief | X + d,x - d | 0,0 |
We identify a convention of peace with the strategy Ali Baba in the game Ali Baba and the Thief. In our model this game is repeatedly played by a given number of agents. Each agent adapts its strategy using a learning rule between different rounds of play. We say a convention has emerged in the population if:
- All agents are choosing and will continue to choose the action prescribed by the convention.
- Every agent believes that all its neighbours will choose the action prescribed by the convention in the next round.
- Every agent believes that all its neighbours want it to choose the action prescribed by the convention.
The above three criteria of convention emergence is a reformulation of Lewis’ famous analysis of conventions: “Everyone conforms, everyone expects others to conform, and everyone has good reasons to conform because conforming is in each person’s best interest when everyone else plans to conform” (Lewis 1969). In our game, we are interested in the situation where all agents choose Ali Baba. This can be understood as no agent is willing to be Thief, which shows a convention saying “everyone is peaceful” has emerged.
Our main contribution in this paper is the discovery of critical points in convention emergence. Our experimental results suggest that when the quotient of the amount of robbery and the initial utility is smaller than the critical point, the probability of convention emergence is high. The probability drops dramatically as long as the quotient is larger than the critical point. To the best of our knowledge, such critical points have never been found in the literature of convention emergence.
The structure of this paper is the following: in Section 2 we review some background knowledge on learning in games. Then in Section 3 we study how conventions emerge in Ali Baba and the Thief. Section 4 summarizes this paper with suggestions of future work.
Background: learning by imitating the best
Imitate-the-best is a very natural and common learning rule in the modeling literature (Nowak & May 1992; Epstein 1998; Alexander 2007; Tsakas 2014). Compared to other learning rules in the literature (Fudenberg & Levine 1998) such as fictitious play and regret matching, imitate-the-best is less cognitively demanding and extremely simple to follow for agents of bounded rationality. According to this rule, at each round of play, every agent surveys the utility of its neighbours and adopts in the next round the strategy of the agent who does the best in this round, where “best” means “receives the highest utility”. Here the neighbourhood is defined in the setting of a social network. A social network is a graph where every node in this graph is an agent and every edge connecting two agents means that the two agents are neighbours. Formally,
| $$s_i^{t+1}= s_k^t {with} k \in \mbox {argmax}_{j\in N_i} u^t_j$$ | (1) |
It is also assumed that an agent will not switch its strategy unless it has some incentives to do so. If the best neighbours of an agent still managed to get lower utility than it, the agent will not switch its strategy. Ties between best neighbours are broken randomly. So, for example, if the highest utility in an agent’s neighbourhood was obtained by 2 agents following strategy \(s_1\), 1 agent following strategy \(s_2\), and 2 agents following strategy \(s_3\), that agent will adopt strategy \(s_1\) with probability \(\frac{2}{5}\), strategy \(s_2\) with probability \(\frac{1}{5}\), and strategy \(s_3\) with probability \(\frac{2}{5}\) . An important aspect of this learning rule is that the agents discard most of the available information. They ignore whatever happened in the previous rounds and even from this round they take into account only the piece of information related to the most successful agent.
Ali Baba and the Thief
In this section we study convention emergence in Ali Baba and the Thief. We use imitate-the-best as the rule of learning. We run simulations using the Netlogo platform[2]. In all our experiments, we fix the population (nodes in the network) to be 100 and set the initial utility x = 1000. We then study how the amount of robbery d changes the probability of convention emergence. The initial percentage of agents choosing Thief is set to be 50%. Over time, however, through agent-agent interactions, a bias toward Ali Baba spreads through the entire network until 100% of the population choose Ali Baba. If this happens, then we say that a convention specifying peaceful behaviour has emerged because:
- All agents are choosing and will continue to choose Ali Baba.
- All agents believe that most agents will choose Ali Baba in the next round. Here we conceive such belief is formed in the process of interactions: if an agent sees another agent keeping choosing a specific strategy for a long time, by default it believes that agent will keep choosing that strategy.
- Every agent believes that all its neighbours want it to choose Ali Baba. Indeed, every agent even knows that it is always beneficial for its neighbours that it chooses Ali Baba.
However, this process may sometimes demonstrate complexity. Note that when all agents choose the same action at a round, they will choose that action forever because the learning rule they use is imitate-the-best. Therefore those rounds are stable (or absorbing) rounds.
We are interested in studying how different network topologies affect the emergence of conventions. In particular, we experiment with (a) lattice networks, (b) ring networks, (c) small world networks, (d) scale-free networks. Lattice and ring networks represent realistic situations where the agents are physically situated in space and are more likely to interact with other agents in their physical proximity. Small world and scale-free networks, on the other hand, characterize complex networks. If we pay attention to the topology of real networks in our life, we will find out that most of them have a very particular topology: they are complex networks (Adamic 1999) with non-trivial wiring schemes. The Internet is among the most prominent complex networks found in the real world. Complex networks are well characterized by some special properties, such as the connectivity distribution (either exponential or power-law) or the small-world property (Amaral et al. 2000). Small world networks are highly clustered graphs with small characteristic path lengths. Scale-free networks represent situations where the node degrees of the network follow a power law distribution.
In each round of our simulation, every agent plays Ali Baba and the Thief with his neighbours one by one. Their utility in this round is the average utility of the plays with all their neighbours. At the end of a round, each agent compares its utility to all its neighbours. If the agent’s utility is higher than all its neighbours, then the agent does not change its strategy in the next round. Otherwise the agent adopts the strategy chosen by its neighbour of highest utility. The stopping rule for our simulation is either all agent choose the same strategy, or the rounds of play reaches 100.[3] We say the convention of peace emerges if the simulation stops with all agents choosing Ali Baba.
Lattice network
Lattice networks are a special kind of social networks in which the connections between agents are defined spatially. Each agent is considered to be located at some cell on an 2-dimensional grid, and every cell in the grid is occupied by exactly one agent. In a lattice, every agent who does not live in the boundary has exactly 8 neighbours. As it is show in Figure 1, the agent in blue has 8 grey neighbours surrounding him.
The data of our experiment on lattice networks is recorded in Table 2 . We let the amount of robbery d vary from 200 to 800. We run the simulation for 100 times for each d \(∈ {200, 400, 600, 800}\).
In general, our experiments show that when the amount of robbery is high, the probability of convention emergence is low whereas the probability of the emergence of all-Thief equilibrium is high. When the amount of robbery decreases, the probability of convention emergence quickly increases. When d is less than 400, the convention “everyone is peaceful” emerges for certain. Intuitively, we can imagine that there are two neighbouring agents (agent a and b) who are Ali Babas and all their other neighbours are Thieves. Those agents who choose Thief will often meet another thief and receive utility close to 0. Although a and b will frequently meet a thief as well, but since they are choosing Ali Baba, their utility will be close x - d. When d is relatively small, a and b are the best neighbours for each other and doing better than all their other neighbours. Therefore other agents will mimic a and b and the convention will eventually emerge.

| Amount of robbery (d) | Probability of convention emergence | Probability of all-Thief equilibrium |
| 200 | 1.00 | 0.00 |
| 400 | 1.00 | 0.00 |
| 600 | 0.00 | 0.42 |
| 800 | 0.00 | 1.00 |
Some readers may think that the convention of peace is not stable because the best response to having only Ali Babas in one’s neighbourhood is to turn into a Thief. This intuition is, however, not true. According to imitate-the-best, an agent does not calculate its best response, but imitate its best neighbour. Therefore even though Thief is the best response for an agent surrounded by Ali Babas, it is does not mean the agent will adopt Thief in the next round.
Note that there is a leap of the probability of convention emergence from d = 600 to d = 400. We are curious about such a leap. To have a better understanding we perform a second experiment in which the amount of robbery varies from 400 to 600.
| Amount of robbery (d) | Probability of convention emergence | Probability of all-Thief equilibrium |
| 400 | 1.00 | 0.00 |
| 420 | 1.00 | 0.00 |
| 440 | 0.60 | 0.00 |
| 460 | 0.79 | 0.20 |
| 480 | 0.73 | 0.22 |
| 500 | 0.00 | 0.16 |
| 520 | 0.00 | 0.08 |
| 540 | 0.00 | 0.22 |
| 560 | 0.00 | 0.26 |
| 580 | 0.00 | 0.27 |
| 600 | 0.00 | 0.42 |
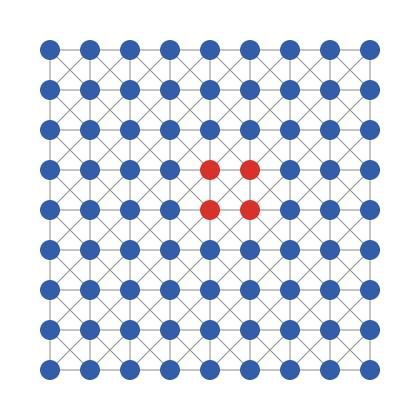
The leap still exists, as Table 3 shows. Now the leap takes place when d decrease from 500 to 480. The existence of such a leap in the lattice network can be explained as follows. Assume x = 1000; d = 500. Suppose in round t an agent i chooses Thief and 3 of its neighbours also choose Thief while other 5 neighbours choose Ali Baba. The utility of agent i in round t is \(u_i^t = (0+0+0+1500+1500+1500+1500+1500)/8 =937.5\). For i’s neighbour j who chooses Ali Baba, in the best case the utility of j in round \(t\) is \(u_j^t = (500+1000+1000+1000+1000+1000+1000+1000)/8 =937.5\). Therefore according to the learning rule imitate-the-best, i will keep choosing Thief in round t + 1. This explains why the state shown in Figure 2 is a stable state. In this figure, there is a red zone of thieves in which each thief is neighboured by exactly 3 thieves. When x = 1000; d = 500, none of these thieves would change to Ali Baba and none of the Ali Babas would change to Thief. Therefore this is a stable state (in which not all agents choose Ali Baba and not all agents choose Thief).[4] The existence of such states explains why the probability of convention emergence drops dramatically in the lattice model when d ≥ 500.
Ring network
We also examine ring networks, where nodes are connected in a ring. We consider rings in which each node is linked to all other nodes within a certain distance \(\delta\), the neighbourhood size. In our experiments we set \(\delta\) = 2. Just like in the lattice model, in our experiments on ring networks, we set the population to be 100, the initial utility x = 1000 and study how the amount of robbery d changes the probability of convention emergence. The data of our simulations are recorded in Table 4 .
| Amount of robbery (d) | Probability of convention emergence |
| 400 | 1.00 |
| 420 | 1.00 |
| 500 | 1.00 |
| 600 | 0.61 |
| 700 | 0.00 |
Our experiment shows that the probability of convention emergence increases when the amount of robbery decreases. Note that there is also a leap of the probability of convention emergence from d = 700 to d = 600. To have a better understanding we perform more experiments to find the critical points. The results of those experiments are presented in Table 5 and 6 . Those data confirm the existence of critical points. For ring networks, the critical point is reached when \(\frac{d}{x} \approx 0.66\).
| Amount of robbery (d) | Probability of convention emergence |
| 620 | 0.67 |
| 640 | 0.82 |
| 660 | 0.63 |
| 680 | 0.00 |
The critical point of ring networks can be partially explained as follows. Suppose there is a sequence of 9 agents, denoted them from left to right as as \(\{-4,-3,-2,-1,0,1,2,3,4\}\). Suppose agent 0 and all agents larger than 0 choose Thief and all other agents choose Ali Baba. Then the utility for agent 0 is \(u_0= (2x+2d)/4\). Moreover we have \(u_{-2}= (4x-d)/4\), \(u_{-1}= (4x-2d)/4\), \(u_{1}= (x+d)/4\), \(u_{2}=0\). Therefore agent 0 will choose Ali Baba in the next round iff \(u_{-2} > u_0\), which is equivalent to \(\frac{d}{x} < \frac{2}{3}\). This means when \(\frac{d}{x} <\frac{2}{3}\) , more and more agents will choose Ali Baba, which explains why the probability of convention emergence is high when \(\frac{d}{x} < 0.66\).
| Initial utility (x) | Value of d at critical points | \(\frac{d}{x}\) |
| 100 | 66 | 0.66 |
| 300 | 199 | 0.66 |
| 500 | 330 | 0.66 |
| 700 | 469 | 0.67 |
| 900 | 594 | 0.66 |
Small world network
The principal merit of lattice and ring networks is that they work well for modeling social networks in which the social relations are associated with the spatial positions of the agents. For social systems in which the relevant relations are not associated with spatial position, other networks need to be developed.
A lot of social networks are well characterized by the small-world property, which says that any two agents in the network are connected by a short sequence of friends, family and acquaintances. A small-world network is a type of graph in which most nodes are not neighbours of one another, but most nodes can be reached from every other node by a small number of edges. We choose the small-world network provided by the NetLogo models library.[5]
| Amount of robbery (d) | Probability of convention emergence |
| 100 | 1.00 |
| 200 | 0.68 |
| 300 | 0.06 |
| 400 | 0.02 |
| 500 | 0.00 |
Just like in the lattice and rings networks, in our experiments on small world networks, we set the population to be 100, the initial utility x = 1000 and study how the amount of robbery d changes the probability of convention emergence. The data of our simulations are recorded in Table 7.
Our experiment again shows that the probability of convention emergence increases when the amount of robbery decreases. Now a leap of the probability of convention emergence takes place from d = 300 to d = 200. More experiments are performed and the results are presented in Table 8 and 9. Those data confirm the existence of critical points. For small world networks, the critical point is \(\frac{d}{x} \approx 0.26\). Due to the complexity of small world networks, we have no analytic explanation of the existence and the exact value of the critical point yet.
| Initial utility (x) | Probability of convention emergence |
| 100 | 1.00 |
| 200 | 0.86 |
| 300 | 0.25 |
| 400 | 0.00 |
| 500 | 0.00 |
| Amount of robbery (d) | Probability of convention emergence |
| 220 | 0.73 |
| 240 | 0.75 |
| 260 | 0.72 |
| 280 | 0.05 |
Scale-free network
Lots of complex networks have the scale-free property: the connectivity of the network follows a power law distribution. This means that the network has a small number of nodes which have a very high connectivity. However, most of the nodes in the network are sparsely-connected. Two examples that have been studied extensively are the collaboration of movie actors in films and the co-authorship by mathematicians of papers.
In our experiments on scale-free networks, we again set the population to be 100 and the initial utility to be x = 1000. The data of our simulations are recorded in Table 10 . In contrast to other networks, there is no critical point in scale-free networks. Instead, there is a critical interval (from d = 300 to d = 200) in which the probability of convention emergence drops rather fast. Within the critical interval, there are butterfly effects in the sense that 2% change in the amount of robbery causes 20% of change in the probability of convention emergence.
| Amount of robbery (d) | Probability of convention emergence |
| 100 | 1.00 |
| 200 | 0.86 |
| 300 | 0.25 |
| 400 | 0.00 |
| 500 | 0.00 |
| Amount of robbery (d) | Probability of convention emergence |
| 220 | 0.65 |
| 240 | 0.80 |
| 260 | 0.53 |
| 280 | 0.32 |
Summary and future work
In this paper we propose a model that supports the emergence of conventions via multi-agent learning in social networks. In our model, individual agents repeatedly interact with their neighbours in a game called Ali Baba and the Thief. An agent learns its strategy to play the game using the learning rule imitate-the-best. We show that some conventions prescribing peaceful behaviours can emerge after repeated interactions among agents inhabited in some social networks. Our experiments suggest that there are critical points of convention emergence in Ali Baba and the Thief. Those critical points are summarized in Table 12. When the quotient of the amount of robbery and the initial utility is smaller than the critical point, the probability of convention emergence is high. The probability drops dramatically as long as the quotient is larger than the critical point.
| Networks | lattice | ring | small world | scale free |
| critical point | 0.5 | 0.66 | 0.265 | 0.2-0.3 |
In the future we will include noise in our learning rule and study the stochastic stability of the convention emergence. We are also interested in studying the problem of convention emergence for agents using some other learning rules such as fictitious play and highest cumulative reward. Shoham & Tennenholtz (1997) proposes a reinforcement learning approach based on the highest cumulative reward rule to study the emergence of conventions. According to this rule, an agent chooses the strategy that has yielded the highest reward in the past iterations. The history of the strategies chosen and the rewards for each strategy are stored in a memory of a certain size. Their experiments show that the rate of updating strategy and interval between memory flushes had a significant impact on the efficiency of convention emergence. In the future, we will investigate whether critical points still exist if agents adopt highest cumulative reward as their learning rule in Ali Baba and the Thief.
Acknowledgements
We are sincerely grateful to the reviewer of JASSS for his/her valuable comments. Xin Sun and Xishun Zhao have been supported by the National Social Science Foundation of China grant “Researches into Logics and Computer Simulations for Social Games” under grant No.13&ZD186.Notes
- https://en.wikipedia.org/wiki/Chicken_(game).
- http://ccl.northwestern.edu/netlogo/index.shtml .
- Here the choice of 100 is based on an empirical observation that most agents will not change its strategy after 100 rounds. Although it is possible to find more convention emergence when the simulation run longer, we believe the probability of such an event is negligible. We also would like to point out that experiments suggest that there seems to be some correlation between the population of agents and the rounds which are need for agents to stop changing their strategy. The larger the population is, the more rounds it takes for agents to stop changing. An in-depth study of such correlation is left as future work
- Here we remind the readers that the existence of this special stable state depends heavily on the parameter d and the structure of the network. It is hardly predictable whether such a special stable state will be reached in a complex network.
- http://ccl.northwestern.edu/netlogo/models/SmallWorlds.
References
ADAMIC, L. A. (1999). The small world web. In S. Abiteboul & A. Vercoustre (Eds.), Research and Advanced Technology for Digital Libraries, Third European Conference, ECDL’99, Paris, France, September 22-24, 1999, Proceedings, vol. 1696 of Lecture Notes in Computer Science, (pp. 443–452). [doi:10.1007/3-540-48155-9_27]
ÅGOTNES, T., van der Hoek, W. & Wooldridge, M. (2012). Conservative social laws. In L. D. Raedt, C. Bessière, D. Dubois, P. Doherty, P. Frasconi, F. Heintz & P. J. F. Lucas (Eds.), ECAI 2012 - 20th European Conference on Artificial Intelligence. Including Prestigious Applications of Artificial Intelligence (PAIS-2012) System Demonstrations Track, Montpellier, France, August 27-31 , 2012, vol. 242 of Frontiers in Artificial Intelligence and Applications, (pp. 49–54). IOS Press.
ÅGOTNES, T. & Wooldridge, M. (2010). Optimal social laws. In W. van der Hoek, G. A. Kaminka, Y. Lespérance, M. Luck & S. Sen (Eds.), 9th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2010), Toronto, Canada, May 10-14, 2010, Volume 1-3, (pp. 667–674).
ALEXANDER, J. M. (2007). The Structural Evolution of Morality. Cambridge University Press. [doi:10.1017/CBO9780511550997]
AMARAL, L. A. N., Scala, A., BarthÃľlÃľmy, M. & Stanley, H. E. (2000). Classes of small-world networks. Proceedings of the National Academy of Sciences, 97(21), 11149–11152. [doi:10.1073/pnas.200327197]
BICCHIERI, C. (2006). The Grammar of Society: The Nature and Dynamics of Social Norms. Cambridge: Cambridge University Press.
EPSTEIN, J. (1998). Zones of cooperation in demographic prisoner’s dilemma. Complexity, 4(2), 36–48. [doi:10.1002/(SICI)1099-0526(199811/12)4:2<36::AID-CPLX9>3.0.CO;2-Z]
FUDENBERG, D. & Levine, D. (1998). The Theory of Learning in Games. MIT Press.
GINTIS, H. (2010). Social norms as choreography. Politics, philosophy & economics, 9(3), 251–264. [doi:10.1177/1470594X09345474]
LEWIS, D. (1969). Conventions: a philosophical study. Cambridge: Harvard University Press.
MORALES, J., López-Sánchez, M. & Esteva, M. (2011). Using experience to generate new regulations. In IJCAI'11 Proceedings of the Twenty-Second international joint conference on Artificial Intelligence - Volume One, (pp. 307–312): http://ijcai.org/papers11/Papers/IJCAI11-061.pdf
MORALES, J., López-Sánchez, M., Rodríguez-Aguilar, J. A., Wooldridge, M. & Vasconcelos, W. W. (2015). Synthesising liberal normative systems. In G. Weiss, P. Yolum, R. H. Bordini & E. Elkind (Eds.), Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2015, Istanbul, Turkey, May 4-8, 2015, (pp. 433–441). ACM: http://dl.acm.org/citation.cfm?id=2772936
NOWAK, M. & May, R. (1992). Evolutionary games and spatial chaos. Nature, 359, 826–829. [doi:10.1038/359826a0]
SEN, O. & Sen, S. (2010). Coordination, Organizations, Institutions and Norms in Agent Systems V: COIN 2009 International Workshops. COIN@AAMAS 2009, Budapest, Hungary, May 2009, COIN@IJCAI 2009, Pasadena, USA, July 2009, COIN@MALLOW 2009, Turin, Italy, September 2009. Revised Selected Papers, chap. Effects of Social Network Topology and Options on Norm Emergence, (pp. 211–222). Berlin, Heidelberg: Springer Berlin Heidelberg. [doi:10.1007/978-3-642-14962-7_14]
SEN, S. & Airiau, S. (2007). Emergence of norms through social learning. In M. M. Veloso (Ed.), IJCAI 2007, Proceedings of the 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, January 6-12, 2007, (pp. 1507–1512): http://dli.iiit.ac.in/ijcai/IJCAI-2007/PDF/IJCAI07-243.pdf
SHOHAM, Y. & Tennenholtz, M. (1996). On social laws for artificial agent societies: Off-line design. Artificial Intelligence, 73(1-2), 231–252. [doi:10.1016/0004-3702(94)00007-N]
SHOHAM, Y. & Tennenholtz, M. (1997). On the emergence of social conventions: Modeling, analysis, and simulations. Artificial Intelligence, 94(1-2), 139–166. [doi:10.1016/S0004-3702(97)00028-3]
SKYRMS, B. (2014). Evolution of the Social Contract. Cambridge University Press. [doi:10.1017/CBO9781139924825]
TSAKAS, N. (2014). Imitating the Most Successful favour in Social Networks. Review of Network Economics, 12(4), 33: https://ideas.repec.org/a/bpj/rneart/v12y2014i4p33n4.html [doi:10.1515/rne-2013-0119]
ULMANN-MARGALIT, E. (1977). The Emergence of Norms. Oxford: Clarendon Press.
VAN DER HOEK, W., Roberts, M. & Wooldridge, M. (2007). Social laws in alternating time: effectiveness, feasibility, and synthesis. Synthese, 156(1), 1–19. [doi:10.1007/s11229-006-9072-6]
VANDERSCHRAAF, P. (1995). Convention as correlated equilibrium. Erkenntnis, 42(1), 65–87. [doi:10.1007/BF01666812]
VILLATORO, D., Sabater-Mir, J. & Sen, S. (2011). Social instruments for robust convention emergence. In IJCAI'11 Proceedings of the Twenty-Second international joint conference on Artificial Intelligence - Volume One (pp. 420–425).
WALSH, T. (Ed.) (2011). IJCAI 2011, Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Catalonia, Spain, July 16-22, 2011. IJCAI/AAAI: http://ijcai.org/proceedings/2011
