Introduction
As an inevitable and influential process within daily social, economic, and political life, social dynamics is tightly connected with opinion formation. The study of opinion dynamics includes a wide range of social phenomena, such as the evolution of voting preferences, variations in market demand for products or competitor trademarks, emergence and popularity of topics, dissemination and preservation of minorities’ opinions, decision-making, political party development, rumour spreading, and emergence and influence of extremists, among others (Xia et al. 2011). Even though formal defining of the opinion is not an easy task (it can be quantified as a degree of satisfaction, desire, or preference), opinion dynamics seen as an evolutionary problem can be considered within the frame of a dynamical system. There has been an increasing interest in analyzing and mathematical modelling of different aspects of opinion formation in networked societies. Since one of the substantial elements defining opinion dynamics is ideology, its inclusion in mathematical models of opinion formation should clarify the role of ideology in different social scenarios.
Agent-based modelling of networks is an efficient and rapidly growing, quasi-deterministic approach to social dynamics for studying collective effects resulting from the interaction of a number of “simple” agents in a social network (Schweitzer 2003). Members of social groups are considered to be adaptive rather than rational agents, and no individual strategy is involved except a common rule for opinion updating. Bounded Confidence, Relative Agreement (BC/RA) models of opinion dynamics are effective agent-based modelling methods (Deffuant et al. 2000; Amblard et al. 2004; Deffuant et al. 2002; Deffuant et al. 2006; Hegselmann & Krause 2002; Lorenz 2007). Opinion dynamics models usually consider homogeneous societies of agents, they do not distinguish between agents by their psychological profiles. To overcome this limitation, a BC/RA nonhomogeneous model with agents of two psychological types (partial antagonism and concord, or PA/C model), was proposed by Kurmyshev et al. (2011); although this model describes quite realistic dynamics of opinion formation and opinion distribution patterns in different networks of agents based on model parameters, the effect of ideology was not explored.
In social sciences, it is hardly possible to find a unique - in a mathematical sense - definition of ideology. Definitions differ from source to source, and they usually emphasize different aspects of ideology. Van Dijk (2011) states that ideologies “are basic systems of social cognition, a configuration of mental representations shared by and specific to a group, which fall within the general beliefs (knowledge, opinions, values, criteria of truth, etc.) of societies or cultures”. Franzoi (2006) considers ideology as the theory a social group has on itself. Althusser (1970) understands ideology as a (social cognition) system imposed on and acting through individuals, in such a way that individuals do not configure that ideology. Porras-Velasquez (2011) writes: “what characterizes ideologies, paying attention to their practical function, is that they are structures unconsciously assimilated by members of a society (persons) and constantly reproduced in everyday practice”. Leadership is deemed a group phenomenon, which strongly determines the behaviour of followers and leaders themselves, and can originate these assimilated structures. This idea persists since the theory of social identity (Tajfel & Turner 1979) and the self-categorization theory (Turner et al. 1987) were proposed. Tajfel (1972) defines social identity as “an individua’s knowledge of belonging to certain social groups together with the emotional or evaluative significance of that membership”. So, for the group to exist, there must be a shared social identity, for example in the form of an ideology.
In this paper, we employ a synthesized definition that captures the main features of the concept as far as we have investigated (see, in addition, Delli 1981, Vela-McConnell 1999 and https://en.wikipedia.org/wiki/Ideology). An ideology is a set of fundamental ideas about the transformation or preservation of a society in regard to a variety of social, economic, political, and scientific-technological and cultural affairs; those are usually entangled with each other. Ideologies characterize different social groups or institutions, and usually consist of a representation of the system and an action program. The first provides an analysis of the current state of the system, usually in comparison with an alternative, real or ideal system; the second aims to bring, as much as possible, the existing real system to the intended ideal system. An ideology is a social control tool that acts on the formation of opinions and shapes individuals towards social group cohesion, and it has different purposes. It is often the emergence of a person (leader) or a small group of people, who induce their ideas into society. When an ideology is accepted by part of a society, it first changes and then maintains (for a certain while) the way in which people think and act; in such a way, it serves as a socio-psychological frame for people’s behaviour in regard to opinion formation and decision-making. When accepted, ideology becomes an agents’ attribute to some extent. From real life we may infer that ideologies result in the separation of societies in different social, political, and economic movements (groups). On the other hand, an ideology aims at consolidating a group of ideological partners. This groupthink behaviour, introduced by Janis (1982), refers to a search for consensus regardless of a series of antecedents (conditions), including group cohesion, which is considered to be the necessary but not sufficient condition for groupthink (Huici et al. 2012). So, we would expect a model including some sort of ideology variable to manifest that ideological separation of agents as well as the consolidation of the opinion of agents sharing the same ideology.
The substantial part of an ideology is an individual’s affinity with their social group vision expressed in terms of their opinion; hereafter, we will refer to this as opinion affinity. Sociology (Vela-McConnell 1999) sees social affinity as an adaptation, sympathy, trend, or similarity of characters, likes, and preferences among the agents of a society; for example, a person may have an inclination towards certain political party, which represents his individual ideas. Previous works have introduced the concept of affinity or similar notions into the study of opinion dynamics models. Salzarulo (2006) introduced the measure of self-identification of a person with a group, based on the self-categorization theory (Turner et al. 1987; Oakes et al. 1991; Oakes et al. 1994). People’s typical behaviour is defined by their self-categorization with respect to the situational context because people identify themselves and behave in specific ways in different situations. Ramirez-Cano & Pitt (2006) define mentality as a set of beliefs, attitudes, assumptions, and trends that predetermine how an agent evaluates an accepted opinion. In this way, the closeness between an agent and a group of agents sharing the same mentality is defined as a function of affinity. This function evaluates the linear similarity between an opinion and a constant \(mu\), which is a reference value for the agent’s mentality to a given problem. Finally, Yang & Xi (2010) crystalized agent personality in a simplified Deffuant model; such personality is defined as the attitude agents display when their opinions are incompatible with others’ opinions during the course of a discussion; personality is thus represented by the convergence rate parameter \(mu\) in opinion updating equations.
In this paper, following up on previous research by Kurmyshev et al. (2011), we propose an extension of the PA/C opinion dynamics model introducing ideological affinity between agents in artificial societies. The aim is to analyze opinion dynamics in specific scenarios in societies including concord (C-) and partial antagonism (PA-) agents, taking into account their ideological preferences by means agent opinion affinity. The following section describes the PA/C model with opinion affinity, section 3 presents a computer experiment design for the application of this model, section 4 shows the simulations results, and finally, section 5 presents our conclusions and discussion.
PA/C model with opinion affinity
In order to be validated, mathematical opinion dynamics models must be based on the key elements of Social Influence, Social Judgment, and Social Identity theories that are psycho-sociological approaches dealing with the manner in which individuals change thoughts, feelings, opinions, and behaviours of others. Social influence theory is focused on the interaction between psychological processes and social factors involved in-group behaviour (Asch 1951; Sherif 1936). Bounded confidence (BC) models (Wood 2000; Deffuant et al. 2000; Hegselmann & Krause 2002), based on the concept of Social Influence, assume that two interacting agents change their opinion (i.e., come closer to each other) if and only if their initial opinions are close enough. Otherwise, they ignore each other. Another theory used in these models is the Social Judgment theory (Sherif & Hovland 1961), which argues that the success of a message depends on the relationship between the message and the receiver’s beliefs. Relative agreement models use principles from the Social Influence and Social Judgment theories.
An ideology influences and interacts with the agent’s psychological profile during the process of opinion formation and changes their attitudes (Sherif & Hovland 1961). That is definitely observed when interacting agents support different ideologies; agents act their psychological profiles out during their decision-making processes and, on the other hand, they must adhere to an accepted ideology - this can cause an agent’s socio-psychological conflict, which can be interpreted as cognitive dissonance. This concept, developed by León Festinger (1957), refers to the stress or disharmony of a system of ideas, beliefs, and emotions perceived by an agent experimenting simultaneous conflicting thoughts, or whose behaviour is in conflict with their beliefs. The question is, which one of the two trends is stronger? When interacting agents are in the same ideological group, they do not have this conflict. So, agents can act naturally, representing their psychological profiles when interacting with ideological friends, or in the opposite way, opposing their own psychological profiles when interacting with ideological opponents.
Mathematical models of opinion dynamics in networked societies are characterized by four basic elements (Fan et al. 2012, 2014; Kurmyshev et al. 2011). Opinion space - a discrete or continuous set of values that represent the opinions of agents. Updating rule - basically, the model equations describing opinion change as a result of agent interaction. Updating dynamics - establish the manner and conditions under which agents update their opinions. Social network (networked society) - represents the communication channels between agents of a society by means of a graph where nodes represent agents and communication channels between agents are represented by links. Usually, opinion dynamics models are distinguished by their specific updating rules and updating dynamics, while other elements are shared.
In order to define the opinion model including ideological (opinion) affinity between agents, we used the concepts, definitions and, to some extent, the methodology of the PA/C model (Kurmyshev et al. 2011). Note that relative agreement (RA) models, along with the opinion variable xi, use a new variable ui, to account for uncertainty, which can be interpreted as the tolerance of an agent “i” to the opinions of others or the level of confidence that an agent has in their own opinion xi. In RA models with one pair of agent interactions, the degree of social influence depends on the overlap hij = min{xi + ui , xj + uj} − max{ xi − ui , xj − uj } of opinion segments [xi − ui, xi + ui] and [xj – uj, xj + uj] of a (i, j)-pair of agents that interact. The more confident an agent is in his opinion (small value of ui), the more influential and less prone to influence the agent will be. As in the PA/C model, we considered agents of two psychological types: partial antagonism (PA) and concord (C). The psychological composition of society was characterized by the parameter p in [0,1], which partitions society in two disjoint subsets, SC and SPA of sizes pN and (1−p) N respectively, where the total number of agents is N.
Our updating dynamics is stochastic, and based on unidirectional interaction in pairs of agents. In each updating stage, N edges of a network are randomly chosen. Then, in the pair (i, j) of agents associated with each of these edges, one agent is considered passive (influenced) and the other active (influential), also randomly. If hij ≥ 0, the passive agent of the pair, say j, updates their opinion xj and uncertainty uj according to the psychological profile. Note that, in the PA/C model (Kurmyshev et al. 2011), the interaction of passive C-agents is always attractive in the opinion space, while the interaction of passive PA-agents can be repulsive-attractive according with relative agreement, as is explained below. In order to include the influence of ideology on opinion formation, we modified the PA/C model updating rules by introducing the opinion affinity function Aij(t), defined below. So, if the passive agent j is C-agent, then:
| $$\begin{split} x_j(t+1)=x_j(t)+\mu_1\cdot A_{ij}(t) \cdot \frac{h_{ij}(t)}{u_i(t)} \cdot \big[x_i(t)-x_j(t) \big] \\ u_j(t+1)=u_j(t)+\mu_2\cdot \frac{h_{ij}(t)}{u_i(t)} \cdot \big[u_i(t)-u_j(t) \big]\\ \end{split}$$ | (1) |
If the passive agent j is PA-agent, then:
| $$\begin{split} x_j(t+1)=x_j(t)+\mu_3\cdot A_{ij}(t) \cdot \frac{h_{ij}(t)}{2u_i(t)} \cdot \Bigg[ \frac{h_{ij}(t)}{u_i(t)}-1 \Bigg] \cdot \big[x_i(t)-x_j(t) \big] \\ u_j(t+1)=u_j(t)+\mu_4\cdot \frac{h_{ij}(t)}{2u_i(t)} \cdot \Bigg[ \frac{h_{ij}(t)}{u_i(t)}-1 \Bigg] \cdot \big[u_i(t)-u_j(t) \big] \\ \end{split}$$ | (2) |
In the above equations, the multipliers μs in (0, 0.5) are convergence parameters (s = 1, 2, 3, 4). In this work, being limited by the one-topic opinion model, we used a very simple mathematical function to express ideological (opinion) affinity: the signum function. So, hereafter:
| $$A_{ij}(t)= \begin{cases} 1 & \text{if $x_i(t)x_j(t)>0$}\\ 0 & \text{if $x_i(t)x_j(t)=0$}\\ -1 & \text{if $x_i(t)x_j(t)<0$}\\ \end{cases}$$ | (3) |
Note that Kurmyshev et al.’s (2011) PA/C model is a special case of our proposed model, where the ideological affinity function is always equal to Aij(t) = 1. As previously stated, our model uses ideas developed by the Social Influence (Asch 1951; Sherif 1936), Social Judgment (Sherif & Hovland 1961), and Social Identity (Tajfel 1972) theories. Particularly, social influence is expressed by the distance between opinion segments of pairs of agents and their overlap, while the basic concepts of Social Judgment and Social Identity theories (beliefs of agents and group belonging) are modelled by the psychological profile of PA- or C-agents and opinion affinity Aij.
In order to better understand the model interaction mechanism between ideological affinity and agent psychological type, we replicate the basic features of the original PA/C model. In that model, the opinions of C-agents tend to come closer to the opinions of active agents, so that the interaction is always attractive. Nevertheless, the relative agreement of PA-agent in the interval −0.125 ≤ (hij/2ui) (hij/ui −1) ≤ 1, can take negative, positive, or zero values. Thus, a passive PA-agent “j” can refuse (when (hij/ui −1) < 0) or accept (when hij/ui −1 > 0) the opinion of an active agent “i”; if hij/ui − 1 = 0, the PA-agent is indifferent. The PA/C model is doubly heterogeneous:
- Parameter p in [0,1] regulates the psychological composition of the society.
- Parameter 0 ≤ l ≤ 1 manipulates the initial political preference of agents.
The initial opinions of lN “left-wing” oriented agents are drawn from the interval [−1, 0], while the opinions of (1−l)N “right-wing” oriented agents are drawn from the interval [0, 1]. As we can see, the proposed PA/C model with opinion affinity, as a natural extension of the original PA/C model, belongs to the class of RA opinion dynamics models. It also has a multiplicative heterogeneity caused by a number of ideologies induced into the society. The ideological affinity of agents, defined in this study as a signum function (Equation (3)), expresses two important issues. First, society can be seen as governed by the two fuzzy, equally powerful ideologies, say rightist and leftist. Second, it indicates the conflict of consciousness between an agent’s ideology and psychological behaviour. There is only one ideology in society when Aij(t)=1, so opinion formation takes place in accordance to the psychological reaction of agents, as in the PA/C model. However, in a society with various ideologies, particularly when Aij(t) is the signum function, the reaction of an agent is influenced by their ideology and psychological profile: this ideological affinity inverts the psychological reaction of an agent to the opposed point of view when the agent interacts with an ideological opponent.
Opinion affinity, seen through the effects of demographic composition on team cohesion and performance, was studied with a model by Flache and Mäs (2008). Even though the PA/C with affinity and Flache-Mäs models are both based on the same social mechanisms, they cannot be considered an extension of one another due to differences in the way each model considers agent affinity and opinion updating (see Table 1); in particular, they operate in different feature spaces. Social influence, rejection, homophily, and heterophobia are the four social mechanisms used in both models, but they are treated in different ways. In the Flache-Mäs model, the mathematical representation of social mechanisms is based on fixed and flexible attributes and their combinations. Specific (dis)-similarities between the PA/C and Flache-Mäs models are as follows. While Flache-Mäs considers a continuous dimension K opinion space (= 4 in the experiment), where agent’s opinions (flexible attributes) are related to team-work, we consider a 1-D continuous opinion space which can be interpreted as an aggregate of K's opinions. An agent’s flexible attributes are entangled with each other through social influence wij. The influence wij agent j has over agent i changes depending on the differences between demographic attributes (fixed attributes) and opinions. With Flache-Mäs, the group similarity of agents i and j is measured in terms of both demographic and flexible attributes; in our model, we consider agent similarity in terms of ideological affinity and opinions. In the PA/C model, agent ideological affinity, Aij can be regarded as a combination of the fixed, correlated attributes of the Flache-Mäs model. In the Flache-Mäs model, social influence wij is a qualitative analog of relative agreement in the PA/C model, a combination of opinion difference and opinion uncertainty; the latter is a psychological more than social entity and there is no equivalent concept in the Flache-Mäs model. We consider PA- and C-agents from the two psychological types. In these terms, homophily or heterophobia can be associated with a combination of (PA/C + Ideological affinity + Uncertainty). Social influence is expressed in the PA/C model by a combination of (Opinion difference + Uncertainty + Ideological affinity + PA/C). Rejection in the PA/C model is determined by a combination of (PA/C + Ideological affinity). As for opinion updating, we use the pair (i, j) interaction dynamics, while Flache-Mäs appeals to the modified Hegselmann-Krause updating rules when the opinion of i is changed in function of the opinion differences of i and all members of the team. Even though in some scenarios these dynamics show similar overall behaviour (consensus, polarization), they can differ in particularities (convergence rate, extremists, fixed points). It should be noted that the work team of the Flache-Mäs model is necessarily a small social group of agents, whereas the PA/C model is focused on large societies.
An extension of Huet et al.’s (2008) bounded confidence model was proposed by Alizadeh et al. (2015), in a 2-dimensional opinion space, in order to resolve the problem of cognitive dissonance in social systems including in-group favouritism and social identity. In both models, Cooperative Bounded Confidence (CBC) and PA/C with affinity, opinion dynamics are based on the theories of social influence, social identity, and cognitive dissonance. Both models use similar social notions, such as opinion, uncertainty, and opinion rejection: their difference lies in their specific variable updating mechanisms and model parameter interpretations. In the CBC model, opinion updating is governed by the distance between the opinions of interacting agents only, whereas the relative agreement PA/C model updates opinions in accord with the distances between agents’ opinions and their uncertainty magnitude (see Table 1 ). In the CBC model, the updating dynamics is bidirectional and invariant to the commutation of agents’ indices (i, j), which causes double rejection or attraction of opinions in a pair of interacting agents. Both the CBC and PA/C models describe attraction, rejection, and no opinion change. In our PA/C model with ideological affinity, these changes are determined by relative agreement, which in turn depends on the psychological type of an agent (PA- or C-agent) and their affinity with an ideological group, Aij. In order to represent opinion rejection, the CBC model uses the opinion space of at least two dimensions. A “secondary” opinion is used to determine if the “main” opinion is rejected or attracted. In addition, a new parameter δ, named intolerance threshold, is introduced to describe the cognitive dissonance (psychological discomfort) of agents. In the PA/C model with affinity, the state of an agents’ cognitive dissonance and its evolution are the result of an interaction between the ideological affinity and psychological type of interacting agents. It should be noted that cognitive dissonance is a psychological characteristic of an agent, and it is difficult to expect this feature to be described by means of the unique parameter δ for all agents and scenarios in nonhomogeneous societies.
As an attempt to better describe the proposed model’s place among RA models, this paper offers a comparison of components from the most widespread of these models. Xia et al. (2011) provide an exhaustive multidisciplinary review including the best known opinion dynamics models, both in discrete and continuous opinion spaces. Table 1 summarizes the principal components of continuous opinion space models: the Deffuant (2000) model and its extension (Deffuant et al 2002), the Hegselmann-Krause (2002) model, the demographic fault-line model (Flache and Mäs, 2008), the PA/C model (Kurmyshev et al. 2011), the CBC model (Alizadeh et al 2015) and the PA/C model with opinion affinity; each of these models can be applied to social networks of any topology.
| Model | Variables’ space | Parameters and characteristics | Type of interaction | Updating rule |
| Deffuant et al. (2000) | Opinion xi[0, 1] | Threshold, d Convergence, μ | Bi-directional pair interaction | Homogeneous linear system xj(t+1) = xj(t)+ μ [xi(t) – xj(t)] The similar way for the agent i |
| Deffuant et al. (2002) | Opinion xi [−1, 1] Uncertainty ui [0, 1] (Note: the opinion dynamics is studied only) | Convergence, μ Initial agent’s tolerance, U Relative agreement hij/ui Fractions of extremists:p+, p− | Bi-directional pair interaction | Homogeneous nonlinear system xj(t+1) = xj(t)+ μ [(hij/ui) − 1][xi(t) – xj(t)] uj(t+1) = uj(t)+ μ [(hij/ui) − 1][ui(t) – uj(t)] The similar way for the agent i |
| Hegselmann-Krause (2002) | Opinion xi [0, 1] | Agent’s confidence εi Set of neighbours Ni(t) | Nearest neighbour interaction | xi(t+1) = | Ni(t)|−1 Σ j in Ni(t) xj(t)
where Ni(t) = {1 ≤ j ≤ N : | xi(t)- xj(t)| ≤ εi} |
| Demographic fault-line model (Flache-Mäs, 2008) | Fixed attributes (opinion) afixid Flexible attributes aflexik The interpersonal relations wij | The fault-line strength f Number of flexible attributes K Number of fixed attributes D | Neighbour interaction | With, Δaflexik,t = |2(N−1)|−1 Σ j≠i wij (aflexjk,t − aflexik,t) If Δaflexik,t > 0 then, aflexjk,t+1 = aflexjk,t + Δaflexik,t (1− aflexik,t) If Δaflexik,t ≤ 0 then,aflexjk,t+1 = aflexjk,t + Δaflexik,t (1+ aflexik,t) Where, wij,t+1 = 1 – (D – K)−1 (ΣDd=1 |afixid,t − afixjd,t| + ΣKk=1 |aflexik,t – aflexjk,t|) |
| PA/C model (Kurmyshev et al. 2011) | Opinion xi[−1, 1] Uncertainty ui [0.1, 1.2] (Note: the opinion dynamics is studied only) | Psychological profile of agents Medium initial uncertainty or tolerance, U Nonlinear relative agreements | Uni-directional pair interaction | Homogeneous nonlinear system C-agent: xj(t+1) = xj(t)+ μ [hij/ui][xi(t) – xj(t)] uj(t+1) = uj(t)+ μ [hij/ui][ui(t) – uj(t)] PA-agent: xj(t+1) = xj(t)+ μ [hij/2ui][(hij/ui)− 1][xi(t) – xj(t)] uj(t+1) = uj(t)+ μ [hij/2ui][(hij/ui)− 1][ui(t) – uj(t)] |
| CBC model (Alizadeh et al. 2015) | Opinions (x1i, x2i) in [−1, 1] × [−1, 1] Uncertainty (u1i, u2i) in [0, 1]×[0, 1] | Uncertainty in-group Uint and out-group Uout; with Uout ≤ Uint Number of groups m The intolerance threshold δ | Bi-directional pair interaction | Homogeneous linear system If |xt1i – xt1j| ≤ U and |xt2i – xt2j| ≤ U then xt+11j = xt1j + μ [xt1j – xt1i] xt+12j = xt2j + μ [xt2j – xt2i] If |xt1i – xt1j| > U and |xt2i – xt2j| ≤ U then if |xt1i – xt1j| ≤ (1+ δ)U then xt+11j = xt1j xt+12j = xt2j + μ [xt2j – xt2i], if |xt1i – xt1j| > (1+ δ)U then xt+11j = xt1j xt+12j = xt2j – μ psing(xt2j – xt2i) (U – |xt2j – xt2i|) Note: if agents i and j belong to the same group, then U=Uint; otherwise U=Uout. |
| PA/C model with opinion affinity | Opinion xi [−1, 1] Uncertainty ui [0.05, 1] (Note: Both the opinion and uncertainty dynamics are studied) | Psychological profile of agents Medium initial uncertainty or tolerance, U Nonlinear relative agreements Ideological affinity Aij | Uni-directional pair interaction | Homogeneous nonlinear system C-agent: xj(t+1) = xj(t)+ μ1 Aij(t) [hij/ui][xi(t) – xj(t)] uj(t+1) = uj(t)+ μ2 [hij/ui][ui(t) – uj(t)] PA-agent: xj(t+1) = xi(t)+ μ3 Aij(t) [hij/2ui][(hij/ui)− 1][xi(t) – xj(t)] uj(t+1) = uj(t)+ μ4 [hij/2ui][(hij/ui)− 1] [ui(t) – uj(t)] |
The cited models and their variants exhibit, in general, three types of attractors (Mathias et al. 2016): central cluster (the group of agents with a centrist opinion), double extreme (opinion polarization in two groups of agents with opposed opinions tending to extremism), and single extreme clusters (a unique group of agents sharing an extreme opinion).
Computer experiment design
Everyday life itself shows that opinion dynamics in real-world societies are not always unique, and their results are not always predictable. Social group members can come to the same opinion, a consensus, in different ways and by means of different dynamics or, on the contrary, social agents can come to different conclusions via similar—if not identical—dynamics; this is due to the instabilities of some social processes. Those features have to be taken into consideration in the modelling and simulation of opinion dynamics. Although the updating rules of opinion and uncertainty are deterministic (see Equations. 1 and 2), the proposed model is characterized by important stochastic elements: updating dynamics and initial distributions of both opinion and uncertainty, psychological distribution of agents on the social network. This combination makes it difficult, if possible, to undertake an analytical study of the model. So, a computer agent-based simulation of the model was used. Due to the stochasticity of the proposed model, we were faced by the difficult decision of studying particular scenarios or the averaged results of many individual experiments. Pilot simulations showed that averaging the results of many experiments (see also (Kurmyshev et al. 2011)) made it possible to capture quite general opinion evolution tendencies, although very interesting and important characteristics of each particular scenario remained hidden. On the other hand, the study of one particular scenario shows rather general trends of opinion evolution in addition to salient particularities. For that reason, in this work we decided to explore systematically individual scenarios in a wide range of parameters offered by the model.
In order to make the description of the experiments more understandable, we will clarify a few notions. Society is for us a network (graph), with specific psychological types (C or PA) assigned to each agent. It should be noted that for a given value of the p parameter, two societies represented by the same graph are considered to be different if they have different psychological type distributions over the nodes. A particular scenario of opinion formation is defined by the following elements: the society itself, the initial opinion distribution, and the particular realization of updating dynamics, which is stochastic in our model. The evolution of opinion and uncertainty can be simulated on a social network with any topology. In this study we used small-world networks. The simulation of a particular scenario begins with setting initial conditions:
- A network of N = 1000 nodes with a small-world topology is fixed as per the Watts-Strogatz model with an edge redirecting probability of 0.25, being <d> = 40 the average degree of each node (Boccara 2010).
- A uniform distribution of C- and PA- agents in the network is controlled by the value of parameter p.
- The uniform opinion distribution in the interval [−1, 1] is used at the initial time t = 0. We use the same array of data for all p and U
- The uniform probability distribution in the interval [U−0.15, U+0.15] is employed to assign initial uncertainty to agents. The average initial uncertainty of agents U is varied in the interval 0.2 ≤ U ≤ 0.7.
After the initial conditions have been fixed, the experiment is conducted as per the following algorithm:
- N = 1000 edges are chosen randomly.
- In each edge (i, j), the passive agent is chosen randomly.
- The overlap hij of opinion segments is calculated.
- If hij ≥ 0, the opinion and uncertainty of the passive agent are updated according to their psychological type, Equations. 1 for the C-agent or Equations. 2 for the PA-agent, with μs = 0.5 for each s.
- In regard to hij < 0, neither opinion nor uncertainty of the passive agent are modified.
It should be noted that opinions are maintained within the opinion space [−1, 1] as follows: if it happens that xj(t) > 1 or xj(t) < −1, then we assign xj(t) equal to 1 or −1, respectively. Similarly, uncertainty uj(t) is maintained in the interval [0.05, 1]. It is important to note that agents with uj(t) = 0 values are not expressive since they are not willing to change their opinion neither their tolerance despite being related in the network, because they have zero opinion segment overlap with other agents. These agents can be considered as apathetic or socially closed because they do not admit interaction with other agents. In order to maintain at least a nominal interaction, a small margin (0.05) was left in uncertainty for keeping opinion exchange.
In order to monitor the evolution of opinion distribution (to a stochastically steady state, if it was the case), a convergence measure was defined as follows. Opinion space is divided into 2m+1 subintervals. At a time t, the opinion distribution function is given by the set of Nk(t) numbers of agents with opinions in each subinterval (k = 1, …, 2m+1) so that
| $$\sum_k^{2m+1}N_k(t)=N $$ | (4) |
| $$D(t)=\frac{1}{2}\sum_k^{2m+1}|N_k(t+1)-N_k(t)| $$ | (5) |
To visualize and analyze the opinion formation process, we opted for presenting the results by way of opinion and uncertainty temporal evolution plots. However, sometimes these plots are confusing as to how they represent the number of agents in the opinion groups. To avoid this confusion we used opinion distribution histograms as a complementary representation. To calculate opinion histograms, we divided the opinion space [−1, 1] into 21 subintervals, in order to have statistically significant opinion differences between the opinions of agents in different subintervals. Regarding histograms for uncertainty distributions, the same number of subintervals was used in the interval [0.05, u*], where u* = max{ui(t) : i = 1… N; t ≥ 0}.
Simulation results
Using the PA/C model as a framework and incorporating ideological opinion affinity, fifteen scenarios were simulated and analyzed. The following model parameters were varied: psychological composition of society p = 0, 0.2, 0.5, 0.7, and 1; initial average uncertainty U = 0.2, 0.5, and 0.7. It should be mentioned that the same society (a network with a given psychological type distribution) and the same initial opinion distribution were used for each p-value, so that particular scenarios differed from each other in their value of U and in stochastic updating dynamics. Hereafter, simulation results are presented in groups for each psychological composition p, varying the values of U.
Society of C-agents
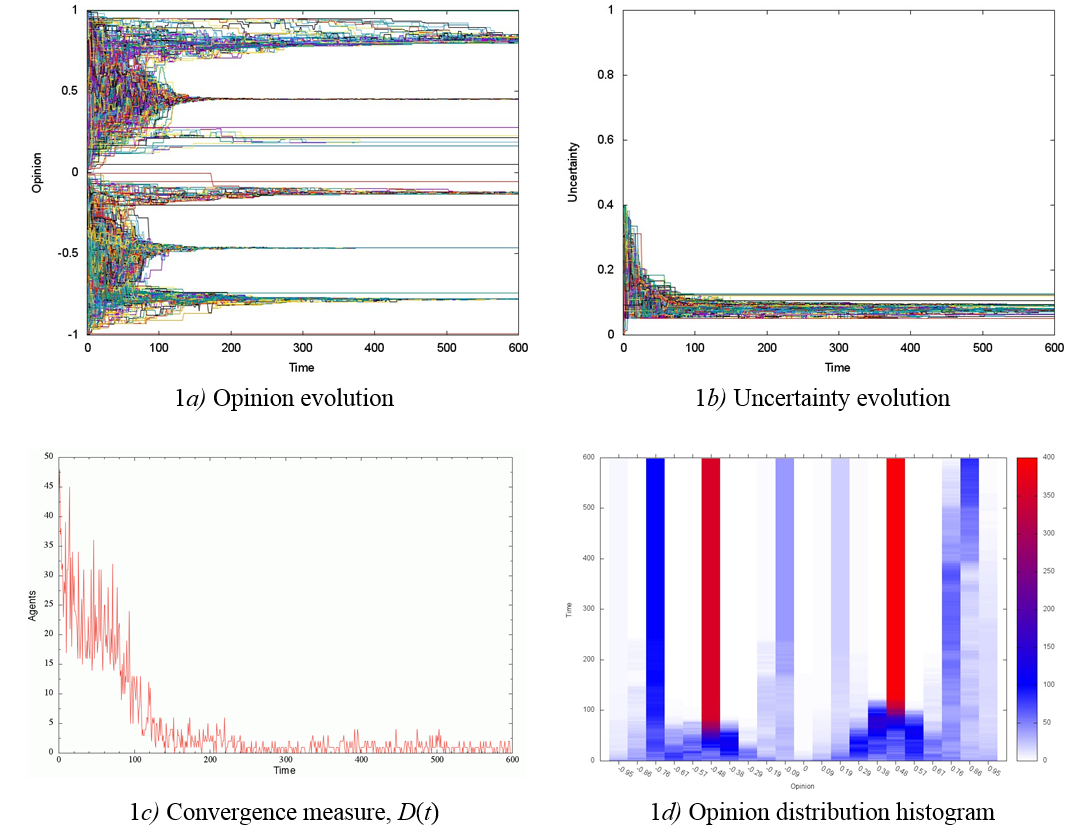
Figure 1 shows results for the society composed of concord agents (p = 1) with initial average uncertainty U = 0.2. The opinion evolution results in consolidation of several groups, see Figure 1a. In order to monitor group size, Figure 1d shows opinion distribution histograms in each time lapse. Six opinion groups, four of them having more than 100 agents each, are formed by time t ≈ 140 (Figures 1a , c). Uncertainty converges to values close to 0.09 (Figure 1b), which explains the stabilization of the convergence measure for the values of t > 140 (Figure 1c) and the attainment of a statistically steady state opinion by the society. In addition, the separation of the society into two opinion subgroups (x in (−1, 0) and x in (0, 1)) divided by opinion affinity is noteworthy, and it clearly shows ideological preferences.
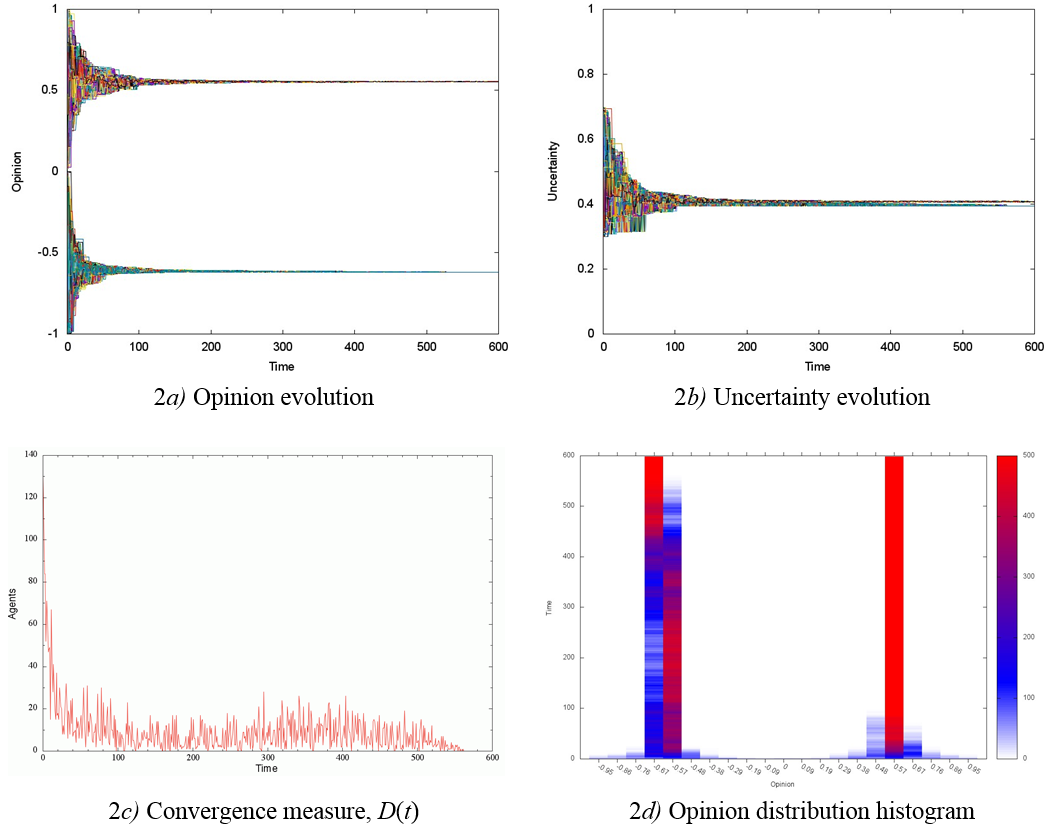
At the initial average uncertainty U= 0.5, we observed the formation of only two opinion groups with an equal number of agents, centred at x = ±0.6, in an even shorter time t > 40 (Figures 2a, d). In contrast to the previous case, uncertainty converged to a value of u = 0.4, approximately (Figure 2b). Additional experiments showed that increasing the initial average uncertainty U renders opinion fragmentation polarized (compare Figure 1d with Figure 1a, 2d), evincing the increased separation between ideologically opposed groups. For example, when U = 0.7, we found that the opinion groups were centred in x = ±0.75, and uncertainty converged to a value of u = 0.6. Similar dynamics to those described above were obtained in societies with 0.95 ≤ p ≤ 1.
Mixed society with 70% of C-agents
The simulations results for a society with p = 0.7 and initial average uncertainty U = 0.2 are shown in Figure 3. The presence of more opinion groups when decreasing the proportion of C-agents is noticeable (see Figure 3d and 3d). At the end of evolution, the four most representative opinion groups (> 200 agents) are observed, as well as two groups of extremist agents (Figure 3d). Uncertainty converges to values close to u = 0.07 (Figure 3b), similar to Figure 1b. The opinion convergence measure shows that society comes to a stochastically steady opinion state in a time t ≈ 200, Figure 3c.
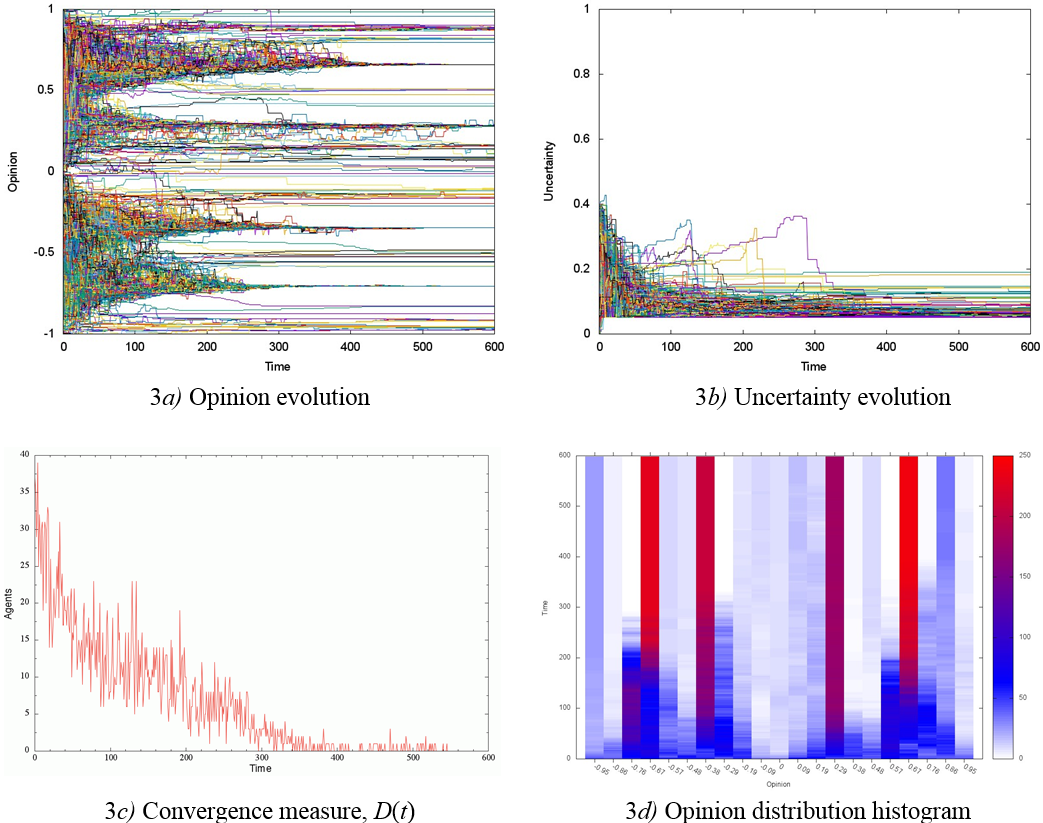
When U = 0.5, three representative opinion groups were formed in the society: a relatively small group of centrists and two large extremist groups (Figures 4a, d). The stabilization of the groups ended at t ≈ 300 (Figures 4c), while uncertainty converged to values close to 0.08. These results differ from those shown in Figures 2a and 4a, since the decreasing of concord agents’ fraction in a society with U = 0.5 stimulated the emergence of a centrist group and a dramatic polarization of opinions in the rest of the society. Moreover, uncertainty converges to different values, u = 0.4 for p = 1 and u = 0.08 for p = 0.7 (Figures 2b and 4b).
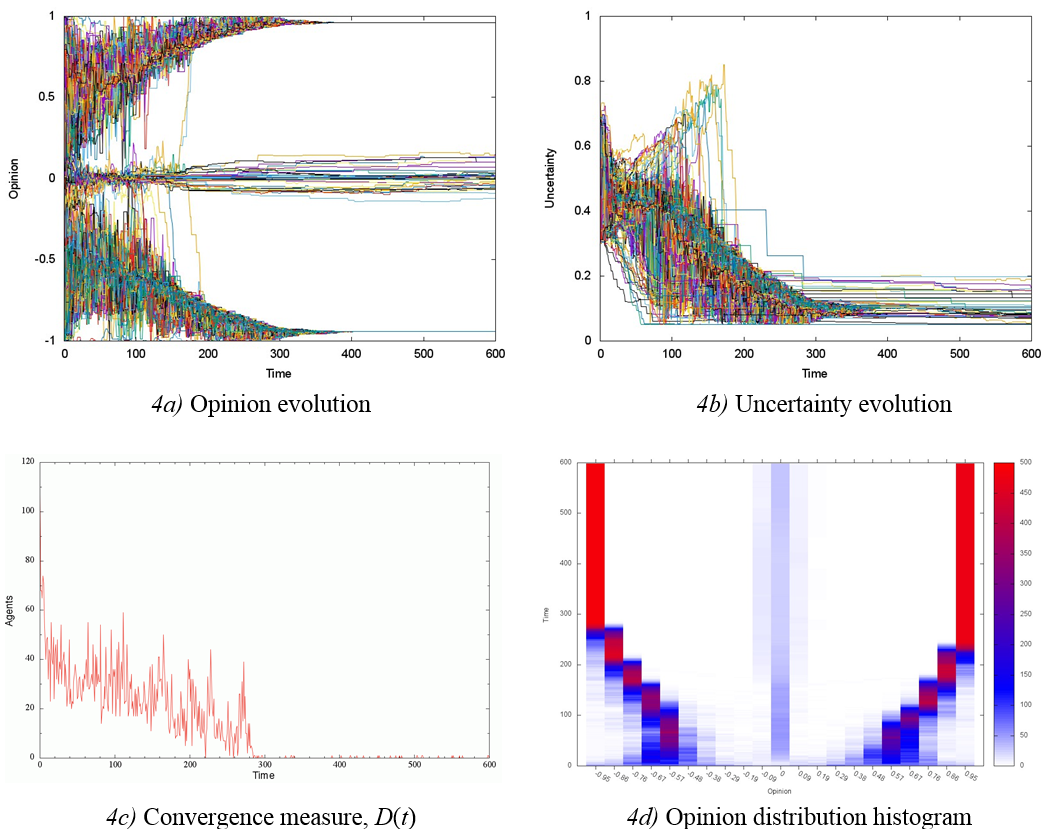
When U = 0.7 in societies with p = 0.7, we observed notable transient processes in opinion dynamics and uncertainty over a time lapse t < 250, approximately; the distributions became statistically stable after this time (Figures 5a, b, c). Regarding opinion, the initial uniform distribution evolved basically in two groups of agents with mass centers at x = −0.9 and x = 0.6, respectively, and a relatively small group of centrists (Figures 5a, c). It is remarkable how the initially uniform distribution of uncertainty transformed into a distribution with two well-defined peaks, of almost equal magnitude, at u = 0.1 and u = 0.33 (Figures 5b, d).
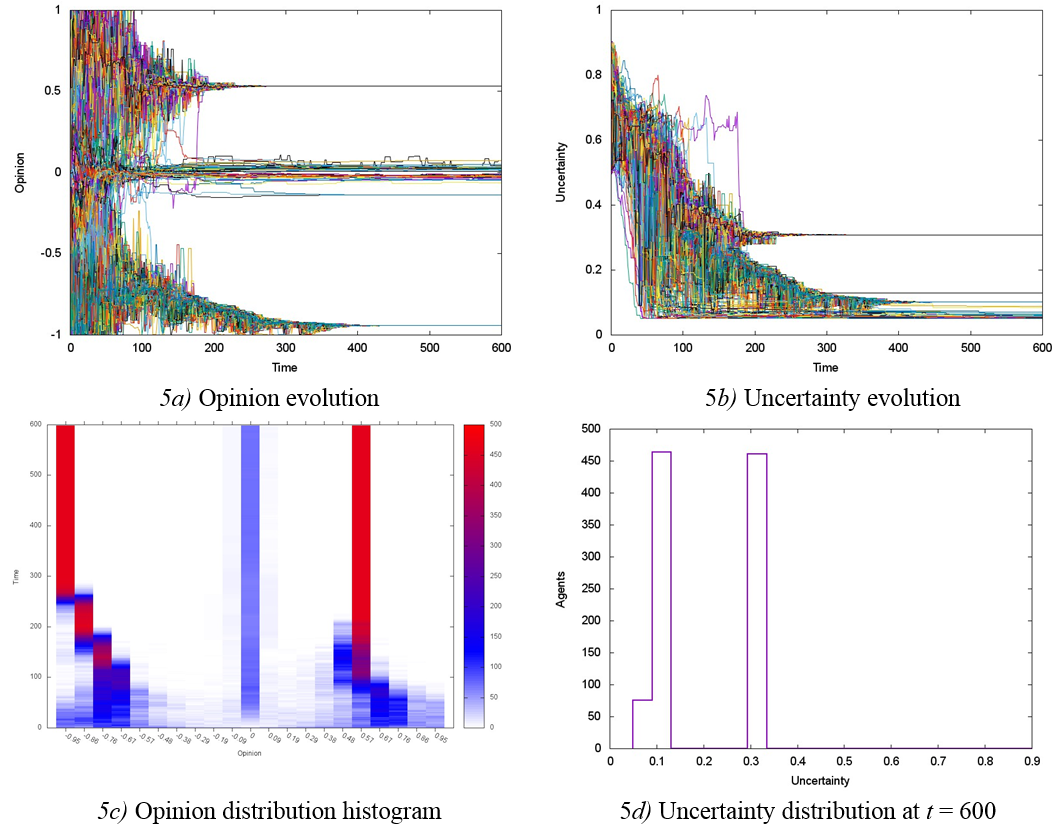
In societies with 0.7 ≤ p ≤ 0.95, variations of parameter U showed simulation results qualitatively similar to those reported for p = 0.7, and so they are not presented here.
Mixed society with 50% of C-agents
The graphs in Figure 6 show simulation results in a society with equal number of C- and PA-agents (p = 0.5) for U = 0.2. This society is seen finally to be fragmented in various opinion groups (Figures 6a, Figures 6d), and the convergence of uncertainty to values close to 0.065 (Figure 6b) is similar to p = 0.7 and p = 1 with U = 0.2. Although the convergence measure looks noisier in comparison with the two previously mentioned cases, fluctuations are not statistically significant (Figure 6c).
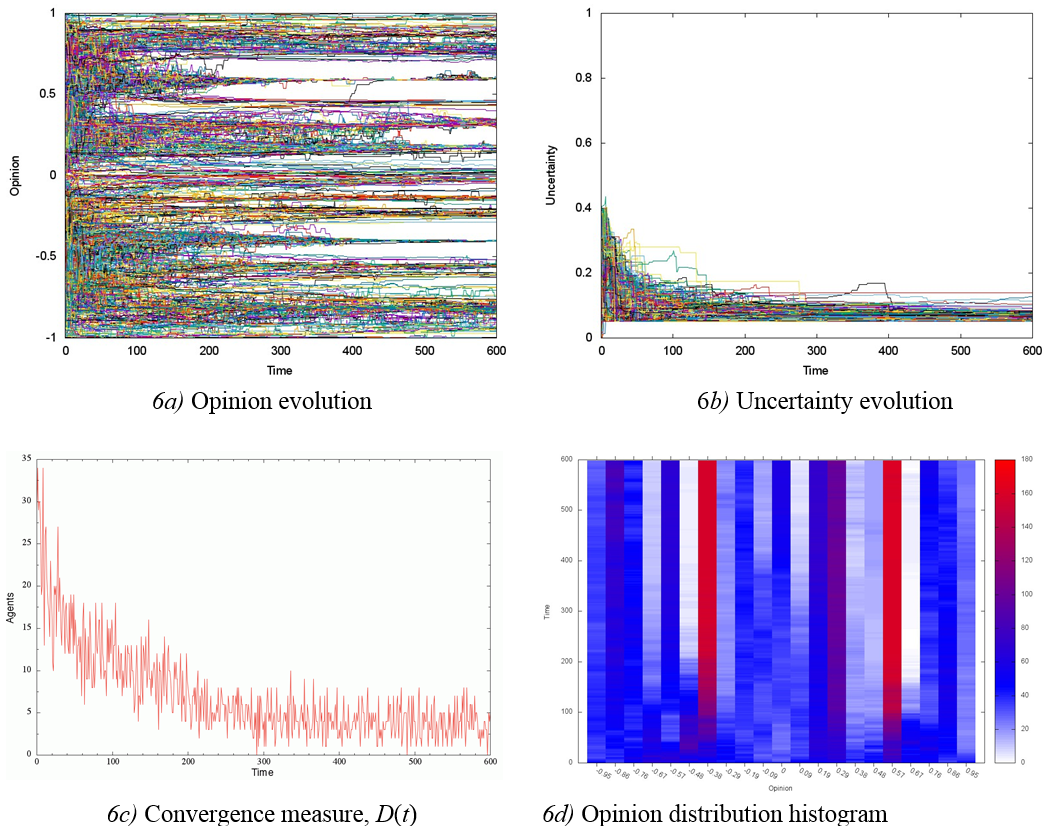
For U = 0.5, our results showed three opinion groups (Figures 7a, c), with an increased number of agents in the centrist group in comparison with Figure 4d. In addition, when we compared Figures 7a and 7c against 4a and 4d, respectively, we observed that a lower percentage of C-agents from p = 0.7 to p = 0.5 transformed the two extremist groups of opinion into two groups of polarized opinion, centered at x = ±0.55 and x = −0.45. Group formation occurred at a time t > 200. Uncertainty converged to three values, two of them with the same amount of agents (425) and close u values (u = 0.3 and u = 0.36), plus a group of 150 agents with u = 0.05 (Figures 7b, 7d).
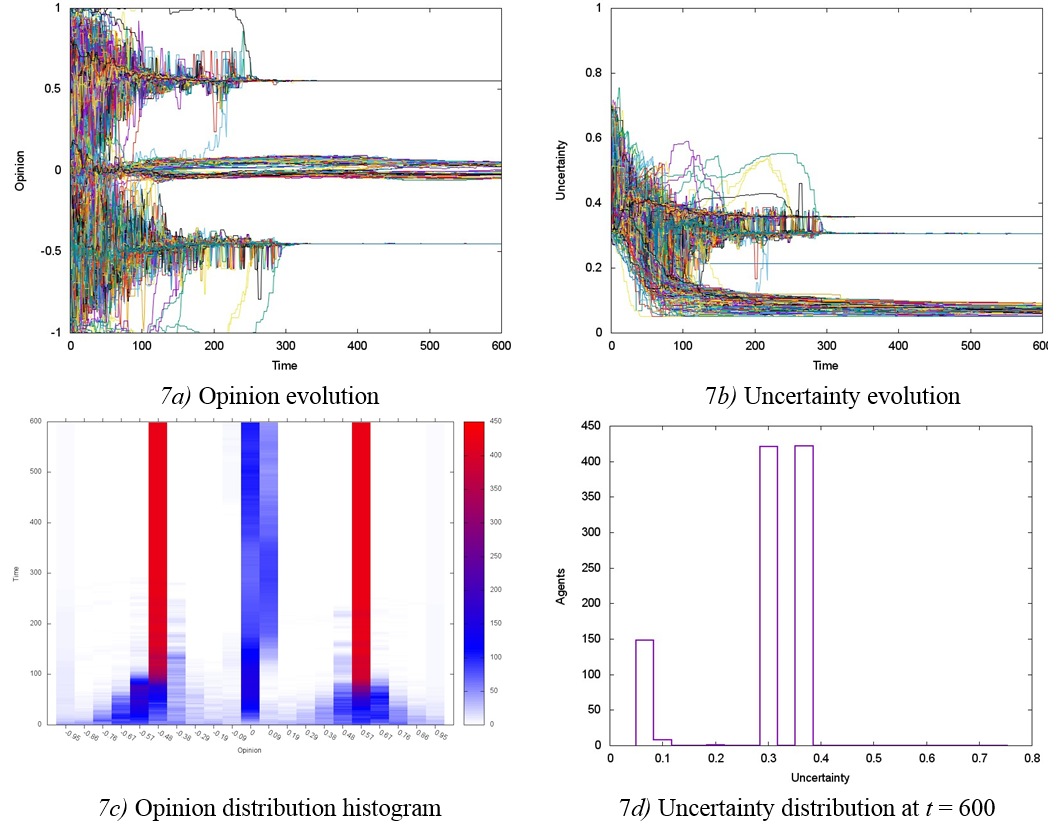
The increase of initial average tolerance to U = 0.7 in a society with p = 0.5 shows decreased opinion polarization along with a significant growth of the centrist group (compare Figures 7c and 8c). The centrist group dynamics is peculiar: in a time interval of 100 < t < 300, an important group of centrist agents is formed, accompanied by a close left-wing group; subsequently, a significant number of agents leave the centrist group to join the left-wing group (see Figure 8c, time interval 400 < t < 470). This behaviour can be interpreted as an indication of ideological preferences that lead to the splitting of a centrist group fraction (Figure 8c). The uncertainty is observed to converge to values below the initial average U with a clustering trend near u = 0.1 (Figures 8b, 8d).
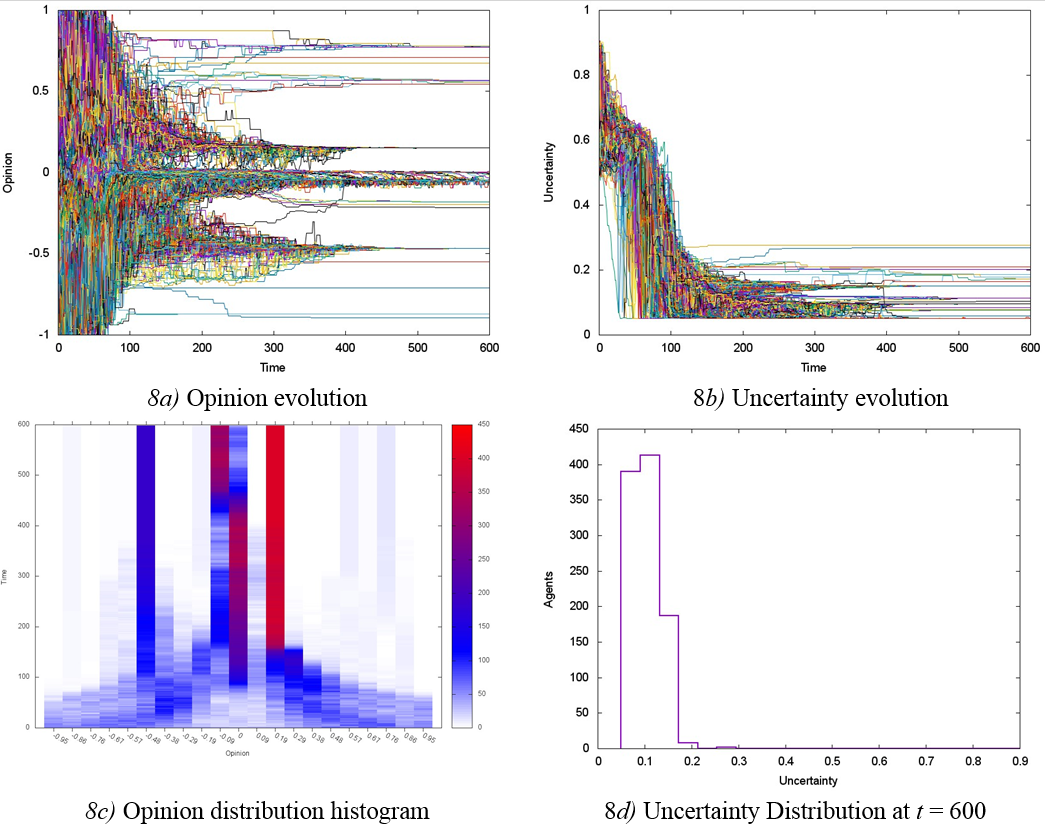
Mixed society with 20% of C-agents
In societies with p = 0.2, we carried out simulations with initial average uncertainty values U = 0.2, 0.5, and 0.7. For the low initial tolerance U = 0.2, evolution of opinion, uncertainty, and convergence measure were similar to those in the case of p = 0.5 and U = 0.2 (see Figure 6), showing the fragmentation of opinion and uncertainty convergence to u = 0.05.
Increasing the initial average uncertainty to the value of U = 0.5, uncertainty tends to two values, u = 0.05 and u = 0.35 approximately (Figures 9b, 9d). The formation of a notable group of agents (≈ 30% of the society) with uncertainty values near u = 0.35 leads to the formation of a smaller number of opinion groups (Figures 9a, c) unlike the previous case, leaving the society separated in three main opinion groups. Nevertheless, the centrist group actually breaks into two well-defined subgroups of opinion close to x = 0 (Figure 9a), since it consists of a group of agents with low uncertainty u = 0.05 and different ideological preferences. Since the convergence measure shows a similar behaviour to the case presented in Figure 6c, the graph was omitted.
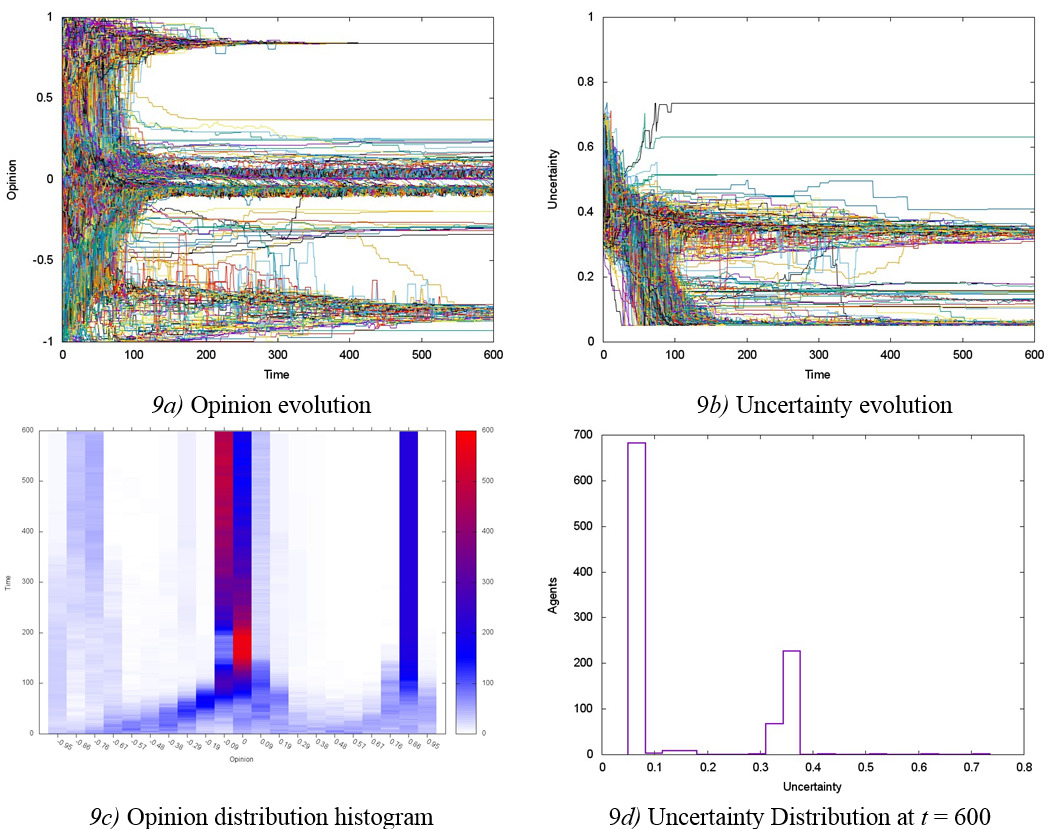
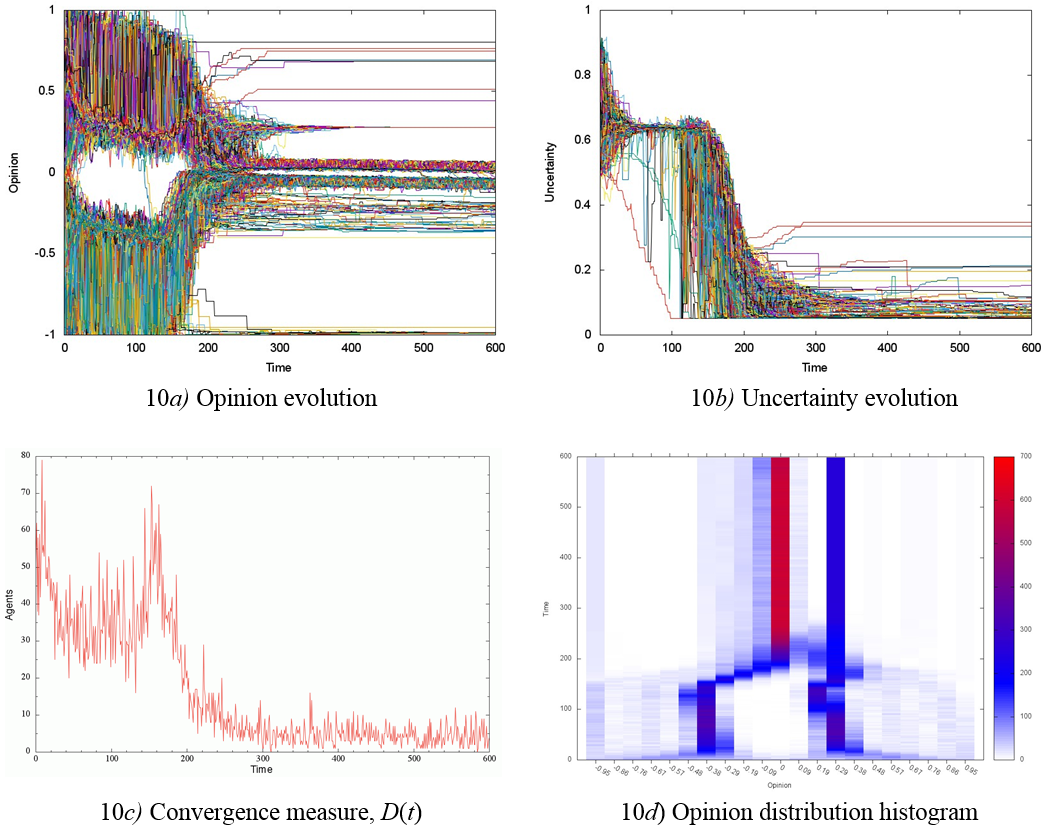
For simulations with high initial uncertainty, U = 0.7, the partition of society into two opinion groups shows the influence of ideological preferences in the time lapse from 1 to about 180 units (Figure 10a). Later, in a time interval close to t = 200, such opinion groups show an important approach each other. However, it does not result in a complete confluence, since the centrist group actually consists of two well-defined subgroups with opinions very close to x = 0 (Figures 10a, d), again due to their low-uncertainty agents u = 0.075 (time t > 250) and different ideological preferences. In addition, in early evolution stages, the distribution of uncertainty converges to a value near u = 0.65, is maintained during the time lapse from 1 to 180 units, and then it abruptly falls to a rather small value of u = 0.075 (Figure 10b) in a relatively short interval 180 < t < 250. Accordingly, the convergence measure graph shows an intense change of opinion in two groups of agents in the lapse from 1 to 160 units of time. After that, a peak in the vicinity of t ≈ 160 on the convergence measure graph marks the just mentioned approaching of opinion between the two groups (see Figures 10a, c, d).
Additional simulations with societies with 0.05 ≤ p ≤ 0.2 and U = 0.2, 0.5, 0.7 showed qualitatively similar simulation results to those described in sections 4.11-4.13.
Society of PA-agents
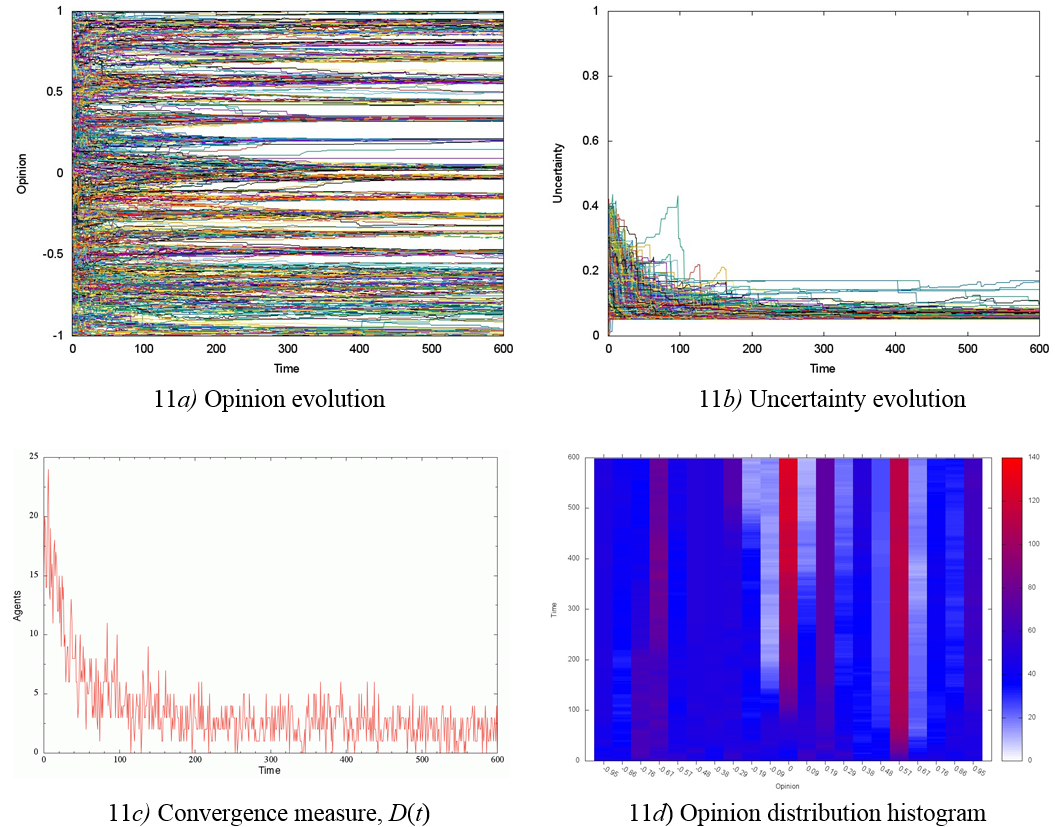
Figure 11 shows the results obtained when U = 0.2 for the society composed only by PA-agents (p = 0). It is observed that the society becomes fragmented in opinion groups (Figures 11a, d) and agent uncertainty converges to values near u = 0.06 (Figure 11b). The convergence measure shows that opinion distribution reaches a stochastically steady state (Figure 11c).
At the initial average uncertainty U = 0.5, the society manages to form three well-defined groups at a time interval of 0 < t < 150, a centrist group, and two extremist groups (Figures 12a, d). Yet, in the opinion evolution plot it can be observed the centrist group divided into two sub-groups of different ideological preferences, but sharing very close opinions. Besides, interaction among these groups is observed at time intervals centered in t ≈ 200, 300, 350, and 500 which is expressed by the convergence measure graph (Figures 12a, c). Uncertainty evolution exhibits two groups of agents: a group of n1 ≈ 700 agents with uncertainty near u ≈ 0.075, and another of n2 ≈ 270 agents with uncertainty near u ≈ 0.375 (Figure 12b). The presence of the n2 agent group with relatively high uncertainty (tolerance) explains the interaction between the centrist opinion subgroups mentioned before.

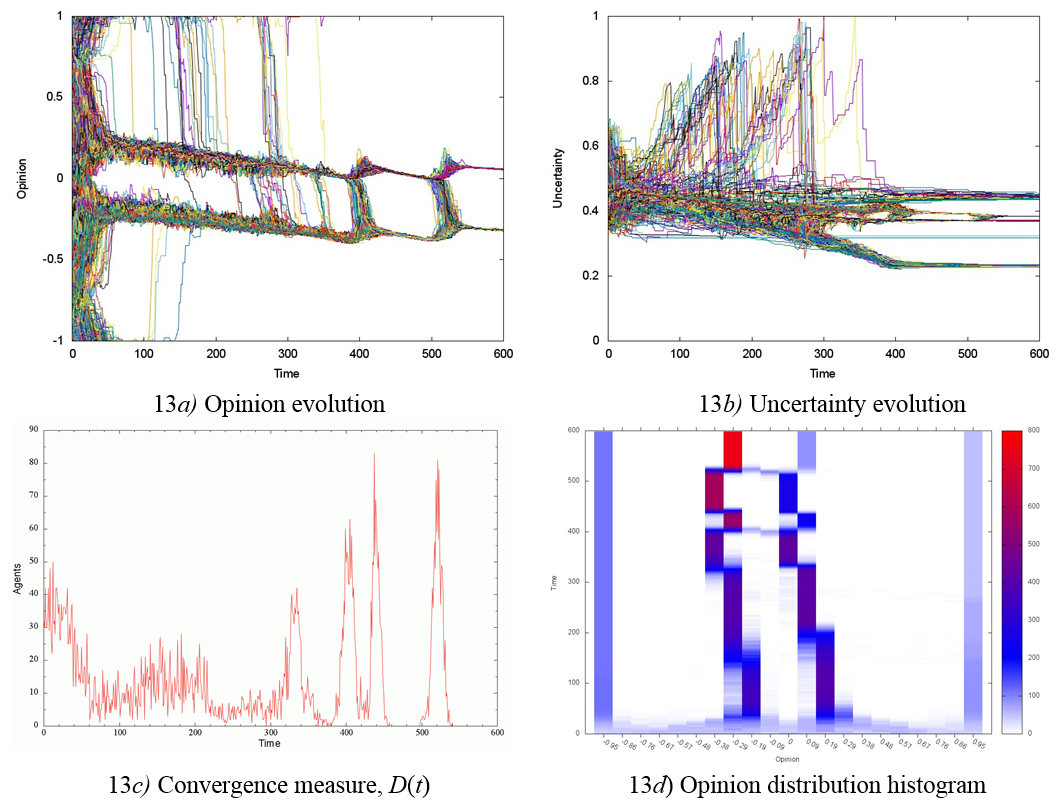
However, in another experiment using a new seeding of data for the initial uniform distribution of uncertainty and keeping all other parameters unchanged, we find significant variations in both the dynamics and the final distribution of opinion and uncertainty (compare Figures 12 and 13). Figure 13a, shows evolution of opinion in an interval 0 < t < 350 where there are two predominant opinion groups with different ideological preferences, not so close together as in the case of Figure 12a. Nonetheless, Figures 13a and 13d, show the transitions of agents between the two groups at t ≈ 400 and 520, which makes the centrist group dissipate. Finally, four opinion groups are formed in the society: a dominant group centered on opinion x ≈ −0.3, a small group with an almost centrist opinion x ≈ 0.1, and two small groups of extremists (Figure 13d). The interactions between groups of different ideological preferences (t ≈ 400 and 520), along with the internal processes in groups (t ≈ 330 and 440), are reflected in the convergence measure graph (Figures 13c and 13d). We found that the final uncertainty distribution consists of a group of n1 ≈ 105 agents with uncertainty near u ≈ 0.235 and another of n2 ≈ 770 agents with uncertainty near u ≈ 0.39 (Figure 13b). Significant differences between the results of those two experiments, shown in Figure 12 and Figure 13, show the sensitivity of the society with p = 0 and U = 0.5 to initial conditions; in other words, the instability of the dynamical system is observed.
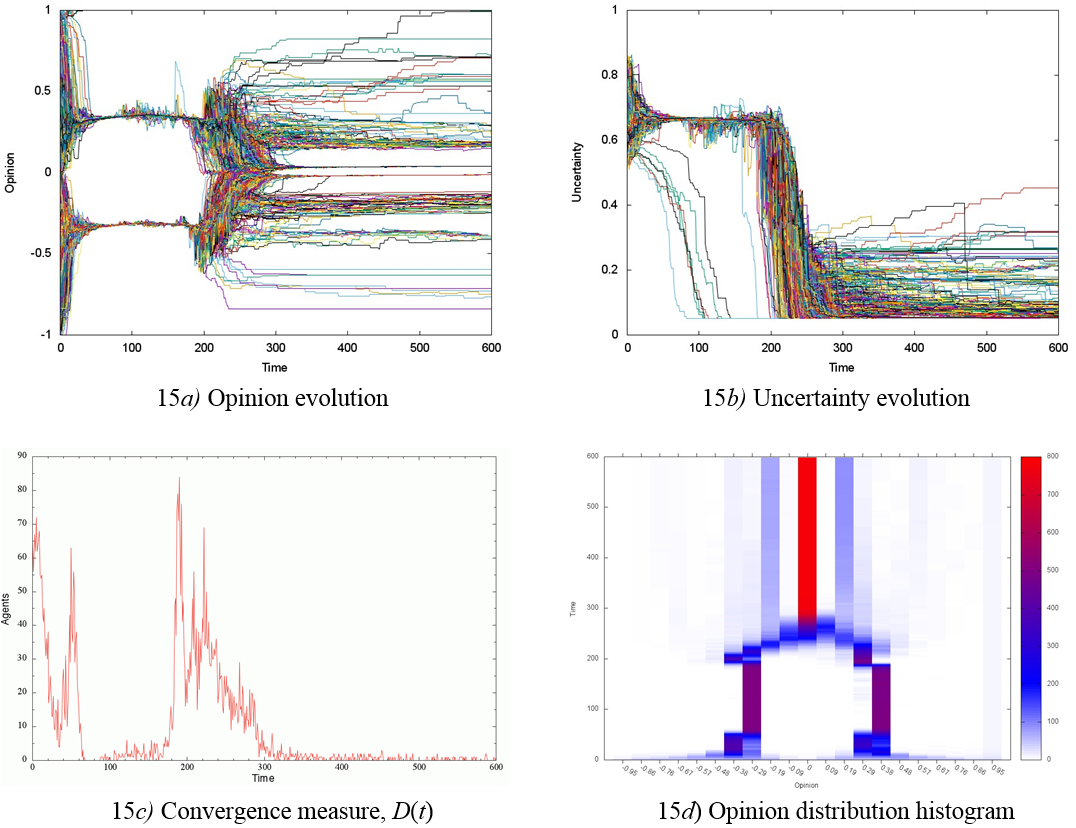
When p = 0 and U = 0.7, we observed even higher social system sensitivity to small changes in initial uncertainty distribution and updating dynamics. Figure 14 and 15 show results of two almost identical experiments that differ only in the seeding of data for the initial uncertainty distribution, as well as in the updating dynamics, since the latter is stochastic and therefore cannot be replicated.
The graphs in Figure 14 show the formation of two well-defined opinion groups of ideological opponents in a very short time interval 0 < t < 40 (Figures 14a, d) with high uncertainty value u = 0.62 (Figure 14b). The convergence measure marks an opinion displacement of the “rightist” group at around t ≈ 135, further away from the opposing group (Figures 14c, d).
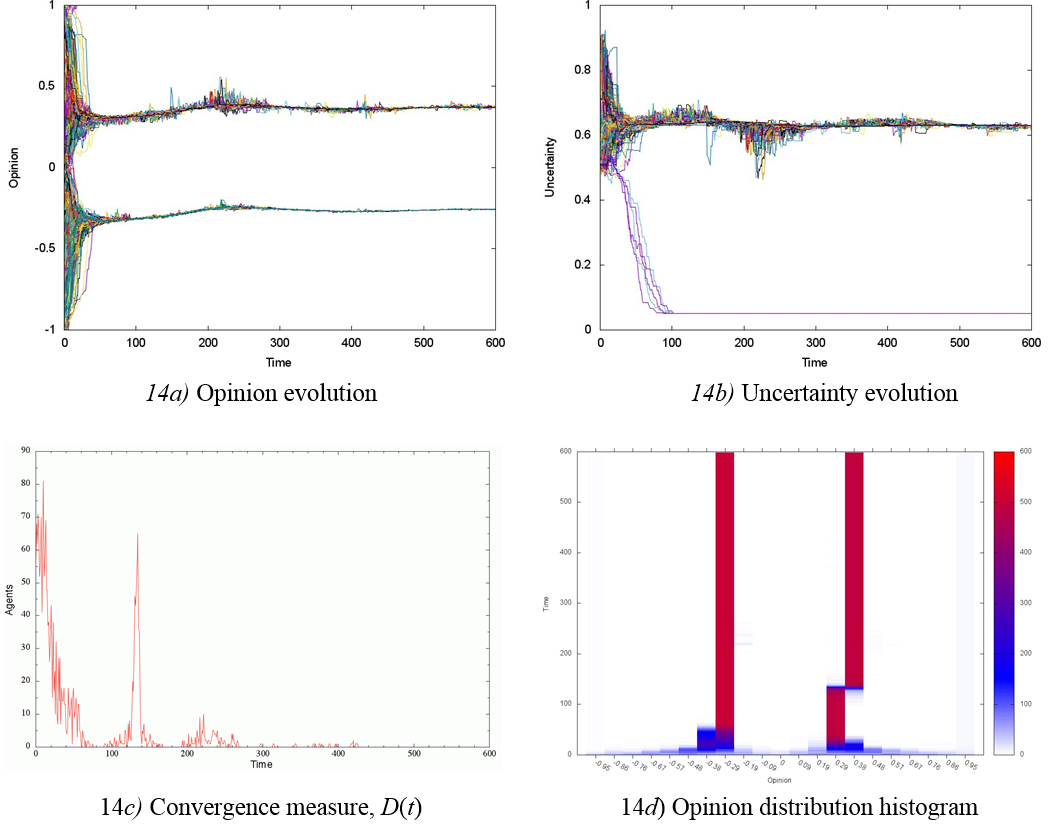
Figure 15a shows that two groups of ideological opponents are formed in the time interval 0 < t < 40, similar to Figure 14a. However, after t ≈ 180, there is an intensive opinion exchange between the protagonist groups at the time interval 180 < t < 290, see Figures 15a, 15c, and 15d. As a result, the opinions of the two groups approach each other until they practically become one centrist group, however separated into two sub-groups by ideological differences (see Figures 15a and 15d). In the time interval 0 < t < 40, uncertainty converges to a value of u = 0.67, falling afterwards to a value of u = 0.07 in the time interval 180 < t < 290, Figure 15b.
Conclusions and discussion
The importance of ideology in the realm of opinion formation motivated us to include it as an element in the PA/C model, and to study its influence via agents’ opinion affinity. In our study, the simulation the opinion dynamics in artificial societies composed of C- and PA-agents (two psychological types of agents) with opinion affinity, revealed a variety of behaviours distinctive of human societies, such as fragmentation and polarization of opinion, consensus within the ideological groups and, in addition, the emergence of groups with different ideological preferences up to their becoming extremist groups. Each social scenario, described by the combination of the model parameters (p, U and initial distributions of opinion and uncertainty), exhibits quite particular opinion and uncertainty dynamics, showing the richness of behavioural characteristic of human societies.
The temporal evolutions of opinion and uncertainty were studied in a relatively long time interval (2000 units of time), which allowed us to accurately determine characteristic times when opinion converged into a stochastically steady state, if that occurred. We noted that, in general, convergence into a steady state occurs in much shorter times, and therefore computer simulations may be performed for shorter time lapses, let us say 400. However, the anticipated completion of the simulation might match a quasi-stationary state, causing the loss of significant transient events in the dynamics of the system (see Figures 15a, b). In addition, real-life time frames of election campaigns are imposed in an administrative-legal manner, and the end of a campaign may fall in times when the opinion state of society is stationary (in this case, voting results are expected to be predictable) or in time intervals when substantial transient processes are taking place (voting results are little predictable). So, since the time of convergence depends on a particular scenario, we recommend that computer simulations be designed using relatively long time lapses to prevent the loss of important particularities of the system’s dynamics.
The dynamical system under study has important stochastic elements: the psychological distribution of the agents in the social network, the initial distributions and the updating dynamics for opinion and uncertainty. To facilitate the analysis of transitions between the states of the system in the opinion space, we have introduced a measure of opinion convergence. The temporal evolution of the convergence measure allowed us to observe and quantify the transition of the social system to a stochastically steady state. Through the measure of convergence, events such as social agitation (intensive change of opinion) could also be modelled. Real-life proves that social agitation can lead a society’s opinion and consciousness towards new states, or societies may end up in the same state as well. A change of state or the return to the state before agitation is predicted by comparing the opinion states at the times when agitation starts and ends. The degree of social agitation can be evaluated by calculating the area below the agitation crest in the convergence measure curve.
In model simulations, we observed that events such as social agitation occur in societies with a dominant fraction of PA-agents or, in some cases, when the initial average uncertainty U is high. When initial average uncertainty U is high, the opinion segments are relatively large, which increases the frequency of interactions between agents. As a consequence, due to the conflict between the ideology and the psychological behaviour of the agents, the interaction between agents of ideologically opposite groups close to the centrist opinion x = 0 lasts a long time and sometimes becomes intensified, in comparison with societies without ideology. This interaction produces so-called ‘activity revivals’ in opinion dynamics (see convergence measure plots). In each scenario, these events occur in quite a particular way, at different magnitudes and emergence times. These events are indicators of the instability of the dynamical system, evinced by a noteworthy increase in social activity as represented by the convergence measure graphs. Another instability manifestation, although in the parameter space, is the high sensitivity of the social system to initial conditions, in particular, the initial distribution of uncertainty, accompanied by the stochastic updating dynamics clearly observed in PA-agent societies, p = 0 and 0.5 ≤ U ≤ 0.7, Figures 14 and 15. On the other hand, in societies with a dominant presence of C-agents, the separation of agents into two groups of ideologically opposite opinion occurs quickly and definitely (see Figure 2).
The competition of two ideologies, defined in this study as the affinity of opinions within “leftist-rightist” groups, is usually manifested through the partition of societies into two sub-societies in the opinion space, with or without subsequent interaction between them. In this context, in societies with a low initial average tolerance U = 0.2, we found that increasing the percentage of C-agents in the interval 0 ≤ p < 0.7 has little effect on dynamics and the final distributions of opinion and uncertainty: opinion remains fragmented and uncertainty converges to a value near u = 0.05. When the initial average tolerance is low, the rate of interaction between agents decreases, and so opinion dynamics stabilizes more rapidly and ideology lacks enough time to produce an effect. When C-agents predominate in a society with 0.7 ≤ p ≤ 1, affinity separates the society into two opinion groups of different ideologies, each group having a dominant subgroup (see Figures 3 and 1). With U = 0.2 and 0 ≤ p ≤ 1, uncertainty converges to low values near u = 0.07 (see the sequence of Figures 11b, 6b, 3b, and 1b).
It should be noted that, in societies with initial average tolerance-uncertainty U = 0.5 and psychological composition in a range 0 ≤ p ≤ 0.5, the centrist group breaks into two opinion subgroups as a result of conflicting ideologies, even though the opinion of such groups may be very close in some cases. In real life, the emergence of a centrist group of agents slightly separated in two ideologically opposite subgroups can favor to coalitions, for example, between two political parties. On the other hand, in a group consisting of centrist or indecisive agents, ideology can be a key factor when voting for a party, x > 0 or x < 0 (see the sequence of Figures 13, 12, 9, and 7).
In mixed societies with high initial average uncertainty U = 0.7, two opinion groups influenced by ideology are initially formed, which then merge into a quasi-centrist opinion group; the result of confluence is observed in the final state of opinion distribution. As the value of p increases, the formation of opinion groups is manifested at an earlier time. Also, the increase in the percentage of C-agents causes the polarization of opinion groups and the splitting of uncertainty distribution into two well-defined peaks. That is, in societies with a high initial tolerance value, the effect of ideology is more visible.
Although affinity tends to form groups of ideological opponents in the early stages of opinion evolution, we see that the ideological differences diminish at a later time, leaving only one predominant opinion group in most scenarios (Figures 12 to 15). It can be said that in some societies the effect of ideologies does not last forever.
Since its introduction in relative agreement models, agent opinion uncertainty has been regarded as a half-hidden variable of little interest. However, social system dynamics are strongly influenced by the interaction of the two groups of variables, opinion, and uncertainty. In this work, we studied the dynamics of uncertainty along with the opinion dynamics, which allowed us to make relevant observations on their mutual influence. The importance of understanding the interaction between the two groups of variables comes from the conceptual difference between them; opinion is a social characteristic, whereas uncertainty, interpreted as tolerance, is more psychological than social. Having observed the dynamics of the two groups of variables, we conclude that the influence of opinion on uncertainty is manifested as follows: the average of uncertainty (tolerance) distribution reaches a steady state value lower than the initial average value, sometimes reaching a value near zero. Moreover, in some occasions, the formation of two or three groups of agents with different uncertainties is observed. Agents showing an uncertainty close to zero can be considered socially apathetic, since they do not interact with other agents, which can be appreciated in opinion and uncertainty evolution graphs.
It should be noted that the Alizadeh et al.’s (2015) CBC model uses an a priori partitioning of society in social groups, without specifying any characteristic property. Instead, ideological affinity in the PA/C model characterizes the agents’ belonging to a social group; this partitioning can be easily extended to any number of ideological groups. In certain scenarios, we observe inter-group consensus in ideological groups as well as in the centrist group, the latter being split into two groups of different ideologies by a small distance between opinions. In addition, fragmentation, polarization, and emergence of extremists are observed in the CBC and PA/C models.
Ideologies are “sets of ideas” applied to real or idealized societies. In this respect, the proposed one-topic opinion model (say, political or economic one) is rather limited; nevertheless, it may provide useful insights for further research with more complicated and complex models. The analysis of our results shows that the model can be used for further investigation on opinion dynamics, and that it may also be employed as a tool to explore conflicts between ideologies and the psychological behaviour of agents in social, economic, and political phenomena using other functions for ideological affinity.
Acknowledgements
The authors express their gratitude to the Laboratorio de Fisicoquímica Teórica del CULagos, Universidad de Guadalajara, for providing the computer facilities based on CentOS Operating System. N.L. Abrica-Jacinto thanks the Consejo Nacional de Ciencia y Tecnología (CONACyT) of Mexico for being supported by grant No. 262442. We are sincerely grateful to anonymous reviewers for their stimulating observations, comments and suggestions that helped us to improve the presentation of our work. The code for the model and supplementary documentation are available in https://www.openabm.org/model/5250/version/1/view.References
ALIZADEH, M., Cioffi-Revilla, C., and Crooks, A. (2015). The effect of in-group favoritism on the collective behavior of individuals’ opinions. Advances in Complex Systems, 18(01n02) 1550002. [doi:10.1142/S0219525915500022]
ALTHUSSER, Louis (1970). Ideologie et Appareils Ideologiques d’Etat, La Pense, Ediciones Sociales, París, No. 151.
AMBLARD, F. and Deffuant, G. (2004). The role of network topology on extremism propagation with the relative agreement opinion dynamics. Physica A343, 725–738. [doi:10.1016/j.physa.2004.06.102]
ASCH, S. E., (1951). Effects of group pressure upon modification and distortion of judgment. In Groups, leadership and men (pp. 177-190), Ed. H. Guetzkow. Pittsburgh: Camegie Press.
BOCCARA, N. (2010). Modeling Complex Systems. Springer-Verlag, New York. [doi:10.1007/978-1-4419-6562-2]
CASTELLANO, C., FORTUNATO, Santo and LORETO, Vito (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2):591–646. [doi:10.1103/RevModPhys.81.591]
DEFFUANT, G., Neau, D., Amblard, F. and Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems 3 (1–4) 87–98. [doi:10.1142/S0219525900000078]
DEFFUANT, G., Amblard, F., Weisbuch, G. & Faure, T. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), 1: https://www.jasss.org/5/4/1.html.
DEFFUANT, G. (2006). Comparing extremism propagation patterns in continuous opinion models. Journal of Artificial Societies and Social Simulation, 9 (3), 8: https://www.jasss.org/9/3/8.html.
DELLI S., A. (1981). En torno al concepto de ideología. Multidisciplin@ primera época, Revista Electrónica de la Facultad de Estudios Superiores Acatlán I(11), 27–44.
FAN, P., Li, P., Wang, H., Jiang, Z. and Li, W. (2012). Opinion Interaction Network: Opinion Dynamics in Social Networks with Heterogeneous Relationships. In Proceedings of the ACM SIGKDD Workshop on Intelligence and Security Informatics (pp. 4:1–4:8). New York, NY, USA: ACM. [doi:10.1145/2331791.2331795]
FAN, P., Wang, H., Yu, W., Li, P. and Hu, Y. (2014). Opinion Dynamics in Social Networks with Heterogeneous Relationships. Journal of Information & Computational Science. [doi:10.12733/jics20103170]
FESTINGER, L., (1957). A theory of cognitive dissonance, Stanford, CA: Stanford University Press.
FLACHE A., and Mäs, M. (2008). Why do faultlines matter? A computational model of how strong demographic faultlines undermine team cohesion. Simulation Modelling Practice and Theory, 16(2), 175-191. [doi:10.1016/j.simpat.2007.11.020]
FRANZOI, S., (2006). Social Psychology. McGraw-Hill.
HEGSELMANN, R. and Krause, U. (2002). Opinion Dynamics and Bounded Confidence: Models, Analysis and Simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html
JANIS, I. L. (1982). Victims of groupthink, 2ª Ed. Boston: Houghton Mifflin.
HOLYST, J. A., Kacperski, K. and Schweitzer, F. (2001), Social impact models of opinion dynamics. Annual Reviews of Computational Physics, 9(22), 253–273. [doi:10.1142/9789812811578_0005]
HUET, S., Deffuant, G., and Jager, W. (2008). Rejection mechanism in 2D bounded confidence provides more conformity. Advances in Complex Systems. 11(4), 529-549 [doi:10.1142/S0219525908001799]
HUET, S., and Deffuant, G. (2010). Openness leads to opinion stability and narrowness to volatility. Advances in Complex Systems. 13(3), 405-423. [doi:10.1142/S0219525910002633]
HUICI, Casal C., Molero Alonso F., Gómez Jiménez Á. Morales Domínguez J. Fco. (2012). Psicología de los grupos. Ed. UNED, ISBN: 978-84-362-6522-4.
KURMYSHEV, E., Juarez, H. A. and González-Silva, R. A. (2011). Dynamics of bounded confidence opinion in heterogeneous social networks: Concord against partial antagonism. Physica A: Statistical Mechanics and Its Applications, 390(16), 2945–2955. [doi:10.1016/j.physa.2011.03.037]
LORENZ, J. (2007), Continuous opinion dynamics under bounded confidence: a survey. International Journal of Modern Physics C, 18 (12) 1819–1838. [doi:10.1142/S0129183107011789]
MATHIAS, Jean-Denis, Huet S., Deffuant, G. (2016). Bounded confidence model with fixed uncertainties and extremists: the opinions can keep fluctuating indefinitely. Journal of Artificial Societies and Social Simulation, 19(1), 6: https://www.jasss.org/19/1/6.html [doi:10.18564/jasss.2967]
OAKES, P. J., Haslam, S. A. and Turner, J. C. (1994). Stereotyping and social reality. Blackwell, Oxford, Cambridge.
OAKES, P. J., Turner, J. C. and Haslam, S. A. (1991). Perceiving people as groups members: The role of fit in the salience of social categorizations. British Journal of Social Psychology. [doi:10.1111/j.2044-8309.1991.tb00930.x]
PORRAS-VELÁSQUEZ, N. R., (2011). Lo ideológico en la psicología social y en la guerra en Colombia. Revista de Psicología GEPU, 2 (2), 138-157.
RAMIREZ-CANO, D. and Pitt, J. (2006). Follow the Leader: Profiling Agents in an Opinion Formation Model of Dynamic Confidence and Individual Mind-Sets. In Proceedings of the IEEE/WIC/ACM International Conference on Intelligent Agent Technology (pp. 660–667). Washington, DC, USA: IEEE Computer Society. [doi:10.1109/iat.2006.67]
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of meta-contrast. Journal of Artificial Societies and Social Simulation, 19(1), 13: https://www.jasss.org/19/1/13.html.
SCHWEITZER, F. (2003). Brownian Agents and Active Particles: Collective Dynamics in the Natural and Social Sciences. Springer Verlag.
SHERIF, M., (1936). The psychology of social norms. New York: Harper.
SHERIF, M. and Hovland, C. I. (1961). Social judgment: Assimilation and contrast effects in communication and attitude change. Oxford, England: Yale Univer. Press (xii, pp. 218)
TAJFEL, H. (1972). La catégorisation sociale. In S. Moscovici (ed.), Introduction à la psychologie sociale. Paris: Larousse.
TAJFEL, H. and Turner, J. C. (1979). An integrative theory of intergroup conflict. In W.G. Austin and S. Worchel (eds.), The social psychology of intergroup relations.
TURNER, J. C., Hogg, M.A., Oakes, P. J., Reicher, S. D. and Wetherell, M. S. (Eds.) (1987). Rediscovering the social group: A self-categorization theory. Blackwell, Oxford.
VELA-MCCONNELL, J. A. (1999). Who is my neighbor?: social affinity in a modern world. State University of New York Press, Albany.
VAN DIJK, T. A (2011). Discourse Studies. A multidisplinary Introduction. Second Edition, pp. 379-407. London:Sage. [doi:10.4135/9781446289068.n18]
WOOD, W., (2000). Attitude change: persuasion and social influence. Annuual Review of Psychology 51, 539-570. [doi:10.1146/annurev.psych.51.1.539]
XIA, H., Wang, H. and Xuan, Z. (2011). Opinion Dynamics: A Multidisciplinary Review and Perspective on Future Research. International Journal of Knowledge and Systems Science, 2(4), 72–91. [doi:10.4018/jkss.2011100106]
XIE, J., Sreenivasan, S., Korniss, G., Zhang, W., Lim, C., and Szymanski, B. K. (2011). Social consensus through the influence of committed minorities. Phys. Rev. E (84) 011130. [doi:10.1103/physreve.84.011130]
YANG, L. and Xi, P. (2010), Opinion dynamics under different agents’ personality. International Symposium on Computer, Communication, Control and Automation (Vol. 1, pp. 342–345).

