Introduction
Metamodeling refers to modeling a model. Within ABM there are two metamodeling approaches: (1) top-down and (2) bottom-up. The top down approach enables users to decompose high-level mental models into behaviors and interactions of agents. In contrast, the bottom-up approach constructs a relatively small, simple model that approximates the structure and outcomes of a dataset typically gathered from the runs of a large and complex ABM.
While both approaches provide abstractions of an ABM, the purpose of the abstraction is different. Top-down metamodels are used in the design phase of modeling to capture requirements and organize the architecture of the ABM, while bottom-up metamodels are constructed after implementation to make behavior of the model comprehensible and exploratory analyses feasible (Goldspink 2000; Bigelow & Davis 2002).
The process of developing a bottom-up metamodel proceeds as follows: (1) the user creates an experimental design for the inputs of the ABM, (2) runs the ABM according to the experimental design, (3) collects the results in a dataset and (4) uses statistical methods to generate a model that enables the user to understand why the ABM behaves the way it does (Barton 1994; Kleijnen & Sargent 2000; Bigelow & Davis 2002; Friedman 2012). The most common implementation of this process predicts the ABM output as a sum of input variables using first-order regression analysis without any bounds on the input space of the model. We refer to metamodels constructed in this manner as baseline metamodels.
Unfortunately, baseline metamodels assume that critical thresholds within a single input or relative relationships among multiples inputs of the ABM do not exist. Due to this assumption the baseline metamodel can be misleading because it gives impression that one can compensate for a component of the system by improving some other component even if such a substitution is inadequate or invalid (Friedman & Pressman 1988; dos Santos & Porta 1999; Kleijnen & Sargent 2000; Meckesheimer 2001; Bigelow & Davis 2002).
We propose to address the aforementioned deficiency by augmenting widely used first-order regression analysis with Boolean conditions that highlight when tradeoffs and substitutions among variables are valid. These Boolean conditions and the regions that they bound reflect critical components within ABMs. The term critical component refers to a threshold within a single input or among multiples inputs that affect the behavior of the ABM. Our approach to capture critical components is inspired by the field of software engineering, which uses predicates to identify critical components that cause errors within computer programs (Liblit 2007; Gore et. al 2011).
The remainder of this paper proceeds as follows. First, we present background material needed to understand our approach and relate it to existing metamodel research. Then we demonstrate how a user employs our approach to produce an augmented metamodel. Next, we compare the efficiency and the effectiveness of our augmented metamodels to baseline metamodels for three established ABMs. Our evaluation also compares the effectiveness of our augmented metamodels to alternative metamodels constructed by applying machine learning methodologies. Finally, we discuss the validity of our analysis and the limitations of our work, summarize our contributions and provide direction for future research.
Background
Top Down Metamodeling
Recall, top-down metamodels capture requirements and system interactions to serve as a template for the implementation of an ABM. Two of theses approaches, Agent-oriented-programming (AOP) and Gaia, provide mechanisms to the decompose agent-behaviors and agent-roles (Wooldridge, Jennings & Kinny 2000). Another approach, the Unified Modeling Language (UML) captures the mental composition of agents through their perception of their environment, their ability to act within their environment, and their reasoning to interpret and solve problems (Hayes-Roth 1993; Wagner 2003; Jouault & Bezivin 2006). Communication between agents can be captured using the Agent extension to UML (AUML) (Odell, Parunak & Bauer 2000). Agent roles or attitudes can also be represented through a set of beliefs, desires, and intentions (BDI) using informal or formal semantics (Rao & Georgeff 1991).
Other top down approaches take a less modular approach to describing the components of an ABM. The Agent-Object-Relationship (AOR) approach employs object-oriented methodologies, including static structure and structural relationships, dynamic interactions, and functional data flow methods (Iglesias, Garijo & Gonzalez 1999). The AOR approach conceptually integrates static, dynamic, and mental components of organizational systems (Shoham 1993). The Kernel MetaMetaModel (KM3) serves as a metamodel definition language by defining a domain definition metamodel (DDMM) of a Domain Specific Language (DSL) (Jouault & Bezivin 2006). Cassiopeia identifies elementary agent behaviors (Wooldridge, Jennings & Kinny 2000) to study the effects of global or organizational behaviors (Collinot, Drogoul & Benhamou 1996).
While the process of abstraction in top down metamodeling is related to our work, its purpose is orthogonal. Our goal is to construct bottom-up metamodels from data collected from an ABM to make trends comprehensible and exploratory analyses feasible. This process is independent of methodology related to the requirements and architectural design of the ABM. In future work, we will explore how the existence of a top down metamodel could improve our approach to constructing bottom-up metamodels.
Bottom-Up Metamodeling
Bottom-up approaches focus on creating a model generated from data gathered from the ABM to make trends comprehensible and exploratory analyses feasible. A myriad of different statistical methods can be applied to generate bottom-up metamodels. However, most techniques fall into one of three broad categories: (1) regression analysis, (2) structural equation modeling or (3) machine learning.
Regression Analysis
Regression analysis estimates the relationship between an output of the ABM and one or more input variables. The structure of the model is determined by minimizing the variance between the model and the data by using as few variables as possible. In this paper, we focus on creating bottom-up metamodels by employing first-order regression analysis. In these metamodels input variables are only included as linear terms (i.e the first power) that are combined through addition and subtraction. We choose first-order regression analysis because it is the most commonly employed method to generate metamodels. Its popularity is largely due to its simplicity and accessibility. As a result, improving the accuracy and validity of these metamodels will benefit the most users in the ABM community.
Structural Equation Modeling
Structural equation models reflect a second generation of analysis methodology (Fornell 1984; Chin 1998). Within the family of SEM techniques are many methodologies, including confirmatory factor analysis (Harrington 2008), causal modeling (Bentler 1980), causal analysis (James, Mulaik & Brett 1995), simultaneous equation modeling (Chou & Bentler 1995), and path analysis (Wold, Esbensen & Geladi 1987). To begin SEM modeling an expert specifies the dependency structure among the variables in a model. This additional information allows for simultaneous analysis of all the variables in a potential model and which can provide a better fit to the collected data. This aspect of SEM is different from regression analysis where all the input variables are assumed to be independent of one another and each potential model must be analyzed incrementally.
Machine Learning
A variety of advanced analysis techniques use machine learning to overcome the deficiencies of structural equation modeling and linear regression analysis. Machine learning algorithms employ feature selection, decision trees, inductive logic programming and neural networks to construct metamodels that support non-linear tradeoffs among input variables that traditional analysis techniques cannot identify and/or represent. Recently, researchers studied the performance of ten different machine learning algorithms for identify the structure of bottom-up metamodels for a variety of simulations. They found that combining feature selection with decision trees produced more accurate metamodels than any other tested combination of machine learning algorithms (Khawli et al. 2015).
New experimental designs guided by machine learning have been proposed as well to develop accurate metamodels more efficiently. Formalisms based on state machines and features diagrams have been employed to support the definition of a valid metamodel so it can distinguished from an invalid metamodel (Wooldridge, Jennings & Kinny 2000). Leveraging this representation, inductive logic programming and genetic algorithms are used to select and deduce valid metamodels that best reflect the data produced by the simulation (Faunes et al. 2013). In addition, Radial Basis Function Networks (RBFNs) have been used to generate accurate metamodels by iteratively adding new sampling points, to approximate responses with discrete changes according to experimental designs (Bandaru et al. 2014). Similarly, recent research has employed Latin hypercubes to choose the sampling points and support vector regression (SVR) to develop a metamodel for buckling loads of composite plates under compression (Koide et al. 2013). Finally, other researchers have compared the efficacy of Neural Networks (NNs) and RBFNs for constructing a metamodel to estimate overheating and air pollution in buildings produced from physics simulations. NNs are shown to perform around 15% better than RBFNs when estimating overheating and air pollution metrics determined in physics models (Symonds et al. 2015).
Statistical Debugging
Our approach to automatically creating augmented metamodels employs predicates that are used in statistical debuggers. Predicates enable statistical debuggers to analyze relationships within and among variable values. Using predicates the debuggers isolate the causes of software bugs to guide developers in locating and fixing faults in buggy programs (Liblit 2007; Gore et al. 2015).
Within statistical debuggers two different types of predicates (single variable, scalar pairs) at two different levels of specificity (static and elastic) are employed to localize bugs. The choice of type and the specify-level defines a unique combination of conditions related to a variable(s) that the predicate captures. Two or more predicates can also be combined by generating compound predicates to gather insight about the behavior of a variable(s) at an additional level of granularity.
A single variable predicate partitions the set of possible values that can be assigned to a variable x. Single variable predicates can be created at two levels of specificity: the static level and the elastic level. The most basic single variable predicates are static. Static single variable predicates are employed to partition the values for each variable x around the number zero: (x > 0), (x≥ 0), (x = 0) and (x ≤ 0), (x < 0). These single variable predicates are referred to as static because the decision to compare the value of x to 0 is made before execution (Liblit 2007). In contrast, the single variable elastic predicates use summary statistics of the values given to variable x to create partitions that cluster together values which are a similar distance and direction from the mean. For the variable x with mean μx and standard deviation σx, the elastic single variables predicates created are: (x > μx + σx), (x > μx + 2σx), (x > μx + 3σx), (μx + σx > x > μx - σx), (μx + 2σx > x > μx - 2σx), (μx + 3σx > x > μx - 3σx), and (x < μx - σx), (x < μx - 2σx) and (x < μx - 3σx). These predicates reflect values of variable x that are well above their normal value, within their normal range of values and well below their normal value (Gore et. al 2015).
Scalar pair predicates capture the important relationships between two variables that elude single variable predicates. The most basic scalar pair variables are static. Static scalar pair predicates are employed to partition the difference between a pair of variables, x and y, around the number zero: (x - y > 0), (x - y ≥ 0), (x - y = 0), (x - y ≤ 0) and (x - y < 0). These scalar pairs predicates are referred to as static because the decision to compare the difference between x and y to 0 is made before execution (Liblit 2007). In contrast, the scalar pairs elastic predicates use summary statistics of the difference between x and y to create partitions that cluster together values which are a similar distance and direction from the mean. For the pair of variables x and y with mean difference μx-y and standard deviation σx-y, the elastic scalar pairs predicates created are: (x - y > μx-y + σx-y), (x - y > μx-y + 2σx-y), (x - y > μx-y + 3σx-y), (μx-y + σx-y > x - y > μx-y – σx-y), (μx-y + 2σx-y > x - y > μx-y – 2σx-y), (μx-y + 3σx-y > x - y > μx-y – 3σx-y), (x - y < μx-y – σx-y), (x - y < μx-y – 2σx-y) and (x - y < μx-y – 3σx-y). These predicates reflect differences between the values of x and y that are well above the normal value, within the normal range of values and well below the normal value (Gore et. al 2015).
Compound predicates reflect any combination of single variable and scalar pair predicates that can be composed using the logical operators ∧ (and) and ∨ (or). For any two predicates P and Q, two compound predicates are tested: (1) the conjunction of the predicates (P && Q) and (2) the disjunction of the predicates (P Ι Ι Q). Once created a compound predicate can be combined with another compound predicate (Nainar et al. 2007).
Automatically Creating Enlightened Metamodels
Despite differences in purpose, we hypothesize that the same Boolean conditions predicate-level statistical debuggers employ to localize bugs in software are capable of bounding regions in the input space where tradeoffs and substitutions among variables are valid. Here, we provide a small example to demonstrate the process and applicability of our approach. Then we address the implementation of our approach in more detail.
Approach
Recall, the most common process users follow to create a baseline metamodel begins with running the ABM for many trials where the inputs are varied according to an experimental design. The resulting output data from the simulation is collected and a statistical model from the data is computed using first-order regression analysis. Based on the analysis, inputs that appear insignificant are discarded while others that seem redundant are combined. Ultimately, the bottom-up metamodel of the simulation is finalized. Recall, we refer to a metamodel created in this manner as a baseline metamodel. The baseline metamodel is significantly simpler than the simulation and produces answers in a fraction of the time (Barton 1994; Kleijnen & Sargent 2000; Bigelow & Davis 2002; Friedman 2012).
Using this method, the output of the simulation is treated as a sum of terms, where each term is composed of one or more input variables. This process assumes that critical thresholds within a single input or relative relationships among multiples inputs of the larger simulation do not exist. Due to this assumption the resulting baseline metamodel can be misleading because it gives the impression that one can compensate for one input of the simulation with another input even if such a substitution/tradeoff is inadequate or invalid (Friedman & Pressman 1988; dos Santos & Porta 1999; Kleijnen & Sargent 2000, Meckesheimer 2001; Bigelow & Davis 2002).
To remedy this shortcoming we augment the terms within a baseline metamodel with predicates used by statistical debuggers. Augmenting the terms in a baseline metamodel encodes the set of valid tradeoffs and substitutions from the ABM into the metamodel. The result is improved accuracy and validity. To elucidate this process and the utility of our contribution, we demonstrate in a small example how our augmentation approach can produce an improved metamodel.
Simple Example
An example helps elucidate our approach to employing predicates to improve the validity and accuracy of baseline metamodels. We suppose a user has constructed a simulation called MED which takes three integers (x, y, and z) as input and outputs the median value.
We construct a metamodel for MED by specifying the experimental design. For this example, we specify a full factorial design for inputs x, y and z over the range of inputs values [1,3]. Next, we run the simulation for each of the inputs. The inputs and output of each run are recorded in a data set. Using the data set we create the single variable, scalar pair predicates at the static and elastic specificity levels for the input variables. Using these predicates we generate compound predicates to explore the captured input conditions in combination. Finally, we augment the collected data to show the truth-value of each generated predicate in the data set. The values of the inputs, an important subset of the generated predicates and the output value of the simulation are shown in Table 1. We use the convention that if the predicate is true for the inputs a value of 1 is recorded and if the predicate is false for the inputs a value of 0 is recorded.
Once the data is collected, analysis is performed to identify those predicates and variables that should be retained, combined and discarded (Calcagno & de Mazancourt 2010). The resulting augmented bottom-up metamodel identified by our approach is shown in Equation 1:
| $$(X\ast Predicate_1)+(Y\ast Predicate_2)+(Z\ast Predicate_3)=MED$$ | (1) |
| Input | Subset of Generated Predicates | Output | ||||
|---|---|---|---|---|---|---|
| Predicate1 | Predicate2 | Predicate3 | ||||
| X | Y | Z | (X-Y≤0) ∧ (X-Z≥0) ∨ (X-Z≤0) ∧ (X-Y≥0) | (X-Y>0) ∧ (Y-Z≥0) ∨ (Y-Z ≤0) ∧ (X-Y<0) | (X-Y<0) ∧ (X –Z>0) ∨ (X-Z<0) ∧ (X-Y>0) | MED |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 2 | 1 | 0 | 0 | 1 |
| 1 | 1 | 3 | 1 | 0 | 0 | 1 |
| 1 | 2 | 1 | 1 | 0 | 0 | 1 |
| 1 | 2 | 2 | 0 | 1 | 0 | 2 |
| 1 | 2 | 3 | 0 | 1 | 0 | 2 |
| 1 | 3 | 1 | 1 | 0 | 0 | 1 |
| 1 | 3 | 2 | 0 | 0 | 1 | 2 |
| 1 | 3 | 3 | 0 | 1 | 0 | 3 |
| 2 | 1 | 1 | 0 | 1 | 0 | 1 |
| 2 | 1 | 2 | 1 | 0 | 0 | 2 |
| 2 | 1 | 3 | 1 | 0 | 0 | 2 |
| 2 | 2 | 1 | 1 | 0 | 0 | 2 |
| 2 | 2 | 2 | 1 | 0 | 0 | 2 |
| 2 | 2 | 3 | 1 | 0 | 0 | 2 |
| 2 | 3 | 1 | 1 | 0 | 0 | 2 |
| 2 | 3 | 2 | 1 | 0 | 0 | 2 |
| 2 | 3 | 3 | 0 | 1 | 0 | 3 |
| 3 | 1 | 1 | 0 | 1 | 0 | 1 |
| 3 | 1 | 2 | 0 | 0 | 1 | 2 |
| 3 | 1 | 3 | 1 | 0 | 0 | 3 |
| 3 | 2 | 1 | 0 | 1 | 0 | 2 |
| 3 | 2 | 2 | 0 | 1 | 0 | 2 |
| 3 | 2 | 3 | 1 | 0 | 0 | 2 |
| 3 | 3 | 1 | 1 | 0 | 0 | 3 |
| 3 | 3 | 2 | 1 | 0 | 0 | 3 |
| 3 | 3 | 3 | 1 | 0 | 0 | 3 |
Given the limited scope of the example one can see that this metamodel exactly predicts the MED’s output for: (1) the inputs over the range [1,3] and (2) all inputs that can ever be given to this simulation. While this may seem like an expected outcome from such a simple example, it is not. Using only sums of the terms created from the three input variables (x, y and z) to model the output of MED will not accurately predict the output of the model for unseen inputs because there is no way to capture that the output is not a direct combination of the inputs. For example, consider the baseline metamodel shown in Equation 2.
| $$\Bigl(\frac{1}{3}\ast X\Bigr)+\Bigl(\frac{1}{3}\ast Y\Bigr)+\Bigl(\frac{1}{3}\ast Z\Bigr)=MED$$ | (2) |
Equation 2 does not employ predicates in its regression analysis and as a result it metamodels the median of X, Y and Z as the arithmetic mean. Unfortunately, this representation can be invalid. For example, parameterizing Equation 2 with X=3, Y=30, and Z = 3,000 results in a prediction of 337, when the actual system output is 30. In general, the baseline metamodel enables one to maximize a single variable (i.e Z) to compensate for shortcomings in the other variables (i.e. X and Y). The actual simulation does not have this property. Without the inclusion of predicates to control when substitutions and tradeoffs among variables are valid an accurate first order linear regression metamodel is not possible.
It is important to note that goal of this example is not to set a standard of 100% accuracy over observed and unobserved inputs for our augmented metamodels. Instead, the goal is to demonstrate how our approach employs predicates to encode some of the valid tradeoffs and substitutions from the ABM into the metamodel to improve validity and accuracy.
In the following subsection we provide more details about: (1) how predicates and input variables are combined within the structure of an augmented metamodel and (2) how we conduct an automated search using a genetic algorithm to identify the augmented metamodel that retains the most information from the ABM.
Implementation
The MED example in the previous section demonstrates the improvements that are possible if metamodels are augmented with predicates. However, it also highlights several questions we must address in the implementation of our approach. These questions include:
- The metamodel featured in the example contains three compound predicates applied to three input variables. What does this imply about the structure of the augmented metamodels built for ABMs?
- What mechanism is used to identify the augmented metamodel that retains the most information from the ABM?
The remainder of this section answers these questions in detail.
Structure of the Metamodels
Our approach augments baseline metamodels with predicates. Within an augmented metamodel, each predicate is a Boolean expressions multiplier that is applied to an input variable in the metamodel. In other words, given a vector of predicates P, and a vector of input variables V, the prediction of the metamodel is the result of applying P to V. For example in the augmented metamodel for MED shown in Equation 1, predicates 1,2 and 3 are applied to the terms X, Y and Z respectively.
This strategy ensures that any metamodel generated by our approach will include one predicate for every term included in the metamodel. This includes cases where qualifying a term with a Boolean condition does not improve the fit of the model. In these cases a predicate that is universally true will be applied to the input variable (i.e. x = 0 ∨ x ≠ 0). It also includes cases where including a variables does improve the fit of the model. In these cases a predicate that is universally false will be applied to the input variable (i.e. x > 0 ∧ x < 0). Furthermore, to ensure that each predicate does not become overly complex we only generate compound predicates that include a maximum of four Boolean conditions.
Finding the Best Metamodel
The process of creating augmented metamodels begins with the data collected from the simulation. First, the input variables and an output across a set of test cases is used to generate and score the truth-values of the predicates employed in augmented metamodels. Then using the data, we apply, an automated model selection approach called glmulti. glmulti uses a genetic algorithm to identify the augmented metamodel that retains the most information from the data collected from the ABM.
The genetic algorithm in glmulti begins by generating an initial population of 500 first-order augmented models that match the structure specified in the previous section. Each model in the population is encoded as a string of 0s and 1s. This encoding indicates which of the possible input variables and predicates in the model are present (1) and absent (0). The string serves as the model’s chromosome that will undergo adaptive evolution and each bit in the string is a locus for possible adaption.
Every generation, each model is treated as a first order linear regression model and the Information Criterion (IC) of the model of is used to determine the model’s fitness. An indepth discussion of the IC we employ is provided in the Evaluation section. The fitness of a model is computed using Equation 3 where ICmodel is the IC value of the current model and ICbest is the best IC in the current population of models.
| $$fitness_{model}=e^{\bigl(-(IC_{model}-IC_{best})\bigr)}$$ | (3) |
Based on the previous generation, 500 models in the next generation are produced through three different genetic operators applied in combination. These operators are: (1) asexual reproduction (45 %), (2) sexual reproduction (45 %), and (3) immigration (10 %).
A model produced by asexual reproduction is simply a copy of its parent. The parent is drawn from the previous generation with a probability proportional to its fitness. Then the states of some the model’s loci are changed by mutation. In our implementation, each locus is changed with a 10% probability.
A model produced by sexual reproduction has two parents whose chromosomes are recombined. Again, parents are drawn from the previous generation with a probability proportional to their fitness. In addition to recombination, each locus can mutate. Within sexual reproduction mutations occur with 10% probability.
A model produced by immigration has the state of each locus assigned randomly. As a result its application can produce big changes in the structure of the models that will be fitted (Yang 2004).
Three rules to define when the algorithm should stop looking for better models. The first two rules reflect target improvements in the best IC and the average IC found in a given generation. In our implementation, if the observed improvements in the IC are below 0.1, then the genetic algorithm is declared not to have significantly improved. The final rule reflects how many times in a row a lack of improvement has to occur to declare the model converged. In our implementation if the best and average IC do not improve above the 0.1 threshold for five consecutive times we declare convergence and the best model is output.
Evaluation
We evaluate the efficiency and effectiveness of our automated approach to augmenting regression analysis with Boolean conditions that highlight when tradeoffs and substitutions among variables are valid. Recall, these Boolean conditions and the regions that they bound reflect critical components within ABMs. The term critical component refers to a threshold within a single input or among multiples inputs that affect the behavior of the ABM. First we introduce the three established ABMs we use as subjects in our evaluation. Then we discuss our experimental setup and our measure of effectiveness. Finally, we present the results of our evaluation.
Established Subject ABMs
Boids
Boids models the flocking behavior of birds on a two-dimensional canvas. The term boid refers to a bird like object. Within the simulation three parameters control the behavior of each boid: separation, alignment and cohesion. The degree of separation controls the extent to which the boids avoid crowding each other. Alignment controls the degree to which each boid steers to the average head of the other boids in the simulation. The cohesion parameter controls the amount that each boid moves toward the average position of the other boids. More complex parameters can be added, such as obstacle avoidance and goal seeking but they are not included in the version of the simulation (Reynolds 1987; Gilbert 2004; Epstein 2006; Salge & Polani 2011). The output of the boids simulation is the mean flocking index of the boids calculated over a period of 1,000 timesteps (Quera et al. 1999). Figure 1 shows a visualization of the Boid ABM.

Schelling’s Model of Segregation
The Schelling model of segregation illustrates how an individual’s satisfaction with their neighbors can lead to segregation. It has been extensively used to study residential segregation of ethnic groups who relocate in urban areas. In the model, each agent belongs to one of two groups and aims to reside within a neighborhood populated by similar agents from the same group. Agents in the simulation continually relocate based on their neighbors. The degree of satisfaction people have is referred to as mean satisfaction. This measures the percent of people that are satisfied living in the current position. The percentage of agents on the landscape that belong to a group, the density of the landscape and the threshold of each agent’s preference to reside with similar agents influence the mean satisfaction (Schelling 1978; Hatna & Benenson 2012; Hegselmann 2012). Figure 2 shows a visualization of the Schelling ABM with two groups (red and blue) where a steady state has been achieved.

Spread of Influenza
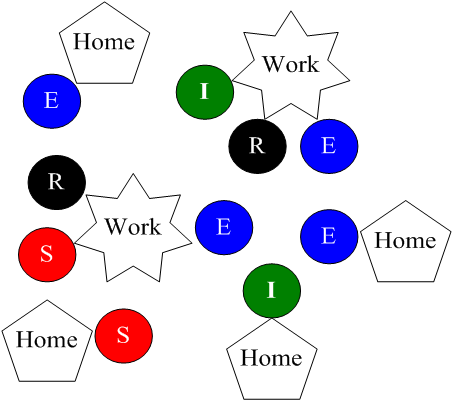
The spread of influenza can be modeled by simulating interactions between agents on a 2-D lattice. In the simulation 1,000 individuals commute between their home and work over the course of a flu season. At home and work infections individuals search for susceptible individuals within a specified radius and spread their infection with a given probability (Carpenter 2004; Dunham 2005, Epstein 2009; O'neil & Sattenspiel 2010; Parker & Epstein 2011).
The results of the model match real-world influenza data. Furthermore, with proper parameterization, the model can be used to predict the peak number of influenza infections that occur during the course of a given season. Several parameters control how the flu is spread and determine the peak number of infections during the course of a given season. These are: the probability with which agents’ infect one another, and the average number of individuals within a workplace and a home. An image showing the structure of the Influenza Spread ABM is shown in Figure 3. In Figure 3 the colored circles reflect the four different states an agent can be in related to influenza: (S) – Susceptible, (E) – Exposed, (I) – Infected and (R) – Recovered.
Creation of Baseline and Augmented Metamodels
For each of the agent-based simulations we construct an experimental design by applying Latin hypercube sampling with 10,000 samples to the simulation’s parameters. A Latin hypercube design yields a sample where each of the dimensions of each variable is divided into equal levels and that there is only one point (i.e. sample) at each level. We use an optimized random procedure to determine the point locations so that good coverage of the design space is ensured. Such an experimental design is recommended by (Meckesheimer 2001; Meckesheimer et. al 2002) in their review of metamodel design and assessment.
Next, we run each simulation for all of the specified inputs in the experimental design and collect the results. Once all the data has been gathered we construct predicates. Then using glmulti we generate augmented and baseline metamodels for each simulation. The name, minimum value and maximum value of the parameters varied and the output metamodeled for each ABM are shown in Table 2.
| ABM | Parameter Min Ι Max | Parameter Min Ι Max | Parameter Min Ι Max | Parameter Min Ι Max | Output |
|---|---|---|---|---|---|
| Boids Flocking | # of Boids 1 Ι 1,000 | Separation 1 Ι 20 | Alignment 0 Ι 1 | Cohesion 0 Ι 1 | Flocking Index |
| Schelling | Satisfaction Threshold 0 Ι 1 | % Agents in One Group 0 Ι 100 | Agent Density 0 Ι 1 | Mean Satisfaction | |
| Influenza Spread | Infection Rate 0 Ι 1 | Work Mean
1 Ι 100 | Home Mean 1 Ι 10 | Peak # of Infections |
Effectiveness
To study the effectiveness of the baseline and augmented metamodels we considered two different Information Criteria: (1) the Akaike Information Criterion (AIC), (2) the Bayesian Information Criterion (BIC). Here we review the similarities and differences of each criterion and describe why we chose to use the BIC to measure effectiveness in our evaluation.
| $$Information\, Criterion=kp-2 ln\, L$$ | (4) |
Equation 4 defines the form for the AIC and BIC information criterion. Both are measures of fitness that estimate the amount information lost by using a metamodel instead of the data set generated by the ABM. Lower AIC and BIC values for a metamodel are preferable because they reflect a metamodel where less data is lost from the ABM.
Within in Equation 4, L is the function measuring the amount of information retained by the metamodel, p is the number of terms in the metamodel and k is penalty coefficient. Given the dynamics of the Equation 4, as k and p increase, the metamodel needs to retain more information to maintain the same IC value. In the computation of AIC, k = 2. However, in the computation of BIC k is the natural log of the number of data points used to fit the model. Recall, we use 10,000 observations for each ABM. This results in a k-value of 9.21 in the computation of the BIC.
The different k-values the AIC and BIC penalize the fit of models differently. The larger k-value employed in the BIC penalizes metamodels containing more terms (i.e. predicates and input variables) more heavily than the AIC. Since our augmented metamodels include predicates they will include more terms than baseline metamodels. Thus, choosing to evaluate the effectiveness using the BIC allows us to conservatively measure the extent to which employing our augmented approach reduces the amount of information lost from the ABM in the resulting metamodel. This choice is noteworthy. Even when an augmented metamodel more accurately reflects the data generated from the ABM it will be aggressively penalized because of the predicates it uses to model the ABM output. As a result, for an augmented metamodel to outperform a baseline metamodel it must produce results that are significantly more accurate.
In addition, it is important to recall how the predicates are formed in the augmented metamodels. They reflect the elastic and static conditions formed from single variable, scalar pair and compound predicates generated from data collected by running the simulation for the experimental design specified in Table 2. Comparing the input values and the difference in input values to zero forms static conditions. Conversely, comparing the input values and difference in the input values to the mean and standard deviations of the values they take on during data collection form elastic predicates. The experimental design is based on Latin hypercube design that employs an optimized random procedure. This ensures good coverage of the input space but also injects some randomness into the input values that are gathered during data collection.
Boids
The two metamodels generated for the Boids simulation are shown along with the BIC values of each metamodel in Table 3. The values of coefficients and intercepts employed in the model have been moved from the table into the caption to improve readability. Recall, a smaller BIC value is preferable because it reflects less information lost from the ABM.
| Type | Metamodel of Flocking Index | BIC |
|---|---|---|
| Baseline | B1*Boids – B2*Separation– B3*Alignment + B4*Cohesion - ε | 205.3 |
| Augmented | A1*P1*Boids + A2*P2*Separation + A3*P2*Alignment + A4*P2*Cohesion+ ε where P1 =(Boids > 1.5) P2 = (0.31>Cohesion>0.73)∧(0.28>Alignment>0.69)∧(2.5<Separation< 12.7) | 204.7 |
The BIC values shown in Table 3 demonstrate that augmenting the Boids model with predicates improves the accuracy of the metamodel. In particular the predicate P2 ensures that if the value of any input variable controlling the Boids flight pattern contributes to the estimation of the flocking index, then all the input variables controlling the flight pattern will contribute to the estimation. This property prevents an extreme value from being assigned to any input variable to compensate for another. For example, improving the alignment of Boids, even to an extreme degree, cannot compensate for insufficient cohesion.
We are not the first researchers to identify this sensitivity of the model. It has been identified by others (Stonedahl and Wilensky 2010). However, our approach automatically generated an accurate metamodel that makes this constraint (i.e. P2 ) explicit to the user. The baseline metamodel does not share this constraint. As a result, it enables users to invalidly maximize or minimize any input variable to overcome an extreme value assigned to another input variable.
Schelling’s Model of Segregation
The two metamodels generated for the Schelling model are shown along with the BIC values of each metamodel in Table 4. The values of coefficients and intercepts employed in the model have been moved from the table into the caption to improve readability. Recall, a smaller BIC value is preferable because it reflects less information lost from the ABM.
| Type | Metamodel of Mean Satisfaction | BIC |
|---|---|---|
| Baseline | -B1*Threshold + B2*PrctInOneGroup– B3*Density + ε | 215.4 |
| Augmented | A1*P1*Threshold + A2*P1* PrctInOneGroup + A3*P2* Density - ε where P1 = ( Threshold - PrctInOneGroup < 0) P2 = ( Density < 0.38 ) | 213.8 |
The BIC values in Table 4 show that augmenting the Schelling model with predicates improves the accuracy of the metamodel. Specifically, the scalar pair predicate P1 employed in the augmented metamodel highlights a critical threshold that exists between the satisfaction threshold of agents in the model and the percentage of agents in the model that belong to one group. When the mean satisfaction threshold of agents is less than the percentage of agents that belong to one group, the mean satisfaction level of agents is high. Intuitively, this makes sense. Both conditions make agents easier to satisfy because: (1) the threshold to be satisfied is lower and (2) there are more similar agents to surround them. Conversely, once the satisfaction threshold of agents in the model exceeds the percentage of agents that belong to one group the mean satisfaction drastically decreases. To enforce this property in the metamodel the scalar pairs predicate P1 is assigned to both variables in the augmented metamodel that are featured in the condition (Threshold and PrctInOneGroup).
This non-linear behavior cannot be represented in the baseline metamodel because it is impossible to compare the values of Threshold and PrctInOneGroup. As a result the baseline metamodel misrepresents the dynamic that exists between these two variables and information from the ABM is lost in the metamodel.
Spread of Influenza
The two metamodels generated for the Influenza Spread model are shown along with the BIC values of each metamodel in Table 5. The values of coefficients and intercepts employed in the model have been moved from the table into the caption to improve readability. Recall, a smaller BIC value is preferable because it reflects less information lost from the ABM.
| Type | Metamodel | BIC |
|---|---|---|
| Baseline | B1*InfRate + B2*WorkMean+ B3*HomeMean + ε | 312.1 |
| Augmented | A1*P1*InfRate + A2*P2*WorkMean + A3*P3*HomeMean + ε where P1 =(InfRate > 0.26) P2=[(WorkMean > HomeMean)∧(WorkMean > 18.4)] P3=[(HomeMean > WorkMean)∧(HomeMean > 2.7)] | 310.9 |
Once again the BIC values shown in Table 5 demonstrate that augmenting the Influenza Spread model with predicates improves the accuracy of the metamodel. In this case a compound predicate that combines a scalar pairs predicate with a single variable predicate imposes a constraint on the metamodel to improve its accuracy and validity. Specifically, the compound predicate highlights the relationship between the value of the mean number of people within a home and the mean number of people within a work place. Within the Influenza Spread model, the peak number of infections in a given season is largely determined by the opportunity to spread the infection (Dunham 2005). When agents work with a larger number of agents than they cohabitate with the number of co-workers dominates the contribution to the number of peak infections. Conversely, when agents cohabitate with more than they work with the number of cohabitators dominates the contribution to the number of peak infections. However, in each case there is a quorum on the number of people needed to provide a significant contribution to the peak number of infections in a season.
These relationships cannot be represented in a baseline metamodel because there is no mechanism to compare values of input variables against one another or identify thresholds needed in a single variable to achieve a quorum. Instead input variables are modeled as strictly continuous functions with coefficients to scale them to the output. All three metamodels constructed in this manner are invalid and lose a significant information from the ABM that is retained in an augmented metamodel.
Evaluation Against Machine Learning Methodologies
Our evaluation shows that each augmented metamodel results in a lower BIC than its baseline counterpart. This is significant; recall a lower BIC means that less information is lost (i.e. more information is retained). Furthermore, BIC, controls for the number of factors included in each model even more aggressively than the AIC measure. This means that the constraints included in augmented models retain significantly information from the ABM even when evaluated under conservative conditions (Bozdogan 1987).
While the existence of this trend is necessary to demonstrate the effectiveness of our approach it is not sufficient. To address this deficiency we evaluate our approach against additional machine learning methodologies that could be employed to construct a baseline metamodel: (1) decision trees and (2) feature selection.
Decision Tree Metamodels
The construction of decision tree metamodels included in our evaluation uses the rpart package available for the R programming language (Therneau and Atkinson 1997). The rpart package builds decision tree metamodels to predict the output of the ABM by constructing a binary tree using a subset of the input variables. The construction process consists of two steps. First a threshold value for the input that best splits the data into two groups is identified. The data is separated, and then this process is applied separately to each sub-group, and so on recursively until the subgroups either reach a minimum size or until no improvement can be made. The BIC of the decision tree metamodel resulting from application of rpart is shown in Table 6.
| Type | ABM Metamodeled | BIC |
|---|---|---|
| Decision Tree | Boids | 307.1 |
| Decision Tree | Schelling’s Model of Segregation | 317.3 |
| Decision Tree | Spread of Influenza | 480.6 |
Table 6 demonstrates that the decision tree metamodels are ineffective compared to the baseline and augmented metamodels shown in Tables 2-5. They result in higher BIC values, which reflect more information, lost from ABM. This is due to an assumption within the decision tree methodology. Decision tree construction assumes that the output space can be discretized by hierarchically nesting conditions related to the ABM inputs. For the ABMs included in our evaluation this is not the case. The output space of each ABM included in our evaluation is either continuous or discretized into fine-grained intervals. As a result, even when the decision tree metamodel correctly classifies the output of the metamodel, it does not produce a prediction that is close to matching the ABM output. Furthermore, the inputs in the ABMs included in our evaluation do not follow a strictly hierarchical order. Under some parameterizations one input will provide the best split of the data. However, under other parameterizations another input will provide the best split of the data. The result of assuming one input will provide the best split of the data for all runs for the ABMs included in our evaluation is an increase in information lost.
Feature Selection Metamodels
The construction of feature selection metamodels included in our evaluation uses the caret package available for the R programming language (Kuhn 2008). The caret package builds a regression metamodel that is similar to a baseline metamodel. The difference between a baseline metamodel and a feature selection metamodel is that a feature selection metamodel is not guaranteed to include all of the input variables while a baseline metamodel is. This ability of select only the most important variables (or features) in a metamodel can enable a feature selection metamodel to produce a lower BIC than a baseline metamodel.
The caret package uses routine that tracks the reduction in the estimate of error of the metamodel for each input variable as it is added to the metamodel. The reduction is used to measure the importance of the input in the metamodel. High reductions in the estimate or error denote important variables while low reductions denote unimportant variables. The minimum reduction in error for an input to be included in the metamodel is determined by the number of inputs in the ABM. The BIC of the decision tree metamodel resulting from application of caret is shown in Table 7.
| Type | ABM Metamodeled | BIC |
|---|---|---|
| Feature Selection | Boids | 205.3 |
| Feature Selection | Schelling’s Model of Segregation | 215.4 |
| Feature Selection | Spread of Influenza | 312.1 |
Table 7 demonstrates that the feature selection metamodels are exactly as effective as the baseline metamodels shown in Tables 2-5. This result demonstrates that each of the inputs in the ABMs in our evaluation are important features. It is important to note that the metamodels included in our evaluation include a relatively small number of inputs (4, 3, 3 and 3). In future work we will explore how the effectiveness of feature selection could be applied to baseline and augmented metamodels for ABMs with more inputs.
Evaluation Summary
Our evaluation shows that each augmented metamodel outperforms its baseline counterpart as well as other metamodels constructed using machine learning methodology. Despite the existence of this trend it is hard to conceptualize the improvement provided by our augmented metamodels. To elucidate improvement we define it as is the number of times the best alternative metamodel is likely to retain more information when compared to an augmented metamodel. This formula is shown in Equation 5.
The best alternative metamodel reflects the baseline, feature selection or decision tree metamodel with the lowest BIC for a given simulation. Using this measure any result greater than 1.0 reflects a situation where the augmented metamodel is more likely to lose information from the ABM than the best alternative metamodel. Similarly, any result less than 1.0 reflects a situation where the best alternative metamodel is more likely to lose information from the ABM than the augmented metamodel.
Equation 5 is an established means to compare the improvement with respect to BIC of two competing metamodels (Konishi & Kitagawa 1996). Within the formula BICAUG is the BIC value for the augmented metamodel and BICALT is the BIC value for the best alternative metamodel.
| $$e^{\Bigl(\frac{BIC_{AUG}-BIC_{ALT}}{2}\Bigr)}$$ | (5) |
| Boids | Schelling Model | Influenza Spread |
|---|---|---|
| 0.7408 times | 0.4493 times | 0.5488 times |
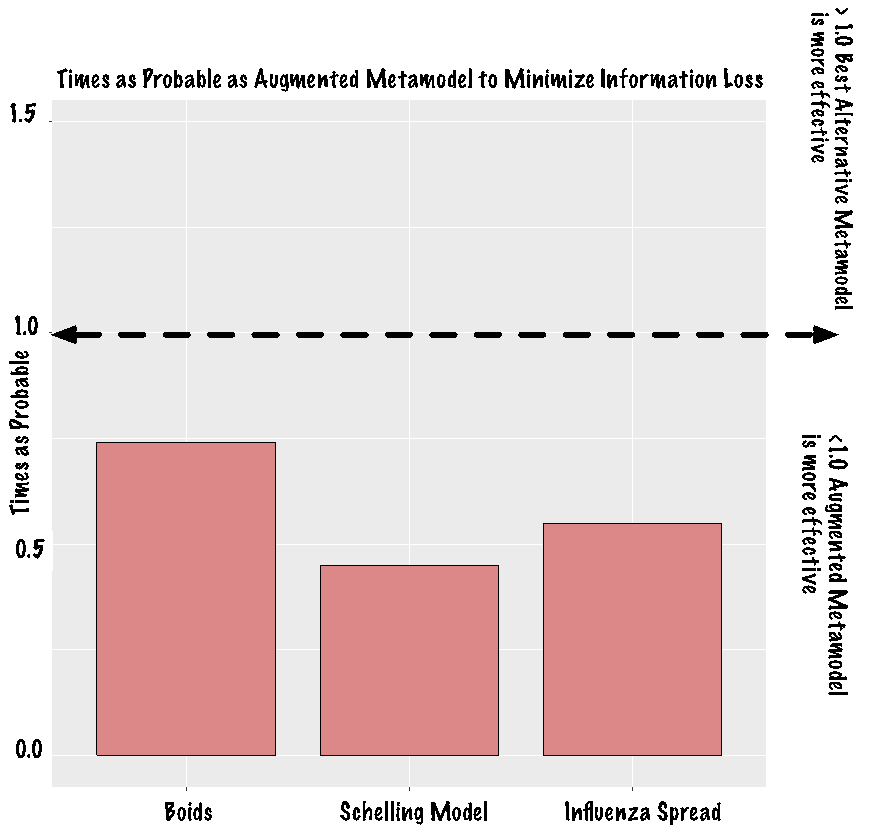
The results from the computation are shown in Tables 8 and visualized in Figure 4. In each of the simulations, the best alternative metamodel is less than 0.75 times as probable as the augmented metamodel to minimize information lost from the ABM. Furthermore, for two of the three models it is ~ 0.50 times as probable as the augmented metamodel to minimize information lost from the ABM. This reflects a significant decrease in accuracy by using any metamodeling methodology included in our evaluation other than our augmented strategy for any of the ABMs included in our evaluation.
In addition to improve accuracy, the inclusion of predicates in the augmented metamodel makes the existence of constraints that limit substitutions and tradeoffs within and among input variables explicit to users. When users employ the augmented metamodels generated for the three established ABMs they will no longer assume that one variable can compensate for another when such a substitution is inadequate or invalid. This is the most powerful capability of our augmented metamodels because even if no additional information from the ABM is retained in an augmented metamodel, the validity of the metamodel is still improved.
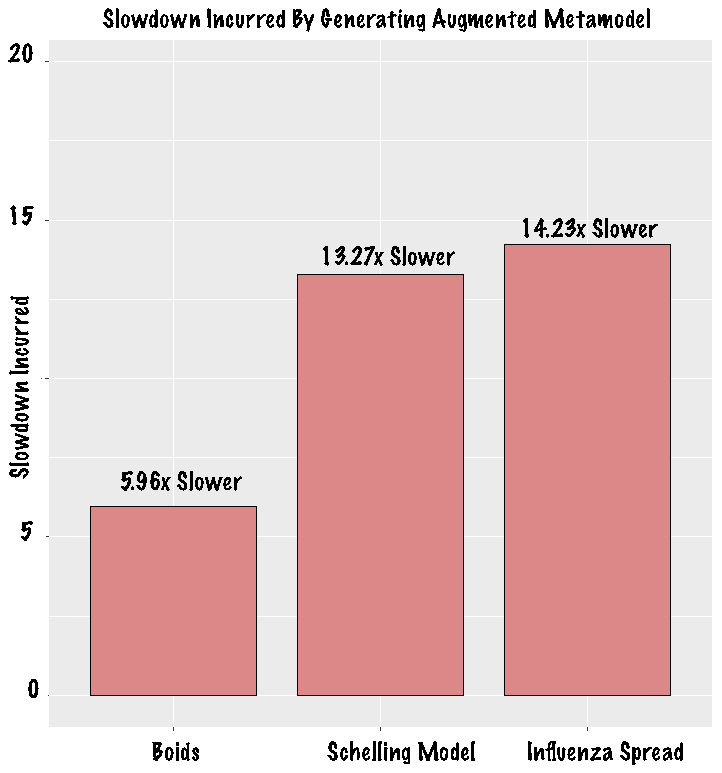
Efficiency
Tables 7 shows the amount of wallclock time that is required to construct the best alternative and augmented metamodels for each simulation included in the evaluation. The slowdown incurred is computed by comparing the time required to create each augmented metamodel to the time required to create the best alternative metamodel. Recall, the best alternative metamodel reflects the baseline, feature selection or decision tree metamodel with the lowest BIC for a given simulation. In the case where there are multiple best metamodels, the metamodel with the shortest construction time is chosen. Formally, this measure is shown in Equation 6.
| $$Slowdown\, Incurred=\frac{wallclockTime_{augmented}}{wallclockTime_{alternative}} $$ | (6) |
| Wallclock Time | Boids | Schelling Model | Influenza Spread |
|---|---|---|---|
| Alternative | 90 seconds | 62 seconds | 73 seconds |
| Augmented | 537 seconds | 823 seconds | 1,039 seconds |
| Slowdown Incurred | 5.96 times longer | 13.27 times longer | 14.23 times longer |
Table 9 and Figure 5 show that the construction of augmented metamodels incurs a 10x - 20x slowdown. In each case, the additional computational time required to construct enlightened metamodels in is spent: (1) generating the predicates from the experimental design and (2) finding the best statistical model in a search space with significantly more factors.
While our approach to creating augmented metamodels is less efficient, it only requires machine time not user time. If users can remain productive while an augmented metamodel is generated, overall efficiency will be improved because the user is given a more effective metamodel. This rationale has made formal software verification methods useful despite execution times measured in days and hours (Silva et al. 2008). Next, we discuss the validity of our study and its limitations.
Discussion
Validity
Validity threats affect our evaluation. Threats to internal validity concern factors that might affect dependent variables without the researcher’s knowledge (Schram 2005). The implementations of the simulations we used in our studies could contain errors. However, these simulations were all gathered from external sources, passed internal code reviews and a face validation of their output was performed before any data was collected. Threats to external validity occur when the results of our evaluation cannot be generalized (Schram 2005). While we performed our evaluations on three established agent-based simulations we cannot claim that the effectiveness observed in our evaluation can be generalized to other agent-based simulations. Threats to construct validity concern the appropriateness of the evaluation metrics used (Cronbach & Meehl 1955). While the BIC information criterion enables the effectiveness of our approach to be conservatively evaluated, some users may prefer different measure of effectiveness. However, our general approach to constructing metamodels can still be applied even if users prefer different measures of effectiveness.
Assumptions and Limitations
It is important to note that our evaluation does not include ABMs that are as complex as some that exist in the wild. This limitation exists because we wanted to employ an established set of ABMs that could be easily understood in the evaluation. Employing our enhanced validation approach on more complicated ABMs is an opportunity for future work.
Related Work
The construction of metamodels is not new. Metamodels have been created for a variety of applications including: modeling output distribution parameters (Santos & Santos 2007), business practice optimization (McHaney & Douglas 1997; Liu 2009; Barton & Meckesheimer 2006; Noguera & Watson 2006), logistics (Stearns 1998), complex social systems (Goldspink 2000; Omicini et al. 2008), multi-resolution modeling (Vo 2012), queueing (Friedman 1989) and estimating artificial neural networks (Fonseca 2003).
These results have improved accuracy and validity of metamodels in specific domains and/or by using advanced analyses. However, none of these efforts have proposed a general approach to address improving accuracy and validity for first-order linear regression bottom up metamodels. Several researchers have attempted to address this issue by complementing the statistical analysis used to construct a metamodel with user knowledge elicited manually (Kleijnen & Sargent 2000; Bigelow & Davis 2002). While these motivated metamodels are capable of capturing critical components they require manual effort and significant input from a user. In contrast, our approach to constructing augmented metamodels is fully automated and requires no user input.
More recently, researchers have conducted a study using an integrated agent-based and metamodel to test the four kinds of policy varying along two dimensions. The results identified thresholds causing non-linear dynamics related to incentives and benefits (Polhill et al. 2013). In future work, we will look to apply our augmented metamodel construction technique to this model to see if it is capable of identifying the same critical thresholds.
Conclusion
The current practice to constructing first-order linear regression bottom-up metamodels needs improvement. The linear sums employed by the statistical methods used to construct the model give the impression that one can compensate for one component of the system by improving another component even if such substitution is inadequate or invalid. As a result the metamodel can fail to accurately reflect the critical components of the system and may be misleading. We propose an approach to constructing augmented metamodels where the predicates employed by statistical debuggers constrain substitutions and tradeoffs among and within variables. We demonstrate that our approach can reduce the information lost in the metamodel while making critical components of the ABM explicit to users. These augmented bottom-up metamodels are more effective than their baseline counterparts and other alternatives. Furthermore, they do not give users the impression that one can compensate for one component of the system by improving another when such substitution is invalid. In future work, we will explore how our augmentation approach can be adapted for advanced analysis techniques and apply our approach to more complex ABMs.
References
BANDARU, S., Ng, A. H., & Deb, K. (2014). On The Performance of Classification Algorithms for Learning Pareto-Dominance Relations. In Evolutionary Computation (CEC), 2014 IEEE Congress On (Pp. 1139-1146). IEEE. [doi:10.1109/CEC.2014.6900641]
BARTON, R. R. (1994). Metamodeling: a state of the art review. In Proceedings of the 26th conference on Winter simulation (pp. 237-244). Society for Computer Simulation International. [doi:10.1109/WSC.1994.717134]
Barton, R. R., & Meckesheimer, M. (2006). Metamodel-based simulation optimization. Handbooks in operations research and management science, 13, 535-574. [doi:10.1016/S0927-0507(06)13018-2]
BENTLER, P. M. (1980). Multivariate analysis with latent variables: Causal modeling. Annual review of psychology, 31(1), 419-456. [doi:10.1146/annurev.ps.31.020180.002223]
BIGELOW, J. H., & Davis, P. K. (2002). Developing improved metamodels by combining phenomenological reasoning with statistical methods. In AeroSense 2002 (pp. 167-180). International Society for Optics and Photonics. [doi:10.1117/12.474911]
BOZDOGAN, H. (1987). Model selection and Akaike's information criterion (AIC): The general theory and its analytical extensions. Psychometrika, 52(3), 345-370. [doi:10.1007/BF02294361]
CALCAGNO, V., & de Mazancourt, C. (2010). glmulti: an R package for easy automated model selection with (generalized) linear models. Journal of Statistical Software, 34(12), 1-29. [doi:10.18637/jss.v034.i12]
CARPENTER, C. V. (2004). Agent-based modeling of seasonal population movement and the spread of the 1918-1919 flu: The effect on a small community (Doctoral dissertation, University of Missouri--Columbia).
CHIN, W. W. (1998). The partial least squares approach to structural equation modeling. Modern methods for business research, 295(2), 295-33.
CHOU, C. P., & Bentler, P. M. (1995). Estimates and tests in structural equation modeling. In Hoyle, R. (ed), Structural equation modeling: Concepts, issues, and applications. Thousand Oaks, CA: Sage, pp. 37–55
CRONBACH, L. J., & Meehl, P. E. (1955). Construct validity in psychological tests. Psychological bulletin, 52(4), 281. [doi:10.1037/h0040957]
COLLINOT, A., Drogoul, A., & Benhamou, P. (1996). Agent oriented design of a soccer robot team. In Proceedings of the Second International Conference on Multi-Agent Systems (ICMAS-96), 41-47.
DOS SANTOS, M., & Porta Nova, A. M. (1999). The main issues in nonlinear simulation metamodel estimation. In Proceedings of the 31st conference on Winter simulation: Simulation---a bridge to the future-Volume 1 (pp. 502-509). ACM. [doi:10.1145/324138.324309]
DUNHAM, J. B. (2005). An agent-based spatially explicit epidemiological model in MASON. Journal of Artificial Societies and Social Simulation, 9(1) 3: https://www.jasss.org/9/1/3.html.
EPSTEIN, J. M. (2006). Generative social science: Studies in agent-based computational modeling. Princeton University Press.
EPSTEIN, J. M. (2009). Modelling to contain pandemics. Nature, 460(7256), 687-687. [doi:10.1038/460687a]
FAUNES, M., Cadavid, J., Baudry, B., Sahraoui, H., & Combemale, B. (2013). Automatically Searching For Metamodel Well-Formedness Rules In Examples And Counter-Examples. In Moreira A. et al. (Eds.), Model-Driven Engineering Languages and Systems (Pp. 187-202). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-41533-3_12]
FONSECA, D. J., Navaresse, D. O., & Moynihan, G. P. (2003). Simulation metamodeling through artificial neural networks. Engineering Applications of Artificial Intelligence, 16(3), 177-183. [doi:10.1016/S0952-1976(03)00043-5]
FORNELL, C., & Larcker, D. F. (1984). Misapplications of simulations in structural equation models: Reply to Acito and Anderson. Journal of Marketing Research, 21(1), 113-117. [doi:10.2307/3151798]
FRIEDMAN, L. W. (1989). The multivariate metamodel in queuing system simulation. Computers & Industrial Engineering, 16(2), 329-337. [doi:10.1016/0360-8352(89)90152-6]
FRIEDMAN, L. W. (2012). The simulation metamodel. Springer Science & Business Media.
FRIEDMAN, L. W., & Pressman, I. (1988). The metamodel in simulation analysis: can it be trusted? Journal of the Operational Research Society, 939-948. [doi:10.1057/jors.1988.160]
GILBERT, N. (2004). Agent-based social simulation: dealing with complexity. The Complex Systems Network of Excellence, 9(25), 1-14.
GOLDSPINK, C. (2000). Modelling social systems as complex: Towards a social simulation meta-model. Journal of Artificial Societies and Social Simulation, 3(2) 1: https://www.jasss.org/3/2/1.html.
GORE, R., Reynolds Jr, P. F., & Kamensky, D. (2011). Statistical debugging with elastic predicates. In Automated Software Engineering (ASE), 2011 26th IEEE/ACM International Conference on (pp. 492-495). IEEE. [doi:10.1109/ASE.2011.6100107]
GORE, R., Reynolds Jr, P. F., Kamensky, D., Diallo, S., & Padilla, J. (2015). Statistical debugging for simulations. ACM Transactions on Modeling and Computer Simulation (TOMACS), 25(3), 16.. [doi:10.1145/2699722]
HARRINGTON, D. (2008). Confirmatory factor analysis. Oxford University Press, USA.
HATNA, E., & Benenson, I. (2012). The Schelling model of ethnic residential dynamics: Beyond the integrated-segregated dichotomy of patterns. Journal of Artificial Societies and Social Simulation, 15(1), 6: https://www.jasss.org/15/1/6.html [doi:10.18564/jasss.1873]
HAYES-ROTH, B. (1995). An architecture for adaptive intelligent systems. Artificial Intelligence, 72(1), 329-365. [doi:10.1016/0004-3702(94)00004-K]
HEGSELMANN, R. (2012). Thomas C. Schelling and the Computer: Some Notes on Schelling's Essay" On Letting a Computer Help with the Work". Journal of Artificial Societies and Social Simulation, 15(4), 9: https://www.jasss.org/15/4/9.html [doi:10.18564/jasss.2146]
IGLESIAS, C. A., Garijo, M., & González, J. C. (1999). A survey of agent-oriented methodologies. In Intelligent Agents V: Agents Theories, Architectures, and Languages, 317-330. Springer. [doi:10.1007/3-540-49057-4_21]
JAMES, L. R., Mulaik, S. A., & Brett, J. M. (1982). Causal analysis: Assumptions, models, and data (Vol. 1). SAGE Publications, Incorporated.
JOUAULT, F., & Bézivin, J. (2006). KM3: a DSL for Metamodel Specification. In Formal Methods for Open Object-Based Distributed Systems, 171-185. Springer. [doi:10.1007/11768869_14]
KHAWLI, T., Eppelt, U., & Schulz, W. (2015). Advanced Metamodeling Techniques Applied To Multidimensional Applications With Piecewise Responses. In Machine Learning, Optimization, and Big Data (Pp. 93-104). Springer International Publishing. [doi:10.1007/978-3-319-27926-8_9]
KLEIJNEN, J. P., & Sargent, R. G. (2000). A methodology for fitting and validating metamodels in simulation. European Journal of Operational Research, 120(1), 14-29. [doi:10.1016/S0377-2217(98)00392-0]
KOIDE, R. M., Ferreira, A. P. C., & Luersen, M. A. (2013). Latin hypercube design of experiments and support vector regression metamodel applied to buckling load prediction of composite plates.
KONISHI, S., & Kitagawa, G. (1996). Generalised information criteria in model selection. Biometrika, 83(4), 875-890. [doi:10.1093/biomet/83.4.875]
KUHN, M. (2008). Caret package. Journal of Statistical Software, 28(5).
LIU, H. (2009). Taylor kriging metamodeling for simulation interpolation, sensitivity analysis and optimization. Dissertation. Auburn University.
LIBLIT, B. (2007). Cooperative bug isolation: winning thesis of the 2005 ACM doctoral dissertation competition (Vol. 4440). Springer.
MCHANEY, R. W., & Douglas, D. E. (1997). Multivariate regression metamodel: A DSS application in industry. Decision Support Systems, 19(1), 43-52. [doi:10.1016/S0167-9236(96)00037-1]
MECKESHEIMER, M. (2001). A framework for metamodel-based design: subsystem metamodel assessment and implementation issues (Doctoral dissertation, The Pennsylvania State University).
MECKESHEIMER, M., Booker, A. J., Barton, R. R., & Simpson, T. W. (2002). Computationally inexpensive metamodel assessment strategies. AIAA journal, 40(10), 2053-2060. [doi:10.2514/2.1538]
NAINAR, P., Chen, T., Rosin, J., & Liblit, B. (2007, July). Statistical debugging using compound Boolean predicates. In Proceedings of the 2007 international symposium on Software testing and analysis (pp. 5-15). ACM.
NOGUERA, J. H., & Watson, E. F. (2006). Response surface analysis of a multi-product batch processing facility using a simulation metamodel. International Journal of Production Economics, 102(2), 333-343. [doi:10.1016/j.ijpe.2005.02.014]
ODELL, J., Parunak, H. V. D., & Bauer, B. (2000). Extending UML for agents. Ann Arbor, 1001, 48103.
OMICINI, A., Ricci, A., & Viroli, M. (2008). Artifacts in the A&A meta-model for multi-agent systems. Autonomous agents and multi-agent systems, 17(3), 432-456. [doi:10.1007/s10458-008-9053-x]
O'NEIL, C. A., & Sattenspiel, L. (2010). Agent-based modeling of the spread of the 1918–1919 flu in three Canadian fur trading communities. American Journal of Human Biology, 22(6), 757-767. [doi:10.1002/ajhb.21077]
PARKER, J., & Epstein, J. M. (2011). A distributed platform for global-scale agent-based models of disease transmission. ACM Transactions on Modeling and Computer Simulation (TOMACS), 22(1), 2. [doi:10.1145/2043635.2043637]
POLHILL, J. G., Gimona, A., & Gotts, N. M. (2013). Nonlinearities in biodiversity incentive schemes: a study using an integrated agent-based and metacommunity model. Environmental modelling & software, 45, 74-91. [doi:10.1016/j.envsoft.2012.11.011]
QUERA, V., Herrando, S., Beltran, F. S., Salas, L., & Minano, M. (2007). An Index for Quantifying Flocking Behavior 1, 2. Perceptual and motor skills, 105(3), 977-987. [doi:10.2466/pms.105.3.977-987]
RAO, A. S., & Georgeff, M. P. (1991). Modeling rational agents within a BDI-architecture. Knowledge Review, 91, 473-484.
REYNOLDS, C. W. (1987, August). Flocks, herds and schools: A distributed behavioral model. In ACM Siggraph Computer Graphics (Vol. 21, No. 4, pp. 25-34). ACM. [doi:10.1145/37402.37406]
SALGE, C., & Polani, D. (2011). Digested information as an information theoretic motivation for social interaction. Journal of Artificial Societies and Social Simulation, 14(1), 5: https://www.jasss.org/14/1/5.html. [doi:10.18564/jasss.1699]
SANTOS, I. R., & Santos, P. R. (2007). Simulation metamodels for modeling output distribution parameters. In Simulation Conference, 2007 Winter (pp. 910-918). IEEE. [doi:10.1109/WSC.2007.4419687]
SCHELLING, T. C. (1978). Micromotives and macrobehavior. WW Norton & Company.
SCHRAM, A. (2005). Artificiality: The tension between internal and external validity in economic experiments. Journal of Economic Methodology, 12(2), 225-237. [doi:10.1080/13501780500086081]
SHOHAM, Y. (1993). Agent-oriented programming. Artificial intelligence, 60(1), 51-92. [doi:10.1016/0004-3702(93)90034-9]
SILVA, V. D., Kroening, D., & Weissenbacher, G. (2008). A survey of automated techniques for formal software verification. Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions on, 27(7), 1165-1178. [doi:10.1109/TCAD.2008.923410]
STEARNS, D. E. (1998). Logistics simulations metamodel for F404-GE-400 engine maintenance (Doctoral dissertation, Monterey, California. Naval Postgraduate School).
STONEDAHL, F., & Wilensky, U. (2010). Finding forms of flocking: Evolutionary search in ABM parameter-spaces. In Multi-Agent-Based Simulation XI (pp. 61-75). Springer Berlin Heidelberg.
SYMONDS, P., Taylor, J., Chalabi, Z., & Davies, M. (2015). Performance of Neural Networks Vs. Radial Basis Functions When Forming A Metamodel For Residential Buildings. World Academy of Science, Engineering and Technology, International Journal Of Civil, Environmental, Structural, Construction And Architectural Engineering, 9(12), 1446-1450.
THERNEAU, T. M., & Atkinson, E. J. (1997). An introduction to recursive partitioning using the RPART routines.
VO, D. A., Drogoul, A., & Zucker, J. D. (2012, February). An operational meta-model for handling multiple scales in agent-based simulations. In Computing and Communication Technologies, Research, Innovation, and Vision for the Future (RIVF), 2012 IEEE RIVF International Conference on (pp. 1-6). IEEE. [doi:10.1109/rivf.2012.6169849]
WAGNER, G. (2003). The Agent–Object-Relationship metamodel: towards a unified view of state and behavior. Information Systems, 28(5), 475-504. [doi:10.1016/S0306-4379(02)00027-3]
WOLD, S., Esbensen, K., & Geladi, P. (1987). Principal component analysis. Chemometrics and intelligent laboratory systems, 2(1), 37-52. [doi:10.1016/0169-7439(87)80084-9]
WOOLDRIDGE, M., Jennings, N. R., & Kinny, D. (2000). The Gaia methodology for agent-oriented analysis and design. Autonomous Agents and multi-agent systems, 3(3), 285-312. [doi:10.1023/A:1010071910869]
YANG, W. X. (2004). An improved genetic algorithm adopting immigration operator. Intelligent Data Analysis, 8(4), 385-401.
