Introduction
Extortion is the demand for money using the threat of violence. An extortion racket is the continuous, regular and systematic extortion of several victims by a criminal or (more usually) a criminal organisation. Extortion is different from other property crime such as burglary or fraud because of the long term, explicit and exploitative relationship between perpetrator and victim. It is also different from blackmail because extortion is often endemic in a community or even society.
There are some well-known examples of protection or extortion rackets. Probably the best known is the Italian Mafia, both in Italy (in particular the South and Sicily) and in migration countries such as the US and Germany (Gambetta 1994). In 2012 the estimated turnover of the Italian Mafia was thought to be around £116bn, which, at 7% of GDP, makes it Italy’s biggest business[1]. By definition, extortion racketeering is an essential feature of a Mafia Type Organisation (MTO), distinguishing MTOs from other organised crime groups (La Spina 2008). Other MTOs include the Russian Mafia (Smith & Varese 2001), motorcycle gangs such as the Hell’s Angels and Bandidos, the Yakuza and a variety of gangs and drug cartels in Central and South America (Anzola & Elsenbroich 2015).
One of the most prevalent scientific approaches to extortion rackets is a formalisation of the interdependent choices of extorters and entrepreneurs in game theory (such as Gambetta 1994; Konrad & Skaperdas 1998; Smith & Varese 2001). This formalisation adopts the rational choice paradigm underlying much of criminology (Becker 1968). But whereas usually the focus is on the decision of the criminal to commit a crime given a probability of punishment if caught, here the focus is the victim’s decision to pay given the probability of being punished by an extorter. This punishment probability is influenced by exogenous factors such as the presence of police (so that Mafiosi are deterred from punishing) and, in some cases, the presence of fakers. Fakers are agents posing as Mafiosi and demanding payment but who will not punish resistors, due to fear of detection by police and real Mafiosi. We discuss these approaches in more detail in Section 2.
Inspired by this approach we develop an agent-based model (ABM) of extortion racketeering to understand the dynamic interdependencies between punishment (for both deterrence and reputation) and levels of acquiescence in a society. The agent behaviour in our model also uses the rational paradigm. However, we take advantage of the dynamic nature of ABMs to allow the memory of a punishment to fade over time. This contrasts with the Game Theory approach of examining the rational decision for di erent fixed probability values.
The ABM is presented in two steps. The first is a discussion of an implementation that, like Game Theory, focusses only on information obtained through direct experience; perceived probability of punishment is high immediately a er being punished but reduces over time. The model is then extended to allow the entrepreneur’s decision to comply or resist an extorter to also depend on events in their neighbourhood. This model is an intuitive implementation of reputation for the Mafia. The neighbourhood model requires much lower levels of punishment, which is more consistent with real life extortion racket phenomena.
This paper is structured as follows: In Section 2, we discuss major game theoretic approaches to extortion rackets (developed in Konrad & Skaperdas 1998; Gambetta 1994; Smith & Varese 2001). In Section 3, we discuss existing agent-based models of extortion and related dynamics, such as reputation and deterrence. In Section 4, an agent-based model inspired by the game theoretic framework from Section 2 is presented and analysed. In Section 5, this agent-based model is extended to incorporate social aspects of Mafia reputation and the two approaches compared. In Section 6, we conclude and discuss future work.
Game Theoretic Approaches to Extortion Rackets
The extortion situation intuitively reads as an iterated decision tree. The extorter demands money from an entrepreneur, the entrepreneur decides to pay or not to pay, and then the extorter decides whether to punish. The demand and decision occurs multiple times between a paired extorter and entrepreneur. In the game theoretic literature on extortion rackets (Konrad & Skaperdas 1998; Gambetta 1988, 1994; Varese 1994, 2001), the payment decision depends on the entrepreneur’s expectation of being punished for refusal to pay. If the payment demand is smaller than the expected loss from damage (that is, the probability of punishment multiplied by the damage cost), the entrepreneur will pay the extorter. Usually protection demands are small and punishments potentially very high (such as arson attacks on the shop taking away the livelihood). This means the important variable to assess for the entrepreneur is the probability of being punished. Two broad approaches can be distinguished in the literature.
The first approach (Konrad & Skaperdas 1998) treats the probability of punishment as endogenous, arising from the efforts invested by extorters and police. The game described in Konrad & Skaperdas (1998) formalises the interdependent choice between the three actors: the extorter, the entrepreneur and the police. The approach sets out to find equilibria for investment into punishment by extorters and efforts by the police to undermine extortion. Entrepreneurs simply calculate the payoff compliance or resistance, given levels of police presence and e ort compared to extorter aggression.
On the other hand, Gambetta (1994) and Smith & Varese (2001) have levels of police presence as an exogenous variable, focussing instead on the extorter-victim interaction. The game originates with Gambetta (1988) who uses it as a setting to discuss reputation, signalling and piracy of symbols. Extorters are split into two types, the real Mafiosi and fakers. Mafiosi establish a reputation for punishing resistance and fakers can free-ride on this reputation if they manage to signal as belonging to the real Mafia. Entrepreneurs decide whether to pay or not depending on their individual expected punishment probability calculated from whether they think an extorter is a faker or not, given knowledge of the level of police presence. High police presence lowers the probability of a Mafioso to punish and also the probability of fakers to extort.
The game has been formally analysed in detail in Smith & Varese (2001). Police presence is either high or low, determined probabilistically. From the construction of the various risks and costs, both Mafiosi and fakers demand in some situations, but only Mafiosi punish resistance and only when police presence is low.
The single iteration Mafia-faker game results in three equilibria. Region 1 describes situations with a high probability of high police presence. Entrepreneurs never pay as they feel safe from punishment due to the high police presence. Thus, fakers do not even attempt extortion as there is no benefit. Only Mafiosi demand, and they only punish refusal when police presence is low (a low probability occurrence). Region 2 has a lower probability of high police presence and hence higher probability that refusal will result in punishment if the extorter is a Mafioso. In this region, the cost of punishment to the entrepreneur is high and entrepreneurs believe that extorters are (mostly) Mafiosi, so they pay the relatively small demands of all extorters. This provides an opportunity for fakers to free-ride on the Mafia reputation and the incentives for fakers partly depend on the risk of encroaching on Mafia territory. As entrepreneurs always pay, they are unable to use their own experience to recognise whether extorters are real Mafiosi.
Region 3 is characterised by uncertainty and leads to the most interesting behaviour. While Mafiosi always demand, fakers also demand sometimes. Entrepreneurs pay sometimes, depending on the interplay of their belief that an extorter is a faker and the levels of police presence. Refusal only leads to punishment where the extorter is a Mafioso and police presence is low. Fakers are more likely to make demands when their expectation of being paid is higher; because entrepreneurs believe that extorters are Mafiosi, police presence is low (so there is risk of punishment) or demand amount is small (so lower cost than the risk of punishment).
These regions are also important in describing the repeated version of the game, analysed in detail in Smith & Varese (2001) and the inspiration for the ABM presented here. While the three regions are substantially similar to the single iteration situation, behaviour near the borders is changed once future interactions are also considered. In particular, there is a stronger incentive for Mafiosi and fakers to extort and punish, and a stronger incentive for entrepreneurs to reject the demands. However, entrepreneurs also recognise the stronger incentive for extorters to punish, which creates a countering influence to pay. For extorters, the expensive decision to risk detection (by police or Mafia for fakers, or by police for Mafia) is potentially repaid with two payments. For entrepreneurs, the risk of punishment for refusal is being judged against the cost of two payments. That is, an expensive risk is spread because it establishes behaviour for two turns, or acts as a "signal of type" (Smith & Varese 2001, 367). Instead of the three regions, these competing incentives lead to six equilibria in the two iteration game. In contrast with the single turn game, even fakers will punish a refusal in one of the regions.
As well as identifying these equilibria, Smith & Varese (2001) noted counterintuitive results concerning levels of violence. In particular, violence is a sign of incomplete control by the Mafia; violence only occurs where entrepreneurs refuse a demand. This may arise either because they know police presence is generally high (region 1) or believe the extorter could be a faker (region 3). With low police presence, there is no violence once the Mafia has established control (by eliminating fakers). Violence then erupts from shocks to the system, such as changes in police presence or the size of demands.
Agent-based Modelling Approaches to Extortion Racketeering
In this paper we develop an ABM of extortion racketeering using the Mafiosi-faker game described above as a conceptual base.
There are three published ABMs directly concerning extortion racket dynamics. Sonzogni et al. (2011) presents a model to investigate the social and economic influences on extortion of entrepreneurs, recruitment to a criminal organisation and judicial punishment on the social entrenchment of extortion rackets. It includes individual labour market conditions and risk perception, combined with a social influence mechanism based on imitating economic success. The model is used to investigate the combined effect of state punishment of, and recruitment to, a criminal organisation.
Nardin et al. (2016) describes a model focussed on extortion racketeering in Sicily and southern Italy. Based on the cognitive agent architecture Emil-A, developed to understand normative behaviour, the model represents in particular cultural dimensions of extortion racketeering. It explicitly investigates a change in culture in Italy of both law enforcement and bottom-up behaviour change through normative communication.
Troitzsch (2014, 2015) presents a model to investigate the effects of extortion racketeering on the distribution of wealth in society and the interactions between state, civil society and criminal organisations regarding compliance, resistance, denunciation and prosecution of criminals. Law enforcement plays a major role in this model as policemen are in charge of arresting Mafiosi and interact with entrepreneurs that denounce extortion. The model simulates effects of extortion racket at the systems level, using thresholds and probabilities. This implementation allows a systematic exploration of the parameters potentially relevant to an extortion racket, such as propensity to pay. The model suggests that the main influence on the success of an extortion racket is the effectiveness of prosecution of extorters by the state, followed by the probability of victims to denounce extorters.
Agent-based modelling has also been used to examine deterrence in social compliance phenomena more generally, outside of the extortion racket application. Mafia punishment to induce payment through fear is a specific application of deterrence models, which have been widely used in ABM, for example to engender pro-social behaviour with utility maximising agents in models of social norms (Elsenbroich & Gilbert 2013, Chapter 3). ABM has implemented deterrence with punishment in a variety of ways, with di erent punishment structures (e.g. central or distributed) and various cognitive mechanisms (e.g. memory of past experiences or perceiving whether others are punished).
A model of tax evasion developed and analysed in van Baal (2004) includes punishment in a way that is most similar to its role in extortion dynamics as we discuss here. The model uses the cellular automata approach, with each location on a grid representing one agent. Agents situated next to each other are neighbours and in each others’ social networks. At each step, agents decide whether to evade tax or not. Tax evasion without getting caught has a positive payoff, while norm compliance has a payoff of zero and being found out to evade tax is sanctioned by a negative payoff (a cost). A law enforcement agency checks agents at random, representing the probability of getting caught through audit. The agent bases its decision on whether the expected payoff of crime is greater than the expected payoff for compliance. The expected payoff is calculated, following Becker (1968), by weighing the potential payoff of transgression against the probability and cost of getting caught.
Agents commit a crime if they perceive crime as profitable. The payoff and cost of transgression is known to the agent. The probability of being audited is estimated by the agent from its social network. The model shows that higher sanctions and higher audit probabilities lead to higher levels of compliance.
This paper draws on the game theoretic and ABM deterrence literatures to operationalise a Mafia-faker conceptual framework for ABM. The narrative of the Italian Mafia is transferred from the original game theory article (Smith & Varese 2001) and what our model sets out to show is that a model of an extortion racket that does not take into account the neighbourhood effects on deterrence (and Mafia reputation by proxy) misses one of the most important aspects of extortion racketeering. The model allows for a detailed analysis of the role of punishment to be extended to a community setting, where entrepreneurs learn from the experience of others, as well as their own.
An Agent-Based Model of the Mafia-Faker-Game
We present an ABM of the interaction game between Mafiosi, fakers and entrepreneurs. The model consists of two kinds of agents: extorters and entrepreneurs. Extorters can be real Mafiosi or fakers. The difference between Mafiosi and fakers is that Mafiosi punish resistance whereas fakers, whilst making extortion demands just like Mafiosi, do not punish. Police presence is deliberately left out of this model as it is an exogenous influence on punishment probability (following Smith & Varese 2001) rather than an active agent. This means the model focusses on the equilibrium regions in which entrepreneurs make decisions uncertain of the situation (Regions 2 and 3 in Section 2).
Entrepreneurs are the targets of extortion demands by both fakers and Mafiosi. Extorted entrepreneurs decide in each simulation step whether they pay the pizzo (the amount of the payment requested) or start resisting. An ABM to model the dynamics of extortion rackets needs to implement the conditions under which entrepreneurs pay or resist (decision mechanism), punishment of an entrepreneur by the Mafia in case of resistance and how this punishment influences an entrepreneur’s future decision making. Consequently, factors to be operationalised include an extorter’s reputation to punish and the entrepreneur’s fear.
If all extorters are real Mafiosi (and police are ineffective), anyone approached should pay as punishment costs exceeds the pizzo and the probability of punishment is very high. In the game theoretic analysis the faker introduces incomplete knowledge into the game (Gambetta 1994), replacing the certainty of being punished with a probability. This probability is the essential feature of the Mafia-faker game. The decisions of the entrepreneurs depend on how they assess the probability of being punished and the expected damages arising from punishment by the Mafia:
| $$ \label {eqRule} \text{Decision: } \begin{cases} \mbox{If } pP \times D \geq E, & \mbox{pay} \\ \mbox{otherwise}, & \mbox{refuse}, \end{cases}$$ | (1) |
Game theory itself does not provide a cognitive mechanism through which an agent might obtain the punishment probability. Instead, expected behaviour is presented for different regions of the probability space. If the agent assesses the probability at some value, it adopts a specific behaviour (pay or resist) based on that assessment. The adopted behaviour is the option calculated to maximise the expected payoff, the probability of an outcome multiplied by the payoff of that outcome for each behaviour choice.
In an ABM, the agent perceives its environment and chooses a behaviour based on a combination of that environment and its own characteristics. In the model presented here, the perceived punishment probability is determined by an entrepreneur’s past experience on refusing to pay. If the refused extorter is a Mafioso, the entrepreneur may get punished, if it is a faker, there will be no punishment. If an entrepreneur is punished, its perceived punishment probability becomes 1. This is then divided by 1.1 (representing a decay of 0:09) each step the entrepreneur is not punished as the agent ‘forgets’ about the trauma of being punished and increasingly wishes to reassess the situation. Input parameters in this model are the territory of an extorter (the extorter-radius), some financial inputs (the amount of money requested (pizzo) and the damaged incurred by an entrepreneur if it is punished (damages), the overall number of entrepreneurs and the number of Mafiosi and fakers.
One additional input needs to be discussed in a little more detail. The ability of Mafiosi to punish resistant entrepreneurs is dependent on the wealth of the Mafia being in excess of the cost of punishing. In the experiments, the cost is varied at 1, 300 and 1000. Although a punishment has some actual monetary cost associated, like the gasoline needed for the arson attack, the cost represents the disutility associated with the risk of being arrested by the police. Thus, a level of 1 means the Mafia has almost total impunity, 300 means there is some cost associated and 1000 stands for a relatively high level of authority interference. These particular values were chosen to demonstrate di erent patterns in the model results. At 300, punishment is regular but not constant, and Mafiosi were successfully undermined at 1000 (corresponding to high police presence).
The model is initialised with 1000 entrepreneurs randomly located on a 33 x 33 grid. The appropriate number of extorters are located in a fixed circle of radius 5 around the centre of the grid. The extorter-radius determines the area of each extorter’s territory. Territories overlap, but each entrepreneur is extorted by at most one extorter. Extorters are initialised with 1000 units of capital. Entrepreneurs have a monthly income, normally distributed with a mean of 500 and a standard deviation of 100. Every 30 time steps entrepreneurs are paid their monthly income and extorters are paid their pizzo by the entrepreneurs they extort.
Every time step, each extorter chooses a random entrepreneur within their territory and if the entrepreneur is not already extorted, they make an extortion request (if the entrepreneur is already extorted nothing happens). In response, the entrepreneur decides whether to pay. In addition, entrepreneurs who are already being extorted reassess whether they will continue to pay. In both cases, the decision to pay is based on the expected probability of punishment as described at Equation 1 above. If the extorter is a Mafioso and has su icient resources, it chooses an entrepreneur to punish from those resisting.
Experimentation focusses on the analysis of how the extorter radius and ratio of Mafiosi or fakers together influence levels of resistance and the number of punishments. The financial inputs are kept constant, the pizzo at 100 and the potential damages an entrepreneur expects at 1,000,000. We vary the number of extorters overall, the ratio of Mafiosi and fakers, the extorter radius and, as discussed above, the cost of punishment for the Mafia. Table 1 describes the parameter combinations, with 126 simulations.
| Parameter | Range |
| Probability Update Type | Memory |
| Mafiosi only | 3, 5, 7, 10 |
| Mixed Mafiosi:fakers | 7:3, 5:5, 3:7 |
| Extorter Radius | 1, 2, 3, 4, 5, 10 |
| Punishment Cost | 1, 300, 1000 |
Results and Analysis
Analysis focussed on how resistance and punishment are influenced by changes in the extorter population, extorter radius, and cost of punishment. To eliminate run-in effects, model results ignore the first 500 time steps and are reported as the average value over the following 1000 time steps.
The model produces a broad range of levels of resistance, from 1% to 100% of entrepreneurs approached by extorters. Resistance is clearly related to the extorter radius, cost of punishment for the Mafia and the presence of fakers (see Figures 1 and 2). A full interpretation also relies on the interplay between levels of resistance and punishment.
Focussing on the Mafia only scenarios (Figure 1), as the cost of punishment increases and their territory expands, the Mafia have too few resources to retain control and resistance increases. With a punishment cost of 1000, each punishment consumes the resources obtained from 10 acquiescent entrepreneurs and there is insufficient revenue to regularly punish resisters. Unpunished resistance leads to lower revenue and worsens the problem (from the Mafia perspective), with the consequent overall behaviour of no punishment and total resistance for any extorter radius. At the other extreme, only a single acquiescent entrepreneur is required to allow a Mafioso to punish at every time step if the punishment cost is 1. The Mafia are able to punish as frequently as required and maintain control until their territory becomes too large. At extorter radius of 10, the constraint of a single punishment per time step (per Mafioso) leads to imperfect control. Despite continual punishment (Figure 1, right), a significant proportion of the entrepreneurs are resisting at any one time step (Figure 1, left) in those scenarios with 3, 5 or 7 Mafiosi. At 10 Mafiosi, however, the territories overlap sufficiently that there are fewer entrepreneurs per Mafioso and they are able to maintain control and reduce the punishment level.
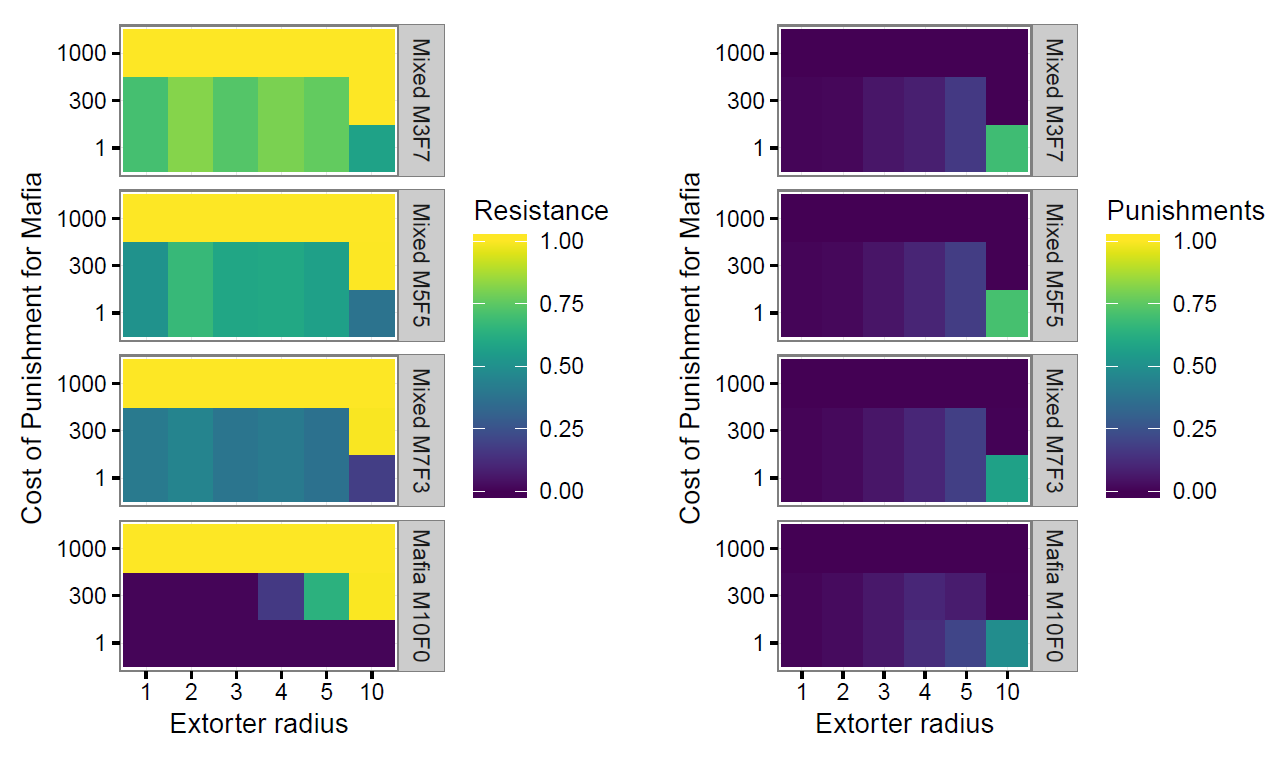
The presence of fakers increases entrepreneur resistance and, for the scenarios with punishment cost of 300, increases the punishments that must be made by the Mafia (Figure 2). The increased resistance is straightforward, many entrepreneurs are in the territory of fakers but not Mafia and, once they realise they are not being punished, they continue to resist.
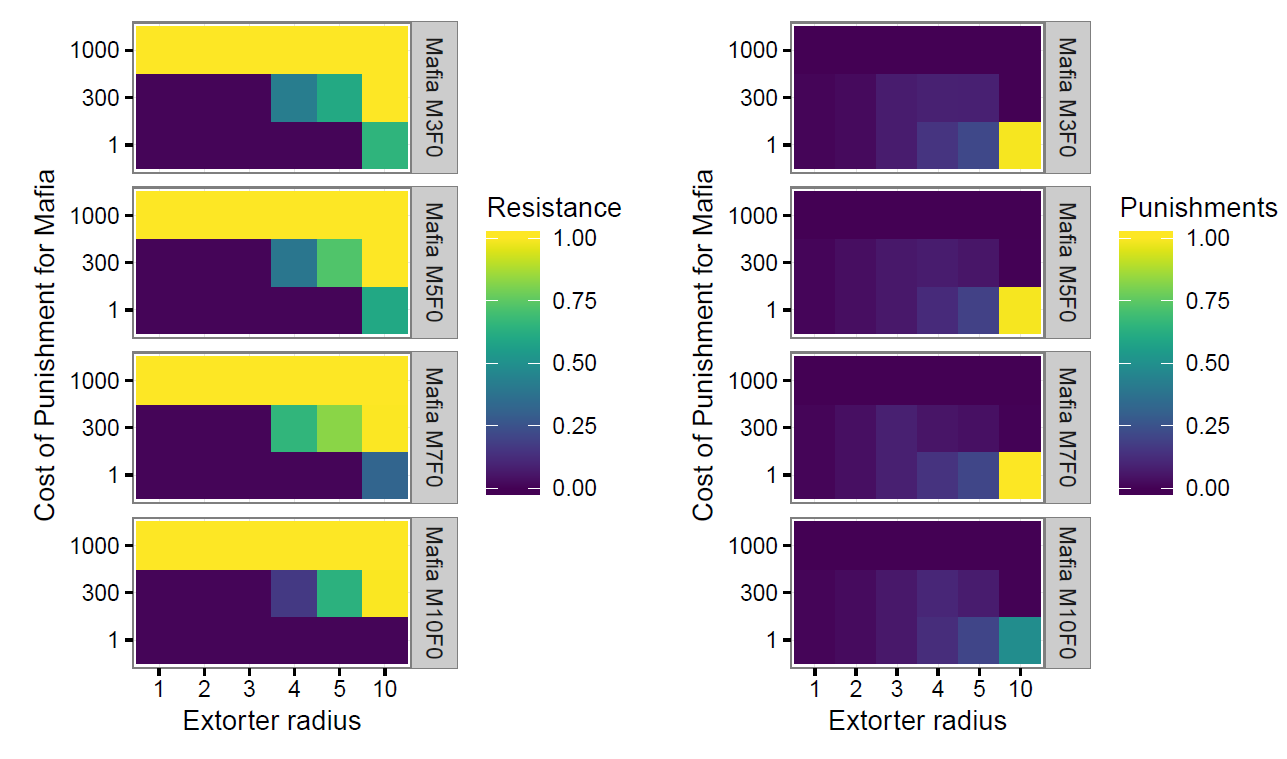
The punishment effect is more interesting. The introduction of fakers makes no difference in the number of punishments per Mafioso per time step where the punishment cost is 1 or 1,000. At a cost of 1, Mafia are able to punish whenever they like and adding fakers does not change the frequency they need to punish to maintain control. At a cost of 1,000, Mafia do not have the resources to punish once their initial allocation has been consumed and adding fakers does not add to their resources so they are also unable to punish in the faker scenarios.
The additional punishments in the faker scenarios for punishment cost of 300 arise from the particular interaction of entrepreneur density and different financial elements in the experiments. The combination of decay rate (1 11:1) in assessment of punishment probability, pizzo size (100) and damages arising from punishment (1,000,000) means that an entrepreneur resists 102 time steps a er being punished (by equation 4.3), during which time they make 3 (or sometimes 4) payments and therefore generally provide sufficient resources to pay for only one punishment. Having been punished, the extorter will acquiesce the next time they are approached and will continue to pay for the remainder of 102 time steps after the punishment. With different parameter variables, the same behaviour would occur but at a different punishment cost. The general principle is that at a moderate punishment cost, the territory of each Mafioso must be small enough to support regular revisits. For the Mafia only scenarios, the territory is too large once extorter radius reaches 4, and financial resources constrain the number of punishments (compare cost 300 cells to cost 1 cells at (Figure 1 right). However, when sharing entrepreneurs with fakers, the Mafia territories are reduced and they have sufficient resources to punish whenever they require for radius 4 and 5 but not radius 10 (Figure 2 right).
The model we have presented recreates some of the results of the game theoretic model. In particular, resistance is high when there is a high punishment cost (equivalent to high police presence) and, at lower punishment cost, resistance increases as the proportion of fakers increases. In addition, violence (punishment) increases as the Mafia try to exert control over a greater number of entrepreneurs. However, this model falls short of replicating one of the most stable stylised facts of extortion rackets: high levels of compliance with low levels of punishment. This combination only occurs for small extorter territories. In this model, deterrence of entrepreneurs is implemented in a purely individualistic way using their memory of being punished, and the Mafia must immediately punish resisters to keep control of a territory. This is costly and leads to Mafiosi ‘running out of resources’ and loss of control. In the next section, we extend the model to implement a reputation mechanism for Mafiosi.
An Agent-based Model of Mafia Reputation
The presented ABM applies a strongly individualistic interpretation of deterrence, chosen to stay as close as possible to the game theoretic model of Smith & Varese (2001). In this section, we develop an ABM that allows entrepreneurs to also gain information from the experience of their neighbours. That is, an entrepreneur is not only deterred by what happened to him or herself but also by experiences of others nearby. The individualistic memory based calculation of the punishment probability does not take this social aspect of deterrence into account.
In the extended model, the memory based calculation is replaced by a mechanism where the punishment probability is determined by the observation of punishment of others as well as personal experience. If an entrepreneur observes a punishment in a certain neighbourhood, its perceived punishment probability becomes 1, decaying each step the entrepreneur does not observe a punishment. The input parameters in this model are the same as above, i.e. extorter-radius, pizzo, damages and cost of punishment, number of Mafiosi, number of fakers, number of entrepreneurs, but in addition entrepreneurs have a neighbourhood-radius, determining the size of the neighbourhood in which observed punishments affect their perceived punishment probability.
The neighbourhood based calculation is expected to enhance the deterrence of each punishment as it not only deters the punished entrepreneur but also those in that are closer than the neighbourhood radius (see Figure 3). This socially enhanced deterrence of punishments should lead to:
- lower levels of resistance, in particular as the neighbourhood radius increases;
- lower levels of punishment for similar levels of resistance; and
- easier free-riding for fakers on the Mafia’s reputation.
We run similar scenarios as in the memory case discussed in Section 5 but, in addition to varying the extorter-radius, we also vary the neighbourhood-radius. Punishment cost is set to 1,000 for all experiments, which is the value at which the previous model had no punishments and fully resistant entrepreneurs because the Mafia had insufficient resources to maintain control. Table 2 describes the parameter combinations, with 504 simulations.

| Parameter | Range |
| Probability Update Type | Neighbourhood |
| Mafiosi only | 3, 5, 7, 10 |
| Mixed Mafiosi:fakers | 7:3, 5:5, 3:7 |
| Extorter Radius | 1, 2, 3, 4, 5, 10 |
| Neighbourhood Radius | 1, 2, 3, 4, 5, 10 |
| Punishment Cost | 1, 1000 |
Results and Analysis
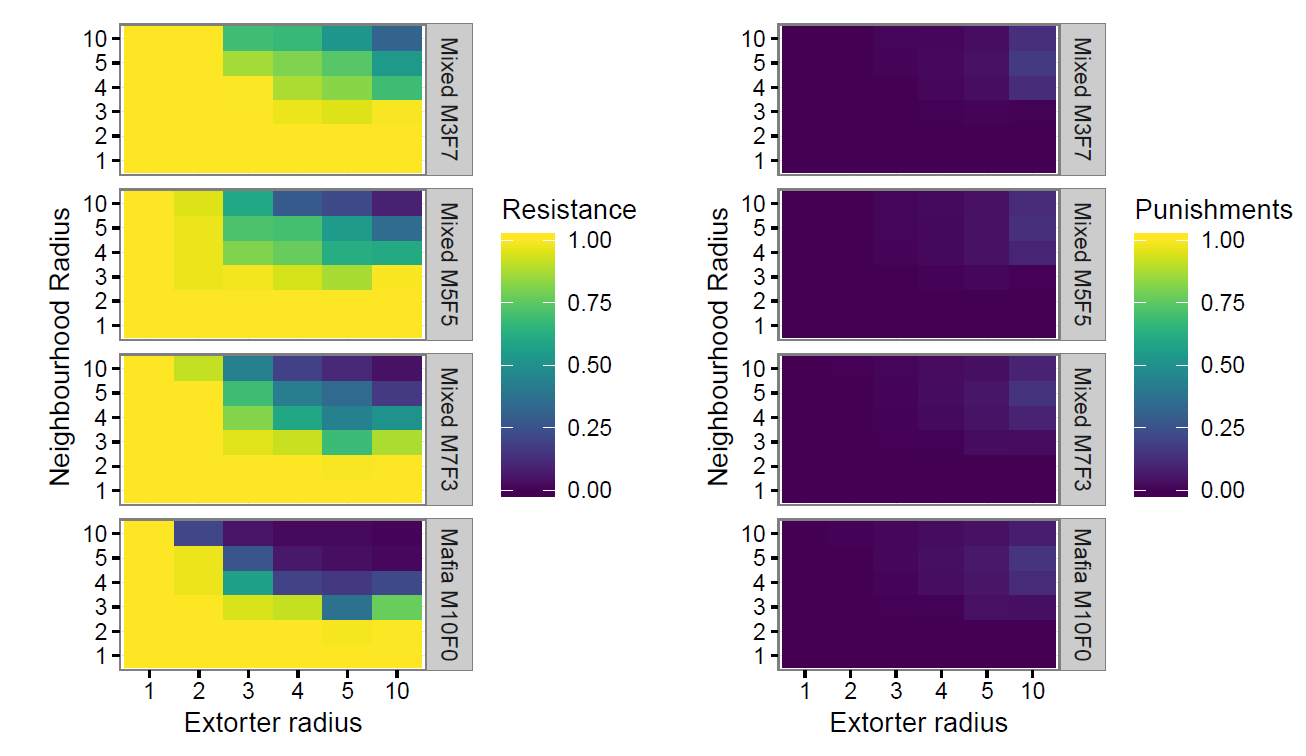
As for Section 5, the presented results are the average value over 1,000 time steps, after discarding the first 500 to eliminate run in effects. In Figures 1 and 2, the 1,000 punishment cost scenarios had full resistance (yellow) and no punishments (blue) for all extorter combination and extorter radius combinations (top lines of each panel). In the extended model (Figures 4 and 6), this same pattern is observed for neighbourhood radius up to 2, but begins to break down as neighbourhood radius increases.
For the Mafia only scenarios (Figure 4), the constraining factor is the resources available for punishment, as can be seen by the existence of at least some resistance combined with punishment levels below 1. This constraint controls the model behaviour; a larger extorter territory allows greater revenue but also requires more punishments. As the neighbourhood radius increases, each punishment potentially influences the behaviour of a larger number of entrepreneurs and therefore allows control over a greater territory.
For the particular experiment values, resistance generally decreases as the number of Mafiosi increases. However, this is not true for extorter radius of 2, where resistance is high for the 3 and 10 Mafiosi scenarios and lower for the 5 and 7 scenarios. At 3 and 10 Mafiosi, there are too few entrepreneurs in each territory to provide resources for punishment because the territories are, respectively, too small or too overlapping.

For all Mafia only scenarios, resistance decreases and punishment increases as extorter radius increases, and resistance decreases with little change in punishment as neighbourhood radius increases. As extorter radius increases for a fixed neighbourhood size, the pizzo revenue increases and enables more punishment. Provided the entrepreneurs are able to observe sufficient nearby punishments (neighbourhood radius of at least 3), these punishments induce enough acquiescence to fund further punishments. As neighbourhood radius increases for a fixed extorter territory, each punishment is observed by more entrepreneurs and resistance decreases, which increases extorter revenue and funds a small increase in punishments.
A different pattern emerges where the Mafia don’t need to rely on multiple entrepreneurs to provide the resources for punishment. With punishment cost set to 1, the number of punishments consistently decreases as the neighbourhood increases (Figure 5, right). That is, the need to punish consistently decreases if there is no resource constraint. Resistance shows a different pattern, decreasing for initial increases in neighbourhood size, but then increasing where the neighbourhood radius is larger than the extorter radius (Figure 5, left). This increase arises because all the entrepreneurs are influenced by the same punishment and thus become resistant again in the same time step. Where there are few (and therefore distant) extorters, the synchrony leads to high resistance at regular time steps, which is resolved with a single punishment on each occasion.

As with the initial model, the presence of fakers increases entrepreneur resistance but there is no effect on punishment levels compared to the Mafia only scenarios (Figure 6). Some entrepreneurs are in the territory of fakers but not Mafia and, if their neighbourhood radius does not extend to the Mafia territory, they cannot observe punishments and continue to resist. As the neighbourhood radius increases, there is a smaller difference between the Mafia only and mixed Mafia / faker scenarios.
One consequence of the Mafia punishing in the mixed Mafia and faker scenarios is that entrepreneurs may acquiesce to a faker’s extortion attempt. As fakers do not bear the cost of punishment, fakers who successfully use the Mafia’s reputation to extort can accumulate greater wealth than Mafia. At time step 1,000, the average wealth of fakers is between 1.2 and 101.7 times that of the Mafia. This ratio increases as extorter radius increases but has no clear relationship with neighbourhood radius (Figure 7).

Conclusion and Future Work
We have presented two ABMs of extortion rackets inspired by the game theoretic analysis of extortion by Gambetta (1994) and Smith & Varese (2001). This approach uses a three player game consisting of a Mafioso, a faker and an entrepreneur, with the latter having some belief about probability of being punished for resisting extorter attempts. The analysis identified regions of punishment probability space with different entrepreneur decisions about resisting and extorter decisions to punish. A key result is that there are regions with high compliance and low punishment, with high levels of violence indicating loss of Mafia control. However, the game theory framework does not provide a mechanism by which entrepreneurs can assess punishment probability, it is exogenous.
The ABM were implemented with the same three active kinds of agents; Mafiosi, fakers and entrepreneurs. The entrepreneur decision-mechanism calculates the utility of complying or resisting, determined by the entrepreneur’s belief about the probability of being punished and the impact of the punishment.
In the first model the punishment probability belief is calculated using a memory based mechanism; if an extorter is punished, it will have a high punishment probability, slowly decreasing over time. The model recreated most of the game theoretic results, showing how increasing punishment is a sign of Mafia weakness and also showed the detrimental effect fakers have on the Mafia reputation. It failed, however, to recreate one of the most stable stylised fact of extortion rackets: the combination of low levels of resistance and low levels of punishment. In order to achieve low resistance levels Mafiosi had to punish constantly. Further, if punishment is costly (representing risk of police detection), the Mafia may collect insufficient resources from the acquiescent entrepreneurs to punish the resisters and a spiral of increasing resistance occurs.
We then extended the memory based ABM by an alternative decision-mechanism based on observing punishments in the neighbourhood rather than only relying on personal experience. This model implements some social aspects of deterrence and reputation through social amplification Kasperson et al. (1988) of the effect of each punishment. This model resulted in much more realistic extortion behaviour, where low levels of resistance are paired with low levels of punishment.
Although the memory mechanisms leads to results with high levels of acquiescence, it is clear that social transmission of reputation renders punishment much more effective. One consequence of this extension, however, is that fakers who are sufficiently close to a Mafioso are able to take advantage of the Mafia propensity to punish and extort without the cost of punishing. Even with non-overlapping extorter radii, if the neighbourhood observation radius is large enough, fakers can survive in the shadow of the Mafia.
The models presented are quite simple and abstract, but allow the exploration of some fundamental dynamics of punishment, reputation and resistance. They suggest that some form of reputation is required in order to achieve compliance without substantial punishment. In future work we will implement extensions on the same level of abstraction that examine different social structures in which the agents operate. In particular we will investigate ways in which extortion rackets can be undermined or fought by both bottom up strategies, such as normative reasoning and collective reasoning spreading resistance and top down interventions such as police pressure and surveillance.
Acknowledgements
This research has received funding from the European Union Seventh Framework Programme (FP7/2007D2013) under grant agreement no. 315874 ( http://www.gloders.eu, Global Dynamics of Extortion Racket Systems).Notes
- Cf. http://news.bbc.co.uk/1/hi/world/europe/7724071.stm [accessed on 27/03/2015].
Appendix
The Model Code is reported in the pdf version of the article, which is downloadable by clicking on the PDF icon at the right of the article's title.References
ANZOLA, D. & Elsenbroich, C. (2015). A typology of extortion racket systems. Deliverable 1.3, Global Dynamics of Extortion Racket Systems.
BECKER, G. S. (1968). Crime and punishment: An economic approach. Journal of Political Economy, 76(2), 169–217. [doi:10.1086/259394]
ELSENBROICH, C. & Gilbert, N. (2013). Modelling Norms. Springer: Heidelberg.
GAMBETTA, D. (1988). Fragments of an economic theory of the mafia. European Journal of Sociology, 29(1), 127-145. [doi:10.1017/S0003975600005610]
GAMBETTA, D. (1994). Inscrutable markets. Rationality and Society, 6, 353–368. [doi:10.1177/1043463194006003005]
KASPERSON, R. E., Renn, O., Slovic, P., Brown, H. S., Emel, J., Goble, R., Kasperson, J. X. & Ratick, S. (1988). The social amplification of risk: A conceptual framework. Risk analysis, 8(2), 177-187. [doi:10.1111/j.1539-6924.1988.tb01168.x]
KONRAD, K. A. & Skaperdas, S. (1998). Extortion. Economica, 65(260), 461-477. [doi:10.1111/1468-0335.00141]
LA SPINA, A. (2008). Recent anti-mafia strategies: The Italian experience. In D. Siegel & H. Nelen (Eds.), Organised Crime: Culture, Markets and Policies. Springer, Dortrecht.
NARDIN, L. G., Andrighetto, G., Conte, R., Székely, Á., Anzola, D., Elsenbroich, C., Lotzmann, U., Neumann, M., Punzo, V. & Troitzsch, K. G. (2016). Simulating protection rackets: a case study of the Sicilian mafia. Journal of Autonomous Agents and Multi-Agent Systems. (pp. 1–31). [doi:10.1007/s10458-016-9330-z]
SMITH, A. & Varese, F. (2001). Payment, Protection and Punishment: The Role of Information and Reputation in the Mafia. Rationality and Society, 13, 349-393. [doi:10.1177/104346301013003003]
SONZOGNI, B., Cecconi, F. & Conte, R. (2011). On the interplay between extortion and punishment. An agent based model of camorra. In Computational Social Science Society of America Annual Conference (CSSSA 2011). Santa Fe, New Mexico.
TROITZSCH, K. G. (2014). Distribution effects of extortion racket systems. In Proceedings of Artificial Economics, LNEMS. Springer, Heidelberg.
TROITZSCH, K. G. (2015). Extortion racket systems as targets for agent-based simulation models. Comparing competing simulation models and empirical data. Advances in Complex Systems, 18, 5-6. [doi:10.1142/S0219525915500149]
VAN BAAL, P. (2004). Computer Simulations of Criminal Deterrence. The Federation Press.
VARESE, F. (1994). Is Sicily the future of Russia? Private protection and the rise of the Russian mafia. European Journal of Sociology, 35, 224-258. [doi:10.1017/S0003975600006858]
VARESE, F. (2001). The Russian Mafia: Private Protection in a New Market Economy. Open University Press. [doi:10.1093/019829736X.001.0001]
