Introduction
This paper introduces Polias, a new agent-based model of attitude dynamics, rooted in sociopsychological theories. Attitude is a central concept to study human behavior. As many constructs in psychology, there are several ways to define it. Broadly speaking, it is "an overall evaluation of an object that is based on cognitive, affective and behavioral information" (Maio & Haddock 2009, p.4). Allport also suggested that an attitude is a predisposition to act, being "a mental and neural state of readiness organized through experience, exerting a directive or dynamic influence upon the individual’s response to all objects and situations with which it is related" (Allport 1935). Thus, an attitude is an evaluative judgment, and it has a valence to express a positive (in favor), neutral or negative (disfavor) predisposition toward this object. It has also a valence, where one could slightly dislike spinach while another really hates it. Moreover, when several people are interested in an object, and exert a social behavior on this object (share it, exchange opinions about it, etc.), this object will be called (according to social psychology) a social object.
According to scientists in social psychology, the concept of attitude plays a major role in various mechanisms such as the construction of mental representation (e.g., Fazio 2007), self-maintenance (e.g, Steele 1988) or behavior (e.g., Fishbein & Ajzen 1981). This is the reason why Attitude dynamics is one of the trending topics in the field of social simulation (e.g., Castellano et al. 2009; Xia et al. 2010; Edmonds 2013).
However, Chattoe-Brown (2014) points out two critical shortcomings in existing works. First, at the microscopic level, most of the models are not grounded on actual social science theories on attitudes. Indeed, the majority of works are based on the bounded-confidence model (Deffuant et al. 2000; Hegselmann & Krause 2002) that sees attitude formation process as a black box. Second, on the macroscopic level, the studied sociological phenomenon are not confronted to any empirical data such as opinion polls results. These two points will be further discussed in next sections below.
In this paper, (1) we propose a model anchored on major theories in social psychology that articulates a cognitive and an emotional dimensions of attitudes, (2) we perform a functional analysis of the model’s behavior and (3) we calibrate the model’s parameters in order to reproduce real world opinion polls results given a reconstituted military scenario that took place in Kapisa (Afghanistan) between 2010 and 2012. Due to this application context, many examples given in the paper are from the military domain. However, the proposed model is general enough to be used in other context.
In the next section, we will first present attitude dynamics models in social simulation and review some related works in social psychology that constitute the foundation of our model. We will then present our model (section 3) and its functional properties (section 4). This model will be then investigated through a functional analysis and calibrated on a real world study case that we present in section 5.
Related Works
In this section, we discuss related works on attitude dynamics. We first present existing models in social simulation and we show how the definition of micro-founded models and validation based on empirical studies has developed recently. We then discuss existing models in social psychology that serve as the foundation of our own model.
Attitudes in social simulation
Many agent-based models of attitude treat the attitude formation process as a black box, and focus on how one individual’s attitude is influenced by others. The first models were inspired by statistical physics, with binary valued attitudes, and applied to voting (Galam 2008). They usually view opinions and attitudes as the same thing. Then models appeared with attitudes of continuous values, like the well-known bounded confidence model (Deffuant et al. 2000; Hegselmann & Krause 2002) , where two individuals (selected randomly) have attitude values close to each other (with a fixed threshold), each one modifying its attitude so that it gets closer to its peer’s (see e.g. for a review on these models Castellano et al. 2009). This is not a suitable approach for two reasons: 1) due to its black-box nature, bounded confidence models the consequences of attitude formation, not the formation process itself (the causes); 2) such models are not rooted in any socio-psychological theory, raising the question of their empirical plausibility (Chattoe-Brown 2014) .
There are however some agent-based models aiming at implementing socio-psychological elements. Urbig & Malitz (2007) take inspiration from Fishbein and Ajzen (1975; 2005), where an attitude is composed of different impressions that are made of two elements: beliefs (also called cognitions) about the presence of some attributes and evaluations of these attributes (Ajzen 1991). The attitude value is computed as the sum of the evaluations (that also includes a belief value) of the object’s features. The attitude revision is based on a variation of bounded confidence model, inheriting its shortcomings. Moreover, all the features contribute to the attitude computation and are equally accessible (regardless whether this information is recent or old, important or not for the individual), which contradicts experimental findings and bounded rationality (Simon 1955).
Kottonau & Pahl-Wostl (2004) go further in this approach by deeply anchoring their model on empirical studies in social psychology. The model simulates the dynamics of political attitudes among a population during an election campaign and the out coming voting behavior. The attitude formation process and the communication mechanisms are based on various human science theories such as memorization, confirmation bias and also Fazio’s attitude model (Anderson & Schooler 1991; Lord et al. 1979). Another contribution is the introduction of the concept of scenario: political parties stimulate the population through communication activities which intensities vary in time depending on a function given as a simulation parameter. For instance, a function can specify that advertising e orts are highly active at the beginning, at the end or constant over the campaign. This enables the comparison in effectiveness of different scenarios. However, a scenario is reduced to a continuous function, thus the model lacks expressiveness and fails to capture real world data such as the variety of communications’ contents, their varying impacts, the major events that occurred etc. Moreover, this model is not confronted to any empirical, quantified phenomenon (e.g. real world study case using actual election results or opinion polls during a campaign).
To overcome these shortcomings and attempt to answer Chattoe-Brown’s criticism (2014), we propose to anchor our agent-based model into social psychology. Following psychomimetism (Kant 1999, Kant 2015), we design our model in order to mimic and implement several socio-psychological theories, presented in the next section.
Attitudes in social psychology
According to the multicomponent approach (Rosenberg & Hovland 1960; Zanna & Rempel 1988; Eagly & Chaiken 1993), attitudes have three components:
- the cognitive component, referring to the beliefs, thoughts and attributes associated with the object. This is the cognitive part of the attitude formation, and many models based on cognitive judgment theories may apply. Typically, the subject will weigh the pros and cons, positive and negative consequences, and aggregate them.
- the affective component refers to feelings and emotions attached to the object. Linked to physiological reactions, triggered by the confrontation with the social object (or representation of this object), emotions affect the cognitive judgment in terms of information processing[1].
- the behavioral component is the link with past or future actions. Past actions influence present attitudes values: for instance making a donation in favor of a cause tends to reinforce attitudes toward it (Festinger 1957). Symmetrically, an attitude may influence future behaviors (e.g. when in the act of buying or voting).
However, the transition from an attitude to a behavior is not straightforward and has been externalized from the definition of the attitude (Simon 1955; Wicker 1969; Fishbein & Ajzen 1975; Fazio 2007). For this reason, our model will exclude the behavioral component of attitude to focus on cognitive and emotional processes.
There are many models of attitude formation and change proposed in social psychology, since the introduction of this concept in 1935 by Allport (for recent reviews, see e.g. Crano & Prisline 2006; Maio & Haddock 2009; Bohner & Dickel 2011). Models differ whether attitudes are stable entities stored in long-term memory (e.g., Fazio 2007), or, according to the constructionist view, "constructed on the spot" as evaluative judgments constructed from scratch, based on current available information (e.g., Schwarz 2007). The main argument in favor of the later is to account for attitude changes when context varies. However, as summed up by Fazio (Fazio 2007), there are many empirical evidences that contradicts the constructionist view: pre-existent evaluations and attitude values have an impact on attitude. Moreover, the importance of prior learning is not taken into account by the constructionist perspective. This is why we adopted in our model Fazio’s approach with attitudes stored in memory.
There is also a debate on the way information is processed to compute the attitude. For several models, including ELM (Petty & Cacioppo 1986) and HSM (Chaiken et al. 1989), a dual process underlies the attitude formation, where arguments (in a message) and external cues associated to the message (like source expertise) are processed differently. Also, in ELM and HSM, two processes coexist depending on the motivation (high or low) and the ability (high or low) to process information. In the APE model (Gawronski & Bodenhausen 2006), two mental processes coexist: an associative evaluation (like a connectionist network) that is implicit, occurs unintentionally and without awareness of the subject, and an explicit process, intentional and with awareness, which is based on logical reasoning. Further research works, including (Fazio 2007; Petty et al. 2007), suggest that there is only one unique process, and the differences between implicit and explicit results mainly on two different ways of measuring the attitudes (Fazio 2007). Again, we will take Fazio’s side, as there are many experimental evidences that support the unified perspective (Fazio 2007; Bohner & Dickel 2011).
Thus, to build our agent-based model, we departed from the object-evaluation associations framework introduced by Fazio and his colleagues in 1995, where attitudes are "associations between a given object and a given summary evaluation of the object-associations that can vary in strength and, hence, in their accessibility from memory" (Fazio 2007). The evaluation process we propose combines analytic and emotional processes, it is based on available information about the social object and past emotional experiences with it. The varying strength of the association enables variability in the attitudes for one person and across several individuals as well. The stronger the association is, the more it will impact other cognitions, behaviors and social processes. As stated by Fazio (Fazio 2007): "attitudes form the cornerstone of a truly functional system by which learning and memory guide behavior in a fruitful direction". The next section presents our multi agent model for simulating attitude formation, based on the following hypothesis from the literature: attitude composed of a cognitive and emotional components, attitude represented as a set of memory associations between evaluations and the social object with varying accessibilities.
The Polias model
The goal of the Polias model is to model the impacts on attitudes, within a population, of a series of actions (e.g. commercial operation, change in public policy or, in our application context: medical support, military intervention, bombing..) by some external actors called forces (e.g. company, NGO or in our military application context: United Nation force, terrorist or others) over time. These impacts are (subjectively) evaluated by the individuals through an evolving attitude value toward each force at stake. The attitude depends on the beliefs the person has that this action 1) actually occurred and 2) produced an impact of a given payoff value (positive or negative). These beliefs are memorized and communicated through other individuals via messages, therefore potentially influencing their attitudes as well.
We will first present the key concepts needed to construct the simulation: the different protagonists (the population represented by individuals grouped into different factions, and the social actors), the actions, their corresponding beliefs, the attitudes and finally the messages. Then we describe the attitude dynamics, including communication of beliefs and attitudes computation.
Key elements
The individuals of the population are represented by computational agents and are characterized by a unique social group defined as a set of individuals sharing similar characteristics or goals. We denote \(SG=\{SG_1,SG_2,...,SG_n\}\) the set of social groups and \(Ind\) the set of all individuals. Each individual \(i\in Ind\) is defined by a tuple \(i = \langle sg, Blf, Cnt \rangle\) with \(sg \in SG\) the social group of the individual, \(Blf\) the set of all the beliefs on actions present in the individual's memory and \(Cnt \subset Ind - \{i\}\) the set of all the contacts of the individual in a social network.
The actors represent entities that can act in the simulation and for which we want to analyze the attitudes evolution among the population. Each of them corresponds to a computational automaton executing its actions list given by the user (for instance, in the context of military interventions, the UN can secure a zone, the terrorists can perform a bombing attack ...). For each \(actor \in Actors\), we denote \(actionList_{actor}\) the ordered list of actions to be executed during the simulation, defined by the user.
We call social object an abstract or concrete, human or artificial entity on which people (at least two) exert a social behavior (attitude formation, opinion exchange, formation of social representation, etc.). Here, the social objects are: the actors and the social groups. We denote SO = SG \(\cup Actors\) the set of all social objects.
An action represents an accomplished task by an actor that impacts a beneficiary individual with a certain amount of quantified payoff. Individuals capture information about these actions either directly or indirectly through communication and add them into their belief base \(Blf\). Besides this information is associated to a certain degree of credibility accorded to its source. We call this information action beliefs[2] and denote them \(a\in AB\):
| $$a = \langle name, actor, coresp, date, bnf, pyf, \sigma \rangle$$ |
For a given individual, each social object is associated to at least one attitude value (positive when in favor, negative when in disfavor and null when neutral). We must distinguish between two types of attitude: We must distinguish between two types of attitude: attitudes toward social groups and attitudes toward the actors.
People have attitudes toward the different social groups that emanate from social tensions present within the population. We define a table \(aTable_{|SG|, |SG|}\) with values in \([-1,1]\), parameter of the simulation, which contains the inter social groups attitudes, that are considered fixed in our model. The attitude of an agent toward a social group follows this equation:
| $$\forall i \in Ind, \forall s \in SG, attSG(i,s)= aTable(i.sg,s)$$ |

The heart of this model consists to simulate the dynamics of the attitudes of the population toward the actors that we denote \(att(i,actor)\). We conceptualize this dynamics as the result of individual’s perceptions of the actors’ actions (cf. section 3.10 below).
During a simulation, actors communicate on their actions to the population in which the information is propagated. These communications are emitted through messages defined by:
| $$ m = \langle emitter, date, a, Adr \rangle$$ |
Attitude dynamics
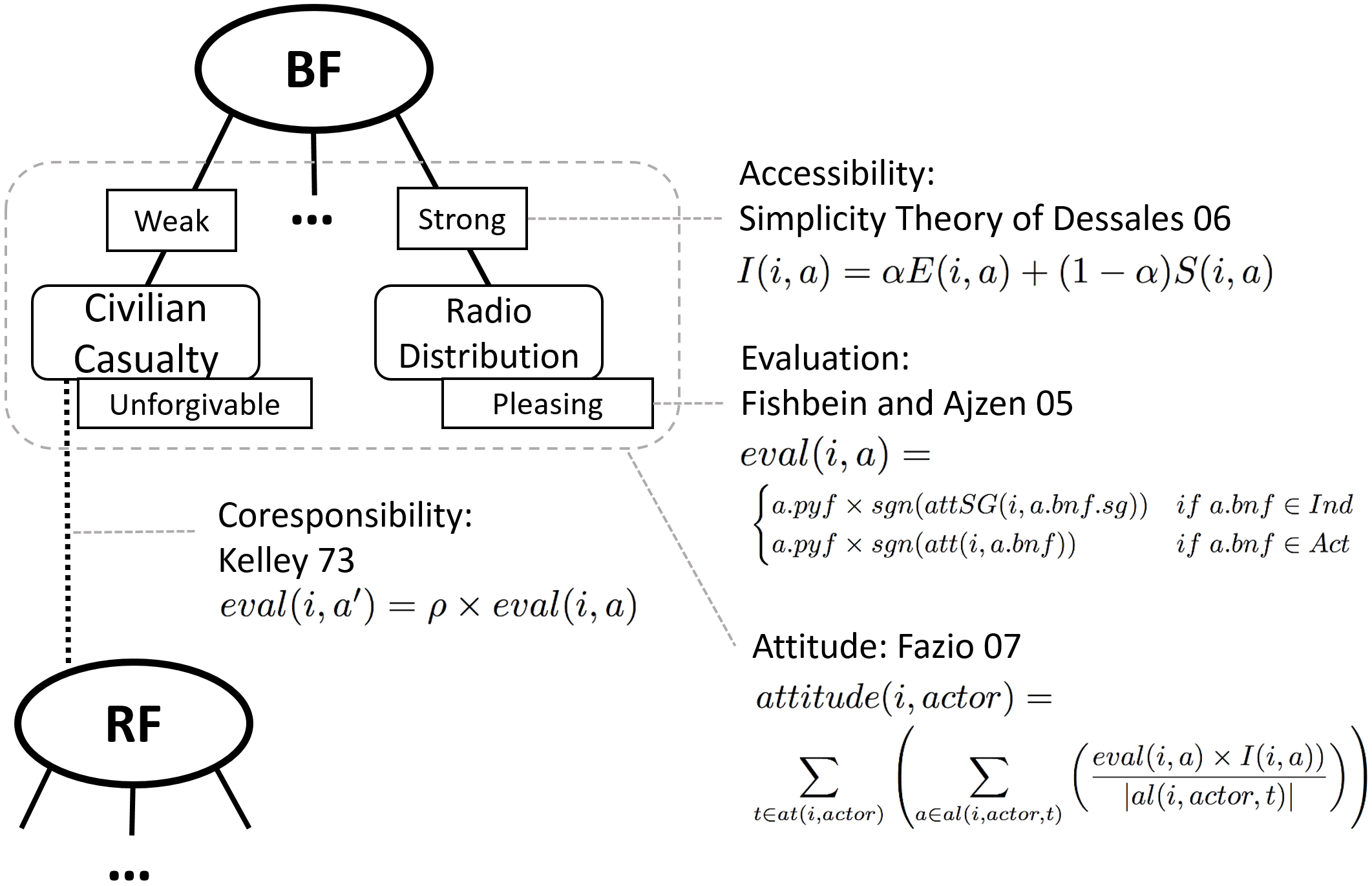
Our model for attitude construction is depicted in Figure 2 and based on action beliefs’ evaluations associated to the object, as proposed by Fazio (2007). The attitude toward an object is computed from a set of beliefs connected to it, weighted by an accessibility in memory factor (continuous value). As shown in Figure 2, in the case of our applications, objects are forces, and beliefs are about actions that might have occurred. Figure 3 summaries the relations between our attitude model’s components and can be used throughout this section to facilitate your reading.
The attitude dynamics process unfolds mainly in 5 steps during one tick. (1) At first, the agent perceives an information that some action happened (whether it is the subject of this action or just witnesses it). (2) Then, it will evaluate the interest of this action, such interest will impact (as a weight) on both attitude computation and communication (to decide whether it wants to send this information). (3) The communication process is then triggered: the agent decides to send (or not) to its contacts the information it acquires during this time step. (4) When it receives messages from contacts, it updates its belief bases through a belief revision process. (5) Finally, the attitude values towards forces are updated. Let us now detail these steps.

(1) Action perception
The agent could receive information in three different ways:
- Direct perception: the agent either is subject to the action or directly witnesses it (e.g. the UN Force brings food to the village and the agent is a member of the village or was around when the action was done);
- Intra-population communication: the agent is given information about a previously perceived action by a neighbor in the social network, through a message;
- Actor communication: an actor communicates about an action toward the population and the agent is one of the addressees (for instance, a force broadcasts propaganda messages or send leaflet).
(2) Interest of an action
In order to select the relevant information to use for constructing their attitudes and also to communicate to other individuals, agents estimate a model of narrative interest of the actions in their belief base. This interest is derived from Dessalles’s Simplicity Theory (Dessalles 2006), a cognitive theory based on the observation that human individuals are highly sensitive to any discrepancy in complexity. Their interest is aroused by any situation which appears simpler to describe than to generate it[3]. To our knowledge, it is the only theory that combines narrative interest and cognitive representation of events that are key concepts in our model.
An extension of the Simplicity Theory proposes to define the information’s narrative interest based on the emotion \(E\) and the surprise level \(S\) it causes to the individual (Dimulescu & Dessalles 2009) . We used the following formula to compute the interest:
| $$I(i,a)=\alpha E(i,a)+ (1-\alpha)S(i,a)$$ | (1) |
The emotional intensity follows a logarithmic law in conformity with Weber-Fechner’s law of the stimuli (in our case, the action ’s payoff \(a.pyf\)):
| $$E(i,a)= log_2\left(1+\frac{|a.pyf|}{\xi}\right)$$ | (2) |
In the Simplicity Theory, several dimensions are considered for the computation of surprise (e.g. geographical distance, recency etc). In our model, we use two dimensions: the temporal distance and the social distance. We chose these dimensions since they are already modeled in our architecture: simulation ticks represents time and the social network enables us to measure social distance between agents. Hence, the surprise value is the sum of a temporal component \(S^{time}\) (where an infrequent event will have more impact than an usual one) and a social component \(S^{social}\), which is a temporal component combined with a personal perspective (i.e. events that affected the individual’s social network):
| $$S = S^{time} + S^{social}$$ | (3) |
The computations of social and temporal surprises are detailed in the Appendix at the end of the document. The core of this model is that the surprise in each dimension is the result of the comparison between the generation complexity (in the sense of Shannon’s information theory (Shannon & Weaver 1949); for instance a bombing attack is a rare event in the US) and the description complexity (e.g. a bombing attack is a simple thing to describe).
Emotion and surprise are used to compute the interest of an action, as presented on equation 1.
(3) Intra-population communication
Each agent can communicate through a given social network, and has a set of potential contacts (neighbors in the network). For each individual \(i \in Ind\), for each action \(a\) acquired during the current time step, the probability that agent \(i\) sends a message about \(a\) to a contact is given by:
| $$p_{send}(i,a)=\begin{cases} 2^{[I(a)-I_{max}]} & if \; 2^{[I(a)-I_{max}]}>T_{com} \\ 0 & otherwise \\ \end{cases}$$ | (4) |
(4) Belief revision
The belief revision mechanism is directly inspired by the model COBAN (Thiriot & Kant 2008). Here we take 3 possible levels of credibility: \(\sigma_3\) (highest credibility) for direct experience, \(\sigma_2\) for messages from families and friends, and \(\sigma_1\) for others (unknown people, institutional message,...). Hence \(\sigma_1 \prec \sigma_2 \prec \sigma_3\).
When an agent \(i\) receives an incoming information in the form of an action belief \(a_{in} \in AB\), of credibility \(\sigma_{s}\), \(s \in \{1,2,3\}\), it updates its belief base \(Blf_i\) as follows:
- If the action \(a_{in}\) does not already exist in \(Blf_i\) (i.e. there is no identical action with the same name, actor, beneficiary's social group and date), the agent adds this action as a new belief. Its level of credibility is given by:
When it is not a direct observation, the belief's credibility is decreased by one level: when a friend tells me he observed an event (\(\sigma_3\) for her), it is still a indirect observation for me (\(\sigma_2\)).$$a_{in}.\sigma =\begin{cases} \sigma_3 & \text{{if this is a direct observation}}\\ \sigma_{max(s-1,1)} & otherwise \\ \end{cases}$$ (5) - If an action \(a_{ex}\) (with credibility \(\sigma_{e}\)) equivalent to \(a_{in}\) exists in \(Blf_i\) (i.e. they have the same name, actor, co-responsible, date, beneficiary, but differ by payoff), two situations can occur:
- (a) Compatible case, reinforcement: if \(|a_{ex}.pyf-a_{in}.pyf|\leq\varepsilon\) with \(\varepsilon\) a fixed threshold, the beliefs are considered to be close enough to refer to the same action. In that case, the credibility value\(a_{ex}.\sigma\) is updated as follows:
or instance, if the existing credibility is \(\sigma_1\) and a friend told me s/he saw an action (\(\sigma_3\) for her), then the credibility for me is increased and becomes \(\sigma_2\).$$a_{ex}.\sigma =\begin{cases} \sigma_3 & \text{{if this is a direct observation}}\\ \sigma_{max(s-1,e)} & otherwise \\ \end{cases}$$ (6) - (b) Incompatible case, revision: if \(|a_{ex}.pyf-a_{in}.pyf| > \varepsilon\), the actions are incompatible. In that case, there is a probability that the agent replaces his belief \(a_{ex}\) by \(a_{in}\). This will depend on the revision probability value given by Table 1, where \(\pi_i \in [0,1]\; i \in \{0,..,2\}\) are the model parameters for credibility revision[6]. A random value is drawn from an uniform distribution: if it is greater then the revision probability, action belief \(a_{ex}\) is replaced by \(a_{in}\).
- (a) Compatible case, reinforcement: if \(|a_{ex}.pyf-a_{in}.pyf|\leq\varepsilon\) with \(\varepsilon\) a fixed threshold, the beliefs are considered to be close enough to refer to the same action. In that case, the credibility value\(a_{ex}.\sigma\) is updated as follows:
| \(a_{ex}.\sigma\) \(\a_{in}.\sigma\) | \(\sigma_3\) | \(\sigma_2\) | \(\sigma_1\) |
|---|---|---|---|
| \(\sigma_3\) | \(X\) | \(1-\pi_1\) | \(1-\pi_0\) |
| \(\sigma_2\) | \(\pi_1\) | \(\\pi_2\) | \(1-\pi_1\) |
| \(\sigma_1\) | \(\pi_0\) | \(\pi_1\) | \(\pi_2\) |
(5) Attitude update
Whenever the reception of a new information about an action \(a\) done by an \(actor\) resulted in a belief revision in \(Blf_i\) or in a modification of the interest of an action belief, individual \(i\) will adapt its attitude toward \(actor\) based on its new mental state. S/he engages a three-stages process: S/he engages a three-stages process that are described in the following sections.
The benefit of an action \(a\) is determined subjectively, i.e. in respect to agent i\(i\)’s attitude and beliefs, using the evaluation model proposed by Ajzen and Fishbein (2005). This model combines the payoff of an action for a beneficiary with the attitude of the individual toward this impacted beneficiary. In this way, an individual judging an action that is beneficial for her or for some of her "friends" (positive attitude), the overall benefit would be positive. Conversely, if the action is beneficial for his "enemy" (negative attitude), the action would have be evaluated with a negative value.
| $$eval(i,a)= \begin{cases} a.pyf \times sgn(attSG(i,a.bnf.sg)) & if \; a.bnf\in Ind \\ a.pyf \times sgn(att(i,a.bnf)) & if \; a.bnf\in Act \\ \end{cases}$$ | (7) |
| $$sgn(x)= \begin{cases} 1 & if \; x \geq 0 \\ -1 & otherwise \end{cases}$$ | (8) |
Individuals tend to make responsible for an action other people, groups or institutions than the direct actor (Kelley 1973; Jones & Harris 1967). For instance, one could blame the police force for occurring terrorist attacks since their role is to maintain the security and prevent such incidents. Hence, we introduce a co-responsibility mechanism that enables individual to attribute a fraction \(\rho \in [0,1]\), parameter of the simulation, of an action payoff to the co-responsible. This mechanism occurs when an individual faces an action a in which (1) there is a co-responsible actor, (2) its impact is negative (i.e. there is no co-responsibility for beneficial actions) and (3) its evaluation is negative. In that specific case, the individual adds a belief \(a'\) with \(actor(a)=coResp(a)\) and \(eval(i,a')=\rho \times eval(i,a)\).
Once all the components of Fazio’s attitude model have been computed, the individual can finally construct his attitude. It corresponds to the aggregation of all actions’ evaluations for a given actor weighted by their corresponding accessibilities (i.e. interest value in our case). However, we propose that this aggregation proceeds in two steps. First, the agent aggregates all the action that share the same action type (e.g. patrol, health-care, etc.) for a given actor. Let \(at(i,actor)\) be the list of all action types made by \(actor\) and \(al(i,actor,t)\) the list of all actions of type \(t\) performed by \(actor\), in agent \(i\)'s belief base. The attitude \(att(i, actor)\) of the individual \(i\) toward the \(actor\) is given at each time of the simulation by:
| $$att(i,actor) = \underset{t \in at(i,actor)}{OWA} \left( \underset{a \in al(i,actor,t)}{OWA} \left( eval(i,a) \times I(i,a) \right) \right) % \label{eq:att-polias}$$ | (9) |
Figure 3 below summaries our attitude construction model and the relations between the components.
Functional analysis of the model dynamics
The model has been implemented in Java using the Repast[7] multiagent platform. In this section, we present several sensitivity analyses that have been conducted to study the model dynamics, the impact of the parameters and some emerging macroscopic behaviors.
Sensitivity to Emotion
We study the impact of the parameters \(\alpha\) and \(\xi\) used in the computation of information interest on attitude dynamics using an abstract scenario. 150 individuals are daily exposed to 10 different positive actions which payoffs vary between 0 and 50[8] during 100 days. The probability that an action occurs is 0.1 and each occurrence reaches 5% of the population. We follow the population’s attitude mean at the end of each simulation while varying \(\alpha\) and \(\xi\) . Also, to limit the stochasticity effect, we replicate each experience 100 times (each ( \(\alpha,\xi\)) couple). The represented results in Figure 4 correspond to the averages over replica (over 60 000 runs).
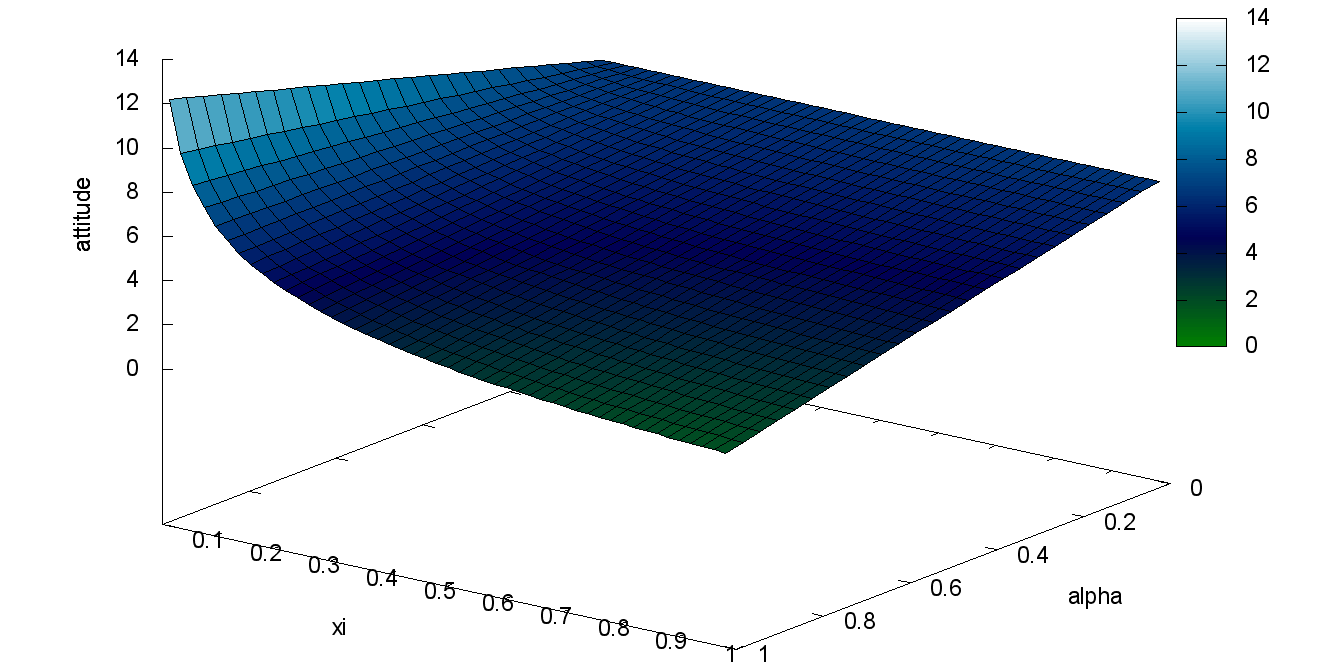
Overall, when \(\alpha\) or \(\xi\) increases, the attitude increases. \(\xi\) plays the role of a scaling factor, triggering the strength of the emotional response. Also, big values for \(\xi\) appear to inhibit its impact, i.e. the function is virtually linear with \(\xi>0.3\). In our simulations, the value of \(S\) varies between 0 and 10. \(\xi \simeq 0.01\) enables values of \(E\) on the same range as \(S\) with impact values ranging from 0 to 100 (payoff's interval that we apply in our work). For these two reasons, we will set \(\xi = 0.01\) from now on. \(\alpha\)'s impact is linear since it only balance the surprise and the emotional components. We thus define 3 types of cognitive profiles:
- Highly emotional agents with \(\alpha\) = 0.9 (90% of interest is based on the stimuli’s impact to the cost of surprise) ;
- Weakly emotional agents with \(\alpha\) = 0.1 (only 10% of interest is based on the stimuli’s impact in favor for surprise) ;
- Balanced agents \(\alpha\) = 0.5 interest is equally based on the stimuli’s impact and surprise .
Impact of social groups
In order to study the impact of social groups on the attitude dynamics, we put in place a scenario where 300 agents are equally divided in 3 groups, SGA, SGB and SGC. These groups are linked with inter-group attitudes as defined in the previous Figure 1 (SGA and SGB are allied against SGC). Inside each group, members are connected by a Watts and Strogatz’s (1998) small-world network with a mean degree of 4. These 3 networks are also tied to each other so that 10% of each group are randomly connected to the other groups. Thus, individuals are highly connected within their own group and some inter-group connections enable the diffusion of information over the whole network. Three phases of positive actions stimulate turn by turn each group (i.e. positive actions on SGA, then SGB and finally SGC). We performed this experiment on the three different cognitive profiles we’ve established. Figures 5, 6 and 7 present the attitude mean over time of each group for each experiment.
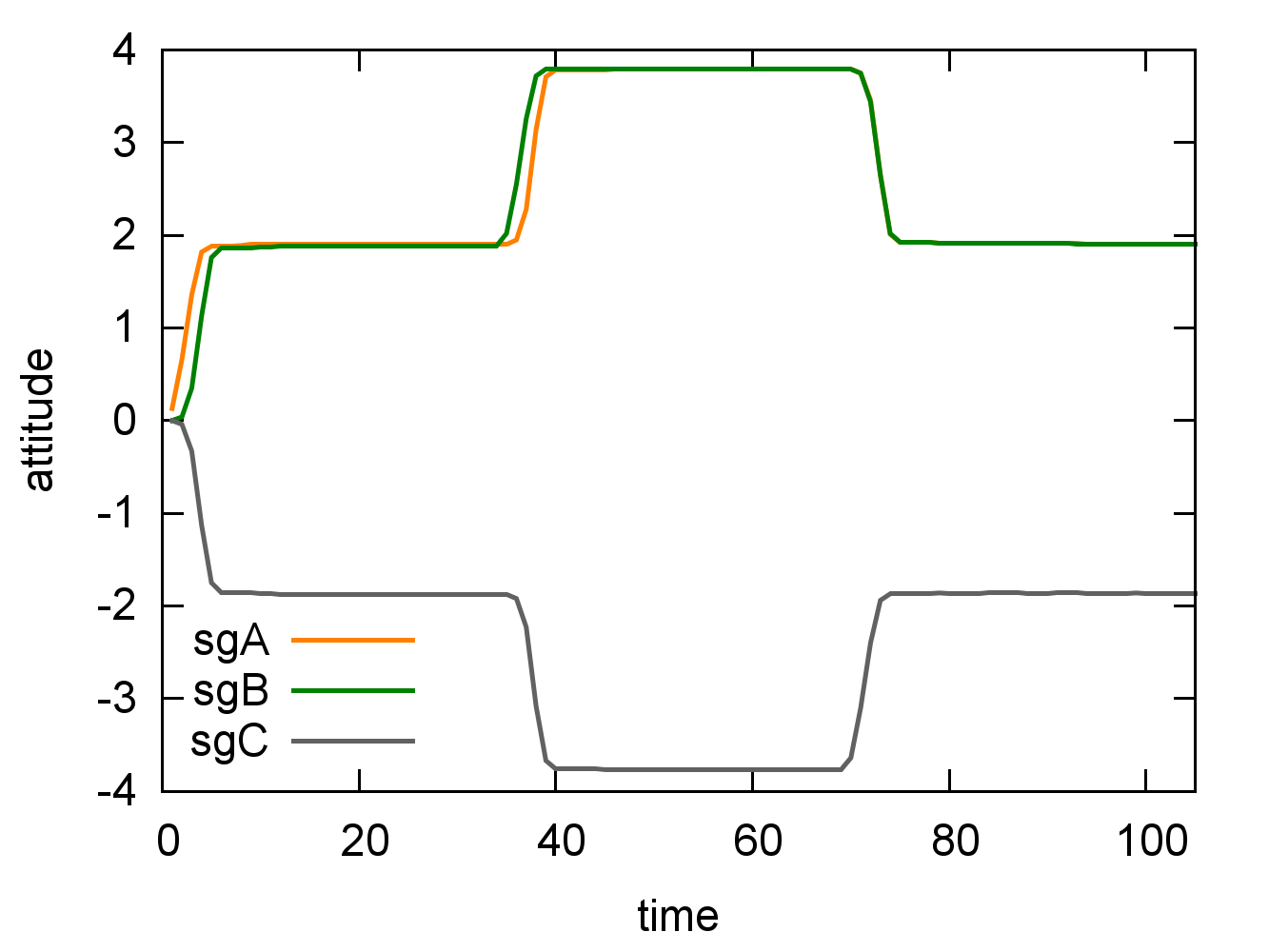

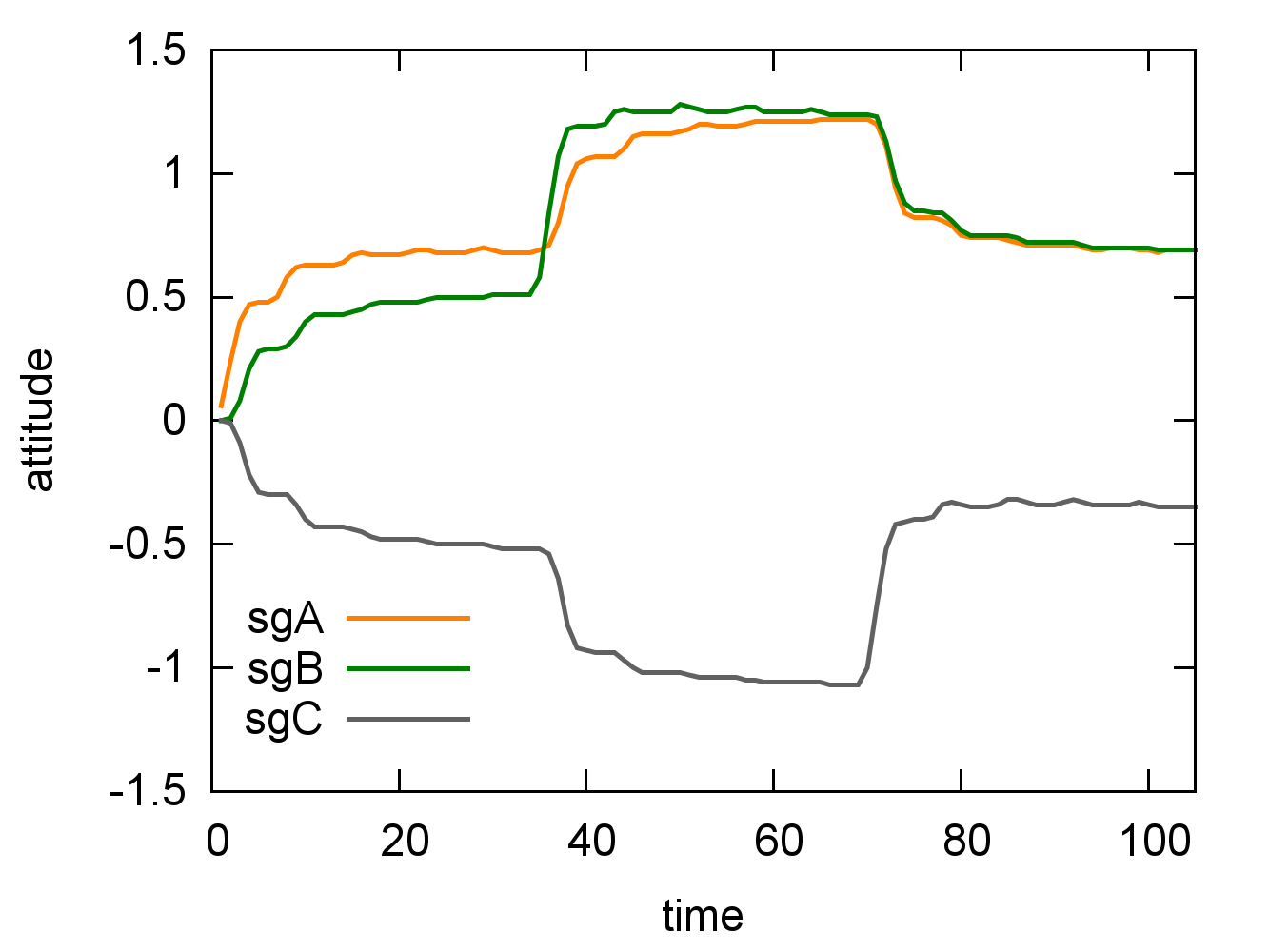
We can observe that all groups react to all actions even if they are not the beneficiary (for example, on the fist series of action impacting SGA, SGB’s and SGC’s attitude means are also impacted). This is enabled by the communication network that ties all the groups, the information about an action is propagated amidst the social network.
Also, we can notice that the attitude dynamics progress correspondingly to the inter-group attitudes: when SGA is rewarded, SGA and SGB’s attitude increase, in contrast, SGC decreases because they are against SGA.
When agents face events affecting other social groups (than their own), weakly emotional agents (and balanced ones, to a lesser extent) react less steeply and less rapidly than highly emotional agent. This is because, when the emotion weight is low, the surprise weights a lot, and interest decreases with the social distance between the agent and the one affected by the event. Thus, lesser individuals get to know the information, mitigating in this way the attitude change amplitude.
Information spreading
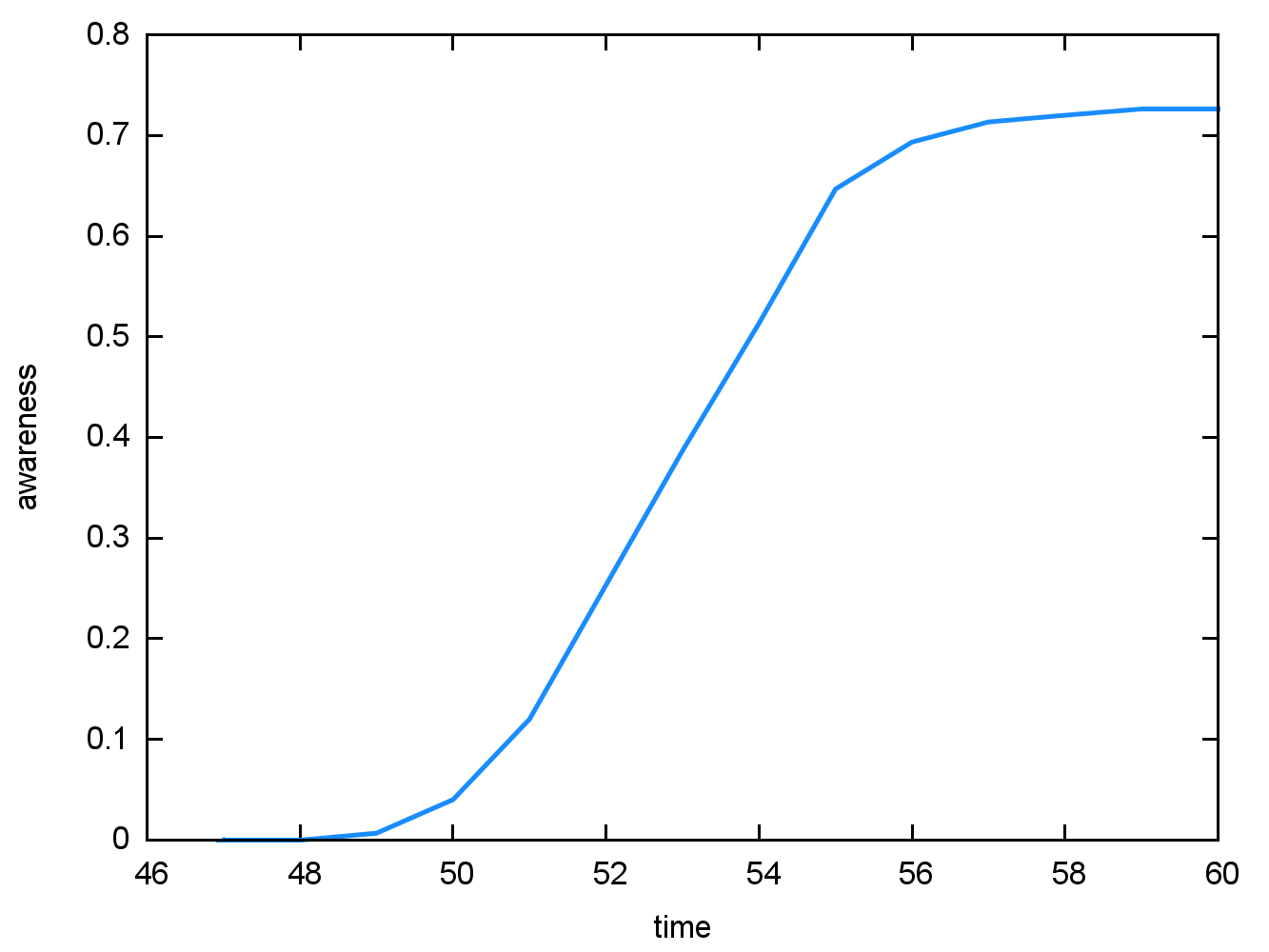
As we saw in the previous section, attitude dynamics heavily depends on the way information spreads through the communication network. To study this, we use a simple scenario where only one agent is aware of an information at the beginning of the simulation and analyze how it spreads in the population. The population is here composed of 150 agents, with a balanced cognitive profile, connected through a small-world network with a mean degree of 4. Figure 8 shows the evolution of the population percentage that came to know the information over time (awareness). We obtain the classic S-form shape of adoption curve (Rogers 2003).
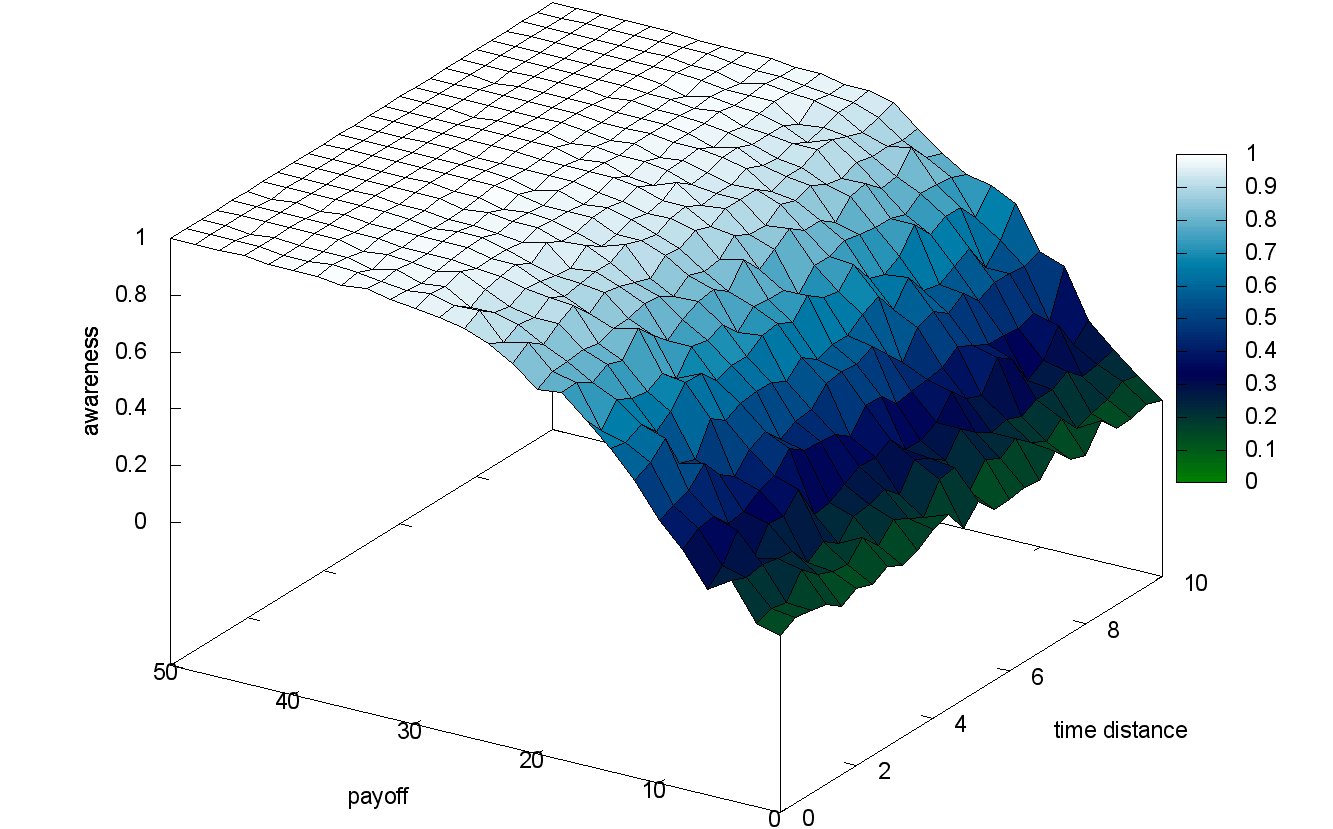
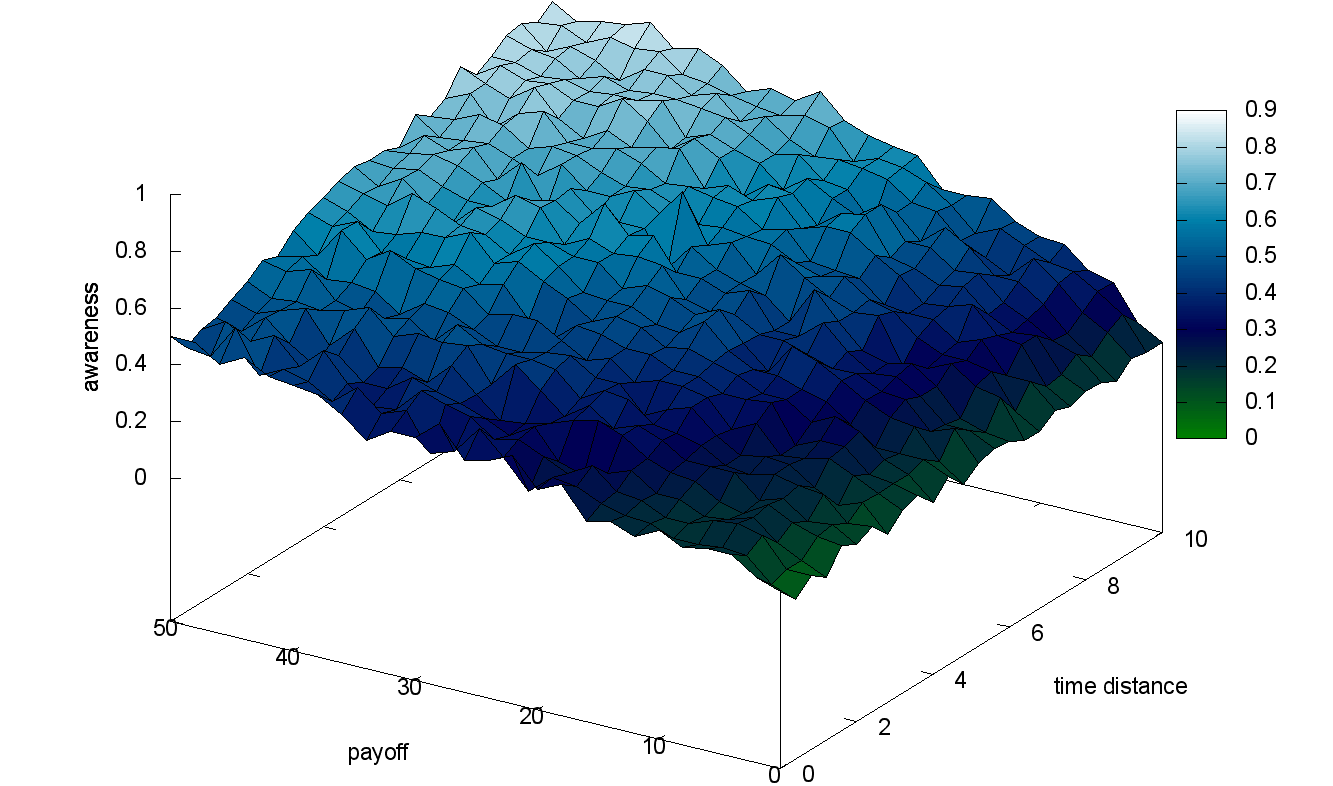
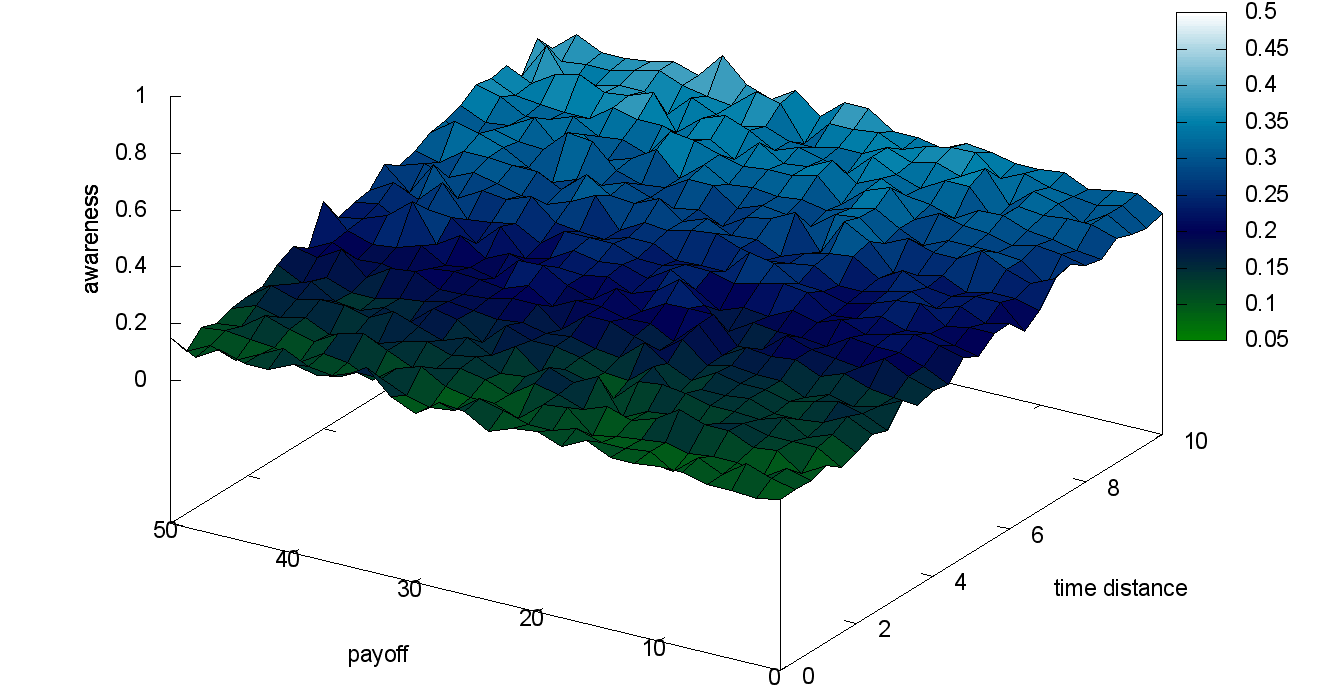
We now study the impact of an action’s parameters on its di usion: the payo and the time distance (time gap between the current occurrence and the last one). Figures 9, 10 and 11 present the awareness at the end of the simulations, each simulation being characterized by a (payoff; timedistance) couple and a different cognitive profile.
We can observe that the awareness always increases with the payo and the time distance since the interest of an action directly depends on them. However, the time distance has no effect on the awareness with highly emotional agents. Similarly, the payoff has no effect with weakly emotional agents. We decide to use agents with a balanced cognitive profile henceforth.
Belief revision and adoption
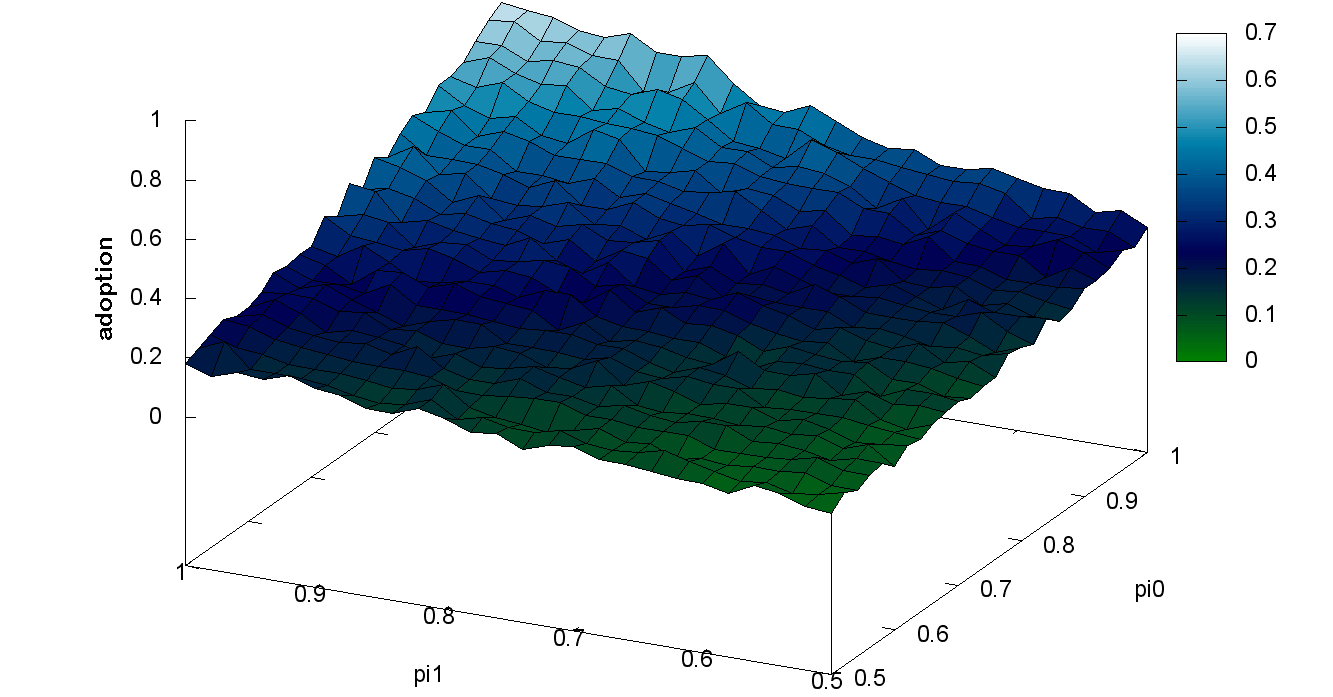
In this section, we study the impact of revision probabilities on the adoption of information. The belief revision mechanism enables agents to decide whether or not they will believe a new information that is contradictory with an already existing belief in their knowledge base (c.f. section 3.20). To do so, we set a scenario where there is a daily broadcast of a false information denoted \(FI\) (for instance, geocentricism) and one agent come to know the truth \(TI\) (for instance, heliocentrism) on the first step of the simulation. The objective consists to study the proportion of the population that came to adopt \(TI\) instead of \(FI\) at the end of each simulation by varying the revision probabilities. We reuse the probability table presented in the information that is contradictory with an already existing belief in their knowledge base (c.f. Table 1 above, and define \(\pi_2\) = 0.5, that is to say two information with the same source’s credibility have equal chance to be retained. We vary \(\pi_0\) (the probability to replace an information with a lowest credibility with a highest credible one) and \(\pi_1\) (the probability to replace an information with a one step more credible one). We set the credibility of the broadcaster as the lowest one ( \(\sigma_1\)), it daily reaches the whole population. The credibility of the first witness of \(TI\) (e.g. Galileo) is the same as any other individuals ( \(\sigma_3\) for herself and \(\sigma_2\) for his neighbors).
Figures 12, 13, 14 show the \(TI\) adoption rates of this experiment conducted on three small-world topologies with an average degree of \(k\) = 4; \(k\) = 6; \(k\) = 8. Each experiment results are averaged on 50 simulations in order to reduce the stochasticity effect (over 30 000 runs). We can observe that the adoption rates increase with the revision probabilities. However, with low probabilities, the first witness can come to believe \(FI\). Indeed, in our model, even if an agent believes strongly an information, the probability to revise it is not null. It can yield to the social influence and believe its neighbors. This phenomenon matches the process of conformity (Crutchfield 1955; Kelman 1958) that yields an individual to adopt majority’s belief due to the social pressure.
Another finding is that when increasing the density of the network, the adoption rate won’t necessarily increase in all situations as we may have predicted. With high probabilities (\(\pi>0.75\)), the increase of communication boosts the adoption of \(TI\). However, with low probabilities, the low credibility information is advantaged, thus individuals are most likely to believe the \(FI\) .
Finally, we found that the maximum adoption rate is never higher than 69% even with maximum revision probabilities. Meanwhile, with the same action’s parameters, population and network, without disinformation broadcast, the adoption rate reaches 78%. In the frame of our model, propaganda has a negative effect even when the population is highly skeptical.


Case study from field data
As was underlined in the introduction, it is very important to confront social simulation models of attitude to concrete scenario and field data, such as opinion polls. We present in this section the evaluation of the Polias model on a case study within a military context.
Scenario
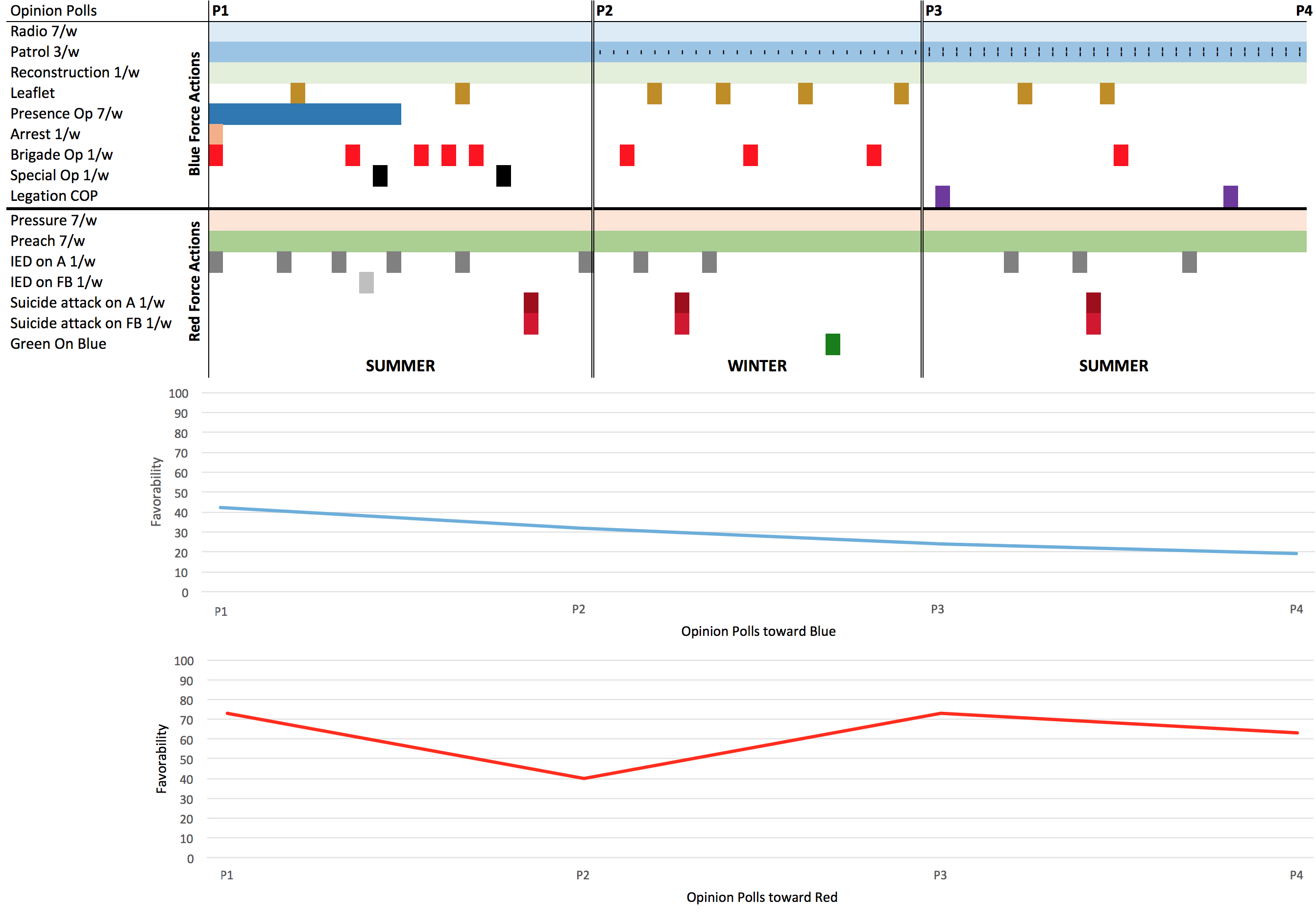
Through our research effort, we have been given an access to polls results about opinions of the population toward the different present Forces (foreign Force and Taliban) in an area of Afghanistan where French forces conducted stabilization operations. In the course of the NATO intervention in Afghanistan to stabilize the country, the French Forces were tasked to maintain security in the regions of Kapisa and Surobi between 2008 and 2012. As part of a more comprehensive maneuver, the Joint Command for Human Terrain Actions[9] were tasked to complement conventional security operations by positively influencing the population and its key individuals through communication, reconstruction and humanitarian actions. Through a set of six interviews with all the successive officers in charge (3 colonels and 3 commanders) from the CIAE, we managed to rebuild the sequence of the events that took place during their tenures, originating both from the NATO and from the Taliban insurgents. This sequence takes the shape of a scenario (see a Figure15).
Each action is characterized by a reach, a frequency and a payoff: how many people were directly affected by the action, how many times per week if it is frequent, how each individual is impacted. These values were defined based on subjective assessments of domain’s experts.
We can observe that both Forces have a constant background activity toward the population composed of non-kinetic actions. However, the Red Force activity is heavily decreased during winter which corresponds to the second period on the scenario. One reason is that local Taliban leaders leave the region to avoid the arid climate. On the Blue Force side, the activity decreases constantly due to the political decision taken to retreat troops after the big human losses on the first period (suicide attack of Joybar on July 13th 2011, which caused considerable human casualties among the Blue Forces).
In order to follow the progress of population’s sentiments and to link them to foreign Forces activities, the French Ministry of Defense financed opinion polls in Afghan regions where the French forces were operating. Those surveys were conducted by Afghan contractors between February 2011 and September 2012 with an interval of approximately 6 months issuing into four measure points P1, P2, P3 and P4 of the opinion of the population of Kapisa toward (1) the Blue Force and (2) the Red Force on the period corresponding to our scenario. The results are displayed in Table 2 below. Since the polls did not asked directly the opinion toward the Red Force but "whether they represent a threat", we decided to take the opposite of these results as the opinions values in the following sections.
| Polls dates | P1 | P2 | P3 | P4 |
|---|---|---|---|---|
| ”The Blue Force contributes to security” | 40 | 32 | 24 | 19 |
| ”The Red Force is the principal vector of insecurity” | 27 | 60 | 27 | 37 |
Simulation settings and initialization
We input the action sequence presented in the scenario of both Red and Blue Forces into the simulation scheduler; one tick corresponds to one day. The simulation covers the period between the first and last opinion polls in 554 ticks. The two agents corresponding to each Force will then operate their actions according to the scenario. The artificial population representing the inhabitants of Kapisa is composed of 500 agents connected by an interaction network based on a small-world topology (Milgram 1967) with a degree of 4 (i.e. each individual has 4 neighbors in average).
Before running the actual simulation, we initialize the population with a personal history for each individual and an attitude corresponding to the value given by P1. Indeed, one of our model’s originality resides in the fact that the attitude depends on the agent’s cognitive state characterized by its beliefs and accessibility values. Thus, we must give individuals an initial belief with a certain reach and payo for both attitudes toward Red and Blue Forces. These beliefs represent the interactions with Forces preceding to the simulation span or cognitive history. Another subtle point in our model is that individuals are surprised when they witness a totally new action, resulting in an overestimation of the action’s impact. In order to habituate them to certain regular actions (such as patrols, preaches, radio broadcasts etc.) we need to run an initialization scenario before the actual one in which the population is confronted to these actions, until we reach a stable point (approximately 200 ticks). This scenario is depicted in Figure16 below.
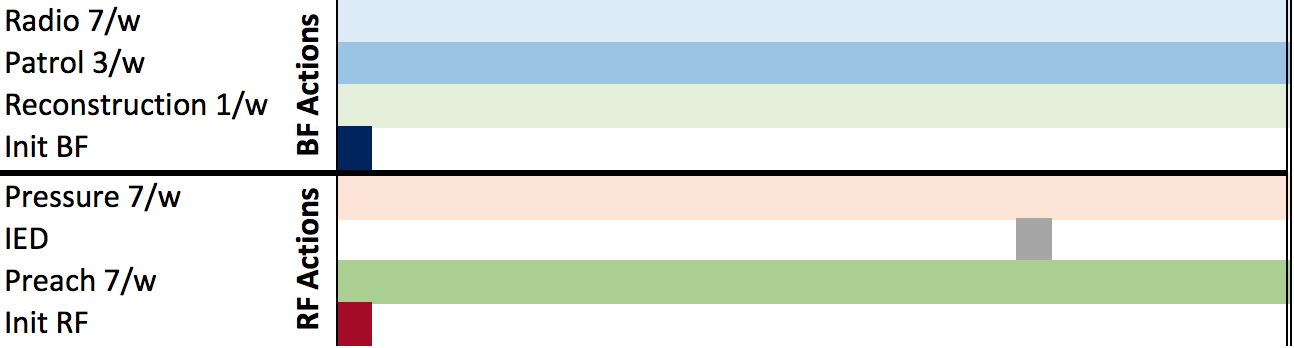
Calibration method
Once the simulation is properly initialized, we calibrate the model parameters using each opinion polls results as objectives. We have four points to calibrate per Force, thus totaling 8 points of calibration. 8 model parameters are shared among all individuals of the population:
- \(\alpha\), the weight of emotional sensibility toward the surprise factor
- \(\xi\), the level of sensibility to a stimuli (i.e. payoff)
- \(\rho\), the co-responsibility factor of Blue Forces for harmful Red actions
- \(T_{com}\), the communication threshold
- 4 parameters of initialization actions to attain the first point P1[10].
The other parameters are set to the following values: \(\pi_0=0.9, \pi_1=0.75, UT_0= 10, \epsilon=0\). The social network is a Watts and Strogatz (1998) small-world network, with mean degree k = 4.
We define our fitness function as the sum of differences’ squares between each point of the opinion poll results and its corresponding percentage of favorable individuals in the simulation. We choose to minimize this fitness using the evolutionary algorithm CMA-ES that is one of the most powerful calibration method to solve this kind of problem (Hansen et al. 2003). Once the fitness stops progressing over 500 iterations, we interrupt the calibration process and save the parameters. Each calibration iteration is based on the average output on over 20 simulations replica since the model is stochastic. It took about 36 hours (7500 runs) on a grid made of 5 x 20 processors (4GHz Intel Xeon).
Calibration results
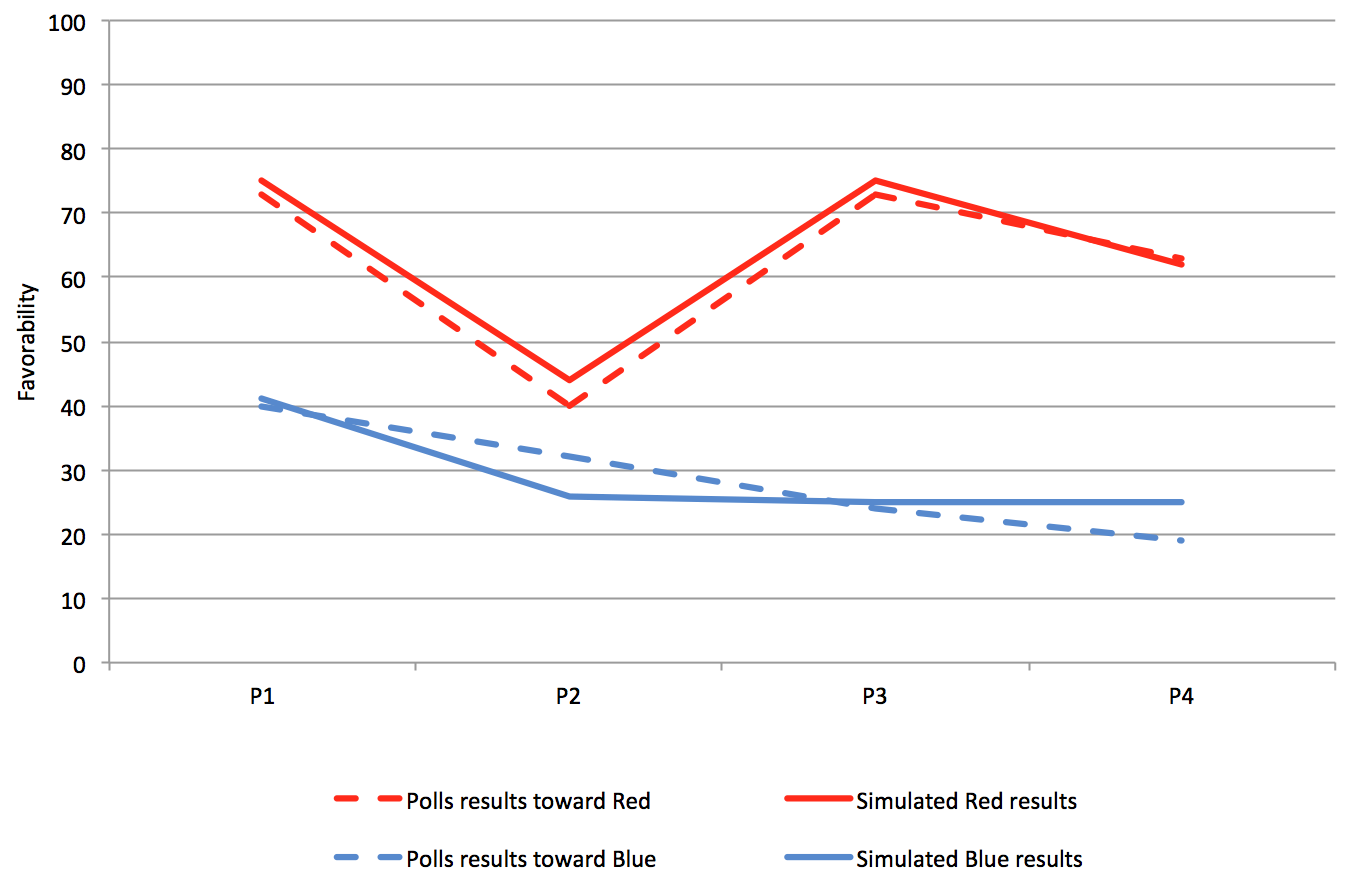
Figure17 shows the results of our model once its parameters have been calibrated. Plain curves represent the objectives to reach that are based on the collected opinion polls results, dashed curves correspond to the simulation results, with \(\alpha\) = 0.77, \(\xi\) = 0.01, \(\rho\) = 0.21 and \(T_{com}\) = 0.15 (as obtained by the calibration). Hence, the individuals appear to be quite emotional, and blame the Blue Force to be co-responsible for 21% of the negative effects.
We can observe that the attitude dynamics tendencies are well reproduced. The average difference between results and objective points is 2.9% with a maximum of 6% for the P2 and P4 blue points. This gap between survey and simulation results could be explained by several factors. First, the established scenario is based on subjective assessments of some Blue Force officers and do not capture all the military events that took place on the terrain. Furthermore, the parameters of action’s models (i.e. payoffs, frequency and reach) have been assessed based on qualitative appraisal of subject matter experts since there is no scientific method to assess them. Second, the sampling of the opinion survey could not be maintained through the survey process, due to the dynamics of the conflict: certain villages could not be accessed constantly over time due to their dangerousness. Moreover, as it was pointed earlier, the questionnaire did not directly ask the opinion toward Red Force which might increase the gap between our model outputs and the polls results. Finally, our field data is limited to the context of military events. Even if our study concerns attitudes toward Forces in the military/security context, other events might also have influenced these attitudes such as economic or daily activities. In view of these limitations, the reproduction of the general tendencies of attitude dynamics between each polls seems encouraging.
Attitude Dynamics
We proceeded to an automatic classification of individual attitudes, using a Kohonen neural network (Kohonen 1998) made of 9 neurons (3x3 grid). The input vector are the attitude values at each point P1,..P4 and for both forces, therefore 8 values for each of the 500 agents. The results are displayed in Figure18. As one can see, we can identify three groups:
- The pro-Blue group (cells 8 and 9), where initial attitudes are favorable to the blues, and increase through the simulation and the attitudes towards red forces move from neutral to negative. It represents 122 agents.
- The anti-Blue group (cells 2 and 3), with initial attitudes are unfavorable to the blues, and decrease through the simulation, while the attitudes towards red forces move from slightly positive to neutral. It contains 299 agents.
- The neutral group (cells 1, 4, 5, 7), whose attitudes are close to zero, slightly decreasing for both forces during the simulation. This group is made of 79 agents.
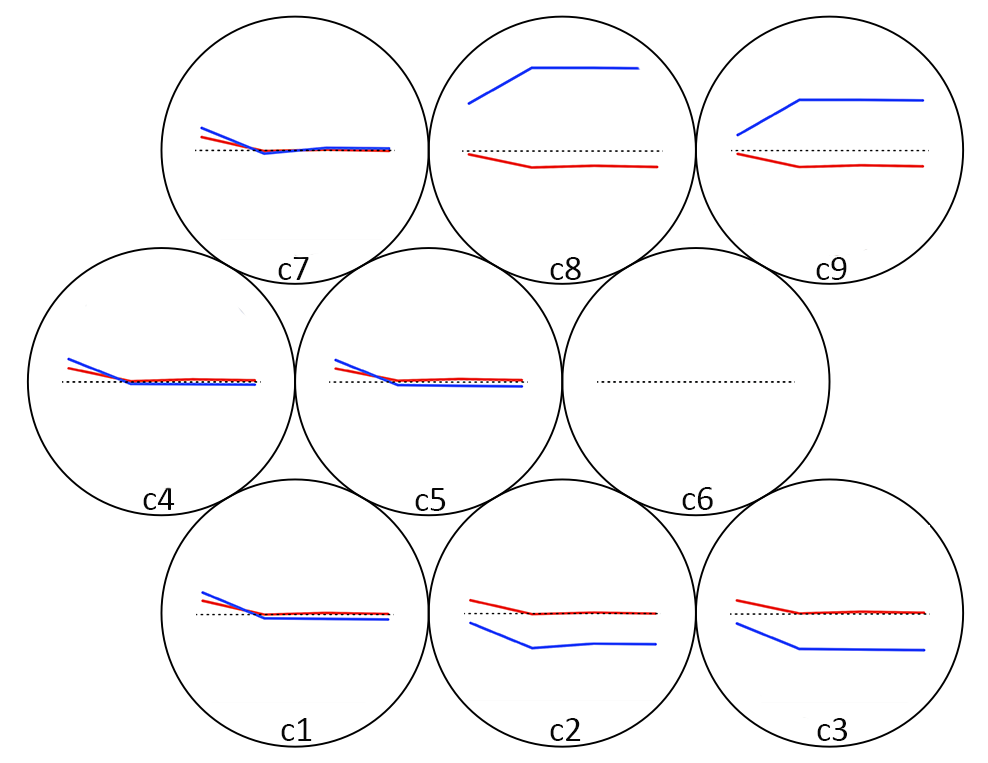
This post-simulation analysis provides useful fine-grained information about the population behavior and the different kinds of attitude dynamics in the population. While a further investigation of the agent’s mental states would be required to better understand how the policy adopted by the UN did impact the population’s attitude, it gives a first glimpse to the power of explanation through introspection in the Polias model.
Conclusion & perspectives
In this paper, we presented Polias, a comprehensive agent-based generative model of attitudes. Strongly grounded on social psychology, it integrates a cognitive and an emotional component, combined with a communication mechanism based on belief revision. It has a relatively small number of parameters (8), and has been calibrated to account for field data. Polias is a generic model of attitude formation, and could be applied to any application domain.
The model dynamics has been studied through a functional analysis of each sub-component with abstract scenarios. This study enabled the understanding of the parameters’ effect on the overall behavior. Moreover, we observed emergent phenomenon such as an S-shaped information diffusion, social pressure and the ability of the population to resist to disinformation.
We also have evaluated our model on a real world case study. We have collected opinion polls results and related events chronology on a period of one year and a half during the French military intervention in Kapisa (Afghanistan) between 2010 and 2012. The model has been able to reproduce the polls results with less than 3 points of error after a calibration phase of the parameters based on the collected field data. The resulting attitude dynamics of the individuals have been classified using a self-organizing map and showed some insight on the different tendencies inside the population.
While the case study was situated in the context of military operations, the model can be applied to civilian use: the actors can represent any kind of active social object such as political parties, institutions, companies or brands, as long as their actions can be represented in terms of positive or negative impacts on individuals (e.g. tax increase, environmental changes, promotions...).
In future works we intend to take full benefit of the introspection capabilities of this agent-based model by conducting a deeper analysis on the individuals’ belief bases in order to bring further explanations about their attitude dynamics and their differences: which event impacted the possible attitude changes, to which extent is it a strong (in terms of interest) element in the agent’s memory, and what are the different agents profiles in this regard.
Some contextual mechanisms could also be added, while we know that an opinion or attitude will differ depending on the context (e.g. professional, personal, political, ...) we are in when we use it.
Our work did not address the notion of social identity (Swann & Bosson 2010) and the impact of norms and group behavior on the interpretation of events. However, it is a interesting prospect to study in the future.
Moreover, we would like to implement the transition from attitudes to behaviors based on the abundant researches on this topic in social psychology: agents would then not only change their attitude, but also change their behavior toward the forces. This could be used in participatory simulation in which actors see the change in the attitude behavior in real time.
Notes
- For instance, certainty-related emotions (happiness, anger, ...) make people process information less carefully (and then with much readiness to be persuaded) than uncertainty-related emotions (surprise, fear,...) (Tiedens & Linton 2001).
- Note that in our model an action is only described as information about it. Therefore, in following sections, an action, information about an action and an action belief will be synonyms.
- For details, see http://www.simplicitytheory.org/.
- On the other hand, in a region where a tornado happens several times a month, the impact of the deaths will be lowered.
- We introduce nStep N, a fixed parameter to encode the number of time steps during which an information could remain the most important one (i.e. a dramatic event in the news). A er nStep steps, other information will be considered to become the most important one.
- Note that the case \(\sigma_3\) versus \(\sigma_3\) is impossible since one cannot witness twice the same action occurrence (it will at least have a different date.
- http://repast.sourceforge.net/.
- Negative actions would have yield attitudes to zero.
- Centre Interarmées des Actions sur l’Environnement in French.
- We must add in the initialization scenario a positive action done by the Red Force, and a negative action done by the Blue Force to balance the habituation effects where most of the time the Blue Force actions are positive and negative for the Red Force. We have to set for each of these two additional actions a payoff and a reach, so a total of 4 values.
Appendix
The temporal surprise is given by the relative impact of the Raw temporal unexpectedness \(U^{time}_{raw}\) diminished by the level \(U^{time}_{perso}\) of this unexpectedness from the person’s view. For instance one could be surprised to witness a tsunami since it is rare \((U^{time}_{raw}\)). However, if this particular individual has personally lived it in the past, the unexpectedness is diminished \(U^{time}_{perso}\).
| $$S^{time} = U^{time}_{raw}-U^{time}_{perso}$$ | (10) |
| $$S^{social} = U^{social}_{raw}-U^{social}_{perso}$$ | (11) |
This leads to four unexpectedness values: \(U_{raw}^{time}\), \(U_{raw}^{social}\), \(U_{perso}^{time}\) and \(U_{perso}^{time}\)l. In all four cases, the unexpectedness of the event (in our model, the action) can be defined by the discrepancy between its generation complexity and its description complexity: \(U^{x}=C_w^{x} - C_d^{x}\) with \(x\) the dimension. The description complexity \(C_d\) must be understood in the meaning of Shannon’s information theory (Shannon & Weaver 1949), i.e. the size of the smallest computational program that could generate this event.
Raw temporal distance (\(U_{raw}^{time}\)) The temporal complexity of generation refers to the probability that the action occurs at a given time. This notion could be interpreted as the usual time gap between two occurrences of the action: the more the action is rare, the bigger the gap is, the less it is probable, the more it is unexpected. Therefore we define the usual time gap using the difference between the occurrence date \(a.date\) of the action a and its last occurrence date \(a_{old}.date\): \(C_w^{time}=log_2(a.date-a_{old}.date)\). The temporal complexity of description corresponds simply to the elapsed time between the action and the current time \(t\): \(C_d^{time}=log_2(t-a.date)\).
Thus, the unexpectedness level for the temporal dimension is given by \(C_w^{time}-C_d^{time}\), that is:
| $$U_{raw}^{time}(a)= \begin{cases} log_2(a.date-a_{old}.date) - log_2(t-a.date)=log_2\left(\frac {a.date-a_{old}.date} {t-a.date} \right) & if \; a_{old}\neq \emptyset\\ UT_0 - log_2(t-a.date) & otherwise % = log_2\left(\frac{date(a)-date(a_{old})}{t-date(a)}\right) \end{cases} $$ | (12) |
Raw social distance (\(U_{raw}^{social}\)) The social complexity of generation refers to the probability that the action occurs on a beneficiary who belongs to a particular social group. We define it with \(C_w^{social}=-log_2(\frac{nbOcc_{SG}(a,i.sg)}{nbOcc(a)})\) with \(nbOcc_{SG}(a,i.sg)\) the occurrence number of the action \(a\) whose beneficiary is a member of the same social group \(i.sg\) as the agent.
The description complexity \(C_d^{social}\) corresponding to the social distance between the individual and the beneficiary of the action depends on two factors: the distance in the social graph and the average degree in the graph. Indeed, the higher the degree, the more complex it will be to describe a single step in the graph (in terms of information theory) and this influence is linear. However, the distance in the graph has an exponential impact on the social distance generation (since it requires to describe all possibilities at each node). Thus, \(C_d^{social}=log_2(v^d)\) with \(v\) the degree of the graph and \(d\) the shortest distance between \(i\) and \(a.bnf\) in the graph.
Hence we obtain the following formula:
| $$U_{raw}^{social}(a)=-log_2\left(\frac{nbOcc_{SG}(a,i.sg)}{nbOcc(a)}\right) - log_2(v^d) % = -log_2\left(v^d \times \frac{nbOcc_{SG}(a)}{nbOcc(a)}\right) $$ | (13) |
Personal temporal distance \(U^{time}_{perso}\) and personal social distance \(U^{social}_{perso}\) The personal unexpectedness is based on the last occurrence of the action \(a\) which has personally affected the individual, \(i.e.\) the last occurrence of the action (with the same \(name\) and \(actor\)) for which \(a.bnf\) is the agent \(i\) itself. We denote \(a_{perso}\) this particular occurrence.
The computation of the unexpectedness values is the same as above (eq. 12), except that the search of experienced occurrences in the belief base is limited to actions with \(i\) as the beneficiary:
| $$\begin{align}U_{perso}^{time}(a)&=log_2(a.date-a_{perso}.date) - log_2(t-a.date)) =log_2\left(\frac {a.date-a_{perso}.date} {t-a.date} \right)\end{align}$$ | (14) |
| $$\begin{align}U_{perso}^{social}(a)&=-log_2\left(\frac{nbOcc_{SG}(a_{perso},i)}{nbOcc(a)}\right)\end{align} $$ | (15) |
| $$S^{time}(a) = \begin{cases} log_2\left(\frac {a.date-a_{old}.date} {t-a.date} \right) - log_2\left(\frac {a.date-a_{perso}.date} {t-a.date} \right) & if \; a_{old}\neq \emptyset\\ UT_0 - log_2(t-a.date) - log_2\left(\frac {a.date-a_{perso}.date} {t-a.date} \right) & otherwise % = log_2\left(\frac{date(a)-date(a_{old})}{t-date(a)}\right) \end{cases}$$ |
| $$S^{social}(a)=-log_2\left(\frac{nbOcc_{SG}(a,i.sg)}{nbOcc(a)}\right) - log_2(v^d) + log_2\left(\frac{nbOcc_{SG}(a_{perso},i)}{nbOcc(a)} \right)$$ | (15) |
| $$S^{time}(a) = \begin{cases} log_2\left(\frac {a.date-a_{old}.date} {a.date-a_{perso}.date} \right) & if \; a_{old}\neq \emptyset\\ UT_0 - log_2({a.date-a_{perso}.date}) & otherwise % = log_2\left(\frac{date(a)-date(a_{old})}{t-date(a)}\right) \end{cases}$$ | (16) |
| $$S^{social}(a)= log_2\left(\frac{nbOcc_{SG}(a_{perso},i)}{v^d \times nbOcc_{SG}(a,i.sg)} \right) $$ | (17) |
Thus, \(S^{time}\) will increase when the event is infrequent (\(a.date-a_{old}.date\) increases) and/or it happened recently to the individual (\(a.date-a_{perso}.date\) is small). \(S^{social}\) will increase when the event happens more frequently to me than in general (\(\frac{nbOcc_{SG}(a_{perso},i)}{nbOcc_{SG}(a,i.sg)}\) increases) and/or it concerns someone close to the individual in the social network (small \(v^d\)).
References
AJZEN, I. (1991). The theory of planned behavior. Organizational behavior and human decision processes, 50(2), 179–211. [doi:10.1016/0749-5978(91)90020-T]
AJZEN, I. & Fishbein, M. (2005). The Influence of Attitudes on Behavior. In: The handbook of attitudes (Albarrac, D., Johnson, B. T. & Zanna, M. P., eds.). Mahwah, NJ, US: Lawrence Erlbaum Associates Publishers, pp. 173–221.
ALLPORT, G. W. (1935). Attitudes. In: Handbook of social psychology (Murchison, C., ed.). Clark University Press.
ANDERSON, J. R. & Schooler, L. J. (1991). Reflections of the environment in memory. Psychological science, 2(6), 396–408. [doi:10.1111/j.1467-9280.1991.tb00174.x]
BOHNER, G. & Dickel, N. (2011). Attitudes and attitude change. Annual Review of Psychology, 62(1), 391–417. [doi:10.1146/annurev.psych.121208.131609]
CASTELLANO, C., Fortunato, S. & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics 81(2), 591. [doi:10.1103/RevModPhys.81.591]
CHAIKEN, S., A, L. & AH, E. (1989). Heuristic and systematic information processing within and beyond the persuasion context. In: Unintended Thought (Uleman, J. & Bargh, J., eds.). Guilford, pp. 212–252.
CHATTOE-BROWN, E. (2014). Using agent based modelling to integrate data on attitude change. Sociological Research Online 19(1), 16: http://www.socresonline.org.uk/19/1/16.html. [doi:10.5153/sro.3315]
CRANO, W. H. & Prisline, R. (2006). Attitudes and persuasion. Annual Review of Psychology, 57, 345–374. [doi:10.1146/annurev.psych.57.102904.190034]
CRUTCHFIELD, R. S. (1955). Conformity and character. American Psychologist, 10(5), 191. [doi:10.1037/h0040237]
DEFFUANT, G., Neau, D., Amblard, F. & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems 3(01n04), 87–98. [doi:10.1142/S0219525900000078]
DESSALLES, J. L. (2006). A structural model of intuitive probability. In: Proceedings of the Seventh International Conference on Cognitive Modeling (Fum, D., Del Missier, F. & Stocco, A., eds.). Edizioni Goliardiche.
DIMULESCU, A. & Dessalles, J.-L. (2009). Understanding narrative interest: Some evidence on the role of unexpectedness. In: Proceedings of the 31st Annual Conference of the Cognitive Science Society: http://csjarchive.cogsci.rpi.edu/proceedings/2009/papers/367/paper367.pdf.
EAGLY, A. H. & Chaiken, S. (1993). The psychology of attitudes. Harcourt Brace Jovanovich College Publishers.
EDMONDS, B. (2013). Review of Squazzoni, Flaminio (2012) “Agent-based computational sociology”. Journal of Artificial Societies and Social Simulation, 16(1): https://www.jasss.org/16/1/reviews/3.html.
FAZIO, R. H. (2007). Attitudes as object-evaluation associations of varying strength. Social Cognition, 25(5), 603. [doi:10.1521/soco.2007.25.5.603]
FESTINGER, L. (1957). A theory of cognitive dissonance, vol. 2. Stanford University Press.
FISHBEIN, M. & Ajzen, I. (1975). Belief, Attitude, Intention and Behavior: An Introduction to Theory and Research. Addison-Wesley Pub (Sd).
FISHBEIN, M. & Ajzen, I. (1981). Acceptance, yielding, and impact: Cognitive processes in persuasion. Cognitive responses in persuasion, Petty, R. E., Ostrom, T. M., Brock. T. C. (eds.), Hillsdale, New Jersey, Lawrence Erlbaum Associates, 339–359.
FISHBEIN, M. & Ajzen, I. (2005). The influence of attitudes on behavior. The handbook of attitudes. Mahwah, NJ: Lawrence Erlbaum Associates, Editors: D. Albarracín, B. T. Johnson, M. P. Zanna, 173–222.
GALAM, S. (2008). Sociophysics: A review of Galam models. International Journal of Modern Physics C, 19(03), 409–440. [doi:10.1142/S0129183108012297]
GAWRONSKI, B. & Bodenhausen, G. V. (2006). Associative and propositional processes in evaluation: An integrative review of implicit and explicit attitude change. Psychological Bulletin, 132(5), 692–731. [doi:10.1037/0033-2909.132.5.692]
HANSEN, N., MÃller, S. & Koumoutsakos, P. (2003). Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evolutionary Computation, 11(1), 1–18. [doi:10.1162/106365603321828970]
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation 5(3) 2: https://www.jasss.org/5/3/2.html.
JONES, E. E. & Harris, V. A. (1967). The attribution of attitudes. Journal of Experimental Social Psychology, 3(1), 1–24. [doi:10.1016/0022-1031(67)90034-0]
KANT, J. D. (1999). Modeling human cognition with artificial systems: some methodological considerations. Proceedings of HCP 99, 501–508.
KANT, J.-D. (2015). Agent-based approaches to the study of human behaviors. Habilitation thesis, UPMC.
KELLEY, H. H. (1973). The processes of causal attribution. American psychologist, 28(2), 107. [doi:10.1037/h0034225]
KELMAN, H. C. (1958). Compliance, identification, and internalization: Three processes of attitude change. Journal of Conflict Resolution, 51–60. [doi:10.1177/002200275800200106]
KOHONEN, T. (1998). The self-organizing map. Neurocomputing, 21(1), 1–6. [doi:10.1016/S0925-2312(98)00030-7]
KOTTONAU, J. & Pahl-Wostl, C. (2004). Simulating political attitudes and voting behavior. Journal of Artificial Societies and Social Simulation, 7(4) 6: https://www.jasss.org/7/4/6.html.
LORD, C. G., Ross, L. & Lepper, M. R. (1979). Biased assimilation and attitude polarization: the effects of prior theories on subsequently considered evidence. Journal of Personality and Social psychology, 37(11), 2098.
MAIO, G. & Haddock, G. (2009). The Psychology of Attitudes and Attitude Change. Sage, London.
MILGRAM, S. (1967). The small world problem. Psychology today , 2(1), 60–67.
PETTY, R. & Cacioppo, J. T. (1986). Communication and Persuasion: Central and Peripheral Routes to Attitude Change. Springer. [doi:10.1007/978-1-4612-4964-1]
PETTY, R. E., Briñol, P. & DeMarree, K. G. (2007). The meta-cognitive model (MCM) of attitudes: Implications for attitude measurement, change, and strength. Social Cognition, 25(5), 657–686. [doi:10.1521/soco.2007.25.5.657]
ROGERS, E. M. (2003). Diffusion of Innovations. New York: Free Press, 5th ed.
ROSENBERG, M. J. & Hovland, C. I. (1960). Cognitive, affective, and behavioral components of attitudes. Attitude organization and change: An analysis of consistency among attitude components, 3, 1–14.
SCHWARZ, N. (2007). Attitude construction: evaluation in context. Social Cognition, 25(5), 638–656. [doi:10.1521/soco.2007.25.5.638]
SHANNON, C. E. & Weaver, W. (1949). The mathematical theory of information.The Bell System Technical Journal, 27, pp. 379–423, 623–656. [doi:10.1002/j.1538-7305.1948.tb01338.x]
SIMON, H. A. (1955). A behavioral model of rational choice. The Quarterly Journal of Economics, 69(1), 99–118. [doi:10.2307/1884852]
STEELE, C. M. (1988). The psychology of self-affirmation: Sustaining the integrity of the self. Advances in experimental social psychology 21, 261–302. [doi:10.1016/S0065-2601(08)60229-4]
SWANN, W. B. & Bosson, J. K. (2010). Self and identity. In D. T. Gilbert, S. T. Fiske, & G. Lindzey (Eds.), Handbook of social psychology, Hoboken, NJ: John Wiley & Sons, pp. 589-628. [doi:10.1002/9780470561119.socpsy001016]
THIRIOT, S. & Kant, J.-D. (2008). Reproducing stylized facts of word-of-mouth with a naturalistic multi-agent model. In: Second World Congress on Social Simulation, vol. 240.
TIEDENS, L. & Linton, S. (2001). Judgment under emotional certainty and uncertainty: The effects of specific emotions on information processing. Journal of Personality and Social Psychology, 81(6), 973–988. [doi:10.1037/0022-3514.81.6.973]
URBIG, D. & Malitz, R. (2007). Driving to more extreme but balanced attitudes: Multidimensional attitudes and selective exposure. In: ESSA European Social Simulation Association Conference 4th: http://www.diemo.de/documents/UrbigMalitz-ESSA2007.pdf.
WATTS, D. J. & Strogatz, S. H. (1998). Collective dynamics of ’small-world’ network. Nature, 393(6684), 440–442. [doi:10.1038/30918]
WICKER, A. W. (1969). Attitudes versus actions: The relationship of verbal and overt behavioral responses to attitude objects. Journal of Social Issues, 25(4), 41–78. [doi:10.1111/j.1540-4560.1969.tb00619.x]
XIA, H., Wang, H. & Xuan, Z. (2010). Opinion Dynamics: Disciplinary Origins, Recent Developments, and a View on Future Trends: http://www.iskss.org/KSS2010/kss/10.pdf.
ZANNA, M. P. & Rempel, J. K. (1988). Attitudes: A new look at an old concept. I D. BarTal & AW Kruglanski (Red.) The social psychology of attitudes (sid. 315-334). New York: Cambridge University Press. I.
