Juliette Rouchier (2003)
Re-implementation of a multi-agent model aimed at sustaining experimental economic research: The case of simulations with emerging speculation
Journal of Artificial Societies and Social Simulation
vol. 6, no. 4
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/4/7.html>
Received: 13-Jul-2003 Accepted: 13-Jul-2003 Published: 31-Oct-2003
 Abstract
Abstract
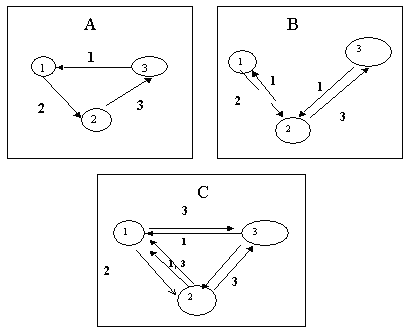
|
| Figure 1. A) From producer to consumer: the ideal circulation of goods (impossible to achieve on this market which is governed by bilateral trading); B) Fundamental strategies in the context of the model (neither agents 1 or 3 are interested in trading for the good i +2); C) Ideal speculative equilibrium pattern, which can be reached for certain values of costs and utility |
| γ(i+1) = - C(i+1) +β u, | (1.1) |
the expected gain for an agent who keeps good i+1 and sells it at the next time-step ; and
| γ( i+2) = - C(i+2) + β u, | (1.2) |
the same gain for good i+2.
Def 1:
SR (i,t) = Speculative ratio of agents of type i at time t ;
NAS (i,t) = Number of speculative trades that are accepted by agents of type i at time t;
NPS (i,t) = Number of possible speculative trades for agents of type i at time t.
Then SR (i,t) = NAS (i,t) / NPS (i,t)
A participant of type i is said to accept an exchange for speculation if he/she proposes to give good i+1 to get good i+2.
| Table 1: Offer frequencies over each half of 5 sessions with real agents. Results are given as the average speculative ratio for each type over the first half of the simulation and over the second half of the simulation | ||||||
| Agents type 1 offers 2 for 3 | Agents type 2 offers 3 for 1 | Agents type 3 offers 1 for 2 | ||||
| first half | second half | first half | second half | first half | second half | |
| R1 | 0.13 | 0.18 | 0.98 | 0.97 | 0.29 | 0.29 |
| R2 | 0.38 | 0.65 | 0.95 | 0.95 | 0.17 | 0.14 |
| R3 | 0.48 | 0.57 | 0.96 | 1.00 | 0.13 | 0.14 |
| R4 | 0.08 | 0.24 | 0.92 | 0.98 | 0.12 | 0.02 |
| R5 | 0.06 | 0.32 | 0.93 | 0.97 | 0.25 | 0.18 |
| Average on R1-R5 | 0.23 | 0.37 | 0.95 | 0.96 | 0.20 | 0.16 |
| Table 2: Offer frequencies over each half of 5 sessions with real agents mixed with automated artificial agents | ||||||
| Agents type 1 | Agents type 2 | Agents type 3 | ||||
| Time-step for the first half | Time-step for the second half | Time-step for the first half | Time-step for the second half | Time-step for the first half | Time-step for the second half | |
| R1 | 0.84 | 0.83 | 1.00 | 1.00 | 0.00 | 0.00 |
| R2 | 0.52 | 0.53 | 1.00 | 1.00 | 0.00 | 0.00 |
| Average on two sessions | 0.69 | 0.71 | 1.00 | 1.00 | 0.00 | 0.00 |
| νi+1 = Σ (ISi+1) * γi +1 - Σ(IFi+1) * γi +2 | (2.1) |
| νi+2 = Σ (ISi+2) * γi +2 - Σ(IFi+2) * γi +1 | (2.2) |
where both (I i+1) are functions which are defined on the set of time-step when the agent possessed good i+1 and:
IS = 1 if the agent traded i+1 for i; and = 0 if it didn't.
IF = 1 if the agent failed to trade i+1 for i; and = 0 otherwise.
With the same definition for both (I i+2).
| xji = νji+1 - νji+2 | (3) |
and:
| P [s=0] = exp xji / (1 + exp xji) | (4) |
is the probability for the agent to reject the exchange. Eventually:
| P [s=1] = 1 - P [s=0] | (5) |
is the probability for the agent to accept the exchange.
| yji = νji+2 - νji+1 | (3') |
to use probability:
| P [s=0] = exp y/ (1 + exp y) | (4') |
Hence, for Duffy, agents have no memory of how they obtained the good.
| Table 3: The names and repartition of rationality for the agents, depending on their rationality. Agents in italic letters are the one that are used by John Duffy in his simulations | |||
| Name of the agent | Agents of type 1 | Agents of type 2 | Agents of type 3 |
| Rational agents | Compare I(2) and I(3) | Compare I(3) and I(1) | Compare I(1) and I(2) |
| Stable rational agents | Never exchange 3 for 2 | Never exchange 1 for 3 | Never exchange 2 for 1 |
| Var-rational agents | Compare J(2) and J(3) | Compare J(3) and J(1) | Compare J(1) and J(2) |
| Automated agents | Compare I(2) and I(3) | Always exchange 3 for 1 | Never exchange 1 for 2 |
| Fi = Ai / number of possibilities to speculate = Ai/ (Ri+Ai) | (5) |
| Table 4: Simulations that were led. The series of simulations reproducing Duffy's are indicated in italic, and the ones I added are in normal format | |||
| Rational agents | Stable rational agents | Var-rational agents | |
| Homogenous rationality | SIM 1 Duffy: 5 simulations Me: Average and MSD over 100 simulations | SIM 2 Average and MSD over 100 simulations | SIM 3 Average and MSD over 100 simulations |
| Heterogenous rationality | Series of 5 simulations SIM 1 - 23 Agents of type 2 and 3 are automated - | Series of 100 simulations SIM 2 - 23 Agents of type 2 and 3 are automated - | Series of 100 simulations SIM 3 - 23 Agents of type 2 and 3 are automated - |
| Table 5: Duffy's results for each of 5 artificial sessions, average for these 5 sessions. The values are the average speculation ratio over the first half and the second half of the simulations | ||||||
| Agents type 1 | Agents type 2 | Agents type 3 | ||||
| first half | second half | first half | second half | first half | second half | |
| A1 | 0.06 | 0.15 | 0.73 | 1.00 | 0.37 | 0.07 |
| A2 | 0.23 | 0.31 | 0.88 | 0.98 | 0.20 | 0.07 |
| A3 | 0.33 | 0.50 | 0.78 | 0.98 | 0.15 | 0.00 |
| A4 | 0.18 | 0.42 | 0.81 | 1.00 | 0.17 | 0.00 |
| A5 | 0.10 | 0.18 | 0.67 | 0.98 | 0.23 | 0.07 |
| Average on A1-A5 | 0.19 | 0.32 | 0.77 | 0.99 | 0.22 | 0.04 |
| Table 6: My results for simulations of all types with homogenous agents that are either: rational agents, var-rational agents and stable agents. Here I give the average speculation ratio of the first half and the second half of the simulations, as well as the MSD of this value for the set of simulations | |||||||
| Agents type 1 | Agents type 2 | Agents type 3 | |||||
| first half | second half | first half | second half | first half | second half | ||
| SIM 1 Rational agents | Average speculation rate | 0.74 | 0.68 | 0.80 | 0.93 | 0.73 | 0.81 |
| MSD | 0.03 | 0.10 | 0.08 | 0.09 | 0.01 | 0.11 | |
| SIM 2 var-rational agents | Average speculation rate | 0.45 | 0.42 | 0.53 | 0.47 | 0.42 | 0.52 |
| MSD | 0.19 | 0.27 | 0.14 | 0.27 | 0.3 | 0.24 | |
| SIM 3 Stable agents | Average speculation rate | 0.68 | 0.77 | 0.76 | 0.79 | 0.66 | 0.66 |
| MSD | 0.07 | 0.12 | 0.01 | 0.09 | 0.04 | 0.12 | |
| Table 7: Duffy's results and my results for simulations of all types with agents 2 and 3 being automated and agents 1 being either: rational agents, var-rational agents and stable agents. Then I took the average and MSD over the remaining simulations (over 90) of the speculation rate for each half of simulation for each type of agents | |||||||
| Agents type 1 | Agents type 2 | Agents type 3 | |||||
| first half | second half | first half | second half | first half | second half | ||
| Duffy: Average on 5 sessions | Average speculation rate | 0.62 | 0.73 | 1.00 | 1.00 | 0.00 | 0.00 |
| SIM 1' Rational agents | Average speculation rate | 0.91 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 |
| MSD | 0.04 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | |
| SIM 2 ' var-rational agents | Average speculation rate | 0.80 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 |
| MSD | 0.15 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | |
| SIM 3 ' Stable agents | Average speculation rate | 0.80 | 0.88 | 1.00 | 1.00 | 0.00 | 0.00 |
| MSD | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | |
2 Meaning that they evolve in a discrete-time environment, where they are randomly paired at each time-step and judge at that time if they want to perform an exchange with the other agent.
3 In a economic paper, it is not necessary to say that agents want to increase their utility. In his paper, Duffy explains how his experiments are organised to induce humans to get as many "utility points" as possible, and that the artificial agents are built with that innate will.
4 As Duffy would say: "An agent speculates when he accepts a good in trade that is more costly to store than the good he is currently storing with the expectation that this more costly-to-store good will enable him to more quickly trade for the good he desires to consume." (page 3)
5Just as an indication of my building of rationality, the memory of an agent is constituted of the collection of its interaction along the time, represented, for agents A meeting agents B as: [good possessed by A; good possessed by B ; proposition of exchange by A ; proposition of exchange by B ; time-step] with: (proposition of exchange) = 1 if the agent does propose the exchange (proposition of exchange) = 0 if the agent does not want the exchange
6 I ran 100 simulations, among which some results were not suitable because the time of simulation was too short and agents did not have the opportunity to speculate: I considered that simulations with less than 40 time-steps were not long enough to study our topic. I then calculated the average and MSD over the remaining simulations (over 90) of the speculation rate for each half of simulation for each t type of agents.
7 About 10% of the simulations gave results that were not suitable because the time of simulation was too short and agents did not have the opportunity to speculate.
8 This is what is stated in the requirement for publishing for JASSS <https://www.jasss.org/admin/submit.html >.
9 However, I don't want to get into a discussion on platforms, knowing that the sharing of code could mean that I have monopolistic views for one platform on other: it is not the case.
10 Experiments are short because humans cannot play for a very long time that kind of game, and with few people because each participant is paid and Research is poor.
11 I don't condemn John Duffy's choice, since he had to build both experiments and simulations on that topic. His idea is really wise, considering that he had to find a straightforward way to build comparable societies on both side. The idea that the combinatorial dimension of the problem could be at stake - as well as all other ideas - only appeared to me thanks to his extremely clear work.
BROWN P.M. (1996) Experimental evidence on money as a medium of exchange, Journal of Economic Dynamics and Control, 20, pp 583-600.
CONTE R and Gilbert N (1995) "Introduction: Computer Simulation for Social Theory", In Conte R and Gilbert N , Artificial Societies. The Computer Simulation of Social Life, UCL Press, London.
DORAN, J. (2001) Intervening to Achieve Co-operative Ecosystem Management: Towards an Agent Based Model. Journal of Artificial Societies and Social Simulation vol. 4, no. 2,
DUFFY J (2001) Learning to Speculate: Experiments with Artificial and Real Agents, JEDC, 25, pp 295-319.
DUFFY J and Ochs J (1999) Emergence of money as a medium of exchange: An experimental study, American Economic Review, 89, pp 847-877.
EDMONDS B. (2001) The Use of Models - making MABS actually work. In. Moss, S. and Davidsson, P. (eds.), Multi Agent Based Simulation, Lecture Notes in Artificial Intelligence, 1979, pp 15-32.
EDMONDS B and Hales D (2003, this issue) Replication, Replication and Replication - Some Hard Lessons from Model Alignment. Journal of Artificial Societies and Social Simulation.
KANIOVSKI Y M, Kryazhimskii A V and Young P (2000) Adaptive Dynamics in Games Played by Heterogeneous Populations, Games and Economic Behavior, 31, pp 50-96
KIYOTAKI N and Wright R (1989) On money as a medium of exchange, Journal of Political Economy, 97, pp 924-954.
MARIMON R, McGrattan E R and Sargent T J (1990) Money as a medium of exchange in an economy with artificially intelligent agents, Journal of Economic Dynamics and Control, 14, 329-373.
ROUCHIER J, Bousquet F., Requier-Desjardins M. and Antona M. (2001) A Multi-Agent Model for Describing Transhumance in North Cameroon: Comparison of Different Rationality to Develop a Routine, Journal of Economic Dynamics and Control, 25, pp 527-559.
STAUDINGER S (1998) Money as a medium of exchange: An analysis with genetic algorithms, working paper, Technical University, Vienna.
SMITH V. (1994) Economics in the Laboratory, Journal of Economic Perspectives, Vol. 8, No. 1, Winter 1994, 113-131.
SMITH V. (2002) Method in Experiment: Rhetoric and Reality, Experimental economics 5, pp 91-110.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]