Yuya Sasaki and Paul Box (2003)
Agent-Based Verification of von Thünen's Location Theory
Journal of Artificial Societies and Social Simulation
vol. 6, no. 2
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/2/9.html>
Received: 17-Jul-2002 Accepted: 16-Feb-2003 Published: 31-Mar-2003
 Abstract
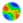
Abstract| Table 1: Generalized agricultural categories in von Thünen's scheme | ||
| I | Intensive Agriculture | Fruits, vegetables, and dairy; products that perish quickly and must be transported immediately to market. |
| F | Forestry | Woods, both for construction and firewood. In von Thünen's time these were the primary sources of energy and a daily necessity within the city. |
| G | Grain Farming | Grain and staple production. |
| L | Livestock | Ranching and animal husbandry for meat, hides, and other non-dairy products. |
|
| Figure 1. von Thünen's isolated state |
|
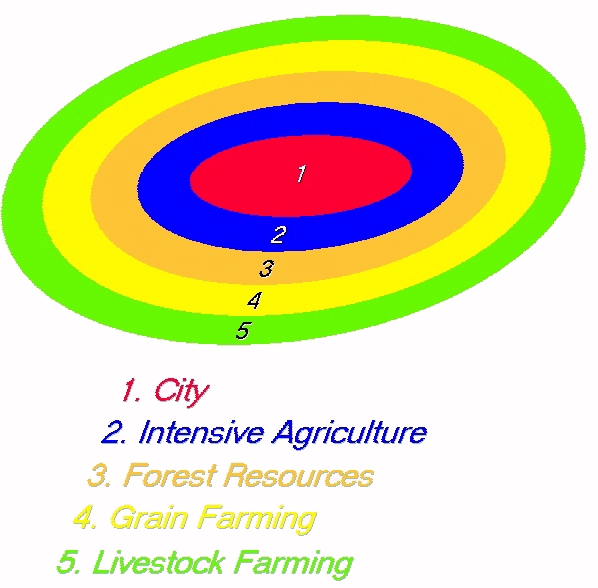
| Figure 2. Cost distributions of commodity with and without transportation included |
|
|
(1) |
where QSf(Pi) is the cumulative quantity on the supply curve on Pi and QCDf(Pi) is quantity of the cost distribution Pi. This is more appropriate for our study than the standard theoretical method of calculating supply, where one calculates the marginal cost curves for all individuals in the population and adds them together. For computational efficiency, we are considering the state as an individual producer, and approximating the supply curve this way for reasons that should become apparent in section 3.3.
|
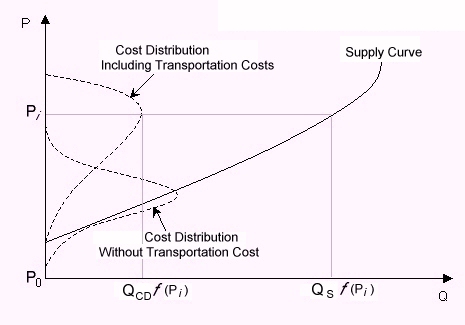
| Figure 3. Conditions forcing an increase in equilibrium price |
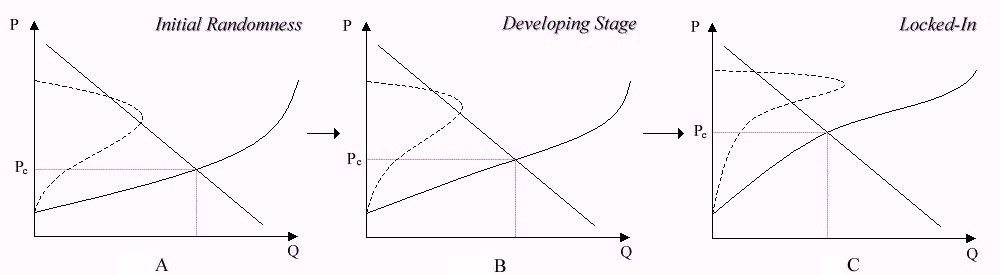
|
| Figure 4. Increase in cost curve causing increasing equilibrium price. Feedback results in convex shape of curve at lock-in |
|
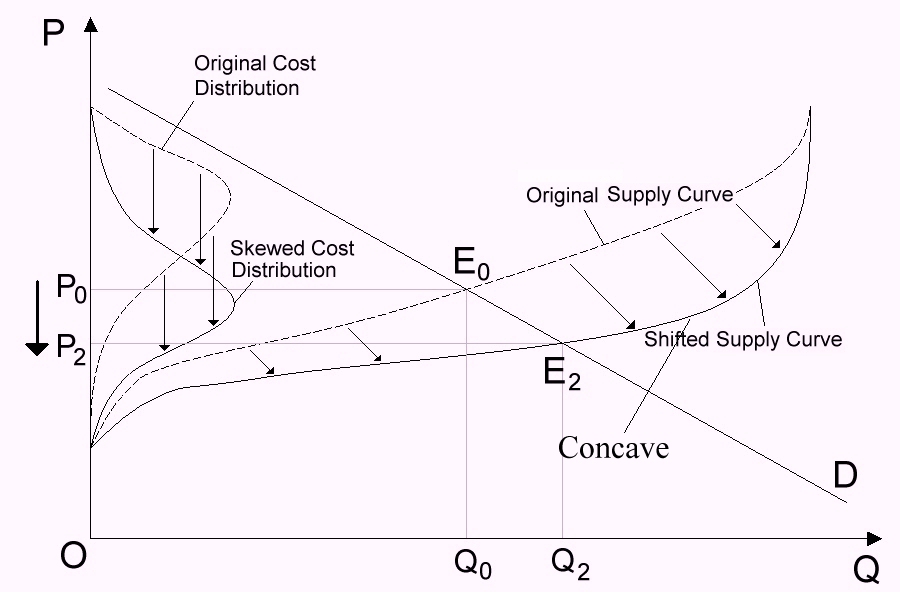
| Figure 5. Conditions forcing a decrease in equilibrium price |
|
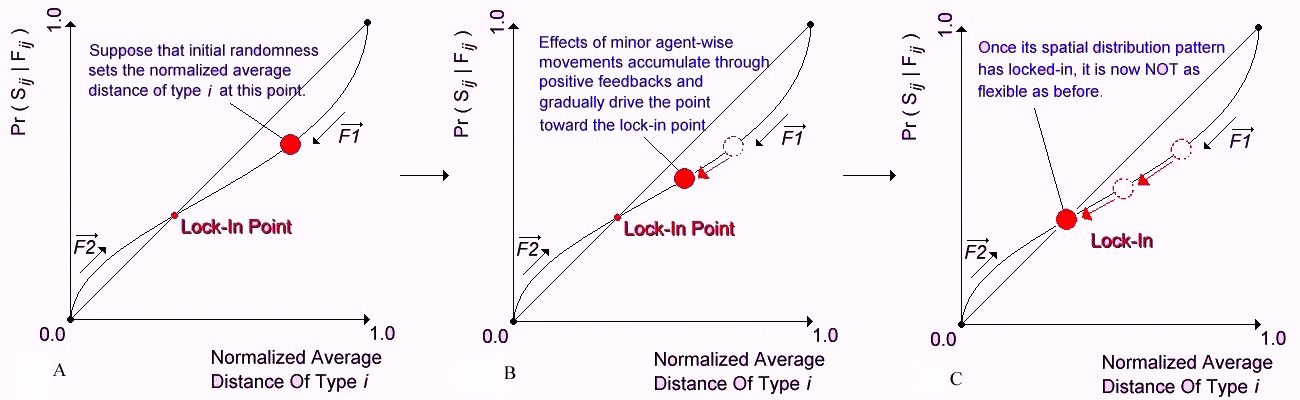
| Figure 6. feedback from individual agents causing lock-in of price |
|
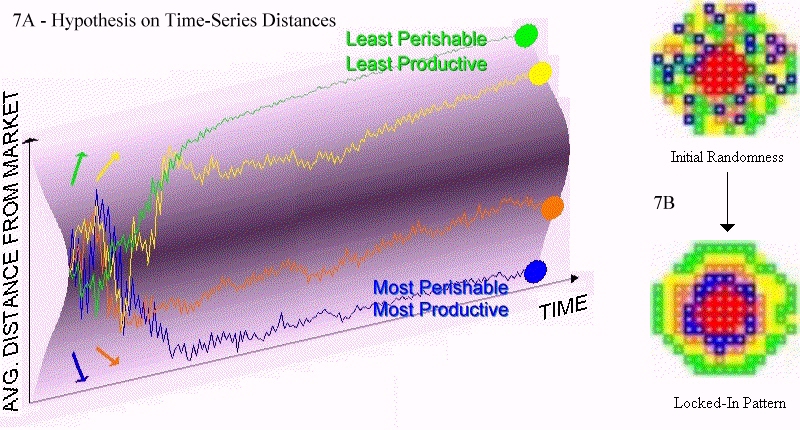
| Figure 7. Lock-in of prices represented in time and space |
| Table 2: Objects defined in this simulation |
Economic Agent: these are families who are farming or could be farmers. They make decisions to settle and farm in different areas depending on market conditions and their own economic state. They have the following properties: Market: an object which collects production and demand statistics from all of the economic agents, and synthesizes this information into reports of equilibrium prices for each agricultural type. The market has the following properties: Supply and demand curve graphs for each agricultural product iLandscape: two-dimensional raster world in which economic agents live. Each raster cell is occupied by a cell object; the landscape is effectively a 2d collection of cell objects. Each cell object has the following properties: Position (x, y) (does not change through simulation) |
| Table 3: Initial parameters for simulation | ||
| variable | value | description |
| worldXSize | 100 | size of world |
| worldYSize | 100 | |
| initNumFamily | 15000 | number of families in world |
| maxNumFamily | 150 | Maximum number of families in a cell |
| avgFamily | 5 | average family size |
| stdvFamily | 1 | Std.dev. of family size |
| naxArea | 5 | maximum area of plot, in number of cells |
| areI | 1 | maximum area occupied by ag type I |
| areF | 2 | maximum area occupied by ag type F |
| areC | 4 | maximum area occupied by ag type C |
| areR | 5 | maximum area occupied by ag type R |
| prodI | 1800 | productivity of ag type I |
| prodF | 2500 | productivity of ag type F |
| prodC | 900 | productivity of ag type C |
| prodR | 400 | productivity of ag type R |
| initiUnitPriceI | 8 | initial unit price of ag type I |
| initiUnitPriceF | 3 | initial unit price of ag type F |
| initiUnitPriceC | 5 | initial unit price of ag type C |
| initiUnitPriceR | 7 | initial unit price of ag type R |
| demandI | 30 | initial demand for ag type I |
| demandF | 80 | initial demand for ag type F |
| demandC | 80 | initial demand for ag type C |
| demandR | 30 | initial demand for ag type R |
| perishI | 0.05 | perishability of ag type I |
| perishF | 0.01 | perishability of ag type F |
| perishC | 0.01 | perishability of ag type C |
| perishR | 0.00 | perishability of ag type R |
| transportCost | 0.05 | transportation cost per unit distance per unit amount |
| cityIncome | 2500 | income for city dwelling families |
| minSatisfaction | -5 | minimum level of satisfaction |
| resoluteness | 0.01 | resoluteness of families |
| Table 4: Relative values for parameters between four agricultural types | |
| Productivity | F ≈ I > G > L |
| Max Area | L > G > I > F |
| Initial Unit Price | I > L < G < F |
| Demand | F > G > I ≈ L |
| Perishability | I > F ≈ G > L |
if agent is farmer then revenue := marketPrice(i) * productivity(i) * area costs := labor_and_capital(i) + transportation income := revenue - costs else if agent is city_dweller then income := cityIncome end if
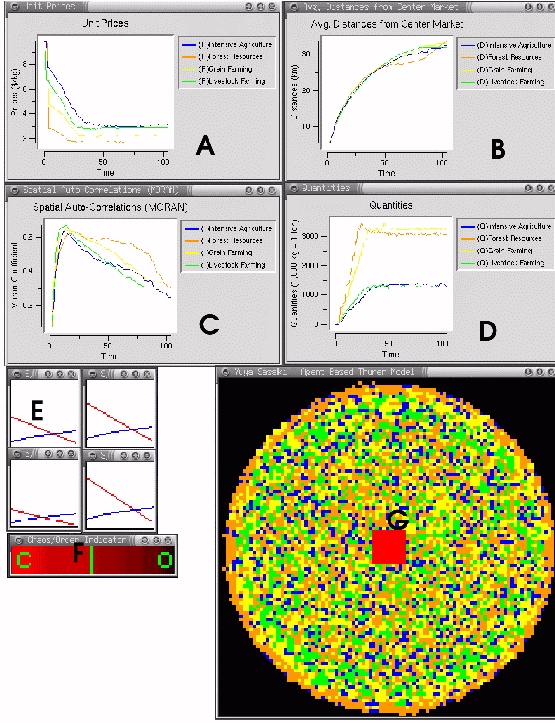
|
| Figure 8. Graphical interface to agent-based model. A: Unit price for each agricultural product (x: time y: price) B: Average distance of agricultural type from city (x: time y: distance) C: Spatial autocorrelation of each agricultural type (x: time y: autocorrelation) D: Total quantity produced of each crop (x: time y: amount) E: Supply and demand graphs for each crop F: Chaos/Order graph G: Spatial representation of model |
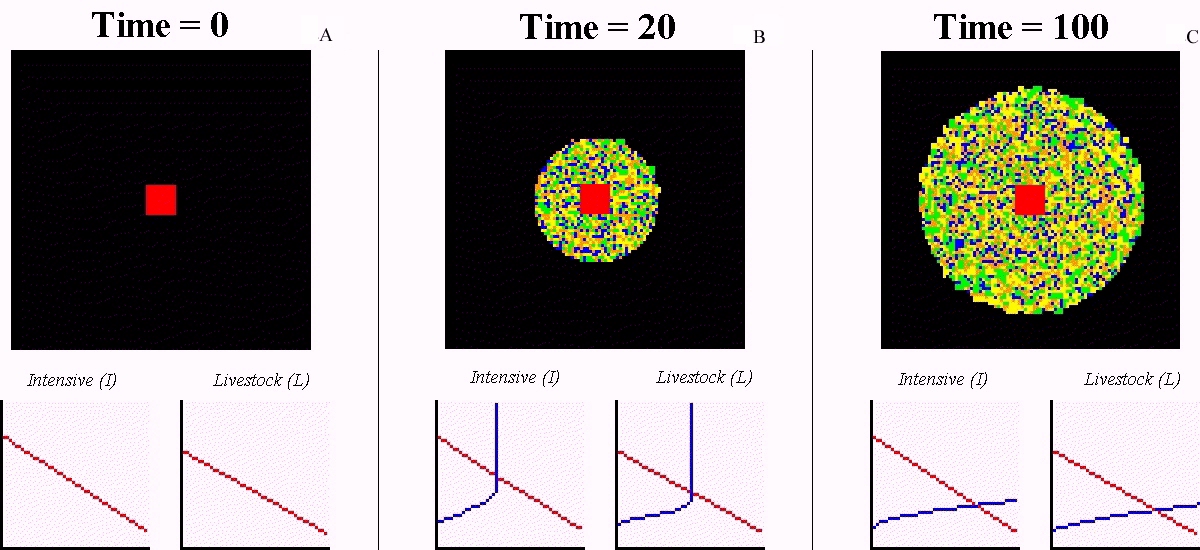
|
| Figure 9. Simulation results for first 100 time steps |
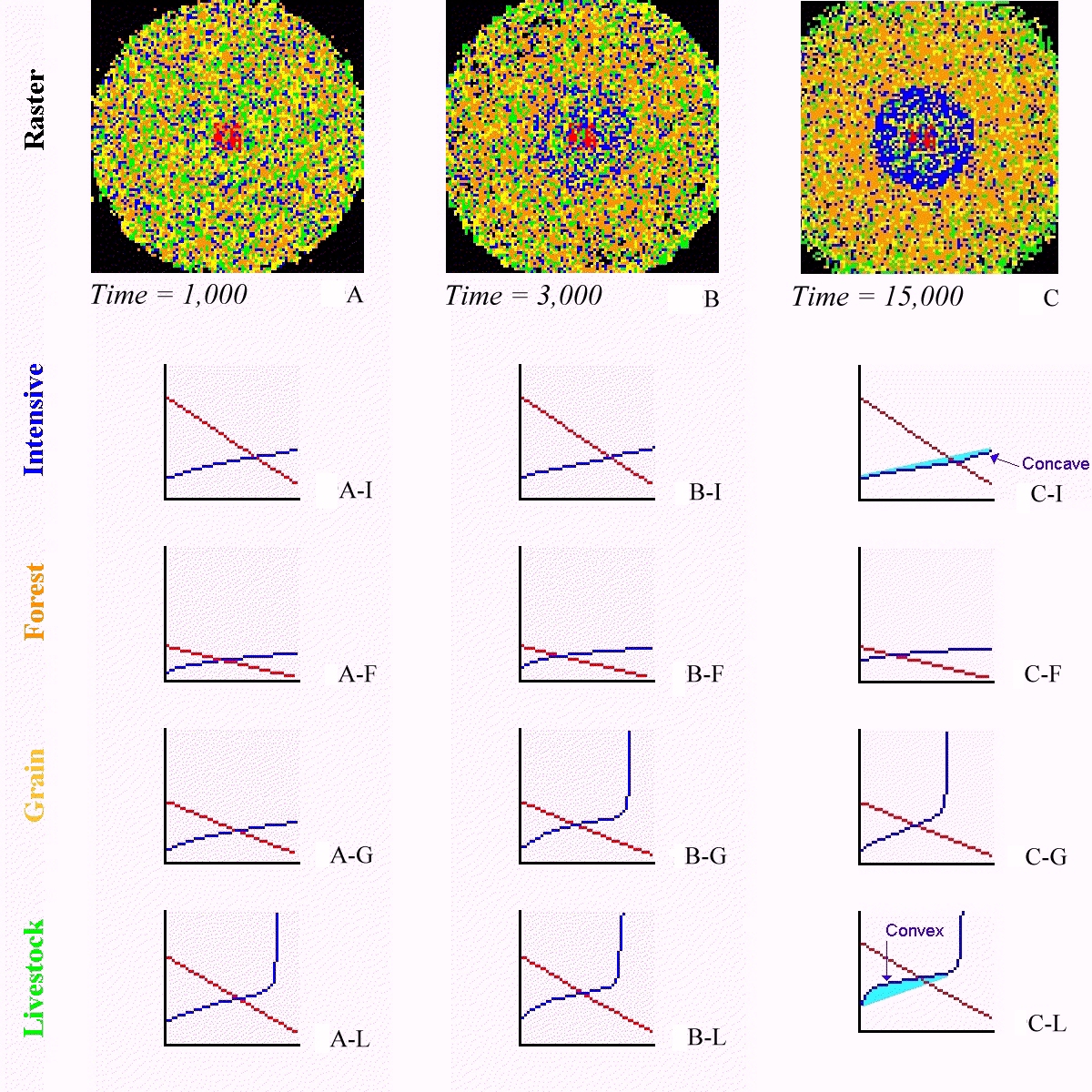
|
| Figure 10. Simulation results from 1000 to 15,000 time steps |
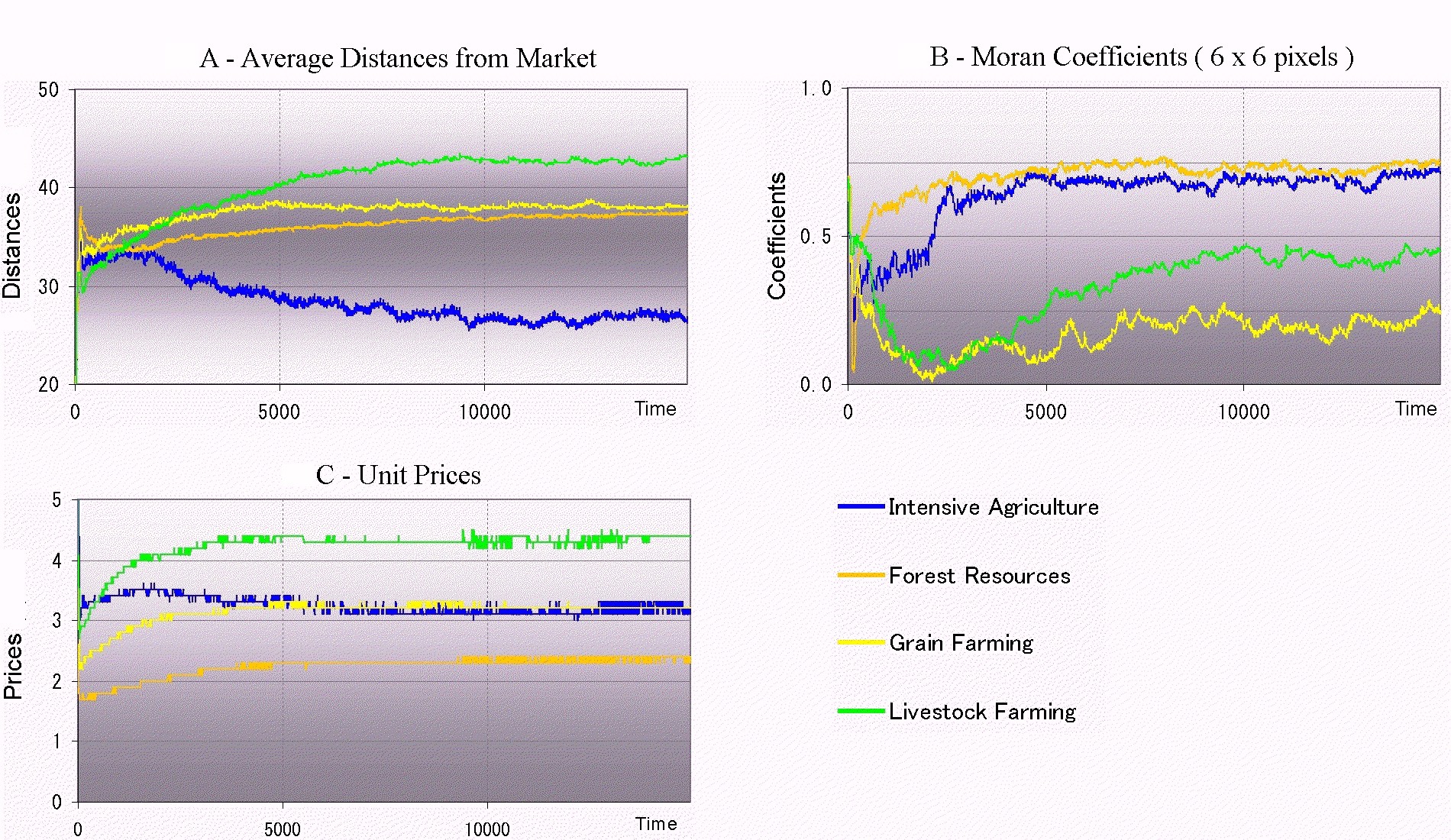
|
| Figure 11. Time series of spatial and market trends for a single simulation run of 15,000 steps |
|
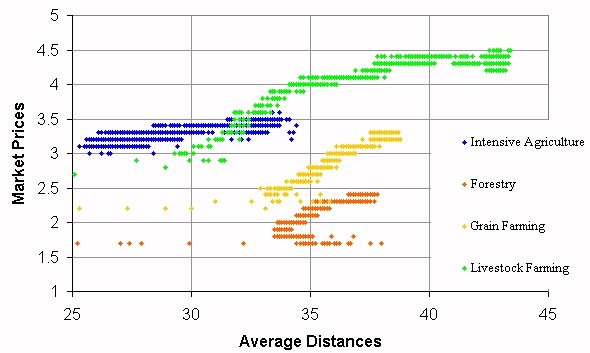
| Figure 12. Correlation between average distance to market and unit price of crops |
| Table 5: Correlations of crop prices with distance to markets for 15,000 agents after 15,000 time steps | |||
| Coefficient | t | Coeff. Dependency | |
| I | .47 | 65.21 | 100% |
| F | .70 | 120.04 | 100% |
| G | .70 | 120.04 | 100% |
| L | .79 | 157.80 | 100% |
|
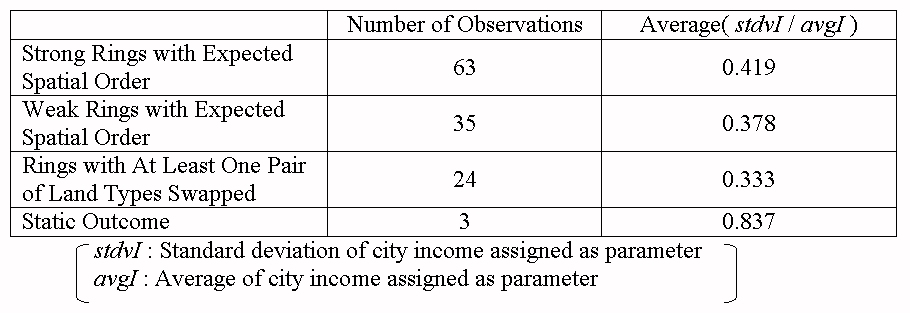
| Table 6. Number of observations and average coefficient of variation of city income for each output category |
|
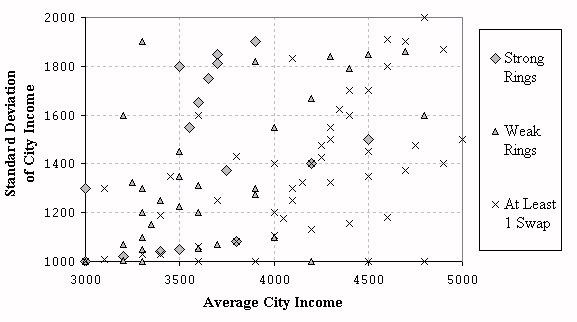
| Figure 13. The plot of output categories over standard deviation and average city income |
|
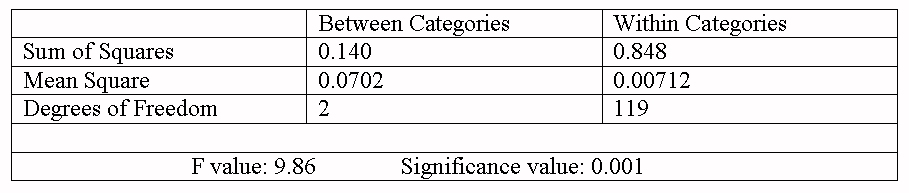
| Table 7. ANOVA table |
ARTHUR B W (1987) Path-dependent processes and the emergence of macrostructure. European Journal of Operational Research, 30. pp. 294-303.
ARTHUR B W (1990) Positive Feedbacks in the Economy. Scientific American, Feburary 1990. pp. 92-99.
AXELROD R (1997) "Advancing the art of simulation in the social sciences". In R. Conte, R. Hegselmann and P. Terna (Eds) Simulating Social Phenomena. Springer
AXELROD R M (1984) The Evolution of Cooperation. Basic Books, New York.
BLOCK D and DuPuis M E (2001) Making the country work for the city: von Thünen's ideas in geography. American Journal of Economics & Sociology, 60(1). pp. 79-99.
BOUSQUET F and Gautier D (1998) Comparasion de deux approches de modélisation des dynamiques spatiales par simulation multiagents: les approches spatiales et acteurs. CyberGéo, 89.
BOX P W (2002), "Spatial units as agents: Making the landscape an equal player in agent-based simulations". In Gimblett H R (Ed.), Integrating Geographic Information Systems and Agent-Based Modeling Techniques for Understanding Social and Ecological Processes, Life Sciences, Oxford. Oxford University Press. pp. 59-82.
CHISHOLM M (1981) Rural Settlement and Land Use: An Essay in Location. Nethuen Drama.
CLARKE K C, Hoppen S, and Gaydos L (1997) A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area. Environment and Planning B: Planning and Design, 24. pp. 247-261.
DEADMAN P J (1999) Modeling individual behavior and group performance in an intelligent agent-based simulation of the tragedy of the commons. Journal of Environmental Management, 56. pp. 159-172.
DEAN J S, Gummerman G J, Epstein J M, Axtell R L, Swedland A C, Parker M T, and McCarroll S (2000), "Understanding Anasazi culture change through agent-based modeling". In Kohler T A and Gumerman G J (Eds.), Dynamics in Human and Primate Societies: Agent-Based Modeling of Social and Spatial Processes, Studies in the Sciences of Complexity. Santa Fe Institute, Oxford University Press. pp. 179-206.
HOLLAND J H (1995) Hidden Order: How Adaptation Builds Complexity. Perseus Books, Cambridge, MA.
KOHLER T, Kresl J, Van West C, Carr E, and Wishusen R H (2000), "Be there then; a modeling approach to settlement determinants and spatial efficiency among late ancestral pueblo populations of the Mesa Verde region, U.S. southwest". In Kohler T A and Gumerman G J (Eds.), Dynamics in Human and Primate Societies: Agent-Based Modeling of Social and Spatial Processes, Studies in the Sciences of Complexity. Santa Fe Institute, Oxford University Press. pp. 145-178.
KOHLER T and Van West C (1996) "The calculus of self interest in the development of cooperation: Sociopolitical development and risk among the northern Anasazi". In Tainter J A and Tainter B B (Eds.), Evolving Complexity and Environment: Risk in the Prehistoric Southwest, volume XXVI of Santa Fe Institute Studies in the Sciences of Complexity, Reading, MA. Addison-Wesley. pp. 171-198.
LANGTON C G (1991), "Computation at the edge of chaos: Phase transitions and emergent computation". In S. Forrest. Emergent computation : Self-organizing , collective, and cooperative behavior in natural and artificial computing networks. Cambridge MA: MIT Press, pp.12 - 37.
LIM K, Deadman P, Moran E, Brondizio E, and McCracken E (2002), "Agent-based simulations of household decision making and land use change near Altamira, Brazil". In Gimblett H R (Ed.), Integrating Geographic Information Systems and Agent-Based Modeling Techniques for Understanding Social and Ecological Processes, Life Sciences, Oxford. Oxford University Press. pp. 277-310.
MANSON S M (2000), "Agent-based dynamic spatial simulation of land-use/cover change in the Yucatán peninsula, Mexico". In 4th International Conference on Integrating GIS and Environmental Modeling (GIS/EM4): Problems, Prospects and Research Needs, Banff, Alberta, Canada. NCGIA. Sept 2-8, 2000.
MINAR N, Burkhart R, Langton C, and Askenazi M (1996) The Swarm simulation system: A toolkit for building multi-agent simulations. Santa Fe Institute Working Paper 96-06-042.
NAGEL, E. (1961) The Structure of Science: Problems in the Logic of Scientific Explanations. Harcourt, Brace, and World, NY.
OTTER H S, van der Veen A, and de Vriend H J (2001) ABLOoM: Location behaviour, spatial patterns, and agent-based modeling. Journal of Artificial Societies and Social Simulation, 4(4). <https://www.jasss.org/4/4/2.html>.
PARKER D C (2000) Edge-Effect Externalities: Theoretical and Empirical Implications of Spatial Heterogeneity. PhD thesis, University of California, Davis, CA.
PEET J R (1969) The spatial expansion of commercial agriculture in the nineteenth century: a von Thünen interpretation. Economic Geography, 45. pp. 283-301.
TORRENS P M and O'Sullivan D (2001) Cellular automata and urban simulation: Where do we go from here? Environment and Planning: B, 28. pp.163-168.
VON THÜNEN J H (1826) Die isolierte Staat in Beziehung auf Landwirtshaft und Nationalökonomie. Pergamon Press, New York. English translation by Wartenberg C M in 1966, P.G. Hall, editor.
WARTENBERG C M (1966) The Isolated State: an English Edition of Der isolierte Staat. Pergamon Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]