© Copyright JASSS


Franco Malerba, Richard Nelson, Luigi Orsenigo and Sidney Winter (2001)
History-Friendly models: An overview of the case of the Computer Industry
Journal of Artificial Societies and Social Simulation
vol. 4, no. 3,
<https://www.jasss.org/4/3/6.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 10-Oct-00
Accepted: 30-May-01
Published: 30-Jun-01
 Abstract
Abstract
-
This paper presents and discusses the methodological rationale, the basic structure and some first results of a new approach to the analysis of processes of industry evolution: "history-friendly" models, concerning the history of the computer industry. The specific purpose of this paper is to evaluate in more general terms the potential and limits of this approach, rather than the formal structure or results of a particular case.
The paper illustrates first the philosophy beneath the use of "history-friendly" models. Then, after a brief summary of the main stylized facts about the evolution of the computer industry and of the main theoretical issues raised up by our investigation, we go on presenting the structure of the model. We then discuss the main results and some preliminary exercises involving different hypotheses on agents' behavior (strategies of product diversification) and policy issues.
- Keywords:
- computer industry, history-friendly models, Schumpeterian economics
 Introduction
Introduction
- 1.1
- This paper presents and discusses the methodological rationale, the basic structure and some first results of a new approach to the analysis of processes of industry evolution: "history-friendly" models.
- 1.2
- In order to present an example of this approach, we base our discussion on the first of these models, about the history of the computer industry. However, the purpose of this paper is to evaluate in more general terms the potential and limits of this approach. For this reason we give more attention to the methodological nature than to the formal structure of a particular case. Similarly, we don't aim now to discuss specific results but to present a survey of the first exercises made around the model.
- 1.3
- The paper is organized as follows. Section 2 illustrates the "philosophy" beneath the use of "history-friendly" models. Then, one model is presented, with reference to the computer industry. Section 3 briefly resumes the stylized facts about computer evolution and the main theoretical issues raised up by our investigation. Section 4 describes the structure of the model. In section 5 we discuss main results and some preliminary exercises involving different hypotheses on agents' behavior (strategies of product diversification) and policy issues. Section 6 concludes, suggesting further developments and uses of this approach.
 Purposes and rationale of "history-friendly" models.
Purposes and rationale of "history-friendly" models.
- 2.1
- "History-friendly" models have the ambition to be a new generation of evolutionary economic models. They are formal models which aim to capture - in stylized form- qualitative theories about mechanisms and factors affecting industry evolution, technological advance and institutional change put forth by empirical research in industrial organization, in business organization and strategy, and in the histories of industries. They have been developed as the consequence of some reflections about the uses and the results of "first generation" economic evolutionary models.
- 2.2
- The main purpose of those models was to broadly explore the logic of evolutionary economic processes and to demonstrate the feasibility of the theoretical and methodological approach. Some - but not all- of those models aimed to "mimic" and explain empirical phenomena such as economic growth, the relationship between industrial structure and innovation, the diffusion processes, and other stylized facts about issues of industrial dynamics. The best known example concerns the analysis of the relationship between industrial structure and innovation in Nelson and Winter (1982). Other models share this same approach. For example, Silverberg et al. (1988) generate the typical "S-curve" of diffusion processes; Dosi et al. (1995) reproduce at the same time some important stylized facts of industrial dynamics: patterns of entry and exit, survival and growth of firms, the emergence of asymmetrical distribution of firms' size, etc.
- 2.3
- Even if the linkage to empirical evidence was considered an essential and characterizing element of the evolutionary approach, most of these "first-generation" models shared rather simple and abstract features. Also when they had a very complex formal structure, the description of phenomena under observation was not very exhaustive. The methodology they adopted was the following: they recognized - rather parsimoniously- one or more stylized facts and they developed a model able to reproduce those phenomena in accordance with an evolutionary explanation. In most of cases, the core of the exercise was a test about the asymptotical properties - or metastable properties - of a system characterized by a complex dynamic structure, whether or not they led to the stylized facts previously presented. For example, the model developed by Nelson and Winter (1982) aimed mainly to demonstrate that - in an evolutionary context - high innovation rates generate a very concentrated industrial structure. Likewise, Dosi et al. (1995) showed that, according to certain hypotheses about the nature of firms' learning processes and the kind of market selection, a model - also a very simple one - can generate industrial structures with very different characteristic pertaining to rates of entry and exit, concentration, patterns of stability or turbulence, distribution of firms' size, etc
- 2.4
- At the same time, the formal structure of these models was often very stylized, too. In most cases, the only agents explicitly modeled were firms. Moreover, the way their internal structure and their behavior were featured was very simplified. Also the demand side was not represented in any depth. These features were plausibly justified by the characteristics of topics under investigation, and also by an obvious aim for simplification. Anyway, they made not possible to analyze key topics like the processes of vertical integration/disintegration or product diversification. The role of the demand side of the market, and the importance of different kind of institution in affecting features and dynamics of industrial structure has been explored only to a little extent, until now.
- 2.5
- Our opinion is that this "first-generation" of evolutionary economic models were a remarkable success. But this very success explains the need to go a step further.
- 2.6
- First, the fact that even simply evolutionary economic model are able to reproduce and to explain a huge variety of relevant empirical phenomena feeds a greater ambition. In a provocative way, one could ask if it hasn't been too easy to achieve current results. If even very heterogeneous evolutionary models seem often able to reproduce stylized facts, then two questions emerge. On the one hand, it might well be that the explanatory mechanisms embodied by evolutionary economic models are really "powerful". In this case, it is necessary to identify more precisely these mechanisms and to try to "generalize" current results using more parsimonious models. In other words, one has to search for the minimal set of hypotheses which leads to results equal to the ones given by more complex models. When possible, this ought to be done analytically. Recent works by Giovanni Dosi, Yuri Kaniovski and Sidney Winter (Dosi, Kaniovski and Winter, 1999) go in this direction.
- 2.7
- On the other hand, paradoxically, one must question if, maybe, those facts were so easy to explain because they weren't sufficiently specified, and conditioned to restrictions. They might be "unconditional objects" (Brock, 1999), which can result from very different dynamic processes. Thus, it is also necessary and possible to follow another direction, different but entirely complementary to the previous one. That is to say, one may seek to enrich models, both as the kind of theoretical fact they try to explain and their internal structure are concerned. The imposition of a tighter "empirical discipline", is necessarily a more demanding test for the model[1]. Moreover, this approach emphasizes the traditional argument that evolutionary theory could -and should- retain solid linkages with empirical research and it forces the modeler to specify to a greater extent and to a greater care the causal relationships and the dynamical processes behind the model.
- 2.8
- Against this background, a field of study that seems particularly interesting and challenging is given by the analysis of the evolution of specific industries. Noticeably, this is a subject strictly linked, but at the same time conceptually different from what is usually defined as "industrial dynamics" (Malerba e Orsenigo, 1996, Dosi et al, 1997). The latter investigates regularities and differences among industries concerning some features of industrial dynamics like rates of entry and exit, extent of heterogeneity between firms, the persistence of some characteristics of actors (innovations, profits, productivity etc.). On the other side the analysis of industrial evolution focuses on the very history of sectors, trying to identify microeconomics determinants for time series of variables like concentration, rates of entry and exit, innovation, etc.
- 2.9
- A huge literature is now available that investigates the history of different economic sectors, in different countries, for different spans of time. Often, but clearly not always, these models share an evolutionary insight. They present empirical evidence and suggest powerful explanations. Usually these "histories" are very rich and detailed. Actors and variables like the educational system, policies, institutions, the internal organizational structure of firms, the structure of demand play a fundamental role in these accounts. Finally, almost always these analysis adopt the methodology which Nelson and Winter labeled "appreciative theorizing", i.e. non formal explanations of observed phenomena based on specific causal links proposed by the researcher.
- 2.10
- Conversely, there are practically no theories - formalized or not - which try to generalize this particular histories and to extract robust regularities from the observed patterns of industrial evolution. The only example is given by the various version of the model of the "life-cycle" of industries or products (Klepper, 1996, Abernathy and Clark, 1978, Teece and Pisano, 1994)
- 2.11
- The analysis of the pattern of evolution of specific industries provides an ideal ground for the development of evolutionary economic models. First, the richness of the histories implies that, from the modeler's point of view, there are more stylized facts to explain jointly, and thus more restrictions to be imposed. These restrictions do not concern only the joint consideration of different agents and variables. Equally, and perhaps even more important, the purpose of this type of models is not only to determine the asymptotic properties of a system but also the ability to mimic real histories, i.e. time series and specific sequences of events involving jointly many variables[2].
- 2.12
- Second, modeling the history of industry necessarily implies a more rigorous dialogue with empirical evidence and with non-formal explanations of those histories, i.e. with "appreciative theorizing". The researcher is forced to spell out in a satisfactorily detailed way the hypotheses used as bases for an "appreciative" explanation of the evolution of a certain sector. This allows testing the robustness of those assumptions, clarifying the key hypotheses and causal mechanisms, identifying variables and relationships that were not adequately considered in non-formal models. This is particularly relevant because many explanations ("appreciative" models) used in historical analysis are so rich and complex that only a simulation model can capture (at least in part) the substance, above all when verbal explanations imply non-linear dynamics. But it is worth observing that a "history-friendly" model doesn't necessarily need to be based upon simulation, nor on an evolutionary approach.[3].
- 2.13
- Finally, this approach provides the grounds for building, in an inductive way, theoretical generalizations about industrial evolution. As an example, at the very beginning of the development of a model, one must obviously identify the distinctive features of the industries under investigation. This means coming back to one of the main issues in industrial economics, i.e. why industrial structure is often so different across sectors. In all probability, then, a model built to deal with the computer industry should be different from a model of the pharmaceutical industry. But the deliberation about which features have to be different and which can be similar is a basic inductive exercise, which paves the way for subsequent generalizations.
- 2.14
- Thus, a "history-friendly" approach can allow us to face and to reformulate some general questions, typical in industrial dynamics and to propose new hypotheses that have an intrinsic theoretical nature: for example, how the characteristics of supply and demand interact in order to shape industrial structure and its evolution.
 A stylized history of computer industry.
A stylized history of computer industry.
- 3.1
- The history that our model aims to capture draws from different sources, mainly Flamm (1988), Langlois (1990), Bresnahan and Greenstein (1995), Bresnahan and Malerba (1999).
- 3.2
- In brief, the evolution of this industry can be divided in four eras. The first began with early experimentation with computers and culminated in designs sufficiently attractive to induce their purchase by large firms with massive computational needs and by scientific laboratories. This opened the era of mainframe computer. The second era began with the introduction of integrated circuits and subsequent development of minicomputers. The third era is the one of personal computer, made possible by the invention of the microprocessor. The fourth era is the current one, characterized by the presence of networked PCs and the Internet.
- 3.3
- The model focuses on a particular feature of this history: the evolution of industrial structure, which includes several discontinuities concerning both components technology (transistors, integrated circuits, and microprocessors) and the opening of new markets (minicomputers, PCs). One firm - IBM - emerges as a leader in the first era and keeps its leadership also in the successive ones, surviving every potential "competence-destroying" technological discontinuity. In each era, however, new firms (and not the established ones) have been the vehicles through which new technologies opened up new market segments. The old established leaders have actually been able to adopt the new technologies and - not always and often facing some difficulties - to enter in the new market segments, where they gained significant market shares but did not acquired the dominant position they previously had.
- 3.4
- The model then focuses on the following questions: what determines the emergence of a dominant leader in the mainframe segment? What are the condition that explain the persistence of one firm's leadership in mainframe computer, despite a series of big technological "shocks"? What allowed IBM to enter profitably into new markets (PCs) but not to achieve dominance?
 The model
The model
The basic structure of the model
- 4.1
- Given space constraints, we sketch in this section only a simple description of our model, trying to provide the gist of its basic features. The model clearly shares the distinctive characteristics of the evolutionary approach. Agents are characterized by "bounded rationality", i.e. they don't completely understand the causal structure of the environment in which they are set. Moreover, they are unable to elaborate exceedingly complex expectations about the future. Rather, firms' actions are assumed to be driven by routines and rules that introduce inertia in their behavior. Agents, However, can learn and are able to improve their performance along some relevant dimensions, in particular technology.
- 4.2
- Given earlier period's conditions, firms act and modify their performance. Specifically, profitable firms expand, and unprofitable ones shrink. Thus, the model is mainly driven by processes of learning and selection. Jointly, the actions of all agents determine aggregate industry conditions, which then define the state for the next iteration of the model.
- 4.3
- Strong non-linearities are present in this structure. They generate a complex dynamics and prevent an analytical solution of the system. Moreover, we do not impose equilibrium conditions: on the contrary, "ordered" dynamics emerge as result of interactions far from equilibrium.
- 4.4
- The model is made up of different modules.
The era of transistors, entry and the mainframe industry
- 4.5
- At the beginning of our episode, the only available technology for computer designs is transistors. N firms engage in efforts to design a computer, using funds provided by "venture capitalists" to finance their R&D expenditures. Some firms succeed in achieving a computer that meets a positive demand and begin to sell. This way they first break into the mainframe market. Some other firms exhaust their capital endowment and fail. Firms with positive sales uses their profits to pay back their initial debt, to invest in R&D and in marketing. With R&D activity firms acquire technological competencies and become able to design better computers. Different firms gain different market shares, according to their profits and their decision rules concerning pricing, R&D and advertising expenditure. Over time firms come closer to the technological frontier defined by transistor technology, and technical advance becomes slower.
The introduction of microprocessors
- 4.6
- After a period t', microprocessors become exogenously available. This shifts the technological frontier, so that it is possible to achieve better computer designs.
- 4.7
- A new group of firms tries to design new computers exploiting the new technology, in the same way it happened for transistors. Some of these firms fail. Some enter the mainframe market and compete with the incumbents. Some others open up the PC market. Incumbents may choose to adopt the new technology to achieve more powerful mainframe computers.
Adoption and diversification
- 4.8
- The adoption of new technology by old firms is costly and time-consuming: microprocessors do not diffuse immediately among incumbents. In order to switch to the new technology it is necessary that firms first perceive the potential of microprocessors. This depends on the current technological position of incumbents, on the progress and the potential of the new technology, on the competitive threat posed by potential entrants. Adoption then entails a fixed cost. and a variable expenditure proportional to firm's size. Moreover, adoption entails a reduction of the experience firms have accumulated in computer design.
- 4.9
- After they have switched to the new technology, incumbents may decide to diversify into the PC market. The incentive for diversification is a function of the size of the PC market, as compared to the mainframe market. In the model, the diversifying firm founds a new division, thus imitating current PC firms. The initial competencies of the new division are initially located near to the current "average practice". After that, the divisional firm acts exactly as a new entrant, with independent profits, budget, and technological advance. Diversification entails a fixed cost for the parent company, which confers to the new division a fraction of its budget and of its experience in technology and marketing.
- 4.10
- The model includes different actors, "objects" and processes.
Computers.
- 4.11
- Computers are defined by two characteristics, "cheapness" (defined as X1 = (1/p), where p is the price of a given computer) and X2, "performance". These characteristics are the results of the application of each firm's technical competencies, which improve over time because of R&D spending. Every computer has a finite life, which lasts T periods.
- 4.12
- Computer can be designed using two different technologies, characterized by the type of components they embody: transistors (TR) and microprocessors (MP). These technologies become exogenously available at different periods: at the beginning of the episode there are only transistor, while microprocessors become available t' periods later. These technologies define the maximum levels of the two characteristics that can be achieved by a computer design, as shown in Figure 1.
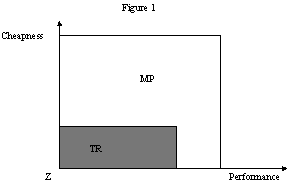
|
|
Figure 1. |
- 4.13
- Note that the use of microprocessors allows to design computers that are "better" that transistor-based computers regarding both performance and cheapness. However, the most dramatic improvement lies in the cheapness direction.
Costumers and Markets
- 4.14
- Computers are offered to two quite separate groups of potential customers. One group, which we call "large firms", greatly values performance and wants to buy mainframes. The second group, which we will call "individuals", or "small users", has less need for high performance but values cheapness. It provides a potential market for personal computers.
- 4.15
- Each of the two user groups requires a minimum level" of performance and cheapness before they are enticed to buy any computer at all. Once these threshold levels of the computers characteristics are reached, the value that customers place on a computer design is an increasing function of its performance and its cheapness.
- 4.16
- Consumer preferences are modeled as follow:
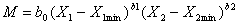
|
|
(1)
|
M is the "level of utility" associated with a computer with particular attributes. Then, the "utility" of a computer with cheapness X1 = 1/p and performance X2 for the user class s is given by a Cobb-Douglas function with the arguments that measure the extent to which threshold requirements (X1min and X2min) have been exceeded. If threshold requirements are not met, M=0. The sum of the exponents in the functions acts like a sort of generalized demand elasticity reflecting performance as well as price, while b0 is a scale parameter.
- 4.17
- Consider now the existence of two consumer groups. If there isn't any other computer available on the market, the (integer) number of a computer, with given characteristic, that each group would acquire is set equal to the utility level "M". In other words, the greater the "value" of a computer, the greater the number of sold products. This way, the utility function (1) has a cardinal interpretation and can be heuristically treated as a demand function.
- 4.18
- Markets for mainframes and for PCs consist of a large number (a parameter in the model) of independent submarkets. They are sub-groups of purchasers with identical preferences. Each submarket buys computer either because it is the first time it enters the market or to substitute computers which have exhausted their life. Besides, the number of "active" submarkets is a function of the number of firms in the market. Thus, over time the demand for computers increases both because the quality of computer improves (and this increases the number of computers each submarkets buys), and because the number of consumers (submarkets) grows.
- 4.19
- If there is more than one kind of computer that meets threshold requirements, our analysis of demand involves variables other than M. Consumers buy computer valuing its "merit", Mi, compared to other products. In addition, markets are characterized by brand-loyalty (or lock in) effects and respond to firms' marketing policies.
- 4.20
- A simple and direct way to account for these factors is the following:
- 4.21
- The probability, Pi, that a particular submarket will buy a computer i is:
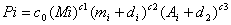
|
|
(2)
|
c0 is specified so that the sum of the probabilities adds to one. Mi denotes the "value" of computer i. "mi" is the market share of the firm who produces computer i, in terms of the fraction of total sales accounted for by that computer. Note that the market share variable can be interpreted either in terms of a "bandwagon" effect, or a (probabilistical) lock-in of consumers who previously had bought products of a particular brand. The constant parameter d1 assures that even computers that have just broken into the market, and have no previous sales, can attract some sales. "A" is the advertising expenditure of a firm. The constant parameter d2 performs here a similar role to d1 for firms who have just broken into the market and have not yet invested in advertising. If consumers in a particular submarket decide to buy computer i, then M is the number of machines they buy.
- 4.22
- Note that, if there is only one computer that meets threshold requirements, then each submarket will buy a number M of it with probability 1. On the other side, assume there is more than one computer that passes the threshold. Then demand behavior is influenced by the exponents of equation (2). For example, if c1 is much greater than c2 and c3, virtually all the consumers will buy the computer with the greater M. On the other hand, if c1 is relatively low, a higher merit computer may be "sold out" by a rival computer that has a higher market share, or which has been advertised very intensively, or both.
- 4.23
- Without lock-in effects or marketing, demand would be similar to a standard demand curve. It would tend to converge towards the higher quality product, even if a positive probability of surviving for computers with lower design would always remain. The inclusion of brand-loyalty and bandwagon effects changes considerably the way market dynamics work. Inertial phenomena and forms of increasing returns now characterize the model.
Firms: technological and market competencies, finance and pricing decisions:
- 4.24
- Our model of firm behavior is meant to capture significant elements of the theory of the firm based on "dynamic competencies" (Winter 1987, Dosi, Marengo 1993, Teece et al, 1996). Firms are represented by sets of technological and marketing competencies that are accumulated over time, and by rules of action. These rules concern the research trajectories followed by firms, the pricing decisions, R&D and marketing expenditure, the adoption of new technologies and the diversification into new markets.
- 4.25
- There is no explicit representation of production per se, or of investment in capacity. It is assumed that the requisite production capabilities can be hired at a price per computer that reflects the "cheapness" attribute of the design.
- 4.26
- The model also aims to capture some aspects concerning finance; in particular, the development of products able to meet consumers' preferences can be time consuming, and it requires financial resources. Clearly, this is especially relevant for new entrants.
- 4.27
- At the beginning of our episode, with the introduction of transistors, we assume that there are a number of firms, endowed by "venture capitalists" with an initial budget to spend on R&D, who hope to exploit the new technological opportunities. All firms starts with the initial design capabilities, represented by point Z in Figure 1. Firms start off with randomly assigned budgets, IB, which they spend to finance their R&D activities in equal amounts over a pre-specified and common number of periods. During these initial periods, firms invest every period a constant fraction of their budget. If the initial endowment is exhausted before a firm meets products threshold, it fails.
- 4.28
- Outcomes of R&D activities depend on the research direction each firm decide to follow, and on latent technological opportunities (i.e. the technological frontiers, defined by the outer limits of the boxes in Figure 1). Firms start off with different randomly assigned trajectories concerning computer characteristics, in terms of cheapness and performance. In order to account for the fact that firms' competencies cannot change rapidly and costlessly, we assume that the directions of technological progress are different for each firm, and cannot change over time. Thus, after the initial period, different firms in the industry will be achieving different computer.
- 4.29
- Through their R&D expenditures, firms accumulate technical capabilities. These are modeled as a stock that increases over time. Technological progress is represented as a shift in the characteristics of each computer, along the two relevant dimensions, that is caused by the application of those specific capabilities.
- 4.30
- Competencies can be thought as the result of the shared experience by two different kind of engineers: some oriented towards the reduction of production costs and some other who care about enhancements of computer performance. The joint action of these efforts results in the technological direction each firm follows. Over time, each firm will hire new engineers, but it keeps groups' proportion constant.
- 4.31
- In each period t, R&D expenditures, Rt, are used to pay the stock of engineers active in the previous period, Rt-1. Along each of the technical dimension, if the fraction of R&D expenditure allocated to a particular group of engineer increases (i.e. Rit > Rit-1) then firm i invests this surplus hiring new people in that group, at a given cost, ceng per person. If, instead, Rit < Rit-1, current employment is reduced by a certain fraction (1/10). If Rit < 0.9 Rit-1, firm uses budget B to cover the difference.
- 4.32
- In every period the "merit " of the computer each firm is able to achieve along its technological trajectory --performance and cheapness— improves according to the following equation:
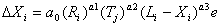
|
|
(3)
|
3)
- 4.33
- The first variable, R, is the firm's R&D expenditure, where i=1 is performance and i=2 is cheapness. As mentioned before, in the first periods this expenditure is a constant fraction of the initial budget. T represents the number of periods that a firm has been working with a particular technology. Obviously this variable is common to all the firms that start off in the very same period. Yet, when microprocessors become available, incumbents will adopt the new technologies in different periods, and thus they will have a different experience. The third variable in the equation, Li-Xi, measures the distance of the achieved design from the technological frontier. The closer one gets to the frontier, the more technological progress slows down, for every given level of R&D expenditure. There is also a random element to what firm achieves, given by e.
- 4.34
- When a firm becomes able to design a computer that meets threshold requirements, and so to sell its products, then it can invests its profits in R&D or marketing activities.
- 4.35
- Profits (which more precisely are modeled as gross margins on production costs), π, in every period are equal to:
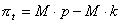
|
|
(4)
|
where M is the number of computers sold, p is the computer price and k is the production cost of a single computer.
- 4.36
- Production costs, k, are determined by the technical progress function. Price is obtained by adding a constant mark-up, µ, to costs:
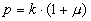
|
|
(5)
|
- 4.37
- The mark-up parameter, µ, is initially equal for all firms. Afterwards, it increases over time depending on each firm's market share. In other words, firms partially exploit their monopolistic power by charging higher prices. Specifically:
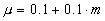
|
|
(6)
|
where m defines the market share of firm i.
- 4.38
- Profits are used in different ways. Firms spend a constant fraction of their profits σ (set equal to 15% for all firms) to repay their initial debt with investors (which is the initial debt capitalized at the current interest rate, r) until it is extinct. What is left is invested in R&D and marketing activities.
- 4.39
- R&D expenditures, Rt, are simply determined as a constant fraction, φ, of what is left after the repayment of their debt:
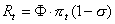
|
|
(7)
|
- 4.40
- Advertising expenditures, A, are calculated in a similar way. They generate marketing competencies that are grow over time. If firms do not invest, their competencies deteriorate and the productivity of a given volume of expenditure decreases. We assume, thus, that the effect of advertising expenditures on sales follows a logistic curve. Specifically, the model first computes advertising expenditures, A*:
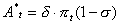
|
|
(8)
|
- 4.41
- This value is then divided by a number that defines the amount of advertising expenditures beyond which the elasticity of sales to advertise is equal to zero (i.e. the asymptote of the logistic curve). This ratio is then inserted into a logistic curve to yield the value of variable A in the demand equation.
- 4.42
- What is left of profits after debt repayment, R&D expenditures and advertising is invested in an account, Bt, that yields the interest rate, r, in each period. Firms treat this account like a reserve.
Transition dynamics
- 4.43
- An essential element of the "dynamic competence" approach to the theory of the firm concerns the cumulative nature of firms' competencies: firms tend to improve gradually following rather rigid directions. As a consequence, they can face great difficulties when trying to do something radically different from their past experience. Competence traps and lock-in phenomena are distinctive features of this approach. For example, Tushman and Anderson (1986), and Henderson and Clark (1990), have documented the difficulties that firms often face when the technologies underlying their products change significantly. Quite often extant firms cannot switch over rapidly enough to counter the threat posed by new firms using the new technology. Christensen and Rosenbloom (1991) have highlighted similar difficulties that incumbents have in recognizing new markets when they open up.
Adoption of new technologies
- 4.44
- In our model, existing transistor-based mainframe firms are able to switch over to microprocessor technology, but this transition may be takes time and costs. It is new firms that do the initial work of advancing computer designs using microprocessors. The probability that an incumbent firm will try to switch over is a function of two variables. The first is how much progress has been achieved by microprocessor computer designs. The second is the distance of a transistor firm from the frontier of technological possibilities defined by transistor technology. The former is clearly a signal to extant firms that "there is a potential powerful new technology out there and we may be in trouble if we don't adopt it ". The latter is an indication that "we can't get much further if we keep on pushing along the same road".
- 4.45
- When an "old" transistor firm decides to switch over, it faces some significant disadvantage, but also has an advantage. The disadvantage is that the experience accumulated in the transistor-technology counts for little or nothing if it shifts to microprocessors (recall equation 3). Thus, in its first efforts after adoption, its computers will have only about the average quality of extant microprocessors-based mainframe computers. Further, it must incur a once and for all switchover cost in order to start designing, producing and marketing microprocessors-based mainframes. However, extant firms have the advantage of large R&D budgets, which, at a given cost, can be switched over to working with the new technology, and a stock of cumulated earnings on which they can draw to cover any transition cost.
- 4.46
- To sum up, adoption takes place in two steps. First, firms must "perceive" the potential of microprocessor technology. Probability of perception is a function of the current technological position of the firm in relation to the frontier in transistor technology and of the progress realized by microprocessors:
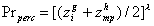
|
|
(9)
|
where Pperc i the probability of perceiving, zi is a fraction of the transistors technological frontier covered by firm i and zmp is the fraction of microprocessor frontier covered by the best-practice microprocessor firm. The parameter λ measures the general difficulty of perceiving the new technology.
- 4.47
- Once firms have perceived the possibility of adoption, they have to invest in order to acquire the new technology. Adoption costs (Cad) entail a fixed cost, Fad, equal for all firms, and the payment of a fraction q of firms' accumulated budget, linked to factors like the training of engineers etc. Thus,
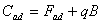
|
|
(10)
|
- 4.48
- Firms whose budget does not cover these costs cannot adopt microprocessors. Moreover, the competence-destroying nature of the new technology is captured by the notion that adoption implies that experience accumulated on the old technology now counts much less. In the model, experience (T) is reduced by a factor that is a parameter of the model.
Diversification
- 4.49
- Once firms have adopted the new technology, they have access to the new technological frontier and can innovate faster. However, they maintain their original trajectory. These firms now have the possibility to diversify, producing computers for the PC market. The incentive for diversification is a function of the size of the PC market, defined in terms of sales, as compared to the mainframe market. Specifically, diversification becomes possible when the ratio between the size of the PC market and the size of the mainframe market is bigger than a threshold value, which is a parameter of the model.
- 4.50
- The old trajectory of technological progress will not be - in general - the best suited one to design PCs. As a matter of fact, IBM entered the PC market founding a completely new division. The procedures governing diversification in the model mimic the actual strategy used by IBM.
- 4.51
- The parent company starts a new division in the attempt to exploit the available competencies specific to PCs, rather than applying its own competencies to the new market. The new division inherits from the parent company a fraction of its budget and of its technical and advertising capabilities. The size of these fractions is a parameter of the model. The position of the new division in the design space is determined as the average merit of design prevailing in the PC markets at the time diversification occurs. In other words, the parent company exploits "public knowledge" in the PC market and partly imitates PC firms. Further, the technical progress trajectory is randomly recalculated. After birth, the new division behaves exactly as a new entrant, with independent products, profits and budget. It faces the disadvantage that there are already firms selling in the PC market, with designs that already exceed threshold, positive market shares, established advertising budgets and experience in the PC market. However, the new "daughter" firm has the advantage of being able to dip into the "deep pockets" and resources of its parent firm, which can transfer a sizeable fraction of its extant R&D and advertising budgets into the new division.
 The simulation runs
The simulation runs
- 5.1
- This model can be used for different purposes. First, obviously, it is necessary to verify that the model is able to reproduce the history of the industry, using parameters' settings that reflect the main hypotheses on the determinants of stylized facts. Second, one has to test the robustness of hypotheses, checking that different values of parameters effectively lead to results which are quantitatively and qualitatively different. After that, the model can be used to analyze different hypotheses concerning agents' behavior, or to investigate the effects of different policies. One can also try to explore more general theoretical questions about industrial evolution.
History replicating and history divergent simulations
- 5.2
- The model is able to replicate the industry history, with a parameter setting - the "standard set"- that reflects the basic key assumptions that economists who have studied the computer industry suggested were behind the pattern that happened. The details of the simulations are discussed in a previous paper and, for reason of space, we do not discuss them here again. (Malerba et al. 1999).
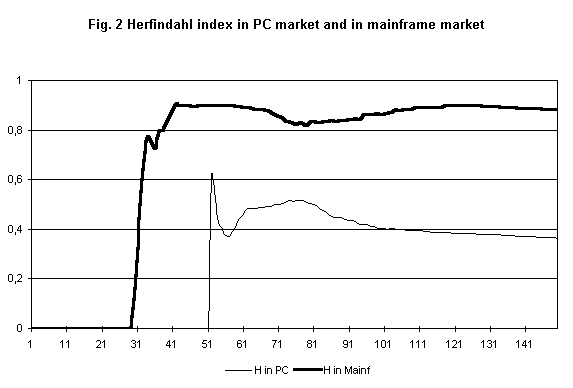
- 5.3
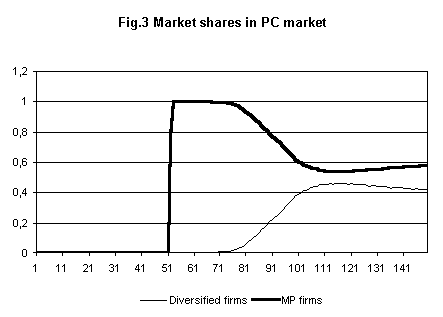
- A dominant transistor-based firm (IBM) emerged relatively quickly in the mainframe market (Figure 2). That firm holds on to its large market share, even when new microprocessor firms entered that market and challenged it. Part of the reason is given by the fact that dominant firm shifted over to microprocessors technology in a relatively timely manner. IBM then diversifies into the PC market, and gained a nontrivial, but not a dominant, share (Figure 3).
- 5.4
- The parameter setting beneath these simulations was based on the following key hypotheses. First, the dominant position of IBM in the mainframe market was due to significant effects of brand-loyalty and consumer lock-in. This raised substantial entry barriers to new entrants. In terms of our model, we set relatively high values for the parameter that captures the role of extant market share into the demand function. Thus, a firm that has a high market share in mainframes will attract a sizeable share of new purchases. Second, by the time microprocessors became available, computer design under the old technology was reasonably advanced, and the leader, IBM, responded to the availability of the new technology pretty rapidly. In terms of our model, soon after the first microprocessor firms enter the mainframe market, the dominant transistor firms in that market switches over to microprocessors. Third, IBM's massive resources enabled it quickly to mount an R&D and advertising effort sufficient to catch up with the earlier entrants into the PC market.
- 5.5
- However, in PC market lock-in and brand-loyalty processes were less significant: for example, the software used by several PC producers was compatible with the software used by IBM. So there wasn't any particular lock-in to IBM. And within the class of IBM compatibles, customers were quite sensitive to the merit of the computer being offered, particularly to price. In our model, thus, in the PC market the coefficient on quality is high and the coefficient on specific market share is low.
|
|
Figure 2.
|
- 5.6
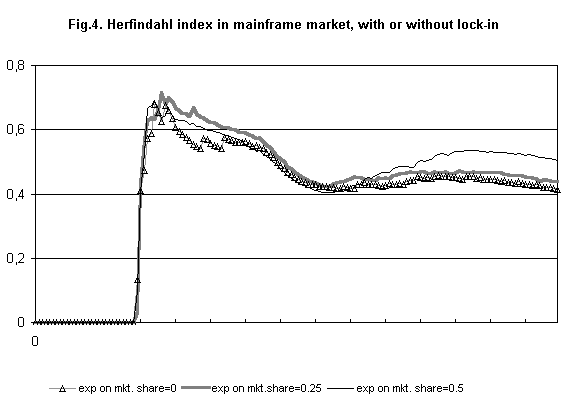
- Changes in this standard set of parameter actually lead to different results, corresponding to the fundamental causal factors of the observed history. (Figure 4). A reduction of the market share's parameter in the demand function of mainframe market lowers significantly market's concentration.
|
|
Figure 3. |
|
|
Figure 4.
|
- 5.7
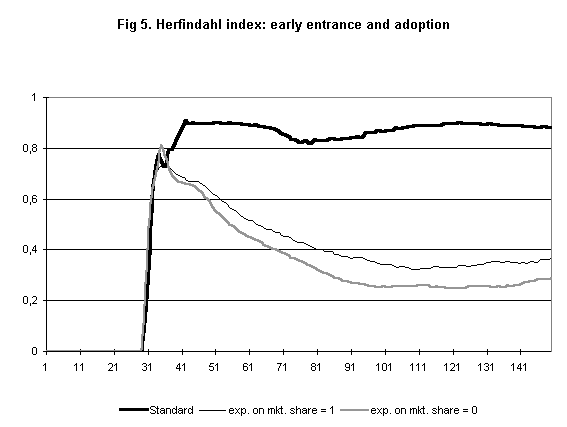
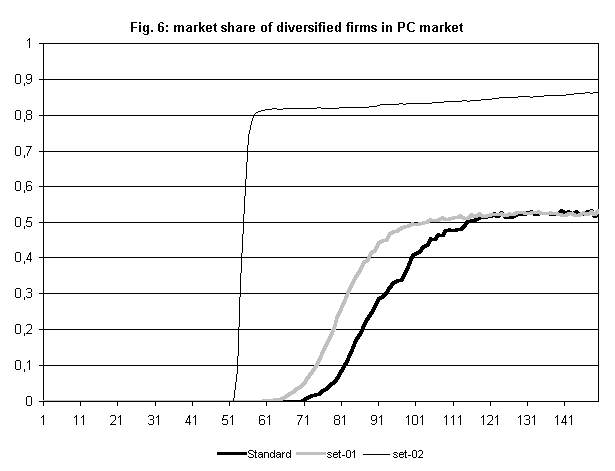
- In another counterfactual exercise, we anticipate the time of introduction of microprocessor technology. When this happens, new firms break into the market before the emergence of a dominant firm. Indeed, the process of microprocessor adoption is then slower and more costly. Facing this environment, IBM is not able to achieve a significant market share in the PC market because it must compete with firms who have already a dominant position in the new segment. (Figure 5). Conversely, IBM becomes able to dominate also the PC market, when we modify the parameters concerning technical progress and demand and when we ease the diversification process. In particular, in the function that drives technological change, we increase the value of the coefficient of the variable R and decrease the coefficient for variable T : i.e. scale economies in R&D become more important while experience loses importance. In the demand function, the coefficient of variable A (advertising) is significantly increased. This new set of parameters (Set 01), if taken alone, modifies only slightly IBM's market share in the PC market (Figure 6). If we add to these changes also a reduced costs of diversification and a greater percentage of the budget being transferred from the parent company to the new division (set 02), then IBM is able to break into the PC market quite rapidly and, exploiting resources accumulated by the parent company, is able to dominate the new market too.
|
|
Figure 5.
|
|
|
Figure 6.
|
Alternative diversification strategies
- 5.8
- As we said earlier, the diversification strategy used by mainframe producers to enter the PC market was modeled so to mimic - in a stylized way - the actual procedure IBM adopted. The logic of this strategy is based on the assumption the technological and market competencies built in the mainframe market might not be adequate in the PC market. (Christensen and Rosenbloom, 1995).
- 5.9
- Would another strategy had performed better? To explore this issue, we modeled a different stylized diversification behavior, which we label "competence-driven" (Malerba et al, 1999). Here firms try to apply their specific "mainframe" competencies to the new product, the PC. So, after adoption, the diversifying firms set up a new internal division which designs a PC using the company's competencies and start selling it. The new division is founded endowed with a fraction of the parent company's budget, of technological and marketing competencies. However, it also inherits the extant trajectory of technological progress and begins its activities starting from the position reached by the parent company in the space of technological characteristics.
- 5.10
- Competence driven diversification may entail the disadvantage that the new division's trajectory of advance might fare relatively badly in a markets that values more cheapness rather than performance. Conversely, the strategy based on the acquisition of new knowledge from external sources can be much more expensive and, in general, the new random selected trajectory might well turn to be a very bad one.
- 5.11
- Let us compare the consequences of the two strategy in the standard set of parameters. "IBM" strategy performs indeed better than "competence- driven" strategy", leading to a much faster growth in market share. However, the difference is not dramatic and, above all, in the long run, when the technological frontier is approached and technological progress becomes slower, the "competence-driven" strategy catches up and generates in the end a (marginally) higher market share.
- 5.12
- The main reason for this result is that when IBM's independent division is launched, its position in the technological and market space is set around the average of the firms already selling in the PC market and its new trajectory is picked up at random. Thus, the "new IBM" is advantaged mainly by its availability of large financial resources to invest in R&D and in marketing, but it might as well pick up a "wrong" trajectory while trying to challenge new entrants. A "competence- driven" strategy, instead, would not perform badly if the design of PC did not require a drastic re-orientation in the competencies mix (i.e. in the trajectory of technological advance) and if the PC market were not too distant from the mainframe market (i.e. the threshold defining the PC market were not too far away from IBM's position at the moment of diversification). In these case, even progressing along the old trajectory would quickly lead IBM into the PC market. IBM-PC would be disadvantaged in terms of cheapness, but it would probably be much better off in terms of performance.
- 5.13
- To test the logic of this argument, we modified the parameter setting as follows. First, the technological frontier after the introduction of microprocessors is significantly widened and its corner is now positioned so to further increase the scope for progress in the cheapness direction relative to performance. In other words, the old trajectory, which led IBM to dominate the mainframe market, is now strongly disadvantaged. Second, the thresholds defining the PC market are significantly shifted upwards. That is to say, the distance that needs to be covered by IBM in order to enter the PC market starting from its old position and adopting a "competence-driven" strategy is now much larger as compared to the previous parameter setting.
- 5.14
- Results of this exercise show coherently that a "competence-driven" strategy performs now much worse than the "IBM" strategy. This is particular evident for the very first periods after diversification. In sum, "competence-destroying" technological change and the emergence of new segments that favor significantly different product characteristics tend to lower the performance of competence-driven strategies. (Figure 7).
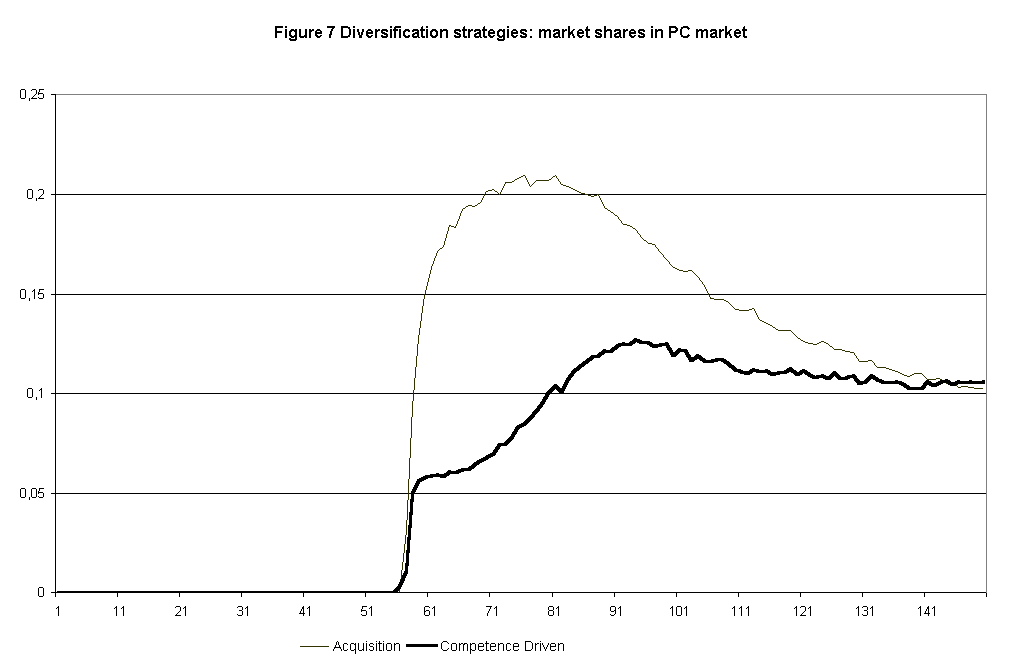
|
|
Figure 7.
|
Industrial policies
- 5.15
- The model embodies different form of dynamic increasing returns, as it has been emphasized by virtually all appreciative contributions concerning the history of the computer industry. In particular, two kinds of dynamic increasing returns play key roles. First, there is cumulativeness in firms' efforts to advance product and process technologies. Firms learn from their past successes and, since technological success generally leads to greater sales and profits, have the funds to further expand they R&D efforts ("success breeds success").
- 5.16
- Second, the model presents dynamic increasing return on the demand side, because of the existence of features like brand-loyalty and lock-in effects. This is particular evident in the market for mainframe computers.
- 5.17
- The result of these dynamic forces is the rise of IBM as a near monopolist in mainframes. On the other hand, IBM was not able to transfer its monopoly position to personal computers, where marketing dynamic increasing returns were less substantial. Our model suggests that, given the structure of dynamic increasing returns, this pattern was nearly inevitable. Note that the interaction of these processes tend to reinforce each other: even a small initial technological advantage is amplified both by the cumulativeness of technological progress and by the lock-in effect on the demand side. Beside, the tendency toward a monopolistic structure remain even when we increase the importance of computer merit - as compared to market share and advertising expenditure - in the demand function. As a matter of fact, the product which initially achieve the higher merit will end to dominate the market, as a consequence of dynamic increasing returns on the technological side and to the effects of the "success breeds success" process (i.e.: more profits, more R&D expenditure, more technical improvements). The result, quite paradoxically, is that a more "competitive" market - with little inertia in consumers behaviour - can generate more concentration than a market where inertia is greater.
- 5.18
- Against this background, several policy questions become relevant. First, the Schumpeterian trade-off: to what extent technological advance necessarily imply monopoly power? Second, could industrial policies have changed these patterns?
- 5.19
- The exercises we now present do not address directly the former question, about the desirability of public intervention to promote competition[4]. Rather, it aims at investigating questions about the effectiveness of public policies under conditions of dynamic increasing returns. How can these policies affect industry evolution over time? How big the intervention should be, to be effective? Is the timing relevant? Do policy interventions have indirect consequences on the dynamics of a related market?
- 5.20
- We have analyzed two sets of policies: antitrust and interventions aiming at supporting the entry of new firms in the industry (Malerba et al, 2001a). To cope with space, we further discuss only antitrust policies.
- 5.21
- In our model, the antitrust authority (AA) intervenes when the monopolist reaches a share equal to 75% of the market[5]. It acts by breaking the monopolist in two smaller companies. The two new firms originating from the old monopolist have half of size and resources of the mother company: budget, engineers, cumulated advertising expenditures (and thus also bandwagon effect). They keep on, however, the same position in terms of product attributes (cheapness and performance), experience and technology of the old monopolist[6]. The two new firms differ only in terms of their trajectory: one of the two inherits the monopolist trajectory, the other a randomly selected one[7].
- 5.22
- AA may intervene at different periods. In one case intervention is set very soon, 1 year (4 periods) after the first firm has reached a share equal to 75% of the market. This is a very unrealistic run, because most of the time AA breaks the very first entrant, when no other competitors exist. In other cases AA intervention is not immediate (5 years), late (10 years), or very late (20 years).
- 5.23
- Results (Figure 8) show that, when AA intervenes very early, the market becomes concentrated again very soon, albeit at a lower level than in the standard case.
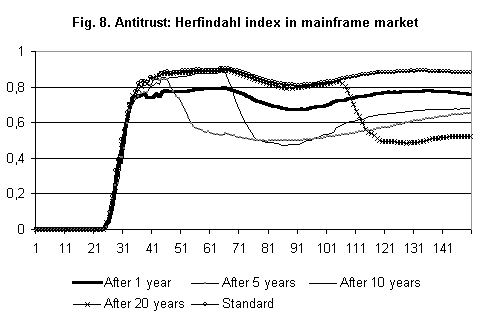
|
|
Figure 8.
|
- 5.24
- In the case of "not immediate" intervention (5 years), all the firms have already entered the market but they are still small in absolute terms. The break up of the largest firm has the effect of making firms more similar in terms of size and resources, so that the emergence of a new monopolist takes more time and the Herfindahl index reaches at the end a lower level (though still a significant one) than the standard case (between .6 e .7). On the contrary, if the intervention comes "late" (10 years), the monopolist has already reached a certain size and the new firms resulting from the intervention are already rather large with respect to other competitors. Therefore, one of the two firms will gain the leadership and the market will tend toward concentration, with the Herfindahl level higher than in the previous case (and similar to the standard one). Finally, if the intervention occurs after 20 years, the market will be divided into two oligopolists, which won't be able to profit any longer from the possibility of gaining market leadership, because dynamic increasing returns are limited (technological opportunities are almost depleted).
- 5.25
- These results show the relevance of the timing of the intervention in dynamic markets. It makes a big difference whether AA intervenes too early or too late Another interesting result concerns the effects on the second market (PC) of an antitrust intervention in the mainframe market. In general, even if the intervention has limited effects on the first market, it produces noticeable consequences on a proximate market, i.e. the PC segment. In this second market the level of concentration is lower than in the standard case. (Figure 9). The reasons o this result are the following: when AA intervenes early (after 1 or 5 years), both new firms are able to diversify into the PC market. As compared to the standard case, two firms enter in the new market, not one only. As a consequence, the PC market will be shared by a greater number of firms. In case AA intervenes "late" (after 10 o 20 years), only one firm will be able to diversify, as it happens in the standard set. However, this firm will be smaller and the overall concentration in the PC market will decrease.
- 5.26
- Finally, in a third group of simulations, we have tested the effect of antitrust when one of the two sources of increasing returns is not present. In order to do that the exponent on the market share is set equal to zero in the demand equation (this way we rule out bandwagon effects). Results (Figure 10) show both a reduction in the overall concentration index and, above all, a bigger effect of antirust policies. Compared to the previous cases, we still observe differences linked to the timing of the intervention but the Herfindahl index is always lower. Moreover, once the monopolist is halved, concentration does not tend not to grow again.
- 5.27
- To sum up, this exercise suggests some consideration. First, in strongly cumulative markets, where substantial dynamic increasing return are present, - either because of the cumulativeness of technological advance or the existence of lock-in on the demand side- there is a strong tendency towards concentration and some sort of "natural monopoly". Our main result is that it is extremely difficult to contrast this tendency. Quite often, the antitrust intervention is ineffective in significantly modifying the degree of concentration, above all in the long run. Even when one source of increasing returns is ruled out, we have a lower level of concentration compared to other cases, but still a tendency towards the emergence of a dominant firm[8].
- 5.28
- The reasons for this "policy ineffectiveness" lay in the strongly cumulative nature of the market. Small initial advantages tend to grow bigger and bigger over time and catching up is almost impossible. Leaders do not only have a "static" advantage: they also run faster than laggards. Policies of the kind we have been examining are somehow designed to "leveling the playing field". But this does not seem to be enough. In order to get effective and long-lasting results, some form of "positive discrimination" might be necessary. That is to say, in the presence of strong dynamic increasing returns, policies should make competitors able to run (much) faster than the monopolist, and not just remove static disadvantages.
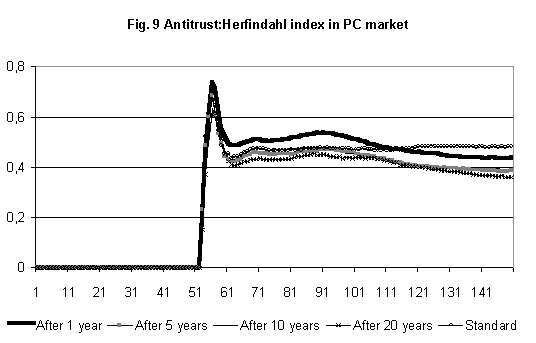
|
|
Figure 9.
|
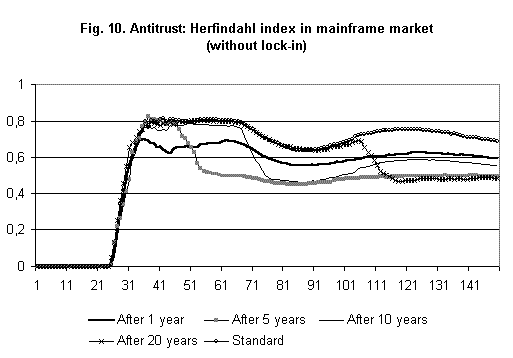
|
|
Figure 10.
|
 Conclusions
Conclusions
- 6.1
- The model presented here - even if very simple- has shown to be adequately flexible and "powerful" to perform the purposes at the base of its creation. It captures in a stylized and simplified way the focal points of an appreciative theory about the determinants of the evolution of the computer industry. It is able to replicate the main events of the industry history with a parameter setting that is coherent with basic theoretical assumptions. Changes in the standard set of parameters actually lead to different results, "alternative histories" that are consistent with the fundamental causal factors of the observed stylized facts.
- 6.2
- Having accomplished this result, the model can be used for different purposes. In this paper we have sketched some exercises aimed at exploring different hypotheses about agents' behavior and the conditions which determine the profitability of different strategies. Further, we have investigated alternative designs for industrial policies in markets characterized by dynamic increasing returns.
- 6.3
- These exercises are just few examples of the feasible application of the model. Other topics are obviously possible and necessary. Beside, this is a first and particular version of the model. Different insights and analytical settings can and must be developed.
- 6.4
- The model seems suitable also to start tackling more ambitious and general theoretical issues. We believe that this version already highlights some interesting suggestions for the theoretical investigation of matters such as the relation between innovation and dynamics of industrial structures. For example, the model shows the significant role of demand's features in shaping market structure and innovation rates. The overall importance of different variables like lock-in, brand-loyalty, frictions and other imperfections characterizing consumers' behavior is illustrated. At the same time the model takes in account the emergence of new products and new markets. The presence of these frictions and the relevance of dynamic increasing returns are powerful mechanisms, which tend to generate concentration and the persistence of leaders' advantages. Conversely, the existence and emergence of new products and new markets tend to lower concentration and make market shares less stable.
- 6.5
- The second theoretical insight concerns the consequences of discontinuities -due to technological shifts or to the emergence of new markets - on incumbents. Such discontinuities create different kinds of problems to extant firms. On the one hand, they face the challenge linked to the adoption of the new technologies. Further, they must manage to acquire the competencies that allow them to successfully break into new markets. The current version of the model, coherently with stylized facts, suggests that this latter challenge has been the most difficult for mainframe producers. In other context, obviously, we could face different conditions but the model provides a formal conceptual tool for deeper investigations of these issues. The third insight concerns entry and its importance for market evolution. In the model new firms, and not established ones, open up new markets. They play also a fundamental role by stimulating incumbents to adopt new technologies and to diversify into new markets. Again, this particular history might be quite different in other industries or under other conditions. This model, however, seems a suitable starting point for further analysis of this subject.
- 6.6
- At a higher level of abstraction, our model lends support, some original insights and suggestions for the study of the evolution of industrial structures. For example it supports, with new and dynamically-based explanations, some conclusions recently proposed by John Sutton (Sutton, 1999) about the relation between innovation and market structure. Moreover, the model embodies some of the stylized facts at the heart of the industry life cycle theory (Klepper, 1996) - e. g. the relevance of first mover's advantages, shake-outs, etc. - but, again, the explanation of these features is grounded on different insight and reaches different conclusions, above all as it concerns the role of demand and the emergence of new markets.
- 6.7
- Finally, the model starts to examine the dynamic properties of structures characterized by several sources of increasing returns. Until now, typically, economic literature focused on cases where only one source of increasing returns is present. For example, models that share an evolutionary approach have investigated the consequences of the cumulativeness of technical advance. Others have analyzed the importance of network externalities on the demand side (Arthur 1985, David 1985, etc.). We think that the joint consideration of these aspects can be a promising trajectory of analysis, showing the possible differences in these processes and, above all, illustrating the consequences -which are not always intuitive- of their interaction. From another point of view, the model provides some preliminary suggestions on how lock-in phenomena deriving from path-dependent processes might sometimes be broken by new technological shocks and the emergence of new markets, i.e. by the appearance of new opportunities for innovation and by heterogeneity in consumers' beheviour.
- 6.8
- This model is only a preliminary attempt and there are many opportunities for further research along these lines. As we mentioned in the Introduction, two directions of work seem to us particularly worthwhile pursuing - beside the further development and improvement of the current model. Along both these directions, some work is already in progress. The first direction of analysis concerns the processes of vertical integration and specialization. The computer industry is an ideal field to investigate, with a dynamic approach, the determinants of firms' boundaries, the emergence of new specialized industries for components' production (semiconductor and software industries) and their co-evolution. Another direction is provided by the analysis of another industry - pharmaceuticals - which has radically different features from computers as it concerns the dynamics of technological change, the structure of demand, the key role played by universities and regulatory authorities. The study of this case might constitute a further step for verifying the robustness of this approach and for broadening its scope through comparative dynamics.
 Notes
Notes
-
1 The pledge for a closer relation with empirical evidence becomes even more important every time that the analytical modeling efforts run the risk to be driven more by the application of specific techniques, rather than by the attempt at explaining certain well-defined empirical regularities, as it tends to happen also in the evolutionary approach.
2 From this point of view, these models are similar to models about economic growth, like Nelson and Winter 1982, Chiaromonte and Dosi, 1993, Dosi et al. 1994.
3 For example, the model presented by Jovanovic and MacDonald (1993) could be thought a neoclassical antecedent of "history-friendly" models
4 The model does not include a robust and clear definition of welfare. To get a preliminary insight, in every set of simulation we compared industry-wide outcomes in terms of cheapness and performance. In general, different levels of concentration do not lead to dramatically different results. In other words, the "Schumpeterian trade-off" does not seem to play a role in current version of the model. More competitive markets actually produce lower mark-ups and prices, but also less profits and technical progress. In monopolistic conditions, the mark-up is higher, but greater profits imply also greater R&D expenditure and costs' reduction. However, the model does not adequately captures one of most important feature of competition in evolutionary contexts: the possibility for heterogeneous firms to explore radical new technological opportunities. Some preliminary results suggest, indeed, that industrial policies supporting new firms can be more successful when enacted in periods closer to technological discontinuities, i.e.- in this version of the model- when microprocessors emerge.
5 Given model's characteristics, the 75% share could be modified without substantially changing the results. In fact, the dominant firm (IBM) in few years reaches a share between 80% and 90% of the mainframe market and does not fall below this level in the course of the whole simulation.
6 In a simulation we have halved the monopolist in two but have maintained the overall endogenous bandwagon effect to one of the two new firms. Of course, the firm that inherits this effect very rapidly regains a dominant position. This result points out the fact that an antitrust intervention that aims just to break in two the R&D and the size of the monopolist, without paying attention to bandwagon effects in a market with lock-in, is doomed to sure failure.
7 In another set of simulation, the two firms shared the same trajectory. Results do not differ from the new random trajectory case.
8 We got similar results in the analysis of policies supporting the entry of new firms. In Malerba et al (2001) different forms of intervention are compared: support to potential new entrants during the "exploration" period (before they begin to sell); support to small firms after they break into the market; support for the creation of new firms (aiming to increase the number of competitors). In most exercise we obtain an analogous result, that only an extremely sizeable intervention is effective in lowering concentration. Also a mix between antitrust and entry-support policies gives similar results.
 Referencies
Referencies
-
ABERNATHY W. and J. UTTERBACK (1978) Patterns of Industrial Innovation,
Technology Review, pp. 41-47
ARTHUR, W.B. (1985), Competing Technologies and Lock-in by Historical Small Events: The Dynamics of Allocation Under Increasing Returns", Technological Innovation Project Working Paper No. 4, Center for Economic Policy Research, Stanford University
BRESNAHAN T.F. and S. GREENSTEIN (1995), Technological Competition and the Structure of the Computer Industry, Journal of Industrial
Economics, 47, 1, pp.1-40
BRESNAHAN T.F., and F. MALERBA (1999), Industrial Dynamics and the Evolution of Firms' and Nations' Competitive Capabilities in the World Computer Industry, in D. Mowery and R.Nelson (ed) The Sources of Industrial Leadership Cambridge University Press
BROCK, W.A. (1999), "Scaling in Economics: A Reader's Guide", Industrial and Corporate Change, 8,3, 409-446
CHIAROMONTE, F. and G. DOSI (1992), "The Microfoundations of Competitiveness and Their Macroeconomic Implications", in C. Freeman and D. Foray (eds.), Technology and the Wealth of Nations, Pinter Publishers, London.
CHRISTENSEN, J.L. and R. ROSENBLOOM (1994), Technological Discontinuities, Organizational Capabilities, and Strategic Commitments, Industrial and Corporate Change,3 , pp 655-686
DAVID, P.A. (1985)"Clio and the Economics of QWERTY", American Economic Review, 75, 332-337
DOSI, G., S. FABIANI, R. AVERSI and M. MEACCI (1994), The Dynamics of International Differentiation: A Multi-Country Evolutionary Model, Industrial and Corporate Change, 3, 1, 225-242
DOSI G., and L. MARENGO (1993), Some Elements of an Evolutionary Theory of Organizational Competence, in Evolutionary Concepts on Contemporary Economics, England R. W. (ed.), University of Michigan Press, Ann Arbor
DOSI, G. , F. MALERBA, O. MARSILI and L. ORSENIGO (1997), "Industrial Dynamics: Stylized Facts, Empirical Evidence and Theoretical Interpretations", Industrial and Corporate Change, Special Issue on Technological Regimes and the Evolution of Industrial Structures", 6(1), pp. 3 - 4
DOSI, G., MARSILI O., ORSENIGO L. and SALVATORE R. (1995), ""Technological Regimes, Selection and Market Structures", Small Business Economics.pp. 411-436
FLAMM K. (1988), Creating the Computer. The Brookings Institution.
HENDERSON R., and K.B.CLARK(1990), Architectural Innovation: The Reconfiguration of Existing Product Technologies and the Failure of Established Firms, Administrative Sciences Quarterly, 35, 9-30
JOVANOVIC, B., and G.M. MACDONALD (1993), The Life Cycle of a Competitive Industry, Working paper No. 4441, National Bureau of Economic Research, Cambridge (Ma).
KLEPPER, S. (1996) , "Entry, Exit and Innovation over the Product Life Cycle", American Economic Review, 86(3), 562-582.
LANGLOIS R.N.(1990), Creating External Capabilities: Innovation and Vertical Disintegration in the Microcomputer Industry, Business and Economic History, 19, 93-102
MALERBA, F., and L. ORSENIGO (1996), "The Dynamics and Evolution of Industries", Industrial and Corporate Change,5(1), pp. 51-87.
MALERBA F. NELSON R. ORSENIGO L. WINTER S. (1999)"History friendly models of industry evolution: the computer industry", Industrial and Corporate Change, 1, 3-41
MALERBA F., NELSON R., ORSENIGO L. and WINTER S. (2001a), "Competition and Industrial Policies in a "History-Friendly" Model of the Evolution of the Computer Industry", International Journal of Industrial Organization, 19, 613-634.
NELSON R. and WINTER S.(1982), An Evolutionary Theory of Economic Change, Harvard University Press
SILVERBERG, G., DOSI, G. and L. ORSENIGO (1988), Innovation, Diversity and Diffusion: A Self-Organization Model, The Economic Journal 98, pp. 1032-1054
SUTTON J. (1999), Technology and Market Structure, Cambridge (Ma.), MIT Press.
TEECE, D. and G. PISANO (1994) The Dynamic Capabilities of Firms: An
Introduction, Industrial and Corporate Change, 3, pp. 537-555
TUSHMAN M.L. and ANDERSON P.(1986), Technological Discontinuities and Organizational Environments, Administrative Science Quarterly, 31, 439-456
WINTER S. (1987), Knowledge and Competence as Strategic Assets, in Teece D. J. The Competitive Challenge, Cambridge (Mass), Ballinger, pag 159-184
WINTER S., KANIOVSKI Y. and DOSI G. (1999), "Modeling Industrial Dynamics with Innovative Entrants", mimeo, LEM Working Papers 1999/01, S. Anna School of
Advanced
Studies, Pisa , Italy

 Return to Contents of this issue
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999
 Abstract
Abstract![]() Introduction
Introduction![]() Purposes and rationale of "history-friendly" models.
Purposes and rationale of "history-friendly" models.
![]() A stylized history of computer industry.
A stylized history of computer industry.
![]() The model
The model

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() The simulation runs
The simulation runs









![]() Conclusions
Conclusions![]() Notes
Notes![]() Referencies
Referencies![]()
Return to Contents of this issue