© Copyright JASSS


Klaus Auer and Tim Norris (2001)
"ArrierosAlife" a Multi-Agent Approach Simulating the Evolution of a Social System: Modeling the Emergence of Social Networks with "Ascape"
Journal of Artificial Societies and Social Simulation
vol. 4, no. 1,
<https://www.jasss.org/4/1/6.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 10-Jan-01
Published: 31-Jan-01
 Abstract
Abstract
-
The behavior of cellular automata is a very close representation of the evolution of complex social systems. We developed the simulation model "ArrierosAlife" to explore the behavior of changes in social networks over time. The model is based on empirical data, a result out of a longitudinal field work. The focus of this research is a comparison of network changes over time in the "real world" compared with the emergence of social networks in an artificial society. "Ascape" was used as a modeling frame work to facilitate the development and analysis of the simulation model. We will give a brief overview of the developed model and describe the experiences using "Ascape" as a framework.
- Keywords:
- Cellular automata, multi-agent model, evolution, social networks, object oriented programming language, artificial landscape
 Introduction
Introduction
- 1.1
- The aim of the research carried out by Klaus Auer (Department of Anthropology - University of Cologne / Germany) was to uncover the process underlying changes of social networks over time. Field research was done in the Cordillera Blanca (Perú) from 1998 till 2000. Five donkey driver (Arrieros) associations have been observed over three years and data on network changes, economic activities, kinship and life histories was collected. For more information about the ongoing research please see http://www.uni-koeln.de/phil-fak/voelkerkunde/forsch/peru/0-initial.htm.
- 1.2
- Observing the "real world" of Arriero communities resulted in a rich data base (qualitative and quantitative data) but a time span of three years is not sufficient for any conclusions about emergent phenomena. The histories of the associations, size of communities and the composition of their resource (tourists) differ significantly even if they are all located relatively close by in the northern part of the mountain range.
- 1.3
- Due to limited financial resources an observation of the social system under investigation was not possible. A simulation model based on the rich data gained during field work is the perfect solution to investigate changes and emergent properties over a longer time period (Gilbert 1995). An artificial society, representing the Arriero communities, delivers the data we needed for the analysis necessary to answer research questions about changes of networks over time. In silica we can perform experiments with the society by varying parameters and analyze the phenomena occurring during a time span of 10 or 15 years. The experiments will not harm the "real world"; they don't need large financial resources; they don't last much longer than a few minutes, and they satisfy the needs of the researcher.
 Complexity theory and agent based modeling
Complexity theory and agent based modeling
- 2.1
- The complex arrangement of inter-linked components forms a social system, a complex system with the potential of evolving new structures over time. As an assumption we can say that the smallest parts of a social system (human agents) produce their own emergent properties and form the next level of structure in the system (e.g. a norm). The basic assumption is that complexity arises out of internal diversity (Heylighen 1999). Complex systems perspective explains, across disciplines, how complex and adaptive behavior can arise in systems composed of large numbers of relative simple components with no central control and with complicated but limited interactions (Kauffman 1993, Kauffman 1995; Nicolis and Prigogine 1989). Applied in social anthropology the aim of Complexity Theory is to explain the formation and transmission of cultural patterns.
- 2.2
- A System is a finite number of interacting components functioning as a whole and distinguishable from its surroundings by boundaries. New system structure appears without explicit involvement from outside of the systems boundaries ( Nicolis and Prigogine 1989: 238-242). It is the result of systems interacting components. The organization can evolve in either time or space. Emergence is a characteristic of the complex (self organizing) systems. It is the appearance of a property not previously observed ( Nicolis and Prigogine 1989: 138-141).
- 2.3
- Following these ideas there is no need for attempting to find a complete representation of the "real world" because a representation is necessarily incomplete. An agent-based model might discover that a set of simple rules iterated across a collection of agents produces a particular dynamic as we may observe similar phenomenon occurring in the real world ( Hegselmann 1998). Agent based modeling combined with the principles of cellular automata is an approach covering the theoretical findings for the simulation of complex social systems ( Hegselmann and Flache 1998).
 Ascape as a modeling base for the development of "ArrierosAlife"
Ascape as a modeling base for the development of "ArrierosAlife"
- 3.1
- The Brookings Institution provides on the world wide web a software framework for developing and analyzing agent-based models called "Ascape" (http://www.brook.edu/ES/dynamics/models/ascape/). Among others Epstein and Axtell's Sugarscape model ( Epstein and Axtell 1996) is implemented in "Ascape" (Parker 1998). The framework is entirely written in the object-oriented programming language "Java" (the Java Development Kit JDK was developed by Sun Microsystems and is available at http://java.sun.com). Java applications are platform independent and can be run on PC, UNIX, Mac or other platforms.
 From Empirical Data to Simulation Model
From Empirical Data to Simulation Model
- 4.1
- "Ascape" has been generally used to develop models for social and economic phenomena. With it's 2-dimensional matrix capabilities, we were able to adapt the base model to provide a semi-geographic area in which we could simulate the empirical data collected. The greatest challenge that we encountered is that the empirical data represents many aspects of societal behavior, i.e. changing norms, education status, social and economic interactions, etc. In order to meet these challenges we needed to draw from various accepted modeling techniques (i.e. 'Norms' - Epstein 2000, and parts of TradingSugarAgents within 'Sugarscape' - Epstein and Axtell 1996) and integrate them into one model.
 General Overview
General Overview
- 5.1
- The "ArrierosAlife" model simulates an artificial 'arriero' (donkey driver) society in which agents (Arrieros) can move over a 50 ( 50 cell grid, an artificial landscape called a 'scape'. The abstract two-dimensional structure consisting of 2500 locations is a torus.
|
|
Figure 1. Torus
|
- 5.2
- The scape has what is know as Von Neumann geometry which dictates that the agents on the scape can only see and move in the four principle directions (up, down, left, and right) giving the agents a limited view of the landscape that surrounds them. The lack of diagonal vision represents limited information and functions as bounded rationality of agents (Adami 1998; Epstein and Axtell 1996).
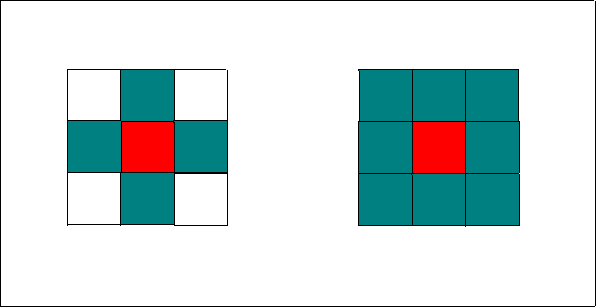
|
|
Figure 2. Von Neumann neighborhood and Moore neighborhood
|
- 5.3
- Certain base cells in the scape have resources for consumption by the agents, some in the form of tourist agencies (permanent grid locations - an office) and some in the form of independent tourists (random grid locations). In order to survive the agents have to find the resource (tourists needing pack animals to carry their gear to the mountains) and consume it (provide the service) if they are able. The ability to find the resources is based on the vision (a representation of education and migration) of the agent. Analysis of empirical data showed a positive correlation of education / migration and economic success. High vision represents a high level of education as well as mobility and vice versa. The ability to consume is based on number of donkeys owned and, if not enough donkeys are owned, friends who would be able to rent donkeys to fill the need. Renting donkeys is based on developing networks of friends (other agents with donkeys available) and on cooperation status of the agent. The income from consuming the resource will be accumulated as wealth and can be invested in buying pack animals (donkeys) and/or fields. Wealth is also consumed on a daily basis to support the family of the agent (metabolism) but the agents do not die (the simulations are generally 3-10 years, well within a lifetime of a human being).
Model Start - Resources
- 5.4
- Tourist agencies (yellow cells) and independent tourists (green cells) are distributed randomly across the scape and each is given a number of clients (tourists that need donkeys) as well as an intended trip length (in days). For the agency cells the client number is set between the particular agencies maximum and minimum capabilities which are based on global limits. The trip time for agency cells is randomly set between global limits. For the tourist cells the client number and trip time are set randomly between respective global limits. The agency cells are in a fixed location and after being consumed by an agent (donkey driver providing donkeys) will grow back to a random number between their individual minimum and maximum client capability with a new random trip time between the global limits. Once an independent tourist group is consumed they will not necessarily regenerate, but instead within each iteration there is a set (e.g. 1 in 4 - a new tourist cell will appear within the scape within four iterations) chance that in a random location (other than a tourist agency cell) a random number of tourists will appear (between the global limits) with an according trip time (also between global limits). The following variables regarding these characteristics can be set in the 'parameters' tab in the settings dialog from the control bar settings button [numbers in brackets are the initial settings and are set to best simulate the empirical data]:
|
| [10] | NumAgencyLocations | the number of agency cells |
| [10] | MaxAgencyClients | the maximum number of tourists an agency can support |
| [1] | MinAgencyClients | the minimum number of tourists an agency will support |
| [15] | MaxAgencyTripTime | the maximum trip time for an agency (days) |
| [5] | MinAgencyTripTime | the minimum trip time for an agency (days) |
| [10] | NumTouristLocations | the initial number of tourist cells |
| [5] | MaxTouristClients | the maximum number of independent tourists to appear |
| [1] | MinTouristClients | the minimum number of independent tourists to appear |
| [10] | MaxTouristTripTime | the maximum trip time for an independent tourist (days) |
| [3] | MinTouristTripTime | the minimum trip time for an independent tourist (days) |
| [4] | TouristGowBack | the chance for the grid that tourists will appear (as 1/x ) |
|
Model Start - Agents
- 5.5
- The agents ('Arrieros' or 'donkey drivers') are also distributed randomly across the scape and given a set of characteristics on which to base their actions. The pseudo code for their initialization is as follows:
|
| [1] | setLocation (as random unoccupied cell in the grid) |
| [2] | setVision (random from min to max) |
| [3] | setNormVision (as Vision) |
| [4] | setChildren (random from min to max) |
| [5] | setFieldsOwned (random from min to max) |
| [6] | setBurrosOwned (random from min to max accounting for number of fields owned) |
| [7] | setWealth (as a product of vision and burros owned) |
| [8] | setFriends (as a blank list) |
| [9] | setCooperation (as random boolean) |
| [10] | setName (as a number according to numerical order in initialization) |
|
- 5.6
- The variables for Location, NormVision, FieldsOwned, BurrosOwned, Wealth, Friends, and Cooperation can and will vary, but Vision, Children, and Name are set as constants for each agent. The following variables regarding the above characteristics can be set in the 'parameters' tab in the settings dialog from the control bar settings button [numbers in brackets are the initial settings and are set to best simulate the empirical data]:
|
| [30] | NumAgents | the number of agents |
| [5] | MaxInitialBurros | the maximum initial number burros |
| [0] | MinInitialBurros | the minimum initial number of burros |
| [2] | MaxInitialFieldSize | the maximum initial field size |
| [0] | MinInitialFieldSize | the minimum initial field size |
| [5] | MaxVision | the maximum vision |
| [1] | MinVision | the minimum vision |
|
- 5.7
- Note that the variable Vision is used for locating resources and new friends while the variable NormVision is used for updating cooperation status. We need two variables due to the nature of the geometry of the Von-Neumann neighborhood for locating actors (other agents or clients) and the one dimensional geometry on which the theory behind changing norms is based (adapted from Epstein 2000). Please see the Cooperation section (5.15) for further details.
Model Start - Global Variables
- 5.8
- Certain global variables are needed for the iteration of the agents across the scape as they 'live' their lives. The list below includes all the global variables that can be accessed through the 'parameters' tab in the settings panel from the settings button in the control bar. They are grouped by the functions or rules that are used to iterate the agents across the scape. Please see the complete discussion of each rule below for more information. [numbers in brackets are the initial settings chosen to best simulate the empirical data]
|
| Guide Rule | | |
| [5] | BurroRental | the cost to rent a burro from a friend (daily) |
| [5] | TripCost | the profit from taking one client to the mountains (daily) |
| | |
| Live Rule | | |
| [100] | BurroCost | the cost to buy a new burro |
| [150] | FieldCost | the cost to buy a new field |
| [0.33] | FieldForBurro | number of fields needed for maintaining one burro |
| [30] | PercentToSave | lower limit on what part of wealth can be spent |
| [0.1] | ChildCost | the daily cost to maintain a child |
| | |
| Change Cooperation Epstein 2D Rule | | |
| [0.05] | CoopCutOffFreq | limit on comparing various frequencies of cooperating and not cooperating neighbors (within this limit they are considered equal) |
| [0.1] | CoopNoise | factor for agents to change cooperation randomly (01) |
| [0.20] | CoopReset | lower limit of cooperating population (%) before cooperation values are reset |
| | |
| Saving Model Snapshots (not a rule) | | |
| [120] | DrawInterval | iteration count between saving snapshots of the model |
|
- 5.9
- The snapshot" of the social network at a particular point in time (saved in ArrierosAlife at defined time intervals) actually represents the data gained during the field research. The snapshot-approach implicitly assumes that there is something fixed and stable but ignores the instability and constant flux in our networks. The limitations of such a single snapshot approach have been recognized but financial and organizational constraints have limited efforts to study the dynamic processes and changes that occur in social networks over time. Network models have often been criticized for being static and not covering the real world" of social relations. The main point is the lack of empirical data because this requires continuos records of networks, which are often hard to collect. Stanley Wassermann and Katherine Faust, leading scientists on social network analysis call dynamic and longitudinal network models as the hottest trend to fill the gaps in current network methods (Doreian and Stockman 1997: 233; Wassermann and Faust 1994: 727-731). The ArrierosAlife model is one possible solution. Based on empirical snap shots we can observe at low costs the emergence of a society (Epstein and Axtell 1996; Gilbert and Troitzsch 1999). As an example see a 3D graphic of a snap shot, the evolved network in simulation run No. 306 after 300 iterations (about network visualization see Freeman, Webster and Kirke 1998; Freeman 2000).
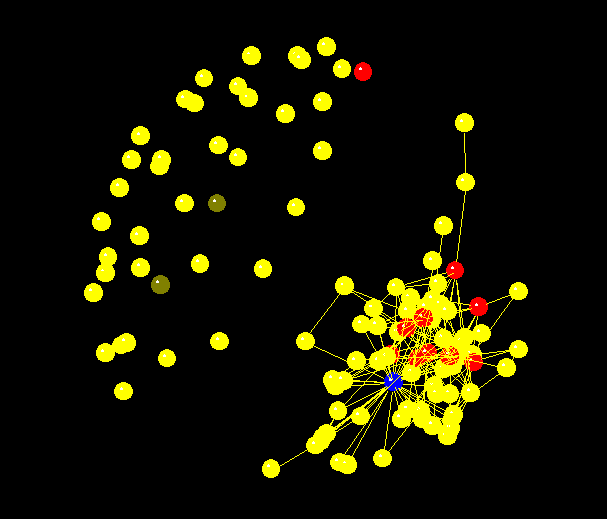
|
|
Figure 3.1. Snap shot of evolved network after 300 iterations
(all actors and all social ties; arrieros = yellow; travel agencies = red;
individual travelers = blue)
|

|
|
Figure 3.2. All Arrieros (N = 100) and their ties
of borrowing/lending donkeys are displayed
|
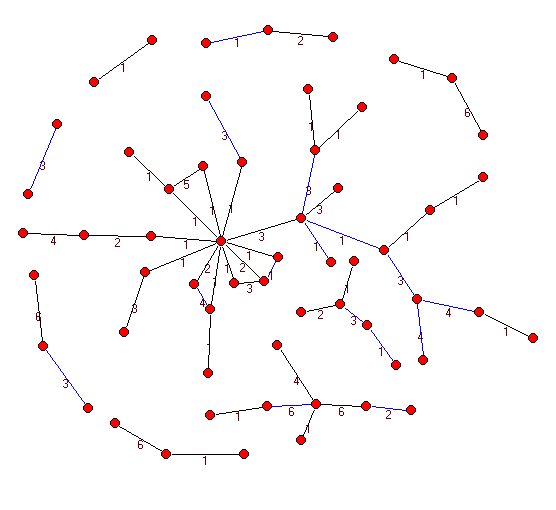
|
|
Figure 3.3. Only Arrieros who have a borrowing relation established are shown
(blue ties are bi-directed; numbers on the lines indicate the frequency)
|
Rules for Iteration ('life')
- 5.10
- In the language of Ascape there are certain rules that dictate the life on the scape. As mentioned in relation to the resources regeneration, there are rules to 'grow back' the agencies and tourists. Literally the 'Agency-Grow Back In Three Steps' Rule and the 'Tourist-Grow Back Random Rule' which can be observed in the settings window on the 'Rules' tab by selecting '2D lattice' from the 'Select Scape' menu. In the case of the resource rules, the user can modify the behavior of the rules by changing global variables that are used within the grow back rules or simply toggle the rules on and of in the settings window. The extendibility of a simulation model is recommended by several authors (Axelrod 1997: 211; Doreian and Stockman 1997). One of the best examples is the Sugarscape model developed by Epstein and Axtell (1996). For the life of the agents there are five rules necessary for ArrierosAlife. Specifically 'Guide', 'Change Cooperation Epstein 2D', 'Live', 'Movement', and 'Track Social Network'. All can be found in the settings window on the 'Rules' tab by selecting 'Arriero Agents' from the 'Select Scape' menu. As indicated above there are variables attached to certain rules and the user can modify the behavior of the rules by altering the appropriate parameters. The user can also turn on or off rules in the settings window on the 'rules' tab.
Live Rule
- 5.11
- The live rule could be compared to metabolism in cellular automata models. Each agent has a wealth characteristic which is dictated by income from clients (Guide Rule) as well as child expenses. Included in the live rule is an option to buy more fields or burros if there is enough wealth (i.e. by buying a burro or field the agent will still have a certain percentage of his wealth to pay for child expenses), thereby giving the agent greater capability to gain income. What follows is the pseudo code for one day of life for an Arriero agent in ArrierosAlife.
/* regular expenses */
[1] Wealth = Wealth - NumChildren * ChildCost
/* investment options */
[2] If FieldsOwned > (BurrosOwned + 1) * FieldsForBurro Then
[3] If BurroCost < WEALTH(1-PERCENTTOSAVE) THEN
[4] BURROSOWNED = BurrosOwned + 1
[5] Wealth = Wealth - BurrosCost
[6] End If
[7] Else
[8] If FieldCost < Wealth(1-PercentToSave) Then
[9] FieldsOwned = FieldsOwned + 1
[10] Wealth = Wealth - FieldCost
[11] End If
[12] End If
Movement Rule
- 5.12
- The model ArrierosAlife is based in a Von-Neumann neighborhood and this geometry dictates how the agents look for resources (agencies, tourists, or new friends) as well as move. For example if an agent has a vision of two he/she will 'see' eight cells as shown below.
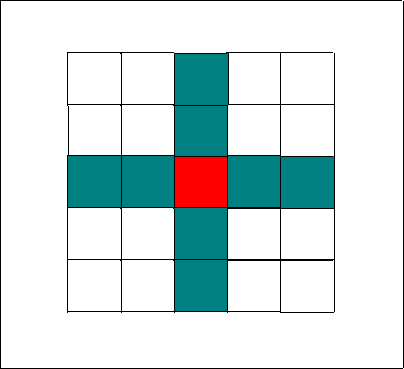
|
|
Figure 4. Von-Neumann neighborhood - vision two
|
- 5.13
- The prime motivation for an agent to move is to consume or locate resources (find and take clients on treks or expeditions) unless they are already occupied with a group of clients. To consume, the agent will look for nearby base cells with available clients (not occupied by another agent) and then move to the location of the best available resource. The agent will be forced to move if he/she is sitting on a good resource but cannot consume it (due to lack of burros). If there are no resources in view the agent moves in a random direction with the distance of the move being dictated by vision (the same movement if an agent is working with clients). The pseudo code for the movement rule follows.
[1] If Not Guiding Then
[2] VisibleCells[array] = CellsVisible Within Vision (includingCurrentLocation)
/* note that VisibleCells[1] is the CurrentLocation of the agent */
[3] BestValue = ResourceValue of VisibleCells[1]
[4] Loop Through All VisibleCells[array]
[5] If (ResourceValue of VisibleCells[step] > BestValue) Then
[6] If (VisibleCells[step] is Available) Then
[7] BestValue = ResourceValue of VisibleCells[step]
[8] End If
[9] End If
[10] End Loop
/* if the agent found a resource */
[11] If BestValue <> 0 Then
/* This if makes sure that the agent is not sitting on a resource */
[12] If Location of BestValue <> CurrentLocation Then
[13] Move To Location of BestValue
[14] Else
[15] Move in Random direction within Vision
[16] End If
/* if the agent found no resources move randomly */
[17] Else
[18] Move in Random direction within Vision
[19] End If
/* move randomly if agent is Guiding */
[20] Else
[21] Move in Random direction within Vision
[22] End If
Guide Rule
- 5.14
- The guide rule is the heart of ArrierosAlife and includes components to take clients on treks if enough burros are owned, and to look for friends to rent burros from if more burros are needed. This rule also does the accounting for wealth gained from guiding as well as counting the days for each trip that is taking place. When the trip is over the guide rule also makes sure that burros are returned to their respective owners (if burros were rented) and that the respective owners get paid for renting burros. The pseudo code for the guide rule follows.
/* the first part is to start consuming a resource and rent burros if needed */
/* if the agent is located at a resource */
[1] If ResourceValue of CurrentLocation > 0 Then
/* can the agent consume without help */
[2] If BurrosOwned > ResourceValue of CurrentLocation Then
[3] Start Consuming Resource
[4] Set Guiding flag to TRUE
/* can the agent consume with help of friends */
[5] Else
[6] If Can Rent needed burros from Friends[] Then
[7] RentBurros from Friends[first with enough]
[8] Start Consuming Resource
[9] Set Guiding flag TRUE
/* can the agent find a new friend to help consume */
[10] Else
[11] VisibleAgents[array] = AgentsVisible Within Vision exclude Self
[12] Loop Through VisibleAgents[]
[13] If VisibleAgent[step] is Cooperating Then
[14] If BurrosOwned by VisibleAgent[step] > BurrosNeeded Then
[15] RentBurros from VisibleAgent[step]
[16] Add VisibleAgent[step] to Friends[]
[17] Start Consuming Resource
[18] Set Guiding flag to TRUE
[19] Set Renting flag TRUE
[20] Exit Loop
[21] End If
[22] End If
[23] End Loop
[24] End If
[25] End If
[26] End If
/* The second part is to take care current trips and ending trips */
/* if agent is guiding do the bookkeeping */
[27] If Guiding is TRUE Then
[28] DayCount = DayCount + 1
/* if the trip is over take care of business */
[29] If DayCount = TripLength Then
[30] Wealth = Wealth + (TripLength * NumClients)
[31] If Renting is TRUE Then
[32] ReturnRentedBurros to Friends[who rented burros]
[33] Pay Friends[who rented burros] for Rent
[34] Set Renting flag FALSE
[35] End If
[36] Set Guiding flag FALSE
[37] End If
[38] End If
Cooperation Rule
- 5.15
- As mentioned above the model was designed to simulate the emergence of social networks. One feature of the network is about borrowing and/or lending donkeys among community members (actors). Most donkey drivers depend on borrowing donkeys from other community members to perform their economic activity in the tourism industry. If a member of the association does not respect the norms he will be sanctioned by others. The most straight forward sanction is not lending donkeys to the person not respecting the norms. To keep the model as simple as possible the following cooperation (norm) rule affecting the network is applied.
-
- If an agent cooperates means he is respecting the norms of the association and he can borrow donkeys from other community members. He by himself will only lend donkeys to others who cooperate.
- If an agent defects means he is not respecting the norms of the association and he can borrow donkeys only from other community members who are defecting. He by himself is free to lend donkeys to others either who cooperates or defects.
- 5.16
- The cooperation (norm) rule applied in the "ArrierosAlife" model was developed by Joshua Epstein (Epstein 2000). The JAVA-Applet and the paper for Epstein's model is available on line at http://www.brook.edu/es/dynamics/models/norms. The core of the model is : Once a pattern of behavior (norm) is established, we conform thoughtlessly. Bicchieri mentions a similar idea but has not developed a formal model (Bicchieri 1997). Epstein's one dimensional model was adopted to the two dimensional lattice sites in the "ArrierosAlife" model (for details on one and two dimensional update rules in cellular automata see Adami 1998).
- 5.17
- In the theory from Epstein the agents will look to their surrounding peers and change their mode of thought according to what they see in their neighbors behavior. The agent would need to see at least two other agents to make a decision, but might look further if warranted (for more details please see Epstein 2000). We encountered a problem as Epstein's model is one dimensional and ArrierosAlife is in two dimensional. Another problem was the low density of cell occupancy in ArrierosAlife. To resolve this problem we allowed the agents to look in all directions (not just the four principle directions - Moore neighborhood) when trying to decide what norm to follow, in this manner we can have the minimum of two agents seen to make a decision and it is possible that an agent will look to the entire society if he/she is having a hard time deciding to cooperate or defect. For this reason we have the two variables Vision, for locating resources, and NormVision, for deciding on cooperation or defection from the norm. We also added the feature that if more than 80% of the population is defecting, then the cooperation status of all agents will be randomly reset. This leads over time to a cooperative majority of all simulation runs. During field work it was observed that the associations are calling for a meeting if most of the members do not respect the established rules. The "80%" feature is simulating the data where a meeting would be called to discuss the problem of defection with a random outcome (as an example see Figure 5).
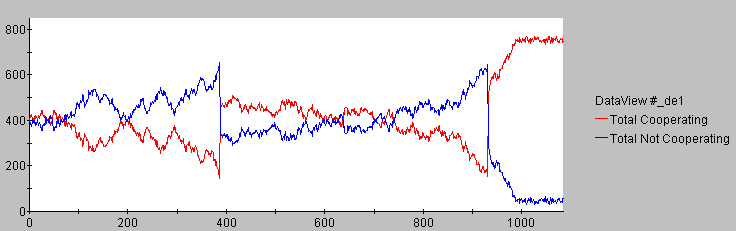
|
|
Figure 5. Example for the emerging cooperative behavior of 800 agents (simulation run No.201; all defaults; 1100 iterations)
|
- 5.18
- What follows is the pseudo code for the Cooperation Rule.
/* first check to see if noise will not change the cooperation status */
[1] If RandomNumber(0-1) > CoopNoise Then
/* make sure we have the minimum agents in view required (3 including self) */
[2] AgentsVisible[array] = AgentsVisibleMoore within NormVision include Self
[3] While Size AgentsVisible[] < 3 THEN
[4] IF NORMVISION < GRIDSIZE THEN
[5] NORMVISION = NormVision + 1
[6] AgentsVisible[array] = AgentsVisibleMoore within NormVision include Self
[7] Else
[8] Break While
[9] End If
[10] End While
/* get values for plus and minus one from NormVision */
[11] MoreAgentsVisible[array] = AgentsVisibleMoore Within (NormVision + 1) include Self
[12] LessAgentsVisible[array] = AgentsVisibleMoore Within (NormVision - 1) include Self
/* If the frequency is different with NormVision plus one, then increase NormVision and use the higher NormVision to base decision about changing cooperation status */
[13] If Abs(FreqCooperation(MoreAgentsVisible[array]) - FreqCooperation(AgentsVisible[array])) > CoopCutOffFreq Then
[14] If NormVision < GRIDSIZE THEN
[15] NORMVISION = NormVision + 1
[16] ChangeCooperationFlag if different from norm shown in FreqCooperation(MoreAgentsVisible[array])
/* takes care of case where we cannot look further */
[17] Else
[18] ChangeCooperationFlag if different from norm shown in FreqCooperation(AgentsVisible[array])
[19] End If
/* If the frequency is the same with NormVision minus one, then decrease NormVision and use the lower NormVision to base decision about changing cooperation status */
[20] Else
[21] If Abs(FreqCooperation(LessAgentsVisible[array]) - FreqCooperation(AgentsVisible[array])) < CoopCutOffFreq Then
[22] NormVision = NormVision -1
[23] ChangeCooperationFlag if different from norm shown in FreqCooperation(LessAgentsVisible[array])
/* takes care of case where NormVision will be used to make decision */
[24] Else
[25] ChangeCooperationFlag if different from norm shown in FreqCooperation(AgentsVisible[array])
[26] End If
[27] End If
/* Change due to noise factor */
[18] Else
[19] ChangeCooperationFlag Random
[20] End If
Track Social Network Rule
- 5.19
- This rule is superficial and only controls whether the renting interactions are shown between the agents in the screen view of the scape. It has no actual control over the interaction of the agents and also does not influence the social network data that is written in the save files.
 Saving and Loading Model Runs
Saving and Loading Model Runs
- 6.1
- The model ArrierosAlife has the ability to save model runs and load previously saved model runs. The user will encounter two buttons on the control bar, 'Save Model' as a diskette icon, and 'Load Model' as a opening folder with a red arrow pointing to the left (not to be confused with the 'Open Model' icon as an opening folder with a blue arrow pointing up) located as the first two icons on the left. These features are extremely useful as the screen appearance of the actual model runs are not of importance, but the social network that grow within the model is the feature we are interested in. The save feature allows the user to save matrices of the evolving network (literally a count of agent-agent, agent-agency, and agent-tourist interactions; all coded with the names of the agents) which can then be used in analysis software. The matrices are ready to use for standard social network analysis software such as UCINET ( Borgatti; Everett and Freeman 1990) or PAJEK ("Program for Large Network Analysis" Vladimir Batagelj & Andrej Mrvar - University of Ljubljana, Slovenia http://vlado.fmf.uni-lj.si/pub/networks/pajek/).
Saving the output
- 6.2
- The user can save a model at any point during a model run, BUT, the save will only include the data after the save command was executed if the 'Continue Model' option is chosen from the save dialog and if the option to 'Restart Model' is chosen a new Random Seed is set and the model runs again with the same parameters as the previous run. If the model is restarted a folder with the model name is created and three files are written to the folder 'modelName-settings.txt', 'modelName-initialConfig.txt', and 'modelName-0Agents.txt'. The model will then write two files at each iteration count divisible by the DrawInterval 'modelName-Agents.txt' and 'modelName-'. If the model is continued a folder with the model name will be created but the modelName-InitialConfig.txt file will not be written. In each case the model will continue saving data until the 'Stop Saving' button is clicked (with the icon of a diskette with a red X).The files are as follows:
|
| modelName | InitialConfig.txt | The file to be loaded with the load command. It contains all initial parameters, locations, and characteristics of all players (agents, agencies, and tourists). |
| modelName | Settings.txt | This file is for documentation only and is a formatted list of initial parameters. |
| modelName | <iteration#>Agents.txt | This file is simply the list of agents with their characteristics. It is formatted to be easily opened with Excel or other graphing software (space delimited). |
| modelName | <iteration#> | This is the Social Network matrix formatted to be easily used with social network analysis software (DL files; space delimited). |
|
Loading
- 6.3
- To load a model the user simply clicks the 'Load Model' button and selects any 'modelName-InitialConfig.txt' file. The model will restart with the exact same locations of all players and characteristics, but with a different Random Seed (good for seeing the butterfly effect - Lorenz 1993: 25-76).
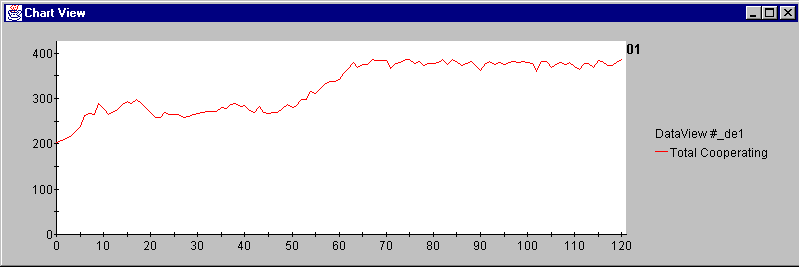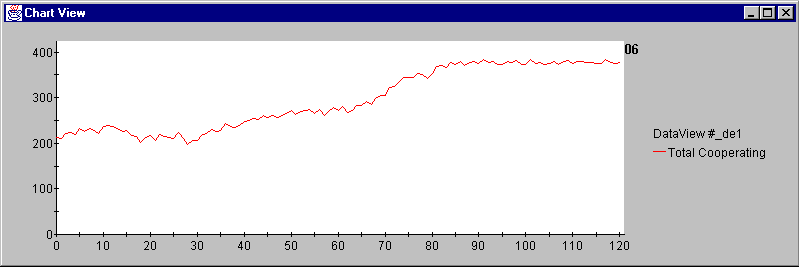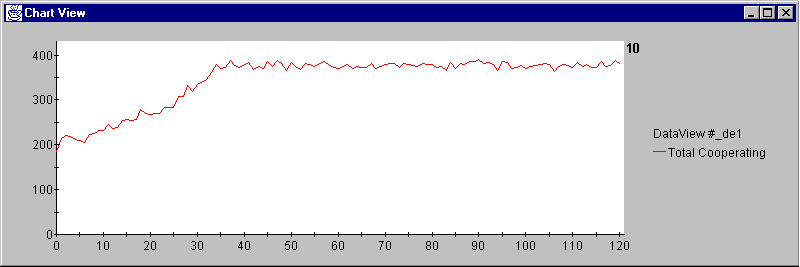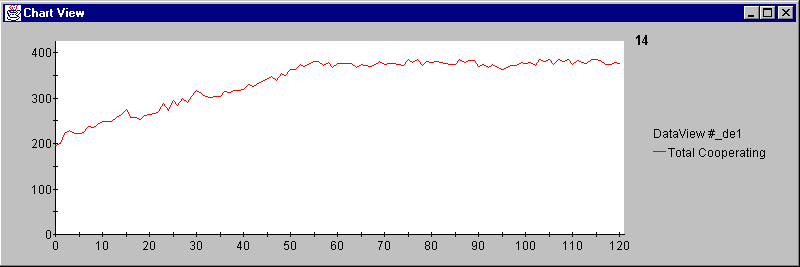
|
|
Figure 6. Example of coop-butterfly effect (100 agents, all defaults, 120 iterations)
|
All simulation runs (N = 13) were started from the same init-config file with the same starting agents, agencies, and tourists. With different random number seeds for the two simulations we can see a good example of the butterfly effect.
 Analysis
Analysis
- 7.1
- Besides some statistical measures (mean, sum, standard deviation) the simulation software does not offer tools for analyzing the data produced in the simulation runs. The files saved with the button 'Save Model' (a diskette icon on the control bar) can be analyzed with any standard tools.
- 7.2
- The aim of the ArrierosAlife model is generating data of an evolving social system and focusing on the analysis of the social networks ( Schweizer 1996; Wasserman and Faust 1994). The files for the matrices are written as a dl-format, ready to import in the UCINET Network Analysis Software (Borgatti, Everett and Freeman 1990). The cell values show the contact frequency of the social ties (a valued matrix). The file containing the parameters for all agents (e.g. sim39-600Agents.txt) can be imported and analyzed in any standard statistical tool (e.g. EXCEL, SPSS). As a final example we will demonstrate the evolution of an Arriero network simulated with the ArrierosAlife model.
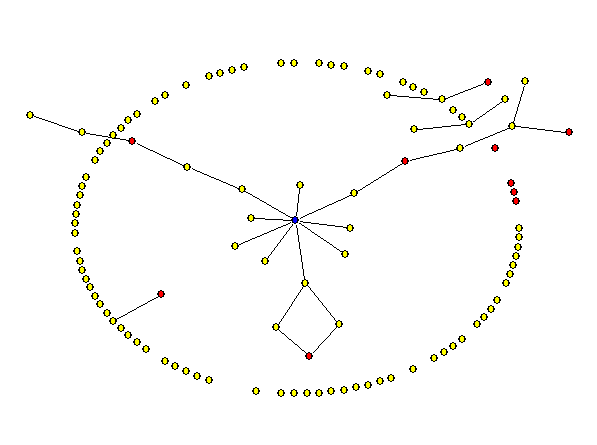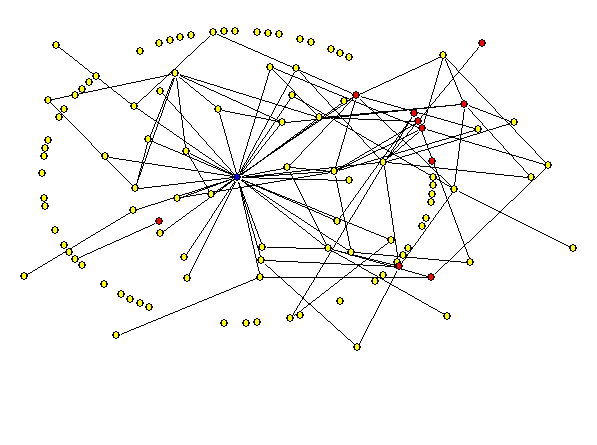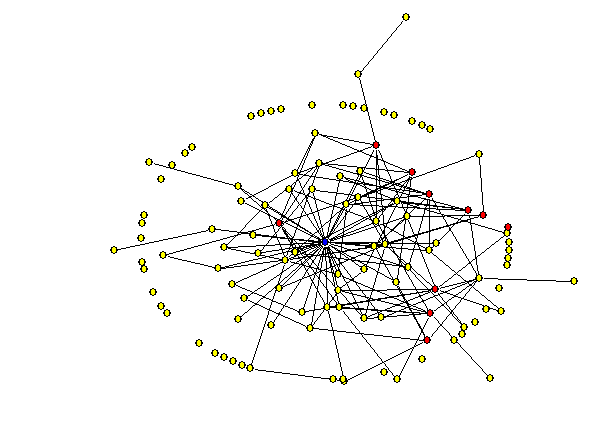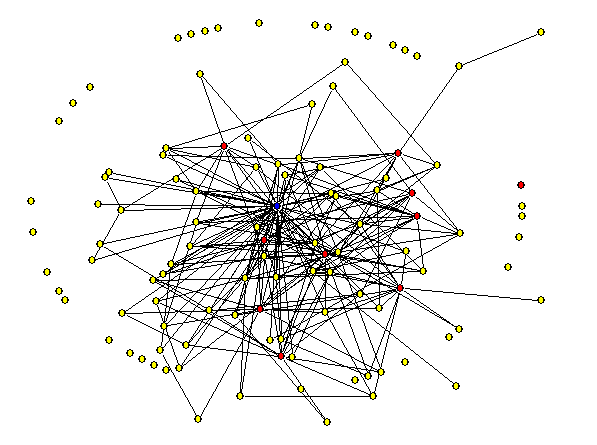
|
|
Figure 7. Animation of an evolving network
|
 Conclusion and Future Work
Conclusion and Future Work
- 8.1
- The implementation of ArrierosAlife within the Ascape framework was successful to a degree. While most characteristics of the empirical data were simulated well, certain aspects of the data collected in the Cordillera Blanca of Peru could not be integrated in this version of the model. Two specific problems have not yet been solved.
- 8.2
- The first is that in the empirical data it is much more common for Arrieros (agents) to form teams to meet the needs of clients instead of renting burros from other agents. This would mean implementing a method that would allow more than one agent (presumably friends) to consume the same resource location. In the language of Ascape, multiple cell occupancy. This is theoretically possibly, but not yet attempted.
- 8.3
- The second problem is simulating the cooperation behavior. The empirical data shows that, along with following rules to rent or lend burros, when Arrieros are cooperating they take turns at consuming local resources following an order decided upon in meetings, when they are not cooperating they will consume the first resource they find without respect to the order. This should also be possibly to implement by playing two agent vectors, one cooperating and one not, on the scape and having agents switch vectors when they change status. This has also not been attempted as of yet.
- 8.4
- Not only would it be interesting to resolve the two problems presented above, but it would also be of great interest to integrate the agent simulation onto a more realistic landscape such as a GIS (geographic information system). The GIS could include data regarding landscapes, trails, physical distances traveled, impacts to the landscape, physical influences on the networks formed, etc. With a little imagination the possibilities for a more realistic simulation, and in turn a more realistic prediction tool, are almost limitless. A valid simulation model could be applied as an important tool for policy and decision making (Auer 2000, Gimblett, Durnota and Itami 1996). The question that starts to arise is what are the cost/benefit relationships of developing such a model and prediction tool. Perhaps some of the answers lie with the work of Dr. Randy Gimblett and his work with 'RB-Sim' (Gimblett 1997; Gimblett Itami and Durnota 1996), an GIS agent based simulation program, or with future work in the Cordillera Blanca - Perú.
- 8.5
- Ascape is a very interesting tool for the development of models based on cellular automata. It offers a variety of interesting features. What we see as the weak point is analyzing the simulation runs (the latest release offers a cell listener - see Miles Parker in this issue). For our purpose we implemented a feature to save the runs as ASCII-files which can be imported to standard analysis tools. Another point at our wish list is the possibility of writing macros in Ascape. A macro enables the user to record a sequence of primitive commands into a file (e.g. load model, show chart view, save simulation run). This file can be used later to execute the saved sequence of commands without typing one by one. To compare the chart views for a sample of simulation runs it would be useful to set defaults (e.g. a fixed size for the x-axis in the time series). This feature would allow to compare a sample of chart views all the same size.
The executable files for "ArrierosAlife" can be downloaded from
http://www.uni-koeln.de/phil-fak/voelkerkunde/forsch/peru/initial-0.htm
 Acknowledgements
Acknowledgements
-
The authors thank Miles Parker (The Brookings Institutions-Washington) for advice and support developing the simulation model. Tim Norris particulary thanks the late Dr. Bernard Nietschmann (Dept. of Geography - UC Berkeley) for inspiration in studying third world development and Don Bain (Dept. of Geography - UC Berkeley) for advice on computer applications in geographical research. Klaus Auer particularly thanks Prof. Dr. Michael Casimir (Dept. of Anthropology- University of Cologne) and Prof. Dr. Douglas White (Dept. of Anthropology- UC Irvine) for helpful comments and advice during the research. Special thanks go to Prof. Dr. Thomas Schweizer for his kind support and for making it possible to realize the research.
 References
References
-
ADAMI, C. 1998. Introduction to Artificial Life. New York
AUER, K. 2000. Conservation versus Tourism Development. Local Polotics and Contextual Factors at Parque National Huascarán - Perú. Documentos de Trabajo-IM No.3, Lima
AXELROD, R. 1997. The Complexity of Cooperation. Agent-Based Models of Competition and Collaboration. Princeton
BICCHIERI, C. 1997. Learning to cooperate. In: Bicchieri, C.; Jeffrey, R. and Skyrms, B. The Dynamics of Norms. Cambridge 1997: 17-46
BORGATTI, S. P.; Everett M. G. and Freeman L. C. 1990. UCINET IV. Columbia: Analytic Technologies. http://www.analytictech.com/borgatti
DOREIAN, P. and Stokeman, F. (eds.) 1997. Evolution of Social Networks. Amsterdam
EPSTEIN, J. and Axtell, R. 1996. Growing Artificial Societies. Social Science from the Bottom Up. Washington.
EPSTEIN, J. 2000. Learning to be Thoughtless: Social Norms and Individual Computation. Center on Social Economic Dynamics Working Paper No. 6 revised January 2000. Forthcoming in Computational Economics
FREEMAN, L. 2000. Visualizing Social Networks. Journal of Social Structure, 1, 2000, (1)
FREEMAN, L., Webster, M. and Kirke, M. 1998. Exploring Social Structure Using Dynamic Three-Dimensional Color Images. Social Networks, 20, 1998: 109-118
GILBERT, N. 1995. Simulation: an emergent perspective
GILBERT, N. and Troitzsch, K.. G. 1999. Simulation for the Social Scientist. Milton keynes: Open University Press
GIMBLETT,R., Durnota, B. and Itami, R. 1996. Conflicts in Recreation Use in Natural Areas: A Complex Adaptive Systems Approach. Third Australian Complex Systems Conference. Charles Stuart University. Albury, Australia.
GIMBLETT, R., Itami, R. and Durnota, B. 1996. Issues in Designing and Calibrating Artificial Human Agents.Workshop Comparing Reactive (ALife-ish) and Intentional Agents. Charles Stuart University. Albury, Australia.
GIMBLETT, R. 1997. Simulating Recreation Behaviour in Complex Wilderness Landscapes Using Spatially-Explicit Autonomous Agents. Unpublished Ph.D.dissertation. University of Melbourne, Australia.
HEGSELMANN, R. 1998. Modelling Social Dynamics by Cellular Automata In: Liebrand, W.; Nowak, A. and Hegselmann, R. (eds.) Computer Modeling of Social Processes. London 1998: 37-64
HEGSELMANN, R. and Flache, A. 1998. Understanding Complex Social Dynamics: A Plea For Cellular Automata Based Modeling. Journal of Artificial Societies and Social Simulation vol. 1, no. 3, https://www.jasss.org/1/3/1.html
HEYLIGHEN, F. 1999, http://pespmc1.vub.ac.be:80/papers/PapersFH.html
KAUFFMAN, S. 1993 The Origins of Order. Oxford
KAUFFMAN, S. 1995. At Home in the Universe. The Search for the Laws of Self-Organization and Complexity. Oxford
LORENZ, E. 1993. The Essence of Chaos. Seattle
NICOLIS, G. and Prigogine, I. 1989. Exploring Complexity. An Introduction. New York
PARKER, M. 1998. Ascape: Abstracting Complexity http://www.brook.edu/es/dynamics/models/ascape
SCHWEIZER, T. 1996. Muster sozialer Ordnung: Netzwerkanalyse als Fundament der Sozialethnologie. Berlin.
WASSERMAN, S. and Faust, K. 1994. Social network analysis: Methods and applications. New York.

 Return to Contents of this issue
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999
 Abstract
Abstract![]() Introduction
Introduction![]() Complexity theory and agent based modeling
Complexity theory and agent based modeling
![]() Ascape as a modeling base for the development of "ArrierosAlife"
Ascape as a modeling base for the development of "ArrierosAlife"
![]() From Empirical Data to Simulation Model
From Empirical Data to Simulation Model
![]() General Overview
General Overview







![]() Saving and Loading Model Runs
Saving and Loading Model Runs

![]() Analysis
Analysis

![]() Conclusion and Future Work
Conclusion and Future Work
![]() Acknowledgements
Acknowledgements
![]() References
References
![]()
Return to Contents of this issue