Introduction
Over the past decade, political campaigns have increasingly used data to inform models of the electorate in order to run their election campaigns as effectively as possible (Hersch 2015; Nielsen 2012). Aside from general insights into population-level data, campaigns may also use personalized data to build individualized models of the electorate (see e.g., Bimber 2014; Issenberg 2012). These models can then be used to find the most effective persuasion or get-out-the-vote efforts for that segment of the population. The drive behind data-driven campaigns is to escape gut-feelings, intuitions, and heavy reliance on the past, and instead take a scientific approach to finding the most relevant citizens, developing appropriate persuasive material, and finding the best way to motivate one’s base to turn out on Election Day.
Campaigns may use two broad categories of data to run their campaigns. First, societal-level data provides general insights into the population (e.g., which political concerns permeate that particular society). This provides the campaign with a rough guide to figure out which issues might be relevant for a particular election – for example, should the campaign focus on the economy, the environment, healthcare, and so forth. Further, some democracies, such as the UK and the USA, operate a first-past-the-post electoral system. For example, in the USA a Presidential candidate will gain 100% of a state’s Electoral College votes even if they only get 50.1% of the popular vote in that state. In these systems, some states or constituencies may not be competitive (e.g., California is almost guaranteed to support a Democratic candidate while Mississippi almost certainly supports a Republican). In these systems, societal-level data can inform campaigns to where they should spend campaign finances by calculating the expected electoral gain per persuaded voter, across each state. In this way, societal-level data has been used for decades to run political campaigns more effectively (Hersch 2015; Nielsen 2012).
More recently, a second data category has been used in political campaigning: personal-level data. While societal data can be used to describe population-level political preferences, regional electoral impact, and general voter turnout, personal data can be used to model political preferences, electoral impact, expectation of turnout, and psychological proclivities at the individual voter level (Bimber 2014; Issenberg 2012). That is, while the general population may find the economy to be the most important political issue, a subset of voters may feel the environment is the most important issue when choosing their candidate. Personal data can be used to describe individual political preferences, psychological dispositions, and whether that voter is likely to vote. In other words, using personalized data, campaigns can segment the electorate into any number of increasingly specific categories to determine who to contact, what to contact them about, and how best to contact them. Crucially, this also allows campaigns to determine who not to bother contacting; an important factor when considering the time and financial constraints on complaining. These are psychologically informed, data-driven analytic micro-targeted campaigns (Madsen 2019)1.
Unquestionably, Cambridge Analytica is the most famous case of political micro-targeting to date (Cadwalladr 2017). They reportedly used psychometric and demographic data to segment American voters into categories in order to develop optimized persuasion and get-out-the-vote efforts in order to assist Donald Trump’s election campaign. There has been considerable disagreement as to whether or not Cambridge Analytica influenced the 2016 presidential election in the USA. Indeed, some suggest they had a significant impact on the elections while others contend that their methods are ineffective and that predicting people generally is very difficult (Chen 2018; Nyhan 2018; Trump 2018).
Micro-targeted campaigns acknowledge that the electorate is heterogeneous: voters have different political desires and priorities, see candidates as more or less credible, are more or less likely to vote, and so forth. For example, one voter may be concerned about climate change, women’s rights, and the economy, while another may be concerned about gun rights, worker’s rights, and the military. For campaigns, it is imperative to know which voters to approach and in what manner, rather than simply contact each voter, and as such one needs to understand why each voter chooses one candidate over another. Thus, while societal-level data may inform the campaign to talk about jobs in Iowa, individual-level data break down Iowa into segmented populations in order to describe what they desire and rate as important, how they see the candidate, and how likely they are to turn up on Election Day. If the campaign has representative models of the electorate that are informed by diagnostic and relevant data, segmentation of the electorate enables candidates to figure out who to talk to (voter relevance), what to talk about them about (their political preferences), and how to talk about it (optimizing the persuasive efforts to fit that segment of the electorate). If the model of the electorate is good and data is diagnostic, this should yield strategic advantages.
Studies on campaigning and political advertisement tend to focus on specific case studies. For example, they have focussed on how Facebook was used in a particular election to advertise (Borah 2016), the consequences of misinformation and online advertisement (Allcott and Getnzkow 2017), and the impact of television compared with YouTube advertisements (Borah, Fowler, and Ridout 2018). Similarly, research projects have used data from specific elections (Bimber 2014; Issenberg 2012), or the exploration of party data sets (Nielsen 2012).
While these studies are important to understand how personalized political adverts function in situ, they cannot – by nature of the specific context – address the fundamental impact of micro-targeted campaigning as a general tool. Put another way, whilst these studies have significant diagnostic value, due to the risk of being over-fitted, their predictive value is limited. For example, following the use of Facebook data in political campaigns, the company changed the API, disabling this access. As such, while papers discussing the use of Facebook data in 2016 provide relevant insights into that election, they no longer apply to current campaign management, as access to data has changed. Further, it is difficult to assess the causal impact of one feature of a single-outcome event like an election, as these cannot be repeated.
We can expect micro-targeting to become more prevalent in future elections, as psychological models of the electorate become more accurate and personalized electorate data expands (in addition, micro-targeted campaigns may also be used to disseminate disinformation more or less effectively, which is becoming a societal issue). Consequently, we need to understand how micro-targeting works in principle (which may then be applied to specific contexts). That is, how effective are micro-targeted campaigns in comparison with campaigns that do not use data to find the most appropriate segments of the electorate?
Modelling Micro-Targeting
To test the effect of micro-targeting, we implement and extend an existing agent-based model (ABM, see description of this modelling technique below) (Madsen and Pilditch 2018). This model contains components for exploring the effectiveness of micro-targeted campaigns, as it encompasses voters, politicians, and persuasive connections between voters and politicians. In the model, voters entertain beliefs about a series of political issues (e.g., climate change, the state of the economy, etc.). In addition, the voters rank how much they care about each of these issues. Finally, voters perceive the competing political candidates as more or less credible, enabling them to revise their beliefs in the political issues when a political campaign contacts them. Politicians in the model, conversely, attempt to persuade the electorate that their position on the various political issues is appropriate. In the model, they do this by contacting members of the electorate during the election campaign. When a politician makes contact with a voter, the politician transmits a persuasive attempt with regards to one of the policy issues. The voter then uses a belief revision function (see below) to update their belief with regards to that policy. Work in the simulation of voter preferences has investigated the role of voter political attitudes (Kottonau and Pahl-Wostl 2004), and interactions between opinions and campaigns / candidates in traditional campaigns (Hegselmann et al. 2015) and primaries (Stiles et al. 2020). Critically, this model contains two types of politicians: a stochastic campaigner that contacts voters at random, and a micro-targeting campaigner that selects the most appropriate voters to contact (using knowledge of the electorate to locate voters who are likely to vote, who finds the candidate credible, and which political issues the voter cares about).
By formalizing connections, beliefs revision processes, and keeping confounding factors related to specific election campaigns out of the model, it can be used to formally test the difference between stochastic campaigns that contact any voter randomly and micro-targeted campaigns that use personal-level data to inform campaign outreach strategies. The model thus provides a new method to test the effectiveness of competing campaign strategies and tactics (for example, the candidates can have any function for choosing who to target, making the model framework capable of testing different types of micro-targeting strategies).
The paper expands the original model considerably. In Madsen and Pilditch (2018), voters only consider one political issue. While this allows comparisons of micro-targeted campaigns and stochastic campaigns for single-issue campaigns (e.g., the proportion of the electorate who believe children should be vaccinated), voters are more complex in election campaigns. They may choose a candidate in relation to multiple policy issues that may carry more or less weight for the individual voter (see e.g., Horiuchi, Smith, and Yamamoto 2018). Further, preferences may be driven by individual factors such as social status (Brown-Iannuzzi et al. 2015). In other words, the electorate is likely strongly heterogeneous in terms of their political preferences and motivations for choosing one candidate/party over another. Following this, the paper extends the Madsen and Pilditch model considerably by including multiple political preferences and individual weights for each political preference. This enables simulations of a heterogeneous electorate (in the paper, we test multiple policy preferences) and how this impacts the strategic capacity of micro-targeted campaigns.
In simulating the outcome of the engagement between the voters and the politicians, we test the effectiveness of micro-targeted campaigns given an increasingly heterogeneous electorate. Specifically, we implement multiple policy considerations. The resulting simulations show that micro-targeting can take advantage of electorate heterogeneity, side-stepping issues facing more traditional campaigns. Micro-targeted campaigns do this by using insights about the electorate to push the most relevant issues with the most relevant weight. As differences within the population increases, so does the tactical and strategic advantage of knowing the electorate. Methodologically, the paper extends the Madsen and Pilditch (2018) model considerably and offers a tool for researchers to investigate the effect of information strategies on more increasingly heterogeneous populations. While it is not possible to re-run campaigns in real life, the model can test differing scenarios (e.g., different types of voters) and the effectiveness of competing campaigns strategies in these contexts. Moreover, the model quantifiably measures the effectiveness of strategies.
It is difficult to assess the precise impact of micro-targeting campaigns in an election, or to know the election outcome if they had not been active, or if other campaign strategies were used instead. The presence of myriad confounding variables complicates the analyses of elections. For example, campaigns may have used inaccurate models of the electorate, poor or irrelevant data, bad data management, or conversely, experienced favourable conditions in that election, encountered poor opposition, or any number of other factors, which may influence the outcome of a specific election. Thus, while it is historically interesting to explore the role of micro-targeted campaigns, such as the impact of Cambridge Analytica in the 2016 presidential election, it is uninformative of the effect of micro-targeted campaigns in principle. To measure the impact of micro-targeting, we require events where comparable conditions can be repeated and analysed statistically. While this is traditionally done with experimental methods, elections campaigns pose a methodological challenge due to their interactive, dynamic, and highly complex nature.
Systems, such as election campaigns, that are dynamic and involve multiple agents interacting over time, are technically complex (Johnson 2007). As systems become increasingly complex, individual and collective behaviours in that system become characterised by how they adapt and change over time (which may in turn cause system-wide changes). For example, voters may change their beliefs about political issues as they hear campaign messages from candidates, campaigns may change who they target as voters develop (e.g., some voters may consider switching to a different party at the onset of the election, but may be committed voters the day before Election Day), and campaigns may adopt entirely different strategies if competing campaigns change how they act (e.g., a campaign may initially forego attack ads, but may choose to do so later if they get desperate or if the opposing campaign deploys them). Models and tests of complex systems require dynamic models. Agent-based models (ABMs) can represent how individual agents act and react to changes in the system, making it an ideal method to simulate and test the effectiveness of micro-targeted election campaigns.
Method: An Agent-Based Model of Micro-Targeted Campaigns
ABMs are simulated multi-agent systems that describe the behaviour of and interactions between individual agents operating in some environment (Bandini, Manzoni, and Vizzari 2009; Gilbert 2008). In the current model, the voters and political candidates are the agents. They are interactive (Bonabeau 2002), meaning that agents can engage with each other and with their environment (if needed). Further, they are self-organizing (Niazi and Hussain 2009), meaning that agents can adapt when the context changes (e.g., a voter might be reachable by a campaign at the beginning of an election, but may have become entrenched and therefore unreachable by the end – an adaptive campaign can update who to target as the election unfolds. Finally, ABMs can be used to test cognitive, social, and tactical or strategic models (Madsen et al. 2019).
ABMs consist of three broadly defined components: Agents, interactions, and the synthetic environment. Agents (the actors within ABMs) can be endowed with any functions that are computationally expressible (e.g., learning, decision-making, memory, etc.). Further, the agents can be heterogeneous within a class (e.g., 10,000 voter agents within the system may set their function parameters by drawing the value from a Gaussian distribution) and between classes (e.g., voter agents may be endowed with some functions while candidate agents may be endowed with entirely different functions). Interactions are any function that link agents with each other, which can facilitate agent functions such as information transmission. Links can be direct (one agent passes information to another who uses its learning function to update its beliefs) or indirect (an agent may physically displace when other agents come near). Finally, the environment describes the synthetic world in which the agents live and act. The environmental features can be enabling (e.g., information transmission) or disabling (e.g., geographical distance between agents may preclude information transmission). They have been used in economics (Grazzini and Richiardi 2015), opinion dynamics (Hegselmann and Krause 2002; León-Medina 2019), social sciences (Schelling 1978; Epstein and Axtell 1996; Heath, Hill, and Ciarallo 2009), and to simulate human-environment systems (Bailey et al. 2019; Carrella, Bailey, and Madsen 2019).
To go beyond individual case studies and just-so stories, Madsen and Pilditch (2018) developed a model to simulate interactions between key components of micro-targeted campaigns: The electorate, the political candidates, and candidate strategies. In their model, Madsen and Pilditch simulate voters, political candidates, and interactions between the candidates and the voters. Voters consider a hypothesis, \(H\) (this is a proxy for ‘which candidate should I support in the election?’). Throughout the simulation, voters’ subjective H may change as a result of their interactions with the MTC or stochastic candidates. To update their belief about whom to vote for (\(H\)), voters use a Bayesian source credibility model where the posterior degree of belief in a hypothesis given a report from another person, \(P(H|Rep)\) depends on the perceived trustworthiness, \(P(T)\), and the perceived expertise, \(P(E)\), of that reporter (here, a political campaign candidate) (see Bovens and Hartmann 2003; Hahn, Harris, and Corner 2009; Harris et al. 2015).
The use of the source credibility model is motivated by the fact that perceived trustworthiness and expertise have been shown to be important in political persuasion (Madsen 2016), civic participation (Levi and Stoker 2000), the intention to participate in an election (Householder and LaMarre 2014), and in persuasion and argumentation more broadly (Chaiken and Maheswaran 1994; Petty and Cacioppo 1984). Further, social psychological findings corroborate the division of credibility into perceived expertise and trustworthiness (Cuddy, Glick, and Beninger 2011; Fiske, Cuddy, and Glick 2007). In other words, the inclusion of perceived credibility in the model is empirically supported, and provides a formal (Bayesian) frame to explore belief revision over the duration of an election campaign, furnishing the voters in the model with the capacity to change their beliefs in a hypothesis depending on their perception of the candidate’s credibility. Specifically, when a candidate contacts the voter with a report (persuasive message), the voter updates their belief thusly:
| $$P(H|Rep)= \frac{P(H)P(Rep|H)}{P(H)P(Rep|H)+P(\lnot H)P(Rep|\lnot H)}$$ | (1) |
\(P(H|Rep)\) represents the probability that the hypothesis, \(H\), is true given a confirming statement (\(Rep\)). \(P(H)\) represents prior belief in the hypothesis, and \(P(Rep|H)\) and \(P(Rep|¬H)\) represent the probability that the source provides a confirming statement if the hypothesis was true (\(H\)) or false (\(¬H\)). Perceived trustworthiness, \(P(T)\), and expertise, \(P(E)\), are integrated within \(P(Rep|H)\) and \(P(Rep|¬H)\)2. Finally, the required conditional probabilities (i.e., if a candidate is truthful (\(T\)) and an expert (\(E\)), what is the probability they will provide a true report? repeated for the 4 combinations of trustworthiness and expertise) are taken from Madsen (2016) who derived these empirically (see Table 1).
| \(T, E\) | \(T, ¬E\) | \(¬T, E\) | \(¬T, ¬E\) | |
| \(H\) | 0.80 | 0.58 | 0.34 | 0.18 |
| \(¬H\) | 0.22 | 0.42 | 0.59 | 0.71 |
To illustrate this function in action, imagine a candidate who contacts a voter about a political issue. The voter’s prior belief is marginally positive (e.g., \(P(H) = 0.57\)) and the voter perceives the credibility of the candidate pretty favourably (e.g.,\(P(E) = 0.63; P(T) = 0.71\)). In the model, as the voter receives the positive report from the candidate (\(H = 1\)), the voter uses the above model to revise their belief. In this case, the voter would revise their prior belief (mildly) positively given the report, making the posterior belief in the hypothesis given the report, \(P(H|Rep) = 0.66\), as the candidate is (mildly) perceived to be credible. Comparatively, if the voter believed the candidate to be extremely credible (e.g., \(P(E) = 0.97; P(T) = 0.93\)), they would revise their belief more strongly (in that case, \(P(H|Rep) = 0.79\)). Conversely, positive reports from candidates deemed discredited (i.e., \(P(T)\) and/or \(P(E) < .5\)) would result in a dissuading effect, pushing the belief (\(P(H)\)) in the negative (unintended) direction.
The fact that the source credibility model allows for negative effects of campaign outreach is in line with two pieces of evidence. First, the so-called backfire effect has been observed in psychological literature (see e.g. Nyhan and Reifler 2010; Wood and Porter 2018). This refers to instances when participants entrench and even strengthen their prior beliefs when faced with evidence contrary to this belief. That is, not only would the participant fail to adjust their belief in line with observed evidence – or even ignore the evidence altogether – but actually move their beliefs in the opposite direction. Second, in line with the backfire effect, Madsen (2016) used the above Bayesian source credibility model to predict voters’ beliefs in the goodness of an unknown policy if a political candidate supported or attacked the policy. Despite no knowledge of the policy, participants reported posterior degrees of belief in the goodness of the policy given their perceptions of the political candidate who supported or attacked the policy. In line with the backfire effect, this effect was bi-directional, as voters who rated a candidate as very credible (high expertise and trustworthiness) increased their belief in the goodness of the policy. Conversely, if they rated the candidate as not credible (low expertise and trustworthiness), they lowered their estimation of the goodness of the unknown policy. Party affiliation had no impact on this effect, as Democrat and Republican voters updated their beliefs in the same manner. As such, the Bayesian source credibility model has been empirically tested (e.g. Harris et al. 2016), applied to political reasoning (Madsen 2016), and approximates the well-known backfire effect (Nyhan and Reifler 2010). As such, we believe the model is appropriate to include as the main belief revision function in the current agent-based model. Given the probabilistic nature of the Bayesian source credibility model, we can consequently map \(P(H)\) on to a voting preference dimension, with \(P(H) > .5\) corresponding to favoring one candidate, and \(P(H) < .5\) corresponding to favouring the other.
Finally, voters are more or less likely to turn up on Election Day to cast their vote. In the model, this is represented by the probability of voting, \(P(Vote)\). At the end of the simulation (after 100 “days” or time-points, known as “ticks” within ABMs), each voter decides whether to vote with a probability corresponding to \(P(Vote)\). That is, voters with \(P(Vote) = 0.25\) will typically vote in ¼ of elections while a voter with \(P(Vote) = 1\) will always participate in the election. If voting, the voter consults the state of their belief, \(1(P(H)\). If \(P(H) < 0.5\), the voter supports the stochastic candidate; If \(P(H) > 0.5\), the voter supports the MTC candidate. In the model, stochastic campaigns target voters randomly. By comparison, micro-targeted campaigns can make use of knowledge of the individual voters (their beliefs, whether or not they perceive the candidate as credible, and whether or not they are likely to actually vote in the ensuing election). This provides the micro-targeting candidate with a significant tactical advantage. By measuring the outcomes of multiple simulated elections, the model can test the general effectiveness of micro-targeted campaigns. Moreover, the model can be used to run different scenarios (e.g., setting the credibility of candidates differently) and compare how the outcome of the elections in these differing scenario simulations.
The agent-based model allows for voter heterogeneity, so as to represent the diversity of beliefs and dispositions found in an electorate. When the model is initiated, each voter sets their individual function parameters. These include their beliefs regarding their voting intention, \(P(H)\), how trustworthy they perceive each candidate to be \(P(T_{CANDIDATES})\), how expert they perceive each candidate to be, \(P(E_{CANDIDATES})\), and their likelihood of voting in the election, \(P(Vote)\). Each voter in the model draws each value from a Gaussian distribution (e.g., \(µ= 0.5, σ = 0.25\)). By drawing the parameter values from a normal distribution, the electorate becomes heterogeneous as voters can differ in their belief in the hypothesis, their perception of the candidates, and their probability of voting.
As the electorate is heterogeneous, campaigns with knowledge of the individual voters can use this information to their strategic advantage. For example, a voter may be amenable to supporting the candidate (e.g., \(P(H) = 0.52\)), and would respond favourably to persuasive attempts (\(P(T) = 0.8\) & \(P(E) = 0.8\)). This voter would represent a swing voter who sees the candidate as credible, but who is still undecided with regards to the specific issue3. However, if that voter is incredibly unlikely to participate in the election (e.g., \(P(Vote) = 0.02\)), they may no longer be relevant. Thus, candidates with information about individual voters can develop data-driven strategies to identify the most relevant segments of the electorate and contact them as needed.
In sum, Madsen and Pilditch initiate a heterogeneous electorate (who differ in belief in the hypothesis, perception of each candidate, and likelihood of voting) who are contacted by candidates throughout the election. The model can measure the impact of having information about the electorate and compare this with stochastic campaign strategies. To make the comparison more direct, candidates in the model reach \(n\) number of voters each “day” (tick) in the simulation. For example, the stochastic campaign may reach 100 randomly chosen voters per day while the MTC candidate only reaches 20. Fig. 1 describes the model flow.
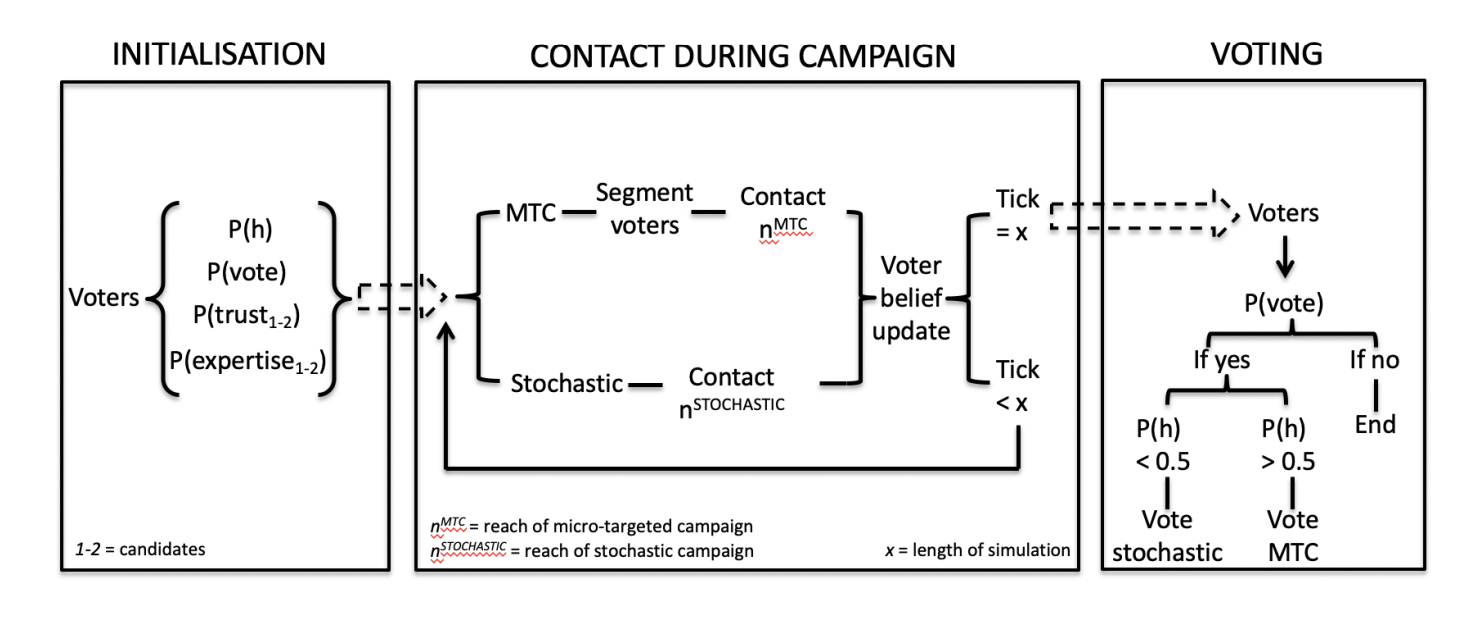
The Madsen and Pilditch model (2018) offers a quantifiable method for testing the effect of information dissemination strategies. Specifically, they compare the persuasive success of a stochastic campaign with that of a micro-targeted campaign that may target voters who will be favourably disposed toward the candidate, \(P(Cred) > 0.5\)4, are swing voters, \(0.3 < P(H) < 0.7\), and who are likely to vote, \(P(Vote) > 0.5\).
The current strategy is motivated by three observations. First, as the simulated election campaign does not allow for Get-Out-The-Vote efforts to increase the probability of voting (Green and Gerber 2008), it becomes increasingly ineffective to persuade voters, as they are increasingly unlikely to turn out on Election Day. This motivates the strategy of only trying to persuade voters who are likely to turn out, \(P(Vote) > 0.5\). Further, as voters in this model use perceived candidate credibility to update their beliefs given reports from that candidate, the candidate should only contact voters who will be positive toward a report. In the Bayesian model, this means any voter with \(P(Cred) > 0.5\). Finally, the candidate only engages with swing voters. The candidate will not gain anything from trying to persuade voters who are already in the candidate’s base (strongly supporting of the candidate). Comparatively, it might be possible to persuade voters who are strongly opposed to the candidate, but this requires significant effort that might be more effectively spent elsewhere. Thus, in the model, the micro-targeting candidate only contacts swing voters, \(0.3 < P(H) < 0.7\), for maximum gain. Of course, if voters who used to be in the candidate’s base are persuaded by an opposing candidate during the course of the campaign, they once again become relevant, as they enter the realm of swing voters – in this way, the micro-targeting campaign can react to changes to the electorate, as the campaign unfolds.5
As illustrated in Fig. 1, the model progresses thusly. In the initialisation, voters and candidates are spawned. Voters draw their cognitive parameters, \(P(H)\), \(P(T)\), \(P(E)\), \(P(Vote)\), as described above. Having generated the electorate, the model begins running. In each simulated step, the candidates contact \(X\) voters (\(X\) is defined by their ‘reach’). The stochastic candidate contacts voters at random, and the micro-targeting candidate identifies relevant voters as described in the above and contacts them. Having made contact, voters update their beliefs using the Bayesian model described in the above. This process of contact and belief revision continues until the end of the campaign (here, 100 rounds of contact and revision). Finally, at the end of the campaign, the voters decide whether or not to vote and if so, for whom, as described in the above.
Extending the model: multiple policy issues and relative weights
While providing the formal framework for testing the effectiveness of micro-targeted campaigns in principle, voters in Madsen and Pilditch (2018) only consider one policy issue. That is, the voting agents vote for one candidate or the other given interactions with those candidates, perceived as more or less credible. However, as discussed in the introduction, modern societies are diverse and complex. Consequently, the electorate can be expected to also be increasingly heterogeneous where elections revolve around a series of political questions such as taxation, the economy, jobs, security, individual’s rights, and many other things. As the electorate becomes increasingly diverse in hopes, political preferences, and opinions, knowledge of the electorate can, in principle, be used to gauge the most effective message topic for a voter (e.g., contacting voter 1 with economic messages while voter 2 is contacted with environmental messages).
To capture the increased heterogeneity within a population, we extend the Madsen and Pilditch model to enable voters to consider specific policy issues. In the current model runs, voters consider up to 3 policies. However, given the formal instantiation described below, the model can in principle be expanded so that voters may consider any number of policies. This enables the model to test MTC effectiveness as the electorate becomes more multi-facetted. Additionally, while voters may be aware of a political issue, they may not consider it relevant or important. For example, some voters may choose their preferred candidate for their stance on labour rights and environmental issues while another may choose the candidate due to their views on foreign and economic policies. In this scenario, both voters may hold positions on four political issues, but weigh the issues differently. For example, two voters may hold the same position on labour policies (e.g., both are pro workers’ rights), but the two may differ in terms of how important they feel this is (e.g., given current economy, other issues, etc.), resulting in different weights (e.g., \(w = 0.85\) vs \(0.25\)). Thus, if the first voter remains somewhat unconvinced about a candidate’s labour policy, we should expect the voter to refrain from supporting that candidate. Comparatively, if the second voter does not approve of the candidate’s labour policy, it should not impact the voting outcome much, as the weight is low. Of course, the two voters could also hold similar or different positions on another policy (e.g., foreign policy), but weight these in an entirely different manner. In other words, voters do not merely have a rank-order of policies (1, 2, 3), but may imbue these ranks with weights to reflect what really makes them choose one candidate over another. This allows for a voting population that includes single issue voters (1 policy highly weighted), multiple-issue / highly engaged voters (multiple highly weighted policies), disengaged voters (all policies have low weights), and combinations thereof.
Weighted preferences over multiple policies add an additional information layer that micro-targeted campaigners may use. Formally, in the current model, an MTC candidate uses their knowledge of the electorate to gradually “zero-in” on viable targets. This unfolds in several stages. First, the contactable voters are restricted to those who perceive the candidate positively \((P(Cred) > 0.5)\), of these, those are more inclined to vote \((P(Vote) > 0.5)\). At this point we depart from the Madsen and Pilditch (2018) model by restricting this subset further to those with a policy position in the acceptable (persuadable) range \((0.3 < P(Pol_H) < 0.7)\), where \(P(Pol_H\)) corresponds to \(P(H)\) in the previous model) and of sufficient weight (\(P(Pol_W) > 0.6)\). If the resultant subset is larger than the possible reach of the MTC (i.e., there are more viable voters than the MTC can target that day), the remaining viable subset is selected based on those with the highest viable policy weights. After targeting is completed, the remaining subset has their highest weighted viable policy “pushed” or persuaded by the campaign. In comparison to the original model, this enables the micro-targeted campaign to target the most potent policy issue with regards to the voter’s preferences and relative weights. A stochastic campaign, by contrast, having selected their voters for targeting randomly, also selects the policy to “push” to those voters randomly as well.
At the conclusion of campaigning, all voting agents will then vote with a probability corresponding to their \(P(Vote)\) value. Who to vote for is decided based on a weighted average of policy positions, wherein the distance of a policy position (\(P(Pol_H)\)) away from 0.5 (towards 0 favoring one candidate, towards 1 towards the other) is multiplied by the weight of that policy. These weighted policies are then averaged, with a final voting decision based on whether this aggregate is greater or less than 0.5 (with voters left at 0.5 deciding between the two candidates randomly). In the simulated experiment below, we implement these functions to track the effectiveness of micro-targeted campaigns for increasingly heterogeneous electorates.
Simulation Results
Our simulations, programmed with Netlogo and run within R using the RNetlogo package (Thiele 2014), entail an election campaign with 2 campaigns (a stochastic, traditional campaign agent, and an MTC campaign agent), who are each trying to persuade a voting population (10,000 “voter” agents) towards their candidate. This is defined along a dimension from 0 (favouring the stochastic campaign candidate) to 1 (favouring the MTC campaign candidate). The model used here is also described by Fig. 1 above, with the exception of policies (\(P(Pol_H)\)), rather than a single belief in the candidates (\(P(H))\) forming the basis of targeting, updating, and eventual voting.
Across simulations, we manipulate a number of parameters independently via shifting the Gaussian distributions from which voters sample their parameter values. Whilst the \(P(Vote)\) distribution is held constant (\(P(Vote): \mu = 0.5, \sigma = 0.25\)), the perceived credibility of campaigns are manipulated independently (\(P(Cred): \mu_{MTC} = [0.4, 0.5, 0.6]\), \(\sigma_{MTC} = 0.25\); \(\mu_{Stochastic} = [0.4, 0.5, 0.6]\), \(\sigma_{Stochastic} = 0.25)\) between simulations. The policy positions (\(P(Pol_{H})_{n-1}\)) and weights of those positions (\(P(Pol_{w})_{n-1}\)) held by each voter are manipulated within each simulation.
On each campaigning “day” (or tick), each campaign reached out to a set number of voters (whether targeted in the case of the MTC, or randomly selected in the case of the stochastic campaign). Stochastic campaign reach was increased in multiples of the MTC campaign reach, such that the latter remained at 20 voters per day, whilst the former increases from 20 to 200, in steps of 20 (and thus in ratio from 1:10).
Along with the manipulation of each respective candidate/campaign’s perceived credibility and campaign reach, the number of policies voters took into consideration was increased from 1 (essentially replicating previous work without policy differences, see Madsen and Pilditch 2018) to 2, to 3. These policies were all independently drawn from truncated Gaussian distributions for both positions (\(P(Pol_{H})_{n-1}\): \(\mu = 0.5\), \(\sigma = 0.25 \)) and weights (\(P(Pol_{w})_{n-1}\): \(\mu = 0.5\), \(\sigma = 0.25\)), such that although each individual voter will have a random collection of policy positions, with those positions randomly assigned weights. We note that as all weight parameters, much like credibility and voting parameters, were drawn from truncated Gaussian distributions, parameters were always between 0 and 1. In this way, although each individual voter will have a random collection of policy positions and weights, the global aggregate across voters and positions does not favor either campaign. Given the independent random sampling of these positions and weights, it thus remains possible for voters to be highly engaged / multiple issue voters (e.g., multiple policies with high weights), disengaged (e.g., multiple policies with low weights), or single issue voters (e.g., one policy with a high weight, the rest low) – irrespective of the policy positions themselves.
After the end of the campaigning stage, consisting of 100 “days” or ticks – with voters updating their policy beliefs in relation to the two campaigns accordingly, each voter casts their vote (with probability \(P(Vote)\)) based on the weighted averaging of policy positions described above, and the simulation concludes. Each combination of manipulated variables (i.e., permutations) is run 100 times, with the results (the proportion of votes between the two campaigns) averaged per permutation.
Manipulations summary
Across the simulated voting population of agents, the likelihood of voting (P(Vote)), the positions voters take on policies (\(P(Pol_H)\)) and the weights assigned to those policies (\(P(Pol_W)\)) are heterogeneous across voters, and are re-sampled at the start of each model run. These variables, along with the campaign duration (100 days or “ticks”), reach of the MTC (20 voters per day), and the size of the voting population (10,000 voters) are not manipulated across simulations.
Campaign Manipulations: Only the reach of the stochastic campaign is manipulated across simulations, from 20 voters per day (on par with the MTC reach), up to 200 voters per day (in increments of 20, resulting in 10 levels).
Voter Manipulations: There are three variables manipulated across simulations among voting agents. First, the number of policies voters consider is manipulated across simulations from 1 to 3 (3 levels). Second, the mean of the distribution from which voters draw their perceived credibility of the MTC campaign (MTC \(P(Cred)\)) is manipulated as either less credible (0.4), neutral (0.5), or more credible (0.6) across simulations (3 levels). Lastly the perceived credibility of the stochastic campaign (Stochastic / non-MTC \(P(Cred)\)) is manipulated independently in the same fashion (3 levels).
Consequently, the simulation consists of 10 x 3 x 3 x 3 = 270 permutations, with each permutation run 100 times (resulting in 27,000 runs), with the results of the 100 runs averaged for each permutation.
Simulation results
In replication of Madsen and Pilditch (2018) we find that in single policy (Fig. 2, solid lines) scenarios, the MTC generally outperforms the stochastic campaign (lines below break-even point mean a lower percentage of votes for the stochastic campaign, and a corresponding higher percentage of votes for the MTC). The only exception to this is when the stochastic campaign is generally perceived as being credible (Fig. 2, bottom row, nonMTC \(P(Cred) = 0.6\)) and is sufficiently larger than the MTC campaign (approximately 2.5 times the size) – a finding that also replicates previous work.
When the stochastic campaign is generally perceived to be less credible (Fig. 2, top row, nonMTC \(P(Cred) = 0.4\)) we find a “backfire” effect of the stochastic campaign as it increases in size. In essence, as the stochastic campaign tries to (randomly) reach more and more voters per day (left to right on X axis), the campaign unintentionally dissuades more voters than they persuade. That is, if the candidate targets a voter who finds the candidate to be unbelievable, the persuasive message backfires and makes the voter believe the candidate less than before the persuasive attempt. More intuitively, we can think of this as an increased chance of voters who may otherwise have aligned with the campaign being “put off” by the low credibility candidate being the source of the persuasive message (“I was inclined towards party \(X\), but then their candidate contacted me…”). As in previous work, this trend is mitigated as the perceived credibility of the candidate increases (e.g., Fig. 2, middle row, nonMTC \(P(Cred) = 0.5\)).6.

Given the targeting capability of MTCs, we find that the MTC avoids the aforementioned backfire effects. This is illustrated by the similarity of results across the differing perceptions of credibility for the MTC campaign (Fig. 2, columns) where MTC can yield the same advantage whether their candidate / campaign is generally perceived to have low (left-hand column), neutral (middle column) or high (right-hand column) credibility.
Finally, we turn to the increasing complexity of voters, represented by the increasing number of policies under consideration (Fig. 2, solid line = 1 policy, short dash = 2 policies, long dash = 3 policies). Here we find that despite the inclusion of this complexity, MTCs generally retain their advantages over stochastic campaigns, successfully navigating the possibilities of single-issue voters, multiple issue voters, generally disengaged voters, and more. We do note that this complexity, when considered in light of the voting decision, tempers the capacity of the stochastic campaign – both to mitigate backfire effects (slower decreasing trends when perceived stochastic campaign credibility is generally low, Fig. 2, top row) and reduce persuasive efficacy (delayed upward trends when perceived stochastic campaign credibility is generally high, Fig. 2, bottom row).
Discussion
The paper extends an agent-based model of micro-targeted campaign strategies through adding additional heterogeneity and sophistication to the voter within the model. In particular, we extend the model in two central ways. One, rather than considering just one policy, voters can now consider multiple political issues when they decide whom to support in the election. In real life, this is closer to how voters approach candidates, as studies show citizens consider multiple political questions (e.g., Horiuchi, Smith, and Yamamoto 2018). Two, we enable voters to rank political issues as more or less important. Similar to considering multiple issues when choosing a candidate, voters may find some issues to be more important than others. This is reflected in weighted preferences across the multiple policy issues. This allows us to heterogeneously produce various forms of voters; single issue (one policy highly weighted), multiple issues / high engagement (multiple policies highly weighted), and disengaged voters (all policies have low weights). These are of course crossed with differing political positions (i.e., a single-issue swing-voter, single issue party voter, etc.). Thus, the paper explores the principled benefits of MTCs when the electorate becomes increasingly complex and heterogeneous.
In line with expectations, we find MTCs to be effective and efficient in navigating this more complex voter-space, consistently yielding a voting advantage over their stochastic counterparts. Furthermore, whilst the increasing reach of a stochastic campaign can either result in increasing backfire effects when they are perceived to have low credibility, or gradual advantage if perceived to have high credibility, MTCs appear to be effective irrespective of general perceptions of credibility. We note these twin effects are critical to bear in mind when considering prospective political campaigns. Those with a candidate who (perhaps unusually) is generally perceived to be highly credible can benefit from an increasingly large campaign reach, though this can arguably be curtailed by campaign finance laws – something that speaks to the general advantage of MTCs in terms of potential efficiency. Contrary to the case with a candidate perceived to be highly credible, if one either knows the prospective candidate to have a perceived credibility that is neutral or low, or one does not know the perceived credibility of the candidate, then an MTC will always yield an advantage among a diverse electorate, with necessary reach being dictated by the credibility of the opponent.
There is one further important implication of the current findings. When an election campaign revolves around a single issue, identity, or candidate (e.g., US presidential campaigns), as opposed to more nuanced, multi-facetted campaigns (e.g., multi-party parliamentary elections), the former is in fact more susceptible to a micro-targeting advantage. This in part is explained by the cumbersomeness of traditional campaigning (i.e., the aforementioned potential to incur backfire effects on prospective voters) being more exposed. Put another way, a single poorly-targeted message is likely to completely turn away a voter if there is only one issue under consideration, but when multiple issues are under consideration, a voter is only likely to be partially turned away.
Extending the cognitive components of the original model allows for increased realism within model simulations. Additionally, as the electorate becomes increasingly complex, the model can test different information dissemination strategies by varying whom to contact, when to contact them, and with what to talk to them. In the current simulations, the micro-targeted campaign targets the swing voters who are favourably disposed towards the candidate and who are likely to vote. However, more sophisticated choice models can be implemented (e.g., calculating expected gain for segments of the electorate in order to optimize targeting). In other words, as the population becomes more realistic, the model offers a formal method to test the effectiveness of competing information strategies.
While the model offers a step towards greater cognitive realism on part of the simulated electorate, there are several avenues for future research. First, while voters in the current model represent a significant step towards a more realistic voter model, there are several models in political theory and science to describe how voters choose a candidate (see e.g., Lodge and Taber 2013). For the purpose of the model framework presented here and in Madsen and Pilditch (2018), it is irrelevant whether there is a universal model or if voter models are culture-specific. The model enables users to input any computational voter assumption within the model, which can be used to test the effectiveness of micro-targeted campaigns (or other campaign strategies) for that voter model and for that electorate. Future work should collate voter models and explore the effectiveness of micro-targeting for different voter assumptions, including the impact of “backfire effects” on findings (but see also e.g., correlating policy positions and weights, and thus stepping towards representations of political polarization among an electorate). Second, research in social psychology has identified psychometric traits as a possible factor in political decision-making (see e.g., Block and Block 2006; Sibley, Osborne, and Duckitt 2012). Future work might explore the appropriateness of these assumptions and whether they impact campaign strategies (for a study on impact of the effect of campaigning via social media, see Bright et al. 2020). Lastly, the assumption of MTC data accuracy used in the present model is a strong one. Although campaigns have been shown to have access to the type of data used here, there remain open questions regarding the influence of “noisiness” in this data, both on general MTC efficacy, and the selection of optimal strategies for (repeated) contacting. This trade-off between data fidelity and MTC strategic efficacy is an important avenue for future research. More broadly, it is not clear what parameters are most diagnostic for segmenting the electorate (personality traits, policy preferences, etc.). As such, the degree of noise concerning electorate data, the most diagnostic signals, and the availability of data throughout a given election cycle will be incredibly context-dependent. As these parameters of the proposed model can be adjusted to fit a given situation, the paper provides a foundational state-of-the-art methodological tool that enables researchers in political science to test assumptions, intuitions, and models in a formal, repeatable manner. Here, we have reported simulations for a situation where data about the electorate is clear and campaigns have access to shifting data throughout the election cycle (e.g. via polls or other means).
Third, information dissemination models and models of beliefs cascading show that bottom-up connectivity between citizens may drive how information is spread, belief formation, and emergent echo chambers (e.g., Duggins 2017; Madsen, Bailey, and Pilditch 2018; Ngampruetikorn and Stephens 2016). In the current model, communication is top-down, as candidates contact voters. To represent the complex information systems inherent in 21st Century election campaigns, future work should integrate social structure and voter-to-voter communication. Fourth, the micro-targeting candidate in the current paper follows one set strategy. As demonstrated within game-theoretic paradigms, competitive agents may adopt different strategies, may switch strategy during the game, or may cancel out strategic advantages of an opponent. Future work may explore different micro-targeting strategies, the evolution of campaign strategies between micro-targeted campaigns, and what happens in multi-party systems.
Finally, agent-based models can be used to calibrate and validate competing models against observable data and be used to test plausible system interventions to make election as equal and fair between candidates as possible (Madsen 2019). While all of these represent intriguing avenues of future research, the current paper, in line with Madsen and Pilditch (2018), provides the foundational computational method through which all of these inherently complex and dynamic questions can be explored. Critically, the model enables researchers to test the impact of information dissemination strategies in principle. That is, the model goes beyond the just-so stories of specific elections where multiple factors may have caused the candidate with access to data to win or lose. By implementing assumptions within the present model framework, we can quantifiably test the specific advantage of knowing the electorate.
The paper focuses on political micro-targeting. However, the method describes how information can be disseminated most effectively in principle and can thus be applied to any number of domains such as public health campaigns, PSAs, and advertisement (the latter is familiar to anyone who has Googled ‘holidays in Berlin’ and subsequently gotten advertisements for flights to or hotels in that city). It is likely that personal- and societal-level data becomes increasingly accessible in the coming years. In addition, the electorates in most representative democracies are becoming increasingly heterogeneous and complex. This paper shows data-driven, psychologically informed campaigns gain strategic advantages when heterogeneity increases. For this reason, it is imperative that we understand and model when and how micro-targeting strategies work in order to ensure fair and democratic elections going forward.
Model Documentation
The agent-based model is written and simulated in NetLogo (release 6.0.4). The simulations were run and data collected and processed using the RNetlogo package in R (Thiele 2014). All files containing the simulation model’s code are accessible at https://www.comses.net/codebases/0ecd5574-99ed-40da-b190-6a1b5786edd5/releases/1.0.0/. The model folder also contains a separate pdf file (“MTC_Model_Basic_Use_Documentation.pdf”) detailing the information needed to understand the model and replicate results.Notes
- In addition to using demographic data, digital data, such as people’s search history, can be used to explore interesting facets of desires, beliefs, and social phenomena (Stephens-Davidowitz 2017). This, in turn, can be used to generate increasingly sophisticated voter profiles for micro-targeting purposes.
- For a full formal model of conditional probabilities, see the complete Bayesian Source Credibility model description in the Appendix.
- While election outcome in this model framework is dependent on the beliefs of the electorate, there are many theories and models of candidate choice (see e.g., Lodge and Taber 2013). Critically, the model presented here is able to test the effectiveness of micro-targeting campaigns for any computationally expressible voter theory/model. Thus, the agent-based method presented provides a canvas that can be used for exploring competing voter theory and how campaign strategies would unfold, given those assumptions.
- This can be considered an amalgam of \(P(T)\) and \(P(E)\) for the purposes of the model.
- As discussed in the above, the model can represent any computationally expressible voter theory/model. Similarly, the model can represent and test the effectiveness of any computationally expressible campaign strategy (i.e., different strategies to segment and target the electorate).
- Of course, the reported backfire effect is a product of the particular cognitive model implemented for belief revision. Some initial empirical evidence suggests that this happens when disliked candidates provides political suggestions (Madsen 2016), it remains an open question as to whether or not this happens for real-life political messages and how best to represent this function computationally. However, as the current paper provides a method in principle, competing voter models may, as discussed in the above, be tested.
Acknowledgements
Both authors were involved in conceptualization, T.D.P. designed and built the model, ran simulations and conducted the analysis, and both authors contributed to the writing and preparation of the manuscript. This research received no external funding. The authors declare no conflict of interest.Appendix
Breakdown of the Bayesian Source Credibility Model
As described in the manuscript (see Equation 1), the probability that a hypothesis is true given a positive report from a source can be calculated using the theorem from Harris et al. (2016).
\(P(H)\) is simple, as it merely represents the current belief of the recipient (ranging from 0 to 1). To integrate perceived expertise, \(P(E)\), and perceived trustworthiness, \(P(T)\), the conditional probability, \(P(Rep|H)\) can be used. To calculate this, Harris et al. (2016) provide the following equation on p. 17:
| $$P(Rep|H) = P(Rep|H, E, T) * P(E) * P(T) + P(Rep|H, E, ¬T) * P(E) * P(¬T) + P(Rep|H, ¬E, T) \\ * P(¬E) * P(T) + P(Rep|H, ¬E, ¬T) * P(¬E) * P(¬T)$$ |
Unpacking this equation, we find complicated conditional probabilities such as \(P(Rep|H, E, T)\). This particular conditional should be read as the probability that the source would say the hypothesis is \(TRUE\) in a world where the hypothesis is actually \(TRUE\) and where the source has total expertise in the relevant field (i.e. relating to the hypothesis) and where the source is completely trustworthy. For example, if a medical professional who has total expertise and is completely to be trusted, what is the probability that they would provide a true report if the report happens to be true?
To integrate perceived expertise, \(P(E)\), and trustworthiness, \(P(T)\), these are multiplied with the relevant conditional probability. For example, if the recipient believes that a fully trusted and expert witness is very likely to provide a positive report given a true hypothesis (\(P(Rep|H, E, T) = 0.8\)), the impact of the report is moderated by the perceived expertise and trustworthiness. Thus, if \(P(E) = 0.34\) and \(P(T) = 0.61\), even a true report from that source would not impact the recipient much. To calculate \(P(Rep|¬H)\), the same equation is used (with \(H\) replaced with \(¬H\)). That is:
| $$P(Rep|¬H) = P(Rep|¬H, E, T) * P(E) * P(T) + P(Rep|¬H, E, ¬T) * P(E) * P(¬T) + P(Rep|¬H, ¬E, T) \\ * P(¬E) * P(T) + P(Rep|¬H, ¬E, ¬T) * P(¬E) * P(¬T)$$ |
Here, conditional probabilities should be read in a similar way. That is, \(P(Rep|¬H, E, T)\) represents the probability that the source would say the hypothesis is \(FALSE\) in a world where the hypothesis is actually \(TRUE\) and where the source has total expertise in the relevant field (i.e. relating to the hypothesis) and where the source is completely trustworthy.
As described in the manuscript, values for the 8 conditional probabilities are taken from Madsen (2016) who sourced these empirically from respondents, yielding Table 1 from the manuscript.
Given the above, the Bayesian Source Credibility model can now compute the posterior degree of belief in the hypothesis, \(H\), given a positive report, \(Rep\), from a source. As described in this appendix and in the manuscript, the impact of this report depends on the prior belief, \(P(H)\), perceived expertise, \(P(E)\), and perceived trustworthiness, \(P(T)\).
References
ALLCOTT, H., & Gentzkow, M. (2017). Social media and fake news in the 2016 election. Journal of Economic Perspectives, 31 (2), 211-236. [doi:10.1257/jep.31.2.211]
BAILEY, R. M., Carrella, E., Axtell, R., Burgess, M. G., Cabral, R. B., Drexler, M., Dorsett, C., Madsen, J. K., Merkl, A. & Saul, S. (2019). A computational approach to managing coupled human-environmental systems: the POSEIDON model of oceans fisheries. Sustainability Science, 14, 259–275. [doi:10.1007/s11625-018-0579-9]
BANDINI, S., Manzoni, S., & Vizzari, G. (2009). Agent Based Modeling and Simulation: An Informatics Perspective. Journal of Artificial Societies and Social Simulation, 12 (4), 4: https://www.jasss.org/12/4/4.html. [doi:10.1007/978-1-0716-0368-0_12]
BIMPER, B. (2014). Digital media in the Obama campaigns of 2008 and 2012: Adaptation to the Personalized political Communication Environment. Journal of Information Technology & Politics, 11 (2), 130-150.
BLOCK, J., & Block, J. H. (2006). Nursery school personality and political orientation two decades later.* Journal of Research in Personality*, 40 (5), 734-749. [doi:10.1016/j.jrp.2005.09.005]
BONABEAU, E. (2002). Agent-Based Modeling: Methods and Techniques for Simulating Human Systems. Proceedings of the National Academy of Sciences of the United States of America,99 (10), 3, 7280-7287. [doi:10.1073/pnas.082080899]
BORAH, P. (2016). Political Facebook use: Campaign strategies used in 2008 and 2012 presidential elections. Journal of Information Technology & Politics, 13 (4). [doi:10.1080/19331681.2016.1163519]
BORAH, P., Fowler, E., & Ridout, T. N. (2018). Television vs. YouTube: political advertising in the 2012 presidential election. Journal of Information Technology & Politics, 15 (3). [doi:10.1080/19331681.2018.1476280]
BOVENS, L., & Hartmann, S. (2003). Bayesian Epistemology. Oxford, UK: Oxford University Press.
BRIGHT, J., Hale, S., Ganesh, B., Bulovsky, A., Margetts, H. & Howard, P. (2020). Does campaigning on social media make a difference? Evidence from candidate use of Twitter during the 2015 and 2017 UK elections, Communication Research, 47 (7), 988-1009 [doi:10.1177/0093650219872394]
BROWN-IANNUZZI, J. L., Lundberg, K. B., Kay, A. C., & Payne, B. K. (2015). Subjective status shapes political preferences. Psychological Science, 26 (1) , 15-26. [doi:10.1177/0956797614553947]
CADWALLADR, C. (2017). The great British Brexit robbery: How our democracy was hijacked. The Guardian, May 7: https://www.theguardian.com/technology/2017/may/07/the-great-british-brexit-robbery-hijacked-democracy.
CARRELLA, E., Bailey, R. M., &. Madsen, J. K. (2019). Repeated discrete choices in geographical agent based models with an application to fisheries. Environmental Software, 111, 204-230. [doi:10.1016/j.envsoft.2018.08.023]
CHAIKEN, S., & Maheswaran, D. (1994). Heuristic Processing Can Bias Systematic Processing: Effects of Source Credibility, Argument Ambiguity, and Task Importance on Attitude Judgement. Journal of Personality and Social Psychology, 66 (3) , 460-473. [doi:10.1037/0022-3514.66.3.460]
CHEN, A., & Potenza, A. (2018). Cambridge Analytica’s Facebook abuse shouldn’t get credit for Trump. The Verge, March 20: https://www.theverge.com/2018/3/20/17138854/cambridge-analytica-facebook-data-trump-campaign-psychographic-microtargeting
CUDDY, A. J., Glick, P., & Beninger, A. (2011). The dynamics of warmth and competence judgments, and their outcomes in organizations. Research in Organizational Behavior, 31, 73-98. [doi:10.1016/j.riob.2011.10.004]
DUGGINS, P. (2017). A Psychologically-motivated model of opinion chance with applications to American politics. Journal of Artificial Societies and Social Simulation, 20 (1), 13: https://www.jasss.org/20/1/13.html. [doi:10.18564/jasss.3316]
EPSTEIN, J., & Axtell, R. (1996). Growing Artificial Societies: Social Science from the Bottom Up, Cambridge, MA: The MIT Press. [doi:10.7551/mitpress/3374.001.0001]
FISKE, S. T., Cuddy, A. J., & Glick, P. (2007). Universal dimensions of social cognition: warmth and competence. Trends in Cognitive Sciences, 11, 77-83. [doi:10.1016/j.tics.2006.11.005]
GILBERT, N. (2008). Agent-Based Models. London, UK: SAGE Publications.
GRAZZINI, J., & Richiardi, M. (2015). Estimation of ergodic agent-based models by simulated minimum distance. Journal of Economic Dynamics and Control, 51, 148-165. [doi:10.1016/j.jedc.2014.10.006]
GREEN, D. P., & Gerber, A. S. (2008). Get Out the Vote: How to Increase Voter Turnout. New York: Brookings.
HAHN, U., Harris, A. J. L., & Corner, A. (2009). Argument content and argument source: An exploration. Informal Logic. 29, 337-367. [doi:10.22329/il.v29i4.2903]
HARRIS, A. J. L., Hahn, U., Madsen, J. K., & Hsu, A. S. (2016). The Appeal to Expert Opinion: Quantitative support for a Bayesian Network Approach. Cognitive Science, 40, 1496-1533. [doi:10.1111/cogs.12276]
HEATH, B., Hill R., & Ciarallo, F. (2009). A survey of agent-based modelling practices (January 1998 to July 2008). Journal of Artificial Societies and Social Simulation, 12 (4), 9: https://www.jasss.org/12/4/9.html.
HEGSELMANN, R., König, S., Kurz, S., Niemann, C. & Rambau, J. (2015) Optimal opinion control: The campaign problem. Journal of Artificial Societies and Social Simulation 18 (3), 18: https://www.jasss.org/18/3/18.html. [doi:10.18564/jasss.2847]
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence: models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5 (3), 2: https://www.jasss.org/5/3/2.html.
HERSCH, E. D. (2015). Hacking the Electorate: How Campaigns Perceive Voters. New York, NY: Cambridge University Press.
HORIUCHI, Y., Smith, D. M., & Yamamoto, T. (2018). Measuring voters’ multidimensional policy preferences with conjoint analysis: Application to Japan’s 2014 election. Political Analysis, 26 (2), 190-209. [doi:10.1017/pan.2018.2]
HOUSEHOLDER, E. E., & LaMarre, H. L. (2014). Facebook Politics: Toward a Process Model for Achieving Political Source Credibility Through Social Media. Journal of Information Technology & Politics, 11 (4), 368-382.
ISSENBERG, S. (2012). The Victory Lab: The Secret Science of Winning Campaigns. New York, NY: Broadway Books.
JOHNSON, N. (2007). Simply Complexity: A Clear Guide to Complexity Theory. Oxford, UK: One World.
KOTTONAU, J. & Pahl-Wostl, C. (2004). Simulating political attitudes and voting behaviour. Journal of Artificial Societies and Social Simulation, 7(4), 6: https://www.jasss.org/7/4/6.html.
LEÓN-MEDINA, F. J. (2019). Endogenous changes in public opinion dynamics. Journal of Artificial Societies and Social Simulation, 22 (2), 4: https://www.jasss.org/22/2/4.html. [doi:10.18564/jasss.3967]
LEVI, M., & Stoker, L. (2000). Political Trust and Trustworthiness. Annual Review of Political Science, 3, 475-507. [doi:10.1146/annurev.polisci.3.1.475]
LODGE, M., & Taber, C. S. (2013). The Rationalizing Voter. New York, NY: Cambridge University Press.
MADSEN, J. K. (2016). Trump supported it?! A Bayesian source credibility model applied to appeals to specific American presidential candidates’ opinions. In Proceedings of the 38th Annual Conference of the Cognitive Science Society, (eds.) A. Papafragou, D. Grodner, D. Mirman, and J.C. Trueswell, 165-170. Austin, TX: Cognitive Science Society.
MADSEN, J. K. (2019). The Psychology of Micro-Targeted Election Campaigns. London, UK: Palgrave Macmillan.
MADSEN, J. K., Bailey, R. M., Carrella, E., & Koralus, P. (2019). Analytic versus computational cognitive models. Current Directions in Psychological Science, 28(3), 299-305. [doi:10.1177/0963721419834547]
MADSEN, J. K., & Pilditch, T. D. (2018). A method for evaluating cognitively informed micro-targeted campaign strategies: An agent-based model proof of principle. PLoS One, 13 (4): e0193909, 1-14. [doi:10.1371/journal.pone.0193909]
MCCLANE, A. J., Semeniuk, C., Mcdermid, G. J., & Marceau, D. J. (2011). The role of agent-based models in wildlife ecology management. Ecological Modelling, 222 (8), 1544-1556. [doi:10.1016/j.ecolmodel.2011.01.020]
NGAMPRUETIKORN, V., & Stephens, G. J. (2016). Bias, belief, and consensus: Collective opinion formation on fluctuating networks. Physical Review E, 94, (5), 052312. [doi:10.1103/physreve.94.052312]
NIAZI, M., & Hussain, A. (2009). Agent-based tools for modeling and simulation of self-organization in peer-to-peer, ad hoc, and other complex networks. IEEE Communications Magazine, 47 (3), 166-173. [doi:10.1109/mcom.2009.4804403]
NIELSEN, R. K. (2012). Ground Wars: Personalized Communication in Political Campaigns. Princeton, NJ: Princeton University Press.
NYHAN, B. (2018). Fake news and bots may be worrisome, but their political power is overblown. The New York Times, February 13: https://www.nytimes.com/2018/02/13/upshot/fake-news-and-bots-may-be-worrisome-but-their-political-power-is-overblown.html.
NYHAN, B. & Reifler, J. (2010) When corrections fail: The persistence of political misperceptions, Political Behavior, 32 (2), 303-330 [doi:10.1007/s11109-010-9112-2]
PETTY, R. E., & Cacioppo, J. T. (1984). Source factors and the elaboration likelihood model of persuasion. Advances in Consumer Research, 11, 668-672.
SCHELLING, T. C. (1978). Micromotives and Macrobehavior, New York, NY: W. W. Norton & Company.
SIBLEY, C. G., Osborne, D., & Duckitt, J. J. (2012). Personality and political orientation: Meta-analysis and test of a threat-constraint model. Journal of Research in Personality, 46 (6), 664-677. [doi:10.1016/j.jrp.2012.08.002]
STEPHENS-DAVIDOWITZ, S. (2017). Everybody Lies: What The Internet Can Tell Us About Who We Really Are. London: Bloomsbury Publishing.
STILES, E. A., Swearingen, C. D., Seiter, L. & Foreman, B. (2020) Catch me if you can: Using a threshold model to simulate support for presidential candidates in the invisible primary. Journal of Artificial Societies and Social Simulation, 23 (1), 1: https://www.jasss.org/23/1/1.html. [doi:10.18564/jasss.4158]
THIELE, J. C. (2014). R Marries NetLogo: Introduction to the RNetLogo Package. Journal of Statistical Software, 58 (2), 1-41.
Trump, K-S. (2018). Four and a half reasons not to worry that Cambridge Analytica skewed the 2016 election. The Washington Post, March 23: https://www.washingtonpost.com/news/monkey-cage/wp/2018/03/23/four-and-a-half-reasons-not-to-worry-that-cambridge-analytica-skewed-the-2016-election/.
WOOD, T. & Porter, E. (2018). The elusive backfire effect: Mass attitudes’ steadfast factual adherence. Political Behavior, 41, 135–163. [doi:10.1007/s11109-018-9443-y]

