Introduction
In April 2009, an earthquake struck L’Aquila, a medieval town in Central Italy, killing 309 people. In 2010 six scientists were put under investigation for allegedly giving false and fatal reassurances to the public a few days ahead of the earthquake (Hall 2011). They were members of the “National Commission for the Forecast and Prevention of Major Risks” (Commissione Grandi Rischi), a governmental body which was asked to provide advice about tremors and earthquakes in the area. According to prosecutors, the fact that these scientists and their spokesperson issued a statement reassuring the population made many people feel safe enough not to leave their houses after the initial shocks on the same night. Many of the survivors reported having interpreted the statement issued by the National Commission, which was immediately and widely reported by the national media, as a reliable and trustworthy indication that no catastrophic events were to be expected and to have behaved accordingly. In 2015, the six scientists were formally acquitted, but their evaluation of the risk and the way it was communicated to and perceived by the population had had a profound impact on society, raising awareness of the consequences of institutional communication and media influence in risky situations.
Sadly, the importance of this behavior had already become evident during the aftermath of Hurricane Katrina in New Orleans, four years before the earthquake in L’Aquila. Katrina was a powerful hurricane that caused extensive destruction and casualties (at least 1,836 people died in the hurricane and subsequent floods), but the many management mistakes during the emergency aggravated the situation. Mayor Nagin of New Orleans and Louisiana Governor Blanco were criticized for ordering residents to a shelter of last resort without any provisions for food, water, security, or sanitary conditions. Furthermore, the information they provided to the population was often incomplete and late (Selected Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina 2006).
These two examples indicate the importance of informing endangered or already affected populations about the risks of a catastrophe without, at the same time, spreading panic. Natural and anthropogenic disasters are characterized by a varying degree of uncertainty about their occurrence, their magnitude and the ensuing consequences. In the decision-making literature, risk is traditionally defined as a function of (a) the likelihood and (b) the value of possible future events. Risk arises from the uncertainty, actual or perceived, surrounding the event and it varies as a function of the kind of hazard. Underestimating the likelihood of disasters is as dangerous as exaggerating them. The latter might result in hoarding behavior, riots and other undesirable consequences, both on the individuals’ health (Rochford Jr & Blocker 1991) and on the community’s well-being (Kaniasty & Norris 2004). Providing accurate and valid information about an uncertain event is obviously very difficult, but even if experts and institutions succeed in doing so, this does not necessarily translate into an equally accurate perception of collective risk.
This occurs because citizens are not passive and unbiased recipients of neutral information, but they actively revise information in light of what they already know and believe (Giardini et al. 2015), and share their own opinions with each other, in an attempt to make sense of what is happening. This process of risk interpretation (Eiser et al. 2012) creates a collective perception of risk that can significantly differ from the initial message sent by the institutions or the media, with varying consequences on emergency preparedness and management. The question is: what are the consequences of different sources of information on collective risk assessment and how does the message interact with individual features (trust in institutions, sensitivity to risks, propensity to communicate with others)? How do social network structures amplify or reduce the collective perception of risk?
There is a long tradition of research in complex systems (Deffuant et al. 2000) and sociology (Flache et al. 2017) concerning the complex relationships between social influence at a micro-level and its macro-consequences for integration or divisions in society. A parallel and unconnected research tradition is disaster studies (Lindell 2013), which address the social and behavioral aspects of disasters. Here, we want to bridge this disciplinary divide by developing an ABM model of collective risk assessment as the result of the interplay between agents’ traits and opinion dynamic processes. If applied to risk interpretation, consensus means that there is a shared perception of a given risk, more or less correct, whereas polarization would result in people holding different beliefs about the occurrence of the event or its consequences. By modeling the determinants and the processes of risk interpretation and social influence it could be possible to understand what causes risk amplification, whereas by understanding the mechanisms behind consensus and polarization in opinions about risks can prove useful to define effective communication campaigns, to avoid the traps of misinformation and to ensure a fact-based view of the emergency.
The aim of this work is threefold. First, we are interested in modelling the interplay between individual factors, information transmission and social aspects of risk perception. Micro-level characteristics like trust in institutions or individual attitudes towards risk can be amplified or reduced in the interaction with other individuals, with unintended effects at the macro-level. Second, we want to compare the role of two different information sources, institutions and the media, on opinion polarization and consensus. Risk interpretation can occur from a more general process of social influence, in which comparing opinions and collecting information from others can lead to more or less consensus about the risk, and then to a heightened collective preparedness in face of a major hazard. Finally, this study investigates the role of network topologies on collective risk assessment by comparing a set of different topologies, also by using two different empirically calibrated networks.
In order to understand collective risk assessment and its emerging macro-effects, we developed an agent-based model in which heterogeneous agents form opinions about risk events depending on information they receive from the media, institutions and their peers. We also used different network topologies in order to get a better understanding of the role of structural features in the spreading of opinions.
The rest of the paper is organized as follows. introduces the problem of risk perception and presents the current state of the art. introduces the distinctive features of the Opinions on Risky Events, O.R.E., model, while presents the results of different simulation experiments. is devoted to discussion. Finally, in we draw some conclusions and suggestions for future research.
Factors Affecting Risk Perception and Collective Risk Assessment
Accuracy in judgment about the world is of primary importance, but it becomes fundamental when individuals have to cope with uncertain and dangerous events. When natural disasters and anthropogenic catastrophes are unavoidable, awareness of their consequences and the preparedness to deal with them is necessary to reduce physical damage, prevent casualties and minimize their repercussions. Earthquakes, flooding, storms, volcanic hazards, industrial disasters and epidemics present very diverse challenges, but they are all characterized by varying levels of uncertainty about whether, when, or where they are going to happen and by largely unforeseeable consequences. Equally difficult to predict is the reaction that individuals will have towards the information, i.e., how they will perceive the risk, both individually and as a result of collective processes (Eiser et al. 2012).
Risk perception: Individual factors and the social amplification of risk
In decision theory, the tradition of studies on risk perception is well established (Slovic 1987), and a number of factors have been claimed to play a role in it. Humans tend to overestimate the risk of catastrophic but unlikely events compared to more common but less disastrous ones (Slovic et al. 1982), although there are several factors affecting risk perception. Wachinger and colleagues (Wachinger et al. 2013) reviewed more than 30 European studies on floods, heat-related hazards, and alpine hazards (flash floods, avalanches, and debris floods) published after 2000. They identified four main categories of factors affecting risk perception: risk factors associated with the scientific characteristics of the risk, informational factors, such as source and level of information, and media coverage, personal factors, which also include age, gender, and trust, and contextual factors, related to the specific situation. These factors are intertwined, and their interplay gives rise to complex and emergent dynamics at the collective level. In this paper, we are going to focus on trust and risk sensitivity as personal factors interacting with informational factors, i.e., peers, institutions and the media as different sources.
Trust is a cornerstone of human societies, and in situations of uncertainty and risk the amount of trust individuals place in different sources of information can become decisive (Earle & Cvetkovic 1995; Luhmann 1989). There are cultural and individual differences in people’s beliefs in the possibility of avoiding and controlling risk, which create different levels of trust in others. For instance, personality and cognitive styles contribute to determining people’s confidence in their judgement and therefore the decision to turn to others to obtain more information (Eiser et al. 2012). The source of the message has the potential to enhance the effectiveness of risk communication (Wogalter et al. 1999) and trust in the source tends to be higher when the source is perceived to be knowledgeable and has little vested interest, as reported by Williams & Noyes (2007). When deciding whether to accept or not a risk message trustworthiness and credibility play a key role, according to Petty et al. (1994). The experts, the government, or a neighbor can all be trustworthy sources of information, especially in times of danger and uncertainty, and their opinions can have important consequences. Sharing and comparing information and interpretations with other individuals is crucial for making sense of what is happening, and this phenomenon, called "social milling" (Mileti & Peek 2000), allows to reach a shared, or allegedly so, interpretation of what is happening.
Alongside peer influence, institutional sources are also very important. Previous research has shown that when considering situations perceived as being risky (for instance, GMO-technologies, stocking of radioactive waste, etc.), individuals who report higher trust in institutions (government, companies, scientists, etc.) also consider catastrophic events as less probable (Bassett Jr et al. 1996; Siegrist 1999). Analogously, general trust in institutional sources is closely related to the perception and acceptability of different risks(Bord & O’Connor 1992; Eiser et al. 2012; Flynn et al. 1992; Freudenburg 1993; Jungermann et al. 1996; Pijawka & Mushkatel n.d.).
There are a variety of sources from which end-users may obtain information regarding hazards and disasters. For instance, mass media (e.g., television, newspapers, radio, etc.) play an extremely important role in the communication of hazard and disaster related news and information (King 2004 and Fischer 1994) and significantly influence or shape how the population and the government view, perceive and respond to hazards and disasters (Rodríguez et al. 2007).
Although relevant, these theories treat risk perception mostly as an individual phenomenon. An interesting exception is offered by the theory of "Social amplification of risk". In the words of Kasperson and colleagues (Renn et al. 1992) the social amplification of risk is "the phenomenon by which information processes, institutional structures, social-group behavior, and individual responses shape the social experience of risk, thereby contributing to risk consequences". In this framework, a proper assessment of a risk experience requires us to take into account the interaction between physical harm attached to a risk event and the social and cultural processes that shape the interpretations of that event, their consequences, and the institutional actions taken to manage the risks.
The importance of understanding the interaction between risks and the context in which they are evaluated has been advocated also by other scholars (Wachinger et al. 2013), but the exact role played by each factor and the consequences for risk perception and individual choices has not been assessed yet. For collective risk assessment to emerge, it is necessary to account for dynamic processes of social influence, but also for the way in which actors integrate what they already know with information coming from other sources, like their peers, the media or institutional sources. Can we identify what drives collective risk interpretation towards alarm (and eventually panic), transforming individuals in scare mongers, or towards indifference, with the result that people underestimate risks and are not prepared?
Social influence and opinion dynamics for collective risk assessment
Collective risk assessment does originate from processes of social influence and communication between individuals and supra-individual actors, such as institutions and the media. Here, we propose to model this process in terms of opinion dynamics, in order to focus on the determinants of opinion spreading in a population, and the conditions under which they become polarized (Deffuant et al. 2000; Hegselmann et al. 2002; Sen & Chakrabarti 2014). A recent review paper by Flache and colleagues (Flache et al. 2017) offers a broad overview of existing models of social influence, and it details the different ways in which a complex relationship between social influence as a micro-level process and its macro-consequences for integration or divisions in society might emerge. The authors systematically review the existing literature by grouping the models according to their core assumptions and showing that these determine whether opinion convergence can be achieved or not. Thanks to this corpus of work, it is possible to explore the conditions under which differences in opinions, considered as the agent’s property affected by social influence, may eventually disappear. The term "opinion" is used in a very general manner, and it can equally apply to attitudes, beliefs and behavior, thus allowing its generalization to different contexts, and its applicability to multiple domains.
More germane to the topic of risk perception is a model of opinion formation specifically designed to address risk judgments, such as attitudes towards climate change, terrorist threats, or children vaccination, developed by Moussaı̈d et al. (2013). In this individual-based model of risk perception there are two main classes of actors, e.g., the individuals and the media, with the former receiving or searching for information provided by the latter, and then communicating about the risk with others. The model also introduces a cognitive bias whereby individuals integrate and communicate information in accordance with their current views. Results show that two variables explain whether individual opinions about risk may converge or not: how much agents search for their own independent information and the extent to which they exchange information with their peers. Although interesting, Moussaid’s model makes very simplistic assumptions about the internal processes determining confidence in the information received, trust in the different sources and the ensuing decision to share that information.
In times of uncertainty when how risks are interpreted and experienced is more relevant than their objective likelihood, dimensions such as trust and risk sensitiveness can offer a better tool to understand collective risk perception and to minimize the risks of exaggeration or underestimation of the danger in the population. In order to model the perception of risks as different opinions, we moved from the cognitive model of opinions developed by Giardini et al. (2015). They define opinions as complex cognitive constructs resulting from the combination of:
- subjective truth-value, which expresses whether and how much someone believes an opinion to be true;
- confidence, i.e., the extent to which someone’s opinion is resistant to change;
- sharedness.
The latter encapsulates the popularity of an opinion according to a given agent and it is a way to model social pressure, which means that believing that one’s own opinion is shared by the majority makes opinion change less likely to happen (Kelman 1958).
The internal dynamics of these traits change as a result of social influence, and it leads to more or less consensus depending on the initial distribution of traits in the population, and on the system topology (Giardini et al. 2015). This tripartite model, though still very simplified, was used to explore which individual traits are responsible for opinion change, and which configuration of traits will lead to consensus.
The O.R.E. (Opinions on Risky Events) Model
Overview - Design concept - Details
We have a population of \(L\) agents (if not differently specified, we will usually assume \(L=1000\)). Each agent \(i\) is characterized by an opinion \(O_i\). For the sake of simplicity, we model opinions as the subjective probability that the disaster will actually take place, without taking into account the magnitude of the possible consequences, which would add further unnecessary complexity to the model. Furthermore, there is a huge variation between disasters in which probability and consequences are extremely difficult to predict, such as earthquakes, and disasters such as floods in which weather forecasts and location-specific features make risk calculation less haphazard. Opinions vary between 0, which can be expressed as "I am certain that nothing is going to happen", and 1, which means "I am certain that the disaster will happen". At the onset of the simulation, opinions are randomly assigned to agents, and they are updated on the bases of the interplay between internal characteristics of the agents and three different sources of influence.
Initial conditions – At the beginning of every iteration of the dynamics, the agents are randomly assigned an opinion between 0 and 1, always with uniform distribution. Additionally, internal variables are randomly distributed, although distribution is not necessarily uniform, and it will be specified in each case. Opinions evolve, but individuals’ internal variables remain constant over time. The institutional information \(I\) is set at the start of the dynamics and never changes.
Characteristics of the agents
Each individual agent is described by different parameters: risk sensitivity, tendency to communicate and trust. Risk sensitivity is an integer variable which can assume three possible values, \(R_i\in\{-1,0,+1\}\). Risk sensitivity is characterized independently from the received information and it is randomly distributed in the population, and affects the tendency to inform others about the potential danger, \(B_i\). This means that agents who perceive the risk as more probable will also tend to talk about it more, thus sharing their worries with others. People tend to transmit information that is in accordance with their initial risk perception, neglecting opposing information (Popovic et al. 2020). This, in turn, can lead to an amplification of the initial risk perception of the group, even if the original information supported the opposite view; it also fuels polarization between different groups.
Trust is a real number varying between \(0\) (minimum trust) and \(1\) (maximum). When trust is \(0\) or very close to it, the information received will not produce any change in the initial opinion because the source will be considered untrustworthy and its message will be discarded. On the contrary, when trust is high the influence of the source and its effect on the opinion will be equally high.
Trust plays a key role in risk perception (Flynn et al. 1992). People who trust authorities and experts tend to perceive fewer risks than people who do not trust them, and this effect is higher when people have little knowledge about an issue that is important to them. In his critical review of the literature, Siegrist confirmed the importance of trust, but he concluded that it varies by hazard and respondent group therefore it is not possible to define a single way in which trust interacts with risk perception (Siegrist 2019). In this study we distinguish between trust in institutions and in other individuals. We define trust in institutions as \(T_{i}\) and trust in peers as \(P_i\).
We assume that trust towards institutional information is negatively correlated to trust towards peers:
| \[T_i=1-P_i\] | \[(1)\] |
This assumption is important because it allows us to distinguish the effect of trust in two major sources of risk information, and to model the interplay between inter-individual trust and trust in official communication (Slovic 1993). Studies on misinformation (Lewandowsky et al. 2012) and the link between conspiracist ideation, worldviews and rejection of science seem to suggest that individuals with low trust in government and experts tend to selectively believe people with the same views (Lewandowsky et al. 2013). A recent study on institutional trust and misinformation about the Ebola outbreak in DR Congo shows that participants in the survey with low levels of trust in government institutions and the information they communicated held widespread beliefs about misinformation, and more than 88 per cent of the surveyed participants had received this information from friends or family (Vinck et al. 2019).
Processes of social influence
We define three ways in which social influence may unfold. The first consists of peer-to-peer communication among agents communicating with each other in a horizontal and reciprocal way. The second kind of influence occurs through vertical institutional communication, which spreads unilaterally from the institution to the individuals.
The impact of media on the population in the aftermath of disasters is well-known (Holman et al. 2014; Vasterman et al. 2005), therefore we also model media influence, as neutral, alarming or reassuring depending on the way in which institutional information is reported. Media influence is also unidirectional, i.e., broadcast from the media source to the agents (in this model we do not consider social media).
| Variable | Description | Notes |
| \(O_i\) | Opinion | Real number; evolving |
| \(R_i\) | Risk sensitivity | Integer; constant |
| \(B_i\) | Tendency to communicate | Real number; constant |
| \(T_i\) | Trust towards institutions | Real number; constant |
| \(P_i\) | Trust towards peers | Integer; constant |
Table 1 presents the main variables defining agents’ internal and external behavior, together with their main features.
Algorithm of the dynamics
Step one – Information from the institutional source. At each time step, the Institution informs each and every agent about the official risk evaluation \(I\), which is a real variable between 0 and 1, being \(I=0\) the minimum risk information (\(i.e.\), no risk at all), and \(I=1\) the maximum (\(i.e.\), catastrophic event to happen with probability of \(100\%\)). We will call this variable institutional information. Agents use this information to update their opinions about the communicated risk \(I\) according to their internal variables. An individual \(i\) modifies its opinion \(O_i(t-1)\equiv O_i^o\) following a two-stage process where the first one is the same rule adopted in Deffuant model (Abelson 1964; Deffuant et al. 2000):
| \[ O_i^o\longrightarrow O_i=O_i^o+T_i(I-O_i^o).\] | \[(2)\] |
| \[ O_i\longrightarrow \left\{ \begin{array}{lll} \frac{1}{2}(1+O_i) & \ \ \ \ \ & \mbox{if} \ \ \ \ \ R_i=+1 \\ & & \\ O_i & \ \ \ \ \ & \mbox{if} \ \ \ \ \ R_i=0 \\ & & \\ \frac{1}{2}O_i & \ \ \ \ \ & \mbox{if} \ \ \ \ \ R_i=-1 \ . \end{array} \right.\] | \[(3)\] |
Step two – Information exchange among peers. In each simulation round a pair of agents is picked up at random. Let us define \(j\) as the "speaker" and \(i\) as the "listener" (the symmetrical interaction where \(i\) is the speaker and \(j\) the listener will take place in the same way), \(i\), and \(O_i\) and \(O_j\) their opinions before the interaction takes place, respectively. Now, the probability \(\Pi_x\) that a determinate player \(x\) communicates its opinion to the opponent is
| \[ \Pi_{x}=O_{x}^{1/B_{x}} \,\] | \[(4)\] |
If the speaker decides not to share its opinion \(O_j\) (according previous equation, this happens with probability \(1-\Pi_j\)) with the listener, the latter’s opinion \(O_i\) does not change. If instead agent \(j\) actually shares its opinion, agent \(i\) will change its own according to a rule of the same kind of Equation (???):
| \[ O_i\longrightarrow O_i'=O_i+P_i(O_j-O_i)\equiv O_i'=O_i+(1-T_i)(O_j-O_i).\] | \[(5)\] |
| \[ O_i'\longrightarrow \left\{ \begin{array}{lll} \frac{1}{2}(1+O_i') & \ \ \ \ \ & \mbox{if} \ \ \ \ \ R_i=+1 \\ & & \\ O_i' & \ \ \ \ \ & \mbox{if} \ \ \ \ \ R_i=0 \\ & & \\ \frac{1}{2}O_i' & \ \ \ \ \ & \mbox{if} \ \ \ \ \ R_i=-1 \ . \end{array} \right.\] | \[(6)\] |
Media influence. As a starting point, we assume that in principle, the media can report institutional information in three ways: in a reassuring way, in an alarming way and in a neutral way, i.e., reporting the information without any changes. In this paper we model such effect in a rather simplified manner, leaving a proper refinement for future works: for a discussion about the role of media in disaster preparedness and agenda setting see Barnes et al. (2008) and Moeller (2006).
We therefore implemented the effect of media influence in the model as follows. Every time an agent receives the institutional information, we assumed that with equal probability such information can be distorted towards alarmism, reassurance, or left unaltered:
| \[I\longrightarrow I'= \left\{ \begin{array}{lll} \mbox{random number}\in[0,I/2) & \ \ \ & \mbox{with probability}\ 1/3 \\ \ & \ & \ \\ I & \ \ \ & \mbox{with probability}\ 1/3 \\ \ & \ & \ \\ \mbox{random number}\in\left(\frac{I+1}{2},1\right] & \ \ \ & \mbox{with probability}\ 1/3 \ . \end{array} \right. \] | \[(7)\] |
End of simulation. Every iteration lasts enough to achieve a final state, i.e., a configuration where the dynamics has become constant and the global configuration of the system is stable, that is, the opinions of all the agents do not change anymore. All the simulation results are averaged over 2000 independent realizations (i.e., iterations) for each given condition, unless differently specified.
Topological structure
A key factor in social influence is the way in which the population is structured and the resulting communication flow. For the sake of simplicity, we decided to place agents on different topologies with increasing complexity. First, we place agents on a complete graph, that is, everyone is directly linked with everyone else (well-mixed population or mean-field topology) (Pirnot 2001). Indeed, interactions among people are in general much more complex, being a complete graph a good description of the underlying network only for very small communities, as for instance the students of a single school class, a group of friends and so on. Nevertheless, this extreme configuration does not generally represent the topology of the vast majority of human interactions. Therefore, as soon as we focus on structured and complex communities, such as cities or countries, it becomes largely insufficient, and a different kind of topology has to be considered for different kind of situations. For instance, the physical interactions (i.e., not through mass and social media) among people in large enough populations are better modelled by Strogatz-Watts small-world networks (Watts & Strogatz 1998); on the other hand, the structure of connections among users in virtual communities as Facebook or large mailing lists show topological behavior close to Scale-free networks (Caldarelli 2007).
In this work, we tested our model for different network topologies, starting with well-mixed case as the baseline configuration in order to explore the more noticeable features of the model. Indeed, knowing the behavior of the model in well-mixed and in more realistic topologies permits to figure out the exact role of the topology itself or, if no relevant differences are found, to know that other factors influence the dynamics and outcomes of the model (Vilone et al. 2016). The second step will consist in checking the dynamics on more realistic topologies. More specifically, we consider the following four network structures:
- a one-dimensional ring of \(L=1000\) nodes with connections to second-nearest-neighbors (so that each agent is linked to four other individuals);
- an Erdös-Rényi random network of \(L=1000\) nodes with probability of existence of a link \(p=0.1\);
- a Watts-Strogatz small-world network (Watts & Strogatz 1998), generated from the ring defined above with rewiring probability \(p_r=0.05\);
- a real network of \(L=1133\) users of the e-mail service of the University of Tarragona, Spain (A. Arenas 2003a; Guimerà Manrique et al. 2003), which can be approximated for high degrees with a scale-free network with exponent \(\simeq2\);
- a real network of \(L=4038\) users of Facebook, extracted again by the University of Tarragona, Spain (A. Arenas 2003b), which can also be approximated for high degrees with a scale-free network with exponent \(\simeq2\).
The last two networks are real systems which allow us to test the model on a realistic configuration. The remaining ones are useful for different reasons. The Watts-Strogatz network models accurately important phenomena occurring in real human interactions (Barrat & Weigt 2000; Watts & Strogatz 1998), as for instance the "six degrees of separation", that is, the average distance among agents increases with the logarithm of the total population. The one-dimensional ring and the Erdös-Rény random network, though essentially abstract, have opposite clustering coefficient (that is, two neighbours of a given node have high probability to be neighbours on their turn in the former, very low in the latter).
Results
In presenting the results, we distinguish between simulation experiment 1, in which there is only one source of information about the risk, i.e., the institution, and simulation experiment 2, in which the presence of media is introduced. For both experiments we aimed to study how interaction between individuals’ internal states, information coming from 2 or 3 (including the media) different sources, and topology affects the dynamics of collective risk assessment.
Baseline: No institution
As a starting point, we checked the behavior of the model without any institutional influence. As we have verified in different configurations (varying population size and topology), without any communication by the institution, all the agents tend to maximum level of alarmism (see Fig. 1): indeed, in such configurations the more worried individuals are more prone to share their opinions, driving the rest of the population towards their views. Therefore, institutional information plays a fundamental role in offering a balanced view and avoiding the spreading of panic.
Simulation experiment 1: The O.R.E. model without media influence
In order to have a baseline of the model, we designed a perfectly balanced system in which all initial opinions are uniformly distributed in the real interval \([0,1]\), and the internal variables \(\{B_i, R_i, T_i\}_{i=1,\dots N}\) are picked up at random with a uniform probability. The agents are placed on complete graphs. Of course, this is an unrealistic situation but, as for the topology, we started from this simple case and subsequently we will refine the parameters, in order to single out the role of each feature of the model to develop the dynamics and final opinion configuration.
Our results show that a final stationary state can be effectively reached by the system, as shown in Figure 1. Noticeably, the convergence is quickly achieved: already after very few time steps, the average opinion acquired a stable value.
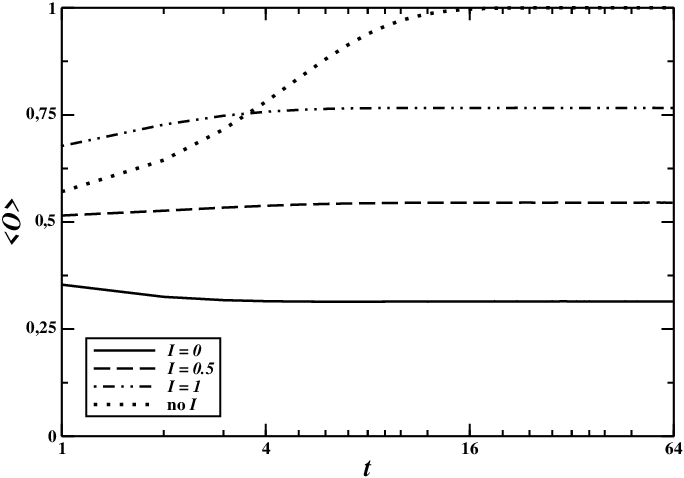

Figure 2 shows how the final average opinion behaves as a function of the institutional information. For both high- and low-probability dangers, the system shows a discrepancy between institutional communication and individuals’ opinions. In general, individuals are more alarmist than the institution for reassuring information, but they are less alarmed if the official information is worrying. However, these results exhibit another interesting asymmetry: the value \(I^*\) of the institutional information for which the response of the population is equal to the input is not \(\bar I=0.5\), as one could expect since the system is balanced, but larger (more precisely, we have here \(I^*\simeq0.58\)). This counter-intuitive result could help explain why alarmist information spreads more easily, especially in highly uncertain situations.
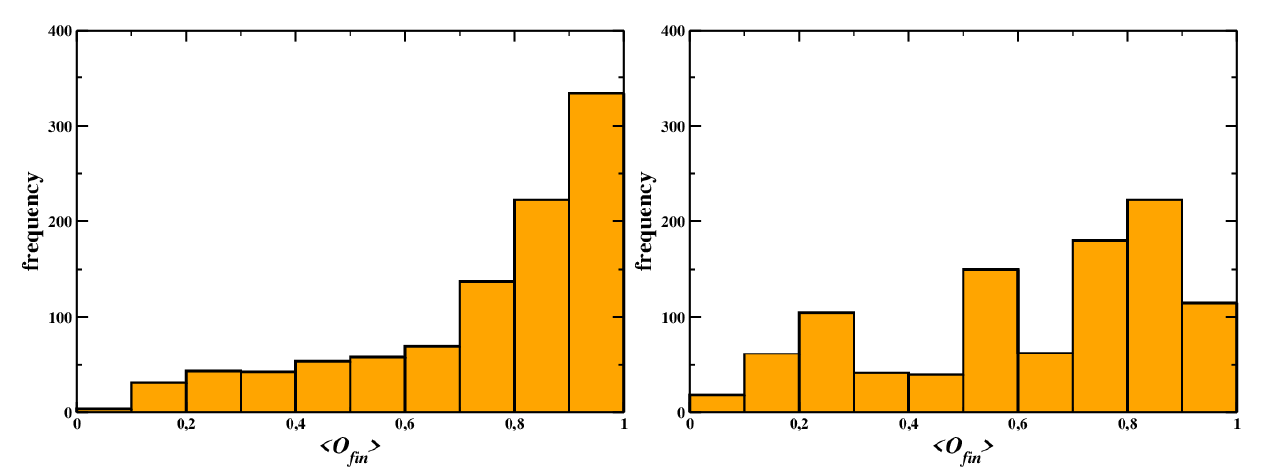
Noticeably, in our model full consensus is never reached: at most, when the average opinion is close to one of the two extreme values, there are fewer agents with an opinion far from the average. Indeed, in the final state there is always a final non-trivial opinion distribution, as shown in Figure 3 (see also Figure 10 in Sec. 7 about a different version of the model), and the median opinions are less common in the final configuration, especially when the system ends up in an alarmist state.
Unbalanced systems in mean-field approximation
In this subsection, we investigate what happens when the system is not balanced, that is, when the distribution of agents’ internal variables is not uniform (equivalently, their average is not equal to their median value). In particular, we studied the behavior of the system by varying the two key features of agents: average risk sensitivity and trust in the institution in order to isolate the effect of the different variables on the final opinion change.
Varying trust, balanced risk sensitiveness
Here we study those systems in which the risk sensitivity is uniformly distributed among agents, while their trust towards the institution has an unbalanced distribution. More precisely, each player \(i\) is assigned with probability \(P_T\) a trust \(T_i\) uniformly distributed between 0.5 and 1 (high trust), and with probability \(1-P_T\) a trust \(T_i\) uniformly distributed between 0 and 0.5 (low trust). Therefore, the average trust is
| \[\langle T\rangle=\frac{1+2P_T}{4}. \] | \[(8)\] |
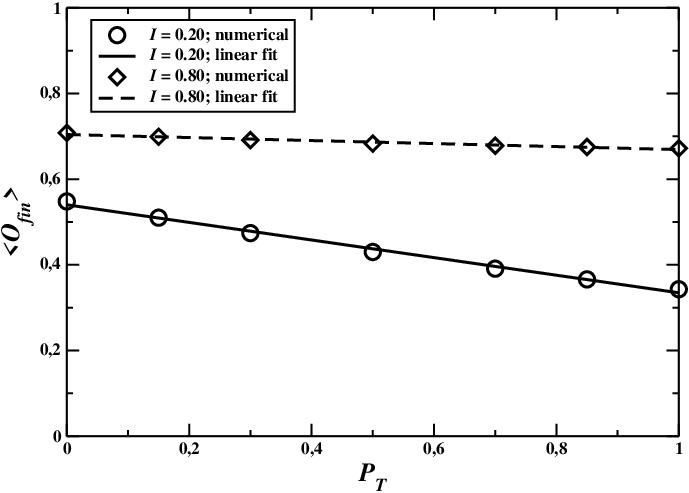
In Figure 4, we show how the population responded to institutional information by varying the average trust towards the institution. Understandably, when the institution communicates a non-alarmist message (\(I=0.20\)), increasing the trust means decreasing the value of the final average opinion. On the other hand, when the input is alarmist (\(I=0.80\)), trust appears to have scarce effect on the dynamics. Indeed, in this case, the system is much less dependent on trust, and the final average opinion is almost constant with respect to \(P_T\) (what is more, it slightly decreases with \(P_T\) increasing).
Varying risk sensitiveness, balanced trust
Here we analyze the opposite case where trust is uniformly distributed, but agents differ with regard to their risk sensitiveness. In particular, each player \(i\) is assigned the neutral risk sensitiveness (\(R_i=0\)) with probability \(1/3\), a positive risk sensitiveness \(R_i=+1\) with probability \(2P_R/3\), and a negative one with probability \(2(1-P_R)/3\). Therefore, the average risk sensitiveness is
| \[\langle R\rangle=\frac{2P_R-1}{3}. \] | \[(9)\] |
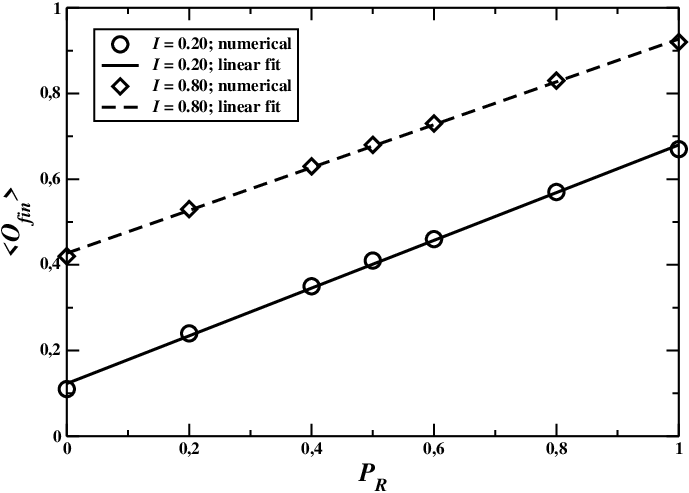
In Figure 5 we show the behavior of the final average opinion as a function of the risk sensitiveness unbalance \(P_R\), again for an alarmist institutional information (\(I=0.80\)) and a non-alarmist one (\(I=0.20\)). As expected, \(\langle O_{fin}\rangle\) increases linearly as the population increases its global risk sensitiveness, in the same way for different values of \(I\).
Network topologies

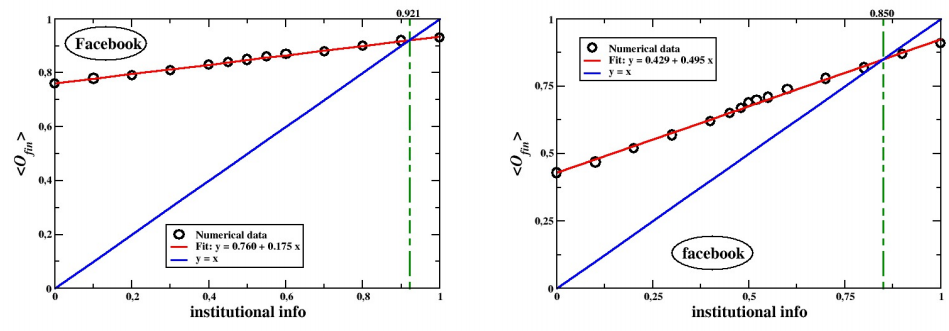
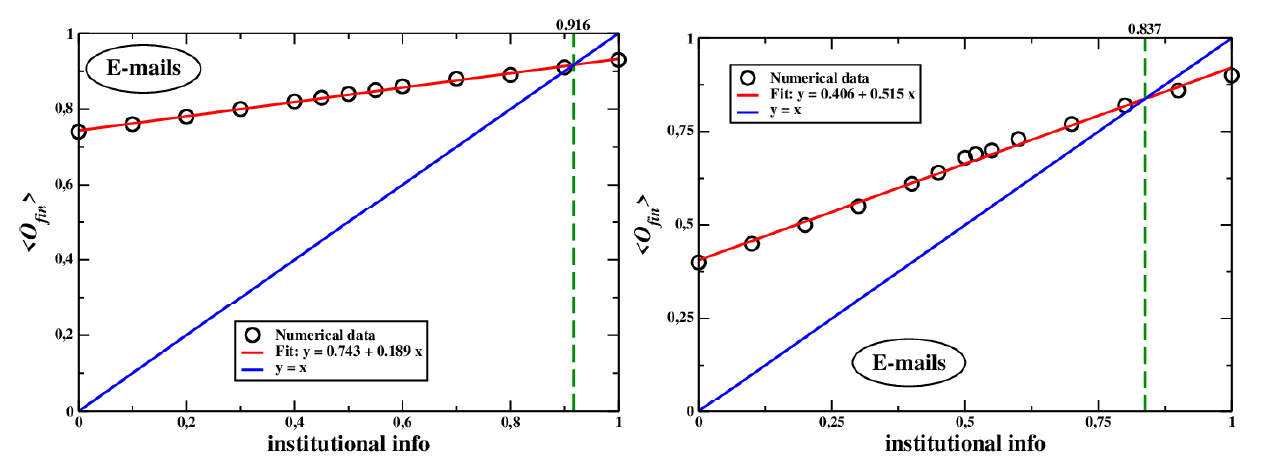
In Figure 6 we show the behavior of the final average opinion as a function of \(I\) in complex topologies, i.e., ring, Erdös-Rényi random network, Watts-Strogatz small-world network, and real e-mail network (we do not show the results with the Facebook network because they are very similar to the e-mail case). As it is clearly visible in the figure, the influence of topology is negligible, meaning that the relevant effects are due to other causes, and in particular the internal variable distributions. Agents’ opinions are not influenced by the position of the local neighbours but rather by the dynamic interplay between individual factors.
Simulation experiment 2: The O.R.E. model with media influence
In the first simulation experiment, we studied the case of perfect information provided by an institutional source in which all agents receive and process the one and only message coming from the institution \(I\). In the real world, however, news information is also transmitted by different kinds of media, either traditional, such as newspapers or TV, or more recent ones, such as online blogs and social media platforms. Here, we model only unidirectional traditional media broadcasting the same message. The role of media sources on collective risk assessment is crucial, because the way the audience processes and transmits the message can produce new dynamics. Therefore, in this last section we focus on the possible effect of media sources on the institutional information and on the dynamics of the system.
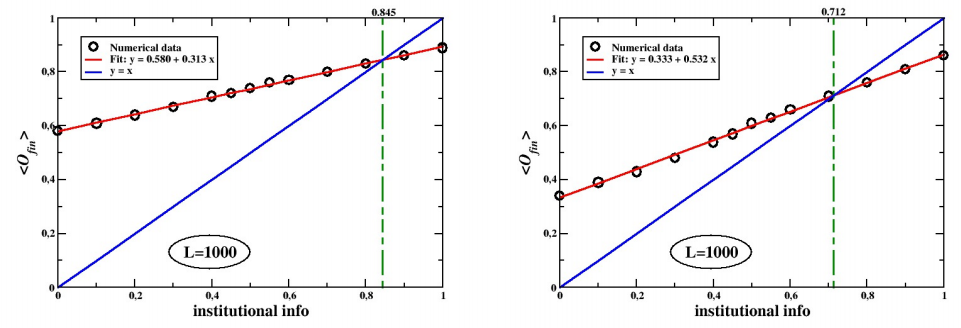
As can clearly be seen in Figures 7, 8, 9 and 10, the effect of media is, in general, to increase the average level of alarm of the population, other things being equal. It is worth stressing that media increase the overall level of alarm both on complete graphs and on the real Facebook and E-mail networks. Despite admitting that it is not enough to make the system reach complete consensus, the asymmetry of the outcome is clearly visible. Even though our simple algorithm creates (on average) as many agents receiving a less alarming input as receiving the more alarming one, the latter tend to communicate their worries to their peers more often than the former. Thus eventually the population ends up being more alarmist than without the media. This result supports the prediction of the Social Amplification of Risk theory (Renn et al. 1992), showing that risk perception heavily depends on the combination between different communication dynamics.
Discussion
Here, we have simulated the dynamics of collective risk perception in a population subject to the risk of natural disasters by modeling the emergence of collective opinions about risk from individual characteristics and their effects on individual agents’ minds (Epstein 2006). The interaction between initial conditions, different sources and network topologies yielded interesting results in terms of collective risk assessment.
First, we observed that in many cases, the average opinion becomes more alarming, even when institutional messages are reassuring. Indeed, the agents are more alarmist than the institution, especially for low values of \(I\), and only when \(I\) gets close to 1, the final average opinion is lower. Such phenomenon also occurs in balanced populations where trust, risk sensitiveness and tendency to communicate are uniformly distributed. This can be explained by the fact that alarmist agents tend to share their opinions more often than non-alarmist agents, all other things being equal. They act as risk amplifiers (Trumbo 1996) who, by increasing others’ exposure to alarmist information, can offset the influence of other variables, like trust or low risk sensitivity. Another explanation for the spread of alarmist opinions can be found in the presence of agents with low trust towards the institution, which systematically disregard and doubt institutional messages, thus weakening their impact.
Our results indicate that agents’ risk sensitivity has a stronger influence than their trust towards the institution. Indeed, by varying the distribution of the former, the final average opinion results much more affected than by changing the latter. This result yields interesting policy implications, suggesting that educating the population in assessing the risks more effectively could counterbalance the negative effects of low trust in institutions.
We have also shown that the topological structure on which the dynamics takes place is substantially irrelevant for the final fate of the system. This result agrees with previous findings showing that there are some social dynamics processes which were experimentally shown to be independent from the details of the networks (Grujić et al. 2010). Moreover, we assessed the effects of the mass-media on the transmission and efficiency of the institutional information. Noticeably, alarmist media condition the opinions of the individuals more than reassuring ones: again, this is due to the higher talkativeness of preoccupied agents.
Finally, we should stress the fact that in our model a global, absolute consensus is never reached, that is, the agents never end up beholding the very same opinion about the risk, and outliers are observed even when a vast majority of agents converged towards a given opinion.
Conclusions and Perspectives
Here, we have applied a numerical approach to the study of collective risk evaluation in order to understand better how horizontal, i.e., social influence, and vertical communication, from institutions and the media, might affect individual opinions in risky situations. In our model, agents receive information about the likelihood of a catastrophic event from two main sources which can transmit either contradictory or converging messages. Institutional sources broadcast their assessment, generally based on experts’ analyses and suggestions, which means that all the agents in the population receive the same information. On the contrary, peer information is based on dyadic interactions between agents placed on different network topologies. These two streams of information are then processed by the agents according to their mental attitudes and beliefs.
Our model of opinion dynamics as a basis for collective risk assessment shows that, even if the agents receive the same initial information about the likelihood of the danger, their perception of the actual risks is modified by individual traits and by the resulting social influence process. For different parameter configurations, our model shows that being an alarmist is more likely, but also that full consensus cannot be reached. This finding is in line with psychological work on misinformation (Lewandowsky et al. 2012), which shows that the widespread persistence and prevalence of misinformation can be attributed to a combination of individual traits and social processes.
Research in psychology has focused on the elements and processes of individual reasoning about uncertain events, uncovering heuristics and biases in making decisions. Various scholars (Eiser et al. 2012; Slovic et al. 2013) convincingly argue that we need to overcome the limitations of traditional "rational choice" models of decision making under risk and uncertainty, by taking into account more realistic theories of human cognition, like heuristics. Although very simplified, our cognitive opinion model takes into account three core aspects, trust, risk sensitivity and a tendency to talk with others. Future work could further develop these characteristics, or it can investigate the role of different heuristics, as suggested by Eiser and colleagues (Eiser et al. 2012).
When an event is dangerous but its likelihood cannot be determined, as in the case of natural disasters or epidemics, individuals need to refer to others to acquire relevant information and to make sense of what is happening. While we know, for example, that individuals in many situations tend to over-estimate the risk of catastrophic events (Lichtenstein et al. 1978), or to be almost indifferent to increasingly dangerous situations, such as climate change (Pidgeon & Fischoff 2011), the current understanding of the effects of risk communication is still limited. According to Trumbo (Trumbo & McComas 2003), individuals and communities tend to perceive institutional agencies as less credible (Fessenden-Raden et al. 1987; Frewer et al. 1996; Kunreuther et al. 1990; McCallum et al. 1991; Slovic et al. 1991). In a complementary manner, there are studies that show that people typically perceive physicians, friends, and environmental groups as the most credible sources, and this also depends on an individual’s familiarity with the risk itself (Frewer et al. 1996; McCallum et al. 1991).
Our study helps us understand the dynamics of risk communication and perception by simulating the joint effect of institutional communication and individual opinion exchange in a population of agents in which those who trust state agencies and the experts are also less likely to trust friends and personal contacts, and the other way around. This simple rule has proven to be powerful enough in determining how individuals who exchange opinions following a similarity bias can become polarized against institutional messages, thus reducing their effectiveness. Empirical data should be collected by future research to calibrate these predictions, and to validate the conclusions of the model.
Even if we designed the O.R.E. model to investigate the determinants of collective risk perception, its application is not limited to risk communication, but it can be usefully applied more generally to opinion diffusion, even if some of its features, such as individual risk sensitivity and the ensuing tendency to inform others, are specific to risk communication and its social amplification. The model could be developed further to account for the differences between specific disasters or for the collective risk perception of different risks, like conflicts and violence.
Another interesting direction for future research is the role of social networks. Even if we tested our model on four different network topologies, a more thorough understanding of the network characteristics and the possibility to collect or have access to real network data could be extremely interesting. Many scholars have highlighted the importance of social capital in the aftermath of a disaster (Aldrich 2012), and our model could be used to simulate communities presenting different levels of social capital, i.e., the resources embedded in the network, and to test its effect on opinion dynamics. Our simulations also highlighted the prevalent role of risk sensitiveness with respect to trust, independently of connectivity. This could provide important indications for policy makers, suggesting that interventions should target risk sensitivity, for instance by offering training and other opportunities to learn about the risks and how to deal with them. Another important implication of our results is that risks can get easily amplified, especially by the media, even when the original message coming from the institutional source is not alarmist. We are aware of the fact that the media is modeled in a very static way, and that social media are becoming a crucial player in the communication of risk (Alexander 2013). Future extensions of the model will broaden the range of media available, including social media
What we set out to explore here is the effect of individual factors and information processes on collective risk perception on different network topologies and with different information sources. The literature on persuasive communication proposes that when individuals believe that they are at risk of confronting dangerous events they will engage in adaptive behavior (Karanci et al. 2005) Thus, in disaster awareness programs it is crucial to develop an awareness of risks involved in disaster events, but also to foster consensus about the risk to build a coordinated and coherent reaction in the population.
As a concluding remark, our work was intended to model the collective perception of risks connected with natural disasters, such as earthquakes, floods, and volcano eruptions, but it also could be extended to model risk evaluation during pandemics. This development would be timely and it could help understanding how to improve risk preparedness and how to promote the adoption of precautionary measures by the population.
Model Documentation
The source code and the real networks datasets can be found in CoMSES online repository at the following link: https://www.comses.net/codebases/17b655a9-5e5e-4175-a6ae-d0a5fd20caab/releases/1.0.0/.Acknowledgements
Work partially supported by the project CLARA (CLoud plAtform and smart underground imaging for natural Risk Assessment), funded by the Italian Ministry of Education and Research (PON 2007-2013: Smart Cities and Communities and Social Innovation; Asse e Obiettivo: Asse II - Azione Integrata per la Società dell’Informazione; Ambito: Sicurezza del territorio).References
ABELSON, R. P. (1964). Mathematical models of the distribution of attitudes under controversy. Contributions to Mathematical Psychology, 3, 1–54.
ALDRICH, D. P. (2012). Building Resilience: Social Capital in Post-Disaster Recovery. Chicago, IL: University of Chicago Press.
ALEXANDER, D. E. (2013). Resilience and disaster risk reduction: An etymological journey. Natural Hazards and Earth System Sciences Discussions, 1(2), 1257–1284. [doi:10.5194/nhessd-1-1257-2013]
ARENAS, A. (2003a). E-mail network URV: https://deim.urv.cat/~alexandre.arenas/data/xarxes/email.zip.
ARENAS, A. (2003b). Facebook network dataset. The dataset is not available anymore in the web but is included in the Model Documentation here: https://www.comses.net/codebases/17b655a9-5e5e-4175-a6ae-d0a5fd20caab/releases/1.0.0/.
BARNES, M. D., Hanson, C. L., Novilla, L. M., Meacham, A. T., McIntyre, E., & Erickson, B. C. (2008). Analysis of media agenda setting during and after Hurricane Katrina: Implications for emergency preparedness, disaster response, and disaster policy. American Journal of Public Health, 98(4), 604–610. [doi:10.2105/ajph.2007.112235]
BARRAT, A., & Weigt, M. (2000). On the properties of small-world network models. The European Physical Journal B-Condensed Matter and Complex Systems, 13(3), 547–560. [doi:10.1007/s100510050067]
BASSETT Jr, G. W., Jenkins-Smith, H. C., & Silva, C. (1996). On-site storage of high level nuclear waste: Attitudes and perceptions of local residents. Risk Analysis, 16(3), 309–319. [doi:10.1111/j.1539-6924.1996.tb01465.x]
BORD, R. J., & O’Connor, R. E. (1992). Determinants of risk perceptions of a hazardous waste site. Risk Analysis, 12(3), 411–416. [doi:10.1111/j.1539-6924.1992.tb00693.x]
CALDARELLI, G. (2007). Scale-Free Networks: Complex Webs in Nature and Technology. Oxford: Oxford University Press.
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87–98. [doi:10.1142/s0219525900000078]
EISER, J. R., Bostrom, A., Burton, I., Johnston, D. M., McClure, J., Paton, D., Van Der Pligt, J., & White, M. P. (2012). Risk interpretation and action: A conceptual framework for responses to natural hazards. International Journal of Disaster Risk Reduction, 1, 5–16.
EPSTEIN, J. M. (2006). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, NJ: Princeton University Press. [doi:10.23943/princeton/9780691158884.003.0003]
FESSENDEN-RADEN, J., Fitchen, J. M., & Heath, J. S. (1987). Providing risk information in communities: Factors influencing what is heard and accepted. Science, Technology & Human Values, 12(3-4), 94–101.
FISCHER, H. W. (1994). Response to Disaster: Fact Versus Fiction and its Perpetuation, the Sociology of Disaster. Lanham, MD: University Press of America.
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2: https://www.jasss.org/20/4/2.html. [doi:10.18564/jasss.3521]
FLYNN, J., Burns, W., Mertz, C., & Slovic, P. (1992). Trust as a determinant of opposition to a high-level radioactive waste repository: Analysis of a structural model. Risk Analysis, 12(3), 417–429. [doi:10.1111/j.1539-6924.1992.tb00694.x]
FREUDENBURG, W. R. (1993). Risk and recreancy: Weber, the division of labor, and the rationality of risk perceptions. Social Forces, 71(4), 909–932. [doi:10.2307/2580124]
FREWER, L. J., Howard, C., Hedderley, D., & Shepherd, R. (1996). What determines trust in information about food-related risks? Underlying psychological constructs. Risk Analysis, 16(4), 473–486. [doi:10.1111/j.1539-6924.1996.tb01094.x]
GIARDINI, F., Vilone, D., & Conte, R. (2015). Consensus emerging from the bottom-up: The role of cognitive variables in opinion dynamics. Frontiers in Physics, 3, 64. [doi:10.3389/fphy.2015.00064]
GUIMERÀ Manrique, R., Danon, L., Dı́az Guilera, A., Giralt, F., & Arenas, À. (2003). Self-similar community structure in a network of human interactions. Physical Review E, 68(6), 065103–065101–065103–065104.
HALL, S. S. (2011). At fault? In 2009, an earthquake devastated the Italian city of L’Aquila and killed more than 300 people. Now, scientists are on trial for manslaughter. Nature, 477(7364), 264–270.
HEGSELMANN, R., Krause, U., & others. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.
HOLMAN, E. A., Garfin, D. R., & Silver, R. C. (2014). Media’s role in broadcasting acute stress following the Boston Marathon bombings. Proceedings of the National Academy of Sciences, 111(1), 93–98. [doi:10.1073/pnas.1316265110]
JUNGERMANN, H., Pfister, H.-R., & Fischer, K. (1996). Credibility, information preferences, and information interests. Risk Analysis, 6(2), 251–261. [doi:10.1111/j.1539-6924.1995.tb00783.x]
KARANCI, A. N., Aksit, B., & Dirik, G. (2005). Impact of a community disaster awareness training program in Turkey: Does it influence hazard-related cognitions and preparedness behaviors. Social Behavior and Personality: An International Journal, 33(3), 243–258. [doi:10.2224/sbp.2005.33.3.243]
KELMAN, H. C. (1958). Compliance, identification, and internalization three processes of attitude change. Journal of Conflict Resolution, 2(1), 51–60. [doi:10.1177/002200275800200106]
KING, D. (2004). Understanding the message: Social and cultural constraints to interpreting weather-generated natural hazards. International Journal of Mass Emergencies and Disasters, 22(1), 57–74.
KUNREUTHER, H., Easterling, D., Desvousges, W., & Slovic, P. (1990). Public attitudes toward siting a high-level nuclear waste repository in nevada. Risk Analysis, 10(4), 469–484. [doi:10.1111/j.1539-6924.1990.tb00533.x]
LEWANDOWSKY, S., Ecker, U. K. H., Seifert, C. M., Schwarz, N., & Cook, J. (2012). Misinformation and its correction: Continued influence and successful debiasing. Psychological Science in the Public Interest, 13(3), 106–131. [doi:10.1177/1529100612451018]
LEWANDOWSKY, S., Gignac, G. E., & Oberauer, K. (2013). The role of conspiracist ideation and worldviews in predicting rejection of science. PloS One, 8(10), e75637. [doi:10.1371/journal.pone.0075637]
LICHTENSTEIN, S., Slovic, P., Fischhoff, B., Layman, M., & Combs, B. (1978). Judged frequency of lethal events. Journal of Experimental Psychology: Human Learning and Memory, 4(6), 551. [doi:10.1037/0278-7393.4.6.551]
LINDELL, M. K. (2013). Disaster studies. Current Sociology, 61(5-6), 797–825. [doi:10.1177/0011392113484456]
LUHMANN, N. (1989). Ecological communication. University of Chicago Press.
MCCALLUM, D. B., Hammond, S. L., & Covello, V. T. (1991). Communicating about environmental risks: How the public uses and perceives information sources. Health Education Quarterly, 18(3), 349–361. [doi:10.1177/109019819101800307]
MOELLER, S. D. (2006). "Regarding the pain of others": Media, bias and the coverage of international disasters. Journal of International Affairs, 59(2), 173–196.
PETTY, R. E., Priester, J. R., & Wegener, D. T. (1994). Cognitive processes in attitude change. Handbook of Social Cognition, 2, 69–142.
PIDGEON, N., & Fischoff, B. (2011). The role of social and decision sciences in communicating uncertain climate risk. Nature Climate Change, 1, 35–41. [doi:10.1038/nclimate1080]
PIJAWKA, K. D., & Mushkatel, A. H. (n.d.). Public opposition to the siting of the highlevel nuclear waste repository: The importance of trust. Policy Studies Review, 10, 180–194. [doi:10.1111/j.1541-1338.1991.tb00289.x]
PIRNOT, T. L. (2001). Mathematics all around. Addison Wesley.
POPOVIC, N. F., Bentele, U. U., Pruessner, J. C., Moussaı̈d, M., & Gaissmaier, W. (2020). Acute stress reduces the social amplification of risk perception. Scientific Reports, 10(1), 1–11. [doi:10.1038/s41598-020-62399-9]
ROCHFORD Jr, E. B., & Blocker, T. J. (1991). Coping with natural hazards as stressors: The predictors of activism in a flood disaster. Environment and Behavior, 23(2), 171–194. [doi:10.1177/0013916591232003]
RODRÍGUEZ, H., Díaz, W., Santos, J. M., & Aguirre, B. E. (2007). 'Communicating risk and uncertainty: Science, technology, and disasters at the crossroads.' In Rodriguez, H., Quarantelli, E. L. & Dynes R. (Eds.), Handbook of Disaster Research (pp. 476–488). Berlin Heidelberg: Springer.
SELECTED Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina. (2006). A FAILURE OF INITIATIVE. Final Report of the Select Bipartisan Committee to Investigate the Preparation for and Response to Hurricane Katrina.
SEN, P., & Chakrabarti, B. K. (2014). Sociophysics: An introduction. Oxford University Press.
SIEGRIST, M. (1999). A causal model explaining the perception and acceptance of gene technology 1. Journal of Applied Social Psychology, 29(10), 2093–2106. [doi:10.1111/j.1559-1816.1999.tb02297.x]
SIEGRIST, M. (2019). Trust and risk perception: A critical review of the literature. Risk Analysis.
SLOVIC, P. (1987). Perception of risk. Science, 236(4799), 280–285. [doi:10.1126/science.3563507]
SLOVIC, P. (1993). Perceived risk, trust, and democracy. Risk Analysis, 13(6), 675–682. [doi:10.1111/j.1539-6924.1993.tb01329.x]
SLOVIC, P., Finucane, M. L., Peters, E., & MacGregor, D. G. (2013). 'Risk as analysis and risk as feelings: Some thoughts about affect, reason, risk and rationality.' In P. Slovic (Ed.), The Feeling of Risk: New Perspectives on Risk Perception (pp. 49–64). London, UK: Routledge. [doi:10.1111/j.0272-4332.2004.00433.x]
SLOVIC, P., Fischhoff, B., & Lichtenstein, S. (1982). Why study risk perception? Risk Analysis, 2(2), 83–93. [doi:10.1111/j.1539-6924.1982.tb01369.x]
SLOVIC, P., Flynn, J. H., & Layman, M. (1991). Perceived risk, trust, and the politics of nuclear waste. Science, 254(5038), 1603–1607. [doi:10.1126/science.254.5038.1603]
TRUMBO, C. W. (1996). Examining psychometrics and polarization in a single-risk case study. Risk Analysis, 16(3), 429–438. [doi:10.1111/j.1539-6924.1996.tb01477.x]
TRUMBO, C. W., & McComas, K. A. (2003). The function of credibility in information processing for risk perception. Risk Analysis: An International Journal, 23(2), 343–353. [doi:10.1111/1539-6924.00313]
VASTERMAN, P., Yzermans, C. J., & Dirkzwager, A. J. (2005). The role of the media and media hypes in the aftermath of disasters. Epidemiologic Reviews, 2(1), 107–114. [doi:10.1093/epirev/mxi002]
VILONE, D., Giardini, F., & Paolucci, M. (2016). 'Exploring reputation-based cooperation.' In F. Cecconi (Ed.), New Frontiers in the Study of Social Phenomena (pp. 101–114). Berlin Heidelberg: Springer. [doi:10.1007/978-3-319-23938-5_6]
VINCK, P., Pham, P. N., Bindu, K. K., Bedford, J., & Nilles, E. J. (2019). Institutional trust and misinformation in the response to the 2018-19 Ebola outbreak in north Kivu, DR Congo: A population-based survey. The Lancet Infectious Diseases, 19(5), 529–536. [doi:10.1016/s1473-3099(19)30063-5]
WACHINGER, G., Renn, O., Begg, C., & Kuhlicke, C. (2013). The risk perception paradox—implications for governance and communication of natural hazards. Risk Analysis, 33(6), 1049–1065. [doi:10.1111/j.1539-6924.2012.01942.x]
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393(6684), 440. [doi:10.1038/30918]
WILLIAMS, D. J., & Noyes, J. M. (2007). How does our perception of risk influence decision-making? Implications for the design of risk information. Theoretical Issues in Ergonomics Science, 8(1), 1–35. [doi:10.1080/14639220500484419]
WOGALTER, M. S., DeJoy, D., & Laughery, K. R. (1999). Warnings and Risk Communication. Boca Raton, FL: CRC Press.


