Introduction
Although models in statistical physics have inspired many interesting analogous developments in the social sciences (cf. Castellano et al. 2009), the emergence of collective properties in social systems can be originated through very different mechanisms from those observed in natural systems (Goldspink & Kay 2007). In particular, humans can perceive environmental patterns, and adjust their mental models and actions according to such perceptions (Castelfranchi 1998). This implies that those who compose social systems are both observers and activate participants of the phenomena they are part of. Such a reciprocal and important relationship between human beings and social phenomena has been roughly termed "reflexivity" in the literature, with many different facets and contexts (cf. Sandri 2009). Nonetheless, current modeling efforts are still far from incorporating reflexive behavior and from investigating whether or not such inclusion would lead to important insights with respect to simpler models.
The present work attempts to put aside the vagueness around the idea of "reflexive behavior". Following the works of Gilbert (2002) and Boero et al. (2008 ), we propose an agent-based model (ABM) that incorporates one of the possible instances of agent reflexivity. Specifically, we endow agents with the ability to recognize an emergent pattern in a diffusion of innovations model, and explore its effect in the generated curves of adoption rate. We find that reflexivity segments the market into groups that adopt at different rates, which explains the observed appearance of slowdowns in the adoption curves of some consumer products. Slowdowns correspond to a sudden decline in adoption followed by a new takeoff, if they occur in the increasing portion of the curve, i.e., before it reaches the global maximum; or to an abrupt growth in the number of adopters, if they appear in the decreasing portion. We also find that, for certain network topologies the effect of reflexivity in the emergence of these slowdowns is stronger than for others.
The next sections discuss the importance of including reflexivity in the study of complex social systems, review previous works on the topic, justify the study of reflexivity in processes of innovations diffusion, present the model and results, and compare our work with other models that deal with similar concepts in computational social science and the modern literature of diffusion of innovations.
Reflexivity and the Complexity of Social Systems
Physicist and Nobel Prize winner Murray Gell-Mann once said "Imagine how difficult physics would be if electrons could think". In this sentence Gell-Mann seems to highlight, on the one hand, that the complexity of social systems is not only a consequence of the amount of human beings that compose them and their interactions. It appears to be qualitatively different from the complexity observed in physical systems (cf. Goldspink & Kay 2007), which makes their study quite more difficult. On the other hand, Gell-Mann points to the main source of this difference: the cognitive faculties that separate human beings not only from the physical world, but also from other species on Earth.
Specifically, symbolic thinking allows humans to create an abstract representation of the world around them (Castelfranchi 1998; Gardenfors 2006, p. 143). Through that representation, they are able to distinguish prominent features of the social processes they belong to (Goldspink & Kay 2007). This “metadata” is then incorporated into their decision strategies (cf. Goldspink 2014, p. 58), with a possible — and endogenous — modification in behavior (Castelfranchi 1998, p. 29).
This implies that social systems present a mutual altering relationship between the system and its participants: participants can change the course of the system with their actions, and a new state during the evolution of the system can lead to a change in its participants’ behavior (cf. Beinhocker 2013). The term “reflexivity” is commonly used in the social sciences to describe this kind of phenomena, i.e. processes that affect themselves recursively (Sandri 2009, p. 2). Figure 1 shows a schematic illustration of this kind of processes.

It is important to note that there are two feedback effects involved in reflexivity (cf. Davis 2013), depending on the starting point in Figure 1’s schema:
- From social phenomena to individuals: Human beings are constantly gathering information about changes in the social phenomena around them. This has the potential to alter people's abstract representation — or mental model — of those phenomena, manifested in new ideas, perceptions or expectations about them.
- From individuals to social phenomena: People can act based on their new ideas or expectations, which has the potential to alter the social phenomena that produced them in the first place.
According to this, the members of social systems take part on two different but interrelated activities: observation and participation (Umpleby 2010). This is contrary to physical — but not biological (Beinhocker 2013) — systems, whose elements are unable to change the evolution of the system by willfully deciding on a different course of action.
To better appreciate the kind of complexity introduced by reflexivity in social systems, we interpret below the development of a well-known historical period as a reflexive phenomenon. The ideas of the Enlightenment — democracy, equality and freedom of thought, among others (Israel 2009, p. vii) — promoted by several philosophers during the 18th century, made people reevaluate their current system of beliefs or ideology (cf. Sandri 2009, p. 40). In turn, that renewed awareness led to profound changes in society, finishing with the French Revolution (Israel 2009)[1]. Nonetheless, the altering effect between individuals and social phenomena did not stop there: the social order that appeared afterwards was the source of new ideas and social changes, among them a strong surge of nationalism across Europe during the 19th century (Dann & Dinwiddy 1988).
Reflexivity in Computational Social Science
A general survey of the social sciences shows that reflexivity has been an important concern for researchers in sociology (Giddens 1984; Bryant 2002), anthropology (Bourdieu & Wacquant 1992), philosophy (Gorton 2006), economics (Soros 2013; Sandri 2009; Filimonov & Sornette 2012) and organizational theory (Argyris & Schon 1978). However, this topic has been studied mostly from a philosophical or descriptive point of view; experimental (cf. Sandri 2009) and theoretical (cf. Filimonov & Sornette 2012) works about reflexivity are still very scarce. This is probably due to the fact that the traditional approach to build scientific theories, which consists in creating objective or observer-free descriptions of reality, cannot be applied to the study of reflexivity: its self-referential character does not allow to separate observers from the system being observed (Umpleby 2010, 2007).
However, some authors (Van Bavel & Grow 2017; Squazzoni 2008) consider that agent-based modeling — one of the most widely used methodologies in computational social science — is better suited for this task, because it allows to represent micro-level features and macro-level properties of social systems at the same time. Pioneering work on reflexivity in this area was done by Arthur (1994), in his now classical analysis of “El Farol bar” problem; and Arthur et al. (1997) their research on asset pricing in an artificial stock market. Arthur and colleagues studied how agents' expectations about a global pattern adapt to continuous fluctuations on it; and how those fluctuations reflect the current state of agents' expectations. Unfortunately, their work does not include interactions among agents. Something most current research in this area considers very important is understanding how global patterns emerge from the combined effect of those interactions (cf. Epstein & Axtell 1996).
After that, only a handful of authors — described in detail below — have studied reflexivity by introducing and analyzing the following feedback effects between emergent structures and agents’ rules of behavior: (i) downward causation, which corresponds to the influence a range of values of the emergent variables have on agents’ behavior (Boero et al. 2008s); (ii) second-order emergence, which is the effect of agents on emergent patterns when they are endowed with the cognitive ability to recognize those patterns during the evolution of the system (Gilbert 2002; Squazzoni 2008); and (iii) tag categorization, which is also the effect of agents on macro-level properties, but when they are allowed to organize in groups endogenously, according to tags that represent qualities such as ethnicity or gender (Gilbert 2002; Boero et al. 2008).
First, Gilbert (2002) created several extensions of the Schelling residential segregation model (Schelling 1971) that separately incorporate all the effects mentioned above. Unfortunately, he was unable to find a different outcome — i.e., other than segregation — from the original model for all of them. Then, Boero et al. (2004) studied how the attitudes and actions of firms that belong to industrial districts are affected by their social context. Their main result is that firms that pay more attention to their context have better economic performance and learning skills after drastic technological and market changes. However, the intricateness of their model — which comprises a large number of traits and behaviors for agents — makes it hard to examine the impact of reflexivity on its outcome.
Finally, Boero et al. (2008) created an abstract model to show the differences in macro-level outcomes obtained when rules of behavior are defined in terms of local interactions alone, versus rules that also incorporate reflexivity through downward causation and tag categorization. The most interesting result of this work is that reflexivity is the only mechanism that allows agents to find a stationary global solution to the coordination problem posed in the model. Unfortunately, their ABM is not related to a specific social process, hence their remarks about reflexivity cannot be easily interpreted in connection to real social systems.
The Case for Reflexivity in Diffusion of Innovations
As shown in the previous section, reflexivity has received several mentions in computational social science; yet, its inclusion and exploration of its implications on ABMs are still exceptional. To expand this study, we propose a new ABM whose agents are able to detect an emergent pattern and change their behavior accordingly. We focus on one of the most studied social processes: diffusion of innovations (cf. Rogers 1983; Kiesling et al. 2012; Watts & Gilbert 2014). We hope our work and results show other researchers the fruitfulness of taking into account reflexivity into their models, contrary to the mixed results of previous studies.
Our decision is based on three major arguments. First, innovation diffusion processes have both a rich variety of models and empirical data that we can compare our model to (cf. Watts & Gilbert 2014). Second, several processes of innovation diffusion have not been completely understood yet. We will focus in one of them: the appearance of slowdown periods of adoption during the evolution of the system (cf. Chandrasekaran & Tellis 2018). We consider slowdowns can occur either in the increasing or decreasing portions of the adoption rate curve, i.e. before or after the curve reaches the global maximum. In the increasing portion, they are characterized by a sudden decline in adoption followed by a new takeoff. In the decreasing portion, they correspond to an abrupt growth in the number of adopters.
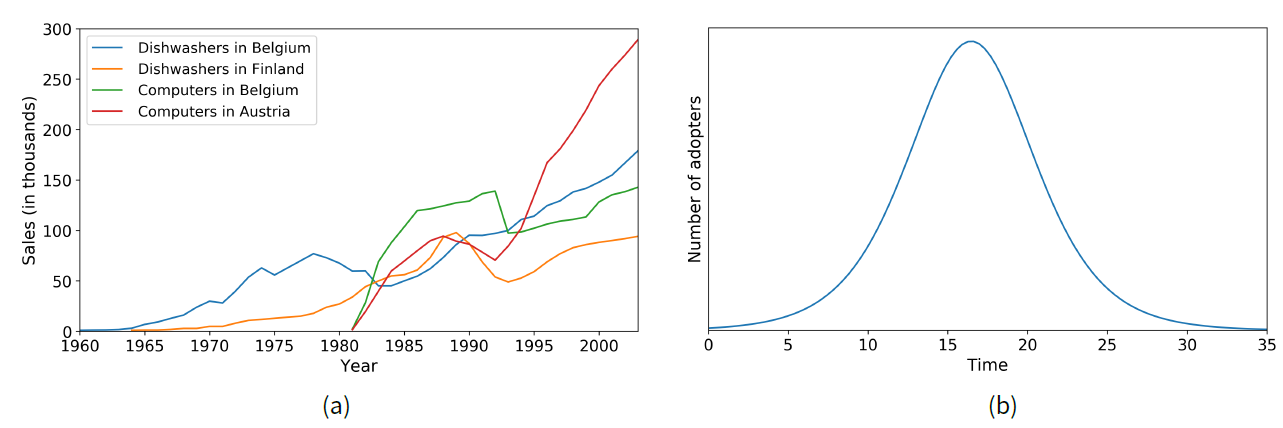
Figure 2 shows the number of sales vs. time for different consumer products in Europe, compared to the curve for the number of adopters obtained from the Bass model (Bass 1969) — one of canonical models in the field[2]. As can be seen, in some cases there is a significant slowdown after the initial takeoff that cannot be explained by the Bass model, which predicts that adopters increase steadily until a peak is reached, then fall to zero as the number of remaining non-adopters becomes scarce.
And third, we consider reflexivity offers a novel mechanism to analyze how fluctuations in the global number of adopters — or global network externalities, as this variable is known in the literature (Kiesling et al. 2012)— affect the diffusion process. Our reasoning is the following: for some consumer products (e.g. mobile phones (Doganoglu & Grzybowski 2007)), the relationship between global externalities and consumers involves an observation/participation cycle similar to the one depicted in Figure 1. This has been described in literature as “the bandwagon effect” (Rohlfs 2003): the more adopters there are in the system, the more the rest of consumers is aware of a widespread adoption pattern around them; and that awareness makes consumers’ decision to participate in the adoption trend more compelling, to not be left out of it.
At this point it is worth mentioning two important things in connection with previous works on this topic. First, there are several models that deal separately with reflexivity (Etzion 2013), the appearance of slowdowns (Golder & Tellis 2004; Goldenberg et al. 2002) and global externalities (Goldenberg et al. 2010) in the case of diffusion of innovations. However, to the best of our knowledge, there is no previous work that have found a relationship between these three concepts, as we purport to show in the next sections.
And second, slowdowns in adoption can be caused by internal or external factors to the system (Chandrasekaran & Tellis 2011). External factors include economic recessions and major technological changes (Chandrasekaran & Tellis 2011). Internal factors result from consumer interactions and they may include a difference in the rate of adoption between two sub-populations (Goldenberg et al. 2002); consumers’ heterogeneity in a market with two competing products (Cadavid & Cardona 2014); and cascades of adoption generated by information consumers derive from the behavior of previous adopters (Golder & Tellis 2004; Geroski 2000). Following most of the marketing literature on diffusion of innovations, we decided to include only marketing as an external factor in our work. Among the internal factors, we focused on markets with a single population and a single product to see if slowdowns can also appear in these simpler situations. Finally, we included a similar mechanism to informational cascades (i.e., reflexivity), but in our case agents can take into account the decisions of all previous adopters to form their own, instead of the decisions of a small number of initial adopters (Bikhchandani et al. 1998) or those of their neighbors (Watts & Gilbert 2014, chap. 3).
The Model
In this section, we present an agent-based model to study the effects of reflexivity in the way innovations spread in a social network. Specifically, we propose to endow agents with a lightweight cognitive mechanism to allow them to recognize an emergent adoption pattern in the system and change their behavior according to that awareness. Our purpose is to study the effects created by the inclusion of reflexivity in the system. We must note that our model is a modified and extended version of a model previously developed by Delre et al. (2007) (our additions to their model will be made clear below).
At the beginning, agents are placed in the nodes of different kinds of social networks — scale-free, small world and random ones — and a small proportion δ of the them is specified as adopters of a new product introduced in the system. Then, at each time step, a non-adopter decides to adopt this product if she comes into contact with another adopter, and either her personal utility is greater than a certain minimal utility or she has been persuaded to adopt because of marketing. If \(D_{i}\) is the decision of agent \(i\) to become an adopter, then
| $$D_{i}=\begin{cases} 1, & U_{i}\geq U_{i,\mathrm{min}}\:\:\mathsf{or}\:\:\lambda>s_{i}\\ 0, & \mathsf{otherwise} \end{cases}$$ | (1) |
We consider that \(U_{i}\) depends on two kinds of social influences. First we have a local influence, which determines how useful it is for an agent to adopt given two factors: the rate of adoption of her closest neighbors and her individual preference.[3] If we call the utility derived from this influence as \(U_{Li}\), we have that
| $$U_{Li}=\beta\cdot x_{i}+\left(1-\beta\right)\cdot y_{i}\label{eq:local-utility}$$ | (2) |
| $$x_{i}=\begin{cases} 1, & A_{i}\geq h_{i}\\ 0, & \mathsf{otherwise} \end{cases}$$ | (3) |
| $$y_{i}=\begin{cases} 1, & p_{i}\leq q\\ 0, & \mathsf{otherwise}\end{cases} $$ | (4) |
It is important to mention that the original model of Delre et al. (2007) goes up to this point. In other words, it describes diffusion of innovations as a process driven only by local influence, through Equations 2, 3 and 4. The rest of this section corresponds to our additions to that model.
Besides local influence, our model also incorporates a global influence, which leads agents to adopt when they notice the appearance of a sizable portion of adopters in the population, even if they cannot perceive a significant change in their surroundings. The simplest measure of the current amount of adoption in the system is the percentage of adopters. However, that does not take into account that agents are placed in a social network. In other words, the percentage disregards the structure of social relations that arise among adopters during the diffusion process, which depends on the underlying network topology. To overcome this limitation, we decided to use instead the average size of connected components in the subgraph of adopters. These components — called components of adopters from now on, for simplicity — correspond to subgraphs composed entirely of adopters and in which any two of them are connected by a path.
As this average size becomes bigger, the more useful it should be for an agent to join the trend and become one more of the crowd. Therefore, we define global utility in our model as
| $$U_{G}=\frac{\overline{C}}{N}$$ | (5) |
| $$\overline{C}=\sum_{j=1}^{n_{c}}\left(\frac{n_{j}}{N}\right)n_{j},\quad n_{j}>1$$ | (6) |
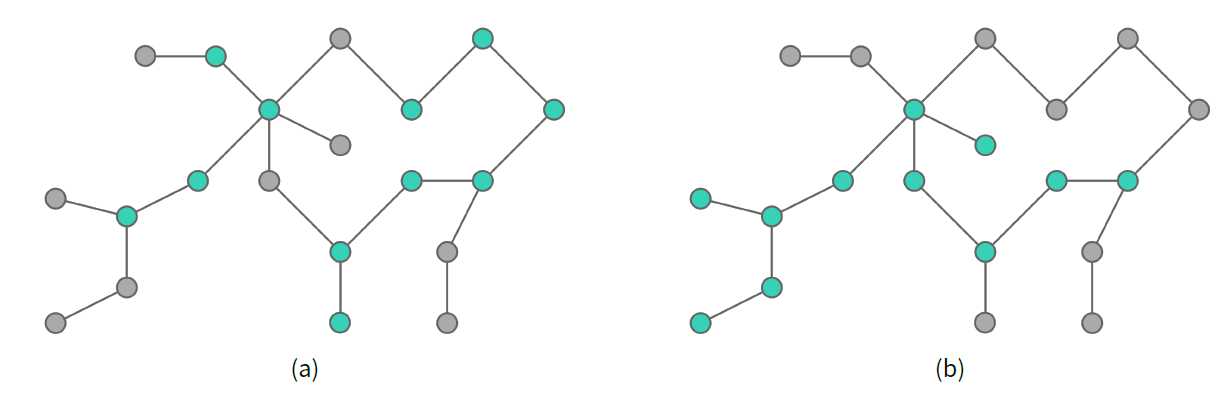
When \(\overline{C}\) is small, global utility also is, hence it should not play a part in agents' decisions. However, as \(\overline{C}\) increases and gets closer to a certain critical mass, its effect should be felt more strongly and start influencing agents accordingly. To model this, we endow agents with a reflexive capacity to allow them to recognize that that critical mass has been reached or it is close to be reached. Only after becoming aware of that fact and being exposed to it for a certain amount of time, an agent can make use of \(U_{G}\) as part of her decision strategy.
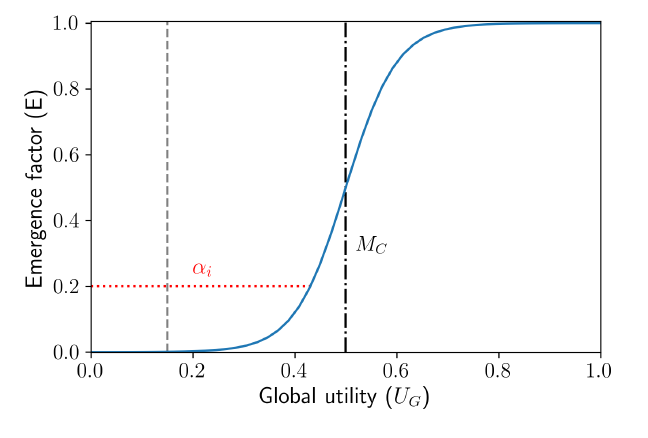
Specifically, we assign agents at the beginning of the simulation a reflexivity index \(\alpha_{i}\sim\mathcal{U}\left(0,1\right)\), to account for heterogeneity in their reflexive abilities. During each time step, we compare this index to an emergence factor \(E\), that increases in value (from 0 to 1) as the global utility approaches the critical mass. We define this factor through the following logistic equation
| $$E\left(U_{G}\right)=\frac{1}{1+e^{-\phi\left(U_{G}-M_{c}\right)}}$$ | (7) |
Finally, agents in our model do not start using the knowledge gained through reflexivity immediately after becoming aware of a global pattern. Instead, we record the amount of time that has passed since each agent detected \(M_{c}\). Only when that time is higher than a personal delay threshold, they can use global utility for their decisions. We obtained this idea from generalized models of contagion (Dodds & Watts 2005, 2004). In these models agents receive one dose of the contagious entity (e.g. a disease or rumor) per time step, and an agent becomes infected when the amount of doses surpasses a threshold. In our case, we use this concept to model that agents need to be exposed to the perception of an emergent adoption trend for a certain period before it can have an effect on them. This seeks to capture the fact that people's responses occur at different time scales because there are several psychological factors (e.g. feelings and willingness to act) that influence their decision process (Sornette 2006).
Given Equations 2, 5 and 7, we define personal utility \(U_{i}\) as
| $$U_{i}=\begin{cases} U_{Li}+U_{G}-U_{Li}\cdot U_{G}, & E\left(U_{G}\right)>\alpha_{i}\,\,\mathsf{and}\,\,t_{a}>d_{i}\\ U_{Li}, & \mathsf{otherwise} \end{cases}$$ | (8) |
Results
This section presents the results obtained by running different simulations of the model introduced in the previous section, with the parameters shown in Table 1 (unless specified otherwise). To generate each plot shown below we took the average over 2000 different initial conditions and network realizations of our model[7]. This was done in order to ensure that our results are independent of the randomness present in the placement of the initial seed of adopters, the network topology and agents’ individual properties (such as their minimal utility and reflexivity index). We also consider this was necessary to get very smooth curves in order to clearly distinguish between the different effects introduced by reflexivity in the system (see Figure 9 below).
Without time delays
We begin with a version of the model that does not include the time delays \(d_{i}\), i.e. \(d_{i}=0\). Our purpose is to examine the generated diffusion curves for noticeable changes in the system when reflexivity is introduced on it. Figure 5 shows the results for a scale-free network generated by the Barabási-Albert model with a new node connected to four previous ones. However, this is not the only kind of network we study in this section. Below we also present results for Erdös-Renyi and small-world networks to analyze if the network topology has an impact on the appearance of slowdowns. Our aim here is to illustrate how reflexivity might be affected by the network topology, without necessarily referring to a real-world network. Thus, we follow a common practice in other theoretical ABMs on diffusion of innovations (cf. Delre et al. 2007; Sáenz-Royo et al. 2015; Yavaç & Yücel 2014), that study how the results of their respective models are affected by different standard theoretical topologies.
| Parameter | Variable | Value |
| Initial proportion of adopters | δ | 0.003 |
| Coefficient of social influence | β | — |
| Product quality | q | — |
| Total number of consumers | N | 1,000 |
| Sharpness of emergence awareness | φ | 30 |
| Critical mass of adopters | Mc | 0.5 |
| Marketing effort | λ | 0.03 |
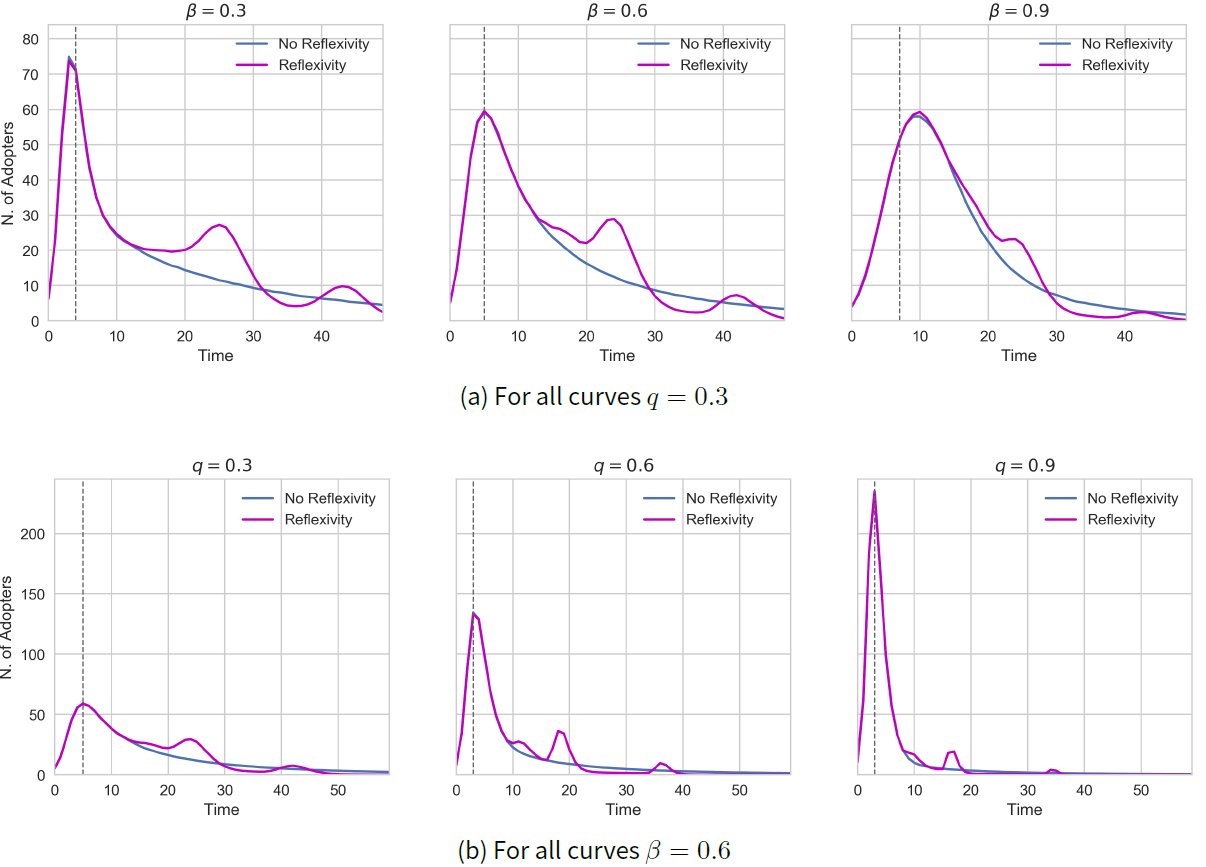
As can be seen in Figure 5, diffusion curves were obtained for three different values of the coefficient of social influence \(\beta\) and the product quality \(q\), while maintaining all other values in Table 1 constant. After running the model with an assorted combination of parameters, we noticed that those have the highest impact in the diffusion process. On the one hand, the initial proportion of adopters \(\delta\) and the marketing effort \(\lambda\) affect the speed of diffusion without altering the results shown in Figure 5. On the other hand, the influence of critical mass of adopters \(M_{c}\) and the sharpness of emergence awareness \(\phi\) will be investigated separately in Section 6.11.

The most interesting fact to highlight from Figure 5 is that, in some cases, the presence of reflexivity generates a slowdown in adoption, i.e. a fall followed by a takeoff afterwards (cf. Chandrasekaran & Tellis 2018). Moreover, the resemblance between these data and those of real diffusion processes — displayed in Figure 2(a) — is evident. This is a consequence of including reflexivity in the model because it moves agents that are not ready to adopt by local influence alone, to do it due to factors beyond their immediate vicinity.
This fact is also quite remarkable because it means we found an instance where agents endowed with the ability to recognize a macro-level feature of the system create a new kind of emergence, i.e. a second-order emergence (see Section 3). Without reflexivity, local interactions produce the familiar bell-shaped curve of adoption at the macro-level, displayed in Figure 2(b) . However, the addition of reflexivity causes a different pattern to emerge, which clearly deviates from the previous one: the system displays two uneven peaks in adoption instead of a single one.
We would also like to mention two other results that can be concluded from Figure 5. First, we found diffusion spreads faster when agents are reflexive. This is attested by the fact that all curves that include reflexivity touch the x-axis before the ones without reflexivity, meaning that the system runs out of agents to adopt more quickly in the first case than in the second. This is to be expected because through reflexivity agents find it more useful to become adopters, thanks to the addition of global utility to their decision strategy. And second, the time of the second takeoff in adoption is preceded by the reflexivity activation time (see Figure 4) represented by the dotted vertical line shown in all plots of Figure 5, and which marks the first moment agents start making use of global utility thanks to their reflexive capacity. This offers another confirmation that our model is working as expected.
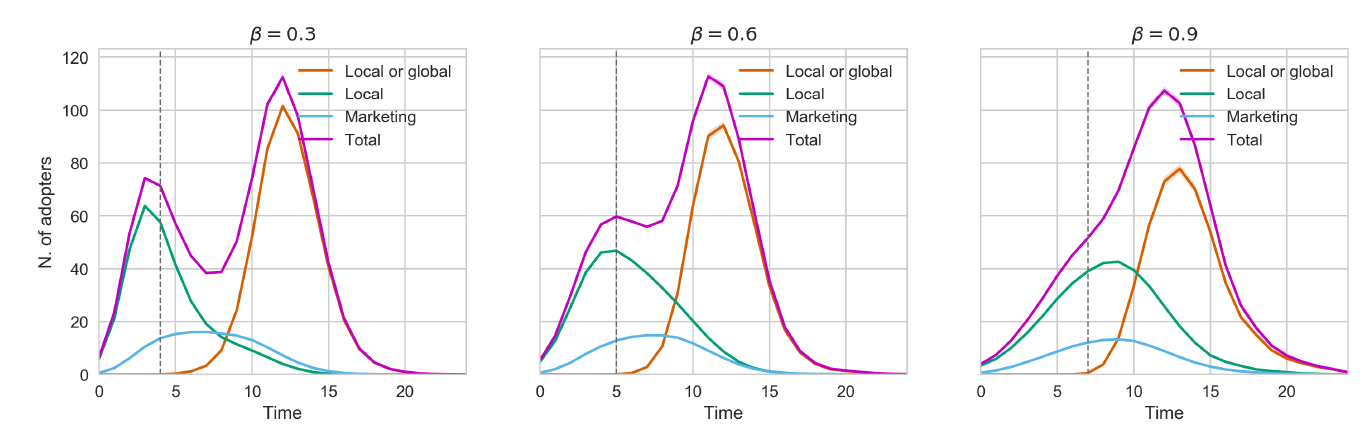
When adopters are divided among those moved by marketing, local utility only and local or global utilities, as shown in Figure 6, it can be appreciated that they constitute distinct groups in the population because each one adopts at different times and in different proportions. Marketing and local utility adopters drive diffusion mostly at the beginning and represent a smaller amount of the population overall, whereas the bulk of consumers adopts thanks to global utility, after they become aware that an adoption trend was set by the previous group.
Goldenberg et al. (2002) postulate that this phenomenon, i.e. the presence of subgroups adopting at different rates — in their case two of them, called early and main markets — is one of the causes for slowdowns in diffusion of innovations processes. According to their reasoning, a temporary decline in the total rate of adoption can be created when diffusion moves from the early to the main market, if there is a significant difference in adoption rates among the two groups. To support this claim, Goldenberg et al. (2002) created a cellular automata model based on this assumption and able to display slowdowns. In their model each consumer is classified at the start as belonging to either the early or main market, and adoption depends on the rate of communication within and among these groups. As can be concluded from Figure 6, our model offers additional support for Goldenberg et al. (2002) hypothesis, but from a conceptually different standpoint. Specifically, there is no artificial distinction between early and main consumers in our model; instead, these categories are generated endogenously during the evolution. Besides, our model does not impose different communication strategies between agents, i.e. the influence of each agent on the others is exactly the same.
With time delays
In this section, we turn our attention to the case of having time delays in agents' inclusion of global utility in their decision to adopt, after detecting a macro-level pattern in the system. At time \(t=0\), each agent is assigned a delay threshold \(d_{i}\) (see Equation 8) drawn randomly from the following discrete distribution
| $$f(d)=\begin{cases} 0.1, & d=5\\ 0.5, & d=12\\ 0.4, & d=30 \end{cases}$$ | (9) |
The results are shown in Figure 7. As can be seen, the inclusion of delays causes a very interesting effect: the appearance of multiple slowdowns along the evolution. A similar phenomena has been observed in the adoption rate curves that span several technological generations of the same product (e.g. DRAM chips, Bass & Bass 2001 or music cassettes, Guseo & Guidolin 2015). However, our model shows that these slowdowns can be caused not only by exogenous changes to the system (i.e., a change in technology), but also endogenously by the way diffusion takes place on it.
Parameters that control reflexivity
Here, we inspect the parameters that control reflexivity to assess their impact on diffusion. We only consider variations in the critical mass of adopters \(M_{c}\) because the results for the sharpness of emergence awareness \(\phi\) are very similar. As shown in Figure 8(a), which uses the same time delay distribution \(f(d)\) of previous sections, the main effect induced by altering \(M_{c}\) is a modification of the reflexivity activation time: the higher the value of \(M_{c}\), the longer it takes for reflexivity to enter into the picture.

This is not a surprising result, given the way our model was defined in Section 5. However, Figure 8(b) and (c) show a more interesting one. In Figure 8(b) we modified \(f(d)\) so that the delay with highest probability be five-time steps instead of twelve. This change makes a slowdown appear for \(M_{c}=0.6\), and to vanish the one the system displays for \(M_{c}=0.5\) in Figure 8(a). We think this occurs because for \(M_{c}=0.6\) the delay with highest probability is longer than the elapsed time between the reflexivity activation time and the peak of adoption without reflexivity, whereas for \(M_{c}=0.4\) and \(M_{c}=0.5\) that delay is shorter. Figure 8(c) offers an additional confirmation of this assertion. In this case 50% of the agents wait 15 time steps before using reflexivity to make their decisions, which is long enough to pass the peak of adoption and generate a slowdown for \(M_{c}=0.4\), as well as for all other values.
These results imply that the presence of slowdowns depends on a subtle interplay between the time delay distribution, the reflexivity activation time, and the time at which occurs the peak of adoption without reflexivity. In essence, a considerable amount of the population (e.g. 50%) needs to first use reflexivity after the peak of adoption to create a slowdown period. Else, reflexivity only makes diffusion spread faster.
The βq space and different network structures
Our last analysis is concerned with an exhaustive exploration of the parameter space composed by the coefficient of social influence β and product quality q, to understand if there are specific conditions that favor the appearance of slowdown periods. For that we varied β and q from 0 to 1, in steps of 0.1, and registered if the obtained diffusion curve displays one out of three observed cases: one or more slowdowns, no slowdown, and a “bending region”. We call “bending region” to a region where the curve changes direction without a drop and surge in adoption. Figure 9 shows typical realizations of these cases. To widen the results, we decided to use several types of networks: a scale-free network with a new node connected to two existing ones, a small-world network generated by the Watts-Strogatz model with an average of four neighbors per node and randomness of 0.1, and an Erdös-Renyi network with a connection probability of 0.004. In all cases, the parameters of Table 1 are maintained constant and f (d) is the same distribution used in Section 6.2.
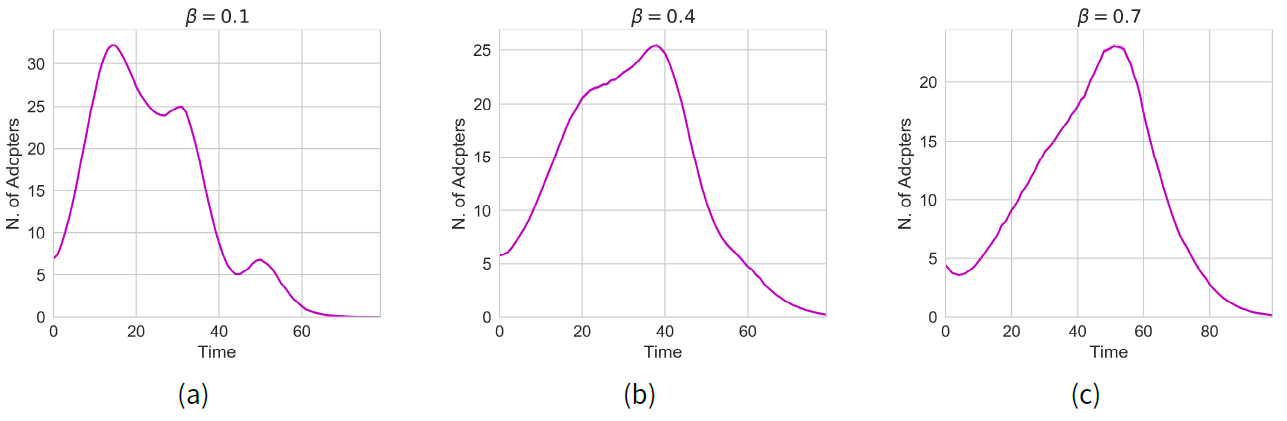
Figure 10 displays the obtained results. As can be seen, the Erdös-Renyi topology is the most favorable to slowdowns, followed closely by the scale-free one. In contrast, small-world networks display much less slowdowns and bending regions. Previous work by Sáenz-Royo et al. (2015) found that diffusion in Erdös-Renyi and scale-free networks is very similar —in their case with respect to the probability of adoption by the whole population and the time for that to happen— and that Erdös-Renyi networks show a slightly higher probability of full adoption than scale-free ones. They also found that this behavior can be clearly differentiated from the one in completely regular networks. In our case, the results shown in Figure 10 are in line with Sáenz-Royo et al. (2015) findings. That is because the presence of slowdowns in Erdös-Renyi and scale-free networks follows a similar pattern, and that pattern is very different from the behavior on small-world networks, whose structure is closer to a regular one for small values of randomness (as it is our case).
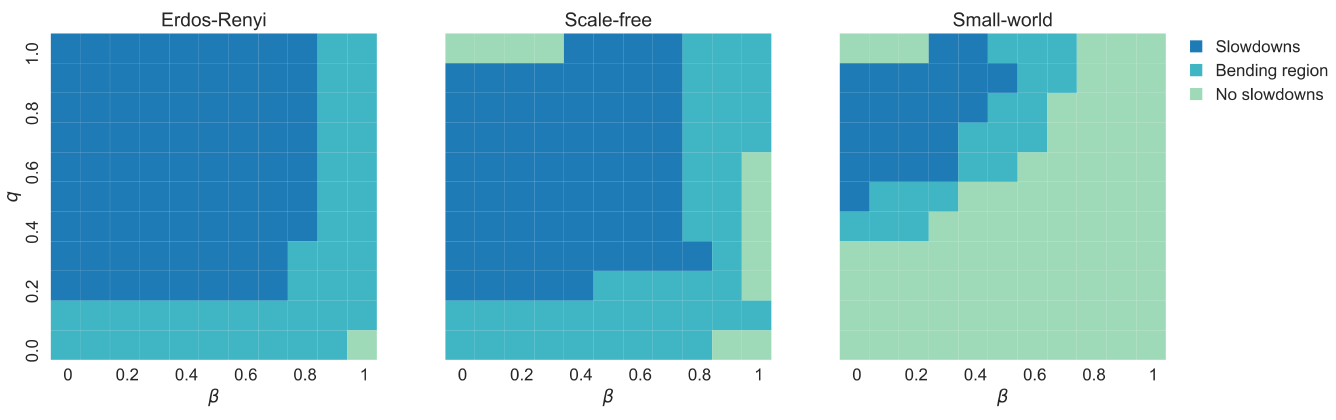
Another important finding that can be concluded from Figure 10 is that slowdowns are not guaranteed to appear under all circumstances. Their presence is highly contingent, depending not only on the network topology but also in the way diffusion takes place on that topology. That is determined by a multitude of factors: the values of \(\beta\) and \(q\), for local influence; and those of \(M_{c}\), \(\phi\) and \(f(d)\), for global influence. This could explain why slowdowns are only observed on some markets and periods of time (Chandrasekaran & Tellis 2018), instead of in all social systems where an innovation is being adopted.
Discussion
The purpose of this section is to compare the model introduced in this paper with previous ABMs that include reflexivity and models that deal with the effect of the total number of adopters in a consumer’s decision, known as global network externalities (Peres et al. 2010) (see Section 4 for the relationship between them and reflexivity).
On the one hand, as described in Section 3, very few ABMs have been proposed to study reflexivity and its effect in social systems, despite its acknowledged importance. Compared to them, (i) our model allows to turn reflexivity on and off, which leads to a better understanding of its impact (in contrast to Boero et al. 2004); and (ii) it was designed by carefully considering the features of a real social process, which makes it easier to interpret its results in connection to empirical data (in contrast to Boero et al. 2008). Although including reflexive behavior in ABMs is a challenging endeavor, we hope these modeling choices can give better methodological insights to other researches on how to address it.
On the other hand, there are also very few models that analyze global externalities in innovation diffusion processes (Kiesling et al. 2012). However, some authors (Peres et al. 2010) consider they are very important to understand adoption in markets such as mobile phones (Doganoglu & Grzybowski 2007) and other consumer electronics (Stremersch et al. 2007), where it becomes more profitable to adopt a new product as the number of its users increases (Rohlfs 2003).
The most discussed model on this topic was proposed by Goldenberg et al. (2010) (cf. Kiesling et al. 2012, p. 27). These authors created a cellular automata where agents decide to adopt with a probability that depends on marketing and the local amount of adopters present. However, adoption only takes place when (i) an agent receives news about the innovation through word-of-mouth; and (ii) the total percentage of adopters in the system is greater than a personal threshold. The main finding of Goldenberg et al. (2010) is that network externalities cause a “chilling” effect, i.e. a prolonged delay in adoption, followed by a sudden surge.
As Goldenberg et al. (2010), we also consider that network effects should not be triggered by any number of adopters. Instead, global externalities should only play a part in agents’ decisions once a personal threshold has been reached. Goldenberg et al. (2010) base their assumption in the collective action literature (cf. Granovetter 1978), whereas we consider it an effect of the reflexive capacity of agents.
Nevertheless, there are important differences between the two models. First, in our model adoption can take place before global externalities start influencing a consumer, thanks to local utility and marketing. We consider this better describes the early phase of diffusion, during which consumers are more driven to adopt due to personal reasons than collective ones (see Section 6.1).
Second, global externalities in Goldenberg et al. (2010) establish a constraint on when adoption can start, whereas in our model they correspond to a factor (given by the global utility UG) that increases the utility to adopt. Rust (2010) and Stremersch et al. (2010) heavily criticized that the main result presented in Goldenberg et al. (2010), i.e. the "chilling" effect of externalities, is built into the model itself. They argued that, since agents are required to meet an extra condition before being able to adopt, it is expected that diffusion be slower with than without externalities. Our results show the opposite effect, i.e. diffusion encompass the entire population in less time with than without reflexivity (see Section 6.1). When agents are endowed with the capacity to be aware of a global adoption pattern and to include that knowledge in their decisions, they feel more inclined to do it, regardless of what is happening in their surroundings. Therefore, agents that would not become adopters under normal circumstances — i.e. without reflexivity —, are now compelled to do it, and that makes diffusion spread faster.
Another ABM that considers the role of global externalities in diffusion of innovations is the one of Etzion (2013). In this model agents need to become aware of an emergent pattern before they can adopt. After doing that, their decision is based on a utility function that depends on the current number of adopters in the system, which is very similar to our model. Although Etzion (2013) model is very interesting (e.g. it can deal with the limited and full diffusion cases and agents are able to drop their current adoption and re-adopt again) it has two main differences with our work: agents do not interact among themselves and they are not connected through a social network. Both limitations prevent to analyze how the influence of agents’ decisions on one another affects the way diffusion takes place in the system.
Summary and Concluding Remarks
In this paper we have explored the implications of including reflexive behavior in one of the most studied social process: diffusion of innovations. Using a previous agent-based model as starting point (Delre et al. 2007), we added to it a global utility that depends on the total number of adopters and a reflexive capacity to agents that allows them to recognize an emergent adoption pattern, even if they cannot perceive a significant change in their surroundings. With this, an agent decides to adopt if she finds the diffusing product useful according to the most preponderant of two utilities: a local one, that depends on the number of adopters among her neighbors and her personal preference; and the global utility described above, which is included in her decision only after she becomes aware of the widespread trend. This section summarizes the main results of our work.
First, we consider our ABM is a good representation of a reflexive process because it captures the mutual altering relationship between a social system and its participants, as depicted in Figure 1. The effect of the system on agents is the following: the states the system reaches through its evolution — represented by the total number of adopters — change the agents’ perception of what is happening in their environment, when they detect an emergent trend at a particular state. Then, this awareness leads agents to a course of action they would have not taken before, if global utility turns them into adopters. Finally, if enough agents modify their behavior accordingly, there appears their effect on the system: the emergence of a different, second-order pattern, characterized by slowdowns along the adoption rate curve.
Second, we found reflexivity partitions agents in sub-populations that adopt at different rates, according to (i) the criteria they use (marketing, local utility only, and local or global utilities), and (ii) the amount of time they need to be exposed to the awareness of an emergent trend before they can use that information. The presence of such sub-populations has been proposed before (Goldenberg et al. 2002) as one of the causes for the observed appearance of slowdowns in the adoption of several consumer products (see Figure 2). However, previous studies only assume that presence without explaining why the population is segmented in such a way.
Third, a novel finding shown by our model and — to be the best of our knowledge — not reported before, is the existence of a link between global network externalities (i.e. the effect of the total number of adopters in a consumer’s decision) and slowdown periods of adoption. Until now, it was assumed that global externalities could only increase (Rust 2010) or decrease (Goldenberg et al. 2010) the speed of diffusion. In contrast, we found that global externalities can generate slowdowns under the appropriate conditions.
And fourth, we have shown that the inclusion of reflexivity is not enough to create slowdowns. Their appearance is a contingent phenomenon, i.e. it depends on the conjunction of other factors as well: (i) The network topology; (ii) the first moment any agent is capable of detecting an emergent pattern in the system, called by us the reflexivity activation time; and (iii) the distribution of time delays before agents can use global utility in their decisions.
For future work is left the use of more realistic network topologies (cf. Cointet & Roth 2007) and empirical data to calibrate our model parameters and compare its results with real innovation diffusion processes.
Model Documentation
The model has been built in Python. In the Appendix, we reported the pseudo-code algorithm used to simulate the model. The code is available on the CoMSES computational model library at this link: https://www.comses.net/codebases/d4055760-2e55-4399-a81d-8f1f7ea6ae3c/releases/1.0.0/.Acknowledgements
We are very grateful to one of the anonymous reviewers for a thorough review and insightful comments, which helped us to clarify the purpose of this work and improve our contribution significantly.Notes
- As the latest scholarship on the Enlightenment clearly establishes it: “[T]he rise ... of ... Enlightenment ... is not merely relevant to the advent of the French Revolution ... but arguably much the most important factor in any proper understanding of how and why the Revolution developed as it did” (Israel 2009, p. 223-224).
- The Gompertz model — another important model in marketing (cf. Michalakelis et al. 2008) — displays a similar behavior.
- This term accounts for the fact that an agent can decide that the product suits her personal needs even if their friends have not adopted it yet.
- If a node has no neighbors, this value is zero.
- Note that UG can only take values between 0 and 1 due to the way it is defined. This will be important in the definition of personal utility below.
- Since ULi and UG vary between 0 and 1, the first part of equation 8 corresponds to a disjunction in probability theory.
- Although not clearly visible, all curves also include one standard deviation at each point around them.
Appendix
A: Pseudo-code of the Model Studied in this Paper
This section presents the algorithm we developed to simulate the model introduced in Section 5. It is written in pseudo-code and divided in two parts: Algorithm 1 describes how we initialize the social network where the innovation diffusion process takes place; and Algorithm 2 describes how this process evolves in the network.


References
ARGYRIS, C. & Schon, D. (1978). Organizational Learning: A Theory of Action Approach. Reading, MA: Addison Wesley.
ARTHUR, W. B. (1994). Inductive reasoning and bounded rationality. The American Economic Review, 84(2), 406–411.
ARTHUR, W. B., Holland, J. H., LeBaron, B., Palmer, R. & Tayler, P. (1997). ‘Asset pricing under endogenous expectations in an artificial stock market.’ In The Economy As An Evolving Complex System II, chap. 2, (pp. 15–44). Reading, MA: Addison-Wesley. [doi:10.1201/9780429496639-2]
BASS, F. M. (1969). A new product growth for model consumer durables. Management Science, 15(5), 215–227. [doi:10.1287/mnsc.15.5.215]
BASS, P. I. & Bass, F. M. (2001). Diffusion of technology generations: A model of adoption and repeat sales. In INFORMS Marketing Science Conference Presentation, (pp. 79–87).
BEINHOCKER, E. D. (2013). Reflexivity, complexity, and the nature of social science. Journal of Economic Methodology, 20(4), 330–342. [doi:10.1080/1350178x.2013.859403]
BIKHCHANDANI, S., Hirshleifer, D. & Welch, I. (1998). Learning from the behavior of others: Conformity, fads, and informational cascades. Journal of Economic Perspectives, 12(3), 151–170. [doi:10.1257/jep.12.3.151]
BOERO, R., Castellani, M. & Squazzoni, F. (2004). Cognitive identity and social reflexivity of the industrial district firms. Going beyond the "Complexity Effect" with agent-based simulations. Lecture Notes in Computer Science, 2934, 48–69. [doi:10.1007/978-3-540-25867-4_4]
BOERO, R., Castellani, M. & Squazzoni, F. (2008). Individual behavior and macro social properties. an agent-based model. Computational and Mathematical Organization Theory, 14(2), 156–174. [doi:10.1007/s10588-008-9025-3]
BOURDIEU, P. & Wacquant, L. J. (1992). An Invitation to Reflexive Sociology. Cambridge, UK: University of Chicago Press.
BRYANT, C. G. (2002). George Soros’s theory of reflexivity: a comparison with the theories of Giddens and Beck and a consideration of its practical value. Economy and Society, 31(1), 112–131. [doi:10.1080/03085140120109277]
CADAVID, L.& Cardona, C. J. F. (2014). Saddle points in innovation diffusion curves: An explanation from bounded rationality. In Advances in Social Simulation, (pp. 73–82). Springer. [doi:10.1007/978-3-642-39829-2_7]
CASTELFRANCHI, C. (1998). Simulating with Cognitive Agents: The Importance of Cognitive Emergence. In Multi- Agent Systems and Agent-Based Simulation, (pp. 26–44). Berlin, Germany: Springer. [doi:10.1007/10692956_3]
CASTELLANO, C., Fortunato, S.& Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591. [doi:10.1103/revmodphys.81.591]
CHANDRASEKARAN, D. & Tellis, G. J. (2011). Getting a grip on the saddle: Chasms or cycles? Journal of Marketing, 75(4), 21–34. [doi:10.1509/jmkg.75.4.21]
CHANDRASEKARAN, D. & Tellis, G. J. (2018). A summary and review of new product diffusion models and key findings. In Handbook of Research on New Product Development, chap. 14, (pp. 291–312). Cheltenham, UK: Edward Elgar Publishing. [doi:10.4337/9781784718152.00025]
COINTET, J.-P. & Roth, C. (2007). How realistic should knowledge diffusion models be? Journal of Artificial Societies and Social Simulation, 10(3), 5: https://www.jasss.org/10/3/5.html.
DANN, O. & Dinwiddy, J. (1988). Nationalism in the Age of the French Revolution. London, UK: The Hambledon Press.
DAVIS, J. B. (2013). Soros’s reflexivity concept in a complex world: Cauchy distributions, rational expectations, and rational addiction. Journal of Economic Methodology, 20(4), 368–376. [doi:10.1080/1350178x.2013.859407]
DELRE, S. A., Jager, W. & Janssen, M. A. (2007). Diffusion dynamics in small-world networks with heterogeneous consumers. Computational and Mathematical Organization Theory, 13(2), 185–202. [doi:10.1007/s10588-006-9007-2]
DODDS, P. S. & Watts, D. J. (2004). Universal behavior in a generalized model of contagion. Physical Review Letters, 92(21), 218701. [doi:10.1103/physrevlett.92.218701]
DODDS, P. S. & Watts, D. J. (2005). A generalized model of social and biological contagion. Journal of Theoretical Biology, 232(4), 587–604. [doi:10.1016/j.jtbi.2004.09.006]
DOGANOGLU, T. & Grzybowski, L. (2007). Estimating network effects in mobile telephony in Germany. Information Economics and Policy, 19(1), 65–79. [doi:10.1016/j.infoecopol.2006.11.001]
EPSTEIN, J. M. & Axtell, R. L. (1996). Growing Artificial Societies: Social Science from the Bottom Up. Washington, D.C.: The MIT Press. [doi:10.7551/mitpress/3374.001.0001]
ETZION, D. (2013). Diffusion as Classification. Organization Science, 25(2), 420–437.
FILIMONOV, V. & Sornette, D. (2012). Quantifying reflexivity in financial markets: Toward a prediction of flash crashes. Physical Review E, 85(5), 056108. [doi:10.1103/physreve.85.056108]
FLEISS, J. L., Levin, B., & Paik, M. C. (2003). Statistical Methods for Rates and Proportions. Hoboken, NJ: John Wiley & Sons, third edn. [doi:10.1002/0471445428]
FLEISS, J. L., Levin, B., & Paik, M. C. (2013). Statistical Methods for Rates and Oroportions. Hoboken, NJ: John Wiley & Sons.
GARDENFORS, P. (2006). How Homo Became Sapiens: On the Evolution of Thinking. Oxford, UK: Oxford University Press. [doi:10.1093/acprof:oso/9780198528517.001.0001]
GEROSKI, P. A. (2000). Models of technology diffusion. Research Policy, 29(4-5), 603–625. [doi:10.1016/s0048-7333(99)00092-x]
GIDDENS, A. (1984). The Constitution of Society: Outline of the Theory of Structuration. Berkeley, CA: Polity Press.
GILBERT, N. (2002). Varieties of emergence. In C. Macal & D. Sallach (Eds.), Proceedings of the Agent 2002 Conference on Social agents: Ecology, Exchange, and Evolution, (pp. 41–50). Argonne, IL: University of Chicago and Argonne National Laboratory.
GOLDENBERG, J., Libai, B. & Muller, E. (2002). Riding the saddle: How cross-market communications can create a major slump in sales. Journal of Marketing, 66(2), 1–16. [doi:10.1509/jmkg.66.2.1.18472]
GOLDENBERG, J., Libai, B. & Muller, E. (2010). The chilling effects of network externalities. International Journal of Research in Marketing, 27(1), 4–15. [doi:10.1016/j.ijresmar.2009.06.006]
GOLDER, P. N. & Tellis, G. J. (2004). Growing, growing, gone: Cascades, diffusion, and turning points in the product life cycle. Marketing Science, 23(2), 207–218. [doi:10.1287/mksc.1040.0057]
GOLDSPINK, C. (2014). Social Norms from the Perspective of Embodied Cognition. In The Complexity of Social Norms, (pp. 55–79). Berlin, Germany: Springer. [doi:10.1007/978-3-319-05308-0_4]
GOLDSPINK, C. & Kay, R. (2007). Social emergence: Distinguishing reflexive and non-reflexive modes. In AAAI Fall Symposium, (pp. 48–55).
GORTON, W. A. (2006). Karl Popper and the social sciences. Albany, NY: State University of New York Press.
GRANOVETTER, M. (1978). Threshold models of collective behavior. American Journal of Sociology, 83(6), 1420–1443. [doi:10.1086/226707]
GUSEO, R. & Guidolin, M. (2015). Heterogeneity in diffusion of innovations modelling: A few fundamental types. Technological Forecasting and Social Change, 90, 514–524. [doi:10.1016/j.techfore.2014.02.023]
ISRAEL, J. (2009). A Revolution of the Mind: Radical Enlightenment and the Intellectual Origins of Modern Democracy. Princeton, NJ: Princeton University Press.
KIESLING, E., Günther, M., Stummer, C. & Wakolbinger, L. M. (2012). Agent-based simulation of innovation diffusion: A review. Central European Journal of Operations Research, 20(2), 183–230. [doi:10.1007/s10100-011-0210-y]
MICHALAKELIS, C., Varoutas, D. & Sphicopoulos, T. (2008). Diffusion models of mobile telephony in Greece. Telecommunications Policy, 32(3-4), 234–245. [doi:10.1016/j.telpol.2008.01.004]
PERES, R., Muller, E. & Mahajan, V. (2010). Innovation diffusion and new product growth models: A critical review and research directions. International Journal of Research in Marketing, 27(2), 91–106. [doi:10.1016/j.ijresmar.2009.12.012]
ROGERS, E. M. (1983). Diffusion of Innovations. New York, NY: The Free Press, third edn.
ROHLFS, J. H. (2003). Bandwagon effects in high-technology industries. MIT press.
RUST, R. T. (2010). Network externalities — Not cool? A comment on "The chilling effects of network externalities".International Journal of Research in Marketing, 27(1), 18–19. [doi:10.1016/j.ijresmar.2009.12.003]
SÁENZ-ROYO, C., Gracia-Lázaro, C. & Moreno, Y. (2015). The role of the organization structure in the diffusion of innovations. PLoS ONE, 10(5), e0126076. [doi:10.1371/journal.pone.0126076]
SANDRI, S. (2009). Reflexivity in Economics. Berlin, Germany: Physica-Verlag.
SCHELLING, T. C. (1971). Dynamic models of segregation. Journal of Mathematical Sociology, 1(2), 143–186
SORNETTE, D. (2006). Endogenous versus exogenous origins of crises. In S. Albeverio, V. Jentsch & H. Kantz (Eds.), Extreme Events in Nature and Society, (pp. 95–120). Berlin, Germany: Springer. [doi:10.1007/3-540-28611-x_5]
SOROS, G. (2013). Fallibility, reflexivity, and the human uncertainty principle. Journal of Economic Methodology, 20(4), 309–329. [doi:10.1080/1350178x.2013.859415]
SQUAZZONI, F. (2008). The micro-macro link in social simulation. Sociologica, 2(1), 1–26.
STREMERSCH, S., Lehmann, D. & Dekimpe, M. (2010). Preface to "The chilling effects of network externalities". International Journal of Research in Marketing, 27(1), 1–3. [doi:10.1016/j.ijresmar.2009.12.001]
STREMERSCH, S., Tellis, G. J., Franses, P. H. & Binken, J. L. (2007). Indirect network effects in new product growth. Journal of Marketing, 71(3), 52–74. [doi:10.1509/jmkg.71.3.052]
UMPLEBY, S. (2007). Reflexivity in Social Systems: The theories of George Soros. Systems Research and Behavioral Science, 24(5), 515–522. [doi:10.1002/sres.852]
UMPLEBY, S. (2010). From complexity to reflexivity: The next step in the systems sciences. Cybernetics and Systems, 10: https://cpb-us-e1.wpmucdn.com/blogs.gwu.edu/dist/d/257/files/2016/11/2010-EMCSR-Complexity-an-Reflexivity-final-1f86cgv.pdf.
VAN BAVEL, J. & Grow, A. (2017). Introduction: Agent-based modelling as a tool to advance evolutionary population theory. In Agent-Based Modelling in Population Sstudies, (pp. 3–27). Berlin, Germany: Springer. [doi:10.1007/978-3-319-32283-4_1]
WATTS, C. & Gilbert, N. (2014). Simulating Innovation: Computer-Based Tools for Rethinking Innovation. Cheltenham, UK: Edward Elgar Publishing.
YAVAÇ, M. & Yücel, G. (2014). Impact of homophily on diffusion dynamics over social networks. Social Science Computer Review, 32(3), 354–372.

