Introduction
The whole is more than the sum of its part (Anderson 2011; Baumeister et al. 2016) is a leitmotif of complex systems research being at the root of the concept of emergence. This sentence has been invoked in many scenarios to explain the onset of ordered self-organised structures (Nicolis & Nicolis 2012). In this work, we propose an application of the former “motto” to social sciences, in particular to the process of task solving. Indeed human beings, like many other social animals, can organise themselves into groups to solve tasks that the single individual is unable to complete (Smith 1994). This can be an incremental support: joining their strengths agents will be capable to overcome the hurdle each one could not separately achieve. It can also be a coordination step where each agent will bring her own knowledge to create something new: a (social) group knowledge capable to solve higher level tasks. The latter can be named Collective Intelligence (\(CI\)), and it is a measure of the advantage of being in a group compared to isolated individuals. In this view, (Szuba 2001) defined the \(CI\) as the property of a social structure that originates when individuals interact and results in the acquisition of the ability to solve new or more complex problems.
The process of social problem-solving that the group implements in order to solve higher-level tasks is the result of the group members cooperation, competition and of their abilities in sharing knowledge. Thus, people tend to turn to groups when they have to untangle complex problems because they believe that groups have better problem-solving skills than a single individual (Forsyth 2018). Researchers found that self-organisation of human crowds, improved nowadays because of the communications technologies that simplify information spread, can lead to original ideas and solutions of notoriously hard problems. These include designing RNA molecules (Lee et al. 2014), computing crystal (Horowitz et al. 2016), improving medical diagnostics (Kurvers et al. 2016), predicting protein structures (Cooper et al. 2010), proving mathematical theorems (Gowers & Nielsen 2009) and collaborative mathematics such as the polymath blog (Gowers 2009) or even solving quantum mechanics problems (Sørensen et al. 2016).
As previously stated, the \(CI\) can be defined as the difference between the rate of success of the group on a specific problem and the average rate of success of its members, on the same issue. This is thus an emergent property of the group as a whole, not reducible to the simple sum of its members’ individual intelligence. The available literature shows that the group performance is affected by several factors, such as: the group members characteristics, the group structure that regulate collective behaviour (Woolley et al. 2015), the context in which the group works (Barlow & Dennis 2016), the cognitive processes underlying the social problem-solving reasoning (Heylighen 1999), the average of members’ Intelligence Quotients (Bates & Gupta 2017) and the structure (Credé & Howardson 2017; Lam 1997), and the complexity of the problem that should be solved (Guazzini et al. 2019; Capraro & Cococcioni 2016; Guazzini et al. 2015; Moore & Tenbrunsel 2014).
During the past few years, the \(CI\) has attracted a large interest from the scientific community, notably from the empirical research side, as individual intelligence did in the last decades. The individual intelligence has been defined as the ability of human beings to solve a wide variety of tasks (Gardner 2011). Adopting an analogous point of view, the \(CI\) has been defined as a general factor able to explain the “group performance on a wide variety of tasks” (Woolley et al. 2010). According to the most recent studies, the latter is able to predict about 43% of the variance of the group performance and it is strongly correlated with three different variables: the first one is the variance of the conversation turnover, the second one is the proportion of women in the group, and the last one is the average of members’ abilities in the theory of mind (Engel et al. 2015, 2014; Woolley et al. 2010).The same studies find that the average of the teammates intelligence quotient (\(\langle{IQ}\rangle\)) is not a significant predictor of group performance (\(\mathit{r} = 0.18\)) (Woolley et al. 2010).
Despite several studies brought empirical evidence about the existence of a unique factor capable of explaining a large part of the group performance, some recent works aimed at resizing the dimensionality of such a model (GRAF et al. 2019; Bates & Gupta 2017; Credé & Howardson 2017). In particular, a recent re-analysis of the four main empirical studies in the field of \(CI\) (Barlow & Dennis 2016; Engel et al. 2015, 2014; Woolley et al. 2010) does not support the hypothesis of a general factor able to explain the performance variation across a wide variety of group-based tasks (Credé & Howardson 2017). Studies conducted in an online environment support the claim that \(CI\) would manifest itself differently depending on the context (Barlow & Dennis 2016). Furthermore, the literature suggests the existence of different models of \(CI\) able to explain the variance of group performance, for different kind of task (Credé & Howardson 2017; Wildman et al. 2012). In this regard, Lam (1997) showed how the structure of the task affected the quality of group communications and decisions. Finally, a complete replication of some standard studies aimed to characterise and measure the \(CI\), conducted with a different sample, shown that sometimes the group performance can be significantly and strongly correlated with IQ. In particular, Bates & Gupta (2017) reported that in their experiments the \(CI\) resulted completely indistinguishable from the members Intelligence Quotients.
Given the different, and sometimes contradictory, available empirical results about the \(CI\) and its characterisation in terms of relevant variables, the aim of our work is thus to shed some light on this issue using a mathematical approach. Even though the literature identified a relationship among \(CI\), group structure and task complexity (Capraro & Cococcioni 2016; Guazzini et al. 2015; Moore & Tenbrunsel 2014), the limited number of studies in this field makes this dynamics still elusive. In particular, it is possible to hypothesise the existence of a non-linear interaction between the potential of the group, e.g., the average of members’ intelligence, and the difficulty of the problem that the group has to solve. This interaction may explain the variance of group performance reported by literature. Thus, it could be relevant for this research field to clarify the intertwined relationship between the two fundamental dimensions introduced above (i.e., task complexity and members’ intelligence) in order to develop a model allowing to understand the group performance. A possible way to achieve this goal is going through the analysis of the cognitive processes underlying the social problem-solving dynamics developed inside the group. In this regard, Heylighen (1999), thorough an interesting formal model, suggested that groups, solving a task, would develop a Collective Mental Map (CMM), as a product of the interaction between some psychosocial processes, such as the cross-cueing (Meudell et al. 1995) and the information and knowledge sharing. The Heylighen’s framework allows to study the \(CI\) dynamics taking into account the merge of the group members’ representations of the problem in a single representation labelled as Member Map (MM). The MMs are usually defined as composed by a set of problem states, a set of possible steps for the solution of the task, and a preference fitness criterion for selecting the preferred actions (Heylighen 1999). Here, adopting the Heylighen framework, we propose a mathematical model of \(CI\) able to shed light on the process resulting from the interaction between the average of group members’ intelligence and the difficulty of the task, and thus open the way to a better understanding of the \(CI\).
The paper is organised as follows. In the next section, we introduce the formal model based on the Heylighen hypothesis and an operational definition of \(CI\). Then, we will present the theoretical consequences of our model and we corroborated them with some numerical results. We finally conclude our study with a discussion about the potential follow-ups of this work and the empirical studies one could organise to check its goodness.
Methods
As already stated, our work is grounded on the Heylighen theoretical model of collective mental maps; the stylised model we derive, allows us to provide a possible explanation of the discording results recently presented in the literature about the \(CI\) and its determining factors, more precisely the existence of a correlation between the \(CI\) and the teammates \(IQ\) (Bates & Gupta 2017) and the absence of such correlation (Woolley et al. 2015). Based on simple rules inspired by cognitive processes, we will build a formal model that will help us to unravel some open issues about the emergence of \(CI\). We anticipate that our model will be deliberately abstract to clearly identify the main drive for the emergence of the collective intelligence, but on the other hand general enough to allow for practical implementation into a real experiment.
The Heylighen hypothesis
Assuming the Heylighen framework to study the dynamics under scrutiny, it appears necessary to distinguish between the construct of intelligence and knowledge. One of the most shared definitions of intelligence suggests separating fluid intelligence from the crystallised one. Fluid intelligence is a set of skills and abilities useful during the reasoning processes and in the acquisition of new knowledge (Bates & Shieles 2003; Stankov 2003). Crystallised intelligence is the set of already stored knowledge needful to the effective problem-solving reasoning (Bates & Shieles 2003; Horn & Masunaga 2006). In the light of the proposed distinction between the two sub-components of intelligence, the crystallised and the fluid one, we can assume that the individual Intelligence Quotient is the result of a complex function among several factors, including the stored knowledge (Cattell 1943). The latter is a factor of interest because it is both cause and effect of the \(IQ\): the ability to acquire knowledge depends on the fluid intelligence (Beier & Ackerman 2005), and, at the same time, the ability to solve a wide variety of tasks, namely \(IQ\) (Spearman 1904), is determined by the previously stored knowledge, or crystallised intelligence (Bates & Shieles 2003). So, we can argue that the agents knowledge is the best marker for their intelligence.
Adopting the Heylighen topological metaphor of human intelligence, the knowledge of the \(i\)-th agent can be described by a vector made of \(D\) entries (knowledge nodes), denoting the previously introduced set of problem states or set of possible steps for the solution of the task, \(\vec{K}^{(i)}=({K}_1^{(i)},\dots,{K}^{(i)}_D)\). In the following, we will refer to the latter as a generic agent's knowledge on a topic. To simplify the notation, we assume to normalise this vector, such that its components can assume a value in \([0,1]\), the smaller (resp. the larger) the value the lower (resp. the higher) is the knowledge on this specific topic. The total knowledge of an agent can be captured by the sum of the entries of her knowledge vector, \(IQ^{(i)}=\sum_{j=1}^D{K}_j^{(i)}\), the latter can thus be used as a proxy of the Intelligence Quotient (\(IQ\)) of the agent. Adopting such a metaphor, in Figure 1 we report a schematic representation of the agent knowledge vector. For each of the \(D\) topics, the agent has a knowledge level schematically represented as a bar of different heights.
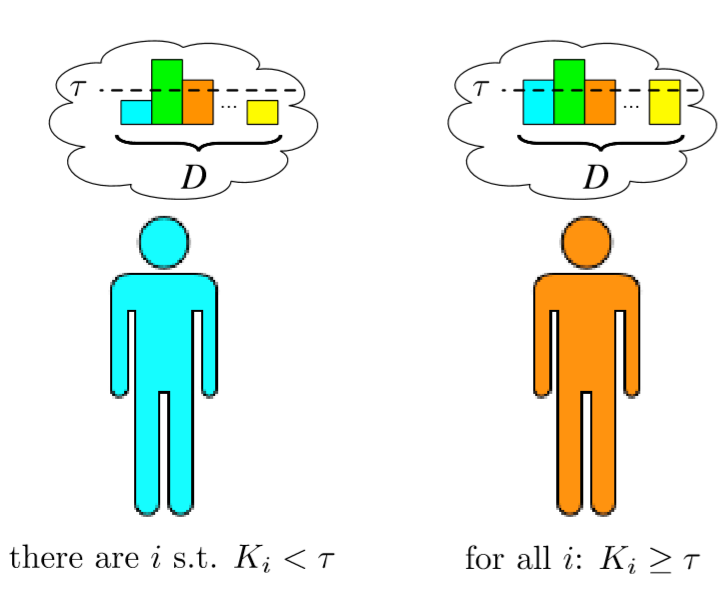
For the sake of simplicity, we assume that an agent is able to solve a task with difficulty \(\tau\), a real number in \([0,1]\), if all the entries in her knowledge vector are larger than \(\tau\), namely \(\min_{j}K^{(i)}_j\geq \tau\) (see Figure 1). Let us observe that the dimension \(D\) participates, even if indirectly, to make a task hard or not, indeed if \(D\) is large it can be difficult (i.e., less probable) for the agents to have all the entries of their knowledge vector larger than \(\tau\). Secondly, we remark that we can relax the definition of task difficulty by assuming the need for different levels of knowledge in each topic to achieve a task, that is the latter would be a \(D\)-dimensional vector, \(\vec{\tau}=(\tau_1,\dots,\tau_D)\in [0,1]^D\), and an agent would be able to solve this task if \(K^{(i)}_j\geq \tau_j\) for all \(j=1,\dots,D\). For a sake of simplicity, we decided to adopt the former simpler assumption and we deserve the latter one for a more detailed further analysis.
The last required ingredient is a set of rules driving the merge of different mental maps (agents’ knowledge) into a common one (group knowledge) in order to model the group problem solving process. Since no previous research explored the connection between task difficulty and group knowledge potential in order to explain the \(CI\) dynamics, we choose to build an abstract model under the assumption of perfect communication between group members, neglecting thus in first approximation all the biases that could affect the group discussion and decision making or problem solving. In this way, we will able to capture the main drive for the emergence of the collective intelligence. Let us observe that some of the above mentioned biases could be easily inserted in the model (see Discussion and Model Documentation Sections), we nevertheless stick to our initial choice in this first analysis.
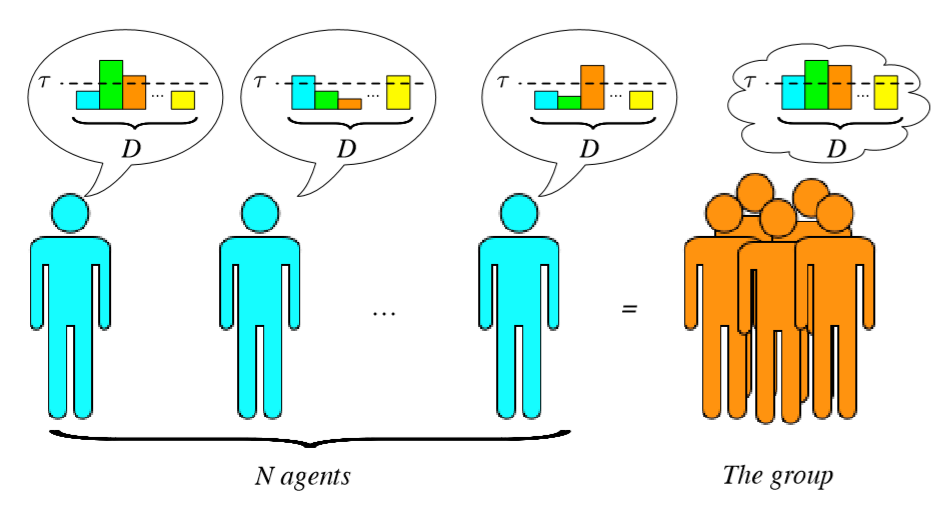
In particular, Heylighen suggested that groups facing with a certain task solving problem, develop CMMs (Heylighen 1999), that, in the absence of any communication issue and/or social hierarchy, can be obtained with agents “juxtaposing” their knowledge vectors, that is the CMM will result to be a \(D\)-dimensional vector, \(\vec{G}=(G_{1},\dots,G_{D})\), whose entries are the “best ones”, (i.e., the ones with the largest values), among the agents, more precisely \(G_{j}=\max_{i}K^{(i)}_{j}\) (see Figure 2). The total knowledge of a group can be measured by the sum of the agents \(IQ\), that is \(IQ_{(G)}=\sum_iIQ^{(i)}\).
Based on the above, a group is able to solve a task of difficulty \(\tau\in[0,1]\) if \(\min_j G_{j}\geq \tau\). Clearly if the group contains agents capable to solve by their own a task of a given difficulty, the group would also do the same but in this case, the \(CI\) will be null because there is not an added value to be together. On the other hand, a group made by agents unable to solve individually a task of a given difficulty, but excelling in sufficiently many different topics, could perform well and solve a problem where each agent will fail. In this latter case one can consider such achievement an emergent property of the group and assign a large \(CI\) (see Figure 2).
An operational definition of Collective Intelligence
Given a task of difficulty \(\tau\in[0,1]\) in a knowledge space of \(D\) dimensions, we can define the \(CI\) as the difference between the rate of success of the group and the rate of success of the average agent composing the group. This function depends thus on \(\tau\) and \(D\), it is non negative and positive values are associated to tasks too hard for the individual agent while solvable by the group.
Let us consider a group made by \(N\) agents and consider a task with difficulty \(\tau\) in a \(D\) dimensional knowledge space. Assume also that the knowledge of the \(i\)-th agent on the \(j\)-th topics is a stochastic variable with a probability distribution \(p(x)\) with support \([0,1]\). Without loss of generality, we hereby hypothesise that \(p(x)\) is the same for all topics; observe however that this working assumption will not substantially modify our conclusions. One can thus determine (see Appendix A for more details) the probability for the \(i\)-th agent to exceed a level \(\tau\) of knowledge on the \(j\)-th topic. From the assumption that the entries of the knowledge vector are i.i.d. random variables, we can obtain the probability, \(\pi^{(i)}(\tau,D)\), that the \(i\)-th agent is able to solve the \(D\) dimensional task characterised by a difficulty \(\tau\), namely to exceed the level \(\tau\) on all the \(D\) dimensions of the task.
By its very first definition, the Collective Mental Map is obtained by letting the agents to interact, compare and exchange their knowledge levels; eventually determining the group knowledge vector obtained by taking the largest values among all the agents knowledge vectors, across each dimension of the task. Hence from the previous result concerning each single agent, one can straightforwardly compute the probability distribution, say say \(\Pi_N(\tau,D)\), for the \(j\)-th component of the Collective Mental Map to be larger than \(\tau\) (see Appendix A).
Finally, the Collective Intelligence for a group of size \(N\) would result the difference among the previous two functions:
| $$CI_N(\tau,D):=\Pi_N(\tau,D) - \pi^{(i)}(\tau,D)\, .$$ | (1) |
A Simple Agent Based Model
The process described in the previous section can be schematically represented by the flow diagram reported in Figure 3 and described in full with the algorithm presented in the Model Description Section. To initialise the model, we have to set the number of agents, \(N\), the size of the knowledge vector, \(D\), and the task difficulty, \(\tau\). Then, we have to fix the probability distribution of the entries of the knowledge vector. Let us observe that we also allows for the possibility of choosing the number of agents actually discussing simultaneously, \(2\leq k \leq N\). Therefore, the process goes on and we can extract the results.
As already stated, we decided to concentrate on small groups, e.g., made by \(N=5\) agents, in order to assume perfect transmission among agents and avoid any hierarchical structure in the group. Focusing on a small number of agents would allow to transfer our conclusions and test them with real experiments, which typically involve small size groups, whose dynamics are simpler than larger groups, being the former characterised by no division in subgroups, rapid communication, absence of delay or memory effects, just to mention few aspects. These assumptions can be implement in a simple ABM as follows. \(N\) agents meet and discuss about one among the \(D\) topics, they have in their knowledge vectors; such topics, say \(j\), are randomly chosen with uniform probability from the \(D\) available ones. At the end of the interaction, each agent leaves the group having learnt the highest value on the topics under discussion from the teammates, i.e., each agent replaces her \(K^{(i)}_j\) with the \(\max_i K^{(i)}_j\). One time step is fixed by performing sufficiently many meetings is such a way that all the \(D\) topics have been discussed at least once (see Appendix B).
Of course, we could relax the assumption that all agents interact at the same time and on the contrary hypothesise that only \(k\) agents discuss simultaneously (\(2\leq k \leq N\)). In our opinion, this scheme will be relevant once \(N\) is large such that many body interactions are forbidden by the system size and the cognitive capacities of agents. These limitations led us to avoid such a scheme.
At the beginning of the process, we evaluate each individual agent against the task. Then after the meetings, we evaluate the whole group against the task and measure the (possible) improvement of the group over the single agent, that as previously stated is a proxy for \(CI\).
Results
The ABM described in the previous section is schematically represented by the flow diagram reported in Figure 3 and presented in the algorithm in the Model Description Section. This model can be analytically solved, as we will hereby show. First, we fix the distribution of agent knowledge; we assume agent knowledge on each topic to follow an unimodal distribution with a peak at some intermediate value \(\beta\in (0,1)\), denoting thus the most probable level of knowledge for each topic. For the sake of simplicity, we assume each entry in agent knowledge vector to follow a “tent distribution” with parameter \(\beta\) (see Figure 4). In the Appendix C, we briefly present the case of uniformly distributed agents knowledge and we can observe that the results are qualitatively similar to the ones hereby presented.


The \(CI\) (given by (9) in Appendix A) can be explicitly computed in the case of the tent distribution and it results to be
| $$CI^{(tent)}_N(\tau,D)= \left[1-\left(\frac{\tau^2}{\beta}\right)^N\right]^D-\left(1-\frac{\tau^2}{\beta}\right)^D \text{, if $0\leq \tau\leq \beta$}\, ,$$ | (2) |
| $$CI^{(tent)}_N(\tau,D)= \left[1-\left(1-\left(\frac{(1-\tau)^2}{1-\beta}\right)\right)^N\right]^D-\left(\frac{(1-\tau)^2}{1-\beta}\right)^D\text{, if $\beta\leq \tau\leq 1$}\, .$$ | (3) |
To check the goodness of (2) and (3), we performed some dedicated numerical simulations of the ABM involving a small group made by \(N=5\) agents, each one endowed with a \(D=5, 10\) and \(20\) dimensional knowledge vector, whose entries are drawn according to the tent distribution with parameter \(\beta\). We also let the group have a sufficient number of meetings to discuss on every topics (see Appendix B for more details). Results are reported in Figure 5 and show that in all cases \(CI\) has a similar behaviour: it starts very small, then it increases up to a maximum value for a given value of the task difficulty to then decrease again toward zero.
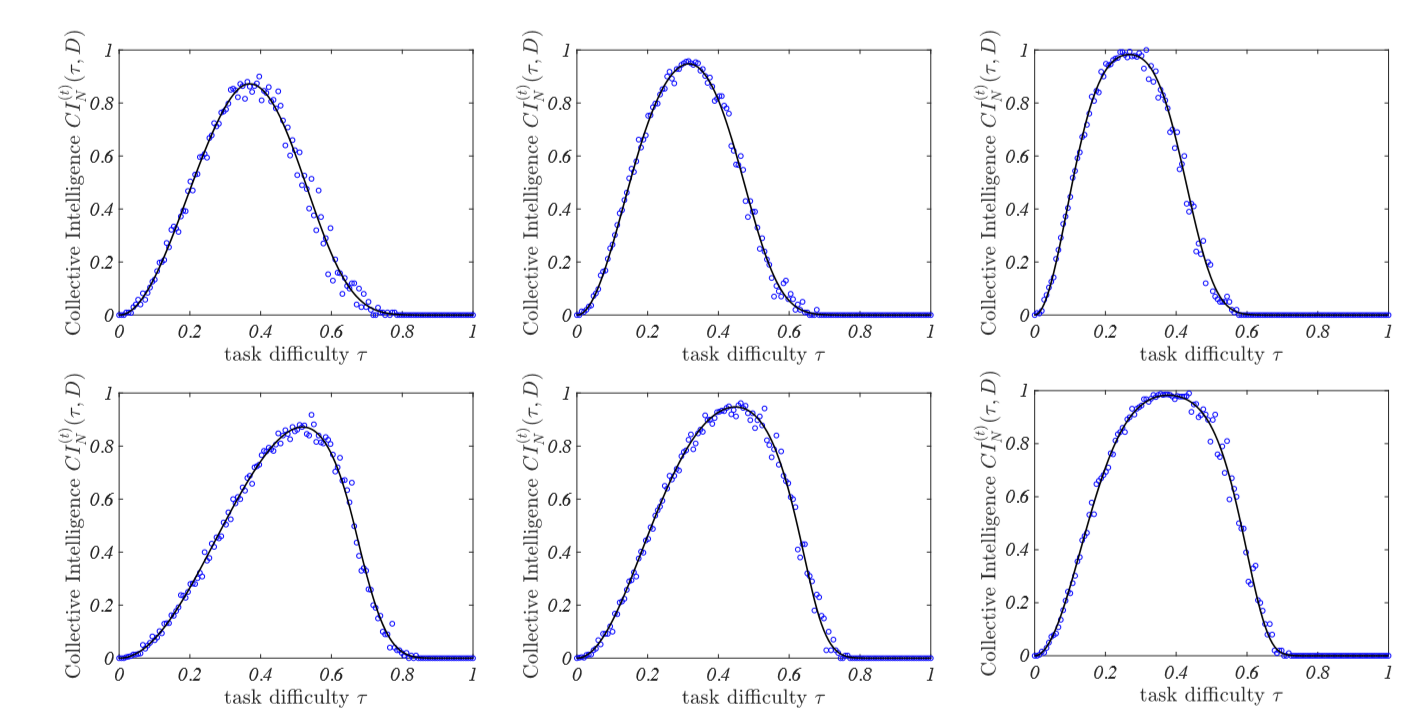
Indeed, for very easy tasks, \(\tau \ll 1\), the \(CI\) is very small: both the average agent and the group are able to solve the task and thus there is no gain in participating to a group discussion. As the difficulty increases, the average agent is less and less capable to solve the task while the group perform excellently. For much larger thresholds, nor the agent nor the group are able to solve the task and thus \(CI\) gets again very low.
The \(IQ\) of an agent with a D-dimensional knowledge space can be exactly computed under the assumption of values distributed accordingly to the tent distribution as follows:
| $$\langle IQ \rangle =\frac{1+\beta}{3}D\, ,$$ | (4) |
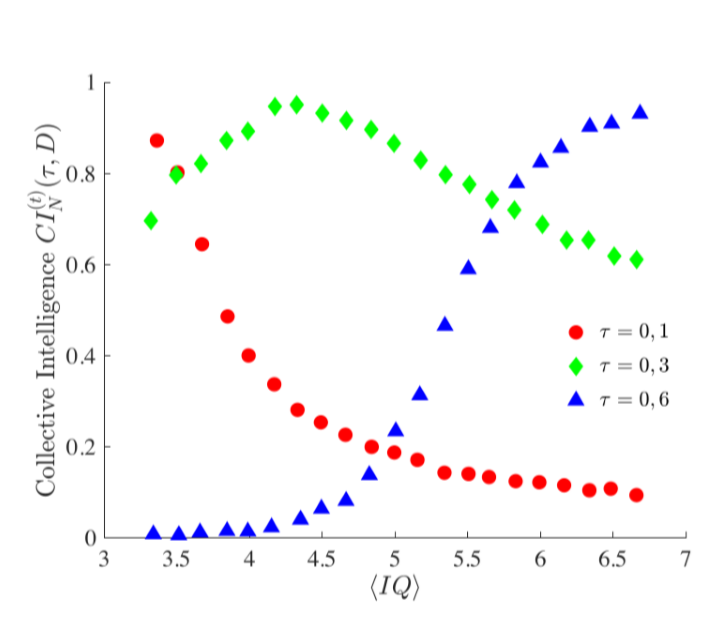
It is thus an increasing function of the parameter \(\beta\). We can hence study the dependence of the \(CI\) on the average \(IQ\), for fixed task difficulty \(\tau\) and dimension \(D\), by varying \(\beta\). Results are reported in Figure 6 for an easy task (\(\tau=0.1\) red circles), a simple task (\(\tau=0.3\) green diamonds) and a more difficult one (\(\tau=0.6\) blue triangles). One can observe three clearly different behaviours; in case of the simple task, the average agent is not able to solve the task once the average \(IQ\) is small while the group does, hence \(CI\) is positive and increasing because the group still performs better than the average agent even for larger \(IQ\). Once \(IQ\) increases even more, the average agent fills the gap and she starts to perform better; \(CI\) thus decreases because there is no longer an incentive in being in a group. On the other hand, in case of more difficult tasks, \(CI\) is always positive and increasing meaning that the average agent never performs as well as the whole group. While for an easy task, \(CI\) is always positive but decreasing meaning that the group is always able to solve the task and the average agent very soon is able to do the same.
To provide a global view, we report in Figure 7 \(CI\) values for a group made by \(N=5\) agents, as a function of \(\tau\) and \(D\) for two values of the \(\beta\)-parameter of the tent distribution. One can observe that as the dimensionality \(D\) increases, the group will always perform better than the single agent even for small \(\tau\), indeed the blue zone on the left part of each plot shrinks as \(D\gg 1\). Comparing both panels of Figure 7 one can conclude that the group performs better than the single agent, i.e., it is able to solve more difficult tasks - large \(\tau\) and \(D\) - as \(\beta\) increases; this somehow counter intuitive phenomenon can be explained by the fact that even if the average agent has a large \(IQ\) for large \(\beta\), the high dimensionality of the task makes almost impossible for the agent to exceed in all the topics and thus she will be unable to solve the task. This is not the case of the group because it will gather the best from each agent.
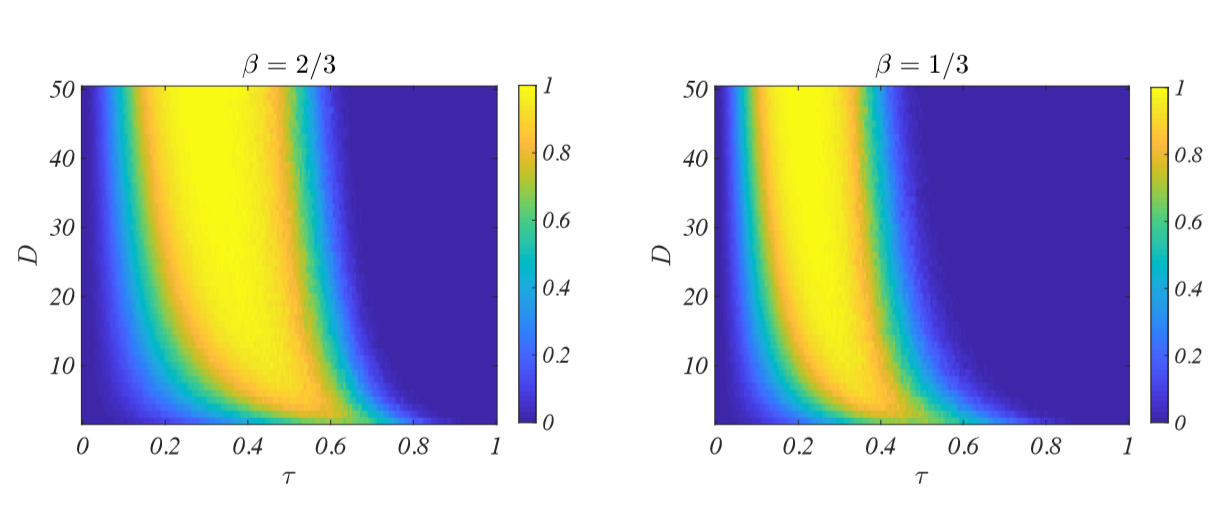
This non monotone behaviour of \(CI\) as a function of the average \(IQ\) can explain the different experimental results available in the literature, where some authors find an increasing correlation between \(CI\) and the average \(IQ\), such as the ones reported by (Bates & Gupta 2017) while other ones find a weak correlation between the same variables, see for instance Woolley et al. (2015). Our model and the resulting analysis suggest that both studies are right. The point is that the chosen groups (or the tasks) were sitting in different locations of the parameter space: one where the relation is increasing (see triangles or diamond curves in Figure 6), the other where it is decreasing (see circle or diamond curves in Figure 6), but the underlying mechanism has always been the same. Now, it is possible to design new experiments where we can control and tune the above variables.
Discussion
The present study aimed to develop an abstract formal model to analyse the Collective Intelligence process, namely the ability of a group to better perform on problem solving than each isolated teammates. Our formal model was based on a minimal set of fundamental assumptions derived from the literature (Woolley et al. 2010; Bates & Gupta 2017; Heylighen 1999), and analysed the (complex) interaction existing among the task difficulty, the average teammate intelligence and \(CI\). In particular, the model focussed on the interaction between the agent ability to solve a task, i.e., her intelligence, and \(CI\), namely the group capability to solve the task.
The results obtained from our ABM, corroborated by analytical ones, supported the hypothesis of the existence of a non-linear relation between the Collective Intelligence of a group and the average Intelligence Quotient of group members, mediated by the task difficulty under study. Indeed for simple tasks, the \(CI\) is a decreasing function of \(IQ\), namely the combination of agents’ knowledge rapidly becomes redundant because of the “simplicity” of the problem to solve. A second and more interesting regime emerges for tasks with intermediate difficulty. Within this regime, the relation between \(CI\) and \(IQ\) exhibits a non-monotone behaviour: initially, \(CI\) increases with \(IQ\) but then a tipping point is reached, beyond which an increasing \(IQ\) produces a decreasing \(CI\). In this regime, there is an optimal combination of task difficulty and average group IQ. A third regime shows that for tasks with a strong difficulty, the \(CI\) monotonically increases with \(IQ\). Moreover, a (almost sharp) phase transition emerges by varying \(IQ\): beyond this value, the group would be always much better than its members, even if the rate of successes would decrease because of the task complexity itself.
We deliberately built an abstract and simple ABM to unravel the role of each constituting element considered. Every model is a partial representation of the reality, we had thus to leave out some factors, that would be considered in future work, such as the imperfect information transmission, group structure, kind of leadership and specific features of the agents (e.g., teammates’ empathy, and social abilities, hierarchical position in the group). We are aware that the latter ones represent two fundamental factors in the modelling of group dynamics. We hypothesised that the two experimental frameworks (Woolley et al. 2010; Bates & Gupta 2017) that motivated our research, have been performed on randomly assembled small groups of unknown people, without giving them any set of rules regarding communication, status and role. We can thus conclude that even if during the tasks, teammates spontaneously adopted some of such communication channels, their net effect would average out in the repeated experiments because of the random assembling of the groups and the absence of any rule, leaving hence the sole interplay between task difficulty, \(IQ\) and \(CI\).
Let us however emphasise that the results of our model suggest a possible interpretation for the, apparently, contradictory results from the literature regarding the existence of a \(CI\) factor, as well as the more challenging question about its magnitude (Woolley et al. 2010; Bates & Gupta 2017). The correlation between \(CI\)and \(IQ\) appears not to be the right observable to answer the above questions, because of the presence of hidden variables among which we have pointed out the main role played by the task difficulty. First of all, the relation between \(CI\) and \(IQ\) appear to be non-linear, and as a consequence, any linear statistics approach (e.g., factor analysis) would fail to capture the problem on the whole. Second, the role of the task difficulty, which is of course frequently an elusive concept to measure in ecological conditions, appears to determine non-linear effects on the relation between \(CI\) and \(IQ\), changing as a consequence the magnitude and the sign assumed by the parameter of any linear statistics relating them. In particular, if an experiment is realised within the first scenario (i.e. simple tasks, e.g. circle curves in Figure 6), the sign of a correlation statistics between \(CI\) and \(IQ\) would be negative, while it would be positive within the third scenario (i.e., very hard tasks; e.g., triangle curves in Figure 6). Finally, within the second scenarios, a small or even an absent correlation between \(CI\) and \(IQ\) would appear; small correlation would result from a positive correlation for small values of \(IQ\) , followed by a negative one for larger values, e.g., see diamond curves in Figure 6.
Our model allowed us to capture an interesting non-linear interaction between the potential of a group (i.e., the average of its members’ intelligence), and the difficulty of a task. In particular, our numerical results seems to capture the qualitative trends provided by the recent literature (Woolley et al. 2010; Bates & Gupta 2017), confirming a good agreement between theory and experimental data. Based on our results, we propose to design experiments where the task difficulty is a controlled variable and thus check the dependence between \(CI\) and \(IQ\).
In order to explain our results according to the Heylighen framework of Collective Mental Map, we hypothesised that the process of merging of subjects’ mental maps would introduce several non-linear effects simplified by the proposed linear analysis provided by previous studies (e.g., Woolley et al. 2010; Bates & Gupta 2017). Even assuming perfect communication between subjects, who would not be affected by any bias in group interaction (e.g., hierarchies, roles, leadership, status), our implementation of the Heylighen CMM shows that the \(IQ\) of the most intelligent member of the group should be the most important factor to solve simple tasks (Bates & Gupta 2017), but no longer strongly related with group outcomes for intermediate task complexity. According to our results, this can happen when the task difficulty overcomes the capacity of most intelligent member, who still would need a support from other members to build a collective mental map to solve the task. As a consequence, we argue that the tasks proposed in Woolley et al. (2010) were appropriate for the level of intelligence of the sample used in these studies, fitting thus with our second regime. On the other hand, the same tasks could be too simple for the sample of the second study (Bates & Gupta 2017) and the average \(IQ\) of the teammates was too high to solve them.
In conclusion, we proposed a simple and abstract model able to explain some relevant results in the literature about group problem solving (Woolley et al. 2010; Bates & Gupta 2017). We are notwithstanding aware that we did not consider certain important actions that groups adopt to increase collective performance once faced to such problems, e.g., division of labour, hierarchies and cooperation devices, just to mention few. However, we believe that the latter can be considered sort of “second order corrections” and so are confident that our model includes the main ingredients and with the sufficient level of abstraction to describe interaction in small groups as found in experiments, where agents cannot explore complex behaviours. We also simplified inter-agent communication by excluding features such as communication biases or hierarchy. We nevertheless show that these features could be easily implemented in our model in future developments.
Model Documentation
We used Matlab (MATLAB 2019) to develop our codes for both the ABM and the analytical study. In this way, we have a full control on the whole framework and we can adapt it at our will. The core of the ABM is presented hereby (algorithm) using the Matlab syntax; such main module is the used by varying the several parameters to perform the numerical simulations presented in the work.
As already stated, our model suffers from some limitations in the way exchanges among teammates can arise in real cases, e.g., we assumed perfect information transfer. Let us however observe that such transmission bias can be straightforwardly included into the model, e.g., it is sufficient to modify line 20 by adding a noise term once computing the maximum values of agent knowledge values on the discussion topic, the size of the noise will be a proxy for the transmission bias. So in conclusion, although simple and abstract, our model is flexible and can be easily adapted to include new factors.

Acknowledgements
T.C. would like to thank the University of the Reunion Island for providing him partial financial support within the call “Expert invité 2018”.Appendix
A: About the mathematical details of the Collective Intelligence
The aim of this section is to provide all necessary mathematical details to compute the \(CI\) starting from the probability distribution of the knowledge of each agent. Consider thus a group made by \(N\) agents and assume to deal with a task with difficulty \(\tau\) in a \(D\) dimensional knowledge space. Assume also that the knowledge of the \(i\)-th agent on the \(j\)-th topics is a stochastic variable with a probability distribution \(p(x)\) with support \([0,1]\), hence the probability the \(i\)-th agent exceed a level \(x\) of knowledge on the \(j\)-th topic is given by:
| $$\text{Prob}\{K^{(i)}_j\geq x\}=1-\int_0^xp(\xi)\, d\xi\,.$$ | (5) |
| $$\pi^{(i)}(\tau,D)=\left[1-\int_0^{\tau}p(\xi)\, d\xi\right]^D\,.$$ | (6) |
By its very first definition, the probability distribution of the \(j\)-th component of the Collective Mental Map is given by:
| $$\text{Prob}\{G_j\geq x\}=1-\left(\int_0^xP(\xi)\, d\xi\right)^N\,,$$ | (7) |
| $$\Pi_N(\tau,D)=\left[1-\left(\int_0^{\tau}P(\xi)\, d\xi\right)^N\right]^D\,.$$ | (8) |
Finally the Collective Intelligence for a group of size \(N\) would result the difference among the previous two functions:
| $$\begin{eqnarray}CI_N(\tau,D)&:=&\Pi_N(\tau,D) - \pi^{(i)}(\tau,D)\\&=&\left[1-\left(\int_0^{\tau}P(\xi)\, d\xi\right)^N\right]^D-\left[1-\int_0^{\tau}P(\xi)\, d\xi\right]^D\notag\, . \end{eqnarray}$$ | (9) |
B: More details about the ABM
As already stated, the ABM has been deliberatively chosen to be simple enough to be able to control the impact of the different parameters and to obtain an analytical understanding of the process. This last fact relies strongly on the number of meetings we let agents to have in order to discuss about the topics and thus modify their knowledge vectors. The aim of this section is thus to show some results in this direction.
Roughly speaking, the analytical solution provided in Appendix A is based on the assumption that agents have met sufficiently many times to discuss any of the \(D\) topics of their knowledge vector; indeed, if a topics has never been considered, then the group doesn’t have any knowledge about it.
By definition, we assume that all agents do attend a team meeting, hence a first bound on the previous condition can be mathematically formulated by solving follows problem: Which is the probability, \(P_{N,M}\), that drawing \(M\) numbers, with reinsertion, from the set \(\{1,\dots,N\}\) will return each number at least one time? Requiring a bound for such probability to being larger than a given threshold, say \(1-\varepsilon\), will determine the number of meetings, i.e., \(M\), once we have fixed \(N\). Mathematically one can prove that
| $$P_{N,M}=1-\sum_{l=1}^N(-1)^l \binom{N}{l}\left(1-\frac{l}{N}\right)^M\,,$$ |
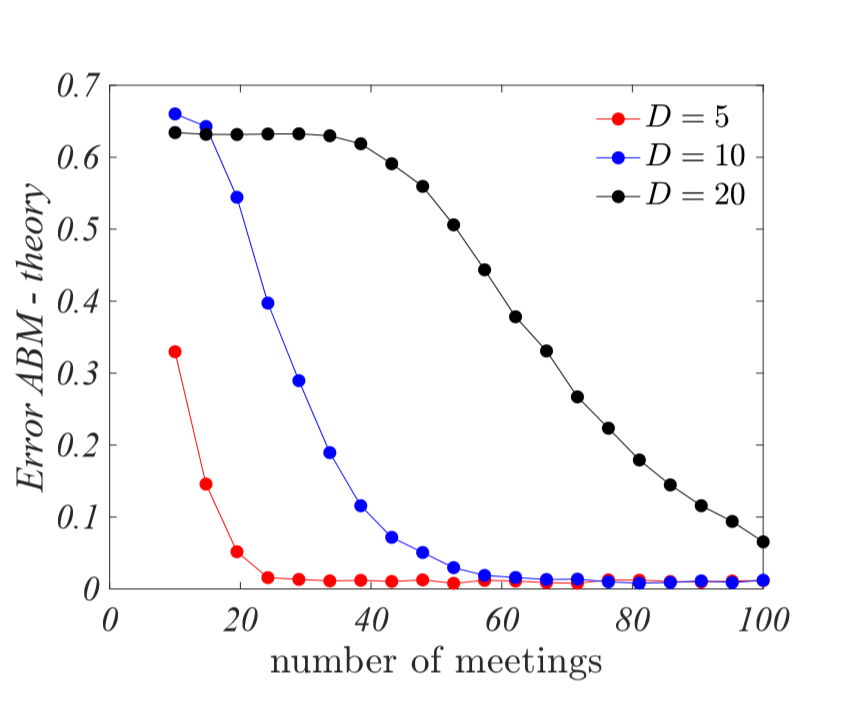
So one can determine \(M\) such that \(P_{N,M}\geq 1-\epsilon\), obtaining thus a bound on the number of meetings needed to get an agreement between the analytical results and the ABM. In Figure 8 we show the error, computed using the \(2\)-norm, between the ABM and the analytical results as a function of the number of meetings once all the agents attend the exchange phase for different lengths of the knowledge vectors, whose entries are distributed according to a tent distribution with parameter \(\beta=1/3\). As expected, for a given size of the error, the larger \(D\) the larger is the number of meetings needed.
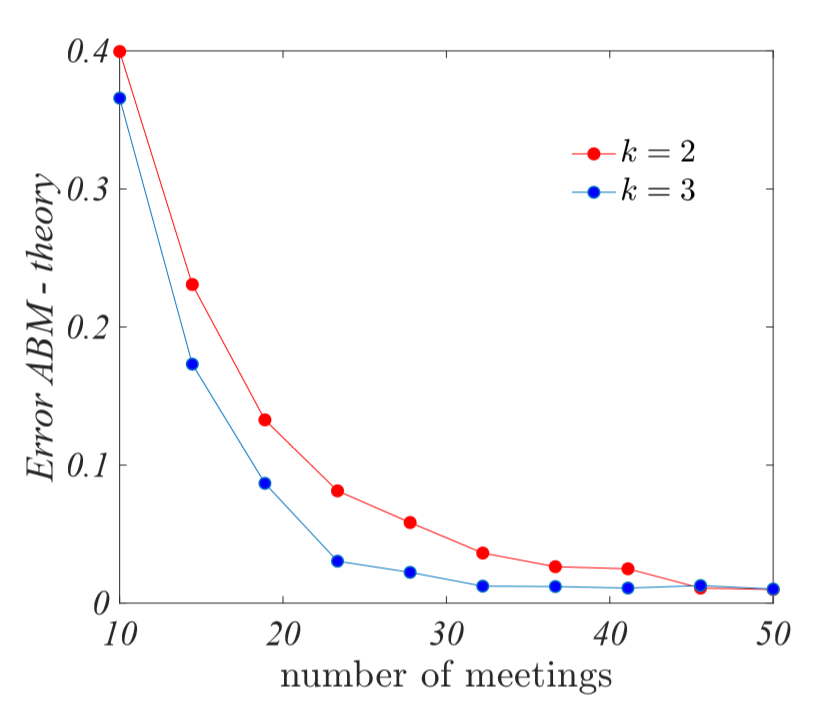
Another quantity that affect the agreement between the ABM and the analytical solution is the number of agents that participate to the groups meeting; indeed if a number \(k\), strictly smaller than \(N\), of agents do attend, it can happen that agents with large entries of their knowledge vector will not share their views and thus the group will not reach the best level. Again, to circumvent this issue one has to let the agents to meet sufficiently many times. In Figure 9 we report the error, computed using the \(2\)-norm, between the ABM and the analytical results as a function of the number of meetings once \(k We hereby assume that agent knowledge is uniformly distributed in \([0,1]\), namely \(p(x)=1\), hence the general formula for the Collective Intelligence given by Equation 5 (main text) rewrites as In Figure 10, we report results of some numerical implementations of the ABM together with the analytical pre- diction. First, it is worth noting the very good description provided by the analytical model. One can also observe that for small \(\tau\), namely once the task are simple, then both the group and the average agent perform well, and thus the collective intelligence is small, the added value of the group is negligible with respect to the average agent. Once \(\tau\) increases, the agent starts to do poorly while the group maintains its high level of success, determining a large value for the collective intelligence. Once \(\tau\) gets even larger, also the groups rate deteriorates and the collective intelligence drop again to \(0\). Increasing the dimension space \(D\) makes the emergence of the collective intelligence even sharper; for \(\tau\sim 0.2\) the average agent performs quite well in a \(5\)-dimensional space (left panel), indeed the collective intelligence is about \(0.6\), while if the dimension doubles (middle panel), then the agent behaviour worsen and the collective intelligence goes beyond \(0.8\). Let us conclude that beside such difference the behaviour of \(CI\) versus task difficulty is similar in the case of uniformly distributed knowledge vectors or with a preferred value, e.g. the tent distribution. This motivates our claim that the model we built is quite robust with respect to the fine details of the used distributions. ANDERSON, P. W. (2011). More and Different: Notes from a Thoughtful Curmudgeon. Singapore: World Scientific.
BARLOW, J. B. & Dennis, A. R. (2016). Not as smart as we think: A study of collective intelligence in virtual groups. Journal of Management Information Systems, 33(3), 684–712. [doi:10.1080/07421222.2016.1243944]
BATES, T. C. & Gupta, S. (2017). Smart groups of smart people: Evidence for IQ as the origin of collective intelligence in the performance of human groups. Intelligence, 60, 46–56. [doi:10.1016/j.intell.2016.11.004]
BATES, T. C. & Shieles, A. (2003). Crystallized intelligence as a product of speed and drive for experience: The relationship of inspection time and openness to G and GC. Intelligence, 31(3), 275–287. [doi:10.1016/s0160-2896(02)00176-9]
BAUMEISTER, R. F., Ainsworth, S. E. & Vohs, K. D. (2016). Are groups more or less than the sum of their members? The moderating role of individual identification. Behavioral and Brain Science, 39, 1–56. [doi:10.1017/s0140525x15000618]
BEIER, M. E. & Ackerman, P. L. (2005). Age, ability, and the role of prior knowledge on the acquisition of new domain knowledge: promising results in a real-world learning environment. Psychology and Aging, 20(2), 341. [doi:10.1037/0882-7974.20.2.341]
CAPRARO, V. & Cococcioni, G. (2016). Rethinking spontaneous giving: Extreme time pressure and ego-depletion favor self-regarding reactions. Scientific Reports, 6, 27219. [doi:10.1038/srep27219]
CATTELL, R. B. (1943). The measurement of adult intelligence. Psychological Bulletin, 40(3), 153.
COOPER, S., Khatib, F., Treuille, A., Barbero, J., Lee, J., Beenen, M., ... & Popović, Z. (2010). Predicting protein structures with a multiplayer online game. Nature, 466(7307), 756-760. [doi:10.1038/nature09304]
CREDÉ, M. & Howardson, G. (2017). The structure of group task performance - A second look at “collective intelligence”: Comment on Woolley et al. (2010). Journal of Applied Psychology, 102(10), 1483-1492. [doi:10.1037/apl0000176]
ENGEL, D., Woolley, A. W., Aggarwal, I., Chabris, C. F., Takahashi, M., Nemoto, K., ... & Malone, T. W. (2015, April). Collective intelligence in computer-mediated collaboration emerges in different contexts and cultures. In Proceedings of the 33rd annual ACM conference on human factors in computing systems (pp. 3769-3778). [doi:10.1145/2702123.2702259]
ENGEL, D., Woolley, A. W., Jing, L. X., Chabris, C. F. & Malone, T. W. (2014). Reading the mind in the eyes or reading between the lines? Theory of mind predicts collective intelligence equally well online and face-to-face. PLoS ONE, 9(12). [doi:10.1371/journal.pone.0115212]
FORSYTH, D. R. (2018). Group Dynamics. Boston, MA: Cengage Learning.
GARDNER, H. (2011). Frames of Mind: The Theory of Multiple Intelligences. London, UK: Hachette.
GOWERS, T. (2009). The polymath blog: https://polymathprojects.org.
GOWERS, T., & Nielsen, M. (2009). Massively collaborative mathematics. Nature, 461(7266), 879-881. [doi:10.1038/461879a]
GRAF, V., GIMPEL, H. & BARLOW, J. B. (2019). Clarifying the Structure of Collective Intelligence in Teams: A Meta-Analysis. Proceedings of the Collective Intelligence, Pittsburgh, PA, USA, 12-14.
GUAZZINI, A., Stefanelli, F., Imbimbo, E., Vilone, D., Bagnoli, F. & Levnajić, Z. (2019). Humans best judge how much to cooperate when facing hard problems in large groups. Scientific reports, 9(1), 5497. [doi:10.1038/s41598-019-41773-2]
GUAZZINI, A., Vilone, D., Donati, C., Nardi, A. & Levnajić, Z. (2015). Modeling crowdsourcing as collective problem solving. Scientific Reports, 5(1), 1-11. [doi:10.1038/srep16557]
HEYLIGHEN, F. (1999). Collective intelligence and its implementation on the web: Algorithms to develop a collective mental map. Computational & Mathematical Organization Theory, 5(3), 253–280.
HORN, J. & Masunaga, H. (2006). A Merging Theory of Expertise and Intelligence. In K. A. Ericsson, N. Charness, P. J. Feltovich, & R. R. Hoffman (Eds.), The Cambridge Handbook of Expertise and Expert Performance.Cambridge, MA: Cambridge University Press, pp. 587–611. [doi:10.1017/cbo9780511816796.034]
HOROWITZ, S., Koepnick, B., Martin, R., Tymieniecki, A., Winburn, A. A., Cooper, S., ... & Jain, N. (2016). Determining crystal structures through crowdsourcing and coursework. Nature Communications, 7(1), 1-11. [doi:10.1038/ncomms12549]
KURVERS, R. H., Herzog, S. M., Hertwig, R., Krause, J., Carney, P. A., Bogart, A., ... & Wolf, M. (2016). Boosting medical diagnostics by pooling independent judgments. Proceedings of the National Academy of Sciences, 113(31), 8777-8782. [doi:10.1073/pnas.1601827113]
LAM, S. S. (1997). The effects of group decision support systems and task structures on group communication and decision quality. Journal of Management Information Systems, 13(4), 193–215. [doi:10.1080/07421222.1997.11518148]
LEE, J., Kladwang, W., Lee, M., Cantu, D., Azizyan, M., Kim, H., ... & Das, R. (2014). RNA design rules from a massive open laboratory. Proceedings of the National Academy of Sciences, 111(6), 2122-2127. [doi:10.1073/pnas.1313039111]
MATLAB (2019). 9.7.0.1247435 (R2019b). The MathWorks Inc: https://nl.mathworks.com.
MEUDELL, P. R., Hitch, G. J. & Boyle, M. (1995). Collaboration in recall: Do pairs of people cross-cue each other to produce new memories? The Quarterly Journal of Experimental Psychology, 48(1), 141–152. [doi:10.1080/14640749508401381]
MOORE, C. & Tenbrunsel, A. E. (2014). “Just think about it?” Cognitive complexity and moral choice. Organizational Behavior and Human Decision Processes, 123(2), 138–149. [doi:10.1016/j.obhdp.2013.10.006]
NICOLIS, G. & Nicolis, C. (2012). Foundations of Complex Systems: Emergence, Information and Prediction. World Scientific Publishing Company. [doi:10.1142/8260]
SMITH, J. B. (1994). Collective Intelligence in Computer-Based Collaboration. London, UK: CRC Press.
SØRENSEN, J. J. W., Pedersen, M. K., Munch, M., Haikka, P., Jensen, J. H., Planke, T., ... & Sherson, J. F. (2016). Exploring the quantum speed limit with computer games. Nature, 532(7598), 210-213. [doi:10.1038/nature17620]
SPEARMAN, C. (1904). “General intelligence” objectively determined and measured. The American Journal of Psychology, 15(2), 201–292. [doi:10.2307/1412107]
STANKOV, L. (2003). Complexity in Human Intelligence. American Psychological Association.
SZUBA, T. (2001). A formal definition of the phenomenon of collective intelligence and its IQ measure. Future Generation Computer Systems, 17(4), 489–500. [doi:10.1016/s0167-739x(99)00136-3]
WILDMAN, J. L., Thayer, A. L., Rosen, M. A., Salas, E., Mathieu, J. E. & Rayne, S. R. (2012). Task types and team-level attributes: Synthesis of team classification literature. Human Resource Development Review, 11(1), 97–129. [doi:10.1177/1534484311417561]
WOOLLEY, A. W., Aggarwal, I. & Malone, T. W. (2015). Collective intelligence and group performance. Current Directions in Psychological Science, 24(6), 420–424. [doi:10.1177/0963721415599543]
WOOLLEY, A. W., Chabris, C. F., Pentland, A., Hashmi, N., & Malone, T. W. (2010). Evidence for a collective intelligence factor in the performance of human groups. Science, 330(6004), 686-688. [doi:10.1126/science.1193147]
C: Uniformly distributed knowledge vectors
$$CI^{(u)}_N(\tau,D)=\left[1-\tau^N\right]^D-\left[1-\tau\right]^D\,.$$
(10) 

References
