Introduction
The study of opinion dynamics is a well-established topic in socio-physics (Castellano et al. 2009), which has continued to attract the attention of scholars for more than two decades. A vibrant research community of physicists and social scientists has shown increasing interest in describing opinion spreading, as a potential determinant of norm formation and behavioral change, by modelling the interactions of virtual agents in social networks. Various models and corresponding simulations have been proposed to explain how consensus or diversity is reached for a group of interacting agents with different opinions (Vazquez et al. 2003; Svenkeson & Swami 2015). Among these models, the voter model serves as one of the simplest, most elegant, and most well-known example of completely-solved opinion dynamics (Sood & Redner 2005). It assumes that an agent would adopt "the opinion of a randomly chosen neighbor" (Krapivsky & Redner 2003). Based on this minimal assumption, the voter model describes the formation of global consensus (Krapivsky et al. 2010) and also produces fruitful non-trivial behaviors when extended or modified (Mobilia 2003; Vazquez et al. 2003; Lambiotte & Redner 2007; Wang et al. 2014), or applied to various network forms (Castellano et al. 2003; Suchecki et al. 2005). Besides the voter model, other notable models of opinion dynamics, just to name a few, includes the Sznajd model (Sznajd-Weron 2005), social influence model (Flache et al. 2017) and contagion model (Valente 1996; Pacheco 2012). Each of them has captured important aspects of opinion dynamics.
Regardless of the differences among these models, they predominantly assume that agents have the ability to directly observe the opinions of other agents, and then update their own opinions according to the observation. This notion of “learning opinions by observing opinions” is based on the implicit assumption that opinions are directly observable; or alternatively, that, when agents interact, they ask for each other’s opinion, and express it to each other –truthfully– when asked for. However, in most situations, and particularly so for sensitive topics, such assumptions seem to be unrealistic: what we can learn from everyday life is that opinions are usually unobservable, and talking about opinions is not the most common way for people to exchange them. Although the term "opinion" may be used in a generic way to represent the property (e.g. attitude, belief, evaluation) affected by others (Flache et al. 2017), there is no question about the latency of opinions. Instead of learning opinions directly, we usually infer other people’s opinions by interpreting their actions. Actions can be, for in-stance, choosing between cycling and driving for one’s daily commute. These actions are observable, but the opinions that induce them are not. However, the relation between opinions and actions helps us learn the unobservable opinions by interpreting observable actions. For example, an observer might interpret someone’s choice to cycle to work as evidence of an environmentally-conscious mindset. The action-opinion relation, however, is not always clear: sometimes the observer is confused about which opinion in fact governs the observed action. For instance, the cyclist could simply be highly cost-sensitive, or care about health a lot, while not caring about the environment at all. Likewise, believers in one opinion can take various actions: both cycling and driving an electric car are reasonable options for an environmentalist (Moons & De Pelsmacke 2012). The possible multiplicity in the relations between opinions and actions has not been captured by previous models yet.
In social psychology, the relation between opinions and actions has been extensively studied with a different term called attitude-behaviour consistency/ inconsistency, where attitudes resemble opinions, and behaviors resemble actions in this paper. Intuitively, early studies assumed that "attitudes predict overt behaviors" (Zanna et al. 1980), but this notion has been challenged by psychologists who found that the attitude-behavior relationship is considerably weak (Wicker 1969), and may be influenced by other factors (Liska 1984). It is called the problem of attitude-behavior inconsistency. One of the most influential and successful models that aims to explain the problem should be the Fishbein-Ajzen model (Fishbein & Ajzen 1975). The model proposes that behavior is directly driven by behavioral intention, and intention depends on both attitudes and subjective norms (Liska 1984), providing a conceptualized framework to analyze multiplicity in attitude-behavior relations, which might shed light on opinion-action relations that will be used in our paper.
In this paper, we propose a simple alternative model of opinion-learning to simulate opinion dynamics in an artificial society. The central assumption embedded in this so-called action-opinion inference (AOI) model is the notion of “learning opinions by observing actions”, which means that the agent attempts to learn the opinions of others by observing and interpreting their actions. Crucially, our model assumes that actions are noisy signals of underlying opinions, which follows from the above-discussed multiplicity. Agents try to infer opinions from actions in a Bayesian way, acknowledging the uncertainty inherent to the opinion-action relation. More specifically, acknowledging the multiplicity of action-opinion relations, our model is able to describe the situation where an action is permitted by more than one opinion, and one opinion could result in various actions. Therefore observing an action will in most cases only allow the observer to partially update her beliefs about the other agent’s underlying (latent) opinions. The model postulates that agents update their opinions and actions by a three-stage mechanism: the agent first uses Bayes’ rule to update her beliefs regarding her neighbors’ opinions, based on their actions which she observes. The inference of opinions from observed actions is determined by an action-opinion matrix, which defines, for each action and each opinion, if the action is either prohibited, permitted, or obliged by that particular opinion. In the second stage, the agent chooses her new opinion for the next time step according to the relative probability of each opinion in the neighborhood, calculated from the inferences of different opinions. In stage three she updates her action according to the new opinion she selected just now. Having performed an extensive literature review, we only found one model whose conceptualization of latent opinions and observable actions relates to our work in physics. This so-called CODA model (Martins 2008) and its relation to our work will be described in Section 3.8.
We compare the AOI model systematically with the voter model, which we will prove can be formulated as a reduced form of the AOI model. More specifically, the AOI model is equivalent to the voter model when each action is only obliged by one opinion, and each opinion only obliges one action (when there is no uncertainty as to which opinion causes which action). The model setup offers an opportunity for us to explore different action-opinion relations, which have rarely been studied before. In the paper we employ cellular automata (CA) to simulate the model with different action-opinion relations and analyze the simulation results both numerically and spatially, focusing on the density of each opinion in the final stable state, as well as the clustering features of the dynamic process. The key question we investigate in this paper is as follows: "what action-opinion relations induce consensus or diversity?" In other words, we would envisage the role of the action-opinion relations in the formation of macroscopic features of the society. This question is closely related to the well-known Axelrod’s question, which asks why consensus is not always reached given that agents learn opinions from others (Axelrod 1997). In this sense, the AOI model provides an alternative approach to answer Axelrod’s question besides the conventional models mentioned before.
The rest of the paper is organized as follows: Section 2 Public & Private Characteristics: A Brief Review, as the name indicated, briefly reviews the relevant works on public and private characteristics, a similar concept to our notion of learn opinions by observing actions. Section 3 Model Setup presents the Action-opinion inference model in detail. Section 4 Two-action Situation and Section 5 Three-action Situation illustrate the simulation results of the model with two and three actions respectively. Additionally, a brief mathematical analysis is given in Section 4 for the system with two opinions and two actions only. The mathematical analysis provides the first step towards validation of the simulation results, and helps us better understand the dynamic process. Section 6 Conclusion and Discussion summarizes the major findings and discusses some critical issues concerning the AOI model and other complex system models. Furthermore, we discuss several avenues for further research.
Public & Private Characteristics: A Brief Review
Although the notion of learning opinions by observing actions was not frequently acknowledged in previous literature, a similar pair of concepts – private and public characteristics – has been employed in previous opinion dynamics studies to capture the discrepancy in the learning process. Here, the term "characteristics" may refer to opinions, attitudes, actions, or any property of an agent that is open to the influences from others. "Public characteristic" represents the observable characteristic publicly expressed by an agent. Conversely, a private characteristics is defined as an agent’s privately held characteristic. Therefore, a public characteristic can be observed directly but is not necessarily the same as the agent’s private characteristic. An early example comes from information cascade. Information cascade, which is defined as the situation when agents simply follow the actions of the others sequentially without considering their own private information (Bikhchandani et al. 1992), is a powerful tool to explain localized conformity and its systematical fragility (Bikhchandani et al. 1992; Wu & Huberman 2006). Both information cascade and the AOI model have roots in the same idea that the public characteristic obtained from a neighbor may not be the same as the neighbor’s private characteristic, and the agent takes actions by making inference from that possibly inaccurate public characteristic. In our notation, an action serves as the public characteristic, and the opinions beneath is the true but private characteristic. The discrepancy between public and private characteristic in information cascade originates from the fact that agents simply ignore their own private characteristic (i.e. opinions) when taking actions, but in the AOI model, it is because of the unobservable relations between actions (public characteristic) and opinions (private characteristic). Therefore the two notions have different underlying principles.
A more recent representative of public and private characteristic is the persuasion model (Mäs et al. 2013; Mäs & Flache 2013; Mäs & Bischofberger 2015) based on psychological theories (e.g. Fishbein 1963; Petty et al. 1981). Different from traditional opinion dynamics models, the persuasion model assumes that opinions are formed based on arguments, and agents only exchange arguments, so opinions are not directly influenced by others (Mäs & Bischofberger 2015). One may realize that the underpinning of our AOI model is inherently close to this assumption in the persuasion model. In both models, opinions (i.e. the private characteristic) play no role in the communication (not necessarily verbal) directly, while some other public characteristics, which refer to actions in the AOI model and arguments in the persuasion model, serve as the messenger between agents. In the persuasion model agents learn arguments from others, and form new opinions based on the arguments; Meanwhile, in the AOI model agents observe actions of others, and update their opinions according to the interpretation of the observations. The primal difference of the two models lies in the relations between private characteristic (i.e. opinions) and public characteristic (i.e. action or argument): in the persuasion model, opinion is a function of some relevant arguments, and thus arguments can affect opinions, but not vice versa. In other words, an agent’s opinions are only affected by another agent’s arguments. On the contrary, the opinion in the AOI model, together with the action-opinion matrix, determines the action; and only another agent’s actions, via the inference process, can affect the agent’s opinion. That is, actions are a function of opinions. This structural disparity distinguishes the two models at a microscopic level, and thus will lead to distinct outcomes at a macroscopic level (see further below). It is noteworthy that in practice, persuasion models usually adopt opinion homophily, that is, each agent selects an agent she wants to interact with based on the similarities of their opinions (Mäs & Flache 2013), so opinions are still observable in such models, playing the role of labels in the partner selection phase. Opinion homophily should be partly responsible for the persuasion model’s ability to explain opinion polarization.
Another famous phenomenon describing disparities between public and private characteristics is pluralistic ignorance, in which most members of a society privately disapprove of, or are undecided about, an opinion but incorrectly believe that most other members accept it (Miller & McFarland 1987; Huang & Wen 2014). Considering themselves as the only dissident, they would express their approval of the opinion that they do not actually support. Pluralistic ignorance results in a global consensus although most members disagree with it, and hence the consensus is so fragile that it could be broken by the so-called minority influence (Huang & Wen 2014). As Seeme and Green explained, the term "opinion" in studies of pluralistic ignorance, rather than in the AOI model, refers to "the expression or behavior of a person towards a topic", instead of one’s "true internal opinion" (Seeme & Green 2016). The "true internal opinion" is called "attitude" by Seeme and Green (2016) to avoid confusion. According to this claim, we find that the AOI model and the pluralistic ignorance studies both describe the discrepancy of the observable "public characteristic", which is actions in the AOI model and publicly expressed opinions in pluralistic ignorance, and the "private characteristic", which refers to the (underlying) opinions in the AOI model and (private) attitudes in pluralistic ignorance. The critical difference between these studies is obvious: the dynamics of public characteristics (actions) in the AOI model is driven by the dynamics of private characteristic (opinions). As stated in 2.2, public characteristics (actions) are not directly influenced. However, in pluralistic ignorance models, public characteristics are directly affected by the "the pressure to conform" (Seeme & Green 2016) or "normative social influence" (Huang & Wen 2014), and private characteristics (attitudes) are later updated according to either "self-perception theory", "cognitive dissonance" (Seeme & Green 2016), or other psychological theories.
Table 1 summarizes the three models involving discrepancies between public and private characteristics as well as the AOI model itself. One of the relevant references for each model is listed inside the parentheses below.
| Model | PC | PrC | Dynamics of PC | Dynamics of PrC |
| AOI | Action | Opinion | Driven by PrC | Observe-Infer |
| (this paper) | ||||
| Information Cascade | Action | Opinion | Observe-Infer | Ignored by agents |
| (Bikhchandani et al. 1992) | ||||
| Persuasion Model | Argument | Opinion | Exchange | Driven by PC |
| (Mäs & Bischofberger 2015) | ||||
| Pluralistic Ignorance | Opinion | Attitude | Pressure to conform | Psychological theories |
| (Seeme & Green 2016) |
The table shows the similarities as well as differences between some notable earlier work and the AOI model. In all, although previous researches have noticed the existence of public and private characteristics and described them in various models, these models do not capture the inference process that enables agents to learn the private characteristics of others by observing public characteristics. The absence of an inference process leads to the omission of uncertainty: in these three models, the relations between public and private characteristics are either deterministic (persuasion model & pluralistic ignorance) or unspecified (information cascade). In contrast, the AOI model creates a smokescreen between public characteristics (actions) and private characteristics (opinions), which represents the multiplicity of the action-opinion relations. This type of uncertainties, although rarely acknowledged in opinion dynamics papers, could lead to misunderstanding or obfuscation, and the role of the uncertainties in opinion dynamics will be one of the central problems we investigate in the rest of the paper.
Model Setup
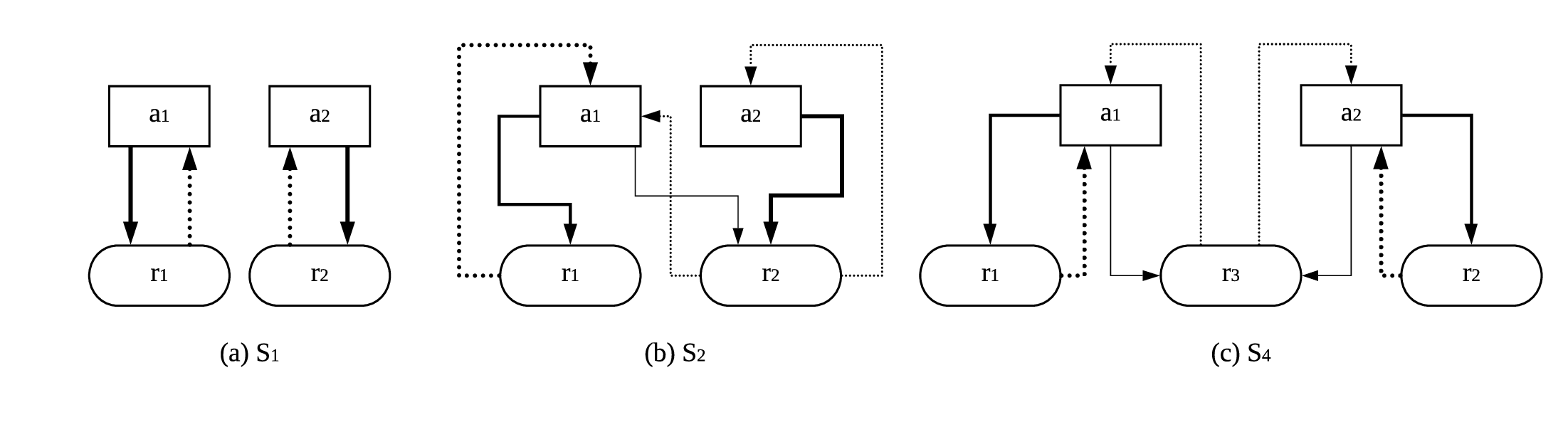
We consider a population of \(N\) agents on an \(L\times L\) regular lattice with periodic boundary conditions as well as a Von Neumann neighborhood. Each cell of the lattice is occupied by an agent, and we set \(L^2=N\) to avoid empty cells. Agent \(i\) (\(i=1,2,...,N\)) chooses one action \(a^{(i)}\) from the action set \(A=\{a_1,...,a_g,...,a_G\}\) based on her opinion, described by a rule \(r^{(i)}\) selected from the rule set \(R=\{r_1,...,r_k,...,r_K\}\). Note that, in terms of terminology, we choose to use the term “opinion” in colloquial discussions, and we use the term “rule” in the context of the mathematical model and simulations. The evaluation of action \(a_g\) by rule \(r_k\) is denoted by \(s_{kg}\). In case that \(r_k\) is an exclusive rule, \(s_{kg}\in \{+,-\}\) \(a_g\) is either obliged (\(+\)) or prohibited (\(-\)) by \(r_k\); however, if \(r_k\) is an inclusive rule, then \(s_{kg}\in \{0,-\}\), where \(0\) implies that the action is permitted but not obliged by the rule. An exclusive rule can only oblige one action, but an inclusive rule always permits more than one action. All \(s_{kg}\) (\(g=1,...G\); \(k=1,...,K\)) constitute a \(K\times G\) matrix \(S\), called the action-opinion matrix, summarizing the action-opinion relations in the system.
The behaviors of the agents are described as follows: if an agent follows an exclusive rule \(r_k\), then she will certainly take the action obliged by the rule, that is, \(P(a_g|r_k)=1\) if \(s_{kg}=+\). Otherwise \(P(a_g|r_k)=0\). If she believes in an inclusive rule \(r_k\), then \(P(a_g|r_k)=1/W\) if \(s_{kg}=0\), where \(W\) is the number of actions permitted by \(r_k\); \(P(a_g|r_k)=0\) if \(a_g\) is prohibited (i.e. \(s_{kg}=-\)). Besides, the agent can observe the actions of her Von Neumann neighbors but cannot observe their opinions (in the form of rules) directly. In addition, each agent has full knowledge of \(A\), \(R\), \(S\), and she assumes that other agents choose actions and update rules in the same way as she does so herself.
Proceeding on the preliminary setup, the action-opinion inference process takes the following steps. Initially, each agent (say agent \(i\)) is randomly assigned a rule \(r^{(i)}\in R\), then chooses the action based on the assigned rule. At each time unit \(\tau\), an agent (say agent \(i\)) is randomly chosen to update her probabilistic inference about which rule is adopted by her neighbor \(j\) (\(j\in M_i\), \(M_i\) is the von Neumann neighbors of agent \(i\)) based on the observation of \(j\)’s action \(a^{(j)}(\tau)\). Specifically, agent \(i\)’s inference that neighbor \(j\) adopts \(r_k\) after observing \(a^{(j)}(\tau)\) takes the form:
| $$P^{(i)}(r^{(j)}(\tau)=r_k|a^{(j)}(\tau))=\frac{P(a^{(j)}(\tau)|r_k)}{\sum_{k=1}^{K}[P(a^{(j)}(\tau)|r_k)]}$$ | (1) |
Equation 1 is derived from the Bayes’ rule by setting equal prior probabilistic beliefs \(P(r_k)\) for all \(k\), that is, \(P(r_k)=1/K\), \(\forall k\). The intuition behind this is that the agent a priori assumes that each rule is equally likely to be taken by her neighbor \(j\). This assumption is reasonable in light of the fact that in each time unit only one agent is selected to observe the neighborhood and then update rules and actions, so it is highly likely that she did not observe her neighbor’s action in a recent time unit.
By updating her probabilistic inference of all neighbors’ rules, agent \(i\) learns the local opinion distributions, based on which she will update her own opinion (i.e. rule). To do so, agent \(i\) evaluates the accumulative probability of each rule across the neighborhood:
| $$\hat{P}^{(i)}(r_k, \tau)=\sum_{j\in M_i}P^{(i)}(r^{(j)}(\tau)=r_k|a^{(j)}(\tau))$$ | (2) |
After the rule-updating process, the world moves to the next time unit \(\tau+1\). Because in each time unit only one agent updates, it is inefficient to study the dynamics between time units. Instead, we denote \(N\) consecutive time units as one time step \(t\) so that each agent has been selected once during one time step on average. This is a common practice adopted by many opinion dynamics models (Suchecki et al. 2005). We will present the dynamics of key variables in the scale of time step in the rest of the paper.
The voter model is chosen as the benchmark for the AOI model not only because of its long-standing popularity in the discipline of opinion dynamics for explaining the emergence of consensus (Sood & Redner 2005; Barrat et al. 2008; Krapivsky et al. 2010), but also due to the fact that the AOI model is built upon the framework of the voter model: despite the AOI model’s learning process, the basic dynamics of the two models are the same, thus using the voter model as a benchmark helps derive implications regarding the effect of the inference. Moreover, variations of the voter model have been applied to a wide range of social phenomena besides opinion dynamics, which provides examples for the AOI model to be modified for other disciplines. The reason why we use the voter model as the basis of the AOI model is also related to its simplicity. As argued by many, the voter model is the simplest and minimal model for the study of opinion dynamics, so its basic framework helps maintain the simplicity and comprehensibility of the new model. For example, if the social influence model were chosen as the basis, we might have trouble deciding which type of social influence we would like to use – positive, negative, assimilative, or similarity biased. Combining the action-opinion inference with various social influence models is a promising line of further research, but for the first work on the AOI model, it is better to avoid unnecessary subtleties arising from model setup and focus on the role of action-opinion inference process in governing dynamics.
The voter model is an example of discrete opinion models, where opinion is represented by a discrete variable. Therefore in the AOI model, rules and actions are also discrete. Besides discrete opinion models (e.g. voter model, majority rule model (Galam 2002), Sznajd model (Sznajd-Weron 2005), many sociological models describe variables of interest in a discrete way, including Latané’s social impact theory (Latané 1981) and Axelrod’s model of cultural dissemination (Axelrod 1997). Continuous opinion models have taken an alternative approach, where opinions can vary between extreme values smoothly (Castellano et al. 2009). Deffuant model (Deffuant et al. 2000), Hegselmann-Krause model (Hegselmann & Krause 2002) and social influence models (Flache et al. 2017) are famous examples of continuous opinion models. A model, mentioned in the introduction, which shares with our model its distinction between latent opinions and observable actions, is the so-called CODA model (Martins 2008). That model differs from ours in the following fundamental ways: the CODA model postulates that opinions refer to a ground (or: universal) truth, which agents attempt to uncover by learning from each others’ actions in a Bayesian fashion. In contrast, the AOI model is not concerned with learning truths, but inferring the latent beliefs of neighbours, induced by a wish to conform with those neighbours in terms of their latent beliefs. This is why the AOI model postulates that opinions and actions are discrete and multinomial, as opposed to the CODA model whose actions are discrete and binary, and whose opinions are statements in the form of a continuous probability function about something being true or not. For this same reason, the AOI model distinguishes between an inference step in which agents try to infer (learn) each others’ opinions, and an update step in which agents update (adjust) their own opinion as a probabilistic function of neighbours’ opinions. This distinction is absent in the CODA model, which is logical given that it is concerned only with learning about truths. Conceptually, the CODA model is related to literature about truth-seeking agents (Prelec 2004), whereas the AOI model is focused on opinion-conformity among agents with diverse latent opinions. An important distinction between the models in terms of what macro-level phenomena they tend to predict, is that the CODA model tends to generate extremism, whereas the AOI model, depending on the structure imposed on action-opinion relations may generate either consensus, coexistence of various opinions, or extremism. This difference in predicted outcomes is rooted in the fact that whereas the CODA model features one relation between binary actions and an underlying opinion, whereas the AOI model features a broader set of relations between various actions and various opinions which may either be exclusive or inclusive (see Section 3.1).
Two-action Situation
For simplicity, we first focus on the two-action AOI model (i.e. \(G = 2\)). Given a two-action set \(\{a_1, a_2\}\) there are in total 4 possible action-opinion matrices \(S_1\) to \(S_4\) for \(K\leq 3\), if one does not allow for duplication.
| $$S_1= \left( \matrix{~ & a_1 & a_2 \cr r_1 & + & - \cr r_2 & - & +\cr} \right) \hspace{1cm} S_2= \left(\matrix{~ & a_1 & a_2 \cr r_1 & + & - \cr r_2 & 0 & 0 \cr} \right) \hspace{1cm} S_3= \left(\matrix{~ & a_1 & a_2 \cr r_1 & - & +\cr r_2 & 0 & 0 \cr} \right) \hspace{1cm} S_4= \left(\matrix{~ & a_1 & a_2 \cr r_1 & + & -\cr r_2 & - & + \cr r_3 & 0 & 0 \cr} \right)$$ |
AOI model with \(S_1\) and the voter model
When taking \(S_1\) as the action-opinion matrix for the system, the AOI model reduces to a two-state voter model, a naive spin model where agents observe and learn opinions directly. This serves as a simple but representative example of studies in opinion dynamics and consensus formation (Krapivsky et al. 2010). In the voter model, a randomly chosen agent adopts the opinion of a neighbor who is also chosen at random (Dornic et al. 2001). The voter model can therefore be interpreted as a special case of the AOI model, the two models being equivalent when in the AOI model, each action is only obliged by one rule, and each rule only obliges one action (i.e. \(S_1\)). Unsurprising, the AOI model with \(S_1\) shows all the features of a two-state voter model (Figure 1). Starting with a random initial configuration, the population eventually converges to an absorbing state of consensus where everyone takes the same opinion (and action). Also, the emergence of opinion clustering and coarsening shown in Figure 1 is a typical pattern of the voter model (Krapivsky et al. 2010).
Simulations of AOI models with \(S_4\) and \(S_2\)
An inclusive rule (\(r_2\) in \(S_2\) and \(r_3\) in \(S_4\)) that permits both actions is introduced in \(S_2\) and \(S_4\). \(S_4\) constitutes a typical case in politics where both supporters of a party (believe in \(r_1\) or \(r_2\)) and indifferent voters (believe in \(r_3\)) exist. See Sections 6.1 and 6.2 for a discussion of how these indifferent voters can be seen as centrists. A striking observation from the simulation of the system with \(S_2\) (Figure 2) is that the two key features of the voter model (i.e. the AOI model with \(S_1\)), clustering and consensus, are no longer valid when an inclusive rule is introduced (i.e. using \(S_4\)). Figure 3 shows the interface densities of rules or actions for both \(S_1\) (voter model) and \(S_4\). Interface density, sometimes called density of domain walls, is defined by the fraction of neighboring agents with different rules or actions (Krapivsky et al. 2010), therefore a lower interface density indicates a higher level of clustering. We find that the inclusive rule r3 significantly reduces the clustering of opinions (or actions) compared to the voter model. Meanwhile, the population reaches a dynamical disordered state, where all three rules coexist and the density of each rule remains relatively stable over time (Figure 2 (a) and (c)). Please be aware that the y-axis scales of (a) and (b) in Figure 2 are different, and other figures in the rest of the paper may show different sections of the scale.
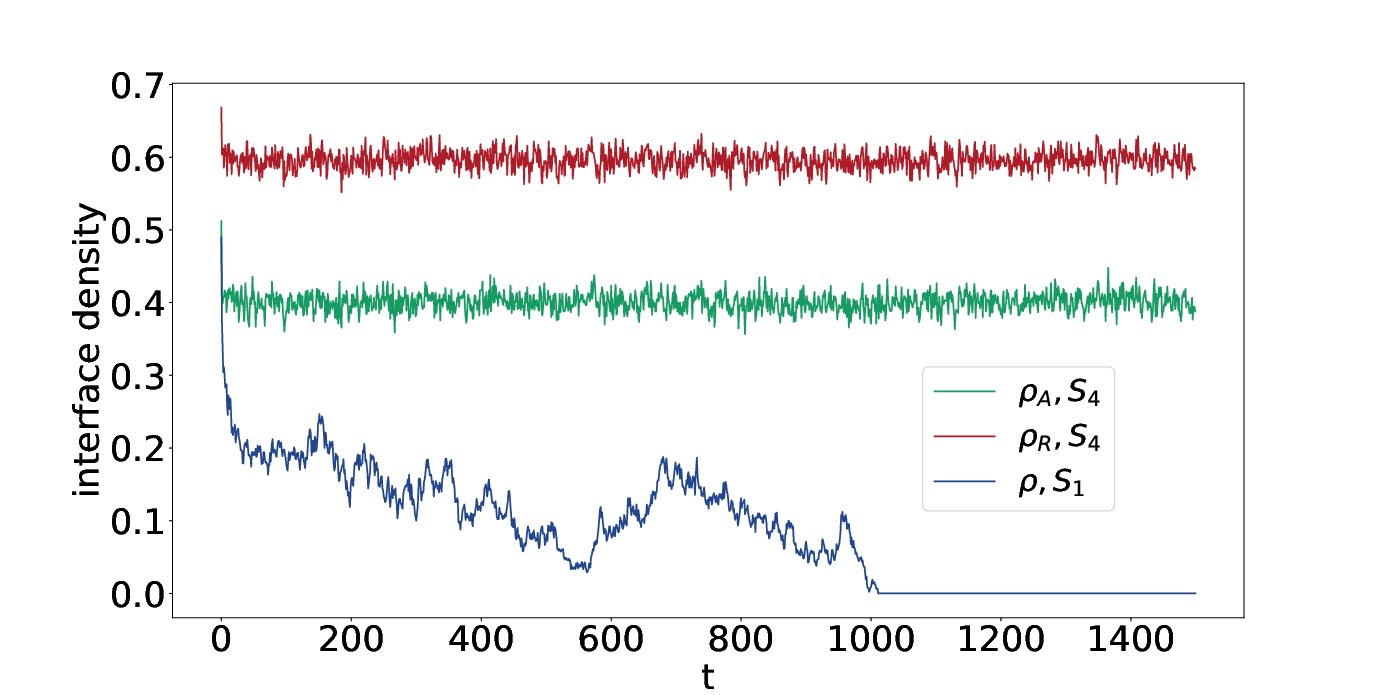
Holley and Liggett (1975) have proved that coexistence of opinions is impossible in a two-dimensional voter model, and many efforts have been made to modify the model in order to reach a mixed state where more than one opinion survives. Such modifications include the threshold voter models (Liggett 1994) where the agent adopts the opposite opinion only when the number of neighbors with opposite opinions is large enough, and the three-state constrained voter model (Vazquez et al. 2003), where the leftists and rights only interact with the centrists. Additionally, if the voter model is run on a small-world network (Watts & Strogatz 1998), the system will be temporarily trapped in a metastable state where different opinions coexist, although it will escape from the metastable state and reaches consensus eventually (Castellano et al. 2003; Castellano et al. 2009). In Figure 2 we have already found that the AOI model, which is an extension of the voter model, can reach the mixed state of opinions by simply introducing an inclusive rule (e.g. \(r_3\) in \(S_4\)) without restricting the interactions of agents (as in the threshold and constrained voter models) or modifying the network structure (as in the small-world network).
The intuition behind the coexistence of opinions in Figure 2, which concerns \(S_4\), is straightforward. For example, if an observer (the focal agent) sees a neighbor acting as \(a_1\), she considers the neighbor believes in \(r_1\) with probability \(P(r_1|a_1)=\frac{1}{1+0.5}=\frac{2}{3}\), and \(r_3\) with a smaller probability \(P(r_3|a_1)=\frac{0.5}{1+0.5}=\frac{1}{3}\) according to \(S_4\). So a neighbor acting as \(a_1\) will increase the observer’s probability of adopting \(r_1\) as well as (albeit less so) \(r_3\). Similarly, an action \(a_2\) of a neighbor will not only increase the observer’s probability of adopting \(r_2\), but also increase her probability of adopting \(r_3\). The underlying opinion dynamics imply that \(r_3\) will never die out. Likewise, an agent employing \(r_3\) will take \(a_1\) and \(a_2\) with equal probabilities, and therefore a reciprocal loop of opinions is constituted (Figure 4 (c)). The loop shows that each action or rule can reach any other action or rule through a finite number of arrows, which implies that all rules and actions are "beneficial" to all the others. This explains the coexistence of different opinions (and actions) in the AOI model with \(S_4\). Contrarily, Figure 4 (a) shows that in \(S_1\), \(r_1\) and \(r_2\) are disconnected, so the ultimate consensus is always reached.
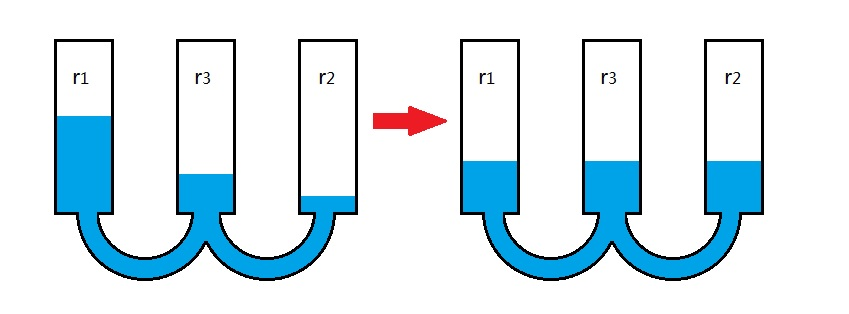
In Figure 2, we imposed an initial configuration with equal densities of the three rules, but this is not the reason why eventually the three rules have almost equal densities. Figure 5 gives four cases of extreme initial configurations, which implies that regardless of the initial densities of the rules, the system will always reach a state where all rules have approximately the same density. On the contrary, the opinion (rule) in the final state of consensus in the voter model is completely determined by the initial configuration. Precisely, the consensus of \(r_1\) occurs with probability \(P_1=p_0\) and the consensus of \(r_2\) occurs with \(P_2=1-p_0\), given that the system was initially composed of a fraction \(p_0\) of agents believes in \(r_1\) and a fraction \(1-p_0\) of agents believes in \(r_2\) (Krapivsky et al. 2010). To summarize, the initial configuration determines the result of the voter model, but has no effect on the result of the AOI model with \(S_4\). The different roles of the initial configurations, obviously, result from the emergence/ absence of the inclusive rule \(r_3\). Comparing Figure 4 (a) with (c), we can see that \(r_3\) plays the role of a bridge connecting the two opposite pairs \((r_1, a_1)\) and \((r_2, a_2)\), and the bridge helps to balance the densities of rules dynamically. Figure 6 illustrates the dynamics in a simple way using the cartoon of a set of communicating vessels.
In Figure 7 we present the simulation result of the AOI model with \(S_2\). \(S_2\) constitutes another interesting case where \(a_1\) is obliged by \(r_1\) and permitted by \(r_1\), while \(a_2\) is only permitted by \(a_2\). Clearly, a1 holds a major advantage over \(a_2\), but as we can see in Figure 7(b), \(a_2\) still survives and holds a small but stable fraction of population with the help of \(r_2\). Again the composition of the stable state has no dependence on the initial configurations (Figure 8). The flowchart corresponding to \(S_2\) can be found in Figure 4 (b).
To summarize, the inclusive rule has three non-trivial effects on opinion dynamics. First, the inclusive rule prohibits the clustering process; second, consensus is never reached if an inclusive rule is present; finally, the composition of the final population is not determined by the initial densities of rules when inclusive rules are present. In other words, the three key features of the voter model, namely clustering, consensus, and the dependence on the initial configurations, disappear due to the introduction of the inclusive rule. Instead, the inclusive rule leads to a non-clustering dynamics of opinions and a diverse final state of opinions that is not related to the initial configuration at all.
Mathematical derivation
Given the various forms of action-opinion relations, obtaining a general analytical solution for the AOI model is very difficult, and therefore we have so far used the cellular automata approach to investigate the evolution of the opinions in the previous subsections. However, it is beneficial to provide analytical results for some simple action-opinion matrices, which would help us better understand the evolution dynamics, especially the feature of (in)dependence of initial configurations in a precise manner. In this subsection, we provide the mathematical analysis for \(S_1\) and \(S_2\), whose simulation results have been displayed in Figure 1 and Figure 7 already. The following derivation generally follows the path that solves the voter model (Krapivsky et al. 2010).
In \(S_1\) or \(S_2\) there are only two rules in total, thus we can define the rules in a binary way: the rule adopted by the agent \(i\), \(r^{(i)}\), can be either \(+1\) (which means \(r^{(i)}=r_1\)) or \(-1\) (which means \(r^{(i)}=r_2\)). We write \(r^{(i)}(\tau)=r^{(i)}\) to keep the notation simple. According to equation (1) and (2), the flip rate that the agent \(i\) changes her rule \(r^{(i)}\) is:
| $$w_i(\textbf{s})=\frac{1}{2}\{1-\frac{r^{(i)}}{4}[\sum_{j\in M_i}P(r^{(j)}=r|a^{(j)})r]\}$$ | (3) |
The master equation is easy to derive, but difficult to solve. Instead, we focus on the average opinion (rule) for each agent, namely \(R(i)\equiv<r^{(i)}>\), where \(<.>\) is the average notation, defined by \(<x>=\sum_{x'}P(x=x')x'\). In a short enough time interval \(\Delta \tau\), the rule of agent \(i\) changes according to:
| $$r^{(i)}(\tau+\Delta \tau)= \begin{cases} & r^{(i)}(\tau) \hspace{2cm} with\hspace{0.2cm} probability\hspace{0.2cm} 1-w_i(\textbf{s})\Delta \tau \\ &-r^{(i)}(\tau) \hspace{1.7cm} with\hspace{0.2cm} probability\hspace{0.2cm} w_i(\textbf{s})\Delta \tau \\ \end{cases}$$ | (4) |
| $$\frac{dR(i)}{d\tau}=\frac{d<r^{(i)}>}{d\tau}=lim_{\Delta \tau\rightarrow 0}<\frac{r^{(i)}(\tau+\Delta \tau)-r^{(i)}(\tau)}{\Delta \tau}>=-2<r^{(i)}w_i(\textbf{s})>$$ | (5) |
| $$\frac{dR(i)}{d\tau}=-<r^{(i)}\{1-\frac{r^{(i)}}{4}[\sum_{j\in M_i}P(r^{(j)}=r|a^{(j)})r\}]>=-R(i)+\frac{1}{4}\sum_{j\in M_i}<\sum_r P(r^{(j)}=r|a^{(j)})r>$$ | (6) |
| $$\frac{dR(i)}{d\tau}=-R(i)+\frac{1}{4}\sum_{j\in M_j}R^{\star}(j)$$ | (7) |
In the voter model, \(R(j)=R^{\star}(j)\), so the equation reduces to \(\frac{dR(i)}{d\tau}=-R(i)+\frac{1}{4}\sum_{j\in M_j}R(j)\). Analogous to magnetization in the vote model, we define the mean magnetization of the system as: \(m\equiv\sum_iR(i)/N\), which measures the average opinion of the whole system, and \(m=+1\) means the system reaches the consensus of \(r_1\), while \(m=-1\) means the consensus of \(r_2\). Summing Equation 7 over all agents
| $$N\frac{dm}{d\tau}=-\sum_iR(i)+\frac{1}{4}\sum_i\sum_{j\in M_i}R^{\star}(j)$$ | (8) |
| $$\small{R^{\star}(j)\equiv <\sum_r P(r^{(j)}=r|a^{(j)})r>=<P(r^{(j)}=1|a^{(j)})-P(r^{(j)}=-1|a^{(j)})>=2<P(r^{(j)}=1|a^{(j)})>-1}$$ | (9) |
\([\color{blue}{S_1}]\) From \(S_1\), we know:
| $$P(r^{(j)}=1|a^{(j)})= \begin{cases} & 1 \hspace{1cm} with\hspace{0.2cm} probability\hspace{0.2cm} P(a^{(j)}=a_1)\\ & 0 \hspace{1cm} with\hspace{0.2cm} probability\hspace{0.2cm} P(a^{(j)}=a_2)\\ \end{cases}$$ | (10) |
| $$<P(r^{(j)}=1|a^{(j)})>=P(a^{(j)}=a_1)$$ | (11) |
| $$R(i)=<r^{(i)}>=P(r^{(i)}=1)-P(r^{(i)}=-1)=2P(r^{(i)}=1)-1$$ | (12) |
| $$N\frac{dm}{d\tau}=-\sum_i(2P(r^{(i)}=1)-1)+\frac{1}{4}\sum_i\sum_{j\in M_i}[2P(a^{(j)}=a_1)-1]$$ | (13) |
| $$N\frac{dm}{d\tau}=2\sum_i[P(a^{(i)}=a_1)-P(r^{(i)}=1)]$$ | (14) |
For \(S_1\), it is clear that \(P(a^{(i)}=a_1)=P(r^{(i)}=1)\) because believing in \(r_1\) is equivalent to acting as \(a_1\), and vice versa. Therefore we have \(N\frac{dm}{d\tau}=0\), which means the magnetization \(m\) is conserved in the AOI model with \(S_1\) (voter model). The conserved magnetization helps to understand the features of the voter model stated in Section 3.4. Also, the result is identical to the result solved for the voter model.
\([\color{blue}{S_2}]\) From \(S_2\), it can be calculated that:
| $$P(r^{(j)}=1|a^{(j)})= \begin{cases} & \frac{2}{3} \hspace{1cm} with\hspace{0.2cm} probability\hspace{0.2cm} P(a^{(j)}=a_1)\\ & 0 \hspace{1cm} with\hspace{0.2cm} probability\hspace{0.2cm} P(a^{(j)}=a_2)\\ \end{cases}$$ | (15) |
| $$<P(r^{(j)}=1|a^{(j)})>= \frac{2}{3}P(a^{(j)}=a_1)$$ | (16) |
| $$N\frac{dm}{d\tau}=2\sum_i[\frac{2}{3}P(a^{(i)}=a_1)-P(r^{(i)}=1)]$$ | (17) |
| $$P(a^{(i)}=a_1)=P(r^{(i)}=1)P(a_1|r^{(i)}=1)+P(r^{(i)}=-1)P(a_1|r^{(i)}=-1)$$ | (18) |
| $$P(a^{(i)}=a_1)=P(r^{(i)}=1)+\frac{1}{2}P(r^{(i)}=-1)=\frac{1}{2}P(r^{(i)}=1)+\frac{1}{2}$$ | (19) |
| $$N\frac{dm}{d\tau}=2\sum_i\{\frac{1}{3}-\frac{2}{3}P(r^{(i)}=1)\}=\frac{2}{3}N-\frac{4}{3}\sum_iP(r^{(i)}=1)$$ | (20) |
Thus the fixed point is \(\sum_iP(r^{(i)}=1)=N/2\), that is, the probability of believing in \(r_1\), averaged over the population, is \(1/2\). Starting from any configuration that \(\sum_iP(r^{(i)}=1)>N/2\), for example, the configuration where \(r^{(i)}=1\), \(\forall i\), since \(N\frac{dm}{d\tau}<0\), will always converge to a (dynamic) state where \(\sum_iP(r^{(i)}=1)=N/2\), which is the stable state shown in Figure 7(a). Similarly, the system starting with the configuration where \(\sum_iP(r^{(i)}=1)<N/2\), because \(N\frac{dm}{d\tau}>0\), will still evolve to the same state where \(\sum_iP(r^{(i)}=1)=N/2\). The analytical result helps us understand that in the model with \(S_2\), why the composition of the stable state is independent of the initial configuration (Figure 8), and why the mixed state of rules is always the final stable state (Figure 7(a)).
Three-action Situation
Although most studies only deal with two-state voter model due to simplicity, it is promising to study the AOI model with three actions because a larger number, and more subtle, action-opinion relations are possible compared to the two-action situation. For reasons of space limitations, we will not go through all the possible situations, but focus on the cases shown by \(S_5\), \(S_6\) and \(S_7\) specifically:
| $$S_5= \left( \matrix{~ & a_1 & a_2 & a_3 \cr r_1 & + & - & -\cr r_2 & - & + & -\cr r_3 & - &- & +\cr} \right) \hspace{1cm} S_6= \left(\matrix{~ & a_1 & a_2 & a_3\cr r_1 & + & - & -\cr r_2 & - & + & - \cr r_3 & - &- & + \cr r_4 & 0 & 0 &-\cr} \right) \hspace{1cm} S_7= \left(\matrix{~ & a_1 & a_2 & a_3\cr r_1 & + & - & -\cr r_2 & - & + & - \cr r_3 & - &- & + \cr r_4 & 0 & 0 & 0\cr} \right)$$ |
The AOI model using \(S_6\) is nothing but a three-state voter model, which is widely used in the studies of language competition (Castelló et al. 2006, Hadzibeganovic et al. 2008). Unsurprisingly, all features of the two-state voter model (Figure 1) are still valid in the three-state voter model: Figure 9 illustrates that consensus is always reached, and each type of consensus (i.e. Figure 9 (a), (b), and (c)) has the same probability to become the final absorbing state because the initial densities of all rules are set equal. Additionally, the clustering phenomenon of the three rules is shown in Figure 10.
\(S_6\) is constructed by introducing an inclusive rule \(r_4\) (that permits \(a_1\) and \(a_2\) but prohibits \(a_3\)) to \(S_5\), so the difference between the simulations result of \(S_5\) and \(S_6\) implies the role of what we call a preferentially inclusive rule. Rule \(r_4\) in \(S_6\) is called a preferentially inclusive rule because it shows strict preference for \(a_1\) and \(a_2\) over \(a_3\), although it is indifferent between \(a_1\) and \(a_2\). On the other hand, \(r_2\) in \(S_2\), \(r_3\) in \(S_4\), and \(r_4\) in \(S_7\) are called non-preferentially inclusive rules because they are completely indifferent to any action.
It is reported that there are two types of outcomes given the action-opinion matrix \(S_6\), namely case A (Figure 11 (a) and (b)) and case B (Figure 11 (c) and (d)). In case A, \(r_4\) dies out rapidly, while \(r_1\), \(r_2\), and \(r_3\) coexist. Specifically, one of \(r_1\) and \(r_2\) is in a momentary majority alternatively, but \(r_4\) holds a relatively stable share over time (Figure 11 (a)). The dynamics of rules lead to similar evolutionary paths for actions (Figure 11 (b)), where \(a_3\) go extinct and \(a_1\) and \(a_2\) coexist. In case B, consensus of \(r_3\) is reached eventually, and \(r_1\), \(r_2\) and \(r_4\) die out gradually. One cannot predict which case we will obtain from one realization of the simulation. There relation between case A and B mimics a trade-off between a smaller chance to become the sole superpower that dominates everyone (\(r_3\) in case B), and a larger chance to dominate around 1/3 of the population (\(r_1\), \(r_2\) and \(r_4\) in case A). In 100 independent trials, we find that 74% trials are in case A, and 26% trials are in case B. The distribution of case A and B suggests that the trade-off is in equilibrium: consider a finite system with equal density for each rule \(r_1\), \(r_2\), \(r_3\) and \(r_4\). Ultimately, the system reaches the consensus of \(r_3\) with probability \(P_B\), and reaches the mixed state of \(r_1\), \(r_2\), and \(r_4\) with probability \(P_A\). So the expected number of agents believes in \(r_3\), \(<N_3>\), should be \(P_BN\), and the expected number of believes in any other rule, \(<N_k>\) (\(k=1,2,4\)), is \(\frac{1}{3}P_AN\). In our trials, we observed that 74 trials are in case A and 26 in case B, so the estimated \(P_A\), \(\hat{P_A}\), is 0.74, and the estimated \(P_B\), \(\hat{P}_B\) is 0.26. Substitute the two estimated probabilities, we find that:
| $$\frac{1}{3}\hat{P}_AN\approx \hat{P}_BN$$ | (21) |
| $$<\hat{N}_1>=<\hat{N}_2>=<\hat{N}_3>=<\hat{N}_4>$$ | (22) |
The evolution of case B is illustrated in Figure 12, describing how the system reaches the consensus of \(r_3\) from a mixed state of all rules. An interesting observation is that besides the single-rule clusters of \(r_3\), there are also some mixed-rule clusters composed of \(r_1\), \(r_2\) and \(r_4\). Comparing Figure 12 with Figure 10, we can see that the preferentially inclusive rule \(r_4\) reduces the ability of \(r_1\) or \(r_2\) to form a single-rule cluster of its own. The results of the AOI model with \(S_6\) shows that there are two categories for exclusive rules: \(r_1\) and \(r_2\) form a category that coexist with \(r_4\) and cannot form single-rule clusters, and \(r_3\) itself is another category, as \(r_3\) and \(r_4\) are completely incompatible. Here we define that two rules are compatible with each other if there exists at least one action that is allowed (i.e. obliged or permitted) by both of them, and otherwise we say that they are incompatible. If we look at \(S_6\) carefully, it is clear that \(r_1\) and \(r_2\) are compatible with \(r_4\) respectively: both \(r_1\) and \(r_4\) allow \(a_1\), and both \(r_2\) and \(r_4\) allow \(a_2\). On the contrary, the two actions permitted by \(r_4\) (i.e. \(a_1\) and \(a_2\)) are prohibited by \(r_3\), and the only action obliged by \(r_3\) (i.e. \(a_3\)) is forbidden by \(r_4\), so \(r_3\) and \(r_4\) are incompatible. The different relations between exclusive rules and inclusive rule explain the different clustering features of each rule. Because both \(r_1\) and \(r_2\) are compatible with \(r_3\), the three rules coexist and no single-rule clusters can be formed. Meanwhile, \(r_3\) and \(r_4\) are incompatible, so \(r_3\) is unlikely to coexist with \(r_4\). Since \(r_1\) and \(r_2\) coexist with \(r_4\), \(r_3\) cannot coexist with \(r_1\) and \(r_2\) either. Thus the single-rule cluster of \(r_3\) emerges if it dominates the population (i.e. case B in Figure 11).
The only difference between \(S_6\) and \(S_7\) lies in the inclusive rule. In \(S_6\), \(r_4\) is a preferentially inclusive rule that permits \(a_1\) and \(a_2\) but prohibits \(a_3\). However, in \(S_7\) we are having a non-preferentially inclusive rule \(r_4\), which permits all actions. Given \(S_7\), now all exclusive rules and the inclusive rule are compatible, so all rules can co-exist (Figure 13). It should be noted that although all rules share almost the same fraction of population on average, the variation of the population believing in \(r_4\) is significantly smaller than other rules. It is equivalent to saying that the share of the population which employs exclusive rules is more likely to be either very small or very large, while the share of the population which employs the inclusive rule is of intermediate magnitude and relatively stable through time.
To summarize, the inclusive rule "forms an alliance" with all the exclusive rules that are compatible with it (e.g. \(r_4\) and \(r_1\), \(r_2\) in \(S_6\)) to compete with, if it exists, the exclusive rule with which it is incompatible (e.g. \(r_3\) in \(S_6\)). In \(S_6\) \(r_1\), \(r_2\) and \(r_4\) form an alliance against \(r_4\), while in \(S_7\) all rules constitute a large alliance. In both cases, the expected population of the believers in each rule in the alliance should be the same (Figure 11 & Figure 13).
Discussion and Conclusion
Discussion: constrained voter model, language competition, and the AOI model
The above simulations have proved that the action-opinion matrix is the most important factor determining the results obtained from the AOI model. A question that arises naturally is where the matrix originates from? Actually, this question concerns the relations between actions, something which we have not discussed in depth yet. In \(S_1\), \(a_1\) and \(a_2\) are two excluding actions, in the sense that it is impossible to be indifferent between \(a_1\) and \(a_2\), and agents must have a strict preference. On the contrary, in \(S_4\), \(r_3\) offers an option for centrists (i.e. the believers in inclusive rules): believers in \(r_3\) are indifferent between \(a_1\) and \(a_2\), and thus they choose actions randomly. This is related to the constrained voter model (Vazquez et al. 2003) and its modification (de la Lama et al. 2006) where agents can be extremists (including leftists and rightists) or centrists. In those models, the centrists, or the undecided agents, serve as an intermediate group that can be converted to one of the extremists, while the extremists do not interact with each other (Castellano et al. 2009). This is also a common method to implement a bilingual state in language competitions, where any change between the two monolingual states must go through an intermediate state called the bilingual state (Castelló et al. 2006; Colaiori et al. 2015).
Although having different formats, the inclusive rule in the AOI model, the centrists in the constrained voter model, and the bilinguals in the language competition model all describe an intermediate state that bridges the other two (or possibly more than two in the AOI model) non-excluding states. Pioneering researchers have already acknowledged the existence of an intermediate state, but the absence of action-opinion relations limits the scope: the intermediate state must include all existing states in the constrained models and the language competition model (but not in the AOI model). To summarize, the two-state classic voter model resembles the AOI model with \(S_1\), while the constrained voter model and the bilingual language competition model resemble the AOI model with \(S_4\). Obviously, the AOI model provides more possibilities other than \(S_1\) and \(S_4\) by introducing various action-opinion relations. Finally, it is worth mentioning that although the constrained voter model and the bilingual language competition model are similar to the AOI model with \(S_4\), due to the different dynamical rules to update agent’s opinion, the three models lead to completely different results. In the constrained voter model, the final states are a consensus in one of the three states or a mixture of the extremists. The bilingual language competition model always ends up with one of the monolingual consensuses (Castellano et al. 2009). Conversely, the AOI model with \(S_4\), as stated in Figure 2, provides another outcome where the mixed state of all states: \(r_1\) (resembles one of the extremists or monolingual states), \(r_2\) (the same resemblance as \(r_1\)), and \(r_3\) (resembles the centrists, or the bilingual state), which is an impossible outcome for the other two models.
Brief conclusion and outlook
The most important contribution of this paper is to provide an alternative and -in our view- more realistic approach to model the spreading of opinions compared to existing models of opinion dynamics. The new approach, called the Action-Opinion Inference (AOI) Model, is based on the postulate that opinions themselves are unobservable, but may be learned by observing the actions that governed by the opinion; this learning process may be partial given that actions are noisy signals of underlying opinions due to the multiplicity of action-opinion relations. The AOI model captures the "learning opinions by observing actions" process, which is an intuitive assumption but has been ignored in the studies of opinion dynamics. In the AOI model, an agent first observes the actions of her neighbors, and then infers her neighbors’ opinions (represented by rules) according to the observations. Then the agent updates her own rule based on the perceived probabilities of each rule among her neighbors.
We show that the outcome of the AOI model strongly depends on action-opinion relations, described by the action-opinion matrix. When the mapping of the action set A to the rule set R (or vice versa) is a bijective function (e.g. \(S_1\) and \(S_5\)), the AOI model reduces to a classic voter model. When introducing an inclusive rule that permits all actions to the bijective relation (e.g. \(S_4\)), the model resembles the constrained voter model. The variation of the action-opinion matrix enables us to investigate a broad range of opinion dynamics. A striking finding from the simulation results for the two-action AOI model is the role of inclusive rules, defined as the rules that permit more than one action, in a competition with other rules. An inclusive rule bridges the actions it permits, which means the rule also bridges the exclusive rules that oblige these actions. An exclusive rule is defined as a rule that obliges only one action. The connection between exclusive rules via the inclusive rule(s) leads to a final mixed state of all these rules, regardless of the initial density of each rule. This phenomenon has never been found in either constrained voter models or bilingual language competitions. The three-action AOI model is more complex, where the inclusive rule forms an alliance with all the exclusive rules that share at least one allowed action to compete with the exclusive rule(s) that shares no allowed actions with the inclusive rule (i.e. \(S_6\)). The competition between the alliance and the incompatible exclusive rule is a winner-take-all game, but if the alliance wins the whole population, the members share the population equally on average.
Admittedly, the major limitation of the AOI model is the difficulty to incorporate complex reality into a simple action-opinion matrix. As mentioned before, the simulation outcomes, as well as the analytical solutions, are based on the relations between actions and opinions, which in this paper are represented by a series of simple action-opinion matrices. In fact, the reality is far more complicated than all the matrices we have shown in the paper. First, we are not sure how many underlying opinions can people infer from an action, and some-times multiple opinions collectively lead to one action. Taking the example of cycling again, it is unfeasible to list all the possible opinions that lead to the action of cycling: besides being environmentally-friendly or cost-sensitive, the cyclist may simply love this sport, or actually he just randomly choose a travel mode and it happens to be cycling today. Moreover, we are not sure if every agent in the society is aware of all the possible opinions. With a slightly different matrix, the simulation result could be different. Given this limitation, we would recommend first applying the model to some simple and obvious situations. Second, further modifications on the design of action-opinion matrices can be a major challenge in future work to enhance the model’s capability to describe reality. It should also be noted that changing the current assumption of discrete opinions, described by "\(+\)", "\(-\)" and "\(0\)", to a more realistic but complicated assumption of cardinal opinions might fit the reality better. Cardinal opinions offer more ways to describe evaluations, rather than simply referring to an action being completely forbidden and completely obliged (or permitted); a consequence would be that a matrix of finite size would no longer represent the full set of possible action-opinion relations. Given that the central concept of the uncertainty in the relations between actions and opinions, which is the key to explaining simulation outcome’s independence of initial configurations (see Sections 4 and 5), remains unchanged, we optimistically speculate that the main result of the discrete opinion version should be robust in the cardinal opinion version of the model.
In all, the AOI model establishes a new framework for researchers to cope with the latency of opinions and with a variety of presumed action-opinion relations. We believe that the AOI model does not only serve as another modification of the voter model, but also constitutes an attempt to study the spreading of both actions and opinions while opening the floor for further discussions in opinion dynamics. Despite the fact that there are still some possible action-opinion matrices that we have not tested yet in the three-action situation, several avenues for further research are promising. First, the AOI model can be extended or adapted by employing other methods that represent processes of “learning opinions by observing actions” to make the model more realistic. For instance, a similarity-based mechanism may assume that an agent is more likely to take the opinion that is similar to her previous opinion (Teşileanu & Meyer-Ortmanns 2006; Flache et al. 2017). In addition, it would be interesting to explore opinion dynamics in the situation where (some) agents are reluctant to signal their opinions through their actions. Such obfuscation behavior, which is characterized by an agent choosing an action that provides minimal information to a focal agent regarding her underlying opinion, has been formalized in recent work (Chorus 2018). Second, the model can be tested in various network structures. We only test the model in the von Neumann neighborhood in the paper, and it is promising to analyze the dynamics of the AOI model in different networks to investigate the role of randomness, degree distribution, and dimensionality. Furthermore, analytical solutions to the model with general action-opinion relations (a simple example has been given in Section 4) would be helpful to understand the simulation results. Finally, an obvious and important direction for further research consists of empirically validating - at a micro and macro level - our behavioral model and the emergent properties it generates.
Acknowledgements
This research has received funding from the European Research Council: Consolidator Grant BEHAVE (grant agreement No. 724431). A prior version of this research has been presented at the 21st International Conference on Principles and Practice of Multi-Agent Systems (PRIMA 2018). T. Tang would like to acknowledge the helpful comments from session chair Michael Mäs and other participants of the conference. The authors would also like to thank the anonymous referee for helpful suggestions.References
AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203-226. [doi:10.1177/0022002797041002001]
BARRAT, A., Barthelemy, M., & Vespignani, A. (2008). Dynamical Processes on Complex Networks. Cambridge, MA: Cambridge University Press.
BIKHCHANDANI, S., Hirshleifer, D., & Welch, I. (1992). A theory of fads, fashion, custom, and cultural change as informational cascades. Journal of Political Economy, 100(5), 992-1026. [doi:10.1086/261849]
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591. [doi:10.1103/revmodphys.81.591]
CASTELLANO, C., Vilone, D., & Vespignani, A. (2003). Incomplete ordering of the voter model on small-world networks. EPL (Europhysics Letters), 63(1), 153. [doi:10.1209/epl/i2003-00490-0]
CASTELLÓ, X., Eguíluz, V. M., & San Miguel, M. (2006). Ordering dynamics with two non-excluding options: bilingualism in language competition. New Journal of Physics, 8(12), 308. [doi:10.1088/1367-2630/8/12/308]
CHORUS, C. G. (2018). A simple model of obfuscation-based decision-making by human and artificial agents. Working paper, under review.
COLAIORI, F., Castellano, C., Cuskley, C. F., Loreto, V., Pugliese, M., & Tria, F. (2015). General three-state model with biased population replacement: Analytical solution and application to language dynamics. Physical Review E, 91(1), 012808. [doi:10.1103/physreve.91.012808]
DE LA LAMA, M. S., Szendro, I. G., Iglesias, J. R., & Wio, H. S. (2006). Van Kampen’s expansion approach in an opinion formation model. The European Physical Journal B-Condensed Matter and Complex Systems, 51(3), 435-442. [doi:10.1140/epjb/e2006-00232-8]
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87-98. [doi:10.1142/s0219525900000078]
DORNIC, I., Chaté, H., Chave, J., & Hinrichsen, H. (2001). Critical coarsening without surface tension: The universality class of the voter model. Physical Review Letters, 87(4), 045701. [doi:10.1103/physrevlett.87.045701]
FISHBEIN, M. (1963). An investigation of the relationships between beliefs about an object and the attitude to-ward that object. Human Relations, 16(3), 233-239. [doi:10.1177/001872676301600302]
FISHBEIN, M., & Ajzen, I. (1975). Belief, Attitude, Intention, and Behavior: An Introduction to Theory and Research. Reading, MA: Addison-Wesley.
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of Social Influence: Towards the Next Frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2: https://www.jasss.org/20/4/2.html. [doi:10.18564/jasss.3521]
GALAM, S. (2002). Minority opinion spreading in random geometry. The European Physical Journal B-Condensed Matter and Complex Systems, 25(4), 403-406. [doi:10.1140/epjb/e20020045]
HADZIBEGANOVIC, T., Stauffer, D., & Schulze, C. (2008). Boundary effects in a three-state modified voter model for languages. Physica A: Statistical Mechanics and its Applications, 387(13), 3242-3252. [doi:10.1016/j.physa.2008.02.003]
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.
HOLLEY, R. A., & Liggett, T. M. (1975). Ergodic theorems for weakly interacting infinite systems and the voter model. The Annals of Probability, 643-663. [doi:10.1214/aop/1176996306]
HUANG, C. Y., & Wen, T. H. (2014). A Novel Private Attitude and Public Opinion Dynamics Model for Simulating Pluralistic Ignorance and Minority Influence. Journal of Artificial Societies and Social Simulation, 17(3), 8: https://www.jasss.org/17/3/8.html. [doi:10.18564/jasss.2517]
KRAPIVSKY, P. L. & Redner, S. (2003). Dynamics of majority rule in two-state interacting spin systems. Physical Review Letters, 90(23), 238701. [doi:10.1103/PhysRevLett.90.238701]
KRAPIVSKY, P. L., Redner, S., & Ben-Naim, E. (2010). A Kinetic View of Statistical Physics. Cambridge, MA: Cambridge University Press. [doi:10.1017/cbo9780511780516]
LAMBIOTTE, R., & Redner, S. (2007). Dynamics of vacillating voters. Journal of Statistical Mechanics: Theory and Experiment, 2007(10), L10001. [doi:10.1088/1742-5468/2007/10/l10001]
LATANÉ, B. (1981). The psychology of social impact. American Psychologist, 36(4), 343.
LIGGETT, T. M. (1994). Coexistence in threshold voter models. The Annals of Probability, 764-802. [doi:10.1214/aop/1176988729]
LISKA, A. E. (1984). A critical examination of the causal structure of the Fishbein/Ajzen attitude-behavior model. Social Psychology Quarterly, 61-74. [doi:10.2307/3033889]
MARTINS, A. C. (2008). Continuous opinions and discrete actions in opinion dynamics problems. International Journal of Modern Physics C, 19(04), 617-624. [doi:10.1142/s0129183108012339]
MÄS, M., & Bischofberger, L. (2015). Will the Personalization of Online Social Networks Foster Opinion Polarization? Paper presented at Lorenz Workshop on Socio-Economic Complexity, Lorenz Center Leiden, The Netherlands. Available at SSRN: https://ssrn.com/abstract=2553436.
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining opinion bipolarization without assuming negative influence. PLoS ONE, 8(11), e74516. [doi:10.1371/journal.pone.0074516]
MÄS, M., Flache, A., Takács, K., & Jehn, K. A. (2013). In the short term we divide, in the long term we unite: Demographic crisscrossing and the effects of faultlines on subgroup polarization. Organization Science, 24(3), 716-736. [doi:10.1287/orsc.1120.0767]
MILLER, D. T., & McFarland, C. (1987). Pluralistic ignorance: When similarity is interpreted as dissimilarity. Journal of Personality and Social Psychology, 53(2), 298-305. [doi:10.1037//0022-3514.53.2.298]
MOBILIA, M. (2003). Does a single zealot affect an infinite group of voters?. Physical Review Letters, 91(2), 028701. [doi:10.1103/physrevlett.91.028701]
MOONS, I., & De Pelsmacker, P. (2012). Emotions as determinants of electric car usage intention. Journal of Marketing Management, 28(3-4), 195-237. [doi:10.1080/0267257x.2012.659007]
PACHECO, J. (2012). The social contagion model: Exploring the role of public opinion on the diffusion of anti-smoking legislation across the American states. The Journal of Politics, 74(1), 187-202. [doi:10.1017/s0022381611001241]
PETTY, R. E., Cacioppo, J. T., & Goldman, R. (1981). Personal involvement as a determinant of argument-based persuasion. Journal of Personality and Social Psychology, 41(5), 847. [doi:10.1037/0022-3514.41.5.847]
PRELEC, D. (2004). A Bayesian truth serum for subjective data. Science, 306(5695), 462-466. [doi:10.1126/science.1102081]
SEEME, F. B., & Green, D. G. (2016). Pluralistic ignorance: Emergence and hypotheses testing in a multi-agent system. Proceedings of IEEE International Joint Conference on Neural Networks (IJCNN). [doi:10.1109/ijcnn.2016.7727896]
SOOD, V., & Redner, S. (2005). Voter model on heterogeneous graphs. Physical Review Letters, 94(17), 178701. [doi:10.1103/physrevlett.94.178701]
SUCHECKI, K., Eguíluz, V. M., & San Miguel, M. (2005). Voter model dynamics in complex networks: Role of dimensionality, disorder, and degree distribution. Physical Review E, 72(3), 036132. [doi:10.1103/physreve.72.036132]
SVENKESON, A., & Swami, A. (2015). Reaching consensus by allowing moments of indecision. Scientific Reports, 5, 14839. [doi:10.1038/srep14839]
SZNAJD-WERON, K. (2005). Sznajd Model and Its Applications. Acta Physica Polonica B, 36, 2537.
TEŞILEANU, T., & Meyer-Ortmanns, H. (2006). Competition of languages and their hamming distance. International Journal of Modern Physics C, 17(02), 259-278. [doi:10.1142/s0129183106008765]
VALENTE, T. W. (1996). Social network thresholds in the discussion of innovations. Social Networks, 18(1), 69-89. [doi:10.1016/0378-8733(95)00256-1]
VAZQUEZ, F., Krapivsky, P. L., & Redner, S. (2003). Constrained opinion dynamics: Freezing and slow evolution. Journal of Physics A: Mathematical and General, 36(3), L61. [doi:10.1088/0305-4470/36/3/103]
WICKER, A. W. (1969). Attitudes versus actions: The relationship of verbal and overt behavioral responses to attitude objects. Journal of Social Issues, 25(4), 41-78. [doi:10.1111/j.1540-4560.1969.tb00619.x]
WANG, Z., Liu, Y., Wang, L., & Zhang, Y. (2014). Freezing period strongly impacts the emergence of a global consensus in the voter model. Scientific Reports, 4, 3597. [doi:10.1038/srep03597]
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 440. [doi:10.1038/30918]
WU, F., & Huberman, B. A. (2004). Social structure and opinion formation. arXiv preprint cond-mat/0407252.
ZANNA, M. P., Olson, J. M., & Fazio, R. H. (1980). Attitude–behavior consistency: An individual difference perspective. Journal of Personality and Social Psychology, 38(3), 432. [doi:10.1037/0022-3514.38.3.432]

