The Value of Values and Norms in Social Simulation

Introduction

Social simulations gain strength when explained in understandable terms. This paper proposes to explain agent behaviour in term of values and norms following (Hofstede 2017; Dechesne et al. 2012; Atkinson & Bench-Capon 2016). Values are generally understood as ‘what one finds important in life’, for example, privacy, wealth or fairness (Poel & Royakkers 2011). Norms generally refer to what is standard, acceptable or permissible behaviour in a group or society (Fishbein & Azjen 2011). Using values and norms in explanations has several advantages: they are shared among society (Hofstede 2017), they have moral weight (Poel & Royakkers 2011), they are applicable to multiple contexts (Miles 2015; Cranefield et al. 2017) and operationalized (Schwartz 2012). Moreover, humans use value and norms in folk explanations of their behaviour (Malle 2006; Miller 2018). Agents that use values and norms could thus lead to social simulation results that meet human needs for explanations.

To understand the relevance of agents with values and norm for social simulation, we need to know to what extent they can represent humans. Models are always simplifications from the system they are meant to represent, but understanding these differences clarifies the relevance of the model. Previous research primarily focussed on constructing agents that use human values and norms in their decision-making (Dechesne et al. 2012; Atkinson & Bench-Capon 2016; Cranefield et al. 2017). They gained insights in possibilities to synthesize theories on values and norms or how to formally argue in favour of an action in terms of values and norms. This paper aims to take the next step by comparing empirical data on human behaviour to simulated data on agents with values and norms.

We approach this by creating four agent models: a homo economicus model, an agent model with values, an agent model with norms and an agent model with both values and norms. By comparing several agent models we gain more insight into the relative properties of the models. We do not expect the models to fully reproduce human behaviour, but we want to know how they compare and in what expects they differ. In particular, the homo economicus model is used as a baseline as it is often used to represent humans (e.g., in game theory).

We simulate the behaviour of the agents in the ultimatum game (UG). In the UG, two players (human or agent) negotiate over a fixed amount of money (`the pie'). Player 1, the proposer, demands a portion of the pie, with the remainder offered to Player 2. Player 2, the responder, can choose to accept or reject this proposed split. If the responder chooses to `accept', the proposed split is implemented. If the responder chooses to `reject', both players get no money. We use two different scenarios: a single-round scenario and a multi-round scenario. In the single-round scenario, we test if the human behaviour can be reproduced by letting the agents evolve and converge to stable behaviour. In the multi-round scenario, we test if the change in behaviour humans display over multiple rounds of UG-play can be reproduced by the different agent models.

We compare the simulated data to empirical data from a meta-analysis that studied how humans play the ultimatum game. We focus on aggregated results: the mean and standard deviation of the demands and acceptance rate. We find that based on these measures a combination of agents with values and norm produces aggregate behaviour that falls within the 95% confidence interval wherein human plays lies more often than the other agent models. Furthermore, we find specific cases (responder behaviour in the multi-round scenario) for which agents with values and norms cannot reproduce the learning nuances human display. We interpret this result as showing that agents with values and norms can provide understandable explanations that reproduce average human behaviour more accurately than other tested agent models. Furthermore, it shows that social simulation researchers should be aware that agents with values and norm can differ from human behaviour in nuanced learning dynamics. We find several insights on what aspects agents with values and norms outperform agents with solely values, the role of values and norms as static and dynamic components and how norms can produce different behaviour in different cases. We discuss the generalizability of these results given the dependence of these results on our translation from theory to model, parameter settings, evaluation measures and the use case.

The remainder of the paper is structured as follows. The next Section presents theories on how agents use a homo economicus view, values, norms or, values and norms in their decision making. Section 3 presents the two UG scenarios and the data on human behaviour in these scenarios. Section 4 presents our translation from theories to domain specific computational agent models. Section 5 presents the simulation experiments and the resulting behaviour of the different agent models. Section 6 discusses the interpretation and generalizability of these results.

Theoretical Framework

We use theories on the homo economicus, values and norms to model the simulated agents. These theories are briefly summarized in this section.

Homo Economicus

The homo economicus (HE) agent is the canonical agent in game theory (Myerson 2013) and classical economics (John Stuart Mill 1944), that only cares about maximizing its direct own welfare, payoff or utility. As the agent only cares about its own direct welfare it will accept any positive offer in the UG. Humans in contrast reject offers as high as 40% of the pie (Oosterbeek et al. 2001).

One approach to explaining these findings is by extending the HE agent model to incorporate learning (Gale et al. 1995; Roth & Erev 1995). The core of this explanation is that humans have learned through the feedback of repeated interaction to reject low offers to force the proposer into making higher offers. In this view, humans can be represented as learning homo economicus agents for which, roughly said, fairness only exist as an instrument for wealth.

Our theory on the learning homo economicus encompasses:

• LHE.1 Humans only care about maximizing their own welfare.
• LHE.2 Humans can learn that forgoing short-time welfare might lead to a higher long-term welfare.

Values

We view values as `what a person finds important in life' (Poel & Royakkers 2011) that function as 'guiding principles in behaviour'. In the remainder of this subsection, we will describe some of the work on values in psychology, sociology and philosophy focusing on how we can use values in the decision making of agents.

Schwartz developed several instruments (e.g. surveys) to measure values (Schwartz 2012). Based on these measurements Schwartz (2012) can distinguish ten different basic values: self-direction, stimulation, hedonism, achievement, power, security, conformity, tradition, benevolence and universalism. (These basic values, in turn, represent a number of more specific values like wealth and fairness.) Schwartz shows that although humans differ in what values they find important there is a general pattern in how these values correlate. For example, people who give positive answers to survey questions on wealth are more likely to give negative answers to survey questions on fairness. These findings on intervalue comparison have been extensively empirically tested and shown to be consistent across 82 nations representing various age, cultural and religious groups (Schwartz 2012; Schwartz et al. 2012; Bilsky et al. 2011; Davidov et al. 2008; Fontaine et al. 2008).

Values have a weak, but general connection with actions (Miles 2015; Gifford 2014). Miles (2015) used data from the European Social Survey to show that values predict 15 different measured actions over six behaviour al domains and in every country included in the study. Gifford (2014, p. 545-546) reviews environmental psychology and concludes that the correlation between action and values is consistent, but weak, such that moderating and mediating variables are needed to predict actions from values. Following this research, we view values as abstract fixed points that actions over many context can be traced back to.

When making a decision between two actions there might be a conflict between two values. For example, when choosing to give away money or to keep it one might experience a conflict between the value of wealth and fairness. (Poel & Royakkers 2011, p.177-190) discusses different ways to resolve a value conflict: a ‘multi-criteria analysis’ or threshold comparison. In multi-criteria analysis, the different actions are weighted on the values and compared on a common measure; in threshold comparison an option is good as long as both values are promoted above a certain threshold. If one action upholds both thresholds, while the other one does not the former is chosen. If both options uphold both thresholds, threshold comparison does not specify what option to take. This paper uses multi-criteria analysis as this allows our agent to always make a concrete choice and therefore serve as a computational model for simulation.

Our theory on values thus encompasses:

• V.1 There are ten different basic universal values (i.e., self-direction, stimulation, hedonism, achievement, power, security, conformity, tradition, benevolence and universalism.) that each represent a number of specific values (e.g., wealth and fairness) Schwartz (2012)).
• V.2 Humans are heterogeneous in the values they find important.
• V.3 The importance one attributes to these values is correlated according to the findings of Schwartz (2012). For example, the values of wealth and fairness are negatively correlated.
• V.4 Values are (for the aim of this study) the direct and only cognitive determiner for actions.
• V.5 When values are at conflict in a decision, humans use a multi-criteria analysis to resolve the conflict.

Norms

We follow Crawford & Ostrom (2007) in that norms have four elements referred to as the ’ADIC’-elements: Attributes, Deontic, aIm and Condition^[1]. The attribute element distinguishes to whom the statement applies. The deontic element describes a permission, obligation or prohibition. The aim describes the action of the relevant agent. The condition gives a scope of when the norm applies. One example in the context of the UG can be found in Table 1.

Table 1: A norm decomposed according to the ADIC-elements.

A	D	I	C
Proposers	should	demand 60% of the pie	when in a one-shot Ultimatum Game

What norms exists in a scenario? We say a norm exists when it influence the behaviour of an agent. We follow Fishbein & Azjen (2011) in that norms influence behaviour either because of perceptions of what others expect or what others do^[2]. Fishbein & Azjen (2011) use the term ‘perceived norm’ (or: subjective norm) to make clear that it is a person’s individual perception that influence behaviour and that these perceptions may or may not reflect what most others actually do or expect. Thus, a norm exists, for a particular person, when that persons perceives other people do or expect it. To put it in terms of the ADIC syntax: a norm exists, for a particular person, if and if only the attribute perceives others do or expect the aim given that the condition holds.

Empirical work shows that there is a correlation between norms and action. For example, a meta-analysis on the theory of planned behaviour shows an average \(R^2\) of .34 between subjective norms and intentions. In other words, a linear model that takes measurements on the subjective norm as input can on average explain 34% of the variation of the measured intentions (Armitage & Conner 2001). (Intentions, in turn, can explain about half of the variance in behaviour). There are many different theories on how this relation between action and norm precisely works. For the purpose of this study, we aim to explore to what extent we can explain agent behaviour using only an understandable concept as norms.

Our theory on norms thus encompasses:

• N.1 A statement is a norm if and if only it has the following four elements: Attributes, Deontic, aIm and Condition.
• N.2 A norm exists, for a particular person, when that persons perceives other people do or expect it.
• N.3 The action a human does is the same as what they perceive as the norm.

Values and Norms

We follow Finlay & Trafimowm (1996) in that some humans use values while others use norms. In a meta-analysis covering \(30\) different behaviours, they found that some humans are primarily driven by attitude (which strongly correlates with values) and some individuals are primarily driven by norms. We choose this theory for its simplicity and postpone more complex combinations of values and norms to future work.

Our theory on norms and values thus combines our theory on values (V.1 - V5) and norms (N.1 - N3) and adds:

• VN.1 Some humans always act according to the norm and other humans always act according to their values.

Note that V.4 and N.3 in the case of the third theory only attribute to a subset of the agents.

The Scenario

In this Section, we describe how humans behave in two UG scenarios. We will use the simulations to check if our models, which we will describe in the next Section, can reproduce this behaviour.

The UG has been the subject of many experimental studies since its first appearance in Güth et al. (1982). In this study, we use the meta-analysis by Cooper & Dutcher (2011) as our main data source for human behaviour. We obtained the data of 5 of the 6 studies from the authors, namely: Roth et al. (1991), Slonim & I (1998), Anderson et al. (2000), Hamaguchi (2004) and Cooper et al. (2003). We obtain a total of 5950 demands and replies with on average the following specifics:

• An experiment has 32 players: 16 proposers and 16 responders.
• The pie size \(P\) is \(1000\)^[3].
• A proposer can demand any \(d\in D =[0,P]\)
• A responder can choose a reply \(z \in Z = \{accept,reject\}\)
• The players are paired to a different player each round, but do not changes roles.
• Players are anonymous to each other.

These studies can be separated on the amount of rounds the subjects play. One round comprises one demand for each proposer and one reply for each matched responder. We consider two scenarios: the one-round ultimatum game and the multi-round ultimatum game.

Scenario 1: One-shot ultimatum game

The ultimatum game where players only play one round is called the one-shot ultimatum game. We subset the dataset on first-round games and depict what humans do in these rounds in Table 2.

Table 2: First-round human behaviour according to our adapted dataset. We display the estimated average demand (with its confidence interval (CI)) and acceptance rate.

datapoints	demand (\(\mu\))	with CI	Demand (\(\sigma\))	accept (\(\mu\))	with CI	accept (\(\sigma\))
310	562	547-576	129	0.81	0.76-0.85	0.40

this in repeated interactions with other humans. When scholars talk about this type of learning, they mean an evolutionary sort of learning that takes place over long periods of time. Debove et al. (2016) reviewed 36 theoretical models that all aim to explain first-round UG behaviour with such an evolutionary model. The idea behind these studies is that one simulates many rounds of behaviour in the ultimatum game and checks if this results in the demands human make in one-shot games^[4]. In Section 5, we will check if our theories can explain the data in a similar way.

Scenario 2: Multi-round ultimatum game

The original study of Cooper & Dutcher (2011) focuses on how behaviour of responders evolves over \(10\) rounds. In Figure 1, we use the obtained data to represent two of their main findings.

In the left figure, we see that the share proposers demand slightly rises over time. In the right figure, we see that the responder's acceptance rate slightly falls and then rises. According to Cooper & Dutcher (2011), the behaviour in the first five rounds significantly differs from the behaviour in the last five rounds^[5]. Although the differences are small Cooper and Dutcher analyze them as they believe they can be informative. They assume that the mechanisms that are responsible for the change in behavior over time, are also the mechanisms that bring about the behavior in the first round. In Section 5, we present experiments that check if our theories can explain this change in behavior over time.

Model

If we want our results to be relevant for our theory (instead of an ad-hoc model), we need to be clear about the relation between the theory and a domain-specific model. In this Section, we present our ultimatum-game specific implementation of our normative and value-based agent theory. The normative model has been implemented in Repast Java (North et al. 2013), the value-based model has been implemented both in Repast Java and in R for verification. The code, documentation and a standalone installer are provided at the CoMSES Library^[6] and GitHub^[7].

Learning homo economicus agent

In case of the learning homo economicus agent there are already a few models available that can be applied to the UG. This paper uses the reinforcement learning models presented in Roth & Erev (1995) and Erev & Roth (1998), because in our view they focus on the core mechanisms of the homo economicus and they are well documented.

In these models, each player keeps track of an utility \(u\) for a range of portions of the pie \(A\) (in our case \(A = \{0, 0.1P, 0.2P,\dots, P\}\).) For the proposer, this number represents the demand it makes. For the responder this number represents a threshold; if the demand is above this threshold it will reject, if the demand is equal or below the threshold it will accept. The model is initiated by letting each player (\(n\)) attribute an initial utility (\(i\)) to each pie-portion \(a \in A\), such that, \(u_n(t=1,a) =i\).

Each round the agent does the following:

1. Each round a player picks a pie-portion according to the distribution of these utilities. In other words, the probability \(H\), to pick a pie-portion \(a\), is defined by the following function \(H(a) = \frac{u_n(t,a)}{\sum\limits_{a\in A}u_n(t,a)}\).
2. The proposer's demand is equal to that chosen pie-portion. The responder accepts the demand if its below its chosen pie-portion and rejects otherwise.
3. Each player \(n\) updates the utility \(u_n\) of the played action \(\hat{a}\) by adding the obtained money \(r\) to the previous utility, i.e. \(u_n(t+1,\hat{a}) = u_n(t,\hat{a}) + r\). The utility of the other actions remains the same.

Roth & Erev (1995); Erev & Roth (1998) present two versions of the homo economicus that differ in their approach to the initial utilities. Before introducing them we first introduce the parameter \(s(1)\), the initial strength of the model, defined as the ratio between sum of the initial utilities and the average reward, i.e. \(s(1) = \frac{\sum\limits_{a_{i}\in A_{i}}u(a)}{0.5P}\). The initial strength determines the initial learning speed of the agent. The two versions of the model are:

1. The initial utilities are all equal to each other i.e. u(a) = u(b) for all actions \(a,b \in A\). (But \(s(1)\) is free.)
2. The initial utilities sum to 1, i.e. s(1) = 500. (But are randomly distributed.)

For pragmatic reasons, we aim to test only one of the models to reproduce human behaviour. For neither of the models Roth & Erev (1995); Erev & Roth (1998) show explicitly if UG results can be reproduced. In Erev & Roth (1998) the authors show that for many games data can be reproduced with the simple reinforcement learning agent introduced and equal initial utilities, but do not treat the UG in this paper. In Roth & Erev (1995), the authors show that crudely UG results can be reproduced with random utilities and a fixed strength of \(500\), but do not provide the exact parameter settings nor specifically compare the learned distributions to first round play. In this study, we choose to further explore the first model (with equal utilities) as the parameter space is more manageable. Future work should explore other reinforcement models including versions where one can vary the learning rate of the agents.

We now aim to specify which extra assumptions have been made when translating the theory to a domain-specific model:

• LHE+.1Players attach utilities to pie-portions that represent the demand for the proposer and a threshold for the responder.
• LHE+.2The initial utilities for these pie-portions are all equal to each other in the first round.
• LHE+.3There is a one-to-one relation to the utility of a pie-portion and the sum of the rewards it got you (e.g., no discount factor or utilities attached to sequences of actions).

Value-based agent

Given V.1 there are ten basic values that each represent a number of specific values. In the context of the UG, we assume that the value of wealth and fairness are more relevant than other values. This is an educated guess based on that the behavioural economics literature frames the decision in these terms (Cooper & Kagel 2013) and the meaning we associate with the values of wealth and fairness.

Given V.2 humans are heterogeneous in the values they find important. We represent this in the model by a parameter \(i_{v}\) that represents the importance (or weight) one attributes to the value.

Given V.3 this importance is correlated according to the findings of (Schwartz 2012). According to (Schwartz 2012) the two values are strongly negative correlated. For pragmatic reasons, we will assume these values are perfectly negative correlated. This allows us to simplify the model to have two parameters \(\mu\) and \(\sigma\) that specify a normal distribution from which the difference (\(di\)) in value strengths is drawn, i.e. for every agent

$$i_w = 1.0 + 0.5di $$

(1)

and

$$i_f = 1.0 - 0.5di$$

(2)

such that, \(di = i_w - i_f\), represents how much more an agent values wealth over fairness.

Given V.4 values are the only cognitive determiner of actions. To make a computational model, we propose a procedure where the agent attributes a utility to every action and chooses the action with the highest utility. This utility should be determined by both the value of wealth and fairness. In other words, the agent will do a multi-criteria analysis to decide on the best action (V.5).

We present the decision-making model in three steps: (1) we relate to what extent a value is satisfied to the resulting money the agent obtains in one round of UG-play (2) we relate this value-satisfaction and the importance one attributes to the value to a utility per result (3) we relate this utility to the action the agent chooses.

First, to relate to what extent a value is satisfied to the resulting money the agent, we have to interpret the meaning of wealth and fairness. Given the meaning of wealth, we assume that the higher one values wealth the higher the demands one makes (and expects). Given the meaning of fairness, we assume that the higher one values fairness the more equal the demands one makes (and expects). We represent this in the following function:

$$s_{w}(r) = \frac{r}{1000}$$

(3)

$$s_{f}(r) = 1-\frac{|0.5P-r|}{0.5P}$$

(4)

where \(s_{x}\) specifies the extent to which the resulting money (of one round UG) \(r\) satisfies value \(x\) and \(P\) is the pie size. The satisfaction of wealth thus increases as one gets more money and the satisfaction fairness peaks around an equal split^[8].

Second, to relate this value-satisfaction (\(s\)) and value importance (\(i\)) to a utility (\(u\)) per result (\(r\)), we can combine \(s\) and \(i\) in several ways. This paper evaluates three possibilities. A divide function

$$u(r) = -\frac{i_{w}}{s_{w}(r) +ds} - \frac{i_{f}}{s_{f}(r)+ds},$$

(5)

a product function

$$u(r) = i_{w} * s_{w}(r) + i_{f} * s_{f}(r),$$

(6)

and a difference function

$$u(r) = i_{w} - s_{w}(r) + i_{f} - s_{f}(r)$$

(7)

Every utility-function thus represents a different model. In the next Section, we will evaluate which model can best reproduce human behaviour.

Third, to relate this utility to the action the agent chooses we postulate that:

• the proposer now demands that \(d \in [0,P]\) for which the utility (as given by \(u(r)\)) is maximal.
• the responder chooses to accept if (and only if) the utility of what it receives - \(u(P - d)\) - is higher than the utility of a reject.

We choose to model the utility of rejection by filling in the chosen utility function with \(s_w(0)\) and \(s_f(0.5P)\), i.e. the agent interprets it as getting maximum fairness (as in the r= 0.5P case), but getting almost no wealth (as in the \(r=0\) case).

In summary, to translate our theory to our domain we have added the following parts to our theory:

• V+.1 Wealth and fairness are the only relevant values in the ultimatum game.
• V+.2 The importance one attributes to wealth and the importance one attributes to fairness are perfectly negatively correlated.
• V+.3 The higher one values wealth the higher the demands one makes (and expects). The higher one values fairness the more equal the demands one makes (and expects).
• V+.4 Humans compare to what extent wealth and fairness are satisfied by
  1. a divide function (function (5)).
  2. a product function (function (6)).
  3. a difference function (function (7)).

Given N.1 a statement is a norm if and if only it has the attribute, deontic, aim and condition element. In the context of the ultimatum game we consider the types of norms stated in Table 3. Note that according to our theory, all sorts of possible norms could be considered. For example, `responders should reject in all cases'. We consider only the type of norms in Table 3 as we think those are likely to exist in this domain.

Table 3: The norms considered in the ultimatum game split out according to the ADIC-syntax, where \(p\) refers to a proposer, \(q\) to a responder, \(d\) to a demand and \(t\) to a threshold.

label	A	D	I	C
\(N_{p\hat{d}}\)	Proposers	should	demand \(\hat{d}\)	in the UG
\(N_{qt}\)	Responders	should	reject	if and if only the demand is above threshold \(t\) in the UG

Normative agent

This part of our theory states that a norm exists, for a particular person, when they perceive other people do or expect it. Note that in our scenario an agent does not switch roles (i.e. proposers stay proposers, responders stay responders). Proposers thus never see the actions other proposers do, but can only rely on what they think responders expect (from proposers). The situation is analogous for responders. The question is thus, how does one derive what the opponent expects from you given his or her actions?

In the case of the responder this is fairly straightforward. What does a proposer expect from a responder when demanding X% of the pie? He or she probably expects that the responder would accept that demand (and lower), but reject everything higher than that. In other words, the demand becomes a certain threshold for acceptance. For multiple rounds, we assume this threshold is calculated by averaging over all seen demands. Formally, this amounts to that norm \(N_{qt}\) exists for responder \(q \in A\) and a threshold \(t \in D\) if and if only

$$t = \frac{\sum\limits_{d \in OD}d}{|OD|},$$

(8)

where \(OD\) are the demands responder \(r\) has observed in the games it participated.

For the proposer, it's a bit more tricky to deduce what behaviour is expected. We postulate that the demand a proposer is expected to make is equal to the average of two indicators: the lowest demand that is rejected and the highest demand that is accepted. Formally, this amounts to that the norm \(N_{pd}\) exists for a proposer \(p \in A\) and demand \(\hat{d} \in D\) if and if only

$$\hat{d} = \frac{\min\limits_{d\in RD} d + \max\limits_{d \in AD} d} {2},$$

(9)

where \(RD\) is the set of demands that the proposer \(p\) has seen rejected and \(AD\) is the set of demands that the proposer \(p\) has seen accepted.

For most cases the action of the proposer and responder is now clear: they act according to what they perceive as the norm (N.3). However, our theory does not specify what agents should do when they perceive no norm. For the sake of making a computational model we postulate that if no norm exist the agent draws a random action from a uniform distribution. Section 5 explores uniform distribution with different means to gain insight into the relevance of this assumption on our results.

We postulate that if no norm exist the agent does a random action. Note that to translate our theory to our domain we have added the following parts to our theory:

• N+.1 Proposers expect that responders accept their demands, but reject everything higher than that.
• N+.2 Responders expect that proposers demand the average of the lowest demand that is rejected and the highest demand that is accepted.
• N+.3 If no norms exist, then humans draw a random action from a uniform distribution.

Experiments & Results

In this Section, we test four agent models in both the one-shot and multi-round scenario. We evaluate the models on their ability to reproduce human behaviour by comparing the 95% CI wherein human behaviour lies to the simulated behaviour.

Reproducing first-round behaviour

To test our theories on their ability to reproduce human first-round behaviour we let the agents interact until their behaviour stabilizes. To set-up this experiment we thus need to simulate a number of 'pre-rounds'. We assume that these 'pre-rounds' are similar to the scenario as described above. For example, the amount of players is \(32\) and the agents do not switch roles. If the stable behaviour is the same as the human first-round behaviour, then the theory serves as an explanation of how humans have learned to make the demands and rejects they display.

We find that if we average over \(100\) runs per parameter set-up the confidence interval around the estimated means is very small. The remainder of this Section thus treats the estimated mean as the true mean.

Testing our learning homo economicus model

We test our learning homo economicus model on its ability to reproduce first round behaviour in the UG. We can run different versions of the model dependent on the initial utilities the agents attribute to their actions (which are given by parameter \(s\)). Using explorative simulations we find that behaviour stabilizes around pre-round `500'.

We run simulations for \(s \in [0.00005, 8]\) with a logarithmic stepsize as exploration learns that the result of simulations outside this interval do not significantly differ from the result of the bounds. We calculate for each parameter set-up the distance between human demand and acceptance rate and the simulated demand and acceptance rate and find that for \(s=0.03\) this distance is minimal; the results for this parameter setting are displayed in Table 4. Furthermore there is a negative exponential relation between \(s\) and the distance.

Table 4: The demand and acceptance rate of the lhe agent. Note that 'avg.' and 'sd.' refer to the average and standard deviation of the demand and acceptance rate over one run

avg. demand	sd. demand	avg. accept	sd. accept
551.2	258.7	0.60	0.10

We conclude from Table 4 that the learning homo economicus agent particular differs from humans in the distribution of demands and acceptance rate. Although the learning homo economicus can reproduce human demands it can only do this when other agents force it into making lower demands by rejecting enough. This model cannot explain why proposers make relatively equal demands while responders accept almost all demands (81 %).

Testing our value-based agent model

We test our value-based agent model (V) on its ability to reproduce first-round behaviour in the UG. We can run different versions of our value-based agent depending on which function the agent uses to combine the satisfaction of different values (V.+4) and with which \(\mu\) and \(\sigma\) the difference in value strength (\(di\)) is normally distributed.

By calculating which value-based agent model leads to which distribution of demand we can gain insight in which model best reproduces the demands human make. Figure 2 compares the three different agent models by showing what the best demand for each agent is given the importance it attributes to its values. Recall, that human demands are normally distributed. Given that \(di\) is normally distributed, we can see that the divide function is the only function for which the demands agents make will be normally distributed. We conclude that our value-based agent model with extension V.+4a has the best chance of reproducing human behaviour.

To find out if the value-based agent can reproduce the demand and acceptance rates human display we simulate the agent. ^[9] We run experiments for \(\mu \in [-2,2]\) and \(\sigma \in [0,2]\) with stepsize \(0.01\) and denote the average demand and the average reject rate they result in. We calculate for each parameter set-up the distance between human demand and acceptance rate and the simulated demand and acceptance rate (i.e., the error). We find that for \(\mu = -0.55\) and \(\sigma = 1.14\) the distance is minimal; the results for this parameter setting are displayed in Table 5. Note that the resulting behaviour fall within the 95% CI wherein human play lies (see Table 2). The distance between human play and simulated play increases with a linear relation to how far \(\mu\) and \(\sigma\) move away from this optimal setting.

We conclude that our value-based model can for a specific parameter range quite accurately reproduce human demands and acceptance rates.

Table 5: The demand and acceptance rate of the value-based agents. Note that 'avg.' and 'sd.' refer to the average and standard deviation of the demand and acceptance rate over one run.

avg. demand	sd. demand	avg. accept	sd. accept
560.9	103.7	0.82	0.37

Testing our normative agent model

We test our normative agent model (N) on its ability to reproduce first-round behaviour in the UG. We can run different versions of our normative agent depending on what the agent does when no norm is specified (i.e. round 1). Using explorative simulations we find that behaviour stabilizes around pre-round `15'.

In our first experiment, the normative agents draw their demand from \(U(0,P)\) and their acceptance rate from \(U(0,1)\). Table 6 presents the demand and acceptance rate the agents demonstrate when their behaviour stabilizes. The average demand and acceptance rate clearly significantly differ from human play (see Table 2). The agents demand just a bit less than half of the pie, where the humans demand more than half. The agents have an accept rate of \(0.5\) and humans \(0.85\). This experiment gives some evidence that a normative theory cannot serve as an explanation for first-round behaviour. However, the stable behaviour is close to the initial behaviour: the mean of the uniform distributions the agents draw their initial actions from is close to \(494.0\) and \(0.50\). This raises the question how dependent our results are on the initial conditions (N+3) and if other initial conditions might reproduce first-round human behaviour.

Table 6: The demand and acceptance rate normative agents display when their behaviour is stabilized (pre-round 15). Note that 'avg.' and 'sd.' refer to the average and standard deviation of the demand and acceptance rate over one run.

avg. demand	sd. demand	avg. accept	sd. accept
494.0	178	0.50	0.5

To test if our normative model could reproduce human behaviour under different conditions, we run analogue experiments for different uniform distributions. Figure 3 depicts the resulting demands and acceptance rate for different initial demands and acceptance rates. We find that the resulting demands are fairly close to the initial demands. The demands can converge to higher or low than the initial demands depending on the initial acceptance rates. For some initial conditions human demands can be reproduced. In contrast, the acceptance rate converges to either 0.5 or 1.0, but never comes close to the human 0.85. Although hard to display in this Figure, inspection of the data shows that its the edge cases (e.g., where the initial demand is 0 or 1000) that convert to an acceptance rate of 1.0.

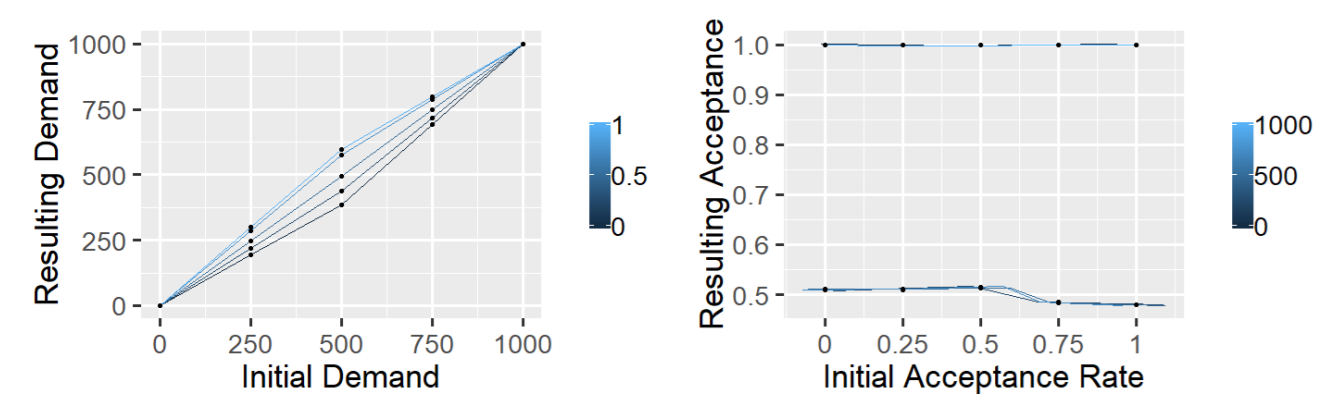
To gain more insight in the role norms can have in human decision-making we highlight a few more aspects of these results. First, Figure 3 shows that although one might expect a normative agent model to 'normalize' both the demand and acceptance rate can converge on different values than they started. Second, Table 6 shows a fairly large standard deviation for both the resulting demand and acceptance rate. This shows that although agents act according to a norm there are still individual differences per agent.

We conclude that our normative model can reproduce human demands, but not simultaneously reproduce human acceptance rates. The simulation shows though that normative models can have counter-intuitive results where resulting norms drift away from the original norm and where agents can have individual norms and reproduce a similar variance behaviour as humans do.

Testing a combination of normative and value-based agents

In our second experiment, we test if we can reproduce human behaviour with our theory that some people act according to their values, while others act according to their norms (VN). In Figure 4, we depict the demand and acceptance rate for different amount of normative agent.

We compare the average demand and acceptance rate of our agents against the confidence interval wherein human play lies (grey area)^[10]. As we already knew, we can reproduce human behaviour by simulating only value-based agents (under the specific parameters mentioned in 5.9. We find that we can also reproduce the demands if we allow up to half of the agents to act out of norms. This can be explained by that if we allow enough value-based agents to make realistic demands, the normative agents will learn to adhere to the norm these agents set. In contrast, only for a very small range of normative agents we can reproduce the acceptance rate as well.

We conclude that our theory on values and norms (VN) reproduces human demands and acceptance rate as long as the amount of normative agents is limited.

Reproducing multi-round behaviour

For multi-round behaviour, we are interested in the behaviour agents display in round 2-10. In contrast to the one-shot scenario, we have empirical data on what the real demand and acceptance rate is humans initially display (round 1). Therefore, we initiate the model based on the empirical data and then test if the agents reproduce human behaviour in subsequent rounds. We evaluate the simulated data on if it falls in the 95% confidence interval in which human play lies. In addition, we highlight aspect of the learning dynamics the agents display.

Testing our learning homo economicus agent model

The learning homo economicus agent is tested on its ability to reproduce multi-round behaviour in the UG. We assume here that the learning homo economicus agent already reproduces human play in the first-round, and see if it can reproduce the learning process humans display. We can run different version of the model depending on the initial utilities the agent attributes to their action (which are given by parameter \(s\)).

We run simulations for \(s \in [0,50]\) as exploration learns that the result of simulations outside this interval do not significantly differ from the result of the bounds. We depict the results in Figure 5. We can see that for both the average demand as well as the average acceptance rate the simulated behaviour does not fall into the confidence interval in which human behaviour lies. However, we can see some similarities in the learning dynamics between the simulated behaviour and the empirical data. In case of the proposer, on round \(3\), \(5\), \(6\) and \(8\), the simulated data shows a similar rise and fall as the empirical data for most values of \(s\). In case of the responder, from round \(5\) onwards the simulated data shows a similar rise and fall as the empirical data for some values of \(s\).

One explanation of these results is that the learning homo economicus differs from humans in wanting to explore other (on average different) options than first-round behaviour. The other behaviour yields enough utility to not change it mind back.

We conclude that the learning homo economicus agent cannot reproduce the average demand and acceptance rate humans display. For some values of \(s\) the learning homo economicus agent reproduces some of the learning dynamic humans display.

Testing our value-based agent

For our value-based agent model we can analytically see that it will not be able to reproduce the human dynamics of multi-round behaviour. The value-based agent behaviour does not change over time and it does not learn.

Testing our normative agent model

The theory on norms (N) is tested on its ability to reproduce multi-round behaviour in the UG. We assume here that the normative agent already reproduces human play in the first-round, and see if it can reproduce the learning process humans display. In other words, we adapt our normative agent such that it does not act randomly the first round, but does the demand and average accept humans do (i.e. we change N.+3).

In Figure 6, we depict the demand and acceptance rate of the normative agent over multiple rounds. We found that the average demands normative agents display is very similar to the average demands humans display. For almost all the individual points we can say with 95% confidence that they are the same as human play^[11]. In contrast, the acceptance rates of the normative agents does not match that of humans. In the case of the proposer, the dynamics of the simulated data and the empirical data match in the general rise, but not in the small fluctuations. In case of the responder, the dynamics primarily differ. In particular, the initial drop in the simulated data and the drop on round \(5\) of the empirical data have no counterpart.

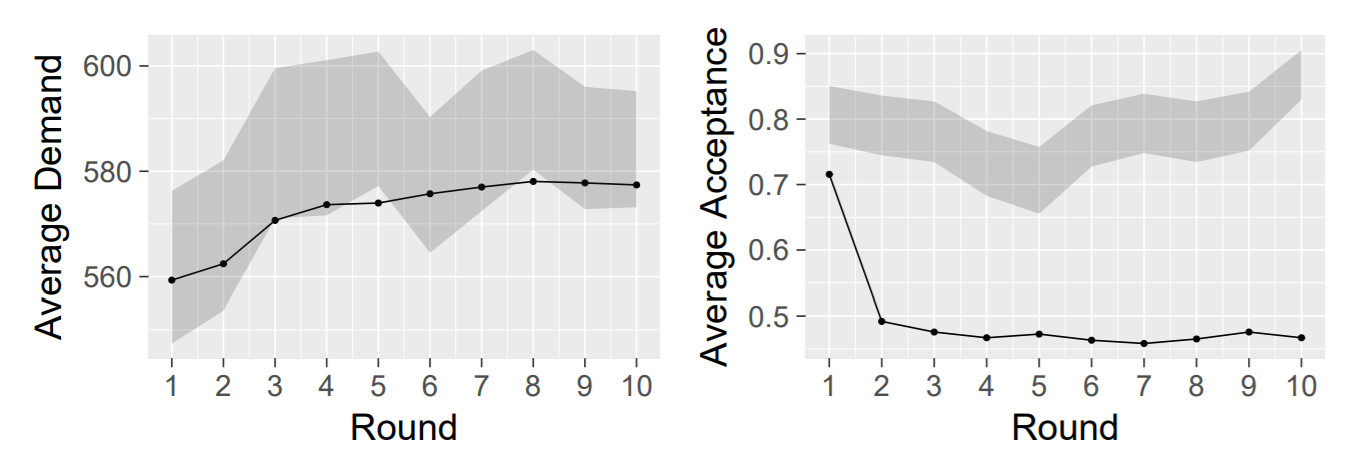
We can explain the initial drop in acceptance rates as follows. After the first turn, the responders set their threshold to the first demand they saw (N.+1). After this, about half of the demands are above and about half of the demands are below this threshold leading to the 0.5 acceptance rate.

We conclude that the normative model cannot reproduce both human demands and acceptance rate. The learning of the proposer agent is similar to that of humans, but (at the same time) responder learning strongly differs.

Testing a combination of value-based and normative agents

In our last experiment, we test if we can reproduce human behaviour with our theory that combines both values and norms (VN). We depict the results in Figure 7.

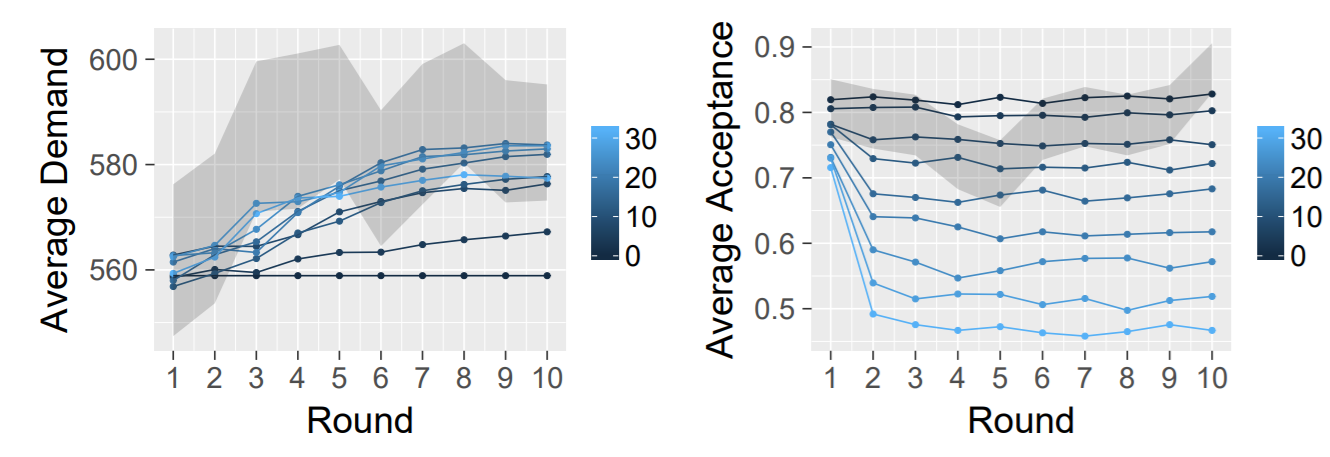
We found that no single combination of value-based and normative agent completely reproduces human play. However, when the amount of normative agents is limited (e.g., 10) the proposer and responder learning is similar to that of humans. In this case, most of the simulated data points fall within the 95% confidence interval wherein human play lies. Note that in the proponent case human behaviour is best matched with a large majority of normative agents, while in the respondent case a majority of value-based agents gives the best fit. We find that the dynamics of the proposer agents match the slight increase in demand humans display. The dynamics of the simulated responders differ from those of humans. In particular, a rise in acceptance rate after round \(5\) is not reproduced.

We conclude that no single combination of normative and value-based agent can completely reproduce human play, but that for some particular combinations the average demand and acceptance rate often lies within the 95% confidence interval humans display. In addition, some of the dynamics of the proposer or reproduced. The dynamics of the simulated responder strongly differs from human play.

Discussion

This paper compared empirical data on human behaviour to simulated data on agents to gain insight in to what extent agents with values and norms can represent human behaviour. We found that agents with values and norms can both evolutionary reproduce one-shot UG behaviour and, for most rounds, reproduces aggregate human behaviour in a multi-round scenario. Given the methodology of this paper, an agent with values and norms thus outperforms a learning homo economicus agent or an agent that uses solely values and norms in its ability to reproduce human behaviour. It outperforms the learning homo economicus agent and the normative agent in the one-shot UG and the learning homo economicus, value-based and normative agent in the multi-round UG. The remainder of this Section discusses to what extent this means agent with values and norms could represent human behaviour in explainable terms.

The generalizibility of these results is namely dependent on the fact that they hold under a specific translation from theory to model, specific evaluation, specific parameter settings and a specific use case.

We aimed to be transparent in our translation from theory to model so that other researchers can pinpoint on what aspects they agree and disagree and how these aspects influence the results. On aspects of the model we found necessary out of a pragmatic viewpoint, but not fundamental to the theory we aimed to study their influence on the output. For example, we showed that the normative model cannot reproduce human acceptance rate independent of its initial conditions. We hope this paper can serve a discussion between the social and computational sciences to pinpoint essential and accidental properties of values and norms.

We evaluated the agent models on to what extent aggregate measures of simulated behaviour fall inside a 95% confidence interval wherein aggregate measures of human behaviour lie. We find that based on this evaluation measure, we can differentiate models that cannot possibly reproduce human behaviour from models that can. For example, our learning homo economicus agent cannot (under any parameter setting) come close to both humans demand and acceptance rate in the one-shot UG. Our value-based agent and agent with values and norms can reproduce human demand and acceptance rates. However, this latter result depends on specific parameter settings for these models (i.e., difference in values follow a certain normal distribution and there are a specific amount of normative agents). In future work, these parameter settings can be evaluated by using empirical data on how values are normally distributed and how many humans act out of norms (i.e., what Moss & Edmonds 2005 call cross-validation). Based on this, we argue that interviews that measure how humans individually explain results would be a valuable addition to the data available on the UG.

We compared our simulated agents on data obtained on human behaviour in the UG: a lab experiment. Lab experiments have the advantage of allowing measurements in a reproducible controlled settings, which is the reason we were able to obtain a relatively large homogenous dataset of a meta-study. Natural decision making criticizes the lab setting as being unrepresentative for real-life decision making (Klein et al. 2008). In the case of the UG, it is indeed unclear what real-life process the ultimatum game is exactly meant to represent. This has at least two consequences. First, it is unclear what modelling assumptions should be made about the setting (e.g., what do the initial conditions means in an evolutionary setting). Second, in a setting with unstable conditions, high stakes and more uncertainty humans could use a different decision-making process than in the UG. Future work should balance findings from this lab context with findings in a more natural context.

By comparing an agent with values and norms to other agent models we gained several insights. First, we found that in the one-shot UG a value-based agent can reproduce human behaviour just as well as an agent model with values and norms. We conclude that both agent models can be used to explain aggregate human behaviour in this scenario. Note that although an agent model with values and norms introduces another concept, a reason to choose it over a value-based model is that it can explain behaviour in a more general context (i.e., the multi-round scenario) or fits better with explanations humans give (e.g., in interviews). Second, the experiments show that values act as a static component that anchors the agent to certain behaviour, where norms form a dynamic component that can allow agent behaviour to drift away from human behaviour (e.g., in the one-shot UG) or towards human behaviour (e.g., in the multi-round UG). This gives insight into the role values and norms can have in humans and agents (i.e., as anchors and as dynamic learning components). Furthermore, this is relevant for creating ethical AI: AI that we create according to our ideas of values and norms can still drift away from behaviour we find acceptable. Third, we found that normative agents can still individually differ in behaviour just like humans. This is because agents can form different ideas of 'the norm' based on the different interactions they had.

Although social simulation focusses on reproducing general aggregate patterns in human behaviour, we should be aware that there are aspects of human behaviour agents with values and norms do not reproduce. The most notable difference is that nuances in the learning dynamics of the proposer and (especially) the responder behaviour in the multi-round scenario are not reproduced. Furthermore, if one is primarily interested in nuanced learning dynamics, then this research suggests that other agent models should be used over agents with values and norms. For social simulation researchers, this means that they should be aware of possible differences between their agents with values and norms and humans in learning dynamics.

We suggest a few directions for future work to find agent models that on an aggregate level reproduce human behaviour. First, we could specify in more detail when to use norms and when values^[12]. The results in the multi-round scenario show that for the proponent case human behaviour is best matched with a large majority of normative agents, while in the respondent case a majority of value-based agents gives the best fit. We are careful to not conflate this with the claim that proposers mainly use norms while responders mainly use values. The average demand, acceptance rate and the different rounds all depend on each other. There are simulation runs with predominantly normative agents (that explain proposer behaviour) and value-based agents (that explain responder behaviour), but this is not the same as one run where both results are explained simultaneously by agents first proposing out of norms and then the same agents responding out of values. It could very well be that the low acceptance rate in runs with a high amount of normative agents is due to the fact that in that same run the demands are higher (and not because the agents use norms). Future work should use simulations to check if agents that sometimes use values and sometimes use norms can explain aggregate UG behaviour.

Second, there are other deontic operators than 'should' that can be used to improve the normative agent model (Wright 1951). For example, the deontic operator 'may' can represent a range of possible demands the proposer considers permissible. Future work could test to what extent these different deontic operators allow the normative agent to reproduce human aggregate behaviour.

Third, in experimental economics, there are several models that have been used to reproduce human behaviour (Cooper & Kagel 2013). As discussed, one of these models, the learning homo economicus outperforms the agent with values and norm by being able to reproduce some of the nuanced learning dynamics. Future work could look at how to combine the benefits of both models to reproduce human behaviour more accurately.

Last, considering that the motivation for this work is to use understandable terminology to explain the agent behaviour, we are more inclined towards using concepts humans use in their explanation. For example, Fehr & Fischbacher (2003) suggested that the concept of reputation can explain the learning dynamics in the UG: a responder could aim to build a reputation as a strong ('selfish') player.

Conclusion

This paper aimed to compare empirical data on human behaviour to simulated data on agents with values and norms. We found that agents with values and norms can both evolutionary reproduce average one-shot UG behaviour and, in most rounds, reproduces the average demands and acceptance rates humans display in a multi-round scenario. We interpret this result as showing that agents with values and norms can provide understandable explanations that reproduce average human behaviour more accurately than other tested agent models (e.g., the homo economicus).

We gained several insights into the role of values and norms in agent models. First, we found that our agents with values and norms cannot reproduce the nuanced learning dynamics humans display (in particular the responder behaviour in the multi-round scenario). Second, we found that agent models with solely values or solely norms can reproduce some human behaviour in one scenario, but to reproduce behaviour in both scenarios a combined model is necessary. Third, the experiments show that values act as a static component that anchors the agent to certain behaviour, where norms form a dynamic component that can allow agent behaviour to drift away from human behaviour (e.g., in the one-shot UG) or towards human behaviour (e.g., in the multi-round UG). Fourth, normative agents can still individually differ in behaviour just like humans, because agents can form different ideas of 'the norm' based on the different interactions they had.

We discussed the dependence of these results on our translation from theory to model, parameter settings, evaluation and use case. Future work should be directed at pinpointing essential and accidental properties of values and norms, interviews that measure how humans individually explain results to validate micro aspects of the model and balance findings from this artificial lab context with findings on natural decision-making.

Our study is a first step that shows how agents with values and norm can provide an improvement over simpler models in representing human behaviour in explainable terms.

References

ANDERSON, L. R., Rodgers, Y. V. & Rodriguez, R. R. (2000). Cultural differences in attitudes toward bargaining. Economics Letters, 69(1), 45–54. [doi:10.1016/S0165-1765(00)00287-1]

ARMITAGE, C. J. & Conner, M. (2001). Efficacy of the Theory of Planned Behaviour: A meta-analytic review. British Journal of Social Psychology, 40, 471–499. URL

ATKINSON, K. & Bench-Capon, T. (2016). Value Based Reasoning and the Actions of Others. In Proceedings of ECAI, (pp. 680–688).

BILSKY, W., Janik, M. & Schwartz, S. H. (2011). The Structural Organization of Human Values-Evidence from Three Rounds of the European Social Survey (ESS). Journal of Cross-Cultural Psychology, 42(5), 759–776.

CASTELFRANCHI, C. (2014). For a science of layered mechanisms: beyond laws, statistics, and correlations. Theoretical and Philosophical Psychology, 5(June), 536. [doi:10.3389/fpsyg.2014.00536]

COOPER, D. J. & Dutcher, E. G. (2011). The Dynamics of Responder Behavior in Ultimatum Games: A Meta-Study. Experimental Economics, 14(4), 519–546.

COOPER, D. J., Feltovich, N., Roth, A. E. & Zwick, R. (2003). Relative versus absolute speed of adjustment in strategic environments: Responder behavior in ultimatum games. Experimental Economics, 6(2), 181–207. [doi:10.1023/A:1025309121659]

COOPER, D. J. & Kagel, J. H. (2013). Handbook of Experimental Economics, vol. 2

CRANEFIELD, S., Winikoff, M., Dignum, V. & Dignum, F. (2017). No pizza for you: Value-based plan selection in BDI agents. IJCAI International Joint Conference on Artificial Intelligence, (pp. 178–184). [doi:10.24963/ijcai.2017/26]

CRAWFORD, S. E. S. & Ostrom, E. (2007). A Grammar of Institutions. Political Science, 89(3), 582–600.

DAVIDOV, E., Schmidt, P. & Schwartz, S. H. (2008). Bringing values back in: The adequacy of the European social survey to measure values in 20 countries. Public Opinion Quarterly, 72(3), 420–445. [doi:10.1093/poq/nfn035]

DEBOVE, S., Baumard, N. & Andre, J. B. (2016). Models of the evolution of fairness in the ultimatum game: A review and classification. Evolution and Human Behavior, 37(3), 245–254.

DECHESNE, F., Di Tosto, G., Dignum, V. & Dignum, F. (2012). No Smoking Here: Values, Norms and Culture in Multi-Agent Systems. Artificial Intelligence and Law, 21(1), 79–107. [doi:10.1007/s10506-012-9128-5]

EREV, I. & Roth, A. E. (1998). Predicting HowPeople Play Games: Reinforcement Learning in Experimental Games with Unique, Mixed Strategy Equilibria. American Economic Review, 88(4), 848–881

FEHR, E. & Fischbacher, U. (2003). The nature of human altruism. Nature, 425(6960), 785–791. [doi:10.1038/nature02043]

FINLAY, D. & Trafimowm, K. A. (1996). The Importance of Subjective Norms for a Minority of People: between Subjects and within-Subjects Analyses. Personality and Social Psychology Bulletin, 22(8), 820–828.

FISHBEIN, M.& Azjen, I. (2011). Predicting and Changing Behavior: The Reasoned Action Approach. Psychology Press. [doi:10.4324/9780203838020]

FONTAINE, J. R. J., Poortinga, Y. H., Delbeke, L. & Schwartz, S. H. (2008). Structural Equivalence of the Values Domain Across Cultures: Distinguishing Sampling Fluctuations From Meaningful Variation. Journal of Cross-Cultural Psychology, 39(October), 345–365.

GALE, J., Binmore, K. G. & Samuelson, L. (1995). Learning to be imperfect: The ultimatum game. Games and Economic Behavior, 8(1), 56–90. [doi:10.1016/S0899-8256(05)80017-X]

GIFFORD, R. (2014). Environmental psychology matters. Annual Review of Psychology, 65, 541–79.

GÜTH, W., Schmittberger, R. & Schwarze, B. (1982). An experimental analysis of ultimatum bargaining. Journal of Economic Behavior and Organization, 3(4), 367–388. [doi:10.1016/0167-2681(82)90011-7]

HAMAGUCHI, Y. (2004). Does Observation of Others Affect People’s Cooperative Behavior? An Experimental Study on Threshold Public Goods Games. Osaka Economic Papers, 54(2), 46–81.

HOFSTEDE, G. J. (2017). GRASP agents: social first, intelligent later. AI and Society, 0(0), 1–9. [doi:10.1007/s00146-017-0783-7]

JOHN Stuart Mill (1844). On the definition of political economy, and on the method of investigation proper to it. In Essays on some unsettled questions of Political Economy, (p. 326)

KLEIN, G., Associates, K. & Ara, D. (2008). Naturalistic Decision Making. Human Factors, 50(3), 456–460. [doi:10.1518/001872008X288385]

MALLE, B. F. (2006). How the Mind Explains Behavior: Folk Explanations, Meaning, and Social Interaction. New York, NY: MIT Press

MILES, A. (2015). The (Re)genesis of Values: Examining the Importance of Values for Action. American Sociological Review, 80(4), 680–704. [doi:10.1177/0003122415591800]

MILLER, T. (2018). Explanation in artificial intelligence: Insights from the social sciences. Artificial Intelligence.

MOSS, S.& Edmonds, B. (2005). Sociology and Simulation: Statistical and Qualitative Cross-Validation. American Journal of Sociology, 110(4), 1095–1131 [doi:10.1086/427320]

MYERSON, R. B. (2013). Game theory. Harvard university press

NORTH, M. J., Collier, N. T., Ozik, J., Tatara, E. R., Macal, C. M., Bragen, M. & Sydelko, P. (2013). Complex adaptive systems modeling with Repast Simphony. Complex Adaptive Systems Modeling, 1(1), 3. [doi:10.1186/2194-3206-1-3]

OOSTERBEEK, H., Sloof, R. & van de Kuilen, G. (2001). Cultural Differences In Ultimatum Game Experiments: Evidence From A Meta-Analysis. SSRN Electronic Journal, 188, 171–188.

POEL, I. v. d. & Royakkers, L. (2011). Ethics, Technology, and Engineering: An Introduction. Hoboken, NJ: John Wiley & Sons.

ROTH, A. E., Prasnikar, V., Okuno-Fujiwara, M., & Zamir, S. (1991). Bargaining and market behavior in Jerusalem, Ljubljana, Pittsburgh, and Tokyo: An experimental study. The American Economic Review, 1068-1095.

ROTH, A. E. & Erev, I. (1995). Learning in extensive-form games: Experimental data and simple dynamic models in the intermediate term. Games and Economic Behavior, 8(1), 164–212. [doi:10.1016/S0899-8256(05)80020-X]

SCHWARTZ, S. H. (2012). An Overview of the Schwartz Theory of Basic Values. Online Readings in Psychology and Culture, 2, 1–20.

SCHWARTZ, S. H., Cieciuch, J., Vecchione, M., Davidov, E., Fischer, R., Beierlein, C., Ramos, A., Verkasalo, M., Lönnqvist, J.-E., Demirutku, K., Dirilen-Gumus, O. & Konty, M. (2012). Refining the theory of basic individual values. Journal of Personality and Social Psychology, 103(4), 663–688. [doi:10.1037/a0029393]

SLONIM, B. Y. R. & I, A. E. R. (1998). Learning in High Stakes Ultimatum Games: An Experiment in the Slovak Republic. The Econometric Society Stable, 66(3), 569–596

WRIGHT, G. H. (1951). Deontic logic. Mind, 60(237), 1–15. [doi:10.1093/mind/LX.237.1]