Introduction
No doubt, there are many positive effects when people congregate together. However, there are also several negative outcomes when the density of people grows too high, such as crowd disasters, severe traffic delays, and pollution. Further, densely populated areas could also lead to emergency evacuation where people attempt to move away immediately from the threat, due to the proximity of people and their frequent interactions. Emergency evacuation could also happen due to natural disasters, fire, traffic accidents, building structural failure and so on.
The prevailing evacuation management systems depend mainly on human power to assist the evacuees during an emergency evacuation scenario. Although the organisers of large gatherings might have done the necessary preparation, it is difficult to anticipate the behaviours of a crowd during an event that may lead to a possible crowd disaster. Uncertainty issues such as the lack of information about other agents’ actions, location, the severity of the emergency evacuation, and the safer evacuation exits during evacuation scenarios could add complexities to the evacuation management tasks (Ibrahim et al. 2016). Evacuation simulation of crowd dynamics (Christensen & Sasaki 2008; Pluchino et al. 2014) have important applications in evacuation management system relevant to organizing safer large-scale gatherings. Crowd dynamic models has been classified into different types depending upon how the scheme treats the pedestrians and the level of detail of the models, viz. macroscopic models, mesoscopic models and microscopic models. Macroscopic models (Colombo & Rosini 2005; Hughes 2002, 2003) consolidate the whole crowd as a single entity, while mesoscopic models (Helbing et al. 2000b; Henderson 1971; Hoogendoorn & Bovy 2000; Klar & Wegener 2000) separate the crowd into different small groups.
Macroscopic and mesoscopic models ignore the importance of the behaviour and characteristics of individual agents where individual agents are considered as irrelevant to the movement of the whole crowd. A microscopic model is considered as a complex system (Helbing et al. 2001) that involves both physical laws and each agent’s characteristic in a crowd (Ma 2013). Through microscopic models, each agent’s behaviours can be simulated and the consequences of emergent behaviours of the whole crowd can be observed (Chen 2006). The microscopic model is intended to model and simulate the actions and interactions of autonomous agents in order to examine their effects on the whole evacuation process.
In this regard, game-theoretic models prove to be efficient for assessing the outcome of the dynamic behaviours of a whole crowd. This is because by utilizing game theory-oriented evacuation simulations, the agents will be able to examine all of the available options and choose the best strategy based on their preferences. However, each agent’s final payoffs will depend on the strategies chosen by other agents. Although the social force evacuation model (Helbing et al. 2000a; Helbing & Molnar 1995) is based on behavioural aspects as well, the underlying assumption that all agents have homogeneous properties seems to be unrealistic. In the evacuation scenario, a crowd is typically composed of different types of individuals (You et al. 2016). Studies of behavioural evolution of crowds take into account the behaviours associated with both cooperators as well as defectors (Huang et al. 2015; Sabar et al. 2017). In this regard, evolutionary game theory can be used to elucidate this. Basically, evolutionary game theory offers efficient computational models to make meaningful and robust decisions among interacting agents. Besides that, evolutionary game-theoretic evacuation models have also been proven to be effective to study the crowd dynamics in terms of individual interactions that are featured in microscopic models (Hao-Nan et al. 2014). Consequently, in recent years a number of evolutionary game theory oriented research contributions have been proposed to model crowd behaviours during evacuation scenarios (Bouzat & Kuperman 2014; Chizari et al. 2013; Hao-Nan et al. 2014; Heliövaara et al. 2013; Ibrahim et al. 2017; Pärnänen 2015; Shi & Wang 2013; Sun et al. 2010; Suryotrisongko & Ishida 2011; von Schantz & Ehtamo 2015; Zheng & Cheng 2011).
Besides that, in a \(n \times 2\) (\(n\) agents, two strategies) symmetric evacuation game as proposed in Bouzat & Kuperman (2014), Hao-Nan et al. (2014), Heliövaara et al. (2013), Ibrahim et al. (2017), Pärnänen (2015), Shi & Wang (2013), von Schantz & Ehtamo(2015), there are only two different strategies that can be adopted by agents which are either cooperator (C) and defector (D). However, in reality, there can be more strategies adapted by agents during evacuation scenarios such as evaluator and retaliator. By convention, cooperators usually don’t fight to attain the desired position. In contrast, defectors tend to be very aggressive in attaining a desired position. An evaluator will assess the opponent in terms of size. The evaluators will act as a cooperator if the opponent is large in size and act as a defector if the opponent is at most equal in size. On the other hand, a retaliator escalates only when the adversary escalates. When two retaliators meet, both would act as cooperator.
Up to now, evacuation models under certainty (Heliövaara et al. 2013; Pärnänen 2015; von Schantz & Ehtamo 2015) and uncertainty (Ibrahim et al. 2017) has been proposed where both scenarios are separately considered, which is inconsistent with reality. In contrast to previous work, we intend to study the effect of heterogeneous populations (Herrera & Lozano 2000; Knoester et al. 2013) where agents of uncertain behaviour (risk seeking, risk averse and risk neutral behaviours of agents) and certain behaviour (best-response agents) are combined. Evacuation simulation in the area of uncertainty and certainty is important in order to study the crowd behaviours during emergency scenarios.
Furthermore, Wirz et al. (2013) suggested that it is crucial to understand the behaviours and situation of the crowd. The connection of crowd behaviours and evolution of different types of behaviours towards escape flow remain unexplored in previous literatures. Therefore, in this work we intend to investigate the effect of various crowd behaviours towards egress flow and the relationship between evolution of crowd behaviours and the occurrences of the crowd turbulence which is believed as potential indicators to alarm crowd disasters (Friberg & Hjelm 2015; Helbing et al. 2007; Helbing & Mukerji 2012; Johansson et al. 2008; Johansson 2008).
Methods
Proposed spatial evacuation model
Regarding agents’ movement in continuous space, we utilized the social force model as described in Ibrahim et al. (2017). Next, we present spatial evacuation as defined in Ibrahim et al. (2017). Each agent has its own estimated evacuation time, Ti as defined by
| $$T_{i}=\frac{d_{i}}{\|v(\textbf{r},t)\|},$$ | (1) |
| $$\|v(\textbf{r},t)\|=\frac{\sum _{j}v_{j}}{n},$$ | (2) |
We perceive the crowd evacuation process as an evacuation game that is played with the objective to reduce the evacuation time. At each time step, the agent interacts with its nearest neighbours. All the conflicting neighbouring agents are identified and solved according to certain rules. Thus, the winners of the conflicts and the agents who are not involved in conflicts with their neighbouring agents move to their desired positions. The simulation ends when all the agents have finally evacuated the room.
In order to resolve the conflicting agents, at first we need to find the conflicting neighbours. The proposed neighbourhood rules in Ibrahim et al. (2017) have been utilized in this work. Then, taking into account the interaction of neighbouring agents between \(i\) and \(i_{c}\) (\(i_{c}\) are the agents other than \(i\) in the scenario (analogous to the complement of i)), the mean estimated evacuation time of these neighbouring agents is defined as \(T_{i(i_{c})}=\frac{T_{i}+\sum_{i_{c}}T_{i_{c}}}{1+n_{i_{c}}}\), where \(n_{i_{c}}\) refers to the number of neighbouring agents for \(i\). In cases where the neighbouring agents tend to interact with each other, we need to solve the conflicts so that only one winner will be able to move. The winner can overtake other agents and reach the desired position and gain the utility by reducing his estimated evacuation time by \(\Delta t\), while the loser(s) will remain in the current location and lose the utility where the loser's estimated evacuation time will increase by the same quantity \(\Delta t\). As a result, the cost of each winner agent will get reduced to a utility that amounts to \(\Delta u(T_{i(i_{c})})\) and the cost of each loser agent(s) increases by the same amount.
For each step taken by an agent, the distance \(d_{i}\) between the agent and the exit eventually gets reduced by \(\Delta d\) which is defined as \(\Delta d=\|v(\textbf{r},t)\|\times \Delta t\) where \(\|v(\textbf{r},t)\|\) is the local speed of an agent \(i\) as defined in Equation 2. \(\Delta t\) is assumed to be a constant value of \(0.8s\) as proposed in as proposed in Ibrahim et al. (2017). Then, we define the difference in estimated evacuation time of conflicting agents for each step as \(\Delta u(Ti(i_{c}))=\frac{\Delta d}{|v_{i}^{0}|}\) where \(|v_{i}^{0}|\) refers to the preferred speed of an agent. When there is an empty space available, the winner of the conflicts will try his best to utilize his preferred speed in order to move to that empty space. This justifies the fact that we have deployed the preferred speed instead of the local speed of an agent in calculating the cost function \(\Delta u(T_{i(i_{c})})\).
Compared to work in Ibrahim et al. (2017), in this work, a new \(n \times 4\) (\(n\) agents, four strategies) symmetric evacuation game is proposed which consists of proposed strategies viz., cooperator C, defector D, evaluator E and retaliator R. Previous works have assumed that payoff of an agent is not influenced by the size of the opponent(s). However, in reality, size of the opponent(s) indeed influences the payoffs that have been received by the conflicting agents. For example, when two defectors are competing to move to a desired position, the larger and mightier agent will usually be able to dominate the move towards the target, while the smaller agent usually will not be able to do so. For simplicity the larger and mightier agent(s) will be simply referred to as larger agents in the rest of the discussions. Here, large opponent(s) for current agent \(i\) is set if the centre of mass distance between agents \(i\) and \(i_{c}\) is less than or equal to \(2cm\), \(d_{i(i_{c})}\leq2cm\). While equal opponent(s) for current agent \(i\) is set if \(-2cm < d_{i(i_{c})} < 2cm\). Thus, large opponents(s) for current agent \(i\) is about \(10kg\) and more, while, equal opponent(s) for current agent \(i\) is between \(-10kg\) and \(10kg\) (these values were obtained by using equation mass of an agent as described in Ibrahim et al. (2017)). If there is no large opponent and equal opponent for current agent \(i\), then it indicates that agent \(i\) is the largest from among the conflicting agents.
Besides that, the conflicting neighbours will also face a conflict cost which could be attributed due to some energy loss, the possibility of getting injuries, time delay in movements, losing some favourable positions in the pedestrian space and so on. When the conflicting neighbours (especially in the case where the conflicting neighbours consist of at least two defectors) attempt to push each other in order to move, there will be a little delay in time. In this work, conflict cost is denoted by the time delay \(t_{d}\) where \(t_{d}> 0\). Then, we can define the rules that will enable us to decide the winner of the conflicts as follows:
- (1) For the case of a conflict with \(n_{def}\) defectors and \(n_{coop}\) cooperator(s) where \(n_{def}>1\), \(n_{coop}\geq~0\):
- (1.1) When large defector, \(L_{n_{def}}\) is single, the large defector will be able to move while all the other defectors and cooperators will remain at the same location. The payoff for the large defector is to gain the utility by reducing the cost of \(\Delta u(T_{i(i_{c})})\). Whereas, the payoff for the other defectors and cooperator(s) is to decrease the utility by penalizing the cost to \(-\Delta u(T_{i(i_{c})})\).
- (1.2) When the number of large defectors are more than one, the large defectors will try and deliberately rush in order to move towards the target. As a result of this conflict one of the large defectors will be able to move while the rest of the defector(s) and all the cooperators would remain at the same location. Due to the equiprobable chance available in getting to the next move by the large defectors, the payoff for the large defectors is to gain the utility by reducing the cost of \(\frac{\Delta u(T_{i(i_{c})})}{L_{n_{def}}}\). Besides that, the large defectors will face a conflict cost which is denoted by the time delay \(t_{d}\). When the large defectors try to push each other in order to move, there will be a little delay in time. Thus, the payoff for the large defectors is to gain the utility by reducing the cost of \(\frac{\Delta u(T_{i(i_{c})})}{L_{n_{def}}}-~t_{d}\) . While the payoff for the other defectors and cooperator(s) is to lose the utility by increasing the cost of \(-\Delta u(T_{i(i_{c})})\).
- (1.3) When there is no large defector, the defectors will try and push in order to move. As a result of this conflict one of the defectors will be able to move while the rest of the defector(s) and all the cooperators would remain at the same location. The payoff for the defectors is to gain the utility by reducing the cost of \(\frac{\Delta u(T_{i(i_{c})})}{n_{def}}-~t_{d}\) . While the payoff for the cooperator(s) is to lose the utility by increasing the cost of \(-\Delta u(T_{i(i_{c})})\).
- (2) For the case of a conflict with \(n_{coop}\) cooperators, \(n_{coop}~\geq~1\) and one defector, the defector will be able to move while all the cooperators will remain at the same location. The payoff for the defector is to gain the utility by reducing the cost of \(\Delta u(T_{i(i_{c})})\). Whereas, the payoff for the cooperator(s) is to decrease the utility by penalizing the cost to \(-\Delta u(T_{i(i_{c})})\).
- (3) For the case of a conflict with \(n_{coop}\) cooperators, \(n_{coop}~>~1\) and no defector, no winner is selected. Even though there is no winner and loser, the payoff is set as if all were cooperators, as the conflicting agents will move together with the crowd based on the social force model. Therefore, the payoff for the cooperators is set to increase the utility by reducing the cost of \(\frac{\Delta u(T_{i(i_{c})})}{n_{coop}}\).
The overall rules in order to decide the winner of the conflicts as described above can be summarized in Algorithm 1.

Based on the aforementioned assertions in Algorithm 1, a new \(n\times4\) game matrix is built as shown in Table 1. The payoff shown in Table 1 accounts only for the row wise agents since all the other agents will get an identical payoff for similar type of interactions. When a strategy is chosen by the agents in the row, the payoff received for the concerned agent is given in the corresponding cell of the matrix.
| \(L\geq1\) | \(L=0\) and \(EQ\geq1\) | \(L=0\) and \(EQ=0\) | ||||
| \(o_{1}\) | \(o_{2}\) | \(o_{1}\) | \(o_{2}\) | \(o_{1}\) | \(o_{2}\) | |
| \({0D}\), \({yC(y\geq1}\) | \({xD}\), \({yC(x\geq1}\), \({y\geq0}\) | \({0D}\), \({yC(y\geq1)}\) | \({xD}\), \({yC(x\geq1}\), \({y\geq0)}\) | \({0D}\), \({yC(y\geq1)}\) | \({xD}\), \({yC(x\geq1}\), \({y\geq0)}\) | |
| \(s_{1}\,(C)\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(-\Delta u(T_{i(i_{c})})\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(-\Delta u(T_{i(i_{c})})\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(-\Delta u(T_{i(i_{c})})\) |
| \(s_{2}\,(D)\) | \(\Delta u(T_{i(i_{c})})\) | \(-\Delta u(T_{i(i_{c})})-t_{d}\) | \(\Delta u(T_{i(i_{c})})\) | \(\frac{\Delta u(T_{i(i_{c})})}{EQ+1}-t_{d}\) | \(\Delta u(T_{i(i_{c})})\) | \(\Delta u(T_{i(i_{c})})-t_{d}\) |
| \(s_{3}\,(E)\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(-\Delta u(T_{i(i_{c})})\) | \(\Delta u(T_{i(i_{c})})\) | \(\frac{\Delta u(T_{i(i_{c})})}{EQ+1}-t_{d}\) | \(\Delta u(T_{i(i_{c})})\) | \(\Delta u(T_{i(i_{c})})-t_{d}\) |
| \(s_{4}\,(R)\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(-\Delta u(T_{i(i_{c})})-t_{d}\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(\frac{\Delta u(T_{i(i_{c})})}{EQ+1}-t_{d}\) | \(\frac{\Delta u(T_{i(i_{c})})}{y+1}\) | \(\Delta u(T_{i(i_{c})})-t_{d}\) |
Proposed updating strategies
Each agent intends to play the aforementioned game with its nearest neighbours, except the agents who are behind. A parallel update scheme (Smith & Wilson 2007) is utilized where strategies of all agents are updated simultaneously. Here we assume that agents update their strategies at each step taken, which is \(0.8s\). We study four types of agent behaviours viz., best-response, risk-seeking, risk-averse and risk-neutral. Under uncertainty conditions, risk-seeking, risk-averse and risk-neutral agents are considered. These type of agents have been discussed in Ibrahim et al. (2017). Under certainty conditions, the best-response agent is considered. In the context of an evacuation scenario, certainty condition refers to the ability of agents to respond by observing other agents' strategies in their neighbourhood during previous instances. Hence, best-response agents are myopic since they do not consider the future or past strategies of other agents in their neighbourhood (Heliövaara et al. 2013; von Schantz & Ehtamo 2015).
Here, a strategy of an agent \(i\) is considered as best response if the strategy of this agent at time \(t\) is at least as good as every other strategy of this agent against any other action of other agents \(i_{c}\) at the previous period \((t-1)\) as defined in Equation 3. In Equation 3, \(s_{i}^{t}\) refers to strategy of agent \(i\) on period \(t\), \(s_{i_{c}}^{(t-1)}\) refers to strategy of other conflicting agents, \(i_{c}\) on period \(t-1\),
| $$s_{i}^{t} \in BR(s_{i_{c}}^{(t-1)}) iff \forall s_{-i}^{t} \in S_{i}^{t}, u_{i}(s_{i}^{t},s_{i_{c}}^{t-1}) \geq u_{i}(s_{-i}^{t},s_{i_{c}}^{t-1})$$ | (3) |
In this proposed automated evacuation model, agents update their preferred speed based on the Available Safe Egress Time (\(T_{ASET}\)) and the Required Safe Egress Time (\(T_{RSET}\)). The \(T_{ASET}\) is the amount of time that elapses between the beginning of an emergency evacuation and the development of untenable conditions. The \(T_{RSET}\) is the amount of time (also measured from the beginning of emergency evacuation) required for agents to safely evacuate. Here, \(T_{ASET}\) is modelled using Equation 2.11. In Equation 3, \(T_{ASET_{o}}\) refers to the total available safe egress time at the beginning of the emergency evacuation, while, \(T_{elapsed}\) refers to the total time elapsed since the beginning of the emergency evacuation. \(T_{RSET}\) has been modelled in a new way as shown in Equation 5. In Equation 5, \(T_{i}\) refers to the agent’s estimated evacuation time and \(T_{i_{REQ}}\) refers to agent{'}s estimated evacuation time due to the total agents in front of the current agent \(i\). \(T_{i_{REQ}}\) is defined as in Equation 6, where \(n_{i}\) refers to total number of agents in front of the current agent \(i\) up to the exit, while \(\beta\) refers to the current flow at the exit door which means number of agents evacuated in a second. We assume that if no exit flow at the current period of a second, then the agents' estimated evacuation time depends on their speed and distance only as defined in Equation 1. Thus, \(T_{i_{REQ}}\) is assumed to be \(0\) if there is no exit flow at that particular second as modelled in Equation 6.
| $$T_{ASET}=T_{ASET_{o}}-T_{elapsed}$$ | (4) |
| $$T_{RSET}=T_{i}+T_{i_{REQ}}$$ | (5) |
| $$T_{i_{REQ}}= \begin{cases} n_{i}/\beta,& \text{if } \beta>0\\ 0,& \text{if } \beta=0 \end{cases}$$ | (6) |
Previous work (Heliövaara et al. 2013; Lakoba et al. 2005; Moussaïd et al. 2011; Saboia & Goldenstein 2012; von Schantz & Ehtamo 2015; Yu 2011) on crowd evacuation simulation do not relate available safe egress time \(T_{ASET}\) and agents' preferred speed, which is not fully realistic. In reality, agents will increase their preferred speed when they are in risky conditions where the required safe egress time \(T_{RSET}\) is quite low compared to the available safe egress time \(T_{ASET}\). In order to achieve realistic crowd evacuation simulation, we propose a new speed parameter, \(r\) which will be multiplied with preferred speed whenever \(T_{RSET}\) is more than \(0.8 \times T_{ASET}\) which intends to indicate high risk for the agents as modelled in Equation 7. In this Equation 7, preferred speed of agents is assumed to be \(1.34 m/s\) because this value is considered as the approximate mean value of walking speed for agents as specified in Helbing et al. (2002); Yu (2011). Agents will try their best in order to reach a safe place prior to facing a worst condition, thus agents will exert themselves to reach the safer place by updating their preferred speed. Here, we assume that the agents could be evacuated safely if \(T_{RSET}\) is not greater than \(0.8 \times T_{ASET}\).
| $$ |v_{i}^{0}|= \begin{cases} 1.34 \times r,& \text{if } T_{RSET} > 0.8 \times T_{ASET}\\ 1.34,& \text{otherwise} \end{cases}$$ | (7) |
Simulations
In this section, we present our computer simulations with respect to the proposed spatial evacuation model. Here, we examine evacuation under potential threat conditions. Thus, we set \(T_{ASET_{o}}\) which refers to the total available safe egress time at the beginning of the evacuation to \(60s\) to indicate evacuation under threat condition. For our simulations, we consider a rectangular room of size \(18m\times17m\) which consists of a single door of length \(1m\) located at the centre of one of the walls. The pedestrian room space at the range of locations \(x = 18\) and \(y = 0\) to \(y = 17\) belong to the walls and cannot be occupied by agents except at \(x = 18\) and \(y = 8\) to \(y = 9\) where the door is symmetrically located. Initially, \(200\) agents are placed at random positions in the range \(0 < x < 17\), \(1 < y < 16\) at time, \(t = 0\).
Critical conditions of the crowd can be characterised using three main attributes, namely, density, speed and flow of the crowd (Johansson 2008). Smith (1995) has investigated the relationship between these three characteristics in the context of large crowds and concluded that higher density will reduce the walking speed of the crowd and vice versa. Meanwhile, flowrate is a product of density and speed. Johansson (2008) has proposed a measure called crowd pressure which can be seen as an early warning sign for critical crowd situations. Crowd pressure is computed as a product of local velocity variance and local crowd density as shown below:
| $$P(\vec{r},t)=\rho(\vec{r},t)\times Var_{\vec{r},t}(\vec{V}),$$ | (8) |
Usually a typical crowd will want to leave the room very fast near the exit door and hence clogging will happen near the exit door (Helbing et al. 2002; Heliövaara 2007; Lakoba et al. 2005; Yang et al. 2014). This clogging will affect the evacuation time, flow and pressure of the crowd (Parry 2007; Saboia & Goldenstein 2012). Thus, we investigate the effect of crowd behaviours towards density and crowd pressure near the exit door at the location of \(x = 17\) and \(y = 8.5\) and at \(x = 15\) and \(y = 8.5\) which are at distance of \(1m\) and \(3m\) respectively from the centre of the exit door.
We perform simulations with respect to a heterogeneous population where agents of uncertainty behaviours viz., risk-seeking, risk-averse and risk-neutral behaviours of agents and certainty behaviours pertaining to best-response agents are combined in order to study the effect towards egress. For better comprehension of crowd dynamics during egress, we study the density and the local crowd pressure for various time delays caused by conflicts by repeating the simulations for \(10\) runs with different random frequencies of cooperators, defectors, evaluators and retaliators placed at random initial locations. We observe that for the aforementioned average values for the time frame of \(15s\) to \((0.7\times Total Escape Time)s\) a typical crowd could form an arch-like blocking near the exit. For each type of simulation, the number of agents with regard to one of the behaviours has been fixed, while the number of agents with the other three behaviours were randomly selected. For instance, if the number of risk-averse agents is fixed to \(50\) agents, the remaining \(150\) agents will be chosen randomly from the remaining three types of agents, viz. risk-seeking, risk-neutral and best-response agents. Then, the average values from \(10\) simulation runs will be studied as will be discussed in the following section. Here, we have included only two sources of randomness in the simulation model, viz. the random initial locations, and the number of the other three behaviours in each of the simulation runs.
Results and Discussion
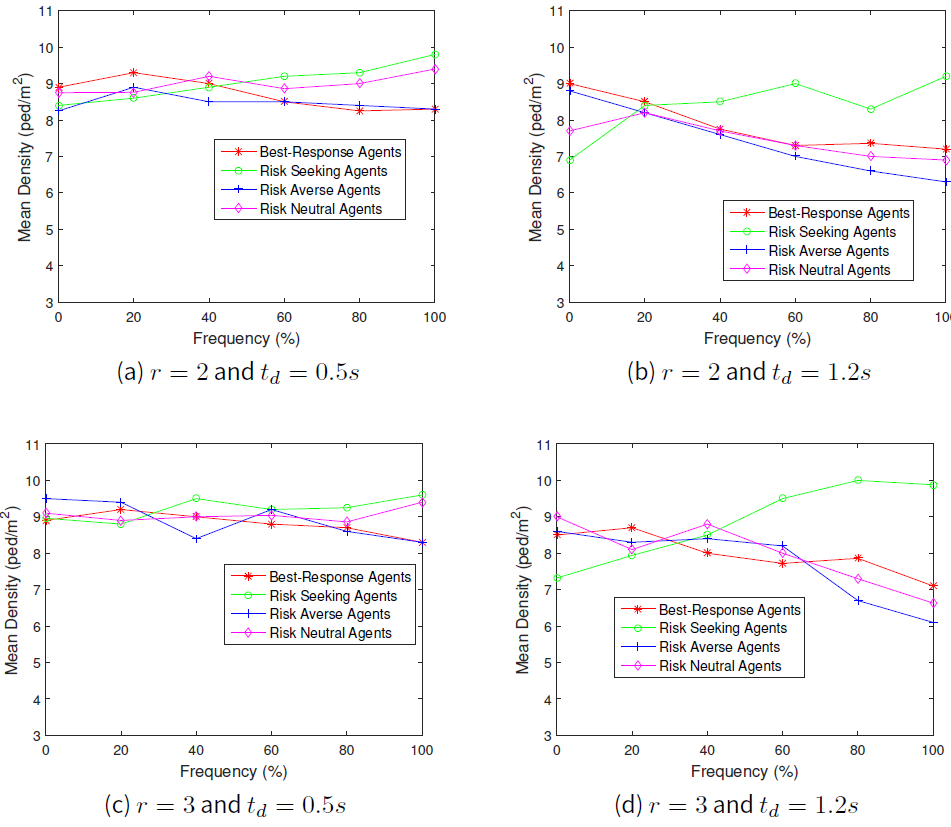
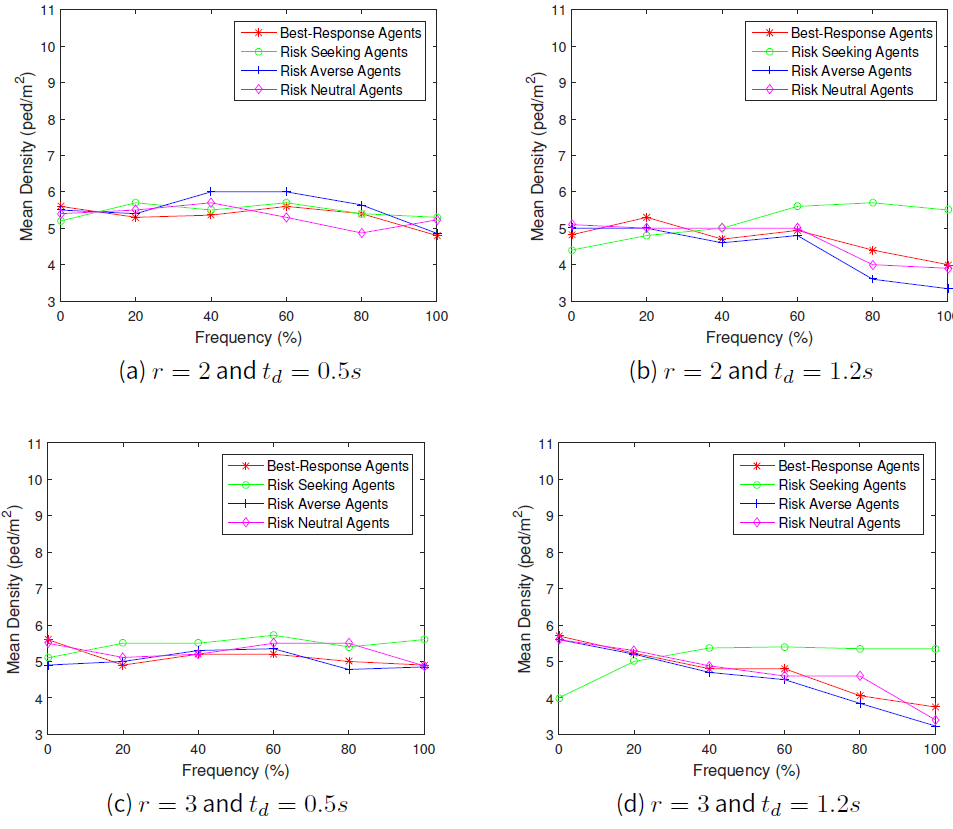
First of all, we set the speed parameter, \(r=2\) and then followed by \(r=3\). The results for average crowd pressure for the case \(1m\) distance and that of the \(3m\) distance from the exit door are shown in Figures1 and 2 respectively, while average local density at \(1m\) distance and at \(3m\) distance from the exit door are shown in Figures 3and 4 respectively.
Johansson (2008) has analysed video recordings of the crowd disaster that was encountered on January \(12\), \(2006\) at Mina during the last day of the Hajj, where \(363\) pilgrims lost their lives. The results in Johansson (2008) showed that crowd turbulence started when the local crowd pressure is more than \(0.02 s^{-2}\), while crowd disaster happens when the crowd pressure is between \(0.03\) to \(0.05 s^{-2}\). Besides that, it is reported in Helbing et al. (2000a); Smith & Dickie (1993) that agents are injured if the pressure acting on the agents, which is the total value of radial forces directed to them divided by their circumference, is more than \(1600Nm^{-1}\).
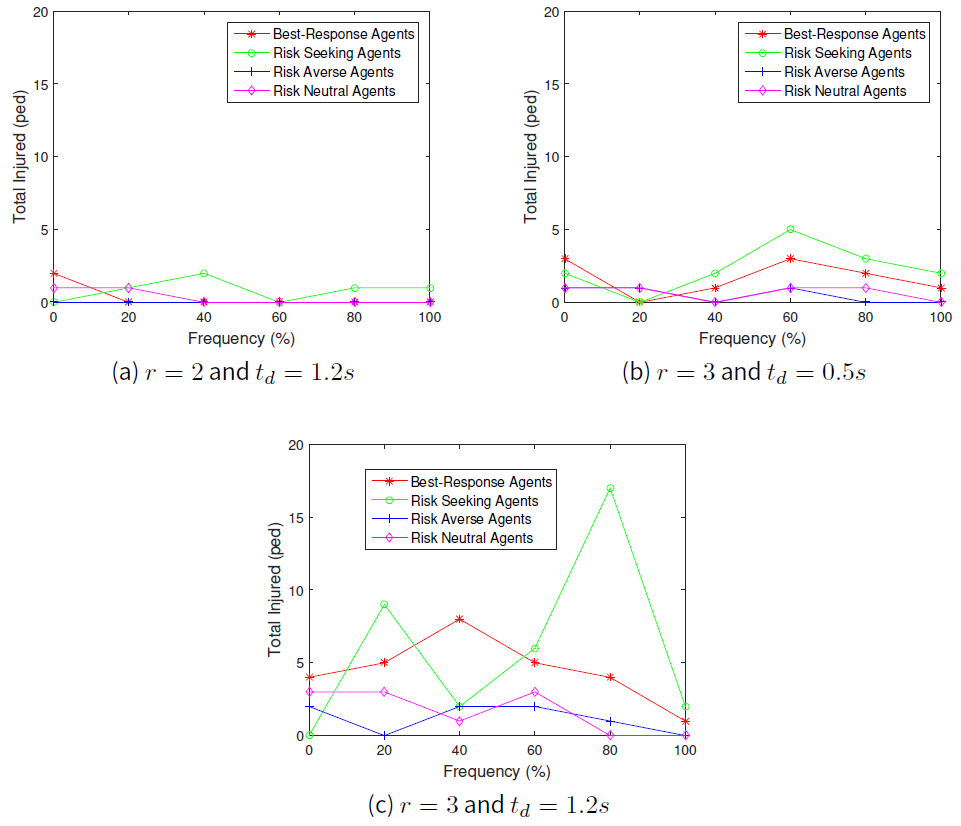
Our simulation results shows the relation between the local crowd pressure and number of injured agents as shown in Figures 2b and 5a, 2c and 5b and also 2d and 5c. Based on these simulation results, we observe that agents are getting injured when the value of local crowd pressure is more than \(0.02 s^{-2}\). In terms of the behaviours of the crowd, we observe that when the proportion of agents in a population of risk seeking agents gets increased, the average crowd pressure, average local density and the number of agents injured increases as well except for the crowd pressure at \(1m\) distance from the exit door as shown in Figure 1. Although the local density is quite high at the \(1m\) distance from the exit door as displayed in Figure 3, the value of the average crowd pressure at that specific location is less than \(0.02 s^{-2}\). This indicates that high density alone, which means overcrowding alone, cannot be utilized as a critical crowd condition and this is in agreement with the previous work of Johansson (2008).
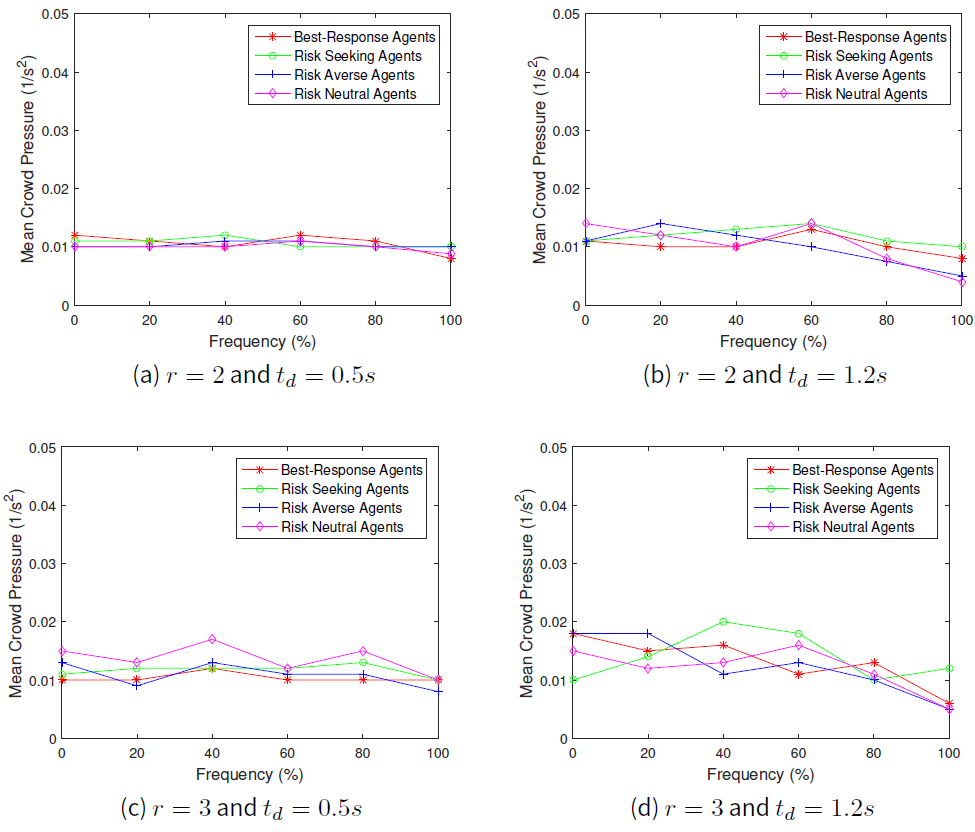
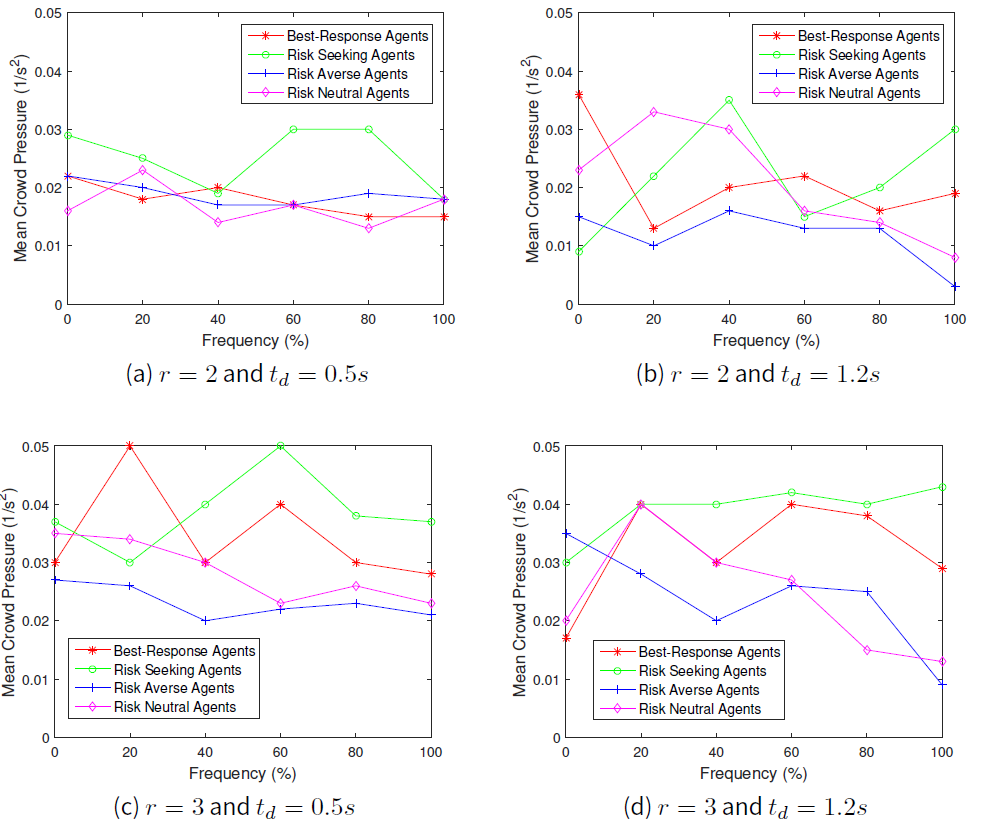
We also found that when the proportion of agents in a population of risk averse and risk neutral agents increased to \(100\) percent, the average crowd pressure is quite low with a small number of injured agents even though the speed parameter \(r\) and the conflict time delay \(t_{d}\) are set to \(3\) and \(1.2s\) respectively. Therefore, we perceive that crowd disaster could be prevented if the agents' population are full of risk averse and risk neutral agents even under potential threat conditions.
Besides that, we observed that crowd pressure is high when the speed parameter \(r\) is set to three and the conflict time delay \(t_{d}\) gets increased to \(1.2s\). Even when the speed parameter \(r\) is set to two, our results in Figure 2b indicate that when \(t_{d}\) is increased to \(1.2s\), the average crowd pressure is getting above \(0.03 s^{-2}\) while Figure 5a shows that there are few agents who are prone to injuries. Thus, our results indicate that conflict time delay can be a means also for the occurrences of crowd accident when the available safe egress time \(T_{ASET}\) is quite low than the required safe egress time \(T_{RSET}\).
Simulation for the case of a homogeneous population
Based on the simulation results discussed above, we further hypothesize that increasing the risk-seeking agents' population could lead to crowd disasters, while increasing risk-averse and risk-neutral agents could prevent crowd disaster. Thus, how these behaviours of agents get evolved and how they update their strategies during evacuation scenarios needs to addressed as well. To empirically justify these potential issues, we have run computer simulations in a typical homogeneous population where we assume that the agents' behaviours are unchanged throughout the simulations. This helps us to better study how these agents update their strategies based on a particular mode of behaviour. Table 2 shows the average equilibrium achieved by different types of behaviours for different conflict time delays. In Table 2, we assume a conflict time delay, \(t_{d}=0.5s\) for a low density condition, while conflict time delay, \(t_{d}=1.0s\) for a high density condition. The justification is that more time delay is required for the winning agents amidst conflicts as the density grows higher.
Based on Table 2, when the density of the crowd is less, we observe that risk-averse agents will act as cooperators half of the time and act as defectors or evaluators during the remaining half. While risk-neutral agents will act as a cooperators approximately one out of five times and as defectors or evaluators during the rest of the time. When the density grows higher, both risk-averse agents and risk-neutral agents will act mostly as cooperators. Thus, we perceive that in order to prevent crowd disaster, agents should exhibit risk-averse or risk-neutral behaviour as aforementioned.
| \(r=2\) \(t_{d}=0.5s\) | \(r=2\) \(t_{d}=1.0s\) | \(r=3\) \(t_{d}=0.5s\) | \(r=3\) \(t_{d}=1.0s\) | |
Risk-seeking | D = 37% E = 62% C = 0% R = 1% | D = 46% E = 53% C = 0% R = 1% | D = 47% E = 52% C = 0% R = 1% | D = 48% E = 51% C = 0% R = 1% |
Risk-averse | D = 16% E = 16% C = 51% R = 17% | D = 0% E = 2% C = 94% R = 4% | D = 19% E = 21% C = 42% R = 18% | D = 2% E = 2% C = 93% R = 3% |
Risk-neutral | D = 34% E = 46% C = 19% R = 1% | D = 13% E = 15% C = 70% R = 2% | D = 38% E = 42% C = 19% R = 1% | D = 11% E = 13% C = 72% R = 4% |
Best-response | D = 26% E = 28% C = 37% R = 9% | D = 18% E = 17% C = 62% R = 3% | D = 28% E = 28% C = 34% R = 10% | D = 19% E = 22% C = 56% R = 3% |
Comparison with an experimental evacuation
The Stapelfeldt experiments
The Stapelfeldt experiments were conducted in 1986, where 100 police cadets were grouped and evacuated (Stapelfeldt 1986) from a room in a chosen school gymnasium. The experimental evacuations were conducted through a single exit of variable width, utilising exit widths of 0.75, 0.80, 1.50 and 1.60m. The exit widths are changed by the opening and closing of a set of double doors. The experimental information revealed here concerns the evacuation of the room under ordinary conditions, without the effect of threat conditions. The dimensions of the experimental room are not revealed, but it has been stated that the room was rectangular in shape (Gwynne et al. 2005; Paulsen et al. 1995; Stapelfeldt 1986).
The data generated from this experiment is presented and compared against the model of the classical social force model (Helbing et al. 2000a), the social force model in Li et al. (2015) and our proposed spatial evacuation model as shown in Table 3. For our proposed spatial evacuation model, in order to indicate normal evacuation, we have set the \(T_{ASET_{o}}\) which refers to the total available safe egress time at the beginning of evacuation to \(250s\). Besides that, we have utilized dynamic conflict time delay \(t_{d}\) in which \(t_{d}\) is updated for each agent depending on the local crowd density (Equation 8). When the density is about \(4 person/m^2\) walking contact among the agents started to occur (Smith 1995; we have set \(t_{d}=0.5s\) if the local crowd density is less than \(4 person/m^2\). When the local crowd density is between \(4 person/m^2\) and \(5.55 person/m^2\), we have set the conflict time delay \(t_{d}=1.0s\). This is because it is reported in Fruin (1981) that possible crowd forces begin to occur when density reaches \(5.55 person/m^2\). Thus, we chose more conflict time delay. When local crowd density is more than \(5.55 person/m^2\), we have set \(t_{d}=1.5s\) indicating that more time delay is needed for the agents to be a winner of the conflict as the density grows higher.
As can be seen in Table 3, the average escape times by using the social force model of Helbing et al. (2000a) and Li et al. (2015) generate significantly longer escape times than our proposed model. Compared to experimental results, the social force model proposed in Li et al. (2015) produced an average escape time quite similar to our proposed model when the exit widths are \(1.5m\) and \(1.6m\). However, when the exit widths are \(0.75m\) and \(0.8m\), model of the Li et al. (2015) produced an average escape time longer than our proposed model (Table 3). These results show that our proposed spatial evacuation model produced robust and relevant results since the average escape times produced by our proposed model are quite similar to the experimental results in Stapelfeldt (1986) for all exit widths.
| EW = 0.75m | EW = 0.80m | EW = 1.50m | EW = 1.60m | |
| Experimental Results (s) | 55 | 50 | 30 | 26 |
| Social Force Model in Helbing et al. (2000a) (s) | 130 | 115 | 38 | 33.8 |
| Social Force Model in Li et al. (2015)(s) | 94.37 | 87.64 | 31.3 | 29.24 |
| Proposed Model (s) | 66.15 ± 1.43(SD) | 60.75 ± 2.5(SD) | 31.36 ± 1.5(SD) | 30 ± 1.5(SD) |
Conclusion
We have systematically investigated the effect on egress under uncertainty and certainty scenarios that could possibly arise during emergency evacuations. In particular, we examine the best-response, risk-seeking, risk-averse and risk-neutral behaviours of agents (pedestrians) using the norms of a typical evolutionary game theory approach. The model code can be found at https://www.comses.net/codebases/6e50a83d-e41d-456b-9fc2-10e73e533e20/releases/1.0.0/. We have simulated evacuation scenarios in a continuous space using the classical social force model, where the impatient and patient agents have been modelled with different individual parameter settings. In summary, the main contributions of our research are as follows:
- Systematic investigation of the effect of evolution of crowd behaviours that are prevalent in the heterogeneous population pertaining to critical conditions of the crowd via evolutionary game theory-oriented simulations under potential threat conditions.
- Formulation of the dynamical cost function for each of the agents with the incorporation of the size of the agents and conflict time delay.
- Development of an automated spatial evacuation model.
- Important findings on how a typical crowd should evolve and behave in order to prevent crowd disaster.
We have set out a framework that can be used by designers of crowd control and evacuation systems. They will have to re-run our model with their specific values for parameters such as room size, repulsive force and its range, angle under which agents are in conflict, etc. Our simulations transparently show what kind of crowd behaviours can be expected during various evacuation scenarios. One of the limitations of the proposed work is we have assumed that the agents interact only with their neighbours. It would also be interesting in future to consider also groups of agents that act as a cluster (e.g. families) that would surely show another behaviour with respect to each other. Another limitation of the current proposed work is we have included only two sources of randomness in the simulation model, viz. the random initial locations, and the other three behaviours in the simulation. For future avenues or research, we would examine the effect of random behaviour of the crowd towards evacuation. In the near future, we will also consider a detailed investigation of evacuation scenarios in rooms of different sizes subject to the presence of obstacles.
Acknowledgements
This research is supported by the LRGS Grant: 203/PTS6728001 and the RUI Grant: 1001/PKOMP/811290 awarded by the Ministry of Education, Malaysia and Universiti Sains Malaysia respectively. The first author would like to thank the International Islamic University Malaysia (IIUM) and the Ministry of Higher Education Malaysia (MOHE) for providing a PhD scholarship. The authors also thank Julian Schmidt and Alexander Späh for sharing their Panic Simulator which simulates the escape panic behaviour proposed by Helbing et al. (2000a).References
BOUZAT, S. & Kuperman, M. (2014). Game theory in models of pedestrian room evacuation. Physical Review E, 89(3), 032806 [doi:10.1103/PhysRevE.89.032806]
CHEN, X. (2006). Microsimulation of Evacuation Strategies. Ph.D. thesis, Texas State University - San Marcos.
CHIZARI, H., Malekinezhad, F., Embi, M. R., Yatim, Y. M., Razak, S. A., bin Haji Ahmad, M. H. & Bakhtiari, M. (2013). Agent-based approach for modeling evacuee uncertainty behavior using game theory model. Life Science Journal, 10(3), 1350–1355
CHRISTENSEN, K. & Sasaki, Y. (2008). Agent-based emergency evacuation simulation with individuals with dis-abilities in the population. Journal of Artificial Societies and Social Simulation, 11(3), 9: https://www.jasss.org/11/3/9.html.
COLOMBO, R. M. & Rosini, M. D. (2005). Pedestrian flows and non-classical shocks. Mathematical Methods in the Applied Sciences, 28(13), 1553–1567 [doi:10.1002/mma.624]
FRIBERG, M. & Hjelm, M. (2015). Mass evacuation-human behavior and crowd dynamics-what do we know? Department of Fire Safety Engineering Lund University, Sweden.
FRUIN, J. (1981). Crowd disasters-a systems evaluation of causes and countermeasures. Inc. US National Bureau of Standards, pub. NBSIR, (pp. 81–3261)
GWYNNE, S., Galea, E., Owen, M., Lawrence, P. & Filippidis, L. (2005). A systematic comparison of building exodus predictions with experimental data from the Stapelfeldt trials and the Milburn house evacuation. Applied Mathematical Modelling, 29(9), 818–851
HAO-NAN, W., Dong, C., Wei, P., Yu, X. & Hong-Di, H. (2014). Evacuation of pedestrians from a hall by game strategy update. Chinese Physics B, 23(8), 080505 [doi:10.1088/1674-1056/23/8/080505]
HELBING, D., Farkas, I. & Vicsek, T. (2000a). Simulating dynamical features of escape panic. Nature, 407(6803), 487–490.
HELBING, D., Farkas, I. J., Molnar, P. & Vicsek, T. (2002). Simulation of pedestrian crowds in normal and evacuation situations. Pedestrian and evacuation dynamics, 21(2), 21–58.
HELBING, D., Farkas, I. J. & Vicsek, T. (2000b). Freezing by heating in a driven mesoscopic system. Physical Review Letters, 84(6), 1240.
HELBING, D., Johansson, A. & Al-Abideen, H. Z. (2007). Dynamics of crowd disasters: An empirical study. Physical Review E, 75(4), 046109. [doi:10.1103/PhysRevE.75.046109]
HELBING, D. & Molnar, P. (1995). Social force model for pedestrian dynamics. Physical Review E, 51(5), 4282.
HELBING, D., Molnár, P., Farkas, I. J. & Bolay, K. (2001). Self-organizing pedestrian movement. Environment and Planning B: Planning and Design, 28(3), 361–383. [doi:10.1068/b2697]
HELBING, D. & Mukerji, P. (2012). Crowd disasters as systemic failures: analysis of the love parade disaster. EPJ Data Science, 1(1), 7.
HELIÖVAARA, S. (2007). Computational Models for Human Behavior in Fire Evacuations. Master thesis, Department of Engineering Physics and Mathematics, Helsinki University of Technology.
HELIÖVAARA, S., Ehtamo, H., Helbing, D. & Korhonen, T. (2013). Patient and impatient pedestrians in a spatial game for egress congestion. Physical Review E, 87(1), 012802.
HENDERSON, L. (1971). The statistics of crowd fluids. Nature, 229, 381–383. [doi:10.1038/229381a0]
HERRERA, F. & Lozano, M. (2000). Gradual distributed real-coded genetic algorithms. IEEE Transactions on Evolutionary Computation, 4(1), 43–63.
HOOGENDOORN, S. & Bovy, P. (2000). Gas-kinetic modeling and simulation of pedestrian flows. Transportation Research Record: Journal of the Transportation Research Board, (1710), 28–36. [doi:10.3141/1710-04]
HUANG, K., Zheng, X., Yang, Y. & Wang, T. (2015). Behavioral evolution in evacuation crowd based on heterogeneous rationality of small groups. Applied Mathematics and Computation, 266, 501–506.
HUGHES, R. L. (2002). A continuum theory for the flow of pedestrians. Transportation Research Part B: Methodological, 36(6), 507–535. [doi:10.1016/S0191-2615(01)00015-7]
HUGHES, R. L. (2003). The flow of human crowds. Annual Review of Fluid Mechanics, 35(1), 169–182.
IBRAHIM, A. M., Venkat, I. & De Wilde, P. (2017). Uncertainty in a spatial evacuation model. Physica A: Statistical Mechanics and its Applications, 479, 485–497. [doi:10.1016/j.physa.2017.03.024]
IBRAHIM, A. M., Venkat, I., Subramanian, K., Khader, A. T. & Wilde, P. D. (2016). Intelligent evacuation management systems: A review. ACM Transactions on Intelligent Systems and Technology (TIST), 7(3), 36.
JOHANSSON, A., Helbing, D., Al-Abideen, H. Z. & Al-Bosta, S. (2008). From crowd dynamics to crowd safety: a video-based analysis. Advances in Complex Systems, 11(04), 497–527. [doi:10.1142/S0219525908001854]
JOHANSSON, A. F. (2008). Data-Driven Modeling of Pedestrian Crowds. Ph.D. thesis, Dresden, Techn. Univ., Diss., 2008.
KLAR, A. & Wegener, R. (2000). Kinetic derivation of macroscopic anticipation models for vehicular traffic. SIAM Journal on Applied Mathematics, 60(5), 1749–1766. [doi:10.1137/S0036139999356181]
KNOESTER, D. B., Goldsby, H. J. & McKinley, P. K. (2013). Genetic variation and the evolution of consensus in digital organisms. IEEE Transactions on Evolutionary Computation, 17(3), 403–417.
LAKOBA, T. I., Kaup, D. J. & Finkelstein, N. M. (2005). Modifications of the Helbing-Molnar-Farkas-Vicsek social force model for pedestrian evolution. Simulation, 81(5), 339–352. [doi:10.1177/0037549705052772]
LI, M., Zhao, Y., He, L., Chen, W. & Xu, X. (2015). The parameter calibration and optimization of social force model for the real-life 2013 Ya’an earthquake evacuation in China. Safety Science, 79, 243–253.
MA, W. (2013). Agent-Based Model of Passenger Flows in Airport Terminals. Ph.D. thesis, Queensland University of Technology.
MOUSSAÏD, M., Helbing, D. & Theraulaz, G. (2011). How simple rules determine pedestrian behavior and crowd disasters. Proceedings of the National Academy of Sciences, 108(17), 6884–6888.
PÄRNÄNEN, I. (2015). Spatial Game Approach to Describe Risky Agents in Evacuation Situations. Master’s thesis, School of Science, Aalto University.
PARRY, G. W. (2007). The Dynamics of Crowds. Master’s thesis, Department of Mathematical Sciences, University of Bath.
PAULSEN, T., Soma, H., Schneider, V., Wiklund, J. & Lovas, G. (1995). Evaluation of simulation models of evacuation from complex spaces. SINTEF Report STF75 A, 95020.
PLUCHINO, A., Garofalo, C., Inturri, G., Rapisarda, A. & Ignaccolo, M. (2014). Agent-based simulation of pedestrian behaviour in closed spaces: a museum case study. Journal of Artificial Societies and Social Simulation, 17(1), 16: https://www.jasss.org/17/1/16.html. [doi:10.18564/jasss.2336]
SABAR, N. R., Abawajy, J. & Yearwood, J. (2017). Heterogeneous cooperative co-evolution memetic differential evolution algorithm for big data optimization problems. IEEE Transactions on Evolutionary Computation, 21(2), 315–327. [doi:10.1109/TEVC.2016.2602860]
SABOIA, P. & Goldenstein, S. (2012). Crowd simulation: applying mobile grids to the social force model. The Visual Computer, 28(10), 1039–1048.
SHI, D.-M. & Wang, B.-H. (2013). Evacuation of pedestrians from a single room by using snowdrift game theories. Physical Review E, 87(2), 022802. [doi:10.1103/PhysRevE.87.022802]
SMITH, D. A. & Wilson, R. E. (2007). Dynamical pair approximation for cellular automata with shuffle update. Journal of Physics A: Mathematical and Theoretical, 40(11), 2651.
SMITH, R. (1995). Density, velocity and flow relationships for closely packed crowds. Safety Science, 18(4), 321– 327. [doi:10.1016/0925-7535(94)00051-4]
SMITH, R. A. & Dickie, J. F. (1993). Engineering for Crowd Safety. Amsterdam, NL: Elsevier.
STAPELFELDT, J. (1986). Angst-und paknikstande aus der sicht des brandschutzes (conditions of anxiety and panic from the viewpoint of fire protection). Vfdb-Zeitschrik, 2, 41.
SUN, X.-Y., Jiang, R., Hao, Q.-Y. & Wang, B.-H. (2010). Phase transition in random walks coupled with evolutionary game. EPL (Europhysics Letters), 92(1), 18003.
SURYOTRISONGKO, H. & Ishida, Y. (2011). Emergence of cooperation as the impact of evacuee’s solidarity. In Safety, Security, and Rescue Robotics (SSRR)2011 IEEE International Symposium on,, (pp. 265–271). IEEE. [doi:10.1109/SSRR.2011.6106783]
VON Schantz, A. & Ehtamo, H. (2015). Spatial game in cellular automaton evacuation model. Physical Review E, 92(5), 052805.
WIRZ, M., Franke, T., Roggen, D., Mitleton-Kelly, E., Lukowicz, P. & Tröster, G. (2013). Probing crowd density through smartphones in city-scale mass gatherings. EPJ Data Science, 2(1), 5. [doi:10.1140/epjds17]
YANG, X., Dong, H., Wang, Q., Chen, Y. & Hu, X. (2014). Guided crowd dynamics via modified social force model. Physica A: Statistical Mechanics and its Applications, 411, 63–73.
YOU, L., Hu, J., Gu, M., Fan, W. & Zhang, H. (2016). The simulation and analysis of small group effect in crowd evacuation. Physics Letters A, 380(41), 3340–3348. [doi:10.1016/j.physleta.2016.08.012]
YU, W. (2011). Agent-Based Modeling of Human Cooperation and Coordination in Social Systems. Ph.D. thesis, Shanghai University.
ZHENG, X. & Cheng, Y. (2011). Modeling cooperative and competitive behaviors in emergency evacuation: A game-theoretical approach. Computers & Mathematics with Applications, 62(12), 4627–4634. [doi:10.1016/j.camwa.2011.10.048]

