Introduction
We present a spatial agent-based model of the emergence and proliferation of premodern complex societies in an isolated region initially inhabited by simple societies.
The concepts of simple societies and premodern complex societies are controversial, and authors define them in different ways. We use the following definitions, which emphasize their differences in social organization, scale, and food production methods.
The archetypal simple society has no social classes and little division of labor beyond gender- and age-specific tasks. People produce food using extensive methods, such as persistence hunting, honey and plant gathering, slash-and-burn agriculture, and nomadic pastoralism. Simple societies range in scale and complexity from a single family to an alliance of clans led by a Big Man. Examples of simple societies are the !Kung, Machiguenga, Nganasan, Yanomami, Inupiaq, Tsembaga, Turkana, Central Enga, and Kirghiz (Johnson & Earle 2000).
The archetypal premodern complex society is socially stratified, and each social class performs specific tasks. Elites govern the society and are responsible for its defense, while commoners produce food using intensive methods, such as gillnetting, sedentary agriculture, and pastoral farming. Premodern complex societies range in scale and complexity from simple chiefdoms to ancient empires. Examples of premodern complex societies are the Trobriand and Hawaiian islanders, the Basseri, Medieval France and Japan, and the Inca Empire (Johnson & Earle, op cit.)[1].
The model connects intrasocietal processes with geographical processes that give rise to dynamics that are qualitatively consistent with four case studies: the Ubaid period in Mesopotamia, the Mississippian chiefdoms of the Savannah River, Ancient Mesoamerica, and Zomia.
At the intrasocietal level, the model integrates the following processes:
- Malthusian-Ricardian demographics: the assumption that fertility is an increasing function of per capita income and that the marginal productivity of labor is a decreasing function of the number of laborers (Malthus 1798; Ricardo 1817).
- Scalar stress: the pressure exerted by population size on the institutions that hold society together. In general, the institutions of complex societies are more stress resistant than the institutions of simple societies (Johnson 1982).
- Social fission: the splitting of a social group into two or more separate groups (Seymour-Smith 1986).
- Sociocultural evolution: the transit of a society from lower to higher levels of complexity (Seymour-Smith 1986).
- Societal collapse: A drastic decrease in a society's complexity and population size (Diamond 2005).
At the geographical level, the model includes warfare for territory and captives, territorial division due to social fission, and territorial disintegration due to societal collapse.
Evidence from archaeology and history shows that more complex societies geographically displace simpler ones over time, but this process is not linear: there is an ebb and flow, in which complex societies emerge for a while, and then disappear. The reason for this pattern has remained elusive: none of the theories proposed so far have been able to simultaneously explain all of the phenomena observed. We integrated elements of these theories into a single model, and conducted simulations to see how social complexity would emerge over time. The model we tested produces a geographical and temporal pattern that fits the historical facts: it produces a progression from simple to complex societies, the complex societies arise and disappear---sometimes collapsing en masse---and three qualitatively distinct eras emerge. Slow change in a single variable drives all of these results: technological progress in intensive food production methods, which takes place at an almost imperceptible pace.
In Sections 1.11-1.31, we outline the model in a story-like format and justify the model assumptions on empirical and theoretical grounds. In Sections 1.32-1.39, we review related models.
The rest of this paper is organized as follows: In Section 2, we formalize the model. In Section 3, we present and discuss the results. In Section 4, we make final remarks.
The model as a story
Here we describe our model in an intuitive way. We justify its assumptions in footnotes scattered throughout the text. Some of these footnotes point to appendices A and B, where we elaborate on the evidence and theories that inspire the model. In appendix Appendix A, you will find alternative theories and pieces of evidence that the model abstracts away.
In the model, there are two types of artificial societies: simple societies and complex societies.
Simple societies produce food using extensive methods. In simple societies, everybody participates in food production, and they form a militia in case of war. We call the members of simple societies “free people” because they are free from servitude. Simple societies are computational representations of acephalous local groups and Big Man collectivities[2].
Complex societies practice intensive agriculture. In complex societies, the populations separate into two hereditary social classes: a peasantry and landed warrior elite[3]. The peasants work the land to produce food. They take a fixed percentage of the food produced, and they constitute a professional army[4]. Complex societies are computational representations of agrarian chiefdoms, archaic states, and ancient empires.
Simple and complex societies coexist in a simulated continent. This continent has two areas: a core land and a marginal land. The core land is flat and clear. It can be ploughed using draft animals and irrigated by means of artificial dams and canals. Extensive food production is feasible there, but intensive agriculture is more productive; for any combination of labor and land, intensive agriculture yields a larger quantity of food than extensive food production methods. The marginal land, however, is rugged, impassable to draft animals, and impossible to irrigate artificially. For these reasons, only extensive food production methods are feasible there [5]. (We imagine the simulated continent as a valley surrounded by mountains, steppes, and marshes. But the continent can also represent other topographies, such as a plateau surrounded by deserts and jungles. The relevant geographic variables are roughness and suitability for intensive agriculture.)
Whether a society uses an extensive method of food production or practices intensive agriculture, the marginal productivity of labor is a decreasing function of the number of laborers. That is, for a given amount of land, each additional laborer produces less food than the previous one[6].
Simple societies diversify the risk of food production failure; for example, hunter-gatherers target a wide variety of species, slash-and-burners do intercropping, nomadic pastoralists traverse vast territories and supplement their diet by hunting, and so forth. Complex societies, alternatively, grow few high-yield crops, typically cereals, tubers, or legumes. These crops are vulnerable to global productivity shocks, for instance, spells of good or bad weather affecting the entire simulated continent, or a pest that damages the crops throughout the core land[7].
There is no progress in extensive food production methods. Intensive agriculture, however, progresses over time, though almost imperceptibly[8]: Crops improve continuously through intentional or unintentional selective breeding. Over the course of centuries, more advanced technologies replace the established ones, for instance, the hoe replaces the digging stick, the ard replaces the hoe, and the moldboard plow replaces the ard. In between technological innovations, technologies are incrementally refined[9]. The constant technological progress translates into a slow but steady increase in productivity; the same number of peasants on the same amount of land produces a little more food in each period than in the previous period, discounting the effect of random productivity shocks.
In the simulated continent, societies constantly fight each other with two objectives: snatching land from neighboring societies and, in the case of complex societies, taking captives that the warrior elite force into peasant servitude[10].
The only strategic consideration in the decision to attack a neighboring society is the probability of success, which depends on relative military strength. This implies that stronger societies are more likely to attack and less likely to be attacked than weaker societies. Military strength, in turn, depends on the size of the militia or professional army and its effectiveness in different types of terrain. In the core land, where the ground is flat and clear, a phalanx of heavily armed warriors can easily crush an equal number of militiamen scantly equipped with mallets and wooden shields. In the marginal land, the militiamen have the advantage: the terrain is irregular and full of obstacles, the horses cannot cross it, and the heavily armed warriors trudge their way through narrow and uncharted roads and are easily ambushed by the same number of militiamen[11].
We assume that simple societies are less belligerent than complex societies: everything else being equal, simple societies are less likely than complex societies to launch an attack[12].
The rate of population growth of a simple society, a peasantry, or a warrior elite is equal to the fertility rate of its members, minus the mortality rate, plus the net inflow of captives from neighboring societies. The fertility rates of free people, peasants, and warriors are directly proportional to their incomes and inversely proportional to the cost of childrearing, which is different for the three groups. This cost is significantly higher for warriors than for free people and peasants because warriors have to intensively train their children for war and provide them with expensive equipment (e.g., horses, iron swords, plate armor)[13]. The mortality rates of free people, peasants, and warriors are partly explained by war and partly by other causes. The mortality rate from war for a particular society depends on how often it fights against its neighbors and the casualty rate in battle. The mortality rate from other causes, including natural deaths, is exogenous to the model.
Combined, the assumptions about labor productivity and endogenous fertility imply that each simple society, each complex society, each social class within a complex society, and the simulated continent as a whole follow Malthusian-Ricardian demographic dynamics[14].
The clans that constitute a simple society compete to obtain a larger share of the society's resources and to increase their political influence. Clan competition acts as a centripetal force that pushes society apart; however, the competing clans are held together by bonds of reciprocity made through gift-exchange and intermarriage, by the mediation of the society's leader, and by ceremonies that foster group identity (for example, the cult of a mythical common ancestor that creates the illusion of kinship between clans). These institutions of social cohesion are effective only when a simple society is small. When the population of a simple society grows beyond a certain threshold, clan feuds cause the society to fission into two smaller simple societies---in almost every case[15]. The threshold is a measure of institutional effectiveness[16].
Moreover, the population threshold for an internal crisis is not fixed. It can be raised or lowered by a "political shock". Positive political shocks are events that reduce the probability of an internal crisis, for example, the marriage between the son of a clan leader and the daughter another, sealing an alliance between the two clans. Negative political shocks are events that increase the probability of an internal crisis, for example, the discovery of a sexual affair between a man and a woman from rival clans[17].
There is, however, a small probability that a populous simple society will stay together by reorganizing itself as a complex society. Complex societies develop institutions that coordinate large groups of people and deter antisocial behaviors. For example, a written legal code; a priestly bureaucracy that enforces the law, collects taxes, and organizes the construction of public works, such as intricate irrigation systems, paved roads, and defensive stone walls; an organized religion that sanctifies class structure and provides a sense of identity to a multi-ethnic population; and extravagant religious ceremonies that confirm that the monarch is god[18].
Complex societies face two types of internal crises: civil war and collapse.
Civil war is a risk for lcomplex societies. Large populations stress the formal and informal institutions that maintain social cohesion (e.g., the bureaucracy and asabiyya). If the population of a complex society exceeds a critical threshold, institutions fail, the warrior elite starts a civil war, and the complex society fissions into two[19].
The population threshold for a civil war, however, is not fixed. It can be raised or lowered by a political shock. Positive political shocks are events that reduce the probability of a civil war. An example is a king successfully predicting an eclipse, thereby proving to his subjects that he is a god. Negative political shocks are events that increase the probability of a civil war; for example, the death of a sage king who is succeeded by an incompetent son.
Collapse occurs when peasants' per capita incomes drop below a “catastrophic level”. Starved, the peasants revolt or flee, the impoverished elite disbands, and the complex society disintegrates into a myriad of simple societies[20].
Finally, the initial state of the model is the following: when history begins, a great number of simple societies populate the continent. Complex societies are yet to emerge.
Related models
The model we propose integrates elements from several prior models.
Dow and Reed (2013), and Rowthorn, Guzmán, and Rodríguez-Sickert (2014) formalized various elements of conflict and functionalist theories of social stratification. They used microeconomic models augmented with Malthusian-Ricardian dynamics.
In Dow and Reed's model, a group of people reside in an open access region. A subgroup encloses the most productive land, creating economic inequality between insiders and outsiders. The insiders thrive and eventually cease to work, at which point they turn into a hereditary elite and let outsiders in to serve as peasants.
Rowthorn and colleagues modeled an isolated archaic state, divided into a peasantry and a landed warrior elite. In line with the historical evidence systematized by Andreski (1968), the model predicts that the cost of raising, training, and equipping a warrior determines the relative sizes of both social classes and the degree of economic inequality. Rowthorn and colleagues also derived conditions under which the social contribution of the warrior elite discourages a peasant revolution.
Cioffi-Revilla (2005) proposed a macro-level simulation model of the path to social complexity. In his model, an initially simple society experiments with a series of random situational changes, such as a drought or the threat of an invasion. A situational change leads to a sequence of political events that have three possible outcomes: the society becomes extinct, it survives without change, or it develops new political traits, for instance, the specialization of labor, the emergence of social norms, or social stratification.
Doran pioneered the use of agent-based models to explore the trajectories to social complexity, focusing on Paleolithic social change (Doran 2000; Doran & Palmer 1994; Doran et al. 1995). Doran has also studied the role of communication in societal processes that support or undermine social structure. For example, he built a model that shows that boundedly rational agents can elaborate collective false belief systems that enhance social welfare (Doran 1998). He also built a model of insurgency that shows that communication is crucial to a successful rebellion (Doran 2005).
Younger (2002) created MICROS, a flexible platform to program agent-based models of simple and complex societies. He has used MICROS to investigate a wide range of social phenomena related to social complexity: in simple societies, resource sharing and theft, reciprocity, sanctions, and reputation (2003;2004; 2005); in complex societies, leadership, centrally managed food storage, warfare, interpersonal violence, and social norms (2010; 2011). In a recent book, Younger applied his models to explain the social organization of pre-contact Polynesian island societies (2012).
Turchin et al. (2013) developed a spatial model of the emergence of large-scale complex societies. In their model, societies coexist on a landscape that represents Eurasia between 1,500 BCE and 1,500 CE. Each society is a set of adjacent cells, and each cell has a vector of “ultrasocial traits” representing the presence or absence of prosocial norms and institutions. Societies compete in war and expand geographically by conquering cells. The military power of a society depends on its size and on its stock of ultrasocial traits. Warfare intensity depends on the spread of military technologies and on geographical factors. Ultrasocial traits develop in regions where warfare is intense, and tend to be lost elsewhere.
The Formalized Model
Here we formalize the simulation model described in the introduction. For future reference, Table 1 summarizes the parameters of the model, and Table 2 summarizes the variables whose values change over time.
| Parameter | Symbol | Default values |
| Number of periods | \(T\) | 10,000 |
| Geography | ||
| Area of the continent in number of cells | \(M^2\) | 10,000 |
| Area of the core in number of cells | \(M^2\) | 4,900 |
| Intersocietal wars | ||
| Belligerence coefficient of simple societies | \(\beta\) | 0.5 |
| Relative military advantage of armies in the core land | \(\phi\) | 10 |
| Relative military advantage of militias in the marginal land | \(\psi\) | 10 |
| Rate of death in war | \(\delta\) | 0.1 |
| Food production and distribution | ||
| TFP of extensive food production methods | \(A_{extensive}\) | 10 |
| Growth rate of the TFP of intensive agriculture | \(g\) | 0.01 |
| Weight of land in production / warriors’ share of the crops | \(\alpha\) | 0.3 |
| Scale parameter of the lognormal productivity shock | \(\sigma\) | 0.05 |
| Reproduction and deaths unrelated to war | ||
| Cost of children for free people | \({\kappa}_{freepeople}\) | 5 |
| Cost of children for peasants | \({\kappa}_{peasant}\) | 5 |
| Cost of children for warriors | \({\kappa}_{warrior}\) | 100 |
| Rate of deaths unrelated to war | \(\mu\) | 0.33 |
| Population of simple societies in period 1 | \(N_{simple,1}\) | 100 |
| Internal crisis in simple societies | ||
| Population threshold for an internal crisis | \(N_{simple}^*\) | 1,000 |
| Scale parameter of lognormal political shocks | \(\tau\) | 0.1 |
| Probability that a simple society will become complex during a crisis | \(\pi\) | 0.001 |
| Internal crisis in complex societies | ||
| Catastrophic income level | \(y^*\) | 2 |
| Population threshold for a civil war | \(N_{complex}^*\) | 107 |
| Scale parameter of lognormal political shocks | \(\upsilon\) | 0.1 |
| Parameter | Symbol |
| Geography | |
| Area of a simple society | \(L_{simple}\) |
| Area of a complex society | \(L_{complex}\) |
| Area of a complex society suitable for intensive agriculture | \(L_{intensive}\) |
| Population | |
| Total population of a simple society | \(N_{simple}\) |
| Peasant population of a complex society | \(N_{peasant}\) |
| Warrior population of a complex society | \(N_{warrior}\) |
| Total population of a complex society | \(N_{complex}\) |
| Military participation ratio | MRP |
| Territorial wars | |
| Military strength of a hostile society | \(S_{hostile}\) |
| Military strength of a threatened society | \(S_{threatened}\) |
| Probability that the hostile society will win the battle | \(p_{win}\) |
| Inherent belligerence of the hostile society | \(b_{hostile}\) |
| Probability that the hostile society will attack | \(p_{attack}\) |
| Food production and distribution | |
| TFP of intensive agriculture | \(A_{intensive}\) |
| Quantity of food produced by a simple society | \(Y_{simple}\) |
| Quantity of food produced by a complex society | \(Y_{complex}\) |
| Per capita income of free people | \(y_{freepeople}\) |
| Per capita income of peasants | \(y_{peasants}\) |
| Per capita income of warriors | \(y_{warriors}\) |
| Lognormal productivity shock | \(x\) |
| Income inequality in a complex society | INEQ |
| Reproduction and deaths unrelated to war | |
| Fertility rate of free people | \(n_{freepeople}\) |
| Fertility rate of peasants | \(n_{peasant}\) |
| Fertility rate of warriors | \(n_{warrior}\) |
| Population growth | |
| population growth rate of free people | \(r_{freepeople}\) |
| population growth rate of peasants | \(r_{peasant}\) |
| population growth rate of warriors | \(r_{warrior}\) |
| Internal conflict in simple societies | |
| Lognormal political shock | \(y\) |
| Internal conflict in complex societies | |
| Lognormal political shock | \(z\) |
Geography
The continent is a grid of \(M\times M\) cells divided into two areas: a core land and a marginal land. The core land is a square of size \(M_{core}\times M_{core}\) cells. The marginal land is a square frame that encloses the core land, consisting of \(M^{2}-M_{core}^{2}\) cells. Figure 1 depicts the topography of an example continent.
One or more societies exist in the continent, occupying its entire surface, as illustrated by the political map in Figure 1B. The territory of a society is a set of adjacent cells. Two cells are adjacent if they share one of their four sides. Cells that share only a corner are not adjacent. A territory can be located in the core land, in the marginal land, or in both. The area of a society is the number of cells that constitute its territory. The minimum area is one cell, and the maximum area is \(M^2\) cells, corresponding to the whole continent.
The frontier of a society is the subset of its cells that are adjacent to one or more cells belonging to another society. Figure 1C highlights the frontiers on the political map of the example continent. If two societies have frontier cells that touch each other, the two societies are neighbors. Figure 1D shows the network of neighboring societies implied by the frontiers in Figure 1C.
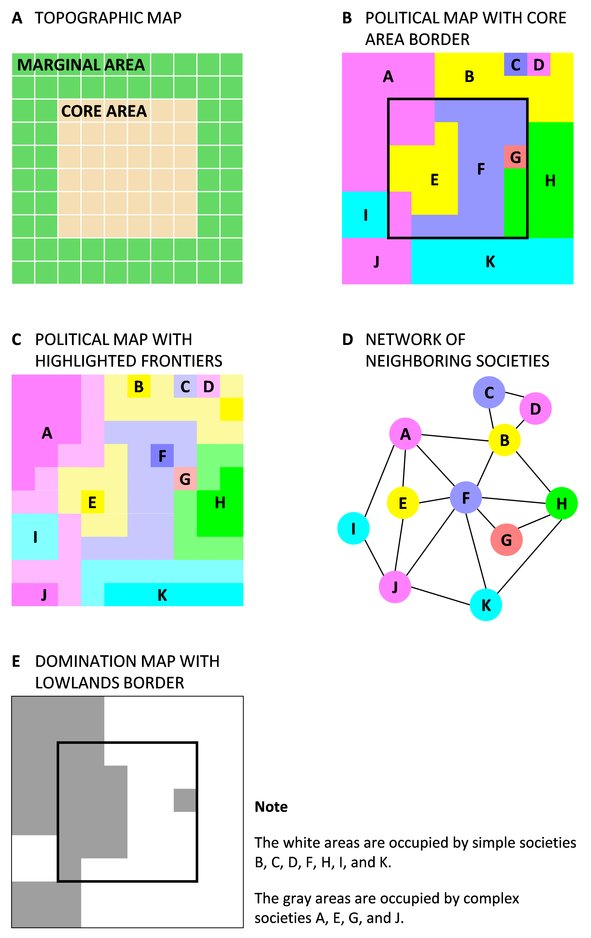
Figure 1E is the “domination map” of the example continent. It shows the zones dominated by simple societies and the zones dominated by complex societies.
We use variable \(L_{simple}\in\mathbb{N}_{>0}\) to denote the area of a simple society. The value of \(L_{simple}\) increases when the simple society expands its territory and decreases when it contracts. Different simple societies have different values of \(L_{simple}\).
Analogously, we use variable \(L_{complex}\in\mathbb{N}_{>0}\) to denote the area of a complex society. The value of \(L_{complex}\) increases when the complex society expands its territory and decreases when it contracts. Different complex societies have different values of \(L_{complex}\).
The sum of the areas of all societies is always \(M^{2}\).
Population
Variable \(N_{simple}>0\) denotes the population of a simple society. The value of \(N_{simple}\) increases when the society grows in population and decreases when its population declines. Different simple societies have different values of \(N_{simple}\). Everyone in a simple society participates in war, so the size of its militia is also \(N_{simple}\).
A complex society has two hereditary social classes: a peasantry and a landed warrior elite. We use variable \(N_{peasants}>0\) to denote the number of peasants and variable \(N_{warriors}>0\) to denote the number of warriors. Different complex societies have different values of \(N_{peasants}\) and \(N_{warriors}\). The value of \(N_{peasants}\) increases when the peasantry grows in population and decreases when its population declines. Analogously, the value of \(N_{warriors}\) increases when the warrior elite grows in population and decreases when its population declines. The total population of a complex society is
| $$N_{complex}=N_{peasants}+N_{warriors}.$$ | (1) |
The “military participation ratio” of a complex society is the size of its army relative to its total population:
| $$\text{MPR}=\frac{N_{warriors}}{N_{complex}}.$$ | (2) |
History of a continent
The history of a simulated continent is a sequence of periods. In the initial period of the simulation, all societies are simple societies. These societies are identical: Each occupies one cell and has a population of \(N_{simple,1}>0\), where \(N_{simple,1}\) is a parameter.
Each period has five stages:
- Intersocietal wars.
- Food production and distribution.
- Reproduction and natural deaths.
- Internal conflict in simple societies, leading to fissioning or complexification.
- Internal conflict in complex societies, leading to collapse or civil war.
In the following sections, we describe these five stages.
Intersocietal wars
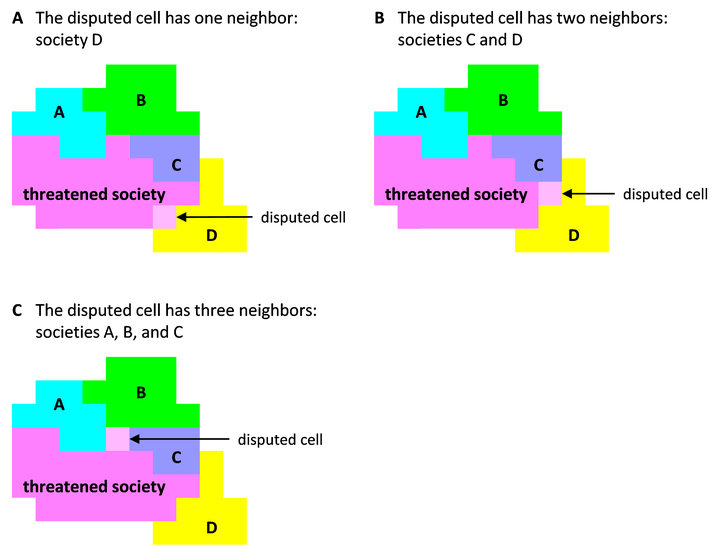
Battles take place in a random sequence, according to the following iterative routine. The routine is repeated \(K\) times, where \(K\) is the number of frontier cells on the political map at the beginning of the period, or until no frontier cells are left (this will happen if and only if, during the routine, a society takes over the whole continent). For example, the map of Figure 1C has 71 frontier cells, so \(K=71\).
An iteration begins by randomly choosing a frontier cell from the set of all frontier cells of all societies. This frontier cell will be the “disputed cell”. The society that owns the disputed cell will be the “threatened society”. Take note that the same cell could be randomly chosen again in subsequent iterations of this routine. Also, note that the cells that comprise the set of frontier cells can change from one iteration to the next, because frontiers change when societies steal cells from each other.
The disputed cell can be adjacent to one, two, or three societies that neighbor the threatened society. Figure 2 gives examples for these three cases. One of the neighboring societies is randomly chosen. It will be the “hostile society”.
The hostile society then considers attacking the threatened society. In making the decision to attack, the hostile society takes into account the probability of winning the battle. The probability of winning is
| $$ p_{win}=\frac{S_{hostile}}{S_{hostile}+S_{threatened}},$$ | (3) |
| $$p_{attack}=b_{hostile}p_{win},$$ | (4) |
Military strength depends on the size of the militia or army and its effectiveness in different types of terrain. In the core land, the military strength of a simple society is \(N_{simple}\), whereas the military strength of a complex society is \(\phi N_{warriors}\), where \(\phi >1\) is a parameter. In the marginal land, the military strength of a simple society is \(\psi N_{simple}\), where \(\psi >1\) is a parameter, and the military strength of a complex society is \(N_{warriors}\).
If the hostile society refrains from attacking its neighbor, the iteration ends with no consequences. However, if the hostile society attacks, there are two possible outcomes: the hostile society wins the battle and annexes the disputed cell, or the hostile society loses the battle and the threatened society keeps the disputed cell.
A fraction of the defeated society's population dies in battle. If the defeated society is simple, then \(\delta N_{simple}/L_{simple}\) people die, where \(\delta \in(0,1)\) is the probability of death in war. If the defeated society is complex, then \(\delta N_{warriors}/L_{complex}\) warriors die, and \(\delta N_{peasants}/L_{complex}\) peasants die.
In addition to annexing the disputed cell, a hostile complex society that wins a battle captures people from the threatened society and assimilates them as peasants. If the threatened society is simple, then the hostile society captures \((1-\delta)N_{simple}/L_{simple}\) people, where \(N_{simple}\) is the population of the threatened society, and \(L_{simple}\) is its area. If the threatened society is complex, then the hostile society captures \((1-\delta)N_{peasants}/L_{complex}\) peasants and \((1-\delta)N_{warriors}/L_{complex}\) warriors, where \(N_{peasants}\) and \(N_{warriors}\) are the peasant and warrior populations of the threatened society, and \(L_{complex}\) is its area.
Often, a society that loses a disputed cell preserves the unity of its territory, but there are two other cases. In the first case, the disputed cell is the entire territory of the threatened society. When it loses its only cell, the threatened society becomes extinct. Otherwise, it has chance to recover. In the second case, the disputed cell divides the threatened society into two or three disconnected territories. Each of these territories becomes a new society. The new societies inherit the social organization of the society from which they originated, and the population is divided among the new societies in proportion to their areas. Figure 3 presents examples of territory division.
A new iteration starts if any remain. Otherwise, the intersocietal wars routine ends.

Food production and distribution
A society's total food production is an increasing function of two inputs: labor and productive land. Labor is measured in the number of laborers, and land is measured in the number of cells. In a simple society, the amount of labor is equal to its total population, and the amount of productive land is equal to its entire territory. In a complex society, the amount of labor is equal to the size of its peasantry, and the amount of productive land is equal to the portion of its territory located in the core land.
A Cobb-Douglas production function determines the quantity of food produced by a simple society:
| $$Y_{simple}=A_{extensive}L_{simple}^{\alpha}N_{simple}^{1-\alpha},$$ | (5) |
In economese, TFP is an efficiency parameter that multiplies the output of any combination of labor, capital, and land. If the value of TFP increases due to improvements in tools, methods, or institutions, a society produces more without having to increase the amount of any of the inputs. Societies with higher TFPs produce more with the same resources.
Cobb-Douglas production functions exhibit constant returns to scale, which means that increasing the amount of land and labor in equal proportions increases the quantity of food produced by the same proportion (e.g., doubling both the number of laborers and the area of productive land doubles food production). Cobb-Douglas production functions also imply a diminishing marginal productivity of labor. That is, for a given amount of land, each additional laborer produces less food than the previous one.
A Cobb-Douglas production function determines the quantity of food produced by a complex society:
| $$ Y_{complex}=xA_{intensive}L_{intensive}^{\alpha}N_{peasants}^{1-\alpha},$$ | (6) |
In period 1, the TFP of intensive agriculture is equal to the TFP of extensive food production methods. Thereafter, the TFP of intensive agriculture grows at a near-zero constant rate \(g>0\).
The distribution of food among the members of a society depends on its social organization.
In simple societies, everyone gets the same amount of food. This means that the per capita income of its members is
| $$y_{simple}=\frac{Y_{simple}}{N_{simple}}.$$ | (7) |
In complex societies, the warrior elite takes a fraction \(\alpha\) of the food produced by the peasants, where \(\alpha\) is the weight of land in food production. The peasants keep the rest of the food. Within a social class, each person gets the same amount of food. Therefore, the per capita incomes of warriors and peasants are
| $$ y_{warriors}=\frac{\alpha Y_{complex}}{N_{warriors}},$$ | (8) |
| $$y_{peasants}=\frac{(1-\alpha)Y_{complex}}{N_{peasants}}. $$ | (9) |
Finally, from the incomes of its warriors and peasants, we get a measure of income inequality for a complex society:
| $$\text{INEQ}=\frac{y_{warriors}}{y_{peasants}}. $$ | (10) |
Reproduction and deaths unrelated to war
The parameters representing the cost of rearing a child for free people, peasants, and warriors are \(\kappa_{freepeople},\kappa_{peasants},\kappa_{warriors}>0\), respectively (recall that “free people” is the name given to members of simple societies). Childrearing is costlier for warriors than for free people and peasants. This means that \(\kappa_{warriors}>\kappa_{freepeople},\kappa_{peasants}\).
The fertility rate of free people is directly proportional to their per capita income and inversely proportional to their cost of childrearing:
| $$n_{freepeople}=\frac{y_{simple}}{\kappa_{freepeople}}. $$ | (11) |
| $$n_{warriors}=\frac{y_{warriors}}{\kappa_{warriors}}, $$ | (12) |
| $$n_{peasants}=\frac{y_{peasants}}{\kappa_{peasants}}. $$ | (13) |
The rate of deaths unrelated to war is given by parameter \(\mu\in\left( 0,1\right)\). It summarizes all causes of death other than being killed in war.
From the rates of fertility and of deaths unrelated to war, we get the rates of population growth. The population of a simple society grows at the following rate:
| $$r_{simple}=n_{freepeople}-\mu,$$ | (14) |
| $$r_{warriors}=n_{warriors}-\mu,$$ | (15) |
| $$r_{peasants}=n_{peasants}-\mu,$$ | (16) |
Internal conflicts in simple societies
When the population of a simple society exceeds a critical threshold, an internal crisis ensues, and its population separates into two conflicting factions. Formally, an internal crisis happens if \(N_{simple}>yN_{simple}^{\ast}\), where \(N_{simple}^{\ast}>0\) is a parameter that quantifies the effectiveness of simple society institutions, and \(y\) is a lognormal “political shock” that affects that specific society. The underlying normal shock, \(ln(y)\), has a mean of 0 and a standard deviation of \(\tau>0\). By raising or reducing the threshold, a political shock changes the probability that a simple society will experience an internal crisis. A new political shock affects each simple society in every period, and shocks are independent and identically distributed across simple societies and through time.
An internal crisis can end in two ways: fission or reorganization as a complex society.
Fission is the almost certain outcome of a crisis. The population divides into two conflicting groups, which divide the territory into two territories of random size. There, the separate factions start new simple societies. People join the new societies in proportion to their territories. There is, however, an exception to this rule: If the society has only one cell, its territory cannot be divided. In this case, one of the conflicting factions slays the other and keeps the one-cell territory. As a result, a random number of people die.
A simple society in crisis has a small chance of becoming a complex society instead of fissioning. In order to become a complex society, a simple society has to have at least part of its territory in the core land. Having territory in the core land is essential to complex societies, because they practice intensive agriculture, which is only feasible in the core land. If this condition is met, a simple society will become a complex society with probability \(\pi\), where \(\pi\in\left( 0,1\right)\) is a parameter, and the value of \(\pi\) is close to zero.
In a nascent complex society of size \(N_{complex}\), the population immediately divides into a warrior elite and a peasantry. The size of the new warrior elite is given by
| $$N_{warriors}=m^{\ast}N_{complex}%$$ | (17) |
| $$ \begin{equation} m^{\ast}=\frac{\alpha\kappa_{peasant}} {\alpha\kappa_{peasant}+\left( 1-\alpha\right)\kappa_{warriors}} \end{equation}$$ | (18) |
Internal conflicts in complex society
Complex societies face two types of crises: collapse and civil wars.
If the peasants' per capita incomes drop below a catastrophic level, given by parameter \(y^{\ast}\), a complex society collapses. A collapsed society disintegrates into many simple societies. Each of these new simple societies has a territory of one cell, and a population of \(N_{complex}/L_{complex}\).
When the population of a complex society exceeds a critical threshold, an internal crisis breaks out, and the warriors separate into two enemy factions. Formally, a civil war breaks out if \(N_{complex}>zN_{complex}^{\ast}\), where \(N_{complex}^{\ast}>0\) is a parameter that quantifies the effectiveness of complex society institutions, and \(z\) is a lognormal “political shock” that affects that specific complex society. The underlying normal shock, \(ln(z)\), has a mean of 0 and a standard deviation of \(\nu>0\). By raising or reducing the threshold, a political shock changes the probability that a complex society will experience an internal crisis. A new lognormal political shock affects each complex society in every period, and shocks are independent and identically distributed across complex societies and through time.
We assume that \(N_{complex}^{\ast}\gg N_{simple}^{\ast}\), which means that complex societies can hold together larger populations than simple societies can.
After a civil war, the territory of a complex society is randomly divided between two new complex societies. Warriors and peasants join the new complex societies in proportion to their territories. There is, however, one exception to this rule: If the original complex society has only one cell, its territory cannot be divided. In this case, one of the conflicting factions obliterates the other, and a random number of people dies. Peasants and warriors die in the same proportions.
Parameter values and code
Table 1 shows the parameter values that we used in our simulations. We programed the model in Matlab version R2016a. The code is available for download, so that the readers can replicate the simulation results and experiment with the model.
Results
We discovered that the simulations go through three consecutive, qualitatively different “eras”. Below, we analyze each of these eras and compare the simulation results with real-world cases.
We use one simulation run as an example. A video of this run is available here: https://www.youtube.com/watch?v=1MDKvY9Ee1o&t=13s.
In the video, the first era starts in minute 0:00, the second era starts in minute 2:12, and the 3rd era starts in minute 13:20.
1st era: Complex societies emerge intermittently but disappear shortly after
Figure 4 illustrates this cycle.
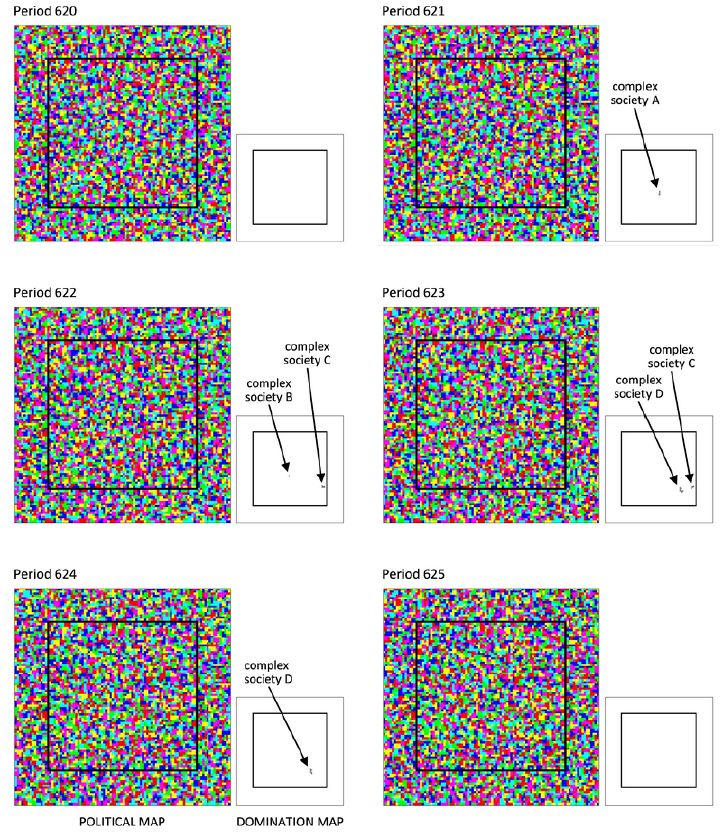
The first era of the simulation resembles the cycles of emergence, expansion, and collapse characteristic of chiefdoms (Wright 1984; Earle 1989). Usually, but not always, these cycles last a decade or so (Wright 1984). In some regions, chiefdoms have survived a hundred years or more (Stein 1994).
Let us compare the model's first era with the Ubaid period (c.5500--c.3800 B.C.). During the Ubaid period, the first intensive farmers of whom we have record settled down in the alluvial plain of Mesopotamia (the equivalent of our “core land”. At least since 4800 BC, these farmers organized themselves into chiefdoms (Stein 1994). Artificial mounds, formed by repeated occupation and abandonment of the same sites, evidence the transience of the Ubadian chiefdoms. The Eridu mound, for example, has nineteen layers corresponding to successive occupations, fourteen of which are prehistoric and date from the Ubaid period (Oates 1960).
The Ubad period is exceptional in that the archaeological sites contain virtually no traces of war, neither between chiefdoms, nor between chiefdoms and the simpler societies that coexisted with them. The Ubadian chiefdoms were also unusually stable, as is to be expected when there is little danger of being wiped out by your neighbors (Wright 1984).
The model's first era (c.1100-c.1600) also approximates the Mississippian chiefdoms of the Savannah River basin. The Mississippian chiefdoms exhibited the characteristic cycle of emergence, expansion, fragmentation, and collapse. There is archaeological and paleoclimatological evidence that this cycle was driven by a combination of environmental and political forces, mainly food shortages caused by prolonged droughts and the rise of competing chiefdoms in nearby drainages (Anderson 1996). Note that the model includes environmental shocks but excludes political competition between societies.
Like the Ubadians, the Mississippians of the Savannah River were peaceful people.
2nd era: Complex societies emerge, expand by conquest, and disappear
During the second era, some complex societies are destroyed in war; others collapse. From time to time, complex societies collapse en masse. However, some complex societies avert early collapse and annihilation, and expanding through conquest. At all times, complex societies coexist with simple societies.
Figure 5 shows a cycle of emergence, expansion, and collapse. Figure 5 shows the last mass extinction of complex societies.

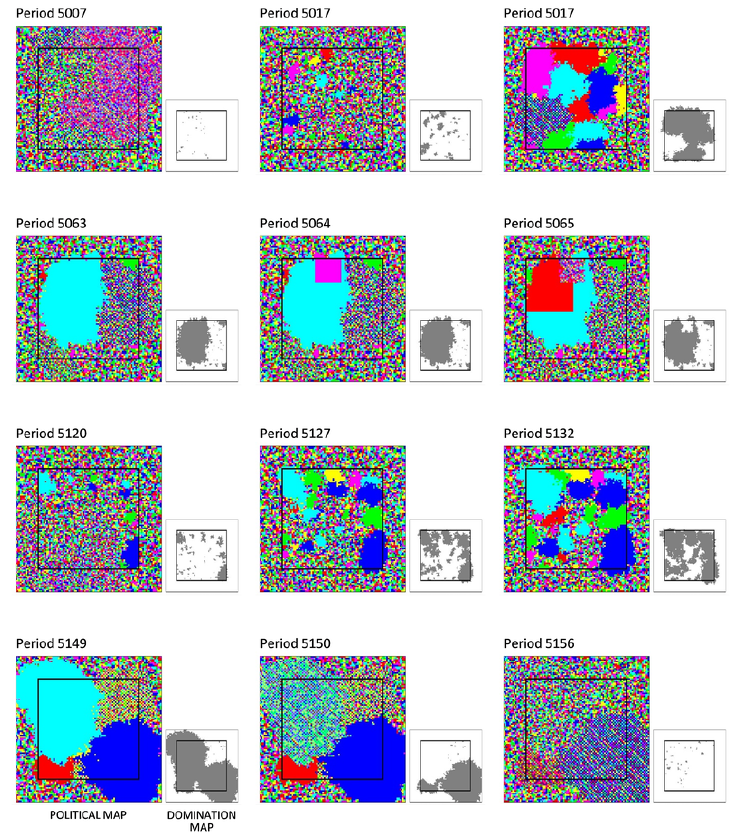
The history of Ancient Mesoamerica is similar to the dynamics of the model's second era.
Around 3500 BC, farmers established sedentary societies on the arable lands of Mesoamerica (Roush 1997). Maize, beans, and squash were the mainstays of their diet (Casas et al. 1998).
During the following 52 centuries, the Mesoamericans intensified agriculture, developing and refining a variety of methods and technologies, including the milpa cycle (a form of shifting agriculture), pet kots (forest gardens), irrigation with canals, coo yuu (terraces), and chinampas (floating gardens) (Challenger 1998). Their TFP of intensive agriculture steadily increased.
In parallel with the agricultural intensification, sedentary Mesoamerican societies became more complex. City-states emerged. The wars between them were frequent and exacerbated over time. Some city-states expanded by conquest or alliance, and a few became civilizations (Bueno 2007; Hassig 1992). The Olmec was the first civilization to appear. It originated circa 1400 BC in the lowlands of the Gulf Coast. At its peak, the Olmec civilization reached a population of approximately 350,000 inhabitants (Fernandez 2004).
Collapse was a constant threat to Mesoamerican regional polities. The Olmec, for example, declined between 400 and 350 BC for uncertain reasons. One theory is that changes in the Gulf's riverine environment drastically reduced agricultural productivity, making it impossible to maintain a large population (Pool 2007).
Mass collapses also occurred in Mesoamerica. For example, in the middle of the eighth century AD, prolonged droughts and political crises led to a mass collapse in the northern region. The region was abandoned by the Mesoamerican people and later occupied by Aridamerican nomads (Solanes & Vela 2000).
Civil wars were another threat to Mesoamerican complex societies. A well-documented example is the Mayan civil war of the seventh century AD. The war was started by two sons of K'inich Muwaan Jol II. The (probably half) brothers disputed the royal emblem glyph of Tikal and the sovereignty over its vassal city-states (Guenter 2003).
3rd era: A moving frontier separates simple and complex societies
In the third era, there are no more mass collapses. Complex societies slowly expand until they dominate the core land, and simple societies take refuge in the marginal land. In an ebb and flow, complex societies invade the marginal land and withdraw to the core land.
Figure 7 and Figure 8 show two cycles of invasion and withdrawal.
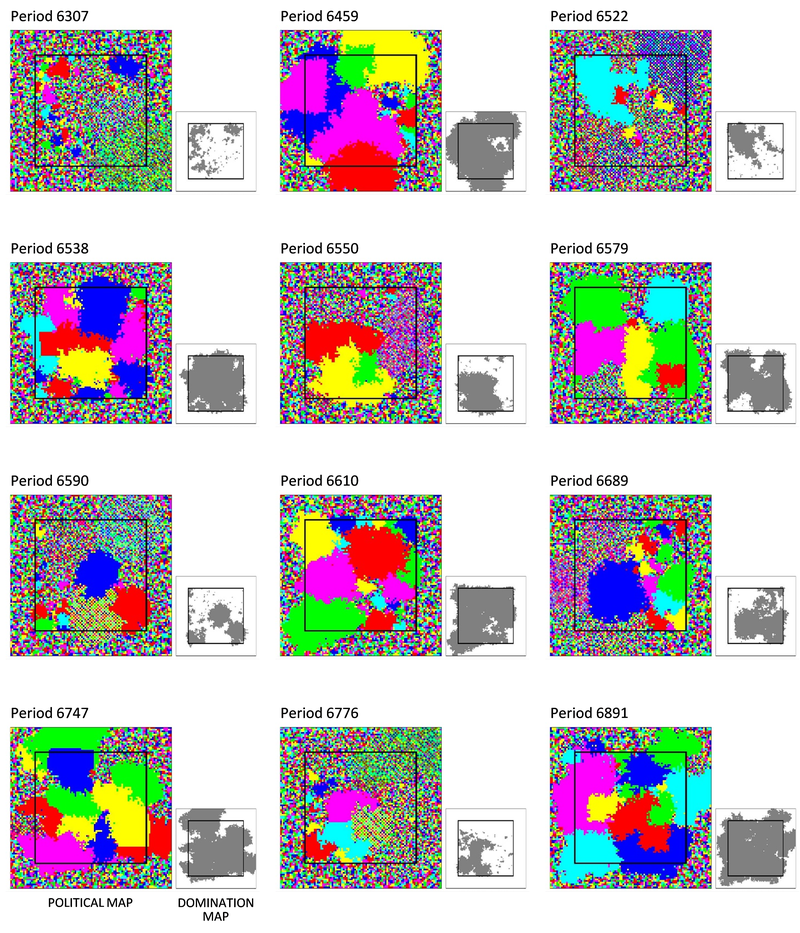

The cycle in Figure 7 takes place early in the third era. In that time, complex societies have not yet consolidated their dominance over the lowlands.
The cycle in Figure 8 takes place late in the third era. In that era, complex societies dominate the entire lowlands. Intermittently, they expand into the highlands, where they impose an ephemeral domain. Shortly after, simple societies expel the conquerors. Complex societies are confined to the lowlands, until a new cycle of conquest begins.
The third era of our model is analogous to the historical case of Zomia, as documented by Scott (2009).
Zomia, the Southeast Asian mainland massif, is perhaps the largest region in the world to remain mostly outside the control of states. Its territory is hilly, rough, and with wide areas covered by forests. For centuries, Zomia has been home and refuge to simple societies of hunter-gatherers, slash-and-burners, and pastoralists. Today, the population of Zomia is about eighty to one hundred million, fragmented into hundreds of ethnic identities.
Until recently, the lowlands of mainland Southeast Asia were occupied by archaic states that specialized in wet-rice agriculture. Many of these states sought to dominate different areas of Zomia by means of force, but they succeeded only temporarily. Their main military objective was to capture barbarians, civilize them, and use them as corvée labor in paddy fields. Other military objectives were to establish tributary relationships with Zomia's simple societies, and to control trade routes that crossed the highlands.
There was also an outflow of people from the lowlands to Zomia. Slaves fled, and peasants revolted and took refuge in the highlands. There, in Scott's words, the refugees “rebarbarianized”.
As is characteristic of archaic states, one would collapse on the border with Zomia from time to time. Collapsed states released people who took refuge in “shatter-zones” that formed in the periphery of the lowlands. Every so often, new states arose in the periphery, absorbing and recivilizing barbarians.
The Han-Chinese state was the archenemy of Zomia. In the mid-nineteenth century, the Ming and Qing dynasties launched large-scale military campaigns against the hill peoples. The campaigns culminated in uprisings that left millions of people in search of refuge. The Burmese and Thai states were also enemies of Zomia, which they constantly raided for slaves.
Scott claimed that the case of Zomia is not unique and that similar historical processes occurred during the formation of most Western nation-states.
Concluding Remarks
By integrating elements of different social science theories, our model reproduces a sequence of geographical dynamics that usually accompany sociocultural evolution:
- The cycle of emergence, expansion, and collapse characteristic of chiefdoms.
- The emergence of the first premodern states and their tendency to collapse, sometimes en masse.
- The expansion of premodern states until they dominate those lands where agricultural intensification is possible, the confinement of simpler societies in marginal lands, and the separation between both types of societies by a moving frontier.
In the model, the transition between these eras is caused by the continuous increase of a single variable: the total factor productivity of intensive agriculture. This model is the first to simultaneously explain the eventual progression from simple to complex societies; why complex societies emerge and disappear, sometimes en masse; and why this process often resolves into three relatively distinct eras, as outlined above.
The model could be extended in several ways to explore other aspects of sociocultural evolution.
A possible extension has to do with the decision to attack another society. In the model, this decision to attack is based on a probabilistic rule that only considers the probability of success. In an extended model, this decision could depend on a cost-benefit analysis, which considers the risks of defeat and the value of the resources in dispute.
Another possible extension is the formation of alliances between societies, for two reasons. First, alliances are common in war. Second, allies sometimes merge and give rise to a larger society. In a similar vein, an extended model could include peaceful cooperation between states, such as commerce.
There is evidence that intersocietal conflict affects a society’s asabiyya (Turchin 2007). Societies at conflict with their neighbors accumulate asabiyya—roughly, a sense of social solidarity and shared purpose—while societies at peace dissipate it. The model could be extended to include asabiyya as a protecting factor against social decomposition.
In the model, the total factor productivity of intensive agriculture increases indefinitely without society needing to reorganize itself at some point. In addition, civil wars and collapse are inevitable consequences of population growth, while in reality, societies can avoid decomposition by upgrading their institutions (Johnson & Earle 2000). To account for these facts, an extended version of the model could include the transformation of premodern complex societies into modern complex societies (e.g., nation states).
Acknowledgements
For their generous help and advice, the authors thank Leda Cosmides, Bob Rowthorn, and Rosita Candia.Notes
- Johnson and Earle classify societies into three broad types of increasing levels of complexity: family-level societies, without and with domestication; local groups, subdivided into acephalous local groups and Big Man collectivities; and regional polities, subdivided into chiefdoms, archaic states (including ancient empires), and nation-states. In Appendix A, we summarize their typology.
- Simple societies use extensive methods of food production, such as hunting and gathering, slashand-burn agriculture, or nomadic pastoralism (Johnson and Earle 2000).
- There is evidence that a society's level of social complexity correlates with both its degree of dependency on agriculture and the intensity of agriculture. Johnson and Earle (2000) theorized that the intensification of all types of food production methods requires increasingly professionalized and centralized management, which eventually mutates into social stratification. We present their theory of social stratification in Appendix A. It must be noted that, outside the model world, complex hunter-gatherer and pastoralist societies do exist, though they are exceptional cases. See Appendix A.
- These assumptions about the social organization of simple and complex societies are taken from Rowthorn and colleagues (2014).
- We base the topography of the simulated continent on Scott's (2009) observations of Zomia. We explain his theory in Appendix A.
- This is David Ricardo's (1817) law of diminishing returns.
- In reality, extensive methods of food production are also affected by productivity shocks, though less affected than intensive agriculture (Scott 2009).
- There could be progress in extensive food production methods too. Assuming that they do not progress is a convenient way of capturing the fact that intensive agriculture progresses much faster (albeit very slowly).
- For an in-depth account of agriculture in premodern times, see Mazoyer & Roudart (2006).
- In the real world, each type of society has a different approach to war: Family-level societies almost never engage in war. Local groups fight over land and other natural resources, but they rarely take captives. Premodern regional polities wage wars of conquest. See Appendix A.
- We base this assumption on Scott's (2009) observation that terrains that are suitable for intensive agriculture are usually favorable for regular warfare, whereas terrains that are unsuitable for intensive agriculture are usually favorable for guerrilla warfare.
- It is a stylized fact that belligerence correlates with social complexity. See Appendix A for details.
- Andreski (1968) presents historical evidence of a positive correlation between economic inequality within a complex society and the cost of raising, training, and equipping professional warriors.
- In Appendix B, we work out a Malthusian-Ricardian demographic model of an isolated simple society.
- In Appendix A, we elaborate on the issue of social conflict.
- We base this assumption on scalar stress theory (Johnson 1982). See Appendix A.
- If clans dwell in the same village---as is the norm among shifting agriculturists---sexual infidelities and accusations of sorcery are recurrent motives for conflict (Johnson & Earle 2000).
- Johnson & Earle (2000) gave an extensive account of institutional development in regional polities. Turchin attributed a crucial role to informal institutions, in particular, to asabiyya. We summarize their ideas in Appendix A.
- The assumption is based on scalar stress theory.
- This assumption captures the gist of Diamond's (2005) theory of societal collapse. We present his theory in Appendix A.
- There are other widely used typologies. Service (1962) distinguished four types: bands, tribes, chiefdoms, and states. Fried (1967) distinguishes three: egalitarian societies, rank societies, and stratified societies.
Appendix
Appendix A: Evidence and social science theories of social complexity
This appendix offers a brief discussion of social science theories of social complexity. The collection of theories is not exhaustive; we have selected those that are closely related to our model. Before discussing theory, we summarize the evidence about the transition from simple to complex society, as described by Johnson and Earle in The Evolution of Human Societies (2000). We have organized the evidence as a list of stylized facts.
The transition from simple to complex society: Stylized facts
In premodern times, societies of increasing levels of complexity coexisted on Earth: family-level groups, with and without domestication; local groups, subdivided into acephalous local groups and Big Man collectivities; and premodern regional polities, subdivided into chiefdoms and archaic states (including ancient empires)[21].
Societies can follow multiple trajectories from lower to higher levels of social complexity (Steward 1955), yet there are strong positive correlations between a society’s level of complexity and its scale, intensity of food production, degree of dependency on agriculture, extent of political integration, degree of hierarchization, and belligerence:
- Scale. Family-level societies have fewer than ten members, typically a couple, their children, and one or two close relatives (e.g., a grandparent). Local groups are clan alliances. The majority range in population from a few hundred (in the case of acephalous local groups) to a few thousand (in the case of Big Man societies). Most premodern regional polities have populations from a few thousand (in the case of simple chiefdoms) to several million (in the case of ancient empires).
- Intensity of food production. Simple societies (family-level groups, local groups) use extensive food production methods and technologies: persistence hunting, bowhunting, spear hunting, angling, spearfishing, poisoning fishing, wild-plant gathering, honey harvesting, shellfish gathering, forest gardening, slash-and-burn agriculture, intercropping, digging sticks, hand plows, dry farming, wild flooding irrigation, nomadic pastoralism, and transhumance, to mention only a few. Complex societies (regional polities) use intensive food production methods and technologies: gillnetting, trawling, fishing weirs, sedentary agriculture, monocropping, controlled flood irrigation, artificial dams and canals, paddy fields, draft animals, the moldboard plow, pastoral farming, dairy farms, and so forth.
- Dependence on agriculture. Family-level societies depend almost exclusively on hunting and gathering, although some supplement their diet with primitive forms of agriculture, such as forest gardening. The majority of local groups practice traditional agriculture, typically shifting agriculture or nomadic pastoralism. Nevertheless, many local groups obtain a significant part of their diet from hunting and gathering. Almost all regional polities are agricultural societies and practice intensive agriculture, although they supplement their diets, to a greater or lesser extent, with hunting and gathering (e.g., fishing). Exceptional cases exist of chiefdoms that do not practice intensive agriculture, such as the Calusa, who were intensive fishers, and the Basseri, who are intensive pastoralists.
- Extent of political integration. Family-level societies are not territorial. They gather opportunistically in camps or hamlets. Local groups live in village-sized settlements and dominate the surrounding territory, where they have their farms or pastures. Regional polities have multi-level settlement hierarchies with some degree of centralized control.
- Degree of hierarchization. Family-level groups are egalitarian societies. Supra-familial leadership is always task-specific and ephemeral. Local groups have formal leadership, but they are not stratified societies: In local groups, all men have the right to own weapons and means of production and the right to contest the role of leader. Regional polities are stratified societies and have at least two social classes: a ruling hereditary elite and a food-producing class of commoners. As premodern regional polities grow in complexity from simple chiefdoms to ancient empires, the economy diversifies, new levels of control appear, and governance becomes increasingly bureaucratic.
- Belligerence. Family-level societies are peaceful. They avoid conflict by staying out of each other’s way. Local groups are warlike. They constantly fight over fertile land, fresh pastures, and concentrated resources (e.g., an exceptionally rich fishing site). They rarely take captives—except perhaps for women. In local groups, all able men are warriors. Regional polities are extremely violent. They wage wars of conquest to seize land and the people it contains in order to exploit them. The military profession is reserved to the male members of the elite.
There are, of course, exceptions to these rules.
Theories of social stratification
Most theorists find the cause of stratification in either social conflict or social function. Conflict theorists claim that stratification occurs when a faction of the local group, the “aggrandizers,” monopolizes weapons and appropriates the means of production (Fried 1967; Hayden 1995). Functionalist theorists claim that the elite provides public goods that benefit the commoners and that these benefits outweigh the cost of supporting the elite—otherwise, the elite would be quickly overthrown (Childe 1954; Davis 1949; Service 1962; Wittfogel 1957).
Johnson and Earle (2000) proposed a theory of social stratification that synthesizes elements of conflict and functionalist theories. They argued that the driving force of social stratification is population pressure. According to Johnson and Earle, the need to support a growing population creates incentives to intensify food production. Intensification, in turn, poses adaptive problems that a society can only address through professional and centralized management: the provision of large-scale technologies (e.g., irrigation systems, whaling boats); the storage of great quantities of food for a rainy day; trade with other societies for essential goods (e.g., meat from pastoralists who want to buy grain); and warfare against neighboring societies for fertile land, fresh pastures, people, and other resources. In order to carry out their work, the managers are granted increasing amounts of power. Once the managers have accumulated enough power, they use it to subjugate the rest of the population and become a hereditary elite. Suddenly, the local group has become a chiefdom.
Other authors argue that social stratification, as a rule, cannot originate within societies, because people would violently resist subjugation. These authors suggest that many or most stratified societies must be born when one society conquests another: The conquerors become a ruling elite, and the conquered become commoners (Andreski 1968; Carneiro 1970; Oppenheimer 1926).
Through a long succession of conquests, a small regional polity can become an empire (Ardant & Tilly 1975; Carneiro 1970; Turchin 2007, 2009). Another path to empirehood is the union of neighboring societies that face a common mighty enemy (Turchin 2007, 2009). Several Big Man collectivities unite and become a chiefdom, several chiefdoms unite and become an archaic state, several archaic states unite and become an ancient empire.
Theories of social conflict and collapse
In complex societies, conflicts arise within and between social classes. Power disputes between factions of the elite sometimes result in civil war, and tensions between the elite and the common people can trigger a revolution.
Complex societies develop institutions that act as “social glue” and contain social conflict.
Johnson and Earle (2000) claim that the main ingredients of social glue are leadership in collective action, an ideology of dominance that justifies the class system, and a sense of group identity that binds together a diverse population. Religion and ceremonies deliver the social glue. Like Johnson and Earle, Turchin (2013) attributed a crucial role to informal institutions, in particular, to bureaucracy, education, and ideology.
However, Turchin (2007) went further and claimed that the fundamental ingredient of social glue is asabiyya: a society’s capacity for collective action, made up of people’s prosocial dispositions and based on a sense group identity. Societies gain asabiyya when they compete with rival societies, especially in wars at meta-ethnic frontiers. Alternatively, complex societies that achieve peace and prosperity lose asabiyya. Populous and multi-ethnic societies (usually created by conquest) also lose asabiyya because they have weaker social ties.
Population growth stresses institutions. Leaders lose their capacity to control their subordinates as their numbers increase. Johnson (1982) called this phenomenon “scalar stress.” Scalar stress can break the social glue and lead a society to fission or disintegration. Alternatively, a society can overcome scalar stress by upgrading its institutions so that the population can keep growing (Carneiro 1967; Simmel 1902; see also Alberti 2014; Bandy 2004; Johnson 1982).
Diamond (2005) identified a pattern in the rise and fall of complex societies: Prosperity leads to population growth. Population growth forces a complex society to intensify agriculture by adopting a succession of increasingly advanced technologies. In the process, farming deteriorates the soil, ruins the water sources, and irreparably damages the environment. At some point, no further intensification is possible. From that moment on, population growth causes per capita food production to decline steadily (Malthus 1798; Ricardo 1817). Eventually, food shortages occur, causing starvation, disease, and violence. The starving masses overthrow the governing elites, and society collapses.
Geographic dynamics of simple and complex societies
According to Carneiro (1970), “circumscription” is necessary for complex agricultural societies to develop. By circumscription, he means the inability of peasants to flee from their masters and relocate elsewhere. Carneiro distinguishes two complementary types of circumscription: An area is “environmentally circumscribed” if it is surrounded by marginal lands where life is even harsher than under a masters’ yoke (steppes, mountains, deserts, forests, jungles, etc.). A region is “socially circumscribed” if every plot of land is occupied so peasants are blocked from all sides.
Elaborating on Carneiro’s ideas, Webster (1975) claimed that a region’s densely populated core will eventually overflow people into marginal lands. Subsistence is possible in marginal lands, but these have low carrying capacity. Simple societies will survive there at very low densities.
Unlike Carneiro, Scott (2009) claimed that marginal lands are, in general, hospitable places where people take refuge from complex societies. Peasant servitude is nasty, brutish, and short, whereas life in the margins is free, leisurely, and affluent (or, at least, not completely miserable).
Scott conjectured that simple societies use extensive food production methods, mainly because such methods involve a nomadic or semi-nomadic way of life. Living in motion and hiding in marginal lands are tactics aimed at circumventing the clutches of complex societies.
According to Scott, complex societies opt for intensive agriculture, not for its productivity, but for tax purposes. Intensive agriculture is sedentary in nature and is practiced in clear valleys and plateaus, which implies that peasants can be enclosed and enrolled. Moreover, the crops used in intensive agriculture (e.g., wheat, potatoes) are difficult to hide and easy to confiscate and hoard.
Scott claims that states are not interested in farming marginal lands, even in those places where intensive agriculture is potentially feasible, such as a patch of mountain forest that could be cleared to build terraces. This is so because transporting crops from marginal lands to the center of a state demands greater amounts of calorie consumption than that contained in the transported crops, which is due to the length and excruciating conditions of the journey. As a reference, a yoke of oxen eats the equivalent of a cartload of grain for every 250 kilometers traveled over flat terrain.
Scott noted that complex societies tend to expand until they become states and control all of the core land. They then venture into marginal lands, primarily because such lands constitute sources of forced labor, but also to establish tributary relationships with local simple societies and to secure trade routes that cross these areas. People from simple societies oppose fierce resistance or simply flee to even more remote areas, thus creating cycles of conquest and withdrawal.
Scott found the explanation for geographical segregation in a peculiar geographic fact—that core lands tend to be flat and clear. They are, thus, favorable for professional warriors, who move in large numbers and charge ahead as blocks. Scott called this type of terrain “lowlands” because they are often valleys, but they can also be plateaus, as is the case of the Altiplano. Conversely, marginal lands tend to be rugged and wild and are, thus, favorable for militiamen who move in small numbers and attack by surprise. Scott called this type of terrain “highlands” because they are often in the mountains, though they can also be elsewhere: in steppes, jungles, marshes, and so forth.
Finally, Scott acknowledged that simple and complex societies also interact in a peaceful ways. For example, they exchange goods that are only found in the highlands or lowlands (ebony from the mountain forests, dried fish from the estuaries, etc.).
Appendix B: Fundamentals of Malthusian-Ricardian demography
The following model captures the fundamentals of Malthusian-Ricardian demography in an isolated simple society. The model assumes that the TFP of agriculture grows at a constant rate. Using this model, we show how to calculate the subsistence income and the steady state population growth rate. We also show how to calculate the carrying capacity of the environment when the TFP of agriculture does not grow or grows at an almost imperceptible rate. Finally, we explain the short-term and long-term effects of adopting a more intensive agricultural technology.
- A society has a fixed amount of land, given by \(L>0\).
- Labor supply is perfectly inelastic and equal to the society’s population. Variable \(N(t)>0\) represents society’s population in time \(t\), where \(t>0\) is a continuous time index.
- Total food production is given by a Cobb-Douglas function:
- TFP grows at a constant rate \(g>0\). Thus, TFP in time t is given by
- Every person gets the same amount of food:
- The fertility rate is directly proportional to the per capita income and inversely proportional to the cost of childrearing:
- The rate of population growth is equal to the fertility rate minus the mortality rate:
- The rate of population growth stabilizes when the fertility rate is constant.
| $$Y(t)=A(t)L^{\alpha}N(t)^{1-\alpha},$$ | (19) |
| $$A(t)=A(0)e^{gt},$$ | (20) |
| $$y(t)=\frac{Y(t)}{N(t)}=L^{\alpha}N(t)^{1-\alpha},$$ | (21) |
| $$n(t)=\frac{cy(t)}{\kappa}$$ | (22) |
| $$\frac{\dot{N}(t)}{N(t)}=n(t)-\mu,$$ | (23) |
Through algebraic manipulations, the above equations can be reduced to the following two:
| $$\frac{\dot{N(t)}}{N(t)}=\frac{cy(t)}{\kappa}-\mu$$ | (24) |
| $$y(t)=A(0)e^{gt}L^{\alpha}N(t)^{-\alpha},$$ | (25) |
| $$\frac{\dot{N(t)}}{N(t)}=\frac{g}{\alpha}$$ | (26) |
| $$y(t)=\frac{\kappa}{c}\left(\frac{g}{\alpha}+\mu\right) $$ | (27) |
These two equations describe the steady state of the model.
Note that, in equilibrium, population grows at a constant rate (see Equation 26). The growth rate depends on how fast the TFP increases. The faster the TFP increases, the faster the population grows. If the TFP remains constant (i.e., if \(g=0\)), the population remains constant as well.
The steady-state per capita income is often called the “subsistence wage.” Note that the subsistence wage is not a biological minimum. Rather, it is an increasing function of three parameters: TFP growth rate (\(g\)), mortality rate (\(\mu\)), and the cost of childrearing (\(\kappa\)). The subsistence wage remains constant through time, unless one or more of these parameters changes for exogenous reasons.
The main implication of the model is that the equilibrium subsistence wage does not depend on the TFP level. All shocks to the TFP level, either temporary or permanent, will be neutralized by transient changes in the population growth rate. This is Malthus’ (1798) famous insight.
Now, suppose that the TFP of agriculture does not grow; if \(g\approx 0\), we can safely make this assumption for a short time window. Replacing \(g=0\) in Equation 27, we get the subsistence income in the time window:
| $$y^{\ast}=\frac{\kappa\mu}{c}.$$ | (28) |
Then, replacing this value in Equation 25 and solving for \(N(t)\), we get the steady-state equilibrium population in the time window:
| $$N^{\ast}=\left(\frac{cA}{\kappa\mu}\right)^{\frac{1}{\alpha}}L$$ | (29) |
| $$ \frac{N^{\ast}}{L}=\left(\frac{cA}{\kappa\mu}\right)^{\frac{1}{\alpha}}$$ | (30) |
At some moment in the time window, the society might abandon its agricultural technology to adopt a more intensive one. This is equivalent to a permanent positive shock to the TFP. The positive TFP shock translates into a sudden increase in the per capita income. People react to the increase in the per capita income by increasing their fertility, and, thus, population starts to grow. As a result, the per capita income begins to diminish, and the fertility rate diminishes accordingly. Population growth slows down until it is once again near zero. Simultaneously, the per capita income converges from above to the subsistence wage, which is the same as before the shock, because it does not depend on TFP.
References
ALBERTI, G. (2014). Modeling group size and scalar stress by logistic regression from an archaeological perspective. PLoS ONE, 9(3), e91510. [doi:10.1371/journal.pone.0091510]
ANDERSON, D. G. (1996).' Chiefly Cycling and Large-Scale Abandonments as Viewed from the Savanna River Basin.' In Scarry, J. F. (Ed), Political Structure and Change in the Prehistoric Southeastern Unite States. Gainesville, FL: University Press of Florida, pp. 231-52.
ANDRESKI, S. (1968). Military Organization and Society. Cambridge, UK: Cambridge University Press.
ARDANT, G. & TILLY, C. (1975). The Formation of National States in Western Europe. Princeton: Princeton University Press.
BANDY, M. S. (2004). Fissioning, scalar stress, and social evolution in early village societies. American Anthropologist, 106(2): 322-333. [doi:10.1525/aa.2004.106.2.322]
BUENO, M. I. (2007). Mesoamerica, territorio en guerra. Revista de Historia Militar 101, 11-40.
CARNEIRO, R. L. (1967). On the relationship between size of population and complexity of social organization. Southwestern Journal of Anthropology, 23(3), 234-243. [doi:10.1086/soutjanth.23.3.3629251]
CARNEIRO, R.L. (1970). A theory of the origin of the state. Science 169(3947), 733-738.
CASAS, A., Caballero, J., Mapes, C., & Zárate, S. (1998). Manejo de la vegetacion, domesticacion de plantas y origen de la agricultura em Mesoamerica Bol. Soc. Bot. Mex, 61, 31-47.
CHALLENGER, A., & Caballero, J. (1998). Utilización y conservación de los ecosistemas terrestres de México: Pasado, presente y futuro. Comisión Nacional para el Conocimiento y Uso de la Biodiversidad, Universidad Nacional Autónoma de México, Agrupación Sierra Madre, SC, México, DF.
CHILDE, V. G. (1954). 'Early forms of society.' In C. Singer, E. J. Holmyard, A. R. Hall & T.I. Williams (Eds.), A History of Technology, vol. 1. Oxford: Clarendon Press, pp. 38-57.
CIOFFI-REVILLA, C. (2005). A canonical theory of origins and development of social complexity. Journal of Mathematical Sociology, 29(2), 133-153.
DAVIS, K. (1949). Human Society. New York: Macmillan.
DIAMOND, J. (2005). Collapse: How Societies Choose to Fail or Succeed. New York: Viking.
DORAN, J. (1998) Simulating collective misbelief. Journal of Artificial Societies and Social Simulation 1(1), 3. https://www.jasss.org/1/1/3.html.
DORAN, J. (2000). 'Trajectories to complexity in artificial societies: Rationality, belief, and emotions.' In T. A. Kohler & G. J. Gumerman (Eds.), Dynamics in Human and Primate Societies: Agent-Based Modeling of Social and Spatial Processes. New York: Oxford University Press, pp. 89-105.
DORAN, J. (2005). Iruba: An agent-based model of guerrilla war process. In Representing Social Reality, Pre-proceedings of the Third Conference of the European Social Simulation Association (ESSA), (pp. 198-205).
DORAN, J., & PALMER, M. (1995). 'The EOS project: Integrating two models of Palaeolithic social change.' In N. Gilbert & R. Conte (Eds.) Artificial Societies: The Computer Simulation of Social Life. London: UCL Press, pp. 103-25.
DORAN, J., PALMER, M., GILBERT, N., & MELLARS, P., (1994). The EOS project: Modelling Upper Palaeolithic social change. In N. Gilbert & J. Doran (Eds.), Simulating Societies: The Computer Simulation of Social Phenomena. London: UCL Press, pp. 195-221.
DOW, G. K., & REED, C. G. (2013). The origins of inequality: Insiders, outsiders, elites, and commoners. Journal of Political Economy, 121(3), 609-641.
EARLE, T. (1989). The evolution of chiefdoms. Current Anthropology, 30(1), 84-88. [doi:10.1086/203717]
FERNANDEZ, I. (2004). Historia de México, Segunda Ediciòn. México: Pearson Educaciòn.
FRIED, M. H. (1967). The Evolution of Political Society: An Essay in Political Economy. New York: Random House.
GUENTER, S. P. (2003). The inscriptions of Dos Pilas associated with B'ajlaj Chan K'awiil. Mesoweb. Retrieved from: http://www.mesoweb.com/features/guenter/DosPilas.pdf.
HASSIG, R. (1992). War and Society in Ancient Mesoamerica. Berkeley: University of California Press. [doi:10.1525/california/9780520077348.001.0001]
HAYDEN, B. (1995). 'Pathways to strength.' In T. D. Price & G. M. Feinman (Eds.), Foundations of Social Inequality. New York: Plenum Press, pp. 15-85.
JOHNSON, G. A. (1982). 'Organizational structure and scalar stress.' In C. Renfrew, M. Rowlands & B. A. Seagraves (Eds.) Theory and Explanation in Archaeology. New York, NY: Academic Press, pp. 389-421.
JOHNSON, A., & EARLE, T. (2000). The Evolution of Human Societies: From Foraging Group to Agricultural State. Stanford: Stanford University Press.
MALTHUS, T.R., (1798). An Essay on the Principle of Population as it Affects the Future Improvement of Society, with Remarks on the Speculations of Mr. Goodwin, M. Condorcet and Other Writers. London: J. Johnson in St Paul's Churchyard.
MAZOYER, M., & ROUDART, L. (2006). A History of World Agriculture: From the Neolithic Age to the Current Crisis. New York: Monthly Review Press.
OATES, J. (1960). Ur and Eridu, the prehistory. Iraq, 22(1-2), 32-50. [doi:10.2307/4199667]
OPPENHEIMER, F. (1926) The State (J.M. Gitterman, trans.). New Yok: Vanguard.
POOL, C. A. (2007). Olmec Archaeology and Early Mesoamerica. Cambridge and New York: Cambridge University Press. [doi:10.1017/CBO9781139167147]
RICARDO, D. (1817). On the Principles of Political Economy and Taxation (1st edition). London: John Murray.
ROUSH, W. (1997). Squash seeds yield new view of early American farming. Science 276(5314), 894-895. [doi:10.1126/science.276.5314.894]
ROWTHORN, R., Guzmán, R. A., & Rodríguez-Sickert, C. (2014). The economics of social stratification in premodern societies. The Journal of Mathematical Sociology, 38(3), 175-202.
SCOTT, J. C. (2009). The Art of not Being Governed: An Anarchist History of Upland Southeast Asia. New Haven: Yale University Press.
SERVICE, E. R. (1962). Primitive Social Organization: An Evolutionary Perspective. New York: Random House.
SEYMOUR-SMITH, C. (1986). Macmillan Dictionary of Anthropology. London: Macmillan. [doi:10.1007/978-1-349-08037-3]
SIMMEL, G. (1902). The number of members as determining the sociological form of the group. I. American Journal of Sociology, 8(1), 1-46.
SOLANES, C. M., & E. VELA. (2000). Atlas del México prehispànico. Arqueologìa Mexicana (5), 5-18.
STEIN, G. (1994). 'Economy, ritual and power in Ubaid Mesopotamia.' In G. Stein & M. Rothman (Eds.), Chiefdoms and Early States in the Near East. Madison, WI: Prehistory Press, pp. 35-45.
STEWARD, J. (1955). Theory of Culture Change. Urbana: University of Illinois Press.
TURCHIN, P. (2007). War and Peace and War: The Rise and Fall of Empires. New York: Penguin.
TURCHIN, P. (2009). A theory for formation of large empires. Journal of Global History, 4(2), 191-217. [doi:10.1017/S174002280900312X]
TURCHIN, P (2013). 'The puzzle of human ultrasociality: How did large-scale complex societies evolve?' In Richerson, P. J. & M. H. Christiansen (Eds.), Cultural Evolution: Society, Technology, Language, and Religion. Cambridge, MA: MIT Press, pp. 61-74.
TURCHIN, P., Currie, T. E., Turner, E. A., & Gavrilets, S. (2013). War, space, and the evolution of Old World complex societies. Proceedings of the National Academy of Sciences, 110(41), 16384-16389. [doi:10.1073/pnas.1308825110]
WEBSTER, D. (1975). Warfare and the evolution of the state: A reconsideration. American Antiquity, 40(4), 464-470.
WITTFOGEL, K. A. (1957). Oriental Despotism: A Study of Total Power. New Haven: Yale University Press.
WRIGHT, H. T. (1984). 'Prestate political formations.' In T. Earle, (Ed.), On the Evolution of Complex Societies: Essay in Honor of Harry Hoijer, 1982. Malibu: Undena Publications, pp. 41-77.
YOUNGER, S. M. (2002). Discrete Agent Modeling as a Tool For the Study of Individual and Social Development: The MICROS Code (Version 8.0). Los Alamos National Laboratory Report LA-UR-02-7009.
YOUNGER, S. M. (2003). Discrete Agent Simulation of the effect of simple social structures on the benefits of resource sharing. Journal of Artificial Societies and Social Simulation, 6(3), 1: https://www.jasss.org/6/3/1.html.
YOUNGER, S. M. (2004). Reciprocity, sanctions, and the development of mutual obligation in egalitarian societies. Journal of Artificial Societies and Social Simulation, 8(2), 9: https://www.jasss.org/8/2/9.html.
YOUNGER, S. M. (2005). Violence and revenge in egalitarian societies. Journal of Artificial Societies and Social Simulation 8(4), 11: https://www.jasss.org/8/4/11.html
YOUNGER, S. M. (2010). Leadership in small societies. Journal of Artificial Societies and Social Simulation 13(3), 5: https://www.jasss.org/13/3/5.html. [doi:10.18564/jasss.1573]
YOUNGER, S. M. (2011). Leadership, violence, and warfare in small societies. Journal of Artificial Societies and Social Simulation, 14(3), 8: https://www.jasss.org/14/3/8.html. [doi:10.18564/jasss.1784]
YOUNGER, S. M. (2012). Calculating Chiefs: Simulating Leadership, Violence, and Warfare in Oceania. LAP LAMBERT Academic Pub.

