Introduction
Discourse and communication patterns in small groups have received attention because certain patterns seem to be connected to successful task performance or good learning outcomes. The beneficial discourse patterns are often characterised by bidirectional mutuality, which is caused by the reciprocity in turn taking in discourse and responses (Barron 2003; van Boxtel et al. 2000; Hogan et al. 1999; Stahl et al. 2014). A widely held notion is that discourse patterns in a small group not only reflect the competencies and cognitive capacities of the group members, but also how they evaluate and appreciate each other (Bonito 2000, 2002) and how tasks or knowledge needed to complete the tasks are organised (Tschan 2002).
A closer look on published research shows that although the discourse patterns depend on diverse factors such as context, the structure of tasks and group composition, certain structural features are recurring. These recurring features include at least: successful strong dyads (two partners strongly connected) and egalitarian triads (three partners all connected) (Bonito 2000, 2002; Barron 2003; Hogan et al. 1999; Stahl et al. 2014) while in some cases one also finds dyads to which a third partner is more weakly connected (Heo et al. 2010; van Boxtel et al. 2000). Very often, however, one finds isolation, with some group members remaining weakly connected or not connected at all to other members in a group (Bonito 2000, 2002; Janssen et al. 2007). The common trend revealed by the empirical studies is that strongly reciprocated dyadic and triadic patterns of interaction are characteristic to successful and high achieving groups (Bonito 2000; Hogan et al. 1999; Stahl et al. 2014) and similar findings have also been reported in studies focusing on task related group performance (Lusher et al. 2014).
The beneficial roles of discourse on group performance and group learning have led to many suggestions to enhance discourse and cooperation in such groups. One persistent problem is that despite repeated attempts it has proved difficult to engage the whole group in discourse that is productive as regards of task or learning outcomes (Barron 2003; Bonito 2000; Janssen et al. 2007). Very often one or more of the group members remain passive, are not engaged in the discussion or gradually drop out from the discourse (Janssen et al. 2007). These problems seem, at least to some degree, to be generic since similar situations are found in different contexts. Isolation and marginalisation also seems to be more common in groups of five and larger than in groups of three or four, independent of the type task (Bonito 2000, Bonito 2002; Janssen et al. 2007). Recent results on participation in groups of seven reveal on closer inspection that even if isolation does not happen, participation and engagement in group activities is in many cases unequal; a significant fraction of group members are much less engaged in group activities than the most active members (Heo et al. 2010).
One possibility to consider is that such generic phenomenon of discourse pattern formation as the emergence of strong dyads, egalitarian triads and isolates in a task engaged small groups is related to the inherent social dynamics of the group and status generation within the group. Several theories of social dynamics addressing the formation of social ties in fact either indirectly support such a view or even explicitly claim that such a connection exists. Two examples of such theories are the affect theory of social exchange (Lawler et al. 2000; Lawler 2001; Lawler et al. 2008) and the expectation state structuralism model (Skvoretz & Fararo 1996; Skvoretz et al. 1996).
The affect theory of social exchange (ATSE), for example, attributes formation of mutual ties through engagement in a common task and how goal orientation in a group generates positive feedback, which enhances the reciprocation of ties when the interaction is found to be satisfying by the interacting partners. The peers in a group have expectations for their performance and roles in completing the task, and when these expectations are felt to be fulfilled, this increases satisfaction and future engagement and exchange (Lawler et al. 2000; Lawler 2001; Lawler et al. 2008). In the ATSE this self-enhancing reciprocation of ties then leads to the formation of social patterns, which have strong dyads and strongly connected triads (Lawler et al. 2008; Yoon et al. 2013).
The expectation state structuralism model (ESSM) posits an explicit connection between the mutual comparisons and participation pattern formation in a task performing group. In ESSM the group members expectations of their peers’ competencies decides how each member is given a chance to participate in task completion or in discussion, and that participation then affects the member’s status in a group. There is dynamic, bidirectional relationship between performance and status (Skvoretz & Fararo 1996; Skvoretz et al. 1996). In the ESSM the basic mechanisms are such that they generate status hierarchies, which are reflected as cyclic and transitive patterns of interactions (Skvoretz et al. 1996). In ESSM the so called by-stander effect is central in deciding whether or not highly transitive patterns emerge. Although the ESSM is designed to describe formation of social hierarchies and does not directly address the reciprocation of ties as ATSE, the basic notion of a close relationship between status and participation patterns is similarly at the core of the ESSM as it is in the ATSE.
A key feature of both ATSE and ESSM is the central role they attribute to peer-to-peer comparisons as a driving force of formation of ties in a group or in status generation. This parallels with the social learning theory (SLT) that posits that individuals in a group constantly compare their performance with their peer’s performance and form not only a conception of themselves as learners but also of their peer’s as learners (Bandura 1997, 2006). In fact, ATSE directly refers to SLT in seeking support for the role of satisfaction and affection in shaping the social ties in task performing group. The mechanisms of peer-to-peer comparison and how these comparisons affect the formation of ties, appreciations or status in task engaged groups are thus basically very similar not only in ATSE and SLT but also in ESSM and SLT. In all these views, it is recognised that individuals’ conceptions of how they are appreciated in social groups essentially determine how much e ort they put into the performance, or the others are expected to put into the cooperation. However, it is important to note that such competition in a task engaged group is not usually or at least is not meant to be only discriminative or differentiating, but contains also a component of mutual support and cooperation. The aspect of support and cooperation arises from the fact that activities and discursivities are evaluated in regard to the task to be performed and there are mutual benefits to be gained if the interacting partners are both active and discursive (Bonito 2000, 2002; Lusher et al. 2014).
The formation of discourse patterns in task engaged groups is here approached from the viewpoint that the key driving forces in the formation of discursive connections are to be found in competitive comparisons and cooperation in a very similar way as the ATSE and SLT posits. As in ATSE and SLT, the focus here is on individual’s participation within the group, which aims to found a consensus concerning a solution of task or problem. It is assumed that participation in discourse concerning the consensus requires activity, and that this activity is self-reinforcing but constrained by competition and boosted by cooperation. The competition in this case is for floor in discussions and gaining visibility in contrast to others, while cooperation is about seeking a cooperation between the discursive and active group members. The formation of discourse patterns under such conditions is approached here through the agent-based model, where interaction rules between agents simulate the comparisons based on competition and cooperation in discourse. Recently, some similar kinds of systems have been studied through agent-based models. For example, the generation of status as it is described by ESSM has been studied through an agent-based model, which allowed a detailed investigation of how status hierarchies are formed, and when they have emerged, how they may lead to the formation of transitive patterns of social ties (Grow et al. 2015). Another recent agent-based model describes the formation of elite and egalitarian groups and how vanity (i.e. seeking praise) shapes group formation in social and political life (Deffuant et al. 2013).
The model introduced here is most closely related to an agent-based model (ABM) recently introduced for description of the generation of mutual appreciation patterns through competitive comparisons in small groups (Koponen & Nousiainen 2016). In that model, many patterns of interaction that emerge correspond patterns found typically in cooperation or discourse in task-engaged small groups. The model, however, was not able to reproduce transitive patterns and cyclic patterns, which, though not common in cooperative learning groups, are found in certain situations. Even more seriously, the model was not able to produce the effect of isolation or marginalisation, except in the very high competitive case. In this study we introduce a closely related model which performs better in these aspects. In the new model, the essential difference is that advantage seeking cooperation is included as a part of the model dynamics. We focus here on groups of sizes from 4 to 7 individuals because this size range is of most interest for small group dynamics, for emergence of isolation effects, and is very common in practical discourse situations (Barron 2003; Heo et al. 2010; Hogan et al. 1999; Tschan 2002; Bonito 2000, 2002). In addition, the previous models based on similar kind of dynamics as the model introduced here, suggest that the most interesting and representative group dynamics is manifest groups of sizes between 4 and 7; group of size 3 is too simple and predictable (Koponen & Nousiainen 2016) and groups larger than 6 individuals appear to behave qualitatively similarly (Koponen & Nousiainen 2016; Grow et al. 2015) as is confirmed by the results presented here. In summary, the model introduced here, its basic assumptions and rules of interactions, are designed to reproduce the phenomena of interest for discourse in relatively small task focused groups, where competition and cooperation govern the discourse dynamics.
Agent-Based Model of Discourse Pattern Formation
We present here an agent-based model (ABM) to simulate how competitive comparisons and cooperation affect the formation of discourse patterns in a small group. The model assumes that the agents’ decision to interact and participate in a discussion depends on two properties of it; activity and discursivity:
- The activity is agents’ potential, inherent activity to participate in a discussion. Activity as agents’ inherent property is not directly observable but related to willingness to send queries or responses to other agents in discursive events. The activities indirectly prompt the interaction (e.g. query-response events) but do not determine it in direct way. Agents’ activities, however, are assumed to be indirectly manifest to peers through discursivity, which is assumed to depend on activity.
- The discursivity is directly proportional to realised and externalised discourse events (e.g. query-response events) that connect two agents. These events can be observed empirically. The discourse patterns, on the other hand, are then patterns formed out of the discursivities between agents.
Basic assumptions
The basic assumptions of the agent’s state (its knowledge of itself and its peers) in the present model can be comprised more formally as states \(\kappa\)characterising the agent as follows:
- An agent \(i\) has activity \(\kappa_{ii}\).
- An agent \(i\) is aware of its peer \(j\)’s activity \(\kappa_{jj}\).
- An agent \(i\) has discursivity \(\kappa_{ij}\)towards its peer \(j\).
- An agent \(i\) is aware that its peer \(j\) has a discursivity \(\kappa_{ji}\) towards it.
The second assumption concerning the agent’s inherent property of activity as a property sensed by its peers is based on additional assumption that discursivity is proportional (or nearly linearly correlated) to activity. Similar assumption of how agents sense the internal states of other agents is made in modelling collective decision making (Zafeiris et al. 2017). In addition, in models based on update rules similar to Equations 4-6 values of variables \(\kappa_{ii}, \kappa{ij}\) and \(\kappa_{ji}\) are strongly correlated when discourse patterns are stabilised (Koponen & Nousiainen 2016).
Competitive comparisons are assumed to affect both activities and discursivities and these changes take place through pair-wise comparisons. The comparisons are competitive in the sense that an agent, through comparison, seeks to increase its floor in discourse by using the information that is available to it of its peers’ activities and discursivities. In the present model changes in activities and discursivities due to competitive comparisons take place as follows:
- Change in the agent’s activity \(\kappa_{ii}\). If in the comparative interaction event agent \(i\) finds that its activity \(\kappa_{ii}\) is lower than its peer \(j\)’s discursivity \(\kappa_{ji}\) towards it, then \(i\) tends to increase its activity because it tries to compete for floor in the discussion. If agent’s activity is higher than its peer’s discursivity, then agent tends to decrease its activity because there is no need to compete.
- Change in the agent \(i\)’s discursivity \(\kappa_{ij}\) is affected by two competitive comparison contributions. First, the agent’s discursivity \(\kappa_{ij}\) towards its peer \(j\) increases/decreases if the agent finds that its peer’s discursivity towards it \(\kappa_{ji}\) is higher/lower than its own activity \(\kappa_{ii}\) This is a similar competitive effect as in case of the agent’s change in activity. Second, the discursivity \(\kappa_{ij}\) is decreased if it is higher than peer \(j\)’s activity \(\kappa_{jj}\). This effect reduces the discourse activity towards agents that have low activity.
The agents also seek cooperation. Cooperation changes agent’s discursivities so that if both interacting agents have high activities the discursivities increase. In cooperation, agents with high activity benefit from interacting with other similar agents, thus mutually reinforcing each other. The pay-off in increase of discursivity is higher for agents of high activity than for agents of low activity. Such a mutual reinforcement mechanism leads to synergy, characteristic for collaborative actions (Caram et al. 2015, 2010). This reflects the assumption that cooperation is a multiplicative rather than additive feature; for success or mutual benefits in gaining floor, both agents need to be active. The cooperation is thus assumed to change the discursivity between agents so that the change is proportional to the interacting agents’ activities as follows:
- Change in agent \(i\)’s discursivity \(\kappa_{ij}\) due to cooperation towards its peer \(j\). This change is proportional to the geometric mean \(\sqrt{\kappa_{ii} \kappa_{jj}}\) of the agents’ activities. Agents’ activities, however, are not assumed to change directly through cooperation.
Agents have different sensitivity to competitive comparisons and to cooperation. The sensitivity described how easily agent changes its state due to comparisons or cooperation. Insensitive agents, despite of their interaction with other agents, maintain their states more robustly, while sensitive agents are more susceptible to change. These inherent sensitivities of agents are referred as sensitivity \(\alpha\) to competitive comparisons (competitivity) and affinity \(\lambda\) to cooperation (cooperativity). The operationalisation of these properties is explained in more detail later on, when the rules corresponding the different possible changes of states are formulated.
Decision probabilities
The agents’ decision to interact is assumed to be probabilistic, guided by how the agent’s activity and discursivity compare to the activities and discursivities of other agents. In all interactions the basic model is dyadic interaction model D, where agent \(i\) randomly selects a partner \(j\) to interact with, but it depends on the activities and discursivities whether or not this interaction actually leads to any changes in the agent’s state (i.e. activity and discursivity). In addition, a second peer \(k\) may also be selected as a partner in the interaction. This second agent, however, is included only collaterally so that only \(\kappa_{ik}\) changes. This model, introduced in (Koponen & Nousiainen 2016) is referred to as the triadic collateral model T because it promotes the formation of pat-terns consisting of three agents. Similar type of collateral participation is also used in modelling formation of egalitarian and elite groups (Deffuant et al. 2013). Both models D and T contain the probabilities whether the interaction leads to any change, but the magnitude of the change depends in a more complex way of on the interacting agents’ states.
In both cases, for competitive comparisons and for cooperation the probability to change state in an event is formally taken as a probabilistic decision, where two factors A and B affect the choice. To these factors A and B we assign utilities \(U_A(i,j)\) and \(U_B(i,j)\) which both may depend on states of agents \(i\) and \(j\). These utilities are related to decision to compete or cooperate and they depend on the agents’ state (to be defined in more detail later on). In the general case the probability that agent \(i\) adopts a new state when it interacts with \(j\) is then given as the canonical probability (Laciana & Oteiza-Aguirre 2014; Sîrbu et al. 2013)
| $$p_{i j} = \frac{\exp[U_{A} /\sigma]}{ \exp[U_{A} /\sigma]+\exp[U_{B} /\sigma] } =\frac{1}{ 1+\exp[-\delta_{ij}/\sigma] }$$ | (1) |
The utilities for competition are here taken to be \(U_{A}(i,j)=\kappa_{ij}\)and \(U_{B}(i,j) =\kappa_{ii}\) in which case \(\delta_{i j}=\kappa_{i j}-\kappa_{i i}\) is the difference between activity and discursivity toward its peers. This choice reflects the assumption that if agent’s \(i\) activity is already higher than its discursivity towards agent \(j\), it is not likely that \(i\)’s interaction with \(j\) will lead to further changes in its activities or discursivities, whereas in the opposite case, it is very likely that change will take place. In this case the parameter \(\sigma=\sigma_{\alpha}\) describes the agents’ tolerance to diversity in the context of competitive comparisons, when they interact with other agents. It is thus referred to as the diversity in competition in what follows. Such diversity is closely related to homophily, with a large diversity indicating a low homophily and a low diversity indicating a high homophily.
The utilities for cooperation are here taken to be \(U_{A}(i,j)=\kappa_{ji}\) and \(U_{B}(i,j) =\kappa_{ij}\) in which case \(\delta_{ij}=\kappa_{ji}-\kappa_{ij}\) is the difference between agents’ \(j\) and \(i\) discursivities towards each other. This reflects the assumption that when agent \(i\) has chosen to interact with \(j\), the cooperation is more likely to take place the higher is \(j\)’s discursivity towards \(i\). Interpreted differently, this is a condition of rewarding reciprocation where agent \(i\)’s partner’s high attention towards \(i\)’s boosts cooperation. In the case of cooperation the parameter \(\sigma=\sigma_\lambda\) describes the agents’ tolerance to diversity in cooperation.
Evolution of activities and discursivities
The evolution of agents activities and discursivities are described stochastically, where the probability \(p_{ij}\) is central in deciding whether the change takes place. The mathematical form of probability is the same for competitive comparisons and for cooperation. The agents’ sensitivity to the competitive comparison is regulated by the parameter \(\alpha \in [0,1]\), referred to as the competitivity in what follows. If \(\alpha=0\), there is no effect. If \(\alpha= 1\), the effect is maximal. The affinity of agents to cooperation is described through the parameter \(\lambda \in [0,1]\), called cooperativity. The probabilities for competitive comparisons and cooperation with corresponding differences in associated utilities are briefly denoted as
| $$p_{ij} = p_{ij} (\delta_{ij}) \text{,} \quad \text{where} \, \, \delta_{ij} = \kappa_{ij} - \kappa_{ii} \, \, \text{for competition}$$ | (2) |
| $$p^*_{ij} = p_{ij} (\delta^*_{ij}) \text{,} \quad \text{where} \, \, \delta_{ij} = \kappa_{ji} - \kappa_{ij} \, \, \text{for cooperation}$$ | (3) |
The update rules for agent \(i\)’s activity \(\kappa_{ii}\) and discursivity \(\kappa_{ij}\) in the dyadic (D) model, and in the triadic collateral model (T), where agent \(i\) holds also the discursivity \(\kappa_{ik}\) towards agent \(k\), are now expressed in the form
| $$\begin{align} & \kappa_{ii} \leftarrow k_{ii} + \pi_o [ \Delta \kappa_{ii}] \kappa_{ii} (1 - \kappa_{ii})\end{align}$$ | (4) |
| $$\begin{align}& \kappa_{ij} \leftarrow k_{ij} + \pi_o [ _{\alpha} \Delta \kappa_{ij} + _{\lambda} \Delta \kappa_{ij} ] \kappa_{ij} (1 - \kappa_{ij})\end{align}$$ | (5) |
| $$\begin{align}& \kappa_{ik} \leftarrow k_{ik} + \pi_o [ _T \Delta \kappa_{ik} ] \kappa_{ik} (1 - \kappa_{ik})\end{align}$$ | (6) |
| $$\begin{align} \Delta \kappa_{ii} & = \begin{cases} (\kappa_{ij} - \kappa_{ii}), & \qquad R_{\alpha} < p_{ij} \\ 0, & \qquad R_{\alpha} \geq p_{ij} \end{cases}\end{align}$$ | (7a) |
| $$\begin{align}_{\alpha} \Delta \kappa_{ij} & = \begin{cases} \alpha(\kappa_{ji} - \kappa_{ii}) + (1 - \alpha) (\kappa_{jj} - \kappa_{ij}), & \quad R_{\alpha} < p_{ij} \\ \alpha (\kappa_{ji} - \kappa_{ii}), & \quad R_{\alpha} \geq p_{ij} \end{cases}\end{align}$$ | (7b) |
| $$\begin{align} \Delta \kappa_{ik} & = \begin{cases} (\kappa_{jk} - \kappa_{ik}), & \qquad R_{\alpha} < p_{ij} \\ 0, & \qquad R_{\alpha} \geq p_{ij} \end{cases}\end{align}$$ | (7c) |
| $$\begin{align} _{\lambda} \Delta \kappa_{ij} = \begin{cases} \lambda \frac{\delta^*_{ij}}{|\delta^*_{ij}|} \sqrt{\kappa_{ii} \kappa_{jj}}, & \qquad R_{\lambda} < p^*_{ij} \\ 0, & \qquad R_{\lambda} \geq p^*_{ij} \\ \end{cases} \end{align}$$ | (7d) |
In all incremental/decremental changes in Equations 4-7, the model takes into account that activities and discursivities do not increase/decrease without limit and are constrained to the maximum value, which is here 1. Similarly, the lowest possible discursivity and activity has a value of 0. The discursivity and activity values 0 mean no participation in discourse and thus isolation, while values 1 mean maximal possible participation and thus equal division of available floor for discourse. In real discourse, these extremes are probably not avail-able, except in case of isolation in which case also activity as it is defined here must have a value 0. In order to take these constraints into account, the equations are of the logistic type and contain the term \(\kappa(1-\kappa)\). Due to the logistic growth activities and discursivities are nearly always in range from 0.15 to 0.9 except in case of isolation when they approach a value 0. The parameter \(\pi_{\rm o}\) is the overall sensitivity of agents to changing their discursivities and activities. This parameter is treated stochastically, thus simulating the randomness in strengths of individual decisions. In practice, we have assumed that \(\pi_{\rm o}\) is normally distributed with an average value of \(\langle \pi_{\rm o} \rangle < 0.3\) and a standard deviation of \(0.3 \pi_{\rm o}\). These values are small enough to prevent instabilities in iteration and to ensure convergence to results that do not depend on exact values of \(\langle \pi_{\rm o} \rangle\). Then the exact value affects only the number of steps needed so that the iterations converge to dynamically stable values of discursivities and activities.
Simulations and parameters
The simulations are carried out by selecting stochastically the agents that interact (two agents for the dyadic model D and three agents for the triadic collateral model T). The initial values of activities and discursivities \(\kappa\) are assigned randomly from a uniform distribution in the range \(0.333 < \kappa <0.667\). This is a practical choice and a wider/narrower distribution of initial values does not affect the distribution of stable patterns; stabilisation of patterns just takes more/less iterations. The parameter \(\alpha\) is varied from 0 to 1, with steps of 0.2, thus spanning the effect of competitivity from a nonexistent effect to a maximal effect. The cooperativity is studied for no cooperation at all \(\lambda\)=0.0, and for intermediate and high cooperation \(\lambda\)=0.1 and 0.3, respectively. The value \(\lambda=0.3\) is high enough so that an increase in cooperation does not significantly change the results. The tolerance to diversity is explored for \(\sigma_{\alpha}\)=0.10, 0.20 and 0.30, where the lowest and highest values are chosen so that there are no essential changes in results beyond these limits. The tolerance to diversity in cooperation \(\sigma_{\lambda}\) was not found to affect much the results and a moderately high value \(\sigma_{\lambda}\)=0.25 and the denotation \(\sigma_{\alpha} =\sigma\) will be used throughout.
| Parameter | Symbol | Role | Values |
| Competitivity | \(\alpha\) | Sensitivity in competitive comparisons | \(\alpha \in [0,1]\), step 0.2 |
| Cooperativity | \(\lambda\) | Sensitivity in cooperation | \(\lambda=0.0, 0.1, 0.3\) |
| Diversity in competition | \(\sigma_{\alpha}\) | Tolerance to diversity in competitive comparisons | \(\sigma_{\alpha}=0.1,0.2,0.3\) |
| Diversity in cooperation | \(\sigma_{\lambda}\) | Tolerance to diversity in cooperativity | \(\sigma_{\lambda}=0.25\) |
The decision to interact is done by simple application of the Monte-Carlo rejection based rule (Koponen & Nousiainen 2016; Laciana & Oteiza-Aguirre 2014; Lipowski & Lipowska 2012). This is done by selecting two random numbers \(R_{\alpha}, R_{\lambda} \in [0,1]\) at a time. If \(R_{\alpha} >p_{ij}\) the activity and discursivity are updated according to Equations 1 - 3 and Equations 4 - 7. If also \(R_{\lambda} >p_{ij}\), discursivity is affected also by cooperation and is updated accordingly by following the rule in Equation 6. In addition, \(\pi_{\rm o}\) in Equations 4 - 6 is also treated as a stochastic variable and selected from a uniform distribution between the values \(\pi_{\rm o} \pm \delta \pi_{\rm o}\), where \(\delta \pi_{\rm o}=0.33 \pi_{\rm o}\). Other technical details of implementation are given in (Koponen & Nousiainen 2016; Laciana & Oteiza-Aguirre 2014; Lipowski & Lipowska 2012). All the simulations were carried out for 2500 repetitions of each parameter combinations. Some simulation runs were done with different choices of initial values as well as different choices of \(\pi_{\rm o}\) to test the robustness of the results in regard to the choice of parameters regulating the computation.
Discourse Patterns
Important characteristics of the relationships in discourse and associated discourse patterns can be under-stood by focusing on different dyadic and triadic sub-patterns and how the ties in these sub-patterns are reciprocated. Given the background assumptions, the expectation is that reciprocated dyads and triads, as well as reciprocated dyads embedded as parts of different triads, are important as expected on the basis of task or engagement based interactions as expected by ATSE (Lawler et al. 2000; Lawler 2001; Lawler et al. 2008). One can also expect to find patterns of the leadership type containing directed ties in which one agent is more central than the others, as predicted by ESSM (Skvoretz & Fararo 1996; Skvoretz et al. 1996). Cyclic (i.e. three agents A, B and C connected cyclically as A \(\rightarrow\) B \(\rightarrow\) C \(\rightarrow\) A), transitive (A \(\rightarrow\) B,C and B \(\rightarrow\) C) and completely non-reciprocated triadic patterns, however, are expected to be rare under situations favouring reciprocation (Yoon et al. 2013; Block 2015). The 16 possible dyadic and triadic patterns are shown in Figure 1 where we have indexed the patterns according to the common structural indexing (Moody 1998) (see the caption of Figure 1 for details). Such triadic census of the patterns acts as a fingerprint of the group dynamics and structure (Moody 1998; Itzkovitz et al. 2003). In what follows the patterns are given short-hand names on the basis of their roles in the social dynamics in discourse, and they are roughly of three different types; triadic, dyadic and leadership-type patterns. The short-hand names of the patterns in Figure 1 and their indexing are given in Table 2. In simulations, we were looking for these patterns and counting their abundances at the stage of simulation where patterns were stabilised (roughly the last 30% of update events in the simulations). In region where patterns are stabilised discursivities which are higher than threshold 0.05 are taken into account. Nearly all such discursivities are close to value 1 in stabilisation of patterns. Variation of threshold does not thus significantly affect the pattern counts.
- Triadic patterns are groups in which all three agents are linked to each other in different ways. In the egalitarian triad (300), all links are reciprocated. In the collateral triad (120D), only two agents are connected by a reciprocated link and the third agent is collaterally connected to them both by an incoming but non-reciprocated link. This is a broker’s position, where a single agent is appreciated by a dyad and can thus influence the dyad. By contrast, in the broker triad (120U), the two agents are connected to the third one by an outgoing link (a pattern known as tertius gaudens (Simmel 1964)). The cyclically connected (CC) triad (120C) has a cyclic pattern 030C as a part of it. Finally, one triadic pattern of interest is transitive triad 030T, typically found in hierarchical patterns (Skvoretz & Fararo 1996; Skvoretz et al. 1996).
- Dyadic patterns are groups in which a reciprocated dyad is the most dominant structural element. In an egalitarian dyad (102), both agents are in symmetrically reciprocated positions but not connected to a third party at all. In a collateral dyad (111U), one of the agents in the dyad is connected collaterally but unidirectionally to another agent, whereas in a broker dyad (111D), one collateral agent connects to one of the agents in the dyad. These patterns have very different roles in discourse; the one who is always contacted but never responds (U), and the one who always contacts but is never responded to (D). These two latter structures are often transitory structures not only in forming corresponding balanced triadic patterns but also in situations in which balanced triadic patterns fall apart.
- Leadership patterns are groups in which one agent attains a special position as a leader. The simplest of such structures is the endorsed leader (021U), in which one agent is contacted by others but which is not responsive towards any of the other agents. Such a position is expected in cases of strong dominance and competition. A similar type of pattern in which one agent affects two other agents is a broker type pattern 021D. A more egalitarian type of leadership is the dyadic leader (201), in which two dyads share a common agent, which then have a leader-type position. This pattern can evolve to or from a triadic leader (210), in which the agents, which are not in a leader-positions, are non-reciprocally connected.
In addition to the patterns listed in Table 1 also totally isolated (no connections at all) triads 003 were recorded in the simulations. The simulations provide the matrix \({\rm K}'\) of all connections in terms of discursivities, and from this matrix, the abundance \(n\) of different patterns (see Table 2) can be obtained (Moody 1998; Itzkovitz et al. 2003). Details and proofs of the formulas provided in Table 1 to count the patterns are given in (Moody 1998; Itzkovitz et al. 2003) and are not reproduced here.
| index | name | Number \(n_{ind}\) | index | name | Number \(n_{ind}\) |
| 300 | triad | \(\sum (S^{3} )/6\) | 021D | broker L | \(\sum (A^{T} A \circ \tilde{E})/2\) |
| 201 | dyadic L | \(\sum (S^{2} \circ \tilde{E})/2\) | 021U | endorsed L | \(\sum (A A^{T} \circ \tilde{E})/2\) |
| 102 | dyad | \(\sum (\tilde{E}^2 \circ S)/2\) | 021C | cyclic L | \(\sum (A^2 \circ \tilde{E})\) |
| 210 | triadic L | \(\sum (S^{2} \circ A)\) | 111D | B dyad | \(\sum (S A \circ K \circ \widetilde{K^T})\) |
| 120D | B triad | \(\sum (A^{T} A \circ S)/2\) | 111U | C dyad | \(\sum (S A^{T} \circ K \circ \widetilde{K^T})\) |
| 120U | C triad | \(\sum (A A^{T} \circ S)/2\) | 030T | transitive | \(\sum (A^2 \circ A)\) |
| 120C | CC triad | \(\sum (A^{2} \circ S)\) | 030C | cyclic | \(\sum ((A^{T})^2 \circ A)/3\) |
| 003 | isolate | \({\rm Tr} \tilde{E}^{3} /6\) | 012 | Link | \(\sum (\tilde{E}^2 \circ A)/2\) |
Results
The formation of the discourse patterns is examined here for groups of 4, 5, 6 and 7 agents. The three agent group is omitted because in a three agent group, G3, the pattern formation is essentially constrained by the geometry, and only egalitarian triads, leadership dyads and dyads are observed (Koponen & Nousiainen 2016). Most results are shown for four- and five agent group G4 and G5. This is due to the fact that G5 is large enough so that its geometry does not essentially constrain the formation of patterns. The four agent group G4 is interesting because it easily splits into two independent dyads. It is expected that the five agent group G5 will provide a different collection of dyadic and triadic patterns and more isolated patterns in comparison to G4. The six-and seven agent group, G6 and G7, and higher are expected to be in many ways very similar to G5 as far as our interest is in the basic units of dyads and triads. The most important difference between G5 and groups with higher number of agents is that as the number of agents increases also the relative number of isolated agents (isolates) increases. Consequently, G5 is of interest as a transitory case between G4 and G6 or larger groups.
The different patterns are counted throughout the simulations, and average values over 1000 final steps (the stabilised stage) of 6000 total steps in each case and 2500 repetitions (ensembles) are reported in what follows. The parameters used in simulations are as listed in Table 1. In all simulations, the competitivity is the most important parameter that affects how the discourse dynamics change and what patterns are dominant.
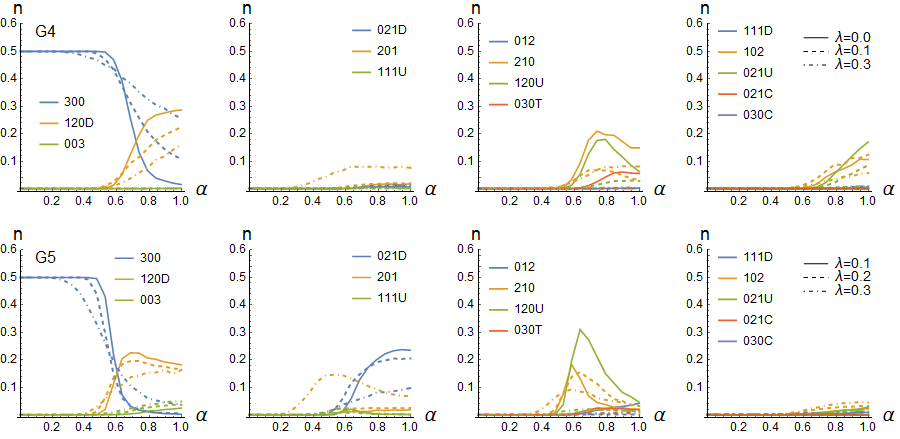
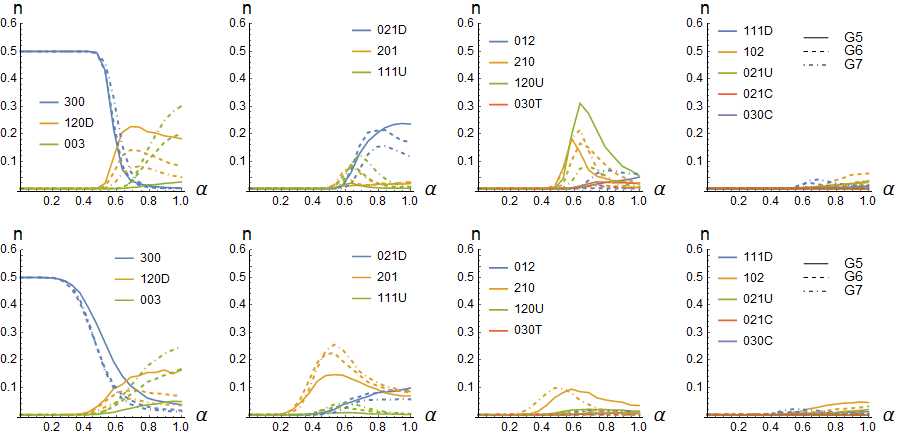
First, we show the average abundance of patterns \(n\) for G4 and G5 and study the effect of diversity for \(\sigma\)=0.10, 0.20 and 0.30 in Figures 2 and 3. In all cases, for each group, the values of \(n_{ind}\) for each pattern \(ind\) are normalised so that \(n_{300}=1\) for fully connected triads. For low \(\alpha\) triads dominate and therefore, for ease of comparisons, we have divided the number of triads by a factor of two in all figures (i.e. in all figures triads with \(n_{300}=1\) correspond to the value of 0.5). Second, the effect of collaterality on pattern formation in terms of models D and T is explored for G4 and G5 in Figure 4. Third, and last, the effect of group size on pattern formation is explored up to G7 for model D in Figure 5 and for model T in Figure 6.
Competitivity, cooperativity and diversity
The effects of competitivity and cooperativity are most prominent in G4 and G5 with dyadic interactions (model D), shown in Figure 2 (all other patterns except the nearly nonexistent single link 012 are shown). The results for moderate tolerance to diversity in competitive comparisons \(\sigma\)= 0.2 and for cooperation \(\lambda\)= 0.0 (no cooperation), 0.10 and 0.30 are shown in Figure 1 (upper panel) and for comparison, for \(\lambda\) = 0.3 with \(\sigma\)= 0.1, 0.2 and 0.3 (lower panel) in order to see how tolerance to diversity affects the results. Cooperativities higher than \(\lambda\)= 0.3 give essentially similar results as \(\lambda\)= 0:3 which is thus chosen to be the highest cooperativity studied. The results for G4 show that the most dominant patterns for low competitivity \(\alpha < 0.4\) are fully connected egalitarian triads (300), while for intermediate competitivity \(0.3 < \alpha < 0.6\) the dyadic leadership patterns (201) are dominant. Increase in cooperativity increases the abundance of these dyadic leadership patterns, and they persist even for the high competitivity region \(\alpha > 0.6\). Cooperativity thus increases the tendency to dyadic leadership type patterns very clearly. In the high competitivity region \(\alpha > 0.5\) dyads (102) become increasingly prominent patterns and also the abundance of broker triads (120D) increase. This signals transition to the strong dyadic interaction when competition is high. This is an outcome of the self-reinforcing feedback effect between highly discursive agents, which become engaged in a mutually reinforcing cycle of discursive interactions while reducing interactions with their less discursive partners.
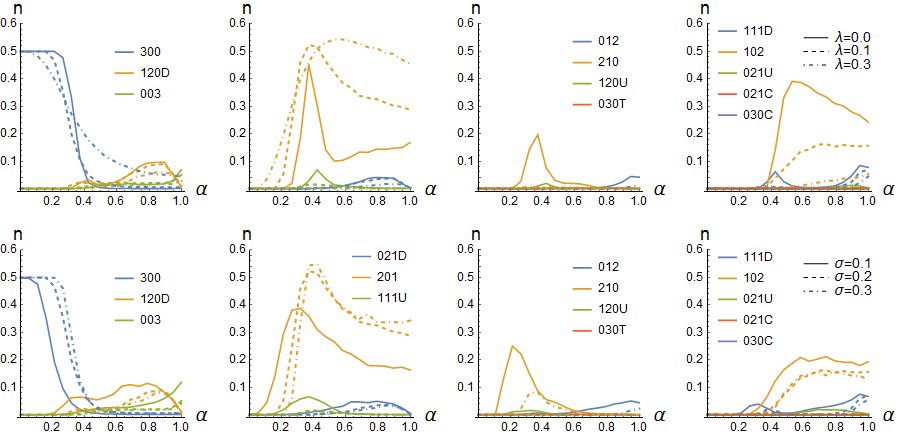
The effects of tolerance to diversity in discourse pattern formation for G4 in case of model D are shown in Figure 2, lower panel. Somewhat unexpectedly the increased tolerance to diversity has very similar effects to increased cooperativity. In both cases, the effect in comparison to no cooperation or low diversity is to increase the dyadic leadership patterns (201) while the number of dyads (102) decreases. This behaviour results, when with increased cooperation or tolerance to diversity, dyads are combined to connected dyads (i.e. to dyadic leadership patterns). This notion is interesting because it supports the anticipated beneficial effects in discourse when participants are cooperative or alternatively tolerant to different opinions. The effects of competitivity, cooperation and tolerance to diversity for G5 and model D are shown in Figure 3 with similar parameters as those for G4 shown in Figure 2. The comparison of results in Figures 3 to those in Figure 2 show that the most significant difference between G5 and G4 is that in G5 the abundance of dyads (102) is significantly lower and abundance isolates significantly higher than in G4 with corresponding parameters. Thus, the bigger group enhances the tendency for isolation and drop-outs. This result agrees with the notion that in big discourse groups face-to-face contacts tend to decrease and risk of isolation increases (Bonito 2000, Bonito 2002). The model results suggest that transition to this kind of behaviour takes place at G5 and it is expected that the number of isolates is even larger in G6 and G7.
In addition to the patterns shown in Figures 2 and 3, we also checked the abundance of cyclic patterns (030C and 120C) and their sub-patterns (021C), but their abundance was so low that they were not of interest. The absence of cyclic patterns is known to be a typical feature of social dynamics in which the formation of reciprocated ties is common, e.g. when social ties are based on mutual trust or engagement in common tasks (Lawler et al. 2008; Yoon et al. 2013). In what follows, we focus on the six patterns that are the most abundant in all cases: egalitarian triads (300), dyadic leaders (201) and single dyads (102), which are the most abundant patterns, and triadic leader (210), broker and collateral dyads (120D and 120U), and isolates (003) which are the patterns most abundant and also most indicative of sociodynamic changes.
Collaterality
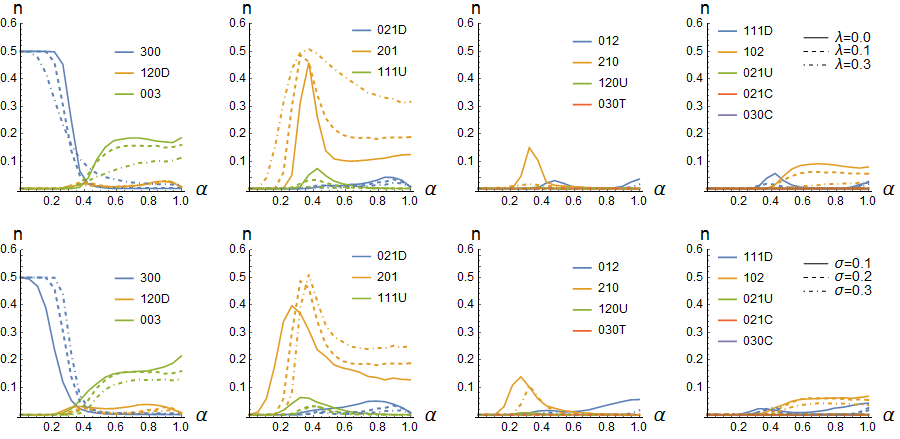
Collaterality refers to relationships in which one agent in a reciprocal dyadic pair of agents connects to a third. This model of interaction is as a triadic collateral model (model T). In Figure 4 is shown the effect of collaterality for G4 (upper panel) and G5 (lower panel) for model T. The results show that inclusion of collaterality increases the abundance of triadic leaders (210) and collateral and broker triads (120D and 120U, respectively), while abundances of dyads (102) and dyadic leaders (201) are decreased in comparison to model D. This is as expected because collaterality tends to add a third agent to the reciprocated dyads. As the results in Figure 4 show the effect of collaterality for G5 is nearly similar to the G4 case. In G5, in high competitivity region, however, also collateral triads (120U) are abundant, while they are absent in the dyadic model D. An interesting feature in G4 is the appearance of endorsed leaders (021U) at very high competitivity, a feature absent in G5.
Increased collaterality causes the egalitarian triads (300) to survive in the region of higher competitivity. As a result, egalitarian triads are now prominent for high competitive regions too. This is as expected, as increasing the tendency to include collateral partners in discourse, and increasing cooperation, make completely connected egalitarian triads become favoured patterns. The effect of collaterality on the abundance of different patterns is qualitatively similar in G4 and G5. In G4, the abundance of dyads (102) and dyad-dependent patterns (e.g. 120D and 120U) is higher than in G5. This is obviously due to fact that a group with an odd number of agents can be split into mono-dyadic units. Therefore, dyads and dyad-dependent collateral and broker pat-terns are more abundant in G4. For dyadic and triadic leadership patterns, group size dependent differences are insignificant in comparison to the differences caused by collaterality.
In summary, if the collaterality of social interactions can be controlled in real groups (as presumably it can be), opportunities are provided to tune the reciprocated dyadic discourse patterns. By increasing collaterality we can suppress the formation of dyadic and dyadic leader patterns and the group can be maintained in a balanced egalitarian mode. However, whether or not the egalitarian mode is more preferred than the dyadic mode is, of course, a decision that depends on the goals and task engagement of the group. In addition, as can be expected, in a small group, it matters whether the group consists of an even or odd number of agents. If egalitarian patterns are of interest, the best option is a group consisting of an odd number of agents and the triadic collateral interaction mode (T), in which case collateral and broker positions become more abundant in comparison to the dyadic interaction mode (D), which leads eventually to the stabilisation of egalitarian triads and connected dyads.
Group size
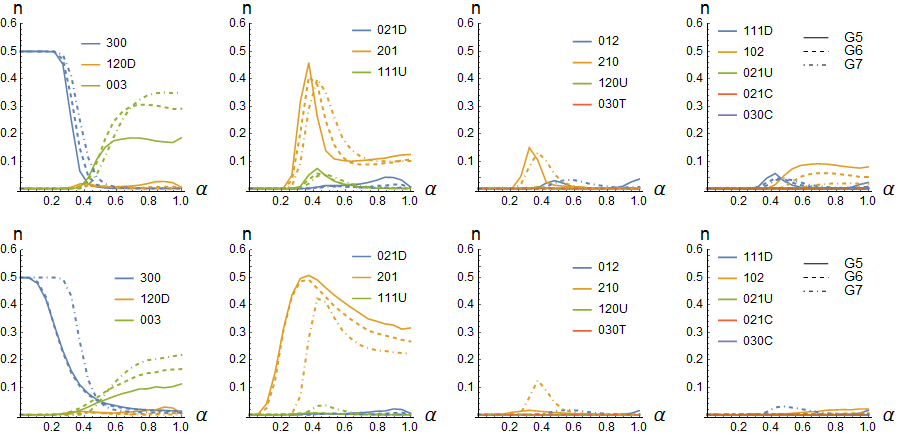
The dyadic and triadic patterns are the elementary blocks of higher-order social patterns and it is of interest to see how group size affects the relative proportions of these elementary units. In order to examine the effect of group size, simulations were also carried out for groups of sizes 6 and 7 (groups G6 and G7) in addition to G4 and G5. The results for G5-G7 are shown in Figure 5 for model D and in Figure 6 for model T. The results in Figure 5 for model D show that for G6 and G7 the results are very similar to G5. With increasing group size, the number of isolated agents increases, the number of triadic leadership patterns (210) and collateral (120U) and broker (120D) triads decrease. In G6 for model D, the dyadic leaders are also quite common in situations of high competitivity, which is as expected because the larger the group the more it provides combinatorial freedom to form connected pairs of dyads as dyads become more abundant. In model T dyadic leadership patterns are nearly absent for low cooperativity but increasing cooperativity increases the number dyadic leadership patterns, as in case of G5. In general, the differences between the results for model D and T is also similar to what is seen in case of G5.
The results for different group sizes show that the most egalitarian triadic discourse patterns are always obtained for low competitivity independent of group size. The larger the group, the higher competitivity it can tolerate while maintaining the egalitarian mode in which all members can equally participate in discourse and discursive moves are reciprocated. The larger the group size the more transition to dyads and dyadic leadership patterns occur at high values of the competitivity \(\alpha\). However, with increasing group size, the relative amount of dyads increases and the larger groups break up into dyadic groups more easily after the transition has taken place. This is expected when reciprocation is high at high competitivity. The comparison of results for G5-G7 with the results obtained for G4 confirm the assumption that G4 is qualitatively different from the larger groups, while larger groups behave rather similarly in regard to triadic census.
Discussion and Conclusions
We have here demonstrated that many patterns of interaction that are found to be typical in cooperation or discourse in task-engaged small groups are reproduced by the agent-based model in which the interaction of agents is based on their activity and discursivity, which dynamically evolves through mutual competitive comparisons and cooperation. The model introduced here is a minimal model in which only very basic competitive comparative evaluations and very simple forms of cooperation are taken into account. Two notions concerning the realism of the model must be made. First, the implicit assumption in constructing the model is that agents perceive not only their own states (activity and discursivity) but also their peers’ states. Though the assumption that discursivities (which are externalised actions and thus observable for all agents) are fully perceived is plausible, the assumption that peer’s activity is also perceived may raise doubts because it is not directly available through e.g. query-response events or discourse moves. However, the activity of agents can be taken as property which is manifest in group level and as such, agents can nevertheless make estimates of their peer’s activity on basis of how peers have participated in discourse in long run. Such an assumption is justified by notion that in models obeying the update rules similar to Equations 4 - 6 values of variables \(\kappa_{ii}, \kappa{ij}\) and \(\kappa_{ji}\) become strongly correlated when their values (and thus discourse patterns) are stabilised (Koponen & Nousiainen 2016). A similar problem with how agents sense the internal states of other agents is common with models of collective decision making, where internal state of the agent also appear as a factor in the model. In those models the problem is resolved by assuming that such internal state corresponds to how that property is manifest in group level and is thus also equated with the value perceived by the agent itself (Zafeiris et al. 2017). Also, the model depends on group level parameters of sensitivity to competitive comparisons (\(\alpha\)) and to cooperativity (\(\lambda\)), which in principle are parameters related to a single agent, but are treated here as being the same for all agents. The phenomenological meaning of these parameters corresponds to how the social learning theory views the roles of cooperation and collaboration. However, the exact values of the parameters can not be derived or deduced from the underlying theory because there is no direct correspondence how the qualitative notions of theory are operationalised. Instead, the values which correspond “high” or “low” sensitivity, must be deduced a posteriori on basis how they affect the evolution of the discourse patterns. Such a model is phenomenological and generative; it gives rise to observable states based on underlying unobservable states and interactions, not derivable from an underlying theory, but yet based on plausible behavioral rules (Nowak et al. 2013). Keeping these limitations and idealisations in mind generalisation to real discourse situations seems possible and useful.
The results show how delicately the discourse patterns depend on mutual comparisons, how the competition of gaining better discursivity (i.e. floor in discourse) shapes the patterns, and how by raising the competition the tendency to reciprocated dyadic patterns is raised. In practice, this means that highly discursive agents have the tendency to strengthen their mutual ties and ignore their less discursive peers, thus forming tightly connected dyads. When competition becomes very high, pure dyads begin to emerge while some group members lose all connections and become isolated. Only when competition is moderate or low, do all the partners in discussion receive attention (i.e. are given the floor in discussions) and no special dyadic patterns arise. This picture is very close to Simmel’s notions (Simmel 1964; Yoon et al. 2013) of the formation of strong, mutually dependent dyads vs. the formation of more egalitarian groups.
While the regions of very high and very low competition turned out to be rather unsurprising, the region of moderate competition shows a richer collection of patterns. When competition is moderate the leadership-type patterns and broker-type patterns emerge, where the basic unit is still a strong dyad, but now connected unidirectionally to a collateral agent. The discourse is still intense between tightly connected dyads, but now a third agent in different roles, either a collateral or broker role, is included. These roles can be seen as either the role of adviser (broker) or the adviced (tertius gaudens).
In addition to the competitive comparisons also the effect of cooperation was investigated. Cooperation here is a kind of advance seeking cooperation, where agents look for partners willing to active mutual discourse (in expectation that discourse is useful). How cooperation then reinforces the mutual discursivity of agents depends, on the other hand, on agents’ activities (i.e. potential willingness to participate in discourse, independent of the partner). As expected, such cooperation helps to maintain the egalitarian discourse patterns even if the agents’ sensitivity to competitive comparison is high and it also helps to maintain the collateral agents attached to the groups. This is seen as a higher abundance of patterns where in addition to strong dyads also single links to collateral agents are maintained. Also the tendency for isolation is reduced. Somewhat unexpectedly it turned out that agents’ increased tolerance to diversity, a kind of homophily, affects the pattern formation in very similar way as the increased cooperation. On closer examination, however, this similarity is reasonable since both mechanisms increase the tendency to reciprocate the ties between the agents, although in a different manner.
In regard to modelling and simulations of group processes in discourse pattern formation the model introduced here is most closely related to model describing formation of appreciation patterns on basis of competitive comparisons (Koponen & Nousiainen 2016), designed to follow the social learning theory (Bandura 1997, Bandura 2006). The major extension of the present model in comparison to model introduced before (Koponen & Nousiainen 2016) is inclusion of cooperation, which leads to richer pattern formation than competitive comparisons alone. The model discussed in this study shares similarities also with models of competition and cooperation (Caram et al. 2010, 2015; Lipowski et al. 2014), elite and egalitarian group formation (Deffuant et al. 2013), and status construction in groups (Grow et al. 2015). Some previous agent-based models for cooperative and competitive small groups have modelled the effect of status comparisons as direct comparisons of the statuses of individual agents (Caram et al. 2010, 2015). Also, in these cases, agents of similar statuses form sub-groups or cliques. These models, like ours, also include the notion that such a status is often bounded and cannot increase or decrease without limits, thus requiring the introduction of logistic growth type terms in update rules. This restriction clearly has an effect on how the groups are formed (Caram et al. 2015). More refined agent-based models of sub-group formation in small groups take into account the fact that the dynamics and status comparisons depend not only on agents’ status but also on other agents’ beliefs or expectations about other agents’ statuses. This effect is taken into account in agent-based models for small groups in which agent-to-agent relations are reinforcing (Lipowski et al. 2014). Such models lead to the formation of different types of leadership patterns, and depending on the strength of the reinforcement, the leadership can be absolute, symmetric (all links of equal strength) or asymmetric (one link stronger than others). These patterns are very similar to the leadership patterns found in the present study. Some agent-based models of the formation of social ties take a further step by taking into account both the agents’ status and the reinforcement of agent-to-agent links so that the comparisons are between the agent’s status and the other agents’ expectations of that status. Comparison to models where the statuses of agents are compared directly or where only agent-to-agent connections are the basis of comparison, such models add an important sociological component: how an individual’s self-conception is affected by peer evaluations. Such factors are included in agent-based models of the formation of elite and egalitarian groups, within the so-called Leviathan model (designed to follow Thomas Hobbes's view and thus named Leviathan) of the role of vanity in human social and political life (Deffuant et al. 2013). The Leviathan model illuminates how self-appraisal and vanity, when very strong, leads to the formation and consolidation of elite groups, and simultaneously, to the isolation of those outside the elite. In all these cases, status, status expectations and their comparisons essentially affect the social structure of groups. This kind of structure generative dynamics is demonstrated by a recent agent-based model describing the formation of status hierarchies (Grow et al. 2015), based on the sociological model of the creation of status hierarchies (Skvoretz & Fararo 1996; Skvoretz et al. 1996). The agent-based model presented here is, in its spirit and aim, very closely related to the Leviathan model (Deffuant et al. 2013) and the status construction model (Grow et al. 2015) in that it also identifies the relevant micro-level mechanism of how individual relations are formed.
In regard to the empirical results, the model provides insight on formation of strong dyads and egalitarian triads in discourse groups (Barron 2003; Heo et al. 2010; Hogan et al. 1999; Tschan 2002) and to the phenomenon of isolation (Bonito 2000, 2002). Empirical research has recognised the strong dyads and egalitarian triads as common discourse patterns emerging and stabilising in real discourse situations. However, research has lacked means to address the underlying social or psychological mechanism behind pattern formation dynamics. This is due to fact that empirical access to learners’ internal mental or psychological states and how they perceive their social status is far from straightforward and usually not accessible at all. The present model suggests that strong competitive comparison is a behaviorally plausible factor behind the formation of dyads, while cooperation facilitates the formation of egalitarian triads. The isolation effect, known also from several empirical studies of discourse, emerges already in groups of four, although not significantly, and increases with increasing group size. In groups of seven the isolation is quite pronounced when competitive comparisons dominate the group dynamics. The isolation effect that increases with group size is also known from empirical studies and it is known that it can be moderated or suppressed only with special arrangements (Bonito 2000, 2002). The model results presented here suggest that one possibility to moderate the formation of strong dyads and isolation is by forcing collateral triadic interaction (T model) instead of dyadic interaction (D). In practice, this means that in exchanges of opinions or in each query-response events a collateral partner is included, i.e. directing attention also to the collateral partners.
The similarity of simulation results to empirical findings suggests that empirical research of small group cooperation, learning and performance, should pay close attention to the individuals’ expectations of their own and their peers’ competencies and performances, and how these expectation are mediated through engagement with the task. In addition, information is needed of how sensitive the individuals are to the outcomes of these comparisons. In broad terms, these notions are in line with how the affect theory of social exchange (ATSE) and the expectation state structuralism model (ESSM) conceptualise the social interaction in task engaged groups. This agreement suggests that ATSE and ESSM could be promising candidates to model and understand dis-course dynamics and participation, and could possibly shed light on open problems in analysis of participation in small groups (Bonito 2000, 2002; Janssen et al. 2007; Stahl et al. 2014).
The main purpose of the model is to help in identifying factors that might affect the participation and to understand better what kinds of factors affect the isolation and drop-out. The agent-based model proposed here serves as a tool for conceptualisation and reasoning about how individuals’ psychological factors (sensitivity to comparisons, competitivity and cooperativity, etc.) may affect the formation of discourse and participation patterns. The model parameters are partly related to factors that are intrinsic, and partly to factors that can be manipulated. The competitivity and cooperativity are supposedly largely related to individual psychological factors and formation of ties on that basis, but they can be nevertheless enhanced or moderated by the external conditions and instructional strategies that regulate group dynamics. The collaterality and the diversity, however, depend more on the practical arrangements and can be altered according to how the group work is organised. In addition, the group size is of much importance. For example, the specific nature of groups of four members should be recognised. All these factors may be essential in determining how the discourse and dialogue are shaped and what kinds of interaction patterns emerge.
Appendix: ODD+D Documentation of the Program
The documentation follows the ODD+D template provided in Müller et al. (2013).
Overview
Purpose
What is the purpose of the study? The purpose of model is to describe formation of discourse patterns in small-groups. The model is designed to describe patterns of discourse or dialogue when a group is engaged in direct verbal exchanges in discourse.
For whom is the model designed? The model is designed for researchers interested in small group research and dynamics, discourse in small groups, group collaboration and effects of competition and cooperation within a group.
Entities, state variables and scales
What kinds of entities are in the model? The model’s entities are agents that represent individuals in a group engaged in discourse or dialogue.
By what attributes (i.e. state variables and parameters) are these entities characterised? Agents are characterised by their activity, how they intrinsic potential to participate in discourse and discursivity, how the engage in (externalised) interaction of discourse, through query-response acts. The state variables characterising an agent are its activity and discursivity. The parameters regulating how an agent is influenced by other agents are: 1) the agent’s sensitivity to comparisons; 2) affinity to cooperation and 3) tolerance to diversity in discursivities.
What are the exogenous factors/drivers of the model? The exogenous factor is the interaction event of agents. This may be an event involving only two agents (dyadic model D), an event involving three agents (triadic model T).
If applicable, how is space included in the model? Space is not included.
What are the temporal and spatial resolutions and extents of the model? The temporal resolution is deter-mined by the number of steps of the total sequence of interactions. This is varied from 1000 up to 4000.
Process overview and scheduling
What entity does what, and in what order? When an interaction event takes place, all entities (agents): 1) compare their activity and discursivity to their peers’ activity and discursivity (agents are aware of their peers’ states), 2) update their activity and discursivity. All updates are done simultaneously. The pseudocode of pro-cess and scheduling is as follows:
#INITIALISATIONS
MODEL PARAMETERS
competitivity
cooperativity
diversity
AGENTS
N_agents are created.
For each agent, values of activity kappa_ii and discursivity kappa_ij
towards other agents are created.
SIGMOIDAL PROBABILITY
Tabulate probability p_ij for difference/diversity
TABLES FOR PATTERN COUNTS
ntotmotif
#EXECUTION OF ITERATIONS
If number of iteration < maximum number iteration
[ Select randomly interacting agent i and j and collateral agent k
Obtain probability p_ij from tabulation that interaction produces change
in activity and discursivity
Calculate strength of change pi_o
Use roulette wheel method on basis of p_ij to decide if change in
activity and/or discursivity takes place. Total magnitude of
change depends on pi_o and alpha and differences in appreciations
Update activity: kappa_ii
Update discursivity: kappa_ij
Update collateral discursivity kappa_ik
Count number of 12 patterns on basis of discursivities
appreciations. Store counts on ntotmif.
]
Increase number of iterations by 1
#END OF PROGRAMDesign concepts
Theoretical and Empirical Background
Which general concepts, theories or hypotheses are underlying the model’s design at the system level or at the level(s) of the submodel(s)? The model is based on the notion of the importance of reciprocation of query-response sequences and how such reciprocation is self-enforcing.
On what assumptions is/are the agents’ decision model(s) based? Agents change their activity and discursivity as a consequence of pair-wise comparisons. Competitive comparisons affect both activities and discursivities and these changes take place through pair-wise comparisons. The comparisons are competitive in the sense that an agent, through comparison, seeks to increase its floor in discourse by using the information that is available to it of its peers’ activities and discursivities. Cooperation changes agent’s discursivities so that if both interacting agents have high activities the discursivities increase. In cooperation, agents with high activity benefit from interacting with other similar agents, thus mutually reinforcing each other. The changes in activities and discursivities due to competitive comparisons take place as follows:
- Change in the agent’s activity due to competition. If in the comparative interaction event agent finds that its activity is lower than its peer’s discursivity towards it, agent increases its activity because it competes for floor to discourse. If agent’s activity is higher than its peer’s discursivity, then agent decrease its activity because there is no need to compete.
- Change in the agent’s discursivity due to competition. First, the agent’s discursivity towards its peer increases/decreases if the agent finds that its peer’s discursivity towards it is higher/lower than its own activity. This is a similar competitive effect as in case of the agent’s change in activity. Second, agent’s discursivity is decreased if it is higher than its peer’s activity. This effect reduces the discourse activity towards agents that have low activity.
- Change in agent’s discursivity due to cooperation. This change is proportional to the geometric mean of the interacting agents’ activities. Agents’ activities, however, are not assumed to change directly through cooperation.
An agent’s sensitivity to competitive comparison is regulated by the parameter \(\alpha\), which is referred to as competitivity. An agent’s affinity to cooperation is regulated by the parameter \(\lambda\), which is referred to as cooperativity.
Why is/are certain decision model(s) chosen? The decision model is chosen based on the notion of the importance of reciprocation of discursive events in discourse and dialogue and reciprocation of acts in cooperation and collaboration, as recognised by the affect theory of exchange and in the social learning theory.
If the model/submodel is based on empirical data, where do the data come from? The decision model is not directly based on empirical data, yet it is indirectly based on empirical data in that it is supported by data regarding patterns of discourse and dialogue.
At which level of aggregation were the data available? At the level of small groups, from three to seven individuals.
Individual decision-making
What are the subjects and objects of the decision-making? On which level of aggregation is decision-making modelled? Decision-making is modelled on the level of single agents (single individuals). No collective effects are included.
What is the basic rationality behind agent decision-making in the model? Agents seek to increase their activity and discursivity in comparison to their peers. The decision-making is adaptive in the sense that the differences in activities and discursivities are of importance.
How do agents make their decisions? Decisions to change activities and discursivities are made on the basis of mutual comparisons.
Do the agents adapt their behaviour to changing endogenous and exogenous state variables? And if yes, how? Agents adapt only to changes in endogenous variables (activity and discursivity) through constant peer-to-peer-comparisons. The only exogenous variable is the event of interaction (a sort of time step).
Do social norms or cultural values play a role in the decision-making process? No cultural or social norms are included.
Do spatial aspects play a role in the decision process? No spatial aspects are included.
Do temporal aspects play a role in the decision process? No temporal aspects play a role in the decision process (expect for event frequency).
To which extent and how is uncertainty included in the agents’ decision rules? All decision rules include randomicity. All randomicity is distributed normally. The decision to interact follows a cumulative normal distribution, with standard deviation related to tolerance to diversity in discursivities.
Learning
Is individual learning included in the decision process? How do individuals change their decision rules over time as consequence of their experience? No learning is included. Decision rules remain the same over the course of simulations.
Is collective learning implemented in the model? No collective learning is included.
Individual sensing
What endogenous and exogenous state variables are individuals assumed to sense and consider in their decisions? Is the sensing process erroneous? An agent senses its peers’ discursivities towards it. The sensing is assumed to be exact.
What state variables of which other individuals can an individual perceive? Is the sensing process erroneous? Agents sense their own activity, their discursivity towards peers and their peers’ activity and discursivities. All sensing is assumed to be accurate.
What is the spatial scale of sensing? No spatial scale is included.
Are the mechanisms by which agents obtain information modelled explicitly, or are individuals simply assumed to know these variables? Agents are assumed to know the pertinent state variables. No specific modelling is included.
Are the costs for cognition and the costs for gathering information explicitly included in the model? No cost models are included.
Individual prediction
Which data do the agents use to predict future conditions? No future prediction is assumed. All interactions are based on a temporally local situation, defined through pertinent state variables.
What internal models are agents assumed to use to estimate future conditions or consequences of their decisions? No estimation of future conditions is included.
Might agents be erroneous in the prediction process, and how is it implemented? No future prediction is assumed.
Interaction
Are interactions among agents and entities assumed as direct or indirect? Interactions are direct in the pair-wise, dyadic model (D-model). Indirect interactions are included in the triadic model (T-model) in which agent acts towards a third, collateral agent.
On what do the interactions depend? The interactions are assigned at random. The probability to interact (to propagate an effect) in competition depends on how agent’s activity relates to its discursivity towards the peer with which it interacts. In cooperation decision to interact depends on difference in interacting agents’ discursivities. The exact probability depends on agent’s tolerance of diversity in discursivities, described by parameter \(\sigma\).
If the interactions involve communication, how are such communications represented? The interaction does require direct communication. Communications are query-response events.
If a coordination network exists, how does it affect the agent behaviour? Is the structure of the network imposed or emergent? The number of agents in a network is fixed (exogenous variable). The links between agents evolve dynamically and reach stabilised strengths as a consequence of dynamic evolution. The links provide the structure of discourse patterns. Thus, discourse patterns are emergent, based solely on model dynamics.
Collectives
Do the individuals form or belong to aggregations that affect and are affected by the individuals? Are these aggregations imposed by the modeller or do they emerge during the simulation? No collectives are formed, except emergent patterns. Patterns, however, do not affect the individuals.
How are collectives represented? No collectives are assumed.
Heterogeneity
Are the agents heterogeneous? If yes, which state variables and/or processes differ between the agents? Agents are not heterogeneous. All agents are described by the same parameters (competitivity \(\alpha\), cooperativity \(\lambda\) and diversity \(\sigma\)). However, the outcome of decisions depends on state variables (activity and discursivity) describing agents’ state.
Are the agents heterogeneous in their decision-making? If yes, which decision models or decision objects differ between the agents? No. All agents are similar in regard to decision rules.
Stochasticity
What processes (including initialisation) are modelled by assuming they are random or partly random? The agents that interact are assigned at random. Decisions to interact are assigned at random (following sigmoidal probability governed by diversity). The magnitude of strength is distributed normally around average strength.
Observation
What data are collected from the ABM for testing, understanding and analysing it, and how and when are they collected? Data is collected from an agents’ activities and discursivities. In analysis, discourse patterns are based on the discursivities. Exact counting of patterns is used.
What key results, outputs or characteristics of the model are emerging from the individuals? The key results of the model are dynamically stable patterns of mutual appreciation. These patterns are dynamically emergent.
Details
Implementation details
How has the model been implemented? The model is implemented as set of iterative (recursive) equations for activities and discursivities. The iterations are realised on regular intervals (event steps); however, whether or not any changes in activities and discursivities take place is decided stochastically. The selection of events is based on a roulette wheel (event-based) method. Implementation is realised as MATHEMATICA 10.4.
Is the model accessible, and if so where? The model is not accessible. However, interested parties may re-quest it from the authors.
Initialisation
What is the initial state of the model world? Agents’ initial states (state variables) are assigned at random from bounded uniform distribution.
Is the initialisation always the same, or is it allowed to vary among simulations? The initialisation varies. It is random within bounded uniform distribution. Only bounds of distribution remain the same.
Are the initial values chosen arbitrarily or based on data? Initial values correspond to an assumption of average (neutral) activities and discursivities.
Input data
Does the model use input from external sources such as data files or other models to represent processes that change over time? No.
Submodels
What, in detail, are the submodels that represent the processes listed in “Process overview and scheduling”? The submodels are as follows: Equations determining the updates, a logistic model of increments of activities and discursivities are assumed in order to limit them to the bounded region from 0 to 1. In probability to decide if change takes place, sigmoidal distribution is assumed. In deciding the magnitude of change, a normal distribution with fixed average and variance is assumed.
What are the model parameters, their dimensions and reference values? All values are dimensionless. The appreciations are limited to bounded region from 0 to 1. The competitivity \(\alpha\) and cooperativity \(\lambda\) are varied from 0 to 1, with steps 0.1. This corresponds full range of variation from no effect to maximal effect of comparison. The diversity \(\sigma\) is varied from 0.05 to 0.30. The values are selected so that no essential changes are observed for lower or higher values.
How were the submodels designed or chosen, and how were they parameterised and then tested? The submodel for deciding the probability of change is based on canonical distribution, most often used in similar applications. The model is tested separately to ensure correct cumulative distribution of probabilities. The submodel for selecting the magnitude of change is based on sampling the normal distribution. The model was tested separately to ensure correct density distribution results.
References
BANDURA, A. (1997). Self-efficacy: The Exercise of Control. New York, NY: Freeman.
BANDURA, A. (2006). Toward a psychology of human agency. Perspectives on Psychological Science, 1(2), 164–180.
BARRON, B. (2003). When smart groups fail. Journal of the Learning Sciences, 12(3), 307–359. [doi:10.1207/S15327809JLS1203_1 ]
BLOCK, P. (2015). Reciprocity, transitivity, and the mysterious three-cycle. Social Networks, 40, 163–173.
BONITO, J. A. (2000). The effect of contributing substantively on perceptions of participation. Small Group Research, 31(5), 528–553. [doi:10.1177/104649640003100502 ]
BONITO, J. A. (2002). The analysis of participation in small groups: Methodological and conceptual issues related to interdependence. Small Group Research, 33(4), 412–438.
CARAM, L. F., Caiafa, C. F., Ausloos, M. & Proto, A. N. (2015). Cooperative peer-to-peer multiagent-based systems. Physical Review E, 92(2), 022805. [doi:10.1103/PhysRevE.92.022805 ]
CARAM, L. F., Caiafa, C. F., Proto, A. N. & Ausloos, M. (2010). Dynamic peer-to-peer competition. Physica A, 389(13), 2628–2636.
DEFFUANT, G., Carletti, T. & Huet, S. (2013). The Leviathan model: Absolute dominance, generalised distrust, small worlds and other patterns emerging from combining vanity with opinion propagation. Journal of Artificial Societies and Social Simulation, 16(1), 5: https://www.jasss.org/16/1/5.html. [doi:10.18564/jasss.2070 ]
GROW, A., Flache, A. & Wittek, R. (2015). An agent-based model of status construction in task focused groups. Journal of Artificial Societies and Social Simulation, 18(2), 4: https://www.jasss.org/18/2/4.html. [doi:10.18564/jasss.2740 ]
HEO, H., Lim, K. Y. & Kim, Y. (2010). Exploratory study on the patterns of online interaction and knowledge co-construction in project-based learning. Computers & Education, 55(3), 1383–1392. [doi:10.1016/j.compedu.2010.06.012 ]
HOGAN, K., Nastasi, B. K. & Pressley, M. (1999). Discourse patterns and collaborative scientific reasoning in peer and teacher-guided discussions. Cognition and Instruction, 17(4), 379–432.
ITZKOVITZ, S., Milo, R., Kashtan, N., Ziv, G. & Alon, U. (2003). Subgraphs in random networks. Physical Review E, 68(2), 026127. [doi:10.1103/PhysRevE.68.026127 ]
JANSSEN, J., Erkens, G., Kanselaar, G. & Jaspers, J. (2007). Visualization of participation: Does it contribute to successful computer-supported collaborative learning? Computers & Education, 49(4), 1037–1065.
KOPONEN, I. T. & Nousiainen, M. (2016). Formation of reciprocal appreciation patterns in small groups: an agent-based model. Complex Adaptive Systems Modelling, 4(1), 1–19. [doi:10.1186/s40294-016-0035-6 ]
LACIANA, C. A. & Oteiza-Aguirre, N. (2014). An agent based multi-optional model for the diffusion of innovations. Physica A, 394, 254–265.
LAWLER, E. J. (2001). An affect theory of social exchange. American Journal of Sociology, 107(2), 321–352. [doi:10.1086/324071 ]
LAWLER, E. J., Thye, S. R. & Yoon, J. (2000). Emotion and group cohesion in productive exchange. American Journal of Sociology, 106(3), 611–657.
LAWLER, E. J., Thye, S. R. & Yoon, J. (2008). Social exchange and micro social order. American Sociological Review, 73(4), 519–542. [doi:10.1177/000312240807300401 ]
LIPOWSKI, A. & Lipowska, D. (2012). Roulette-wheel selection via stochastic acceptance. Physica A, 391(6), 2193–2196.
LIPOWSKI, A., Lipowska, D. & Ferreira, A. L. (2014). Emergence of social structures via preferential selection. Physical Review E, 90(3), 032817. [doi:10.1103/PhysRevE.90.032817 ]
LUSHER, D., Kremer, P. & Robins, G. (2014). Cooperative and competitive structures of trust relations in teams. Small Group Research, 45(1), 3–36.
MOODY, J. (1998). Matrix methods for calculating the triad census. Social Networks, 20(4), 291–299. [doi:10.1016/S0378-8733(98)00006-9 ]
MÜLLER, B, Bohn F., Dressler, G., Groeneveld, J.. Klassert, C., Martin, R., Schlüter, M., Schulze, J., Weise, H., & Schwarz, N,. (2013). Describing human decisions in agent-based models - ODD + D, an extension of the ODD protocol. Environmental Modelling & Software, 48, 37-48.
NOWAK, A., Rychwalska, A. & Borkowski, W. (2013). Why simulate? To develop a mental model. Journal of Artificial Societies and Social Simulation, 16 (3), 12: https://www.jasss.org/16/3/12.html. [doi:10.18564/jasss.2235 ]
SIMMEL, G. (1964). In: Wolff, K. H. W. (Ed.), The Sociology of Georg Simmel. Glencoe, IL: The Free Press.
SÎRBU, A., Loreto, V., Servedio, V. D. P. & Tria, F. (2013). Cohesion, consensus and extreme information in opinion dynamics. Advances in Complex Systems, 16, 1350035. [doi:10.1142/S0219525913500355 ]
SKVORETZ, J. & Fararo, T. J. (1996). Status and participation in task groups: A dynamic network model. American Journal of Sociology, 101(5), 1366–1414.
SKVORETZ, J., Faust, K. & Fararo, T. J. (1996). Social structure, networks, and e-state structuralism models. The Journal of Mathematical Sociology, 21(1-2), 57–76. [doi:10.1080/0022250X.1996.9990174 ]
STAHL, G., Law, N., Cress, U. & Ludvigsen, S. (2014). Analyzing roles of individuals in small-group collaboration processes. International Journal of Computer-Supported Collaborative Learning, 9(4), 365–370.
TSCHAN, F. (2002). Ideal cycles of communication (or cognitions) in triads, dyads, and individuals. Small Group Research, 33(6), 615–643. [doi:10.1177/1046496402238618 ]
VAN BOXTEL, C., van der Linden, J. & Kanselaar, G. (2000). Collaborative learning tasks and the elaboration of conceptual knowledge. Learning and Instruction, 10(4), 311–330.
YOON, J., Thye, S. R. & Lawler, E. J. (2013). Exchange and cohesion in dyads and triads: A test of Simmel’s hypothesis. Social Science Research, 42(6), 1457–1466. [doi:10.1016/j.ssresearch.2013.06.003 ]
ZAFEIRIS, A., Koman, Z., Mones, E. & Vicsek, T. (2017). Phenomenological theory of collective decision-making. Physica A, 479, 287–298.

