The beginning of the slaves’ revolt in morality occurs when ressentiment itself turns creative
and gives birth to values: the ressentiment of those beings who, denied the proper response of action,
compensate for it only with imaginary revenge.
- Nietzsche (2006 [1887], p. 20)
Introduction
Cooperation among genetically unrelated organisms is a puzzling phenomenon because an individual has to bear a cost to perform it while it provides a benefit in a short run that is smaller than selfishly exploiting others (Clutton-Brock 2009). It is rare among rational individuals, because even if cooperation that strives for a common goal is in everyone's interest, there is no guarantee that it will be achieved unless it is also in every individual's personal interest (Olson 1971).
In this study, we focus on the role of aggressive displays in the emergence of social cooperation. Previous research has shown that humans invest their own resources to harm other individuals without any conscious self-interested motive (Fehr & Gächter 2002). We are interested in the question how such sentiments evolved and whether they foster cooperative order.
While there is agreement on what are the proximate mechanisms controlling cooperation and punishment, their ultimate function remains debated (Alexander 1993; Burnham & Johnson 2005; Hagen & Hammerstein 2006; Krasnow & Delton 2016; Raihani & Bshary 2015; West, Griffin & Gardner 2007; West, El Mouden & Gardner 2011). In other words, while mechanistic explanations of (non-)cooperative decisions seem uncontroversial, the question why and how these mechanisms evolved remains unanswered. Agent-based models are well suited to contribute to such an investigation because they can illustrate how given strategies perform in different environments and what macro-level patterns emerge from local interactions (Bandini, Manzoni & Vizzari 2009).
In general, agent-based models allow rigorous specification of and direct control over agent-internal mechanisms hypothesized to cause a certain behavioral pattern. They also allow large-scale simulations (both in terms of population size and number of interactions) unfeasible in empirical experiments. They can model behavioral patterns emerging within a fixed population (e.g., Shoham & Tennenholtz 1997) or be combined with evolutionary replication dynamics to model multi-generational populations with combinations of genetic and cultural transmission (e.g., Gilbert et al. 2006). Last but not least, the models allow simulating interventions that would be unethical in real experiments.
The main purpose of our research is to explore adaptiveness of different aggression strategies and their impact on rate of cooperativeness in the population. We are also interested in whether effectively spread information about an aggressive reputation can lead to systems of mutual threats and dominance hierarchies that would keep the number of actual fights low. In the next section, we review some interesting findings from experimental studies on cooperation and punishment. We distinguish two types of aggressive behavior: (1) individual aggression among partners directly involved in cooperative interactions, and (2) moralized aggression performed by third parties observing interactions of others. We argue that the uses of these behaviors constitute manifestations of dominance-seeking behavior of increasing complexity, and we investigate emergent properties of societies built on them.
We then formalize verbal theories proposed to explain these findings into two evolutionary agent-based models with the goal of evaluating their feasibility. Both of them model social interactions based on the use of aggressive behavior:
- In the first model, we investigate the effectiveness of different strategies regulating whom agents attack upon encounter. Agents are paired and play the Prisoner’s Dilemma (PD) Game. Depending on their strategy, they can decide to fight against their partners afterwards. We introduce 4 types of agents: those who are never aggressive (pacifists), those who are willing to attack partners who defected against them (avengers), those who are willing to attack those who cooperated with them (bullies) and those who always want to aggress against their partner regardless of his decision (harassers). When agents are observed defeating their opponents, they gain a reputation for toughness which discourages others from attacking them in the future.
- The second model is an extension of the first one, where we investigate how patterns of interactions change when neutral observers become engaged in conflicts. Therein we introduce (morally sensitive) agents who care about the interactions of others and engage in fights after observing an interaction. We consider two additional strategies: agents who fight against defectors (rangers) and agents who fight against cooperators (thugs) also when they merely observe an interaction. That leads to group fighting and analogically to the first model, agents participating in the victorious group gain a reputation for being tough.
We then analyze emergent patterns of interaction within generations and also observe success of different strategies in the long evolutionary run. Based on obtained results, we argue that agents with aggressive and exploitative predispositions in their decision-making faculties can give rise to a system where violence is suppressed due to the existence of credible mutual threats. We conclude that the evolution of moral systems may in part be based on adaptations to secure agents’ own interests. The agent-based models were developed using the NetLogo software (version 5.2) and all data were analyzed using R software (version 3.2.2).
The Logic of Aggression
Individual aggression
The supposed evolutionary reason for the existence of mechanisms motivating aggressive behavior is the need for negotiating status and forcing desirable treatment from others – in a situation of conflict of interests individuals need to fight for their position and the feeling of anger is a proximate mechanism that motivates them to achieve that (Sell, Tooby & Cosmides 2009).
It was observed that such aggressive behaviors are commonly used by dominant individuals in order to enforce cooperation; this stabilizes social functioning through the system of threats (Clutton-Brock & Parker 1995). However, when analyzing patterns of aggression, it is crucial to emphasize that there are no a priori rules regarding who is an acceptable target of violence. Experimental results show an interesting variability in how humans choose targets of aggression. It has been shown that in the context of Public Goods Games, some people are willing to attack those who do not contribute to the common pool, whereas others are inclined to attack prosocial contributors (Herrmann, Thöni & Gächter 2008). While punitive attitudes are usually directed at violators of prosocial norms, it has also been observed that people spitefully attack others only in order to ensure their well-being is relatively worse (Abbink & Herrmann 2011; Abbink & Sadrieh 2009; Houser & Xiao 2010; Sheskin, Bloom, & Wynn 2014). The relative prevalence of these behaviors is supposed to be related to local competitiveness (Barker & Barclay 2016; Lahti & Weinstein 2005; Sylwester, Herrmann, & Bryson 2013; see also Charness, Masclet & Villeval 2013). Due to this variability, it has been argued that researchers need to investigate all possibilities of the direction in which aggression is inflicted (Dreber & Rand 2012).
A relatively common type of aggressive behavior is revenge, targeted at individuals believed to have caused some harm to the aggressor in the past. It seems to be the most hard-wired and inflexible mechanism in determining decisions to inflict harm on others, since it is automatic and can be carried out by an individual without any regard to other information (Carlsmith & Darley 2008; Carlsmith, Darley & Robinson 2002; Crockett, Özdemir & Fehr 2014).
Three main functions of revenge can be distinguished: (1) reducing the relative fitness advantage of the target, (2) changing the target’s expectations about the aggressor who signals his unwillingness to accept similar treatment in the future, (3) changing audience expectations about the aggressor’s status (Giardini & Conte 2015; Griskevicius et al. 2009; Kurzban & DeScioli 2013; McCullough, Kurzban & Tabak 2013; Nakao & Machery 2012; Price, Cosmides & Tooby 2002). Note that these functions do not have to be consciously realized – often the only pursued goal of an individual inflicting such a harm is to make the target suffer (Giardini, Andrighetto & Conte 2010; Andrighetto, Giardini & Conte 2013; Giardini & Conte 2015; see also Marlowe et al. 2011) without understanding of complex social interdependencies by avengers, their victims, and observers. All that matters is the showcase of aggressiveness through which agents prove their toughness.
In such a way, harming another individual serves a self-presentational function, that is, its purpose is to restore challenged self-esteem of the aggressor (Miller 2001). By achieving this, deterrence emerges as another function of such behavior (McCullough et al. 2013). Its adaptiveness depends on a correlation between inflicting harm and benefits received in subsequent encounters (Gardner & West 2004; Jensen 2010; Johnstone & Bshary 2004) and it will emerge only when deterrence is effective and if future interactions with the same agent are likely (Krasnow et al. 2012).
Because of these adaptations, willingness to harm others and fear of others being hostile is an important motivator of human action (Abbink & de Haan 2014; see also Schelling 1960). Aggression serves thereby a self-protective function – it has been shown that reputation for performing aggressive acts decreases the likelihood of being attacked by others in subsequent interactions (Benard 2013, 2015).
It seems that aggression is the default behavioral predisposition of humans that manifests itself in the absence of complex social organizations, as famously observed by Hobbes (1651/2011).
In Model 1, we investigate which of the aggression strategies becomes prevalent in the population and what social order emerges from interactions between aggressive agents who instigate fights after social exchanges they are involved in.
Moralized aggression
What is perplexing about the logic of human intervention is that people are willing to pay a cost to harm others in cases when they are not directly affected by the interaction; this is known as a third-party punishment (Fehr & Fischbacher 2004). People usually perform such behavior with a conviction that they uphold some moral norms. What benefit can humans get from becoming involved in conflicts of others?
Becoming involved in conflicts first and foremost provides an opportunity to signal a dominant social position by performing an aggressive act (Krasnow et al. 2016). It can also appear in case of helping one’s group member or ally, or in the reciprocity case when the third parties can expect a repayment of their investment in the future (Asao & Buss 2016; Marczyk 2015; Rabellino et al. 2016). Additional benefit can be reaped by increasing one’s own trustworthiness in the eyes of norm-followers. In line with this understanding, it was shown that engaging in third-party punishment increases the observer-rated likeability of an individual (Gordon, Madden & Lea 2014; Jordan et al. 2016; but see Przepiórka & Liebe 2016).
This type of aggression is closely related to moralization of actions – targets of aggression are those who are believed to break some social or moral norms. It is typically accompanied by an aggressive use of moral language (accusing, enforcing behavior by claiming one should do it) which emerges if using it is effective in manipulating others (Cronk 1994). In that perspective, moralization should be understood as a process of attributing objective moral properties to actions in order to manipulate others with implicit threats of aggression – if one is able to present some behavior not as serving a particular interest but as serving moral principles, then the manipulation is successful (Maze 1973). An individual benefits from this by engaging third-parties in fight for his case (Petersen 2013).
In conjunction with coalitional psychology, this mechanism paves the way for the emergence of large-scale moral systems by enabling humans to form and assess strength of alliances (Tooby & Cosmides 2010). In such a setting, there is a pressure for developing a common set of rules allowing for dynamic coordination among observers of conflicts (DeScioli & Kurzban 2009, 2013; DeScioli 2016).
Moving from a system based on individual conflicts to a system based on moralized actions evoking group conflicts requires the existence of agents that are more cognitively complex. While in the case of simple revenge it was sufficient to detect harm done to oneself and the agent who caused it, third-party punishment requires some understanding of social relations. Specifically, observers need to negotiate the status of an action – something that is absent in a world ruled by personal revenge only. This created an evolutionary pressure for developing common code and might have aided the evolution of language (Boyd & Matthew 2015).
The evolutionary emergence of such moral alliances is not well understood and has not been investigated in simulation work before. In order to fill this gap, in Model 2 we investigate third-party involvement in conflicts, which presents an attempt to formally examine circumstances under which these strategies can be adaptive and moral order can emerge in the community.
Model 1: Individual Aggression
Model description
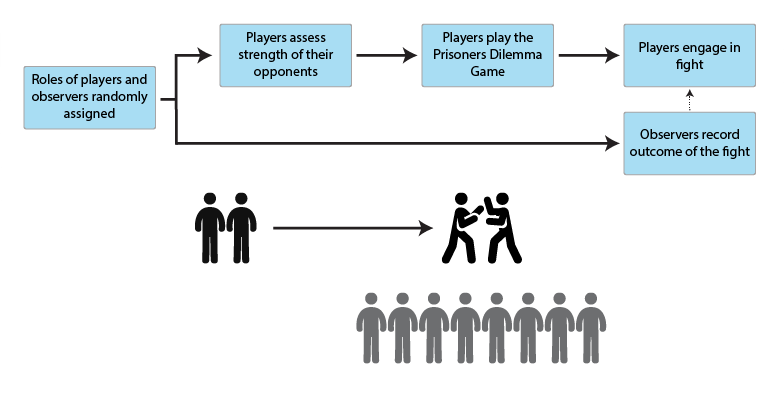
The first model (Figure 1) investigates the role of aggressive displays in enforcing cooperation in a multi-generation evolutionary setting. Agents in each generation engage in interactions, where they can lose or gain fitness. In each interaction round, one fifth of the agents are paired randomly for interaction, with the rest of the agents evenly distributed to be observers of the interactions (8 observers assigned for each interacting pair). The interacting agents first play the Prisoner’s Dilemma Game and afterwards they can decide to fight their opponent based on their fighting strategy (see below) and perceived relative strength. The fitness of the interacting agents is influenced by both the outcome of the game and a potential subsequent fight (see Appendix A for a detailed algorithm).
We are interested in the question of what fighting strategies are most adaptive from an evolutionary point of view. These are a hereditary trait of agents: (1) pacifists are agents who never fight after an interaction, (2) avengers fight against defectors, (3) bullies fight against cooperators, and (4) harassers fight against everyone. In the first generation, the population is composed of pacifists only. See Table 1 for comparison of agent strategies.
| Fight against | ||||
| Cooperators | Defectors | Observed cooperators | Observed defectors | |
| Pacifists | - | - | - | - |
| Avengers | - | + | - | - |
| Bullies | + | - | - | - |
| Harassers | + | + | - | - |
| Rangers | - | + | - | + |
| Thugs | + | - | + | - |
The result of a fight depends on relative strengths of the agents involved[1]. The existence of power asymmetry among agents is the crucial element of the model: stronger agents are more aggressive, decide to fight more frequently, and are more likely to win if a fight takes place.
A behavioral rule for decision whether to cooperate or defect in the PD game is also related to strength, but this time to perceived relative strength of one’s opponent: the agents cooperate when they feel weaker than their opponent and defect when they feel stronger. Thus, decisions to cooperate and decisions not to fight are closely connected in our model, as both of them are manifestations of weak sense of entitlement, a characteristic of people who are physically feeble (Sell et al. 2009; Sell, Eisner & Ribeaud 2016). This belief is established probabilistically according to strength differences among contestants – see Appendix A for details.
The choice of such a decision rule is deliberate since we want to exclude any other factors contributing to these decisions and focus on aggressive displays only. Each time an agent loses a fight against an opponent, the loser and all observers of this fight will add the winner to their fear_list – a privately maintained list of ‘tough’ agents[2]. When assessing the strength of an opponent, the fear_list biases perception, i.e. the opponents in the fear_list are perceived to be stronger than they are (again, for details see Appendix A). This assumption is motivated by the observation that the formation of animal dominance hierarchies depends on organisms observing each other what leads to development of expectations about their status and strength (Chase et al. 2002). In our model this emergent effect coming from observation and experience is conceptualized as deterrence – overestimation of strength of successful agents.
To investigate the influence of information spreading in the population besides the direct observers, the information from the fear_list is further passed on (gossiped) to other randomly chosen agents. After 200 interaction rounds, all the agents die and are replaced with a new generation according to the replicator equation (see Equation 2 in Appendix A), i.e. fighting strategies are spread proportionally to the fitness of their bearers in the previous generation.
The strength parameter that the agents possess can be thought of as the upper-body muscle mass, a feature argued to be the most important for estimating fighting ability (Sell, Hone & Pound 2012) and it is normally distributed within population. It has been shown that the fighting ability influences beliefs of individuals about their entitlements – stronger individuals are more likely to bargain for outcomes advantageous to them and have lower thresholds for aggression (Petersen et al. 2013; Sell et al. 2016).
Although strength is not the only feature determining the assessment of fighting ability (see e.g., Arnott & Elwood 2009; Pietraszewski & Shaw 2015), for the sake of simplicity we assume the agents make decisions based on this value only. We further assume that each agent knows accurately their own fighting ability (but see Fawcett & Johnstone 2010; Garcia et al. 2014) and can observe the fighting ability of others, although these observations are systematically biased, as already noted (Fawcett & Mowles 2013; Prenter, Elwood & Taylor 2006). We also assume that both contestants are equally motivated to compete for resources.
In this way, our model does not suffer from unrealistic assumptions found in previous models – that everybody is, in principle, able to punish everybody else[3]. In real life, it is not true, because individuals differ in their fighting ability. At the same time, the outcome of a fight is never certain (see Gordon et al. 2014). Agents make assessments that are probabilistic in their nature and mistakes are very common in real life (see Figures 10, 11 in the Appendix A). Perfectly rational and omniscient individuals always decide to fight when they are stronger and retreat from the conflict when they are weaker. In a population of all infallible individuals, fights would never occur. The fact they do occur suggests that individuals can make errors in their assessments, some of them resulting from adaptive biases (Johnson & Fowler 2011).
Our primary research question is which fighting strategies become dominant and which conditions promote cooperation in the PD game and reduce number of fights. We were especially interested in the impact of population size (we ran simulations for sizes equal to: 50, 100, or 500), the impact of deterrence effect strength (conceptualized as the number of standard deviations added to the opponent’s strength in case he was observed to have been aggressive in the past), the impact of differing cost of punishing, and the importance of gossiping (to how many agents information about conflict outcome is passed). The number of different agents one can remember (size limit on the fear_list) was equal to 50 and held constant across all simulations. The independent parameters are listed in Table 2 and used in the algorithm described in Appendix A. Particular values were chosen to sample from ranges that make sense relative to one other.[4]
| Parameter | Used values | Description |
| population | {50, 100, 500} | regulates the size of the population |
| punishment | 9 | regulates the magnitude of a punishment inflicted on the agent losing a fight |
| pun_cost | {3, 6, 9} | regulates the cost of inflicting punishment borne by the winner of a fight |
| submit_cost | 6 | regulates the cost of retreating from conflict by submitting to one's opponent |
| deterrence | {1, 3, 6} | regulates the magnitude of overestimation of the opponent's strength if he is known to be aggressive |
| sensitivity | 0.8 | regulates how sensitive the agents are to differences in strength |
| gossip | {5, 20} | regulates to how many individuals one can pass information about the outcome of the conflict |
| memory | 50 | regulates the number of other agents one can remember (stored in fear_list) |
The dependent variable was the rate of Cooperate-Cooperate (CC) outcomes. We put forward the following hypotheses:
- H1: Harassers will be an evolutionary stable strategy under all parameter combinations.
- H2: Cooperation rates will be higher in smaller groups than in bigger groups.
- H3: Cooperation rates will be higher under strong deterrence effect.
- H4: Cooperation rates will be higher when gossiping is more frequent.
- H5: Cooperation rates will be higher when the cost of punishment is low.
Results
The results of Model 1 clearly show that the most adaptive strategy across all various environmental conditions is to fight against everyone (harasser strategy, see Table B1 in Appendix B). This is the case because these agents establish a status of being tough most effectively due to a deterrence mechanism present in our model; this causes more of their opponents to cooperate with them. They have a particular advantage over avenger agents because they attack agents who cooperated with them, effectively showing their aggressiveness, since cooperators are mostly those who are weaker and are easy to damage (this relationship follows directly from the decision rule agents possess).
In our model it is the aggression inflicted upon weaker agents that drives the success of harasser agents – a very cost-effective strategy of increasing one’s own status in a group, as every bully understands. Avenger agents lose this opportunity and cannot establish their status. Thus, we find a support for H1. Nevertheless, an unexpected finding needs to be noted – when the group size is large (n = 500), evolution leads to coexistence of harasser and bully agents (see Figure 3). Bully agents perform well too since they also fight against cooperators after defecting them, but they forego opportunities to fight after Defect-Defect (DD) games. It seems that the extreme aggressiveness expressed by harasser agents pays off in small groups where valuable information about their toughness spreads effectively. In larger groups there exists a significant group of bully agents because harassers’ costly fighting after DD games where both contestants are of similar strength is not so strongly compensated by gaining a tough reputation as it is in smaller populations.
| Hypothesis | Result | Comment |
| H1: Harassers will be an evolutionary stable strategy under all parameter combinations. | Confirmed | The harasser strategy is most adaptive since these agents engage in fights most frequently and build the reputation for being tough |
| H2: Cooperation rates will be higher in smaller groups than in bigger groups. | Confirmed | Cooperation is stronger in smaller groups because agents observe each other fighting frequently what leads them to think others are tough; this is not the case in big groups with anonymous interactions |
| H3: Cooperation rates will be higher under strong deterrence effect. | Partially confirmed | Deterrence promotes cooperation in small groups where agents observe each other frequently; in large groups where repeated interactions are not likely its effect becomes negligible (see also Figure 4) |
| H4: Cooperation rates will be higher when gossiping is more frequent. | Not Confirmed | This parameter did not significantly affect results of our simulations |
| H5: Cooperation rates will be higher when the cost of punishment is low. | Not Confirmed | This parameter did not significantly affect results of our simulations |
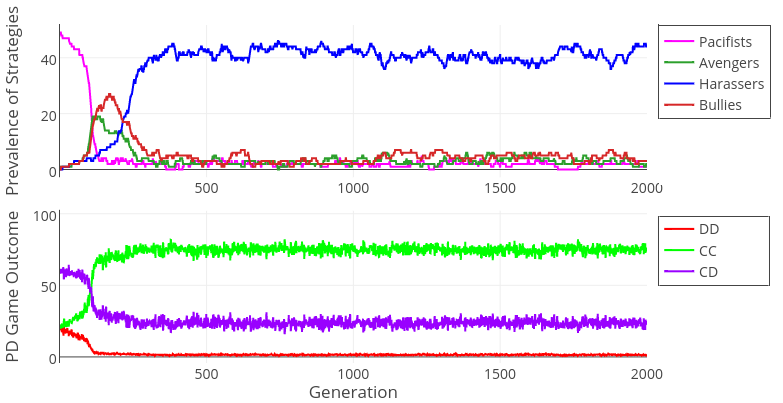

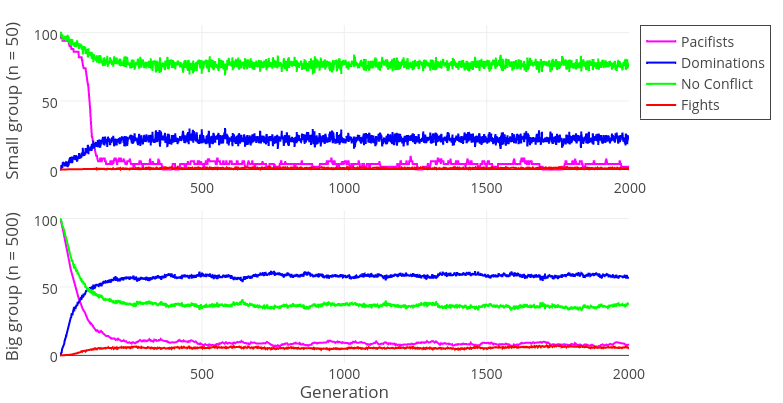
Figures 2 – 4 illustrate simulation dynamics in two different runs. As can be seen in Figure 2, in small groups the CC rate increases as the proportion of aggressive individuals increases. However, this is not the case for large groups (Figure 3). This difference is due to the availability of information about other agents in small, but not large, populations.
In large populations the lack of information about other agents’ past behavior in most encounters leads to a strict dominance hierarchy – most interactions are CD outcomes (Figure 3). This happens because agents assess each other relatively accurately and “correctly” play Defect (the stronger player) and Cooperate (the weaker player). Such interactions are often followed by the weaker agent submitting (Dominations, Figure 4). Interestingly, due to dominance hierarchies, the rate of post-game fights remain low.
In smaller populations agents have information about others’ past behavior in most cases and adjust their decisions accordingly. Because more of the assigned partners are remembered to be aggressive, agents overestimate their fighting ability and “incorrectly” play Cooperate. When both players fear their opponent, it leads to a CC outcome. This situation corresponds to the Hobbesian state of war in which agents live in a system of mutual threats. The rate of fighting is similarly low as in large populations, the rate of dominations is also lower (because agents fear each other, conflicts are instigated less frequently).
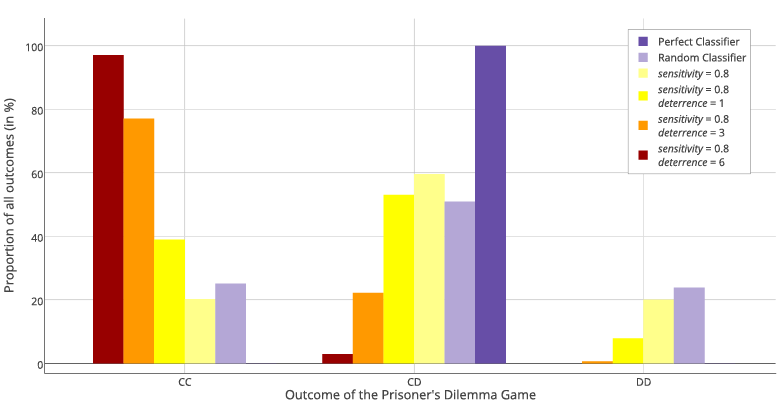
Figure 5 summarizes the rates of CC at the end of different simulations. A baseline to which these rates are compared is a situation when deterrence parameter is set to 0. In this case, agents do not develop reputation for being tough so the mechanism proposed by us is not at work. Under the assumption that agents can classify themselves as either weaker or stronger without making errors, this baseline would be equal to 0, as the only possible outcome would be CD. Because we made more realistic assumption about messy classifier (see Appendix A), random errors lead also to CC and DD outcomes. We verified this by running our model with deterrence parameter set to 0 and the average CC rate achieved was equal to 19.79%[5].
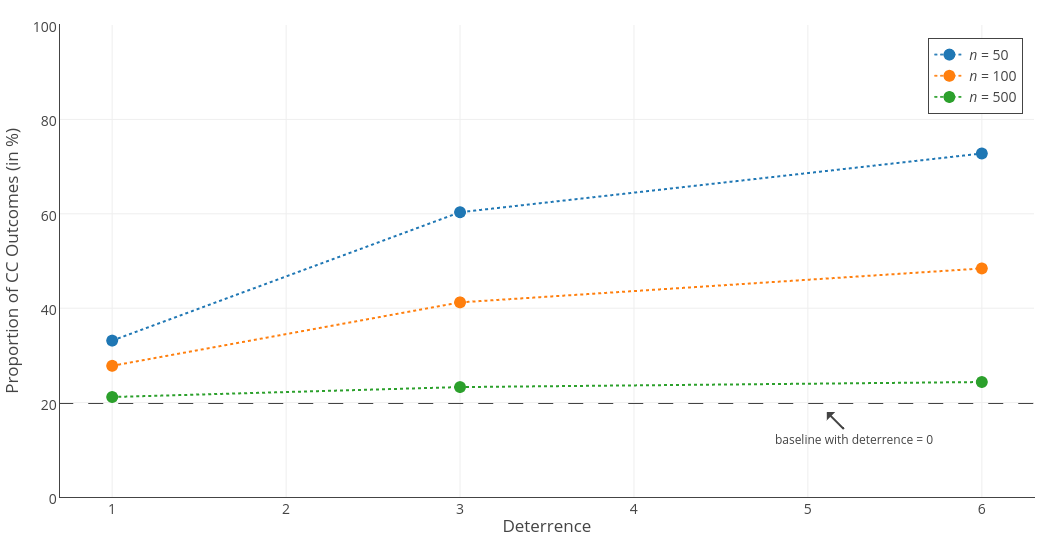
As can be seen in Figure 5, our results indicate an interaction between the group size and deterrence. Effective threats can deter defections and sustain a relatively high ratio of CC outcomes in a population when its size is small. We thus find support for H2 and a limited support for H3. When the population size is large, the deterrence effect becomes irrelevant, because most interactions will be anonymous. In that case the prevailing outcome of PD Game will be Cooperate-Defect (CD, see Figure 3). For the effectiveness of aggressive displays, it needs to be the case that the information is passed to other agents. The group size and the effectiveness of deterrence are contributing to the maintenance of social order. However, we do not find support for hypotheses H4 and H5, as the effects of gossiping and the cost of punishment parameters were negligible (see Appendix B).
Discussion
The results show that the existence of aggressive agents does not lead to a higher number of fights. This is the case because agents who have information about each other’s toughness develop dominance hierarchies that allow them to resolve conflicts without the need to fight. Such dominance hierarchies are frequently observed in various animal societies (Franz et al. 2015; Hsu, Earley & Wolf 2006) and our model illustrates their possible evolutionary emergence.
Our results are also consistent with findings showing that sociality promotes suppression of fights and that conflicts are resolved through submissive displays (Hick et al. 2014).
How is it possible that cooperation is promoted based on a decision rule that promotes defection against everyone who is thought to be weaker? The only way to achieve it is in a situation of mutual fear – when two agents meet each other and both of them think the opponent is stronger. This follows from the formula for estimating the opponent’s strength (see Appendix A). If the two agents have each other in their fear_lists, their perception of the other agent’s strength will be biased by the deterrence value, which causes the stronger agent to choose cooperation and decide not to fight because of its false belief. It follows then that the only way to enforce cooperation is to make oneself stronger in the eyes of others. We assume that it can be achieved through aggressive displays which deter future partners from defecting. Deterrence is conceptualized as a tendency to overestimate the strength of individuals that have been observed to be aggressive. We show that this effect is especially pronounced in small groups (see Figure 5).
In this model, we provide a novel way of conceptualizing deterrence in agent interactions. Previous approaches modeled deterrence in the context of the Public Goods Game by having agents develop a reputation for being a punisher, which in turn enforced contribution when agents observed these punishers in their groups (e.g., dos Santos & Wedekind 2015; Krasnow et al. 2015). In another related model, Nowak et al. (2016) investigated the adaptiveness of different strategies regulating behavior in response to being challenged to fight. A novel feature, missing in their approaches, is the linking of these predispositions to cooperative interactions which, in our model, also affect agents’ fitness. Through this linking, our model focuses on emergent mechanisms curbing agents’ exploitative and aggressive predispositions, which were assumed to be universal.
Model 2: Moralized Aggression
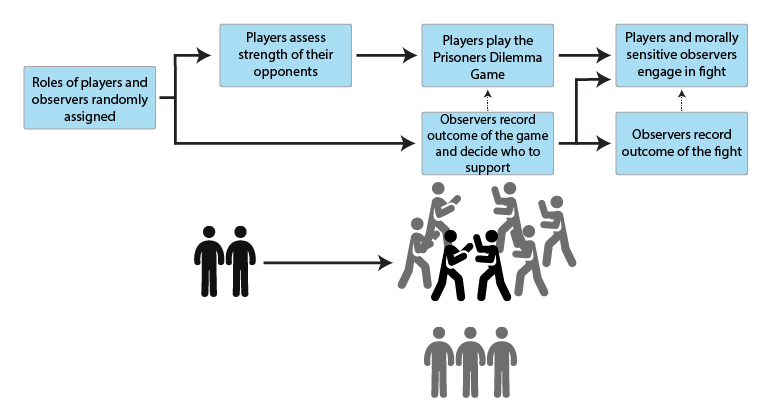
Model description
Model 2 (see Figure 6) is an extension of Model 1 in that some of the observers (so called morally sensitive) will not remain passive bystanders but will actively take sides and join the fight. The outcome of the fight is then determined by relative total strengths of the two fighting groups. The model investigates the adaptiveness of different strategies regulating side-taking rules in conflicts. We introduce two new types of (morally sensitive) agents: (1) Rangers who engage in fights as a third-party supporting cooperators, and (2) Thugs who support defectors.
The latter strategy can be understood as a mafia-like alliance in which antisocial individuals will join their forces to inflict harm and suffering even more effectively. These agents will also possess a different decision rule whether to cooperate or defect in the PD game: in order to defect, they need not be stronger themselves; it suffices if the number of antisocial fighters in the society is high enough to support them: another feature that, this time, a group of bullies perfectly understands[6].
The ranger strategy can be understood as a moral alliance, which demands moral integrity from its members. Thus, the decision rule for these agents is also different. We investigate three possibilities regarding how these agents can behave: (1) they cooperate with everyone (Always Cooperate); (2) they defect against the agents who have been observed defecting in the past (Defect Defectors[7]); (3) they defect against defectors and against the agents who remain neutral in conflicts (Defect Defectors and Neutrals), thereby creating an additional pressure against the agents who do not care about interactions they are not involved in. The algorithmic details of Model 2 are described in Appendix C (see also Table 4 for newly introduced parameters).
| Parameter | Used values | Description |
| coal_sensitivity[8] | 0.3 | regulates how sensitive the agents are to differences in the coalitional strength. Since the variance of strength differences is higher in case of fighting coalitions, this number was set to be smaller than sensitivity |
| Rule | {alwaysC, DefectD, DefectD&N} | regulates the decision rule for rangers: 1) Always Cooperate; 2) Defect against agents who have been observed defecting in the past; 3) Defect against agents who have been observed defecting in the past and against agents who have been observed remaining neutral at conflicts |
Our main research question for Model 2 is which conditions make an intervention performed by a morally sensitive third-party adaptive. To the best of our knowledge, there are no models that would explicitly investigate this effect[9].
The logic behind a potential success of the intervention strategies relies on several factors. The first is that group fighting can decrease the cost borne by the participating individuals (Jaffe & Zaballa 2010; Okada & Bingham 2008). The second factor is that these strategies allow establishment of toughness more easily, especially for weaker agents who can display aggressiveness in coalitions supporting them. Third, fighting coalitions can more easily eliminate lone agents – while this can have a destructive effect on the society, it can very often increase the relative fitness of attackers. Finally, the more individuals are involved in punishment, the stronger the deterrence effect appears to be, even if material losses are the same (Villatoro et al. 2014).
We put forward the following hypotheses:
- H6: Thug will be an evolutionary stable strategy under Always Cooperate decision rule, or when the population size is large.
- H7: Under Defect Defectors and Defect Defectors and Neutrals decision rules, Ranger will be an evolutionary stable strategy, but only when the population size is small (n = 50 and n = 100).
Results
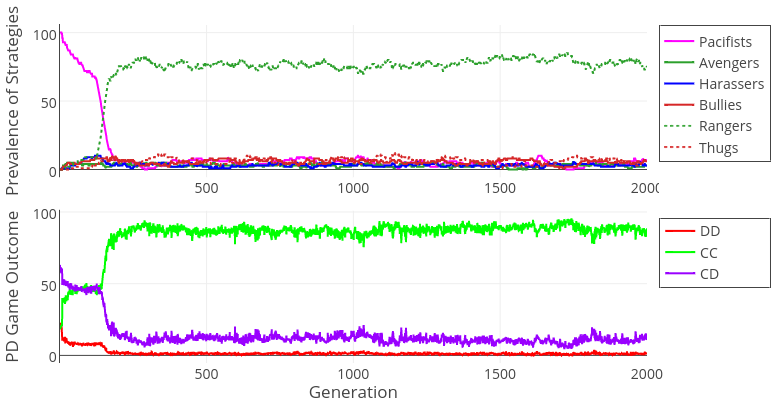
In accordance with hypothesis H6, results of Model 2 show that, under ranger decision rule Always Cooperate, the only possible outcome is that thugs invade the population and the rate of DD outcomes approaches 100%, leading to costly private fights among all members of the population (see Appendix D). Rangers maintain their integrity by having a cooperative reputation; they inflict punishment on defectors, but this is not enough to outweigh benefits acquired by the defectors.
| Hypothesis | Result | Comment |
| H6: Thug will be an evolutionary stable strategy under rangers’ Always Cooperate decision rule, or when the population size is large. | Confirmed | Unconditional cooperation makes agents an easy target of exploitation that leads to the success of thugs This happens both in the case of cooperating with everyone by default (Always Cooperate rule) and when interactions are anonymous (as in large groups) |
| H7: Under Defect Defectors and Defect Defectors and Neutrals decision rules, Ranger will be an evolutionary stable strategy, but only when the population size is small (n = 50 and n = 100). | Partially confirmed | This can happen, but success is not always guaranteed (see Figure 8 and Sections 4.11-4.14). Successful order maintenance happens due to the existence of a moral alliance between rangers |
In the case of the other two rangers’ decision rules, when the group size is large (n = 500), thug agents also invade the population regardless of the values of remaining parameters (see Figure 7). This happens because rangers are not able to keep all individuals in memory, and under these circumstances of anonymity they play Cooperate in cases when they should not, also leading to their demise. Thus, we find full support for H6.

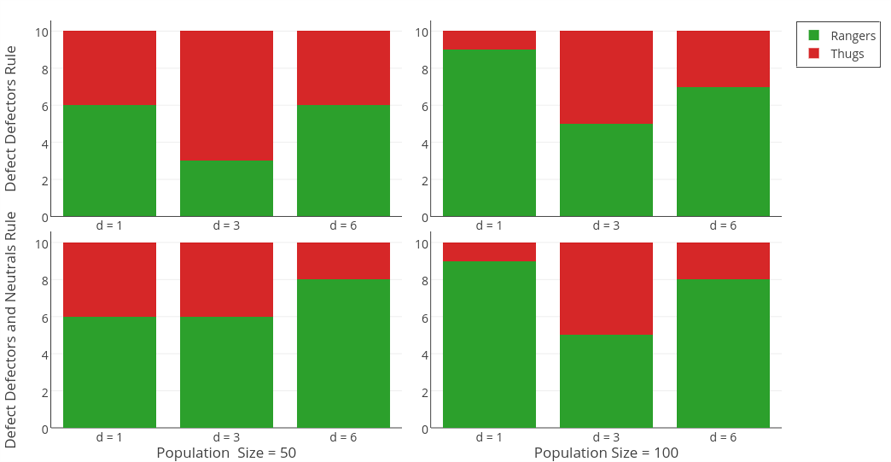
In the case of smaller group sizes, results are sensitive to random differences at the beginning of each simulation run. Figure 8 depicts a simulation run where ranger invaded a population promoting very high rate of CC outcomes. Such a result, however, was not obtained in all parameter combinations (see Table D1 in Appendix D). In order to verify this seemingly random pattern of results, we ran Model 2 again for small and moderate group sizes, as well as Defect Defectors and Defect Defectors and Neutrals decision rules and now each parameter combination was repeated 10 times (with different random generator seeds).
Figure 9 depicts the number of simulations in which these strategies were successful. There appears to be a threshold above which one of the coalitions gets strong enough to intimidate other players in all interactions and spreads very quickly. Once one of the strategies becomes prevailing, it is evolutionary stable. Thus, while it seems that a small group size and efficient information spread help rangers enforce cooperative order, we do not find full support for H7 – under favorable conditions, this strategy invades the population only 65 % of time. Further research needs to identify different factors contributing to the success of emerging coalitions.
Discussion
The results of our simulation suggest there are two factors necessary for the emergence of moral alliances: (1) small group size where agents are not anonymous, and (2) common rules allowing for justified defection (defecting those who have defected, see also Axelrod & Hamilton 1981). The maintenance of social order in runs where rangers prevailed suggests a possible mechanism in which threat of aggression serves a prosocial role. Still, even if these conditions hold, the success of prosocial moral strategies (rangers) is not guaranteed.
In this model, enforcement is based on the presence of individuals willing to fight for a given norm. The success of moral alliance composed of rangers shows the paradox inherent in the use of morality – that the weapon originally invented to fight against others by constraining their behavior turns against its inventors who need to constrain their own behavior as well. We believe that the decision rule possessed by those agents exemplifies the central mechanism of morality – they refrain from exploiting others not because they expect to be beaten (as did the agents present in Model 1), but because they act according to norms (e.g., defecting only against defectors). Adherence to this alliance enforces cooperation on other non-moral agents when they believe they are in a minority, what leads to even higher CC rates than those observed in Model 1.
In this model we formalized the verbal argument regarding the emergence of impartial morality put forward by DeScioli and Kurzban (2009, 2013; DeScioli 2016). We thus provide some support for their proposal by showing that agents committing themselves to a moral alliance and upholding norms agreed upon by them can perform well despite their refraining from exploitation of others. This happens because they effectively bring order into society and promote cooperation.
However, it is not clear what other factors contribute to the success of rangers as opposed to thugs. In our model the success of rangers is not guaranteed. It suggests that other factors such as social exclusion of non-cooperative individuals and forming closed communities with a limited number of partners might also be important in the emergence of cooperation (see e.g., Baumard, André & Sperber 2013; Helbing et al. 2010).
General Discussion
In the current study, we developed two agent-based models of social conflict, each leading to a system of social aggression with characteristic complexities. The models illustrate a way in which social order can be maintained among aggressive agents with minimal assumptions regarding their cognitive capacities.
In the first model, we assumed that agents seek dominance and use aggression in order to fight for resources. Their social life was limited to observing fights performed by others, which helped in making their own decisions regarding escalating conflicts. The results of this model showed that this system would lead to vengefulness and social exploitation of weaker agents by those who had power to do so. Despite such a grim world, we showed that the system of mutual threats established by everyone’s aggressiveness could constitute an effective deterrent discouraging the agents from seeking dominance violently. Interactions of such intimidated agents produced a relatively high level of cooperative outcomes.
We believe that such understanding of evolutionary roots of norm-related behavior sheds light on the existence of moral hypocrisy in social interactions (see Batson 2016). Rather than conceptualizing morality as a device for controlling one’s own behavior, we conceptualized it as a device for controlling others’ behavior. As we argued, this presents a more reasonable approach to the problem from the evolutionary perspective. We have shown that in a group of agents possessing primarily aggressive and other-directed morality, adherence to moral rules can nevertheless be promoted. Adherence happens not because agents intrinsically value adherence to moral rules, as there are no evolutionary reasons for such a sentiment to be adaptive. Instead, adherence happens because agents fear others who are willing to defend their (other-directed) moral rules.
Such a state makes moral hypocrisy an adaptive strategy (when unobserved, agents would try to break the rules themselves) and creates a pressure for the development of behavioral strategies that control one’s own behavior depending on whether others are observing the agent (see also Trivers 1971). We think that such framing illuminates the roots of defensive morality which is concerned with securing a cooperative reputation within a group (Alexander 1987). An emergent property of a system based on aggression is that in the presence of individuals willing to fight for a given norm it is adaptive to follow the norm, because it diminishes the probability of being attacked (or, to be more precise, it is adaptive to appear to be a norm follower in the eyes of others).
In the second model, we made an additional assumption regarding members of the society – we endowed agents with the ability to form alliances and wage group wars. We showed that such a system established a selection pressure for developing common rules for forming alliances and conflict resolution. Our results illustrate that in the absence of moral alliances, societies are invaded by antisocial groups (thugs), whose interactions lead to mutual defections and costly fights. They also show that under favorable circumstances, reliable coalitions can enforce cooperative outcomes. For this to happen, it is necessary for agents promoting moral order to allow for justified defections according to widely accepted norms.
In such a way, our study builds on the philosophical argument on the emergence of morality developed by Nietzsche (1887/2006). Cooperative behavior in the Prisoner’s Dilemma Game is usually thought to be a moral or socially desirable response, while decision to defect is thought to be a selfish or at least distrustful choice. However, on a more basic level, these decisions can be analyzed not on a cooperative versus non-cooperative continuum, but on an inferiority versus assertiveness continuum. It is primarily not a moral choice, but a choice between asserting one’s own superiority and aiming for higher payoffs (defecting) or relinquishing potential payoff to the partner (cooperating). Cooperative behavior in our first model was not chosen by agents who were the fittest, it was chosen by those who were weak and intimidated. Such a conceptualization sheds light on findings suggesting that strictness in moral judgments about one’s own transgressions is typical for individuals who have low power, as they do not feel entitled to fight for their interests (Lammers, Stapel & Galinsky 2010).
In Nietzsche’s terms, moral prescription to cooperate has its roots in the slave morality. It is not based on striving to be superior; it is based on being inferior. The evolutionary emergence of moralization (the slave’s revolt) happens at the moment when agents following cooperative strategies (rangers) form an alliance in which they enforce cooperative norms on others. This corresponds to the moment of transition from the system where cooperation was a necessary manifestation of inferiority when one feared his opponent (Model 1) to the system where, due to the newly-formed alliance, the concept of behavioral consistency enters the picture and rangers need to practice what they preach by following cooperative norm themselves (Model 2).
We would like to conclude our paper with emphasizing some important limitations of our results. While we found support for our hypotheses regarding evolutionary pressures created by modeled mechanism, in both models these failed to promote cooperative outcomes for larger populations. This suggests that there are likely also other mechanisms at play in promoting cooperative outcomes. Specifically, the reason why we obtained such results is that we assumed interactions in well-mixed populations, where each agent is equally likely to be paired with every other member of the group. Modeling variations on this grouping scheme was beyond scope of this study but it could be expected that taking into consideration local interactions within larger population would make information spread more efficient and promote more cooperative outcomes. These effects are not inconsistent with the framework outlined here and future work needs to focus on them in investigating the emergence of moral alliances.
Acknowledgements
We would like to thank the anonymous reviewers for their helpful comments. Figures 1 and 6 contain graphics designed by Freepik.Notes
- The strength of agents is distributed normally within the population (mean = 10, SD = 1).
- At the beginning of every generation this list is empty – agents only start to learn through their experience and observation.
- Bone et al. (2015) criticize previous models for exactly the same reason and explicitly introduce power asymmetries. Nevertheless, they still assume that weak players are able to punish strong ones, albeit inflicting smaller relative damage.
- For example, punishment is roughly the same as benefit from the defection, submit_cost is smaller, because this is the case of accepting defeat to avoid fighting, etc.
- Note that when deterrence parameter is set to 0, values of other parameters should become irrelevant – that was indeed the case – in these simulations, we did not observe any variability in CC rates across combinations of other parameters.
- In the first generation, thugs are born with a belief that they are in majority; this gives them a slight advantage as they defect in the first round. This is motivated by our assumption that they should feel entitled to exploit others by default – they will only stop doing so if they learn they are in minority. In all subsequent generations they are born with the average belief present in the previous generation (see Appendix C for details).
- This is a generalization of the Grim Trigger strategy (Friedman 1971) that is even more grim, since justified defections will follow after merely observing the other player playing defect.
- In case of group conflicts, sensitivity used in decision to fight (Equation 1, Appendix A) needs to be lower as strength differences taken as input increase (see Appendix C for explanation).
- Halevy and Halali (2015) investigate third-party interventions, but in their framework benefits are introduced directly to the payoff structure, which allows strategic rather than morally-motivated interventions.
Appendix
Appendix A: Description of Model 1
In this appendix, we provide an algorithmic description of the first model developed in the study.

| $$sigmoid = \frac{1}{1+\exp{(-diff\cdot sensitivity)}}$$ | (1) |
| $$Pr_{t+1}(i)=\frac{Pr_t(i)\cdot F_t(i)}{\sum_{j=1}^N \, Pr_t(j)\cdot F_t(j)}$$ | (2) |
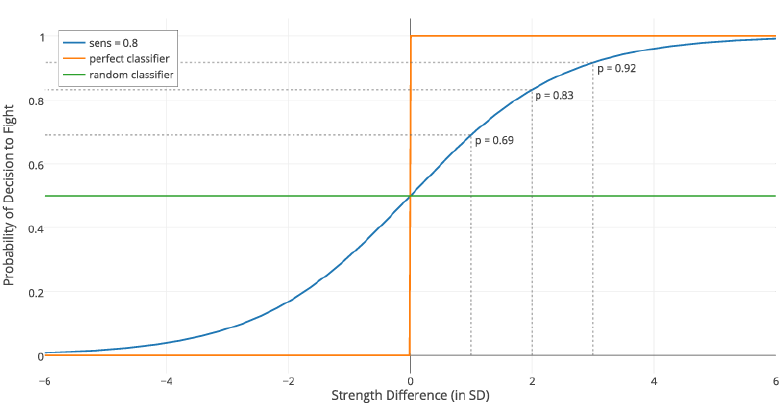
Equation 1 depicts the sigmoid function that returns the probability of feeling stronger. Equation 2 depicts the Replicator Dynamics used in the model. Prt(i) denotes the proportion and Ft(i) denotes the average fitness of agents following strategy i at time t.
Appendix B: Results of Model 1
Table 6 presents the full results of Model 1 runs:
| population | pun_cost | gossip | deterrence | pacifists | avengers | harassers | bullies | DDs | CDs | CCs |
| 50 | 3 | 5 | 1 | 10.00 | 8.00 | 74.00 | 8.00 | 10.200 | 57.770 | 32.030 |
| 50 | 3 | 5 | 3 | 2.00 | 4.00 | 88.00 | 6.00 | 2.950 | 38.490 | 58.560 |
| 50 | 3 | 5 | 6 | 4.20 | 2.00 | 84.20 | 9.60 | 1.830 | 26.790 | 71.380 |
| 50 | 3 | 20 | 1 | 10.00 | 12.60 | 64.60 | 12.80 | 9.850 | 55.460 | 34.690 |
| 50 | 3 | 20 | 3 | 4.40 | 6.00 | 76.00 | 13.60 | 2.560 | 34.810 | 62.630 |
| 50 | 3 | 20 | 6 | 5.60 | 7.00 | 77.80 | 9.60 | 1.560 | 24.030 | 74.410 |
| 50 | 6 | 5 | 1 | 6.00 | 3.40 | 73.00 | 17.60 | 9.360 | 56.860 | 33.780 |
| 50 | 6 | 5 | 3 | 4.00 | 12.60 | 67.40 | 16.00 | 3.110 | 38.580 | 58.310 |
| 50 | 6 | 5 | 6 | 4.60 | 5.40 | 78.00 | 12.00 | 1.950 | 28.000 | 70.050 |
| 50 | 6 | 20 | 1 | 9.20 | 14.60 | 63.00 | 13.20 | 9.630 | 56.640 | 33.730 |
| 50 | 6 | 20 | 3 | 3.00 | 7.00 | 72.80 | 17.20 | 2.330 | 35.850 | 61.820 |
| 50 | 6 | 20 | 6 | 2.00 | 2.80 | 89.20 | 6.00 | 1.280 | 23.660 | 75.060 |
| 50 | 9 | 5 | 1 | 16.00 | 8.80 | 51.20 | 24.00 | 10.440 | 57.960 | 31.600 |
| 50 | 9 | 5 | 3 | 5.80 | 4.00 | 74.60 | 15.60 | 3.360 | 38.420 | 58.220 |
| 50 | 9 | 5 | 6 | 3.80 | 4.00 | 84.20 | 8.00 | 2.120 | 27.150 | 70.730 |
| 50 | 9 | 20 | 1 | 11.80 | 14.00 | 18.00 | 56.20 | 9.900 | 57.130 | 32.970 |
| 50 | 9 | 20 | 3 | 3.80 | 7.20 | 77.60 | 11.40 | 2.450 | 35.100 | 62.450 |
| 50 | 9 | 20 | 6 | 0.00 | 6.00 | 87.40 | 6.60 | 1.360 | 23.600 | 75.040 |
| 100 | 3 | 5 | 1 | 7.90 | 9.00 | 54.70 | 28.40 | 13.710 | 58.335 | 27.955 |
| 100 | 3 | 5 | 3 | 5.20 | 6.30 | 75.90 | 12.60 | 7.435 | 51.465 | 41.100 |
| 100 | 3 | 5 | 6 | 5.60 | 5.20 | 81.90 | 7.30 | 5.955 | 45.800 | 48.245 |
| 100 | 3 | 20 | 1 | 9.00 | 7.90 | 65.50 | 17.60 | 13.520 | 58.495 | 27.985 |
| 100 | 3 | 20 | 3 | 3.90 | 5.30 | 84.20 | 6.60 | 7.455 | 51.325 | 41.220 |
| 100 | 3 | 20 | 6 | 2.00 | 3.00 | 90.30 | 4.70 | 5.685 | 45.855 | 48.460 |
| 100 | 6 | 5 | 1 | 10.00 | 8.40 | 49.20 | 32.40 | 13.590 | 58.180 | 28.230 |
| 100 | 6 | 5 | 3 | 8.10 | 4.70 | 76.00 | 11.20 | 7.405 | 51.815 | 40.780 |
| 100 | 6 | 5 | 6 | 4.70 | 4.20 | 77.50 | 13.60 | 6.055 | 45.970 | 47.975 |
| 100 | 6 | 20 | 1 | 10.10 | 6.80 | 65.50 | 17.60 | 13.135 | 59.495 | 27.370 |
| 100 | 6 | 20 | 3 | 4.80 | 5.10 | 79.80 | 10.30 | 7.415 | 50.865 | 41.720 |
| 100 | 6 | 20 | 6 | 3.60 | 4.60 | 82.70 | 9.10 | 5.775 | 45.280 | 48.945 |
| 100 | 9 | 5 | 1 | 9.50 | 11.20 | 42.70 | 36.60 | 13.470 | 58.955 | 27.575 |
| 100 | 9 | 5 | 3 | 2.30 | 4.20 | 80.90 | 12.60 | 7.530 | 51.715 | 40.755 |
| 100 | 9 | 5 | 6 | 3.00 | 3.50 | 84.70 | 8.80 | 5.895 | 45.155 | 48.950 |
| 100 | 9 | 20 | 1 | 4.70 | 9.20 | 46.00 | 40.10 | 13.235 | 59.115 | 27.650 |
| 100 | 9 | 20 | 3 | 3.40 | 6.20 | 73.60 | 16.80 | 7.235 | 50.945 | 41.820 |
| 100 | 9 | 20 | 6 | 3.50 | 4.70 | 79.70 | 12.10 | 6.080 | 45.970 | 47.950 |
| 500 | 3 | 5 | 1 | 13.50 | 17.54 | 47.42 | 21.54 | 18.368 | 60.754 | 20.878 |
| 500 | 3 | 5 | 3 | 8.24 | 10.40 | 63.56 | 17.80 | 16.704 | 60.263 | 23.033 |
| 500 | 3 | 5 | 6 | 6.60 | 7.02 | 70.00 | 16.38 | 16.634 | 58.965 | 24.401 |
| 500 | 3 | 20 | 1 | 12.76 | 16.96 | 45.04 | 25.24 | 18.506 | 60.219 | 21.275 |
| 500 | 3 | 20 | 3 | 8.04 | 8.58 | 60.34 | 23.04 | 17.065 | 59.551 | 23.384 |
| 500 | 3 | 20 | 6 | 9.80 | 8.36 | 67.72 | 14.12 | 16.450 | 59.134 | 24.416 |
| 500 | 6 | 5 | 1 | 17.38 | 11.78 | 30.16 | 40.68 | 18.366 | 60.251 | 21.383 |
| 500 | 6 | 5 | 3 | 11.12 | 7.44 | 38.66 | 42.78 | 17.034 | 59.735 | 23.231 |
| 500 | 6 | 5 | 6 | 7.40 | 8.00 | 52.90 | 31.70 | 16.316 | 59.205 | 24.479 |
| 500 | 6 | 20 | 1 | 17.72 | 10.46 | 27.46 | 44.36 | 18.304 | 60.512 | 21.184 |
| 500 | 6 | 20 | 3 | 12.04 | 8.46 | 42.12 | 37.38 | 16.971 | 59.448 | 23.581 |
| 500 | 6 | 20 | 6 | 7.68 | 9.34 | 50.22 | 32.76 | 16.720 | 58.872 | 24.408 |
| 500 | 9 | 5 | 1 | 21.42 | 13.18 | 20.94 | 44.46 | 18.411 | 60.330 | 21.259 |
| 500 | 9 | 5 | 3 | 9.38 | 9.88 | 30.38 | 50.36 | 17.098 | 59.740 | 23.162 |
| 500 | 9 | 5 | 6 | 8.28 | 7.20 | 38.42 | 46.10 | 16.081 | 59.770 | 24.149 |
| 500 | 9 | 20 | 1 | 19.36 | 9.76 | 24.24 | 46.64 | 18.271 | 60.617 | 21.112 |
| 500 | 9 | 20 | 3 | 12.46 | 9.28 | 30.90 | 47.36 | 17.086 | 59.573 | 23.341 |
| 500 | 9 | 20 | 6 | 9.82 | 6.86 | 35.02 | 48.30 | 16.736 | 58.975 | 24.289 |
Appendix C: Description of Model 2
In this appendix, we provide a detailed description of the second model developed in the study. The structure of interactions is related to those present in Model 1. Agents are assigned to roles of players and observers just like in Model 1. The difference is in the way types of agents introduced here make decisions regarding playing the PD Game, see lines 9-18 of the algorithm in the Appendix A.
Ranger agents maintain in memory decisions made by other players by updating defector_list and neutral_list (players following strategies present in model 1 who do not engage in group fights).
When rule parameter is set to alwaysC, rangers always cooperate with the partner.
When it is set to DefectD, rangers make the decision in a following way:

When it is set to DefectD&N, rangers make the decision in a following way:

Thug agents maintain an estimate of the frequency of their strategy relative to rangers (rangers / thugs). In the first generation, they are born with an estimate equal to 0.9, which is then subsequently updated as agents observe new contests. This value was chosen such that thugs receive a slight advantage at the beginning of simulation – they decide to defect in their first interactions and stop doing that only if they learn they are in minority (see below).
Within the generation, this estimate is updated in each interaction round 3.
| $$new\_ratio=(0.8\cdot old\_ratio)+(0.2\cdot\frac{ranger}{thug})$$ | (3) |
In subsequent generations, thug agents are born with the estimate equal to the average estimate present in the previous generation.
Thug agents make a decision how to play the PD Game, according to the following rule:

For the punishment stage of the game (lines 21-29 of the algorithm in Appendix A), there are two possibilities: either there are no morally sensitive agents among observers, in which case the conflict resolution will be based on a private fight just like in Model 1, or there are morally sensitive observers, and that will lead to a coalitional fight.
In the latter case, the procedure is the following:

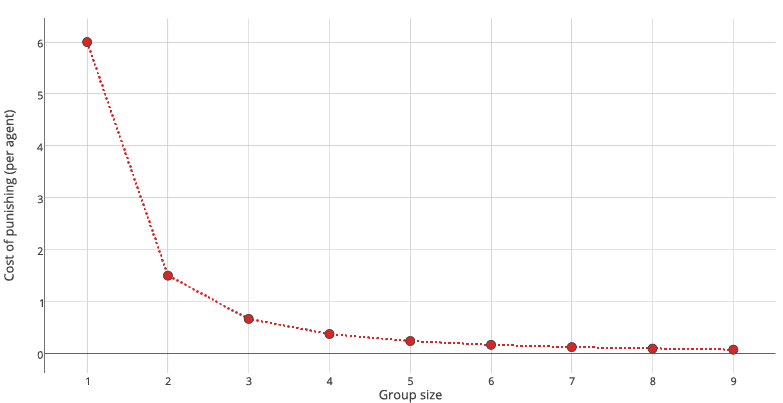
| $$cost = \cfrac{pun\_cost}{\#members^2} $$ | (4) |
Equation 4 shows how the cost borne by one group member is calculated. Agents replicate and mutate in the same way that in Model 1, see Appendix A, the algorithm lines 32-33.
Note that the equation determining decisions to fight (Equation 1, Appendix A) in case of group conflicts uses different sensitivity value than in the case of individual conflicts. This is because strength differences between groups of individuals can be higher than differences between single individuals – in other words, the range of inputs to the sigmoid function increases (see Figure 10). For that reason, in order to keep the baseline of random cooperation similar to the level found in individual contests (see Figure 5), we needed to change the value sensitivity parameter. Assigning higher value would very slightly decrease number of CC outcomes, but would not qualitatively change our results.
Appendix D: Results of Model 2
Table 7 presents the full results of Model 2 runs:
| rule | population | deterrence | pacifists | avengers | harassers | bullies | rangers | thugs | DDs | CDs | CCs |
| AC | 50 | 1 | 2.20 | 0.00 | 3.00 | 0.00 | 2.00 | 92.80 | 89.520 | 10.290 | 0.190 |
| DD | 50 | 1 | 7.00 | 2.00 | 3.60 | 6.60 | 74.80 | 6.00 | 1.360 | 14.990 | 83.650 |
| DD&N | 50 | 1 | 3.00 | 2.00 | 2.00 | 2.00 | 6.20 | 84.80 | 88.400 | 11.140 | 0.460 |
| AC | 50 | 3 | 2.40 | 0.00 | 2.60 | 0.40 | 2.00 | 92.60 | 88.140 | 11.650 | 0.210 |
| DD | 50 | 3 | 6.00 | 0.00 | 6.00 | 11.40 | 67.20 | 9.40 | 0.640 | 11.410 | 87.950 |
| DD&N | 50 | 3 | 2.20 | 2.00 | 3.00 | 4.00 | 82.40 | 6.40 | 2.180 | 21.800 | 76.020 |
| AC | 50 | 6 | 0.00 | 0.00 | 0.00 | 2.20 | 0.40 | 97.40 | 95.550 | 4.450 | 0.000 |
| DD | 50 | 6 | 1.20 | 1.80 | 1.40 | 2.00 | 2.80 | 90.80 | 87.330 | 12.240 | 0.430 |
| DD&N | 50 | 6 | 4.00 | 0.00 | 3.40 | 2.80 | 88.60 | 1.20 | 0.880 | 13.800 | 85.320 |
| AC | 100 | 1 | 1.10 | 1.00 | 1.30 | 0.00 | 1.00 | 95.60 | 93.925 | 6.045 | 0.030 |
| DD | 100 | 1 | 4.90 | 4.40 | 1.60 | 3.10 | 78.10 | 7.90 | 1.355 | 12.210 | 86.435 |
| DD&N | 100 | 1 | 1.80 | 1.50 | 1.00 | 1.00 | 92.20 | 2.50 | 2.595 | 7.460 | 89.945 |
| AC | 100 | 3 | 1.30 | 1.00 | 1.00 | 1.20 | 1.20 | 94.30 | 91.595 | 8.310 | 0.095 |
| DD | 100 | 3 | 7.00 | 3.00 | 3.20 | 6.00 | 74.10 | 6.70 | 1.410 | 12.345 | 86.245 |
| DD&N | 100 | 3 | 1.30 | 1.40 | 1.00 | 0.00 | 1.90 | 94.40 | 94.010 | 5.880 | 0.110 |
| AC | 100 | 6 | 1.50 | 0.50 | 1.00 | 1.20 | 0.90 | 94.90 | 92.160 | 7.775 | 0.065 |
| DD | 100 | 6 | 1.20 | 1.00 | 1.00 | 1.10 | 1.00 | 94.70 | 93.080 | 6.830 | 0.090 |
| DD&N | 100 | 6 | 1.20 | 2.70 | 2.50 | 2.30 | 87.10 | 4.20 | 2.745 | 14.060 | 83.195 |
| AC | 500 | 1 | 0.56 | 0.60 | 0.78 | 0.36 | 0.26 | 97.44 | 96.992 | 2.996 | 0.012 |
| DD | 500 | 1 | 0.40 | 0.60 | 0.54 | 0.74 | 0.24 | 97.48 | 97.137 | 2.844 | 0.019 |
| DD&N | 500 | 1 | 0.64 | 0.40 | 0.50 | 0.36 | 0.30 | 97.80 | 97.604 | 2.387 | 0.009 |
| AC | 500 | 3 | 0.58 | 0.50 | 0.28 | 0.40 | 0.34 | 97.90 | 97.578 | 2.407 | 0.015 |
| DD | 500 | 3 | 0.36 | 0.48 | 0.54 | 0.38 | 0.26 | 97.98 | 97.600 | 2.389 | 0.011 |
| DD&N | 500 | 3 | 0.52 | 0.84 | 0.36 | 0.34 | 0.30 | 97.64 | 97.349 | 2.629 | 0.022 |
| AC | 500 | 6 | 0.70 | 0.52 | 0.56 | 0.46 | 0.36 | 97.40 | 96.833 | 3.144 | 0.023 |
| DD | 500 | 6 | 0.56 | 0.54 | 0.48 | 0.56 | 0.28 | 97.58 | 97.459 | 2.520 | 0.021 |
| DD&N | 500 | 6 | 0.74 | 0.44 | 0.46 | 0.42 | 0.34 | 97.60 | 97.388 | 2.591 | 0.021 |
As can be seen in Table 6, when the population size was large (n = 500) and when the AlwaysCooperate rule was used, the only possible outcome was that thugs invaded the population. When the population size was smaller, the results appeared to be random, so we ran the simulation for the second time, varying the following parameters (Table 7):
| Parameter | Used values |
| population | {50, 100} |
| deterrence | {1, 3, 6} |
| rule | {DefectD, DefectD&N} |
We then counted the number of simulations for each combination of parameters invaded by ranger and thug agents. These results are presented in Table 8.
| Population | Deterrence | Rule | Rangers | Thugs |
| 50 | 1 | DD | 6 | 4 |
| 50 | 1 | DD&N | 6 | 4 |
| 50 | 3 | DD | 3 | 7 |
| 50 | 3 | DD&N | 6 | 4 |
| 50 | 6 | DD | 6 | 4 |
| 50 | 6 | DD&N | 8 | 2 |
| 100 | 1 | DD | 9 | 1 |
| 100 | 1 | DD&N | 9 | 1 |
| 100 | 3 | DD | 5 | 5 |
| 100 | 3 | DD&N | 5 | 5 |
| 100 | 6 | DD | 7 | 3 |
| 100 | 6 | DD&N | 8 | 2 |
We also decided to change the assumption that thugs are born with the estimate equal to 0.9 (see Appendix C) and observe if giving them even more advantage at the beginning will lead to more invasions. We ran our simulation once again varying the parameters as indicated in Table 7, but this time setting initial estimate of thugs to 0.1. It turned out that this does not significantly affect results and leads to similar pattern as depicted in Table 8 (63.33% invaded by rangers if initial estimate set to 0.1 vs. 65% with initial estimate set to 0.9).
References
ABBINK, K., & de Haan, T. (2014). Trust on the brink of Armageddon: The first-strike game. European Economic Review, 67, 190-196. [doi:10.1016/j.euroecorev.2014.01.009]
ABBINK, K., & Herrmann, B. (2011). The moral costs of nastiness. Economic Inquiry, 49(2), 631-633. [doi:10.1111/j.1465-7295.2010.00309.x]
ABBINK, K., & Sadrieh, A. (2009). The pleasure of being nasty. Economics Letters, 105(3), 306-308. [doi:10.1016/j.econlet.2009.08.024]
ALEXANDER, R. D. (1987). The biology of moral systems. Hawthorne, NY: Aldine de Gruyter.
ALEXANDER, R. D. (1993). Biological Considerations in the Analysis of Morality. In M. H. Nitecki & D. V. Nitecki (Eds.), Evolutionary Ethics (pp. 163-196). Albany, NY: State University of New York Press.
ANDRIGHETTO, G., Giardini, F., & Conte, R. (2013). An evolutionary account of reactions to a wrong. In M. Knauff, M. Pauen, N. Sebanz, & I. Wachsmuth (Eds.), Proceedings of the 35th Annual Conference of the Cognitive Science Society (pp. 1756–1761). Austin, TX: Cognitive Science Society.
ARNOTT, G., & Elwood, R. W. (2009). Assessment of fighting ability in animal contests. Animal Behaviour, 77(5), 991-1004. [doi:10.1016/j.anbehav.2009.02.010]
ASAO, K., & Buss, D. M. (2016). The Tripartite Theory of Machiavellian Morality: Judgment, Influence, and Conscience as Distinct Moral Adaptations. In T. K. Shackelford & R. D. Hansen (Eds.), The Evolution of Morality (pp. 3-25). Cham, Switzerland: Springer International Publishing. [doi:10.1007/978-3-319-19671-8_1]
AXELROD, R., & Hamilton, W. D. (1981). The evolution of cooperation. Science, 211(4489), 1390-1396. [doi:10.1126/science.7466396]
BANDINI, S., Manzoni, S., & Vizzari, G. (2009). Agent based modeling and simulation: An informatics perspective. Journal of Artificial Societies and Social Simulation, 12(4), 4. https://www.jasss.org/12/4/4.html [doi:10.1007/978-0-387-30440-3_12]
BARKER, J. L., & Barclay, P. (2016). Local competition increases people's willingness to harm others. Evolution and Human Behavior, 37(4), 315-322. [doi:10.1016/j.evolhumbehav.2016.02.001]
BATSON, C. D. (2016). What's Wrong with Morality? A Social-Psychological Perspective. New York, NY: Oxford University Press.
BAUMARD, N., André, J.B., & Sperber, D. (2013). A mutualistic theory of morality: The evolution of fairness by partner choice, Behavioral and Brain Sciences, 36(1), 59-78. [doi:10.1017/S0140525X11002202]
BENARD, S. (2013). Reputation systems, aggression, and deterrence in social interaction. Social Science Research, 42(1), 230-245. [doi:10.1016/j.ssresearch.2012.09.004]
BENARD, S. (2015). The value of vengefulness: Reputational incentives for initiating versus reciprocating aggression. Rationality and Society, 27(2), 129-160. [doi:10.1177/1043463115576135]
BONE, J. E., Wallace, B., Bshary, R., & Raihani, N. J. (2015). The effect of power asymmetries on cooperation and punishment in a prisoner’s dilemma game. PloS one, 10(1), e0117183. [doi:10.1371/journal.pone.0117183]
BOYD, R., & Mathew, S. (2015). Third-party monitoring and sanctions aid the evolution of language. Evolution and Human Behavior, 36(6), 475-479. [doi:10.1016/j.evolhumbehav.2015.06.002]
BURNHAM, T. C., & Johnson, D. D. (2005). The biological and evolutionary logic of human cooperation. Analyse & Kritik, 27(2), 113-135. [doi:10.1515/auk-2005-0107]
CARLSMITH, K. M., & Darley, J. M. (2008). Psychological aspects of retributive justice. Advances in experimental social psychology, 40, 193-236. [doi:10.1016/S0065-2601(07)00004-4]
CARLSMITH, K. M., Darley, J. M., & Robinson, P. H. (2002). Why do we punish?: Deterrence and just deserts as motives for punishment. Journal of personality and social psychology, 83(2), 284-299. [doi:10.1037/0022-3514.83.2.284]
CHARNESS, G., Masclet, D., & Villeval, M. C. (2013). The dark side of competition for status. Management Science, 60(1), 38-55. [doi:10.1287/mnsc.2013.1747]
CHASE, I. D., Tovey, C., Spangler-Martin, D., & Manfredonia, M. (2002). Individual differences versus social dynamics in the formation of animal dominance hierarchies. Proceedings of the National Academy of Sciences, 99(8), 5744-5749. [doi:10.1073/pnas.082104199]
CLUTTON-BROCK, T. (2009). Cooperation between non-kin in animal societies. Nature, 462(7269), 51-57. [doi:10.1038/nature08366]
CLUTTON-BROCK, T. H., & Parker, G. A. (1995). Punishment in animal societies. Nature, 373(6511), 209-216. [doi:10.1038/373209a0]
CROCKETT, M. J., Özdemir, Y., & Fehr, E. (2014). The value of vengeance and the demand for deterrence. Journal of Experimental Psychology: General, 143(6), 2279-2286. [doi:10.1037/xge0000018]
CRONK, L. (1994). Evolutionary theories of morality and the manipulative use of signals. Zygon, 29(1), 81-101. [doi:10.1111/j.1467-9744.1994.tb00651.x]
DESCIOLI, P. (2016). The side-taking hypothesis for moral judgment. Current Opinion in Psychology, 7, 23-27. [doi:10.1016/j.copsyc.2015.07.002]
DESCIOLI, P., & Kurzban, R. (2009). Mysteries of morality. Cognition, 112(2), 281-299. [doi:10.1016/j.cognition.2009.05.008]
DESCIOLI, P., & Kurzban, R. (2013). A solution to the mysteries of morality. Psychological Bulletin, 139(2), 477-496. [doi:10.1037/a0029065]
DOS SANTOS, M., & Wedekind, C. (2015). Reputation based on punishment rather than generosity allows for evolution of cooperation in sizable groups. Evolution and Human Behavior, 36(1), 59-64. [doi:10.1016/j.evolhumbehav.2014.09.001]
DREBER, A., & Rand, D. G. (2012). Retaliation and antisocial punishment are overlooked in many theoretical models as well as behavioral experiments. Behavioral and brain sciences, 35(01), 24. [doi:10.1017/S0140525X11001221]
FAWCETT, T. W., & Johnstone, R. A. (2010). Learning your own strength: winner and loser effects should change with age and experience. Proceedings of the Royal Society of London B: Biological Sciences, 277(1686). [doi:10.1098/rspb.2009.2088]
FAWCETT, T. W., & Mowles, S. L. (2013). Assessments of fighting ability need not be cognitively complex. Animal Behaviour, 86(5), e1-e7. [doi:10.1016/j.anbehav.2013.05.033]
FEHR, E., & Fischbacher, U. (2004). Third-party punishment and social norms. Evolution and human behavior, 25(2), 63-87. [doi:10.1016/S1090-5138(04)00005-4]
FEHR, E., & Gächter, S. (2002). Altruistic punishment in humans. Nature, 415(6868), 137-140. [doi:10.1038/415137a]
FRANZ, M., McLean, E., Tung, J., Altmann, J., & Alberts, S. C. (2015). Self-organizing dominance hierarchies in a wild primate population. Proceedings of the Royal Society of London B: Biological Sciences, 282(1814). [doi:10.1098/rspb.2015.1512]
FRIEDMAN, J. W. (1971). A non-cooperative equilibrium for supergames. The Review of Economic Studies, 38(1), 1-12. [doi:10.2307/2296617]
GARCIA, M. J., Murphree, J., Wilson, J., & Earley, R. L. (2014). Mechanisms of decision making during contests in green anole lizards: prior experience and assessment. Animal Behaviour, 92, 45-54. [doi:10.1016/j.anbehav.2014.03.027]
GARDNER, A., & West, S. A. (2004). Cooperation and punishment, especially in humans. The American Naturalist, 164(6), 753-764./p> [doi:10.1086/425623]
GIARDINI, F., Andrighetto, G., & Conte, R. (2010). A cognitive model of punishment. In S. Ohlsson & R. Catrambone (Eds.), Proceedings of the 32nd Annual Conference of the Cognitive Science Society (pp. 1282-1288). Austin, TX: Cognitive Science Society.
GIARDINI, F., & Conte, R. (2015). Revenge and Conflict: Social and Cognitive Aspects. In F. D'Errico, I. Poggi, A. Vinciarelli, & L. Vincze (Eds.). Conflict and Multimodal Communication: Social Research and Machine Intelligence (pp. 71-89). Cham: Springer International Publishing. [doi:10.1007/978-3-319-14081-0_4]
GILBERT, N., Besten, M. den, Bontovics, A., Craenen, B. G. W., Divina, F., Eiben, A. E., Griffioen, R., Hévízi, G., Lörincz, A., Paechter, B., Schuster, S., Schut, M. C., Tzolov, C., Vogt, P., & Yang, L. (2006). Emerging Artificial Societies Through Learning. Journal of Artificial Societies and Social Simulation, 9 (2), 9. https://www.jasss.org/9/2/9.html
GORDON, D. S., Madden, J. R., & Lea, S. E. (2014). Both loved and feared: Third party punishers are viewed as formidable and likeable, but these reputational benefits may only be open to dominant individuals. PLoS ONE 9(10), e110045. [doi:10.1371/journal.pone.0110045]
GRISKEVICIUS, V., Tybur, J. M., Gangestad, S. W., Perea, E. F., Shapiro, J. R., & Kenrick, D. T. (2009). Aggress to impress: Hostility as an evolved context-dependent strategy. Journal of Personality and Social Psychology, 96(5), 980-994. [doi:10.1037/a0013907]
HAGEN, E. H., & Hammerstein, P. (2006). Game theory and human evolution: A critique of some recent interpretations of experimental games. Theoretical Population Biology, 69(3), 339-348. [doi:10.1016/j.tpb.2005.09.005]
HALEVY, N., & Halali, E. (2015). Selfish third parties act as peacemakers by transforming conflicts and promoting cooperation. Proceedings of the National Academy of Sciences, 112(22), 6937–6942. [doi:10.1073/pnas.1505067112]
HELBING, D., Szolnoki, A., Perc, M., & Szabó G. (2010). Evolutionary Establishment of Moral and Double Moral Standards through Spatial Interactions. PLoS Computational Biology, 6(4): e1000758. [doi:10.1371/journal.pcbi.1000758]
HERRMANN, B., Thöni, C., & Gächter, S. (2008). Antisocial punishment across societies. Science, 319(5868), 1362-1367. [doi:10.1126/science.1153808]
HICK, K., Reddon, A. R., O’Connor, C. M., & Balshine, S. (2014). Strategic and tactical fighting decisions in cichlid fishes with divergent social systems. Behaviour, 151(1), 47-71. [doi:10.1163/1568539X-00003122]
HOBBES, T. (2011) [1651]. Leviathan: Or the matter, forme and power of a commonwealth ecclesiastical and civill. London: Penguin.
HOUSER, D., & Xiao, E. (2010). Inequality-seeking punishment. Economics Letters, 109(1), 20-23. [doi:10.1016/j.econlet.2010.07.008]
HSU, Y., Earley, R. L., & Wolf, L. L. (2006). Modulation of aggressive behaviour by fighting experience: mechanisms and contest outcomes. Biological Reviews, 81(1), 33-74. [doi:10.1017/S146479310500686X]
JAFFE, K., & Zaballa, L. (2010). Co-operative punishment cements social cohesion. Journal of Artificial Societies and Social Simulation, 13(3), 4 https://www.jasss.org/13/3/4.html. [doi:10.18564/jasss.1568]
JENSEN, K. (2010). Punishment and spite, the dark side of cooperation. Philosophical Transactions of the Royal Society B: Biological Sciences, 365(1553), 2635-2650.
[doi:10.1098/rstb.2010.0146]JOHNSON, D. D., & Fowler, J. H. (2011). The evolution of overconfidence. Nature, 477(7364), 317-320.
JOHNSTONE, R. A., & Bshary, R. (2004). Evolution of spite through indirect reciprocity. Proceedings of the Royal Society of London B: Biological Sciences, 271(1551), 1917-1922. [doi:10.1098/rspb.2003.2581]
JORDAN, J. J., Hoffman, M., Bloom, P., & Rand, D. G. (2016). Third-party punishment as a costly signal of trustworthiness. Nature, 530(7591), 473-476. [doi:10.1038/nature16981]
KRASNOW, M. M., Cosmides, L., Pedersen, E. J., & Tooby, J. (2012). What are punishment and reputation for?. PLoS ONE, 7(9), e45662. [doi:10.1371/journal.pone.0045662]
KRASNOW, M. M., & Delton, A. W. (2016 ). Are humans too generous and too punitive? Using psychological principles to further debates about human social evolution. Frontiers in Psychology, 7, 799. [doi:10.3389/fpsyg.2016.00799]
KRASNOW, M. M., Delton, A. W., Cosmides, L., & Tooby, J. (2015). Group Cooperation without Group Selection: Modest Punishment Can Recruit Much Cooperation. PLoS ONE 10 (4): e0124561. [doi:10.1371/journal.pone.0124561]
KRASNOW, M. M., Delton, A. W., Cosmides, L., & Tooby, J. (2016). Looking under the hood of third-party punishment reveals design for personal benefit. Psychological Science, 27(3), 405-417. [doi:10.1177/0956797615624469]
KURZBAN, R., & DeScioli, P. (2013). Adaptationist punishment in humans. Journal of Bioeconomics, 15(3), 269-279. [doi:10.1007/s10818-013-9153-9]
LAHTI, D. C., & Weinstein, B. S. (2005). The better angels of our nature: group stability and the evolution of moral tension. Evolution and Human Behavior, 26(1), 47-63. [doi:10.1016/j.evolhumbehav.2004.09.004]
LAMMERS, J., Stapel, D. A., & Galinsky, A. D. (2010). Power increases hypocrisy: Moralizing in reasoning, immorality in behavior. Psychological Science, 21(5), 737-744. [doi:10.1177/0956797610368810]
MARCZYK, J. (2015). Moral alliance strategies theory. Evolutionary Psychological Science, 1(2), 77-90. [doi:10.1007/s40806-015-0011-y]
MARLOWE, F. W., Berbesque, J. C., Barrett, C., Bolyanatz, A., Gurven, M., & Tracer, D. (2011). The “spiteful” origins of human cooperation. Proceedings of the Royal Society B: Biological Sciences, 278, 2159–2164. [doi:10.1098/rspb.2010.2342]
MAZE, J. R. (1973). The concept of attitude. Inquiry, 16(1-4), 168-205. [doi:10.1080/00201747308601684]
MCCULLOUGH, M. E., Kurzban, R., & Tabak, B. A. (2013). Cognitive systems for revenge and forgiveness. Behavioral and Brain Sciences, 36(01), 1-15. [doi:10.1017/S0140525X11002160]
MILLER, D. T. (2001). Disrespect and the experience of injustice. Annual review of psychology, 52(1), 527-553. [doi:10.1146/annurev.psych.52.1.527]
NAKAO, H., & Machery, E. (2012). The evolution of punishment. Biology & Philosophy, 27(6), 833-850. [doi:10.1007/s10539-012-9341-3]
NIETZSCHE, F. (2006) [1887]. On the Genealogy of Morality. (C. Diethe, Trans.). Cambridge, United Kingdom: Cambridge University Press.
NOWAK, A., Gelfand, M. J., Borkowski, W., Cohen, D., & Hernandez, I. (2016). The evolutionary basis of honor cultures. Psychological Science, 27(1), 12-24. [doi:10.1177/0956797615602860]
OKADA, D., & Bingham, P. M. (2008). Human uniqueness: self-interest and social cooperation. Journal of theoretical biology, 253(2), 261-270. [doi:10.1016/j.jtbi.2008.02.041]
OLSON, M. (1971). The logic of collective action: Public goods and the theory of groups. Cambridge, MA: Harvard University Press.
PETERSEN, M. B. (2013). Moralization as protection against exploitation: do individuals without allies moralize more?. Evolution and Human Behavior, 34(2), 78-85. [doi:10.1016/j.evolhumbehav.2012.09.006]
PETERSEN, M. B., Sznycer, D., Sell, A., Cosmides, L., & Tooby, J. (2013). The ancestral logic of politics upper-body strength regulates men’s assertion of self-interest over economic redistribution. Psychological Science, 24(7), 1098-1103. [doi:10.1177/0956797612466415]
PIETRASZEWSKI, D., & Shaw, A. (2015). Not by Strength Alone: Children’s Conflict Expectations Follow the Logic of the Asymmetric War of Attrition. Human Nature, 26(1), 44-72. [doi:10.1007/s12110-015-9220-0]
PRENTER, J., Elwood, R. W., & Taylor, P. W. (2006). Self-assessment by males during energetically costly contests over precopula females in amphipods. Animal Behaviour, 72(4), 861-868. [doi:10.1016/j.anbehav.2006.01.023]
PRICE, M. E., Cosmides, L., & Tooby, J. (2002). Punitive sentiment as an anti-free rider psychological device. Evolution and Human Behavior, 23(3), 203-231. [doi:10.1016/S1090-5138(01)00093-9]
PRZEPIÓRKA, W., & Liebe, U. (2016). Generosity is a sign of trustworthiness–the punishment of selfishness is not. Evolution and Human Behavior, 37(4), 255-262. [doi:10.1016/j.evolhumbehav.2015.12.003]
RABELLINO, D., Morese, R., Ciaramidaro, A., Bara, B. G., & Bosco, F. M. (2016). Third-party punishment: altruistic and anti-social behaviours in in-group and out-group settings. Journal of Cognitive Psychology, 28, 4. [doi:10.1080/20445911.2016.1138961]
RAIHANI, N. J., & Bshary, R. (2015). Why humans might help strangers. Frontiers in Behavioral Neuroscience, 9(39), 1-11. [doi:10.3389/fnbeh.2015.00039]
SCHELLING, T. C. (1960). The Strategy of Conflict. Cambridge, MA: Harvard University Press.
SELL, A., Eisner, M., & Ribeaud, D. (2016). Bargaining power and adolescent aggression: the role of fighting ability, coalitional strength, and mate value. Evolution and Human Behavior, 37(2), 105-116. [doi:10.1016/j.evolhumbehav.2015.09.003]
SELL, A., Hone, L. S., & Pound, N. (2012). The importance of physical strength to human males. Human Nature, 23(1), 30-44. [doi:10.1007/s12110-012-9131-2]
SELL, A., Tooby, J., & Cosmides, L. (2009). Formidability and the logic of human anger. Proceedings of the National Academy of Sciences, 106(35), 15073-15078. [doi:10.1073/pnas.0904312106]
SHESKIN, M., Bloom, P., & Wynn, K. (2014). Anti-equality: Social comparison in young children. Cognition, 130(2), 152-156. [doi:10.1016/j.cognition.2013.10.008]
SHOHAM, Y., & Tennenholtz, M. (1997). On the emergence of social conventions: modeling, analysis, and simulations. Artificial Intelligence, 94(1), 139–166. [doi:10.1016/S0004-3702(97)00028-3]
SYLWESTER, K., Herrmann, B., & Bryson, J. J. (2013). Homo homini lupus? Explaining antisocial punishment. Journal of Neuroscience, Psychology, and Economics, 6(3), 167-188. [doi:10.1037/npe0000009]
TOOBY, J., & Cosmides, L. (2010). Groups in mind: The coalitional roots of war and morality. In H. Høgh-Olesen et al. (Eds.) Human Morality and Sociality: Evolutionary and Comparative Perspectives (pp. 191-234), New York, NY: Palgrave Macmillan. [doi:10.1007/978-1-137-05001-4_8]
TRIVERS, R. L. (1971). The evolution of reciprocal altruism. Quarterly review of biology, 35-57. [doi:10.1086/406755]
VILLATORO, D., Andrighetto, G., Brandts, J., Nardin, L. G., Sabater-Mir, J., & Conte, R. (2014). The Norm-Signaling Effects of Group Punishment Combining Agent-Based Simulation and Laboratory Experiments. Social Science Computer Review, 32(3), 334-353. [doi:10.1177/0894439313511396]
WEST, S. A., El Mouden, C., & Gardner, A. (2011). Sixteen common misconceptions about the evolution of cooperation in humans. Evolution and Human Behavior, 32(4), 231-262. [doi:10.1016/j.evolhumbehav.2010.08.001]
WEST, S. A., Griffin, A. S., & Gardner, A. (2007). Social semantics: altruism, cooperation, mutualism, strong reciprocity and group selection. Journal of Evolutionary Biology, 20(2), 415-432. [doi:10.1111/j.1420-9101.2006.01258.x]
