Introduction
People discuss their points of view about many topics that affect them personally and/or socially. These social interactions are influenced by many factors, including prior knowledge, the perception of new information, the judgment of interacting partners, and the situation in which interaction occurs (Martin & Hewstone 2003; Wood 2000; Forgas & Williams 2001). Based on these communications, people form and adapt their opinions. But how does this work? In this study, we want to address this basic question, focusing especially on the content and the form of opinions and using empirical evidence and agent-based modeling (ABM) to analyze a part of the big picture of social interaction.
We based our investigation on models of continuous opinion dynamics under bounded confidence (Deffuant et al. 2000; Deffuant 2006; Hegselmann & Krause 2002; Salzarulo 2006), in which agents gradually adjust their opinions by comparing them with those of other agents. This repeated averaging occurs within the context of bounded confidence, by which agents only interact if they are close in opinion to each other.
An extension of these classical opinion dynamics models includes the implementation of contrast effects (Huet, Deffuant & Jager 2008; Dykstra et al. 2013; Jager & Amblard 2005). Contrast effects refer to the mechanism of shifting away from an advocated position when this position is distant to the receivers’ initial position (see also the Section on theoretical background). For instance, in the model developed by Jager and Amblard (2005), the inclusion of contrast effects permitted shifts in opinion and resulted in the emergence of different patterns, including divergent, convergent, and pluriform distributions.
Another method of understanding why these phenomena of converging or diverging opinions in social interaction occur relates to social influence in terms of attraction (i.e., homophily) and distancing (i.e., heterophobia) (Flache & Macy 2006; Flache & Mäs 2008; Mark 2003; Liu & Srivastava 2015; Macy et al. 2003; Salzarulo 2006). In fact, in addition to positive influence among social groups (i.e., seeking consensus in interactions), negative influence (i.e., moving away from others’ opinions in interactions) is also shaping the way in which social influence occurs. Positive and negative social influences are mainly used in studies that investigate in-group and out-group dynamics, as well as those that examine social dynamics in different cultures (e.g., Axelrod 1997; Mark 1998, 2003; Mäs & Flache 2013; Salzarulo 2006). Experimental studies (Mäs & Flache 2013; Takás, Flache and Mäs 2014) have tested positive and negative mechanisms in social interactions, and their results have revealed the presence of homophily; however, they have not found supporting results for negative social influence.
Despite the various successful studies of opinion dynamics, a commonality among these models is the fact that agents only have their opinions represented as one-dimensional concepts. In such studies, opinions are either positive or negative, with binary or continuum characteristics (e.g., Latané & Nowak 1997; Weisbuch et al. 2002, 2003). Some scholars have pointed out the necessity of viewing opinions as multidimensional (Urbig & Malitz 2005); however, the lack of empirical data in opinion dynamics remains. In fact, what we learn from these models about opinion dynamics is often presented in artificial, abstract terms. The concrete case may differ considerably, and real populations/samples do not always exist in the same homo- or heterogeneous manner, as arbitrary distributions of agent populations assume. With our contribution, we aim to test what happens when we fill these data gaps and explore a more realistic model based on empirical data and a specific real-world issue (related to contested infrastructures).
Switzerland is currently active in a participatory site selection process for the building of deep geological repositories (DGR) for nuclear waste, and citizens’ opinions are important if the overall support of the population is to be obtained (Swiss Federal Office of Energy 2008). Prior research has shown that there are different opinion types regarding this specific topic, such as extreme opinions (against or in favor) and moderate opinions (ambivalent or indifferent) (Seidl et al. 2013).
Thus, it is important to determine how lay people communicate and adapt their opinions on this topic in the long term. In fact, when people discuss any issue, what they compare is usually not a mean value of their overall opinion on the discussed topic. What we observe is that people communicate arguments to each other. An individual’s opinion is not an aggregate; rather, it is split up into subcategories (arguments), which can have different valences.
Usually, each individual identifies pro and con arguments in different amounts and ratios depending on the topic. This is also a reason why moderate opinions (i.e., ambivalence) can occur (see Jonas, Broemer & Diehl 2000 for an overview). The disaggregation of opinions has been inspired by prior work on arguments in opinion dynamic models.
For instance, in their paper on multidimensional opinion dynamics, Urbig and Malitz (2005) emphasize the fact that attitudes are multidimensional by nature. They propose a simple attitude model where evaluations and associations regarding the object are conceived as different opinion dimensions. Mäs et al. (2013) also approached multidimensional opinion dynamics and used arguments to represent the elements that form opinions in order to explain homophily and social influence. These contributions, however, do not include empirical data in their model dynamics. A successful attempt to include empirical data in multidimensional opinion dynamics was performed by Mäs and Flache (2013). These scholars tested their hypotheses regarding social influence through argument communication via a group discussion experiment.
In line with the efforts of these prior research contributions, we concluded that in our simulation, the use of concrete arguments rather than aggregated opinions was the path to follow. Furthermore, we wished to emphasize the inclusion of empirical data in the model parameters. We aim to conduct an opinion dynamic exercise that studies argument communication on a specific topic; this examination will be made on the basis of sociopsychological concepts. The results of this exercise should provide a ground for discussion regarding the implementation of empirical data into opinion dynamic models with disaggregated opinions. Moreover, this study will introduce empirical groundings for simulation models of contrast effects.
Theoretical Background
The theoretical pillar for our investigation on opinion changes comes from social psychology. Social judgment theory (SJT) (Sherif & Hovland 1961) offers a good basis for modelers of social simulations (e.g., Dykstra et al. 2013; Jager & Amblard 2005) because it allows for a good balance between complexity and simplification (Railsback & Grimm 2012; Starfield, Smith & Bleloch 1990). An anchor based on prior knowledge and experience provides the basis for comparison and places the new information on the social judgment continuum, which also determines the persuasive power of the message (O’Keefe 1990; Sherif, Sherif & Nebergall 1965). This social judgment continuum is divided into three latitudes with rejection at one extreme, acceptance at the other, and non-commitment in the middle.
In this process, people might stumble across perceptual errors explained in SJT as contrast and assimilation effects. A contrast effect means that new information that falls within the latitude of rejection is perceived as more opposed to one’s own attitude (because it is perceived as being further away from one’s own anchor or point of view) than it really is. An assimilation effect means that new information that falls within the latitude of acceptance is perceived as less opposed to one’s own attitude (because it is perceived as being much closer to one’s own anchor or point of view) than it really is.
However, changes in opinion might occur during the second step, in which people adjust their own attitude or opinion either toward or away from the new information, depending on whether the new information has been previously judged as being in the latitude of acceptance, non-commitment, or rejection. If the new information is judged to be in the latitude of acceptance, the receiver will adapt his or her attitude or opinion[1] toward it. If the opposite occurs (i.e., the new information is judged to be in the latitude of rejection), the receiver will adjust his or her attitude or opinion away from that of the other person. In both cases, it is believed that the greater the discrepancy between opinions, the larger the change. For new information in the latitude of non-commitment, the common interpretation is that no change occurs (Sherif & Hovland 1961).
Born as a sociopsychological theory in the 1960s (and being under acknowledged in the last few decades), SJT has found some recent applications in communication science. Smith et al. (2006) focused their investigation on the latitude of non-commitment. They found that information presented in social norm campaigns that fell under the latitude of non-commitment provoked a change in attitude and behavior in the direction of the presented norm. The latitudes of acceptance and rejection were not compared, which impedes comparison between these latitudes for possible changes.
In an experimental study on persuasion, Park et al. (2007) focused on argument quality and involvement, which is an additional factor in SJT determining the acceptance or rejection of persuasive messages. They found no evidence of involvement’s relevance to attitude change. However, argument quality was found to be a determinant of the ability of information to provoke attitude change.
All in all, the applicability of SJT is yet to be proven in social simulations of opinion dynamics with empirical cases. In the following section, we will describe our social simulation model, in which we implement SJT and use empirical data for the investigation of opinion dynamics based on arguments.
Method
Empirical study
Sample
Our sample comprised 841 participants (43.4% women and 56.6% men) with an age range between 19 and 84 years (M= 56.2, SD = 16.86); participants completed the online questionnaire in January of 2014. The sample participants lived in the German-speaking part of Switzerland, as the potential sites for nuclear waste repositories are all located in German-speaking regions. We recruited the sample in collaboration with a market research institute. This permitted a wide distribution of the questionnaire based on specific quotes aimed at recruiting a representative sample of the Swiss German-speaking population. Furthermore, the selection of the final sample was directly linked to the quotes and to the completeness of the responses; this allowed us to obtain a complete data set without missing values.
Questionnaire
A short factual description of the topic of nuclear waste in Switzerland and the ongoing repository site selection process introduced the participants to the online questionnaire. In the first part, ten arguments related to this topic were to be evaluated on (a) a valence scale, asking participants if, in their opinion, the argument was in favor of or against a DGR on a seven-point Likert scale (from “ totally against” to “ totally in favor”), with the option of an “I don’t know” answer, and on (b) an importance scale, asking the degree of importance they would attribute to each argument on a seven-point Likert scale (from “ not important at all” to “ very important”).
Of the ten arguments, four focused on the risks of a DGR (e.g., “ A deep geological repository would represent a health risk”), four on the benefits of a DGR (e.g., “ A deep geological repository would create new and lasting job opportunities in the region”), and two on the ongoing site selection process (e.g., “The communication during the site selection process should be transparent”) (see Table 1).
The decision to include the dimensions of risk and benefit was made in order to ascribe to classical research on contested technologies and infrastructures (e.g., Slovic 1972). The focus lies in the evaluative aspect of certain attitudes toward, for instance, nuclear issues, which in many studies is described as the risk and benefit perception (e.g.,Poortinga & Pidgeon 2006; Visschers & Wallquist 2013). However, concerning the specific issue of nuclear waste in relation to its political process, procedural aspects should also be taken into consideration. Factors such as fairness and transparency have been described as fundamental to the participatory processes of contested infrastructures (Krütli et al. 2012). Therefore, we included in our questionnaire the dimension of process, which refers to the procedural aspects of the site selection process in Switzerland.
After the evaluation of the ten arguments, we measured the social judgment continuum of the participants for each argument. For this purpose, we used an adapted measurement called the ordered alternative scale (OAS) (Sherif & Hovland 1961; Sherif et al. 1965; Smith et al. 2006). The adaptation of the original measurement rooted in the studies on conception measurements (see Jackson 1960) was necessary for the best implementation in the ABM[2]. In our online questionnaire, participants had to sort the ten arguments on a three-point scale from "objectionable" to "acceptable," with a neutral position "neither acceptable nor objectionable." This neutral position represented arguments in the latitude of non-commitment. The arguments reported as being objectionable were represented in the latitude of rejection, and arguments reported as being acceptable were represented in the latitude of acceptance.
Results
The results of the evaluations of the arguments are depicted in Table 1. As expected, benefit-oriented arguments were rated as more favorable to DGR in Switzerland (valence). The process-oriented arguments were rated as the most favorable and the most important among the sample. The importance ratings show higher values for risk-oriented arguments than for benefit-oriented arguments.
| Valence | Importance | |||
| Arguments | M | SD | M | SD |
| More working places (BO) | 5.0 | 1.60 | 4.1 | 1.75 |
| Better infrastructure (BO) | 4.3 | 1.81 | 3.8 | 1.68 |
| Lower taxes for citizens (BO) | 4.6 | 1.80 | 3.8 | 1.84 |
| Sustainable development in the region (BO) | 4.0 | 1.78 | 3.8 | 1.69 |
| Environmental damages (RO) | 3.3 | 1.92 | 4.8 | 1.87 |
| Transport accidents (RO) | 3.8 | 1.89 | 4.8 | 1.83 |
| Health risk (RO) | 3.3 | 1.87 | 4.8 | 1.90 |
| Later generations reach into the repository (RO) | 3.1 | 1.79 | 4.2 | 1.99 |
| Fairness of the political process (PO) | 6.1 | 1.31 | 6.0 | 1.38 |
| Transparency of the communication process (PO) | 6.2 | 1.27 | 6.1 | 1.30 |
For the computation of the scales (see Sections5.3-5.6), we ran a factor analysis (FA) on the ten arguments both for the valence and importance dimension. Results of the FA showed a three-factor solution, which was consistent with the argument types defined as risk-, benefit-, and process-oriented. Each scale represented the mean values for valence and the importance of the arguments by type (see Table 2).
| Valence | Importance | |||
| Scale | M | SD | M | SD |
| Benefit-scale | 4.5 | 1.75 | 3.9 | 1.74 |
| Risk-scale | 3.4 | 1.87 | 4.7 | 1.90 |
| Process-scale | 6.1 | 1.29 | 6.1 | 1.34 |
Agent-Based Model
For our simulation, we used an agent-based model (ABM) and described it by following the ODD-protocol (Grimm et al. 2010; Müller et al. 2013). In the following sections, we will only illustrate the protocol subsections relevant to our ABM.
Purpose
The purpose of our ABM was to investigate the mechanisms of opinion dynamics over time on the basis of the assumptions of SJT and arguments related to the specific issue of DGR. The paired agents in the model interact unidirectionally, compare argument-scales, and adapt them (or not) depending on the position of each argument on their own social judgment continuum (see the input data section). Based on the simulation output, we will be able to draw conclusions regarding the applicability of SJT, the differentiation of opinions into arguments for opinion dynamics simulations, and the utilization of empirical data for simulation purposes.
Entities, state variables, and scales
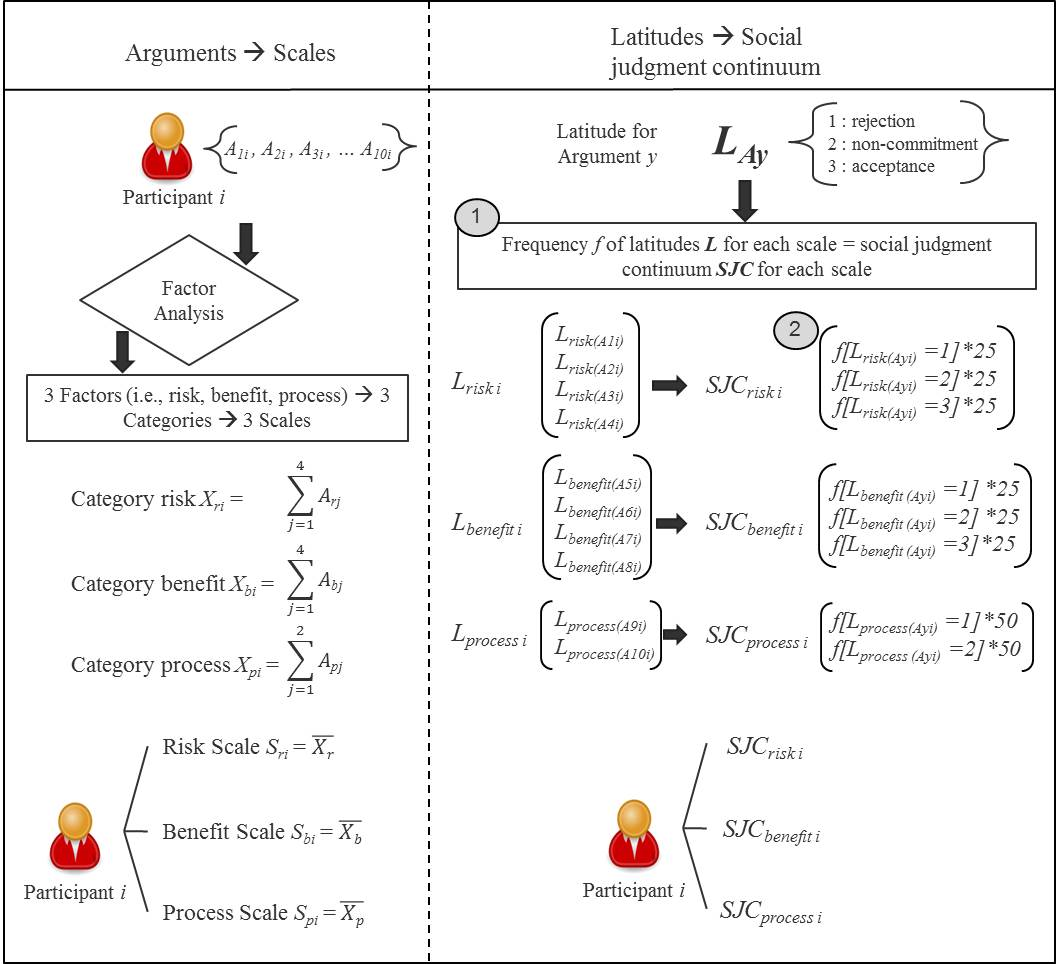
The model consists of 841 agents representing Swiss citizens. The argument values Ai taken from the empirical study have been computed as the product of valence ratings Vi [-1, 1] and importance ratings Ii [0, 1]. The mean values of the arguments belonging to the same category (i.e., risk, benefit, and process) resulted in the argument scales Sx, where x is the related category, assuming values between -1 and 1 (see Figure 1). Therefore, each agent T possesses a set of three argument-scales Sx computed as the mean of the argument values Ai belonging to each category x.
The agents’ profiles were completed using information about the distribution of latitudes (i.e., rejection, non-commitment, and acceptance) for each of the three argument scales Sx on the social judgment continuum SJCx of each agent (see Figure 1, step 1 on the right). This information has been directly implemented using the empirical data that measured the distribution of latitudes (i.e., OAS measurement, see section questionnaire for more details).
This data has been computed as a probabilistic distribution on the social judgment continuum SJCx (see Figure 1, step 2 on the right). This means that for each scale, a minimal probability of p=0.25 (p=0.5 for the process scale) was multiplied by the number of entries for each latitude. As an example: if, for the risk scale, Participant i reported two arguments in the latitude of rejection (Lay = 1), one argument in the latitude of non-commitment (Lay = 2), and one argument in the latitude of acceptance (Lay = 3), the social judgment continuum for the risk scale SJCrisk i would comprise the probabilities [0.5; 0.25; 0.25 ].
Each interaction between all pairs of agents randomly chosen from the social network is represented by a one-time step t. Time in the model was thus a discrete measure and did not represent a real time interval.
Process overview and scheduling
The simulation world consisted of a 29 x 29 two-dimensional grid with wrapped boundaries (i.e., all agents are interconnected) based on a Moore neighborhood (i.e., eight neighbors for each agent). This type of social network and the number of links for each agent was selected based upon empirical information (73.2% of the participants reported having interactions with between one and eight persons about DGR). Because spatial representation was not a focus in our study, the Moore neighborhood was assumed to be a good compromise to facilitate simple, readily explicable dynamics. It should be noted that the implementation of more complex social networks (i.e., small worlds, preferential attachments, etc.) and the inclusion of agent characteristics that can be attributed to the social dynamics of different groups have been explicitly omitted. With the exception of general interaction frequency, we do not have empirical information about the network itself (i.e., to whom people may talk and how often they do so). To assume other mechanisms based on arbitrary assumptions would have been beyond the scope of this exercise.
As described in Figure 2, at each time step t, each agent randomly chose a neighbor from the social network. The one-directional interaction (meaning that only the interacting agent Ta could adapt its argument-scale value Sx) started with the comparison of a similar argument-scale Sx.
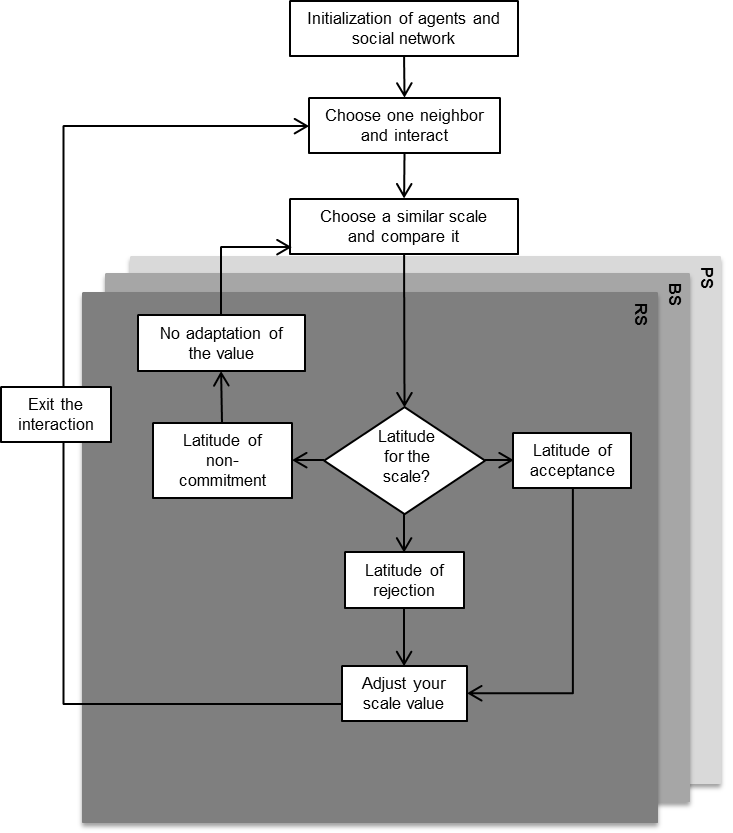
The choice of the latitude to use in the comparison for each agent and each argument-scale depended on a random process using the probabilistic distributions of the social judgment continuum related to each argument-scale SJCx. The occurrence of an adaptation directly depended on the chosen latitude type and on the valence of the compared argument-scale values Sxa and Sxb (i.e., positive or negative).
If the latitude for the chosen argument-scale was in the latitude of non-commitment, no adaptation occurred. The argument-scale value Sxa of the interacting agent Ta remained unvaried, and Ta moved on to the next argument-scale.
An adaptation for agent Ta would only occur if the latitude for the chosen argument-scale was in the latitude of rejection or acceptance. Based on the general quadratic functions 1 & 2 and depending on the latitude (see Tables 3 and 4), the argument-scale value Sxa was permitted to shift up or down to a maximum of 1 or a minimum of -1. The quadratic term in function 1 leads to an asymptotic approach to the extreme positions so as to best represent the two effects of contrast and assimilation described in SJT (see Section 2).
The constant s set at s = 0.01 slowed down the speed of change in the argument-scale values (see also Jager & Amblard 2005). This facilitates better observation during the simulation and better reflects the generally slower changes in people’s opinions in the real world.
| $$f(x) = \pm (x^2 \times s) \rightarrow f(x) = \pm (S_{xb}^2 \times s)$$ | (1) |
| $$S_{xa(t+1)} = S_{xa(t)} \pm y \rightarrow S_{xa(t+1)} = S_{xa(t)} \pm (S_{xb}^2 \times s)$$ | (2) |
| Latitude of acceptance | Sxb | ||
| + | - | ||
| Sxa | + | Sxa(t+1) = Sxa(t) + (Sxb2 * s) | Sxa(t+1) = Sxa(t) – (Sxb2 * s) |
| - | Sxa(t+1) = Sxa(t) + (Sxb2 * s) | Sxa(t+1) = Sxa(t) – (Sxb2 * s) | |
| Latitude of rejection | Sxb | ||
| + | - | ||
| Sxa | + | Sxa(t+1) = Sxa(t) – (Sxb2 * s) | Sxa(t+1) = Sxa(t) + (Sxb2 * s) |
| - | Sxa(t+1) = Sxa(t) – (Sxb2 * s) | Sxa(t+1) = Sxa(t) + (Sxb2 * s) | |
Agent Ta exits the interaction as soon as every argument-scale has been compared and its value Sxa has been updated. For the next time step, another neighbor agent Tb is chosen from the social network, and agent Ta begins the same interaction process again.
Design concepts - Implementation and initialization
The model was implemented in the freely available, multi-agent, programmable modeling environment NetLogo 5.0.3 (Wilensky 1999).
During the initialization, every agent profile was sequentially built upon the following empirical information about its state variables:
- values for each argument-scale (Sx) were computed as the mean of the argument-values Ax and the argument-values Ax were computed as the product of valence Vx and importance Ix and
- the probability for every latitude (i.e., latitude of rejection, acceptance, or non-commitment) of location in each of the three social judgment continuum SJCx related to a category x.
Input data
The input data for every variable described above consisted of the empirical data from an online questionnaire. This investigation was conducted in January, 2014 in the German-speaking part of Switzerland. Thus, at the beginning of the simulation, every agent directly represents one of the participants of the online questionnaire.
Results
We ran several prior sensitivity analyses using our model in order to define a level of stability and to ensure the robustness of the parameters (the simulation was run over 2000 time-steps). Examining the number of runs, the model showed relatively stable patterns at approximately 500 time-steps. After more than 500 time-steps, the change was negligible and no significant deviations or emerging patterns were detected; thus, we decided to adopt this figure as the maximum number of interactions for the purposes of our study. This would represent each individual (i.e., agent) having 500 interactions with other people, which is apparently a great deal of interaction. However, we must bear in mind that the process of DGR takes several decades to complete; therefore, discussions regarding this issue could realistically entail such a large number of interactions.
To test the parameters, we primarily focused on the trajectories of the latitudes to see if the changes in the argument-scale values directly depended on the latitudes. This means that for each argument-scale, only one distribution of the latitudes was taken sequentially, without allowing for changes during the simulation in the first place (no random choice based on the probabilistic distribution). Different runs showed that the trajectories did depend directly on the latitudes and not on random effects not defined in the model.
Results among the entire sample
If we consider the entire sample of 841 agents, the runs on the three different argument-scales (considering the individual social judgment continuum for each agent) showed different pictures for all three scales[3].
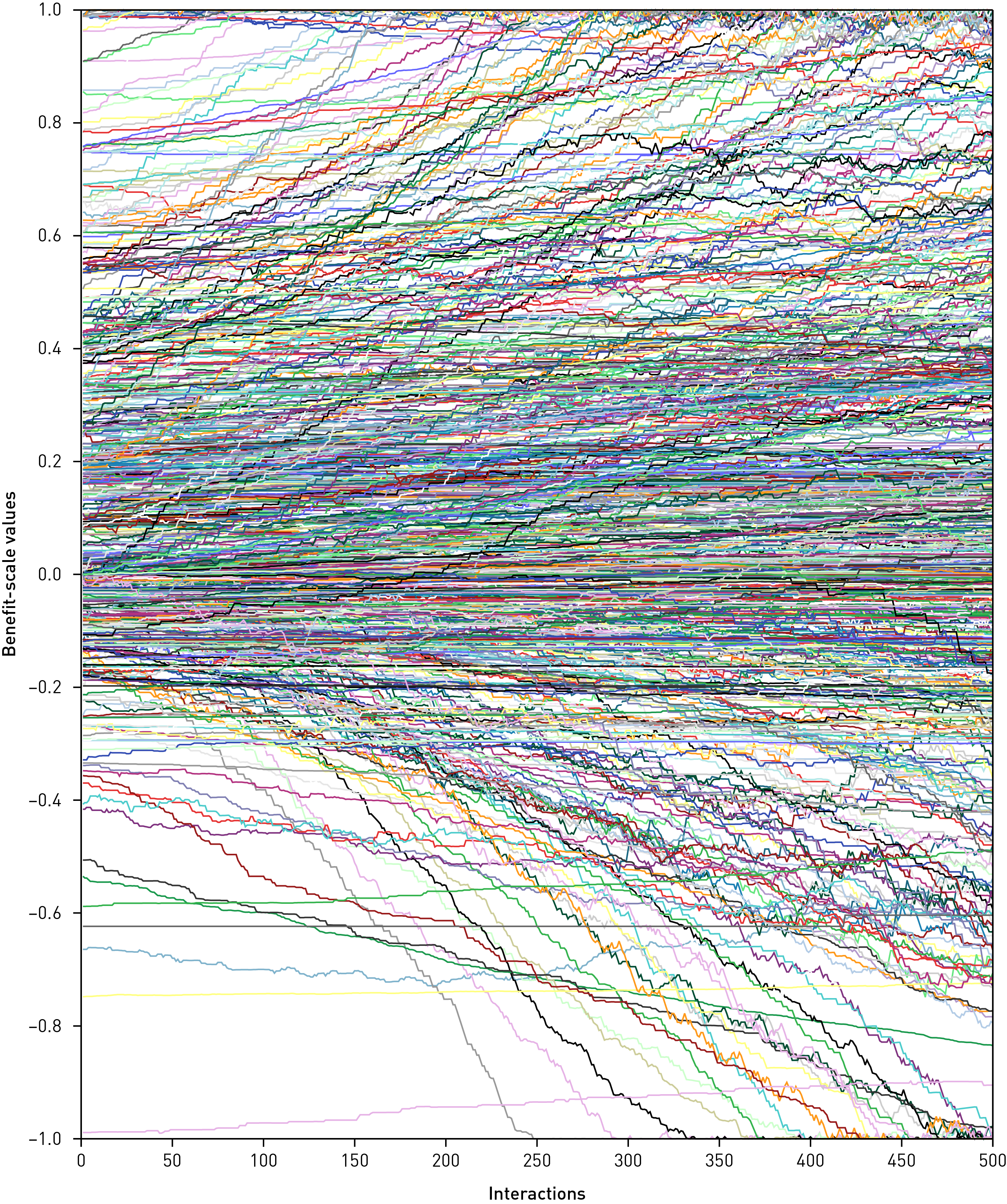
In our sample, the participants (and thus the agents in the model) varied in their evaluations of the risk-scale, showing different initial states along the continuum from absolutely against to absolutely in favor of (Figure 3). We observed a huge variance in the scale-values over the course of the simulation, with a minor tendency to converge on the low extreme of -1 and a diffusion in the middle part. This heterogeneity is also noticeable in the social judgment continuum, resulting in high variance during the simulation exercise. We also noted very different trajectories for the agents (each represented by a curve in the graph), showing that they adapted their values in different ways, without a clear general tendency.

The benefit-scale produced a similar yet horizontally flipped picture of the scale-values in the simulation (Figure 4). The agents possess more heterogeneous initial values compared to those of the risk-scale, which converge to the neutral position with a slight positive tendency. Hence, the lower part (benefit-scale as arguments against a DGR) is less represented, and we noted only a small percentage of the sample in the lower part. During the simulation, we also noted more stable trajectories for the agents in the model than for those in the risk-scale, with distinguishable tendencies. It appears that agents starting with positive values tended to adapt towards more positive values, whereas agents starting with negative values tended to adapt toward more negative values. Additionally, we noted a remarkable number of agents in the middle section, showing stable trajectories and indicating a less prominent adaptation of their scale-values over time.
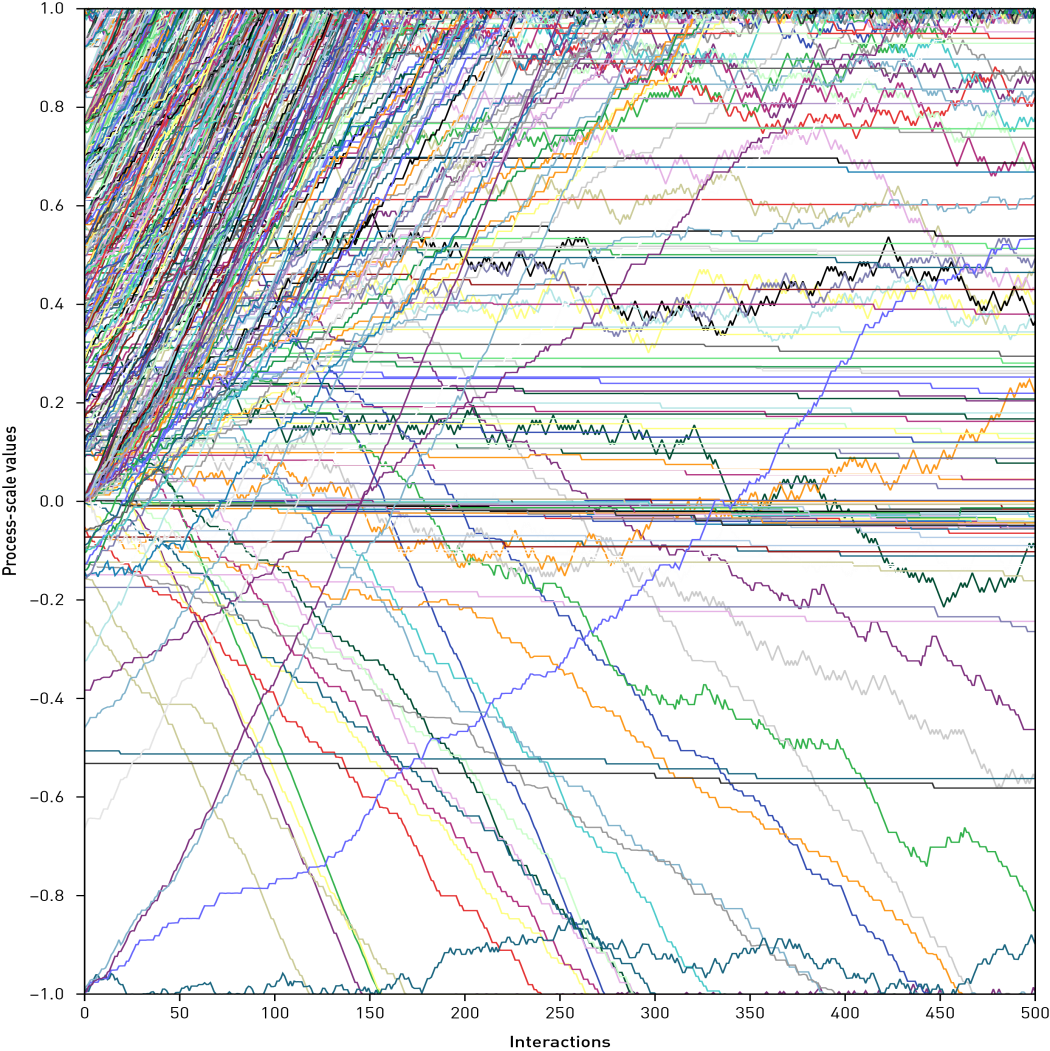
Finally, the process-scale shows a tendency toward a high degree of consensus that occurs significantly more rapidly than in the other two scales (Figure 5). We can observe that already after the first 200 interactions, process-scale agents began to converge to the upper limit of 1. Only a small subset of agents shows either no significant change over the interactions or a falls towards the negative limit of -1. This is related to the initial state values almost exclusively represented in the positive segment, already showing a favorable evaluation of this scale. The rapid adaptation towards a positive consensus is also triggered by a high representation of the social judgment continuum, entailing almost the latitude of acceptance among the agents (see below, Figure 7).
Results among subgroups of the entire sample
To allow for a better comprehension of these graphs, we decided to divide each scale into the different social judgment continua. We divided the sample into groups whose members reported the same latitude distributions in each scale. As an example, Figure 6 illustrates in greater detail the grouping of the sample for the risk scale. We subsequently obtained 15 different cases for both the risk and benefit scales (3 latitudes x 4 arguments) and six cases for the process scale (3 latitudes x 2 arguments). In Figure 7, the cases are described and provided along with the percentage of agents who share the same social judgment continuum across the entire sample.
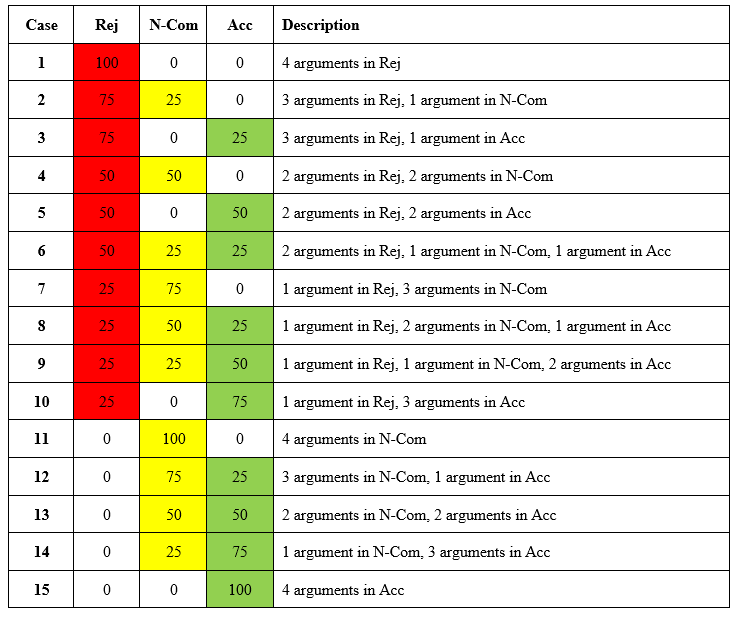
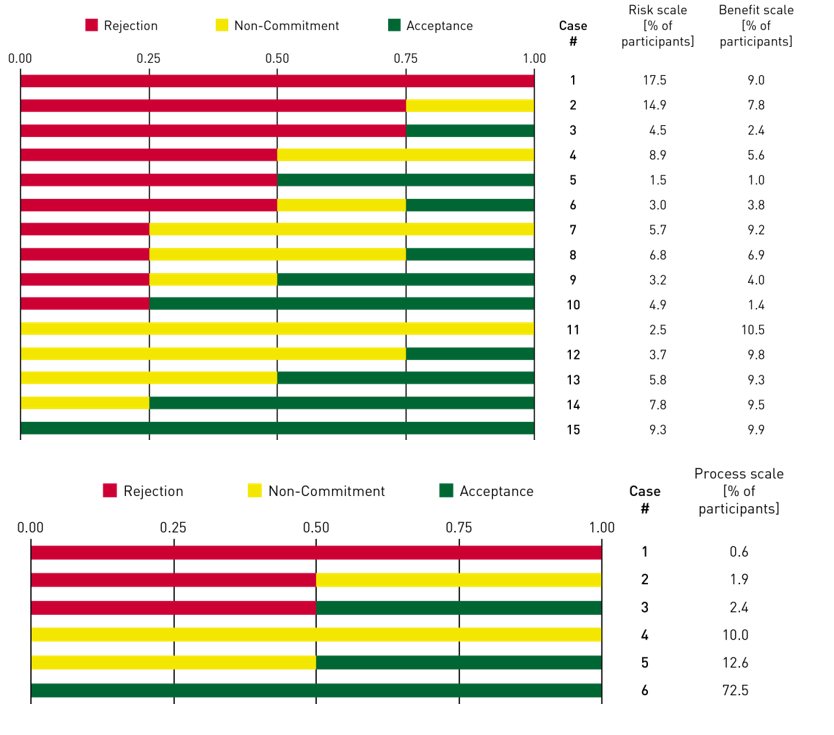
In dividing the sample into subgroups of agents who share the same social judgment continuum (cases), we observed different stylized facts related to this cases. For example, the distribution of the cases among the scales is quite different. The largest difference is observed in the process scale, which clearly indicates a skewed distribution. Only a few participants reported both process arguments to be in their latitude of rejection (0.6%), whereas the majority (72.5%) reported both arguments to be in the latitude of acceptance. The risk scale shows that half of the sample participants (50.3%) reported a latitude of rejection that fell within the scale, at least to a probability of p= 0.5 (which indicates that at least two of four arguments were reported to exist in this latitude). For the benefit scale, however, this was the case for only 29.6% of the sample. Conversely, the probability of an individual having at least p= 0.5 of their arguments fall within the scale reported in the latitude of acceptance is similar for both the risk scale (32.5%) and the benefit scale (35.1%).
Shifting the focus to the dynamics in the simulation, we take the most extreme cases for every scale as examples of the different trajectories in order to relate them to the initial values. Cases 1 and 15 were used for the risk-scale (17.5% and 9.3%, respectively) and the benefit-scale (9% and 9.9%, respectively), and case 6 was used for the process-scale (72.5%). We omitted case 1 for the process scale because of the underrepresented sample (0.6%).

For case 1 (in which the probability for the latitude of rejection in the social judgment continuum equals 100%) we see a major difference in the dynamics if we compare the risk-scale with the benefit-scale. The values for the risk-scale in case 1 (see Figure 8B) present much more variability and less consensus than those for the benefit-scale. Both extreme values of -1 and 1 are reached, and the dynamics of value adaptations do not show any clear tendencies over time. Even if the social judgment continuum is the same for all agents represented in the graph, a clear relationship among the starting values, the adaptations, and the social judgment continuum is absent.
The benefit-scale (see Figure 8A) in case 1 shows more homogeneous starting values and presents a clear tendency in the dynamics. The direction of the dynamics is either negative (reaching the extreme of -1) or more or less stable over time (diffusing the scale-values over the negative spectrum). No changes are visible in the upper positive space of the graph. It seems that agents with prevailing rejection tendencies in their social judgment continua also rate benefit-related arguments as being against a DGR.
For case 15 (in which the probability for the latitude of acceptance in the social judgment continuum equals 100%) differences between the risk-scale and the benefit-scale are visible again. For the risk-scale in case 15 (see Figure 8D), we observe a variability in both the dynamics and in the starting values. Even though there is a tendency for a convergence to the extreme values of -1, the trajectories are of different speeds and in some cases are also of different directions (stable or towards more positive values). Again, no clear relationship among the starting values, the adaptations, and the social judgment continuum is present.
The benefit-scale in case 15 (see Figure 8C) presents more homogeneous values at the start of the simulation than the risk-scale. Almost all agents’ initial values cover the entire positive spectrum, meaning that those agents see the benefit-scale as representing arguments in favor of a DGR. Except for a few outliers, the dynamic is rather stable, with a tendency toward the positive extreme of 1. Thus, after the 500 time steps in the simulation, we notice a slightly stronger consensus toward a favorable position.
Concerning the similar case for the process scale (i.e., case 6, the same social judgment continuum with a 100% probability of acceptance) we observe a strong representation of the initial values in the positive half of the spectrum (see Figure 8E). Moreover, the dynamics are very fast, all in the same direction (positive), and reach consensus in the upper extreme of 1 after around 100 interactions. That is, agents rapidly accept the process-related arguments to be in favor of a DGR.
Discussion
The simulation based on empirical data from an online questionnaire about DGR in Switzerland provides insight regarding the structure of opinions in a context-specific opinion dynamic exercise. The opinion structure is discussed in terms of the process of opinion disaggregation into arguments (empirical basis) and of disaggregation into scales representing different categories of arguments. Our results show different patterns depending on these categories.
We adapted prior models of opinion dynamics based on SJT and contrast effects by allowing for individual differences and variations in the latitudes during the simulation, as well as by including real empirical data, which facilitates a content-based simulation related to a specific topic.
Summing up the results, we can observe a mutual influence between individuals’ current knowledge and what they value (initial state) and how they evaluate new information (dynamics). However, it is important to note the large differences among the scales in this respect.
This suggests that not only do dynamics and the initial values play a role in the simulation but the content-related part is also very important. We see, based on our results, that the risk category has a much more diffused dynamic compared to the other two categories (i.e., the benefit and process categories). In addition, the process category has the most rapid adaptation toward a positive consensus among the other categories (i.e., the risk and benefit categories).
This indicates that the dynamics over time depend on the category of an argument. This category may be valued differently for different topics. Thus, the pattern of risk/benefit/process is most likely linked to the topic at hand. We assume that a very different pattern and set of related dynamics would exist for more controversial topics, such as the fair distribution of refugees from Syria. In this case, for instance, the salience of the topic and the almost constant media coverage might provide different sources of information and could affect the way in which new information is being processed, considering also the cultural issues at hand (see e.g., González-Avella et al. 2007). It could be plausible to have higher importance ratings that lead to stronger and more polarized positions (as the valence of arguments is weighted in opinion communication). Furthermore, the debate would focus on specific arguments that could be related to other categories, such as values or ethics. It is therefore advisable to study the topic carefully and to derive assumptions that are possibly based on empirical evidence.
Why not (only) psychology?
Studying human behavior and cognition is commonly related to the social sciences—such as psychology and sociology, as well as neuroscience and biology—with their respective established methods. So, why should scientists bother to invest time in simulation models to better understand human cognition and behavior?
Observing most social and psychological phenomena, we can state that they are not the results of behaviors and/or cognitions performed by individuals alone. As social beings, people interact with, learn from, and are influenced by each other. People repeatedly interact and hence build their opinions, enhance their experiences, and make decisions.
Yet, domains such as social psychology use suboptimal theory-building and modeling techniques to capture dynamic processes related to social interactions (Smith & Conrey 2007). Social simulations can help overcome these shortcomings (Squazzoni, Jager & Edmonds 2014). However, it is important to acknowledge the importance of keeping the investigations near to the real world. This means that empirical information should be incorporated into the models along with theories.
With our contribution, we provide an example of how this combination can be performed. Sociopsychological theories can be used in empirical investigations and can be translated into codes for computer simulations. Working with these assumptions using empirically-based generated populations of agents can enable a different perspective, which is very helpful in attempting to comprehend thematic social dynamics (Jager 2017).
Why should social simulations incorporate real data, theories, and specific topics?
Our contribution aims to accomplish the following goals. We seek to:
- operationalize a sociopsychological theory,
- find a traceable compromise between very abstract models and very case-specific models to facilitate the investigation of a specific problem, and
- include real data in order to better match real world opinion communications.
Concerning point 1, we can conclude from our examination that SJT applies well to simulation studies. It allows researchers to capture structural information about individuals’ cognitions, provides a way to implement an algorithm that describes social interaction and attitude changes, and captures specific effects such as assimilation and contrast. However, we should note that from a sociopsychological perspective, the theory is not perfectly grounded and has not been put forward in empirical investigations (e.g., Eagly & Telaak 1972; Hovland, Harvey & Sherif 1957).
Obviously, there are other theories that explain cognitive mechanisms related to persuasion and attitude change in greater detail. The more popular dual-system models, such as the elaboration-likelihood model (ELM) (Petty & Cacioppo 1986) or the heuristic-systematic model (HSM) (Eagly & Chaiken 1993) have attracted a great deal of attention and have been widely studied in psychology (for an overview, see Evans 2008). In addition, the social simulation community has successfully implemented these models, albeit with considerable effort (e.g., Mosler et al. 2001).
Nonetheless, the complexity of the latter models restricts the inclusion of empirical data into simulations. Our conclusion is that, in order to better comprehend social interaction and attitude change, one must find the best possible compromise between a suitable theory, a comprehensible model, and empirical information. Moreover, especially for attitude change and persuasion mechanisms, there is still an ongoing debate surrounding the establishment of a standard in social psychology (Evans 2008). This means that there is not one theory one must apply, but several more or less suited for the case at hand.
Referring to point 2, our contribution can be seen as a meso-level approach to the investigation of opinion dynamics. This refers to the multidimensionality of attitudes (e.g., Urbig & Malitz 2005), which claims that an opinion should not be seen as a single general variable, but rather should be divided to the best degree of disaggregation in order to capture differences among the real content of what we call “opinions.” The “best degree,” however, is not evident from the case but instead results from experience with this meso-level approach, which is currently seldom applied. This refers again to the more general issue of complexity and simplification when it comes to social dynamics, and as scientists we must face the fact that we cannot have a perfect model:
"No one knows precisely the dynamics of a single individual, nor the way he interacts with others. Moreover, even if one knew the very nature of such dynamics and such interactions, they would be much more complicated than, say, the forces that atoms exert on each other. […] Therefore, any modeling of social agents inevitably involves a large and unwarranted simplification of the real problem. It is then clear that any investigation of models of social dynamics involves two levels of difficulty. The first is in the very definition of sensible and realistic microscopic models; the second is the usual problem of inferring the macroscopic phenomenology out of the microscopic dynamics of such models. Obtaining useful results out of these models may seem a hopeless task." (Castellano, Fortunato & Loreto 2009, p. 592)
To provide some hope, we assume that a meso-level approach can provide relevant benefits for the investigation of social interaction and opinion dynamics, instead of focusing either on realistic microscopic models that are difficult to generalize or on macroscopic models, which are usually too abstract and out of touch with reality.
We are of course aware of the fact that these types of model (such as the one in this contribution), compared to works for instance by Hegselmann and Krause (2002), may appear “messy” in their results and lack the beauty of the more mathematically exact models. However, as well-done and interesting as such models are, they are devoid of empirical application. As long as we do not apply models to simulate real world opinion dynamics on actual topics, the contribution of social simulation to, for instance, social or environmental psychological research is unclear. Of course, one can learn from the results—for example by gathering stylized facts derived from random distributions as input variables—and find applications from empirical cases.
However, we noted that to some extent, the meso-level between fully empirically grounded simulations (Tobias 2009) and very abstract simulations is missing (for physics-based simulation models, see Sobkowicz 2009). This is obviously because such meso-level simulations are difficult to execute and yield “messy” results. More research and simulation studies are definitely needed to gain more experience and further test the value of empirically-based agent-based models of opinion dynamics.
This leads us to point 3, which highlights the meaningful nature of gathering and using empirical data for simulation purposes. Our study provides an example of how multidimensional opinion dynamics can be investigated on the basis of empirical data that concerns a specific real-world problem. Though limited by the study design, when considered in conjunction with previous research on the topic of nuclear waste, we find that it is not necessarily whole opinions that are communicated between people; rather, people communicate various types of arguments (i.e., the differentiation of issues within an opinion). Thus, in the context of modeling and the simulation of opinion dynamics, heterogeneity with respect to the arguments and their latitudes of acceptance and rejection is of great importance. As stated above, we assume that similar studies on other topics may reveal diverse risk-benefit-process patterns and that simulation of opinion dynamics should consider this.
This insight becomes meaningful if we want to investigate the societal response to complex issues, such as contested infrastructures or other controversial topics that entail risks and benefits and in which the fairness of the process plays a role. From our experience in the domain of nuclear waste and after this combination of empirical information with a social simulation model, we conclude that a differentiation between short- and long-term social discourses should be considered.
Regardless, social interaction is relevant to such debates about contested topics. Besides the more methodological struggle related to social simulations and empirical investigations discussed above, the subject matter of an issue plays a crucial role in how we formulate our hypotheses about said issue. Short-term social discussions—such as those surrounding political elections or the migration crisis—can offer more detailed insights into social interactions. This is related to the usually high salience of those topics in the public and the media, and a relatively manageable timespan. In these cases, one could build a simulation model and initialize it with empirical data based on diary studies, which would allow for more detailed parameters and dynamics.
However, additional work is required to establish a focus on more long-term topics such as the location of nuclear waste repositories, renewable energy transitions, and climate change. In these debates, people are not confronted with the topic on a daily basis. The processes themselves typically encompass several decades prior to the development and communication of concrete decisions that might affect the population. Reliable information about, for instance, the frequency of social interaction concerning this specific topic is difficult to gather. Monitoring would make sense at least for short-term interaction patterns. However, such studies are demanding in terms of the costs and time required for long-term processes, and major process steps usually occur only once per year. Thus, the time perspective is typically not clear or manageable, which impedes the collection of fully satisfactory empirical data on personal evaluations (e.g., about the risks and benefits to study participants).
Conclusion
Based on our simulation exercise, the empirical data gathered, and the results related to both the dynamics and the context of the study, we claim that there is more need for social simulations addressing concrete topics. It is highly important to find a good balance between empirical details and modeling abstractions and to strike this balance on a content-specific level. In fact, speaking about opinion dynamics, one should first define what “opinion” means for the purposes of a given study.
The complexity and the effort of combining empirical information with cognitive theories and of relating them to concrete topics in a social simulation model is very demanding. However, we claim that the insights gained from such efforts could significantly contribute to the implementation of new policies and the building of new infrastructures.
Notes
- The terms “attitude” and “opinion” are often interchangeably used in the literature. In our understanding and for the purpose of the study, we define both as overt evaluations - made up of affective and cognitive elements - of a target or an object (for an overview, see Maio & Haddock 2010).
- The original OAS, developed to assess an individual’s judgment on one issue, comprised a set of statements (usually nine) representing different points of view on a defined issue, arranged from one extreme to the other (Sherif & Hovland 1961). The adaptation in our investigation was that the statements would be represented by the ten arguments on the issue of DGR in Switzerland. Even though we do not have a clear ranking from one extreme to the other, we can confidently assume that we covered the full range of arguments for this specific issue based on prior research (Seidl et al. 2013).
- The results displayed for the entire sample (this section) and those displayed for the subsamples (see Sections 5.23-5.30) are based on the mean data computed over 10 simulation runs.
References
AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 223–226. [doi:10.1177/0022002797041002001]
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of modern physics, 81, 591–646. [doi:10.1103/RevModPhys.81.591]
DEFFUANT, G. (2006). Comparing extremism propagation patterns in continuous opinion models. Journal of Artificial Societies and Social Simulation, 9(3), 8: https://www.jasss.org/9/3/8.html.
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87–98. [doi:10.1142/S0219525900000078]
DYKSTRA, P., Elsenbroich, C., Jager, W., Lavalette, G. R. De, & Verbrugge, R. (2013). Put Your Money Where Your Mouth Is: DIAL , A Dialogical Model for Opinion Dynamics. Journal of Artificial Societies and Social Simulation, 16(3), 4: https://www.jasss.org/16/3/4.html. [doi:10.18564/jasss.2178]
EAGLY, A. H., & Chaiken, S. (1993). The psychology of attitudes. New York: Harcourt Brace Jovanovich.
EAGLY, A. H., & Telaak, K. (1972). Width of the latitude of acceptance as a determinant of attitude change. Journal of Personality and Social Psychology, 23(3), 388–397. [doi:10.1037/h0033161]
EVANS, J. St. B. T. (2008). Dual-processing accounts of reasoning, judgment, and social cognition. The Annual Review of Psychology, 59, 255–278. [doi:10.1146/annurev.psych.59.103006.093629]
FLACHE, A., & Macy, M. W. (2006). Why more contact may increase cultural polarization. arXiv preprint physics/0604196: https://arxiv.org/abs/physics/0604196.
FLACHE, A., & Mäs, M. (2008). How to get the timing right. A computational model of the effects of the timing of contacts on team cohesion in demographically diverse teams. Computational and Mathematical Organization Theory, 14(1), 23–51. [doi:10.1007/s10588-008-9019-1]
FORGAS, J. P., & Williams, K. D. (2001). 'Social influence: Introduction and overview'. In J. P. Forgas & K. D. Williams (Eds.), Social influence: Direct and indirect process (pp. 3–24). Philadelphia: Psychology Press.
GONZÁLEZ-AVELLA, J. C., Cosenza, M. G., Klemm, K., Eguiluz, V. M., & San Miguel, M. (2007). Information Feedback and Mass Media Effects in Cultural Dynamics. Journal of Artificial Societies and Social Simulation, 10(3), 9: https://www.jasss.org/10/3/9.html.
GRIMM, V., Berger, U., Deangelis, D. L., Polhill, J. G., Giske, J., & Railsback, S. F. (2010). The ODD protocol: A review and first update. Ecological Modelling, 2760–2768. [doi:10.1016/j.ecolmodel.2010.08.019]
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html
HOVLAND, C. I., Harvey, O. J., & Sherif, M. (1957). Assimilation and contrast effects in reactions to communication and attitude change. Journal of Abnormal Psychology, 55(2), 244–252. [doi:10.1037/h0048480]
HUET, S., Deffuant, G., & Jager, W. (2008). A rejection mechanism in 2d bounded confidence provides more conformity. Advances in Complex Systems, 11(4), 529–549. [doi:10.1142/S0219525908001799]
JACKSON, J. (1960). 'Structural characteristics of norms'. In N.B. Henry (Ed). The dynamics of instructional groups: Sociopsychological aspects of teaching and learning. Yearbook of the National Society for the study of education, 59, Part II: (pp. 136-163).
JAGER, W., & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-based simulation model of attitude change. Computational and Mathematical Organization Theory, 10, 295–303. [doi:10.1007/s10588-005-6282-2]
JAGER, W. (2017). Enhancing the Realism of Simulation (EROS): On Implementing and Developing Psychological Theory in Social Simulation. Journal of Artificial Societies and Social Simulation, 20(3), 14: https://www.jasss.org/20/3/14.html. [doi:10.18564/jasss.3522]
JONAS, K., Broemer, P., & Diehl, M. (2000). Attitudinal Ambivalence. European Review of Social Psychology, 11(1), 37–41. [doi:10.1080/14792779943000125]
KRÜTLI, P., Stauffacher, M., Pedolin D., Moser, C. & Scholz, R. W. (2012). The process matters – fairness in repository siting for nuclear waste. Social Justice Research, 25(1), 79–101. [doi:10.1007/s11211-012-0147-x]
LATANÉ, B. & Nowak, A. (1997). 'Self-organizing social systems: Necessary and sufficient conditions for the emergence of clustering, consolidation, and continuing diversity'. In G. A. Barnett & F. J. Boster (Eds.), Progress in Communication Sciences, New York: Ablex Publishing Corporation.
LIU, C. C. & Srivastava, S. B. (2015). Pulling Closer and Moving Apart: Interaction, Identity, and Influence in the U.S. Senate, 1973 to 2009. American Sociological Review, 80 (1), 192–217. [doi:10.1177/0003122414564182]
MACY, M. W., Kitts, J., Flache, A., & Benard, S. (2003). ‘Polarization and dynamic networks. A Hopfield model of emergent structure’. In R. Breiger, K. Carley, and P. Pattison (Eds.), Dynamic Social Network Modeling and Analysis: Workshop Summary and Papers (pp. 162–73). Washington, DC: The National Academies Press.
MAIO, G. R., & Haddock, G. (2010). The psychology of attitudes and attitude change. London: SAGE Publications Ltd.
MARK, N. P. (1998). Beyond individual differences: Social differentiation from first principles. American Sociological Review, 63(3), 309–330. [doi:10.2307/2657552]
MARK, N. P. (2003). Culture and competition: Homophily and distancing explanations for cultural niches. American Sociological Review, 68(3), 319–345. [doi:10.2307/1519727]
MARTIN, R., & Hewstone, M. (2003). 'Social influence'. In M. Hogg & J. Cooper (Eds.), Sage handbook of social psychology (pp. 347–366). London: Sage.
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining opinion bi-polarization without assuming negative influence. PLoS ONE, 8(11), e74516. [doi:10.1371/journal.pone.0074516]
MÄS, M., Flache, A., Takács, K., & Jehn, K. (2013). In the short term we divide, in the long term we unite. Demographic crisscrossing and the effects of faultlines on subgroup polarization. Organization Science, 24(3), 716–736. [doi:10.1287/orsc.1120.0767]
MOSLER, H.-J., Schwarz, K., Ammann, F., & Gutscher, H. (2001). Computer Simulation as a Method of Further Developing a Theory: Simulating the Elaboration Likelihood Model. Personality and Social Psychology Review, 5 (3), 201–215. [doi:10.1207/S15327957PSPR0503_2]
MÜLLER, B., Bohn, F., Dreßler, G., Groeneveld, J., Klassert, C., Martin, R., Schlüter, J., Weise, H., & Schwarz N. (2013). Describing human decisions in agent-based models – ODD+D, an extension of the ODD protocol. Environmental Modelling & Software, 48, 37–48. [doi:10.1016/j.envsoft.2013.06.003]
O’KEEFE, D. J. (1990). 'Social judgment theory'. In D. J. O’Keefe (Ed.), Persuasion: Theory and research. Newbury Park, CA: SAGE Publications Ltd.
PARK, H. S., Levine, T. R., Kingsley Westerman, C. Y., Orfgen, T., & Foregger, S. (2007). The effects of argument quality and involvement type on attitude formation and attitude change: A test of dual-process and social judgment predictions. Human Communication Research, 33 (1), 81-102. [doi:10.1111/j.1468-2958.2007.00290.x]
PETTY, R. E., & Cacioppo, J. T. (1986). 'The elaboration likelihood model of persuasion'. In L. Berkowitz (Ed.), Advances in experimental social psychology (pp. 123–205). New York: Academic. [doi:10.1016/S0065-2601(08)60214-2]
POORTINGA, W. and Pidgeon, N. F. (2006). Prior Attitudes, Salient Value Similarity, and Dimensionality: Toward an Integrative Model of Trust in Risk Regulation. Journal of Applied Social Psychology, 36(7), 1674–1700 [doi:10.1111/j.0021-9029.2006.00076.x]
RAILSBACK, S. F., & Grimm, V. (2012). Agent-based and individual-based modeling. A practical introduction. Princeton, NJ: Princeton University Press.
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of meta-contrast. Journal of Artificial Societies and Social Simulation, 9(1), 13: https://www.jasss.org/9/1/13.html.
SEIDL, R., Moser, C., Stauffacher, M., & Krütli, P. (2013). Perceived risk and benefit of nuclear waste repositories: Four opinion clusters. Risk Analysis, 33(6), 1038–1048. [doi:10.1111/j.1539-6924.2012.01897.x]
SHERIF, M., & Hovland, C. I. (1961). Social judgment: Assimilation and contrast effects in communication and attitude change. New Haven, CT: Yale University Press.
SHERIF, C. W., Sherif, M., & Nebergall, R. E. (1965). Attitudes and attitude change: The social judgment-involvement approach. Philadelphia: W. B. Saunders.
SLOVIC, P. (1972). Information processing, situation specificity, and the generality of risk-taking behavior. Journal of Personality and Social Psychology, 22, 128–134. [doi:10.1037/h0032370]
SMITH, S. W., Atkin, C. K., Martell, D., Allen, R., & Hembroff, L. (2006). A social judgment theory approach to conducting formative research in a social norms campaign. Communication Theory, 16(1), 141–152. [doi:10.1111/j.1468-2885.2006.00009.x]
SMITH, E. R., & Conrey, F. R. (2007). Agent-Based Modeling: A New Approach for Theory Building in Social Psychology. Personality and Social Psychology Review, 11(1), 87–104. [doi:10.1177/1088868306294789]
SOBKOWICZ, P. (2009). Modelling opinion formation with physics tools: Call for closer link with reality. Journal of Artificial Societies and Social Simulation, 12 (1), 11: https://www.jasss.org/12/1/11.html.
SQUAZZONI, F., Jager, W., & Edmonds, B. (2014). Social simulation in the social sciences: A brief overview. Social Science Computer Review, 32(3), 279–294. [doi:10.1177/0894439313512975]
STARFIELD, A. M., Smith, K. A., & Bleloch, A. L. (1990). How to model it: Problem solving for the computer age. New York: McGraw-Hill.
STEFANELLI, A. & Seidl, R. (2017). Opinions on contested energy infrastructures: An empirically based simulation approach. Journal of Environmental Psychology, 52, 204-217. [doi:10.1016/j.jenvp.2016.06.003]
SWISS Federal Office of Energy. (2008). Sectoral plan for deep geological repositories – Conceptual part. Bern.
TAKÁCS, K., Flache, A., & Mäs, M. (2014). Is there negative social influence? Disentangling effects of dissimilarity and disliking on opinion shifts. PLoS ONE, 11(6), e0157948.
TOBIAS, R. (2009). Changing behavior by memory aids: A social psychological model of prospective memory and habit development tested with dynamic field data. Psychological Review, 116(2), 408-438. [doi:10.1037/a0015512]
URBIG, D., & Malitz, R. (2005). 'Dynamics of structured attitudes and opinions'. In K. G. Troitzsch (Ed.), Representing Social Reality. Pre-Proceedings of the Third Conference of the European Social Simulation Association, pp. 206–212. Koblenz.
VISSCHERS, V. H. M., & Wallquist, L. (2013). Nuclear power before and after Fukushima: The relations between acceptance, ambivalence and knowledge. Journal of Environmental Psychology, 36, 77–86. [doi:10.1016/j.jenvp.2013.07.007]
WEISBUCH, G., Deffuant, G., Amblard, F. and Nadal, J. P. (2002), Meet, discuss, and segregate! Complexity, 7, 55–63. [doi:10.1002/cplx.10031]
WEISBUCH, G., Deffuant, G., Amblard, F. and Nadal, J. P. (2003). ‘Interacting agents and continuous opinions dynamics’. In R. Cowan & N. Jonard (Eds.), Heterogeneous Agents, Interactions and Economic Performance, Springer Verlag, Berlin, pp. 225–242. [doi:10.1007/978-3-642-55651-7_14]
WILENSKY, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
WOOD, W. (2000). Attitude change: Persuasion and social influence. Annual Review of Psychology, 51, 539–570. [doi:10.1146/annurev.psych.51.1.539]
