Introduction
Micro-simulations such as activity based models for urban transport demand forecasting purposes or agent based models for epidemiology studies usually involve a large number of agents representing the real population living in the area being studied. It is extremely expensive, however, if not impossible (due to stringent privacy laws in certain countries), to carry out a survey that obtains a fully disaggregated data set to describe the demographics and characteristics of the agents of interest. An alternative is to construct a synthetic population that statistically matches the demographics of the real population. Examples of micro-simulation models that require a large synthetic population include those in studies by Fumanelli et al. (2012) and Huynh et al. (2015). Synthetic population generation has consequently attracted increasing attention from various research groups around the world. A number of works, for example those by Huang and Williamson (2001), Bowman (2004), Ryan et al. (2009), Muller and Axhausen (2010), Barthelemy and Cornelis (2012), and Tanton et al. (2014), provide a good review and comparisons between the current population synthesising methods.
The basic principle behind the majority of population synthesisers found in the literature is to integrate an aggregated dataset with a disaggregated dataset. The aggregated dataset is a set of joint distributions (or cross-tabulations) that describes the demographics of a relative small geographical area (the target area), the synthetic population of which must be generated. Such a dataset is normally available from the census data, such as the Summary Files in the US, the Small Area Statistics file in the UK, and the Community Profiles in Australia. The disaggregated data is normally survey data of sample households with demographic attributes of the household and those of its residents. Examples of such survey data is the Public-Use Microdata Samples in the US, the Sample of Anonymised Records in the UK, and the Confidentialised Unit Record File in Australia. The information in the survey data normally covers a much larger geographical area (the seed area) than the area for which the synthetic population is required.
Very often the joint distributions are available only between some, but not all, of the critical demographic attributes (the control variables) required for population synthesis. The well-known iterative proportional fitting (IPF) procedure (Deming and Stephan 1940; Ireland and Kullback 1968; Fienberg 1970) has been widely used to construct the missing joint distributions between control variables based on their marginal distributions. Evaluation of popular techniques for generating joint-distributions (or cross-tabulations), including IPF procedure and hill-climbing algorithms, can be found in Kurban et al. (2011). In conventional population synthesisers, the requirement for these fully joint distributions is that they must preserve not only the correlation between these control variables as observed in the subset of the disaggregated (survey) data associated with the target area, but also the correlation between the marginal distributions of the variables that are specific to that target area. Once the fully joint distributions between all the control variables are constructed, records of individuals in a household are iteratively drawn from the survey data so that joint distributions of attributes of the resulting synthetic population match as closely as possible the distributions obtained from the IPF process. The household, the residents therein, and their attributes (both at household level and individual level) are stored as part of the resulting synthetic population.
The above procedure of population synthesis was first proposed by Beckman et al. (1996). There were a few problems with this approach and these were reported in the literature (Beckman et al. 1996; Guo and Bhat 2007; Ye et al 2009). The first was the incorrect zero cell values in the resulting table of joint distributions (Lovelace et al. 2015). This happens when the demographic distribution in the sample data is not fully representative of the demographic in the target areas (as described by the marginal distributions in the aggregated data). Because of this, the value corresponding to the demographic group that exists in the aggregated data but not in the sample data would remain zero throughout the IPF process and, as a result, these will fail to converge. This problem was investigated by various studies (e.g. Beckman et al. 1996; Guo and Bhat 2007; Ye et al 2009). A comprehensive review and evaluation of different modifications to the implementation of the IPF algorithm for spatial microsimulation was reported by Lovelace et al. (2015). Another shortcoming of the conventional population synthesiser used by Beckman et al. (1996) was that the procedure can control and satisfy joint distributions of attributes at either household level or individual level, but not both. To overcome this difficulty, Guo and Bhat (2007) proposed a mechanism that draws a household from the survey data and adds it to the synthetic population only if it satisfies both a set of joint distributions of household-level attributes and a set of joint distributions of individual-level attributes. Ye et al. (2009) proposed a new iterative proportional updating procedure (IPU) in which the weight corresponding to a household type in the sample is iteratively determined and adjusted by the weights corresponding to individual types in each of the sample households. These weights are then used to determine the probability based on which households are drawn from the survey. Other notable studies that focused on resolving the problem of individual household allocation include the one by Muller and Axhausen (2011), who introduced the hierarchical IPF for multi-level control of the drawing of households from survey data, and the study by Pritchard and Miller (2012) who proposed a method that fitted household and individual zonal attributes simultaneously with a focus application on Canadian census data. PopGen (http://urbanmodel.asu.edu/popgen.html.), developed at the Arizona State University, is a formal package for population synthesis for activity-based model modelling purposes, that is also capable of controlling the matching of both household-level and individual-level attributes.
Huang and Williamson (2001) presented another method, called the combinatorial optimisation approach, for population synthesis, which is slightly different from the above procedures. In this method, the process first randomly picks a set of households from survey data, as an initial estimate of the population to be synthesised for the target area. It then assesses the effects achieved by swapping a random household from this set with one household from the survey data. If the swapping improves the goodness of fit between the attributes of the synthetic population and a set of predefined aggregated demographic attributes of the target area, the swap is made. Otherwise the swap is not made and the process restarts with another household randomly picked from the survey data. This process of assessment and swapping is repeated until a satisfactory goodness of fit is achieved. The fit between the resulting population and the constraining aggregated dataset is measured by the relative sum of squared Z scores, proposed by Huang and Williamson (2001) . Major research efforts to build a synthetic population following this approach include those carried out at the National Centre for Social and Economic Modelling (NATSEM) at the University of Canberra, Australia (Harding et al 2004; Williams 2003; Melhuish et al 2002).
One critical assumption in the aforementioned population synthesisers is the availability of a disaggregated dataset from which household records are drawn to form the resulting population in the target area. This assumption is not always accurate either because such a survey does not exist or, more often, it is inaccessible. Even when such survey data is available, the sample size needs to be large and spatially distributed enough to be fully representative of the demographic distributions of each target area. This condition is critical to the convergence of the iterative processes (IPF, IPU, HIPF) used in the majority of the above approaches. To avoid these difficulties, a sample-free approach was first introduced by Birkin and Clarke (1988) where it was applied to construct microdata of the population in the Leeds Metropolitan District (UK). The approach was then followed by Gargiulo et al. (2010) who developed an algorithm to synthesise population for the Auvergne region (France), and by Barthelemy and Toint (2013), whose algorithm was applied to the Belgium’s population. Similarly, Long and Shen (2013) developed an algorithm that disaggregated not only heterogeneous attributes of the population but also locations of the people from aggregated data, small-scale surveys, and empirical studies.
In the sample-free population synthesiser by Barthelemy and Toint (2013), the joint distributions of attributes at individual level and household level are constructed using only marginal joint distributions of these attributes. Values in the resulting joint distributions at individual level represent the number of individuals of each individual type and are used to construct a pool of individuals. Records of individuals are drawn from this pool and allocated to households so that the resulting households in the synthetic population satisfy the joint distributions at household level calculated above. The joint distributions at individual level also inform this drawing process in terms of the probability an individual type being drawn given the household type being considered and attributes of the existing (previously allocated) residents. Comparisons between sample-free and sample-based approaches on the same target area were made by Lenormand and Deffuant (2013) and by Barthélemy and Toint (2013). The latter authors claimed that the synthetic population from the sample-free approach was more accurate than that from the sample-based approach.
It is worth noting that while sample-free algorithms reported in the literature followed the same principle, i.e. relying solely on aggregated demographics data to reconstruct the microdata record of individuals, they were designed specifically to solve the problems of data quality and availability in different applications, and therefore had limited transferability.
While there have been various studies on using Australian census data to construct the population, they relied on a sample of microdata for this purpose (for example, see Tanton et al. 2014 and Namazi-Rad et al. 2015). We present in this paper a population synthesiser which constructs a computational representation of a population following the sample-free approach and which takes advantage of the wealth of demographics data available in the Australian context. The synthesiser begins by constructing a pool of individuals and a pool of households using only aggregated census data at the individual and household level, respectively. The allocation of individuals into households in this work follows a two-stage process. The first stage is essentially a heuristic allocation which follows a set of constraints which restricts the composition of individual types for the type of household being considered. The second stage iteratively assigns remaining individuals in the individual pool into households aiming at gradually and simultaneously minimising the deviation across various demographic attributes between the resulting population and the census data in the target area. This second stage resembles the combinatorial approach reviewed above. The allocation processes are further constrained by biological restrictions, including the maximal and minimal age gap between the mother and a child in a household and a distribution of age gap of a couple (either married or in a de facto relationship). This feature also existed in the population synthesiser used by Barthélemy and Toint (2013).
There are major differences in the synthesis algorithm in our work compared to other sample-free population synthesisers. The population synthesiser by Gargiulo et al. (2010) relied on a full set of household types constructed based on those of the desired demographic attributes in the final population. The synthetic population was then constructed by drawing households from this set following a predefined distribution until the final population matches satisfactorily with a set of observed demographics. While the algorithm in this approach may be simple (and thus preferred for code writing and maintenance), its application may be limited because any increase in the number of the desired attributes and/or the number of categories in each of these attributes would exponentially increase the set of possible household types. This would likely lead to much higher computational time for the algorithm to iterate through the set before arriving at a satisfactory final population. Our synthesiser, instead, is not constrained by the number of desired demographic attributes or the number of their categories. In fact, the synthetic population that we constructed has seven demographic attributes, compared to three in Gargiulo et al. (2010), with up to 17 categories per attribute.
The difference between the population synthesiser in this work and the one proposed by Barthelemy and Toint (2013) is two-fold. In terms of data availability and quality, we are fortunate that all aggregated census data required for the population synthesis is available for each target area. Therefore the application of IPF processes to reconstruct the joint distributions of population attributes from various data sources (available at various geographical levels), which was an important part of the population synthesiser used by Barthelemy and Toint (2013), was unnecessary in this study. The iterative process for allocating a synthetic individual into a synthetic household in our method is required only for a subset of the population (thanks to the preceding heuristic – and deterministic thus more computationally efficient – allocation step) whereas this process was applied to the whole population in the algorithm Barthelemy and Toint (2013) proposed.
The remaining of the paper is structured as follow. Section 2 presents the method we propose to build a synthetic population, including the input data available for this purpose. Section 3 presents results from the population synthesis for a representative census collection district (CCD) in the state of NSW, Australia in 2006, as well as the resulting synthetic population for all CCDs across the state, including the comparison against census data. The paper is concluded in Section 4 with suggestions for further development of the population synthesiser as well as its potential application particularly for the modelling of urban transport demand.
A modified sample-free approach to synthesise population
This section first introduces the aggregated data used in this study and attributes of the synthetic population to be constructed. The proposed algorithm used to model the population is presented in the subsection that follows. A Java-based open source implementation of the population synthesiser as well as the sample input data used in this research is available at https://github.com/smart-facility/SPGen.
Description of the aggregated data
The aggregated data used in this study is from the Basic Community dataset in the Community Profiles data published by the Australian Bureau of Statistics (ABS) for the year 2006. This dataset is freely available and contains information related to people, families and dwellings that characterise a given geographical area. The data is available at various geographical levels, ranging from CCD to State or Territory, e.g. New South Wales (NSW). CCD is the smallest geographical unit. The dataset was collected and processed in 2006 and was chosen in this study as a unit target area for population reconstruction so that the resulting synthetic population over the whole state of NSW best preserves the geographical heterogeneity of the real population characteristics. To give a perspective of scale, an average CCD in 2006 has around 225 dwellings. It should be noted that the information in this dataset contains information only for population living in private dwellings.
| Census data | Denotation in synthetic population |
| Husband (wife) in a registered marriage | ‘Married’ |
| Partner in de facto marriage | |
| Lone parent | ‘LoneParent’ |
| Child under 15 | ‘U15Child’ |
| Dependent student (aged 15-24 years) | ‘Student’ |
| Non-dependent child | ‘O15Child’ |
| Other related individual | ‘Relative’ |
| Unrelated individual living in family household | |
| Group household member | ‘GroupHhold’ |
| Lone person | ‘LonePerson’ |
| Visitor (from within Australia) | (not included) |
Tables from the Basic Community dataset used for the population synthesis in this work are briefly described below.
- Census table “Relationship in Household by Age by Sex”. This table provides information on the number of males and females in each relationship category in each age group. There are 9 age groups which are “0-14 years”, “15-24 years”, “25-34 years”, “35-44 years”, “45-54 years”, “55-64 years”, “65-74 years”, “75-84 years”, and “85 years and over”. A summary of relationship categories in census data and their corresponding relationship categories used in the population synthesis is in Table 1.
Relationship category ‘Visitor’ is not considered in the population synthesis because of the inconsistent inclusion of this category across the tables. The counts of males and females in categories ‘Husband (wife) in a registered marriage’ and ‘Partner in de facto marriage’ include same sex couples. Categories corresponding to children in a family household are ‘Child under 15’, ‘Dependent student (aged 15-24 years)’, and ’Non-dependent child’ and are inclusive of natural, adopted, step or foster children of a couple or a lone parent. These notations of relationship between individuals are crucial in allocating individuals into households as well as in explaining (very) few exceptional cases in the resulting synthetic population. - “Family Composition”. This table gives the number of family households by type. According to census data, there are 16 categories of family household types, as elaborated in Table 2. It should be noted that couple families in the census data include same-sex families.
- Census table “Family Composition by Sex of Person in Family”. This table gives information on the number of males and females in each family household type. The family household types in this table are identical to the household types in table “Family Composition”.
- Census table “Household Composition by Number of Persons Usually Resident”. This table provides information on the number of family households and the number of non-family households by household size (i.e. the number of people living in these households).
| Census data | Denotation in synthetic population |
| Couple family with no children | HF1 |
| Couple family with children under 15 and | |
| dependent students and non-dependent children | HF2 |
| dependent students and no non-dependent children | HF3 |
| no dependent students and non-dependent children | HF4 |
| no dependent students and no non-dependent children | HF5 |
| Couple family with no children under 15 and | |
| dependent students and non-dependent children | HF6 |
| dependent students and no non-dependent children | HF7 |
| no dependent students and non-dependent children | HF8 |
| One parent family with children under 15 and | |
| dependent students and non-dependent children | HF9 |
| dependent students and no non-dependent children | HF10 |
| no dependent students and non-dependent children | HF11 |
| no dependent students and no non-dependent children | HF12 |
| One parent family with no children under 15 and | |
| dependent students and non-dependent children | HF13 |
| dependent students and no non-dependent children | HF14 |
| no dependent students and non-dependent children | HF15 |
| Other family | HF16 |
| Non family household | NF |
The definition of household types and the definition of categories of household relationship imply a set of requirements of compositional residents for each household type. Such requirements constrain the minimum number of individuals in each category of household relationship for a given household type, as summarised in Table 3.
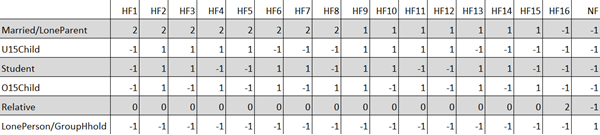
Any cell with value -1 indicates the household type in that column must not have any individuals of the household relationship categories in that row. For example, cells in row ‘Married/LoneParent’ that have value ‘2’ indicate that the corresponding household types must have two individuals of type ‘Married’ of either same or different genders. Similarly, cells on this row that have value ‘1’ indicate that the corresponding household types must have one individual of type ‘LoneParent’. A household of type, for example, HF2 therefore
- Needs exactly 2 individuals of type ‘Married’ (of either same or different genders), and
- Needs at least 1 individual of type ‘U15Child’, and
- Needs at least 1 individual of type ‘Student‘, and
- Needs at least 1 individual of type ‘O15Child’, and
- May or may not have individuals of type ‘Relative’, and
- Must not have any individuals of type ‘LonePerson’ and ‘GroupHhold’.
While the dataset is consistent across all target areas with information highly useful for the purpose of population synthesising, there are mismatches in values between tables that characterise individual attributes and those that characterise household attributes. This is because in order to preserve the confidentiality of the census data, small random adjustments had been introduced into these tables before they were published. These mismatches need to be accounted for in the algorithm synthesising the population, as described in further detail in the following section.
The proposed algorithm to synthesise the population
The modified sample-free population synthesiser presented in this paper starts with the construction of a pool of individuals and a pool of households based on the census tables presented in Section 2.1.
The pool of individuals is a collection of disaggregated records each of which details demographic information of a synthetic individual. This pool, in principle, serves the same purpose as the microdata in sample-based population synthesisers, i.e. individuals are drawn from this pool to construct the final population. The major difference is that the pool is constructed using an aggregated census table for the target area, meaning that the number of synthetic individuals in this pool is exactly the size of the final population. The census table used to construct the individual pool is “Relationship in Household by Age by Sex”. The values in this table inform the number of synthetic individuals which need to be generated for each household relationship category, for each age group, and for a given gender. The specific age of an individual is randomly generated following a uniform distribution between the bounds of his/her age group. At the end of this pool construction process, attributes that will have been assigned to each synthetic individual are household relationship, age, and gender.
The pool of households is a collection of disaggregated records, each of which represents demographic information of a synthetic household. Values in the “Family composition” table inform the number of households in each family household type (i.e. types ‘HF1’ to ‘HF16’) that needs to be constructed. The total number of non-family households (i.e. type ‘NF’) that needs to be constructed is from the table ‘Household Composition by Number of Persons Usually Resident’. At the end of the pool construction process, the attribute that will have been assigned to each synthetic household is the household type.
Once the pools are constructed, the next task assigns individuals into households. Such assignment is constrained by:
- the requirement of individual characteristics for a given household type, and
- the distribution of total number of males and females for each household type, and
- the distribution of households by household size.

An algorithm to allocate individuals into households that simultaneously satisfies the above three constraints would be not only highly sophisticated (which imposes huge burdens on the coding and debugging the algorithm) but likely computationally inefficient. We therefore propose that synthetic individuals in the individual pool be allocated into each synthetic household in the household pool following a two-stage process. The first stage aims at satisfying the requirement of compositional individuals (based on their household relationship) in each household based on its type following the assumptions in Table 3. The second stage aims at simultaneously satisfying the demographic distributions, as set out in table “Family Composition by Sex of Person in Family”, and table “Household Composition by Number of Persons Usually Resident”. The process is demonstrated by the diagram in Figure 1. The allocation algorithm in each step is described in detail in the following subsections.
Heuristic allocation of synthetic individuals into synthetic households
The allocation in this stage includes the following steps. It should be noted that the constraints on age gaps used throughout the allocation of individuals into households in this stage are only a guideline. For a given set of values in the census data of a target area, some allocations may not satisfy these constraints. This can be attributed to the quality of census data as well as exceptions that crisp numerical constraints cannot represent.
Step 1. Assigning a couple of ‘Married’ individuals into each of the households requiring them
The households requiring this step are those with types ‘HF1’ to ‘HF8’ in the household pool. Pairs of ‘Married’ individuals are selected from the pool of individuals so that their age gap follows a predefined distribution, which ideally should be informed by census data. In this study we assume that the age gap distribution of married couples follows a Gaussian distribution. This assumption can be easily replaced by a real distribution (e.g. from surveys or census) if available.
For each of the requiring households, a value of the desired age gap of the ‘Married’ individual pair to be selected for this household is randomly generated following the predefined distribution. A matrix of age gap between all available ‘Married’ individuals in the individual pool is constructed as follows:
| $$DAge_{ij} = MarriedMale_{i}.age - MarriedFemale_{j}.age$$ | (1) |
| $$DAge_{ij} = |Married_{i}.age - Married_{j}.age|$$ | (2) |
The selection of the pair of ‘Married’ individuals to be allocated into a household is further constrained by the minimum age of the female parent (or the younger parent for same sex couple). This minimum age is determined based on the types of children entitled to this household type, as elaborated below
.- Households of types ‘HF2’, ‘HF3’, ‘HF4’, ‘HF6’, ‘HF7’ and ‘HF8’ need at least one ‘Student’ individual and/or one ‘O15Child’ individual. Because the minimum age of an individual of either of these types is 15, the minimum age of the female parent (or younger parent in case of same sex couple) in these households should be older than 15 plus the age of consent. In this study, we assume the age of consent is 16.
- For households of type ‘HF5’ (which require only at least one child under 15 years old) or of type ‘HF1’ (which require no children at all), the minimum age of the female parent (or the younger parent for same sex couple) is the age of consent.
Satisfying the condition of parental minimum age in this step facilitates the more accurate allocation of child individuals (i.e. ‘U15Child’, ‘Student’, and ‘O15Child’ individuals) in later steps. The ‘Married’ pair that (i) has the corresponding age gap in the age gap matrix closest to the desired age gap and (ii) satisfies the above condition of parent minimum age is selected. In case no pair satisfies the second condition, the pair that has the female age (or the younger parent age) closest to the parent minimum age gap is selected. The selected individuals are added to the list of residents of the requiring household being considered. They are removed from the pool of synthetic individuals and will not be considered in the selection of ‘Married’ individuals for the remaining requiring households.
If there is only one ‘Married’ individual remaining in the pool, a new ‘Married’ individual is created. The gender and age group of the new ‘Married’ individual are determined to minimise the root mean square between the distribution of males and females by age group by household relationship in the resulting synthetic population and the distribution from census table “Relationship in Household by Age by Sex”.
This step stops if one of the following conditions is met.
- There are no requiring households remaining. In this case, any remaining ‘Married’ individuals in the individual pool are deleted.
- There are no remaining ‘Married’ individuals in the individual pool. In this case, any remaining households requiring this step in the household pool will be deleted.
Step 2. Assigning a ‘LoneParent’ individual into each of the households requiring it.
The households requiring this step are those with types ‘HF9’ to ‘HF15’. The allocation of a ‘LoneParent’ individual into a requiring household is also constrained by the minimum parent age, which is dependent upon the types of children entitled to this household type, as elaborated below.
- Households of types ‘HF9’, ‘HF10’, ‘HF11’, ‘HF13’, ‘HF14’, ‘HF15’, ‘HF8’ need at least one ‘Student’ individual and/or one ‘O15Child’ individual. Because the minimum age of an individual of either of these types is 15, the minimum age of the female parent (or younger parent in case of same sex couple) in these households should be older than 15 plus the age of consent. In this study, we assume the age of consent is 16.
- For households of type ‘HF12’ (which require only at least one child under 15 years old), the minimum age of the female parent (or the younger parent for same sex couple) is the age of consent.
For each of these households, a ‘LoneParent’ individual is randomly selected from the individual pool and stored to the list of residents of the requiring household being considered. This individual is removed from the pool of synthetic individuals and will not be considered in the selection of ‘LoneParent’ individuals for the remaining requiring households.
If there are no ‘LoneParent’ individuals remaining in the individual pool, a new ‘LoneParent’ individual is constructed to allocate to each of the requiring households remaining. The gender and age of new ‘LoneParent’ individuals are determined to minimise the root mean square between the distribution of males and females by age group by household relationship in the resulting synthetic population and the distribution from census table “Relationship in Household by Age by Sex”.
This step stops if all requiring households have been allocated a ‘LoneParent’ individual.
Step 3. Assigning an ‘O15Child’ individual into each of the households requiring it.
The households requiring this step are those with types ‘HF2’, ‘HF4’, ‘HF6’, ‘HF8’, ‘HF9’, ‘HF11’, ‘HF13’ and ‘HF15’. The existent residents in each of these households are either a couple of ‘Married’ individuals (allocated in Step 1) or a ‘LoneParent’ individual (allocated in Step 2).
The allocation of an ‘O15Child’ individual is constrained by the biological law represented by the minimum and maximum age gap between the child and a parent in a household. The choice of which parent to be considered for this biological constraint depends on the type of parent(s) of the household being considered, as follows:
- In households with two ‘Married’ individuals (i.e. two parents) and one of them is female, the age of the female parent is used in this constraint.
- In households with two parents having same genders, the age of the younger parent is used.
- In households that have ‘LoneParent’ individuals, the age of the ‘LoneParent’ is used.
The households in this step are sorted in descending order of the age of the parent chosen for the child-parent age gap constraint. The list of available ‘O15Child’ individuals in the individual pool is also sorted by their age. For each household in the sorted households, the allocation algorithm looks into the individual pool for the oldest ‘U15Child’ individual satisfying the upper bound and lower bound of the parent-child age gap constraint. This allocation strategy ensures that the parent-child age gap constraint is met as much as possible for the distribution of ‘O15Child’ individuals and the distributions of ‘Married’ and ‘LoneParent’ individuals across the age groups in census data for a given target area.
In cases where no ‘O15Child’ individual satisfies the upper bound and lower bound of the parent-child age gap constraint, the individual whose age is closest to either the upper bound or the lower bound is selected. A possible explanation for the allocation in these cases is that the selected ‘O15Child’ individual is not a natural child to the parent(s) in the household but is either an adopted child, foster child, or step child.
If there are no ‘O15Child’ individuals remaining in the individual pool while there remains at least one household requiring this, a new ‘O15Child’ individual is constructed for each of the remaining households. The age and gender of each of the new ‘O15Child’ individuals are decided to minimise the root mean square between the distribution of males and females by age group by household relationship in the resulting synthetic population and the distribution from census table “Relationship in Household by Age by Sex”.
This step stops when all households requiring this step are assigned with an ‘O15Child’ individual.
Step 4. Assigning a ‘Student’ individual into each of the households requiring it.
The households requiring this step are those with types ‘HF2’, ‘HF3’, ‘HF6’, ‘HF7’, ‘HF9’, ‘HF10’, ‘HF13’ and ‘HF14’. The algorithm assigning a ‘Student’ individual into each of these households resembles the algorithm that allocates ‘O15Child’ individuals into households in Step 3.
Step 5. Assigning a ‘U15Child’ individual into each of the households requiring it.
The households requiring this step are those with types ‘HF2’, ‘HF3’, ‘HF4’, ‘HF5’, ‘HF9’, ‘HF10’, ‘HF11’ and ‘HF12’. The algorithm assigning a ‘U15Child’ individual into each of these households resembles the algorithm that allocates ‘O15Child’ individuals into households in Step 3.
Step 6. Assigning a pair of ‘Relative’ individuals into each of the households requiring them.
The households requiring this step are those with type ‘HF16’. Two ‘Relative’ individuals are randomly selected from the pool of individuals and allocated to each of these households. If there are not sufficient ‘Relative’ individuals in the pool for the number of households requiring them, new ‘Relative’ individuals are constructed. The gender and age group of these new individuals will be constructed to minimise the root mean square between the distribution of males and females by age group by household relationship in the resulting synthetic population and the distribution from census table “Relationship in Household by Age by Sex”. This step stops when all ‘HF16’ households in the household pool are assigned with two ‘Relative’ individuals.
Step 7. Assigning ‘LonePerson’ and ‘GroupHhold’ individuals into each of the non-family households (type ‘NF’)
For each household of type ‘NF’ in the household pool that has one resident, a ‘LonePerson’ individual is randomly selected from the individual pool and assigned to this household. The number of such households is specified in the census table “Household Composition by Number of Persons Usually Residents”. If the number of ‘LonePerson’ individuals in the individual pool is less than the number of 1-resident ‘NF’ households, new ‘LonePerson’ individuals will be constructed under the constraint that minimises the root mean square between the distribution of males and females by age group by household relationship in the resulting synthetic population and the distribution from census table “Relationship in Household by Age by Sex”.
‘GroupHhold’ individuals are randomly drawn from the individual pool and assigned to ‘NF’ households that have more than 1 resident following the distribution of number of non-family households by household size as specified in table “Household Composition by Number of Persons Usually Residents”. If the number of ‘GroupHhold’ individuals in the individual pool is insufficient to satisfy this distribution, new ‘GroupHhold’ individuals will be constructed. Their age and gender are decided to minimise the root mean square between the distribution of males and females by age group by household relationship in the resulting synthetic population and the distribution from census table “Relationship in Household by Age by Sex”.
This step stops when all non-family households are filled with the required number of residents.
Iterative allocation of synthetic individuals into synthetic family households
After the allocation steps in Section 2.2.1, non-family synthetic households (i.e. those with type ‘NF’) in the target area should have been filled with the required number and type of residents following the distribution of non-family households by household size from census data. For this reason, these households will not be considered in the allocation algorithm in this section. On the contrary, each synthetic family household in the target area has been allocated with only the minimum required number of individuals to satisfy its household type. The individual pool at this stage should contain only individuals with relationship categories ‘U15Child’, ‘Student’, ‘O15Child’ and ‘Relative’. The objective of this allocation stage is allocating these remaining individuals into synthetic family households constrained by simultaneously satisfying the distribution of individuals by household type (from census table “Family Composition by Sex of Person in Family”) and the distribution of family households by household size (from census table “Household Composition by Number of Persons Usually Residents”). This allocation is iterative and is detailed below.
For each remaining individual in the individual pool, the allocation algorithm considers each feasible synthetic household and calculates the following root mean square (RMS) errors should the individual be allocated to that synthetic household. It should be noted that a feasible synthetic household is the one whose type does not restrict the household relationship category of the synthetic individual being considered, as defined in Table 3.
- The root mean square error between the distribution of individuals by family household type in the resulting synthetic population and in the census data, as follows:
where$$RMS_{IndCount} = \sqrt{\frac{1}{n_{HFType}} \sum^{n_{HFType}}_{i=1}(PIC_i-PIS_i)^2}$$ (3)
and$$PIS_i = \left\{\begin{aligned} & \frac{IS_i}{1+\sum^{n_{HFType}}_{j=1}IS_j}, & & i\neq k\\ & \frac{1+IS_i}{1+\sum^{n_{HFType}}_{j=1}IS_j}, & & i= k \end{aligned} \right.$$
In Equation 3, IC and IS are the array of counts of individuals by household type in census data and in the existing synthetic population (i.e. before the synthetic individual being considered is allocated to any household), respectively; n_HFType is the number of family household types (which is 16 according to Table 2); k is the index in IS corresponding to the type of feasible synthetic household being considered.$$PIS_i = \left\{\begin{aligned} & \frac{IS_i}{1+\sum^{n_{HFType}}_{j=1}IS_j}, & & i\neq k\\ & \frac{1+IS_i}{1+\sum^{n_{HFType}}_{j=1}IS_j}, & & i= k \end{aligned} \right.$$ - The root mean square error between the distribution of family households by household size in the resulting synthetic population and in census data, as follows:
where$$RMS_{HholdCount} = \sqrt{\frac{1}{n_{HFSize}} \sum^{n_{HFSize}}_{i=1}(PHC_i-PHS_i)^2}$$ (4)
and$$PHS_i = \left\{\begin{aligned} & \frac{HS_i}{1+\sum^{n_{HFSize}}_{j=1}HS_j}, & & i\neq k\\ & \frac{1+HS_i}{1+\sum^{n_{HFSize}}_{j=1}HS_j}, & & i= k \end{aligned} \right.$$
In equation (4), HC and HS are, respectively, the array of family household counts by household size in the census data and the existing synthetic population (i.e. before the synthetic individual being considered is allocated to any household); n_HFSize is the number of valid categories of household size, which are 2 people, 3 people, 4 people, 5 people, and 6 people or more; k is the index in HS corresponding to the new household size category of the feasible synthetic household being considered should the current synthetic individual be allocated to it.$$PHC_i = \frac{HC_i}{\sum^{n_{HFSize}}_{j=1}HC_j}.$$
Each pair of these RMS values represents the errors (between the resulting synthetic population and census data) associated with a possible choice of allocating the synthetic individual being considered to a feasible synthetic household. The best choice (i.e. the most suitable synthetic household this individual belongs to) is the one that results in both the smallest error in the distribution of individual counts by household type and the smallest error in the distribution of household counts by household size. In case such optimal choice is not available, i.e. not any one of the feasible choices strictly outperforms others, a set of choices that are not strictly dominated by any other are selected. These choices are represented by the Pareto front of RMS data points. The algorithm then randomly picks a choice out of this set that allocates the individual being considered into a household. The algorithm in this second allocation stage stops when all remaining individuals in the individual pool are allocated to households in the household pool. The construction of the synthetic population is completed.
The resulting synthetic population
A population synthesising process is normally (and should be) carried out at the smallest possible geographical area where the required demographic attributes (the aggregated data) are available. This ensures that the location information of the synthesised population is retained and thus the heterogeneity of the population over a large geographical area is best preserved. This is particularly required when synthetic households need to be geo-located onto the street network. A population synthesiser therefore needs to be computationally efficient to make it practically feasible to be iteratively executed over a very large number (e.g. many thousands) of small geographical areas in constructing a very large synthetic population (e.g. many millions of people). In the population synthesis presented in this paper, the iterative process allocating individuals into households (the second stage), which normally is the most computationally demanding and time consuming process, is required only for a subset of individuals in the individual pool. This is because a considerable number of individuals are already placed into households in the target area after the first allocation stage, which is based on heuristics, deterministic, and thus fairly fast. As a result, the computation time required for population synthesis in this work is improved significantly.
This section presents the results from applying the algorithm described in Section 2 to construct the synthetic population in 11,678 CCDs in New South Wales (NSW), Australia in 2006. The total population was approximately 6 million people living in over 2.3 million households that resided in private dwellings. The algorithm is executed independently for each CCD. The resulting synthetic population comes in the form of disaggregated records, each of which represents a synthetic individual characterised by six attributes including age, gender, household relationship, household type, identification of the synthetic household he/she belongs to, and the identification of the CCD the synthetic household resides in.
As the algorithm is stochastic, the generator has been run 40 times with different seed values for the pseudo-random generator. The resulting populations from these runs are analysed to assess the accuracy and robustness of the synthesis algorithm.
The total computational time to finish one run was 2 hours and 34 minutes on average (with a standard deviation of 9 minutes). It should be noted that the population synthesiser was implemented using a single threaded Java 7 and executed on a 64 bit Windows environment with Intel Xeon CPU E5-2603 v2 at 1.80GHz and 16GB of RAM. Since the generation process is not time-critical because it is typically executed only once (e.g. in agent-based models by Huynh et al. 2015 and by Barthelemy and Toint 2015), this computational time is deemed satisfactory. Nevertheless the current implementation and execution time could be improved, for example by taking advantage of parallel computing.
Goodness of fit
The Freeman-Tukey (FT) goodness of fit test is used to evaluate the satisfactory matching of demographics distributions from the resulting population to those in the census data of a CCD. Seven demographics distributions from the synthetic population were compared against those from census data. These include
- the distribution of males and females by household relationship (informed by census table “Relationship in Household by Age by Sex”)
- the distribution of family households by type (informed by census table “Family Composition”)
- the distribution of males and females by household type (informed by census table “Family Composition by Sex of Person in Family”)
- the distribution of family households and non-family households by size (informed by census table “Household Composition by Number of Persons Usually Resident”).
The Freeman-Tukey statistics is defined by
| $$FT(T, T^{\prime}) = 4\sum_i\left(\sqrt{T_i}-\sqrt{T_i^{\prime}}\right)^2$$ | (5) |
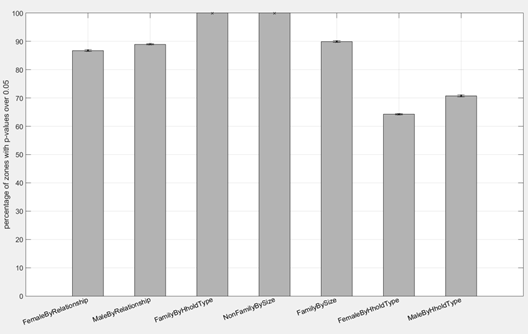
Figure 2 shows the average and associated 95% confidence intervals of the proportions of the CCDs that has a p-value greater than 0.05 for each of the seven demographic attributes examined. The statistics are computed across the 40 replications of the synthetic population of all CCDs. More specifically, according to the FT test, an average of 89.1% of the CCDs has the distribution of males by household relationship in the resulting synthetic population which satisfactorily matches with their census data. Similarly, this average proportion for the distribution of females by household relationship is 86.8%. The same interpretation applies to other demographics categories in Figure 2.
It should be noted that for every run, 100% of the CCDs have the distributions of family households and non-family households by size in the synthetic population which match with their census data. This is because the distributions in the census data are used in constructing the pool of synthetic households, as described at the beginning of Section 2.2. It should also be noted that the distributions of males and females by household relationship are used in constructing the pool of synthetic individuals (see Section 2.2). Figure 2, however, shows that not 100% of the CCDs have distributions which match with the census data. This is attributed to the fact that census data for some CCDs violates the assumptions of minimum number of individuals of each household relationship for each household type (see Table 3). Such a violation is a result of random adjustments introduced into census data before these were released to preserve the confidentiality of the data. The number of males and females in each household relationship category in the individual pool therefore needs to be adjusted for these CCDs and this leads to discrepancies of the distributions of males and females by household relationship between the resulting synthetic population and the census data. Such adjustments and their impacts are better illustrated by closely looking into the population synthesising process for a CCD selected for its relatively poor results compared to the other CCDs, namely CCD 1331103.
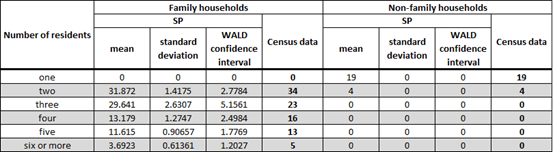
Tables 4 to 6 detail the average counts, their associated standard deviations and the length of the corresponding 95% confidence interval for the demographics attributes in the resulting 40 replications of the synthetic population for CCD 1331103. The census data for this CCD is also included for comparison purposes. As mentioned previously, the lengths of the confidence intervals are small, further indicating the stability of the method regardless of the initial seed value used by the pseudo-random number generator.

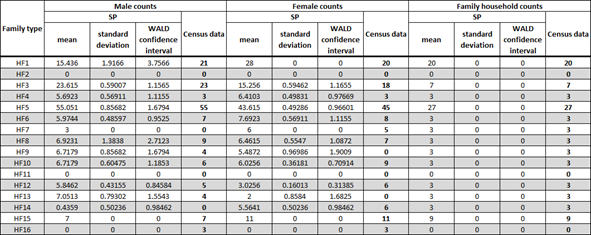
Contradictions between values across the census data of this CCD include:
- The total number of households requiring two ‘Married’ individuals is 66. The total number of ‘Married’ males and females is only 131.
- The number of non-family households requiring exactly one resident is 19. The number of ‘LonePerson’ males and females is 18.
- The total number of households requiring a ‘LoneParent’ individual is 24. The total number of ‘LoneParent’ males and females is 27.
- The total number of households requiring at least a ‘Student’ individual is 25. The number of ‘Student’ males and females is 25.
- The number of non-family households requiring at least two residents is 4. The number of ‘GroupHhold’ males and females is 0.
Adjustments were made to the number of synthetic individuals in this CCD in order to satisfy the assumptions of resident composition in Table 3. It should also be noted that these adjustments need to minimise (as much as possible) the difference between the distribution of males and females by household relationship by age group in the resulting synthetic population and in the census data. It should be noted that these adjustments were done in stage one of the synthesis process (see steps 1 to 7 in Section 2.2.1). Changes to the number of synthetic males and females in the relevant household relationships as a result of these adjustments are shown in Table 4.
The radar graph in Figure 3a shows the p-value of seven demographic distributions for the worst replication of CCD 1331103 in terms of p-values. The change of p-values of these demographics after 40 runs is shown in Figure 3b. While the resulting distribution of synthetic males by household relationship is statistically similar to the one extracted from census data (according to the FT test), the resulting distribution of synthetic females by household relationship is not (i.e. its p-value is lower than 0.05). This unsatisfactory result is attributed to the level of contradictions in the original census data (and thus the level of adjustment required) rather than the adjustment procedure itself. The impacts of these adjustments also contribute to the unsatisfactory match between the distribution of females by household type in the synthetic population and in the census data (p-value: 3.32e-4), particularly in regards to the acceptable performance of the iterative allocation algorithm, as described in the next subsection.
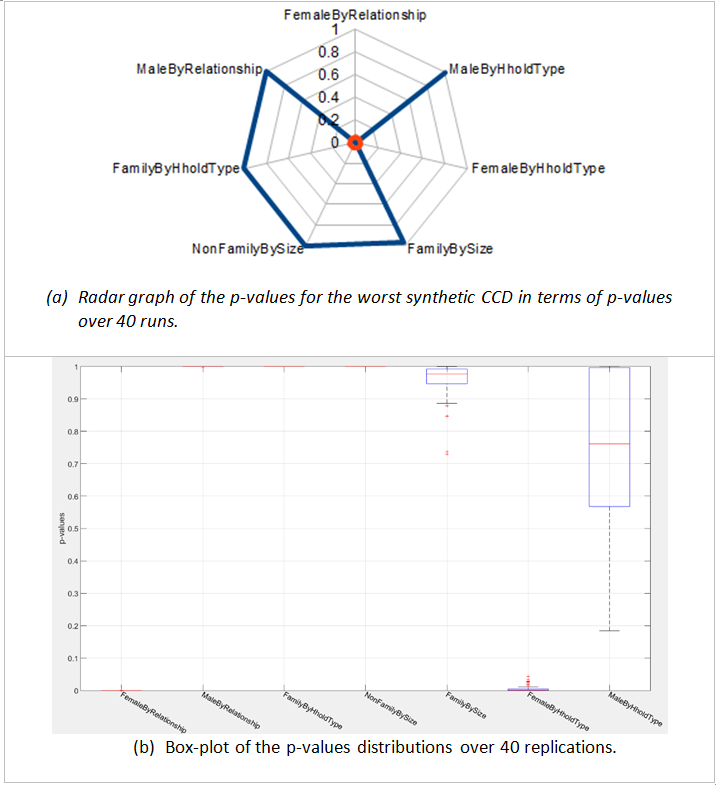
Impact of the iterative allocation algorithm
The adjustments to the number of synthetic males and females were done in stage one of the two-stage process allocating individuals into households (see steps 1 to 7 in Section 2.2.1). Stage two of the process (Section 2.2.2) iteratively allocates individuals remaining from stage 1 into households aiming at simultaneously maintaining the distribution of males and females by household type and the distribution of family household by size as closely as possible to the distributions in census data.
The box plots in Figure 4 represent the distribution of the RMS value at each iteration across the 40 runs for the CCD 1331103. It illustrates that the iterative allocation algorithm effectively improves the (already small) RMS errors described in Equations 3 and 4 throughout the iterations of the allocation process. This improvement in RMS error as shown in Figure 4a is 32%, from 0.019 to approximately 0.013. It should be noted that the number of iterations is the number of individuals at the beginning of stage 2, which need to be allocated to synthetic households. The box plots also show that the process presents little variability across the 40 runs, as indicated by the small length of the boxes (i.e., the difference between the third quartile and the first quartile).
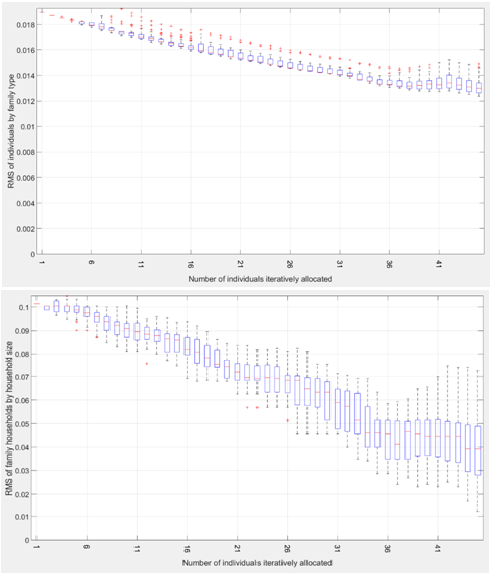
There are certain iteration steps where the RMS errors are higher than that in previous steps. This is because the allocation algorithm in stage 2 considers only the possible solutions of allocating a synthetic individual into a synthetic household within the current step and is not aware of the outcome of the previous allocation step. Simple changes can be made to the algorithm such as adding the data point of RMS errors from previous allocation step(s) into the collection of possible solutions of the current step, to help enable the algorithm to take into consideration the performance of previous steps and this may improve the allocation results.
Absolute percentage deviation across the study area
The population synthesis for CCD 1331103 and its results have detailed typical issues in census data and their impacts on the resulting synthetic population that are applicable to many of the CCDs. The demographics of the total synthetic population over the whole study area, nevertheless, agree quite well with those from the census data.
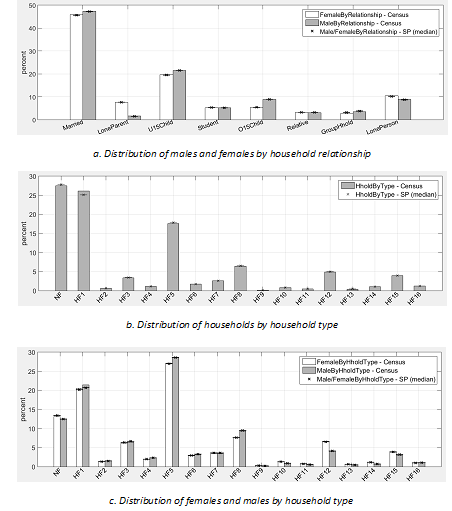
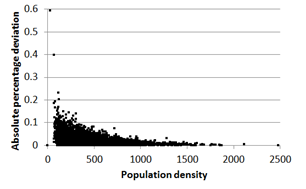
For instance, bar plots in Figure 5 provide visual comparisons of the median of the demographic attributes computed for the 40 replications of the synthetic population and in the census data for the whole study area. The whiskers correspond to the 95% confidence interval of the median of the synthetic data. A heat map of population density for each CCD in the census data and a heat map of the absolute percentage deviation (APD) in the resulting synthetic population are given in Figure 6.
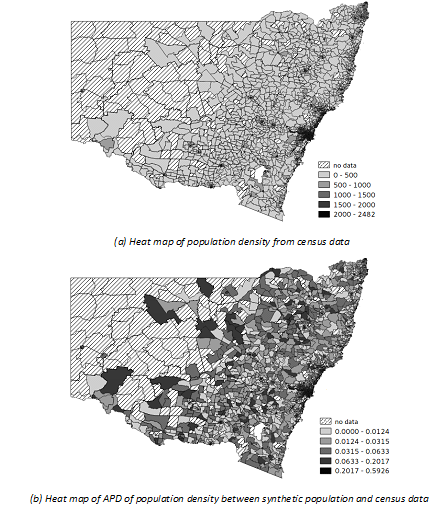
It should be noted that while the APD in some CCDs is as high as 60% (0.5926), these are the CCDs that have relatively small population, as can be seen in Figure 7 which illustrates the distribution of APD by population size. The values in census data for these CCDs are relatively small and thus suffer more from processing errors or any randomisation made to the data. As a result, the adjustments/corrections required during the population synthesising for these CCDs are likely to be substantial, leading to relatively large deviations between the resulting synthetic population and the census data.
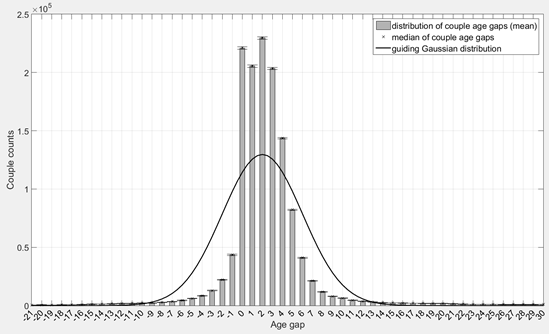
Couple age gap distribution
As described in Section 2.2.1. the selection of two ‘Married’ individuals to form a couple for a synthetic household that needs two parents is constrained by a distribution of age gap of couples in the population. Because such guiding distribution is not available in the census data, we assume in this study that the age gap of couples follow a Gaussian distribution with a mean of 2 years and a standard deviation of 2 years. This hypothetical guiding distribution can be easily replaced by a real distribution once the data becomes available.
Figure 8 shows the average distribution (computed across the 40 replications) of couple counts by their age gap in the resulting synthetic population in comparison with the curve from the hypothetical guiding Gaussian distribution.
While the distribution of couple age gaps in the synthetic population resembles a Gaussian distribution, discrepancies compared to the Gaussian distribution are expected because of a number of factors. First, the guiding Gaussian distribution is used only as a guideline for coupling ‘Married’ individuals during population synthesis and is highly unlikely to be representative of the age gap distribution of couples in the real population. Second, the age of a synthetic individual is randomly generated following a uniform distribution bounded by his/her age group in the census data. Therefore the larger the size of age groups in census data, the less accurate the age of a synthetic individual can be. Such inaccuracy of the age of synthetic individuals contributes to errors in reproducing the true age gap distribution of synthetic couples. Ideally, the age group size should be 1, thus we can accurately assign an age to the synthetic males and females. The size of age groups in the census data available to this study is 10 years, which is relatively large and could be a significant source of errors. In addition, Figure 8 also illustrates the median of the generated distribution and their 95% confidence interval, showing once more the similarities between the different runs.
It is important to note that all confidence intervals shown in Figures 2, 3, 4, 5, 8 and Tables 4, 5, 6 are very small and this indicates that the population synthesising algorithm produces similar results regardless of the seed values. This is a good indication not only of its robustness and but also of its computational efficiency because such insensitivity to randomness infers that the algorithm does not need to be executed multiple times to find a population replication closest to the observed data (i.e. the census) as suggested by Lenormand and Deffuant (2013) to the population synthesiser proposed by Gargiulo et al. (2010).
Conclusions
This paper has presented a hybrid method that utilises heuristics and combinatorial optimisation to synthesise a population for agent based modelling purposes. The method follows the sample-free approach of population synthesis pioneered by Gargiulo et al. (2010) and by Barthélemy and Toint (2013) which do not rely on a set of disaggregated survey data from which household records are drawn to form the resulting synthetic population in the target area.
Unlike the methods proposed by Gargiulo et al. (2010) and by Barthélemy and Toint (2013), however, the population synthesiser in this study comprises two stages. The first stage heuristically allocates synthetic individuals into synthetic households following a set of constraints that restricts the composition of individual types for the type of the household being considered. The second stage iteratively assigns the remaining synthetic individuals into synthetic households aiming at gradually and simultaneously minimising the deviation across various demographic attributes between the resulting population and the census data in the target area. Because of this combined approach, the new population synthesiser is computationally efficient and this means that it can be used to build a large synthetic population (many millions) for many thousands of target areas at the smallest possible geographical level. This capability ensures that the geographical heterogeneity of the resulting synthetic population is best preserved.
The method was applied to construct the synthetic population for 11,678 CCDs in New South Wales (Australia) in 2006. The resulting synthetic population matches very well with the census data across seven demographics attributes that characterise the population at both household level and individual level. Discrepancies between the synthetic population and the census data are primarily due to random adjustments made to the census tables before they were released (to preserve the confidentiality of the data). This led to contradictions between values across the census tables for certain CCDs and thus extensive corrections to these values during the population synthesis. The contradictions in census data, the required corrections, and their impacts on the resulting synthetic population were demonstrated by carefully examining the population synthesis of a sample CCD.
The robustness of the method was also tested by producing several replications of the synthetic population for the same study area using different seed values for the pseudo-random number generator. The results highlighted a small variation between the replications. This observation in conjunction with satisfactory comparisons of the synthetic population against census data indicate that a single run would be sufficient to produce a synthetic population with statistically satisfactory accuracy, hence obviating the need to run the algorithm multiple times to select the best replication as proposed in Lenormand and Deffuant (2013).
The resulting synthetic population comes in the form of disaggregated records, each of which represents a synthetic individual characterised by six attributes including: age, gender, household relationship, household type, identification of the synthetic household he/she belongs to, and the identification of the CCD the synthetic household resides in. Such a synthetic population is highly suitable for agent based models for simulating social behaviours, especially those encapsulating collective decision making at household level, e.g. demographics evolution, transport demands, and residential mobility, among many others. This is because the population accurately replicates the link between synthetic individuals and synthetic households via a number of attributes especially the relationship of the individuals. The application of this population for an agent based model for urban planning for a metropolitan area in South East Sydney, New South Wales (Australia) has been reported by Huynh et al. (2015). More specifically, the agent based model simulated the change of demographics in the urban area of interest, how this change impacts housing and transport needs of the population and the way they make collective decisions regarding residential relocation and mode choice.
Acknowledgements
The authors wish to gratefully acknowledge the help of Dr. Madeleine Strong Cincotta in the final language editing of this paperReferences
BARTHELEMY, J., and Cornelis E. (2012) Synthetic population: review of the different approaches. LISER Working Paper Series, 2012 (18).
BARTHELEMY, J., and Toint P.L. (2013) Synthetic population generation without a sample. Transportation Science, 47 (2) 266-279.
BARTHELEMY, J., and Toint P.L. (2015) A Stochastic and Flexible Activity Based Model for Large Population. Application to Belgium. Journal of Artificial Societies and Social Simulation, 18 (3) 15: https://www.jasss.org/18/3/15.html.
BECKMAN, R. J., Baggerly, K. A., and McKay, M. D. (1996) Creating synthetic baseline populations. Transportation Research Part A: Policy and Practice, 30 (6) 415–429.
BIRKIN, M., and Clarke, M. (1988) SYNTHESIS – A synthetic spatial information system for urban and regional analysis: methods and examples. Environment and Planning A, 20 (12) 1645–1671.
BOWMAN, J.L. (2004) A comparison of population synthesizers used in microsimulation models of activity and travel demand, http://jbowman.net/papers/2004.Bowman.Comparison_of_PopSyns.pdf, accessed on 03/06/2016.
DEMING, W.E. and Stephan, F.F. (1940) On a On a Least Squares Adjustment of a Sampled Frequency Table When the Expected Marginal Totals are Known. The Annuals of Mathematical Statistics, 11 (4) 427-444.
FIENBERG, S.E. (1970) An Iterative Procedure for Estimation in Contingency Tables. The Annuals of Mathematical Statistics, 41 (3) 907–917.
FUMANELLI, L., Ajelli, M., Manfredi, P., Vespignani, A., and Merler, S. (2012) Inferring the structure of social contacts from demographic data in the analysis of infectious diseases spread. PLoS Computational Biology, 8 (9): e1002673.
GARGIULO F., Ternes S., Huet S., and Deffuant G. (2010) An Iterative Approach for Generating Statistically Realistic Populations of Households. PLoS ONE, 5 (1) e8828.
GUO, J.Y. and Bhat C.R. (2007) Population synthesis for microsimulating travel behaviour. Transportation Research Record, 2014 (12) 92–101.
HARDING, A., Lloyd, R., Bill, A., and King, A. (2004) ‘Assessing poverty and inequality at a detailed regional level – New advances in spatial microsimulation’, in McGillivray, M and Clarke, M. (eds), Understanding Human Well-Being, ISBN: 9280811304.
HUANG, Z., and Williamson, P. (2001) A comparison of synthetic reconstruction and combinatorial optimisation approaches to the creation of small-area microdata, http://pcwww.liv.ac.uk/~william/microdata/workingpapers/hw_wp_2001_2.pdf, accessed on 03/06/2016.
HUYNH, N., Perez, P., Berryman, M., and Barthélemy J. (2015) Simulating Transport and Land Use Interdependencies for Strategic Urban Planning—An Agent Based Modelling Approach. Systems, 3 (4) 177-210.
IRELAND, C. T. and Kullback S. (1968) Contingency tables with given marginals. Biometrika, 55 179–188.
KURBAN, H., Gallagher, R., Kurban, G. A., and Persky, J. (2011) A Beginner’s Guide To Creating Small-Area Cross-Tabulations. Cityscape: A Journal of Policy Development and Research, 13 (3) 225–235.
LENORMAND, M., and Deffuant, G. (2013) Generating a Synthetic Population of Individuals in Households: Sample-Free vs Sample-Based Methods. Journal of Artificial Societies and Social Simulation, 16 (4) 12: https://www.jasss.org/16/4/12.html.
LONG, Y., and Shen, Z. (2013) Disaggregating heterogeneous agent attributes and location. Computers, Environment and Urban Systems, 42 14-25.
LOVELACE, R., Birkin, M., Ballas, D., and van Leeuwen, E. (2015) Evaluating the performance of Iterative Proportional Fitting for spatial microsimulation: new tests for an established technique. Journal of Artificial Societies and Social Simulation, 18 (2) 21: https://www.jasss.org/18/2/21.html.
MELHUISH, T., Blake, M., and Day, S. (2002) An evaluation of synthetic households populations for census collection districts created using spatial microsimulation techniques. Australasian Journal of Regional Studies, 8 (3) 269:387.
NAMAZI-RAD, M., Mokhtarian, P., and Perez, P. (2014) Generating a dynamic synthetic population – Using and age-structured two-sex model for household dynamics. PLoS ONE, 9 (7): e94761.
MULLER, K., and Axhausen, K.W. (2010) Population synthesis for microsimulation: State of the art, 10th Swiss Transport Research Conference, Ascona, 2010.
MULLER, K., and Axhausen, K.W. (2011) Hierarchical IPF: Generating a synthetic population for Switzerland, 51st Congress of the European Regional Science Association, Barcelona, 2011.
PRITCHARD, D. R., and Miller, E. J. (2012) Advances in population synthesis: fitting many attributes per agent and fitting to household and person margins simultaneously. Transportation 39 (3): 685–704.
RYAN, J., Maoh, H., and Kanaroglou, P. (2009) Population synthesis: Comparing the major techniques using a small, complete population of firms. Geographical Analysis, 41 (2) 181-203.
TANTON R., Williamson P., and Harding A. (2014) Comparing Two Methods of Reweighting a Survey File to Small Area Data. International Journal of Microsimulation, 7 (1) 76-79.
VOAS, D., and Williamson, P. (2000) An evaluation of the combinatorial optimisation approach to the creation of synthetic micro-data. International Journal of Population Geography, 6 (5) 349–366.
WILLIAMS, P. (2003) Using microsimulation to create synthetic small-area estimates from Australia’s 2001 census, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.95.7310&rep=rep1&type=pdf, accessed on 03/06/2016.
YE, X., Konduri, K., Pendyala, R.M., Sana, B., and Waddell, P. (2009) A methodology to match distributions of both household and person attributes in the generation of synthetic populations, The 88th Annual Meeting of the Transportation Research Board, Washington DC, 2009.
