Introduction
The human development sequence (HDS) theory, proposed by Ronald Inglehart and Christian Welzel (Inglehart & Welzel 2005) is one of the most prominent modernisation theories (Wucherpfennig & Deutsch 2009), stating that economic development, changes in emancipative cultural values and democratisation are intimately linked. These three processes are hypothesised to follow a common causal direction, with economic resources providing the means for emancipation, which in turn provides motivation for more democratic institutions. Over time countries undergo a transition as their citizens’ values change from reflecting the need to survive to the need to live a self-determined life. Ultimately, the way a country is governed changes to reflect these emancipative values (Inglehart & Welzel 2005; Welzel 2013).
The HDS theory has not remained unchallenged (Duch & Taylor 1993; Hadenius & Teorell 2005; Teorell & Hadenius 2006; Teorell 2010). Recent empirical analysis show that the assumed sequence of economic development, emancipation and democratisation is not entirely supported by the data. Spaiser et al. (2014) show that cross-country time-series data suggests that the implementation of human rights and democratisation in fact precedes the emancipation of the wider population. In line with the HDS theory, data analyses confirm that prior to democratisation and emancipation countries need to progress economically. However, data seems to suggest that the emancipation of wider segments of the population requires not only existential security in terms of basic economic well-being but includes also security granted by human rights (ibid.). In this paper we use an agent-based approach in combination with data analysis to further investigate the HDS theory. We contrast the theory against alternative democratisation theories and suggest several revisions of the HDS theory that would make the theory consistent with the data and with some alternative democratisation theories.
The micro-macro link
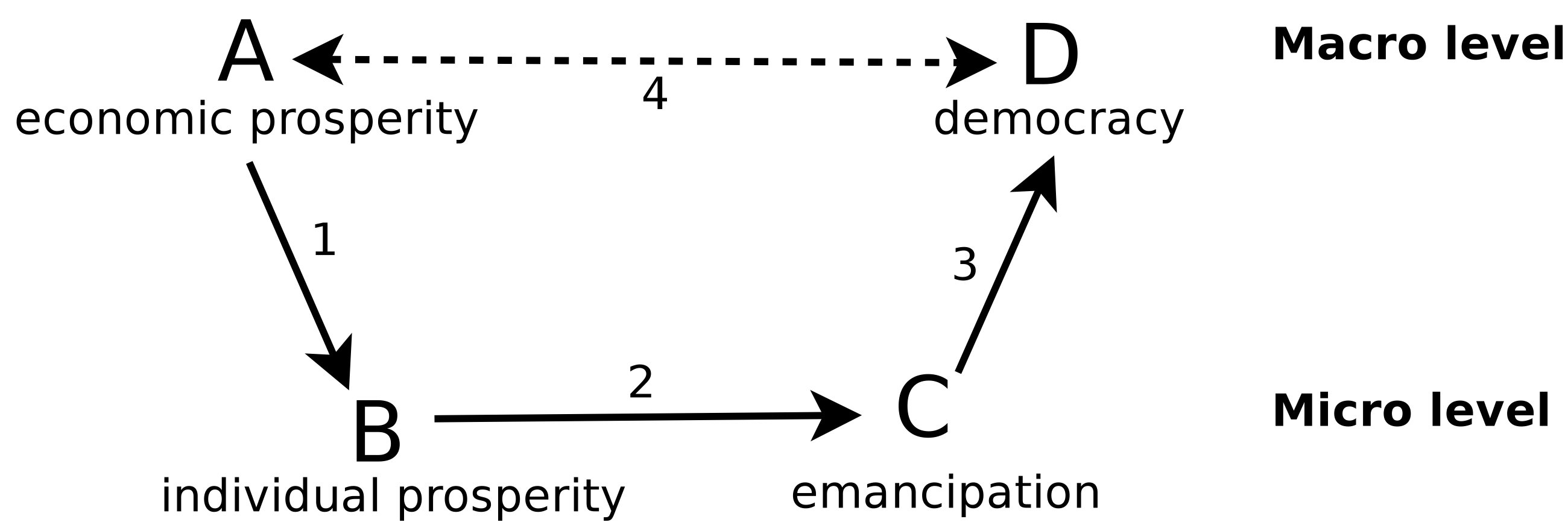
The starting point for our study is that the causes of macro phenomena, like democratisation, can be best understood through underlying mechanisms on the micro-level (Hedström & Swedberg 1998; Hedström 2006; Coleman 1986). Coleman’s (1986) boat diagram provides a useful suggestion of how to link between macro-level variables through a micro-level mechanism to study causality (Figure 1). The diagram replaces a black box correlation with a model of how individuals’ social interactions result in social macro phenomena. There are different assumptions one can make about the individuals: describing them, for example, as rational agents (Olson 1965; Elster 1986; Hedström 1996) or in terms of behavioural heuristics (Durlauf & Blume 2010; Al-Suwailem 2012; Etzioni 2012). However, the key point is that Coleman’s model takes one set of macro-level variables as input and predicts their effect on another set of macro-level variables, while explicitly describing the micro-level mechanisms at work. In terms of Coleman’s boat diagram, the HDS theory (Inglehart & Welzel 2005) assumes that (A) economic prosperity leads to (B) improved economic conditions of individuals who become (C) emancipated and together demand and establish (D) democratic institutions.
While Coleman’s boat provides a conceptual guide to the micro-macro link, it does not in itself provide a set of tools for empirically testing theories. It is here that agent-based modelling is a powerful tool (Raub et al. 2011; Mueller-Benedict 2006; Opp 2011; Macy & Willer 2002). At the micro-level, individual agents are characterised by a set of attributes and a set of interaction rules that specify how agents behave or change in terms of their attributes (Gilbert & Troitzsch 1999; Macal & North 2010). A computer simulation runs a large number of rounds updating the state of each agent in each round according to the rules. This results in some macro-level patterns, for instance a particular distribution of attributes amongst the agents.
Agent-based approach to “Theory Stressing”
Agent-based models come in a variety of forms, ranging from caricatures of reality up to fully quantitative models that match cross-sectional and longitudinal analysis data. Axtell & Epstein (1994) categorise these forms as from level 0 up to level 3, with more quantitative models assigned a higher level. Epstein (2006) further emphasises that there are a range of potential uses of agent-based models: from using them to elucidate concepts, to investigating emergence, to “stressing”, i.e. testing the robustness of standard theories. Our approach lies in this last application: we aim to stress test the underlying assumptions of the HDS theory and then support or reject the HDS theory mainly at, what Axtell and Epstein call, level 1: to identify the degree to which an agent-based model qualitatively agrees with empirical macro-structures in terms of distributions of properties of the agent population ( Axtell & Epstein 1994). We perform some analyses also at level 2, seeking to reach quantitative agreement between the agent-based models and empirical macro-structures.
In order to facilitate empirical comparison we maintain a relatively simple structure in our agent-based model. Specifically, in section Formalising Human Development Sequence theory we develop a well-mixed, site-based model where at each discrete time step, discrete resource units are distributed uniformly at random across different types of individuals (Johansson & Sumpter 2003). The individuals then become emancipated or stay unemancipated, depending on their resource status, and they interact, building or preventing democracy. These processes can then be approximated by a set of coupled difference equations (Johansson & Sumpter 2003; Czárán 1998; Parunak et al. 1998). This dual use of an agent description and approximating equations, some-times referred to as the equation-based model approach (Parunak et al. 1998), places less emphasis on finding emergent phenomena and more emphasis on mathematical tractability and empirical prediction. In section Formalising Human Development Sequence theory we use this approach to derive dynamic equations for emancipation and democracy. This is a common approach in complexity modelling, where the micro-macro link can be established through mean-field approximation (Sugihara et al. 2012; Sawyer 2003; Scholl 2001). Maintaining this relative simple structure in the simulation model, combined with the macro data analyses, allows us, in section Model simulations and data evidence, to perform robust comparison between model predictions and data. We do not calibrate our model with country-specific empirical data, since the goal is to develop a general agent-based model for a revised HDS theory, approximated by difference equations. We show however that our models can be calibrated with empirical data to make for instance (country-)specific predictions (see Appendix A2).
In subsection HDS theory at the macro level: resources and democracy we show that the relationship between economic growth and democracy is consistent with HDS theory. However, in subsection HDS theory at the micro level: emancipation we discuss that the micro-level assumptions of the HDS theory with respect to emancipation is not supported by the available data. We then examine alternative democratisation theories that do match existing data. In subsection Revising the HDS theory: power relations and the role of the elite, we show that democratisation depends on the power relations between the emancipated fraction of the population, that seek democratic change and the unemancipated fraction of the population that seeks to suppress democratisation. If there is a small but powerful emancipated elite in a country, we may expect democratisation to precede emancipation of the wider population. This relation is supported by the available data. We go on, in subsection Revising the HDS theory: economic inequality, to demonstrate that the HDS theory needs to acknowledge the role of inequality in the emancipation of a population and thus in democratisation dynamics. Highly unequal societies are likely to fail to develop into full democracies, since the majority of its population will not attain a sufficiently high level of socio-economic well-being that would allow for emancipation, while its rich elites would become satisfied with the status quo.
Critique of the Human Development Sequence Theory
The HDS theory is a highly influential modernisation theory that assumes that people’s cultural values and beliefs change across the world as nations worldwide become more affluent. With economic development that frees people from extreme poverty and existential struggle, people become less focused on security and conservative, collectivist traditions. They develop more individualistic and liberal views (Inglehart & Welzel 2005). The theory assumes a universal human desire for self-determination. Emancipation is the process of exemption from external constraints and emancipative values thus prioritise freedom of choice and equality of opportunities. However, emancipative values cannot fully unfold and guide people’s actions as long as they are hampered by existential constraints. Only, with improving living conditions emancipative values can gain utility and spread in a society that has reached a sufficiently high economic development level (Welzel 2013).
These fundamental changes in people’s values lead to political changes as the increasingly emancipated people demand to have a say in political decision making (Inglehart & Welzel 2005). Emancipative values are the psychological basis and the major inspiration for democratisation movements and according to Welzel (2013), rulers cannot withstand the mass political action of capable and highly motivated people. Drawing on World Value Survey data, Inglehart and Welzel (Inglehart & Welzel 2005; Welzel & Inglehart 2006) demonstrated the sequence pattern empirically, controlling for prior measures of democracy and thereby arguing that cultural change towards more self-expressive values is a cause and not a consequence of democracy. And Abdollahian et al. (2014) presented recently an agent-based model that supports the HDS theory. The HDS theory and its empirical evidence has however also been repeatedly challenged (Hadenius & Teorell 2005; Teorell & Hadenius 2006; Teorell 2010; Spaiser et al. 2014). Spaiser et al. (2014) have for instance argued that lawlessness and rights violations do constitute existential constraints as well as material living conditions and therefore some level of human-rights democratic rule must be implemented before emancipative values can truly thrive within the majority of a population.
It has been argued that elites are decisive for democratisation to happen and for democracies to stabilise (O’Donnell et al. 1986; Casper & Taylor 1996; Higley & Burton 2006). Democratisation is most likely when there is a regime opposition, often consisting of a highly educated middle class and a fraction of regime elites that build a liberal camp and that split from the status quo regime elite. This liberal camp joins forces with the regime opposition and conjointly they may bring about democratic change (O’Donnell et al. 1986; Casper & Taylor 1996; Higley & Burton 2006). Under this scenario the proportion of emancipated individuals to induce a democratic transition is rather low and democratisation could precede emancipation of the general population.
Inequality may also play a role in democratisation, because extreme inequality may prevent the majority from getting hold of sufficient resources that would allow their emancipation. The relation between democratisation and inequality has been studied for some time with different conclusions (Bollen & Jackman 1995; Muller 1995; Barro 1999; Houle 2009). Acemoglu & Robinson (2006) for instance state that the relation between democratisation and inequality should be an inverted U-shape. Transitions towards democracy are most likely at moderate levels of inequality, while very low and very high inequality make democratic changes unlikely. Boix (2003) on the other hand predicts a straightforward negative relation between inequality and democratisation, holding a country’s level of wealth constant. Contrary to this, Ansell & Samuels (2010) predict that democratisation is most likely “when newly wealthy economic groups accumulate an increasing share of national income, leaving the poor far behind”, as they will be interested in setting up (democratic) rules that protect them “against expropriation of their income and assets by the autocratic governing elite” (Ansell & Samuels 2010, pp. 1544-1545).
The HDS theory but also theories on elite-driven democratisation and on inequality and democratisation focus on a set of endogenous or internal factors (socio-economic, cultural) that contribute to a country’s democratisation. Others have been suggesting rather exogenous factors to explain in particular the diffusion of democratisation, thus the empirically observed geographic and temporal clustering of democracies (Gleditsch & Ward 2006; Doorenspleet 2001). Elkink (2011) for instance has used an agent-based simulation to show that individual attitudes towards democracy can explain democratic diffusion. He argues that not solely socio-economic development results in attitudinal changes that precede democratisation, but public opinion dynamics in neighbouring areas are decisive to understand the changes in cultural values and attitudes in a country prior to democratisation. In fact, Wejnert (2005) suggests that when comparing the different sets of factors, endogenous and exogenous, diffusion factors outperform the endogenous factors in predicting democratisation. The external factors that predict democratisation best are spatial factors such as proximity to neighbouring democratic countries and the density of neighbouring democratic countries, network factors, thus the embededdness of countries in certain international networks that may support or suppress democratisation and media communication that can provide information about democracy (ibid.).
It is certainly the interplay of endogenous and exogenous factors, which can be very context specific, that ex-plains and predicts best why certain countries become democratic and others not. Given the point of departure for our analyses is the HDS theory, which builds on endogenous predictors, we will focus here on endogenous explanatory factors, which can be also more easily integrated in a revised HDS theory that we propose here as a result of our analyses. An integration with the diffusion theories of democratisation goes beyond the scope of this paper but could be an interesting future step. Ultimately, democratisation processes are a (re-)negotiation of power relations within more or less favourable contexts. In the course of this (re-)negotiation institutional innovations are made, often taking neighbouring countries as models. And the process requires time to create stable, enduring democratic structures (Lindenfors et al. 2011; Jansson et al. 2013).
Formalising Human Development Sequence theory
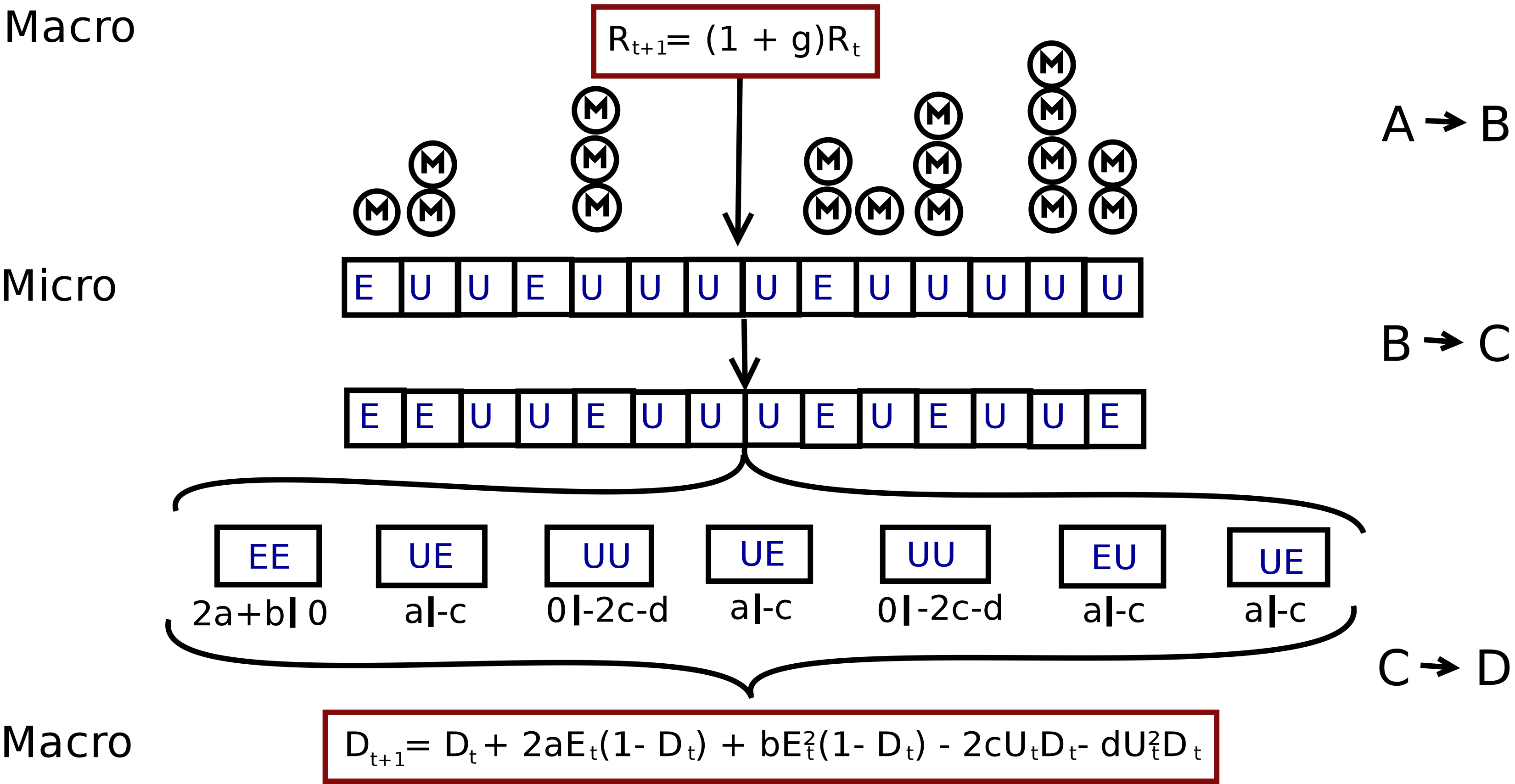
We now elaborate on the HDS theory and formulate an agent-based model. The economy is a macro-level input, which influences whether agents have the means to become emancipated, and then through micro-level interactions the agents produce macro-level democracy. The stages of our model are illustrated in Figure 2. We now explain each of the steps of the model in turn.
Economic growth
We consider an economic situation in which there are limited existential resources. Resources are increasingly available on the micro level if a society’s economy is developing and prospering, so that the expected number of available resources is a function of economy’s development. We assume that existential resources are growing at each time step t — which we assume to represent a year — at a positive constant rate, such that
| $$R_{t+1} = (1+g) R_t$$ | (1) |
In a growing economy the growth constant g is positive and the economy grows exponentially. This assumption is standard to economic development models (Basu 2003) and consistent with observations across countries (Durlauf et al. 2005). Over the last 50 years, most of the world’s nations have experienced a sustained period of economic growth, measured either in GDP (Gross Domestic Product), GNI (Gross National Income) or HDI (Human Development Index) (WorldBank 2009; UNDP 2011).
In terms of Coleman’s boat diagram, the distribution of resources is the step from A to B (see Figure 2). At each time step t we distribute Rt action resource units uniformly at random amongst the whole population N. The assumption that economic resources are distributed uniformly at random between all N individuals is not based on empirical observation. Within societies, resources are typically skewed towards certain individuals. We return to this assumption in subsection Revising the HDS theory: economic inequality. For now, we note that by excluding social inequality from the model at this point, we isolate the effect of emancipation prescribed by HDS theory on the transition to democracy. For large N the number of resources each individual received can be assumed Poisson distributed. Thus, the expression
| $$\frac{\exp \left(-\frac{R_t}{N}\right) \left(\frac{R_t}{N} \right)^k}{k!}$$ | (2) |
The process of emancipation
Based on individuals’ resource status, and thus the resource distribution at any given time step t, we can derive the distribution of emancipated Et and unemancipated Ut = N - Et individuals within the whole population N. Individuals can be assigned to one of two states, emancipated (E) or unemancipated (U), based on their resource level. The step from B to C, is then made via the following rules for emancipation and unemancipation (see Figure 2):
- If an unemancipated individual receives two or three resource units then he/she will become emanci-pated. Otherwise, he/she will remain unemancipated.
- Emancipated individuals remain emancipated, unless they receive no resource units within a time step. In this case, they become unemancipated again.
- If an unemancipated individual receives four or more resources then he/she remains unemancipated.
The first rule reflects individuals’ existential wellbeing. Following the HDS theory, when people have relatively few resources (zero or one), their preferences are focused on materialistic goals, like making a living, ensuring some form of existential security. They also tend to cling to extended family or clan structures. Community is of great value to these people since the community provides support and protection. This focus on existential security that goes along with traditional cultural values makes the unemancipated more receptive to autocratic regimes and collectivist social systems, which claim to guarantee stability, security and order (Inglehart & Welzel 2005; Welzel 2013). The first rule also reflects the prediction that once a certain relative level of resources (two or three in our model) is acquired and existential needs are satisfied then people draw their attention to other objectives in life, such as self-realisation and participation (Inglehart & Welzel 2005; Welzel 2013). A transition back to disempowerment (second rule) is possible, but only in the extreme situation where no resources are available. Once emancipated, some degree of hardship is tolerated but a complete removal of resources leads to a change in perspectives, because people again need to struggle for their and their families’ survival. The third rule is not part of the original HDS theory. It is included for consistency with both theoretical and empirical observations. Empirical evidence suggests that a superfluous amount of resources on the macro-level may lead to an exceeding availability of resources on the micro-level (through spending programs and low taxation for instance), and people are less likely to develop political aspirations (Ross 2001; Vanderwalle 1998; Kessler 1999 ; Bellin 1994). Theoretically this observation is explained by the “spending effect" where governments (for instance Qatar or Saudi Arabia) use their resource revenues for generous patronage and welfare, to lower pressures for democratisation (Ross 2001; Brand 1992; Crystal 1990; Entelis 1976).
The choice of two or three resource units is arbitrary, but since the resource unit is also arbitrary this does not affect the results that follow. Rather, it is the relative level of resource units that is relevant. The key ingredient of these three rules is the existence of a threshold of resources needed for emancipation, and the numerical value of this threshold is unimportant. This corresponds with the assumption that existential needs have to be fully (not gradually) met before people can focus on higher-level needs. It follows from Abraham Maslow theory of a hierarchy of needs (Maslow 1943) that underlies HDS assumptions about emancipation (Inglehart & Welzel 2005 Welzel 2013).
Deriving equations for emancipation
We now turn to the mathematical derivation of equations, which describe the change in emancipation gen-erated by the three rules discussed in the previous subsection. Here we go from the agent-based description to deriving mean-field di erence equations (Johansson & Sumpter 2003; Czárán 1998; Parunak et al. 1998). The expected number of individuals who become emancipated in a time step is determined by the proportion of unemancipated individuals receiving either two or three resources. Specifically, applying rule 1 above and equation 2, the expected increase in emancipation is
| $$U_t \exp \left(-\frac{R_t}{N}\right) \left(\frac{(\frac{R_t}{N})^2}{2} + \frac{(\frac{R_t}{N})^3}{6} \right)$$ | (3) |
| $$E_t \exp \left(-\frac{R_t}{N}\right)$$ | (4) |
| $$E_{t+1} = E_t \left( 1 - \exp \left(-\frac{R_t}{N}\right) \right)+ U_t \exp \left(-\frac{R_t}{N}\right) \left(\frac{(\frac{R_t}{N})^2}{2} + \frac{(\frac{R_t}{N})^3}{6} \right) + \sqrt{V(U_t,R_t)} \epsilon_t$$ | (5) |
| $$V(U_t,R_t) = U_t \exp \left(-\frac{R_t}{N}\right) \left(\frac{(\frac{R_t}{N})^2}{2} + \frac{(\frac{R_t}{N})^3}{6} \right) \left( 1 - \left(\exp \left(-\frac{R_t}{N}\right) \left(\frac{(\frac{R_t}{N})^2}{2} + \frac{(\frac{R_t}{N})^3}{6} \right)\right)\right)$$ | (6) |
From emancipation to democracy
We now turn to the step from C to D in the boat diagram (Figure 1). In line with Inglehart & Welzel (2005), we assume that political change, in terms of the level of democracy Dt, is a function of emancipation. A continuum between 0 and 1 defines the level of democracy. To understand the link between emancipation and democratisation, we see democracy as a public good (Nelson 2015; Barr et al. 2011), since people need to participate in democracy building and democracy maintaining and since democracy is a good from which individuals cannot be effectively excluded and which does not decrease due to people’s utilisation (Ostrom & Ostrom 1999). The process of political change is conceptualised as an interaction between the emancipated and unemancipated individuals. At each time step of the model, the individuals form pairs and interact both with each other and the current democracy level to decide their contribution to democracy (see Figure 3). Specifically, for each pair, their contribution to democracy is determined by Figure 3(a) with probability 1 Dt and by Figure 3(b) with probability Dt. Thus, when democracy is low, then emancipated individuals tend to create democracy (e.g. by building civil society associations, publishing critical information, protesting, etc.), and when democracy is high, then unemancipated individuals tend to hinder democracy (e.g. by strengthening the autocratic government, propaganda, repression, etc.). The conceptualisation of democracy as a public good, allows us to capture the micro-macro dynamic of democracy (arrow from C toD, see Figure 1, Figure 2). Democracy is a public good (macro-level institutions, procedures etc.) which however requires a contributing participation (micro-level). This follows from the democracy understanding advanced by the HDS theory: democracy is not only formal democratic institutions and election procedures, it is likewise a political condition where citizens think and act democratically (Inglehart & Welzel 2005; Welzel 2013).
The parameter a, respectively c, in Figure 3 captures independent contributions to democracy creation, respectively democracy reduction. The parameter b, respectively d, is a collective contribution towards, respectively against, democracy. By collective we mean that two interacting agents may join forces if both are either emancipated or both are unemancipated. The b and d parameters thus reflect our hypothesis that people who have a preference for democracy and join forces (e.g. build civil society associations) are more likely to bring about political change than if they act on their own (e.g. go individually to protests), or only interact with people who do not have a preference for democracy. Equivalently, unemancipated agents actively prefer an autocratic state and when they join forces (e.g. build repression structures) they may prevent or slow down democratic transitions more effectively.
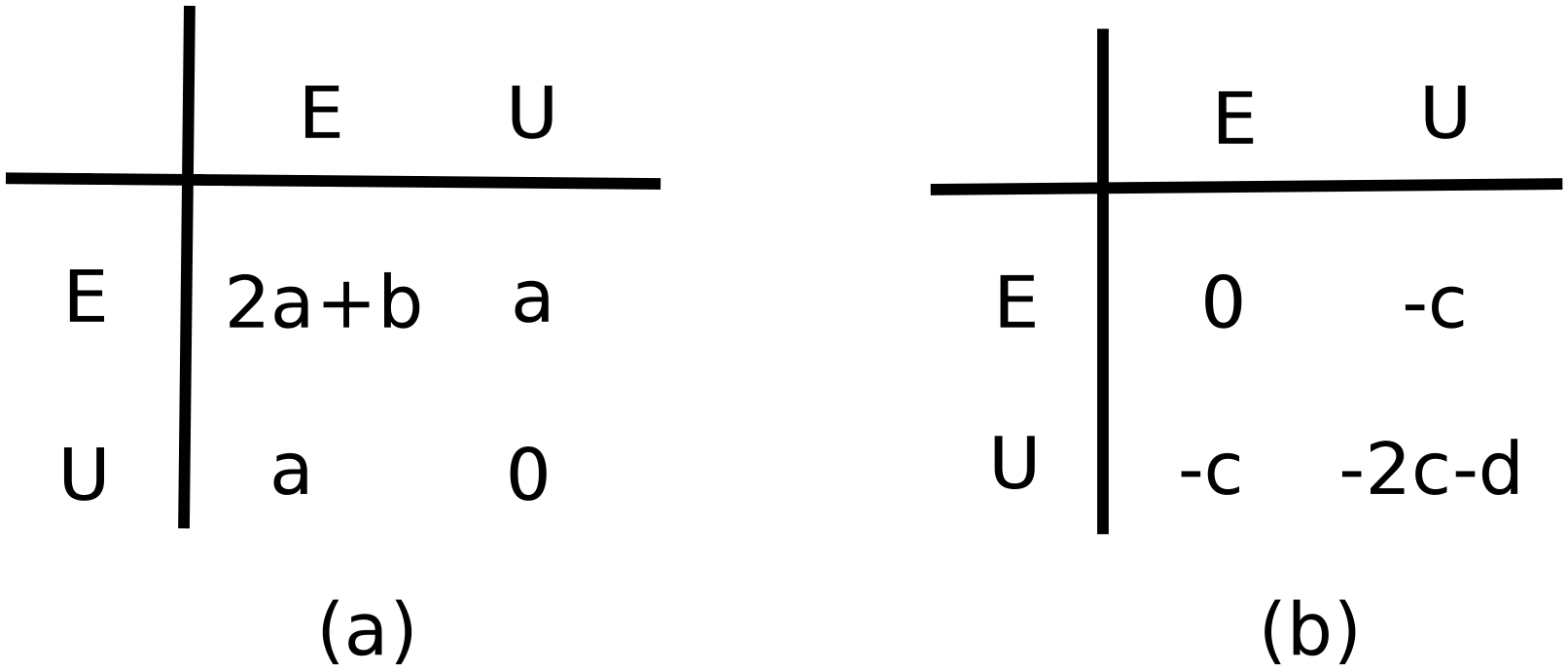
Deriving democracy equations
We can use the rules for interactions in pairs to derive the rate of change of democracy. The derivation is done for each pair of possible interactions, one at a time. For example, the proportion of pairs of two emancipated individuals is \(E_t^2\). From Figure 3 we see that they contribute 2a+b units to democracy with probability 1 Dtand 0 units with probability Dt. Thus the overall contribution to democracy of pairs of two emancipated individuals is \( (2a+b)E_t^2 (1-D_t)\). Similarly, pairs in which one individual is emancipated and the other is not, contribute on average \( 2 E_t U_t \left( a(1-D_t) - c D_t \right),\) and pairs of two unemancipated individuals contribute \( - (2c+d) U_t^2 D_t\).
The interaction contributions are summed up and form the basis of democracy building, which represents the third arrow in Coleman’s boat diagram, C to D (see Figure 1, Figure 2). When all contributions are independent (i.e. b = d = 0) then democracy grows according to:
| $$D_{t+1} = D_t + 2a E_t (1-D_t) - 2c U_t D_t \label{Dtype2}$$ | (7) |
This democratisation model follows the HDS theory, where democratisation is essentially a damped linear function of emancipation. It is important to test this linear assumption, since it ensures that any interesting simulation results obtained arise directly from HDS. Democratic change is often associated with dramatic and sudden increases, rather than the linear increase prescribed by the model. Our aim is that these dramatic changes should emerge from the model, rather than being incorporated directly in the equations. By assuming that the relationship between emancipation and democracy is linear, we can be certain that we have not built in these dramatic changes.
That said, we also test the effect of non-linear interactions, that occur when we include collective democracy building and deconstruction, i.e. b > 0 and d > 0. For these parameter values the collective action of individuals enhances the respective individual contributions. This gives the full non-linear model for democracy:
| $$D_{t+1} = D_t + (2a+b)E_t^2 (1-D_t) + 2 E_t U_t ( a(1-D_t) - c D_t - (2c+d) U_t^2 D_t = D_t + ( b E_{t} + 2a E_t (1-D_t) - ( d U_{t} + 2c) U_t D_t $$ | (8) |
This second, collective democratisation model allows for non-linear threshold effects, where democratisation is made possible even if the majority of the population has not yet become emancipated, if an emancipated minority has sufficient collective “power" (if b is sufficiently big) to trigger political change.
Implementation and Parameters
In the previous sections we have derived stochastic di erence equations for the models that describe the change in emancipation and democracy. The complete model is encapsulated by equations 1, 5, 6 and 8. We implemented the model in Matlab. The pseudocode for the simulation is given in Appendix A1.1 and A1.2.
The model was solved numerically over 100 time steps, with each time step representing a year, for N = 10,000,000 individuals. Resource units were parameterised as described in subsections Economic growth to Deriving equations for emancipation. For the parameters g, a, c, b, d different parameter values were used, examining different scenarios, albeit the standard basis model parameterises g = 0.1 and a = c = 0.1 and b = d = 0.
In order to aid readability we primarily focus on these general parameter values and units in the main results, and refer the reader to Appendix A2 for model validation and sensitivity tests with different sets of parameter values and units (for instance empirically informed resource units) and different time scales (for instance months).
Data
To test Human Development Sequence (HDS) theory hypotheses and agent-based model results against data, we used different open data sources. In particular, we used the same indicators and indices that were previously used for testing the HDS theory (Inglehart & Welzel 2005; Welzel 2013). To measure resources we used log GDP (Gross Domestic Product) per capita data provided by the World Bank (http://data.worldbank.org). GDP per capita is a widely used measure for wealth and resources in development and political science literature.
To operationalise democracy we used a human-rights weighted democracy index, suggested by Christian Welzel in the context of the HDS theory (Welzel 2013). This index is based on Freedom House’s civil liberties and political rights scores (FreedomHouse 2008, 2010), weighted for the actual human right performance in the respective countries, with two indices from the Cingranelli/Richards Human Rights data project (Cingranelli & Richards 1999, 2010). Freedom House relies mostly on the judgement or regional experts, supplemented by officially documented information to rate societies regarding their civil liberties and political rights. The Cingranelli/Richards human-rights data project (CIRI) indices of personal integrity rights and political empowerment rights on the other hand rely on actual rights violations, documented by the US State Department and Amnesty International. Moreover CIRI uses a standard coding scheme to translate the obtained information into scores that measure to what extent particular types of rights are respected in a society (Welzel 2013).
To build the index, Freedom House political rights and CIRI empowerment rights scores are added to give political participation. Similarly, Freedom House civil liberties and CIRI personal integrity rights are added to give personal autonomy. Political participation and personal autonomy are then multiplied to give the human-rights democracy index. Using a product results in low index scores, making human-rights weighted democracy index a rather rigorous indicator for democracy (Welzel 2013). For a discussion of other democracy measures used to test the HDS theory see Spaiser et al. (2014).
We measured emancipation with the World Values Survey emancipative values index. The World Value Survey is a survey of representative sample of citizens from various nations. The survey is carried out by face-to-face interviews or phone interviews in remote areas. The World Values Survey provides longitudinal survey data on the level of individual respondents that may be aggregated on the national level. In our cross-national study we worked solely with aggregated data (for details on aggregation method see http://www.jdsurvey.net/jds/jdsurveyMaps.jsp?Idioma=I&SeccionTexto=0404&NOID=101). Emancipative values are measured on four dimensions: choice, equality, voice and autonomy. These values represent preferences for “decision-making freedom of the individual human being and the equality of all human beings in this decision-making freedom” (Welzel 2013, p. 202). On the choice dimension respondents are asked for instance to what extent they toler-ate abortion, diversity and homosexuality. At the equality dimension, three items measure gender equality in the domain of politics, education and jobs. To measure the emancipation level on the voice dimension, respondents had to indicate to what extent they demand that people have more say on the local and national level and what priority they assign to the freedom of speech. At last, the fourth dimension autonomy was measured by people’s prioritisation of independence and imagination and their rejection of obedience as a desired quality (WorldValueSurvey 2006).
Finally, we included the GINI coefficient to analyse empirically the relation between democratisation and economic inequality. The GINI coefficient data was obtained from the World Bank (http://data.worldbank.org). It measures the statistical dispersion in order to represent national income distributions. The GINI coefficient is frequently used to measure income inequality. However, it has been criticised that the index does not necessary reflect inequality adequately (Bollen & Jackman 1995; Stewart 2002; Ansell & Samuels 2010). We used the GINI coefficient because of data availability and because it is so far still the most common measure for economic inequality.
Model simulations and data evidence
We now analyse the above models and directly test the predictions against the data. We start with the first democratisation model (equation 7), where contributions to democracy-building are independent. This model is our starting point because it implements the Human Development Sequence without any modifications.
HDS theory at the macro level: resources and democracy
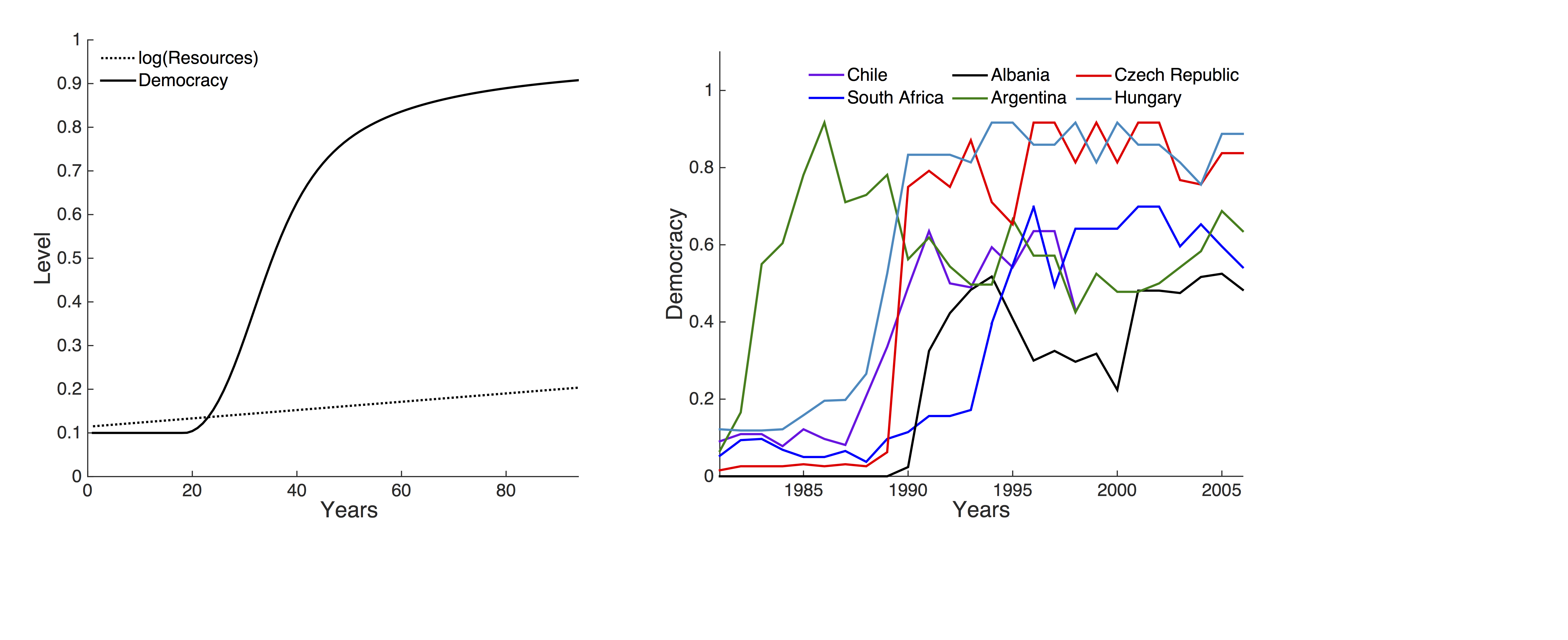
Figure 4a shows the simulated dynamics of the macro-level variables, resources (economic prosperity) and democracy, in countries with initially low levels of economic development, emancipation and democracy. The log of resources grows linearly, as we would expect from equation 1. The level of democracy remains stable on the low initial level for some period, before increasing suddenly and rapidly after 20 years of simulated time. Figure 4b shows changes in democracy in six example countries, where a democratic transition took place between 1980 and 2000. These rapid changes are representative of how democracy has arisen, once low income countries become middle income countries (Huntington 1993; Welzel 2013).
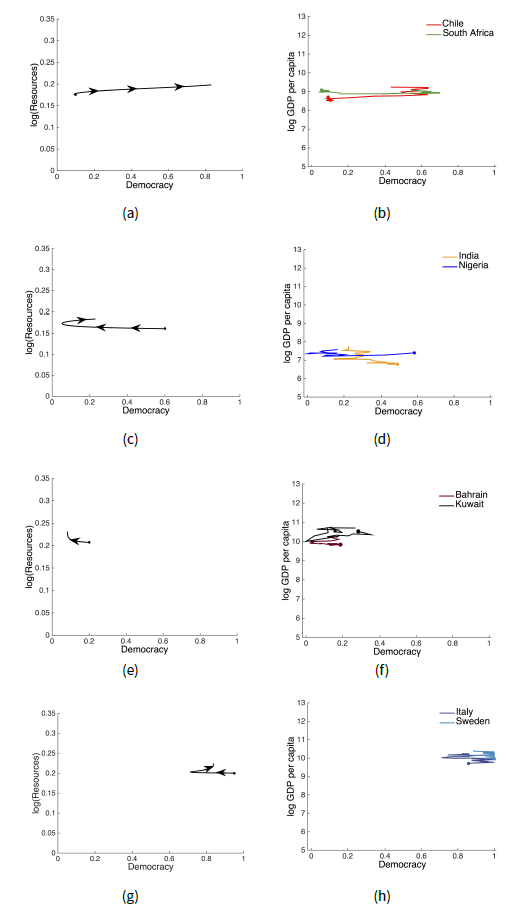
Figure 4 includes only simulation cases and country examples where a democratic transition took place, but the model reproduces other scenarios too, as depicted in Figure 5. In the model, democratisation depends on the availability of sufficient resources. Figure 5a shows a phase space of log resources and democracy, with initial conditions characteristic of middle income countries and parameter values as in Figure 4a. This visualisation illustrates again the rapid increase in democracy, once there are sufficient resources. In Figure 5b, we plot the equivalent data, showing that initially small changes in democracy in two exemplary cases, Chile and South Africa, were followed by sudden rapid shifts.
The relationship between democracy and resources depends on the starting position of the countries. For example, Figure 5c shows that democracy decays in the absence of sufficient resources. A similar pattern is seen in the data for Nigeria and India for instance, where GDP per capita is low and democracy has decreased (Figure 5d). The model predicts that in the near future democracy will increase in these countries, as GDP per capita grows.
The democratic dynamics of rich countries depend on the initial level of emancipation. Democracy fails to increase in extremely rich countries with initial low levels of democracy (Figure 5e) because the excessive resource availability prevents large numbers of individuals demanding democracy. In the data this effect is seen in, for example, Kuwait and Bahrain (Figure 5f). Rich countries with established democracy on the other hand can maintain democracy at a high level (Figure 5g), as is seen in Sweden and Italy (Figure 5h).
Although we only present a subset of the country data here, the model is generally consistent with large scale patterns of rapid democratic change seen across the world in the last 30 years (Spaiser et al. 2014; Lindenfors et al. 2011; Jansson et al. 2013). The model reproduces the macro-level relationship between economic development and democracy: first economies develop and grow, followed by an increase in democracy. The comparison to data provides a validation of the HDS framework at the macro-level, but leaves open the question of whether the implicit micro-level assumptions are correct.
HDS theory at the micro level: emancipation
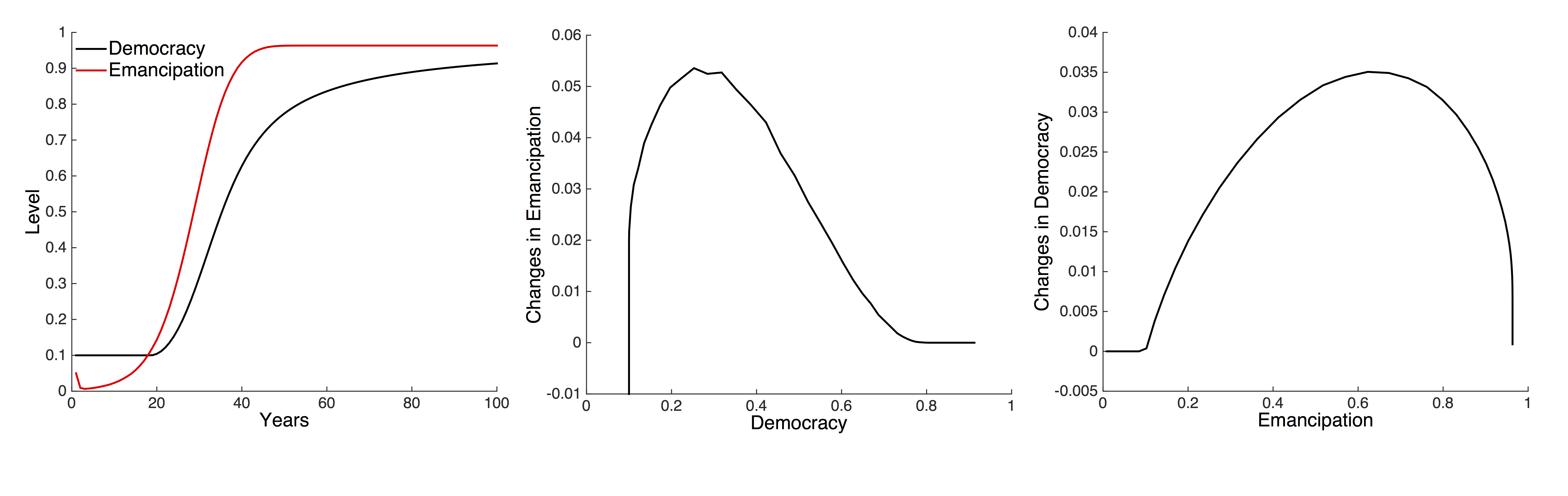
We now look at the micro-level dynamics of the HDS model, starting with the case where democracy is not driven by collective action (i.e. as in equation 7). Figure 6a illustrates the change in emancipation, measured as the proportion of emancipated individuals, and change in democracy in the simulation. All three variables (democracy, resources and proportion of emancipated individuals) are highly correlated. This correlation implies that simply plotting one variable against the other and calculating best fit regressions does not allow us to infer which is the causal factor. However, our ABM model implies a specific causal pathway, and we can use this to make testable predictions about the relationships between the variables under HDS theory. In particular, we can predict how the rate of change of emancipation is determined by levels of democracy, and vice versa. If the model holds then we expect to see the simulated relationships also in the data, while if the model is incorrect then the simulated predictions will fail to represent the data.
In Figure 6a emancipation increases at first, followed by an increase in democracy. This simulation outcome can be viewed in a different way by plotting the rate of change of emancipation as a function of democracy (Figure 6b) and the rate of change of democracy as a function of emancipation (Figure 6c). In line with the HDS theory (Inglehart & Welzel 2005), the model thus predicts that emancipation increases when democracy is low, and the growth of democracy increases with level of emancipation. Once both emancipation and democracy reach a maximum then they stabilise. We would now expect to see a similar pattern of emancipation and democratisation in the data.
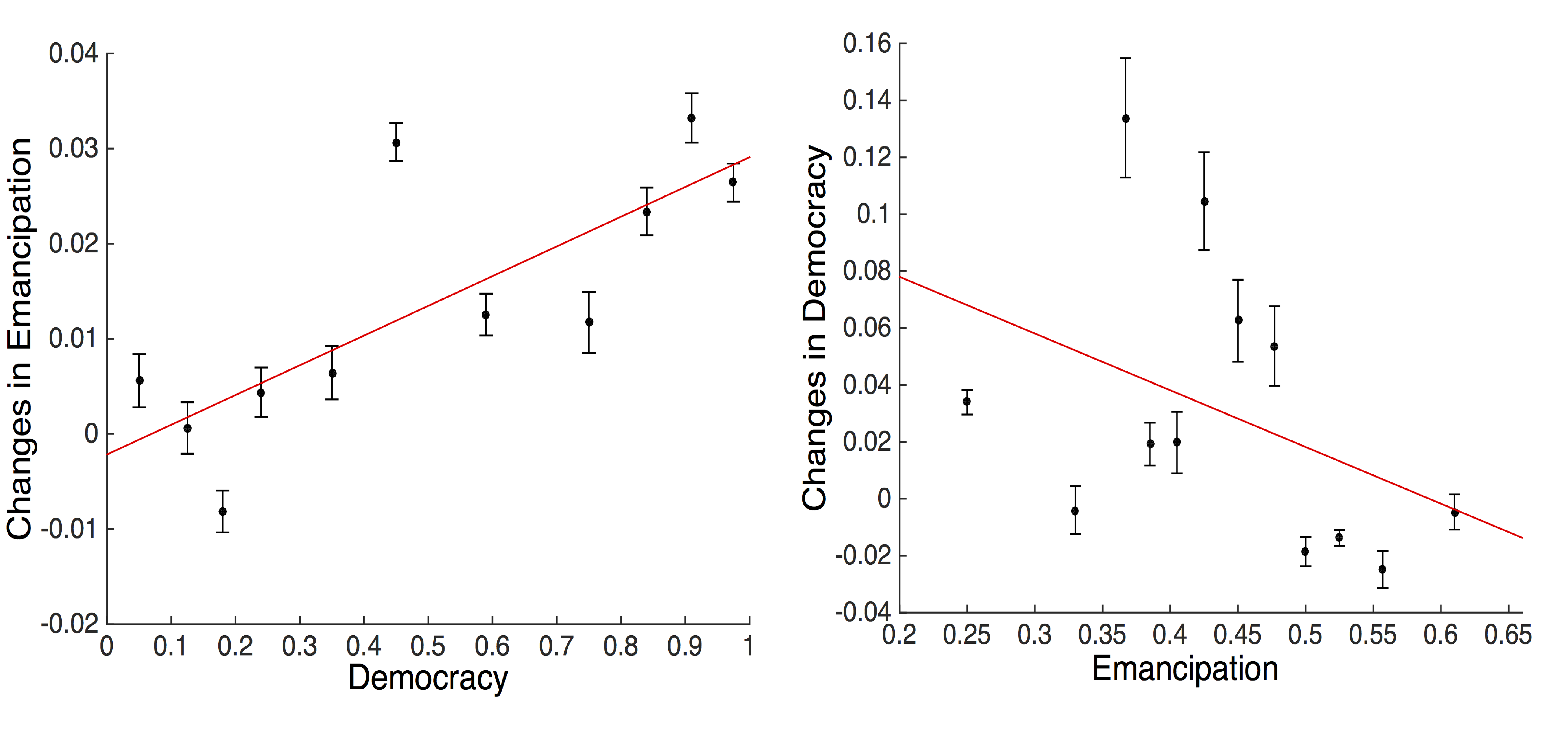
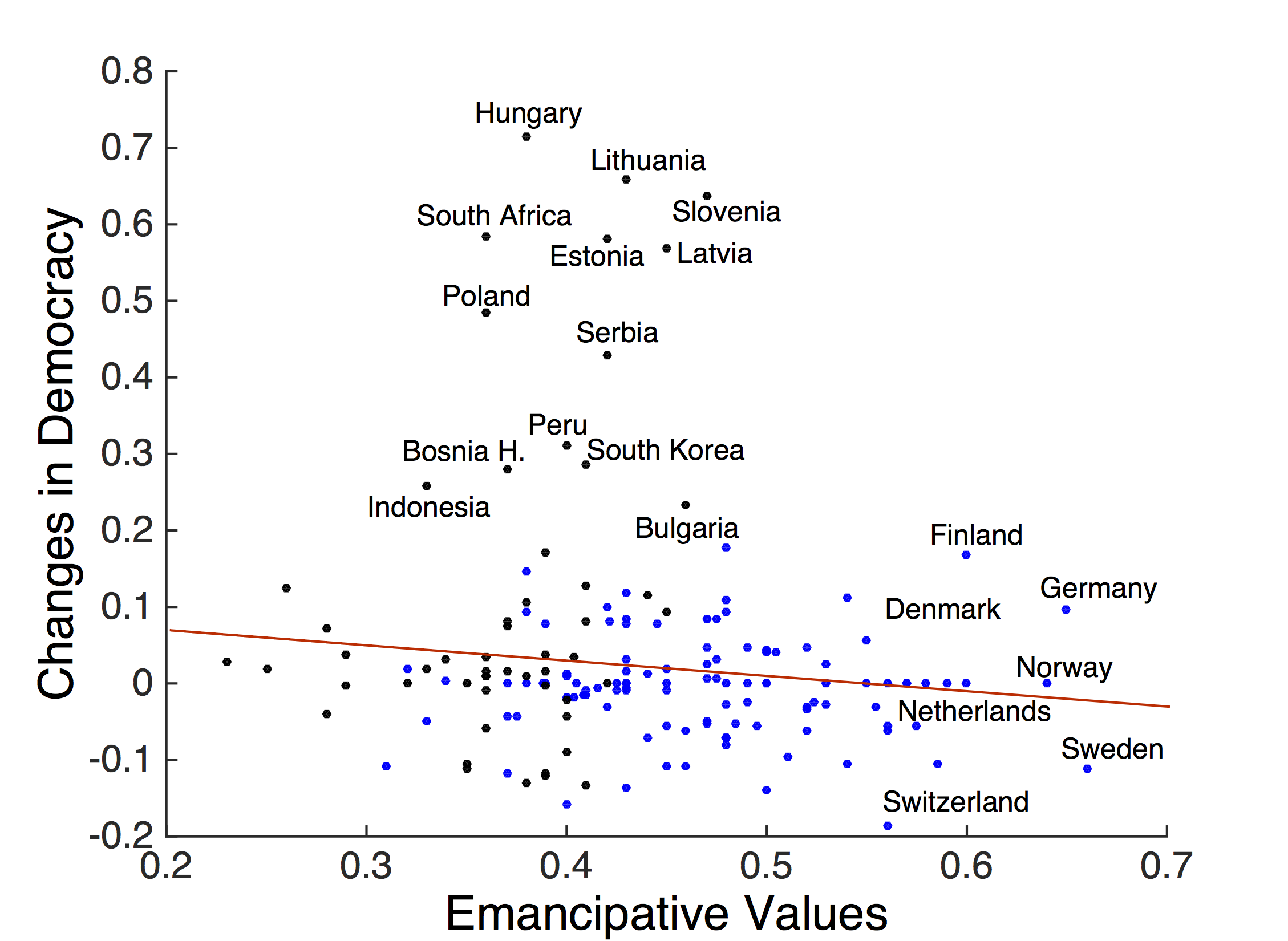
In the World Value Survey data, emancipation can be measured by looking at the aggregate level of emancipative values in the population. We use this data to test the simulation predictions and thus the HDS theory implications against empirical evidence. Figure 7a shows the change in emancipation as a function of the level of democracy derived from the data. Here we see a rather clear pattern of increasing emancipation with level of democracy (F-test with F = 14.2053 and p = 0.0044), which is the opposite pattern than that predicted by the model.
Similarly, Figure 7b shows that changes in democracy appear to be independent of level of emancipative values (F-test with F = 1.9186 and p = 0.196). Moreover the (non-significant) relation between changes in democracy and emancipative values shows the opposite direction than predicted by the model. In the data, emancipative values increase only after democracy has already shown significant increases and democracy increases most frequently with emancipative values scores between 0.35 and 0.45. The fact that the data shows a statistically different relationship between emancipation and democracy than predicted by the standard HDS theory leads us to reject it as a model at the micro-level.
Revising the HDS theory: power relations and the role of the elite
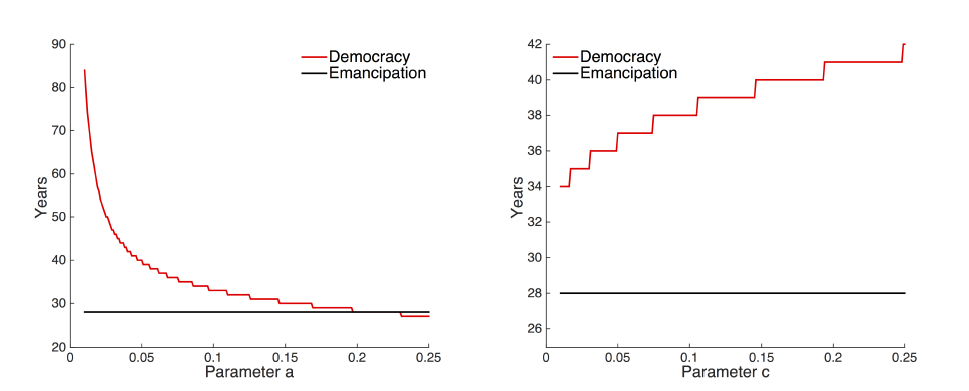
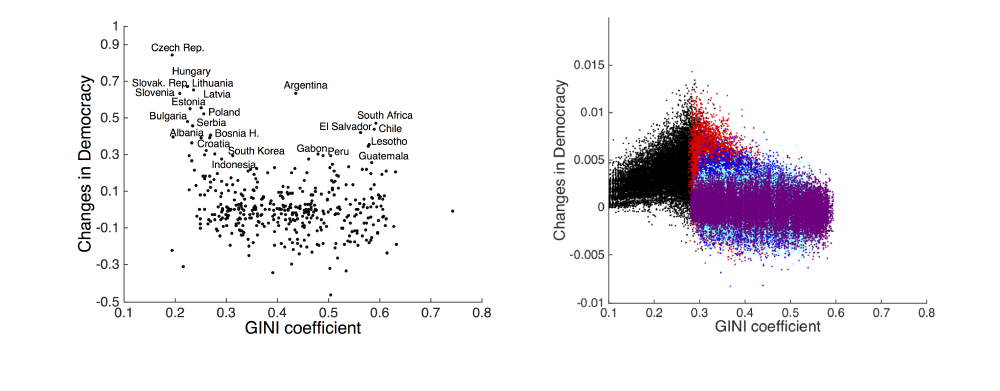
One reason for the discrepancy of the model results and data may be in the way parameters were chosen. To investigate this we now systematically explore the two parameters a, the democracy promoting effect, and c, the democracy inhibiting effect. Figure 8 shows how changes in these two parameters determine the time until democracy and emancipation reach half of their final value. The time until emancipation is half (i.e. the time t at which Et > 0.5) is determined solely by the g parameter, occurring after 28 time steps for g = 0.1. The time at which democratisation exceeds half (i.e. Dt > 0:5) depends on the relative values of a and c. If a is much bigger (around 5 times bigger) than c, then democratisation precedes emancipation (Figure 8a) as seen in the data (Figure 7). A larger value of c relative to a on the other hand has the effect of delaying democratisation (Figure 8b).
The relation of a and c represents the power relation of different groups in a society. If those who favour democratisation are very powerful, that is, if they can make a much higher contribution to political change, then a >> c and democratisation happens even if the majority of the population is not yet emancipated. On the other hand, if anti-democratic individuals are powerful, that is, if they can make a much higher contribution to keep the undemocratic political status quo, i.e. c >> a, then democratisation is delayed until the point when a large majority of the population becomes emancipated and enforces democratic transition. Comparing the model and data, we see that the data seems to be consistent with the former case only: a >> c with democratisation preceding emancipation (Figure 7).
This scenario (i.e. a >> c ) is however not entirely consistent with the way the HDS theory is formulated. According to the HDS theory a rather small but powerful (i.e. a >> c ) and liberal minded group alone would not be sufficient to trigger democracy. Instead it is claimed: “Democratization processes of recent decades have been most far-reaching and most successful where the masses were mobilized into democracy movements in such number and so ubiquitously that state authorities could not suppress them easily" (Welzel 2009, p. 83). Even though Welzel or other authors who made similar claims (Karatnycky & Ackerman 2005; Ulfelder 2005; Schock 2005), do not specify the necessary size of the democracy movement, this statement implies that the proportion of emancipated individuals required to cause a regime shift is rather large. In terms of the simulation model, the HDS assumption is then that a = c or even that c >> a, that is, the emancipated are not particularly powerful, but once their number is large enough their influence becomes sufficient to bring about political change. While our model allows such scenario, the data presented here suggest that this HDS assumption is not correct. Our comparison of model predictions and data is however consistent with the idea that democratisation is started by a liberal minded (i.e. emancipated) and influential (i.e. a >> c) "elite" (O’Donnell et al. 1986; Casper & Taylor 1996; Higley & Burton 2006).
In our second democracy model, equation 8, we additionally include collective contributions b and d of emancipated and unemancipated agents. This assumption results in a threshold democracy model: once there are a sufficient number of emancipated people, their interactions produce rapid increases in democracy. Figure 9 shows how the two additional parameters affect democratisation and emancipation. Assuming a and c being equal (i.e. a = c = 0.1), when b and d are equal then democratisation and emancipation happen almost simultaneously, with emancipation taking place only slightly ahead of democratisation. If b is larger (around 5 times bigger) then d, then democratisation precedes emancipation. On the other hand, if d is larger (around 5 times bigger) then b, then emancipation precedes democratisation and democratisation is delayed.
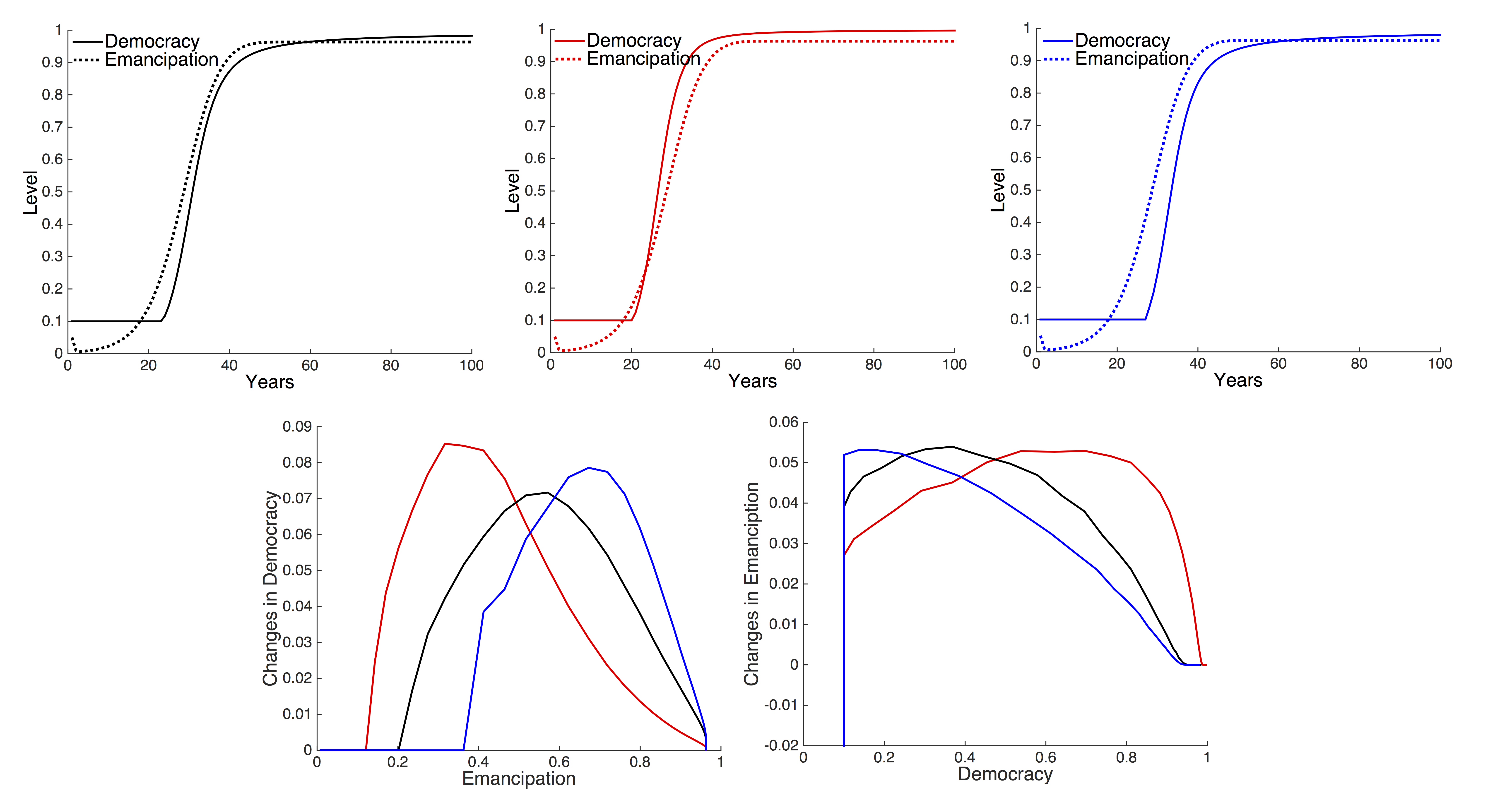
These outcomes confirm our earlier findings with the first democracy model, showing that the relative power relations (in terms of a and c contributions to political change or political status quo) of the emancipated and unemancipated individuals in a society determine the timing of emancipation and democratisation. With or without collective interaction effects, the important factor in determining the sequence of events in the transition to democracy is the relative power relations.
Looking again at the data and the change in democracy as a function of emancipation over all countries (Figure 10), we see that those countries where a rapid democratic transition occurred, had emancipative values scores between 0.33 and 0.45. These scores represent a scenario where a certain proportion, but not the majority of the population was emancipated when the democratic transition occurred. Thus, the available data is again only consistent with models in which democracy starts to increase when a rather small but powerful proportion of individuals is emancipated.
Revising the HDS theory: economic inequality
The assumption in the previous models that resources are equally distributed amongst all individuals, is rather doubtful. We also assumed that the amount of resources obtained by each individual was independent between years. We now remove both these, somewhat unrealistic, assumptions by introducing a tuneable preferential attachment model of resource distribution (Merton 1968; Rigney 2010; Newman 2005). The model we choose, and describe in full below, has a parameter q that determines how equal the distribution of resources is. For q = 1 resources are distributed uniformly at random, producing a Poisson distribution (as in the previous section). For q = 0 the model produces a power law distribution of resources, similar to Zipf’s law (Zipf 1935). While neither the Poisson nor the power law distribution reproduces exactly the empirical distribution of wealth seen in country data (Atkinson & Bourguignon 2003; Benabou 2000), they do produce extremes of equality and inequality, respectively. Thus by investigating the effect of q on model outcomes we can understand how the degree of inequality affects the emergence of democracy.
In our revised model each individual i is represented by two variables: an integer ri (t) which is the amount of resources possessed by the individual; and a state \(x_i(t) \in \{U,E,S\}\) which is the state of emancipation. State U is unemancipated and E is emancipated as in the previous implementation. Moreover, now the individual can also be in the state S, i.e. satisfied. The total resources are now \(R_t=\sum{r_i(t)}\) and the aggregate emancipation Et is the proportion of individuals with state E, St is the proportion of individuals who are satisfied and Ut is the proportion of individuals who are unemancipated. Initially, Ri (0) = 0 and xi (0) = U, for all individuals.
In the inequality model each time step t in the simulation represents a month instead of a year. The changed time unit was necessary, along with a changed economic growth dynamics (linear economic growth, see following paragraphs), as the current model consists of only 1000 individuals. To simulate similar dynamics with N = 1000 as in the previous models with N = 10,000,000, the time and economic growth dynamic had to be adjusted. Reducing the number of individuals on the other hand was necessary as the individuals are tracked in their resource and emancipation status during the simulation in the inequality model. With a large number of individuals, the tracking becomes computationally intensive. The inequality model was run over 600 time steps, which then represents 50 years of simulation (see Appendix A2.4, for model validation result with other time units). With the tracking of individuals over the course of the simulation and the new resource distribution mechanism, our model resembles now a full agent-based model and we can no longer approximate it with equations only (see the pseudo-code in Appendix A1.3).
On each time step all individuals with ri (t) > 0 have probability p of losing one resource unit. These resource units are then redistributed amongst all individuals, together with additional g new resource units. Redistribution is carried out as follows. For each resource unit, we assign the resource unit to one individual selected uniformly at random with probability q (the ’equality’ parameter). Alternatively, with probability 1 - q, we assign the resource unit to individuals in proportion to their current wealth, i.e. the probability that individual i receives the resource unit at time t + 1 is
| $$\frac{r_i(t)+1}{N+\sum_{j=1}^N r_j(t)}$$ |
The rules for updating the emancipation state are similar to the previous models, but we now make the satisfied state explicit. We assume that unemancipated individuals with 2 or 3 resource units become emancipated. Unemancipated and emancipated individuals with 4 or more resources become satisfied. Emancipated or satisfied individuals with zero resource units become unemancipated. The state of individual i is thus updated as follows:
| $$ x_i(t+1) = \left\{\begin{array}{lcl} E & , & \mbox{if } x_i(t) = U \mbox{ and } (r_i(t)=2 \mbox{ or } r_i(t)=3) \\ S & , & \mbox{if } (x_i(t) = U \mbox{ or } x_i(t) = E) \mbox{ and } r_i(t) \geq 4 \\ U & , & \mbox{if } (x_i(t) = E \mbox{ or } x_i(t) = S) \mbox{ and } r_i(t) = 0 \\ x_i(t) & , & \mbox{otherwise.}\end{array} \right. $$ |
We assume that the satisfied individuals make their contributions independently of who they interact with, as they only care about the status quo. These specifications then result in a modified threshold democratisation model:
| $$D_{t+1} = \begin{cases} D_t + \left( b E_{t} + 2a \right) E_t (1-D_t) - \left( d U_{t} + 2c \right) U_t D_t + e S_{t}(D_t - \frac{1}{2})D_t (1-D_t) \end{cases}$$ | (9) |
Simulation results show a strong effect of economic inequality on democratic change. Figure 11a-c show model outcomes for low, middle and high levels of equality, q. Democracy grows faster and reaches higher values when economic inequality is low (q=1) (11a). On the other hand if inequality is extremely high (q=0), then democracy is never achieved: democracy rises at first but then decreases again. For middle inequality levels (q=0.5) a transition to democracy takes place but democracy never reaches very high levels. In the simulation, inequality allows agents to move to the satisfied state before democracy has been achieved. The result is a small rich elite with little interest in developing democracy and a large population of poor unemancipated individuals, preoccupied with existential constraints.
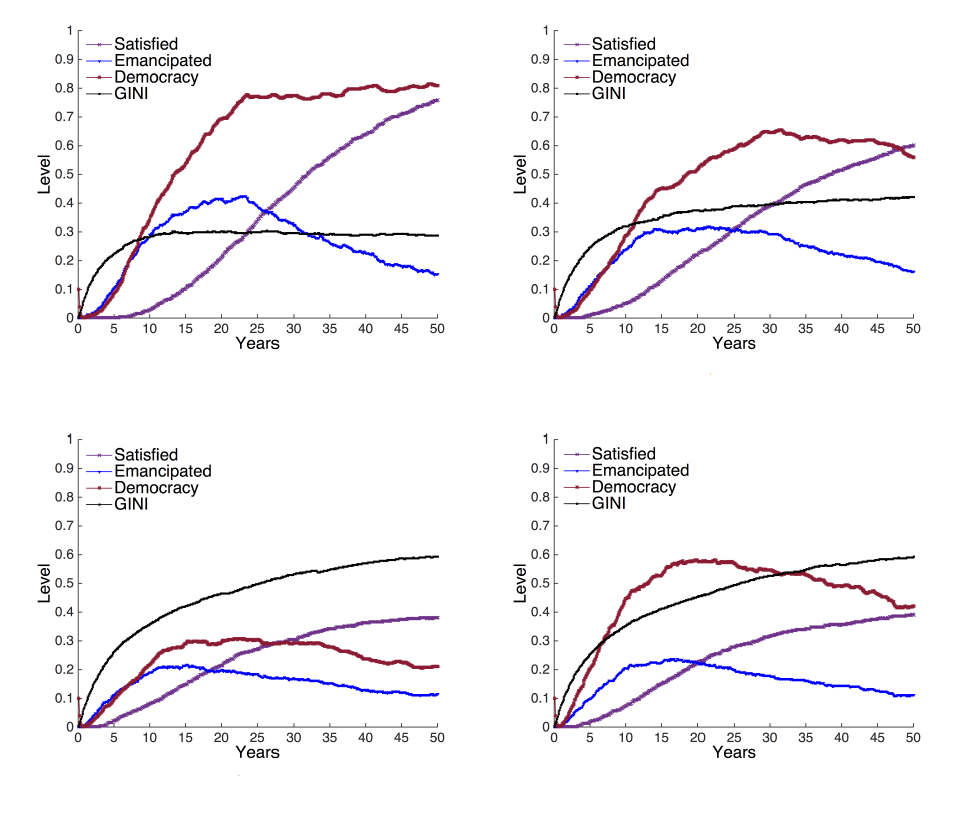
The empirical data support a similar relation between democracy and inequality as we find in our simulation. The data show that democratisation is most likely at a GINI level between 0.2 and 0.3 (see Figure 12a), and this is similar in our model simulations (see Figure 12b). Specifically, between 1981 and 2006 democratic changes happened mostly in rather equal societies. These were typically communist countries before their democratic transitions, and thus countries with low inequality.
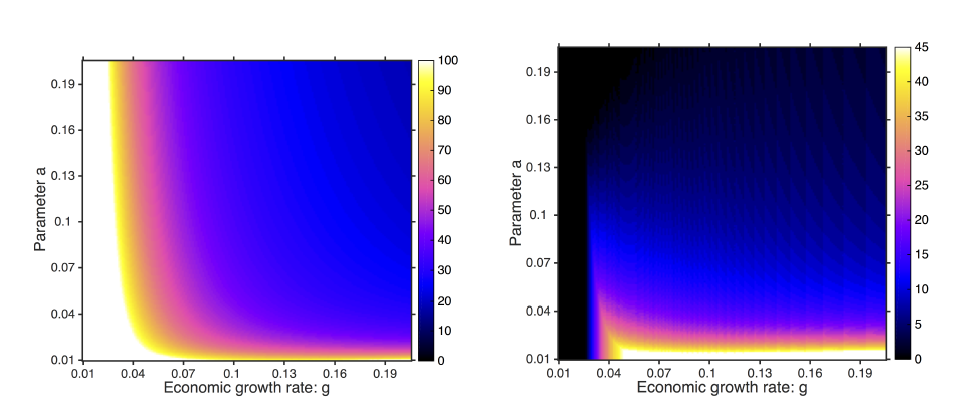
South Africa, which had both economic and political apartheid before its democratic transition, is one of the few exceptions (the others are mostly Latin-American countries, see Figure 12a). These exceptions do not appear in the simulation results in Figure 12b, and can instead be best explained by a change in the balance of power. Democratic transitions in very unequal societies can be reproduced by the simulation when a and b are considerably increased (see Figure 11d) or if economic growth is increased significantly (see Figure 13 for effects of economic growth on democratisation).
These results suggest that any theory about the emergence of democracy needs to take into account inequality. The HDS theory stresses the importance of people’s socio-economic well-being for emancipation without taking into consideration socio-economic inequality and its consequences in terms of emancipation and democratisation. Figure 12a reveals that democratisation can only take place and stabilise, if a sufficient proportion of the population has access to resources to improve its socio-economic situation. In societies with high inequality this is unlikely to happen, as the majority of the population is excluded from socio-economic well-being. As a result emancipation and democratisation will fail to materialise.
Conclusions
The HDS theory establishes a close relation between emancipation and democratisation to explain why democratisation is most likely to occur in countries that have undergone a considerable economic development. The data confirms that there is indeed a relation between democracy and emancipation. Consequently, we do not reject the political culture congruence theory (Sheafer & Shenhav 2013) that underlies the HDS theory and assumes that stable democracies require a congruence between emancipative or broader speaking democratic values among the population and democratic political institutions. The questions is rather does institutional democratisation precede emancipation or is the other way round? Contrary to the postulations of the HDS theory, data shows that human-rights democracy seems to lead to an increase in emancipation. Rather, in accordance with the data, our models suggest that democratisation is led by a influential and emancipated elite of around 10-20% of the population, using their influence to initiate democratic change (O’Donnell et al. 1986; Casper & Taylor 1996; Higley & Burton 2006). That is, the transition to democracy is initiated when a small proportion of the population becomes emancipated and, if this group has sufficient political power relative to other political groups, it triggers political changes. Such a pattern of emancipation is not measurable in aggregated measures of emancipation, but it is reflected in the growth of democracy before emancipation seen in the data.
We arrived at the conclusion above because our agent-based models make predictions that were partly testable against data. Unfortunately, more fine-grained data, panel data on the individual level to track changes in emancipation of individuals for instance, is not available. Such data would have allowed to test the simula-tion model predictions more directly.
In previous empirical tests of the HDS theory, that were supposed to confirm the theory (Inglehart & Welzel 2005; Welzel 2013), a method was applied of looking at correlations in the rate of change of variables. Fitting a model \(y_{t+1}-y_t = c (x_{t+1}-x_t )\) can reveal a correlation in growth of the variables of yt and xt but it can never reveal that a change in xt causes a change in yt or vice versa (Freedman 1997, 2006). Such an approach was nevertheless adopted by Inglehart & Welzel (2005) and Welzel (2013) in their original test of the Human Development Sequence. Changes in GDP, democracy and emancipative values were fitted as a set of three simultaneous di erence equations. The change in the three variables are taken in turn as independent variables in equations where the change in all three variables are included as dependent variables. The argument is that the fitted terms with the most explanatory power in this linear regression provides the strongest possible causal link (ibid.). We would argue that in the absence of a micro-level explanation of why such a correlation should exist, these correlations do not allow us to say anything about the likelihood or otherwise of the HDS theory. Recently, an attempt has been made to formulate the micro-level mechanisms for the HDS theory (Abdollahian et al. 2014), but, the simulation results were not compared against data (ibid.). In Figure 7 we however show that important aspects of the data fail to match the HDS theory. These findings correspond to recently published empirical analyses that similarly suggest the inconsistency of the HDS theory with data (Spaiser et al. 2014).
In our study, after rejecting the initial HDS model, we revised it to account for different power relations of different political groups. These revised models are consistent with the available data. We also went on to test the role of inequality and again found patterns in our model that are reflected in the data. We hypothesised that egalitarian societies do not have wealthy elites who oppose democratisation, because they fear losing their benefits and accumulated wealth. Democratisation is eased by the fact that there are no materialist interest in keeping the undemocratic status quo (Boix 2003). Moreover, the high economic equality allows a sufficient share of the population to get access to existential resource and become emancipated (Inglehart & Welzel 2005; Welzel & Inglehart 2006).
Exceptions, where rich countries have failed to become democratic, could be partially explained by inequality (Acemoglu & Robinson 2006, 2008). In unequal societies there is a strong class of wealthy elites who might lose some of their privileges in a democratic society. However, under certain circumstances they will be supportive of democratic change, for instance if they fear mass uprisings that might threaten their privileges even more then a democratic transition, which they can try to shape according to their preferences. Giving the emancipated more power in relation to the unemancipated and satisfied, i.e. further increasing a and b (see Figure 11d), allows for democratisation even in highly unequal societies. This captures some of the empirical examples of democratisation in highly unequal societies, where a wealthy but emancipated elite advocated democratisation to preserve their privileges and wealth. However, our ABM simulation suggests that democratisation is unstable in highly unequal societies and democracy will decrease eventually (see Figure 11d). Moreover, if the economic growth is big enough then a sufficient number of people becomes emancipated in a short period of time and demands democracy even in an unequal society.
Despite producing models that are consistent with the data, there remain other highly plausible explanations of the relationships observed in the data (Barro 1999; Krieckhaus 2003; Wucherpfennig & Deutsch 2009; Spaiser et al. 2014). For instance, in our models we focused on democratisation processes, not further examining what drives the economy for instance and in how far the economic dynamic itself is linked with democratisation, emancipation or inequality processes. This focus was set by the HDS theory, which we investigated in this paper against data and in terms of mechanism consistency. The HDS theory conceptualises economy as independent of democratisation and emancipation.
It has been also suggested that the third democratisation wave that took place in the 1980s and 1990s was mostly geographically confined to the European continent and in that context other explanations for the diffusion of democracy in these countries have been advanced (Doorenspleet 2001; Elkink 2011). In fact, the diffusion of democracy theory offers an additional explanation for the important role of elites for democratisation. If we conceptualise democracy as an innovation, then, according to the theory of diffusion of innovations (Rogers 1983), the innovation is first adopted by early adopters. These early adopters are typically the educated and resource-rich elite of a country. The majority follows the early adopters somewhat later and the innovation spreads across the society. Research seems moreover to suggest that the diffusion of democracy across countries is geographically and culturally rooted (Wejnert 2005; Elkink 2011). It remains to be seen whether the dif-fusion of democracy will continue globally or whether alternative development models, like the one promoted by China, will become an alternative to the democratisation (Lin et al. 2008). These questions go beyond the scope of this paper, which focuses on the examining and theoretical revision of the HDS theory, but should be more in the focus of research in future.
Our analysis shows how a combination of simulation models and data analysis can be used to examine and revise a theory. Linking models to data as closely as possible, ideally not only to macro-level but equally to micro-level data, can give us some confidence about the validity of simulation models. The combination of the two used here allows us to get closer to an understanding of the relationship between macro-level phenomena and their underlying micro-level processes.
Acknowledgements
The authors would like to thank Ronald Inglehart and Christian Welzel for access to processed World Value Survey data and overall feedback, moreover we would like to thank Gianluca Manzo for his valuable feedback on our simulation model. The research was funded by Vetenskaprådet project grant 2013: Development Space.Appendix
Here is the appendix of the article, including the Matlab pseudocode and supplementary analysis.References
ABDOLLAHIAN, M., Yang, Z. & deWerk Neal, P. (2014). Human development dynamics: An agent based simulation of adaptive heterogenous games and social systems. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2454406. APSA 2014 Annual Meeting Paper [doi:10.1007/978-3-319-05579-4_1]
ACEMOGLU, D. & Robinson, J. A. (2001). A theory of political transition. American Economic Review, 91(4), 938–963
ACEMOGLU, D. & Robinson, J. A. (2006). Economic Origins of Dictatorship and Democracy. New York, NY: Cam-bridge University Press
ACEMOGLU, D. & Robinson, J. A. (2008). Persistence of power, elites, and institutions. American Economic Review, 98(1), 267–293
AL-SUWAILEM, S. (2012). Behavioural complexity. In S. Zambelli & D. A. R. George (Eds.), Nonlinearity, Complexity and Randomness in Economics: Towards Algorithmic Foundations for Economics, (pp. 85–110). Chichester: Wiley-Blackwell [doi:10.1002/9781118300442.ch5]
ANSELL, B. & Samuels, D. (2010). Inequality and democratization: A contractarian approach. Comparative Political Studies, 43(12), 1543–1574
ATKINSON, A. B. & Bourguignon, F. (2003). Handbook of Income Distribution. Amsterdam: North-Holland Elsevier
AXTELL, R. L. & Epstein, J. L. (1994). Agent-based modeling: Understanding our creation. The Bulletin of the Santa Fe Institute 9 (2), 28-32
BARR, A., Packard, T. & Serra, D. (2011). Is turning out to vote a public good contribution? Evidence from a new democracy. Paper presented at the Economic Science Association Meeting.
BARRO, R. J. (1999). Determinants of democracy. Journal of Political Economy, 107(S6), 158–183
BASU, K. (2003). Analytical Development Economics: The Less Developed Economy Revisited. Cambridge, MA: MIT Press
BELLIN, E. (1994). The politics of profit in tunisia: Utility of the rentier paradigm? World Development, 22(3), 427–436
BENABOU, R. (2000). Unequal societies: Income distribution and the social contract. American Economic Review, 90(1), 96–129 [doi:10.1257/aer.90.1.96]
BOIX, C. (2003). Democracy and Redistribution. Cambridge: Cambridge University Press
BOLLEN, K. A. & Jackman, R. W. (1995). Income inequality and democratization revisited: Comment on Muller. American Sociological Review, 60(6), 983–989 [doi:10.2307/2096436]
BRAND, L. A. (1992). Economic and political liberalization in a rentier economy: The case of the hashemite king-dom of jordan. In I. Harik & D. J. Sullivan (Eds.), Privatization and Liberalization in the Middle East. Blooming-ton, IN: Indiana University Press
CASPER, G. & Taylor, M. M. (1996). Negotiating Democracy: Transitions from Authoritarian Rule. Pittsburgh: Uni-versity of Pittsburgh Press
CINGRANELLI, D. L. & Richards, D. L. (1999). Respect for human rights a er the end of the cold war. Journal of Peace Research, 36(5), 511–534
CINGRANELLI, D. L. & Richards, D. L. (2010). Ciri dataset 2008: http://www.humanrightsdata.com
COLEMAN, J. S. (1986). Social theory, social research, and a theory of action. American Journal of Sociology, 91(6), 1309–1335
CRYSTAL, J. (1990). Oil and Politics in the Gulf: Rulers and Merchants in Kuwait and Qatar. Cambridge: Cambridge University Press [doi:10.1017/CBO9780511558818]
CZÁRÁN, T. (1998). Spatiotemporal Models of Population and Community Dynamics. London: Chapman & Hall
DOORENSPLEET, R. (2001). The structural context of recent transitions to democracy. European Journal of Political Research, 43(3), 309–335 [doi:10.1111/j.1475-6765.2004.00156.x]
DUCH, R. M. & Taylor, M. A. (1993). Postmaterialism and the economic condition. American Journal of Political Science, 37(3), 747–779
DURLAUF, S. N. & Blume, L. E. (2010). Behavioural and experimental economics. Basingstoke: Palgrave Macmillan [doi:10.1057/9780230280786]
DURLAUF, S. N., Johnson, P. A. & Temple, J. R. (2005). Growth econometrics. In P. Aghion & S. N. Durlauf (Eds.), Handbook of Economic Growth, vol. 1, (pp. 555–677). Amsterdam: Elsevier
ELKINK, J. A. (2011). The international diffusion of democracy. Comparative Political Studies, 44(12), 1651–1674 [doi:10.1177/0010414011407474]
ELSTER, J. (1986). Rational choice. New York, NY: New York University Press
ENTELIS, J. P. (1976). Oil wealth and the prospects for democratization in the Arabian peninsula: The case of Aaudi Arabia. In N. A. Sherbiny & M. A. Tessler (Eds.), Arab Oil: Impact on the Arab Countries and Global Implications, (pp. 77–110). New York, NY: Praeger
EPSTEIN, J. L. (2006). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, N. J.: Princeton University Press
ETZIONI, A. (2012). Behavioral economics. toward a new paradigm. American Behavioral Scientist, 55(8), 1099– 1119 [doi:10.1177/0002764211412355]
FREEDMAN, D. A. (1997). From association to causation via regression. Advances In Applied Mathematics, 18(1), 59–110
FREEDMAN, D. A. (2006). Statistical models for causation - what inferential leverage do they provide? Evaluation Review, 30(6), 691–713 [doi:10.1177/0193841X06293771]
FREEDOMHOUSE (2008). Freedom in the world. Report: www.freedomhouse.org
FREEDOMHOUSE (2010). Freedom in the world. report: www.freedomhouse.org
GILBERT, N. G. & Troitzsch, K. G. (1999). Simulation for the Social Scientist. Maidenhead: Open University Press
GINI, C. (1913). Variabilita e mutabilita. Journal of the Royal Statistical Society, 76(3), 326–327 [doi:10.2307/2340052]
GLEDITSCH, K. S. & Ward, M. D. (2006). diffusion and the international context of democratization. International Organization, 60(4), 911–933
HADENIUS, A. & Teorell, J. (2005). Cultural and economic prerequisites of democracy: Reassessing recent evi-dence. Studies in Comparative International Development, 39(4), 87–106 [doi:10.1007/BF02686166]
HEDSTRÖM, P. (1996). Rational choice and social structure: on rational-choice theorizing in sociology. Stockholm: Stockholm University Press
HEDSTRÖM, P. (2006). Dissecting the Social: On the Principles of Analytical Sociology. Cambridge: Cambridge University Press
HEDSTRÖM, P. & Swedberg, R. (1998). Social mechanisms: an analytical approach to social theory. Cambridge: Cambridge: Cambridge University Press
HIGLEY, J. & Burton, M. G. (2006). Elite Foundations of Liberal Democracy. Lanham, MD: Rowman & Littlefield
HOULE, C. (2009). Inequality and democracy: Why inequality harms consolidation but does not affect democratization. World Politics, 61(4), 589–622
HUNTINGTON, S. (1993). The Third Wave: Democratization in the Late 20th Century. Norman, OK: University of Oklahoma Press
INGLEHART, R. & Welzel, C. (2005). Modernization, Cultural Change and Democracy: The Human Development Sequence. Cambridge: Cambridge University Press
JANSSON, F., Lindenfors, P. & Sandberg, M. (2013). Democratic revolutions as institutional innovation diffusion: Rapid adoption and survival of democracy. Technological Forecasting and Social Change, 80(8), 1546–1556 [doi:10.1016/j.techfore.2013.02.002]
JOHANSSON, A. & Sumpter, D. J. (2003). From local interactions to population dynamics in site-based models of ecology. Theoretical Population Biology, 64(4), 497–517
KARATNYCKY, A. & Ackerman, P. (2005). How Freedom is Won: From Civic Resistance to Durable Democracy. Freedom House
KESSLER, T. P. (1999). Finance Reform and the State - Mexico as Model. Westport, CT: Praeger Klügl, F. (2008). A validation methodology for agent-based simulations. In SAC ’08 Proceedings of the 23rd Annual ACM Symposium on Applied Computing, (pp. 39–43)
KRIECKHAUS, J. (2003). The regime debate revisited: A sensitive analysis of democracy’s economic effect. British Journal of Political Science, 34(4), 635–655 [doi:10.1017/S0007123404000225]
LIN, J. Y., Cai, F. & Li, Z. (2008). The China Miracle. Development Strategy and Economic Reform. Hong Kong: The Chinese University Press
LINDENFORS, P., Jansson, F. & Sandberg, M. (2011). The cultural evolution of democracy: Saltational changes in a political regime landscape. PLoS ONE, 6(11), e28270 [doi:10.1371/journal.pone.0028270]
MACAL, C. M. & North, M. J. (2010). Tutorial on agent-based modelling and simulation. Journal of Simulation, 4, 151–162
MACY, M. & Willer, R. (2002). From factors to actors: Computational sociology and agent-based modeling. Annual Review of Sociology, 28, 143–166 [doi:10.1146/annurev.soc.28.110601.141117]
MASLOW, A. (1943). A theory of human motivation. Psychological Review, 50(4), 370–396
MERTON, R. K. (1968). The Matthew effect in science. Science, 159(3810), 56–63 [doi:10.1126/science.159.3810.56]
MUELLER-BENEDICT, V. (2006). How do non-linear relations of social macro-variables arise from aggregation. Journal of Mathematical Sociology, 30(2), 137–158
MULLER, E. N. (1995). Economic determinants of democracy. American Sociological Review, 60(6), 805–821 [doi:10.2307/2096435]
NELSON, D. D. (2015). Commons Demoncracy. The Bronx: Fordham University Press
NEWMAN, M. E. J. (2005). Power laws, Pareto distributions and Zipf’s law. Contemporary Physics, 46(5), 323–351 [doi:10.1080/00107510500052444]
O’DONNEL, G. A., Schmitter, P. C. & Whitehead, L. (1986). Transitions from Authoritarian Rule: Comparative Perspective. Baltimore, MD: John Hopkins University Press
OLSON, M. (1965). The Logic of Collective Action. Cambridge, MA: Harvard University Press
OPP, K.-D. (2011). Modeling micro-macro relationships: Problems and solutions. The Journal of Mathematical Sociology, 35(1-3), 209–234
OSTROM, V. & Ostrom, E. (1999). Public goods and public choices. In M. D. McGinnis (Ed.), Polycentricity and Local Public Economices, (pp. 75–103). Ann Arbor: The University of Michigan Press
PARUNAK, H. V. D., Savit, R. & Riolo, R. L. (1998). Agent-based modeling vs. equation-based modeling: A case study and user’s guide. In Proceedings of Multi-agent systems and Agent-based Simulation (MABS’98), (pp. 10–25). Springer, LNAI 1534
PRZEWORSKI, A. (1991). Democracy and the Market: Political and Economic Reforms in Eastern Europe and Latin America. Cambridge: Cambridge University Press [doi:10.1017/CBO9781139172493]
RAUB, W., Buskens, V. & Assen, M. V. (2011). Micro-macro links and microfoundations in sociology. Journal of Mathematical Sociology, 35(1-3), 1–25
RIGNEY, D. (2010). The Matthew Effect: How Advantage Begets Further Advantage. New York, NY: Columbia University Press
ROGERS, E. M. (1983). Diffusion of Innovations. 3rd Edition. New York: Free Pres
ROSS, M. L. (2001). Does oil hinder democracy? World Politics, 53(3), 325–361 [doi:10.1353/wp.2001.0011]
SAWYER, R. K. (2003). Artificial societies. multiagent systems and the micro-macro link in sociological theory. Sociological Methods & Research, 31(3), 325–363
SCHOCK, K. (2005). Unarmed Insurrections: People Power Movements In Nondemocracies. Minneapolis, MN: University of Minnesota Press
SCHOLL, H. J. (2001). Agent-based and system dynamics modeling: A call for cross study and joint research. In Proceedings of the 34th Hawaii International Conference on System Sciences. IEEE
SHEAFER, T. & Shenhav, S. (2013). Political culture congruence and political stability. revisiting the congruence hypothesis with prospect theory. Journal of Conflict Resolution, 57(2), 232–257 [doi:10.1177/0022002712446127]
SPAISER, V., Ranganathan, S., Mann, R. P. & Sumpter, D. J. (2014). The dynamics of democracy, development and cultural values. PLoS ONE, 9(6), e97856
STEWART, F. (2002). Horizontal Inequality: A Neglected Dimension of Development. QEH Working Paper No. 1 Queen Elisabeth House, University of Oxford
SUGIHARA, G., May, R., Ye, M., hao Hsieh, C., Deyle, E., Fogarty, M. & Munch, S. (2012). Detecting causality in complex ecosystems. Science, 338, 496–450
TEORELL, J. (2010). Determinants of Democratization: Explaining Regime Change in the World, 1972-2006. Cambridge: Cambridge University Press [doi:10.1017/CBO9780511762727]
TEORELL, J. & Hadenius, A. (2006). Democracy without democratic values: A rejoinder to Welzel and Inglehart. Studies in Comparative International Development, 41(3), 95–111
ULFELDER, J. (2005). Contentious collective action and the breakdown of authoritarian regimes. International Political Science Review, 26(3), 311–334 [doi:10.1177/0192512105053786]
UNDP (2011). Human development Report 2011 - Technical notes. Tech. rep., UN
VANDERWALLE, D. (1998). Libya since Independence: Oil and State-Building. Ithaca, NY: Cornell University Press
WEJNERT, B. (2005). Diffusion, development, and democracy. American Sociological Review, 70(1), 53–81
WELZEL, C. (2006). Individual modernity. In R. J. Dalton & H.-D. Klingemann (Eds.), The Oxford Handbook of Political Behaviour, chap. 10, (pp. 185–205). Oxford: Oxford University Press
WELZEL, C. (2009). Theories of democratization. In C. W. Haerpfer, P. Bernhagen, R. F. Inglehart & C. Welzel (Eds.), Democratization, (pp. 74–90). Oxford: Oxford University Press
WELZEL, C. (2013). Freedom Rising. Human Empowerment and the Quest for Emancipation. Cambridge: Cambridge University Press [doi:10.1017/cbo9781139540919]
WELZEL, C. & Inglehart, R. (2006). Emancipative values and democracy: Response to hadenius and teorell. Stud-ies in Comparative International Development, 41(3), 74–94
WORLDBANK (2009). World bank data. http://data.worldbank.org
WORLDVALUESURVEY (2006). World value survey questionnaire, root version, 2005-2006 wave: http://www. worldvaluessurvey.org
WUCHERPFENNIG, J. & Deutsch, F. (2009). Modernization and democracy: Theories and evidence revisited. Living Reviews in Democracy, 1: http://www.livingreviews.org/lrd--2009--4
ZIPF, G. K. (1935). The Psycho-Biology of Language. Cambridge: Cambridge University Press
