 Abstract
Abstract
- The different ways individuals socialize with others affect
the conditions under which social norms are able to emerge. In this
work an agent-based model of cooperation in a population of adaptive
agents is presented. The model has the ability to implement a multitude
of network topologies. The agents possess strategies represented by
boldness and vengefulness values in the spirit of Axelrod's (1986)
norms game. However, unlike in the norms game, the simulations abandon
the evolutionary approach and only follow a single-generation of agents
who are nevertheless able to adapt their strategies based on changes in
their environment. The model is analyzed for potential emergence or
collapse of norms under different network and neighborhood
configurations as well as different vigilance levels in the agent
population. In doing so the model is found able to exhibit interesting
emergent behavior suggesting potential for norm establishment even
without the use of so-called metanorms. Although the model shows that
the success of the norm is dependent on the neighborhood size and the
vigilance of the agent population, the likelihood of norm collapse is
not monotonically related to decreases in vigilance.
- Keywords:
- Social Norms, Agent-Based Modeling, Social Networks, Neighborhood Structure, Cooperation
 Introduction
Introduction
- 1.1
- The role of the structure of personal social networks in
the process of diffusion of specific social facts has been now long
acknowledged. Research in social network analysis subscribes to the
structuralist hypothesis which claims that the adoption of social facts
such as norms is not the cause but rather the effect of an individual's
structural location in the complex web of social interactions. That is,
people acquire norms as they acquire information – through ties
structured in the network – and their spread is the direct consequence
of the resources available to each and every individual in the network (Wellman 1983). Granovetter (1973) has famously
validated this point of view in his classic study on the strength of
weak ties. Other studies of diffusion dynamics have since shown that
social network topologies can have important consequences for emergent
patterns of collective behavior (see Newman
et al. 2006). Moreover, most social contagion is complex, in
the sense that multiple channels of communication and exposure are
being exploited concurrently, yet possibly at varying spatial and
temporal scales (Centola &
Macy 2007). Individual-level decision-making thus plays an
ever more important role as social contagion is dependent on strategic
behavior as well as the percieved credibility and legitimacy of the
social fact being diffused.
- 1.2
- In this article special attention is therefore given to
spatial agent-based modeling as a means of providing a powerful
framework for exploring the mechanisms which lie at the foundations of
the norm establishment process. In fact the use of computational
simulation in the form of agent-based models to study social norms is
nothing new. Axelrod (1986)
used a game-theoretical foundation combined with an evolutionary
approach; Axtell et al. (2001)
observed the mechanics of transitions from social inequality to an
equitable state by employing a model of individual action grounded in
behavioral game theory; Epstein (2001)
also explored the role of bounded rationality and thoughtless
conformity on the adoption of norms with an ABM; just to name a few
examples. This work draws heavily from Axelrod's norms game, however it
modifies the original framework to fit the purposes of simulating a
population of a single-generation of adaptive agents in a spatial
environment rather than using an evolutionary approach.
- 1.3
- Thirty years later, the norms game, as Axelrod had dubbed
it, is still a very valuable model because it attempts to account for
the amorphous and opaque, yet much discussed concept of norm emergence
through the lens of individual actions. Moreover, it does so using only
a very simple and clearly understandable framework. However, the
trouble with such abstract models is that they can often fall into the
trap of theoretical instrumentalism, where choice of assumptions is
subject to predictive power or plausible results (Hedström 2005). One can argue
that research in the social sciences should always be led under the
maxim of grounding its explanatory mechanisms in empirical findings (De Marchi 2005). In this article,
the aim is to introduce a modified set of assumptions which draws from
Axelrod's ideas, but at the same time avoids fictionalist temptations
regarding parts of the model design. Moreover the focus is shifted to
simulating agent adaptation in spatial structures within a single
generation.
- 1.4
- In doing this, the hope is to answer the following question: how does the changing nature of individuals' social network structures affect the emergence and internalization of certain social norms? This paper will focus on cooperation-based norms with defections beneficial to individuals yet detrimental to society. Even more specifically, the focus will be on such norms with defection rewards independent of the population size (one example of this type of norm is tax-paying and the issue of tax evasion, where the total sum of money evaded by any individual actor is certainly independent of the size of the population). The goal is to elucidate the answer with the help of a computational model extending and modifying the original norms game in order to study agent adaptation in a multitude of environmental configurations. A background review of sociological theory on communities and social networks is presented first, before demonstrating the re-implementation of the norms game in the MASON package. Most importantly, a full description and specification of the new model follows. Finally, some simulation results are discussed.
 Background
Background
- 2.1
- Bicchieri (2006)
defines a social norm as a behavioral rule such that a sufficiently
large part of the population is aware of its existence and its
application to relevant situations. Moreover, individuals must prefer
to conform to this rule on the condition that others are believed to
conform to it as well, and that others are believed to expect the
individual to conform to it and may sanction behavior. The question of
emergence of social norms is an age-old conundrum of the social
sciences. Sociologists as far back as Durkheim ([1893] 1997) in the 19th
century have hypothesized on the nature of how norms "come to life" and
how they are propagated throughout society and sustained in an emergent
bottom-up manner (see Sawyer 2002).
Later in the second half of the 20th century, Parsons (1964) built his entire theory
around the mechanisms responsible for the adoption of norms and their
spread in modern societies.
- 2.2
- It should be no surprise then, that ever since agent-based
modeling established itself as a specific research domain in the social
sciences, there have been attempts at using such computational
simulation methods to explore the emergence of social norms. Today,
there exists a large amount of research where agent-based models are
used to help answer these questions.
- 2.3
- Savarimuthu and Cranefield (2009)
categorize simulation models of social norms with respect to the ways
they represent a) norm creation, b) norm spreading, and c) norm
enforcement. In different models norms can be designed off-line (Castelfranchi & Conte 1995),
created by leader agents (Kittock
1993), or in other instances they can be cognitively deduced
from the behavior of other agents (Andrighetto et al. 2008). Similarly
the spread of norms can be fueled by leadership (Kittock 1993), imitation (Epstein 2001), as well as
evolution (Axelrod 1986).
The enforcement of social norms has been modeled using sanctioning
mechanisms (Axelrod 1986)
as well as reputation of agents (Hales
2002), among other approaches.
- 2.4
- Such models have been recently used to model a variety of
real-world applications, ranging from the international diffusion of
political norms (Ring 2014),
through the prediction of smoking cessation trends (Beheshti & Sukthankar 2014),
to the mapping of diffusion of safe teenage driving (Roberts & Lee 2012).
These represent only a small fraction of the entiry body of social
norms research utilizing agent-based models. However, perhaps the first
agent-based model concerned with the emergence of norms, and certainly
the most classic one, is Axelrod's (1986)
evolutionary model.
Axelrod's Norms Game
- 2.5
- In his seminal 1986 paper "An Evolutionary Approach to
Norms" (Axelrod 1986),
Axelrod presents a simple agent-based model which seeks to
explain the mechanisms which eventually lead to establishing a norm in
a society. To achieve this goal Axelrod used the game-theoretical
concept of the prisoner's dilemma and extended it to n players (see Manhart & Diekmann 1989).
In the model, agents have a simple choice to either cooperate with
other agents or to defect.
- 2.6
- The agents possess two attributes which govern their
behavior. These attributes are defined as boldness
and vengefulness. Both of these can take on values
between 0/7 and 7/7 (to constrain them to 3 bits). Agents also have a
numerical score assigned to them, which represents how well they are
doing in the "norms game". Finally each agent gets assigned a
probability of being seen during the defection. This probability is a
random number sampled each round from a uniform distribution on the
interval \((0,1)\). An agent will then defect, if its boldness
is higher than the probability of being seen in the given round. Every
time an agent defects it receives a temptation payoff of \(T = 3\); at
the same time all of the other agents get a negative payoff of \(H =
-1\), because they are hurt by the defection.
- 2.7
- On the other hand, if an agent sees a defection, it will
have to decide whether to punish it or not. This happens with a
probability equal to its vengefulness value. After
the punishment the original defector is hurt by \(P = -9\) points,
however the punisher's score is also negatively adjusted by \(E = -2\),
the assumption being that the enforcement of the punishment comes at a
certain cost.
- 2.8
- On top of this game-theoretic design, Axelrod (1986) superimposed an
evolutionary mechanism responsible for selection and reproduction of
high-scoring individuals. Every four rounds of the game, the agents are
evaluated and ranked by their score. Players who are at most one
standard deviation below the population average, but under one standard
deviation above the average are given one offspring, and players who
are at least one standard deviation above the mean are given two
offspring to seed the next generation of agents (the next 4 rounds of
the simulation). The offspring are then mutated, by introducing a small
probability of flipping the bits of their boldness
and vengefulness values.
- 2.9
- Upon analyzing the model, Axelrod discovered that under the
given conditions the norm rarely emerges. Thus, he revised the original
model and introduced "metanorms" — that is, norms which
dictate to not
only punish defectors, but to also punish those who are seen not
punishing defectors. Just as in the norms game, meta-punishment
decreases the punished agent's score (\(\mathrm{MP} = -9\)) and it
comes at an enforcement cost to the meta-punisher (\(\mathrm{ME}=
-2\)). The agent's decision to punish as well as meta-punish is tied to
the same vengefulness value. Only after the
introduction of this new mechanism was Axelrod able to have norms
emerge in the model.
- 2.10
- The model has quickly become a staple of the agent-based
modeling community and a classic in the modeling of norms. As such, it
has also been heavily scrutinized and replicated (e.g. Galán & Izquierdo 2005; Galán et al. 2011; Mahmoud et al. 2012) as well
as criticized. Authors have noted Axelrod's unclear and potentially
weak experimental design, and the nature of model constraints and
conditions, which seems to be arbitrary in certain cases (Galán & Izquierdo 2005).
Another often cited shortcoming (Mahmoud
et al. 2012) is the perfect knowledge which Axelrod's agents
had possessed – in short, the players in the game always knew about the
strategies and defections of all of the remaining players. For example
in Mahmoud et al.'s (2012)
paper the authors used a learning algorithm to overcome this aspect of
the model. Another way of imposing some imperfection onto the agents'
knowledge of their environment is to introduce a topology, or a spatial
concept into the model.
- 2.11
- There have in fact been studies on the norms game played
between agents located on networks. Galán et al. (2011) have studied the effects
of playing the metanorms game on random, small-world and scale-free
networks. Other studies have also demonstrated the ability to establish
norms on different network topologies through meta-enforcement and
meta-punishment (Mahmoud et al.
2012b, 2012c,
2013). However, such
extensions to networks have been singularly focused on the replication
of the metanorms game and have not taken into account the effects of
network topology on the original norms game. And so the possibility of
norm emergence in populations of networked agents without the help of
metanorms has been left as an open question. Moreover, these efforts
have maintained the evolutionary approach first used by Axelrod. This
study seeks to explore the effects of network topology and the ability
of agents to adapt within a single generation in a modified version of
the original norms game. But to understand how norms can emerge in a
social environment where the agents' knowledge is constrained by the
people they know, their culture and the social networks they are
associated with, we must first study the patterns of social network
structure in modern society.
Community Structure
- 2.12
- Social research has concerned itself with the concept of
community in modern society ever since its inception. The terms community
and community structure are here
understood in their sociological context as functional and cohesive
groups of people, and the shape and quality of the interaction networks
within them, as opposed to the more technical definitions employed in
network analysis. Ferdinand Tönnies (1957
[1887]) was one of the first sociologists to address the
issue of community. Others followed suit in the following century (e.g.
Wirth 1938; Fischer 1975, 1984)
- 2.13
- A modern sociological theory on community life, which will
be of interest to the modeling effort presented in this paper, is due
to Wellman (2002).
Wellman establishes a tripartite typology of contemporary patterns of
social aggregation. He calls these types little boxes,
glocalization and networked
individualism respectively. His claim is that there is a
general teleological shift in modern society from the first, to the
second and finally to the third type. He argues that originally people
were living in little boxes: a handful of tightly
bounded, densely knit communities, each of them tied to a specific
locality: the family, the workplace, a club, or an organization. Even
in large cities, people were bound to the neighborhood and visited each
other door-to-door. The place was an essential part of what glued the
communities together. But with the proliferation of expressways,
affordable air transportation and the increasing ease of long-distance
communication, whether it was the home telephone, later on cell-phones
and most recently the Internet, a shift to glocalized networks
occurred. Suddenly, people were not bound by their locale anymore.
Thanks to the above mentioned technologies, individuals can now obtain
the same form of support, solidarity and companionship from physically
distant people, that they would earlier be able to enjoy only from
people living in their neighborhood. The result is a network of
multiple communities, some tightly knit, some more loosely, with sparse
interactions across these communities, but most importantly the
relationships of people across different communities and those even
within their limits are not tied to a specific location.
- 2.14
- Finally, the move away from glocalization
to networked individualism is propelled by the rise
of the Internet and mobile phones. Interactions in little
boxes were door-to-door, glocalized interactions were
place-to-place, but now we are experiencing a shift to person-to-person
interactions. Networks become even sparser, communities less tightly
bounded, linkages are more ad hoc.
- 2.15
- What could this mean for the emergence of norms in societies differentiated by these three types of community life? Perhaps in societies where the glocalization or networked individualism community structure is dominant, one would see norms struggling to emerge due to the fragmentary and diversified nature of the society. Or perhaps, conversely, these societies could be more conducive to the diffusion of norms because the social cross-linking could allow for a richer sampling of the cultural landscape.
 Methodology
Methodology
- 3.1
- To explore the concept of norm emergence in different
spatial topologies, two different versions of an agent-based model
implementing some basic concepts from Axelrod's (1986) original norms
game have been developed. The first version of the model, which from
here on will be referred to as "the network model" incorporates
different network topologies on which the individual agents are allowed
to interact. The second version, referred to as "the grid model"
implements a grid-based environment for the agents' interaction.
Naturally, a grid with some notion of neighborhood is by definition a
network. The distinction between networks per se
and grids is made because the "network model" can serve as a test of
viability and of the general effects of playing the game in space by
studying some well-known types of networks, whereas the grids provide a
convenient way to represent a specific social theory (due to Wellman 2002). Both versions
also simulate only a single generation of agents, who are however able
to change their strategies throughout a simulation run in an attempt to
adapt to changing environments.
- 3.2
- The original model designed by Axelrod was also recreated
for the purposes of comparison and verifying the correct implementation
of the basic model assumptions. Replication and re-implementation
computational models proves to be a very important tool for verifying
the results of experiments (Axelrod
1997; Edmonds &
Hales 2003). Although the technique is not yet wide-spread in
the ABM community, replication is perhaps even more important in the
field of simulation than in others (Wilensky
& Rand 2007). The re-implementation done here serves
as confirmation that the new models arise from the same basic framework
as Axelrod intended it.
- 3.3
- Both of the new models introduced here provide a simulation
environment which for the purpose of this study is instantiated and ran
a large number of times under different model parameter settings and,
importantly, using different topologies. During these runs important
model variables are tracked and recorded. Finally a sensitivity
analysis of the model variables to parameters and topologies is
performed.
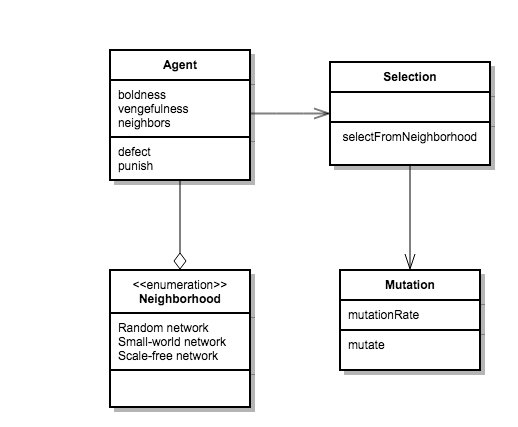
Figure 1. Class diagram of the model. - 3.4
- For the first version of the model three different network
topologies are considered. Apart from random networks, small-world
networks and scale-free networks are also utilized. Every time a random
network is instantiated in the model, it is generated using the
Erdös–Renyi algorithm (Erdös
& Rényi 1959). In a similar vein, small-world
networks are grown using the Watts–Strogatz algorithm (Watts & Strogatz 1998),
and finally scale-free networks in the model are created via the
Barabasi–Albert algorithm (Albert
& Barabasi 2002). For random and small-world networks
we focus solely on graphs with mean node degree \(k = 100\). This
number was chosen somewhat arbitrarily, with the hopes of staying true
to some of the theories on the average number of meaningful social
connections of humans (Dunbar 1992),
while also keeping computational efficiency in mind. The degree
distribution of the scale-free network follows a power law, in which
case the mean and standard deviation are not always well defined.
- 3.5
- As hinted above, the networks' nodes represent the social
actors in the model, in this case, individual people, while links
between nodes represent meaningful social connections, such as
friendship, kinship, professional acquaintances, colleagues,
supervisors, etc. It is assumed, that any time two nodes are connected
via a link, their relationship is such so that any behavior perceived
as non-conforming to the actors' beliefs could potentially be met with
a substantial reaction.
- 3.6
- The model consists of a set number of agents connected
via links in a network, an adaptive mechanism (strategy
selection) which is used to re-seed the network
with agents' new behavioral information at evenly spaced time intervals
based on the attributes of the selected agents, and a mutation
mechanism (Figure 1). The model
includes a single global parameter \(W\) – the mean probability of an
agent witnessing a defection. An agent \(i\) is then assigned its own
probability \(W_i\) of witnessing a defection from the normal
distribution centered at \(W\) with a standard deviation \(\sigma =
0.2W\). This attribute represents an agent's vigilance.
- 3.7
- As in the original norms game each agent possesses a boldness
value \(B\) ranging from 0/7 to 7/7 and a vengefulness
value \(V\) also ranging from 0/7 to 7/7. Moreover every agent is
assigned a numerical score which at the beginning of each simulation
run is set at 0. However, because the motivation for this model is to
model adaptation of behaviors in a network of actors rather than to
simulate the evolution of agents, the payoffs are not reset at the
beginning of each period. Because the model simulates a single
generation of agents, the payoffs continue to accumulate throughout the
entirety of a simulation run. Thus an agent's payoffs do not
necessarily reflect how good its current strategy is. This is done
because one of the aspects of the agents' bounded rationality is their
inability to clearly discern the effects of individual strategies. The
agents will simply emulate the behaviors of successful agents in their
neighborhood. They do not, however, have the ability to discern which
strategies contributed to which portion of the payoffs.
Agent Decision-Making
- 3.8
- The first decision an agent has to make each round is
whether to defect or not. To determine whether agent \(i\) defects we
first need to know its boldness value \(B_i\) and
\(S\), the probability it will be seen, should it decide to defect. The
probability of being seen is directly tied to the number of an agent's
neighbors and their witnessing probabilities. Naturally, the larger an
agent's social network is, the bigger the chance of being caught by at
least some of its neighbors. However, to avoid for the defection
decision to become completely determined by the size of one's
neighborhood, and to account for the diversity of conditions which are
variedly favorable to defection, a certain amount of noise is added to
the equation. Thus:
$$ S = 1- \prod_{i\in N} (1- W_i + R) $$ Here \(N\) is the set of the agent's neighbors, \(W_i\) is the witnessing probability of neighbor \(i\), and \(R\) is the normally distributed random variable with \(\mu = W\), \(\sigma = W\). Apart from this modification it is also assumed that agents only possess bounded rationality and thus will always gauge the probability of being seen with some degree of error. Therefore the perceived probability of being seen must be also calculated for each agent:
$$ S_p = 1- (1- W+R)^n $$ Here \(n\) is the number of agent's neighbors. Finally, an agent will defect only if \(B_i > S_p\), that is, if its boldness value is greater than the perceived probability of being seen by at least one of its neighbors. As the mechanism stands, the boldness label might not be appropriate anymore, opportunity being perhaps a better choice, however for the sake of clarity and continuity the original nomenclature is preserved.
- 3.9
- The second decision an agent has to make, is whether to
punish a defection. This is done for all of the agent's neighbors in
the same way as in the original Axelrod model. That is, if an agent's
neighbor defects, the model first checks whether the agent \(j\) sees
the defection, which happens with probability \(W_j\). If the agent
indeed sees the defection it then punishes the neighbor with
probability equal to its vengefulness value \(V_j\). See Figure 2 for a flow diagram of agent
activity.
- 3.10
- Since \(W\) is an exogenous parameter, in model
configurations with a high value of \(W\), some agents, while being
very vigilant, will never follow through with any sort of punishment,
because of their low vengefulness value. However, the notion behind
vigilance is that it may potentially act as a deterrent even if the
agents do not follow through, because the defecting agents cannot know
with certainty whether the punishment will come or not.[1] The vigilance
parameter also represents the tightness of links between agents.
Tightly-knit communities of agents, such as traditional family
structures, are vigilant "by default" because their members interact
with each other frequently. Thus, vigilance is also a proxy for
frequency and intensity of other interactions which are not directly
modeled.
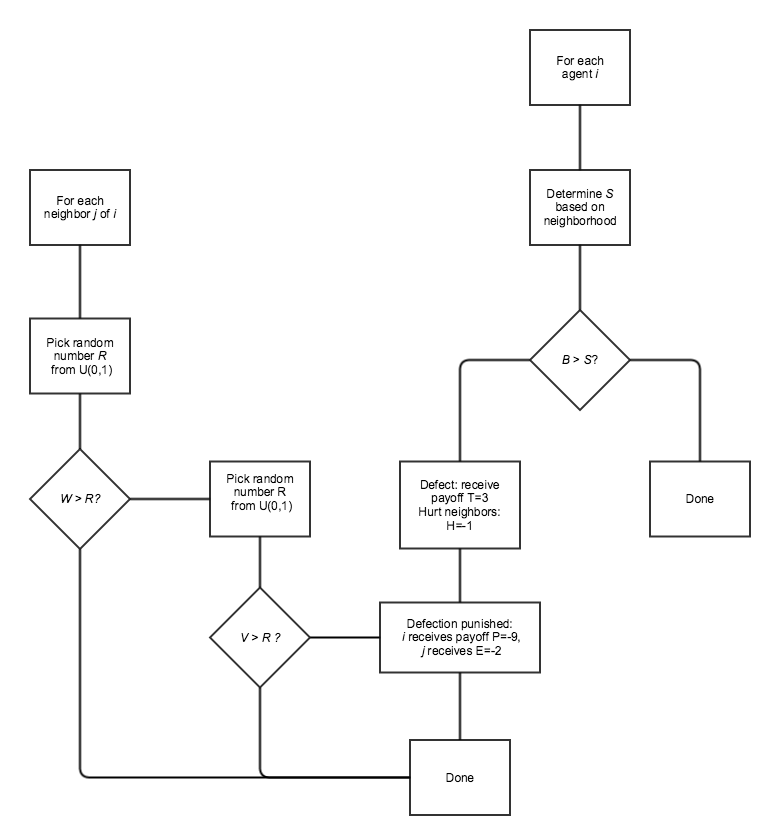
Figure 2. Agent activity in the modified norms game model. 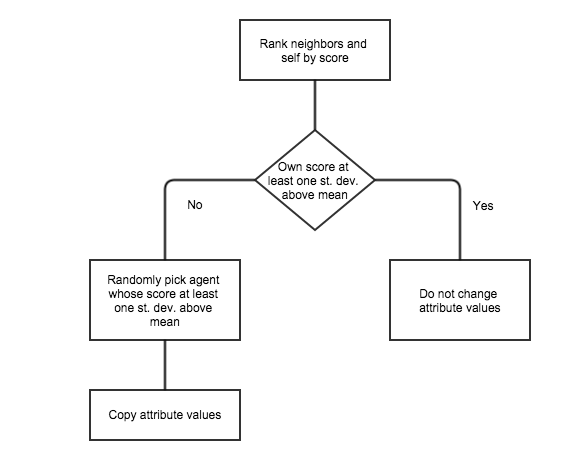
Figure 3. Adaptive mechanism. - 3.11
- All actions undertaken by the agents in the model result in
payoffs distributed according to the same payoff matrix used in the
original norms game.
- 3.12
- After every four rounds each agent is evaluated together
with all of its neighbors. The adaptive process is illustrated in
Figure 3. At the beginning,
the neighborhood is ranked by their payoffs. If the agent itself falls
at least one standard deviation above the neighborhood's mean payoff
value then the agent simply retains its current behavior and does not
consider any further options. If it does not, then it randomly chooses
any neighbor which lies at least one standard deviation above the
neighborhood mean and copies that agent's behavior for its own. The
reasoning behind this choice is simple: the agents have a rough idea of
who in their neighborhood is doing pretty well and who is not. If they
are doing well, then they are content with their current strategy.
Otherwise they attempt to imitate a strategy of some well-off agent in
their neighborhood.
- 3.13
- After the adaptive process is done each agent's behavior
has a small probability of being randomly modified. This represents
imperfect imitation of behaviors. The modification is done as mutation
in the original norms game where each bit has a 1% chance of being
flipped.
- 3.14
- The norm is said to emerge in the model if the average
boldness of the agent population is low and the average vengefulness of
the agent population is high. This represents the agents'
internalization of cooperation-enabling behavior. It should be noted
that cooperative behavior can be present even in agents who do not
internalize the norm. For example an agent might decide not to defect,
even though it has a high boldness value, simply because it thinks that
the probability of getting caught is too high. Thus, it is important to
distinguish between cooperative behavior and the internalization
of cooperation-enabling dispositions.
Grid Model Design
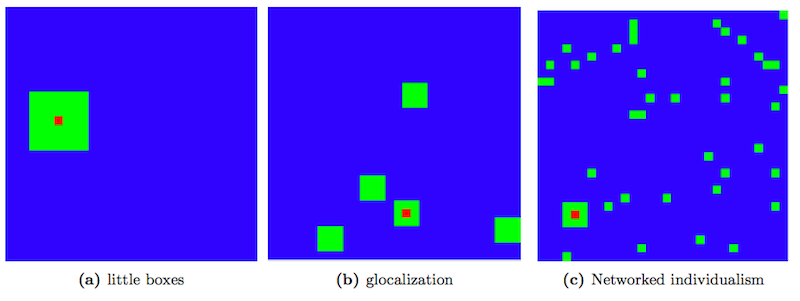
Figure 4. Neighborhood types in the grid model. Red cell is the inspected agent, green cells represent neighborhood cells. - 3.15
- In the second implementation of the model, the network
topology is replaced by a spatial environment based on a rectangular
grid. Each cell in the grid is occupied by a single agent. The most
important way in which the two different models presented here differ
is the way agents' neighborhoods are defined. The grid-based model
makes use of the neighborhood typology introduced by Wellman (2002). Thus, three different
types of neighborhoods were implemented into the model, to reflect the little
boxes, glocalization, and networked
individualism neighborhood patterns.
- 3.16
- The little boxes mode is represented
simply as a Moore neighborhood of radius 3 surrounding the agent's
cell. This gives each agent precisely 48 neighbors. To represent the glocalization
pattern each agent has a "core" neighborhood of the 8 surrounding cells
as well as a number of "satellite" communities composed of \(3\times3\)
cell squares of agents, randomly dispersed throughout the grid. The
total number of communities (including the core) is taken from a normal
distribution with mean \(\mu = 5.5\) and standard deviation \(\sigma =
0.5\). This gives every agent a mean number of 48.5 neighbors. Finally,
networked individualism was implemented in two
different ways. In the first approach the agent retains its core
neighborhood of the 8 surrounding cells, with another 40 agents chosen
randomly on the grid. In the second approach all 48 neighbors were
selected randomly from the grid. Figure 4
provides a visual overview of the different neighborhood types.
- 3.17
- The agent-decision making process as well as the strategy
adaptation and modification processes work in precisely the same way as
described in the network model design, with agents' neighborhoods based
on the definitions of the three types described above.
- 3.18
- All of the model versions described here were developed in
the Java-based MASON package (Luke et
al. 2005) which is specifically tailored for agent-based
model programming. All of the model version were verified for proper
functionality with code walkthroughs using the Java debugger and unit
tests, and with the help of supporting print statements as well as
visual neighborhood displays for neighborhood testing. The source code
for all model versions is available at www.openabm.org/model/4714/.
Experimental Design
- 3.19
- Experimentation consisted of multiple batches of a large number of simulation runs in both model cases. For the network version 100 simulation runs consisting of 1000 agents were executed for 5,000 time steps for each of the three network topologies (random, small-world and scale-free) and for four mean witnessing probability values \(W = 0.2\), \(0.1\), \(0.01\), \(0.001\), for a total of 1200 simulation runs. In the case of the grid version 100 simulation runs consisting of 10,000 agents (laid out on a \(100\times100\) square grid) were executed for 5,000 time steps for each of the four neighborhood types (little boxes, glocalization, and the two versions of networked individualism) and for each of four mean witnessing probability values \(W = 0.2\), 0.1, 0.01, 0.001, giving a total of 1600 runs. For all the results collected for a single parameter setting (neighborhood type/witnessing probability pair) the averages across all such executed simulation runs were recorded and stored. The re-implemented model originally designed by Axelrod was run 100 times for 10,000 time steps. The run lengths for each of the different model versions were chosen so as to allow the system to reach a state of (dynamic) equilibrium.
 Results
Results
- 4.1
- The first test amounted to checking whether running the
re-implementation of the original model, results in behaviors which
resemble those described in Axelrod's paper (that is, almost ubiquitous
collapse of the norm and very rare establishment on the other hand).
Following in the footsteps of others who have re-implemented this model
(Galán & Izquierdo 2005),
the norm was defined to have collapsed at a given time step whenever
the average boldness in the agent population was at
least 6, while at the same time the average vengefulness
was at most 1. Similarly, the norm was defined to have been established
at a given time step whenever the average boldness
was at most 2, and the average vengefulness was at
least 5. Axelrod (1986)
arrives at the correct conclusion that the norm collapses most of the
time, although his results were in fact inconclusive. In their
re-implementation Galán and Izquierdo (2005)
observed that this variability in simulation runs was due to rather
short run times in the original experiments. However, they demonstrated
that in the long run, the norm does indeed collapse a vast majority of
the time. The results obtained from the implementation developed for
the purposes of this study visually match those of Galán &
Izquierdo (2005). Figure 5 shows the proportion of runs
resulting in either norm collapse or establishment over time.
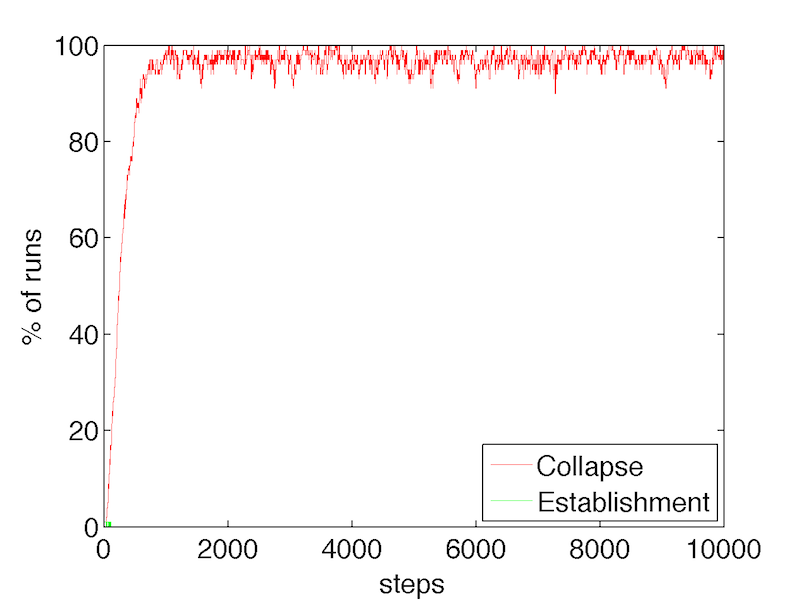
Figure 5. Proportions of runs that result in norm establishment vs. norm collapse in the re-implementation of the original Axelrod model. 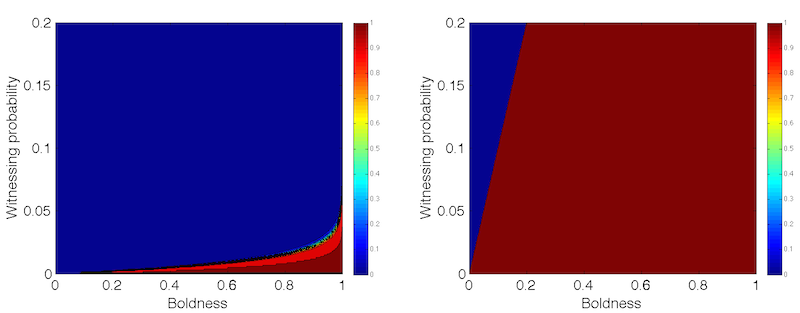
Figure 6. Contour plots of defection probability in small-world/random networks (left) with mean degree 100 and \(\sigma =10\), and scale-free networks (right). - 4.2
- An analysis of the modified network model is provided next.
To begin with, the expected payoffs associated with defection and the
expected costs associated with enforcement are tied to the size of
agents' neighborhoods. Ignoring the effect of noise, the probability of
defection of a random agent with boldness \(b\), assuming a fixed
witnessing probability \(W\) can be calculated as follows:
$$ P(S < b) = P(1-W)^n < b) = P \left( n < \frac{\ln(1-b)}{\ln(1-W)} \right) $$ Here \(n\) is the number of neighbors to which the agent is connected in the network. Thus, for random and small-world networks where node degree is normally distributed the following is true:
$$ P(S < b) = \frac{1}{2} \left[ 1 + \mathrm{erf} \left( \frac{\frac{\ln(1-b)}{\ln(1-W)}-\mu}{\sigma\sqrt2} \right) \right] $$ Here, the right-hand side is obtained by simply substituting into the cumulative distribution function for the generalized normal distribution with mean \(\mu\) and standard deviation \(\sigma\). Similarly, the same expression can be evaluated for scale-free networks where the complementary cumulative degree distribution scales with \(n^{-2}\). Thus, the probability of defection for scale-free networks follows:
$$ P(S < b) = 1- \left( \frac{\ln(1-b)}{\ln(1-W)} \right)^{-2}$$ - 4.3
- The contour plots for both probabilities as functions of
boldness and witnessing probability are shown in Figure 6. Having
expressed the defection probabilities, the expected cost of enforcing
punishment, \(E(C_P)\), can be calculated. Specifically, for an agent
with vengefulness \(v_i\), and assuming \(E=-2\) as enforcement cost,
the following equality holds:
$$ E(C_P) = 2 \cdot W \cdot v_i \cdot \sum^n_{j=1} P(S < b_j) $$ Here \(n\) is the number of neighbors and \(W\) is the mean witnessing probability. Hence, the cost per unit of vengefulness:
$$ c_{UV} = 2 \cdot W \cdot \sum^n_{j=1} P(S < b_j) $$ - 4.4
- Based on the previous analysis of the defection probability
the cost can be derived explicitly. Thus, for random and small-world
networks the cost at the beginning of a simulation run when the
expected boldness is equal to 0.5 approaches zero
for \(W > 0.01\). If \(W < 0.01\), the system undergoes a
phase transition and \(C_{UV}\) scales with \(nW\). As the average
boldness of an agent's neighborhood changes, so does the value of \(W\)
at which the described transition occurs. For scale-free networks the
costs scale with \(nW\) if and only if \(b > W\). The costs
approach zero only when average boldness is lower than or equal to the
witnessing probability. (see Figure 6).
- 4.5
- Similarly the expected payoffs associated with defection,
\(E(P_D)\) can also be derived. For any given agent with boldness \(b\)
and mean witnessing probability \(W\), the following holds:
$$ E(P_D) = 3\cdot P(S < b)-9 \cdot P(S < b) \cdot W \cdot n \cdot \langle v \rangle $$ Here, \(\langle v \rangle\) is the average vengefulness in the agent's neighborhood. Obviously the payoffs are zero in the regions where the probability of defection is zero. However, in regions where \(P(S < b) \rightarrow 1\), the following is true:
$$ E(P_D) = 3- 9 \cdot W \cdot n \cdot \langle v \rangle \qquad \mathrm{if~}P(S < b) \rightarrow 1 $$ And so, payoffs from defection are positive whenever \(Wn\langle v \rangle < 1/3\). This is trivially true whenever \(Wn < 1/3\). One important observation to be made here is that while the temptation payoff remains the same (as it was established that it is in fact independent of the population size) the punishment component grows linearly with the number of neighbors.
- 4.6
- This analysis shows that the agents' propensity to punish
defectors depends heavily on the mean witnessing probability in the
system and the size of the agents' neighborhoods. The larger the social
network of an agent, the more costly it is to be vengeful. On the other
hand, smaller individual probabilities of witnessing defections result
in decreased enforcement costs in the long run. Unlike the original
norms game where population and the expected probability of being seen
remained fixed, these dependencies can have important effects on the
simulation results. It remains to be seen how the addition of noise and
the different spatial topologies affect the behavior of the system.
- 4.7
- Figures 7–8 show that especially in the cases
of random and small-world networks the system results into a state with
low levels of boldness and defections and
tolerable levels of vengefulness (the figures have
semi-logarithmic axes – this was done to illustrate temporal trends in
a more visible manner). Note that in these types of networks agents
have on average 100 neighbors, whereas in the scale-free networks the
typical number of neighbors would be very low (due to the power law
nature of its node degree distribution). It is precisely the way in
which the probability of being seen is implemented in the network model
which dramatically affects the probability of norm emergence. Figure 9 shows the relationship between
neighborhood size (degree) and average agent attributes. The analysis
shows that neighborhood size becomes a factor when witnessing
probability is neither too low nor too high. When \(W = 0.2\)
vengefulness becomes costly. Conversely, when \(W = 0.001\), the impact
of witnessing probability on the expected payoffs begins to exceed that
of neighborhood size by far. This is in line with the previous
mathematical analysis.
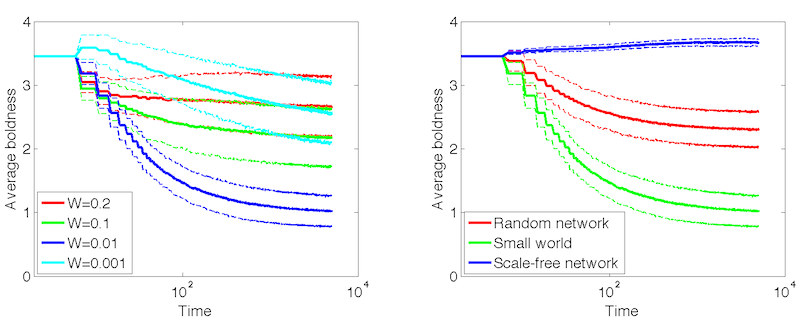
Figure 7. Average boldness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\). 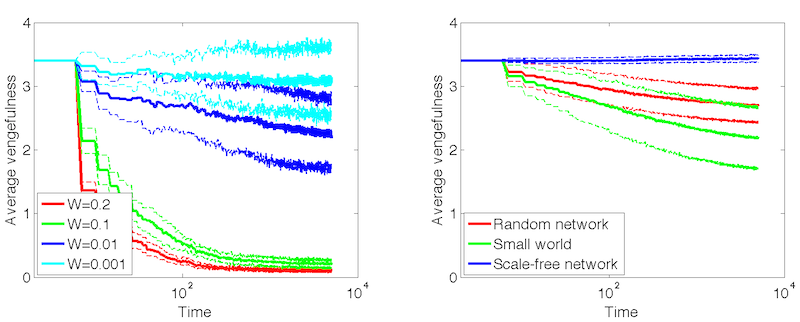
Figure 8. Average vengefulness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\). - 4.8
- It is also worth noticing the different dynamics of the
population boldness with regard to the witnessing probability (see
Figure 7). When \(W \geq 0.1\),
boldness levels decrease only slightly. This is because with perfect
information, the agents' probability of defection would have been zero
for the most part (see Figure 6).
However agents who still defect due to imperfectly estimating
probabilities of being seen or because they represent outliers in terms
of their neighborhood size receive negative payoffs for their action
since \(Wn > 1/3\). This creates adaptive pressure towards lower
boldness levels in this sub-population of agents. When \(W = 0.01\)
boldness decreases because the expected defection payoffs are negative
for most agents. When \(W = 0.001\) there is a small uptick in boldness
followed by a slow decrease even though the payoffs are now positive.
However, once a big enough fraction of agents' neighbors become
defectors, the agents are hurt more than they can receive from their
own defections, due to their large number of neighbors. Thus, small
clusters of cooperators which can appear by chance will have the
opportunity to spread throughout the population.
- 4.9
- Figure 8 shows that
vengefulness decreases only for high values of \(W\). When \(W \leq
0.01\) enforcement is fairly cheap, and since boldness is
self-regulated, there is little adaptive pressure on vengefulness.
Although, the actual cost of punishment is always non-zero,
vengefulness levels of most agents will be allowed to remain fairly
high, since defection ceases to occur due to decreasing levels of
boldness. Moreover, the actual probability of enforcing punishment for
any given agent is low, due to the low likelihood of seeing defections.
In this way, there is no adaptive pressure[2]
exerted on the vengefulness attribute. The effect of added noise is
most noticeable when \(W \geq 0.1\). The expected costs of enforcement
are null, because no one is expected to defect. However, occasional
misguided defectors (those affected by the added noise) still incur
unnecessary costs on enforcers. Thus, for such large values of \(W\),
the population vengefulness will converge to a quiescent state.
Finally, the simulation results show that network topology does play
some role in the rate at which boldness and vengefulness decrease.
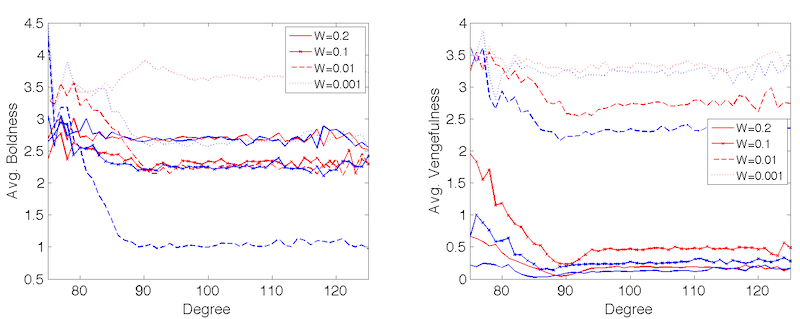
Figure 9. Relationship between neighborhood size (degree) and agent attributes for different values of \(W\). Red lines show values for small-world networks, blue lines show values for random networks. - 4.10
- To examine how the agents' strategy adaptation heuristic
affects the resulting system behavior, the same runs were performed,
but with the payoff mechanism implemented as in Axelrod's norms game,
i.e. letting the payoffs reset after every four rounds. Figures 10–11
shows the results of these runs. It is clear that especially in cases
of low vigilance the system reverts to the state described by Axelrod (1986) with prevailing high
values of boldness and low levels of vengefulness essentially
representing norm collapse. Thus, the heuristic is actually responsible
for a large part of the interesting dynamics that can be seen in the
new version of the model. This suggests that initial small advantages
or disadvantages of certain agents in the beginning of the runs with
accumulating payoffs can have potentially large effects on the
resulting population average. This in turn depends on the initial
conditions of the system – the exact topology of the network and the
initial strategies of agents in specific locations within the network.
To test the sensitivity of the system towards changing these initial
conditions, additional runs were executed. First, For each of the model
configurations described in the Experimental Design section a single,
fixed network was used in 100 runs, randomly perturbing only the
initial strategies of the agents in specific nodes. Figure 12 shows the dispersion of the
resulting population averages at the end of each run. Next, extreme
initial conditions were tested as well. Each of the configurations was
run from four different initial population settings:
- Avg. Boldness: 1/7. Avg. Vengefulness: 1/7.
- Avg. Boldnes: 1/7. Avg. Vengefulness: 6/7.
- Avg. Boldness: 6/7. Avg. Vengefulness: 1/7.
- Avg. Boldness: 6/7. Avg. Vengefulness: 6/7.
- 4.11
- The changes in the average population strategy from these
initial conditions are shown in Figure 13.
The resulting dynamics reveal that the system is in fact fairly "stiff"
in that the initial conditions determine much of the resulting location
of the population average in the strategy state space. Some cases show
less dependence, such as runs with low levels of \(W\), or populations
with low initial vengefulness levels. On the other hand, populations on
scale-free networks are much "stiffer" than the other network
topologies.
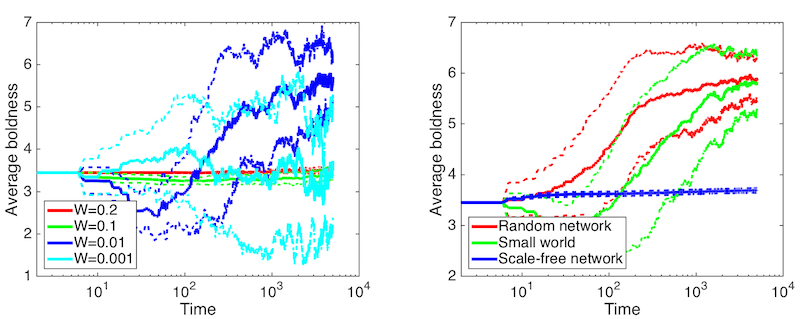
Figure 10. Runs with payoffs resetting every 4 rounds. Average vengefulness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\). 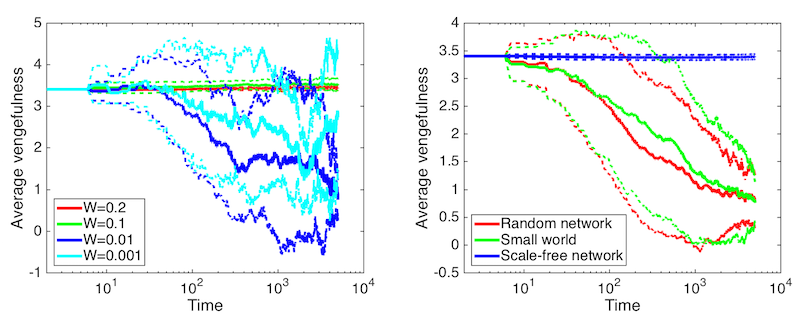
Figure 11. Runs with payoffs resetting every 4 rounds. Average vengefulness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\). 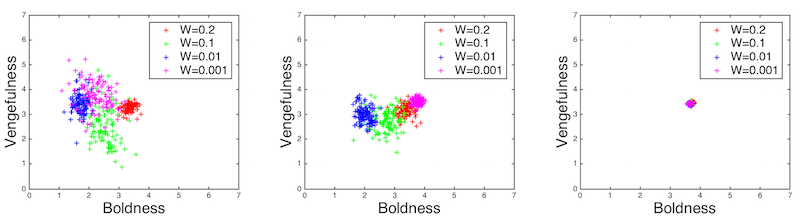
Figure 12. Average population boldness and vengefulness levels at ends of individual runs. LEFT: Small-world network. CENTER: Random network. RIGHT: Scale-free network. 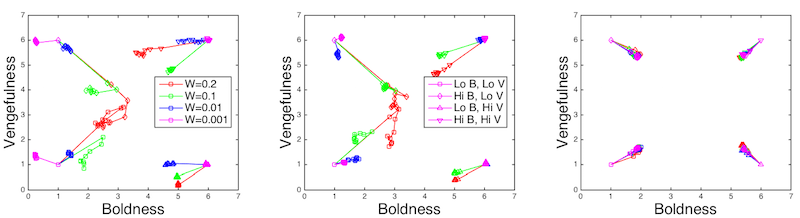
Figure 13. Change of average population boldness and vengefulness levels during runs from extreme initial conditions. Each point represents 1000 steps. LEFT: Small-world network. CENTER: Random network. RIGHT: Scale-free network. - 4.12
- When we turn our attention to the grid-based model the
situation remains similar (see Figures 14–15). It is necessary to keep in mind
that the dynamics are somewhat affected by the smaller average
neighborhood size. However, the decrease in boldness as well as
vengefulness for large witnessing probabilities is still noticeable.
The forces driving the decrease are the same as in the case of the
network model. The main difference lies in the behavior of the system
under low levels of witnessing probability. When \(W = 0.01\) the
expected costs of defection are now positive due to the smaller
neighborhoods. However, just as in the network model, the hurtfulness
of neighbors' defections still quickly exceeds the advantages of one's
own defections, and yet again any clusters of cooperators will be
allowed to spread. Once boldness falls to a certain level, the fraction
of "free" enforcements increases and thus some agents with higher
vengefulness levels will be allowed to survive. This explains the
eventual slight increase in the average vengefulness as well as the
growing variance when \(W = 0.01\). The same arguments hold for
population boldness dynamics when \(W = 0.001\). However, what is most
intriguing are the initial decreases in vengefulness under the lower
levels of \(W\), which eventually taper off to zero in the case when
\(W = 0.001\). Although the rates of defection in the systems are
higher, now that neighborhood sizes are smaller which naturally results
in higher costs of vengefulness, this alone cannot explain the observed
dynamics. Indeed, the qualitative difference between the temporal
trends of vengefulness of the little boxes neighborhoods
and the other neighborhood types are obvious. Hence, some of the
dynamics can only be explained by the chosen neighborhood topology.
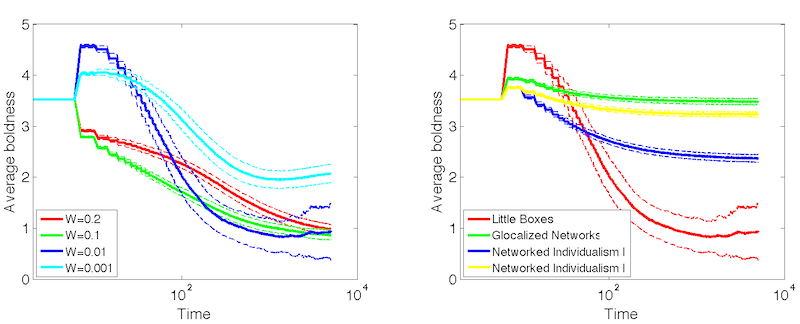
Figure 14. Average boldness over time. LEFT: Little boxes at different witnessing probabilities. RIGHT: Different neighborhood types at witnessing probability \(p = 0.01\). 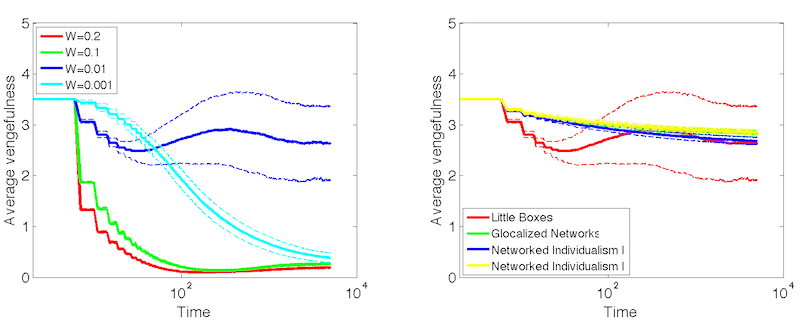
Figure 15. Average vengefulness over time. LEFT: Little boxes at different witnessing probabilities. RIGHT: Different neighborhood types at witnessing probability \(p = 0.01\). - 4.13
- Tracking average population values alone on its own cannot
provide full insight into the dynamics of the model. To this end,
visualizations of a large number of simulation runs were tracked, to
elucidate the system's state over different periods of time. Figures 16–17
show the changes in the spatial distribution of population vengefulness
over a long period of time for two different neighborhood types. One
can notice that under certain configurations, and barring mutation, the
system can reach a state close to a true equilibrium (see Figure 16). On the other hand, when
employing the glocalized neighborhood, the model
reaches a dynamic equilibrium, where the attributes of individual
agents are in flux, yet on average the system retains the same
aggregate state from a qualitative point of view. The same types of
dynamics were witnessed in simulation runs employing the networked
individualism neighborhood types.

Figure 16. Vengefulness in the population after 1,000 steps (left) and 10,000 steps (right) with little boxes neighborhoods and \(W = 0.01\). Showing a single representative run. 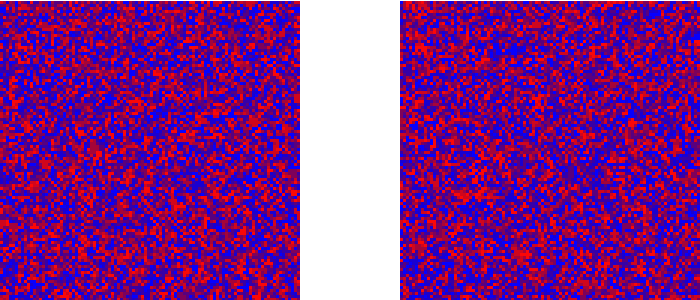
Figure 17. Vengefulness in the population after 1,000 steps (left) and 10,000 steps (right) with glocalized neighborhoods and \(W = 0.01\). Showing a single representative run.
 Discussion
Discussion
- 5.1
- The model results show a number of interesting behaviors.
Firstly, the probability of an individual witnessing a defection plays
an important role in the global behavior of the system, and as the
results have shown even very small probabilities on the individual
level can discourage agents from their defection if they have enough
neighbors. Using the mechanism for witnessing defections (and, perhaps
more importantly, the expectations for witnessing defections) has
prevented cases of norm collapse in the system even without the use of
metanorms. This is achieved by a sort of "distributed vigilance"
mechanism – agents as individuals will rarely witness a defection, but
because of the effect of sheer neighborhood size and the relatively low
costs and low adaptive pressure on enforcement, defectors are still
being continuously policed. Moreover, due to the effect of neighborhood
size and the variation in the spatial distribution of traits, boldness
is effectively self-regulated – pockets of defectors hurt each other
more than they can gain from their individual defections, which allows
pockets of cooperators to fortuitously expand throughout the
environment. On the other hand, a higher probability of seeing an
individual's defection does not necessarily ensure a lower global rate
of boldness, mostly due to low adaptive pressure. However, the
emergence of the norm is not guaranteed. Specifically, in cases of low
vigilance, the average vengefulness level in the population is a result
of random drift. Furthermore, the heuristic which led agents to adopt
other agents' strategies based on their aggregate performance over the
course of the entire run has proved to be a major contributor to the
resulting system states. If agents are unable to clearly judge the
effects of strategies and just blindly copy agents who have had success
in the past, norm collapse actually ceases to be the norm.
- 5.2
- The model also demonstrated sensitivity to the different neighborhood types. The results showed qualitative differences in the overall trends in agents' adaptation across different neighborhood structures. The little boxes neighborhood mode also showed promising population dynamics in terms of boldness and vengefulness with certain levels of vigilance. The first hypothesis of this paper stated that the glocalization and networked individualism types would lead norm instability due to the fragmented and pluralistic nature of communities, while the alternate hypothesis suggested that it is precisely because of this diversity that individuals will be able to better "sample" the fitness landscape and find their way to an optimal solution faster. From the analysis of the simulation runs it would seem that there is more evidence for the first hypothesis. However, it is important to note that this comes at a price: there is always a trade-off between stability (norm emergence) and diversity as shown in Figure 16.
 Conclusion
Conclusion
- 6.1
- Previous modeling efforts have elicited conditions for norm
emergence on networks either with the use of Axelrod's metanorms
mechanisms (Galán et al. 2011;
Mahmoud et al. 2012b,
2012c, 2013), or with entirely
different mechanisms for norm spreading (Anghel
et al. 2004). Conversely, some simulation models have shown
the ability to establish norms with the use of imtitation-based norm
adoption mechanisms, yet without any network structure (Andrighetto et al. 2008)
or for different categories of norms (Epstein
2001). The model analyzed here has shown the dynamics of norm
emergence on network topologies for single-generation populations of
adaptive agents.
- 6.2
- Moreover, the agent-based model presented here showed that
neighborhood structure and social network topology do in fact have an
effect on the emergence of norms. Furthermore, by representing vigilance
as a social phenomenon and by focusing on behavior
adaptation rather than evolution the simulation results showed the
significance of neighborhood size, vigilance itself
and most importantly of the interplay of these two factors.
- 6.3
- The model was intended to be left simple and abstract in
order to provide a first glimpse into the effect of social topologies
on the emergence of norms. There is certainly ample room for
modification. For instance, it might be even more realistic to
introduce and calibrate a dynamic probability of witnessing defections
for individuals rather than use a static one throughout the entire
simulation run. Then there is the question of how many witnesses does
it usually take to prevent a defection? In the model it sufficed to
have just one witness, but this number might be different under certain
circumstances. Perhaps if the model employed a weighted social network,
then agents could possess a weight threshold for witnesses that would
discourage them from defecting. The resulting dynamics would also most
certainly change had the payoffs been calibrated differently. Moreover,
further modifications to the agents' scope of knowledge would certainly
yield new interesting results. For example, how would the outcome
change if agents knew of their neighbors vengefulness levels and would
be able to incorporate this knowledge into their defection decision? In
the model described here the agents will not defect if they think they
will be seen, regardless of the likelihood of actually being punished
upon being caught. One could make the claim that more intelligent
agents will learn from past experiences and tend to defect even in
highly exposed situations, if their neighbors are continually reluctant
to enforce punishment. However, these modifications are beyond the
scope of the current work, which simply sought to extend the original
norms game on networks with defection decisions based on the witnessing
abilities of the agents' direct neighbors.
- 6.4
- Most importantly, it is necessary to constantly test how realistic are the topologies used as a representation for social communities. The faithfulness of the small-world network and scale-free network representations has been recently questioned (Shekatkar & Ambika 2014). The accuracy of Wellman's neighborhood typology is also in question as it has never been thoroughly validated. Thus, it is important to further explore and re-evaluate our view and understanding of community structures in contemporary society, and validate these claims with well-designed studies before we can start to fully consider the validity of models regarding the emergence of norms, such as the one presented in this paper.
 Acknowledgements
Acknowledgements
- I would like to thank Claudio Cioffi-Revilla for his support and guidance. I would also like to thank Andrew Crooks for helpful advice and valuable feedback on drafts of the paper.
 Notes
Notes
-
1 This
is similar to the police strategy of frequent motor patrolling of crime
hot-spots. Studies have shown that just having enough police presence
on its own leads to decreased crime rates in the affected areas (Sherman & Weisburd 1995).
2 The term adaptive pressure is used in a sense similar to "selection pressure" in evolutionary algorithms when changes in the agents' strategies result in a change in the distribution of payoffs.
 References
References
- ALBERT, R., & Barabási,
A.-L. (2002). Statistical mechanics of complex networks. Reviews
of Modern Physics, 74, 47–97. [doi:10.1103/RevModPhys.74.47]
ANDRIGHETTO, G., Campenni, M., Cecconi, F. & Conte, R. (2008). How agents find out norms: A simulation based model of norm innovation. NORMAS, Volume 8, 16–30.
ANGHEL, M., Toroczkai, Z., Bassler, K.E. & Korniss, G. (2004). Competition-driven network dynamics: Emergence of a scale-free leadership structure and collective efficiency. Physical Review Letters, 92(5), 0587011–0587014. [doi:10.1103/PhysRevLett.92.058701]
AXELROD, R. (1986). An Evolutionary Approach to Norms. The American Political Science Review, 80(4), 1095–1111. [doi:10.2307/1960858]
AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. In Conte R, Hegselmann R, Terna P, editors. Simulating Social Phenomena (Lecture Notes in Economics and Mathematical Systems 456). Berlin: Springer-Verlag. [doi:10.1007/978-3-662-03366-1_2]
AXTELL, R., Epstein, J., & Young, P. (2001). The emergence of classes in a multi-agent bargaining model. In S. Darlauf & P. Young (Eds.), Social Dynamics. Cambridge, MA: MIT Press.
BEHESHTI, R., & Sukthankar, G. (2014). A normative agent-based model for predicting smoking cessation trends. In Proceedings of the 2014 international conference on Autonomous agents and multi-agent systems (pp. 557–564). International Foundation for Autonomous Agents and Multiagent Systems.
BICCHIERI, C. (2006). The Grammar of Society. New York, NY: Cambridge University Press.
CASTELFRANCHI, C. & Conte, R. (1995). Cognitive and social action. London: UCL Press
CENTOLA, D., & Macy, M. (2007). Complex Contagions and the Weakness of Long Ties. American Journal of Sociology, Vol. 113, No. 3, 702–734. [doi:10.1086/521848]
DE MARCHI, S. (2005). Computational and mathematical modeling in the social sciences. Cambridge, UK: Cambridge University Press. [doi:10.1017/CBO9780511510588]
DUNBAR, R. (1992). Neocortex size as a constraint on group size in primates. Journal of Human Evolution, 22(6), 469–493. [doi:10.1016/0047-2484(92)90081-J]
DURKHEIM, E. ([1893] 1997). Division of Labour in Society. New York, NY: Free Press.
EDMONDS, B. & HALES D. (2003). Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation, 6 (4) 11 <https://www.jasss.org/6/4/11.html>.
EPSTEIN, J. M. (2001). Learning to Be Thoughtless: Social Norms and Individual Computation. Computational Economics, 18(1), 9–24. [doi:10.1023/A:1013810410243]
ERDÖS, P., & Rényi, A. (1959). On random graphs I. Publicationes Mathematicae, 6 (pp. 17–61).
FISCHER, C. S. (1975). Toward a Subcultural Theory of Urbanism. American Journal of Sociology, 80(6), 1319–1341. [doi:10.1086/225993]
FISCHER, C. S. (1984). The Urban Experience. New York: Harcourt.
GALÁN, J. M. & Izquierdo, L. R. (2005). Appearances can be deceiving: Lessons learned reimplementing Axelrod's Evolutionary Approach to Norms. Journal of Artificial Societies and Social Simulation, 8 (3) 2 <https://www.jasss.org/8/3/2.html>.
GALÁN, J. M., Łatek, M. M., & Rizi, S. M. M. (2011). Axelrod's Metanorm Games on Networks. PLoS ONE, 6(5), e20474. [doi:10.1371/journal.pone.0020474]
GRANOVETTER, M. S. (1973). The Strength of Weak Ties. The American Journal of Sociology, 78(6): 1360–1380. [doi:10.1086/225469]
HALES, D. (2002). Group Reputation Supports Beneficent Norms. Journal of Artificial Societies and Social Simulation, 5 (4) 4 <https://www.jasss.org/5/4/4.html>.
HEDSTRÖM, P. (2005). Dissecting the social: On the principles of analytical sociology. Cambridge, UK: Cambridge University Press. [doi:10.1017/CBO9780511488801]
KITTOCK, J.E. (1995). Emergent conventions and the structure of multi-agent systems. In: Nadel, L. & Stein, D.L. (Eds.), 1993 Lectures in Complex Systems. Boston, MA: Addison-Wesley.
LUKE, S., Cioffi-Revilla, C., Panait, L., Sullivan, K., & Balan, G. (2005). Mason: A multiagent simulation environment. Simulation, 81, 517–527. [doi:10.1177/0037549705058073]
MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2012). Overcoming Omniscience for Norm Emergence in Axelrod's Metanorm Model. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VII (pp. 186–202). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-35545-5_11]
MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2012b). Norm emergence: Overcoming hub effects in scale free networks. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VII (pp. 136–150). Springer Berlin Heidelberg.
MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2012c). Establishing norms for network topologies. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VII (pp. 203–220). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-35545-5_12]
MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2013). Norm Emergence through Dynamic Policy Adaptation in Scale Free Networks. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VIII (pp. 123–140). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-37756-3_8]
MANHART, K., & & Diekmann, A. (1989). Cooperation in 2-and N-Person Prisoner's Dilemma Games: A Simulation Study. Analyse and Kritik, 11(2), 134–153.
NEWMAN, N, Barabasi, A.-L., & Watts, D. (2006). The Structure and Dynamics of Networks. Princeton, NJ: Princeton University Press.
PARSONS, T. (1964). The Social System. New York, NY: The Free Press/Macmillan.
RING, J. (2014). An Agent-Based Model of International Norm Diffusion. Retrieved from http://myweb.uiowa.edu/fboehmke/shambaugh2014/papers/Ring_Diffusion_of_Norms__ABM_Approach.pdf. Archived at http://www.webcitation.org/6WmguxHgN.
ROBERTS, S. C., & Lee, J. D. (2012). Using Agent-Based Modeling to Predict the Diffusion of Safe Teenage Driving Behavior Through an Online Social Network. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 56(1), 2271–2275. [doi:10.1177/1071181312561478]
SAVARIMUTHU, B. T. R. & Cranefield, S. (2009). A categorization of simulation works on norms. In G. Boella, P. Noriega, G. Pigozzi & H. Verhagen (eds.), Normative Multi-Agent Systems , Dagstuhl, Germany: Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Germany.
SAWYER, R. K. (2002). Durkheim's Dilemma: Toward a Sociology of Emergence. Sociological Theory, 20(2), 227–247. [doi:10.1111/1467-9558.00160]
SHEKATKAR, S. M., & Ambika, G. (2014). Mediated attachment as a mechanism for growth of complex networks. ArXiv: 1410.1870 [cond-mat, physics:physics].
SHERMAN, L. W., & Weisburd, D. (1995). General deterrent effects of police patrol in crime 'hot spots': A randomized, controlled trial. Justice Quarterly, 12(4), 625–648. [doi:10.1080/07418829500096221]
TÖNNIES, F. (1957). Community and Society. New York, NY: Courier Dover Publications.
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of "small-world" networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]
WELLMAN, B. (1983). Network Analysis: Some Basic Principles. Sociological Theory 1:155–200. [doi:10.2307/202050]
WELLMAN, B. (2002). Little Boxes, Glocalization, and Networked Individualism. In M. Tanabe, P. van den Besselaar, & T. Ishida (Eds.), Digital Cities II: Computational and Sociological Approaches (pp. 10–25). Springer Berlin Heidelberg. [doi:10.1007/3-540-45636-8_2]
WILENSKY, U., & Rand, W. (2007). Making models match: replicating an agent-based model. Journal of Artificial Societies and Social Simulation, 10 (4) 2 <https://www.jasss.org/10/4/2.html>.
WIRTH, L. (1938). Urbanism as a Way of Life. American Journal of Sociology, 44(1), 1–24. [doi:10.1086/217913]