 Abstract
Abstract
- As they involve relationships between interacting
individuals and groups, social systems can be described at different
levels of resolution. In a number of modeling cases, only one of these
levels is explicitly represented. In order to study phenomena where
both individual and collective representations are needed, multi-level
modeling is a good approach as it explicitly represents these different
levels. We propose to consider a multi-level representation from a
multi-modeling point of view. This perspective allows explicitly
specifying the level's relationships and, therefore, to test hypothesis
about interaction between individuals and groups in social systems. We
define a framework to better specify the concepts used in multi-level
modeling and their relationships. This framework is implemented through
the AA4MM meta-model, which benefits from a middleware layer. This
meta-model uses the multi-agent paradigm to consider a multi-model as a
society of interacting models. We extend this meta-model to consider
multi-level modeling, and present a proof of concept of a collective
motion example, where we show the advantages of this approach for the
study of social phenomena.
- Keywords:
- Multi-Level, Multi-Model, Multi-Agent, Collective Motion
 Introduction
Introduction
- 1.1
- In this article, we are interested in the design or the
study of complex systems. Simulation is an important tool for this
activity because it allows testing different alternatives and different
scenarios while limiting experimentation costs. Complex systems
naturally involve at least two levels of representation: local and
collective. The former corresponds to the micro level while the latter
corresponds to the macro level of the phenomenon.
- 1.2
- As they involve relationships between interacting
individuals and groups, social systems can be considered as complex
systems (Goldspink 2000).
Spatial distribution of the urban population and collective motions
like crowd flow and urban mobility are good examples of such systems.
All these social phenomena involve at least two levels of
representations whereas, in a number of modeling cases, only one is
explicitly represented.
- 1.3
- Let us consider the example of pedestrians walking in a
street. At the micro level, each of them moves individually, according
to his/her personal goal, but the trajectory he/she takes is influenced
by other pedestrians' behaviors. When these pedestrians evolve and
interact at micro level, they can form a collective motion phenomenon
of a crowd at macro level. This macro structure can be considered on
its own with its proper attributes (common goal, average density,
speed) and behaviors (Musse &
Thalmann 1997). In fact, when describing this phenomenon, one
can consider both levels: the micro level (pedestrians walking in the
street) or the macro level (crowd or groups formation, extinction,
evolution and interaction between macro level entities).
- 1.4
- In order to study such phenomena (with individual and
collective representations), multi-level modeling is a good approach as
it explicitly represents these different levels. In this perspective,
the different levels can coexist and influence each other. This
multi-level approach could be used, for instance, when there is a lack
of expressiveness of one level and a second one is needed; when
available data explicitly refer to different levels of representation;
or when the modeling question is explicitly to study the mutual
influences between levels whose dynamics have to be coupled.
- 1.5
- However, the most adapted formalism for describing a system
may depend on the level of resolution. Moreover, each level is more
likely to be described at specific spatial and temporal scales. For
instance, in collective motion phenomena, individual-based formalisms
are more adapted for representing individuals evolving at micro level
while equation-based formalisms are more convenient for describing the
phenomenon as a flow at macro level (Vo
et al. 2012; El Hmam et al.
2006). In other words, a multi-level model may imply
heterogeneity of representations.
- 1.6
- In this case, a multi-level representation corresponds to
different models (one for each level of description). The question
becomes how to integrate these models, which may use different spatial
and/or temporal scales and possibly with different formalisms. Such
integration is not trivial as it underlies issues about the consistency
of the resulting representation: how to manage the different
formalisms? How to have a sufficiently rigorous process to guarantee
some validity of the obtained integration? We have to consider these
issues from the multi-modeling perspective.
- 1.7
- The AA4MM (Agents and Artifacts for Multi Modeling)
meta-model (Siebert et al. 2010a)
answers these integration issues of heterogeneous models using a
co-simulation approach: a formalism-specific simulator executes the
dynamics of each model. AA4MM relies on a multi-agent perspective where
each model is seen as an agent and the interactions between agents
correspond to data exchanges between simulators. The multi-model is
seen as a multi-agent system (MAS).
- 1.8
- The advantage of a meta-model for multi-modeling is that it
allows directly manipulating the multi-modeling's concepts. These
concepts have semantics that put constraints on the design process
preventing the creation of ill-formed multi-model (Sprinkle et al. 2010; Cetinkaya et al. 2010). In
other words, using a meta-model is a mean to bring some rigor in the
multi-modeling process (in that sense our approach can be related to
FURM (Ropella et al. 2005)).
- 1.9
- Moreover, the concepts can be matched with an existing
multi-modeling formalism (for instance the DEVS formalism (Zeigler et al. 2000)). The
meta-model's constraints can then be expressed in this formalism and
the resulting multi-model can be transformed into executable software.
To sum up, this meta-model approach allows passing from the rigorous
design of a multi-model to its implementation as a middleware with a
clear separation of the different levels of question. In this article,
we will be more focused on the conceptual and semantic aspects of
multi-level modeling rather than on the formalism.
- 1.10
- In the next part, we present different facets of multi-level modeling that involve different kinds of interactions between levels and that correspond to different modeling objectives. Based on similarities between them, we propose in section 2.3 a generic framework for multi-level dynamics coupling. In section 3, we detail the implementation of this framework in the AA4MM meta-model. As multi-level representations were not included in AA4MM's original specifications we explain how AA4MM is extended to multi-level modeling with constraints specific to that kind of representation. Finally in section 4, we present the advantages of our approach through the implementation of variations of a multi-level modeled collective motion phenomenon.
 Multi-level
Representations
Multi-level
Representations
- 2.1
- In this section, we present different approaches (Section 2.1) and different examples (Section 2.2) of multi-level representations in
order to show the different facets of the multi-level modeling. We
present then in section 2.3 a
framework describing in a generic way some of these approaches.
Different approaches of multi-level modeling
- 2.2
- Different approaches of multi-level modeling exist
depending on the relation between the levels and the level-changing
policies. Each of them answers to different representational needs.
- 2.3
- A multi-resolution model (MRM) is a model, or a family of
models, managing several levels of resolution (Davis
& Hillestad 1993). A level is said to be at low
resolution when it represents the phenomenon with a coarse description
(with respect to a high resolution level). Different kinds of MRM can
be considered.
- 2.4
- In a selective viewing model, the simulation takes place
only at the high-resolution level for precision needs. The
low-resolution level is obtained a posteriori for presentation or data
analysis purpose (Klir and Šafarik 2004).
Therefore, the low-resolution dynamics is not explicitly represented in
this case. Only one model describing the high-resolution dynamics is
required.
- 2.5
- In the aggregation-disaggregation approach, two kinds of
entities are considered: the High Resolution Entity (HRE), which
corresponds to a micro representation of the phenomenon and the Low
Resolution Entity (LRE), which corresponds to a macro representation.
Here an entity is only represented at one level of resolution at a
time. Aggregation (from HRE to LRE) and Disaggregation (from LRE to
HRE) operations are used in order to change the level of resolution.
The policy for level changing is determined by the separation of the
global modeled space into different areas called play-boxes. Entities
inside a play-box are all represented at the same level of resolution.
Aggregation-Disaggregation operations are also used to put entities
interacting together at the same levels of resolution.
- 2.6
- In a concurrent representation model, the different levels
of resolution are concurrently maintained and can influence each other.
Here an entity is simultaneously represented at different levels and is
called a Multi-Resolution Entity (MRE) (Natrajan
& Nguyen-Tuong 1995). The MRE uses a mapping function
in order to translate from one level to another (Reynolds et al. 1997). The
interest of such an approach is that it is possible to study the mutual
influences between levels.
- 2.7
- The concept of holon refers to an entity which is
simultaneously a whole and a part. This recursive concept can serve to
describe a complex system in a hierarchical way. Such a description is
called a holarchy. A holon can be considered as an agent. In a holonic
multi-agent system (Rodriguez et
al. 2007), agents organize themselves into holons, that can
then again group themself into holons (super-holons). The politics for
grouping and separating holons depends on pre-defined criteria that can
be based for instance on simulation performance (Demange 2012). When agents
group themselves into a holon, their perceptions and actions are
aggregated into this holon. When a holon splits, each agents recovers
its perceptions and actions. The advantage of such approach is that,
contrary to previous approaches that represent the relationships
between different levels of resolution, the holonic approach focuses on
the formation/separation of higher-level structures.
Some examples of multi-level modeling
- 2.8
- In the simulation of the evacuation of Nha Trang City (Vo et al. 2012), the major issue is
to deal with a huge number of citizen agents evolving on the roads,
which considerably slows down the simulation. To increase simulation's
performance, roads are divided into two kinds of patches: crossroad
patches, and segments of the road patches. In the former, citizen
agents are simulated individually, while the later uses a macro model
of pedestrian flow in order to simulate their moves. Each patch is
represented by a road agent. An organizational meta-model for
multi-scale modeling is used in order to ensure transitions between
patches. Road agents use "capture" and "release" operations on citizen
agents. A road agent manages the execution of all of its captured
citizen agents. A captured citizen doesn't have an autonomous behavior
anymore. When a citizen agent is released by a road agent, it recovers
its autonomous behavior. A road agent captures citizens when they reach
the border segments of the road patch. Then, captured citizens are
considered as pedestrians in the macro model of pedestrian flow. Road
patches determine the movements of captured citizens according to the
macro model, and release them when they exit patches' borders.
- 2.9
- In the 3D real-time multi-agent pedestrians simulation of
Gaud et al. (2008), the
major issue is to deal with computation cost in order to ensure an
acceptable performance for the 3D visualization of the simulation while
managing a large number of agents. The solution is to dynamically
change the level of description in order to have the best trade-off
between the accuracy of the simulation and the computation performance.
A holonic model is used in order to organize and dynamically change the
level of description. Then, in a low level of the holarchy, perceptions
and actions of pedestrian holons are aggregated in a pedestrian super
holon. Physics based indicators are used in order to determine whether
pedestrians should be grouped or considered individually.
- 2.10
- In SIMPOP3 (Gil-Quijano
et al. 2010), a micro model SIMPOPNano, describing the
evolution of a city, is coupled with a mesoscopic model, SIMPOP2,
describing the evolution of a system of cities in order to study their
mutual interactions. The challenge here is to ensure an ontological
translation between levels: the concepts of urban function (from macro
to micro) and spatial efficiency (from micro to macro) are used to
ensure the passage from a level to another.
- 2.11
- In simulBogota (Gil-Quijano
et al. 2010), the challenge is to model the evolution of the
city of Bogotá when having a lack of information on the behaviors of
basic entities (household and housing). In order to deal with this
issue, mesoscopic entities are considered (household and housing
groups) with an arbitrary defined behavior. Then, groups are
dynamically detected and reified at mesoscopic level at each simulation
step using an automated classification mechanism of the micro entities.
When reified, household groups share housing with an auction mechanism
and the micro population evolves based on global rules.
- 2.12
- In (El Hmam et al. 2006),
the hybrid traffic flow approach is to jointly use macroscopic and
microscopic models of a traffic flow in order to take advantage of each
kind of representation. The space is divided into several areas that
are not modeled at the same level. A macro model describing in a global
and aggregated way the phenomenon is used for areas that don't
necessitate a high level of detail. At the opposite, areas where the
traffic flow is more subject to abrupt changes, are represented by a
micro (multi-agent) model. The challenge here is to ensure transition
between models that are not of the same nature, between agents and
aggregated values. An upward agent (from micro to macro) and a downward
one (from macro to micro) are defined to fill these roles.
- 2.13
- All these examples use two models to describe the same
phenomenon at different levels of representation (individual and
collective) and mapping functions to translate a state from one level
to another (Natrajan &
Nguyen-Tuong 1995). They can be related to the problem of
multi-perspective modeling where each sub-model of the multi-model
represents a perspective of the phenomenon (here a macro and a micro
perspective) (Yilmaz et al. 2007).
In order to reconcile these different perspectives a bridge model can
be used (Seck & Honig 2012).
This bridge model links the different perspectives as it represents how
the modeled entities are related in the different models. Therefore,
the bridge model can be in charge of the interactions between these
perspectives as it makes conceptual translations between them by
transforming the exchanged data between the models.
- 2.14
- However, the nature of relationships between levels doesn't
convey the same constraints according to the chosen level-changing
policy. The approaches or examples have to be considered separately
according to the kind of representation of one state of the phenomenon.
Some of them (concurrent representation, selective viewing) represent
simultaneously the same states at two levels of representation whereas
others (aggregation-disaggregation, holonic) consider only one level of
representation at a time.
A framework for multi-level modeling
- 2.15
- The framework we propose is a rephrasing of Bourgine (2008). It makes explicit the
relationships between the two levels (micro and macro) in a complex
system. When doing a multi-level modeling of a complex system, this
framework has to be adapted to fit the chosen level-changing policy. In
this article we specify how to implement it in order to consider
simultaneously two levels of representation.
- 2.16
- When representing an upward relationship (e.g. pedestrians
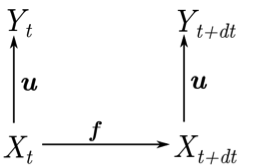
are forming groups), we consider the following elements (see Figure 1):
- Xt is the set of information describing the state of the target system at time t at micro level.
- Yt' is the set of information describing the state of the target system at time t' at macro level. As the macro level is a coarser description of the target system than the micro one, we can state:
- (1) card(Yt') < card(Xt).
- f is a function describing the micro dynamics. It specifies how to pass from Xt to Xt+dt.
- g is a function describing the macro dynamics. It specifies how to pass from Yt' to Yt'+dt'.
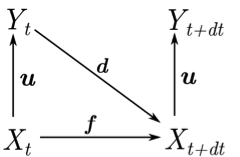
- u is an upward function of integration of Xt ensuring the passage to Yt'. According to constraint (1), it does an aggregation of information describing the phenomenon. This function fills the role of a bridge model as it is a translator between two perspectives of a phenomenon (micro and macro views).
- 2.17
- Time representations at macro and micro levels are
respectively t and t'. This
means that the simulations may a priori have different execution
policies or time steps. By using two notations, we explicitly ask the
question of time correspondence between models. This means that u
has also to manage the temporal mapping between levels.
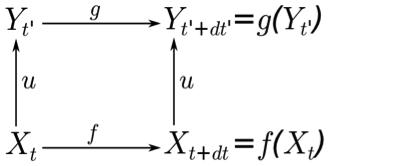
Figure 1. Upward relationship between levels of representation and temporal evolution of the phenomenon. - 2.18
- When representing macro dynamics having an influence on the
micro one (e.g. groups influence pedestrians), a new relationship has
to be added (see Figure 2):
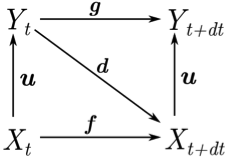
- d is a downward function ensuring the translation of Yt' in terms of influences on f, and f has to integrate this influence. Then the arity of f changes as this function takes two arguments: the micro states of the phenomenon (Xt) and the macro influences (d(Yt')). According to the (1) constraint, d does an augmentation of information. As u, d is also in charge of the temporal mapping between levels. This function can also be considered as a bridge model.
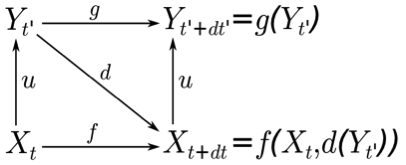
Figure 2. Upward and downward relationships between levels of representation and temporal evolution of the phenomenon. - 2.19
- This way of representing the different levels can be mapped
with some of the cases of section 2.2.
Indeed, the different elements are expressed in a generic way and then
can describe several multi-level modeling examples. Table 1 illustrates how this framework
can be mapped on some of the previous cases. Moreover, as the framework
is modular, it can be adaptated to different approaches of Section 2.1. (see Figure 3).
Table 1: Description of some multi-level modeling cases through our framework. Multi-level modeling cases X Y f g u d Nha Trang City Individual citizen in crossroad patches Aggregated values MAS Equations of pedestrian flow Capture operation Release operation
SIMPOP3 City's districts and micro urban functions Cities and macro urban functions MAS. Micro urban functions localize themselves in districts MAS. Agents localize themselves in cities Determine the spatial performance indicator based on district relationship Determine cities' micro urban function attribute SimulBogota Household and housing Household and housing groups Population evolution rules Auction mechanism Classification mechanism Relocation of household based on auction mechanism result 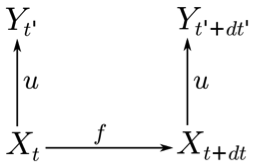

(a) (b) (c) Figure 3. Different configurations of the framework. (a) A simple upward relationships corresponding to a selective viewing modeling. (b) A concurrent representation case (without macro dynamics) (c) A concurrent representation case with macro dynamics. - 2.20
- One can note here that our definition of multi-level
coupling can't describe neither direct interactions between entities
represented at different levels nor approaches considering only one
level of representation at a time. This rules out holonic multi-agent
systems as two holons can interact together even if they are
represented at different levels. Indeed, contrary to the holonic
approach, we focus on interactions between the dynamics rather than on
interactions between the components of these dynamics. As a
consequence, in the following discussion we are not considering holonic
systems anymore. The model's coupling doesn't have the same semantic
for these cases and specifications have to be defined at the conceptual
level in order to keep a rigorous modeling process.
- 2.21
- If our framework seems to fit the cases of Table 1 in the realm of discourse, we have to investigate further with a concrete implementation. The next section describes how this framework can be instantiated with the AA4MM meta-model.
 The
AA4MM meta-model
The
AA4MM meta-model
-
Generalities about AA4MM
- 3.1
- The meta-model AA4MM (Siebert
et al. 2010b) represents a complex system as a set of
interacting models. Its main purpose is to build an heterogeneous
multi-model of a complex system from a set of previously independent
models already implemented in their simulation software.
- 3.2
- The models composing a heterogeneous multi-model may
represent the phenomenon at different spatial and temporal scales using
different formalisms. Then, the major issues of multi-modeling are:
- To integrate heterogeneous representations.
- To preserve the individual validity of the models: integration must be done with the minimum modifications on these models.
- To synchronize the models' executions which are possibly based on different scheduling policies (cyclic time-step, variable time-step, event-based).
- 3.3
- To face these issues, AA4MM relies on the multi-agent
paradigm: each model corresponds to an agent that is associated with
its simulator, and the data exchanges between the models correspond to
the interactions between the agents. The global dynamics of the
phenomenon is simulated thanks to the interactions between the models.
- 3.4
- Originality toward other multi-model approaches is to
consider interactions in an indirect way within the Agents and
Artifacts (A&A) paradigm (Ricci
et al. 2007).
- 3.5
- In A&A, autonomous agents interact together through
a programmable workspace environment composed of artifacts, which are
passive computational entities. Each artifact has a specific function
and provides services in that effect to the agents (Omicini et al. 2008). These
services are expressed independently of the agent's internal
functioning: the only hypothesis made is that the agents know how to
use the artifacts. The strength of the A&A paradigm is to allow
describing the interactions between agents as processes, and then to
allow formalizing these processes (Ricci
et al. 2011).
- 3.6
- AA4MM manages and links the two kinds of dynamics of a
multi-model:
- The models' dynamics: It relies on the execution of the simulators implementing each model.
- The multi-model dynamics: the co-evolution of the different models. This dynamics is made explicit thanks to the behavior of the agents associated with each model.
- 3.7
- By representing such a multi-model as a A&A
multi-agent system, we can then take advantage of the expressive power
of the paradigm to represent a multi-model (Bonneaud
& Chevaillier 2007): the models don't have to be
adapted to interoperate as their interactions are resolved through
their common environment.
- 3.8
- Artifacts allow describing model's interactions as
processes outside of the models, and expressing them independently of
the models' internal functioning. The problem of heterogeneous
representations between models is managed as a transformation service
of the artefact in charge of the interaction.
- 3.9
- In the next section, we detail the concepts of the AA4MM
meta-model.
Concepts of the meta-model
- 3.10
- The original AA4MM's concepts have specifications for a
structural coupling of models (Siebert
2011). The structural coupling is defined as the evolution of
a constant number of entities simultaneously involved in several
dynamics, each dynamics being managed by a model.
- 3.11
- AA4MM relies on three concepts to describe a multi-model
(each of them associated with a graphical notation):
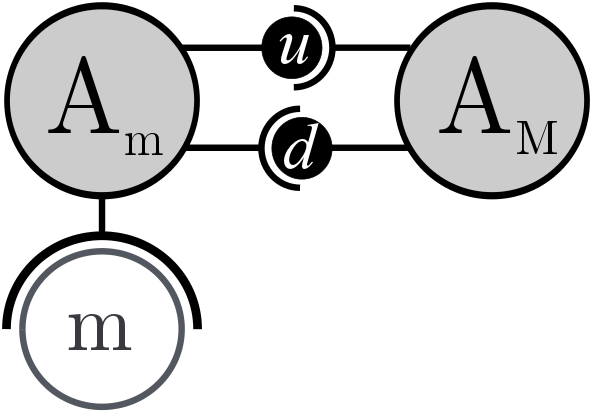
- The m-agent Ai manages a model mi and is in charge of the interactions of this model with the other ones (symbol in Figure 4a),
- Each interaction between two m-agents Ai and Aj is reified by a coupling artifact Cij (symbol in Figure 4b),
- Finally, the interface artifact Ii reifies interactions between an m-agent Ai and its model mi (symbol in Figure 4c),
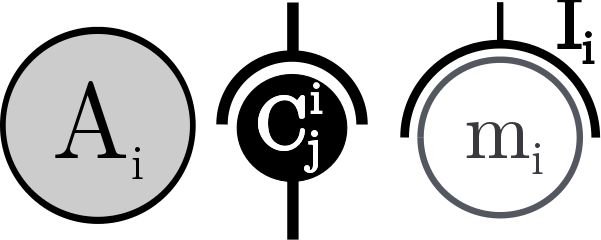
(a) (b) (c) Figure 4. Symbols of the AA4MM components (a) m-agent, (b) coupling artifact, (c) interface artifact and its model mi. - 3.12
- A multi-model simulation corresponds to the behaviour and
interactions of these components.
- 3.13
- The m-agent's behavior (see fig. 6)
corresponds to the cycle:
- Read the new state of the shared entities from the coupling artefact. For instance, it could be a set of pedestrian's positions.
- Update its model's state, and execute its simulator for one time step via the interface artifact,
- Get the new state of the shared entities via the interface artifact and Post this state to the coupling artifact,
- 3.14
- A coupling artifact Cij
has a direction and works like a mailbox: the artifact has a buffer of
data where Ai can post its output data iiout
and Aj can get its input data ijin.
- 3.15
- It proposes three functions (see fig 5):
- post: an m-agent Ai managing a model mi writes data iiout to be transferred to other models.
- transform: transforms the output data iiout of the model mi, into input data ijin for the model mj. This function can make scales changing on the data.
- read: an m-agent Aj reads input data ijin.
- 3.16
- An interface artifact contains primitives for the
manipulation of its simulator: initialization, updating simulator
state, executing for a time step and collecting information about
individuals. Table 2 sums up
the operations proposed by the AA4MM artifacts.
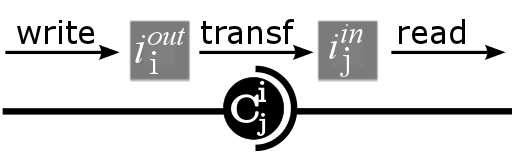
Figure 5. The three functions of a Cij coupling artifacts. - 3.17
- As a consequence of the structural coupling's definition,
the reader may notice that:
- the transform operation is such that length(iiout)=length(ijin) because the number of shared entities is constant,
- there is no creation nor suppression of entities in the models.
- 3.18
- AA4MM relies on operational specifications and proved
algorithms (Siebert et al. 2009)
related to temporal coherence between models. They enable the
implementation of a multi-model and its simulation with only a selected
number of functions specific to the application to define. Conceptual
proofs of this approach with the coupling of Netlogo simulators have
been done (Siebert et al. 2010b).
We applied AA4MM to study the mutual influences between mobility models
and routing algorithms in mobile ad-hoc networks (Leclerc et al. 2010). In the
following, we describe the implementation of a multi-model with AA4MM
(Section 3.3) and how we extend
the original specifications to implement multi-level coupling (Section 3.4).
Table 2.
Table 2: Operations proposed by the AA4MM artifacts (taken from Siebert et al. 2010) Artifact Function Role Model-Artifact Ii init() Initialize the model mi run() Process the next simulation event getOutputData() Return output data iiout of the model mi setInputData(iiin) Set up the model mi with the iiin input data getCurrentData() Return the current simulation time of the model mi getCurrentTime() Return the current simulation time of the model mi getNextTime() Return the simulation time of the next event of the model mi stop() Manage the end of the simulation (data storage, analyse, etc.) Coupling-Artifact Cji post(iiout) Store the iiout output data in the artifact trans(iiout) Transform the output data of the model mi, iiout into input for the model mj data ijin read() Return the ijin input data stored in the artifact Implementation of a multi-model in AA4MM
- 3.19
- When implementing a multi-model with AA4MM we make the
hypothesis that there are pre-existing simulators implementing each
sub-model. In the following, for simplicity purpose, we suppose a
multi-model composed of two models m1 and m2
implemented respectively by two different simulators sim1
and sim2. The pre-existing AA4MM middleware
manages the exchanges of data between the models, and the coordination
of the simulator's executions. It consists of:
- The m-agent behavior corresponds to a proved multi-simulation algorithm (Siebert et al. 2009) inspired from Chandy and Misra (1979).
- The coupling artifact without the transformation function.
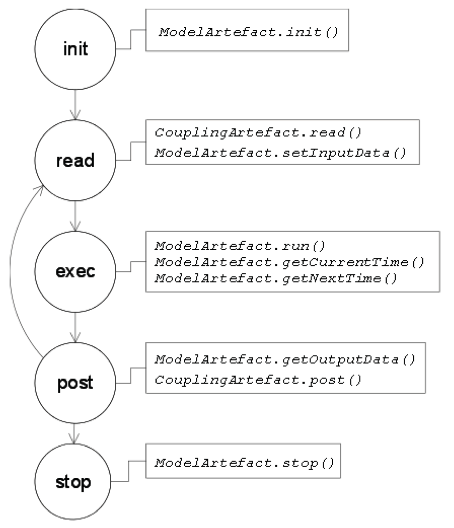
Figure 6. The m-agent behavior (taken from Siebert et al. 2010b) - 3.20
- In order to operationalize a multi-model, the interface
artifacts have to be defined (one for each simulator). Features
specific to the application have also to be defined:
- The data types of the application: the data exchanged between the m-agents (through the coupling artifacts) and the data to be collected from and injected in each simulator.
- Transformation functions between simulators (for example matching time and spatial dimensions). The proved algorithm of AA4MM needs these functions to ensure the consistency between the simulators' executions.
- 3.21
- Figure 7 describes
the coupling of the two models with AA4MM. Starting with an interaction
graph between models (Figure 7a),
a first step is to build its equivalent with the AA4MM meta-model
(Figure 7b).
- 3.22
- The meta-model implementation starts from existing
elements: the AA4MM middleware and the two simulators (Figure 8). They have to be completed with an
interface artifact for each simulation software, with data types and
transformation functions between models (Figure 9).
Figure 10 shows the complete
implementation of a multi-model with AA4MM.
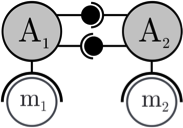
(a) (b) Figure 7. (a) Interaction graph between models m1 and m2, (b) AA4MM corresponding meta-model diagram. 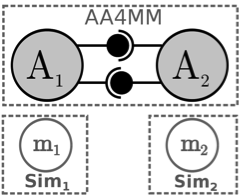
Figure 8. The starting components: the models (here m1 and m2) implemented in their simulators (here sim1 and sim2), the m-agents and the coupling artifacts. 
Figure 9. Features specific to the application: data types and the interface artifacts specific to a simulator. 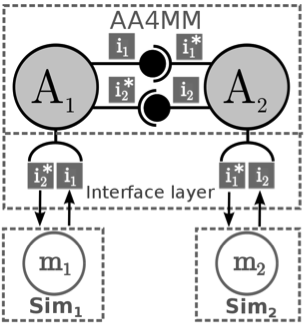
Figure 10. Complete implementation of a multi-model with AA4MM. Each little grey square represents a data type to be defined. Extension of AA4MM for multi-level modeling
- 3.23
- The framework for multi-level representation presented in
section 2.3 is instantiated as
follows in the AA4MM's meta-model. As described above, several steps
are needed to create a multi-model with AA4MM. The first step is to
define the interaction graph between models where the exchanged data
are specified. In our case, each level is associated with a model (m
for micro and M for macro). The interactions are the upward relation
from micro to macro (u) and the downward relation from macro to micro (d)
(see Figure 11a).
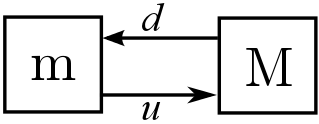
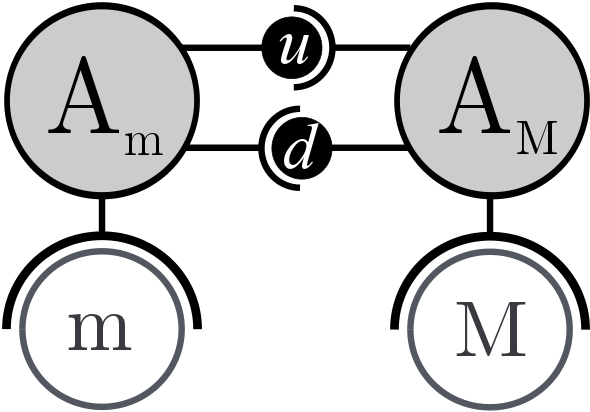
(a) (b) Figure 11. Multi-level within AA4MM. (a) Graph of relations between models. (b) The corresponding AA4MM diagram of multi-level representation. - 3.24
- The next step is to describe this graph with the concepts
of AA4MM. Each model is associated with an m-agent and an interface
artifact. The Am m-agent manages the micro model
and the AM m-agent manages the macro model.
Each relation between models corresponds to a coupling artifact between
the m-agents (Figure 11b). We
define upward and downward artifacts in order to represent the same
named functions. The upward artifact (resp. downward) receives data
from the Am (resp. AM)
m-agent; these data are modified by the upward (resp. downward)
function and send to AM (resp. Am).
- 3.25
- We extended the original AA4MM's specifications by
integrating constraints specific to a multi-level representation.
- 3.26
- As the number of entities is not the same between micro and
macro model, we extended the meta-model with two new kinds of coupling
artifacts:
- The upward artifact (symbol in Figure 12a) allows passing from a micro to a macro representation of the phenomenon. It implements the upward function of the framework instead of the transformation function of the original coupling artifact. This function aggregates the data sent by the micro model therefore this function changes the cardinality of the data: length(imout) > length(iMin). For example, imout corresponds to pedestrians and iMin corresponds to groups of pedestrians.
- The downward artifact (symbol in Figure 12b) allows passing from a macro to a micro representation of the phenomenon. It implements the downward function of the framework instead of the transformation function of the original coupling artifact. This function disaggregates the data send by the macro model therefore length(iMout) < length(imin).


(a) (b) Figure 12. Symbols of the new AA4MM's concepts for multi-level modeling replacing the original coupling artifact. (a) The upward artifact. (b) The downward artifact. - 3.27
- Moreover, to represent the appearance and disappearance of
macro entities in a multi-level modeling, we extended the m-agent
specifications in order to allow creation and suppression of entities
in addition of the updating operation. These extensions, which respect
the original AA4MM's hypothesis, allow the deployment and the
implementation of a multi-level model.
- 3.28
- An advantage of this framework's instantiation is that, as each conceptual elements of the framework is instantiated by one AA4MM's component, we can use the modularity of the framework in the AA4MM's meta-model in order to rapidly implement the different configurations of Fig. 3. This point is developed in the following section.
 Proof
of Concepts
Proof
of Concepts
- 4.1
- In this section, we illustrate through a collective motion
example how to implement different patterns of interactions between
levels. We consider individuals evolving in a toric space. This example[1] of collective motion
phenomena serves as an illustration for showing the advantages of our
approach for the study of social systems.
- 4.2
- The micro level corresponds to moving individuals. Each
individual is defined by an identifier, a position, an orientation and
a color. The behavior of an individual consists of three rules:
- Trying to avoid collisions with obstacles (others individuals),
- Moving closer to others individuals,
- Following other individuals.
- 4.3
- The macro level corresponds to moving groups. A group is
defined as a set of "close enough" individuals with similar
orientations. In the macro model, a group has an identifier, a
position, an orientation, a size and a color (different for each
group). We assume here that the behavior of a group is the same that
the behavior of an individual: a group tries to move closer and to
follow other groups while trying to avoid collisions with obstacles.
- 4.4
- In the experiments, the f and g
functions are each implemented by a Netlogo instance simulating the
dynamics. The advantage of the AA4MM meta-model here is that, as an
interface artifact is specific to a simulator, we only had to define
once the interface artifact for all the following cases. For sake of
clarity, we describe multi-level modeling where spatial scale is the
same at the micro and macro levels. Details for the management of
heterogeneous spatial and temporal scales with AA4MM can be found in
Siebert et al. (2010b).
- 4.5
- In the next parts, we implement different patterns of
interactions between these two levels. Each pattern is expressed in a
generic way as a graph using the functions u, d, f, g. Based
on this graph, the corresponding AA4MM diagram is systematically
described. Then, the software implementation of this graph is performed
thanks to the AA4MM middleware in which we add the domain specific
functions.
- 4.6
- In section 4.1, we
describe how the micro level dynamics influences the macro level:
groups form, move and separate according to individuals' configurations
(corresponding to the framework's configuration of Fig. 3a).
In section 4.2, we add an
influence from the macro level to the micro one: groups determine the
color of their composing individuals (corresponding to the framework's
configuration of Fig. 3b). In
section 4.3, we introduce mutual
influences between the macro and micro levels: individuals form groups
(as previously) but groups have their own behavior and impose their
movement to their composing individuals (corresponding to the
framework's configuration of Fig. 3d).
In section 4.4, contrarily to
three previous examples, the models don't have the same time scale: one
time step at the macro level equals four time steps at the micro one.
In section 5, we discuss what are
the advantages of this modular approach for the study of multi-level
phenomena.
Micro dynamics and upward relationship
- 4.7
- The first example is a selective viewing case
(corresponding to the framework's configuration of Fig. 3a), where we want to study the
formation/separation of groups over time. Individuals (X)
move (f) and form groups. X and f
are implemented by a Netlogo instance. X
corresponds to the turtles' model and f to the
turtles' behavior. An interpretation function u
detects the groups. It transforms individuals (X)
into groups (Y). Since groups don't have their own
behaviors at the macro level, we only need to represent the different
states of the macro level but not their evolution: in this example, we
don't need a simulator instance. Figure 13a
shows the corresponding diagram of relations between the levels in our
framework.
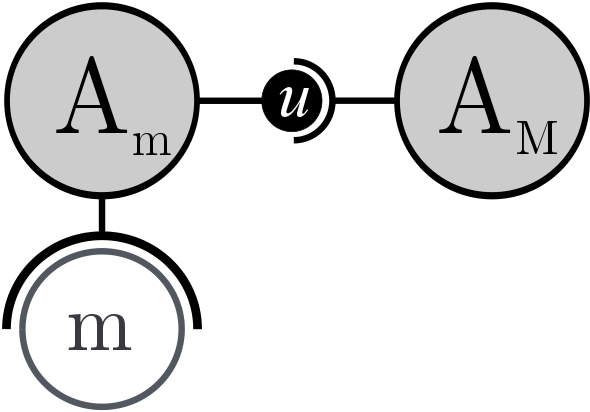
(a) (b) Figure 13. A simple upward relation case. (a) Graph of relation between levels of representation and temporal evolution (b) The corresponding multi-level coupling in AA4MM. - 4.8
- Each level corresponds to an m-agent (Figure 13b). Am
manages the micro model m in order to simulate the micro dynamics
thanks to a Netlogo instance. The upward function is implemented as a
cluster identification algorithm (Ankerst
et al. 1999). It transforms, at each time step, a list of
individuals' position and orientation into groups. This function takes
two parameters: proximity and orientation thresholds. At macro level, AM
collects the number of groups detected by the upward artifact at each
time step. This way, we can study the evolution of the number of groups
as a function of time (Figure 14).
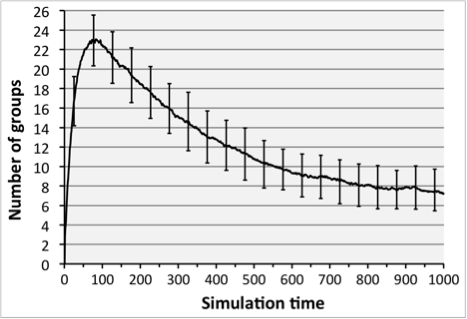
Figure 14. An example of use: studying the number of groups detected in a flocking phenomenon according to simulation time (average over hundred simulations). Error bars indicate standard deviation. Micro dynamics, upward and downward relationships
- 4.9
- In order to visually identify what are the individuals that
compose the detected groups, we assign different colors to the
individuals according to the group they belong to. The macro entities
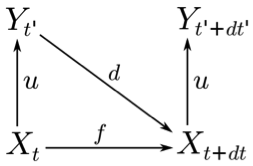
have now an influence on the micro level. Similarly to section 4, individuals (X)
move (f) and form groups. These groups (Y)
are detected with an upward function (u). As the
macro level has an influence on the micro level, a downward function (d)
is required. The corresponding diagram of relations between the levels
of representation and the temporal evolution of the phenomenon can be
seen in Figure 15a.
- 4.10
- AM receives data on detected groups
from the upward artifact. It assigns each detected group to a color and
provides a list of groups and colors to the downward artifact (Figure 15b). The downward function is
implemented in the downward artifact. It assigns groups' color to their
composing individuals and makes this information available to Am,
which changes the color of the individuals accordingly (Figure 16).
(a) (b) Figure 15. A case of micro dynamics with upward and downward relations. (a) Graph of relation between levels of representation and temporal evolution (b) The corresponding multi-level coupling. 
Figure 16. An example of use: visualization of groups on a snapshot of micro level with colors. Micro and macro dynamics, with upward and downward relationships
- 4.11
- We want to model simultaneously the macro and micro
dynamics. The individuals and the groups have their own behaviors, but
when an individual belongs to a group, the macro dynamics determines
its movement: an individual moves with the same vector and has the same
orientation as its group. If an individual is not in a group, its
behavior is the same as in section 4.1
and 4.2.
- 4.12
- As previously, individuals (X) move (f)
and form groups. These groups are detected with an upward function (u).
The detected groups are reified (Y) and move (g).
Y and g are implemented by
another NetLogo simulator. d is an interpretation
function of groups' mouvements. It transforms Y
(movements of groups) to X (movements of
individuals belonging to groups). The corresponding diagram of
relations between the levels of representation and the temporal
evolution of the phenomenon can be seen in Figure 17a.
Figure 17b is the
corresponding representation in the AA4MM meta-model.
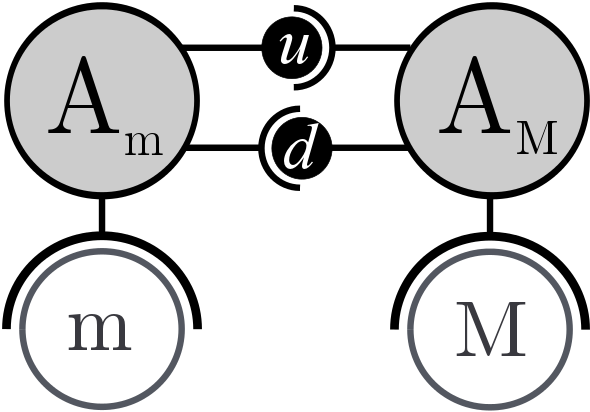
(a) (b) Figure 17. A case of micro dynamics, macro dynamics, upward and downward relations. (a) Graph of relations between levels of representation and temporal evolution (b) Corresponding multi-level coupling. - 4.13
- Am manages the micro model m and
simulates its dynamics. The upward function of section 4.1 and 4.2
is extended. It sets detected groups' attributes by aggregating micro
data as follow: position is the gravity center of the micro cluster,
orientation corresponds to the average direction of its constituent
individuals and size refers to the dispersion.
- 4.14
- AM manages the macro model M and its
dynamics. It receives detected groups from the
upward artifact and adds, removes or updates them in M, executes one
step of simulation, collects data and sends group's vectors and
orientation to the downward artifact. The downward function transforms
groups' movements into individuals' movements. It is implemented in the
transformation function of the downward artifact. Am
receives from this artifact the movements of some individuals (those
that belong to a group). It modifies the states of these individuals
accordingly. For the individuals not belonging to a group, it asks for
a simulation step in order to update their states. Figure 18 is a snapshot of the multi-model
execution. Figure 19 shows an example of use of this pattern of
interactions. The multi-level representation of the collective
phenomenon makes explicit groups crossing and allows studying them
simultaneously at the micro and macro points of view.
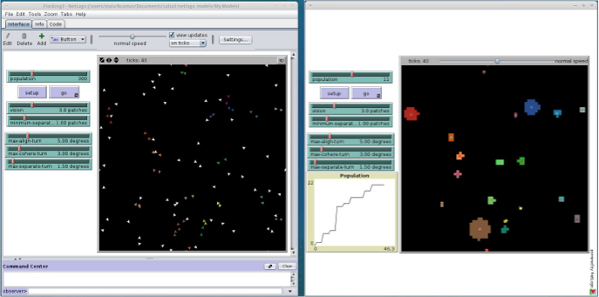
Figure 18. Snapshot of the multi-model execution in a micro and macro dynamics, with upward and downward relationships case. (left: micro level, right: macro level) 

Figure 19. An example of use: studying the groups' crossing at micro (left) and macro (right) levels. Different time scales
- 4.15
- In this section we describe the use of different temporal scales between the two simulators. In this case, one macro simulator's time step corresponds to four micro simulator's time steps. This difference of temporal scale implies that, for the same simulation time period, while the macro model produces one data, the micro model produces four ones. Thanks to the modularity of AA4MM, only the downward artifact has to be changed when taking the previous configurations back: the downward function linearly decomposes now groups' movement vectors it received in four parts. The AA4MM's proved decentralized algorithm automatically managed the models synchronization in this case: the macro model considers only the last of the four micro data received by the upward artifact.
 Discussions
Discussions
- 5.1
- We can see with the different examples of use (Figures 14, 16
and 18) that our approach
preserves the advantages of a multi-level representation. We can study
the formation of higher-level structures (Figure 14),
enhance the visualization of the phenomenon (Figure 15),
and make explicit new phenomenon, for instance group's crossing (Figure
19).
- 5.2
- This modular vision of multi-level modeling facilitates the
study of multi-level phenomena in social systems. As levels'
relationships are reified in an AA4MM multi-level coupling, we can test
hypothesis about the level's influences by comparing different
multi-level representations of the same phenomenon. It is then possible
to study the mutual influence of levels, for instance the mutual
influence of individuals and groups. As shown in section 4, we can rapidly switch from a pattern
of interaction to another with well-focused efforts.
- 5.3
- Figure 20 shows a
comparison of the number of groups detected in simulations using
different level's dynamics (described by Table 3) and influences. These
simulation results could be used for the validation of the multi-model
towards a real collective motion system. In particular, our proposal
enables the assessment of several candidate configurations and their
confrontation with existing data to check what hypotheses about the
relationships between individuals and groups in this social system
hold.
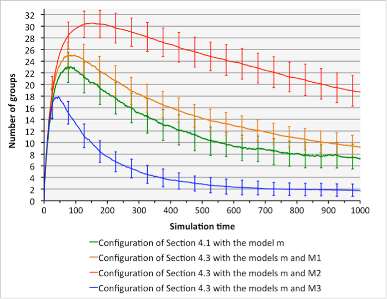
Figure 20. Number of groups detected according to simulation time (average over hundred simulations) in different AA4MM configuration. Error bars indicate standard deviation. Table 3: Values of the parameters of the different models being compared. m correspond to the micro model and Mi to models of the macro dynamics. Models Cohere parameter Align parameter Separate parameter m 3 5 1.50 M1 3 5 1.50 M2 0 0 10 M3 14,25 14,25 0 - 5.4
- The AA4MM's advantages are also preserved with a multi-level coupling. Thanks the modular approach and the clear separation of the different levels of questions, we can change the simulator implementing one model with only changing the interface artifact. It is then possible to compare different implementations of the same model. AA4MM can also be the support to an incremental modeling process as it is possible to test different versions of the same model and to check their interoperability in the multi-model.
 Conclusion
Conclusion
- 6.1
- In this article, we proposed to consider a multi-level
model as a multi-model. This approach relies on a multi-agent vision of
a multi-model. We used the AA4MM meta-model to design and instantiate
the multi-model. We defined a framework that organizes the
multi-level's concepts and their relations. This framework specifies
the patterns of interaction between levels. We translated this
framework into the AA4MM meta-model while respecting the semantic
constraints specific to the simultaneous representation of two levels.
In order to manage multi-level modeling in AA4MM, we proposed two new
kinds of coupling artifacts in order to manage the change of resolution
level: the upward and downward artifacts; and extended the m-agents
possibilities to create or suppress entities in their model. As a proof
of concept, we used a collective motion phenomenon to detail different
kinds of multi-level representation. With different examples of
simulations, we have shown the interests of this approach for the study
of complex system.
- 6.2
- Since we extended AA4MM, we can benefit of its advantages for multi-level representations (reuse of simulators, of meta model concepts, ease to switch from one pattern to another,...). We limited to two simultaneous levels in this article. In future works, two directions can be addressed: representing several levels simultaneously or representing a phenomenon with several levels but considering only one at a time.
 Notes
Notes
-
1This
example can be downloaded at https://www.openabm.org/model/4589/version/1/view.
 References
References
- ANKERST M., Breunig M., Kriegel
H-P., Sander J. (1999). "OPTICS: Ordering Points to Identify the
Clustering Structure". ACM SIGMOD International Conference on
Management of Data. ACM Press. pp. 49–60. [doi:10.1145/304181.304187]
BONNEAUD S., Chevaillier P. (2007). Oriented pattern agent-based multi-modeling of exploited ecosystems. In Proceedings of the 6th EUROSIM Congress on Modelling and Simulation, Ljubljana, Slovenia, September 9–13, 7 pages.
BOURGINE P. (2008). "Distributed Problem Solving in Natural and Artificial Complex Systems." Invited talk in Engineering Societies in the Agents World IX, 9th International Workshop, ESAW.
CETINKAYA, D., Verbraeck, A., Seck, M. D. (2010). A metamodel and a DEVS implementation for component based hierarchical simulation modeling.01/2010. In Proceedings of the 2010 Spring Simulation Multiconference, SpringSim 2010, Orlando, Florida, USA, April 11–15. [doi:10.1145/1878537.1878714]
CHANDY, K. M., Misra, J. (1979). Distributed simulation: A case study in design and verification of distributed programs. Software Engineering, IEEE Transactions on, (5), 440–452. [doi:10.1109/TSE.1979.230182]
DAVIS, P. K., Hillestad, R. J. (1993). Families of models that cross levels of resolution: Issues for design, calibration and management. In Proceedings of the 1993 Winter Simulation Conference. ACM, New York. [doi:10.1109/WSC.1993.718351]
DEMANGE, J. (2012). Un modèle d'environnement pour la simulation multiniveau: application à la simulation de foules. Phd Thesis, Belfort-Montbéliard University (in French).
EL HMAM, M., Abouaissa H., Jolly D., Benasser A. (2006). "Macro-Micro Simulation of Traffic Flow". 12th IFAC Symposium on Information Control Problems in Manufacturing, INCOM, Saint-Etienne, France.
GAUD, N., Galland, S., Gechter, F., Hilaire, V., Koukam, A. (2008). "Holonic Multilevel Simulation of Complex Systems: Application to Real-time Pedestrians Simulation in Virtual Urban Environment." Simulation Modelling Practice and Theory, 16, 1659–1676. [doi:10.1016/j.simpat.2008.08.015]
GIL-QUIJANO, J., Louail T., Hutzler G. (2010). "From Biological to Urban Cells: Lessons from Three Multilevel Agent-Based Models." PRIMA, 620–635.
GOLDSPINK C. (2000). Modeling social systems as complex: Towards a social simulation meta-model. Journal of Artificial Societies and Social Simulation, 3(2)1: https://www.jasss.org/3/2/1.html.
KLÍR, J., Šafarik, J. (2004). Variable resolution modeling in interactive parallel discrete event simulation. In Electronic computers and informatics. Košice: VIENALA Press, s. 353–358. ISBN: 80-8073-150-0
LECLERC, T., Siebert, J., Chevrier, V., Ciarletta, L., Festor, O. (2010). "Multi-modeling and Co-simulation-based Mobile Ubiquitous Protocols and Services Development and Assessment." In: 7th International ICST Conference on Mobile and Ubiquitous Systems – Mobiquitous 2010, Australie Sydney.
MUSSE S.R., Thalmann D. (1997). "A Model of Human Crowd Behavior: Group Inter-Relationship and Collision Detection Analysis," Proc. Workshop Computer Animation and Simulation of Eurographics. '97. [doi:10.1007/978-3-7091-6874-5_3]
OMICINI, A., Ricci, A., Viroli, M. (2008). Artifacts in the A&A meta-model for multi-agent systems. Autonomous Agents and Multi-Agent Systems 17, 3 (December 2008), 432–456. [doi:10.1007/s10458-008-9053-x]
NATRAJAN, A., Nguyen-Tuong, A. (1995). "To disaggregate or not to disaggregate, that is not the question" , ELECSIM, Internet, April-June, 1995, Technical Report CS-95-18, Department of Computer Science, University of Virginia.
REYNOLDS, F. P., Natrajan, A., Srinivasan S. (1997). "Consistency maintenance in multiresolution simulation." ACM Transactions on Modeling and Simulation, 7(3) pp. s368–392. [doi:10.1145/259207.259235]
RICCI, A., Viroli, M., Omicini, A. (2007). "Give Agents their Artifacts: the A&A Approach for Engineering Working Environments in MAS." In AAMAS '07: Proc. of the 6th international joint conference on Autonomous agents and multiagent systems, pp. 601–603, New York, USA.
RICCI, A., Piunti, M., Viroli, M. (2011). Environment programming in multi-agent systems: an artifact-based perspective. Autonomous Agents and Multi-Agent Systems 23(2): 158–192.
RODRIGUEZ S., Gaud N., Hilaire V., Galland S., Koukam A. (2007). "An analysis and design concept for self-organization in holonic multi-agent systems. In ESOA'06, Workshop of AAMAS. [doi:10.1007/978-3-540-69868-5_2]
ROPELLA, G.E., Hunt, C.A., Nag, D.A. (2005). "Using Heuristic Models to Bridge the Gap Between Analytic and Experimental Models in Biology." Proceedings of the 2005 Agent-Directed Simulation Symposium (San Diego, CA, April 2-8), Simulation Series Vol. 37.
SECK, M. D., Job Honig, H. (2012). "Multi-perspective Modelling of Complex Phenomena." Computational & Mathematical Organization Theory, 1–17. [doi:10.1007/s10588-012-9119-9]
SIEBERT, J. (2011). "Approche Multi-agent pour la Multi-modélisation et le Couplage de Simulations. Application à l'étude des Influences entre le Fonctionnement des Réseaux Ambiants et le Comportement de leurs Utilisateurs." Phd Thesis, Henri Poincaré University - Nancy 1 (in French).
SIEBERT, J., Ciarletta, L., Chevrier, V. (2010a). "Agents & Artefacts for Multiple Models Coordination: Objective and Decentralized Coordination of Simulators." In Proceedings of the 2010 ACM Symposium on Applied Computing. Pp. 2024–2028.
SIEBERT, J., Ciarletta, L., Chevrier, V. (2010b). "Agents and Artifacts for Multiple Models Co-evolution. Building Complex System Simulation as a set of Interacting Models." In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2010, May 10, 2010, Toronto, Canada, pp. 509–516.
SIEBERT, J., Rehm, J., Chevrier, V., Ciarletta, L., Mery, D. (2009). "AA4MM coordination model: Event-B specification". Technical Report, INRIA.
SPRINKLE, J., Rumpe, B., Vangheluwe, H., Karsai G. (2010). Metamodelling State of the Art and Research Challenges. In Proceedings of the 2007 International Dagstuhl conference on Model-based engineering of embedded real-time systems. Pages 57–76 . Springer-Verlag Berlin, Heidelberg.
VO, D., Drogoul, A., Zucker, J.-D. (2012). "An Operational Meta-model for Handling Multiple Scales in Agent-based Simulations." Research, Innovation, and Vision for the Future (RIVF), Ho Chi Minh: Vietnam.
WILENSKY, U. (1998). "NetLogo Flocking Model". Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL: http://ccl.northwestern.edu/netlogo/models/Flocking
YILMAZ L., Lim A., Bowen S., Oren T. (2007). "Requirements and Design Principles for Multisimulation with Multiresolution, Multistage Multimodels." Simulation Conference, 2007 Winter. IEEE. [doi:10.1109/WSC.2007.4419678]
ZEIGLER, B. P., Praehofer, H., Kim, T. G. (2000). Theory of Modeling and Simulation: Integrating Discrete Event and Continuous Complex Dynamic Systems. Academic Press.