 Abstract
Abstract
- To reduce overpopulation around Seoul, Korea, the
government implemented a relocation policy of public officers by moving
the government complex. This implies that there will be a negative
impact on the suburban area that originally hosted the complex, but we
do not know the magnitude of the impact. Therefore, this paper presents
a micro-level estimation of the impact on the city commerce with an
agent-based model. This model is calibrated by the micro-level
population census data, the time-use data, and the geographic data.
Agent behavior is formally specified to illustrate the daily activities
of diverse population types, and particularly the model observes how
many agents pass by commercial buildings of interest. With the
described model, we performed a virtual experiment that examines the
strengths of factors in negatively influencing the city commerce. After
the experiment, we statistically validated the model with the survey
data from the real world, which resulted in relatively high correlation
between the real world and the simulations.
- Keywords:
- Agent-Based Simulation, Discrete Event Model, Urban Design, Population Modeling, Urban Simulator
 Introduction
Introduction
- 1.1
- Korea has been rapidly industrialized, and its cities have
expanded quickly on the large scale. For instance, Seoul alone has a
population of more than 10 million, and if we include suburban areas,
the population exceeds 20 million. This centralization of population
has resulted in the centralization of commerce, government, culture,
and so on, which benefits the city and its population. However, when
this centralization becomes too extensive, various problems arise, such
as, crime, pollution, traffic jams, and so on. Therefore, the
government strategically started relocating some of its branch offices
to a newly developed city that is distant from the overpopulated city.
This relocation policy may reduce the problems caused by the large
population, but the existing benefits from that population will also
disappear in currently operating shopping centers, restaurants, and
other services (Jun 2007).
Therefore, the relocation policy requires a careful evaluation on the
effect of the policy on the local population as well as the local
environment in the current overpopulated city, i.e., the centralization
of commerce.
- 1.2
- Then, the major question will be how the local area will
change with regard to such aspects as commerce, government services,
and residence after the relocation policy is implemented (Marshall et al. 2005). This
separation of city functions—for instance, the separation of commerce
capital and government capital—is observed in the United States,
Australia, China, and so on. For example, the United States has
Washington, DC, as the government's capital and New York City as a
central city for commerce. Similarly, China separated the city function
between Beijing and Shanghai; Australia's example is Canberra and
Sydney. These examples of the separation of city functions are created
by either historical evolutions or strategic policy implementation. If
the historic evolution induced the separation of functions, i.e., the
United States, the society would not need a careful evaluation on
what-if analyses because the separation would have already been done
through societal evolutions. On the other hand, in the case of
Australia and Korea, if the policy is strategically planned and
implemented, the policy makers should be informed of the potential
disruptions and benefits from the suggested policy. Particularly, such
policy shifts are rare, yet important, so generative simulations on the
questions of interests would be a good support to the policy makers.
- 1.3
- The relocation policy in Korea will affect the whole
spectrum of the suburban environment near Seoul, but estimating the
strength of that effect is a difficult task. Fundamentally, a city is a
complex system with many individual components and interactions. The
individual components are people, buildings, roads and other
infrastructure. These components have relations through usage,
residence, build-ons, and interlinks. Hence, we cannot provide an
estimation of urban area changes by using simple statistics; the
relocation policy will impact these individual city components in
different magnitudes. Instead of simple statistical analyses, many
researchers have utilized simulation models to replicate the city and
its change in a virtual world. Through generating individual components
and their relations, researchers expect to capture what would happen in
the real world from their simulation world. Often, agent-based models
(ABM) have extensively been utilized to generate a potential scenario
of changes (Moon & Carley 2007).
ABM involves the individual's actions and interactions with others as
well as environment (Bae, Lee &
Moon 2012; Carley 2002;
Epstein 1996; Tesfatsion 2002). Through
this property of ABM, insights into dynamic changes could be gained
that are difficult to obtain in other types of models (Holzer & de Meer 2008).
- 1.4
- Following the urban area simulations that generate the potential impacts of a policy shift, we took a similar approach to gauging the impact of the relocation policy in Korea. The current relocation policy in Korea is moving a government complex in a suburban area, Gwacheon city, near Seoul, to a newly built city, Sejong city, located about 100km south of Gwacheon city. Therefore, the local population in Gwacheon might commute to the work place by two-hour highway driving, or the family working at the complex might relocate to the new city. One important issue for local population in Gwacheon as well as the policy makers is the disruption of other city functions in Gwacheon. Many residents and local businesses are concerned about a potential recession in their local commerce as a result of relocating the population. To address this issue, we performed a virtual experiment utilizing an agent-based model. This paper introduces the details of our models, simulations, and virtual experiments. To examine the impact of the relocation, especially in the marketing area, we modeled and simulated agents and environments by varying the reduction ratio of relocating public officers and their family movement together. In the real world, this relocation policy was implemented in 2012, and we were able to gather a dataset for validations of our model, which was unavailable when we initially built and presented the ABM in the late 2012 and the early 2013. Our result indicates that a certain set of parameter values for our simulation model predicts that there will be a negative effect to the local business, and this effect will be varied by the locations in the city, the family relocation ratio, and the commute ratio. The simulation is statistically validated with the survey result gathered after the relocation policy was implemented.
 Previous
research
Previous
research
- 2.1
- Urban modeling has a long history of research that dates
back to the 19th century, such as Thunen's isolated
state theory. We categorized the urban modeling into
system-oriented models and individual-oriented models, and we present
the surveyed research in this section. In addition to the surveys on
modeling methodology, we surveyed on the simulations on urban
development and changes to show how simulations have contributed to the
urban management that is an application domain of this paper.
System-Oriented Model
- 2.2
- A system-oriented model analyzes the problems of a complex
system in a macro view. It models macro parameters, such as distance,
land cost and land use, rather than property of entities. For instance,
system-oriented models have been traditionally used to describe urban
land use. Von Thunen's model (Thünen,
Wartenberg & Hall 1966) is an early model of land
use. It is a basic analytic model with an equation of relationships
between costs and revenue. Land use is determined by way of maximizing
profit. After the analytic model, Burgess developed a descriptive model
that divides a city into six concentric zones (Burgess
2008). Each zone has a different land use, and it is the
result of the observation of several American cities. Furthermore,
compared to the concentric model, sectorial models are developed. The
sectorial model is similar to the concentric model but was developed by
factors overlooked in the concentric model (Hoyt
1939). In the sectorial model, the effect of transportation
is added. The creation of a sector depends on the roads; its pattern is
a polycentric shape. Finally, the multiple nuclei model developed from
the sectorial model. It recognizes a number of separate centers, as
compared to only one center in the previous models (Harris & Ullman 1945).
- 2.3
- Because the above models are close to economic models based
upon demand, supply, and price, researchers solved
the models, not simulated them. However, as
researchers add up more interactions among the macro parameters, the
models become insolvable, so they are simulated. The simulation model
with a macro view is often called the "system-dynamics model." For
instance, Forrester modeled the macro parameters of a city with a
system-dynamics model (Forrester
1971). Another example involves utilizing a system-dynamics
model to plan the city-wide water supply (Zhang
et al. 2008). Also, the methodology is applied to study how
to plan and manage the regional environment (Guo
et al. 2001).
Individual-Oriented Model
- 2.4
- The individual-oriented model approaches the problem from a
micro-perspective. It considers the interactions among individuals and
assumes the actions and interactions of individuals will affect the
overall system. As we mentioned, a city is a complex system. While
representing that the interactions among individuals is critical in
analyzing complex systems, the system-oriented models, such as models
introduced in section 2.1, tends to fail because the method ignores
those interactions among entities. To capture this characteristic, the
components and interactions of urban dynamics should be explained. For
instance, Rodrigue claims that there are five significant components of
urban dynamics: land use, transport network, population and housing,
employment and workspace, and movement of passengers (Rodrigue, Comtois & Slack 2011).
Our model should include such individual components and their
relations.
- 2.5
- Lately, there are many researchers interested in the
agent-based model to deal with complex society. Albatross is one of the
agent-based model (Arentze
& Timmermans 2004). In this model, the agent decides
the activity and schedules it depending on the priority of activities
and several constraints, such as time and spatial constraints. After
deciding the daily schedule, the agent chooses the place for the
activity based on the rule adapted by reinforcement learning and social
learning. A second agent-based model is Aurora (Arentze, Pelizaro & Timmermans
2005). An agent of this model generates the schedule
depending on the utility function of activities. After each activity is
completed, the agent updates his knowledge about the environment and
reconsiders the remaining schedule. Transims is also based on the
agent-based model for regional transportation system analyses (Smith, Beckman & Baggerly 1995).
Transims generate agent and road network models using network and
census data from a target region. Using the generated models, Transims
perform a traffic simulation with the iterations of activity
generation, route planning, micro simulation, and feedback procedures.
- 2.6
- These kinds of daily activity models are applied for the
specific environment. There is a model to evaluate exposure to air
pollution that combines the Albatross and Aurora models with air
quality data (Beckx et al. 2009).
Given the population and traveling schedule of agents, the model
estimates the degree of exposure to pollution. There is also a
shop-around behavior model. It deals with an agent's spatial behavior
in a shop-around environment. It also considers the agent's shop
preference and impulsive visits (Kaneda
& Yoshida 2012). Moreover, there is a diverse amount
of literature on how to model and simulate the urban land use with
agent-based models. Matthews et al provide an extensive review on the
applications of agent-based land-use models (Matthews
et al. 2007). Additionally, The Journal of Artificial
Societies and Social Simulation has featured diverse works on the
land-use and the urban-population models (Filatova,
Parker & van der Veen 2009; Fonoberova et al. 2012; Otter, van der Veen & de Vriend
2001; Schwarz et al. 2012).
Simulations on Urban Development and Management
- 2.7
- Our objective is to perform what-if analyses on the methodologies of modeling and simulations, policy makers, civil engineers, and researchers in urban studies that have applied diverse simulation tools to their real-world problems. Batty wrote an extensive book on how to model the city dynamics with cellular automata and agent-based models (Batty 2004). With his expertise in the geo-graphics and urban planning, his book shows a set of clear examples of how city grows and exhibits complex features over time. When it comes to actual simulation software that simulates urban dynamics, we can name various simulations with various modeling objectives. For example, UrbanSim is designed to simulate a city growth and its impact on the residents in the long term with cellular automata (Waddell 2002). Another example of city-wide simulation is OREMS, which estimates the city-wide population evacuation in the case of disasters (Rathi & Solanki 1993). Also, the city-wide pandemic analysis has been supported by various agent-based model, i.e. BioWar (Carley et al. 2006). These simulations may differ by their modeling purposes, but they model the urban area and its population with agent-based models.
 Method
Method
- 3.1
- Our objective is to perform what-if analyses on changes of
local commerce after the population relocation. The policy affects the
population composition and behavior, yet we do not know the magnitude
of changes in advance. Therefore, we develop an agent-based model
representing population behaviors in a general sense with respect to
their shopping behavior, and we change the population compositions and
behavior with various parameters. This involves developing an ABM as
well as configuring a virtual experiment design. This section describes
1) simulation scenarios with a dataset, 2) formally defined simulation
models, and 3) the virtual experiment design of our simulations.
Simulation Scenario Dataset
- 3.2
- Three datasets are used to provide a simulation scenario
for our model. The first dataset is micro-population data that are
utilized to generate the virtual population in our model. The second
dataset is the statistics of living time that provide the behavior
schedules of the agents. When we acquired the datasets, there was a
one-year time gap between the generations of the two datasets. However,
the impact of this difference would be marginal. The third dataset is
the city environment, particularly district polygons and road
topologies, to distribute the agents geographically. The city
environment and the city population together determine which areas
would be hot spots of city commerce.
Micro-Population Data on City Population
- 3.3
- Micro-population data are detailed statistics about
population in a certain region. In the United States, the
micro-population data are called the Public Use Microdata Sample
(PUMS); in Korea, the data are named the Micro Data Service System
(MDSS). MDSS contains a collection of attributes, such as the
individual's address, occupation, family composition, education level,
and so on. Because there is a concern about privacy violation, the
dataset is usually provided as an anonymized sample. We could obtain a
5% sample of population data, which contains 1,189 population data out
of 23,780 population in Gwacheon city, from MDSS and use them to
generate the agent population in our model. Table 1 is a break-down of
the city population by occupations. Since the city is a suburban area,
or a satellite city, of Seoul with a focus on the government complex,
public officers and workers commuting outside of the city are the
majority. The original MDSS dataset does not provide this occupational
categorization of individuals, so we categorize the sampled individuals
with the flow in Figure 1.
- 3.4
- This categorization of population is important in
estimating the daily activities of population. Considering the impact
of the commerce after the relocation, we hypothesized that the agent's
drop-in and shop-in behaviors would be the focus of this study. These
behaviors are tightly linked to the agent's geospatial locations and
traffic pattern of the agent's daily life. However, there is no direct
dataset describing such patterns, so we modeled such daily activities
by the combination of the agent's occupation, the geospatial
distribution of buildings, and statistics of time-use. The first step
to generate an individual's daily activities is profiling the
individual, and the MDSS and the categorization jointly result in the
individual's profile.
Table 1: Descriptive statistics of 5% sample population in Gwacheon Agent Categorization # of Agents Implication Public Officer Agent 130 Public officer agent works at government complex in Gwacheon Teacher Agent 262 Teacher agent works at school Medical Personnel Agent 10 Medical personnel agent works at hospital Business Agent 27 Business agent works at office such as bank Worker Agent 19 Worker agent works in industry rather than in offices, such as shop Out-of-Town Agent 140 Out-of-town agent has a workplace out of town Student Agent 117 Student agent studies at school Telecommuter Agent 22 Telecommuter agent works at home Homemaker Agent 350 Homemaker agent looks after home and family Kid Agent (not used in Simulation) 112 Kid agent is a child Total 1,189 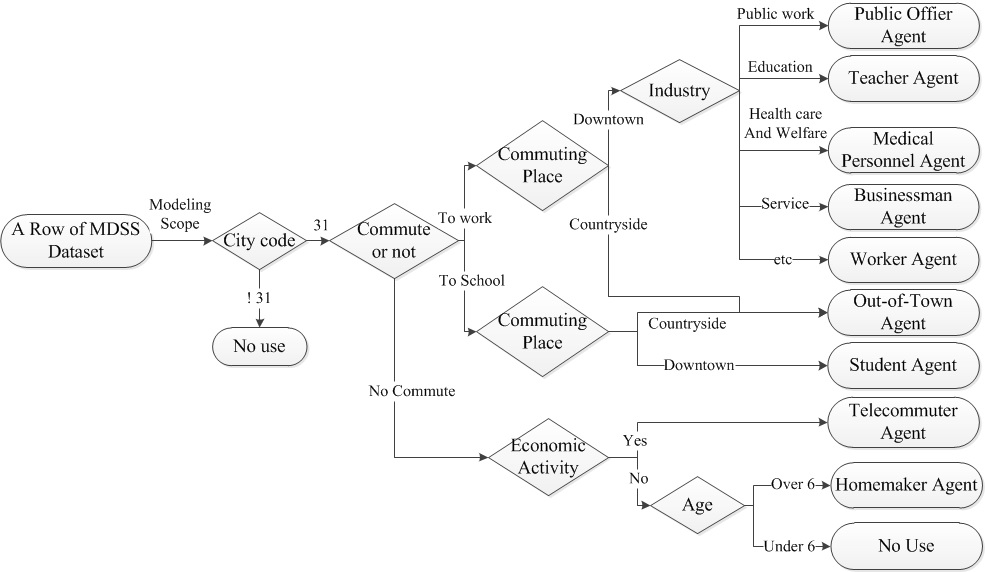
Figure 1. Flowchart of agent-type categorization with MDSS dataset Time-Use Data on City Population
- 3.5
- Many countries perform the time-use survey to gauge
productivity, daily life, and infrastructure efficiency. We used the
time-use survey provided by the Korean National Statistical Office.
This survey provides the timetable of an ordinary individual in daily
life. Particularly, this survey fits well into the MDSS dataset because
the individuals are categorized by their occupations. Figure 2 is a facet of the time-use data,
which specifies how much time an individual with a certain occupation
spends performing a certain activity. The sleeping time is almost
uniform for students, employees, and homemakers, whereas the commuting
time and the leisure time are significantly different by occupations.
This information provides two types of modeling information. First,
from the time-use data, we enumerate activity states of agent types and
their transitions. Second, the transition time for each state is also
specified by the dataset.
- 3.6
- Besides the activity-state duration by occupations, the
time-use data provides individual-level data of a certain activity.
Commuting behavior is important in analyzing and simulating traffic
patterns, shopping-in behavior, and regional characteristics.
Therefore, the time-use dataset provides a sampled set of individual
commuting-time data: when they leave their workplace or home to
commute. Figure 3 illustrates
commute patterns of student agents and other agents. There are two
peaks because the agents have to go back and forth between the home and
workplace. Compared to the other agents, student agents have a
more-concentrated commute period in the morning because every student's
class starts at 9:00 a.m. in Korea. This individual record of commuting
time suggests the distribution parameters, i.e., mean and variance, on
what time the agent commutes in a virtual city.
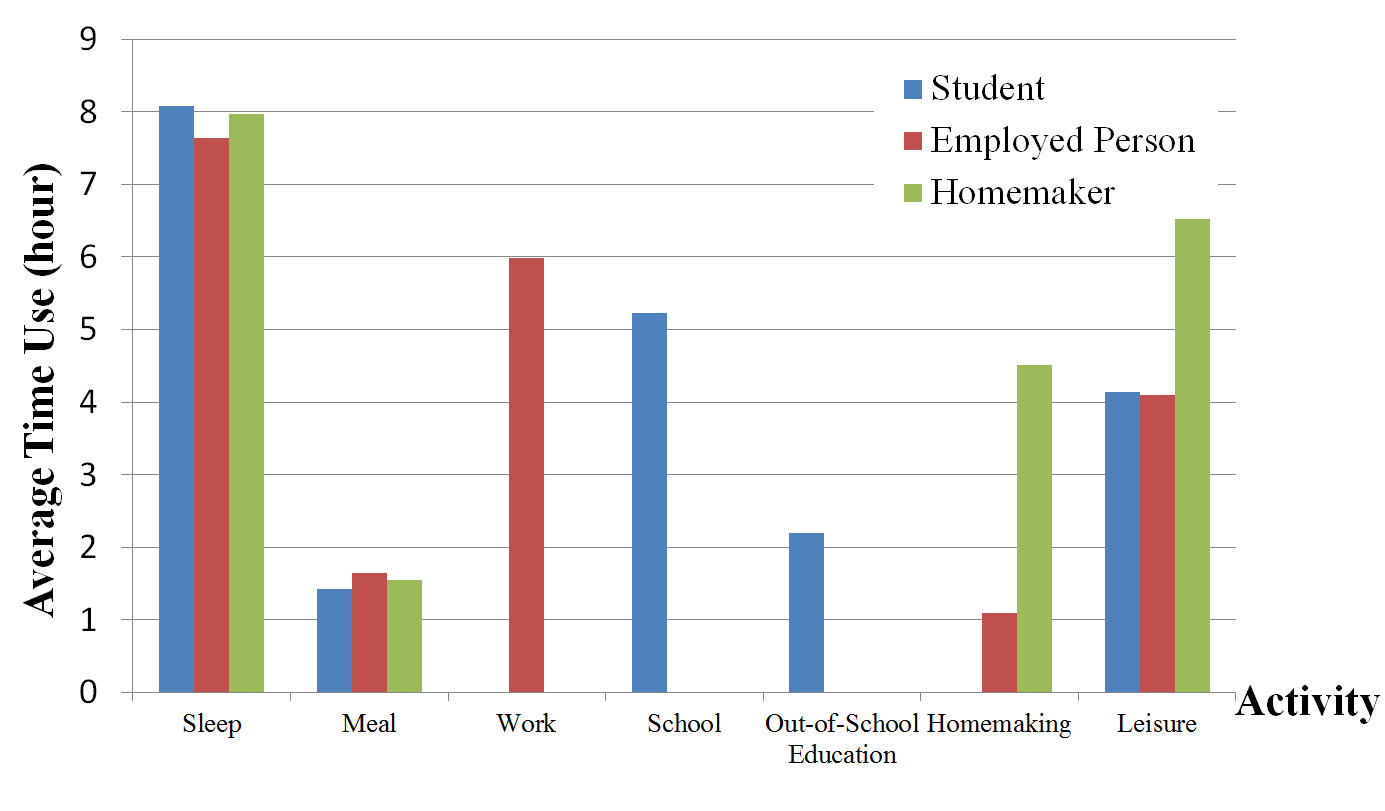
Figure 2. Time-use statistics of daily activity by student, employed person and homemaker 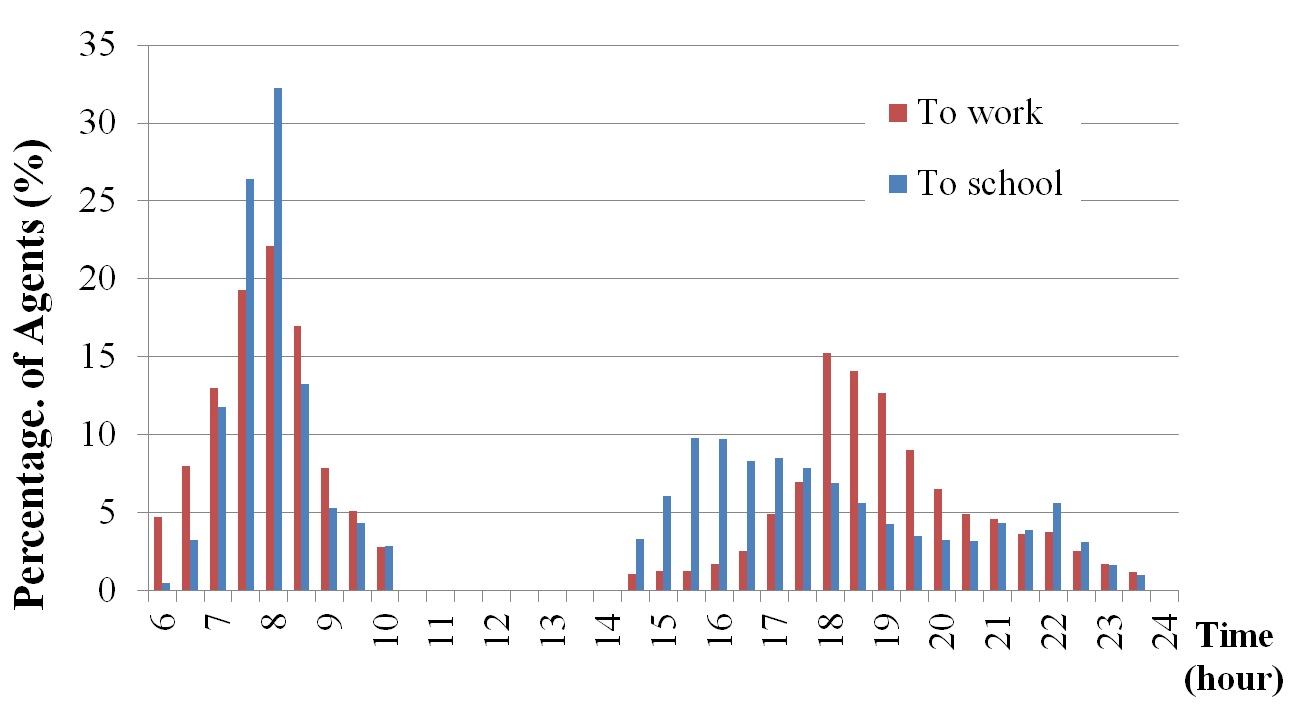
Figure 3. Time-use statistics of commute behavior by student agents and the other agent types Geographic Information Data on City Environment
- 3.7
- In addition to the agent models, we have environment data
that captures the geospatial characteristics of Gwacheon. The data were
downloaded from OpenStreetMap, see Figure 4,
and a data-cleaning process followed because the data of Korean regions
was significantly incomplete. We recovered 56 buildings of five
different types and their geospatial locations. Further, we identified
a road network that has 37 road segments and 31 junctions. The road
network data were structured and stored as a graph data to be used by
agents. The building data were not directly converted into the network
data, yet the in-and-out of the buildings was connected to the closest
road segment of the network. Three types out of the five building types
are closely related to the simulations. First, the governmental
buildings are specified as workplaces, so the worker agents commute to
the locations. Second, the commercial buildings are located at the
sides of road segments, so the passing-by agents can drop-in and shop.
Third, the residential buildings are distributed across the city, and
the agents start their daily activities from the residential buildings.
These three types of buildings become the basic spots to create an
origin-destination matrix for an individual agents, and the
origin-destination matrix of a population may reveal which commercial
areas may have more or less passing-by agents after the policy
implementation.
Figure 4. OpenStreetMap screenshot of city of interest, Gwacheon Agent-Based Model Description
- 3.8
- Since the scenario requires complex interactions between
the city environment and individuals, we chose ABM as our modeling
approach. Figure 5 shows the
structure of our ABM. The model is mainly composed of largely two
parts: the heterogeneous-agent models and the environment data. We
formally modeled the agents and treated the environment as data objects
that are used by agents. This limited the event generation and process
of environment, but those were outside our modeling scope. We
implemented our model with Repast Symphony 2.0[1].
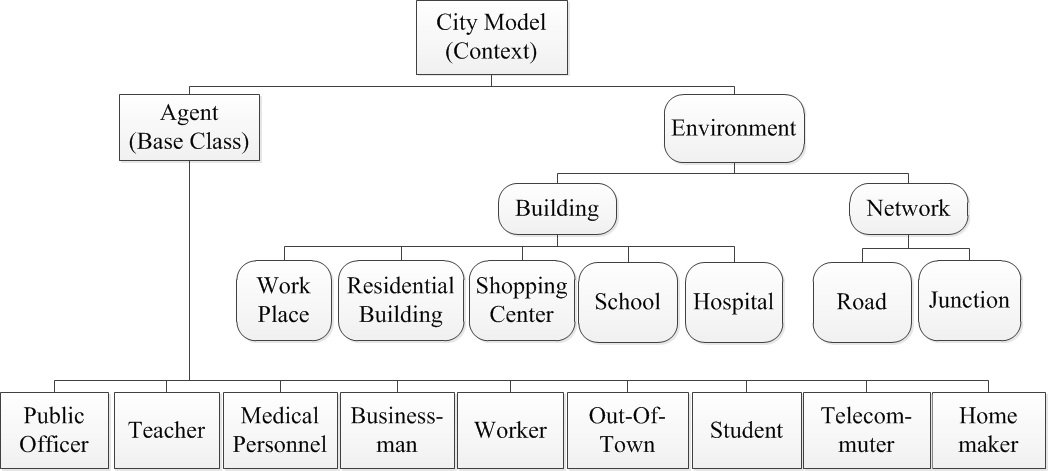
Figure 5. Agent-based model structure hierarchy; rectangles are models, and rounded rectangles are data objects - 3.9
- The agent models are built upon a base class that has basic
functionalities of agents, such as shortest-path finding, agent
generation, and agent removal. Our model depends heavily on the traffic
behavior of agents, so we made a number of assumptions on modeling the
shortest-path finding.
- Agents know the neighborhood, and they are able to find the shortest route with global map information.
- The global map information is just the information of the geospatial layout and road network; it does not include traffic flow speed at a certain time.
- 3.10
- To implement the above shortest-path-finding behavior, we
applied a simple Dijkstra algorithm to the implemented model. After
implementing the base class, diverse agent types were implemented
through the inheritance, and we continued the model description of our
diverse agents, discussed in Section 3.3.
Formal Specification of Agent Behavior
- 3.11
- Though the base function of agents is intuitive without a
detailed explanation, the schedule of agent behaviors is a crucial part
of the models that requires further explanation. One way of specifying
agent behavior is through the utilization of flowcharts. However, the
flowchart is an inadequate expression in the concrete formalism of
models because there is only a weak consensus on symbols and arrows.
Furthermore, the flowchart is useful in a brief description, but it is
less useful in specifying the detailed timings of behaviors because it
is impossible to specify the time advance in the flowchart. Similarly,
the diagram of finite state machines suffers from a number of
weaknesses. Though the finite state-machine diagrams are better than
flowcharts in showing the state transition—which is a primary design of
agent modeling—the diagrams still lack the timing of behavior, the
perception-event handling, the action-event handling, and so on. We
suspect that these shortcomings of agent-behavior representation are
commonly derived from a lack of formalism in the agent-model
description. Thus, we utilize one of the most well-known formalisms in
the discrete event model, DEVS Formalism, to formally specify the agent
behaviors in our model. Our ABM has no part of continuous time models,
so it is a discrete-event model in the big picture. Therefore, our ABM
can be specified by the DEVS formalism, which is known as a full,
complete expression of a discrete-event model. Moreover, a DEVS diagram
that is complete as well as intuitive would be a useful representation
in the agent-behavior transitions.
- 3.12
- In our model, agents make a decision on daily activities
based on their agent type and current state. Figure 6–10 describes 1) the states, 2) their
transitions guided by the external events, and 3) the outputs to the
outside of the agent model. There are five types of agent behaviors
varied by the agent types that come from the occupation date in the
MDSS. Each of the first four diagrams describes the behaviors of
student agent, out-of-town agent, homemaker agent, and telecommuter
agent. The last diagram describes the behavior of commuting agents,
which are the public officer agent, businessman agent, teacher agent,
medical personnel agent, and worker agent. States in the diagram
represents their current behaviors, and time advances that corresponds
to their state indicates time duration for the associated behavior.
- 3.13
- Agent types and the number of agents with an agent type
were set by MDSS data, and by the defined agent types, agents' daily
behaviors, such as where to visit and when to go, would be determined.
Using MDSS data and Time-use data, we developed must-go
buildings according to heterogeneous agent types, which
indicates the buildings that an agent with a certain type should visit
in a day (see Table 2). More
specifically, each agent type should go to several types of buildings
in its daily schedule. For example, in Figure 6,
a student agent prefer to school, and academy, while a homemaker agent,
in Figure 8, has no buildings that the agent must go. Also, for the
variation in simulation, the alternatives of the mandatory schedules
(i.e., going to must-go buildings) are designed. In
Figure 6, a student agent can
go to school with a higher probability (PSC) or
stay at home with a lower probability (PH1)
(i.e., PSC >> PH1).
Such probabilities in the above figures are arbitrarily defined. When
an agent decides to go to a building, the agent moves to the building
through the road network model and stays there for a certain time
duration, or time advance. Such duration time for the behaviors is
fundamentally drawn from the time-use statistics described in Section
3.1.2.
- 3.14
- When an agent goes over all must-go buildings,
its mandatory schedules in a day is over so that the agent could have
leisure time. The leisure time was categorized into two-folds: going to
another places or taking a rest at home. For example, when a student
agent moves around its school and academy, it could go to another
places for its leisure time or go back home for taking a rest. In
Figure 6, when the state of a
student agent is Academy and its duration is over,
the agent makes a decision to go to another place (with PSh1)
or home (with PH2). If an agent decides to go to
another place, the agent can go around buildings except its must-go
buildings and should go back home until its sleeping time
that can be also derived from time-use data.. Such a design method is
adopted to develop other agent types considering their must-go
buildings and time-use data (see Figure 6–10) so that we could generate
calibrated behaviors of the various agent types from the real data.
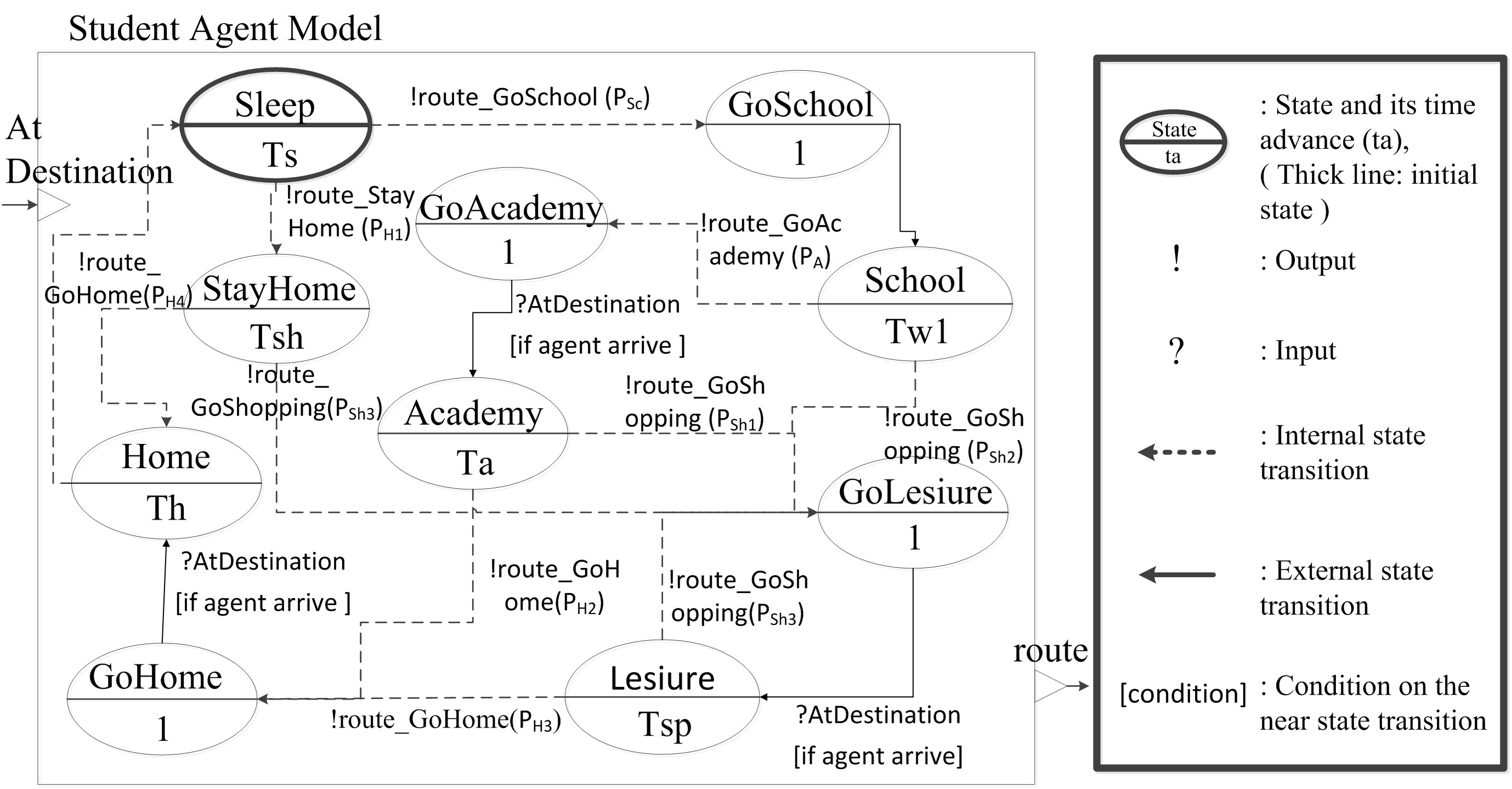
Figure 6. (Left) DEVS diagram for student agent's behaviors (states) and their time schedules (time advances) and (Right) notations on a DEVS diagram 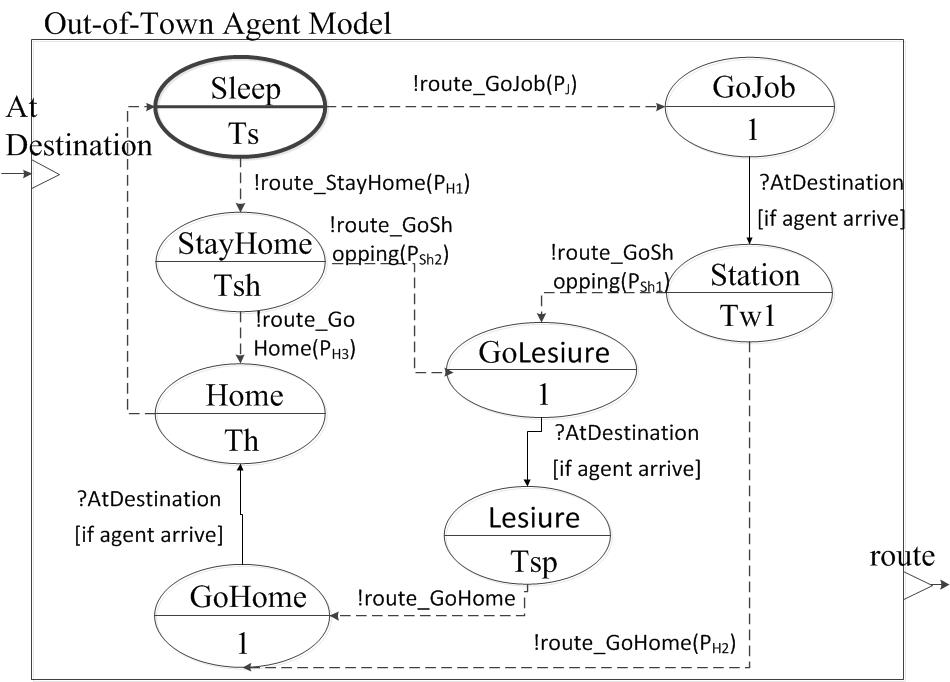
Figure 7. DEVS diagram for out-of-town agent's behaviors (states) and their time schedules (time advances) 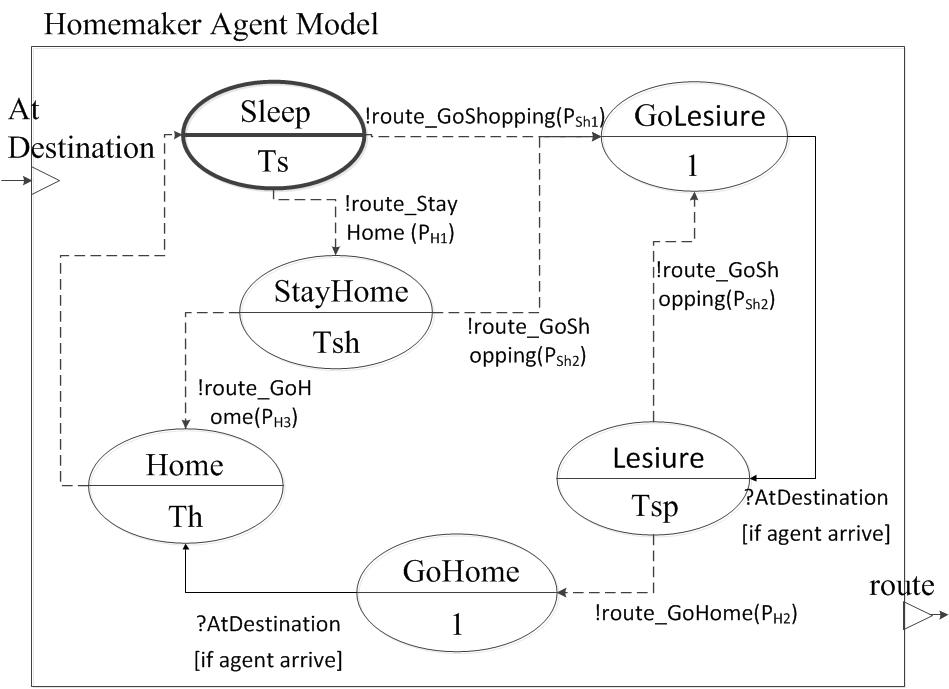
Figure 8. DEVS diagram for Homemaker agent's behaviors (states) and their time schedules (time advances) 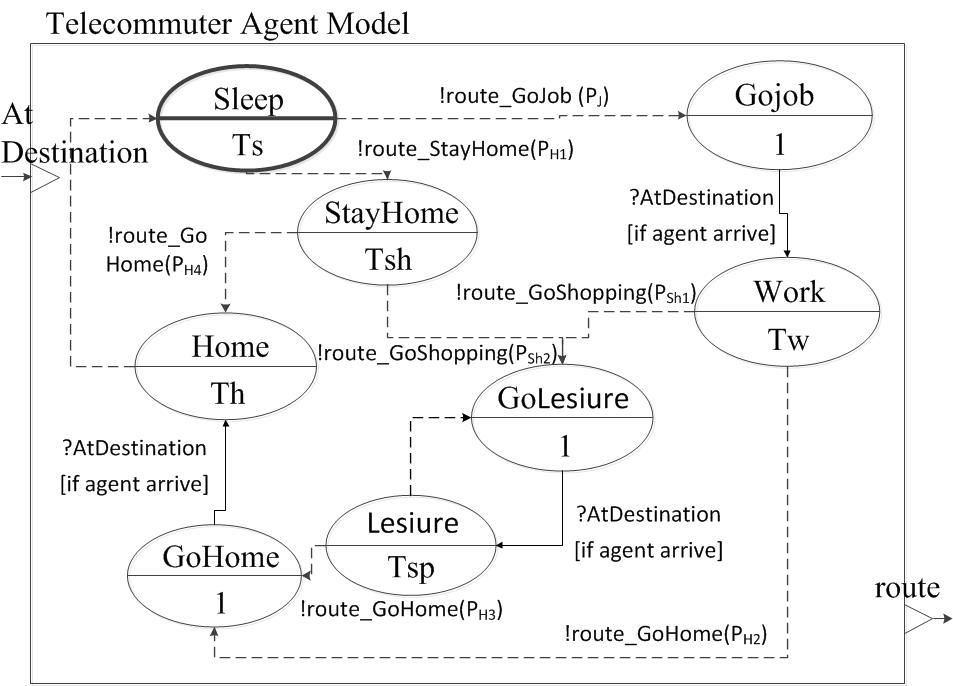
Figure 9. DEVS diagram for telecommuter agent's behaviors (states) and their time schedules (time advances) 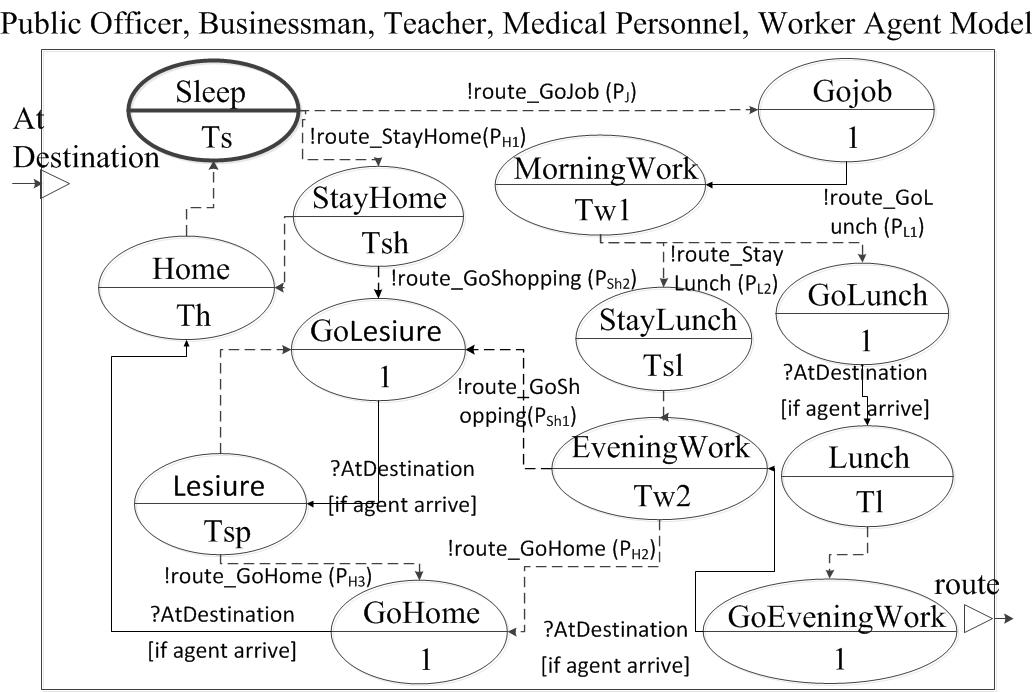
Figure 10. DEVS diagram for public officer, businessman, teacher, medical personnel, and worker agent's behaviors (states) and their time schedules (time advances) Table 2: Must-go building lists according to heterogeneous agent types Building Info. Agent Type Building Type Number Student Out-of-town Home maker Tele commuter Public officer Business man Teacher Medical personnel Worker Public 1 O Office 8 O O O Shopping 8 Traffic 4 O Apartment 10 O O O O O O O O O Hospital 2 O Restaurant 9 O O O O Academy 4 O O School 10 O O Total 56 Model Summary and Virtual Experiment Design
- 3.15
- We built our ABM of daily activities with a focus on
weekday working and shopping behavior to assess the impact of the
population relocation on the city commerce. While the previous sections
described the model architecture and the inside of the agents, Table 3 enumerates the utilized datasets
and generated output for the analysis. We calibrated our agent
activities by the MDSS dataset and the time-use dataset. We obtained
the 5% sample data of overall population in Gwacheon city from MDSS,
which contains only 1,189 members of the population. As the 1,189
population is too small to evaluate the impact on the commerce, we
generated 2,154 agents in our model, which is twice the size of the
population data. The desired output is the potential shop-in behavior
counts of each commercial building in Gwacheon.
Table 3: List of input variables, output variables, and parameters of our agent-based model Type Name Implication Input MDSS Dataset Given attributes of each agent, agent type is determined, and the daily schedule is generated by the type of agent. Time-Use Dataset The daily time consumption on a certain activity state for a certain type of individual GIS Dataset Information of roads and buildings about coordinates, type, and identification Output Number of Passing-by Agents The count of passing-by agents for each building to gauge the commerce activities Number of Agents on Road Segment The count of agents on a certain road segment to gauge the traffic status Parameter Reduction Ratio Portion of relocating public officers over all of the public officers in Gwacheon city Commute Ratio Portion of public officers who commute between Gwacheon and new city without moving out over all of the relocating public officers Family Move Boolean value indicating whether a public officer would move out with his family or not Transportation Speed The speed of walking is 1, and others are x times faster than walking
(walk = 1, bike = 3, bus = 8, car = 10)Simulation time Total simulation time
(default = 24 hours)Initial Position of Agent Determine the house of agent randomly before the simulation
(default = random assignment with the MDSS dataset, see Section 3.3.)Required Place of Agent Determine the mandatory place for agent depending on its type
(default = random assignment with the MDSS dataset, see Section 3.3.)Activity Duration Activity duration of agent depends on its statistics
(default = time-use statistics in Section 3.1.2.) - 3.16
- In the simulation, the model counts the passing-by agents
to gauge the size of local populations at a certain location, and we
assume that the counts on passing-by agents would negatively affect to
the city commerce. This assumption is not an originative one because
the relationship between population in a local area and the local
economy was researched in numerous works (Kuznets
1967; Simon 1986;
Becker, Glaeser & Murphy
1999; Tsen &
Furuoka 2005). For example, Tsen and Furuoka (2005) investigated the
relationship between population and economic growth in Asian economies.
Also, Fesser and Sweeney (1999)
examined significant forms of economic distress that accompanied
out-migration and population loss in U.S. communities from the same
viewpoint of ours. The counts on passing-by agents depend on the
traffic status of the road network, so the number of agents on a
certain road segment is also counted.
- 3.17
- Table 4 is the
virtual experiment design to establish scenarios of interest and
estimate the impact of the relocation policy. The policy to be
implemented will relocate the workplace for public officers in Gwacheon
to the other city, so the public officers and their family in Gwacheon
city are subject to considering the movement by the relocation policy.
Once the policy is executed, we could estimate three possible cases of
the public officers dependent on several conditions:
- When the relocation policy is executed, some of the public officers should relocate to new administrative city
- Among the relocating public officers, some would move out from Gawcheon city, but others would commute between Gwacheon and the new city
- Among the moving out public officers, some would move out with their family, but others would move alone
- 3.18
- Based on the three possible cases, we setup three
experimental variables: reduction ratio, commute ratio,
and family move. Reduction ratio
indicates a portion of the relocating public officers. If the reduction
ratio is 0.1, 10% of public officers in the city should relocate to the
new administrative city. Commute ratio describes a
portion of the relocating public officers who commute between Gwacheon
city and the new city without moving out. If the commute ratio is 0.0,
all of the relocating public officers would move out from Gwacheon
city. Family move represents whether a public
officer's family would go with him or not when he decides to move out.
In our virtual experiments, we developed seven cases of reduction
ratio, five cases of commute ratio and two cases of family move (see
Table 4). Thus, we came up
with 70 simulation cases by the full-factorial experimental design and
added one more simulation case (i.e., baseline) with no relocations.
All of the experiments were repeated 20 times to prevent the effects of
randomness in our model.
Table 4: Virtual experiment design of scenario of interests Experiment
Variable NameExperiment Design Implication Reduction Ratio 0.1, 0.2, 0.3, 0.4, 0.5 0.6, or 0.7 (7 cases) Portion of relocating public officers over all of the public officers in Gwacheon city Commute Ratio 0.0, 0.25, 0.50, 0.75, or 1.00 (5 cases) Portion of public officers who commute between Gwacheon and new city without moving out over all of the relocating public officers Family Move True or False (2 cases) Boolean value indicating whether a public officer would move out with his family or not Total Number of Experiment Cells 70 experiment cells + 1 baseline cell
(= 7 * 5 * 2 + 1 cases)Each cell is replicated 20 times
 Results
Results
- 4.1
- We analyzed the policy impact with the described ABM and
the experiment design. First, this section presents the results of the
policy analysis which is the major objective of this paper. The results
of the policy analysis are provided visually as well as with a
statistical significance test. Second, this section illustrates the
statistical validation results on the model. We present how we gathered
the validation dataset and how we statistically computed the
correlation between the simulated world and the real world.
Result on Relocation Policy Analysis
- 4.2
- We performed a virtual experiment with our model and
experiment design. To assist the intuitive understanding of the result,
we provided a visualization of simulation runs. After the
visualization, we investigated the significance of changes on the
passing-by agents at the building level. One merit of utilizing the ABM
is the micro-level analysis of simulation outputs, so we observed which
areas would be affected more than the other areas.
Illustration on Model Execution
- 4.3
- Our ABM simulates the local population's daily activities
with a focus on traffic and shopping-in behavior. Figure 11 shows a list of screenshots at
6am, 8am, 2pm, and 6pm in the simulation world. The agent types are
color-coded in the screenshots, and the buildings are geospatially
distributed in the region. Figure 3
from the time-use dataset specifies that there is a smaller range of
time for going to the workplace compared to going home in the commuting
activities. Therefore, our model shows the heavier traffic at 8am
compared to the traffic at 6pm. At 6am, there is little traffic because
of random time-advance adjustment for some agents. At noon, agents who
do not commute come out for shopping and other activities.
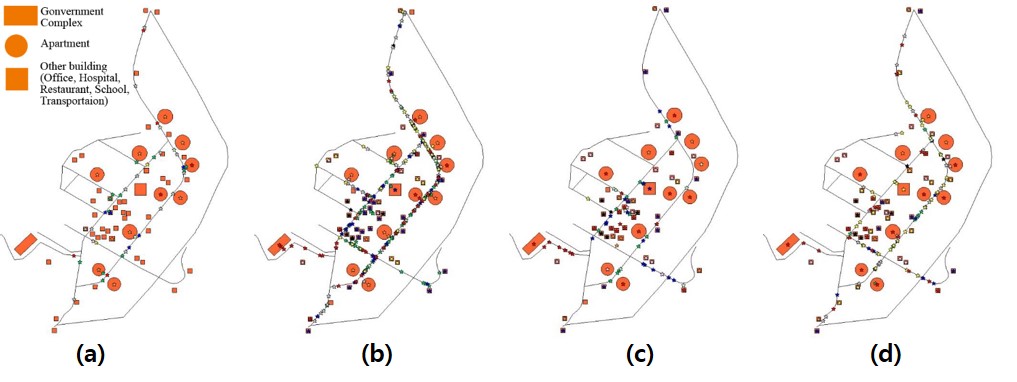
Figure 11. Simulated daily activities of local population at 6am (a), 8am (b), 2pm (c), and 6pm (d) in the simulated city - 4.4
- Figure 12 shows
the impact of reducing passing-by agents at commercial buildings of
interest. The 17 buildings were selected by if they were related to
shopping, dining, or leisure activities, which would be the commercial
buildings in the city. Figure 12
shows the nine cases out of 70 experimental cells in Table 4. When the family does not
relocate, the impact to the counts of passing-by agents was minimal.
Therefore, we selected nine representative cells when the family does
not relocate. We observed that the buildings were affected differently
by the commute ratio and the reduction ratio. Furthermore, the
geographic locations of buildings influenced the impact as well. For
instance, the cell with a high reduction ratio and low commute ratio
showed a greater reduction than the cell with a high reduction ratio
and high commute ratio because the local population diminishes less
with a higher commute ratio. The commuting behavior will lead the
agents to the highway interchange at the north of the city, so some
buildings in the way are almost the same before the policy is
implemented.
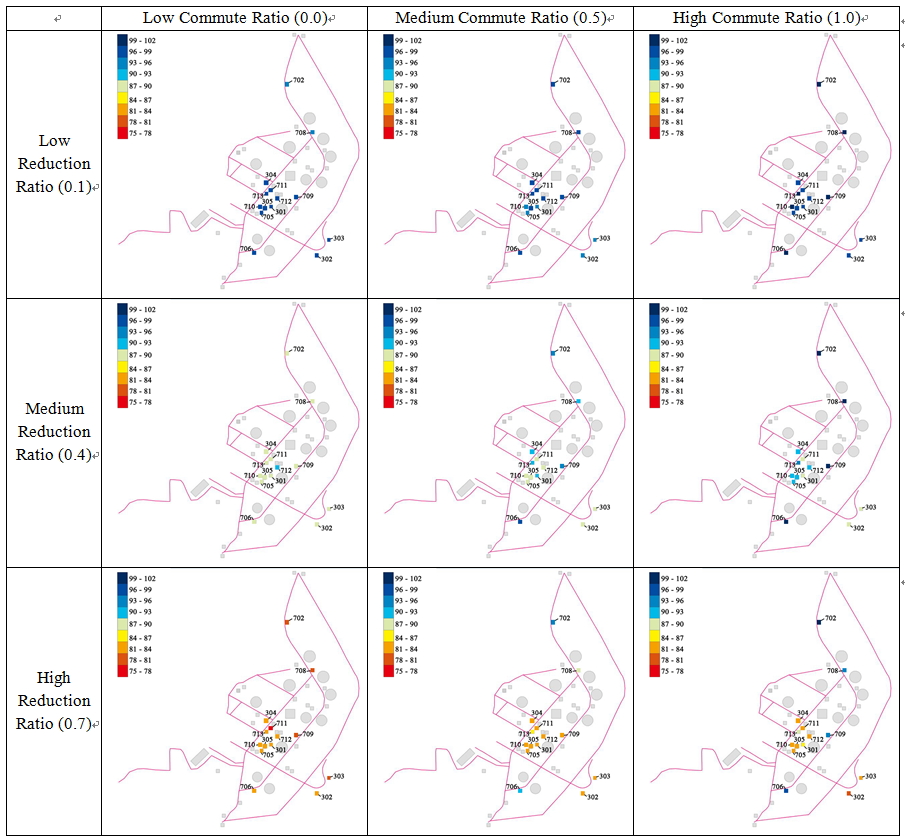
Figure 12. Reduction rate of the number of passing-by agents with various experimental variable settings; north is up, and the percentage indicates the reduction of passing-by agents compared to the baseline - 4.5
- Figure 13
illustrates the aggregated impacts of the city commerce through diverse
factors. Figure 13 implies
that the relocation will not affect much unless it is accompanied by
the family relocation. This relocation of the family is much more
significant than varying the relocation ratio of the public officers.
Actually, this estimation is already being observed in Gwacheon because
there are reports questioning the impact of the relocation policy
without whole family movements.
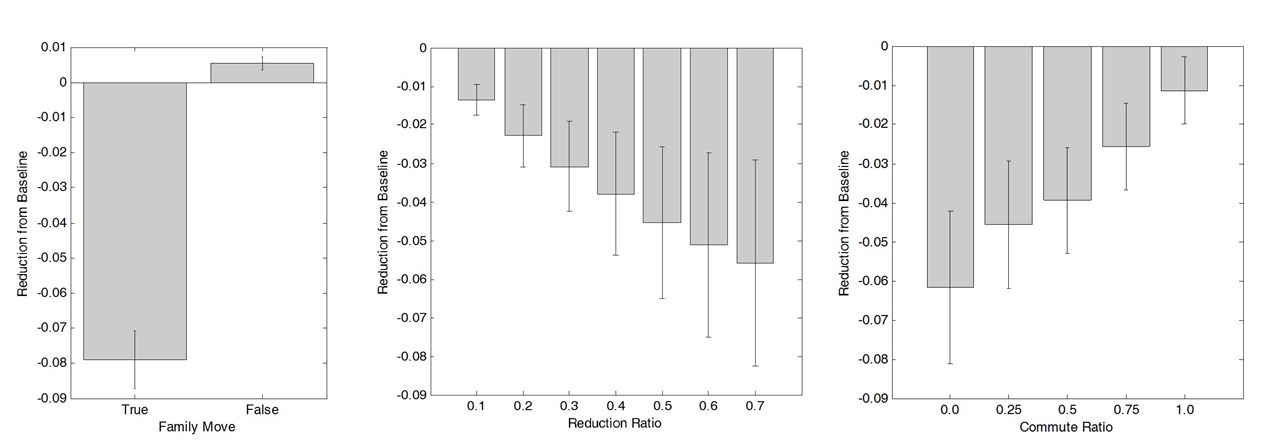
Figure 13. Percentages of reduced passing-by agents compared to the baseline (Left) marginalized by family move parameter, (Center) marginalized by reduction ratio, and (Right) marginalized by commute ratio (marginalization: integrating or summing out results from three parameters to the result of one parameter for concentrating on the effect by each parameter independently) Statistical Analyses on City Commerce
- 4.6
- In our simulations, the counts of passing-by agents of
commercial buildings vary by four factors: building locations, family
move, reduction ratio, and commute ratio. To statistically evaluate the
significance of these factors, we developed a meta-model that explains
the significance of the factors in determining the counts. The
meta-model is a multivariate linear regression between the four factors
and the counts of passing-by agents. Two factors, the building and the
family move, are categorical variables, so we created two corresponding
sets of variables by omitting one case for each of the sets. Table 5 describes the details of the
meta-modeling result. Because we standardized the coefficients, we can
compare the sensitivity of changing variables to increase the counts.
As illustrated in Figure 9, the
counts decrease when the families move, the reduction ratio increases,
and the commute ratio decreases. Table 5
indicates that the strengths of the three factors are in the order of
family move, commute ratio and reduction ratio by observing the
standardized coefficients and the P-value indicates the robustness of
the interpretations. When we compare the three factors to the
commercial building locations, most of the locations have a stronger
influence to the counts than the family move, the reduction ratio, and
the commute ratio. This means that the building locations will be the
strongest factor in determining the rise and fall of the commercial
merits, and this is illustrated in Figure 12.
- 4.7
- Besides the meta-modeling, we performed an analysis of
variance (ANOVA) test on the factors and the counts of passing-by
agents. Table 6 shows the
influence from the treatments, which are experimental variables, to the
counts. The analysis result is consistent with the meta-model. The
building location is the major treatment to change the counts. Then,
the family move, the commute ratio, and the reduction ratio have the
influence to the counts in the order of the strengths.
Table 5: Meta-model of passing-by counts with linear regression of passerby counts by buildings of interest 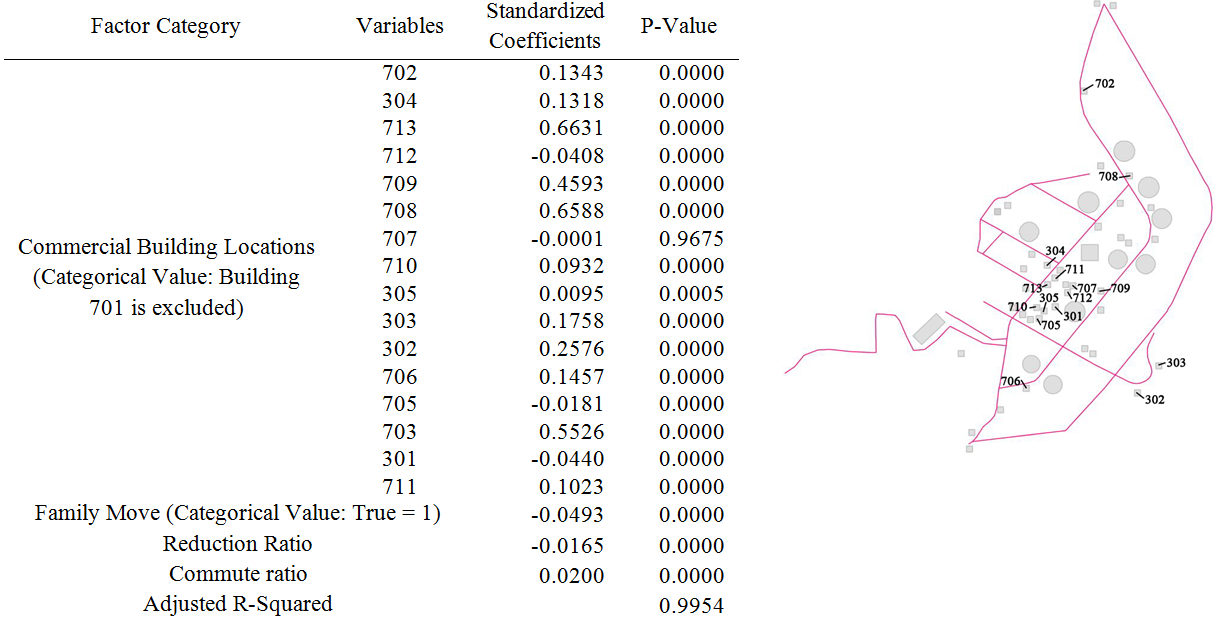
Table 6: ANOVA to show factor significance between the experimental variables and the counts of the passing-by agent Variables 'Sum Sq.' 'd.f.' 'F' 'Prob>F' Commercial Building Locations 4.30E+09 1.60E+01 15820.3738 0.0000 Family Move 1.05E+07 1.00E+00 620.6110 0.0000 Reduction Ratio 1.19E+06 6.00E+00 11.7019 0.0000 Commute Ratio 1.75E+06 4.00E+00 25.8057 0.0000 'Error' 1.97E+07 1.16E+03 'Total' 4.34E+09 1.19E+03 Result of Model Validation Analysis
- 4.8
- This simulation study was designed in the middle of 2012
when the policy was about to be executed. In Aug, 2013, we surveyed the
actual changes in Gwacheon. This study focuses on the impact of the
relocation on the commercial aspect, so we investigated the rent rate
changes of the simulated buildings in the real world. The direct
measure of commercial status would be a sales amount of shops and malls
in the region, but such information is difficult to collect in the
city-wide area. Therefore, we collected the indirect measure, i.e., the
rent rate of the buildings, showing the changes in the commercial
aspect, and this measure is easier to survey. However, objectively
recording the rent rate of commercial buildings was not an easy task
because the contracts were not made often and because the exact rate
was not publicly available, which was very different from finding the
rent rate for residences. Therefore, we contacted 11 major real-estate
agencies and performed the surveys on the rents of the buildings.
Because there were no responses from some of the interviewees, we
recovered only five survey returns. Furthermore, out of 17 buildings of
interest in the simulation, three buildings were not available for
renting spaces for commercial purposes, so 14 buildings became the
targets of validation.
- 4.9
- Figure 14 and
Figure 15 shows the visual
comparison between the measures from the real world and the
simulations. We contrasted the surveyed rent rate and the average
counts of passing-by agents by commercial buildings of interest. It is
difficult to see a strong correlation between the two, yet the scatter
plots show a slight positive correlation between the two sets of
metrics. Whereas there seems to be a positive correlation, some
buildings, Building 711, 706, and 302, are deviated from the fitted
line.
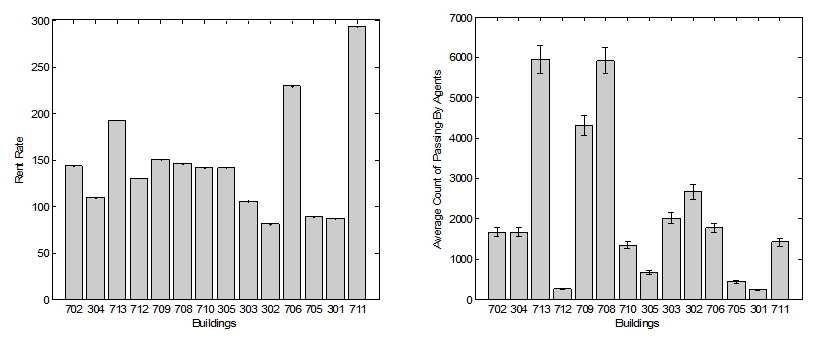
Figure 14. (Left) Surveyed rent rates by buildings in the real world and (Right) average count of passing-by agents in the simulations 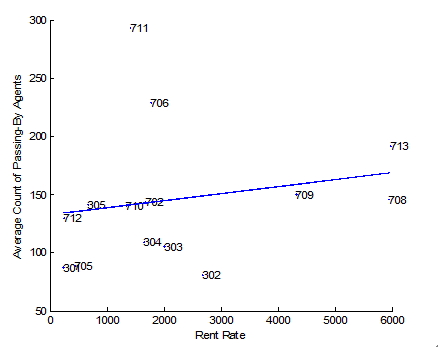
Figure 15. Scatter plot and a linear fitted line between the simulation result and the real world survey - 4.10
- Since we cannot confirm the correlation with only the
visualization of the two distributions, we calculated the correlations
between the two distributions. Specifically, we calculated the
correlations between the surveyed distribution and each virtual
experiment cell, which resulted in 70 sets of correlation results.
Also, we calculated three different correlations: Pearson correlation,
Spearman's rank correlation, and Kendall's tau rank correlation. We
included the rank correlations because simulation results with correct
prediction in ranks, not the continuous value distribution, can be
useful in the real world policy analyses. Table 7
shows the summary of this correlation analysis. When we include every
building of interests, the value correlation is 20.68%, and the rank
correlation is 45.49%. Considering that this is a social simulation
that is very difficult to achieve high validation, we think that this
is an average quality for the validation. When we exclude the buildings
that are deviating from the fitted line in Figure 15,
the value correlation becomes 48.3%, and the rank correlation becomes
85.45%. This would be a good quality of validation considering the
difficulty of the validation of social simulations. Besides the
statistical validation result, we traced which virtual experimental
cells resulted in the maximum correlation. This parameter trace result
might tell us the actual settings of the real world. For example, when
the experimental cells generating the maximum Spearman's rank
correlation simulates when the families do not relocate, the reduction
rate is 0.7, and the commute ratio is 0.5.
Table 7: Correlation analysis between the surveyed rent rate and the simulated passing-by agent counts 14 Buildings 11 Buildings
(Excluding outliers: Building 711, 706, and 302)Max. Correlation Value Simulation Setting of Max. Correlation Max. Correlation Value Simulation Setting of Max. Correlation Family Move Reduction Ratio Commute Ratio Family Move Reduction Ratio Commute Ratio Pearson
Correlation0.2068 True 0.6 1.0 0.4830 True 0.3 0.75 Spearman's Rank Correlation 0.4549 True 0.6 1.0 0.8545 False 0.7 0.5 Kendall's Tau Rank Correlation 0.3187 True 0.6 1.0 0.6727 False 0.7 0.5
 Conclusions
Conclusions
- 5.1
- We studied the impact of the public officer's relocation
policy to the commerce of Gwacheon city. Our agent-based model is
calibrated with the micro-population dataset, the time-use dataset, and
the geospatial environment of the city. The analysis results estimate
that the relocation will reduce the city commerce significantly in
three cases: when the families of the public officers relocate, when
the reduction ratio gets higher, and when the commute ratio becomes
lower. While the city-wide commerce would be damaged in general, the
magnitude of the impacts will differ by the buildings, particularly by
the geospatial locations of commercial buildings. When we gauge the
strengths of the factor influence to the damage, the building location
would be the most significant factor in determining the impact
magnitude. To validate this result, we surveyed the rent rate of the
commercial buildings as a proxy measure to observe the damage to the
city commerce. While there are outlier buildings in the validation, the
value correlation is 48.3%, and the rank correlation is 85.45%.
- 5.2
- Many policies are designed and implemented for a greater good and a strategic purpose. This relocation policy of the government complex is intended to divert a small function of Seoul to a distant city, so the over-population and its accompanying problems could be resolved in the process. However, this policy makes a profound impact on the affected population: the families that needs to relocate, the public officers who might commute for two hours a day, and the local shops and malls with reducing sales. Policy makers might need a tool that enables them to foresee the outside effects of their policies, and this simulation would be such a tool.
 Acknowledgements
Acknowledgements
- Supports from the Public welfare & safety research program through the National Research Foundation of Korea (NRF) (2012-0029881)
 Notes
Notes
-
1This
model can be found at https://www.openabm.org/model/4345/version/1/view
 References
References
- ARENTZE, T. A., Pelizaro, C.
& Timmermans, H. J. P. (2005). Implementation of a model of
dynamic activity-travel rescheduling decisions: an agent-based
micro-simulation framework. Proceedings of the Computers in
Urban Planning and Urban Management Conference, 48.
ARENTZE, T. A. & Timmermans, H. J. P. (2004). Albatross – a learning based transportation oriented simulation system. Transportation Research Part B: Methodological, 38(7), 613–633. [doi:10.1016/j.trb.2002.10.001]
BAE, J. W., Lee, G. & Moon, I.-C. (2012). Formal specification supporting incremental and flexible agent-based modeling. Proceedings of the 2012 Winter Simulation Conference (pp. 1–12). [doi:10.1109/WSC.2012.6465163]
BATTY, M. (2004). Cities and Complexity: Understanding Cities with Cellular Automata, Agent-based Models, and Fractals. MA: MIT press.
BECKER, G. S., Glaeser, E. L. & Murphy, K. M. (1999). Population and economic growth. American Economic Review, 145–149. [doi:10.1257/aer.89.2.145]
BECKX, C., Int Panis, L., Arentze, T., Janssens, D., Torfs, R., Broekx, S. & Wets, G. (2009). A dynamic activity-based population modelling approach to evaluate exposure to air pollution: methods and application to a Dutch urban area. Environmental Impact Assessment Review, 29(3), 179–185. [doi:10.1016/j.eiar.2008.10.001]
BURGESS, E. W. (2008). The Growth of the City: An Introduction to a Research Project (pp. 71–78). Springer US. [doi:10.1007/978-0-387-73412-5_5]
CARLEY, K. M. (2002). Computational organization science: A new frontier. Proceedings of the National Academy of Sciences, 99(suppl 3), 7257–7262. [doi:10.1073/pnas.082080599]
CARLEY, K. M., Fridsma, D. B., Casman, E., Yahja, A., Altman, N., Kaminsky, B. & Nave, D. (2006). BioWar: scalable agent-based model of bioattacks. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 36(2), 252–265. [doi:10.1109/TSMCA.2005.851291]
EPSTEIN, J. M. (1996). Growing Artificial Societies: Social Science from the Bottom Up, (pp. 1–20). Brookings Institution Press.
FESSER, E. J. & Sweeney, S. H. (1999). Out-migration, Population Decline, and Regional Economic Distress (p. 80). Washigton, DC.
FILATOVA, T., Parker, D. & Van der Veen, A. (2009). Agent-based urban land markets: agent's pricing behavior, land prices and urban land use change. Journal of Artificial Societies and Social Simulation, 12 (1) 3: https://www.jasss.org/12/1/3.html.
FONOBEROVA, M., Fonoberov, V. A., Mezic, I., Mezic, J. & Brantingham, P. J. (2012). Nonlinear dynamics of crime and violence in urban settings. Journal of Artificial Societies and Social Simulation, 15(1), 2.
FORRESTER, J. W. (1971). Counterintuitive behavior of social systems. Theory and Decision, 2(2), 109–140. [doi:10.1007/BF00148991]
GUO, H. C., Liu, L., Huang, G. H., Fuller, G. A., Zou, R. & Yin, Y. Y. (2001). A system dynamics approach for regional environmental planning and management: a study for the Lake Erhai Basin. Journal of Environmental Management, 61(1), 93–111. [doi:10.1006/jema.2000.0400]
HARRIS, C. D. & Ullman, E. L. (1945). The nature of cities. The Annals of the American Academy of Political and Social Science, 242(1), 7–17. [doi:10.1177/000271624524200103]
HOLZER, R. & de Meer, H. (2008). On modeling of self-organizing systems. Proceedings of the 2nd International ICST Conference on Autonomic Computing and Communication Systems (pp. 1–6). Turin, Italy. [doi:10.4108/ICST.AUTONOMICS2008.4671]
HOYT, H. (1939). The structure and growth of residential neighborhoods in American cities (p. 178). Washington, D.C: U.S. Govt.
JUN, M. J. (2007). Korea's public sector relocation: Is it a viable option for balanced national development? Regional Studies, 41(1), 65–74.
KANEDA, T. & Yoshida, T. (2012). Simulating shop-around behavior. Proceedings of the 2012 Symposium on Agent Directed Simulation (p. 8). Orlando, Florida: Society for Computer Simulation International.
KUZNETS, S. (1967). Population and economic growth. Proceedings of the American Philosophical Society (pp. 170–193).
MARSHALL, J. N., Bradley, D., Hodgson, C., Alderman, N. & Richardson, R. (2005). Relocation, relocation, relocation: assessing the case for public sector dispersal. Regional Studies, 39(6), 767–787. [doi:10.1080/00343400500213663]
MATTHEWS, R. B., Gilbert, N. G., Roach, A., Polhill, J. G. & Gotts, N. M. (2007). Agent-based land-use models: a review of applications. Landscape Ecology, 22(10), 1447–1459. [doi:10.1007/s10980-007-9135-1]
MOON, I. C. & Carley, K. M. (2007). Modeling and simulating terrorist networks in social and geospatial dimensions. IEEE Intelligent Systems, 22(5), 40–49. [doi:10.1109/MIS.2007.4338493]
OTTER, H. S., van der Veen, A. & de Vriend, H. J. (2001). ABLOoM: Location behaviour, spatial patterns, and agent-based modelling. Journal of Artificial Societies and Social Simulation, 4 (4) 2: https://www.jasss.org/4/4/2.html.
RATHI, A. K. & Solanki, R. S. (1993). Simulation of traffic flow during emergency evacuations. Proceedings of the 1993 Winter Simulation Conference (pp. 1250–1258). New York, New York, USA: ACM Press.
RODRIGUE, J.-P., Comtois, C. & Slack, B. (2011). The geography of transport system. Journal of Urban Technology, 18(2), 99–101. [doi:10.1080/10630732.2011.603579]
SCHWARZ, N., Kahlenberg, D., Haase, D. & Seppelt, R. (2012). ABMland - a tool for agent-based model development on urban land use change. Journal of Artificial Societies and Social Simulation, 15 (2) 8: https://www.jasss.org/15/2/8.html.
SIMON, J. L. (1986). Theory of Population and Economic Growth. Oxford United Kingdom Basil Blackwell.
SMITH, L., Beckman, R. & Baggerly, K. (1995). TRANSIMS: Transportation analysis and simulation (No. LA-UR-95-1641).
TESFATSION, L. (2002). Agent-based computational economics: growing economies from the bottom up. Artificial Life, 8(1), 55–82. [doi:10.1162/106454602753694765]
THÜNEN, J., Wartenberg, C. M. & Hall, P. (1966). Von Thünen's Isolated State. London: Oxford: Pergamon press.
TSEN, W. H. & Furuoka, F. (2005). The relationship between population and economic growth in Asian economies. ASEAN Economic Bulletin, 314–330. [doi:10.1355/AE22-3E]
WADDELL, P. (2002). UrbanSim: modeling urban development for land use, transportation, and environmental planning. Journal of the American Planning Association, 68(3), 297–314. [doi:10.1080/01944360208976274]
ZHANG, X. H., Zhang, H. W., Chen, B., Chen, G. Q. & Zhao, X. H. (2008). Water resources planning based on complex system dynamics: a case study of Tianjin city. Communications in Nonlinear Science and Numerical Simulation, 13(10), 2328–2336. [doi:10.1016/j.cnsns.2007.05.031]