 Abstract
Abstract
- During the 1960s but mainly in the 1970s, large mathematical dynamic global models were implemented in computers to simulate the entire world, or large portions of it. Several different but interrelated subjects were considered simultaneously, and their variables evolved over time in an attempt to forecast the future, considering decades as time horizons. Global models continued to be developed while evidencing an increasing bias towards environmental aspects, or at least the public impact of models with such a focus became prevalent. In this paper we analyze the early evolution of computer-based global modeling and provide insights on less known pioneering works by South American modelers in the 1960s (Varsavsky and collaborators). We revisit relevant methodological aspects and discuss how they influenced different modeling endeavors. Finally, we overview how distinctive systemic approaches in global modeling evolved into the currently well-established discipline of complex systems.
- Keywords:
- Global Models, Social Processes, Complex Systems, History of Science, Computer Simulation, Latin American Modeling
 Introduction
Introduction
- 1.1
- For social scientists interested in mathematical global models, the computer can be regarded as their (virtual) laboratory. Models including social dynamics must either have a strong random structure, or be prepared to analyze several very different scenarios based on a wide range of assumptions, or both. In this context, at least two interesting questions emerge: on the one hand, how much is it possible to characterize developed and underdeveloped countries using as a parameter the "degree of randomness" of the forecasts for any given region? That is, is randomness a characteristic of underdeveloped (or developing) countries? Clearly not: e.g., Argentina has a more developed structure than, say, Namibia, but in spite of that Namibia is more "predictable" than Argentina.
- 1.2
- On the other hand, how sophisticated must be the mathematics employed to formulate a global model in order to offer acceptable levels of confidence? In other words, is there a correlation between the mathematical complexity behind a global model and the accuracy of its forecasting power? In this case, and to the applied mathematicians' disappointment, the answer is also no, or at least not necessarily. As an extreme example, two outstanding works predicting the fall of the Soviet Union, namely Amalrik (1970) and Todd (1976) had been published many years before its actual dissolution[1]; none of them used mathematical models, and it seems that global modelers did not paid attention to them[2]. Meanwhile, considerably complex models of political processes have led to utterly implausible conclusions (e.g. runs of the GLOBUS model in the 1980s predicted the political system in Czechoslovakia, East Germany and Poland to be more stable than that in Western Europe). It is very difficult to forecast political upheavals using exclusively mathematical models. Yet, when used carefully, global models are very powerful tools; in fact, we consider not using them a complete mistake.
- 1.3
- The more satisfied we are with the predictive capacity of a global model the more complex the involved mathematics become, and the more new ideas of potential applications appear calling in turn for new mathematical tools. In this scenario, an important methodological aspect to pay attention to mandates never putting mathematics before the model: the assumptions of the model should suggest the degree of complexity of the mathematics employed. In fact, this is the methodology we should always adhere to when modeling any system, be it a world system or any other (usually for models in physics or engineering, we count on a vast experience of several centuries during which the mathematical tools developed considerably, and it is already known we must begin with technically "hard" mathematics, while in the case of socio-political models the "right" mathematical tools are still a matter of debate[3]).
- 1.4
- None of the remarks made above are original. They are universally known in the context of the involved disciplines. What we shall present in this work is an exemplification of these ideas while analyzing the evolution of global modeling, including a discussion of the pioneering work of South American modelers in the 1960s (Varsavsky and his collaborators' models) and in the 1970s (the Bariloche model).
 Tracing back the origins of
global models
Tracing back the origins of
global models
- 2.1
- In late 1950s, the brilliant engineer turned specialist in management Jay Wright Forrester, already well known because of his participation in the building of an aircraft simulator -that eventually became the Whirlwind digital computer, and then became the Semi-Automatic Ground Environment (SAGE) air defense system for North America- and for having developed the "Multi-coordinate digitally information storage device", forerunner of today's RAM, created System Dynamics, a discipline whose goal is to understand the dynamic behavior of complex socio-natural systems using mathematical tools and computer simulations. His book (Forrester 1961) studied industrial business cycles using System Dynamics as a convenient tool. In 1969, after many discussions with former Boston mayor John F. Collins he published a book (Forrester 1969) modeling social urban problems. His work was extremely important in the process of modeling complex social, industrial and political situations and in formulating current and future feasible scenarios through mathematical models.
- 2.2
- But Forrester did not apply his technique to entire countries –at least during the 1960s–, let alone large regions that include several countries, continents, or the entire world. It seems that the first application of such ambitious approach is due to E.P. Holland (see Holland & Gillespie 1963). As Holland tells in the preface of this book, after trying unsuccessfully to implement a model of these characteristics in an analog computer, he eventually prepared the model to be run on the IBM 704 computer of the MIT Computational Center, using the simulation language DYNAMO, which Forrester and his group were just completing at the MIT School of Industrial Management (moreover, in the process of translation the model became more elaborated: perhaps one can consider the failure with the analog model and the success -and improvement- with the digital one as a symbolic demonstration of the triumph of digital computation). By the way, Holland and his group were helped in the programming by A. L. Pugh, III, and P. A. Fox, designers of DYNAMO (see Pugh 1970). Therefore, one can see Forrester's influence, though Forrester himself did not participate in this project. In this work the economy of a plausible underdeveloped country -that had some of the characteristics of India- was simulated (Holland used considerable data from India, but some considerations important for India were omitted or grossly simplified). The model was dynamic, i.e., with fixed parameters and state variables evolving over time, it showed the supposed changes of the economy of the "India-like" underdeveloped country. It contained around 250 equations (for technical reasons, DYNAMO needed around 400 equations); simulation experiments were performed during 1960. According to Varsavsky and Calcagno (1971), "the model did not pretend to have a practical use, and there was not yet a clear idea of the characteristics, possibilities and difficulties of the approach, but it was a typical example sufficient to suggest its potential".
- 2.3
- At this point, it is appropriate to clarify why we don't mention as antecedents of Holland and Gillespie's model (and of Forrester's models, by the way) some very important economic models of the United States, such as the Klein-Goldberger (1955) and Leontief (1951) models. The reason is simple: the Klein-Goldberger model is econometric (while we are interested in models that take also into account other social -or political- variables), and Leontief's is a static input-output model (while we are interested in dynamical models). In these senses, the type of models which are object of this article uses a very different approach.
- 2.4
- Finally, it is interesting to remark that Holland's interest was the economic development of an underdeveloped nation, as he clearly states in his book; that is, he tried to use his global model as a tool for the development of a country. This was exactly Oscar Varsavsky's approach to global modeling, as we shall see in the following section.
 Early Latin American
applications
Early Latin American
applications
- 3.1
- The beginning of the 1960s was an interesting time in Latin America. Science was considered a fundamental tool for development, and a considerable number of intellectuals and scientists were enthusiastic about the region's future: some of them became very impressed by the Cuban Revolution and wanted to put science and technology "in the service of Revolution", while others were optimistic about the success of democratic institutional changes (remember that several military dictatorships had just been replaced by constitutionally-elected governments). For instance, we may mention the role of FLACSO (Latin American Faculty of Social Sciences), located in Santiago, Chile, whose Latin American School of Sociology, directed between 1960 and 1965 by the Swiss sociologist Peter Heintz, was extremely influential in the development of a generation (perhaps the first) of Latin American sociologists with a global vision of sociopolitical problems in the region along with a training in formalization, modeling and simulation of such problematic. Some of these sociologists were therefore "ready" to be influenced by mathematical models. Only a few years later, an impressive experience took place in Chile during the Allende administration, which was interrupted by the coup-d'état that overthrew Allende in 1973: the Cybersyn project (or Synco, in Spanish, see http://www.cybersyn.cl/) was an attempt to manage through computers the Chilean economy in real time (even including daring ideas about direct democracy through the participation of people from their "interconnected households"). Cybersyn may be considered technically as a sort of practical mixture of Stafford Beer's management cybernetics (through his Viable System Model, VSM, (Beer 1984)) with Forrester's System Dynamics[4]. The models envisioned had the spirit of global models (this time applied at a national scale) in the sense that they tried to capture concurrently interactions among several heterogeneous "layers" in which a socioeconomic reality may be decomposed.
- 3.2
- Perhaps the country where confidence in democratic changes was greatest was Venezuela. On the one hand, the military government of General Marcos Pérez Jiménez had been overthrown (January 23, 1958) and a constitutional civil administration governed since 1959. On the other hand, oil royalties for an important oil exporter such as Venezuela allowed significant investments (compared to the Latin American standards) in higher education and science. Besides, in those years "planning" was considered by many economists at the Economic Commission for Latin America and the Caribbean (ECLAC) a powerful tool for Latin American economic development. That was the political climate in which Holland (and Varsavsky in several opportunities) worked in Venezuela.[5]
- 3.3
- As Oscar Varsavsky and Alfredo E. Calcagno tell in their book, Holland traveled to Caracas, Venezuela, in 1961, to try to apply his models for planning an actual economy (he even wrote an article for a Venezuelan journal (he even wrote an article for a Venezuelan journal, i.e., Holland 1962). Eventually he began to work in 1963 with a small group of collaborators and almost three years later produced the model V-2, with which he reproduced the Venezuelan economic history from 1950 to 1962 taking into account two economic sectors: oil and all the others. Varsavsky met Holland in Caracas, became impressed by the power this type of models could have in social sciences, and organized, in 1962, a group to prepare socio-economic models at the Instituto de Cálculo (a sort of Institute of Applied Mathematics) of the University of Buenos Aires. In 1963 the MEIC-0 economic model (Economic Model-0 of the Instituto de Cálculo) was already working (Varsavsky 1965). Varsavsky and his colleagues prepared several economic, demographic, political and educational models in Buenos Aires, Caracas and Santiago de Chile (there was also an application in Bolivia) during the 1960s. We can mention, among others, short-term models of economic policies in Bolivia and Chile and analyses of results of different styles of development in Venezuela. A mathematical model of Thomas Moore's Utopia was also prepared (Domingo and Varsavsky 1967).
- 3.4
- Varsavsky's idea was that several models were "modules" of a larger one, and outputs of one model should be inputs for other(s). This vision of modularity applied to socioeconomic models was conceptually very advanced for its time. The evolution of modeling for computer simulation until our days has shown that the concept of building models of complex systems by means of the coupling of simpler models has progressed enormously in the engineering domains (mainly concerned with building physical devices, e.g., spaceships, bridges, computers), but is very underexplored in the domain of social and natural sciences[6], leading to knowledge islands of deep specialization too often difficult to interconnect.
- 3.5
- Varsavsky collaborated with and directed many groups in all those countries, and for some years a Latin American network actively worked in those subjects. Some models implemented back then were described in Varsavsky and Calcagno's book, but we may also mention national models related to Brazil (Domingo et al. 1972). In sum, there was an intense activity in Latin America regarding the preparation of global models which, although referred each of them to a single country, contained many ideas that were going to be applied during the next decade for the construction of several world models. In those years, in the mathematical modeling of society, Latin American science was outstanding.
- 3.6
- By the way, it is interesting to remark that this "Latin American network" was very unusual. Latin American scientists not always work together; more often than not (and especially in those times) their contacts originate in the United States or in Europe and the center of their network is (or was) an American or European University.
 The first world models
The first world models
- 4.1
- Meanwhile, Forrester continued working on his models. During the 1960s, Dick Bennett collaborated with Forrester and prepared a compiler for Industrial Dynamic models (SIMPLE: Simulation of Industrial Management Problems with Lots of Equations) and Jack Pugh extended the compiler into the DYNAMO series; we have already mentioned the use of DYNAMO by Holland. DYNAMO may be considered one of the first continuous time simulation languages, and certainly the first System Dynamics simulation language (i.e., the Forrester's approach). An impressive bibliography exists about both continuous time and discrete events simulation languages, and the 1960s was perhaps the decade when simulation models became popular: on the one hand, many mathematical problems didn't have an explicit solution (or at least a technically feasible one) and, on the other hand, computers were already sufficiently developed to deal with problems significantly complex (from the point of view of the size of data and number of equations).
- 4.2
- After Urban Dynamics was published, Forrester began to be known in the circles of urban planners, and, in general, of people interested in prospective scenarios. In 1970, Aurelio Peccei and Eduard Pestel, who had founded the Club of Rome in 1968 as a global think tank, contacted Forrester. After that, Forrester published World Dynamics (1971) and Meadows et al. The Limits to Growth (1972), both with very simple equations. World Dynamics initiallyused five worldwide sectors and assigned one state variable to each of them: Population, Natural Resources, Capital Investment (industrialization), Pollution and Capital Investment in Agriculture Fraction (food production). The Limits to Growth extended the model to 13 sectors represented by 41 state variables. The mathematical models (named World2 and World3 in 1971 and 1972, respectively) were written in DYNAMO.
- 4.3
- The impact of the book by Meadows and collaborators was very strong. In fact, Meadows et al. (1993, 2004) are two updates of their book, both maintaining the original pessimism. What they said, in a sense, could be thought of as a kind of "neo-Malthusianism", that is, the world population was growing much faster than the natural resources available to feed this growth, and so the only solution was to stop the growth. Independently of the merits or flaws of the World3 model, it is evident that for people in the upper classes all over the world the consequences of stopping growth would be very different than the consequences for people in the lower classes, and above all for people in the lower classes in underdeveloped countries -or, as it is more politically correct to say, in developing countries-. Interestingly, it was in one developing country, in Latin America, where a model was prepared to challenge the "doomsday scenario" anticipated by the World3 model: an interdisciplinary group in Bariloche, Argentina, designed and implemented the Latin American World Model, usually better known as the Bariloche Model (Herrera et al. 1976; 2004) 2004). The Bariloche Group preferred a model which would outline the path to sustainable development rather than predict doomsday. The Bariloche Model was a scientific success, and its influence, exposing rigorously and explicitly the pre-assumed points-of-view of researchers from a developing country, was significant: suffice it to say that UNESCO used an interactive version of the model in Paris for teaching courses in planning. Besides, it was an impressive exercise of interdisciplinary work in Argentina, where scientists from different areas seldom endeavor into interdisciplinary projects. It is worth commenting that the GLOBAL 2000 model[7] presented to President Carter in 1980 (Barney 1980), describes six additional models in its Volume 2 (World2, World3, Mesarovic-Pestel, MOIRA - Model of International Relations in Agriculture, Latin American World Model and UNWM - United Nations World Model), and remarks that the Bariloche model replaces the question "What will happen when the structures in place in the world have advanced in time by 20 or 100 years?" formulated by Forrester, Meadows and Mesarovic-Pestel by the question "How can the resources of the world be used most effectively to improve the lots of all people?"
- 4.4
- The Bariloche model was officially presented in 1974 to the IIASA (International Institute for Applied System Analysis). The same year another model was also presented, as the second report to the Club of Rome, but which supposedly corrected the mistakes of which the World3 Model was accused: the Mesarovic and Pestel's World Integrated Model (WIM), (Mesarovic and Pestel 1974).
- 4.5
- The objections –in general very sound– to Meadows' model (and to Mesarovic and Pestel's model) spanned through the decades, are well known, and are not only of political but also of technical nature, but this is not the place to analyze them (see, for instance, Gallopin (2004), Scolnik (1979, 2004), Kalman (1979)[8]).
- 4.6
- Very recently, fresh words started to be heard about those models and the conclusions offered in The Limits to Growth, mainly due to its 40th anniversary (see for instance Bardi (2011)). Interestingly, a somewhat non-traditional reinterpretation of what that work really was (and what its real message was really intended to be) comes from one of its very authors, Jorgen Randers (Randers 2012). These recent retrospective thoughts are more concerned with the non-technical criticisms received by Meadows' World3 model (i.e. the interpretations of "the message"). In the words of Randers: "…[the book] points to the need for a solution to three fundamental and legitimate problems: poverty, unemployment, and old age insecurity that underlie the global fascination with growth. These problems must be solved in a way which is compatible with planned reduction of the human ecological footprint." Here, "planned reduction" instead of 'growth stop", and "ecological footprint" instead of "economic growth", represent alone big conceptual departures from the originally popularized message of the book. Moreover, Randers continues: "… Most likely this [reduction of ecological footprint] will ultimately require equitable allocation of finite global resources on a per capita basis", a sentence suggesting the egalitarian distribution of global wealth among all human societies perhaps not too easy to claim loud in the United States by the time the first incarnation of The Limits to Growth was published.
- 4.7
- All in all, it is fair to say also that the Meadows' model had a great virtue: although Forrester's model can be considered the first world model, Meadows' was the first that became famous, it had an extraordinary impact in the press and in the public opinion, and compelled many scholars to study the characteristics that a global model should have in order to be reliable. Anyway, as the controversial judge Alex Kozinski remarks, sometimes predictive models reflect not reality, but the preconceptions of their creators (Kozinski 2002). There was an excessive "doomsday scenario" in World3 but the endeavor was challenging: while the scenarios were perhaps too pessimistic, it was really important to engage an international scientific community with analyzing projections of plausible global futures.
- 4.8
- A myriad of global models appeared after the ones mentioned above, and it is not necessary to mention them here. For example, Brecke (1990, 1993) discusses the history of many of them, including a not very known Soviet one (Brecke 1995); regarding this one, it is curious that so few Western modelers investigated what the Soviets were doing: it should have been obvious that, in spite of political constraints and control, a country that invented central planning by means of five-year plans probably should be (as in fact was) interested in this methodology. Lazarevic (1979) shows some opinions about global models at the end of the 1970s. During the 1970s this kind of global models was very popular; moreover, the already mentioned IIASA -housed in the Blauer Hof Palace in Laxenburg, near Vienna- was created in 1972 with the main purpose of analyzing and confronting the models.
- 4.9
- Besides those models (and many others) we should not forget to especially mention the International Futures model prepared in the Frederick S. Pardee Center for International Futures at the University of Denver, which has evolved through four generations of models[9] and has produced an impressive bibliography; see for instance the Patterns of Potential Human Progress series: (Hughes et al. 2009; Dickson et al. 2010; Hughes et al. 2011; Rothman et al. 2014). The series has been edited by Barry B. Hughes, and each title indicates its main purpose. A fifth volume, Strengthening Governance Globally, has just been published.
- 4.10
- The timeline presented in Figure 1
(and Table 1)
below depicts a non-comprehensive selection of global models and
publications considered influential (or worth mentioning) in the
discipline.
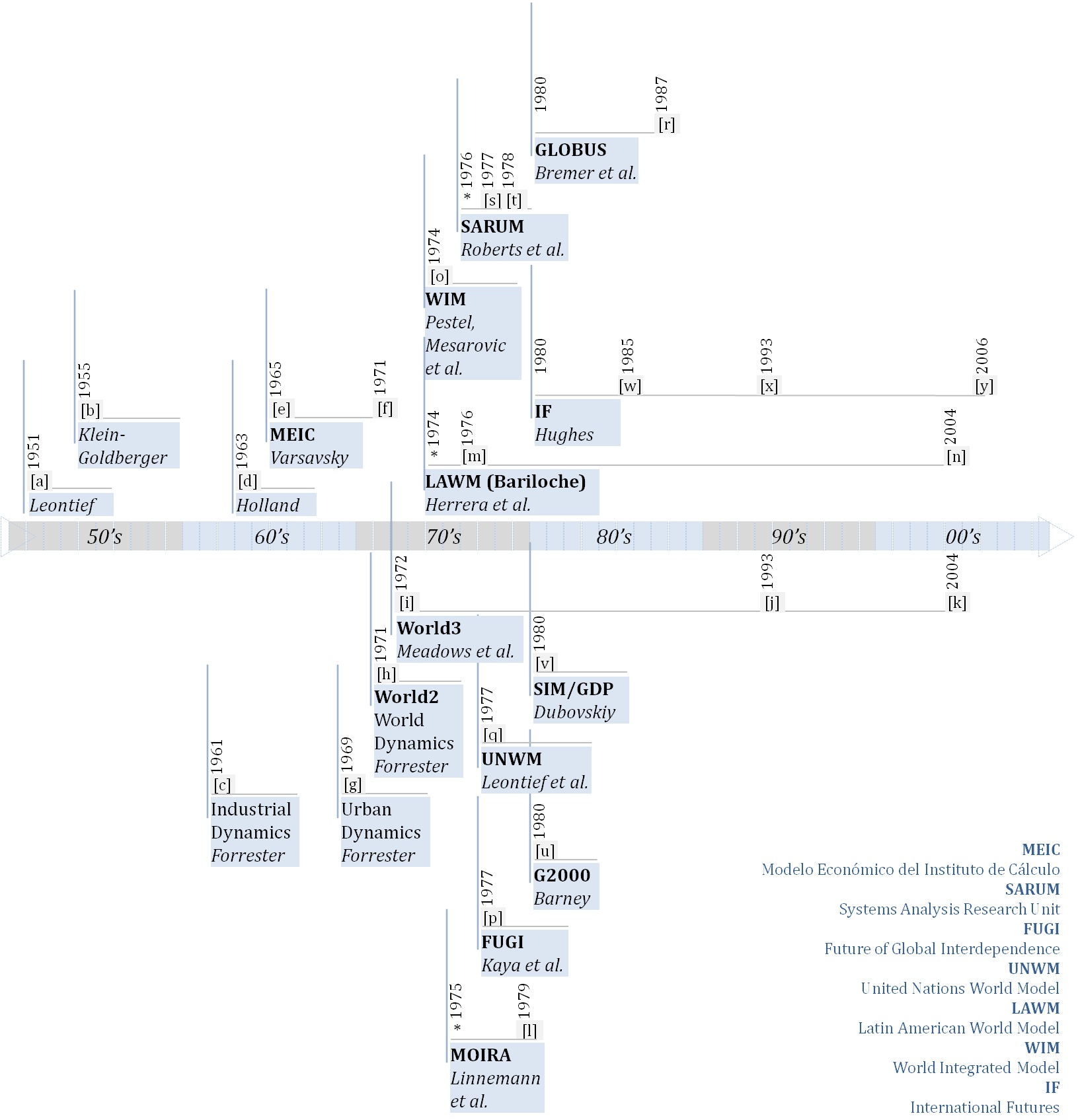
Figure 1.Timeline for a selection of global models and publications influential in the discipline.
Vertical lines | : Approximate earliest activity of the project.
Horizontal lines – : Citations related to the same project.
Acronyms in bold: Global Model.
Names in italic: Main researcher/author/project director.
Asterisks (*): First report presented at IIASA (source: Meadows et al. (1982)).
Table 1: List of publications in Figure 1
a Leontief (1951) j Meadows et al. (1993) s Roberts (1977) b Klein and Goldberger (1955) k Meadows et al. (2004) t SARU (1978) c Forrester (1961) l Linnemann et al. (1979) u Barney (1980) d Holland and Gillespie (1963) m Herrera et al. (1976) v Dubovsky (1980) e Varsavsky (1965) n Herrera et al. (2004) w Hughes (1985) f Varsavsky and Calcagno (1971) o Mesarovic and Pestel (1974) x Hughes (1993) g Forrester (1969) p Kaya et al. (1977) y Hughes and Hillebrand (2006) h Forrester (1971) q Leontief et al. (1977) i Meadows et al. (1972) r Bremer (1987)
 Further methodological remarks
on global models
Further methodological remarks
on global models
- 5.1
- In what sense these global models could be considered "forecasting" models? The models neither predicted the fall of the Soviet Union or the war in Yugoslavia, nor took into account a scenario in which these events could happen. Meanwhile, runs of the GLOBUS model in the 1980s predicted the political system in East Germany, Poland and Czechoslovakia to be more stable than that of Western Europe.[10] It can be argued that for that kind of predictions, a model dealing with political variables should have been used, and we are very far from implementing reliable mathematical models of political events (Domingo and Varsavsky prepared a mathematical model of Utopia, not a real political situation). Nevertheless, in many cases even changes in economic variables (e.g., the oil price) are not easy to forecast.
- 5.2
- Besides, other difficulties appear that should not be overlooked: the models may be too sensitive to parameters whose values are arguable, and the variables not modeled explicitly must be accounted for by the introduction of some "randomness". Of course, a modeler can never introduce in a global model all the variables involved: on the one hand, one does not even know all of them, and on the other hand, the relationships among the known ones are too complicated for all of them to be described explicitly. Therefore, as in many other scientific models, "hidden variables" should be perhaps aggregated into random variables. Moreover, randomness does exist: had it been feasible in January, 1914, to prepare a global model of the world, or at least of Europe, with an horizon of, say, twenty years, it is extremely implausible that the model had taken into account that seven months later the most important countries in Europe would be immersed in a horrific war (which, by the way, most planners in different General Staffs supposed would be short). Unfortunately, lack of predictability cannot be simply associated with lack of data (so that the model "seems more random"); if one assumes that when a country is more developed then more data exist, and thus more reliable the data are, it could be argued that the more developed a country is, the more predictable or robust the model becomes. Unfortunately, it is not so: "robustness" or "predictability" of a global model is not necessarily related to the degree of development of the country or region studied: as we already mentioned, it is likely that an Argentinean model be less robust or less predictable than a Namibian model. Moreover, sometimes population dynamics may be unpredictable: population size may run amok (May 1976).
 Complex systems
Complex systems
- 6.1
- During the 1980s the mass media and public opinion became less and less interested in global models of this kind. For the Latin American groups, the explanation is simple: the optimism, that we already mentioned, of the 1960s, disappeared completely in the 1970s: in Argentina there was a military dictatorship from 1966 to 1973, but scientists interested in political, social and economic problems who abandoned the country or the research at the universities could continue working in other Latin American countries (the "Varsavsky network" is an example) or in non-governmental organizations (as shown by the Bariloche Foundation that funded the Bariloche model).
- 6.2
- In the 1970s the political situation was unhealthy in most South American countries, and global models were not a priority for scientists exiled or silenced. In the developed world the explanation is not so easy: it is likely that pessimism related with doomsday scenarios began to decrease, given that it was obvious that in the 1980s the western powers – especially the United States – were winning the competition against the Soviet Union, and that "normal" scenarios are less attractive, from the mass-media point-of-view, than doomsday scenarios. Anyway, it was impossible not to use this kind of models, or similar ones: since the appearance of the computers at the end of the 1940s, that meant the possibility of making more and more computations with more and more variables in less and less time; it was obvious that complex systems, impossible to work with prior to the computer era, should –and would– be mathematically and computationally treated.
- 6.3
- Continued increasing attention was paid to the study of more general complex systems, not necessarily related to socio-economic worldwide prospective analyses. The study of complex systems is an interdisciplinary field of science, which studies the structure and characteristics of complex interactions among systems in nature and society (García 2006). As complex systems deal with many, many partly independent and autonomous entities involving many, many variables (with many attributes, subject to many relationships which in turn might represent many possible causes), it was unthinkable to try to model them mathematically before the computer. Global models are a class of complex systems that analyze some parts of the society related with different countries, of geographic regions, and in many of them these entities are hidden in the variables and equations.
- 6.4
- What was instead observed was a more intense interest in complex models in general, and in "complexity science". Simultaneously, several institutes -similar in a sense to the IIASA- were created in different places, for instance the Santa Fe Institute, founded in 1984, the Center for Policy Modelling (http://cfpm.org/about/117/centre-for-policy-modelling) of the Manchester Metropolitan University Business School, focused on complexity science and social simulation since 1992, and the New England Complex Systems Institute (NECSI), founded in 1996. All these approaches are necessarily interdisciplinary. NECSI, for instance, defines Complex Systems as "a new field of science studying how parts of a system give rise to the collective behaviors of the system, and how the system interacts with its environment" (http://www.necsi.edu/).
- 6.5
- The applications are varied: NECSI indicates among its applications economics, multiscale methods, ethnic violence, networks, health care, evolution and ecology, management, systems biology, education, engineering, military conflict, development, negotiation. Some of these fields are a priori not supposed to be easily modeled; others may be thought as descendants of game theory models, tracing back to the impressive effort that von Neumann and Morgenstern (1944) invested in their famous book, perhaps one of the first (very simple) attempts to model complex situations under competition. It is amusing to see that almost all the book analyzes scenarios with up to 3 or 4 participants: it was written before the appearance of the modern computer.
- 6.6
- The areas of interest of the Santa Fe Institute (http://www.santafe.edu/) are physics of complex systems; emergence, innovation, and robustness in evolutionary systems; information processing and computation in complex systems; dynamic and quantitative studies of human behavior; and emergence, organization and dynamics of living systems. As it can be seen, a lot of systems may be labeled "complex" and tried to be mathematically modeled. Obviously, multi-disciplinary collaboration is absolutely necessary in this kind of approach. Another institute, the Bath Institute for Complex Systems -this one, like the Centre for Policy Modelling, in Britain (http://www.bath.ac.uk/math-sci/bics/)- has research lines related to modeling and analysis of multiscale problems; structure of biologic populations; deterministic properties of highly disordered systems; numerical methods for multiscale problems; and highly structured stochastic systems. Systems on which these institutes work seem perhaps more difficult to model than systems studied by global models; but, for the above mentioned reasons (among many others), interest gradually changed in the 1980s from global models to complex systems, understood in the sense these three Institutes (and many others) approached them. It could be well regarded as a symptom of the prevalence of domain-oriented specialization over cross-domain analysis at least from the application point of view (even when interdisciplinarity remains a key feature).
- 6.7
- Many valuable and interesting papers have been written on complex systems, as well as dull and uninteresting ones (as in all fields of science, of course). As the definition of complex systems is very broad, many important contributions can be classified as contributions to complex systems. Anyway, many contributions on complex systems are theoretical, so that they cannot be compared with works on global models. Perhaps the most mature organized body of knowledge related with complex systems is the Springer Complexity interdisciplinary publishing program (www.springer.com/physics/complexity) which stems from physics and includes research and teaching-level texts on fundamental and applied aspects of complex systems.
 Environmental models
Environmental models
- 7.1
- In the last couple of decades, a global interest arose in other kind of models, environmental models, which have many common traits with the traditional global models, although more focused, naturally, in environmental problems (notably climate change) than in development problems. Global models in general assumed that what they simulated were feasible situations originated in human decisions on economics, policy, military affairs, fight against poverty, and so on. In current environmental models, on the other hand, human decisions refer especially to their contributions to global warming or climate change; according to most experts, global warming is due mostly to anthropic actions; according to a minority of experts, the anthropic influence in global warming is negligible. In both standpoints, besides anthropic action there exist natural causes, which are always included in the models.
- 7.2
- Most complex systems models are not particularly aimed to foresee the future state of the world. On the other hand, that is precisely the main goal of most global models: to provide a forecast of the future state of the world, or parts of it, using (perhaps many) mathematical equations and assumptions. This is also the main interest of environmental models.
- 7.3
- In both types of models not all the assumptions are explicit; some are hidden in the equations. Environmental models are more "technical", in the sense that they use less political or economic assumptions, which are always subject to discussion (although the fact that a minority of experts challenge the approach of most scientists indicates that, in spite of being "technical", they are not immune to discussions). Considering this, it is probably sound to affirm that, in a sense, environmental models are somehow the heirs of the 1970s global models. This is the feeling one has, for instance, when looking at the IIASA website (http://www.iiasa.ac.at/), and realizes how much this institute, where thirty years ago many global models were presented, is now interested in climate change. It is interesting to remark that environmental models can be regarded as "heirs" of global models, but not "descendants" of them: environmental models evolved from the forecast numerical models that John von Neumann and Jule Charney proposed at the end of the 1940s and in the early 1950s (Jacovkis 2005), and then from the atmospheric general circulation models from 1955 on (Phillips 1956).
 Conclusions
Conclusions
- 8.1
- From all the discussions on global models, and also on environmental models, some words of caution are necessary: equations are sometimes controversial (not only the empirical equations, but also the supposedly "conceptual" ones); parameters must be calibrated whenever feasible (often a difficult task); they may be extremely sensitive to changes (although sometimes we do not know their actual values); initial conditions (state of the system at the beginning of the simulation time) must be given, and sometimes, if they are difficult to obtain, they must be found through a process of "warming up" of the model which does not always converges to the true simulated beginning of the simulation; boundary conditions must be given (sometimes they are difficult to obtain, and when using a model for predicting a future state of a system one has often to invent them); if partial differential equations are used, numerical methods must be robust enough; in socio-economic models, equilibrium points may be unstable.
- 8.2
- On the other hand, if used sensibly and cautiously, they enrich the knowledge of the system under study; a huge number of experiments with different parameters, boundary conditions and initial conditions must be performed before inferring unquestionable conclusions; some experiments must be performed with variables randomly perturbed; a global model must be developed dynamically and iteratively, that is, it must be constantly criticized, modified and improved (besides, a global model must be dynamic in the sense that it evolves in time and usually does not tend to an equilibrium point). Sometimes (and perhaps this is really difficult) if the results of the model are not what we expect, we must change our expectations, not the model. In spite of this, modelers often back their models more than they should.
- 8.3
- More caveats should be included in all models made public, more alternative results should be shown changing selected input data (or parameters) not sufficiently well known, and more scenarios should be explored. Also, the main assumptions embedded in the structure of models should be made clearly explicit, exposing the underlying ideologies and worldviews to which all modellers are unavoidably attached to.
 Acknowledgements
Acknowledgements
- The authors gratefully acknowledge the documents supplied by Prof. Carlos Eduardo de Senna Figueiredo regarding the Cybersyn project, the useful observations made by Prof. Ulrich Müller-Herold on many topics including the role of Peter Heinz in South America, and the valuable comments of two anonymous reviewers. PMJ had the financial support of University of Buenos Aires grant 20020100100536.
 Notes
Notes
- 1In
fact, we can also mention the book by Carrère (1978).
Although the reasons Carrère gave for predicting the fall of the Soviet
Union (an eventual demographic majority of Muslims in the Union) were
wrong, the Soviet Union anyway disappeared and, besides, the Chechen
wars showed that there is a conflict inside Russia where nationalistic
and religious causes are mixed.
2It is appropriate to remark here that preparing global mathematical models cannot be considered exclusively a work for applied mathematicians, computer scientists, engineers, economists and sociologists. Although the usefulness of "political mathematical models" (see later) is extremely arguable, if the global model gets sufficiently ambitious political scientists and in general people from different cultural environments and all professions should be also consulted. This approach makes sense at least if one believes that political circumstances may change dramatically not only the economic and social structure of a country, but also the international relations and the relative power of the different nations, and that the likelihood of these changes are not reflected in the available data (be it because data are insufficient, biased, or deliberately hidden). For instance, in Meadows et al. (1972) (see later) no reference is made to political works, with the exception perhaps of comments on Hardin (1968) and Russell (1935), which are anyway writings of a general character with no mention to actual facts susceptible to be accounted for into a mathematical model.
3The above-mentioned example on the stability of Eastern Europe countries shows how extremely difficult is to prepare political models.
4On the one hand, Cybersin was an intellectual creation of Beer (subject of course to dynamical changes during its implementation, due to the active participation of Chilean professionals in charge of the project); on the other hand, in some parts of the project Forrester's influence may be detected. The DYNAMO programming language was used e.g. to develop the CHECO (CHilean ECOnomy) module, a real time monitoring dashboard and mid- to long-term forecasting panel. The story may be consulted in Medina (2006), or Medina (2011). For a detailed biography of Beer, including especially his contribution to Cybersyn, see Rosenhead (2006); for a theoretical approach to the VSM/SD mixing see Schwaninger et al. (2004).
5In fact, in this context the Center of Studies for the Development (Centro de Estudios del Desarrollo, CENDES) was created in 1961 at the Central University of Venezuela in Caracas. CENDES was (and still is) an influential institution in Venezuela: some of Varsavsky's collaborators and colleagues were affiliated with it.
6In a nutshell, engineering models as compared to social models count on at least two important advantages: i) they rely on well understood first (physical) principles, and ii) the models aim at building devices for which their boundaries and ranges of operation can be delimited at will. Therefore, complexity can be tackled by interconnecting subsystems via well-defined interfaces that transform information and energy from one domain into the other (e.g. digital-mechanical-electrical-hydraulic devices). The latter is seldom possible in social models.
7As Barney says in http://www.geraldbarney.com/G2000Page.html (consulted on November, 27, 2013), "Global 2000 study is based on the integration of a number of sector-specific projections, such as food, energy, population, and environment, most of which were prepared by US Government agencies."
8Anyway, it is interesting to comment on Kalman's paper. His approach is more general from the point of view of the "theory of models", with a touch of epistemological flavor. His reference to Meadows' model is very short; he attacks it from a "pure system-theoretic" angle, and he mentions Vermeulen and de Jongh (1977), who observe that "…the mathematical model basic to the results of The Limits to Growth has been found to be very sensitive to small perturbations". On the sensitivity of Meadows' model to changes in parameters and initial conditions, and on the issue of model's validation against historical data see Castro (2012).
9The fifth generation is underway.
 References
References
- AMALRIK, A. (1970). Will
the Soviet Union Survive Until 1984?. New York: Harper
& Row.
BARNEY, G. O. (Study director). (1980). The GLOBAL 2000 Report to the President. Entering the Twenty-First Century, Volume 2. Washington: US Government Printing Office.
BARDI, U. (2011). The Limits to Growth Revisited. New York: Springer-Verlag. [doi:10.1007/978-1-4419-9416-5]
BEER, S. (1984). The viable system model: its provenance, development, methodology and pathology. The Journal of the Operational Research Society, 35(1), 7–25. [doi:10.1057/jors.1984.2]
BRECKE, P. (1990). A bibliographical report on six contemporary global models. In H. Chestnut, P. Kopacek and T. Vamos (Eds.), International Conflict Resolution using System Engineering. Proceedings of the IFAC/SWIIS Workshop, Budapest, Hungary, 5–8 June 1989 (pp. 93–112), IFAC Workshop Series, Number 1. Oxford: Pergamon Press. [doi:10.1016/b978-0-08-037529-8.50023-x]
BRECKE, P. (1993). Integrated global models that run on personal computers. Simulation, 60(2), 140–144. [doi:10.1177/003754979306000209]
BRECKE, P. (1995). The Soviet global model: SIMIGDP. Simulation & Gaming, 26(1), 17–26. [doi:10.1177/1046878195261002]
BREMER, S. A. (Ed.). (1987). The GLOBUS Model: Computer Simulation of World-wide Political and Economic Developments. Frankfurt am Main: Campus Verlag.
CARRÈRE d'ENCOUSSE, H. (1978). L'Empire Eclaté. Paris: Flammarion.
CASTRO, R. (2012). Arguments on the imminence of global collapse are premature when based on simulation models. Gaia, 21(4), 271–273.
DICKSON, J. R, Hughes, G. G. and Irfan, M. T. (2010). Advancing Global Education. Patterns of Potential Human Progress, Volume 2. Boulder, CO: Paradigm Publishers.
DOMINGO, C. and Varsavsky, O. (1967). Un modelo matemático de la Utopía de Moro. Desarrollo Económico, 7, 3–36. [doi:10.2307/3465759]
DOMINGO, C., Sananes, M. and Bonilla, F. (1972). Numerical Experiments with National Systems Models. Institute of Political Studies, Stanford University.
DUBOVSKY, S.V. (1980). Simulation model of international multiproduct trade within global modeling system. In Systems Modeling of Global Development Processes, Vol. 14. Moscow: VNIISI (Institute for Systems Studies, USSR Academy of Sciences). In Russian.
FORRESTER, J. W. (1961). Industrial Dynamics. Waltham, MA: Pegasus Communications.
FORRESTER, J. W. (1969). Urban Dynamics. Waltham, MA: Pegasus Communications.
FORRESTER, J. W. (1971). World Dynamics. Cambridge, MA: Wright-Allen Press (2nd edition, The MIT Press, 1977).
GALLOPIN, G. (2004), El Modelo Mundial Latinoamericano ("Modelo Bariloche"): tres décadas atrás. In Herrera et al. (2004) (pp. 13–26).
GARCÍA, R. (2006). Sistemas Complejos. Conceptos, Método y Fundamentación Epistemológica de la Investigación Interdisciplinaria. Barcelona: Editorial GEDISA.
HARDIN, G. (1968). The Tragedy of the Commons. Science, 162, 1243–1248. [doi:10.1126/science.162.3859.1243]
HERRERA, A., Scolnik, H., Chichilnisky, G., Gallopin, G., Hardoy, J., Mosovich, D., Oteiza, E., Romero Brest, G. L. de, Suárez, C. E. and Talavera, L. (1976). Catastrophe or New Society? A Latin American World Model. Ottawa: IDRC.
HERRERA, A., Scolnik, H., Chichilnisky, G., Gallopin, G., Hardoy, J., Mosovich, D., Oteiza, E., Romero Brest, G. L. de, Suárez, C. E. and Talavera, L. (2004). Catástrofe o Nueva Sociedad? Modelo Mundial Latinoamericano 30 Años después (2nd edition). Ottawa: IDRC and Buenos Aires: IIED-AL.
HOLLAND, E. P. (1962). Programación simulada y su aplicación a las economías subdesarrolladas. Revista de Economía Latinoamericana (Caracas), 2 (5), Enero-Marzo 1962.
HOLLAND, E. P. and Gillespie, R. W. (1963). Experiments on a Simulated Underdeveloped Economy: Development Plans and Balance-of-payments Policies. Cambridge, MA: The MIT Press.
HUGHES, B. (1985). World Futures. Baltimore: The Johns Hopkins University Press.
HUGHES, B. (1993). International Futures: Choices in the Search for a New World Order. Boulder, CO: Westview (1993; 1996; 1999).
HUGHES, B. and Hillebrand, E. (2006). Exploring and Shaping International Futures. Boulder, CO: Paradigm Publishers.
HUGHES, B., Irfan, M. T., Khan, H., Kumar, K. B., Rothman, D. S. and Solórzano, J. R. (2009). Reducing Global Poverty. Patterns of Potential Human Progress, Volume 1. Boulder, CO: Paradigm Publishers.
HUGHES, B., Kuhn, R., Peterson, C. M., Rothman, D. S. and Solórzano, J. R. (2011). Improving Global Health. Patterns of Potential Human Progress, Volume 3. Boulder, CO: Paradigm Publishers.
JACOVKIS, P. M. (2005). The applied mathematician's laboratory. In V. Marik, P. M. Jacovkis, O. Stepankova and J. Klema (Eds.). Interdisciplinary Aspects of Human-machine Co-existence and Co-operation (pp. 130–141). Prague: Czech-Argentine Biennale Workshop "e-Golems", Czech Technical University.
KALMAN, R. E. (1979). A system-theoretic critique of dynamic economic models. In Lazarevic (1979) (pp. 3–24). [doi:10.1007/bfb0049018]
KAYA, Y., ONISHI, A., SUZUKI, Y., et al. (1977). Report on Project FUGI - Future of Global Interdependence. Fifth Global Modeling Conference. Laxenburg, Austria: IIASA.
KLEIN, R. S. and Goldberger, A. S. (1955). An Econometric Model of the United States 1929–1952. Amsterdam: North-Holland.
KOZINSKI, A. (2002). Gore Wars. Michigan Law Review, 100, 1742–1746. [doi:10.2307/1290465]
LAZAREVIC, L. (Ed.) (1979). Global and Large Scale System Models. Proceedings of the Center for Advanced Studies (CAS) International Summer Seminar, Dubrovnik, August 21–26, 1978. Lecture Notes in Control and Information Sciences, Berlin: Springer-Verlag. [doi:10.1007/BFb0049016]
LEONTIEF, W. (1951). The Structure of the American Economy 1919–1939, 2nd ed. New York: Oxford University Press.
LEONTIEF, W., Carter, A. and Petri, P. (1977). The Future of the World Economy, a United Nations Study. New York: Oxford University Press.
LINNEMANN, H., De Hoogh J., Keyzer M. and Van Heemst H. (1979). MOIRA - Model of International Relations in Agriculture. Amsterdam: North-Holland.
MAY, R. (1976). Simple mathematical models with very complicated dynamics. Nature, 261, 459–467. [doi:10.1038/261459a0]
MEADOWS, D. H., Meadows, D. L., Randers, J. and Behrens III, W. W. (1972). The Limits to Growth. New York: Universal Books.
MEADOWS, D. H., Richardson J. and Bruckmann G. (1982). Groping in the Dark: The First Decade of Global Modelling. Chichester, UK: Wiley.
MEADOWS, D. H., Meadows, D. L. and Randers, J. (1993). Beyond the Limits to Growth. White River Jct., VT: Chelsea Green Publishing Company.
MEADOWS, D. H., Meadows D. L. and Randers J. (2004). Limits to Growth: the 30-Year Update. White River Jct., VT: Chelsea Green Publishing Company.
MEDINA, E. (2006). Designing freedom, regulating a nation: socialist cybernetics in Allende's Chile. Journal of Latin American Studies, 38 (3), 571–606. [doi:10.1017/S0022216X06001179]
MEDINA, E. (2011). Cybernetics Revolutionaries. Technology and politics in Allende's Chile. Cambridge, MA: The MIT Press.
MESAROVIC, M. and Pestel, E. (1974). Mankind at the Turning Point: The Second Report to the Club of Rome. New York: Dutton.
PHILLIPS, N. A. (1956). The general circulation of the atmosphere: a numerical experiment. Quarterly Journal of the Royal Meteorological Society, 82 (352), 123–164. [doi:10.1002/qj.49708235202]
PUGH III, A. L. (1970). DYNAMO User's Manual, 3rd ed. Cambridge, MA: MIT Press.
RANDERS, J. (2012). The real message of The Limits to Growth. A plea for forward-looking global policy. GAIA, 21/2, 102–105.
ROBERTS, P. C. (1977). SARUM 76-Global Modelling Project. London: Research Report No. 19, UK Departments of Environment and Transport.
ROSENHEAD, J. (2006). IFORS' Operational Research hall of fame. Stafford Beer. Intl. Trans. in Op. Res., 13, 577–581. [doi:10.1111/j.1475-3995.2006.00565.x]
ROTHMAN, D. S., Irfan, M. T., Margolese-Malin, E., Hughes, B. B. and Moyer, J. D. (2014). Building Global Infrastructure. Patterns of Potential Human Progress, Volume 4. Boulder, CO: Paradigm Publishers.
RUSSELL, B. (1935). In Praise of Idleness and other Essays. London: Allen and Unwin.
SARU (1978). SARUM Handbook. London: SARU (Systems Analysis Research Unit), UK Departments of Environment and Transport.
SCOLNIK, H. D. (1979). A critical review of some global models. In Lazarevic (1979) (pp. 58–80). [doi:10.1007/bfb0049022]
SCOLNIK, H. D. (2004). Una perspectiva histórica personal del Modelo Bariloche. In Herrera et al. (2004) (pp. 27–37).
SCHWANINGER, M., Pérez Ríos, J. and Ambroz, K. (2004). System dynamics and cybernetics: a necessary synergy. Oxford: Proceedings, International System Dynamics Conference.
TODD, E. (1976). La Chute Finale: Essai sur la Décomposition de la Sphère Soviétique. Paris: Laffont.
VARSAVSKY, O. (1965). Los modelos matemáticos numéricos como herramientas de decisión en problemas difícilmente cuantificables: el MEIC-0. Boletín Interno No. 1 [mimeo]: Instituto de Cálculo, Universidad de Buenos Aires.
VARSAVSKY, O. and Calcagno, A. E. (1971). América Latina: Modelos Matemáticos. Santiago de Chile: Editorial Universitaria.
VERMEULEN, P. J. and de Jongh, D. C. J. (1977). Growth in a finite world – a comprehensive sensitivity analysis. Automatica, 13, 77–84. [doi:10.1016/0005-1098(77)90010-3]
VON NEUMANN, J. and Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton: Princeton University Press (there are several later editions, including a 60th anniversary edition (2007), with an introduction by Harold Kuhn and an afterword by Ariel Rubinstein).