 Abstract
Abstract
- The investigation of how cooperation is achieved on graphs in the field of spatial game or network reciprocity has received proliferating attention in the biological and sociological literature. In line of the research, this paper provides an new account of how cooperation could evolve in complex networks when actors use information of network characteristics to strategize whether to cooperate or not. Different from past work that focuses exclusively on the evolution of unconditional cooperation, we are proposing new strategies that are choosy in whom to cooperate with, conditional on the structural attributes of the nodes occupied by actors. In a series of evolutionary tournaments conducted by computer simulation, the model shows that a pair of simple strategies-cooperating respectively with higher and lower nodal-attribute neighbors-can be advantageous in adaptive fitness when competing against unconditional cooperation and defection. In particular, these strategies of conditional cooperation work well in random graphs-a network known for being unfavorable to the selection of cooperation. This paper contributes to the literature by showing how network characteristics can serve as a mechanism to sustain cooperation in some hostile network environments where unconditional cooperation is unable to evolve. The cognitive foundations of the mechanism and its implications are discussed.
- Keywords:
- Evolution of Cooperation, Complex Network, Spatial Game, Conditional Cooperation
 Introduction
Introduction
- 1.1
- A wide range of collective action essential to the livelihood of social animals, such as food foraging and territory defense, requires cooperation among group members. The emergence of cooperation is difficult to explain in the face of the free-rider problem. To this challenge, evolutionary theorists have proposed a variety of models to explain how cooperation can out-perform defection in adaptive values (Sachs et al. 2004; Nowak 2006; West et al. 2007). Many of these models use the Prisoner's Dilemma game or it's variant to analyze the cooperation problem and investigate different treatments of how individuals interact with one another. Some assume that actors interact in fixed pairs (Axelrod and Hamilton 1981), in specific structural arrangement or network (Nowak et al. 2010), and with others preferentially selected on fixed or evolving partner preferences (Skyrms and Pemantle 2000; Pacheco et al. 2006).
- 1.2
- Different mechanisms were proposed to explain how cooperation evolves in each of the conditions. For example, when interaction is conducted in fixed pairs, cooperation could evolve if players use strategies, such as "tit-for-tat", that would condition their action on the history of partners' play (Axelrod and Hamilton 1981). When interaction is structured in accordance with certain spatial arrangement such as on a grid, the emergence of clusters of cooperators can successfully resist the invasion of defectors (Nowak and May 1992). Other particular structural arrangement, such as the Scale-Free network, is found to benefit the selection of cooperation (Pacheco and Santos 2005). This line of research demonstrates the role network topology plays in the evolution of cooperation. Moreover, when partners are selected on a competitive basis rather than exogenously given, cooperation is possible to evolve if cooperators prefer one another as partners (Noe and Hammerstein 1994; Roberts 1998).
- 1.3
- Along this line of research, this paper offers a new account for how cooperation evolves in networks-a research area termed spatial game or network reciprocity in the literature (Killingback et al. 1996; Nowak 2006; Szabo and Fath 2007; Roca et al. 2009; Nowak et al. 2010). Conventional treatment of this kind of work postulates that individuals are placed on network to interact with adjacent neighbors. Although actors' strategies adapt over evolutionary time, they remain invariant to each network neighbor at a fixed point in time. If an actor cooperates, for example, he would do so with each network neighbor, ignoring that these neighbors might vary in where they stand in network. In other words, this kind of cooperator is an unconditional cooperator who sees his network neighbors as homogenous in the position of the nodes they occupy. As increasing evidence indicates that human and animal social networks are far from homogeneous (Croft et al. 2008), we find it necessary to take into account the heterogeneity of network positions in modeling the evolution of cooperation.
- 1.4
- In contrast to unconditional cooperation, strategies of conditional cooperation are found to be effective in combating the free-rider problem in the evolution of cooperation. The success of conditional cooperation lies in the fact that actors are selective in whom to cooperate with—a mechanism that enables them to shun the exploitation of defectors. Accumulated empirical evidence and theoretical models have introduced an array of successful strategies of conditional cooperation that would render evolutionary advantages: Actors choose to cooperate with genetic-related kins (Hamilton 1964), with members of the same group (Hammond and Axelrod 2006), with strangers with the reputation of either being cooperative to the focal player (direct reciprocity) or to third others (indirect reciprocity) in the past (Nowak 2006), and with strangers with distinct and recognizable biological or cultural marks (Hales 2000; Riolo et al. 2002; Kim 2010). In what follows, we introduce a novel strategy of conditional cooperation built on the structural attributes of nodes occupied by actors on networks. A nodal attribute is a structural feature of a node with respect to particular functions operating in networks, such as the transmission of information or diseases, coordination of work, and exercise of power, to list a few examples. These structural features of nodes are termed network characteristics, network positions or network statistics in the literature of social and biological networks (Wasserman and Faust 1994; Croft et al. 2008). At first glance, it may seem difficult to conceive how a cooperation strategy built on nodal attributes of networks influences the evolution of cooperation. What we aim to achieve in this paper is to provide a thought experiment through computer simulation to see how well these new strategies perform when competing against unconditional cooperation and defection in evolution.
- 1.5
- Unlike unconditional cooperation or defection where nodal attribute has no leverage on shaping an individual's strategy, the new strategies proposed here conditions a focal actor's move toward an alter on their network attributes. Let Ai and Aj denote respectively node i's and j's nodal attribute value. The strategy of conditional cooperation proposed here would map the relation between Ai and Aj to the decision to cooperate or defect in the cooperation game. For example, suppose that node degree is the nodal attribute under investigation. One plausible strategy is to command a focal actor i to cooperate only with those neighbors who have higher degrees than his (Ai -Aj<0). the threshold of (Ai -Aj) to trigger cooperation can be treated as a strategy and its evolutionary advantage can then be tested.
- 1.6
- The tradition of spatial game or network reciprocity has long treated topology of network structure and strategy of individual action as two separate entities when modeling the evolution of cooperation in networks. The major contribution of this paper is to relax the assumption to integrate network attribute into the formation of an actor's strategy of conditional cooperation. The emergence of network science in the past decades has witnessed a great advance in the development of network statistics to understand how network are structured. Researchers have discovered some relationships between network characteristics and the emergence of cooperation (Nowak 2006; Nowak et al. 2010), but none of the past work, to our knowledge, has considered that agents on networks can use the information of network characteristics to strategize their action. There is ample empirical evidence indicating that individuals, ranging from humans to other species of social animals, are capable of perceiving the networks that organize their social lives. Research in cognitive networks shows that people's perception of social networks matches real network pattern with a substantial degree of accuracy, if not perfect (Freeman 1992; Janicik and Larrick 2005; Kilduff et al. 2008). For non-human social animals, biological research found that an individual's position in social network correlates with his physical trait and personality recognizable through observation (Lusseau and Newman 2004; Lehmann and Dunbar 2009; Sueur et al. 2011; Crofoot et al. 2011). These studies all together point out that judging a network is not completely out of question. Not only can individuals perceive social networks, but also they can use their understanding of it to achieve personal gains. For example, the structural-hole theory, proposed by economic sociologists, argues that people in the business domain would strategically occupy certain positions in networks, such as a bridge linking two otherwise disconnected communities, to grasp advantages in brokerage that would not be rendered by other positions (Burt 1995; Buskens and van de Rijt 2008). Similarly, the growing literature on social capital theory shows how individuals use their personal connections to access collective benefits, such as job-opening information, that would flow in social networks (Lin et al. 2001; Mouw 2006). We thus have sufficient reasons to believe that agents are able to use their understanding of network characteristics to guide their decision-making. The current paper provides an example of how this idea can be applied to explaining the evolution of cooperation in networks.
 The Model
The Model
- 2.1
- The cooperation problem is modeled by the helping game described as follows (Nowak 2006; Nowak et al. 2010). Each actor is placed on network of a fixed size (n=150) and endowed with a strategy to govern his choice of cooperating or defecting when interacting with each network neighbor. When cooperating, an individual incurs a cost c=1 to deliver a help valued b=5 to a network neighbor. For a focal node i and a network neighbor j of i, let Ai and Aj denote i's and j's value of nodal attribute A. The decision of actor in node i is formulated as follows.
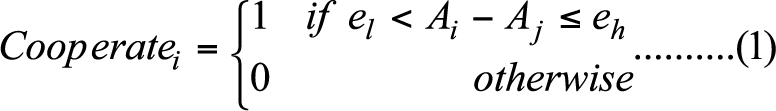
(1) Here, the lower and upper bounds, el and eh, put together represent a strategy in the game. For example, unconditional cooperation can be represented by el = -∞ and eh = ∞, suggesting that cooperation is independent of nodal attributes, whereas unconditional defection can be expressed as el > eh, which would never be satisfied, meaning that cooperation is not possible. Other vectors of (el, eh) that satisfy -∞ << el and eh<< ∞ each represents a strategy of conditional cooperation as a focal player's cooperation is activated only when certain conditions of Ai -Aj are satisfied.
- 2.2
- To investigate the evolutionary advantage of a strategy, we conduct a strategy tournament operated by computer simulation. In the tournament, a contestant strategy, characterized by a vector (el, eh) with el < eh, is played against unconditional cooperation and unconditional defection in the evolutionary dynamics of the helping game. The share of a strategy adopted by actors toward the end of evolution marks its evolutionary advantage.
- 2.3
- We follow the standard approach to modeling the evolutionary dynamics of strategies in the helping game (Szabo and Fath 2007; Roca et al. 2009). In the initial condition, one-third of actors are unconditional cooperators, one-third is defectors and the remaining population adopts a contestant strategy. In each round of the evolution, actors follow their strategy to interact with network neighbors. An actor uses the same strategy to interact with each neighbor at any point in evolution time, but these neighbors might be treated differently depending on their nodal attributes that feed into the strategy used by the focal actor. At the end of each round, each actor compares his fitness with his network neighbors' and adopts the strategy of whoever (including himself) has the highest fitness level. Technically, what was described above is a deterministic "imitating the best" adaption rule, coupled with synchronous updating practiced in a node's (actor's) local neighborhood. Fitness is rescaled to zero at the beginning of the next round. The evolution lasts for 500 rounds—long enough for the evolution of strategies to stabilize. The pseudo-code of the evolution described above is outlined in the appendix. For robustness purpose, we test other kinds of adaptation rules and update dynamics, reported in the following section.
- 2.4
- For network topology, we start with the Erd_s-Rényi random network (the ER-random network hereafter) (Erd_s and Rényi 1959) and then apply the model to the other two well-studied networks: the small-world network (Watts and Strogatz 1998) and the scale-free network (Barabási and Albert 1999). The nodal attributes (A) used to trigger actors' cooperation include degree, clustering coefficient, betweenness and the eigenvector centrality. Degree represents a node's connectedness. Clustering coefficient measures the cohesiveness of connections in a node's local neighborhood. Both betweenness (Freeman 1977) and the eigenvector centrality (Bonacich 1972) assess a node's role in mediating traffic flow in networks. All of these measures have received increasing attention in the biological and social network research (Wasserman and Faust 1994; Croft et al. 2008). Formal calculations of these network measures can be found in the appendix. We conduct independent simulation tournaments for each network attribute respectively.
- 2.5
- Since measures of nodal attributes are sensitive to network size, we standardize each nodal attribute in the following way.
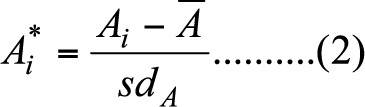
(2) where A ∈ {degree, clustering coefficient, betweenness, the eigenvector centrality }, and
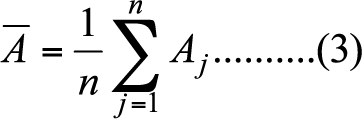
(3) 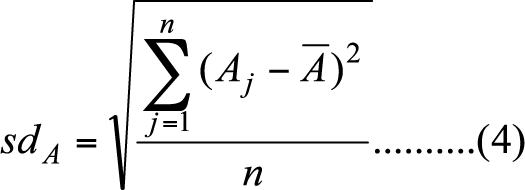
(4) Accordingly, we replace A with A* in equation (1). Standardization of nodal attribute helps us to narrow down our strategy space; otherwise, the number of strategies of (el, eh) in equation (1) would be impossible to manage when network size increases.
- 2.6
- We begin our simulation tournaments with the ER-random networks of fixed size (=150) and density (=0.25). As a preliminary test, we generate a sufficient number of networks controlled by these parameters. Observing these cases, we realize that the following boundary would hold: -6 < A*i - A*j < 6. To construct our strategy space, el ≤ A*i - A*j ≤ eh with el < eh, we fine-tune el and eh with a fixed interval of 0.5 in the range of -6 ≤ el and eh ≤ 6. In addition, we consider one more strategy characterized by el=eh=0, meaning that an actor would cooperate only with those who have strictly the same nodal attribute value. As a result, there are 301 contestant strategies participating in the tournaments, graphically illustrated in Figure 1 with one axis representing el and the other eh. Each of the strategies, (el, eh), shown in Figure 1, is played against unconditional cooperation and unconditional defection in the tournament of the helping game. We track the share of actors using the contestant strategy toward the end of evolution (the last 100 rounds).
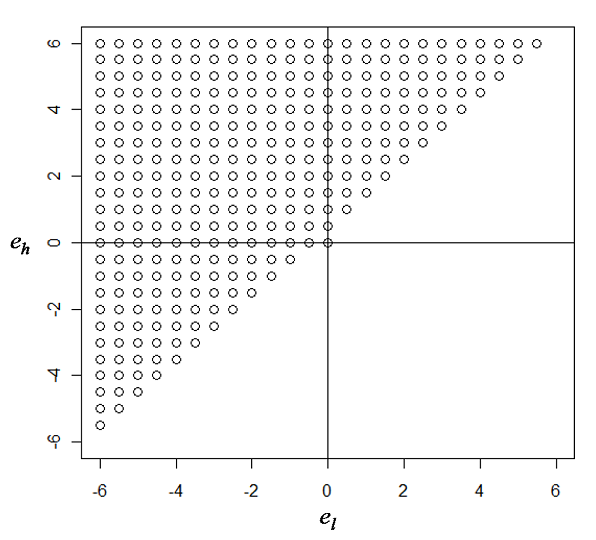
Figure 1. Graphic illustration of the contestant strategies of conditional cooperation participating in the evolutionary tournament against unconditional cooperation and defection in the ER-random networks of fixed size (=150) and density (=0.25). There are 301 contestant strategies. - 2.7
- All of the simulations were conducted in R(R 2011), an open-source statistics language and program, drawing on two supporting packages "igraph" (Csardi and Nepusz 2006) and "sna" (Butts 2008). The former package is responsible for generating different network topologies while the latter package is employed to calculate nodal attributes of networks. Complete R code to run the simulation can be found in the appendix.
 Results
Results
-
Main result
- 3.1
- Figure 2 presents a series of contour plots using terrain color spectrum projected on Figure 1 to quantify the share of each contestant strategy in the ER-random-network tournaments. The result shows that the distributions of adaptive advantages of the contestant strategies are highly similar across the four nodal attributes investigated. The similarity can be attributed to the fact that some of the nodal attributes are highly correlated (Borgatti et al. 2006). Two major types of strategies are found to be advantageous. Strategies that command one to cooperate with neighbors with either higher or lower nodal attributes are advantageous. On the other hand, if one cooperates with both higher and lower nodal-attribute neighbors, he would be less advantageous. As seen in the contour plots, the area circumscribed by el < 0 and eh > 0 is marked with low popularity. Note that this disadvantage cannot be attributed to a wide gap between µh and µl, reflecting less choosiness in the recipients of cooperation. Take el = - 0.5 and eh = 0.5 for example: It is a somewhat choosey strategy as the gap between eh and el is relatively small, yet it is inferior to other strategies with the same width of (eh-el) where eh × el > 0.
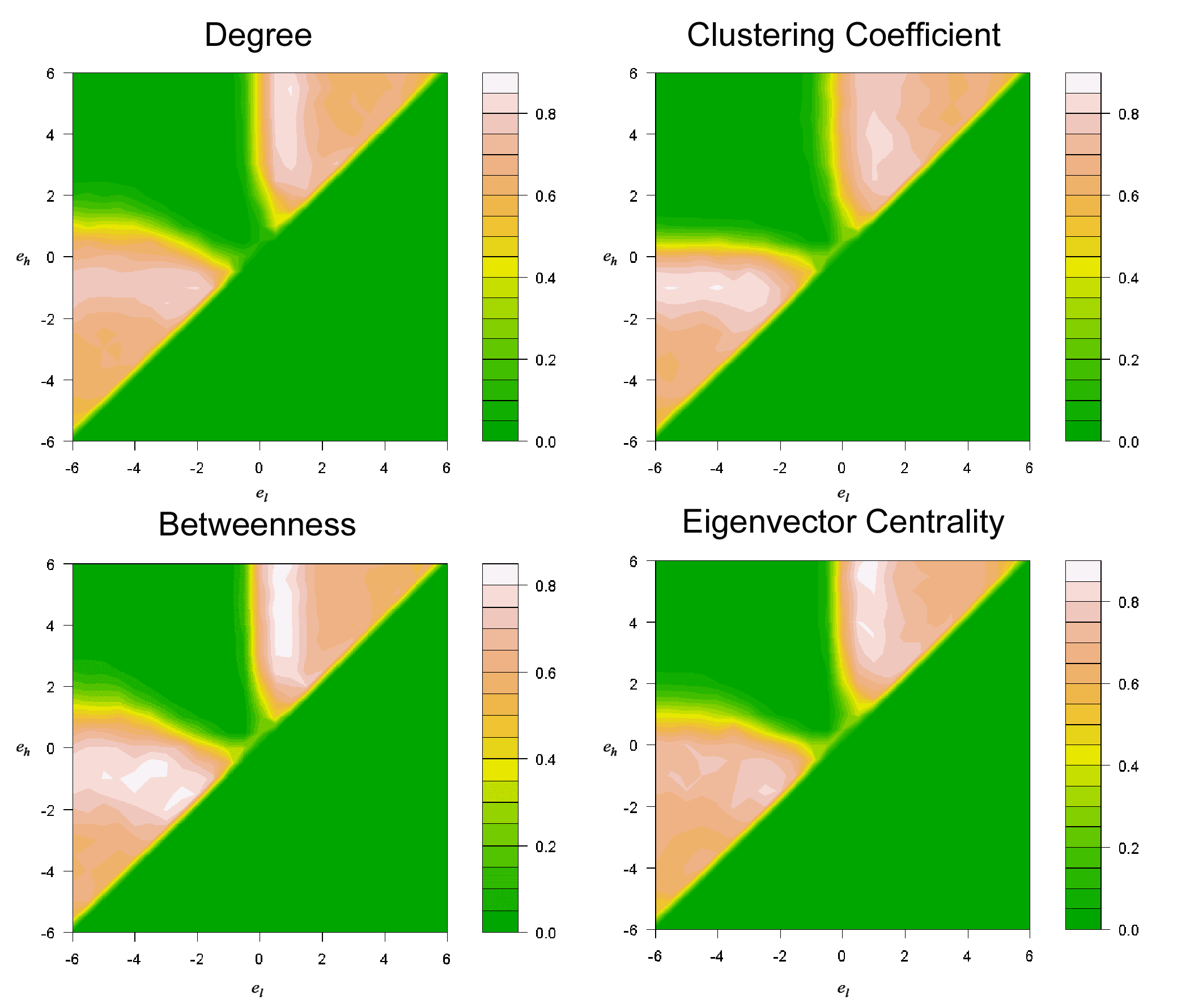
Figure 2. Average share of each contestant strategy (shown in Figure 1) in the last 100 rounds of the evolutionary tournaments. The reported data average over 500 random replications of the tournament conducted in the ER-random network with network size = 150 and network density = 0.25. Four separate sets of simulations were conducted, with each testing a nodal attribute among the choices of degree, clustering coefficient, betweenness and the eigenvector centrality. - 3.2
- The results show that the adaptive advantage of the strategies of conditional cooperation is determined by a single parameter of either eh or el. For the strategies that govern one to cooperate with lower-attribute neighbors (el < eh < 0), the adaptive advantage is related to the upper bound eh. The higher eh, the more advantageous the strategy is, until eh moves close to zero. It means that it is beneficial to cooperate with neighbors whose nodal attributes are higher by at least a small threshold. On the other hand, for those strategies that direct one to cooperate with higher-attribute neighbors (0 < el < eh), the adaptive advantage is determined by the lower bound el. The lower el, the more advantageous a strategy performs, until el gets close to zero. It means cooperating with neighbors whose nodal attributes are lower by at least a small threshold is advantageous.
- 3.3
- The results showed in Figure 2 are based on a model that adopts the Axelrod-type tournament-each contestant strategy competes with unconditional cooperation and defection in their own tournaments. For robustness check, we consider an alternative selection mechanism that puts all contestant strategies in one tournament (Nowak and Sigmund 1992). Details of the model and the results are presented in the appendix. Basically, we found no qualitative difference from the finding reported above.
- 3.4
- The vectors of (el, eh), each representing a strategy of conditional cooperation, entail difference degrees of complexity of execution. For example, a strategy that commands one to cooperate with a network neighbor with higher attribute value should be easier to follow than a strategy that governs one to cooperate with another whose network attribute is larger by an amount between one and two standard deviations. With the cognitive and information cost taken into account, the most advantageous strategy in adaptive value in the tournament may not be necessarily the most efficient one. Nevertheless, our simulation result suggests that a pair of simple strategies-cooperate with whoever has higher attributes (CWH), characterized by el=-6 and eh=0 (see Figure 1), or lower attributes (CWL), characterized by el=0 and eh=6 is not only easy to follow, but also performs considerably well in the tournaments. For this reason and because it is computationally expensive to test all the 301 strategies in different conditions, the remaining sections of the paper will focus on discussing the conditions of these two strategies' evolutionary advantages. Hereafter, we will test CWH represented by el=-∞ and eh=0, and CHL by el=0 and eh=∞.
- 3.5
- We now address two follow-up issues: How does network density influence the performance of the strategies? And how do they perform in networks with different network-attribute distributions? For the first question, we run evolutionary simulations in the ER-random-networks with different network densities from 0.05 to 0.95. Figure 3 plots the average share of the two strategies CWH and CWL in the tournaments. Similarly, there is high consistency in outcome across the four nodal attributes investigated. The result shows that CWH fares better than CWL, and both perform better in sparser networks. The negative relationship between network density and a strategy's evolutionary advantage echoes the mathematical rule derived in the previous work (Ohtsuki and Nowak 2006).
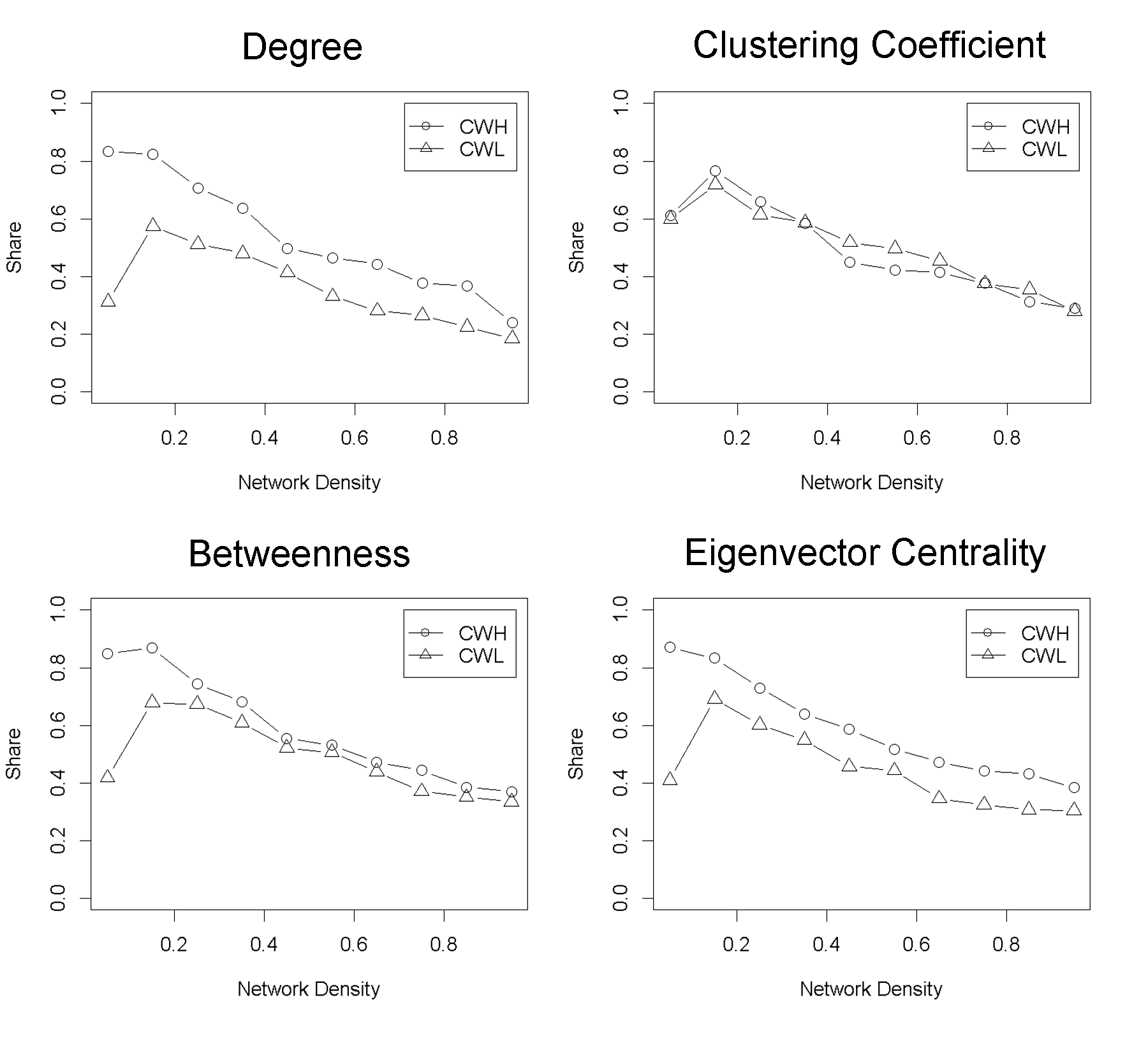
Figure 3. Average shares of the two strategies-cooperating with higher nodal-attribute neighbors (CWH) and lower-attribute neighbors (CWL)-in the last 100 rounds of the evolutionary tournaments. The reported data average over 500 random replications of the ER-random networks with fixed size (=150), but different network densities. Four separate sets of simulations were conducted, with each testing a nodal attribute among the choices of degree, clustering coefficient, betweenness and the eigenvector centrality. - 3.6
- For the second question, we run a series of tournaments in different network structures. We modify the rewiring algorithm used in the small-world network model to generate a wider range of network topologies (Watts 1999). The original version of the algorithm controls the probability of tie-rewiring to let network evolve from regular lattice to the small-world network to random network when the rewiring probability increases from 0 to 1. We modify the algorithm by introducing one more parameter to the model: when a tie is rewired, rather than randomly picking a new node to link to, as was proposed originally by Watts (1999), the choice of the new node is now determined probabilistically by its current degree. To be more formal, let ki denote node i's degree, the probability that it will get chosen as the recipient of a rewired tie is:
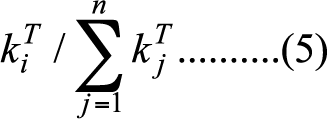
(5) where T is the new parameter that controls the extent to which rewiring is biased to high-degree nodes. When T = 0, the model replicates the original beta-model proposed in Watts (1999), and when the rewiring probability p equals 0, it is a regular lattice network, where each node has the same degree; a small-world network when p deviates slightly from 0, and a random network when p is non-trivial. When both T and p are non-trivial, ties are more likely to be rewired to high-degree nodes so a degree-centralized network, such as the scale-free network, would be generated.
- 3.7
- Figure 4 presents the average share of CWH (on node degree) over 100 random cases of tournament on networks generated in accordance with different combinations of the two parameters p and T. The result shows that CWH is more advantageous in networks where T is small and p is non-zero, which corresponds to the small-world network and random network. On the other hand, CWH performs inferiorly in regular lattices as in this case each node is isomorphic in structure so any strategy conditional on nodal attribute cannot be activated. The result also shows that CWH is comparatively less advantageous in more degree-centralized networks. This is because in such networks the strategy adopted by the central nodes would be most likely to be imitated (Pacheco and Santos 2005). The advantage of a strategy is thus determined mainly by how likely the central nodes would adopt it in the beginning, which is random chance (1/3). Overall, the test on different network topologies reveals an interesting message that while random networks (and even the small-world networks) have proved to be unbeneficial to the selection of cooperation, our study shows that as hostile as the network environment may be, there exist new behavioral strategies that help resist the invasion of defection and make cooperation possible to survive. These strategies are selective in choosing whom to cooperate with, and the criteria of selection can be related to network structural attributes.
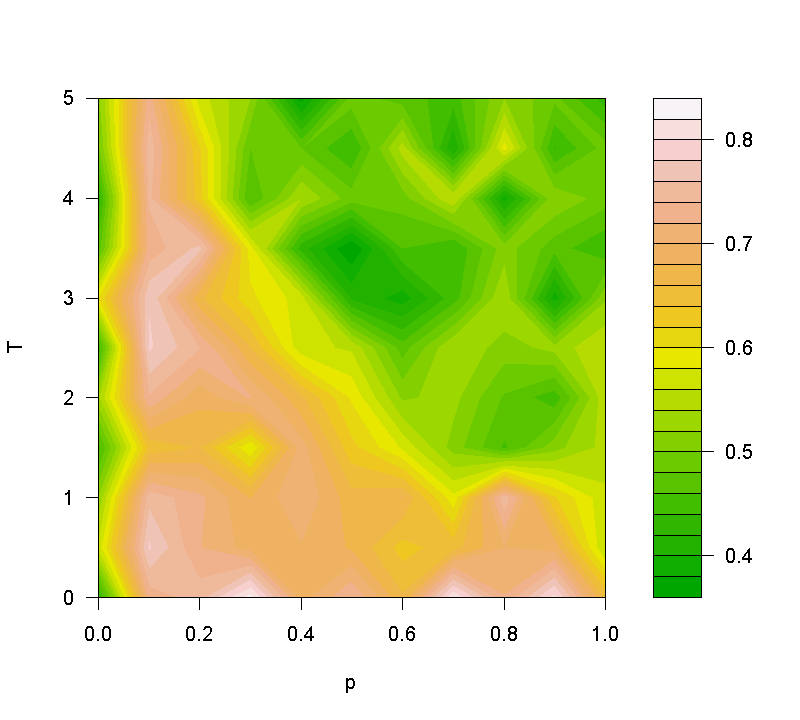
Figure 4. Average shares of the strategy CWH in the last 100 rounds of the evolutionary tournaments. The nodal attribute is node degree. The data report the mean shares over 100 random replications of tournaments in networks generated in reference to the two parameters p and T. In the small-word network model (Watts 1999), p controls the probability of rewiring each tie in a regular lattice (network size = 150 and number of ties per node = 40), while T (a new parameter in the model) governs the extent to which ties are rewired to high-degree nodes, when applicable. Why does the mechanism work?
- 3.8
- The reason why CWH and CWL work in (random) networks can be articulated through the following steps of reasoning. First, a network-attribute-conditional strategy, unlike unconditional cooperation, is selective in choosing the recipients of help. The choosiness prevents an actor from incurring the cost to help aimlessly all network neighbors. The cost of cooperation is saved, but then how can a conditional strategy be lucrative, imitated, and reinforced? In the three-strategy tournament, any actor could receive help from either unconditional cooperators or those who use a conditional strategy. In the latter case, the focal actor receives help because the difference between his nodal attribute and his neighbor's satisfies the criterion of the strategy being used that triggers cooperation. But then how can the evolutionary benefit be sustained and reinforced? Let us consider a hypothetical example for illustration. Suppose node i and node j are network neighbors and Ai > Aj. Assume that the actor in node i adopts CWH, and he is the most successful one in j's network neighborhood. The superiority in fitness prompts j to learn from i and adopts CWH. Because Ai > Aj, even though both i and j adopt CWH now, only j would help i, but not the other way around. That j continues to help i consolidates i's fitness further and reinforces the likelihood that j keeps imitating the strategy of CWH. This forms a virtuous cycle and explains why a conditional strategy such as CWH or CWL is possible to proliferate.
- 3.9
- The simulation result shows that between the two strategies, CWH performs slightly better than CWL in random networks. The evolutionary superiority of CWH over CWL can be attributed to the structural property of the ER-random network (and other networks that share similar property). Suppose actor in node i uses CWH. He incurs the cost of helping neighbors who have higher nodal attribute values. On the other hand, he receives help from neighbors who are either unconditional cooperators or use CWH with lower nodal attribute values. For actor i to be lucrative such that CWH can be imitated, it must be the case that the benefit actor i receives offsets the cost he incurs. It means that the number of i's neighbors who are smaller in nodal attribute value should be larger than the number of i's neighbors who are larger in nodal attribute value. As noted, the reinforcement of CWH's advantage lies in having as many as possible smaller-nodal-attribute neighbors, while the advantage of CWL, quite on the opposite, relies on being surrounded by larger-nodal-attribute neighbors. The difference in the conditions favoring the two strategies' success explains why one performs better than the other in random networks.
- 3.10
- Take node degree for example. It is well established in network science that the distribution of degree in random networks can be approximated by the Poisson distribution. The right-skewedness of the distribution means that there is a small set of nodes that have disproportionally high degrees. For these nodes, they are linked with nodes with smaller degrees. If actors in these nodes adopt CWH, they would have evolutionary advantages to prompt their neighbors to imitate CWH. On the other hand, CWL benefits nodes with low degrees. However, low-degree means that these nodes would not have as many high-degree neighbors as high-degree nodes would have small-degree neighbors.
- 3.11
- For evidence, we simulate an ER-random network (n= 150) and over each node we compute respectively the number of neighbors that have higher or equal degrees and lower or equal degrees respectively. Figure 5 plots each node's degree (k) against the two quantities from a random replication of the ER-random network. The distributions show that high-degree nodes tend to have neighbors with lower degrees, and vice versa. What is noteworthy is the difference in the extent: On average, high-degree nodes have more lower-degree neighbors than low-degree nodes have higher-degree neighbors. The former condition benefits CWH while the latter does CWL so it explains why CWH performs slightly better than CWL in the tournaments.
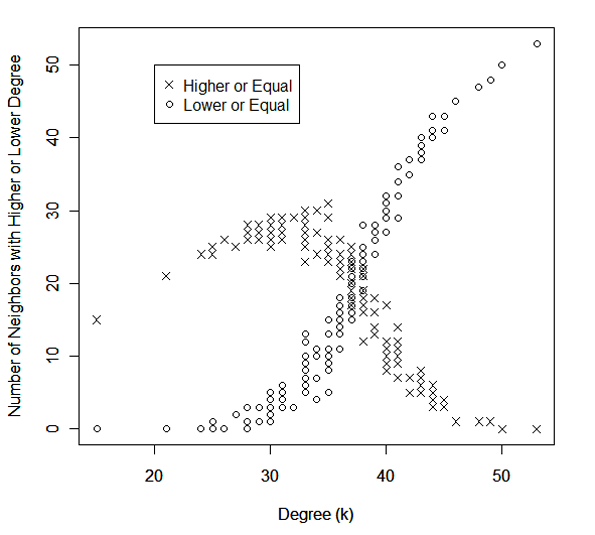
Figure 5. The distribution of the number of neighbors with higher or equal degree (◊) and lower or equal degree (ø) of each node, plotted against its own degree, generated from a random replication of the ER-random network with network size =150 and network density = 0.25. Robustness testing
- 3.12
- The ratio of the benefit of cooperation over the cost of it (b/c) is expected to influence the selection of strategies of conditional cooperation. We manipulate the ratio of b/c by fixing c to 1 and tuning b from1 to 8 in separate simulations. The results, reported in Figure 6, show that shares of the two conditional cooperation strategies, especially CWL, increase with the ratio of b/c. This is not only in line with the findings in the previous simulation studies on unconditional cooperation (Nowak 2006), but also coincides Hamilton's rule (1964) that addresses the relationship between the evolution of cooperation and the ratio of b/c.
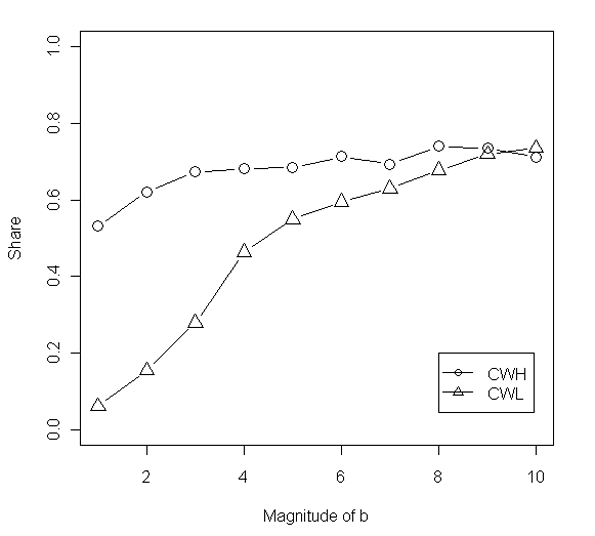
Figure 6. Average shares of the two strategies, CWH and CWL, in the tournaments over different ratios of b/c. Each data point averages 500 replications of the tournaments conducted in the ER-random networks with fixed network size = 150 and network density = 0.25. - 3.13
- The discussion insofar is built on an assumption that actors use a deterministic "imitating the best" adaption rule and update their strategies synchronously in local neighborhoods. It remains a question whether the evolutionary advantages of the strategies would remain robust if actors use alternative adaptation formats. For this inquiry, we run more simulations of tournaments, each of which tests a unique combination of adaptation rule and update dynamics, selected from a recent study (Yamauchi et al. 2010) that summarizes a wide range of evolutionary dynamics formats. Table 1 and 2 report the results. Similar to what was found in the previous study (Szabo and Fath 2007; Roca et al. 2009; Yamauchi et al. 2010), synchronous updating is slightly more favorable to the selection of cooperation. Among the three adaptation rules, imitating the best, which is adopted in the current study, facilitates the selection of conditional cooperation the most effectively. Although the two strategies, CWH and CWL, are less advantageous under the other two adaptation rules, the result is not qualitatively different from what is reported above: In most of the cases, the two strategies of conditional cooperation perform better than unconditional cooperation, which usually ends up with being wiped out in the tournament.
* The adaptation rules and update dynamics defined in the table are referred to Yamauchi et al. (2010).Table 1: Average share of CWH under different evolutionary dynamics rules
Adaptation RuleUpdate Dynamics
Synchronous
AsynchronousFermi Function 0.04 0 Best Imitation 0.71** 0.64 Linear Probability of Payoff Difference 0.15 0.01
**: Adopted in the main model of the paper.
* The adaptation rules and update dynamics defined in the table are referred to Yamauchi et al. (2010).Table 2: Average share of CWL under different evolutionary dynamics rules
Adaptation RuleUpdate Dynamics
Synchronous
AsynchronousFermi Function 0 0 Best Imitation 0.56** 0.55 Linear Probability of Payoff Difference 0.03 0.02
**: Adopted in the main model of the paper.
 Discussion
Discussion
- 4.1
- We have discussed new strategies of conditional cooperation on network characteristics and discussed the circumstances under which they evolve. In particular, we selected two strategies for further investigation-cooperating respectively with higher and lower network-attribute neighbors. These strategies are chosen not only because they have substantially high survival advantages in evolution, but also they are easy to be implemented in decision-making. As increasing psychological research indicates that people tend to make decisions in a cognitively frugal manner (Gigerenzer et al. 1999), we believe that these two strategies are more likely to be selected for due to its relatively low cognitive cost.
- 4.2
- The strategies of cooperation discussed here are particularly useful when actors have little or no information about one another's cooperativeness. In this case, network characteristics could serve as a signal to entice cooperation. We might suspect that a person would be more likely to cooperate with a socially popular stranger, because high sociality ensures that this person be more carefully in maintaining his or her reputation in future interaction-the control mechanism termed by scholars (Buskens and Raub 2002), or because sociality just reflects his or her good record of being cooperative in the past-the learning mechanism (Buskens and Raub 2002). We can develop a behavioral experiment to test the effectiveness of this strategy. For example, running a variant of the prisoner dilemma game experiment wherein the information of the number of friends in social media, such as Facebook, is provided, we can test whether humans tend to cooperate with those who have more Facebook friends.
- 4.3
- The success of these conditional strategies discussed in this paper is built on a number of assumptions. First, there is no limit on the resources an agent can have. Second, one has information about the structural characteristics of a network. Although there is increasing research evidence showing that individuals are capable of perceiving a complex network, investigating the factors that determine the accuracy of it remains a new field to be explored. We suggest that learning how to cooperate with others and learning how one's social network is structured could reinforce each other. Therefore, future research can investigate the co-evolution of the cognitive capacity to read social networks with the formation of cooperation strategies built on maneuvers of network attributes. Future studies can also investigate more complex strategies not covered in this paper, such as switching between cooperating with higher and lower network-attribute neighbors. The success of these more complex strategies, however, would need to take into account the cognitive cost of implementation.
- 4.4
- The recent emergence of research on dynamic networks provides a different perspective for how conditional cooperation evolves in networks (Skyrms and Pemantle 2000; Pacheco et al. 2006; Rand et al. 2011; Suri and Watts 2011; Bravo et al. 2012). Rather than staying in fixed networks, agents in dynamic networks are free to form links as they want depending on how they were treated by others. Based on the premise that "cooperators attract", it is expected that networks would evolve to a state where more cooperative actors end up with receiving more ties. This interesting finding, derived from both simulation work and experimental studies (Eguiluz et al. 2005; Bravo et al. 2012), coincides with what was found in the current paper: The strategy to cooperate with more sociable actors would work because, in light of dynamic network models, more linked actors are usually more cooperative and it is evolutionarily profitable to cooperate with cooperators. Because the two mechanisms address different network conditions, in one of which network is endogenously formed while in the other it is exogenously fixed, it is possible that the two mechanisms function in different stages in network evolution. In the early stage where ties are constantly rewired, strategies that act on individuals' characteristics, but not on network characteristics because networks constantly change, could function well in coping with the cooperation problem. In the latter stages where ties gradually become fixed in steady states, strategies that are triggered by network characteristics, but not by individual characteristics, could become more prominent. Thus, the strategy to cooperate conditionally on network characteristics discussed in this paper can be an evolutionary product of the strategy that emerges in dynamic networks. Future studies can test the relationship between the two mechanisms in different stages of the evolution of real social networks.
- 4.5
- Recent emergence of research interest in biological networks emphasizes the importance of understanding animals' social behavior from a broader network perspective than the limited dyadic view can provide (Krause et al. 2010). The attempt of this paper to link strategies of cooperation to nodal attributes echoes this appeal. As nodal attributes reflect a node's structural property in relation to other parts of the network, cooperation with others conditional on nodal attributes implicitly means that an individual incorporates the global network he is embedded in into the decision of whether to cooperate or not, even though explicitly he interacts with local neighbors only. Some nodal attributes, such as centrality measure, are a global network property in that calculation of these measures considers every other code's position across the network, while other attributes, such as clustering coefficient, are a local property as assessment of them involves only a node's local neighborhood. It remains to be investigated whether there is difference between global and local network properties in their influence on the evolution of cooperation.
 Appendix 1: Simulation code
Appendix 1: Simulation code
-
Pseudo-code of the evolutionary dynamics (deterministic imitating-the-best and synchronous updating)
For each round Fitness level is rescaled to zero For each actor Decide whether to cooperate (contingent on the strategies and nodal attributes) Fitness level updated End # loop over actors For each actor Check fitness levels in local neighborhoods Imitate the strategy of actor with the highest fitness level End # loop over actors End # loop over rounds
Complete R code run for the model:
# A function built to operate the helping game strategy=function(str_index,ego,alters){ # conditional cooperation index=1 if (str_index==index){ attribute_ego=Network_statistic[ego] attribute_alters=Network_statistic[alters] if (attribute_ego!="Nan"){ e_lower=Contestant[1] e_higher=Contestant[2] condition=attribute_ego-attribute_alters action=alters[which(condition<=e_higher & condition>=e_lower)] } else action=NULL } # unconditional cooperation index=index+1 if (str_index==index){ action=alters } # unconditional defection index=index+1 if (str_index==index){ action=NULL } action } # Main program starts here # Import supporting packages library(sna) library(network) # Introduce a contestant strategy (Figure 1): for example, CWH Contestant=c(-6,0) # Run over random replications for (cases in 1:500){ strategy_length=3 # a contestant strategy, plus unconditional cooperation and defection group_size=50 n=strategy_length*group_size # Generate a random graph library(igraph) net=erdos.renyi.game(n,p=0.25) NET=get.adjacency(net) NET[which(NET[,]>0)]=1 detach("package:igraph") net=network(NET,directed=FALSE) # Get network statistics: degree D=degree(net)/2 D=(D-mean(D))/sd(D[which(D!="NaN")]) # standardization Network_statistic=D # The helping game parameters b=5 c=1 # The distribution of strategies in the initial state STRATEGY_RECORD=sample(rep(c(1:strategy_length),group_size),n,replace=FALSE) # File to keep track of strategy distribution S=NULL # main program for (time in 1:500){ fitness=rep(0,n) S=rbind(S,STRATEGY_RECORD) for (actor in 1:n){ friends=which(NET[actor, ]==1) recipients=strategy(STRATEGY_RECORD[actor],actor,friends) fitness[actor]=fitness[actor]-length(recipients)*c fitness[recipients]=fitness[recipients]+b } # for actor # Selection old_strategy=STRATEGY_RECORD for (updated_actor in 1:n){ reference_group=c(which(NET[updated_actor, ]==1),updated_actor) their_fitness=fitness[reference_group] MIN=min(their_fitness) if (MIN<0){ their_fitness=their_fitness+(0-MIN) } model=reference_group[which(their_fitness==max(their_fitness))] if (length(model)>1){ model=sample(model,1) } STRATEGY_RECORD[updated_actor]=old_strategy[model] } # for updated_actor } # for time } # for cases
 Appendix 2: Formal definitions of network attributes
Appendix 2: Formal definitions of network attributes
- A.1
- Let G denote a graph (or network) consisting of two sets: {V, E}, where V=1, 2, ....n represents vertices (or nodes) of the graph, and E, an n × n matrix, has element eij=1 representing an edge (link) between node i and j, and 0 otherwise.
- A.2
- The clustering coefficient of node i is computed in the following way.
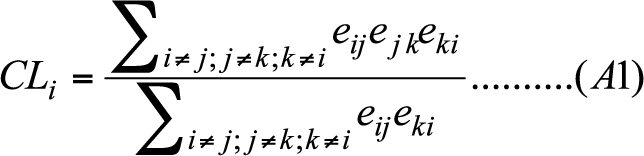
(A1) - A.3
- Let Pi(jk) denote the number of edges in the shortest path between node j and k that passes through node i. Let P(jk) represent the total number of edges in all the paths linking node j and k. The Betweenness of node i is measured as follows.
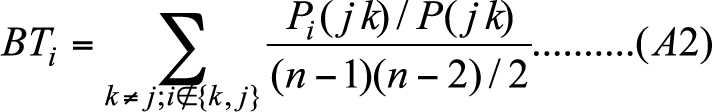
(A2) And the Eigenvector centrality of node i would be obtained by solving the following equation:
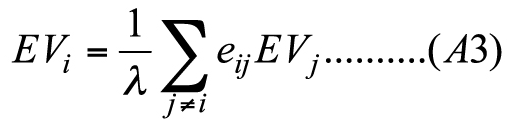
(A3) where λ is the eigenvalue of the matrix form of the equation: λEV(n-1)=E(n × n)EV(n ×n)
 Appendix 3: Alternative selection mechanism
Appendix 3: Alternative selection mechanism
- A.4
- In contrast to the tournaments reported in the paper where a contestant strategy competes alone with unconditional cooperation and defection, here we consider a different selection mechanism that puts all contestant strategies, along with unconditional cooperation and defection, into one "tournament" to examine how they evolve (Nowak and Sigmund 1992). All the modeling details are identical to the model reported in the content, except that now all the contestant strategies, along with unconditional cooperation and defection, are evenly distributed over actors. Since now all the strategies compete in one tournament, the share of each strategy in the initial state is small compared to the old model. We thus consider a smaller strategy space by fine-tuning el and eh with a fixed interval of 1 (rather than 0.5 as was reported in Figure 1) in the range of -6 ≤ el and eh ≤ 6 to make sure that the representativeness of a strategy would not be too trivial. A total of 81 strategies are considered. The simulation result is reported in Figure 7 below.
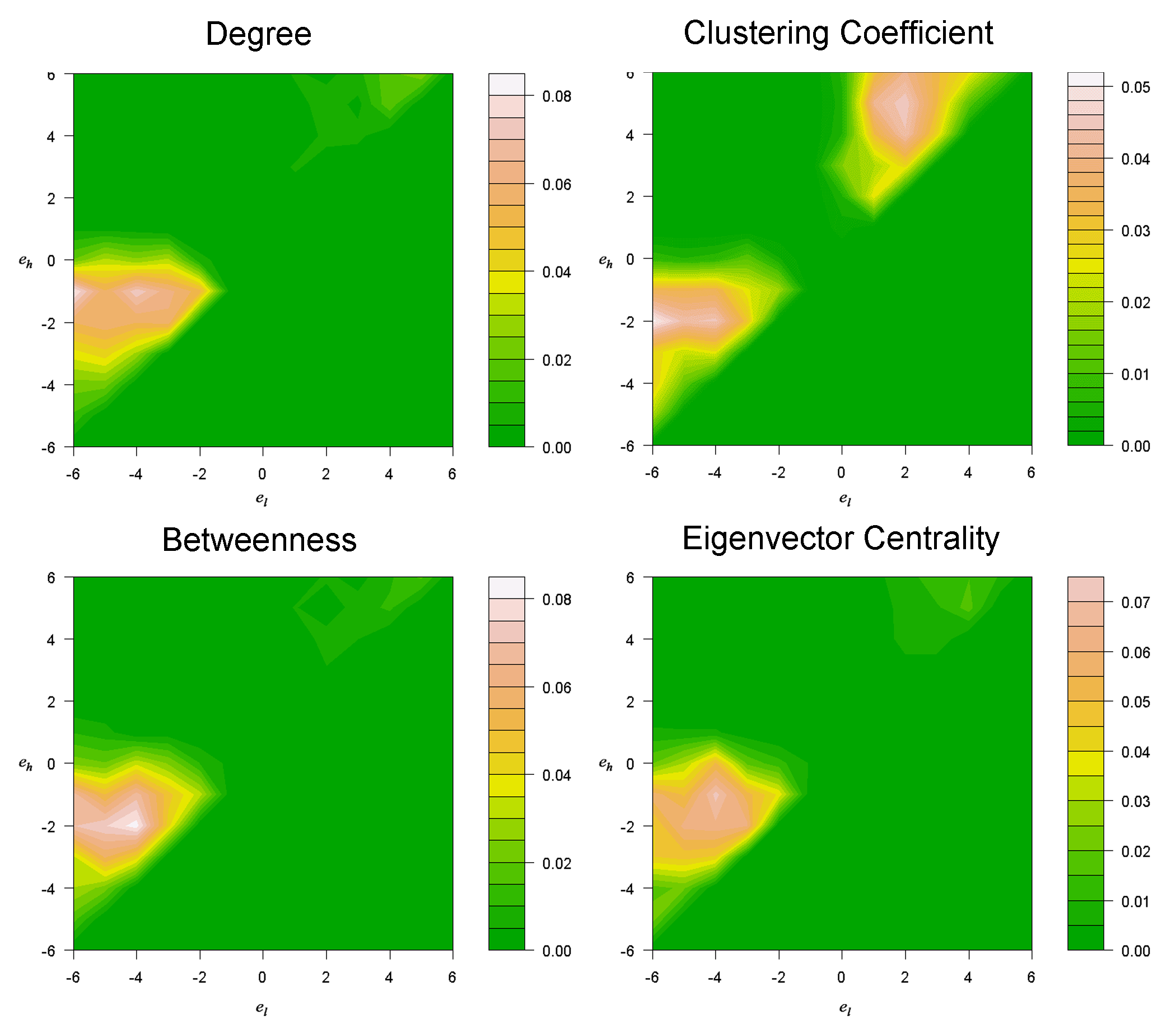
Figure 7. Average share of each contestant strategy in the last 100 rounds of the evolution. The reported data average over 500 random replications of the evolution conducted in the ER-random network with network size = 405 (81 strategies × 5 actors per strategy) and network density = 0.25. Four separate sets of simulations were conducted, with each testing a nodal attribute among the choices of degree, clustering coefficient, betweenness and the eigenvector centrality.
 References
References
-
AXELROD, R. and Hamilton, W.D. (1981). The evolution of cooperation. Science, 211, 1390-1396. [doi:10.1126/science.7466396]
BONACICH, P. (1972). Factoring and weighting approaches to status scores and clique identification. Journal of Mathematical Sociology, 2, 113-120. [doi:10.1080/0022250X.1972.9989806]
BARABSI, A., and Albert, R.(1999). Emergence of scaling in random networks. Science, 286, 509-512. [doi:10.1126/science.286.5439.509]
BORGATTI, S. P., Carley, K.M. and Krackhardt, D. (2006). On the robustness of centrality measures under conditions of imperfect data. Social Networks, 28, 124-136. [doi:10.1016/j.socnet.2005.05.001]
BRAVO, G., Squazzoni, F. and Boero, R. (2012). Trust and partner selection in social networks: an experimentally grounded model. Social Networks, 34(4), 481-492. [doi:10.1016/j.socnet.2012.03.001]
BURT, R.S. (1995). Structural Holes: the social structure of competition. Cambridge: Harvard University Press.
BUSKENS, V., and van de Rijt, A. (2008). Dynamics of networks if everyone strives for structural holes. American Journal of Sociology, 114, 371-407. [doi:10.1086/590674]
BUSKENS, V., and Raub, W. (2002). Embedded trust: control and learning. Volume Advances in Group Processes, 19, 167-202. [doi:10.1016/s0882-6145(02)19007-2]
BUTTS, C.T. (2008). Social network analysis with sna. Journal of Statistical Software, 24. [doi:10.18637/jss.v024.i06]
CROFOOT, M.C., Rubenstein, D.I., Maiya, A.S. and Berger-Wolf, T.Y. (2011). Aggression, grooming and group-level cooperation in white-faced Capuchins (Cebus capucinus): insights from social networks. American Journal of Primatology, 73, 821-833. [doi:10.1002/ajp.20959]
CROFT, D.P., James, R. and Krause, J. (2008). Exploring Animal Social Networks. Princeton: Princeton University Press. [doi:10.1515/9781400837762]
CSARDI, G. and Nepusz, T. (2006). The igraph software package for complex network research. InterJournal Complex Systems, 1695.
ERDÖS, P. and Rény, A. (1959). On random graphs. Publications Mathematicae Debrecen, 6, 290-297.
EGUILUZ, V. M., Zimmermann, M. G., Cela-Conde, C. J. and San Miguel, M. (2005). Cooperation and the emergence of role differentiation in the dynamics of social networks. American Journal of Sociology, 110, 977-1008. [doi:10.1086/428716]
FREEMAN, L.C. (1977). A set of measures of centrality based on betweenness. Sociometry, 40, 35-41. [doi:10.2307/3033543]
FREEMAN, L.C. (1992). Filling in the blanks: a theory of cognitive categories and the structure of social relations. Social Psychology Quarterly, 55, 118-127. [doi:10.2307/2786941]
GIGERENZER G., Todd, P.M. and ABC group. (1999). Simple Heuristics That Makes Us Smart. Oxford: Oxford University Press.
HALES, D. (2000). Cooperation without Space or Memory: Tags, Groups and the Prisoner's Dilemma. In Moss S and Davidson P (Eds.) Multiple-Agent-Based Simulation-Lecture Notes in Artificial Intelligence 1979/2000, Spring-Verlag. Pp. 157-166. [doi:10.1007/3-540-44561-7_12]
HAMILTON, W.D. (1964). The genetical evolution of social behavior I and II. Journal of Theoretical Biology, 7, 1-52. [doi:10.1016/0022-5193(64)90038-4]
HAMMOND, R.A., and Axelrod, R. (2006). The Evolution of Ethnocentrism. Journal of Conflict Resolution, 50, 926-936. [doi:10.1177/0022002706293470]
JANICIK, G.A., Larrick, R.P. (2005). Social network schemas and the learning of incomplete networks. Journal of Personality and Social Psychology, 88, 348-364. [doi:10.1037/0022-3514.88.2.348]
KILLINGBACK, T. and Doebeli, M. (1996). Spatial evolutionary game theory: Hawks and Doves revisited. Proceedings of the Royal Society of London Series B-Biological Sciences, 263, 1135-1144. [doi:10.1098/rspb.1996.0166]
KILDUFF, M., Crossland, C., Tsai, W. and Krackhardt, D. (2008). Organizational network perceptions versus reality: a small world after all? Organizational Behavior and Human Decision Processes, 107, 15-28. [doi:10.1016/j.obhdp.2007.12.003]
KIM, J-W. (2010). A Tag-Based Evolutionary Prisoner's Dilemma Game on Networks with Different Topologies. Journal of Artificial Societies and Social Simulation, 13, 2. https://www.jasss.org/13/3/2.html
KRAUSE, J., James, R. and Croft, D. P. (2010). Personality in the context of social networks. Philosophical Transactions of the Royal Society B-Biological Sciences, 365, 4099-4106. [doi:10.1098/rstb.2010.0216]
LEHMANN, J., and Dunbar, R. I. M. (2009). Network cohesion, group size and neocortex size in female-bonded Old World primates. Proceedings of the Royal Society B-Biological Sciences, 276, 4417-4422. [doi:10.1098/rspb.2009.1409]
LIN, N., Cook, K. and Burt, R.S. (2001). Social Capital. New Brunswick: Transaction Publishers. [doi:10.1017/CBO9780511815447]
LUSSEAU, D. and Newman, M. E. J. (2004). Identifying the role that animals play in their social networks. Proceedings of the Royal Society B-Biological Sciences, 271, 4417-4422. [doi:10.1098/rsbl.2004.0225]
MOUW, T. (2006). Estimating the causal effect of social capital. Annual Review of Sociology, 32, 79-102. [doi:10.1146/annurev.soc.32.061604.123150]
NOE, R. and Hammerstein, P. (1994). Biological markets- supply-and-demand determine the effect of partner choice in cooperation, mutualism and mating. Behavioral Ecology and Sociobiology, 35, 1-11. [doi:10.1007/BF00167053]
NOWAK, M. A. (2006). Five rules for the evolution of cooperation. Science 314, 1560-1563. [doi:10.1126/science.1133755]
NOWAK, M.A, and May, R.M. (1992). Evolutionary games and spatial chaos. Nature, 359, 826-829. [doi:10.1038/359826a0]
NOWAK, M.A., Tarnita, C.E. and Antal,T. (2010). Evolutionary dynamics in structured populations. Philosophical Transactions of the Royal Society B-Biological Sciences, 365, 19-30. [doi:10.1098/rstb.2009.0215]
OHTSUKI, H. and Nowak, M. (2006). The replicator equation on graphs. Journal of Theoretical Biology, 243, 86-97. [doi:10.1016/j.jtbi.2006.06.004]
PACHECO, J.M. and Santos, F.C. (2005). Scale-free networks provide a unifying framework for the emergence of cooperation. Physical Review Letters, 95, 098104. [doi:10.1103/PhysRevLett.95.098104]
PACHECO, J.M., Traulsen, A. and Nowak, M.A. (2006). Active linking in evolutionary games. Journal of Theoretical Biology, 243, 437-443. [doi:10.1016/j.jtbi.2006.06.027]
R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/
RAND, D. G., Arbesman, S. and Christakis, N. A. (2011). Dynamic social networks promote cooperation in experiments with humans. Proceedings of the National Academy of Sciences, 108, 19193-19198. [doi:10.1073/pnas.1108243108]
RIOLO, R.L., Cohen, M.D. and Axelrod, R. (2002). Behavioral evolution (communication arising): Does similarity breed cooperation? Nature, 418, 500. [doi:10.1038/418500a]
ROBERTS, G. (1998). Competitive altruism: from reciprocity to the handicap principle. Proceeding of the Royal Society of London Series B- Biological Sciences, 265, 427-431. [doi:10.1098/rspb.1998.0312]
ROCA, C.P., Cuesta, J.A. and Sánchez, A. (2009). Effect of spatial structure on the evolution of cooperation. Physical Review E, 80, 046106. [doi:10.1103/PhysRevE.80.046106]
SACHS, J. L., Mueller, U. G., Wilcox, T.P. and Bull, J.J. (2004). The evolution of cooperation. Quarterly Review of Biology, 79, 135-160. [doi:10.1086/383541]
SKYRMS, B. and Pemantle, R. (2000). A dynamic model of social network formation. Proceedings of the National Academy of Sciences of the United States of America, 97, 9340-9346. [doi:10.1073/pnas.97.16.9340]
SUEUR, C., Jacobs, A., Amblard, F., Petit, O. and King, A.J. (2011). How can social network analysis improve the study of primate behavior? American Journal of Primatology, 71, 1-17. [doi:10.1002/ajp.20915]
SURI, S. and Watts, D. J. (2011). Cooperation and contagion in web-based, networked public goods experiments, PLoS ONE, 6, e16836. [doi:10.1371/journal.pone.0016836]
SZABO, G. and Fath, G. (2007). Evolutionary games on graphs. Physics Reports-Review Section of Physics Letters, 446, 97-216. [doi:10.1016/j.physrep.2007.04.004]
WASSERMAN, S. and Faust, K. (1994). Social Network Analysis. Cambridge: Cambridge University Press. [doi:10.1017/CBO9780511815478]
WATTS, D. J. (1999). Small Worlds. Princeton: Princeton University Press.
WATTS, D.J. and Strogatz, S. (1998). Collective dynamics of 'small-world' networks. Nature, 393, 440-442. [doi:10.1038/30918]
WEST, S.A., Griffin, A.S. and Gardner, A. (2007). Evolutionary explanations for cooperation. Current Biology, 17, 661-672. [doi:10.1016/j.cub.2007.06.004]
YAMAUCHI, A., Tanimoto, J. and Hagishima, A. (2010). An analysis of network reciprocity in prisoner's dilemma games using full factorial designs of experiment. Biosystems, 103, 85-92. [doi:10.1016/j.biosystems.2010.10.006]