 Abstract
Abstract
- Role playing games (RPGs) can be used as participatory simulation methods for environmental management. However, researchers in the field need to be aware of the influence of the game settings on participants' behavioural patterns and attitudes, before fine tuning the design and use of their games. We developed an agent-based model (CauxAttitude) to assess the framing induced by the conditions of implementation of a specific game, named CauxOpération, on possible changes in participants' attitudes. We designed CauxAttitude on the basis of social psychology theories that describe relations between attitudes and behaviours, as well as on observations of CauxOpération sessions. In this paper, we describe how the model behaved according to variations in the initialization of the parameters, our aim being to explore the effects of subjective choices concerning model design and implementation. The results of our simulations enabled us to identify effects of game settings we explored, including the choice of the population of participants or of the number of participants made by the game designer. Our results also revealed the underlying mechanisms that explain the effects of game settings. These provide clues to the game designer on how to manage them.
- Keywords:
- Agent-Based Social Simulation, Role Playing Game, Companion Modelling, Attitude-Behaviour Relations, Attitude Change, Game Setting Effects
 Introduction
Introduction
- 1.1
- Many authors refer to 'companion modelling' (Commod) in case studies in which role playing games (RPGs) are used to help stakeholders deal collectively with a natural resource management issue. The aim of the game is to enable stakeholders to share their knowledge and learn about the system or the environment they share. The game provides an experimental setting for stakeholders to explore joint solutions to environmental problems that are tailored to the constraints of their own context. This kind of participatory setting in research is increasingly common. Companion modelling approaches are representative of this trend but are far from being the only ones (Voinov and Bousquet 2010; Barreteau et al. 2007).
- 1.2
- Evaluation of the outcomes of such methods for the participants (Etienne 2010), and, more generally, of participatory research (Barreteau et al. 2010), is a relatively new field, both with respect to changes in sharing natural resources by those who are concerned and the rules that are drawn up as a result of the shared experience. Scientists in the field actively focus on learning models as processes that can occur during RPG sessions (Peters and Vissers 2004; Ryan 2000; Tsuchiya 1998). They focus on the changes in the participants' representations generated by the specific settings of a game session and its debriefing. However, these settings (such as the selection of the participants, time management, the facilitation protocol, contextualisation of the game situation, etc.) could frame changes during the game session. Game designers thus need tools to assess how these settings can influence the outcomes for participants.
- 1.3
- Our goal was to develop an agent-based model to grasp some of the underlying cognitive and social mechanisms that can occur during RPG sessions, in order to understand how the effects of a setting can lead a game session towards specific outcomes. This paper presents a model named CauxAttitude, focused on changes in participants' attitudes in a specific RPG named CauxOpération. Here, "attitude is a psychological tendency that is expressed by evaluating a particular entity with some degree of favour or disfavour" (Eagly and Chaiken 1993). According to the MIT model of Williams and Williams (2010), attitudes can easily change in this kind of RPG. In companion modelling in general, components of RPGs fit the aspect of reality they aim to represent as well as the small world with which they interact: participants are concerned by the game's outcome, the game structure matches reality, and participants are free to create and execute a personal strategy and receive feedback on it.
- 1.4
- The aim of CauxAttitude is to explore the specific settings of CauxOpération that can frame the participants' attitude dynamics. The model is based on social psychology theories. Much has been undertaken on attitude change in social psychology in recent decades, e.g., Eagly and Chaiken (1993), Hogarth and Einhorn (1992), Petty and Cacioppo (1986), and on attitude-behaviour relationships, e.g., Ajzen (1991), Festinger (1957), Glasman and Albarracin (2006), social simulations of attitude dynamics; e.g., Galam (2003), Deffuant et al. (2001), Urbig (2003). However, only a few authors have linked social psychology theories with social simulation relative to the attitude topic: Dubois et al. (2007), Jager and Amblard (2007), Mosler et al. (2001), Nowak et al. (1990). In these studies, the authors include social psychology models of attitude change in agent based models. To our knowledge, only one author has connected the attitude-behaviour relationships from the social psychology literature (Richetin et al. 2010) with social simulation, but they do not consider agents in interaction.
 The RPG CauxOpération
The RPG CauxOpération
- 2.1
- In this section, we describe the role playing game, CauxOpération (Souchere et al. 2010). The aim of this RPG is to facilitate coordinated management of a watershed which is prone to erosive runoff, by having stakeholders play a role in a fictional situation dealing with erosion prevention techniques and agricultural practices. The main purpose is to increase participants' awareness of erosive runoff processes and of the cumulated impacts of their activities. Participants do not receive any financial compensation for playing the game.
- 2.2
- The game board represents a 675 ha watershed divided into fields belonging to six farms with a village located at the watershed outlet. The RPG involves eight stakeholders (six farmers, one mayor and one agricultural watershed advisor) who play their real-life roles. Farmers who play the role of farmers choose their cropping pattern and allocate a crop to each field based on their own farming system. Their choice generates a risk of erosive runoff which a computer model calculates for each location in the watershed. The participant playing the role of mayor is informed about the damage caused by erosive runoff to the village and to the roads crossing the watershed. The participant playing the role of the watershed advisor is the technical advisor for the implementation of solutions to reduce runoff. He and the mayor have to design a strategy to manage erosive runoff at the watershed scale. They can provide incentives for cover crops and plant grass strips or build new storage ponds, if they succeed in obtaining the farmers' agreement. They can encourage the farmers to reduce damage by organizing collective meetings to negotiate the planting of grass strips, to build ponds and to negotiate a change in agricultural practices but they cannot offer many financial incentives as their budget is not large enough to solve all the problems.
 Observations of CauxOpération and interviews with participants
Observations of CauxOpération and interviews with participants
- 3.1
- We observed seven sessions of CauxOpération (three sessions with farmers and four with students). We asked all participants to fill in a questionnaire concerning changes in attitudes that occurred during the game session; and 11 participants in the two first sessions with farmers accepted to be interviewed after the game sessions. Field investigations included following tasks:
- Collecting the necessary information to design and validate the model of the game environment, e.g., what are the pattern and the topic of interaction among the participants?
- Judging if an attitude change has taken place during game sessions of CauxOpération.
- If so, analyse causes of attitude change.
- Characterize the game setting effects to be further explored: for example, if feedback is a relevant setting, how is it taken into account by participants? When is it delivered to participants during the game session? etc.
 The agent-based model: CauxAttitude
The agent-based model: CauxAttitude
- 4.1
- We designed a model named CauxAttitude to grasp changes in attitudes during sessions of CauxOpération. The model focuses on one way of change based on the attitude-behaviours relationships captured by social psychology theories. Behaviours in CauxOpération are mainly negotiations between participants about solutions to deal with runoff issues. Here a negotiation is considered to be a situation in which there is at least one individual who wants something from another individual, and which the latter has to accept or reject. In the model, we assume that the attitudes and behaviours displayed during the negotiation process influence each other.
Modelling the game situation based on observations of CauxOpération
- 4.2
- We observed that the main interactions between the participants were negotiations between two individuals. This observation was confirmed by the answers to the questionnaires, as one participant put it: "too many participants in a negotiation make it difficult to solve a problem". Other kinds of interactions were informal discussions, sharing of knowledge about runoff issues, and collective meetings to think together about suitable solutions. Negotiations were about elaborating solutions to deal with runoff issues in the watershed. We observed negotiations about almost all the possible solutions in the game: planting cover crops, grass strips, digging storage ponds, exchanging fields and so on. The most frequently discussed types of solutions were those which required no financial investment by the farmers, like cover crop funding, digging storage ponds or planting grass strips. For instance, a farmer participant said "I agree with all your requests as long as they don't cost me anything". Some solutions were discussed but only rarely: better farming practices with no financial incentives, crop rotations based on agreements between farmers.
- 4.3
- On the basis of these observations, we chose to model interactions between participants as 2-participant negotiations with proposals for solutions to cope with erosive runoff.
- 4.4
- To reduce the number of possible solutions, we grouped 15 possible solutions into two types: solutions for runoff issues with and without funding. By funded solutions, we mean solutions that cost money and the money had to come from another participant, e.g., a participant playing the role of a farmer asked the watershed advisor to cover the cost of planting a cover crop. By solutions without funding, we mean solutions negotiated between several participants but that required no external funds, e.g., a participant playing the role of a farmer suggested to another farmer that they both choose crops that will prevent runoff.
- 4.5
- We assume that participants can change their attitudes to the different types of solutions during ongoing negotiations in CauxOpération. We asked the participants to fill in questionnaires during the game session whenever they ended the negotiations they were involved in. Reading the questionnaires enabled us to observe many changes, which legitimized our choice of focusing on processes leading to changes in attitude.
A model inspired by social psychology theories
Main theories of attitudes-behaviours-relationships
- 4.6
- The prediction of behaviours has been widely studied in social psychology. The main model is the theory of planned behaviour (TPB) proposed by Ajzen (1991; 2004), itself an extension of the theory of reasoned action (Ajzen and Fishbein 1980).
- 4.7
- In the TPB, attitudes toward behaviours and subjective norms (perceived social pressure to perform or not perform the behaviour) influence intentions, which, in turn, influence behaviours. Also, perceived behavioural control (perceived ease or difficulty in performing the behaviour) influences intentions and also directly influences behaviours. Perceived behavioural control was not included in the theory of reasoned action. Figure 1 is a conceptual representation of TPB. In the literature, some authors added other interpersonal and situational factors that compete with attitudes to influence behaviours, like habits (Ronis et al. 1989) or the positive or negative consequence associated with the behaviour (Devine 1989). Moreover, some authors (Sapp 2001 and Grieve 2001, cited in Richetin et al. 2010) showed that the non-rationality of decisions (mostly studied by Simon (1955), Tversky and Kahneman (1986)) can also occur in the relations between attitudes and behaviours.
Figure 1. Theory of planned behaviour (Ajzen 1991; Ajzen 2004) - 4.8
- Individually, attitudes are generally poor predictors of behaviours. However, they can be good predictors under particular circumstances. A meta-analysis by Glasman and Albarracin (2006) showed that the attitude-behaviour association is stronger when attitudes are accessible (easy to recall) and remain stable over time. Because of accessibility, attitudes are better predictors of behaviours when individuals have direct experience with the attitude object and report their attitudes frequently. Because of stability, attitudes are better predictors of behaviours when individuals are confident in their attitudes, when individuals form their attitudes on the basis of information that is relevant to the behaviour, and when they receive or are led to think about one rather than two-sided information about the attitude object.
- 4.9
- Nevertheless, results on relations between attitudes and behaviours in the literature feature correlations. Thus they do not enable us to draw the necessary and sufficient conditions for the prediction of behaviours from attitudes. For instance, when attitudes are confident, they are better predictors of behaviours, but there is no proof that confidence necessarily makes attitudes good predictors of behaviours.
- 4.10
- On the other hand, behaviours can be good predictors of attitudes and can have an impact on future behaviours. Figure 2 describes four possible ways past behaviours can influence cognitions and future behaviours.
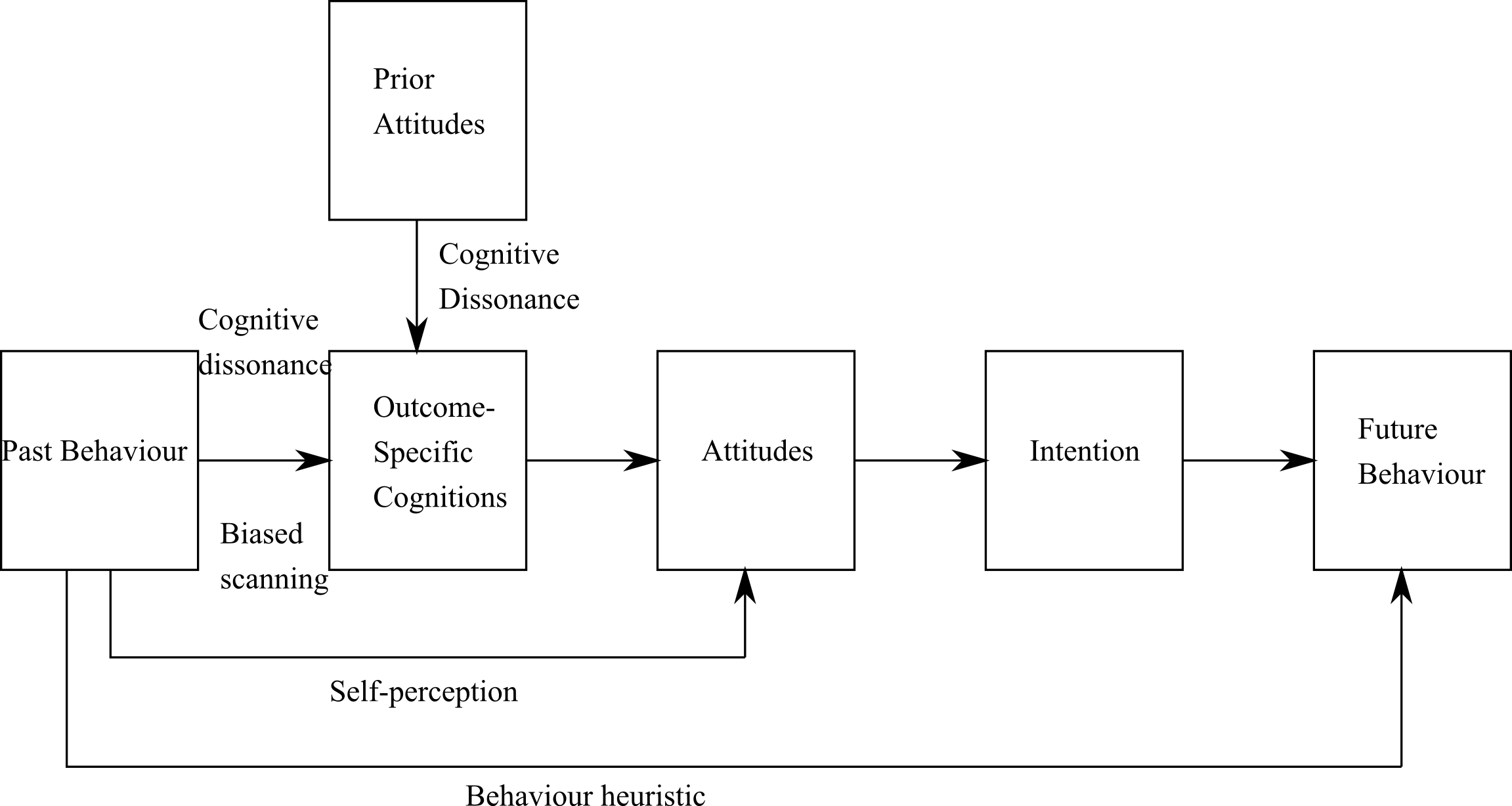
Figure 2. Four ways past behaviours can influence cognitions and future behaviours (Albarracin and Wyer Jr. 2000) - 4.11
- These four ways are supported by four theories from the psychological literature and cited in Albarracin and Wyer Jr. (2000):
- The cognitive dissonance theory (Festinger 1957) assumes that when behaviours and attitudes are congruent, attitudes tend to be consolidated by past behaviours. When they are not congruent, attitudes tend to get closer to past behaviours in order to reduce the cognitive dissonance of the individual, i.e., when an individual has two incompatible cognitions or a cognition that is incompatible with his/her behaviour.
- The biased scanning theory (Janis and King 1954) postulates that when individuals perform behaviours, they scan their memory to find congruent knowledge with the desirability and likelihood of the consequences associated with the behaviours. This leads individuals to update their attitudes, intentions and future behaviours.
- The self-perception theory (Bem 1965; 1972) suggests that when individuals are called on to report an attitude, they often infer this attitude from the implications of a past behaviour. This suggests that the inference may occur independently of their pre-existing attitudes and does not require much mediating cognitive activity. Consequently, it is more likely to happen when individuals are not motivated or unable to think about why they might have performed the behaviour in question.
- Behaviour as a heuristic tool (Bentler and Speckart 1979; Cialdini 1988) suggests that individuals' past behaviours can have a direct impact on their future behaviours that is independent of their attitudes toward the behaviour. This impact is more likely when the behaviour is habitual and occurs in stable contexts (Ouelette and Wood 1998; Triandis 1977; 1980).
- 4.12
- Although the literature reveals correlations between past behaviours, attitude change and future behaviours, the influence of attitudes resulting from past behaviours is not systematic. For instance, if an individual can justify his behaviour with explicit incentives such as receiving money for performing an undesirable behaviour, his attitude does not change (Festinger and Carlsmith 1959). Kelman (1953) also showed that when individuals perform behaviours in order to conform to social norms, they conform more if they are paid to do so, but their attitude change is less extensive.
Modelling choices
- 4.13
- We designed the CauxAttitude model on the basis of several principles:
- The model should be adapted to the conditions of interactions and to the types of attitudes observed in the role playing game sessions: i.e., negotiations between participants about two types of solutions (funded and non-funded) leading to two types of attitudes.
- The model should be in accordance with the psychological literature on attitude behaviour relationships.
- The focus should be on attitudes. As we want to observe the attitude dynamics and not the dynamics of subjective norms or perceived behavioural control, the model should focus on changes in attitudes while still considering the possibility that other factors influence behaviours.
- The model should be simple. As the goal of the study was to understand the dynamics, we chose to build the simplest possible model to understand the main mechanisms behind the dynamics we observed in the RPG sessions. We consequently only included the components that already formed part of our theoretical hypothesis and tuned them to our observations.
- 4.14
- We first chose a parameter x to determine the weight of the factors that involve attitude as a predictor of behaviour. x is an aggregate of accessibility, stability and their implications, e.g., confidence, plus all possible others factors that can have an impact on attitudes for the prediction of behaviours. As mentioned above, results published in the literature are simply correlations: accessibility and stability are not enough to characterize the weight of attitudes in influencing behaviours. For simplicity's sake, in the first stage, we chose to formalize the model at this level of aggregation. We also considered that x can change during a game session. As the game encourages participants to think about their attitudes, these can become both more stable and more accessible. There are several possible ways for x to evolve in a RPG session, but we chose to create the dynamics based on the negotiation process. We assume that during a negotiation, the behaviour of one participant can influence the confidence he/she has in the attitude of another participant, and can thus influence the value of x. This assumption is explained in detail in the formal description of CauxAttitude. Despite the existence of several ways of modelling attitude and opinion dynamics in the literature (e.g., Deffuant et al. 2001), we chose to have our model be a simplification of the most common psychological theories.
- 4.15
-
We chose a parameter y to determine the weight of all the factors that can influence behaviours other than attitudes. y is an aggregate of subjective norms, perceived behavioural control, habits, behaviour associated with positive and negative consequences and all other factors that are not cited in the literature (in as far as the TPB does not explain all the variance in the influence of behaviours).
We chose to aggregate the competitors of attitudes in order to focus on the influence of attitude. Figure 3 summarizes factors that lead to the prediction of behaviours and attitude-behaviour relationships that we took into account for the study. Bringing together in a single model the theoretical framework of factors that imply attitudes as predictors of behaviours with a theoretical framework of relations between attitudes and behaviours (TPB) is appropriate here because the stability and accessibility of attitudes have also already been analyzed in TPB (Doll and Ajzen 1992).
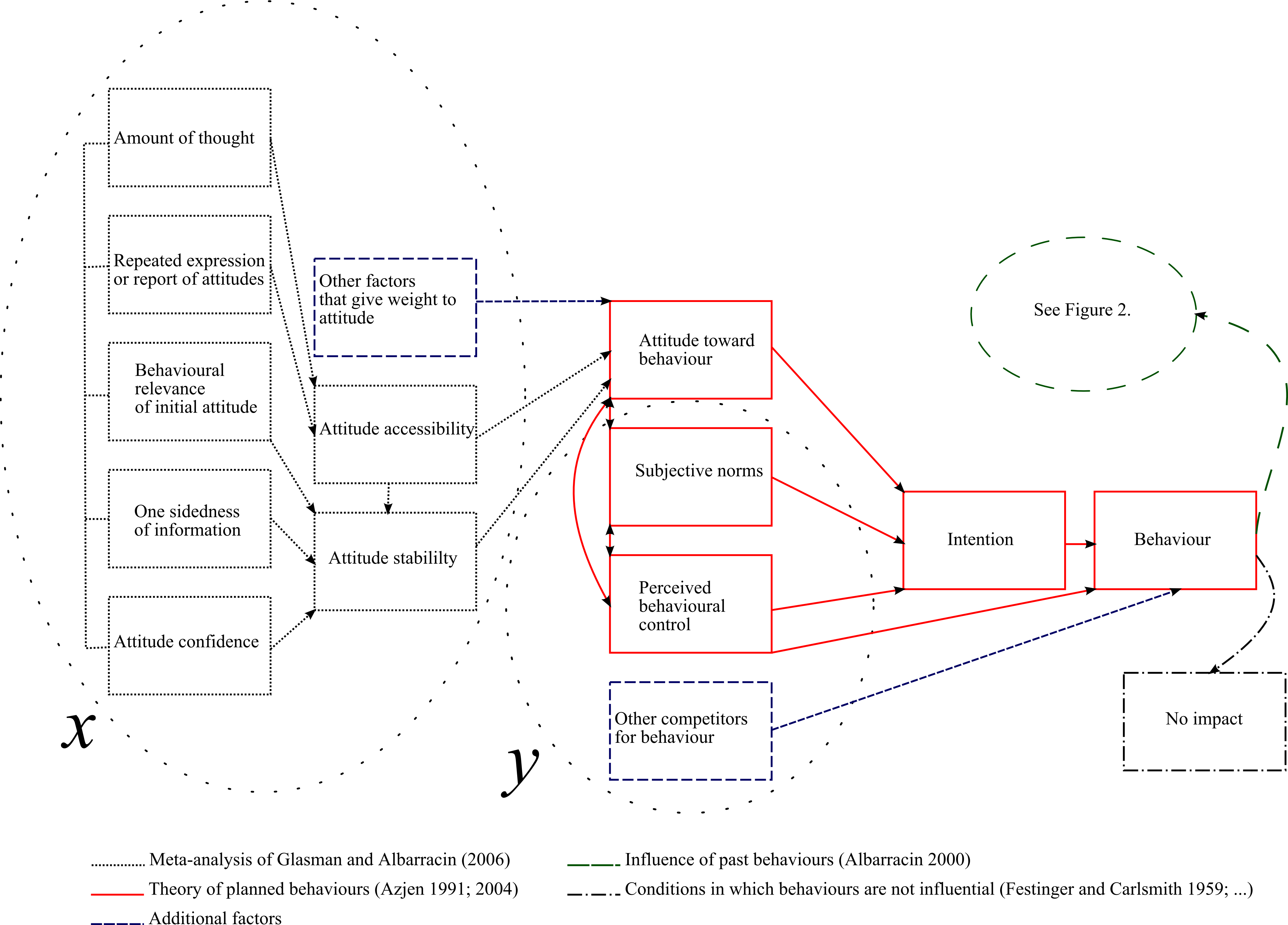
Figure 3. Factors included in attitude-behaviour relationships. Circles explain what is captured by parameters x and y in CauxAttitude - 4.16
- Regarding the TPB, we removed the concept of intention because mathematically speaking, it actually acts only as a filter of probability thus decreasing the occurrence of behaviour relative to attitudes, subjective norms, perceived behavioural control and so on. It is not indispensable to add a filter of probability as long as it is possible to explore all the possible dynamics of the model using the variations in the original parameters (x, y, attitude values). For that reason, consistent with our rule of simplicity, we did not include intention in the model.
- 4.17
- Regarding the influence of attitudes on behaviours, we assume that the choices of behaviours made by the agents (i.e., agents representing participants in the model) can be due to the value of their attitudes (a), their x, and their y. This is a model based on thresholds, i.e., if compared to value of other factors which can influence behaviours (y) the weight of attitude i.e., x × a, is sufficiently high, the behaviour will be performed according to the attitude. Otherwise, the behaviour will be performed according to y.
- 4.18
- Regarding the effects of behaviours on attitudes, we chose to drastically simplify the process and in CauxAttitude, to assume that the relations are entirely deterministic. Behaviours cause attitudes to update themselves to reduce any discrepancy. We thus consider that in CauxAttitude, agents systematically update their attitudes after performing a behaviour. Therefore, we consider that CauxAttitude favours the emergence of processes like cognitive dissonance reduction or biased scanning. As mentioned in the previous section, when past behaviours do not influence attitudes, additional factors are needed to reduce the effects of past behaviours on attitudes (e.g., factors that allow justification). As CauxAttitude is a theoretical model, in this study, we chose to first investigate the simplest possible situation and we assume that this is the situation in which the number of factors is the lowest. Consequently, it refers to the situation in which past behaviours have direct influences on attitudes. Figure 4 shows our simplification of the process.
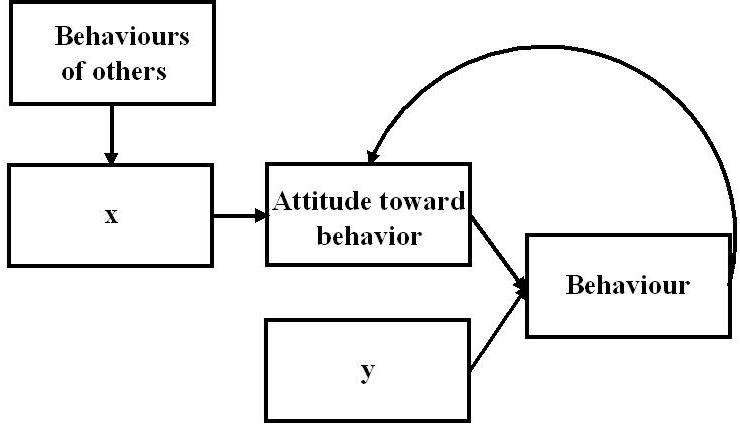
Figure 4. Factors leading the prediction of behaviours and attitude-behaviour relationships in CauxAttitude Formal description of CauxAttitude
- 4.19
- We consider a RPG session as a succession of negotiations between two participants. The agents are randomly chosen at each time step among a set of n agents. The negotiations either concern solution A or solution B.
- 4.20
- Agents can behave in two possible ways:
Initiate a negotiation:
- 4.21
- One of the two agents asks the other for a solution (A or B). The solution is chosen according to the agent's attitudes to the two solutions (aA and aB) and according to x and y.
Suppose (i,j) a pair of agents is randomly chosen among a Population P of agents. Formula (1) describes the initiation of the negotiation.
if aA or aB ≥ 0 if max{ xAi × aAi , xBi × aBi } ≥ yi
if xAi × aAi > xBi × aBi , i asks j for a solution A
if xAi × aAi < xBi × aBi , i asks j for a solution B
if xAi × aAi = xBi × aBi , i chooses a solution at random and asks j for else if max{ xAi × aAi , xBi × aBi } < yi
if aBi< 0, i asks j for a solution A(*)
if aAi < 0, i asks j for a solution B
else, i chooses a solution at random and asks j for it(**)
otherwise, another pair is chosen.
(1) where
aA: Attitude to solution A.
aB: Attitude to solution B. Both attitudes range from -5 (entirely unfavourable) to 5 (entirely favourable).
x ∈ [0,1]: Weight of the factors that imply attitude as a predictor of behaviour.
y ∈ [0,6]: Weight for the agent of other factors than attitude which determine behaviour.
(*): An initiator never asks for a solution when his/her attitude towards it is negative.
(**): We assume that the agent makes a random choice when he/she behaves according to y.
- 4.22
- Let us assume initiator i asks j for solution A, and then his/her attitude then changes due to his/her behaviour. Formula (2) captures the process of revising. The same process is engaged when i asks j for solution B, or if i starts by randomly choosing a solution.
aAi = aAi (t-1)+1
(2) Accepting/rejecting the request
- 4.23
- The receptor j can accept or reject the request. In a similar way, j's answer is influenced by his/her attitude, x and y. Formula (3) describes the response part of the negotiation when i asks j for a solution A.
if xAj × |aAj| ≥ yj and aAj ≥ 0, j accepts and aAj = aAj (t-1)+1 aAj < 0, j rejects and aAj = aAj (t-1)-1 if xAj × |aAj| < yj, j randomly accepts or rejects and j changes his/her attitude as a result.
(3) - 4.24
- We also suppose that the receptor's answer influences the x value of the initiator. Formula (4) describes this feedback process for the same example. Therefore, in this version of the model, x is dynamic and y is static.
if j accepts, xAi = xAi (t-1) + 0,1 xAi ∈ [0;1] if j rejects, xAi = xAi (t-1) - 0,1
(4) When i asks j for solution B or if i starts by choosing a solution at random, formulae (2) to (4) are processed in the same way. The process from (1) to (4) is repeated until the end of simulation. At each time step, a new pair (i,j) is chosen at random.
 Design of simulations
Design of simulations
- 5.1
- Despite its simplicity, we consider that CauxAttitude can at least explore three types of effects of game settings: the choice of participants in a game session, artefacts handled by the game facilitator during the course of the game to fine tune its unfolding, and the number of players. We now explore various initializations of parameters to enable simulations to explore these potential gaming effects.
- Choice of population of participants regarding their initial x, y and attitudes: individuals who play have different initial attitudes, different degrees of confidence in their own attitudes, different perceived behavioural control over the behaviours requested during the game, and so on. In our questionnaires, we observed significant heterogeneity between participants, e.g., participants with high initial confidence in their attitudes, participants with high confidence in their attitudes but only with respect to a few types of solutions, participants with limited confidence in their attitudes, participants with high or low initial attitudes, and so on.
- Certain game constraints which influence the values of x and y: for example, giving (virtual) money to participants can have an impact on their perceived behavioural control of the implementation of a solution. In CauxOpération, at the start of the game, the farmers do not receive any (virtual) money for funding solutions against runoff. However, they can ask the watershed advisor or the mayor for funds.
- Effects of variation of the number of participants.
 Results of simulations
Results of simulations
- 6.1
- Numeric values of the initialization of parameters are listed in a table in each sub-section below.
All our simulations involved 500 steps, which is sufficient to observe possible attractors or convergences of attitudes to an extremity (polarization). We replicated all the simulations 1000 times in order to capture variability, since the model is stochastic. We initialized a and x to their median values (a=0, x=0.5) in order to minimize the effects produced by initialization of parameters that remain the same for all the simulations.
Variation of y
First we simulated four cases (case1a, case1b, case1c and case1d) with different values of y. Table 1 lists the initialization of parameters. Figure 5 shows the proportions of positive and negative updates of attitudes during the negotiations in the four simulations.Table 1: Initialization of parameters for variation of y Case1 n xA xB aA aB y Steps Replicas Case1a 8 0.5 0.5 0 0 0 500 1000 Case1b 8 0.5 0.5 0 0 3 500 1000 Case1c 8 0.5 0.5 0 0 5 500 1000 Case1d 8 0.5 0.5 0 0 6 500 1000 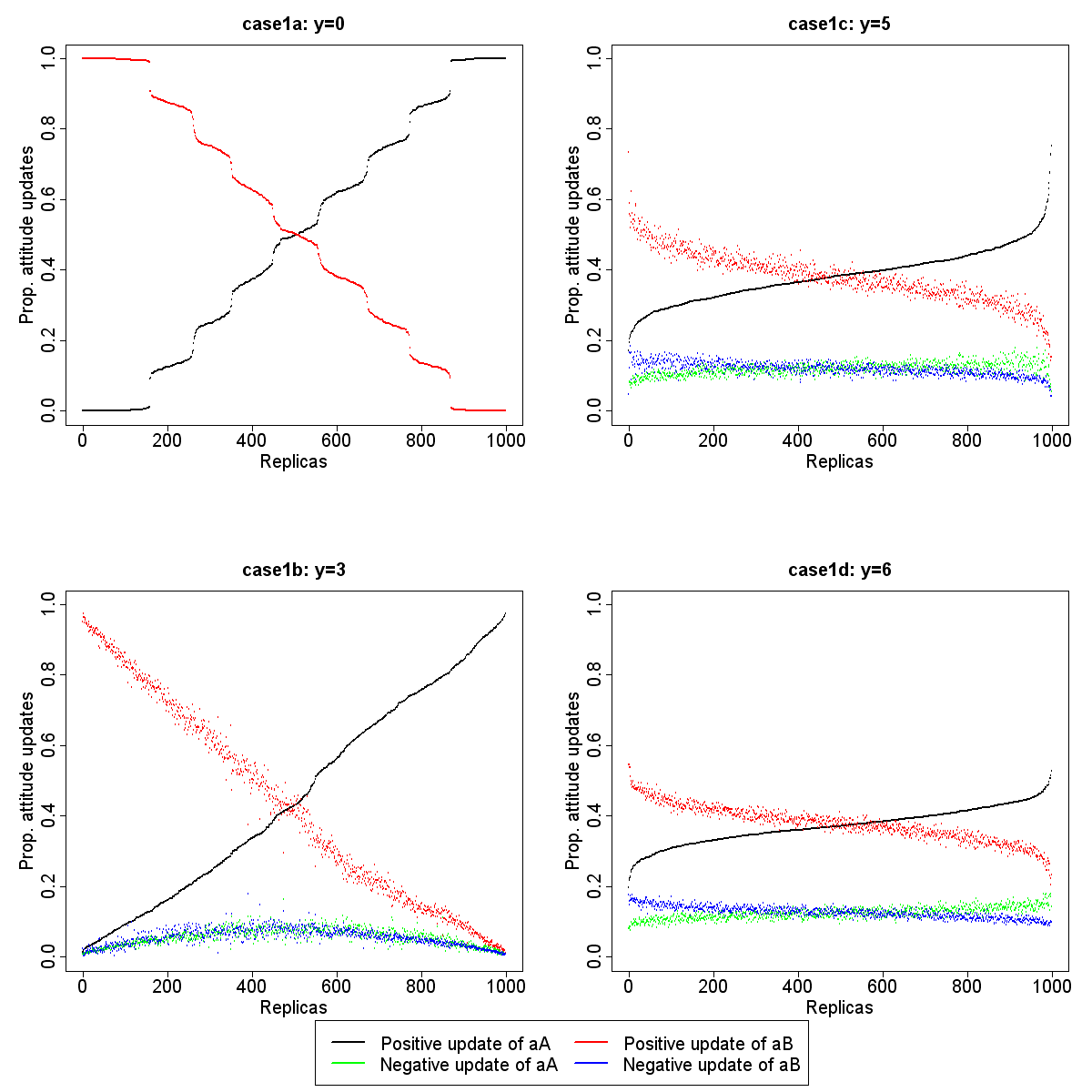
Figure 5. Proportion of positive and negative updates of attitudes during the negotiations in case1a, case1b, case1c and case1d. The replicas are ordered with respect to the positive update of aA. For example: for replica 500 in case1a, 50% of positive updates of aA and 50% of positive updates of aB occur during the negotiations. We also consider cases in which agents had already reached the extreme value of the attitude (5 or -5) and were nevertheless willing to go further as attitude updates - 6.2
- Regarding case1a in Figure 5, only positive updates of attitudes are expressed. Agents' behaviours are only performed in accordance with their attitudes because the condition x × a ≥ y is always satisfied. As the initial attitude values are not negative, receptors of negotiations never reject requests. There are also nine plateaus which reveal the proportion of agents initiating requests for solutions A and the proportion initiating request for solutions B. In this case, it is very difficult for agents to initiate requests for both solutions. Suppose an agent initiating a negotiation for solution A, xA and aA are positively updated (because the receptor accepts the request) and xA × aA (0.6 × 1=0.6) is then greater than xB × aB.(0.5 × 0=0). At this point, the agent has to be designated successively twice as receptor of a request for solution B in order to be able to initiate solution B. Thus, only 5.6% of agents among the 1000 replicas were able to initiate both solutions during one replica. The first plateau refers to replicas in which all agents initiate solution B, the second plateau refers to replicas in which seven agents initiated solution B and one agent in initiated solution A, and so on. The middle of each plateau shows the average proportion per period e.g., when seven agents initiate solution B, the average of positive updates of attitudes concerning solution B is equal to 7/8 (number of agents initiating solution B/number of agents). The non-linear switch from one plateau to the next is due to the fact that according to Gaussian law, the probability of the occurrence of extreme values is low. In fact, each plateau follows a Gaussian law i.e., the middle of the plateau corresponds to the average and the gradient of the plateau gives the deviation. As the model is stochastic, all the replicas belonging to one plateau do not end up with the same proportion of attitude updates.
- 6.3
- In case1b, case1c and case1d, negative updates of attitudes appear but they are still fewer in number than the positive ones, because there are no negative updates of attitudes when agents are initiators. However, there are no more plateaus. As y > 0, stochastic behaviours appear and enable agents to initiate both solutions. Consequently, stochastic behaviours prevent the appearance of plateaus since they were caused by the wish of agents to only initiate the solution they initiated the first time they were engaged in a negotiation in each replica. When y=3 (case1b) or higher, the situation in which some of the population of agents initiates solution A and others initiate solution B is harder to reach. Plateaus can be attractors only if initiators do not receive rejections from the receptors. If they do, their x value decreases and they are likely to change their initiating behaviour (i.e., to initiate the other solution). And when y=3, all the agents have to update their x value at least to 0.6 for the solution they did not initiate in order to avoid rejecting requests (i.e., even if their attitude positively converged, 0.5 × 5 < 3). Consequently, the higher the value of y, the less it is possible for plateaus to be attractors.
- 6.4
- When y=5 or y=6, there is a decrease in heterogeneity between replicas. When behaviours are highly stochastic, the proportion of attitude updates tend to be similar between the replicas because the initiators have an equal probability of choosing solution A or B. Nevertheless, choices are stochastic until x × a reaches the value of y for at least one type of solution. Note than when y=6, behaviours are only stochastic. Also, another attractor can emerge (except for y=6), i.e. group polarization. This refers to a state of the system in which all agents of the population ask receptors for the same type of solution (A or B) until the end of the simulation, and all the receptors accept the requests. Consequently, all agents positively converge to the same attitude, i.e., reach the positive extreme values of x and a (x=1, a=5). Group polarization is achieved when the system reaches a situation defined by several characteristics:
- All agents behave according to their attitudes (versus according to y). In other words, all agents reach x × a≥y.
- All initiators ask receptors for the same solution.
- All receptors accept the requests.
Variation of x and x × y interaction
- 6.5
- We simulated the model taking the extreme values of x in an example in which y=0 and in an example in which y=5. Table 2 summarizes the initialization of the parameters. Figure 6 shows the proportion of positive and negative updates of attitudes that occurred during negotiations in the four simulations.
Table 2: Initialization of parameters for the x variation and x × y interaction Case2 n xA xB aA aB y Steps Replicas Case2a 8 0 0 0 0 0 500 1000 Case2b 8 1 1 0 0 0 500 1000 Case2c 8 0 0 0 0 5 500 1000 Case2d 8 1 1 0 0 5 500 1000 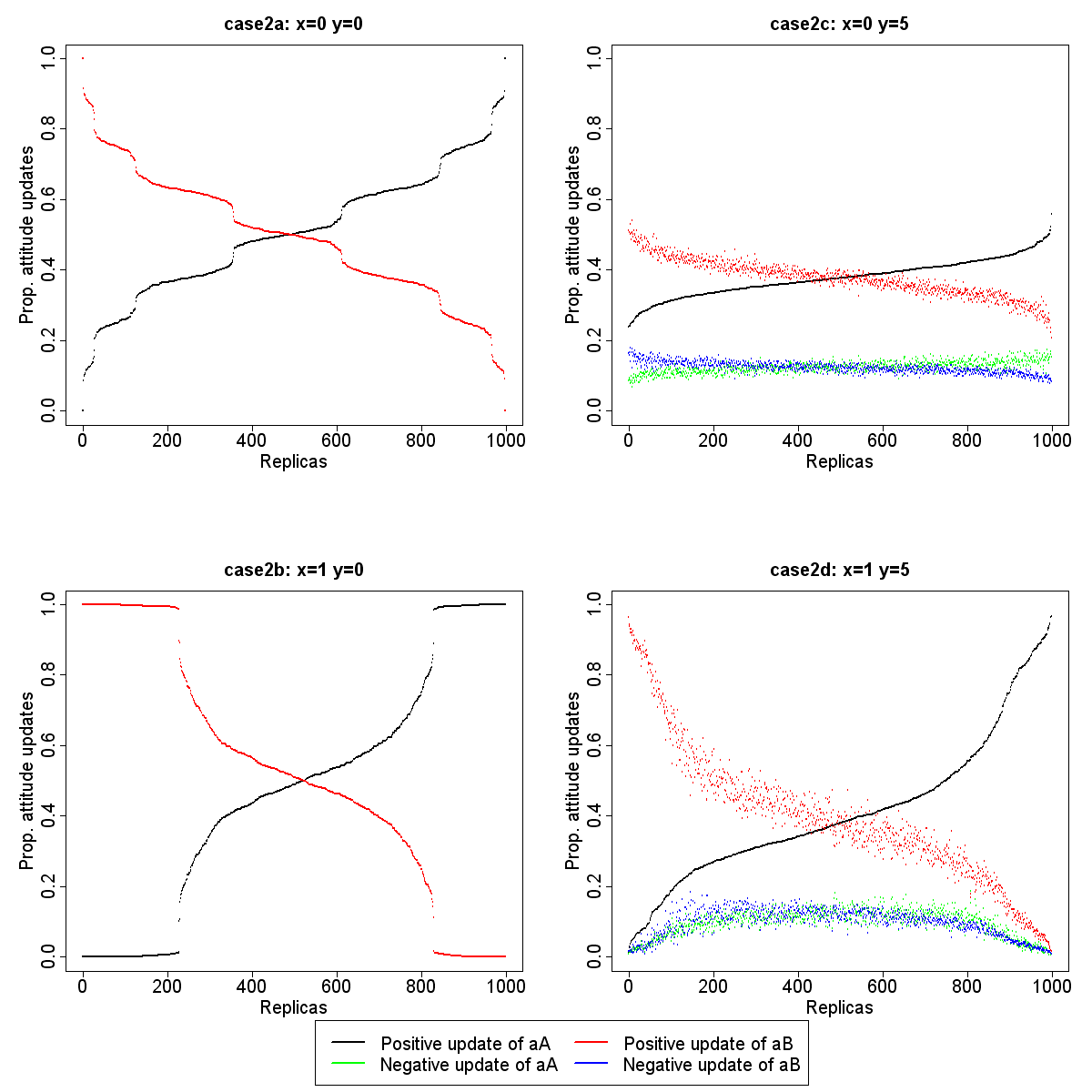
Figure 6. Proportion of positive and negative updates of attitudes during the negotiations in case2a, case2b, case2c and case2d - 6.6
- Regarding case2a in Figure 6, when x=0, plateaus are still present as was the case for case1a with x=0.5 in the previous sub-section. On the other hand, no plateaus correspond to a situation in which 100% of the positive attitude updates were only for one solution for all agents (i.e., group polarization starting from the first time steps. For instance, if the original initiators ask the receptors for solution A, the receptors accept the requests and update their attitudes accordingly. But as x=0 for the receptors, xA × aA = xB × aB and the receptors can still initiate solution B when they switch to the position of initiator.
- 6.7
- When x=1 (case2b), the plateaus corresponding to a group polarization from the first time steps are still present but no other plateaus are visible. As x=1 for both solutions and as the condition implies that agents always accept the requests, all agents positively update both of their attitudes and can then initiate both solutions. The plateaus corresponding to a group polarization from the first time steps correspond to a situation in which the original initiators initiate the same solution. In that case, all attitudes to the negotiated solution become superior to all attitudes to the other solution, and then only the previously negotiated solution will be chosen until the end of the simulation.
- 6.8
- Regarding case2c and case2d, case2c shows the same homogeneous situation as case1c. When x=1 (case1d), the homogeneity is upset because the condition is more favourable for group polarization, i.e., as soon as the value attitude of all agents reaches 5 for the same solution.
Heterogeneity of y among agents
- 6.9
- The value of y can differ among participants. Participants can play different roles during the RPG, and the amount of external constraints (included in y) can be associated with the specific role of each participant.
- 6.10
- We decided to simulate two conditions to explore the potential effect of heterogeneity:
- A condition with a lambda agent (we chose agent2) with y = 0 and y = 5 for the rest of the population (case3b).
- A condition with agent2 with y = 5 and y = 0 for the rest of the population (case3d).
- 6.11
- We focused the results on the proportion of attitude updates by agent2 during the negotiations in which he/she was involved in. We compared these results with the proportion of attitude updates of agent2 when all of the population (including agent2) has the same y value (case3a and case3c). Table 3 summarizes the initialization of parameters for case3a, case3b, case3c and case3d. Figure 7 shows the proportion of attitude updates by agent2 among the four cases.
Table 3: Initialization of parameters for the test of y heterogeneity Case3 n xA xB aA aB y Steps Replicas Ag2 P-ag2 Case3a 8 0.5 0.5 0 0 0 0 500 1000 Case3b 8 0.5 0.5 0 0 0 5 500 1000 Case3c 8 0.5 0.5 0 0 5 5 500 1000 Case3d 8 0.5 0.5 0 0 5 0 500 1000 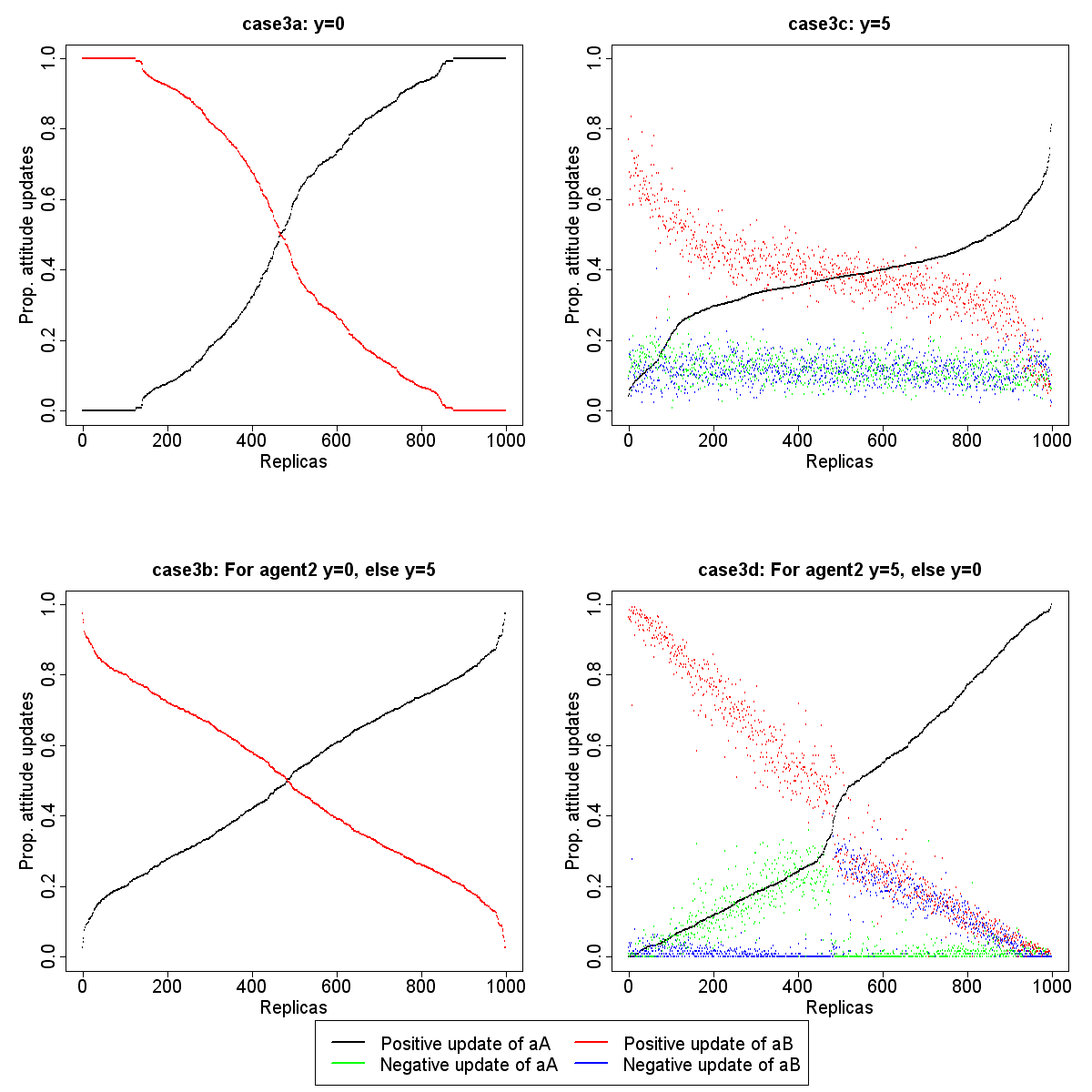 GOES HERE
GOES HERE
Figure 7. Proportion of attitude updates among negotiations by agent2 in case3a, case3b, case3c and case3d - 6.12
- Comparing case3a with case3b, in case3a, agent2 updates more attitudes to one solution than in case3b, in which the curves are nearly linear. In case3a, agent2 is behaving according to his/her attitudes and tends to initiate only one solution because other agents always accept requests (see sub-section "variation of y"). In case3b, agent2 also behaves according to his/her attitudes, but other agents can reject requests from agent2. Consequently, the x values of agent2 can increase and decrease which makes it easy for agent2 to switch between solution A and B during the initiation stage. Agent2 is more likely to massively update only one of its attitudes when other agents also behave according to their attitudes (which are not negatives in this case).
- 6.13
- Comparing case3c and case3d, agent2 performs stochastic behaviours until xA × aA ≥y or xB × aB ≥y. In case3c, other agents also perform stochastic behaviours as they always accept requests in case3d. Consequently, it is harder for agent2 to reach and maintain xA × aA ≥y or xB × aB≥y and then to only positively update one attitude. In case3d, agent2 can easily reach this state and consequently positively updates one attitude. There is also an increase in negative updates of attitudes in case3d. In case3c, agent2 can initiate both solutions while xA × aA ≥y or xB × aB≥y and an agent in the position of initiator always updates attitudes positively. Thus, the proportion of his/her positive updates is greater than the proportion of his/her negative updates. On the other hand, in case3d, agent2 initiates only one solution in most of the time steps. Hence, agent2 is always in the position of receptor for the other solution, and accepts or rejects randomly. Consequently, the positive and negative updates of the attitude towards the solution not initiated by agent2 always appear in the same proportion.
- 6.14
- Considering the four cases, when other agents behave according to their attitudes which are positive, agent2 is likely to positively update one of his/her attitudes to a greater extent than the other.
Variation of the number of agents
- 6.15
- In CauxAttitude, we assumed that eight agents could match the settings of CauxOpération. In CauxOpération (like in other RPGs in companion modelling), the choice of the number of participants is made based on local conditions and the underlying structure of the model, and not because of anticipation of effects that could impact on the outcomes for participants, such as attitudes. We assume that such variation can influence the attitude dynamics in CauxAttitude. In this section we assess the effects produced by variation of the number of participants in two conditions: when y is low and when y is high. We simulated the model with very few agents (2 and 3) and with many agents (100) in order to get the most extreme effects. Table 8 summarizes the initialization of parameters. Figure 8 shows the proportion of positive and negative updates of attitudes during the negotiations between 2, 3 and 100 agents and with y=0. Figure 9 shows the proportion of positive and negative updates of attitudes during the negotiations between 2, 3 and 100 agents and with y=5.
Table 8: Initialization of parameters for the test of the variation of the number of agents Case4 n xA xB aA aB y Steps Replicas Case4a 2 0.5 0.5 0 0 0 500 1000 Case4b 3 0.5 0.5 0 0 0 500 1000 Case4c 100 0.5 0.5 0 0 0 500 1000 Case4d 2 0.5 0.5 0 0 5 500 1000 Case4e 3 0.5 0.5 0 0 5 500 1000 Case4f 100 0.5 0.5 0 0 5 500 1000 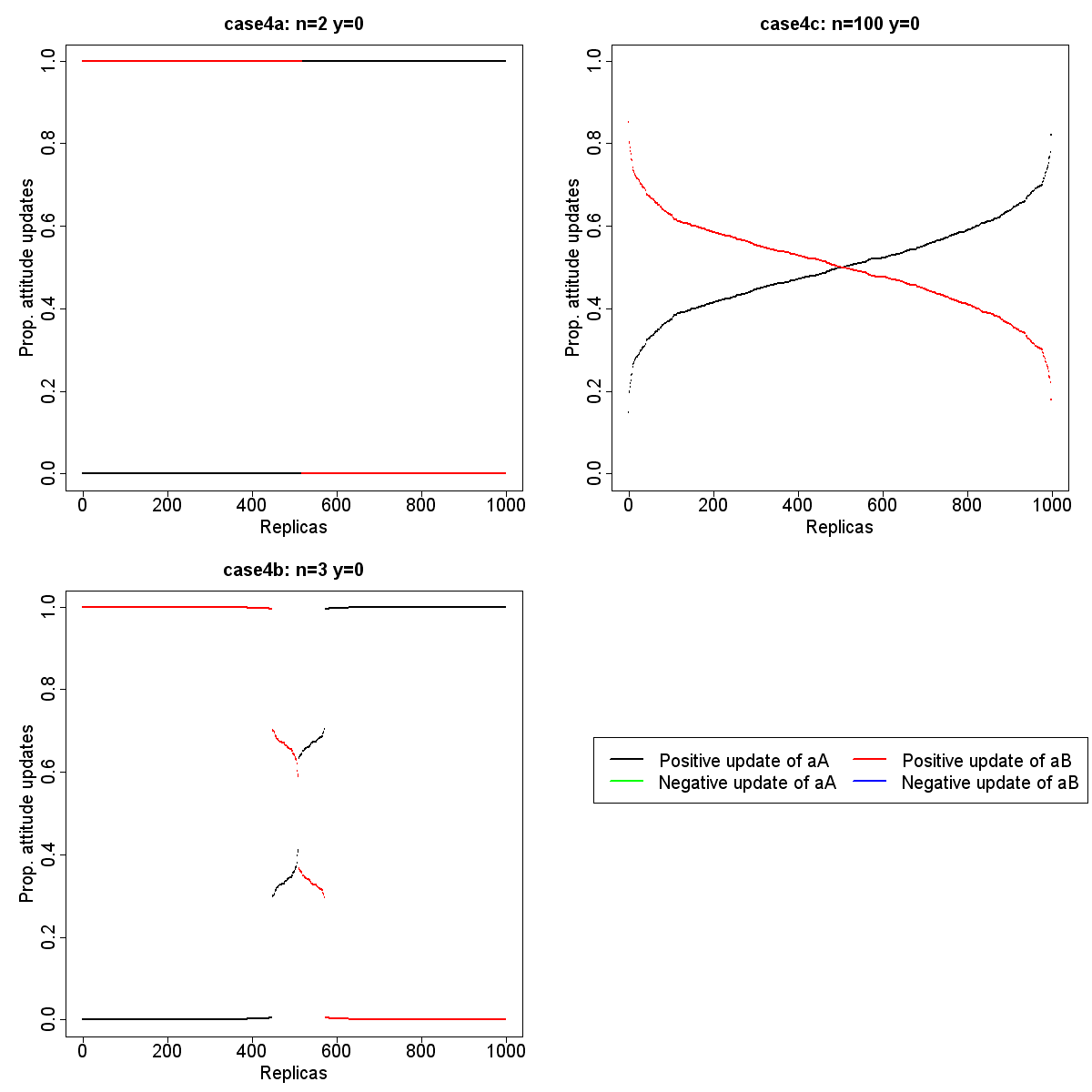
Figure 8. Proportion of positive and negative updates of attitudes during negotiations in case4a, case4b and case4c 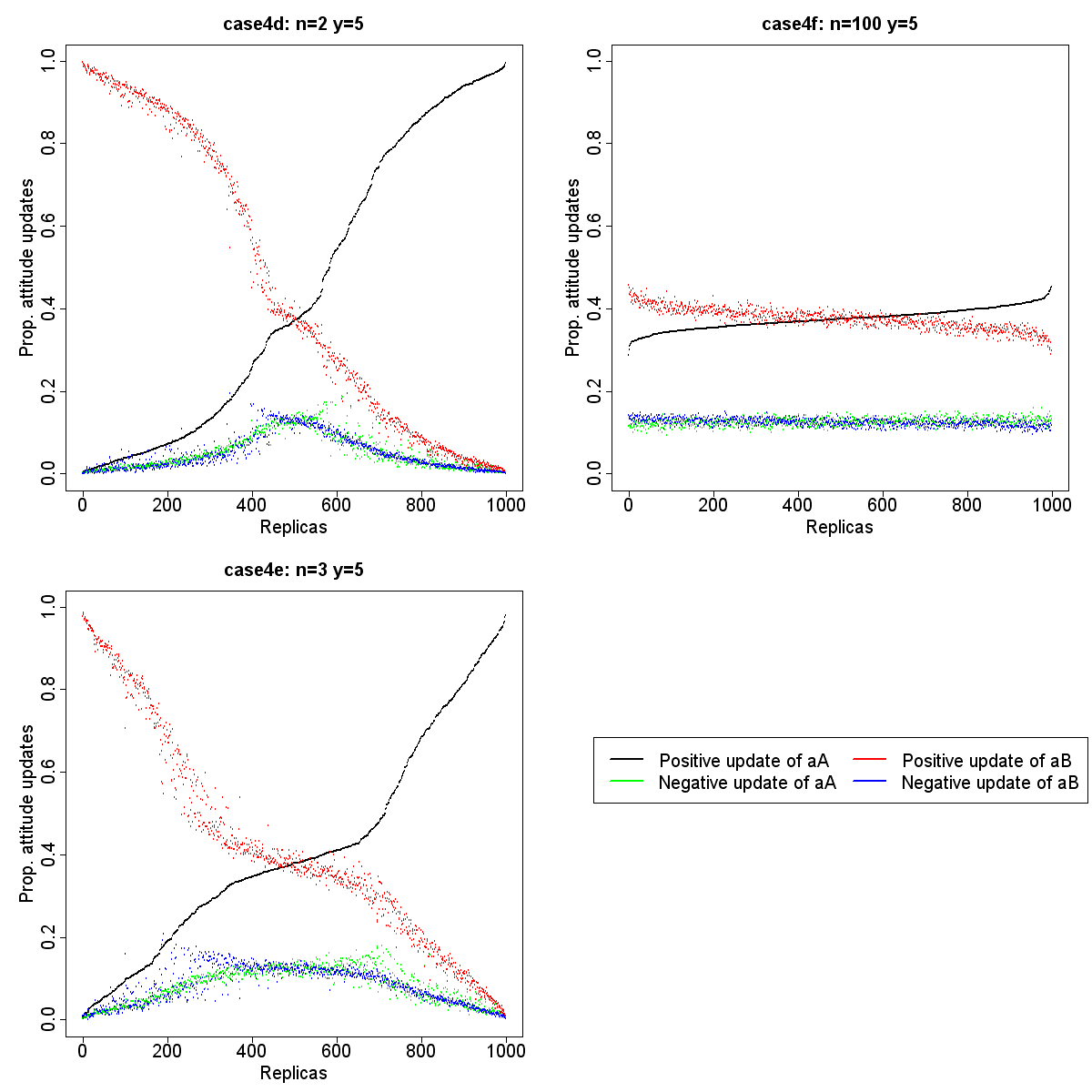
Figure 9. Proportion of positive and negative updates of attitudes during negotiations in case4d, case4e and case4f - 6.16
- Case4a in Figure 8 shows that when there are only two agents and when the agents behave according to their attitudes, only one solution is discussed and subsequently only one attitude is updated (group polarization). This is because when the first agent asks for a solution, the second accepts and updates his/her corresponding attitude. When the second agent then needs to initiate, he/she will do so according to this attitude. When three agents are involved (case4b), only one solution is also usually discussed but in approximately 10% of the replicas both solutions are discussed: the agent who did not take part in the negotiation can still initiate the solution not previously discussed. With 100 agents (case4c), both solutions are discussed and the variation between replicas is linear.
- 6.17
- Case4d in Figure 9 shows that when there are only two agents involved and when their behaviours are stochastic until xA × aA ≥ y or xB × aB > y, in the majority of replicas, only one attitude is updated. In fact, when both agents reach xA × aA ≥ y or xB × aB > y, they will discuss and accept requests only concerning this solution. This effect is reduced when there are three agents, and completely disappears when 100 agents are involved. The fewer the agents, the easier it is for all agents to reach xA × aA ≥y or xB × aB ≥ y.
 Discussion of the results of simulations and their implication for RPGs
Discussion of the results of simulations and their implication for RPGs
- 7.1
- In this section, we come back to the results of simulations of CauxAttitude and explain how these results can help understand the influence of the game setting on outcomes in situation such as CauxOpération sessions. As explained earlier, we designed simulations based on the effects of game settings that CauxAttitude was already able to explore through variation of its parameters.
- 7.2
- Globally, our results displayed different shaped outcomes for possible attitude updates. These shapes represent a set of the possible outcomes with respect to different parameter initialization. The differences between the shapes indicate the effects of the game setting which we investigated through the different initialization of parameters. In addition, the relative simplicity of the model enabled us to understand the processes responsible for creating the different shapes.
- 7.3
- The shapes of dynamic outcomes identify the attractors that the underlying mechanisms can lead to. In summary, our results explain how a game setting can have effects (here on attitudes) and how it can determine the dynamics of the system.
- 7.4
- Regarding the variation of y in case1, it will be recalled that, for the agent, y is the weight of all factors other than attitudes that determine behaviours. It is the aggregation of subjective norms, perceived behavioural control and all other factors that compete with attitude in influencing behaviours. For the participants in a RPG session, the value of y can be due to the choice of the population of participants by the game designer, e.g., people who strongly or weakly account for perceived behavioural control of this topic. It also can be due to game constraints the participants face, e.g., the rules that state which role to endorse, whether funding is available (or not) and so on. In CauxAttitude, a high value of y captures conditions in which these factors strongly influence behaviours, whereas a low value of y captures conditions in which these factors have a weak impact on behaviours.
- 7.5
- In the results of simulations, we identified three differently shaped representations of outcomes:
- Plateaus: the range of possible outcomes is framed in succession of plateaus revealing the number of agents who initiate each solution. This framing is observed when agents only behave according to their attitudes.
- Linear: the range of possible outcomes gives all the possible final proportions of positive updates of attitudes among the replicas. This occurs when agents behave both according to their attitudes and to other factors.
- Homogeneous: the range of possible outcomes is framed in homogeneous proportions of positive updates of attitudes. This framing is observed most often when factors other than their attitudes influence the behaviour of the agents.
- 7.6
- In a case in which a population of individuals has no previous attitude towards the solutions proposed in a negotiation process like in CauxAttitude (original attitudes are equal to 0), the variation in the weight of factors other than attitudes in influencing behaviours induces different framings expressed by different range of possible outcomes.
- 7.7
- Regarding the underlying processes responsible for these attractors, plateaus are due to the difficulty agents have in initiating both solutions when they only behave according to their attitudes. The introduction of additional factors that influence behaviours (captured by adding stochastic behaviours in CauxAttitude) means the range of what is possible can be extended because agents are able to initiate both solutions when they do not behave according to their attitudes. Nevertheless, if the weight of the additional factors is too high, individuals will have difficulty obtaining preferential behaviours and will tend to update their different attitudes to the same extent, which is also a framing.
- 7.8
- In RPGs in the field of companion modelling, the game designer chooses the population of participants and designs the rules of the game based on his/her own constraints. For instance, as RPGs are new methods of resource management and are not yet very well known, it may happen that some stakeholders are reluctant to participate. In this case, the number of participants needed to hold a RPG session may simply be the number of potential participants who agreed to come.
- 7.9
- Nevertheless, even though the game designer's freedom of movement regarding the game design is sometimes limited, as our results show, it can lead to an implicit orientation of game session outcomes and hence to manipulation of participants' attitudes.
- 7.10
- Regarding the variation of x (weight of the factors that imply attitude as a predictor of behaviour) and the interaction x*y in the case2, the different initial values of x can be due, as well as y, to:
- The choice of the population: e.g., strongly or weakly motivated people, people with a high degree of confidence (or the reverse) in their attitude;
- Game constraints set by game designers: e.g., the game may encourage (or discourage) the expression of attitudes when requiring discussion among players.
- 7.11
- When agents have a low value of x, the shapes of dynamic outcomes are mostly influenced by the value of the weight of factors other than attitudes in influencing behaviours: plateaus and the homogeneous situations again appear. Conversely, a high value of x favours group polarization and influences the outcome dynamics by favouring positive attitude updates of one solution. Once again, the game designer's freedom of action in recruiting participants can also influence the attitudes of participants depending on the factors included in x, such as confidence or motivation.
- 7.12
- In CauxOpération, heterogeneity of y between agents refers to the choice of a heterogeneous population or to different designs for roles implying different game constraints. According to the results of our simulations, when a participant is surrounded by a homogeneous population of participants behaving according to their attitudes, the participant is more likely to form a preferential attitude and to behave according to this attitude, even when he/she is strongly influenced in his/her behaviours by factors other than attitudes. In this case, the influence of others also increases the negative updates of attitudes of the isolated participant. In summary, our results suggest that whatever an isolated participant thinks and acts, the majority has implicit power to apply pressure that can influence the range of possible outcomes for the minority.
- 7.13
- Regarding the variation in the number of agents, results of simulations suggest that whether or not participants behave according to their attitudes, the fewer the participants there are, the more group polarization tends to emerge. Although the number of participants is chosen in accordance with local needs the game designer should keep in mind the potential influence of this factor on attitude change.
 Conclusion
Conclusion
- 8.1
- CauxAttitude is a theoretical model that uses a specific point of view through filters of chosen social psychology theories including simplification. Thus, our model provides knowledge on the mechanisms underlying the effects of game settings. Because the model is very simple, it can capture some of the underlying cognitive and social mechanisms that may occur in RPGs, and hence explore how game setting effects can direct a game toward specific outcomes. We chose to focus on the attitude change processes that occur in one particular RPG, CauxOpération. We developed our model based on individual processes of attitude change and attitude-behaviour relationships analyzed in social psychology. We modelled interactions between agents on the basis of observations, questionnaires and interviews with participants during real game sessions of CauxOpération.
- 8.2
- From a methodological point of view, to cope with the lack of laboratory data, we designed our model in two stages. Individual processes are represented on the basis of simplifications of widely accepted psychological theories. Inter-individual processes in the model were designed based on field observations. This proved to be an appropriate way to develop a coherent model and to improve our understanding of a social system that accounts for certain psychological processes.
- 8.3
- Regarding the results of simulations based on variations of the parameters, we show that some game settings have a significant impact on the attitude dynamics and may consequently generate biases in game outcomes:
- The choice of the population of participants and specific game constraints influence factors other than attitude in framing participants' behavioural patterns. Hence the participants' attitudes are limited to a subset of what is theoretically possible. Game settings also frame attitudes which themselves influence participants' behavioural patterns, thus reducing the range of possible outcomes, including cases of group polarization when this influence is high.
- At a collective level, an isolated participant is also pushed towards a preferential attitude when the majority of participants behave according to their own attitudes, without really taking other factors into account.
- The number of participants/agents affects how the group reaches polarization: the smaller the number, the higher the probability of group polarization.
- 8.4
- Our results show that the joint use of social psychological theories and agent based simulations can provide new ways of considering game design. Exploration of scenarios through simulations strengthens the original game design through ex ante identification of potential biases. For example, the number and abilities of the participants in the RPG are generally chosen based on local constraints. As a result, fulfilling the objectives of the game designed to fit local constraints may generate undesirable changes in attitude (in RPGs where attitude change may be the specific objective of the game but also when attitude change is only a side effect of the RPG). Being aware of these possible biases, the game designer can try to exert less influence/introduce fewer biases when designing the game.
- 8.5
- For further studies, we need to add new parameters to the model to investigate other kinds of game settings, such as participants' feedback on their actions or new conditions of interactions.
- 8.6
- We developed CauxAttitude based on a specific game, CauxOpération. However, as mentioned in the introduction, RPGs and other facilitated discussion sessions are being increasingly used for so-called "wicked problems" (Rittel and Weber 1973). CauxAttitude is potentially suitable for the whole range of artefacts as long as they can be reduced to a series of elementary binary negotiations. Upgrading to negotiations with n-participants could be explored quite easily to fit a wide range of situations.
 Acknowledgements
Acknowledgements
- This work has been carried out with the financial support of the Seine-Normandie water agency. We would also like to thank Frédéric Amblard, Marianne Cerf and Sylvie Huet for their helpful comments.
 References
References
-
AJZEN, I. (1991). The theory of planned behavior. Organizational Behavior and Human Decision Processes, 50, 179-211. [doi:10.1016/0749-5978(91)90020-T]
AJZEN, I. (2004). Theory of planned behavior. In A. N. B. (Ed.), Encyclopedia of health and behavior (Vol. 2, pp. 793-796). Thousand Oaks: Sage Publications. [doi:10.4135/9781412952576.n208]
AJZEN, I., & Fishbein, M. (1980). Understanding attitudes and predicting social behavior. Englewood Cliffs: Prentice-Hall.
ALBARRACIN, D., & Wyer Jr., R. S. (2000). The cognitive impact of past behavior: influences on beliefs, attitudes, and future behavioral decisions. Journal of Personality and Social Psychology, 79(1), 5-22. [doi:10.1037/0022-3514.79.1.5]
BARRETEAU, O., Bots, P. W. G., & Daniell, K. A. (2010). A framework for clarifying "participation" in participatory research to prevent rejection of participation for bad reasons. Ecology and Society, 15(2), 22.
BARRETEAU, O., Le Page, C., & Perez, P. (2007). Contribution of simulation and gaming to natural resource management issue. Simulation and Gaming, 38(2), 185-194. [doi:10.1177/1046878107300660]
BEM, D. J. (1965). An experimental analysis of self-persuasion. Journal of experimental social psychology, 1(3), 199-218. [doi:10.1016/0022-1031(65)90026-0]
BEM, D. J. (1972). Self-perception theory. In L. Berkowitz (Ed.), Advances in experimental social psychology (Vol. 6, pp. 2-57). New York: Academic press. [doi:10.1016/s0065-2601(08)60024-6]
BENTLER, P. M., & Speckart, G. (1979). Models of attitude-behavior relations. Psychological review, 86(5 ), 452-464. [doi:10.1037/0033-295X.86.5.452]
CIALDINI, R. B. (1988). Influence: Science and practice. Glenview: Scott, Foresman.
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2001). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(1-4), 87-98.
DEVINE, P. G. (1989). Automatic and controlled processes in prejudice: The role of stereotypes and personal beliefs. In A. R. Pratkanis, S. J. Breckler & A. G. Greenwald (Eds.), Attitude structure and function (pp. 181-212). Hillsdale: Erlbaum.
DOLL, J., & Ajzen, I. (1992). Accessibility and Stability of Predictors in the Theory of Planned Behavior. Journal of Personality and Social Psychology, 63(5), 754-765. [doi:10.1037/0022-3514.63.5.754]
DUBOIS, E., Huet, S., & Deffuant, G. (2007). Primacy effect with symmetric features propagating in a population, ESSA, The fourth conference of European Social Simulation Association (pp. 71-82): Frédéric Amblard.
EAGLY, A. H., & Chaiken, S. (Eds.). (1993). The psychology of attitudes. Orlando: Harcourt Brace Jovanovich College Publishers.
ETIENNE, M. (Ed.). (2010). La modélisation d'accompagnement : une démarche participative en appui au développement durable. Paris, France: QUAE.
FESTINGER, L. (1957). A theory of cognitive dissonance. Stanford: Standford University Press.
FESTINGER, L., & Carlsmith, J. M. (1959). Cognitive consequences of forced compliance. Journal of Abnormal Psychology, 58(2), 203-210. [doi:10.1037/h0041593]
GALAM, S. (2003). Modelling rumors: The no plane pentagon french hoax case. Physica A., 320, 571-580. [doi:10.1016/S0378-4371(02)01582-0]
GLASMAN, L. R., & Albarracin, D. (2006). Forming attitudes that predict future behaviors: A meta-analysis of the attitude-behavior relation. Psychological Bulletin, 132(5), 778-822. [doi:10.1037/0033-2909.132.5.778]
GRIEVE, W. (2001). Traps and gaps in action explanation: Theoretical problems of a psychology of human action. Psychological review, 108(2), 435-451. [doi:10.1037/0033-295X.108.2.435]
HOGARTH, R. M., & Einhorn, H. J. (1992). Order effects in belief updating: The belief-adjustment model. Cognitive Psychology, 24(1), 1-55. [doi:10.1016/0010-0285(92)90002-J]
JAGER, W., & Amblard, F. (2007). Guess you're right on this one too: Central and peripherical processing in attitude changes in large populations. In S. Takahashi, D. Sallach & J. Rouchier (Eds.), Advancing Social Simulation (pp. 249-260): Springer. [doi:10.1007/978-4-431-73167-2_23]
JANIS, I. L., & King, B. T. (1954). The influence of role playing on opinion change. J Abnorm Psychol, 49(2), 211-218. [doi:10.1037/h0056957]
KELMAN, H. C. (1953). Attitude change as a function of response restriction
Human relations, 6(3), 185-214. [doi:10.1177/001872675300600301]
MOSLER, H. J., Shwarz, K., Ammann, F., & Gutcher, H. (2001). Computer simulation as a method of further developing a theory: Simulating the Elaboration Likelihood Model. Personality and social psychology review, 5(3), 201-215. [doi:10.1207/S15327957PSPR0503_2]
NOWAK, A., Szamrej, J., & Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological review, 97(3), 362-376. [doi:10.1037/0033-295X.97.3.362]
OUELETTE, J. A., & Wood, R. (1998). Habit and intention in everyday life: the multiple processes by which past behavior predicts future behavior. Psychological Bulletin, 124(1), 54-74. [doi:10.1037/0033-2909.124.1.54]
PETERS, V., & Vissers, G. A. N. (2004). A simple classification model for debriefing simulation games. Simulation & Gaming, 35(1), 70-84. [doi:10.1177/1046878103253719]
PETTY, R., & Cacioppo, J. T. (1986). Communication and persuasion: Central and peripheral routes to attitude change: NewYork: Springer-Verlag.
RICHETIN, J., Sengupta, A., Perugini, M., Adjali, I., Hurling, R., Greetham, D., et al. (2010). A micro-level simulation for the prediction of intention and behavior. Cognitive Systems Research, 11(2), 181-193. [doi:10.1016/j.cogsys.2009.08.001]
RITTEL, H. W. J., & Weber, M. M. (1973). Dilemmas in a general theory of planning. Policy sciences, 4(2), 155-169. [doi:10.1007/BF01405730]
RONIS, D. L., Yates, J. F., & Kirscht, J. P. (1989). Attitudes, decisions, and habits as determinants of repeated behavior. In A. R. Pratkanis, S. J. Breckler & A. G. Greenwald (Eds.), Attitude structure and function. Hillsdale: Lawrence Erlbaum Associates.
RYAN, T. (2000). The role of simulation gaming in policy making. Systems Research and Behavioral Science, 17(4), 359-364. [doi:10.1002/1099-1743(200007/08)17:4<359::AID-SRES306>3.0.CO;2-S]
SAPP, S. G. (2001). Non-rationality in belief sets: Implications for the theory of rational expectations. Social Behavior and Personality, 29(4), 337-345. [doi:10.2224/sbp.2001.29.4.337]
SIMON, H. A. (1955). A behavioral model of rational choice. Quarterly Journal of Economics, 69(1), 99-118. [doi:10.2307/1884852]
SOUCHERE, V., Millair, L., Echeverria, J., Bousquet, F., Le Page, C., & Etienne, M. (2010). Co-constructing with stakeholders a role-playing game to initiate collective management of erosive runoff risks at the watershed scale. Environmental Modelling & Software, 25(11), 1359-1370. [doi:10.1016/j.envsoft.2009.03.002]
TRIANDIS, H. C. (1977). Interpersonal behavior. Monterey: Brooks/Cole.
TRIANDIS, H. C. (1980). Values, attitudes, and interpersonal behavior. In H. E. Howe Jr. & M. M. Page (Eds.), Nebraska symposium on motivation (Vol. 27, pp. 65). Lincoln: University of Nebraska Press.
TSUCHIYA, S. (1998). Simulation/gaming as an essential enabler of organizational change. Simulation & Gaming, 29(4), 400-408. [doi:10.1177/104687819802900403]
TVERSKY, A., & Kahneman, D. (1986). Rational Choice and the Framing of Decisions. The Journal of Business, 59(4), 251-278. [doi:10.1086/296365]
URBIG, D. (2003). Attitude dynamics with limited verbalisation capabilities. Journal of Artificial Societies and Social Simulation (JASSS), 6(1), 2 https://www.jasss.org/6/1/2.html.
VOINOV, A., & Bousquet, F. (2010). Modelling with stakeholders. Environmental modelling and software, 25(11), 1168-1191. [doi:10.1016/j.envsoft.2010.03.007]
WILLIAMS, R. H., & Williams, A. J. (2010). One for All and All for One: Using Multiple Identification Theory Simulations to Build Cooperative Attitudes and Behaviors in a Middle Eastern Conflict Scenario. Simulation & Gaming, 41(2), 187-207. [doi:10.1177/1046878108319931]