 Abstract
Abstract
- We employ a multimodal logic in a decision making mechanism involving trust and reputation. The mechanism is then used in a community of interacting agents which develop cooperative relationships, assess the results against several quality criteria and possibly publish their beliefs inside the group. A new definition is proposed for describing how an agent deals with the common reputation information and with divergent opinions. The definition permits selecting and integrating the knowledge obtained from the peers, based on their perceived trust, as well as on threshold called critical mass. The influence of this parameter and of the number of agents supporting a sentence over its adoption are then investigated.
- Keywords:
- Agent Based Social Simulation, Trust, Reputation, Cognitive Modeling, Multi-Modal Logic
 Introduction
Introduction
- 1.1
-
In order to maximize their performance, both human and software agents usually need to rely on the abilities or information provided by their peers. Since it is very likely to interact with previously unknown partners, assessing their trustworthiness is of maximum importance. Quite a few mechanisms and formalisms have been designed to cope with this. Trust gains momentum in a number of different areas of research such as multi-agent systems cooperation and delegation (Pinyol et al. 2012), reliable knowledge integration in the Semantic Web (Antoniou & van Harmelen 2008), or service oriented architectures (Uddin et al. 2009).
- 1.2
-
Informally, trust could be regarded as a type of attitude an agent has towards the future evolution of the events she depends upon, which are beyond her control and whose result may be either positive or negative (Gambetta 1988). Therefore trust is a subjective assessment of the potential event outcomes and risks involved by relying on a partner. On the other hand, reputation could be seen as a collective assessment of the same aspects, which is shared by a group of agents. Both trust and reputation are connected to each other and proved to be of high importance for making sensible decisions in multi-agent systems.
- 1.3
-
The goals of the research we pursued were twofold. First, we employed a multimodal logic based on agent trust for grounding an operational decision making mechanism. This serves for selecting the sentences to be adopted as beliefs by an agent and further to make decisions based on them. Then, we dealt with the problem of extending this mechanism with reputation. This is done by modifying the definition of this notion in a manner which allows selecting reliable partners in the group of acquaintances and integrating the knowledge obtained from them. The impact of the newly proposed definition over an agent's internal beliefs over time is then assessed. Reputation modeling gains more and more importance with the development of online social networks which allow consumers to share their information and opinions concerning the purchasing experiences. Coping with the bunch of opinion providers becomes a central issue for nowadays e-commerce. This paper aims to contribute at developing a logic-based approach of this problem.
- 1.4
-
The rest of the paper is organized as follows.
Section 2 introduces the basics of trust modeling for multiagent systems.
After a briefing of the multi-agent paradigm and possible applications, a description of the e-commerce trust and reputation issues is given in subsection 2.1.
The next subsection 2.2 introduces our illustrative running scenario, followed, in subsection 2.3, by a presentation of the multi-modal logic we employed in order to model the scenario details.
Extending the approach for dealing with the notion of reputation, besides trust, is discussed in Section 3.
The influence of the critical mass and number of agents supporting a sentence over its adoption is then assessed. Details about the SPASS implementation of the model and the issues it helps to solve are given in Section 4.
Section 5 positions our work within the context of the state-of-the-art models for trust and reputation and Section 6 presents the conclusions and intended future developments.
 Multiagents Technology and Trust for e-Commerce
Multiagents Technology and Trust for e-Commerce
- 2.1
-
In (Shoham & Leyton-Brown 2008), multiagent systems are defined as "systems that include multiple autonomous entities with either diverging information or diverging interests, or both". Typically, these entities perceive their environment through sensors and act upon it through effectors. Agents are autonomous to some extent, having control over their own behavior, but they are not fully independent as they must fullfill their goals in a manner consistent with their knowledge, perceptions and effectual capabilities at the moment they make that choice. In our example, this would mean to buy the book with the lowest price among all books which meet all other specified quality criteria. No agent is expected to be omniscient or omnipotent. Therefore, agents often have to rely on their peers for cooperating in order to achieve some complex task, for obtaining information they do not possess etc. That means agents will have to adopt supplementary goals as a part of their teamwork, to trade knowledge and capabilities, to be able to communicate with their partners and to model, to learn and to reason over their peers' behavior. Meeting those desiderata is a challenge both for human and artificial agents.
- 2.2
-
The Belief-Desire-Intention architectural model assumes each agent has a set of current beliefs over the current state of environment, a set of desires which are basically the objectives s/he wants accomplished and a set of intentions, consisting of the states of affairs s/he has committed to trying to bring about in the next moment. Beliefs are subject to revision according to the perceptual input and their previous values. Intentions are selected on the basis of current beliefs, desires, and prior intentions and achieved by executing the atomic actions the agent is able to perform.
- 2.3
-
A set of intelligent agents could engage in an electronic commerce activity on the behalf of their human owner, e.g., to monitor goods available for sale in on-line shops, collect opinions on their quality and delivery terms, then purchase the best one. Such an agent will have to know their owner's preferences for products, quality and budget, as well as the similar agent's behavior when it will interact with them (e.g., auctioning, negotiating with the sellers etc.). Collecting high quality knowledge of this type would require building models of the peers' reliability in terms of trust and/or reputation.
Trust Modeling
- 2.4
-
In the pre-digital era of marketing, it become nearly common sense the idea that an unhappy customer will complain to at least five others. Nowadays, this number highly increased due to the possibility of on-line assessment publishing, where the "word of mouth" has been replaced by the "word of mouse". This also came with the possibility of review manipulation, as shown by the episode when the Canadian Amazon website revealed by mistake the identity of some of people who authored book reviews. Some of them turned out to be either publishers of the books themselves or competitors (Jøsang 2009). Therefore, the need of formalisms and instruments able to cope with credibility and reputation in on-line communities.
- 2.5
-
In the centralized approach, systems collect in a single point and then aggregate all ratings received by an agent from prior interactions. This is the case with some sites in the field of e-commerce like eBay 1 or Amazon 2, medicine 3, or even product review collecting sites like epinions 4. The final result depends on the ratio between the number of favorable ratings and of total number of ratings. In the case of distributed approach, e.g., the Rummble recommendations engine 5, agents do not post all their observations and assessments in the same place, but forward them from one to another across a web of trust. Here, both the ratings and the network topology can influence the final result.
- 2.6
-
A twice-yearly survey conducted by Nielsen Global Online 6 showed that consumers trust real friends and virtual strangers the most. Two interesting observations on the customer habits when it comes to confidence arise. First, according to the cited source, 90% of the customers trusted "completely" or "somewhat" the recommendations from people they know. Recommendations by known people outperformed with about 20% the second most trusted source of information, namely the opinions posted by consumers on-line (which usually are not the customer's personal acquaintances). Second, brand websites scored the same as on line consumer opinions. The survey has been conducted on a number slightly over 25,000 of Internet consumers from 50 countries and it is, to our knowledge, the most extensive survey of this type to date. These two things show the importance of reputation in a community from the customers' behavior perspective, hence the need for a formal approach.
- 2.7
-
Two main research lines have emerged in this area. On one hand, we have the mechanisms designed for numerical evaluation of an agent's trustworthiness. This is based on a combination between his recorded prior performances and on peers' opinions.
- 2.8
-
An alternative promising approach is the socio-cognitive model of trust described in (Falcone & Castelfranchi 2010). It struggles to avoid over-simplification of some other approaches, and among them:
- reducing trust to predictability by simply performing statistical analysis over the previous experiences and neglecting competence;
- replacing trust with expectation of good behavior of the peer and neglecting the aspect of trust as decision;
- carelessly collapsing opinions and/or experiences in order to obtain a subjective probability
- 2.9
-
The socio-cognitive model of trust takes into account, in an integrated manner, both agent beliefs and actions, together with their social effects and dynamics over time. It builds an explicit representation of the trust ingredients: the trustor i,
her goal φ,
the trustee j,
his potential action a,
together with i
's beliefs that j
is capable to do a,
intends to do it and, by doing so, will ensure the fulfillment of the goal φ
.
The proposed theory focuses on the truster's ascription of some relevant properties concerning the trustee (e.g. capabilities, intentions, dispositions etc.) as well as the environment in which the trustee is going to act, which are together sufficient to ensure that one of the truster's goals will be achieved (Castelfranchi & Falcone 2010).
- 2.10
-
Trust ingredients are further modeled using a modal logic (Herzig et al. 2010). We adopted the socio-cognitive model for our research and tried to expand the approach in two ways. First, we elaborated on the way the formalism can be used for making sensible decisions in an e-commerce like scenario. Second, we proposed extending the definitions in order to capture the reputation based layer of interaction and assessed their influence over belief adoption.
Running Scenario
- 2.11
-
The issues we try to address with our model are illustrated in the following general scenario.
- 2.12
-
Professor Y
will teach a new course the next year and she thinks of adopting book B
as a textbook. She intends to study the book in detail before making the decision, so she decides to buy a copy for herself as soon as possible. The copy must be in good condition (but excellent condition is acceptable as well!), while the price should be low. We assume for both quality criteria (i.e., condition and price), a finite set of mutually disjoint values is defined, namely
{medium, good, excellent}
for quality and
{low, average, high}
for price. The meaning of each value labels and assumed to be known to each agent in the community, together with the order relationship defined among them (
medium < good < excellent
and
low < average < high
respectively).
In the first stage of the scenario, a copy of the book is on sale on Amazon at a low price, by ann
. Supplier ann
is known by Y,
as she has already bought some books from her before.
- 2.13
-
After a careful examination, professor Y
decides to adopt the textbook B
and to order a number of copies for the University library. This time, the only acceptable condition for the books is
excellent,
but the price could be average
or low
. More, the book supplier must be able to offer copies of the book whenever needed. Professor Y
can address one of the bookstores suggested by the publisher of the book, but unfortunately she has never had any interaction with any of them before. In this case, she might talk first to her colleagues
paula, ralph, sue, ted
and ursula
in order to get reputation information about the book supplier.
Preliminaries of Multimodal Logic
- 2.14
-
The current Section briefly presents the language
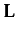 and axioms of the multimodal logic that are implemented and used in our running example. For formal proofs of the properties and any further details, we refer the reader to (Herzig et al. 2010).
Definition 2.1 ( Syntax of language
and axioms of the multimodal logic that are implemented and used in our running example. For formal proofs of the properties and any further details, we refer the reader to (Herzig et al. 2010).
Definition 2.1 ( Syntax of language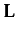 )
)
Given agent i from a nonempty finite set of individual agents AGT = {i, j,...}, action a from a nonempty finite set of atomic actions ACT = {a, b,...} and sentence p from a nonempty set of atomic formulas ATM = {p, q,...}, the syntax of a sentence φ of the language
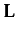 is defined by:
is defined by:
φ ≡ p | ¬ φ | φ 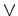 φ |
φ | 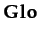 φ |
φ | 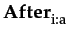 φ |
φ | 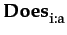 φ |
φ | 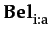 φ |
φ |  φ
φ
- 2.15
-
The primitive operators of
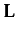 can be read in the following way:
can be read in the following way:
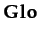 φ
: φ
is globally true (i.e., will hold in every point of the strict future)
φ
: φ
is globally true (i.e., will hold in every point of the strict future)
-
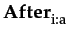 φ
: immediately after agent i
performs action a,
sentence φ
holds (therefore
φ
: immediately after agent i
performs action a,
sentence φ
holds (therefore
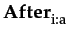 φ
φ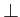 means agent i
cannot do a
)
means agent i
cannot do a
)
-
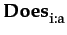 φ
: agent i
is going to do action a
and sentence φ
will hold from that moment on (therefore
φ
: agent i
is going to do action a
and sentence φ
will hold from that moment on (therefore
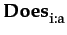
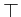 means agent i
is going to do a
)
means agent i
is going to do a
)
-
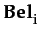 φ
: agent i
believes φ
φ
: agent i
believes φ
-
 φ
: agent i
has chosen φ
as the next goal
φ
: agent i
has chosen φ
as the next goal
- 2.16
-
For syntax sugaring purposes, we will write:
-
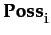 φ
(i
believes φ
is possible) iff
φ
(i
believes φ
is possible) iff
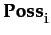 φ
≡
¬
φ
≡
¬
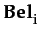 ¬ φ
¬ φ
-
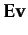 φ
( φ
will eventually hold) iff
φ
( φ
will eventually hold) iff
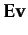 φ ≡ ¬
φ ≡ ¬
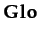 ¬ φ
¬ φ
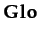 (globally true in the present moment and in the future):
(globally true in the present moment and in the future): 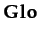 ≡
φ
≡
φ
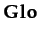 φ
(with
φ
(with 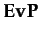 defined in the same way)
defined in the same way)
-
- 2.17
-
Table 1 presents an excerpt of the set of axioms underpinning the the logic described by the language
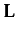 . All modal operators are of type box, except for
. All modal operators are of type box, except for
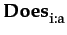 and possess the necessity property. The part of the logic concerning the agent beliefs is similar to that for choice and is KD45.
and possess the necessity property. The part of the logic concerning the agent beliefs is similar to that for choice and is KD45.
Table 1: Axiomatization of 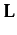 ,
from (Herzig et al. 2010)
,
from (Herzig et al. 2010)Axiom Name all propositional calculus theorems and inference rules PC  φ
φ
 ( φ
( φ  ψ)
ψ) 
 ψ
ψ
KChoice ¬(  φ
φ
 ¬ φ)
¬ φ)
DChoice  φ
φ 

 φ
φ
4Choice ¬  φ
φ 
 ¬
¬ φ
φ
5Choice 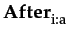 φ
φ
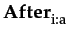 ( φ
( φ  ψ)
ψ) 
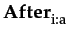 ψ
ψ
KAfter 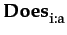 φ
φ
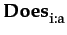 ( φ
( φ  ψ)
ψ) 
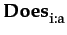 ψ
ψ
KDoes 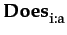 φ
φ  ¬
¬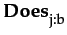 ¬ φ
¬ φ
AltDoes 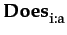 φ
φ  ¬
¬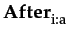 ¬ φ
¬ φ
IncAD ( 
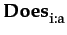
 ¬
¬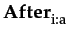
 )
) 
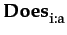
IntAct1 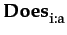


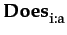
IntAct2
- 2.18
-
Now, we can introduce the definitions of occurrent trust OT
(i.e., performing a
here and now) and dispositional DT
(general disposition to perform a
) respectively:
Definition 2.2 (Occurence Trust)
OT(i, j, a, φ) ≡ COT  BOT
BOT
COT ≡ 
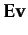 φ
φ
BOT ≡ 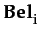 (
(
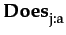

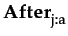 φ)
Definition 2.3 (Dispositional Trust)
φ)
Definition 2.3 (Dispositional Trust)DT(i, j, a, φ) ≡ PDT  BDT
BDT
PDT ≡ 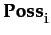
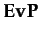 (k
(k

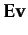 φ)
φ)
BDT ≡ 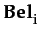
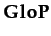 ((k
((k

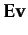 φ)
φ) 
( 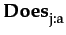
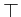

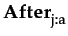 φ))
Example 2.4 The first situation of the illustrative scenario considers professor Y 's decision to buy a book which should be in good or excellent condition, at a low price, so she must establish the occurrent trust regarding the sentence cg
φ))
Example 2.4 The first situation of the illustrative scenario considers professor Y 's decision to buy a book which should be in good or excellent condition, at a low price, so she must establish the occurrent trust regarding the sentence cg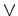 ce
.
ce
.
The book is on sale by a known seller (ann ), whose prior performances allow Y to assert occurrent trust in ann towards selling books in good condition cg . Knowledge concerning and agent's capabilities are stored at this level of granularity; we may assume Y possesses the sentence
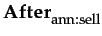 cg
in her memory. In the same time, we may assume a separate module (e.g. a planner) is in charge with generating the agent's current intention; for this situation, this might be the sentence
cg
in her memory. In the same time, we may assume a separate module (e.g. a planner) is in charge with generating the agent's current intention; for this situation, this might be the sentence

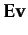 φ
. In this example, the intentions will consist of simple sentences only, which will be taken for granted. Automatically generating them by a planner will be considered for future development.
φ
. In this example, the intentions will consist of simple sentences only, which will be taken for granted. Automatically generating them by a planner will be considered for future development.
In the situation above, with the substitution {i/P, j/ann, a/sell, φ/cg
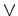 ce},
agent Y
can successively infer:
ce},
agent Y
can successively infer:
-

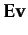 cg
cg 

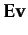 (cg
(cg ce)
ce)
-
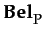 (
(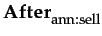 cg
cg
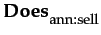
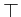 )
) 
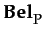 (
(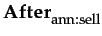 (cg
(cg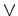 ce)
ce)
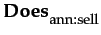
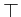 )
)
-
OT(P, ann, sell, cg
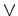 ce)
ce)
-
- 2.19
-
As one can see, Y
has proved the occurrent trust relationship towards ann
about selling books in good or excellent condition, so she is pretty sure she could buy the book from ann
in the desired conditions. The criterion of dispositional trust could be established in a similar way.
 Handling Reputation
Handling Reputation
- 3.1
-
Reputation is defined by the Oxford English Dictionary as "what is generally said or believed about a person's or thing's character or standing". This widely cited definition reveals the difference which might exist between what an agent says versus what she believes on a specific topic. On one hand, agents can communicate some information concerning an individual even if they don't necessarily believe it. On the other hand, one agent may commit to a group belief even if this contradicts her own private one (for example, a member of the ACME Board might be bound to the group belief "The ACME stock price will increase", even if his private opinion is different).
Therefore, one must carefully distinguish between shared beliefs, group belief and merely forwarded information.
- 3.2
-
We argue that, for making a decision, an agent ultimately commits to trust some information, which involves a personal, subjective commitment. It is possible that the information is not gained by first hand experiences, but provided by peers in form of shared beliefs; so trust precedes decision making and reputation precedes trust. The agent will have to select those sources which are more valuable from his own point of view, to commit to giving credit to them and to build up a consensus out of their possibly divergent opinions.
- 3.3
-
In order to deal with reputation, the model in (Herzig et al. 2010) extends the language
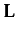 by defining the
by defining the
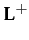 language, which accommodates the I
group beliefs:
Definition 3.1 (Syntax of languageModality
language, which accommodates the I
group beliefs:
Definition 3.1 (Syntax of languageModality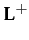 )
)
φ ≡ p | ¬ φ | φ 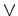 φ |
φ |  φ |
φ | 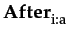 φ |
φ | 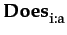 φ |
φ | 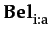 φ |
φ |  φ |
φ | 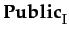 φ
φ
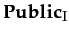 observes the usual axioms KD45, the necessity axiom as well as axioms connecting group beliefs to individual and sub-group beliefs respectively (which we skip here for brevity reasons).
observes the usual axioms KD45, the necessity axiom as well as axioms connecting group beliefs to individual and sub-group beliefs respectively (which we skip here for brevity reasons).
- 3.4
-
Then, the following definition of reputation is introduced:
Definition 3.2 (Reputation)
ReputO(I, j, a, φ, k) ≡ PoTG  PubG
PubG
PoTG ≡ 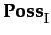
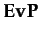 (
(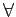 i ∈ I.
(
i ∈ I.
(
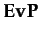 φ
φ
 k))
k))
PubG ≡ 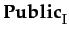
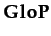 (
( i ∈ I.
(
i ∈ I.
(
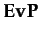 φ
φ
 k)
k)
 (
(
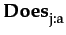
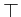

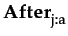 φ))
φ))
- 3.5
-
It states that j
has a reputation in group I
to do a
for achieving φ
in the circumstances k
iff:
- the agents in I do not exclude that, at some time in the future when k holds, each of them will want φ
- it is public (i.e. group believed) in I that j will be able to do a when he will intend to do it and by doing a will ensure φ
- 3.6
-
The definition above is based on the properties of the
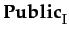 operator, which incorporates the relationship between one agent and the goals and beliefs of the group he belongs to. However, it
does not consider one agent's opinion on her peers, regarded as individuals.
For sample, there might exist a group belief concerning agent A,
but Y
may regard only a fraction of of the agents in the group to be knowledgeable and credible enough in order for their opinions to be significant for the current purpose. These opinions should not be simply discarded by the mere fact their owners belong to a group whose general belief may be altered.
operator, which incorporates the relationship between one agent and the goals and beliefs of the group he belongs to. However, it
does not consider one agent's opinion on her peers, regarded as individuals.
For sample, there might exist a group belief concerning agent A,
but Y
may regard only a fraction of of the agents in the group to be knowledgeable and credible enough in order for their opinions to be significant for the current purpose. These opinions should not be simply discarded by the mere fact their owners belong to a group whose general belief may be altered.
- 3.7
-
To address this issue, we introduce an alternative definition of reputation. It aims to formally model the subjective reputation as described above, based upon the ideas of a critical mass of opinions m
and of a set of trustworthy agents IT
.
Definition 3.3 (Critical Mass based Reputation)
Given τ ∈ (0.5, 1], a real number and IT ⊆ I, a set of agents such that
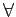 it ∈ IT.
DT(i, it, provide - info, φ),
we define
ReputD(i, I, j, a, φ, k)
by:
it ∈ IT.
DT(i, it, provide - info, φ),
we define
ReputD(i, I, j, a, φ, k)
by:
ReputD(i, I, j, a, φ, k) ≡ PdTG  PubG
PubG CmG
CmG
PdTG ≡ 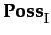
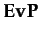 (
(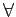 n ∈ I.(
n ∈ I.(
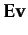 φ
φ k))
k))
PubG ≡ 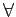 l ∈ IT.
l ∈ IT. (
(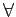 m ∈ IT.(
m ∈ IT.(
 φ
φ k)
k) 
( 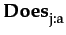

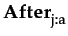 φ))
φ))
CmG ≡ | IT+ | / | IT | ≥ τ IT+ ≡ {m ∈ IT | 
 φ}
φ}
- 3.8
-
The definition asserts that agent i
in group I
should hold ReputD
towards agent j,
action a
in circumstances k,
and sentence φ
iff, among the set of trustworthy information providing agents IT
(from i
's perspective), there exists a subset
IT+ ⊆ IT
whose cardinality is above a critical amount and each agent in IT+
supports φ
. Basically, credible and knowledgeable sources are selected, then the information coming from them is assembled into a consensus.
- 3.9
-
The idea of critical mass based reputation is the main contribution of the present paper. It aims to formalize in an operational manner the decision made by people when they decide to commit to a specific belief provided such a belief is supported by enough peers. Unlike the definition above, the group is delimited according to the assessing agent and context; it is the agent itself who decides the peers' membership to the "circle of trust", which makes the approach more flexible.
- 3.10
-
The intuitions behind this definition could be tracked down to the social consumer theory (Solomon 2010; Kotler & Armstrong 2011), which lists four major categories of factors influencing the consumer behavior: cultural, social, personal and psychological.
Among the cultural factors, one could mention the "sub-culture", namely groups of people having shared value systems, based on common life experiences and situations. Common value systems will generate resembling expectations. This is in line with (Castelfranchi & Falcone 2010), where it is shown that an agent's expectation involves both a prediction relevant for him and the goal of knowing whether the prediction really happens.
Then, social factors include membership groups and online social networks, family, friends, as well as co-workers and neighbors. The IT
set models the aforementioned primary membership group an agent belongs to. This group is built on similarity grounds, in a somehow subjective manner. This is consistent though with the findings in (Ziegler & Golbeck 2007) which show the people trend to trust like-minded partners more than random ones.
- 3.11
-
The newly proposed definition aims to distinguish between a sentence φ
being public in a group and being actually believed by an agent. Figure 2 shows a sentence which is always public ( in the original definition's respect) but which could not be adopted as a belief by an agent at certain moments of time, e.g. in round 3.
- 3.12
-
One should note the suggested definition of reputation in a "dispositional"-like manner. We think this is reasonable for at least two reasons. First, occurrent reputation could be regarded as dispositional reputation at a specific moment of time, namely at the next moment. Second, the membership of an agent to the IT
group at a specific moment in the future depends on some external events and can be decided only in the moment the inference is carried. The next step would be to describe how the set IT
could be selected.
- 3.13
-
First, we introduce operators
Saidi, j φ
, meaning j
has said to i
that φ
and
Seeni, j( φ, k)
, meaning i
has noticed the outcome φ
for an action of j
within context k
. Borrowing from (Demolombe 2001), we define the following four properties of agent j
as assessed by agent i
:
- sincerity:
Sinci, j φ ≡ 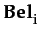 (Saidi, j φ
(Saidi, j φ 
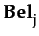 φ)
φ)
- credibility:
Credi, j φ ≡ 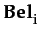 (
(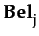 φ
φ  φ)
φ)
- cooperative behavior:
Coopi, j φ ≡ 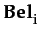 (
(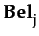 φ
φ  Saidi, j φ)
Saidi, j φ)
- vigilance:
Vigii, j φ ≡ 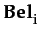 ( φ
( φ 
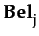 φ)
φ)
- sincerity:
- 3.14
-
For reputation handling, the following axioms are added:
Sinci, j φ  Credi, j φ
Credi, j φ Coopi, j φ
Coopi, j φ Vigii, j φ
Vigii, j φ Saidi, j φ
Saidi, j φ  DT(i, j, provide - info, φ)
DT(i, j, provide - info, φ)
(DTI) Seeni, j( φ, k)  DT(i, j, provide - info, φ)
DT(i, j, provide - info, φ)
(DTS) - 3.15
-
The DTI
axiom says that if an agent i
gets a certain piece of information from an agent j
which is perceived as sincere, credible, cooperative and vigilant, than a dispositional trust relationship from i
to j
should be asserted. Axiom DTS
tells that if agent i
notices a certain decision made by agent j
with respect to a given piece of information φ,
then i
should believe φ
even if not explicitly said by j
. This is similar to passive delegation mentioned in (Castelfranchi & Falcone 1999). Both information sources get counted for the critical mass of opinions.
- 3.16
-
Each agent i
keeps, for each information provider j
and for each of the four aforementioned properties, a Likert-like scale with five levels of satisfaction, as follows:
very disappointed
<
disappointed
<
neutral
<
happy
<
very happy
(henceforth vd,
d,
n,
h,
vh
respectively). Their values could change over time, according to the outcomes of the new experiences. Each time i
gets a piece of information from j,
this is assessed against its observed value. If the results match, i
's quality level about j
increases, otherwise it decreases; e.g. if j
says "I believe the book is in good condition" and the book is actually in bad condition, then credibility of j
in i
's eyes will drop one step, say from h
to n
. Figure 1) depicts the transition diagram corresponding to the Likert scale for credibility. The sentence
Sinci, j φ
gets deleted from the knowledge base of i
if the quality level of j
on i
's scale about credibility hits d
level or below.
- 3.17
-
For the experiments we conducted, we focused on the price (
{low, average, high}
) and product quality (
{medium, good, excellent}
) features. This was done in order to keep things simple, but could be easily extended to some other features, e,g,. products category or availability. On the other hand, the Likert scale based mechanism above has been employed in order to assess the features concerning reputation.
Example 3.4
The second stage of the scenario in Section 2.2 describes the situation in which professor Y decides to buy a number of books for the University bookstore. The books must be in excellent condition (ce ) now, while the price could be either average or low (pa or pl ). Books must be supplied whenever needed. Since Y has no experience with the book suppliers available for this, she must rely on the opinions of her colleagues paula, ralph, sue, ted and ursula about the bookstore BS . Let us assume Y considers ted and ursula not credible about the prices of the books (their Likert level is d and vd respectively), while paula, ralph and sue are considered sincere, credible, cooperative and vigilant about the same topic, having each a Likert level equal to vh .
Let us also assume paula, sue and ted support φ = pa, ralph and ursula support ¬ φ and the critical mass is 0.6 (i.e., agent Y believes sentence φ only if at least 3 out of 5 sources support it). For this situation, the IT set has 3 elements (namely paula, ralph and sue ), while the cardinality of IT+ is 2, hence the ratio gives us 0.67, which is higher than the threshold. Therefore, the inferred trust towards BS will emerge.
Example 3.5We assume the same circumstances as for example 3.4. Now, professor Y has just noticed ted has just bought some excellent quality books at a low price from BS, which will increase the level of ted from d to n and consequently include him into set IT . Now, the IT set has 4 elements (paula, ralph, sue and ted ), while the cardinality of IT+ is 3 (because of paula, sue and ted ), which gives a ratio of 0.75, hence trust towards BS will emerge once again. Had ted supported ¬ φ, the score would have been 0.5, so the action of buying from BS it would have been rejected.
Reputation Evolution over Time
- 3.18
-
No one can expect to always possess the full amount of knowledge she needs, therefore people often depend on the information obtained from their friends.
Since people tend to group based on common preferences, tastes or cultural features, somebody's inner circle of friends could provide knowledge whose quality is judged by similar criteria and expectations. The scenario below aims to show how the proposed definition can help an agent in aggregating and adopting his own opinions out of the ones provided by those sources inside the friends circle which are perceived as trustworthy. The agent consults all of his friends when in need for an opinion, then filters out the opinions coming from the people who are considered not trustworthy (from now on, trustworthy is defined in respect to the prior Dispositional Trust axioms). The scenario assumes the circle of friends is already built. If one would like to add some new acquaintances to her circle of friends, she could employ a method of predicting trust in strangers like those suggested by (Guha et al. 2004) or (Liu et al. 2008).
- 3.19
-
Table 2 presents an 8-round simulation involving a set of artificial agents. The first one is professor Y
, who repeatedly consults 5 friend agents (p,
r,
s,
t
and u
) and reasons upon their reputation in order to establish whether sentence φ
(e.g. "the book quality is good") is to be adopted.
The table aims to illustrate, over 8 rounds, the relations between the trust levels of T
towards each of his 5 friends, the opinions casted by them, the real value of the claimed sentence and its adoption by Y
. The real outcomes are independent of the agents and become available for Y
at the end of each round.
- 3.20
-
The trust level concerning the sincerity of each agent, from Y
's perspective, is presented in the Trust column. The Opinions column shows the opinions casted by each agent in every round when asked by Y
about the truth of the sentence φ
. One should notice that even if Y
considers an agent not sincere, the opinion is still asked; in addition, no information is obtained via Seen
. The opinions casted by different agents could change from one round to another, perhaps due to the new interactions they had meanwhile and are not dictated by the values in column Out
alone.
- 3.21
-
The support rate and the belief of Y
towards φ
are presented in the last 2 columns. The support rate is computed as the ratio between the number of trustworthy agents (i.e., having the trust level at least n
) who support φ
and the total number of trustworthy agents. Sentence φ
gets adopted if an only if the support rate is higher than τ
.
After each round, Y
commits or not to buy based on her belief of φ
; the evaluation of the actual transaction outcome, after the sentence adoption decision, is presented in column Out. Then, the trust level of Y
into her peers gets adjusted. The results corresponding to the scenario in Table 2 are displayed in Figure 2, where the horizontal line τ = 0.51
marks the threshold above which the sentence φ
gets adopted; this actually happens in rounds 1,2,5,6 and 8.
Figure 2: Evolution of Belief of φ over 8 rounds ( τ = 0.51). A sentence is adopted as a belief if its support is higher than the threshold τ ![\includegraphics[width=80mm]{Ex12-51.eps}](7/img41.png)
- 3.22
-
In the first phase, we investigated the impact of the threshold value τ
over the adoption of a certain sentence φ
. The experiments on a set of Epinions data published in (Massa & Avesani 2007) pointed out that in case of many controversial users present, two limit cases of culture, namely "the tyranny of the majority" and "the echo chambers" might arise. The "tyranny of the majority" phenomenon appears when the majority makes all the rules/opinions, thus condemning the minority to absolute silence. This might lead to loosing some valuable opinions if they haven't had yet the chance to gain a sufficient number of supporters.
The "echo chambers" effect consist of a claim made by some source and over-repeated by many like-minded people until most people assume that some extreme variation of the story is true (Massa & Avesani 2007).
Experiments were conducted to see the impact of the critical mass factor over beliefs and the decisions which are based upon them.
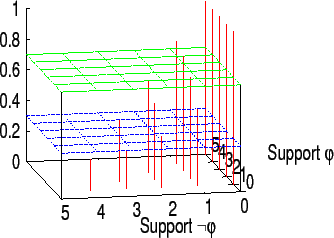
Figure 3: Evolution of Belief in φ (left) and ¬ φ (right) over 8 rounds ( τ = 0.7 ). During rounds 1,2,4 and 7, neither φ nor ¬ φ is adopted as a belief in order to diminish the possibility of the tyranny of a majority ![\includegraphics[width=80mm]{Ex12-7.eps}](7/img42.png)
![\includegraphics[width=80mm]{Ex12-7not.eps}](7/img43.png)
- 3.23
-
Figure 4 displays a similar situation, but with τ = 0.7
. Increasing the threshold means requiring higher support for a sentence before its adoption. This could lead to the situation that, in some rounds, neither φ
nor ¬ φ
is adopted as a belief since none of them gets enough support (see, for example, rounds 1,2,4 and 7). In these rounds, an action having φ
as a precondition cannot be performed, and one having ¬ φ
as precondition cannot either. This way one agent is not always forced to unconditionally follow the majority. Figure 4 displays the possible outcomes for φ
and ¬ φ
in case of a circle of 5 friend agents, for different values of τ
: φ
is believed when its support gets above the superior green plan, while ¬ φ
is believed when the support for φ
falls below the blue plan. A higher value for τ
would require more peer support when making a decision and less power for a majority.
Figure 4: Impact of the number of agents supporting φ and ¬ φ over the belief of φ, for τ = 0.51 (left) and τ = 0.7 (right). Sentence φ is believed when its support gets above the green plan; ¬ φ is believed when the support for φ falls below the blue plan 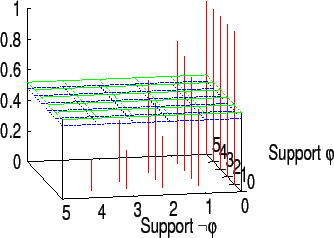
- 3.24
-
On the other hand, one should look at the "echo chambers" effect: a claim made by a source gets repeated by many like-minded people and ultimately is accepted as factual. If we look once again at the Example in Table 2, we can see the agent s
repeatedly copies the opinions casted by agent p
. As a result, p
's experiences get counted twice when professor Y
makes the reputation based assessment of sentence φ
. When comparing the predicted (i.e., believed) value of φ
and the actual supplyer behavior over more rounds, we can observe they are the same only for round 6, while in rounds 2,3 and 7 they do not match (in the other rounds, the actual output of the experience is not available). But if we assumed an "abstain" vote casted by s
instead of snobbishly copying p
's opinions, the match would happen in three out of four rounds, namely 2,3 and 6. A similar result would have been obtained if increasing the value of the threshold τ
up to 0.66, which would have "filtered out" the artificial influence of the copied vote, at the price of narrowing the set of available opinions (and perhaps decisions). Finding the optimal threshold value should be combined with detecting the sources of the echo chambers effect, but we have not investigated this latter part yet.
 Implementation in SPASS
Implementation in SPASS
- 4.1
-
The scenario was tested using SPASS 7, a saturation-based theorem prover which can handle formulas in the first-order logic (FOL) with equality and also modal logic formulas. The latter ones are automatically translated into their first-order counter-parts before the proving process starts. The prover takes as input a formula in the accepted language and produces an output consisting of the proof of its validity in case such a proof was found or signals by a specific message, that the proof searching process has been completed and the formula cannot be proved.
- 4.2
-
Figure 5 presents the significant part of the code used to implement a simplified definition of the dispositional trust in Section 3. This one is used, for example, in deciding the ReputD
for Example 3.4. We define simplified dispositional trust as the trust whose preconditions are only the sincerity and the existence of a Said
fact. This simplified definition is introduced for the sake of simplicity; the proof for the real case comprises similar steps, but it would be a little bit tedious to follow.
- 4.3
-
The modal operator
belrepresents the beliefs of agentP, while predicatebelpaulawill represent the beliefs paula has.saidpaulais be used to represent the act of communication of a sentence by paula to Y . Each agent involved in the community has her own set of operators named accordingly (e.g.,saidralph). The predicates pa and pl represent the price levels average and low in the mentioned example. - 4.4
-
The first part of the
list_of_special_formulae(axioms,EML)section (lines22-32) asserts that paula said to Y the price is average (line25), that Y considers paula is sincere (lines28-29) and introduces the simplified definition of dispositional trust towards paula (predicatesdtpaulain lines31-32). This emerges if φ is said bypaulaandpaulais sincere. Lines33-37give the implementation of the axioms DBel, 4Bel, 5Bel in the equivalent form of properties of relationships between the Kripke worlds which correspond to the Bel operator. For example, line40-41says that Bel φ Bel (Bel φ)
for any sentence φ
. Table 3 gives a synopsis of the equivalences. Similar axioms are implemented for predicate Belpaula
. This latter predicate is generated by
Bel (Bel φ)
for any sentence φ
. Table 3 gives a synopsis of the equivalences. Similar axioms are implemented for predicate Belpaula
. This latter predicate is generated by SPASSwhen translating the modal axioms ofbelpaula. The last part (line47) asks the system to prove the simplified occurrent trust regarding paula for the sentence pa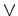 pl
.
pl
.
Table 3: Axioms and corresponding relationships properties (Huth & Ryan 2004) Name Axiom Property First-order definition T □p  p
p
reflexivity 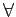 x.R(x, x)
x.R(x, x)
B p  □ ◇p
□ ◇p
symmetry 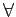 x, y.R(x, y)
x, y.R(x, y)  R(y, x)
R(y, x)
D □p  ◇p
◇p
seriality 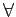 x.
x.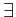 y, R(x, y)
y, R(x, y)
4 □p  □ □p
□ □p
transitivity 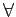 x, y, z.(R(x, y)
x, y, z.(R(x, y) R(y, z))
R(y, z))  R(x, z)
R(x, z)
5 ◇p  □ ◇p
□ ◇p
euclideanness 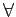 x, y, z.(R(x, y)
x, y, z.(R(x, y) R(x, z))
R(x, z))  R(y, z)
R(y, z)
- 4.5
-
Figure 6 presents the most important fragments of the system's output for this case.
In lines
01-02of this figure, one can see the input modal assertions translated by SPASS into fragments of the FOL. The process imply introducing skolem constants (e.g.,skc3in line02, corresponding toplin input) or predicates, translations of modal operators and their axioms into FOL predicates. - 4.6
-
Line
22contains the textSPASS beiseite: Proof found, stating the deductive process has successfully ended and a proof has been produced. - 4.7
-
Lines from
25to48list the step-by-step proof of the query which was given to the system to prove. The inference rule used at each step is given, together with the clauses it was applied on. For example, line36says that at this step, the resolution was applied on clauses1(line25) and14(line32) and produced the clauseSkQpa(skf6(skc3))* -> SkQpa(skc2) SkQpl(skc2)as a result. The process ends when the empty clause is produced, which means a valid proof of the query exists. This, this could start again for answering some other query. For Example 2, this would mean asking each agent the query on the book quality and counting the cases in which a proof was found in order to see if this number is greater than the critical threshold needed for trusting that sentence.
 Related Work
Related Work
- 5.1
-
The socio-cognitive model of trust (Castelfranchi & Falcone 2010) describes the ingredients of trust rather than regarding it as the result of a statistical analysis of past interactions. The most important ingredients of trust are considered competence (i.e., if an agent is able to perform a given task) and willingness (i.e., the agent wants to perform the same task). In line with this view, (Falcone & Castelfranchi 2010) lists conditions for making the decision of trusting a partner, for trust transitivity in case of delegation and the impact of competence and willingness over the trust transitivity. However, many of the basic beliefs involved are specified at a high level of abstraction (e.g., how to assess the reasons for agent Z
to serve agent Y
versus the reasons for agent Z
to serve agent X
which could lead to different outcomes), hence the need to detail the model in more depth.
- 5.2
-
One line of development is presented in (Herzig et al. 2010), where a formal logical framework for socio-cognitive trust modeling is described. This formal model provides the possibly of automated reasoning and integration into the popular Belief-Desire-Intention agent model. Our work focuses on extending the details of the approach by refining the definition of the reputation and by making it operational in an e-commerce scenario. This extension is grounded on the idea that reputation as public image should offer support for inferring useful beliefs, which will ultimately serve for decision making. It is consistent with the distinction operated by Conte and Paolucci (Conte & Paolucci 2002) between image as shared believed evaluation and reputation as a shared communicated "voice", which is not necessarily a shared belief.
- 5.3
-
The proposed extended definitions match the properties formulated in (Castelfranchi & Falcone 2010). They avoid carelessly collapsing opinions as a selection is performed before integrating and adopting the result. This view is consistent with the psychological propension of people trusting their close friends' opinions more than the aggregate opinions from strangers, as pointed out by some online reputation management studies 8.
- 5.4
-
The selection process relies on the idea of trust as a "decision to trust" in that it filters out peers who are considered untrustworthy. In the same time, by relying on the acquaintances opinions, it assumes similar expectations and competences, thus preferring opinions (i.e., experiences) provided by similar people instead of an equal treatment of all information at hand.
- 5.5
-
In order to deal with uncertainty and opinion divergence, one approach is to employ Subjective Logic (Jøsang 2007), a superset of the Dempster-Shafer theory of beliefs (Shafer 1976; Dempster 1967) and of Nilsson's probabilistic logic (Nilsson 1986).
Each sentence has an opinion attached, which measures the amount of evidence which supports and the amount of uncertainty of the sentence; the corresponding operations over them are defined.
Unlike this approach, we used the simplifying assumption of claiming the truth of a sentence if a large enough majority of agents (the "critical mass") state its truth. In the same time, the uncertainty issue is addressed by incorporating quality levels in sentences.
 Conclusions and Future Work
Conclusions and Future Work
- 6.1
-
We employed a multimodal logic for building a decision making mechanism which involves both trust and reputation.
Reputation information is accepted for building trust relationships in case not enough prior common interactions are available.
In order to deal with this, a new simple definition, based on the notion of "critical mass" convergence, is proposed for describing how an agent deals with the common reputation information and with divergent opinions in order to select and integrate knowledge obtained from its peers. Then, new axioms are added in order to accommodate the definitions.
The mechanism is used in a community of interacting agents which develop cooperative relationships, assess the results against several quality criteria and possibly publish their beliefs and/or assessments inside the group. The illustrative implementation is tested in a multiple rounds e-commerce use case and the influence of the critical mass and number of agents supporting a sentence over its adoption is assessed.
- 6.2
-
As future work, we intend first to test the whole system in more complicated scenarios in order to assess its completeness as well as efficiency. The opinion diffusion model proposed in Malarz et al. (2011) would probably offer a more realistic view over the spreading or information and beliefs among the agents. Within this context, one objective is to develop the mechanism for agent intentions management. So far, intentions are considered already generated, but in the future developments, they should be built automatically, by employing a planner.
- 6.3
-
A second line of investigation would be to improve the agent credibility assessment process by replacing the simple Likert scale with a more sophisticated mechanism aimed to combine the trust feature values into trust levels. One possible approach is to employ a mechanism similar to the log/linear trust model which was proved to favor fewer strong relationships over many weaker Sutcliffe & Wang (2012). The assessment could be further improved by taking into account the acquaintances network structure and by mining the agent decision sequences in order to detect the sources of the echo chambers effect.
 Acknowledgements
Acknowledgements
-
Part of this work was supported by CNCSIS-UEFISCSU, National Research Council of the Romanian Ministry of Education and Research, project number ID_170/2009. We are grateful to the anonymous reviewers for their useful comments.
 Notes
Notes
- 1
- http://www.ebay.com
- 2
- http://www.amazon.com
- 3
- http://www.ratemds.com
- 4
- http://www99.epinions.com
- 5
- http://www.rummble.com
- 6
- http://blog.nielsen.com/nielsenwire/consumer/global-advertising-consumers-trust-real-friends-and-virtual-strangers-the-most (Archived at http://www.webcitation.org/67tP0KGDp)
- 7
- http://www.spass-prover.org
- 8
- Online Reputation Management. Tourism Businness Essentials. Ministry of Jobs, Tourism and Innovation, British Columbia, Canada. http://www.jti.gov.bc.ca/industryprograms/pdfs/OnlineReputationManagementTBEGuide2011_Jun15.pdf (Archived at http://www.webcitation.org/67tPel9hj)
 References
References
-
ANTONIOU, G. & VAN HARMELEN, F. (2008).
A Semantic Web Primer (Second Edition).
Cambridge, MA: MIT Press.
CASTELFRANCHI, C. & FALCONE, R. (1999). The dynamics of trust: from beliefs to action. In: Proceedings of the First International Workshop on Deception, Trust and Fraud in Agent Societies. Seattle, WA.
CASTELFRANCHI, C. & FALCONE, R. (2010). Trust Theory: A Socio-Cognitive and Computational Model. Wiley Publishing. [doi:10.1002/9780470519851]
CONTE, R. & PAOLUCCI, M. (2002). Reputation in Artificial Societies: Social Beliefs for Social Order. Springer. [doi:10.1007/978-1-4615-1159-5]
DEMOLOMBE, R. (2001). To trust information sources: a proposal for a modal logic framework. In: In C. Castelfranchi, Y-H. Tan, editors, Trust and Deception in Virtual Societies. Kluwer Academic Publishers. [doi:10.1007/978-94-017-3614-5_5]
DEMPSTER, A. P. (1967). Upper and lower probabilities induced by a multivalued mapping. The Annals of Mathematical Statistics 38(2), 325-339. [doi:10.1214/aoms/1177698950]
FALCONE, R. & CASTELFRANCHI, C. (2010). Trust and transitivity: a complex deceptive relationship. In: Proceedings of the Thirteenth Workshop on Trust in Agent Societies at AAMAS 2010. Toronto, Canada.
GAMBETTA, D. (1988). Trust. Making and Breaking Cooperative Relations. Oxford: Basil Blackwell.
GUHA, R., KUMAR, R., RAGHAVAN, P. & TOMKINS, A. (2004). Propagation of trust and distrust. In: Proceedings of the 13th international conference on World Wide Web. New York, NY, USA. http://doi.acm.org/10.1145/988672.988727.
HERZIG, A., LORINI, E., HüBNER, J. F. & VERCOUTER, L. (2010). A logic of trust and reputation. Logic Journal of IGPL 18(1), 214-244. http://jigpal.oxfordjournals.org/content/18/1/214.abstract. [doi:10.1093/jigpal/jzp077]
HUTH, M. & RYAN, M. (2004). Logic in Computer Science: Modelling and Reasoning about Systems, 2nd edition. New York, NY, USA: Cambridge University Press. [doi:10.1017/CBO9780511810275]
JøSANG, A. (2007). Probabilistic logic under uncertainty. In: Proceedings of the thirteenth Australasian symposium on Theory of computing - Volume 65, CATS '07. Ballarat, Victoria, Australia. http://dl.acm.org/citation.cfm?id=1273694.1273707.
JøSANG, A. (2009). Trust and Reputation Systems. Tutorial at IFIPTM 09, Purdue University. http://www.webcitation.org/67tQCTDcl.
KOTLER, P. & ARMSTRONG, G. (2011). Principles of Marketing (14th Edition). Prentice Hall.
LIU, H., LIM, E.-P., LAUW, H. W., LE, M.-T., SUN, A., SRIVASTAVA, J. & KIM, Y. A. (2008). Predicting trusts among users of online communities: an epinions case study. In: Proceedings of the 9th ACM conference on Electronic commerce, EC '08. New York, NY, USA: ACM. http://doi.acm.org/10.1145/1386790.1386838. [doi:10.1145/1386790.1386838]
MALARZ, K., GRONEK, P. & KUŁAKOWSKI, K. (2011). Zaller-deffuant model of mass opinion. Journal of Artificial Societies and Social Simulation 14(1), 2. https://www.jasss.org/14/1/2.html.
MASSA, P. & AVESANI, P. (2007). Trust metrics on controversial users: balancing between tyranny of the majority and echo chambers. International Journal on Semantic Web and Information Systems, Special Issue on Semantics of People and Culture . http://www.gnuband.org/papers/trust_metrics_on_controversial_users_balancing_between_tyranny_of_the_majority_and_echo_chambers-2.
NILSSON, N. J. (1986). Probabilistic logic. Artificial Intelligence 28(1), 71-88. [doi:10.1016/0004-3702(86)90031-7]
PINYOL, I., SABATER-MIR, J., DELLUNDE, P. & PAOLUCCI, M. (2012). Reputation-based decisions for logic-based cognitive agents. Autonomous Agents and Multi-Agent Systems 24(1), 175-216. [doi:10.1007/s10458-010-9149-y]
SHAFER, G. (1976). A Mathematical Theory of Evidence. Princeton: Princeton University Press.
SHOHAM, Y. & LEYTON-BROWN, K. (2008). Multiagent Systems. Algorithmic, Game-Theoretic, and Logical Foundations. Cambridge University Press. [doi:10.1017/cbo9780511811654]
SOLOMON, M. R. (2010). Consumer Behavior, buying, having, and being. Prentice Hall.
SUTCLIFFE, A. & WANG, D. (2012). Computational modelling of trust and social relationships. Journal of Artificial Societies and Social Simulation 15(1), 3. https://www.jasss.org/15/1/3.html.
UDDIN, M., ZULKERNINE, M. & AHAMED, S. (2009). Collaboration through computation: incorporating trust model into service-based software systems. Service Oriented Computing and Applications 3(1), 47-63. [doi:10.1007/s11761-009-0037-8]
ZIEGLER, C.-N. & GOLBECK, J. (2007). Investigating interactions of trust and interest similarity. Decision Support Systems 43(2), 460-475. [doi:10.1016/j.dss.2006.11.003]
![\includegraphics[width=145mm]{scale.eps}](7/img40.png)

![\begin{figure}\begin{verbatim}01. Input Problem:
02. 1[0:Inp] \vert\vert -> SD...
...kc2).
...
48. 246[0:MRR:243.0,29.0] \vert\vert -> .\end{verbatim}
\end{figure}](7/img50.png)