 Abstract
Abstract
- Within a universal agent-world interaction framework, based on Information Theory and Causal Bayesian Networks, we demonstrate how every agent that needs to acquire relevant information in regard to its strategy selection will automatically inject part of this information back into the environment. We introduce the concept of 'Digested Information' which both quantifies, and explains this phenomenon. Based on the properties of digested information, especially the high density of relevant information in other agents actions, we outline how this could motivate the development of low level social interaction mechanisms, such as the ability to detect other agents.
- Keywords:
- Information Theory, Collective Behaviour, Inadvertent Social Information, Infotaxis, Digested Information, Bayesian Update
 Introduction
Introduction
- 1.1
- To improve our understanding of social interaction in a developmental context it is important to know what the benefit of social interaction is. Understanding the motivation behind social interaction is a core issue in the study of social systems. Once a collective of individuals is observed to exhibit social interaction, a post hoc analysis and explanation of its advantages is often straightforward. From an evolutionary or developmental point of view, however, the challenge is often to identify a path that would lead towards such an interaction in the first place.
- 1.2
- For several social interactions, such as cooperation, social learning and imitation, the benefits are often obvious, and there are several good accounts that identify and quantify the gain of an agent (e.g. in the mathematical framework of game theory (Maynard Smith 1982; Axelrod 1984), or in current works that try to evaluate the benefits of social interaction (Gotts 2009; Gostoli 2008)). But those phenomena are already very complex, and they normally involve several other agent abilities in an implicit fashion, such as:
- The ability to differentiate other agents from the environment
- Directed attention towards other agents
- Understanding of own actions and consequences
- Understanding of other agents action and consequences
- 1.3
- A naive explanation would be to assume that all those mechanisms needed for complex social interaction developed in one big step, motivated by the final results and its benefits. But this is in conflict with the common step-by-step idea of evolution whereby development is explained via localized incremental improvements, all of which need to selected for in order to prevail. It becomes especially unfeasible in our case, because the benefits of those mechanisms are typically significantly delayed.
Summary
- 1.4
- To counter the criticism of irreducible complexity, we aimed at identifying possible motivations for an agent society to develop some of those mechanisms from localized, short-term knowledge that do not require the agent population to have a model of the delayed benefit of complex social interactions.
- 1.5
- For this purpose, we adopt a hypothesis that has been brought forward already in early cybernetics and has been revived due to new evidence (Barlow 1959,2001;Attneave 1959; Touchette 2004; Nehaniv 1999, Laughlin 2001, Bialek 2001;Polani 2009) namely that organisms attempt to optimize their information processing; more precisely, organisms attempt to maximize the information attained relevant to their goals under the constraints of their particular sensorimotor (and neural) equipment. A detailed discussion is beyond the scope of the present paper and we refer to the aforementioned literature for details; however, we would like to briefly mention two aspects which play an important role in our later discussions:
- First, information acquisition and processing are found to be very expensive in terms of metabolic costs - it therefore makes evolutionary sense to process as much relevant information (information needed to achieve certain life goals) as possible for a given organismic sensorimotor equipment. If the organism could do with less relevant information, its information processing equipment can be expected to be selected against during evolution.
- Second, the informational efficiency of the organism provides an immediate (rather than delayed) gradient for the effectiveness of the organism's behaviour, prior to any particular long-term payoff.
- 1.6
- Point 1 gives us an evolutionary rationale for the plausibility of an informational view of an agent's performance. However, even more central for our original goal is Point 2; there are indications that pure, immediate sensorimotor efficiency already provides powerful local gradients for adaptation and evolution (Klyubin 2005, 2007, 2008;Prokopenko 2006, Ay 2008a, Der 1999,Sporns 2003). Here we will assume a slightly more specific criterion, namely that the agents are interested in maximizing the relevant information about a life goal (the location of food). For this, the agents will have the possibility to detect the food directly or to observe the behaviour of other agents. Our study will investigate whether and how under these circumstances social interaction can emerge simply from the immediate drive to maximize relevant information.
- 1.7
- To implement a quantitative and consistently informational model, we will use an approach based on Shannon's Information Theory, Bayesian Modelling and Causal Bayesian Networks. Using these principles, our agents will build their behaviours from the starting point of quite restricted assumptions; in particular, no a priori social dynamics will be assumed. On top of this universal, low assumption framework we will then introduce the concept of "Digested Information"; this will serve as an argument for why the actions produced by an agent without any direct consequences for another agent might still be interesting for the latter.
- 1.8
- We will support these conceptual arguments by presenting simulations that support the plausibility of the previous argument by verifying its conclusions; in particular, this will also demonstrate that the information-theoretic framework allows us to quantify the concrete benefit of observing another agent.
Related Work
- 1.9
- Further related work can be found in the area of biology, especially by Danchin (Baude 2008; Parejo 2008; Danchin 2004) who describes a phenomenon called "Inadvertent Social Information". Danchin et. al. observe bees (and other animals) and show that the foraging performance of one group of bees increases, if they are operating in an area where another, experienced group of bees if already foraging. Danchin employs an informal notion of information to argue that the actions of other animals provide useful information. This occurs without any explicit form of communication, such as bee dances. Our present paper develops a quantitative framework in the language of information theory to give a precise quantitative characterization of the information exchanged in such processes.
- 1.10
- Danchin (2004) also suggests that this information, once it is replicated and propagated, could give rise to an evolution-like process; an idea closely related to the idea of "memetics" (Blackmore 2000; Dawkins 1990; Lynch 1999). If the presented framework manages to formally describe the information replication process in Danchin's work, it might then also be a step towards a better mathematical understanding of the memetic process.
- 1.11
- But currently our work only tries to model and the most basic processes of social interaction within the framework of information theory, employing the formal notion of information based on Shannon (1948). We are not aware of a fully information-theoretic treatment of agent-agent interaction. But a similar formalisation to ours can be found in the work of Klyubin (2004) where he models stigmergy, which is the information transfer to oneself through time by the use of artifacts or the environment. Also, Capdepuy (2007) demonstrated how coordinated behavior could emerge from agents that tried to maximize their "Empowerment" (Klyubin 2005), another formal information theoretic measure that maximises the channel capacity from one's actuators to one's sensors.
 Information-Theoretic Framework
Information-Theoretic Framework
- 2.1
- This chapter will introduce a universal, purely syntactical, and agent-centric Agent-World-Interaction Framework that we require for our argument. We will demonstrate how to express our computer simulations in the language of Causal Bayesian Networks and furthermore introduce essential notions we require for our information-theoretic discussion.
- 2.2
- The Causal Bayesian Network framework will also serve for the purpose of the later quantitative analysis. It unifies all pertinent agent-world interaction scenarios with respect to their common properties and covers all our simulations. In particular, it will give a precise quantitative meaning to the concept of Digested Information.
- 2.3
- For this purpose, we model all aspects of our simulation which we want to study as a set of random variables. For discrete states (as e.g. in our computer simulation), this is straightforward, but in principle it carries over to continuous scenarios, e.g. from real-world scenarios.
- 2.4
- In the model, we distinguish random variables according to whether they describe agent or non-agent states. These non-agent variables will be used to form a compound random variable, which we will simply call the environment R. Furthermore we divide the agent itself into the sets of random variables, the sensors S, the actuators A and the memory M. To do so we assume a model for the causal connections between the variables. When we construct an explicit model or when the architecture of the system under investigation is known, the causal relation between environment, sensors and actuators is given per default. In this paper, we operate under this assumption. In general, when such a model is not given a priori, the causal structure can still be inferred by interventional experiments and, under some circumstances, also by observation (Pearl 2000; Spirtes 2001).
- 2.5
- In our framework, we define the sensor S as the minimal set of random variables (of the agent) which causally shield the agent's remaining random variables from the environment variables R. So, there is no causal path in the Causal Bayesian Network from any part of R to the variables of the agent that does not pass through S (see also Ay 2008b). Likewise, the Actuators A will be defined as the minimal set of variables that causally shield the environment from the agent. The remaining variables of the agent are internal states which we will interpret as the agent's memory. In the following, we treat each of those three sets as a single random variable each. The resulting network is depicted in Fig. 1.
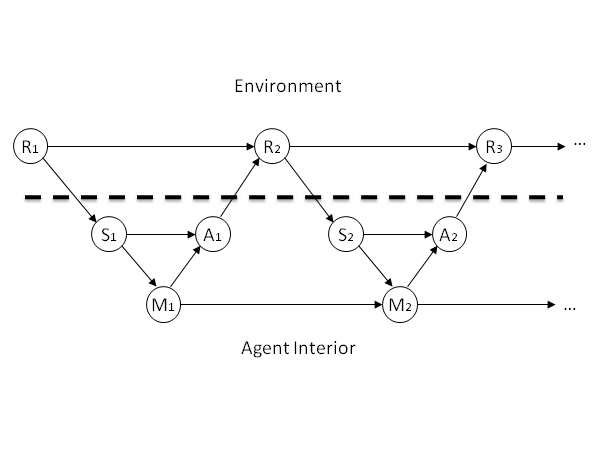
Figure 1. A Causal Bayesian Network visualizing our general Agent-World-Interaction Framework in time. The dashed line shows the divide between the agent and the environment R. The sensors S take in information, and are causally dependent on the environment. The actuators A inject information into the environment. M is used to preserve information through time within the agent. Note that the arrows crossing the dashed line are not under the control of the agent; they are defined by the relation between the agent and the world, and thereby externally determined. - 2.6
- The agent's ability to make decisions is modeled by the fact that it can alter the causal relations between the variables within the agent; which in our case is essentially the relation between sensors, memory and actuators. Note that the agent's ability to interact with the environment is limited by the bandwidth of the sensors and actuators, and all information in and out of the agent has to pass through those variables. For our current purpose, this is going to be our definition of an agent.
- 2.7
- One should note that, assuming the validity of a probabilistic model of the system and assuming that sensors and actuators are split in the way denoted by Fig. 1, this model is universal. For a concrete setting, possible technical difficulties could arise from the random variables being continuous, or the precise causal structure not being known (e.g. in a real-world scenario where the structural knowledge is incomplete). These technical difficulties (which will be dealt with in future work), will, however, not affect the scenarios studied here.
- 2.8
- Importantly, note also that the model is purely "syntactical" (Nehaniv 1999); i.e. there is no external meaning assigned to the states of the random variables. It allows us to inspect decision making from an agent-centric perspective, where it is only possible for the agent to use its sensors, actuator and internal states, without further knowledge of the environment. This is akin to the situation a new mind finds itself in, once it starts to inhabit a body, but has no idea about how that body is formed, or interacts with the environment (Philipona 2003).
Information Theory
- 2.9
- Information Theory (Shannon 1948; Cover 1991) can be used to study the properties of random variables. If a random variable X can assume the states x, and P(X=x) is the probability for X to assume the specific state x, we can define a measure H(X) called entropy as:
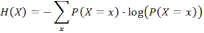
(1) - 2.10
- This is often describe as the uncertainty about the outcome of X, or the average expected surprise, or else the information gained if one was to observe the state of X, without having prior knowledge about X. The entropy has a number of important properties. Among other, the a priori uncertainty (i.e. entropy) is larger if the outcomes are more evenly distributed than if the outcomes are more concentrated on a particular value - in other words, concentrated values are easier to predict than if uniformly spread ones.
- 2.11
- Consider two jointly distributed random variables, X and Y; then we can calculate the conditional entropy of X given a particular outcome Y=y as:
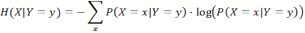
(2) This can also be generalized to the entropy of X, given Y in general, averaged over all possible outcomes of Y:
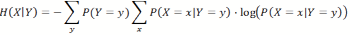
(3) - 2.12
- This is the entropy of X that remains if Y is known. Consider here H(X) and H(X|Y), the entropy of X before and after we learn the state of Y. Thus, their difference is the amount of information we can learn about X by knowing Y. Subtracting one from the other, we get a value called mutual information:
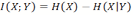
(4) The mutual information is symmetrical (Cover 1991) and measures, in bits, the amount of information one random variable contains about another (and vice versa, by symmetry). This quantity will be of central importance in the following argument.
 Digested Information
Digested Information
- 3.1
- In this section we will introduce the concept of digested information. It forms an extension of the concept of relevant information (Polani 2001) to multiple agents observing each others' actions. Relevant information is a formalism to quantify the minimum amount of Shannon information that an agent requires to decide which action to carry out in order to perform optimally. A more general definition used in the literature (e.g.Polani 2006) defines it as the minimal information needed to attain a certain (not necessary optimal) performance level. Together with the information bottleneck formalism (Tishby 1999), one can utilize relevant information to identify which features in the system are used by an agent to carry out a decision. This indicates that, whatever goal an agent aims to achieve, some part of the information about the goal is going to be "encoded" in the actions it carries out. This will be the starting point for our argument that it would be beneficial for an agent to observe the actions of another.
- 3.2
- At this point, we would like to reiterate that we are operating in a framework where there is no a priori meaning to an agent's sensor inputs, where the other agents' actions have no direct consequences for us, and where the agents are not even able to differentiate between other agents and the rest of the environment. The goal is to show that, even in this very universal, low-level and limited-assumption agent-world interaction model there is a concrete benefit in observing other agents, and therefore a motivation to develop facilities for identification of agents, directing you attention towards them and understanding their actions.
Relevant Information
- 3.3
- Assume that there is an agent that interacts with its environment by perceiving a sensor input from a set of sensor input states, and selecting an action from a set of output actions. Furthermore, assume that the actions of the agent are connected to some unspecified form of utility function (for example survival probability, or fitness) that determines the different payoffs, depending on the agent's action and the state of the environment. In this case, for every state of the environment, there exists a set of actions which result in the highest expected utility; we will call a collection of such actions for each state of the world an optimal strategy.
- 3.4
- Relevant Information is defined (Polani 2001) as the (minimal) amount of information the agent needs to acquire to be able to choose its optimal strategy. This can be measured as the minimum of mutual information between the environment and the optimal action, see Fig. 2 for some examples.
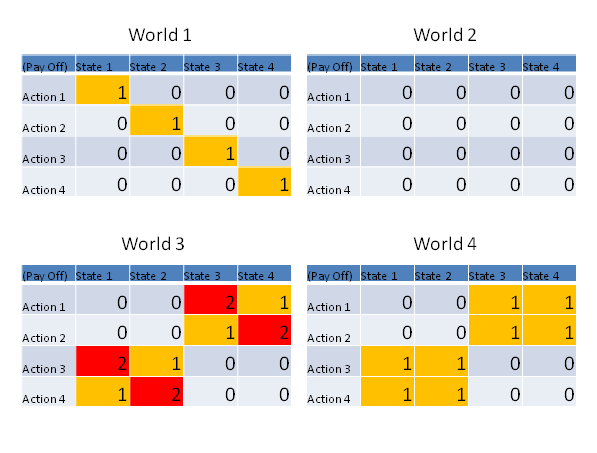
Figure 2. This figure depicts the relation between action and utility, given a certain world state. In world 1 the relevant information can be computed as two bits. The optimal strategy chooses a different action for every state of the world; therefore it has to obtain two bits of information to determine what state the world is in. World 2 is an example of a scenario where there is no relevant information. The actions of the agent do not matter, and it needs to know nothing to make the best choice. World 4 has a relevant information of only 1 bit. One optimal strategy here would still be to choose a different action for every state, but there is also another strategy that just relies on finding out if the world is in the first two or last two states. Since we look for the minimum mutual information across all strategies, the agent only needs to obtain one bit. World 3 demonstrates that a suboptimal pay-off level can be reached with less relevant information. Using the same strategy as in World 4, the agents obtains an average payoff of 1.5, but if the agents would obtain two bits of information he could achieve an average pay-off of two. - 3.5
- But the mutual information cannot only be interpreted as the amount of information the agent has to obtain; it also is the amount of information the agent has to encode in its actions to gain the actual benefit of the relevant information. The agent has to act on its information. And since the mutual information is symmetric, this can also be seen as the amount of information an observer could get about the environment by observing the agents actions. Therefore, an agent should, in its own interest, encode relevant information about the environment in its own actions.
- 3.6
- By extension, it is also possible to calculate the amount of information needed to obtain a certain payoff level, by calculating the minimum relevant information of all strategies that reach at least that level of expected payoff (Polani 2006). It became evident that an increase in the payoff level of a given action strategy always required more or the same amount of information. This means an agent that increases the payoff level of its strategy also increases the amount of encoded information, or at least keeps it the same. It also gives agents, per definition of relevant information, an incentive to increase their relevant information, since it is a by-product of increasing their performance.
- 3.7
- The agent's actions typically have a much smaller state space than the rest of the environment, and hence a much smaller bandwidth. This means in particular that the agent has to compress the relevant information from the environment into its bandwidth-limited actions, thereby creating an "Information Bottleneck" (Tishby 1999). This indicates that the agent's actions could contain a much higher "concentration" of relevant information than other parts of the environment. We will investigate this question later in a precise quantitative sense.
Benefits for Observing another Agent
- 3.8
- We will now consider a scenario with several similar agents; similar in a sense that they have a similar embodiment and utility, and they therefore need to obtain "similar" relevant information from the environment to pick their strategies.
- 3.9
- If we consider one agent's actions to be part of the environment of another agent, then, via the argument from last subsection, these actions contain information not only relevant to the first agent, but also to the observing agent. This information, which we call digested information, is beneficial because:
- Agents encode, by virtue of their own drive, relevant information in their actions
- The better they do, the more likely they are to encode more information
- The actions of an agent might exhibit a higher density of relevant information than other parts of the environment
- These actions might, in addition, provide information that is not available to the agent otherwise
- 3.10
- The first three points follow from the earlier arguments. The last, however, is motivated by the idea that an agent can retain some information. Once an agent is spatially or temporally removed from that information source, it might still be able to act upon it, and thereby propagate this information as to give other agents the chance to acquire this information, which would otherwise not be available in that place or time.
 Nonsocial Agent Simulation
Nonsocial Agent Simulation
- 4.1
- To illustrate and verify the concept of digested information we created a scenario called "Fishworld". In the following experiment we aim to verify that the information in the agent`s actions has the special properties we discussed in the earlier section on digested information.
Fishworld Model
- 4.2
- First we created a model where an agent has a simple information-obtaining task. This model will serve as a baseline for our question asking how the performance of that agent could be enhanced by observing other agents.
- 4.3
- The model considers an agent situated in a grid world of size n × m with periodical boundaries in which there is one single food location. The agent's location, and the location of the food are randomly generated at the start of the simulation, and the goal of the agent is to determine the location of the food source, in the shortest time possible. At each time step the agent can execute a move action which moves it one cell up, down, left or right. The agent then gets new sensor inputs; it is not able to see the state of the world in all cells not more than 2 cells away from it and perceives whether those cells are empty or contain a food source. After the observation, the agent then decides where to move next. This behavior is repeated until the agent finds the food.
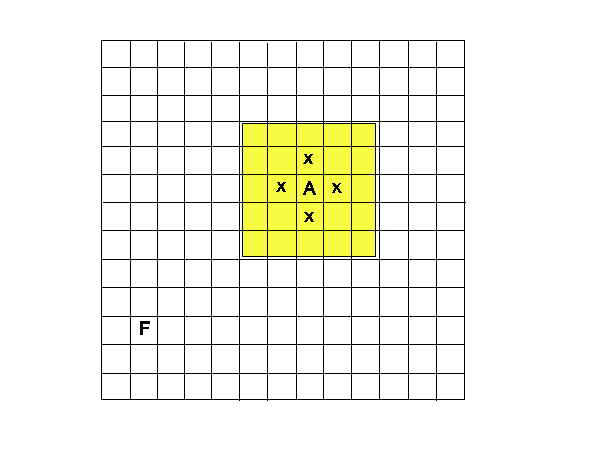
Figure 3. A sample gridworld of the size 13 × 13. A indicates the position of the agent, F the position of the food source. The yellow area is the cells visible to the agent A, and the x shows the cells it can move to in the next turn. - 4.4
- The agents determine their actions by using an internal memory which stores information about the world, in fact, this internal memory acts as a Bayesian model for the location of the food source. More precisely, the internal memory is an array that has the same number of cells as the world. Each memory cell is associated with a cell in the world. Those cells store the probability for a cell to contain food, given the past experience of the agent.
- 4.5
- Initially, all cells have the same probability of 1/n × m. However, as the agent moves around, it discovers that some cells are empty or contain food. The distribution of probabilities is adjusted by setting either the probability of a cell to zero in the case that there is no food in it, or to one in case the cell contains food. In all cases the probabilities over the cells are normalized, to ensure that the sum of probabilities is always one. The remaining uncertainty about the location of the food source position is reflected by the probability distribution and can be measured in terms of entropy H(F), where F is a random variable encoding the expected position of the food. As indicated before, the entropy computes to:
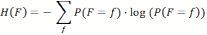
(5) Infotaxis Search
- 4.6
- To generate the agent's behavior, we adopt a greedy information-gain maximization algorithm, called "Infotaxis" (Vergassola 2007). Infotaxis was shown to provide a biologically plausible principle as to how a moth could use the very sparse information provided by their olfactory sensors to determine the source of pheromones inside a wide area. The main idea is to act in a way that increases the expected gain in information at each time step. We adapted the infotaxis approach for our discrete grid world scenario.
- 4.7
- To determine which way to go, the agent considers all its possible moves and decides which move has the highest expected reduction in remaining entropy, according to F*, its internal (Bayesian) model of F, the random variable encoding the food source. At each time step, the calculation of the expected entropy reduction of F* is done by using the respectively current distribution of F*. Thus, the expected reduction of entropy is based on the agent's current "knowledge" about F.
- 4.8
- To formalize this, we first have to define the set
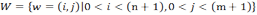
(6) that contains the positions w of all the cells of the grid world. The values i and j are the coordinates of the position on the grid world. Note that the random variable F* that encodes the food source position from the perspective of the agent uses W as alphabet for which one has | W | = n ⋅ m. Also, since we are considering a world with periodical boundaries both sides of the equation ( i, j) = ( i + n,j + m) denote the same position. Depending on the position of the agent wa, there is a set S that includes all the positions that are visible to the sensor of the agent. If the agent now takes an action α from a set of possible actions starting from the current position, one obtains a set Sα as the new set of sensor inputs after the move. To calculate the expected entropy reduction ΔH(α) depending on the action α, two main cases have to be considered. In the first case the actual location of the food source f ∈W would be in Sα , the sensor range after the action was taken by the agent. The agents assumes that this occurs with the probability of
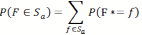
(7) in reference to our internal variable F*. In that case our current uncertainty would be reduced to zero, so the reduction in entropy would be H(F*) .
- 4.9
- The other case assumes that the location f of the food source is not in Sα . This occurs with a probability of 1- P(F ∈ Sα ). In that case we have to calculate an updated probability distribution of F*, which we will call F*α. According to Bayes' rule, we will set all P( F*α = f) = 0 for all f ∈ S α and then normalize the remaining probability values by dividing them by their total sum.
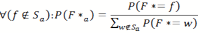
(8) The updated version of F*α can then be used to calculate the reduction of entropy in the second case, which is the difference H(F ) - H(F*α) If we put all this together the expected reduction of entropy is:
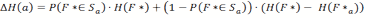
(9) So at every step the agent selects the action a that maximizes ΔH(a). If several directions have the same expected entropy reduction the agent selects one of them at random.
Results of Infotaxis
- 4.10
- As a measure of performance we record the time it took the agents to locate the food source. On average, the agents with the infotaxis behavior outperform agents that chose their direction at random by a significant factor. For a 25 x 25 world, the average search time for the location of food, measured over 50000 trials, is around 76 turns for infotaxis agents, and around 450 turns for random walk agents.
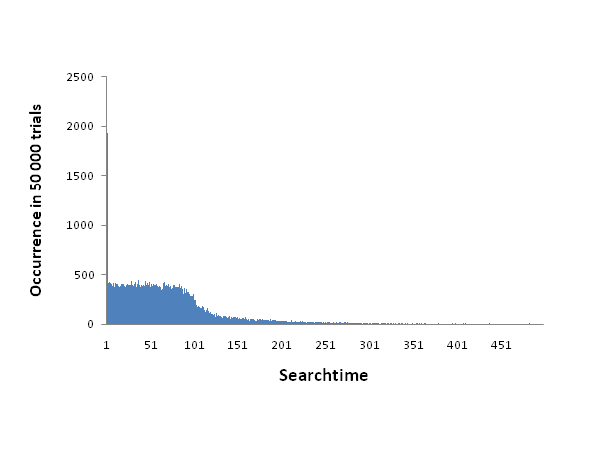
Figure 4. The distribution of time it take the agent to locate the food source with an infotaxis search. The actual numbers correspond to occurrences in 50000 trial runs. The distribution approximates the theoretical optimum, with a rough 4% chance to find the food in round 1, and an even distribution of searchtime between the first 120 rounds. - 4.11
- This compares well against the theoretically optimal searchtime for a non-social strategy which we calculated as follows. A 25 x 25 grid world has 625 positions. The agent perceives 25 positions in t=0, therefore it has a chance of 25/625=1/25 to find the food source in round 0. No matter how the agent moves, the maximum amount of positions that could enter its sensor range that were not previously seen is 5. So it would take at least 120 turns to sense all positions and thus have a probability of 1 to find the food. None of those positions are more or less likely to contain food, so the order in which they are searched can be considered arbitrary. By this reasoning we assume that the probability to discover the food source prior or in round t grows linearly with t. The two different cases have the expected searchtime of 0 and 60 respectively, therefore the optimal search time calculates to: (0 ⋅ 1/25) + (60 ⋅ 24/25) = 57.6.
- 4.12
- This is not too surprising because in this simple scenario infotaxis behaves very similar to exhaustive search. The only difference we observed where a few instances where the agents take a substantially longer time to find the food source. Closer inspections of those runs show that the agents sometimes get trapped in a local optimum of the greedy infotaxis search. Since the agent only considers the information gain for its next step, it is possible that it ends up in a situation where all the cells it could reach with one step are already explored. In this case, the next direction is chosen at random, rather than to move in a line to the closest patch of unexplored territory. Visual inspection of the agent's behavior indicates that in those cases it is entirely possible for the agent to perform a random walk for quite some time before finding an explorable area again. A possible way to circumvent this for future research would be to give the agent the ability to consider a lookahead of several future steps in deciding on an action in order to give it a more directed walk towards areas where its internal model has non-vanishing probabilities.
Relevant Information Encoding
- 4.13
- We now come to one of the core theses expounded earlier: Using our information-theoretic framework, we aim to verify the assumption about the relevant information in the agent's action. We recorded the states of A, the actions of the agents, together with F, the location of the food source relative to the agent. This makes it possible to calculate the joint entropy H(F,A) which can in turn be used to calculate the conditional entropy as H(F|A) = H(F, A) - H(A). This allows us to calculate the mutual information as I(F; A) = H(F) - H(F|A) the value that indicates how many bits of information the action of an agent contains, on average, about the location of the food source. The results for the different sensor ranges can be seen in Fig. 5.
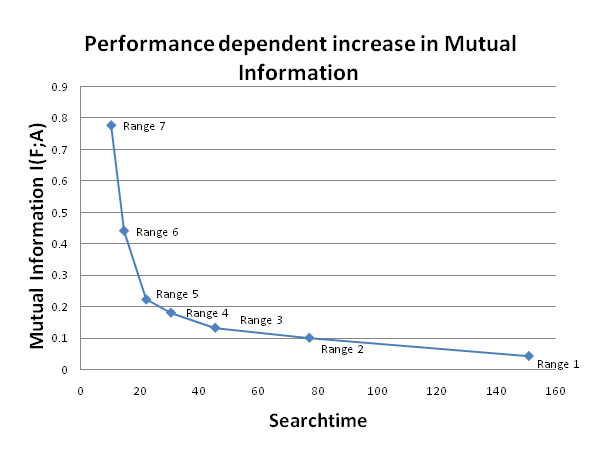
Figure 5. This graph shows how the mutual information increases with the agent's performance. The different points indicate agents with different sensor ranges. A higher range leads to a decrease in average search time, which corresponds to an increase in performance and an increase in mutual information. The mutual information is calculated with statistics recorded over 10,000 trials, and the searchtime is the average over the agents' results in those trials. - 4.14
- If we compare the information gained from the action of an agent with sensor range of 2 (≈ 0.1 bits) , to the information gained from observing a single cell (≈ 0.01 bits), then the information from the agent is significantly higher. This is true, even if we take into account that the cell only has two states, while the agent's actions have four states, and hence twice the bandwidth of the cell.
- 4.15
- This shows that the observation of an agent's actions yields relevant information, and considerably more so than the observation of a cell. This should give an agent which aims to obtain "Relevant Information" of a similar type (i.e. relating to a similar goal, such as food) and which has a limited processing capacity, an incentive to discriminate towards information from other agents rather than from empty cells.
- 4.16
- Furthermore, if we vary the sensor range of the agents in the earlier experiment, we can create agents which perform better because they have access to more information at the same time. As Fig.5 shows, the increase in range, and the ensuing increase in performance also increases the amount of relevant information encoded by the agent. In this case, an agent that performs better also encodes more relevant information.
 Social Agent Simulation
Social Agent Simulation
- 5.1
- If we look at the non-social agent model as a baseline, we can now try to answer the next question: what benefit could an agent gain from observing other agents as compared to observing some other part of the environment? We have already established that other agents encode and concentrate the relevant information from the environment in their actions, now we want to show that it is possible to extract and use this information. Since the calculation shows that the non-social agent cannot do much better with the information it currently perceives, it has to acquire new sources of information. So we will also investigate whether our hypothesis is true and the agents are able to display relevant information in their actions which is not available otherwise.
- 5.2
- Consider now a scenario where the world does not only contain one single agent and a food source, but also several other agents who have a similar set of goals as our agent. The extended version of the Fishworld model populates the grid world with several agents at the start of the simulation. All of the agents try to find the same food source. Also, in addition to the current two sensor states, corresponding to a cell being empty or containing a food source, the sensors of the agents can now assume new states that indicate that another agent moved into the corresponding cell and which direction it came from. So the four new states are {agent that moved in from the north, … south, … east, … west}. So, if an agent senses another agent within its sensor range, it will be able to perceive the direction it entered the cell from; the agent is able to see the last move of that other agent.
- 5.3
- Since we now want to evaluate what an agent could possibly learn from the other agent's actions we had the agents update their own internal model F* of the food source F depending on the other agent's actions. This adjustment of probabilities can be comfortably integrated into our existing infotaxis search.
- 5.4
- Note that for the described simulation all agents are equipped with those new "social" abilities and all of them use the other agents' actions to update their internal world models. But they only use this ability if they accidentally encounter another agent. They do not deliberately seek out other agents.
Bayesian Update
- 5.5
- Let F* be our current internal probability assumption of the location of the food source, and a the states of the random variable A that encodes the last move action of another agent we are observing. We can then use Bayes' Theorem to update the probability distribution of F*. What we are interested in is the probability of the food source to be in a specific location given the evidence of another agent's action and position P(F=w|A=a). According to Bayes' Theorem this could be calculated for every cell f of the environment as:
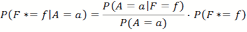
(10) - P(F*=f) the a priori probability, is the internal memory of the agent mapping the probability distribution of F, as gained by their own experience so far.
- P(A = α) is the probability that the agent takes the move action a. Since the grid world is symmetrical to rotation the empirical probability should be initially close to 1/4 for every action α ∈ { north, west, south, east}. Measurements in our single agent simulation confirm this. This is a normalization factor so the overall sum of probabilities is still one.
- P(A = α|F = f) is the probability of another agent performing action a if the food is in position f. Note that the position f in this case is calculated in relation to the position of the observed agent. So the question we are asking is for example "If the food is known to be 3 cells north of the agent what is the probability of the agent performing move action a". We then record all the cases in the past where an agent has been observed 3 cells south of a food source and the action it took.
- 5.6
- To obtain those statistics for the computer simulation we observed 50000 non-social infotaxis agents searching for the food. Note that the agents we used were non-social and thus "blind" to the actions of other agents. They behaved as described in the "Non-social Agent Model" part of this report. So even though all the agents in the simulation now have the ability to sense other agents and update their internal world models they still calculate their Bayesian update under the assumption that all others were non-social agents. We used the data obtained from those agents to create a statistic to calculate the probabilities for P(A=a) and P(A=a|F=f).
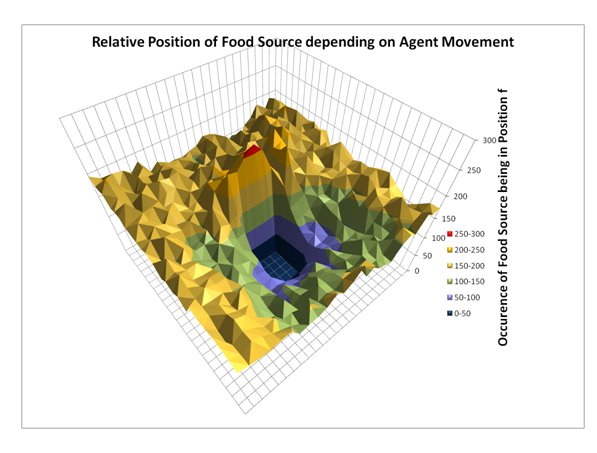
Figure 6. Graph showing P(F|A=north), the distribution of F, the food source position, given a specific agent movement (in this case north). The data was obtained from 10000 single agent simulations. The position of the agent is in the center of the graph. Note that there is a peak north of the agent, meaning that it is more likely for the food source to be directly north of the agent when it moves north. Conversely, it is very unlikely for the food source to be in the southern sensor range while the agent moves north. After the agent updates F*, it resumes the infotaxis behaviour described in the non-social agent model.
- 5.7
- For our current simulation all agents were equipped with the new mechanism, but only the performance of one single agent, chosen at random, was measured. All agents started their search at the same time and were initialized with no knowledge about the world. Agents that had successfully located the food stopped moving and were no longer perceivable by other agents. This was done to increase the challenge since it would have been trivial for another agent to infer from seeing another non-moving agent that the food must be within sensor range of that agent. As a result, the agents could not see any agents which knew where the food was.
Results
- 5.8
- In such a simulation, populated by 10 agents, the average searchtime over 10 000 trials was around 65 rounds for the social agents, as compared to around 76 turns for the non-social infotaxis fishes. Since we did not include any collision detection, or any other means for the agents to interfere with each other, the searchtime for the non-social agents remains unchanged in regard to the amount of other agents in the simulation.
- 5.9
- In the social agent simulation a further increase of the number of agents reduces the average searchtime further, down to a minimum of 48.9 turns for 95 social agents, as seen in Fig. 7. An increase in the number of agents then leads to a slow rise of the average searchtime again.
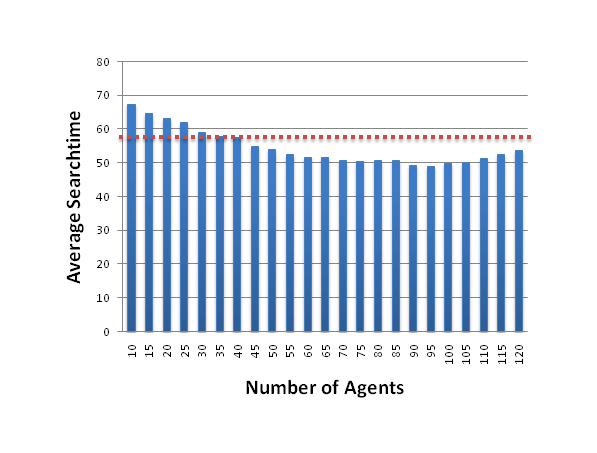
Figure 7. The average time to locate the food (over 10 000 trials for each number of agents), depending on the number of other social agents in the simulation. The line indicates the theoretical optimal searchtime of 57.6 for a non-social agent. Note that several agent populations perform better than that, and must therefore obtain additional information not available to their non-social counterparts. - 5.10
- Prior calculations showed that an agent, who only used its sensors to detect if cells are empty or contain food, could not be faster than an average of 57.6 rounds. Bigger agent populations beat this optimal non-social behavior, and must therefore obtain useful information from their observation of other agents; information that would otherwise not be available to them.
- 5.11
- A possible interpretation for the increase in search time, once the number of agent increase above 100, is similar to the explanation for the large search time of single agents. Visual inspection of the simulations indicates qualitatively that, if an agent observes agents coming at him from every direction (which becomes more probable with a high agent density), then it can rule out the existence of food in any of these directions for the next few unseen cells. This indicates to the agent that there would be no information gain in any direction in the next step forcing it to choose the direction at random. Such behaviour is inefficient and becomes increasingly more common with more agents present in the simulation.
- 5.12
- Another interpretation for the loss in performance might be the increased proliferation of "faulty" information. While, in our simulation, all the sensor data picked up from the environment would lead to the agent being more "correct", it is possible that observing another agent would alter the internal probability distribution so that the agent believes the food is less likely to be in its actual position. This is possible because the agents` actions are only probabilistically determined by the food position; therefore there are improbable cases where the agent's actions can mislead us.
- 5.13
- This in itself should be unproblematic for the Bayesian update, since it is specifically designed to deal with those cases. But our repeated application of Bayesian update is only correct, if the observed events are marginally independent. In our simulation all agents use Bayesian update, so it is possible for them to create a feedback loop where an unlikely event leads other agents to assume an unlikely probability distribution which in turn leads to more unlikely actions being performed by those agents. This could then lead to a proliferation of "faulty" information which in turn would lead to a decrease in agent performance. It seems plausible that such a scenario is more likely with a higher number of agents present. But, as of now, we believe further investigation is necessary to determine the exact nature of this effect.
 Conclusion
Conclusion
- 6.1
- Concluding, the simulation supports the claims of our "Digested Information" argument. The observed agents, motivated only by their own benefit and without any explicit interest in communication, ended up encoding relevant information in their actions. They obtained this information from the environment through their sensors, processed it, and injected it in "compressed" form back into the environment through their actions. The relevant information contained in those actions then had a higher density than any other part of the environment. Furthermore, an increase in the efficiency of the agent's strategy also led to a further increase in the amount of encoded relevant information. Those special properties of another agent's actions offer a nice incentive for another agent to develop the necessary abilities to differentiate agents from the environment and direct its attention at them. Ultimately (but not studied here), it could even prove to be useful to identify other agents separately, e.g. one would be aiming to discern which agents are doing better than others, and focus one's attention onto those. An agent that would be able to observe the actions of other agents could also use them as information pre-processors, and basically "outsource" part of its own information processing to other agents.
- 6.2
- Our simulation also showed that, once those abilities are acquired, an observing agent can use the information obtained from observing another agent's action to increase the performance of its own strategy. This performance increase is so significant that the "social" agent outperforms every agent with a non-social strategy, due to those agents limited information intake. Therefore, the socially observing agent has to acquire information that is otherwise unobtainable, so it must have been transported either through time or space by the other agent. This property of other agents makes them even more useful as external pre-processors of information.
- 6.3
- A major benefit of the introduced framework is the ability to actually formulate the concept on a quantitative basis. In the given Fishworld scenario we were able to show that the information in the agents' actions is not only better encoded, but that it also uses the bandwidth of its respective variables at a roughly 5 times more efficient level. Furthermore, we can exactly quantify how much information about the food location is, on average, encoded in the agent's behaviour. This exact analysis enables us to both understand the limits for the flow of information and it also makes it possible to see exactly how much beneficial (i.e. relevant) information the various information sources offer.
Plausibility
- 6.4
- As simple as our current simulation model is, it already contains all ingredients necessary to produce the effect we hypothesized concerning the "Digested Information" argument. The simplicity and minimality of the model demonstrates that it is already sufficient to show the predicted effects. The argument given in the section "Digested Information" is expected to be valid for all models that can be reduced to the presented framework in that every agent which needs to obtain information from the world to select an action most beneficial to it will encode some relevant information in its actions.
- 6.5
- In this context it is interesting to note that there is some well documented biological behaviour for bees (Baude 2008) and birds (Parejo 2008) which both encode information into their actions without an explicit intent to communicate. Danchin calls this phenomenon "inadvertent social information" and describes several additional cases where this behaviour is also suspected (Danchin 2004). In relation to that work, our contribution is to offer an information-theoretic explanation for this behaviour, including a method to actually quantify it. Of special interest is the work of Parejo (2008), because it looks at groups of birds that are somewhat similar, but not homogenous. Since the usefulness of "Relevant Information" is based on the assumption of homogenous agents, with similar payoff function, this raises the interesting question on how the "Relevant Information" diminishes once the similarity between agents decreases, and whether this kind of agent similarity can actually been measured or quantified.
- 6.6
- Finally, the original behaviour of the agent in our social Fishworld model is based on the "Infotaxis" model of Vergassola (2007) who already demonstrated that the actual behaviour of moth searching for a mate bears a functional resemblance to the infotaxis search principle. Thus, even without a detailed knowledge about the concrete biological mechanism behind search, it is plausible to assume that informational principles could actually drive search behaviours in biology.
Interaction
- 6.7
- Finally, we need to discuss two further remaining questions in regard to this work: whether above mechanism actually leads to a form of social interaction where one social agent reacts in regard to the actions of another, and how this model would deal with the possibility of one agent deliberately trying to deceive another. Both are already implicitly covered by this framework through the way we define relevant information. Since it is defined as the minimal information, on average, that an agent has to acquire to achieve a certain performance level, this is at the same time the information that needs to be reflected in the actions. In other words, it is necessary for the agent to act according to the acquired information. Acquired information that is not, at least potentially, acted upon is useless, and a certain pay-off level can only be reached, if the agent is willing to act accordingly, and encode at least that much information about the environment in its actions.
- 6.8
- That means that, for social interaction, if an agent receives information about another (similar) agent's actions, then he has to react to that information, and thus to that other agents' actions if it wants to improve its own performance.
Deceit
- 6.9
- Currently our model does not model scarcity of resources, since we intended to demonstrate that just informational considerations are sufficient to create a motivation for interaction, even without considering a scenario where the other agent`s actions have consequences that actually change the world. In a scenario where resource scarcity was modelled, it would be difficult to separate the different effects.
- 6.10
- But if there is only a limited amount of resources it might be beneficial for the agent to mislead others, or at least offer only a minimum of useful information. There are two ways how this could be addressed. If there are several strategies with the same pay-off level, the agent could choose one that would reveal the least information about the environment. This is de facto the default principle behind the calculation of relevant information. Therefore, there is a hard limit on how much information an agent has to display, to act on a certain performance limit.
- 6.11
- Now, if the agent wants to display even less information, it has to sacrifice a certain amount of its performance in regard to the environment. A deceit on that level is not possible without accepting a trade-off that moves away from an optimal strategy. Also, there might be a minimum amount of information to perform better than random (see also Klyubin 2007, appendix E for an analogous calculation in a related gradient scenario). Of course, if the loss of pay-off by proliferating information to opponents is greater than the loss of pay-off by committing to a suboptimal strategy than this might be rational. If we include the other agent as part of the agent environment, this situation can be seen as reframing the whole pay-off table, and in this context a deceiving action would again be optimal. The study of such highly interwoven situations in the future promises further significant insights into the role of information in shaping the collective dynamics of agents, under otherwise minimal assumptions.
 References
References
-
ATTNEAVE F (1959) Applications of information theory to psychology: A summary of basic concepts, methods, and results, New York: Holt, Rinehart & Winston, 1959.
AXELROD R (1984) The Evolution of Cooperation, Basic Books, 1984.
AY N, Bertschinger N, Der R, Goettler F and Olbrich E (2008a) Predictive information and explorative behavior of autonomous robots, European Physical Journal B - Condensed Matter and Complex Systems, 63, pp. 329 - 339, 2008.
AY N and Polani D (2008b) Information Flows in Causal Networks, Advances in Complex Systems, 11(1):17-41,2008. [doi:10.1142/S0219525908001465]
BARLOW H B (1959) Possible principles underlying the transformations of sensory Messages, in Rosenblith, W. A., (editors), Sensory Communication: Contributions to the Symposium on Principles of Sensory Communication, pp. 217 - 234, The M.I.T. Press, 1959.
BARLOW H B (2001) Redundancy reduction revisited, Network: Computation in Neural Systems, 12(3):241 - 253, 2001. [doi:10.1080/net.12.3.241.253]
BAUDE M, Dajoz I and Danchin É (2008) Inadvertent social information in foraging bumblebees: effects of flower distribution and implications for pollination, Animal Behaviour, 2008. [doi:10.1016/j.anbehav.2008.08.010]
BIALEK W, Nemenmann I and Tishby N (2001) Predictability, Complexity, and Learning, Neural Computation,13:11, 2409-2463, 2001. [doi:10.1162/089976601753195969]
BLACKMORE S (2000) The Meme Machine (Popular Science). Oxford University Press, USA, May 2000.
CAPDEPUY P, Nehaniv C L and Polani D (2007) Maximization of Potential Information Flow as a Universal Utility for Collective Behaviour, Proceedings of the First IEEE Symposium on Artificial Life, p. 207-213, 2007. [doi:10.1109/alife.2007.367798]
COVER T M and Thomas J A (1991) Elements of information theory, John Wiley and Sons, Inc., 1991.
DANCHIN E, Giraldeau L-A, Valone T J, and Wagner R H (2004) Public information: From nosy neighbors to cultural evolution, Science, 305 (5683), July 2004, pp. 487 - 491. [doi:10.1126/science.1098254]
DAWKINS R (1990) The Selfish Gene. Oxford University Press, September 1990.
DER R, Steinmetz U and Pasemann F (1999) Homeokinesis--a new principle to back up evolution with learning, M. Mohammadian (editors), Computational intelligence for modelling, control, and automation, Amsterdam, IOS Press, (pp. 43-47), 1999.
GOSTOLI U (2008) A Cognitively Founded Model of the Social Emergence of Lexicon, Journal of Artificial Societies and Social Simulation 11 (1) 2, https://www.jasss.org/11/1/2.html.
GOTTS N M and Polhill J G (2009) When and How to Imitate Your Neighbours: Lessons from and for FEARLUS, Journal of Artificial Societies and Social Simulation 12 (3) 2, https://www.jasss.org/12/3/2.html.
KLYUBIN A S, Polani, D and Nehaniv C L (2004) Tracking Information Flow through the Environment: Simple Cases of Stigmergy, In J. Pollack, M. Bedau, P. Husbands, T. Ikegami, and R. A. Watson (editors) Artificial Life IX: Proceedings of the Ninth International Conference on the Simulation and Synthesis of Living Systems, The MIT Press, 2004, pp. 563-568.
KLYUBIN A S, Polani D and Nehaniv C L (2005) All Else Being Equal Be Empowered. In M. S. Capcarrère, A. A. Freitas, P. J. Bentley, C. G. Johnson, and J. Timmis, (editors), Advances in Artificial Life: Proceedings of the 8th European Conference on Artificial Life, volume 3630 of Lecture Notes in Artificial Intelligence, pages 744-753. Springer, Sep 2005.
KLYUBIN A S, Polani D and Nehaniv C L (2007) Representations of Space and Time in the Maximization of Information Flow in the Perception-Action Loop, Neural Computation, 19(9):2387-2432, 2007. [doi:10.1162/neco.2007.19.9.2387]
KLYUBIN A S, Polani D and Nehaniv C L (2008) Keep Your Options Open: An Information-Based Driving Principle for Sensorimotor Systems, PLoS ONE, 3(12):e4018. , Dec 2008. [doi:10.1371/journal.pone.0004018]
LAUGHLIN S B (2001) Energy as a constraint on the coding and processing of sensory information. Current Opinion in Neurobiology, (11):475-480, 2001. [doi:10.1016/s0959-4388(00)00237-3]
LYNCH A (1999) Thought Contagion: How Belief Spreads Through Society. Basic Books, January 1999.
MAYNARD SMITH J (1982), Evolution and the Theory of Games, Cambridge Univ. Press, 1982.
NEHANIV C L (1999) Meaning for observers and agents IEEE International Symposium on Intelligent Control / Intelligent Systems and Semiotics (ISIC/ISAS'99), IEEE Press, 1999, pp. 435 - 440.
PAREJO D, Danchin, É, Silva N, White J F, Dreiss A N and Avilés J (2008) Do great tits rely on inadvertent social information produced by blue tits? A habitat selection experiment. Behavioral Ecology and Sociobiology, 62, pp. 1569-1579, 2008. [doi:10.1007/s00265-008-0586-4]
PEARL J (2000) Causality, Cambridge University Press, 2000
PHILIPONA D, O'Regan J K, Nadal J P (2003) Is there something out there? Inferring space from sensorimotor dependencies, Neural Computation. 15(9):2029-49, Sept 2003. [doi:10.1162/089976603322297278]
POLANI D, Martinetz T and Kim J T (2001) An information-theoretic approach for the quantification of relevance, Proceedings of the 6th European Conference on Advances in Artificial Life, Springer-Verlag, London, 2001, pp. 704 - 713. [doi:10.1007/3-540-44811-X_82]
POLANI D, Nehaniv C, Martinetz T, and Kim J T (2006) Relevant Information in Optimized Persistence vs. Progeny Strategies, in M.Rocha, L., Bedau, M., Floreano, D., Goldstone, R., Vespignani, A., and Yaeger, L., editors, Proc. Artificial Life X, August 2006, pp. 337 - 343.
POLANI D (2009) Information: currency of life? HFSP J. Volume 3, Issue 5, pp. 307-316, October 2009. [doi:10.2976/1.3171566]
PROKOPENKO M, Gerasimov V and Tanev I (2006) Evolving Spatiotemporal Coordination in a Modular Robotic System, in Nolfi, S., Baldassarre, G., Calabretta R., Hallam, J. C. T., Marocco, D., Meyer J.-A., Miglino, O., and Parisi, D., (editors). From Animals to Animats 9: 9th International Conference on the Simulation of Adaptive Behavior (SAB 2006), Rome, Italy, Springer, Lecture notes in computer science, vol. 4095, 558-569, 2006. [doi:10.1007/11840541_46]
SHANNON C E (1948) A mathematical theory of communication, Bell System Technical Journal, 27, July 1948, pp. 379 - 423. [doi:10.1002/j.1538-7305.1948.tb01338.x]
SPIRTES P, Glymour C and Scheines R (2001) Causation, Prediction, and Search, Second Edition, The MIT Press, 2001.
SPORNS O and Pegros T K (2003) Information-Theoretical Aspects of Embodied Artificial Intelligence, Embodied Artificial Intelligence, 74-85, 2003.
TISHBY N, Pereira F C and Bialek W (1999) The information bottleneck method, Proc. of the 37th Annual Allerton Conference on Communication, Control and Computing, 1999, pp. 368 - 377.
TOUCHETTE H and Lloyd S (2004) Information-theoretic approach to the study of control systems, Physica A,331(1-2):140-172, Jan. 2004. [doi:10.1016/j.physa.2003.09.007]
VERGASSOLA M, Villermaux E and Shraiman B I (2007) "info-taxis" as a strategy for searching without gradients, Nature, 445(7126), 2007, pp. 406 - 409. [doi:10.1038/nature05464]