Abstract
Abstract
- We describe a computer model of general effectiveness of a hierarchical organization depending on two main aspects: effects of promotion to managerial levels and efforts to self-promote of individual employees, reducing their actual productivity. The combination of judgment by appearance in the promotion to higher levels of hierarchy and the Peter Principle (which states that people are promoted to their level of incompetence) results in fast declines in effectiveness of the organization. The model uses a few synthetic parameters aimed at reproduction of realistic conditions in typical multilayer organizations. It is shown that improving organization resiliency to self-promotion and continuity of individual productiveness after a promotion can greatly improve the overall organization effectiveness.
- Keywords:
- Organization Productivity, Peter Principle, Agent Based Modeling
 Introduction
Introduction
- 1.1
- Computer simulations have become increasingly popular in describing social phenomena, from traffic jams to opinion formation. The number of topics and works is very large and there are even popular expositions of the discipline, such as Ball (2004). In some cases the new tools provide significant insight into observed phenomena. In some others the simulations may add a level of understanding into already formulated explanations of real world phenomena. In this work we present a computer model of general effectiveness of hierarchical organizations, focused at effects of individual effectiveness of employees. The model aims at extending the the famous Peter Principle (Peter & Hull 1969): "In a hierarchy every employee tends to rise to his level of incompetence". Thus in any hierarchical organization global effectiveness is diminished due to the fact often skills which make a person an excellent worker at a given level in the organization may be unsuited at a higher one. Promotion of the best employees (which looks like a reasonable way of action from the point of view of employee recognition and motivation) results in loss of skilled workers and, possibly, creation of less than optimal managers. Of course, such ineffective manager would no longer be promoted, so eventually everyone would become stuck at their level of incompetence. Peter originally formulated this idea in a joke-like fashion, but once we recognize its importance, it becomes pretty obvious and common sense.
- 1.2
- It should be noted that companies fight against the “incompetence stasis” resulting from Peter Principle via constant pressure on employees: promoting the best is usually accompanied by firing the worst performers at each level of hierarchy. But while this leads to culling of non-performers, it might mean loss of capable lower level employees who have been promoted beyond their skill range. The process creates a bad manager from a good worker, and then gets rid of the bad manager. This problem can in turn be solved by providing horizontal career paths, which ensure that the best specialists could be recognized and awarded without changing the nature of their tasks, so that their skills would not be lost upon promotion. Yet, despite the fact that Peter Principle is known for forty years, examples of loss of productivity due to promoting people beyond their capacities are present in almost all types of hierarchical organizations, from scientific research to commercial companies.
- 1.3
- The topic has already been studied well beyond the original witty insight. Mathematical analyses appeared as early as one year after the original book (for example Kane (1970)). The topic is quite actively researched. For example, a computer model of Peter Principle in action has been recently published by Pluchino et al. (2010), while earlier works on the topic include Fairburn & Malcomson (2001); Lazear (2001); Lazear (2004); Dickinson and Villeval (2007). In this paper we attempt to go beyond the earlier approaches, which assume that the basis for promotions is the actual performance of the organization members. Our motivation comes from experience that decisions to hire and promote are based on perceived performance. Thus, employees or external candidates who focus on presenting themselves and their own results in good light (instead of just working) have better chances of advancement. Such individual public relations activity or self-promotion is quite natural and present everywhere: in commercial companies, universities or political parties. The result is that not only people reach their incompetency level, but also that the whole promotion process often focuses on those who have little to contribute to the organization but rather direct their efforts to (and spend their time on) getting promoted, attempting to cheat the evaluation systems based on measurements of performance. The observation has been made by Scott Adams (Adams (1996)), who, discussing Peter Principle, remarked that "incompetent workers are promoted directly to management, without ever passing through competence stage". While the negative effects of Peter Principle are beyond doubt, as Adams observes, Êit provided a boss who may not understand his present job, but at least understood that of his subordinates. If promotions not only change the nature of the required skills but also depend on superficial characteristics, presented for the benefit of the people who decide promotions, the results can be, and often are, much worse. This combination of the two phenomena, which we propose to call the Dilbert-Peter Principle limits the effectiveness of organizations. The name has already been used by Faria (2000).
- 1.4
- It might seem presumptuous to use fictitious Pointy Haired Boss and other characters featured in the Dilbert strip as “real world” basis for computer modeling. Would it not be better to use official company data, histories and performance figures as a source for inspiration for a simulation model? In our opinion, just the contrary. The official documents are usually written with the purpose of hiding the very mistakes and ineffectiveness we want to discuss. On the other hand, due to the popularity of the strip and its web site( http://www.dilbert.com), the accumulated “database” of cases of stupidity and mismanagement is much better and true to life than the official corporate profiles and annual reports. Author's own experience gathered in the course of over 15 years of work in several commercial companies (Polish, American, German and French) and more than ten years within an academic institution, suggests that Dilbert jokes are often an uncannily accurate descriptions modern organizations. Thousands of letters sent to Scott Adams from all over the world confirm this experience. In many areas we find organizations which share similar activities, sizes and structures, yet which differ widely in their effectiveness. This is true for both commercial companies and public organizations. Our goal is to find which which aspects of the model are crucial in determination of the overall productivity, and perhaps to suggest measures to improve the operations in real life.
 Model description
Model description
- 2.1
- The purpose of the model is to provide a simplified description of effectiveness of a hierarchical organization in which people act to maximize their promotion chances. The promotions are achieved through comparisons of individuals within a given hierarchy level. This is similar to internal tournament models, introduced by Lazear and Rosen (1981). Before we discuss further, a brief note about the meaning of productivity is needed here. We follow Pritchard (1990), who discusses broad range of meanings of the term, used to note output, individual performance, production, profitability competitiveness, work quality of individuals, groups and organization units. Prichard equates productivity with efficiency or effectiveness, defines as measure of outputs divided by inputs and by relationship of outputs to some standards. One of the key differentiators of the model is the division between real or effective productivity (for example sales results, number of research publications, lines of code accepted into a project) and perceived productivity, as seen by the authorities responsible for making promotion decisions. While the effectiveness of the whole organization is measured by accumulating the real output of the contributors, their advancement within the organization is related to comparative perceived results. Observations show that often it is not the best performer that gets promoted (as postulated by the original Peter Principle) but those who appear to be the best workers.
- 2.2
- In our model we assume that all employees are trying to get promoted. The actual incentives (increased salaries, more power and status etc.) and benefits are not discussed. We also assume that the employees understand the real productivity/perceived productivity difference and have therefore the two main strategies to achieve promotion. The first is via improvement of the real output, based on hope that it would be noticed and rewarded. The second strategy, observed all too frequently, is through the use of political games, thanks to which a person appears to be more productive and worthy of advancement. This is an extension of the classical approach in which employees signal their abilities by means of an effort display (MacLeod and Malcolmson (1988)). Here, the effort might be in pure signalling, with less focus on the actual job in hand. Such difference has been stressed many years ago by Spence (1973), who remarked that while job applicants can do little about their actual results and indices measuring them, signals are under employee control and can be subject to manipulation. In many cases, these individual PR activities are done at the expense of the actual work, thereby decreasing the contribution of the individual to the overall organizational effectiveness. Within the model, each agent has a fixed “psychological makeup”, deciding on the actual mix of strategies used. In contrast to real life, agents can not modify their behavior. But, as we are interested in checking who gets promoted and how the process of promotion determines the composition of management levels and overall productivity of the company, keeping agents' characteristics fixed seems a reasonable simplification.
- 2.3
- Following Pluchino et al. (2010) we propose to compare two possible scenarios, differing in description of individual productivity after the promotion. The first one, called continuity scenario ('common sense' in Pluchino et al. (2010)), in which the productivity at the new post is similar to the one at the previous one. Such situation is expected when the range of tasks related to the new position remains similar to the previous ones. The Peter scenario assumes that due to difference in tasks at different levels of the organization the productivity at the new post is unrelated to the old one. In both cases our current model measures the perceived productivity, including effects of internal politics. We investigate the effects of promotion process on key characteristics of the organization: its general productivity, averages of effectiveness at various levels of the hierarchy, dynamics of changes due to the promotion preferences.
- 2.4
- The simulations presented here are designed to include several phenomena associated with modern enterprises and organizations, namely hierarchical organization, management contribution, measurements of effects dependent on both individual qualities and cumulative results of subordinates and interplay between in-company promotion and external hiring. The goal of the model is to provide some predictions regarding the dependence of the measured qualities on a few simple controls: importance of the political gamesmanship for promotion, heritability of skills after promotion (the continuity model versus Peter hypothesis) and tendency for internal or external advancement. Presented results are based on a small number of selected conditions and, we hope, can be a starting point for a more advanced study.
- 2.5
-
The basic model applies to organizations in which activities are uniform,
i.e. where the nature of tasks is the same for all positions at a
given hierarchy level. Examples might be provided by some government
institutions (such as tax offices), research institutions or by specialized
parts of larger bodies, for example sales divisions in large corporations.
While the basic tasks and measurement criteria per level are comparable
throughout the organization, advancing from one level to another might
change (sometimes very significantly) the nature of the job: from
tax collection or sales to management, more and more remote from the
outside world as we move up in hierarchy.
Hierarchical structure
- 2.6
-
We are interested here in department based hierarchical organizations,
such as a commercial company with many local sales offices, or large
software house with multiple project teams. To a certain degree this
description applies to research and government institutions as well. The simplest
way of modeling such organization is via pyramid structure of units
of the same size. Organization is divided into
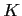 levels, numbered
from top (
levels, numbered
from top (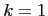 ). Each unit consists of a manager at level
). Each unit consists of a manager at level 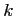 and
and
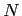 subordinates (workgroup) at level
subordinates (workgroup) at level 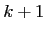 . With the exception of the topmost executive,
each employee has exactly one direct manager and each manager
has exactly
. With the exception of the topmost executive,
each employee has exactly one direct manager and each manager
has exactly
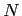 subordinates.
subordinates.
- 2.7
-
The size of the whole organization is thus
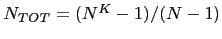 .
To achieve reasonable number of levels and unit sizes we may restrict
ourselves to
.
To achieve reasonable number of levels and unit sizes we may restrict
ourselves to 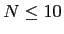 and
and 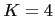 or
or 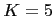 , resulting in organizations
with enough structure and with size greater than 500 people.
This corresponds to businesses above the "Small Business" definition
as described in U.S. Small Business Administration Table of Small Business Size Standards (2008)
The size has been chosen to allow statistical effects and relative anonymity of employees to play significant role
in the organization. In small companies the closer connection between employees and those responsible for promotion
decisions often allows better recognition of actual performance and competences, diminishing effects of Dilbert-Peter
Principle.
, resulting in organizations
with enough structure and with size greater than 500 people.
This corresponds to businesses above the "Small Business" definition
as described in U.S. Small Business Administration Table of Small Business Size Standards (2008)
The size has been chosen to allow statistical effects and relative anonymity of employees to play significant role
in the organization. In small companies the closer connection between employees and those responsible for promotion
decisions often allows better recognition of actual performance and competences, diminishing effects of Dilbert-Peter
Principle.
Agent characteristics
Real work and self-promotion - 2.8
-
Employees are represented by computer agents numbered via subscript
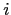 . Each agent is characterized by two parameters. The first,
. Each agent is characterized by two parameters. The first, 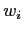 ,
is its capacity to perform real work at its current position,
called also raw productivity. We consider here two types of contributions:
direct work (for example value of sales achieved by a salesman, lines of code written by a programmer or
research papers published by a scientist) and managerial contribution,
related to organizing, coaching and monitoring efforts of others.
Managers, by their actions, may significantly influence the sum of individual results of their subordinates.
This would correspond, to use the above examples, to overall sales figures for a branch office,
code submitted by a software development group or the research standing of a university department.
We have decided to combine the two contributions into
one parameter, to keep the spirit of Peter principle, defining one "competence",
as appropriate for a given position.
,
is its capacity to perform real work at its current position,
called also raw productivity. We consider here two types of contributions:
direct work (for example value of sales achieved by a salesman, lines of code written by a programmer or
research papers published by a scientist) and managerial contribution,
related to organizing, coaching and monitoring efforts of others.
Managers, by their actions, may significantly influence the sum of individual results of their subordinates.
This would correspond, to use the above examples, to overall sales figures for a branch office,
code submitted by a software development group or the research standing of a university department.
We have decided to combine the two contributions into
one parameter, to keep the spirit of Peter principle, defining one "competence",
as appropriate for a given position.
- 2.9
-
The second characteristics of an agent is the effort
he or she puts into internal political positioning (self-promotion)
denoted by
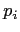 . This parameter may include
activities and skills that are quite commonplace in modern organizations,
for example twisting the facts to present
one's own results in a good light (“Power Point economy”),
doing the opposite with respect to other employee achievements, forming and nurturing of cliques and
power circles. We consider here that effort
. This parameter may include
activities and skills that are quite commonplace in modern organizations,
for example twisting the facts to present
one's own results in a good light (“Power Point economy”),
doing the opposite with respect to other employee achievements, forming and nurturing of cliques and
power circles. We consider here that effort 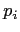 is focused on personal
interest of the agent and does not contribute to actual results –
neither those related to direct output, nor to management contributions.
In this work we separate the “productive” part of political activities
(such as organizing, motivating, ensuring cooperation...),
being an inherent part of management activities and contributing to
the real work done, from activities aimed at personal gain.
is focused on personal
interest of the agent and does not contribute to actual results –
neither those related to direct output, nor to management contributions.
In this work we separate the “productive” part of political activities
(such as organizing, motivating, ensuring cooperation...),
being an inherent part of management activities and contributing to
the real work done, from activities aimed at personal gain.
- 2.10
-
In our simulations we assume that the
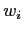 is drawn from Gaussian
distribution centered around
is drawn from Gaussian
distribution centered around 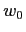 (a good value for
(a good value for 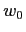 might
be
might
be 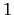 , for reasons explained in the next section)
with distribution width of
, for reasons explained in the next section)
with distribution width of 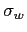 , while for
, while for 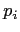 the distribution
is flat from 0 to
the distribution
is flat from 0 to 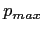 . The two parameters are used to model
the actual results of the work done by the agent and the perception
of the work done within the organization. The resulting contribution
to the organization productivity by the agent is given by the difference
. The two parameters are used to model
the actual results of the work done by the agent and the perception
of the work done within the organization. The resulting contribution
to the organization productivity by the agent is given by the difference
This is a simple way of describing the fact that focusing on improving one's own position by political activities must deduct some time from the time spent on actual work effort. On the other hand, effort spent on political maneuvers improves the perceived results. This is described in a more complex way, depending on additional parameter: organization's susceptibility to self-promotion (Eq. 3). Similar trade-off between technical and social skills has been proposed by Faria (2000). It should be noted, however, that in our approach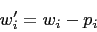
(1) 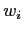 contains
both the technical and social skills as defined by Faria.
The change of responsibility upon promotion might result in a different
optimal ratio of the two types of skills, and therefore, in different
value of
contains
both the technical and social skills as defined by Faria.
The change of responsibility upon promotion might result in a different
optimal ratio of the two types of skills, and therefore, in different
value of 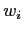 before and after promotion. We have
used values of
before and after promotion. We have
used values of 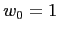 in the
simulations. This choice has been motivated by the use of multiplicative
approach to management contribution (discussed in the next section).
The width of the Gaussian distribution of capabilities used in results presented in this article was,
in the
simulations. This choice has been motivated by the use of multiplicative
approach to management contribution (discussed in the next section).
The width of the Gaussian distribution of capabilities used in results presented in this article was,
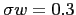 . Such distribution of
. Such distribution of 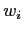 allows occasional differences of individual productivity
in the range of 200% or even more. The treatment of
allows occasional differences of individual productivity
in the range of 200% or even more. The treatment of 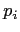 is different: it measures an internal characteristic of a person,
its drive to improve own position, which does not improve the actual
results in any way and has not been considered in the past. The choice of flat distribution
is different: it measures an internal characteristic of a person,
its drive to improve own position, which does not improve the actual
results in any way and has not been considered in the past. The choice of flat distribution 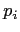 reflects relatively frequent
cases of extreme behavior: from total lack of focus on self-promotion
to giving it large part of the total effort of the employee.
Author personal experiences lead to assumption of
reflects relatively frequent
cases of extreme behavior: from total lack of focus on self-promotion
to giving it large part of the total effort of the employee.
Author personal experiences lead to assumption of 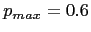 ;
there are people who do spend more than half of time on political
ploys aimed to advance their position.
;
there are people who do spend more than half of time on political
ploys aimed to advance their position. 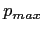 is a fully adjustable parameter of the model.
Moreover, it should be remembered that within the model
is a fully adjustable parameter of the model.
Moreover, it should be remembered that within the model 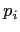 of a given agent is not changed when the agent is promoted to a higher level.
of a given agent is not changed when the agent is promoted to a higher level.
Management contribution - 2.11
-
To take into account the fact that in most organizations managers
are measured on the results of the teams they manage, we introduce
here accumulated versions of the effective work and perceived results,
which combine the results of the manager and his or her subordinates.
We have chosen to use a multiplicative way of describing the influence
of the manager on the results of the department. This is by no means
the only choice, but it provides a simple way of describing situation
where a bad manager (
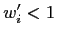 ) would actually decrease the overall
output of his department, while the good manager (
) would actually decrease the overall
output of his department, while the good manager (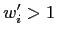 ) would
increase it. This multiplicative approach differs from additive view
of Pluchino et al. (2010), who propose that contributions at higher
levels of hierarchy should be modeled by simple addition of manager's
results multiplied by an artificial factor ranging from 0.2 at the
lowest level to 1.0 at the top management, to simulate the increased
importance of the higher levels of hierarchy. Increase of productivity
of given employee over time is a real phenomenon found in many organizations,
related with accumulation of skills and experiences. It would describe
a horizontal progress from an apprentice to an expert - within
a given level of hierarchy. It is less suited to vertical promotion
and managerial tasks, where the contribution of a manager comes from
organizing the work of the subordinates. Moreover, additive approach
can not describe the Dilbertian influence of idiot bosses who often
decrease the results of the departments they manage. The importance
of the individual contribution must be higher as we move up in the
organization levels. Thus we propose that effective results are given
by
) would
increase it. This multiplicative approach differs from additive view
of Pluchino et al. (2010), who propose that contributions at higher
levels of hierarchy should be modeled by simple addition of manager's
results multiplied by an artificial factor ranging from 0.2 at the
lowest level to 1.0 at the top management, to simulate the increased
importance of the higher levels of hierarchy. Increase of productivity
of given employee over time is a real phenomenon found in many organizations,
related with accumulation of skills and experiences. It would describe
a horizontal progress from an apprentice to an expert - within
a given level of hierarchy. It is less suited to vertical promotion
and managerial tasks, where the contribution of a manager comes from
organizing the work of the subordinates. Moreover, additive approach
can not describe the Dilbertian influence of idiot bosses who often
decrease the results of the departments they manage. The importance
of the individual contribution must be higher as we move up in the
organization levels. Thus we propose that effective results are given
by
where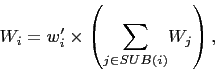
(2) 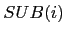 denotes the agents that are directly managed
by agent
denotes the agents that are directly managed
by agent 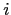 . Due to recursive nature of the above expression, the
effective results of a manager
. Due to recursive nature of the above expression, the
effective results of a manager 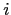 include contributions of all
its subordinates. For the lowest level of hierarchy
include contributions of all
its subordinates. For the lowest level of hierarchy 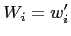 .
In such model, if all agents have the same value of
.
In such model, if all agents have the same value of 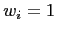 and
and
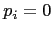 (no effort is wasted on political positioning) the results
at a given layer
(no effort is wasted on political positioning) the results
at a given layer 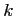 are
are 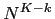 , assigning much greater importance
to the managers that in the additive model. But if
, assigning much greater importance
to the managers that in the additive model. But if 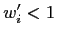 then
the manager decreases the summed contributions of his or hers subordinates.
Such model does not describe well situations where a manager combines
the managerial tasks with the same type of production as his or her
subordinates (e.g. programming team leader writing code, university
department head doing his or her own research or sales manager being directly responsible
for some customers). However, above certain realistic size of the
workgroup, the qualitative results of our model remain unchanged by
such assumption.
then
the manager decreases the summed contributions of his or hers subordinates.
Such model does not describe well situations where a manager combines
the managerial tasks with the same type of production as his or her
subordinates (e.g. programming team leader writing code, university
department head doing his or her own research or sales manager being directly responsible
for some customers). However, above certain realistic size of the
workgroup, the qualitative results of our model remain unchanged by
such assumption.
Perceived results - 2.12
-
In contrast with the actual results, the perceived outcome
for a manager is given by a combination of the real results of his
department (compared to the expected average at the appropriate level)
and the outcome of his political ploys. We have used a simple sum
of these two factors
where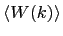 is the average result at the level of the
agent
is the average result at the level of the
agent 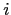 .
.  is a numerical factor used to model self-promotion
importance - one of the key parameters in the simulations.
We use the name “susceptibility” for
is a numerical factor used to model self-promotion
importance - one of the key parameters in the simulations.
We use the name “susceptibility” for  , as it determines the relative importance of self-promotion in the selection of candidates for promotion, and thus the way the organization responds to self interests of employees.
Such form of the perceived results
allows normalization of its two components independently of the level,
number of subordinates etc. Agents with highest and lowest values
of
, as it determines the relative importance of self-promotion in the selection of candidates for promotion, and thus the way the organization responds to self interests of employees.
Such form of the perceived results
allows normalization of its two components independently of the level,
number of subordinates etc. Agents with highest and lowest values
of 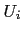 would be the candidates for promotion
and sacking, respectively.
would be the candidates for promotion
and sacking, respectively.
- 2.13
-
Using the assumptions about the distribution of raw output
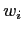 and self-promotion
and self-promotion 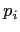 described in Section 2.2.1, it is possible to calculate the averages of actual
and perceived results at each organization level in a situation where
the capabilities of each agent are drawn randomly
described in Section 2.2.1, it is possible to calculate the averages of actual
and perceived results at each organization level in a situation where
the capabilities of each agent are drawn randomly
where
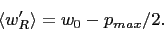
(5) - 2.14
-
The overall outcome of the political activities on the real and perceived
results of an agent at a given position are simply: increase of
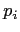 leads
to decrease of real contribution but increase of the perceived one.
Depending on the value of
leads
to decrease of real contribution but increase of the perceived one.
Depending on the value of  playing politics may prove to be advantageous
- or not. As it turns out the result depends on the level of the organization,
making the model more life-like.
playing politics may prove to be advantageous
- or not. As it turns out the result depends on the level of the organization,
making the model more life-like.
Promotion, firing and hiring
- 2.15
-
To model the processes of promotion in an organization we need to
provide some assumptions as to the personnel mobility within it. This
requires balancing between model simplicity and the need to cover
realistic situations. The rules proposed apply to organization levels
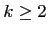 . For the top level, there is no competition and no hiring/firing.
Real organizations certainly experience changes at the CEO level,
and such changes can bring large differences in the overall performance.
Charismatic leaders, by their vision and management
skills can radically change the evolution of their companies. Such
contributions are, however, impossible to simulate in a statistical
computer model. Our goal is to model internal competition and promotion
mechanisms within an organization, coming from lower levels. To allow
such focus in our simulations we have assumed that the top manager
has no influence on the overall productivity, having
. For the top level, there is no competition and no hiring/firing.
Real organizations certainly experience changes at the CEO level,
and such changes can bring large differences in the overall performance.
Charismatic leaders, by their vision and management
skills can radically change the evolution of their companies. Such
contributions are, however, impossible to simulate in a statistical
computer model. Our goal is to model internal competition and promotion
mechanisms within an organization, coming from lower levels. To allow
such focus in our simulations we have assumed that the top manager
has no influence on the overall productivity, having 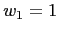 , and
, and
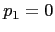 .
.
- 2.16
-
At lower levels the firing and promotion scheme easier to simulate.
At each simulation step there is some chance (given by parameter
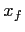 ) that from each workgroup of
) that from each workgroup of 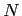 employees one would be fired. Thus the typical churn rate is
the same at every level, being given by
employees one would be fired. Thus the typical churn rate is
the same at every level, being given by 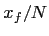 , and the reason
for introducing
, and the reason
for introducing 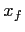 is to allow adjustment of the rate of change
in the model. This would allow the “simulation time” to reflect
actual time for real organizations - we selected
is to allow adjustment of the rate of change
in the model. This would allow the “simulation time” to reflect
actual time for real organizations - we selected 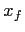 equal to 0.05, for which a single simulation step (corresponding to
3 months "real time") gives realistic ratio of fired employees. For comparison
the U.S. Bureau of Labor Statistics reports in
Job Openings and Labor Turnover Survey that the layoffs and discharges monthly rate for
the period between 2000 and 2009 varied between 1.2% and 2%. The rate calculated with our model parameters
is 0.33%, but it should be remembered that our model does not include mass layoffs and discharges
due to disability or illness.
equal to 0.05, for which a single simulation step (corresponding to
3 months "real time") gives realistic ratio of fired employees. For comparison
the U.S. Bureau of Labor Statistics reports in
Job Openings and Labor Turnover Survey that the layoffs and discharges monthly rate for
the period between 2000 and 2009 varied between 1.2% and 2%. The rate calculated with our model parameters
is 0.33%, but it should be remembered that our model does not include mass layoffs and discharges
due to disability or illness.
- 2.17
-
While the chance of firing is probabilistic, the choice of the agent to be
fired is almost-deterministic: the worst perceived performer in each workgroup
is selected. If two or more agents share the same value of perceived productivity,
the program randomly fires one of them.
The vacant positions can be filled either by internal promotion or
by external hiring. This can by described by assuming two mechanisms
of filling a given empty post, each with probability being a part
of the model.
First, there is a probability
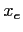 that the post will be
filled by externally hired agent, with values of
that the post will be
filled by externally hired agent, with values of 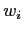 and
and
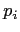 drawn from the same distributions as the original set of employees.
The second option of filling a vacancy is through direct promotion
of the best performer (again, we measure perceived performance!) of
the organizational level directly below the vacancy. In any case, when two agents have the same perceived
performance, the one for promotion is chosen randomly.
In presented simulations we have used 10% probability of external hiring. The actual values of
drawn from the same distributions as the original set of employees.
The second option of filling a vacancy is through direct promotion
of the best performer (again, we measure perceived performance!) of
the organizational level directly below the vacancy. In any case, when two agents have the same perceived
performance, the one for promotion is chosen randomly.
In presented simulations we have used 10% probability of external hiring. The actual values of
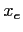 parameter vary considerabley between organizations,
moreover, in real life that vary between varius levels within an organization. For some types of positions (for example
sales management and high level management in commercial companies) the external hiring would be much more probable.
On the other hand in education, research or production companies, internal promotion is dominant.
The choice of the value of
parameter vary considerabley between organizations,
moreover, in real life that vary between varius levels within an organization. For some types of positions (for example
sales management and high level management in commercial companies) the external hiring would be much more probable.
On the other hand in education, research or production companies, internal promotion is dominant.
The choice of the value of 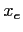 resulted from
intention to keep influence of Peter Principle rather high.
In presented results we used global promotion scope, where anyone from
the lower level can be picked to fill the vacated post.
The promotion will, of course,
leave another vacancy to be filled at a lower level. The hiring process
should start at the highest vacancy and continue down. All the vacancies
at the lowest level are, obviously, filled by external hiring.
resulted from
intention to keep influence of Peter Principle rather high.
In presented results we used global promotion scope, where anyone from
the lower level can be picked to fill the vacated post.
The promotion will, of course,
leave another vacancy to be filled at a lower level. The hiring process
should start at the highest vacancy and continue down. All the vacancies
at the lowest level are, obviously, filled by external hiring.
- 2.18
-
To describe the productivity of the employee after the promotion in the two scenarios introduced before we use the following assumptions. For the Peter scenario, suitable in situations where the new post calls
for totally different set of skills (salesman promoted to sales manager
or to marketing manager position) the post-promotion value of productivity
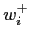 is randomly drawn, without any relation
to previous
is randomly drawn, without any relation
to previous 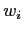 . On the other hand, for the
continuity scenario, in which the
productivity at the higher level remains close to the previous one, agent's
productivity changes by a small random value of
. On the other hand, for the
continuity scenario, in which the
productivity at the higher level remains close to the previous one, agent's
productivity changes by a small random value of 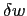
where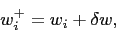
(6) 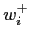 denotes agents capacity on the higher level.
We assumed that
denotes agents capacity on the higher level.
We assumed that
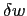 has
normal distribution centered at zero with width of
has
normal distribution centered at zero with width of
 (we used value of 0.2 for
(we used value of 0.2 for  in results presented in this paper).
This hypothesis would be applicable to situations where the tasks
at the higher hierarchy level are largely similar to those at a lower
level (advancement from programmer to programming team leader, for
example).
in results presented in this paper).
This hypothesis would be applicable to situations where the tasks
at the higher hierarchy level are largely similar to those at a lower
level (advancement from programmer to programming team leader, for
example).
- 2.19
-
Depending on the organization the change of the scope of activity
due to promotion, from direct production (writing the code, visiting
customers, conducting experiments) to managerial tasks of organizing,
planning and supervision may be more or less dramatic, pointing to Peter or continuity scenario.
In some real life situations it might be suitable to use a mixed model (for example stressing the change of tasks when someone is promoted from the workpool to managerial levels), but this paper is limited to pure scenarios.
We remind here that we keep the
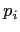 values unchanged for individual agents regardless of their promotions.
values unchanged for individual agents regardless of their promotions.
Simulation considerations
- 2.20
- During simulation process we are looking both at global changes of organization effectiveness depending on the promotion model as well as individual career paths and results of individual strategies . The simulation steps correspond to realistic conditions, e.g. quarters or semesters – periods where typically performance of employees is reviewed and firing/hiring decisions may be taken. We run the simulations up to 64 steps (16 years). By experience, modern commercial organizations stay in the same shape (without major reorganizations) for periods of 3-5 years. Such stasis times are longer in governmental and educational organizations. Of course, major reorganizations are not covered by the simplistic model described above. The individual results of the simulation runs differed significantly (as discussed in Section 3.1) and for each combination of parameters we have accumulated results of 8000 runs, to obtain averages and distribution of key characteristics.
- 2.21
-
The key parameters and characteristics of the simulated organization
were:
- Overall performance of the organization, given by the averages of
effective total result of the topmost manager
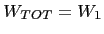 and its
changes during simulation steps, as well as effective performances
of organization units at different levels, as given by their bosses'
and its
changes during simulation steps, as well as effective performances
of organization units at different levels, as given by their bosses'
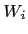 .
We also recorded the number of new hires compared to internal promotions, to check the initial
assumptions It is worth noting that these parameters are comparable to real world data,
as such comparison could lead to improvements
of the model (for example probabilities of external hiring depending
on the level of the vacancy).
.
We also recorded the number of new hires compared to internal promotions, to check the initial
assumptions It is worth noting that these parameters are comparable to real world data,
as such comparison could lead to improvements
of the model (for example probabilities of external hiring depending
on the level of the vacancy).
- Monitoring true productivity and self-promotion factor at various levels of the organization.
Average
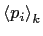 for each level
for each level 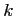 as well as the average value of raw individual
productiveness
as well as the average value of raw individual
productiveness
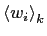 were calculated at each step of the simulations;
to check if it is the political manipulators or the real workers who move
to the upper echelons, as suggested by common sense.
were calculated at each step of the simulations;
to check if it is the political manipulators or the real workers who move
to the upper echelons, as suggested by common sense.
The simulations were coded in Fortran95. The code is available from the Author on request.
- Overall performance of the organization, given by the averages of
effective total result of the topmost manager
 Results
Results
- 3.1
-
The model presented in this work is rather complex, involving several
parameters designed to mimic at least some of the crucial aspects
of modern organizational life. This complexity, however, makes deriving
clear dependencies rather difficult. For the purpose of this preliminary
paper we decided to divide the system controls into two groups. The
first contains those that are static between various simulations,
for example the parameters describing the distributions of
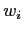 and
and 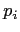 .
We have also kept the firing rate
.
We have also kept the firing rate 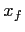 and the external hiring rate
and the external hiring rate 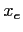 fixed and selected to to keep the “simulation time” as close
as possible to the real world, and to obtain reasonable values of the
churn ratio and average time spent as given position.
fixed and selected to to keep the “simulation time” as close
as possible to the real world, and to obtain reasonable values of the
churn ratio and average time spent as given position.
- 3.2
-
The second group contained controls that were varied between simulated organizations,
describing their main
characteristics: number of levels and workgroup size,
type of
post-promotion efficiency model (Peter hypothesis, continuity model) and
organization susceptibility to self-promotion,
 .
.
- 3.3
-
We present here results for a multi-level hierarchy comprised of 5 levels with
5 people in a workgroup. This choice was motivated by a desire to keep the
overall size moderate. Based
on the distribution of
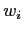 and
and 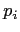 defined in Section 2,
we can derive two “yardstick” measures of the total organization
productivity. The first, is the
average productivity in a wholly random organization, including
the negative effects of time and effort lost on political games. The
defined in Section 2,
we can derive two “yardstick” measures of the total organization
productivity. The first, is the
average productivity in a wholly random organization, including
the negative effects of time and effort lost on political games. The
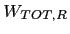 value for random distribution is, with our choice of
parameters, rather low, equal to 105 (Eq. 4). This is, of course, due to the largely negative impact of the
managerial structure, where every manager decreases the production
of his/her department by a factor of
value for random distribution is, with our choice of
parameters, rather low, equal to 105 (Eq. 4). This is, of course, due to the largely negative impact of the
managerial structure, where every manager decreases the production
of his/her department by a factor of
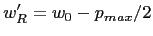 (0.7 for our choice of parameters).
This value is also a starting point of the dynamic
simulations, as the initial conditions use random distribution of
agent characteristics. It should be noted that the random configuration
and associated productivity seems highly unrealistic, as it means
that all managers negatively influence the outcome. For this reason,
we have used productivity of neutral organization as the criterion of the improvement
vs. decline of the total output in the simulations.
Interestingly enough, some combinations of parameters resulted in
simulation runs that were worse than the random one. We should remind here that negative selection
is real, and some organizations may indeed seem to perform worse than if they were staffed through random hiring. This is especially true if the organization itself is under no threat
to its existence nor in competition, as is often true for government structures.
(0.7 for our choice of parameters).
This value is also a starting point of the dynamic
simulations, as the initial conditions use random distribution of
agent characteristics. It should be noted that the random configuration
and associated productivity seems highly unrealistic, as it means
that all managers negatively influence the outcome. For this reason,
we have used productivity of neutral organization as the criterion of the improvement
vs. decline of the total output in the simulations.
Interestingly enough, some combinations of parameters resulted in
simulation runs that were worse than the random one. We should remind here that negative selection
is real, and some organizations may indeed seem to perform worse than if they were staffed through random hiring. This is especially true if the organization itself is under no threat
to its existence nor in competition, as is often true for government structures.
- 3.4
-
The other, more realistic measure of global effectiveness,
which we would call “neutral productivity”,
assumes that no self-promotion take place (
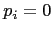 ) and that all workers
and managers have the same effective
) and that all workers
and managers have the same effective 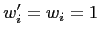 . Then the organization's
output is simply given by the number of lowest level workers (as managers
neither improve nor diminish the results). In the case of the 5-by-5 structure
. Then the organization's
output is simply given by the number of lowest level workers (as managers
neither improve nor diminish the results). In the case of the 5-by-5 structure 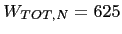 .
Despite the fact that in all simulations the pool of agents' individual
capabilities remained the same, the final long term results of the
model organization, depending on the post-promotion productivity scenario
and the susceptibility to self-promotion varied by almost an order of
magnitude, from much below
.
Despite the fact that in all simulations the pool of agents' individual
capabilities remained the same, the final long term results of the
model organization, depending on the post-promotion productivity scenario
and the susceptibility to self-promotion varied by almost an order of
magnitude, from much below 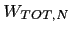 to more than four times better than this value!
to more than four times better than this value!
Simulation statistics - 3.5
-
Due to the multiplicative way the managerial contribution is modeled
here, the influence of individual characteristics of managers, especially
at high positions, can significantly change the overall productivity
of the organization. As a result we observe rather wide distribution
of results between simulation runs. As an example, Figure 1
presents distribution functions of overall productivity
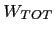 for the Peter
model for various values of the susceptibility factor
for the Peter
model for various values of the susceptibility factor  ,
at different stages of the evolution starting from random configuration: after 3, 5 and 16 years.
Figure 2 presents similar data for a set of simulations
in the continuity model.
,
at different stages of the evolution starting from random configuration: after 3, 5 and 16 years.
Figure 2 presents similar data for a set of simulations
in the continuity model.
Figure 1: Distribution of 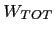 values for Peter model (organization with
5 levels with 5 positions in a workgroup) depending on
values for Peter model (organization with
5 levels with 5 positions in a workgroup) depending on  value
after 3, 5 and 16 years. Probabilities of
value
after 3, 5 and 16 years. Probabilities of 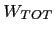 are very well
described by Gaussian distributions. Increased values of
are very well
described by Gaussian distributions. Increased values of  shift
the center of the distribution to smaller values and decrease the
width of the distribution – top left curves in each panel correspond
to
shift
the center of the distribution to smaller values and decrease the
width of the distribution – top left curves in each panel correspond
to 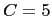 , bottom right to
, bottom right to 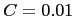 .The distributions
were displaced vertically for clarity for increasing
.The distributions
were displaced vertically for clarity for increasing  values.
values.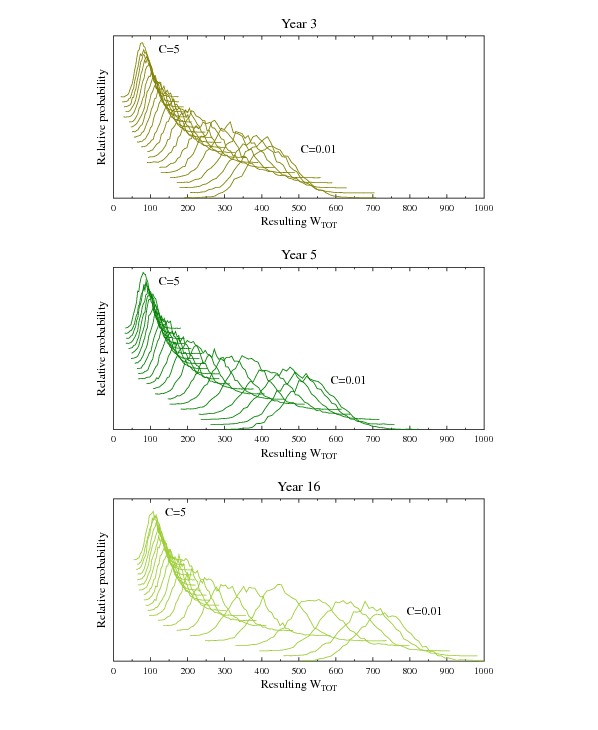
Figure 2: Distribution of 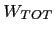 values for continuity model (organization
with 5 levels with 5 positions in a workgroup) depending on C value
after 3, 5 and 16 years. Probabilities of
values for continuity model (organization
with 5 levels with 5 positions in a workgroup) depending on C value
after 3, 5 and 16 years. Probabilities of 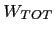 are very well
described by Gaussian distributions.The distributions
were displaced vertically for clarity for increasing
are very well
described by Gaussian distributions.The distributions
were displaced vertically for clarity for increasing  values.
values.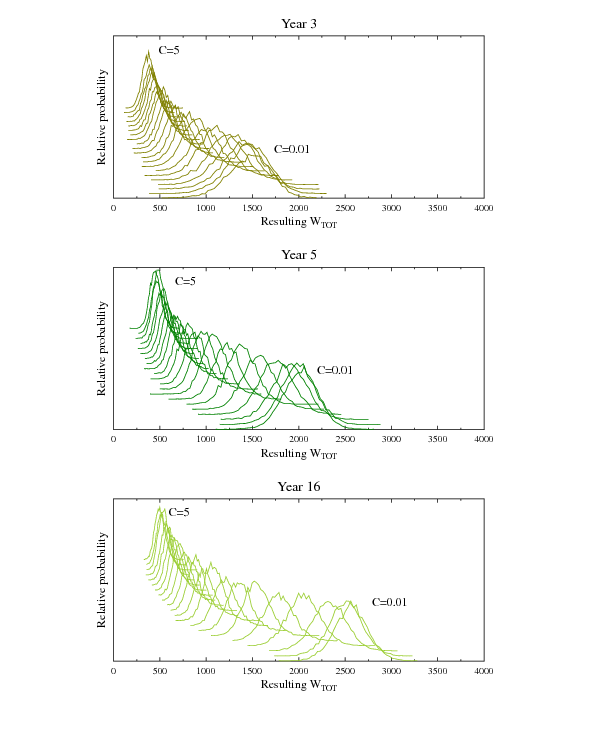
- 3.6
-
The distributions of
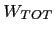 are well described by Gaussian functions. This allows
us to use, in presenting further results, peak center positions. It intersting to observe that
the widths of the distributions are rather high and
strongly correlated with the position of the peak center
(Fig. 3). The half-width and half maximum (HWHM) varied between more than 20% of the average value for the Peter model, 3 years from the start of the simulations to still sizeable 10% for the continuity model after 16 years.
In the continuity model we observe strong
reduction of the width of the distribution of
are well described by Gaussian functions. This allows
us to use, in presenting further results, peak center positions. It intersting to observe that
the widths of the distributions are rather high and
strongly correlated with the position of the peak center
(Fig. 3). The half-width and half maximum (HWHM) varied between more than 20% of the average value for the Peter model, 3 years from the start of the simulations to still sizeable 10% for the continuity model after 16 years.
In the continuity model we observe strong
reduction of the width of the distribution of 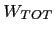 with the
passage of time, but even after 16 years of continuous evolution,
there are still significant differences of results between individual
simulation runs. We note here that the average values of
with the
passage of time, but even after 16 years of continuous evolution,
there are still significant differences of results between individual
simulation runs. We note here that the average values of
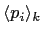 and
and
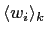 for organization level
for organization level 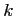 have similar
Gaussian distributions.
have similar
Gaussian distributions.
Figure 3: Correlations between the maximum of the 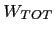 distribution in
multiple simulation runs and the width of the distribution. Point series correspond to situation after
3 and 16 years, and each series is given by different susceptibility
distribution in
multiple simulation runs and the width of the distribution. Point series correspond to situation after
3 and 16 years, and each series is given by different susceptibility
 values, ranging from
values, ranging from 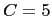 at bottom left corner to
at bottom left corner to 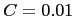 at the top right corner.
at the top right corner.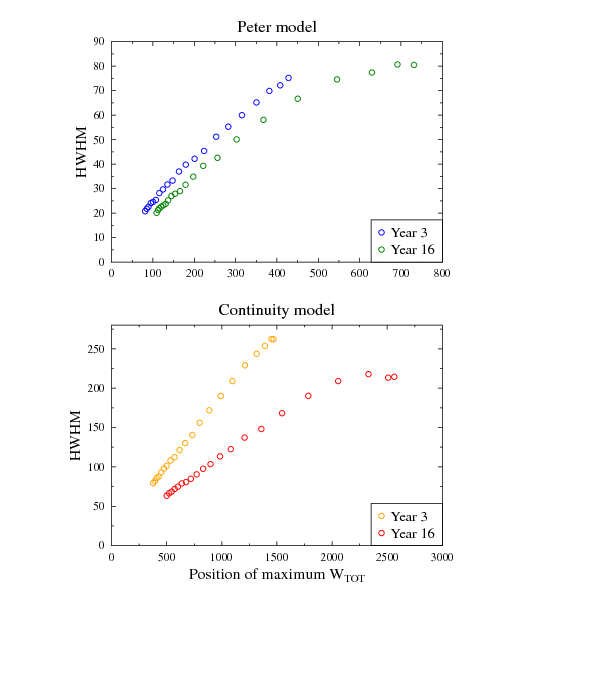
- 3.7
- The time evolution of average values of
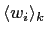 and
and
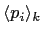 for various organization levels are
– for most parameter combinations – reasonably well described by
exponentially decaying functions of time
for various organization levels are
– for most parameter combinations – reasonably well described by
exponentially decaying functions of time
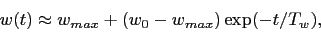
(7)
For very low values of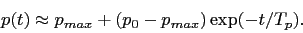
(8)  the self-promotion is selected against,
thus
the self-promotion is selected against,
thus 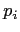 decreases with time for both continuity and Peter models.
For large values of
decreases with time for both continuity and Peter models.
For large values of 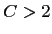 selection favors high political activity
and thus
selection favors high political activity
and thus 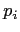 grows. In the intermediate regime of
grows. In the intermediate regime of 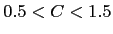 we observe more complex behavior of
we observe more complex behavior of 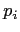 , remaining close to the
average value for random distribution. On the other hand, the true
productivity in both models is observed to grow with time. Obviously
this increase is much higher for the continuity model, where the promotion
preserves, at least partially, the
, remaining close to the
average value for random distribution. On the other hand, the true
productivity in both models is observed to grow with time. Obviously
this increase is much higher for the continuity model, where the promotion
preserves, at least partially, the 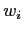 values, so that talent and competencies are not lost.
values, so that talent and competencies are not lost.
Figure 4: Time evolution of average 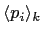 and
and
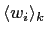 values for the continuity model; 5 levels of 5 positions
in a workgroup. Colors correspond to various values of the susceptibility
values for the continuity model; 5 levels of 5 positions
in a workgroup. Colors correspond to various values of the susceptibility  , ranging from
, ranging from 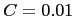 (blue), through
(blue), through  (green),
(green), 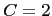 (olive),
(olive), 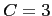 (yellow),
(yellow), 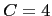 (orange) and
(orange) and 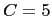 (red).
(red).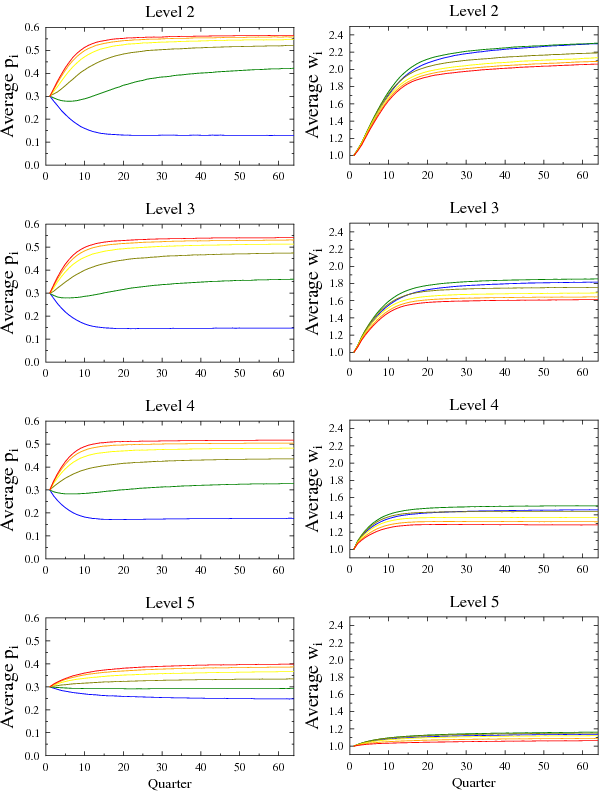
Figure 5: Time evolution of average  and
and
 values for the Peter model; 5 levels of 5 positions in a
workgroup.
values for the Peter model; 5 levels of 5 positions in a
workgroup.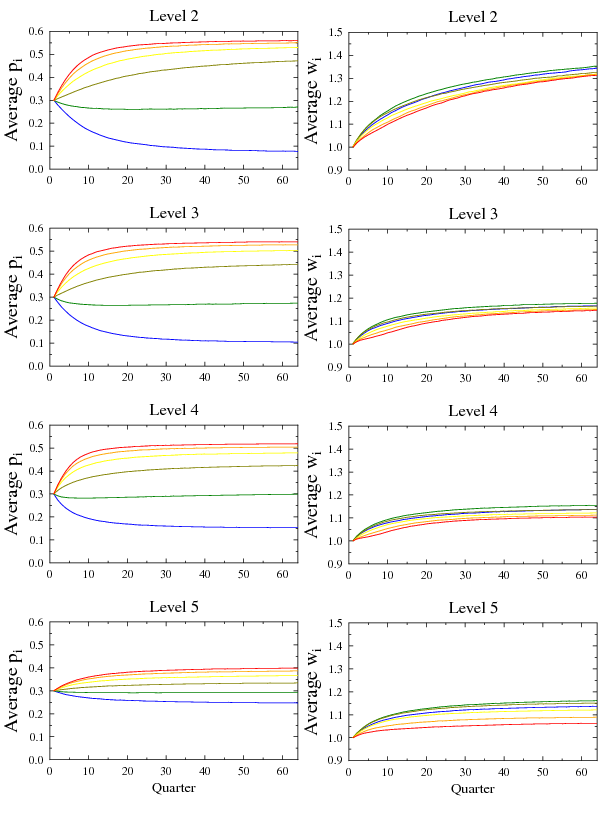
Global effectiveness
- 3.8
-
We shall focus now on the main model controls: the post-promotion
effectiveness model (Peter or continuity) and the organization susceptibility
to internal self promotion,
 . Both factors play a crucial role
in the evolution of the organization effectiveness. Let us discuss
first the differences between the two post-promotion models. The continuity
model, even in the presence of strong susceptibility to internal PR,
predicts improvement of the individual productivity
. Both factors play a crucial role
in the evolution of the organization effectiveness. Let us discuss
first the differences between the two post-promotion models. The continuity
model, even in the presence of strong susceptibility to internal PR,
predicts improvement of the individual productivity 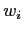 with
time at higher levels of organization. Selection of best (perceived)
performers coupled with limited “inheritance” of the individual
productivity significantly improves the average values, and as result,
leads to much higher values of overall true productivity than in the
Peter model.
with
time at higher levels of organization. Selection of best (perceived)
performers coupled with limited “inheritance” of the individual
productivity significantly improves the average values, and as result,
leads to much higher values of overall true productivity than in the
Peter model.
- 3.9
-
The difference between the productivity in continuity model and Peter
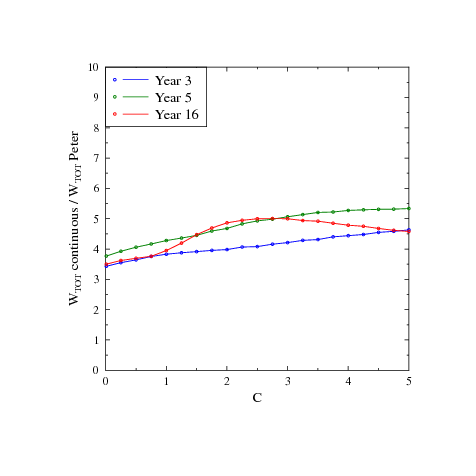
model can be as high as 5 times, as shown in Fig. 6.
Selection process for the continuity model,
even for very large values of susceptibility
 (when agents with high focus on self-promotion are at advantage), leads to performance
better than for the random assignment of agent capacities – but lower
than the neutral configuration, when internal politics plays no role.
For the Peter model at large
(when agents with high focus on self-promotion are at advantage), leads to performance
better than for the random assignment of agent capacities – but lower
than the neutral configuration, when internal politics plays no role.
For the Peter model at large  values the evolution
may lead to decrease of productivity from the starting
random configuration! This seems to be a very bad sign for any organization.
For some combinations of parameters this decrease, happening over
a short period of less than 10 quarters, diminished the productivity
by a factor of 2 (see, for example, Fig. 8).
values the evolution
may lead to decrease of productivity from the starting
random configuration! This seems to be a very bad sign for any organization.
For some combinations of parameters this decrease, happening over
a short period of less than 10 quarters, diminished the productivity
by a factor of 2 (see, for example, Fig. 8).
- 3.10
-
The following figures 7 and 8 show time evolution of average
organization productivity (starting from a random configuration),
dependence of this productivity on the susceptibility
 after 3,
5 and 16 years of evolution and similar dependence of the average
after 3,
5 and 16 years of evolution and similar dependence of the average
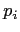 and
and 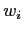 values at various levels of the organization.
Overall productivity has been normalized to that of a neutral
organization. Such normalization allows to see the effects independently
to organization size and number of levels.
For very small susceptibility values,
the continuity scenario, with its positive
selection of productivity
values at various levels of the organization.
Overall productivity has been normalized to that of a neutral
organization. Such normalization allows to see the effects independently
to organization size and number of levels.
For very small susceptibility values,
the continuity scenario, with its positive
selection of productivity 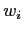 gives results that are 4 times better than neutral organization,
while for the Peter scenario the improvement in only by 20%.
In both scenarios we observe strong, negative influence of increasing susceptibility
gives results that are 4 times better than neutral organization,
while for the Peter scenario the improvement in only by 20%.
In both scenarios we observe strong, negative influence of increasing susceptibility
 on overall results. After 16 years, for
the continuity scenario, the results are slightly below those of neutral organisation,
while for Peter scenario the results are at the level of 15% of the neutral benchmark.
This means that Dilbert
Principle decreases productivity more than fivefold.
Importantly, the drop of performance is significant even for relatively low values of
on overall results. After 16 years, for
the continuity scenario, the results are slightly below those of neutral organisation,
while for Peter scenario the results are at the level of 15% of the neutral benchmark.
This means that Dilbert
Principle decreases productivity more than fivefold.
Importantly, the drop of performance is significant even for relatively low values of
 = 2.
= 2.
Figure 7: Simulation results for the continuity model, 5 layers, 5 positions in a workgroup. Upper panels: time evolution and dependence of overall productivity 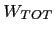 on organization susceptibility
on organization susceptibility
 , divided by productivity of neutral
organization of the same size. Lower panels: dependence of average
, divided by productivity of neutral
organization of the same size. Lower panels: dependence of average
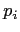 and
and 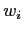 values on
values on  at the end of the third, fifth
and 16th year of evolution.
at the end of the third, fifth
and 16th year of evolution.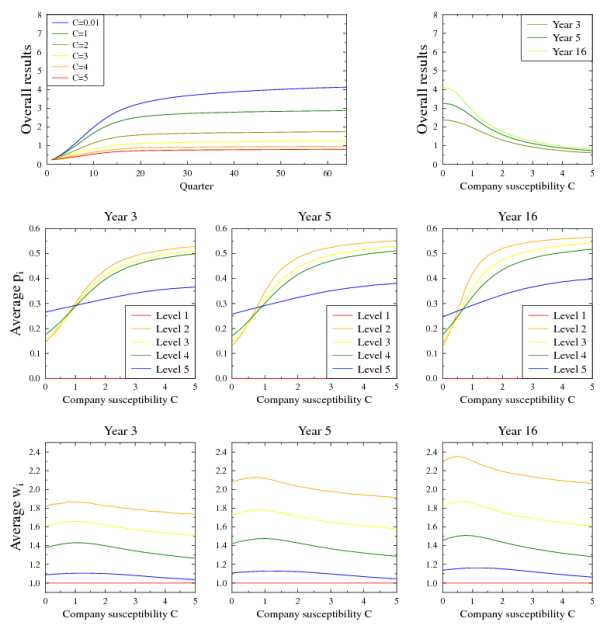
Figure 8: Simulation results for the Peter model, 5 layers, 5 positions in a workgroup. Upper panels: time evolution and dependence of overall productivity 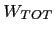 on organization susceptibility
on organization susceptibility  , divided
by productivity of neutral organization
of the same size. Lower panels: dependence of average
, divided
by productivity of neutral organization
of the same size. Lower panels: dependence of average 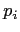 and
and
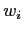 values on
values on  at the end of the third, fifth and 16th year
of evolution.
at the end of the third, fifth and 16th year
of evolution.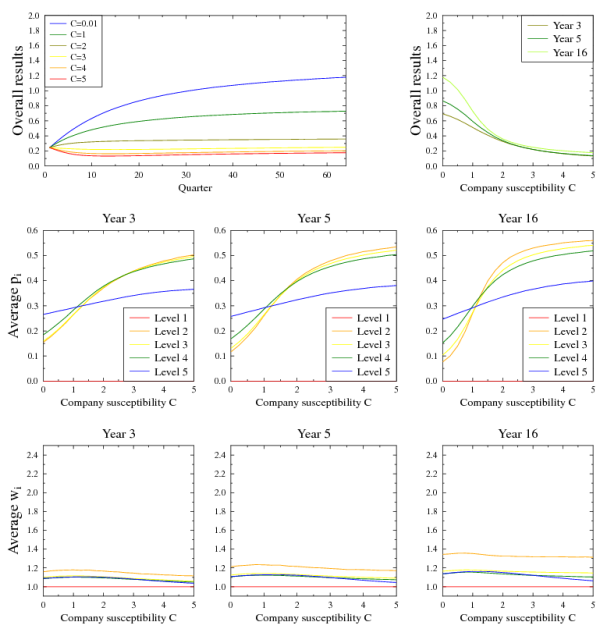
 Conclusions
Conclusions
-
Discussion of results
- 4.1
-
The general results of the simulations are not surprising (just as
the original observations of Peter and Adams are not surprising).
Everyday observations show that there are many organizations, big
and small, commercial and governmental, where promotions and demotions
follow political ploys and not the real capability of
an employee to fulfill specific roles. And it is quite obvious to
both internal and external observers, that the performance of these
organizations may be far from optimal. Thus our model has no “discovery”
value, but is, more or less, a mathematical toy, reflecting
some aspects of the social reality. Obviously, it misses a
lot of factors that are present in real life: individuality and creativeness
of the leaders; innovative, market disruptive products or ideas; well established
processes and organizational culture that effectively guide individual players; capacity to change
the organizational form to adapt to new challenges. All these can
be crucial in determining the success or a failure of the organization.
On the other hand, the processes related to promotion and internal
politics included in the model are present in almost all types of
organizations and can negatively impact their results. The main idea
behind the model is to look for some simple controls that could allow
some general policy suggestions – as it turns out some model parameters
are more important than others. For example, the model allows to include phenomenon of
blame-shifting by the managers. A badly performing manager, threatened with being fired, can
point to one of his or her subordinates as the reason for bad performance
and fire the person to preserve own position. Such phenomenon is quite common.
It turns out that the presence of blame-shifting
influences the simulated overall performance only to a minor degree.
Therefore, if we look to measures improving the organization productivity,
we should note that
such self-preservation instincts are natural (although clearly immoral), and it
is very hard to avoid them. Another model variable, degree of pre-screening
of external candidates, provides much higher influence on the resulting
productivity (especially in the continuity model). But for most of
modern organizations such competitive nature of hiring is already
present, so there is little room for improvement here. The two major
factors are the capability to preserve the skills and efficiency of
an employee after the promotion and susceptibility of an organization
to self-promotion, or, in other words, capacity to recognize the real values.
Here the differences in overall productivity can
be as high as an order of magnitude. Thus, the model suggests that
organizations should focus on measures eliminating negative effects
due to Peter Principle and to self-promotion. Such measures
include:
- Using measurable and objective criteria for employee evaluation. This is relatively easy for some areas (for example in sales departments), but rather difficult in creative environments (scientific research, software engineering). Yet despite the difficulty, such standards would decrease the employee's drive to use political skills for self-promotion, instead of focusing on the needed tasks.
- Giving prospective candidates for promotion tasks related to the nature of duties at the higher level (e.g. temporary management of small groups, responsibility for analysis of results and preparing directions for action for workgroups and departments etc.) and measuring results of such assignments. These results should be used when considering promotion, as they estimate the productivity at the higher level, and thus decrease the effect of Peter Principle.
- Introduction of horizontal advancement paths, in which employees who do not fit into the traditional promotion model (for example brilliant engineers lacking managerial skills) would still be able to achieve satisfaction within a company, without falling prey to the Peter Principle trap.
- 4.2
- There is a large body of literature devoted to consequences of promotion models to individual and general organization productivity, including works that are focused on analysis of Peter Principle (for example Audas et al (2004), Barmby et al (2006), Dickinson and Villeval (2007), Gibbons and Waldman (2006), Koch and Nafziger (2007), Lazear and Rosen (1981), Lazear (2001), Lazear (2004), MacLeod and Malcolmson (1988), Valsecchi (2003) ). Most of these works consider the effects of promotions taking into account both the goals of the employer and the employee. The most important difference between the models used in the quoted sources and our simplified model, is that we did not cover the economic analysis on the employee side. There are no incentives for promotion - it is assumed that all employees, by definition, are interested in moving to higher positions. Such assumption is obviously far from the actual situations in real life, where some employees are risk adverse and prefer to stay in current positions.
- 4.3
-
In our model we compare the relative perceived performance of agents at a given
level of hierarchy as candidates for promotion. This is reminiscent of the tournament
method of promotion selection (Lazear (1981)) as opposed to measurement of performance against a pre-defined standards. The difference in our model is that instead of comparing results of two workers we pick the best relative performers from a much larger pool of candidates. This has, of course a limitation to organizations where cross-departmental promotion is possible.
It should be remarked here that even in the case of traditional tournaments Lazear (2001) has already predicted that in environments where there are "low quality" and "high quality" employees, the low quality employees would attempt to contaminate high quality firms. Direct inclusion of self-promotion in our model provides additional means for such corruption of quality.
- 4.4
-
Additional limitation of our model is in stability of agent's "profile" in time. There is no increase of
productivity at a given post with experience (as discussed, for example, by Koch and Nafziger (2007)). Nor do we introduce positive effects brought by training and learning.
These effects are certainly important in real life. Providing newly promoted employees with training, coaching
and allowing some "starting time", during which measurement criteria are somewhat relaxed, to gather experience are common actions of many organizations. They mitigate, to certain extent, the effects of Peter Principle, but
in Author's opinion they can do little against Dilbert Principle and people who are focused on self-promotion.
Thus, including self-promotion factor in productivity model diminishes the positive effects of greater experience in organization allows agents with high
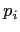 to attain high positions (by having large value of susceptibility
to attain high positions (by having large value of susceptibility  ).
).
- 4.5
- Faria (2000) has presented an analysis of a combination of Peter and Dilbert Principles in a model describing suboptimal choices in an internal job market, with a split of managerial skills into technical and social. The proposed explanation of the origin of Dilbert Principle is different from ours. Faria assumed that organization could promote an employee who is below a competence optimum. Such choice would lead to the Dilbert Principle, but it is hard to understand, within the model proposed by Faria, why such suboptimal choice would be made. Although our model is more simplified than the one proposed by Faria (we do not split the skills into technical/social) it provides some quantifiable "explanation" for the wrong promotion decisions by the employer. Our notion of self-promotion is a practical realization of remark by Faria that if promotion decisions are made on the basis of proxies for the output rather than on measurable output, workers might put more emphasis on proxies than on output itself.
- 4.6
-
Most of the traditional literature focuses on individual contributions to organization output.
The total output is assumed to result from summing of outputs of employees. Thus, promotion decisions
are based on tournaments which compare individual productivity.
In many real life situations this is far from truth. Due to team nature of many tasks the evaluation of promotion criteria often depends not only on the direct contribution of an employee, but also on the contributions of all team members, for example subordinates. Sales manager performance is measured not on his or her individual results, but on sales of the group of people being managed. Research institute head repotation depends not only on what she or he publishes, but on cumulative research achievements of the institute. And so on.
The comparisons of performance used in our model take such teamwork into account.
However, as we already remarked, summing up individual contributions can not reproduce the possible negative
influences of managers on team performance, unless we assume that negative outputs are possible. But even in the last case, additive model can not handle easily situations in which promotion of bad manager can have much larger negative influences simply because after promotion the manager may negatively affect the output of many more people. For these reasons we have opted for rather unusual multiplicative contribution model at management positions, which addresses the issues in a natural way.
Improving organization performance
- 4.7
-
Within the simulation model, even a moderate decrease of the organization susceptibility to political
ploys, and improvement of the “heritability” of skills after
promotion may lead to dramatic improvement of overall productivity,
not by single percentage points but by a significant factor.
To show this we have simulated effects of changes in organization
policies related to promotion and susceptibility to self-interests
in a “mature” environment. In such simulations an organization
resulting from some years of evolution under one set of parameters
would be used as the starting point of a new simulation, for example
with a changed value of
 . This would correspond to corrective measures
undertaken by top management, for example when a new CEO comes on board. The
main question of such studies would be to determine, for example,
the expected improvements due to lowering of susceptibility or the
time it takes to see such improvement take the effect. Figure 9 presents
results of such simulations showing that the improvement of overall effectiveness due to
both possible courses of action: decreasing susceptibility to self-promotion and changing
the post-promotion scenario from Peter to continuity.
We have arbitrarily assumed that the corrective measures are undertaken in the middle of the simulated period
of 16 years, giving the organization the same amount of time to recover as the time of negative impact of
Dilbert-Peter Principle. We studied corrective measures taken only against self-promotion, only against effects of Peter Principle and
combined effort.
The two corrective strategies, although leading to comparable individual improvements in total performance, act
in different ways. Diminishing company susceptibility to self-promotion decreases
. This would correspond to corrective measures
undertaken by top management, for example when a new CEO comes on board. The
main question of such studies would be to determine, for example,
the expected improvements due to lowering of susceptibility or the
time it takes to see such improvement take the effect. Figure 9 presents
results of such simulations showing that the improvement of overall effectiveness due to
both possible courses of action: decreasing susceptibility to self-promotion and changing
the post-promotion scenario from Peter to continuity.
We have arbitrarily assumed that the corrective measures are undertaken in the middle of the simulated period
of 16 years, giving the organization the same amount of time to recover as the time of negative impact of
Dilbert-Peter Principle. We studied corrective measures taken only against self-promotion, only against effects of Peter Principle and
combined effort.
The two corrective strategies, although leading to comparable individual improvements in total performance, act
in different ways. Diminishing company susceptibility to self-promotion decreases
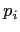 , leaving resulting individual productivities almost unchanged. Changing
post-promotion model from Peter to continuity (achieved, for example by suitable training and/or screening of promotion candidates
with respect to tasks on the higher hierarchy level) increases
, leaving resulting individual productivities almost unchanged. Changing
post-promotion model from Peter to continuity (achieved, for example by suitable training and/or screening of promotion candidates
with respect to tasks on the higher hierarchy level) increases
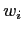 , leaving self-promotion
, leaving self-promotion 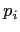 unchanged. In the case when both actions take place the increase of effectiveness is as high as by a factor of 20 for the chosen parameters.
What is important is that the improvement in productivity happens rather fast, so that there can be a positive feedback,
showing to top management that the decisions are bearing fruit and strengthening the resolve.
unchanged. In the case when both actions take place the increase of effectiveness is as high as by a factor of 20 for the chosen parameters.
What is important is that the improvement in productivity happens rather fast, so that there can be a positive feedback,
showing to top management that the decisions are bearing fruit and strengthening the resolve.
- 4.8
-
Our model focuses on negative effects of Peter Principle and distortion of the observed output of
employees due to self-promotion. The improvement strategies described above obviously miss other actions,
such as education and training, which would result in improvement of employee productivity at current post.
Such actions are especially important in promotion situations, to combat the decrease of productivity due to Peter principle,
but they are beyond the scope of the simulations presented here.
Figure 9: Changes in overall organization performance (compared to neutral organization) and average values of 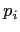 and
and 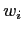 due to changes in organization policies. Starting organization is highly ineffective:
has very high susceptibility to self-promotion and uses Peter model of post-promotion effectiveness
due to changes in organization policies. Starting organization is highly ineffective:
has very high susceptibility to self-promotion and uses Peter model of post-promotion effectiveness 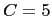 . The effectiveness of such organization, as already noted is very low. Left column: after 8 years of evolution the company changed the susceptibility to minimal value
. The effectiveness of such organization, as already noted is very low. Left column: after 8 years of evolution the company changed the susceptibility to minimal value 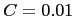 , resulting in rapid decrease of the self-promotion. Middle column: the company changed the post-promotion model to continuity scenario, without changing
, resulting in rapid decrease of the self-promotion. Middle column: the company changed the post-promotion model to continuity scenario, without changing  , resulting in improvement of the productivity. Right column: the company changed both the post-promotion model from Peter to continuity and decreased
, resulting in improvement of the productivity. Right column: the company changed both the post-promotion model from Peter to continuity and decreased  from 5 to 0.01. In the last case the cumulative effects led to dramatic increase of performance of the whole organization. Dotted lines show results when no change is introduced.
from 5 to 0.01. In the last case the cumulative effects led to dramatic increase of performance of the whole organization. Dotted lines show results when no change is introduced.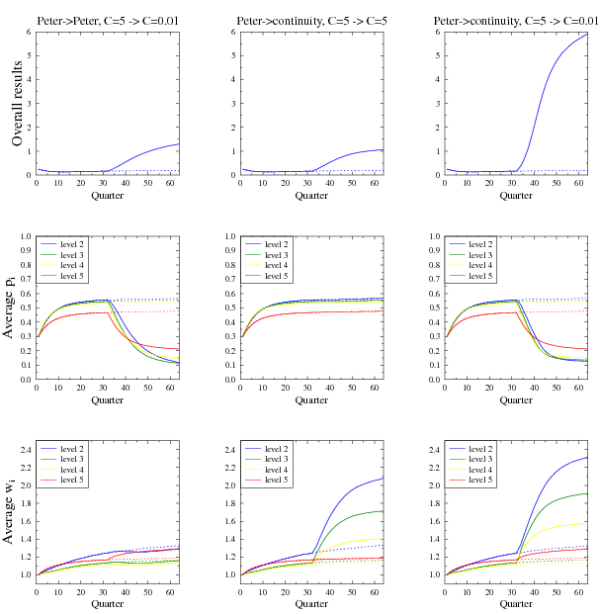
Model extensions
- 4.9
- The initial model presented here can be expanded in several directions. The best source of improvement of the model would be when the computer simulation could be coupled with some “microscopic” sociology studies (for example interviews focused on measuring the payoff of political activities within the organization). Especially, if one could provide comparative studies of general effectiveness of organizations built upon different social models. The model itself is quite flexible and allows many improvements. Such extensions of the computer model would still miss the effects due to individuality of participants and specific nature of the organization but bring the simulated strictures still closer to reality.
- 4.10
- To make the model more realistic one might divide the organization into a few 'divisions'. Promotion within a division (e.g. sales, marketing, manufacturing) should be based on a common sense hypothesis, as a lot of workload remains the same, so the effective results should be changing only partially. On the other hand, promotion across the departments should be less frequent and the new value of raw productivity would be totally uncorrelated.
- 4.11
- Yet another direction of further research is the study of dependence of overall output and effectiveness per employee in a growing organization – as most of real life organizations are dynamically changing their size.
- 4.12
-
The model can also be improved by including
effects evaluation of potential candidates for hiring and of employee dissatisfaction and restlessness when they are
not promoted. It is relatively easy to include effects of pre-screening of external candidates, for example by choosing the best agent from several candidates. This improves the quality even if the number of reviewed candidates is as small as 4. Of course, in the spirit of the current work, the compared quality would be properly normalized perceived potential performance, given, for example by
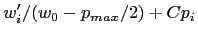 . There is, however, another process which counterbalances such gains due to pre-screening.
In the current paper, the external candidates
come from an infinite pool of agents with random characteristics.
In real life they would be the people from appropriate levels of other
organizations (usually quite similar to the studied one). By symmetry,
these effects should be included in the study: a process of agents leaving
the company to join other ones. In contrast with firing of the worst
perceived performers, here the agents most likely to leave would be
the ones who have relatively high opinion of themselves and willingness
to seek new opportunities. These qualities, in the first approximation
are related to the self-promotion drive
. There is, however, another process which counterbalances such gains due to pre-screening.
In the current paper, the external candidates
come from an infinite pool of agents with random characteristics.
In real life they would be the people from appropriate levels of other
organizations (usually quite similar to the studied one). By symmetry,
these effects should be included in the study: a process of agents leaving
the company to join other ones. In contrast with firing of the worst
perceived performers, here the agents most likely to leave would be
the ones who have relatively high opinion of themselves and willingness
to seek new opportunities. These qualities, in the first approximation
are related to the self-promotion drive 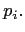 The probability
should increase with time spent at the same position. As a result,
increases of productivity introduced by the pre-screening of external
candidates would be counterbalanced by the outflow of the restless,
disgruntled employees.
The probability
should increase with time spent at the same position. As a result,
increases of productivity introduced by the pre-screening of external
candidates would be counterbalanced by the outflow of the restless,
disgruntled employees.
- 4.13
-
The extensions mentioned above could allow the model to be used for concrete organizations.
This would provide more practical value, extending beyond the current conclusions that
combating the Peter scenario and self-promotion may quickly and significantly improve real productivity of organizations.
 References
References
-
ADAMS, S. (1996).
The Dilbert Principle.
Harper Business.
AUDAS, E., BARMBY, T. & TREBLE, J. (2004). Luck, Effort, and Reward in an Organizational Hierarchy. Journal of Labor Economics 22(2), 379–395. [doi:10.1086/381254]
BALL, P. (2004). Critical mass: How one thing leads to another. Farrar Straus Giroux.
BARMBY, T., EBERTH, B. & MA, A. (2006). Things Can Only Get Worse? An Empirical Examination of the Peter principle. University of Aberdeen Business School Working Paper Series. http://www.dur.ac.uk/resources/dbs/research-papers/TimBarmby27Feb09.pdf.
DICKINSON, D. L. & VILLEVAL, M-C. (2007). The Peter Principle: An Experiment. IZA Discussion Paper No. 3205, Institute for the Study of Labor (IZA), Bonn, Germany .
FAIRBURN, J. & MALCOMSON, J. (2001). Performance, promotion, and the Peter Principle. The Review of Economic Studies 68(1), 45–66. [doi:10.1111/1467-937X.00159]
FARIA, J. R. (2000). An Economic Analysis of the Peter and Dilbert Principles. Tech. rep., UTS Working Paper No. 101. http://www.business.uts.edu.au/finance/research/wpapers/wp101.pdf.
GIBBONS, R. & WALDMAN, M. (2006). Enriching a theory of wage and promotion dynamics inside firms. Journal of Labor Economics 24(12) 59 – 107. [doi:10.1086/497819]
KANE, J. (1970). Dynamics of the Peter Principle. Management Science 16(12) B800 – B811. [doi:10.1287/mnsc.16.12.B800]
KOCH, A. K. & NAFZIGER, J. (2007). Job Assignments under Moral Hazard: The Peter Principle Revisited. IZA Discussion Paper No. 2973, Institute for the Study of Labor (IZA), Bonn, Germany.
LAZEAR, E. & ROSEN, S. (1981). Rank-order tournaments as optimum labor contracts. The Journal of Political Economy 89(5), 841 – 864. [doi:10.1086/261010]
LAZEAR, E. (2001). The Peter Principle: promotions and declining productivity. Tech. rep., NBER Working Paper No. 8094. http://economics.uchicago.edu/download/peterprinciple.pdf.
LAZEAR, E. (2004). The Peter Principle: a theory of decline. Journal of Political Economy 112(S1), 141–163. [doi:10.1086/379943]
MACLEOD, W. & MALCOLMSON, J. (1988). Reputation and hierarchy in dynamic models of employment. The Journal of Political Economy 96, 832–854. [doi:10.1086/261565]
PETER, L. & HULL, R. (1969). The Peter Principle. William Morrow and Company, New York.
PLUCHINO, A., RAPISARDA, A. & GAROFALO, C. (2010). The Peter Principle revisited: A computational study. Physica A: Statistical Mechanics and its Applications 389(3), 467 – 472. [doi:10.1016/j.physa.2009.09.045]
PRITCHARD, R. (1990). Measuring and improving organizational productivity: A practical guide. Praeger Publishers, New York.
SPENCE, M. (1973). Job market signaling. The Quarterly Journal of Economics 87 355 – 374. [doi:10.2307/1882010]
US SMALL BUSINESS ADMINISTRATION, (2008). Table of Small Business Size Standards. http://www.sba.gov/idc/groups/public/documents/sba_homepage/serv_sstd_tablepdf.pdf.
VALSECCHI, I. (2003). Job assignment and bandit problems. International Journal of Manpower 24(12) 844 – 866. [doi:10.1108/01437720310502168]