 Abstract
Abstract
- This paper interprets a particular agent-based social simulation (ABSS) in terms of Conte's third way of understanding agent-based simulation. It is proposed that the normalized compression distance (derived from estimates of Kolmogorov complexity) between the initial and final macrolevel states of the ABSS provides a quantitative measure of the degree to which the results obtained via the ABSS might be obtained via a closed-form expression. If the final macrolevel state of an ABSS can only be obtained by simulation, this confers on agent-based social simulations a special status. Future empirical (computational) work and epistemological analyses are proposed.
- Keywords:
- Agent-Based Social Simulation, Weak Emergence, Social Networks, Kolmogorov Complexity, Upward Causation, Downward Causation
 Introduction
Introduction
- 1.1
- In an account of a third way to understand social simulation, Conte (2009) suggests (in contrast with agent-based social simulation (ABSS) intended to generate bottom-up explanations) a need for the following:
- (Computational) theories of individual systems … Enriched with mechanisms of downward causation … which may occur in the context of emergence [emphasis added] when '[r]ules for interpreting others and forming expectations are affected by social properties and entities (norms, authorities, leaders, etc.)'.
- Upward theories about which mechanisms at the individual agents might lead to observed effects …
- [And] downward theories of possible loops from [social] effects obtained back to individuals, taking advantage of the mechanisms of downward causation … (pp. 44-46)
- 1.2
- All three elements noted by Conte are of general interest and importance. The first element—dealing with emergence—is of particular interest. Is it possible, within the framework of a third way agent-based social simulation, to give a quantitative characterization of emergence?
- 1.3
- Emergence has been (Gilbert 2002) and remains (Squazzoni 2009) a major topic of interest to those who simulate social systems. The term 'emergence', however, is loaded with related, and not so related, meanings. As noted by Baker (2010), "as typically used [following Bedau (1997)], the term 'emergent' is applied to whole systems of interacting parts".
- 1.4
- Huneman criticizes the part-whole characterization of Bedau and asserts that "… emergence is a feature of the whole agent-based simulation process" (Huneman 2008, p. 601). Huneman (p. 597) offers a computational characterization according to which "a state of a computation process is weakly emergent iff there is no shorthand to get to it except by running the simulation". Huneman and Humphreys (2008) refer to this as the "incompressibility criterion of [weak] emergence".
- 1.5
- Broadly speaking, this paper attempts to build on the qualitative insights offered by Conte and the quantitative possibilities disclosed by Huneman. The purposes of this paper are two-fold. First, to provide an example of an ABSS that can be interpreted in terms of Conte's recommendations. Second, to demonstrate a computational method (using the example ABSS) by which we can assess the degree to which a result arrived at by an ABSS might be obtained via a closed form expression that maps simulation inputs to simulation outputs. If the outputs generated by an ABSS from its inputs can be generated only by the ABSS, this is an argument for the methodological superiority of ABSS. If Conte's third way of understanding ABSS is a cognitive value to which practitioners should commit, then the degree to which an ABSS can be interpreted in terms of the three features identified by Conte is an indicator of the quality of that simulation.
 Third Way ABSS: An Example
Third Way ABSS: An Example
- 2.1
- The following discussion, designed to achieve the first purpose, is limited to a particular type of ABSS based on the agent-based model (ABM) specified by Skvoretz and Fararo (1995) to explore the interaction-driven emergence of social order amongst n group members engaged in task-related behavior. For this model, a set of microstates and macrostates can be distinguished and each macrostate is represented by an n by n sociomatrix R. Because the underlying ABM is based on the long-standing theoretical and experimental research program of expectation states, it has considerable internal complexity. For the purposes of this paper, however, a detailed accounting is unnecessary (see (Skvoretz and Fararo 1995) for details).
- 2.2
- In a manner of speaking, the ABM of Skvoretz and Fararo maps an initial macrostate R(0) to some 'final' macrostate R(K). When simulated, the ABM generates sequences of sociomatrices R(i), each defined as follows:
R(0)[x][y]='U' for all x,y ∈ {1, … n}
and
R(i)[x][y] = { one of 'U' or 'd' or 'D'} for all x, y ∈ {1, … n}, x ≠ y.
R(i) represents, then, the social order of the social network at time i. Whenever members interact, new social relational ties may form, generating R(i+1). How this affects subsequent member interaction is described next. - 2.3
- As shown in Figure 1 each simulation is driven by three macro-level inputs: a (changing) sociomatrix R (depicted by the leftmost reddish input element); a set composed of static parameters SC and SP (defined below); and a set RS of arbitrary but fixed random number seeds. These are briefly described as follows.
- 2.4
- A status characteristic (SC) is "any attribute possessed by members of a group whose culturally specified meaning is such as to make it potentially relevant to performance at [or, on] the group's task" (Balkwell 1994). The Skvoretz-Fararo ABM has three system parameters (SP) that determine the computation of expectation states and govern (in the weak, cybernetic, sense) the formation of social relations (via pseudo-random number generation). This use of pseudo-randomness (crudely) operationalizes the view that the behavior of individual human beings is sometimes unpredictable in principle (Collins and Kusch 1998). The above macro-level inputs can be varied according to the purpose of the simulation.
- 2.5
- By virtue of the axioms on which the Skvoretz-Fararo ABM is based, given enough rounds of interaction between group members, the final sociomatrix R(K) will be graphically complete. The sociomatrix R is complete if each actor x has formed a stable disposition to defer to ('d') or dominate ('D') each actor y. Other (similarly symmetric) interpretations of 'd' and 'D' are possible: for example, 'd' may designate a stable disposition to grant precedence, and 'D' to take precedence, in making task-relevant contributions.
- 2.6
- As depicted by the uppermost yellow element in Figure 1, R(i) determines the current expectation state of each actor x. The expectation state of an actor is a real value that indicates how strongly associated (in a cognitive sense) that actor is to task success or task failure. Actors with a positive expectation state are generally granted more opportunities to contribute to task completion. Each simulated actor, and each group of actors, is assumed to act in accordance with the mathematically specified, and experimentally supported, postulates of status characteristics theory (a branch of the expectation states research program). For a tutorial introduction to expectation states theory as it pertains to the model of Skvoretz and Fararo, see Wilson (2007).
- 2.7
- The micro-level of the model is depicted by the greenish element in Figure 1. Given a set of expectation states, a pair (x, y) of group members is selected. These members will engage in a single dyadic interaction. Pair selection is a stochastic function of: R(i) and values of SP, SC and RS.
- 2.8
- Once a pair (x, y) of interactants is selected, the micro-to-macro map (depicted by the lowermost yellow element of Figure 2) is evaluated. This too is a stochastic function: zero or more relational ties involving actors x and y (and the n–2 observers of the direct interaction between x and y) may (but need not) form. If ties do form, then R(i) is updated, which yields R(i+1), the new macrolevel component.
- 2.9
- The ABSS depicted in Figure 1 can be interpreted in terms of the third way of Conte as follows. First, the reddish (greenish) elements specify the macrolevel (microlevel) of the ABM: namely, R(i) (e(x)). The mechanism of downward causation (but see (Doreian 2001)) is specified by the uppermost yellow element: the computation amounts to a macro-to-micro mapping f: R(i) → e(x). Second, the mechanism of upward causation is specified by the lowermost yellow element: the computation amounts to a micro-to-macro mapping g: e(x) → R(i+1). The upward theory is that of status characteristics theory. Last, with mechanisms of both upward and downward causation, we have a loop from effects (via the macrolevel) back to individuals. Hence, a Skvoretz-Fararo ABSS (based on the corresponding ABM) can be understood in terms of the third way described by Conte.
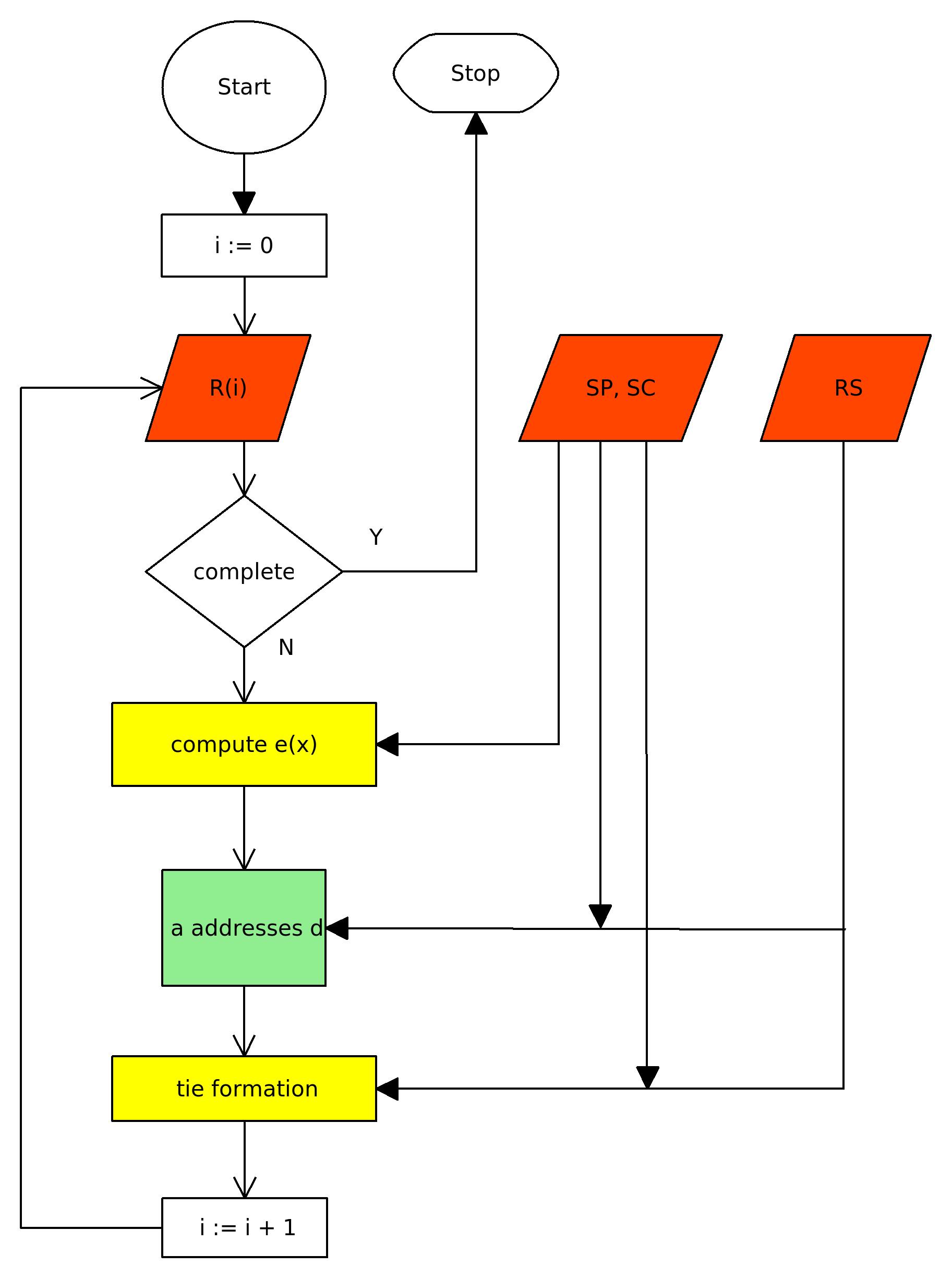
Figure 1. The Skvoretz-Fararo ABSS An objection—Is the ABSS deterministic?
- 2.10
- It turns out that the axioms of the Skvoretz-Fararo ABM are sufficient to guarantee that the corresponding the sequence R(i) converges to a graphically complete sociomatrix R(K), provided enough direct interactions are simulated. Such convergence to a static equilibrium (with respect to R), if it occurs, might seem to suggest convergence to a deterministic sequence of interactions. Though R(K) conditions pair selection for i > K, pair selection incorporates randomness via pseudorandom number generation.
 Assessing the irreducibility of an ABSS result
Assessing the irreducibility of an ABSS result
- 3.1
- This section addresses the second purpose of the paper: namely, to demonstrate a computational method for assessing whether a result arrived at by an ABSS can also be arrived at via a closed form expression that maps ABSS inputs to ABSS outputs. For Huneman (2008),
… the incompressibility criterion … formulates the unpredictability of a given state from knowledge of the rule and initial state [of a cellular automata]—but of course, not [emphasis added] of step n + 1 relative to step n, since this is perfectly … determined. (p. 600)
- 3.2
- Huneman also suggests that the incompressibility criterion is equally applicable to agent-based simulations (as distinguished from simulations based on cellular automata). In order to appreciate the incompressibility criterion, it is necessary to have a sense of what is meant by incompressibility.
- 3.3
- An object o is incompressible if C(o), the length of a compressed version of o obtained via some real-world compressor C, and the length of o, denoted len(o), are related as follows (where C(o) and len(o) are defined in terms of bits): C(o) > len(o) (Li and Vitanyi 2008, p. 116). Formal inference about compressibility (and, therefore, incompressibility) is based on Kolmogorov complexity (which is related to, but distinct from, Shannon complexity). The Kolmogorov complexity function is not computable, but it can be approximated by real-world compressors such as zip, bzip, and pmz (Cilibrasi 2006). It is this approximation that makes it possible to assess the degree to which a result arrived at by a Skvoretz-Fararo ABSS might be instead be obtained by the shorthand of evaluating a closed form expression that takes ABSS inputs as its arguments.
Normalized Compression Distance
- 3.4
- To keep matters simple, let n = 4 and suppose that a Skvoretz-Fararo ABSS generates the sequence R(1) through R(6), with each represented as a string S(i) shown in Table 1. Each S(i) consists of 4 × 4 = 16 bytes or 128 bits. We can assess the compressibility (and, therefore, the incompressibility) of each R(i) using the program ncd (developed by Cilibrasi and available at www.complearn.org along with very accessible documentation).
- 3.5
- Column 3 of Table 1 shows the number of bits in the compressed version of S(i) (using the command ncd -s S(i)) and column 4 shows the Normalized Compression Distance (NCD) between S(i-1) and S(i). The NCD can be computed using the command ncd -d dir dir, where dir contains a file F(i) for each i, and the content of F(i) is precisely the uncompressed S(i). The NCD(a, b) represents the similarity of the objects a and b. Typically 0 ≤ NCD(a, b) < 1.1 and smaller values of NCD represent more similar files/strings.
- 3.6
- As shown in Table 1, for i > 0, C(S(i)) > len(S(i)) = 128, so each S(i) is an incompressible sequence of characters. The large value of NCD(S(0), S(1)) suggests that S(1) contains much more 'information' than S(0). Yet, for i > 1, 0.3 < NCD(S(i-1), S(i)) < 0.50, suggesting more pair-wise similarity than pair-wise difference. Despite this, the dissimilarities accumulate.
- 3.7
- For this artificial example, NCD(S(0), S(6)) = 0.64. The hypothetical Skvoretz-Fararo ABSS transforms the compressible macrostate R(0) into the incompressible macrostate R(6). Hence, it is unlikely that R(6) can be 'deduced' from R(0) (Huneman 2008, p. 600) except by the ABSS.
Table 1: Compressibility and Similarity Step i S(i) C(S(i)) (bits) NCD(S(i-1), S(i)) 0 UUUUUUUUUUUUUUUU 88 Undefined 1 UUUDUUUUUUUUdUUU 136 0.53 2 UdUDDUUUUUUUdUUU 144 0.32 3 UdDDDUUUdUUUdUUU 144 0.37 4 UdDDDUdUdDUUdUUU 176 0.48 5 UdDDDUdDdDUUddUU 192 0.4 6 UdDDDUdDdDUdddDU 168 0.32 An objection—Is incompressibility a trivial property?
- 3.8
- One might argue that, because most strings of an arbitrary but fixed length are incompressible (Li and Vitanyi 2008), the incompressibility criteria of emergence is a trivial one. According to Huneman, an individualized outcome of a simulation inherits the feature of weak emergence from the whole agent-based simulation process. For a Skvoretz-Fararo ABSS, the individualized outcome is the final value of a graphically complete R(K). Hence, the final state of the hypothetical ABSS inherits the non-trivial feature of being weakly emergent.
 Conclusion
Conclusion
- 4.1
- The paper interprets a type of ABSS in terms of Conte's third way of understanding agent-based simulation. It is suggested that the normalized compression distance (NCD) may be taken as a quantitative measure of whether a result obtained by an ABSS might instead have been obtained by evaluating some closed-form expression that maps ABSS inputs to ABSS outputs. Future empirical (computational) work should examine how the NCD varies across a finite number of sample paths (given a fixed set of inputs) and across variations in the fixed set of inputs to a particular ABSS. In addition, the utility of the NCD for comparing ABSSs should be explored. Finally, if the approach taken here is technically reasonable and useful, it nevertheless should be assessed in light of the differing epistemological analyses of weak emergence (as understood by Bedau) carried out by Huneman (2008) and Baker (2010).
 References
References
-
BAKER A (2010) 'Simulation-Based Definitions of Emergence'. Journal of Artificial Societies and Social Simulation 13(1)9, retrieved 10 February 2010, https://www.jasss.org/13/1/9.html.
BALKWELL J W (1994) 'Status'. In Foschi M and Lawler E J (Eds.) Group Processes: Sociological Analyses, Chicago: Nelson-Hall.
BEDAU, M A (1997) Weak Emergence. In James Tomberlin, ed., Philosophical Perspectives: Mind, Causation, and World, vol. 11, pp. 375-399. Oxford: Blackwell Publishers. [doi:10.1111/0029-4624.31.s11.17]
CILIBRASI R (2006) Statistical Inference Through Data Compression. Amsterdam: R. Cilibrasi.
COLLINS H and M Kusch (1998) The Shape of Actions: What Humans and Machines Can Do, Cambridge: MIT Press.
CONTE R (2009) 'From Simulation To Theory (and Backward)'. In Flaminio Squazzoni (ed.), Epistemological Aspects of Computer Simulation in the Social Sciences. Berlin: Springer Verlag, pp. 29-47. [doi:10.1007/978-3-642-01109-2_3]
DOREIAN P (2001) 'Causality in Social Network Analysis', Sociological Methods and Research 30, 81-114. [doi:10.1177/0049124101030001005]
GILBERT N (2002) Varieties of emergence'. In D. Wallach (ed.), Social Agents: Ecology, Exchange, and Evolution. Agent 2002 Conference, University of Chicago and Argonne National Laboratory, pp. 41-56.
HUNEMAN P (2008) 'Emergence Made Ontological? Computational versus Combinatorial Approaches'. Philosophy of Science 75, 595-607. [doi:10.1086/596777]
HUNEMAN P and P Humphreys (2008) 'Dynamical Emergence and Computation: An Introduction'. Mind and Machines 18(4), 425-430. [doi:10.1007/s11023-008-9124-4]
LI M and P M B Vitányi (2008) An Introduction to Kolmogorov Complexity and Its Applications. 3rd ed. Berlin: Springer. [doi:10.1007/978-0-387-49820-1]
SQUAZZONI F (ed.) (2009) Epistemological Aspects of Computer Simulation in the Social Sciences (Lecture Notes in Computer Science). Berlin: Springer-Verlag. [doi:10.1007/978-3-642-01109-2]
SKVORETZ J and T J Fararo (1996) 'Status and participation in task groups: A dynamic network model'. American Journal of Sociology, 101 (5), 1366-1414. [doi:10.1086/230826]
WILSON R W (2007) 'Simulating the Effect of Social Influence on Decision-Making in Small, Task-Oriented, Groups'. Journal of Artificial Societies and Social Simulation 10(4)1, retrieved 16 July 2009, https://www.jasss.org/10/4/1.html.