Bill Tomlinson (2009)

A Proximate Mechanism for Communities of Agents to Commemorate Long Dead Ancestors

Journal of Artificial Societies and Social Simulation vol. 12, no. 1 7
<https://www.jasss.org/12/1/7.html>

For information about citing this article, click here

Received: 04-May-2008    Accepted: 07-Sep-2008    Published: 31-Jan-2009

Abstract

Many human cultures engage in the collective commemoration of dead members of their community. Ancestor veneration and other forms of commemoration may help to reduce social distance within groups, thereby encouraging reciprocity and providing a significant survival advantage. Here we present a simulation in which a prototypical form of ancestor commemoration arises spontaneously among computational agents programmed to have a small number of established human capabilities. Specifically, ancestor commemoration arises among agents that: a) form relationships with each other, b) communicate those relationships to each other, and c) undergo cycles of life and death. By demonstrating that ancestor commemoration could have arisen from the interactions of a small number of simpler behavioural patterns, this simulation may provide insight into the workings of human cultural systems, and ideas about how to study ancestor commemoration among humans.

Keywords:

Agent Based Models, Ancestor Commemoration, Dominance Relationships, Communication, Cooperation, Memory

Introduction

1.1

Ancestor commemoration is an important phenomenon across human history, forming the basis for many complex behaviours in numerous cultures (see Li 2000 for a review). Ancestor veneration, in particular, has been defined by MacAnany as "rituals and practices surrounding the burial and commemoration, by name, of apical ancestors of kin groups." (McAnany 2000) Drawing on this definition, ancestor commemoration can be defined as "practices surrounding the formation and maintenance of shared memories of apical ancestors of kin groups." These kinds of phenomena are often seen as arising from complex cultural processes (e.g., Li 2000; Lucero 2007). In this paper, we offer a potential proximate mechanism by which ancestor commemoration may have arisen in human cultures. Specifically, we take a simulated approach to this problem, creating communities of computational agents programmed to have computational versions of several capabilities found in humans. From the interactions of these capabilities, the agents began to exhibit patterns of behaviour that resemble a simplified version of human ancestor commemoration. This finding provides a functional model of how the complex activities of ancestor commemoration may have arisen in progenitors of modern humans as a result of the combination of several simpler characteristics.

1.2

Computational simulations provide an effective way of exploring apparently complex phenomena that may be derived from simpler parts. For example, human religions have been studied using computational models (Bainbridge 2006; Upal 2005). Flocking, herding, and schooling behaviours in animals have been simulated using groups of agents that adhere to a small number of simple rules (Reynolds 1987). Genetic algorithms have also been used to simulate the evolution of virtual creatures (Sims 1994). The research described here uses an agent-based approach to offer a parsimonious proximate mechanism for the apparently complex phenomenon of ancestor commemoration. More complex explanations of this behaviour, for example involving modelling of kinship, are not necessary. While the simulation cannot prove that this set of human behaviours originated in this way, it does provide support for the idea that ancestor commemoration could have resulted from the interactions of several simple behaviours, rather than the requiring more complex cultural explanations.

Implementation

2.1

The key data structures in this simulation include the Person (the computational model for each individual agent), the PersonModel (the mental representation that one Person forms about another), and the Relationship (an archive of the interaction history between two Persons). At each time step of the program, each living Person enacts the same behavioural code, involving the ability to form relationships with each other and communicate them to each other. Only one Person performs an action at a time. All living Persons act in the same order at each time step.

2.2

When it is an agent's turn to update, it has some probability of initiating an interaction with another agents, some probability of telling another agent about a Relationship that it holds, and some probability of initiating an act of cooperation. After completing these three steps, the agent increments its age. Having interactions and telling other agents about relationships, the key elements in the initial emergence of ancestor commemoration, are described immediately below. Cooperation, a possible mechanism by which ancestor commemoration may have been perpetuated within communities, is described later in the paper.

2.3

At each time step, each agent has the opportunity to interact with another agent. This agent is chosen at random from among the other living agents in the population. We considered implementing a spatial grid or other mechanism for enhancing context preservation, but wished to keep the simulation as simple as possible and therefore decided to have the agents choose their social partners at random. In the interactions between partners, each agent chooses an action, and then both agents exchange actions and update their Relationships based on that information. The three central elements of this system - relationships, communication, and life cycles - were decided upon in an effort to produce a system that was as simple as possible, while maintaining biological plausibility. All three elements exist in many biological species; the three frequently co-occur. The sections below describe the details of the implementation for each of these elements.

Relationships

2.4

The first element of this system is a model of relationship formation among agents. The implemented simulation described below uses dominance relationships; however, other kinds of relationships could work as well, as long as each agent is able to remember the unique identities of other individuals and store information about them. Dominance relationships in particular were used in this system so that this project could contribute to a larger research effort that is beyond the scope of this paper.

2.5

A dominance relationship between two entities can be defined as a learned and remembered construct by which that entity keeps track of its history of competitive interactions with another entity, and allows that history to affect its future interactions with that entity (derived from Tomlinson (2002) and de Vries (1998)). Dominance hierarchies emerge as a consequence of positive feedback among multiple dyadic dominance relationships within a social group (Tomlinson 2002). Context preservation ( Cohen, Riolo, and Axelrod 1999) is the essential function of a dominance relationship - behaving differently toward different social partners, rather than interacting with all entities in the same way. Long-term dyadic social relationships such as dominance relationships exist in many different species, enabling stable alliances in societies of primates (Harcourt and de Waal 1992; Barrett, Henzi, Weingrill, Lycett, and Hill 2000), raiding parties among chimpanzees (Wrangham and Peterson 1996), and inheritance of rank in spotted hyenas and cercopithecine primates (Engh, Esch, Smale, and Holekamp 2000).

2.6

In this simulation, dominance relationships occur via three elements (Tomlinson 2002) - dominance, perception and memory. The agents use a simple model of social dominance - a single number varying from submissive (0.0) to dominant (1.0). This model is a simplified version of Mehrabian and Russell's (Mehrabian and Russell 1974) dimensional model of emotion, which featured Pleasure, Arousal, and Dominance as the three orthogonal axes of emotion.

2.7

The agents' perception mechanism is a simple unique identifier that allows a Person to recognize unique other Persons during successive interactions. Each Person uses this unique ID to create a PersonModel of the other Person, which allows them to recognize that individual on each successive encounter.

2.8

The agents also feature a memory mechanism called a Relationship that creates an association between a dominance value and two PersonModels. The Relationship model supports both first-person Relationships, in which the Person storing the Relationship is one of the participants, and third-person Relationships, in which both participants are not the Person storing the Relationship. First-person Relationships are learned through direct experience, i.e., as a result of engaging in a dominance interaction, in which the Person itself and the social partner each choose dominance displays to exhibit, and forming a mental model of that interaction. Persons learn about third-person Relationships through communication acts from other Persons.

2.9

In first-person Relationships, the Relationship model stores the dominance value that the Person holding the Relationship experiences during its interactions with the Person represented by the PersonModel. On each successive interaction, a Person's dominance behaviour is based on a weighted average between its actual dominance value prior to the interaction, and the dominance value stored in its Relationship with the other Person. These factors are weighted via a confidence value that is also stored in the Relationship. This confidence value increases when an interaction confirms the dominance value stored in the Relationship, and decreases when it conflicts with that value. After each interaction, the Person updates the Relationship's dominance value based on a weighted average of the Relationship's stored value and the Person's actual dominance value in the wake of the encounter.

2.10

In third-person Relationships, both participants have identities that are distinct from the Person holding the Relationship. Third-person Relationships are updated when a Person is told about a Relationship by a different Person, as described below.

Communication

2.11

The second element of the simulation is a system by which agents communicate the details of their dominance relationships to each other. Social communication exists in many different forms in the natural world. Primate greetings, negotiation, and recruiting utilize a vocabulary of signals (Hauser 1998). Baboons exchange social currency through grooming (Barrett et al. 2000). Humans have a great deal of expertise at interpreting social signals and meaning (Brothers 1997).

2.12

At each time step, in addition to potentially initiating an interaction, each Person tells another living Person, chosen at random, about a Relationship that it knows, choosing among several options: the Relationship in which it has the highest confidence, the most recent Relationship that it participated in, or a random Relationship from its memory. The probability of each of these options is specified in advance, and is constant across all Persons for the entire length of the run.

2.13

Each communication act includes the identities of the two PersonModels involved in the Relationship, the dominance value of each of them, and the confidence that the teller has in that Relationship. The receiver learns this information in a similar way as if it had witnessed or participated in the interaction, except that the effect is modified by the confidence that the listener has in the teller. If the listener has low confidence in the teller, the effect of the communication act on the listener's existing Relationships is lessened.

Life Cycles

2.14

The third component of the simulation is a cycle of life and death. In the natural world, organisms are born and die with regularity. The young tend to have lower dominance than adult members of a community, for example among wolves (Mech 1999) and primates (Pereira 1995).

2.15

In this simulation, each run begins with a full population of Persons of varying ages. Thereafter, additional Persons are born at fixed intervals. All Persons starting with low dominance. For the first portion of their lives, they exhibit a reduced ability to act dominant (simulating smaller size). Once they achieve adulthood, their dominance in a given interaction is determined solely by their dominance immediately before the interaction and any Relationships that affect that dominance.

2.16

Persons in the population die after a fixed lifetime. When a Person dies, all of the Relationships that it held in its mind are deleted. However, the PersonModels that other Persons formed about it remain in existence. Persons don't need to be alive to be the subject of communication acts; other Persons continue to communicate Relationships that involve the deceased. This process is similar to communication in the real world, where it is possible to tell stories about people whether they are alive or dead, and whether or not the teller knows whether they are alive or dead.

2.17

Populations run for several generations, where a generation is measured by the length of time it takes for one agent to be born and then die. Once an entire generation has passed, no Persons are still alive from that population who were alive prior to the beginning of that generation.

Source Code

2.18

To assist readers in replicating and/or improving on this research, the full source code for the simulation is available at: http://www.ics.uci.edu/~wmt/code/AncestorVeneration.zip.

Results

3.1

Dominance relationships, communication, and life cycles combine to cause individual agents within a simulated population to exhibit behavioural patterns that resemble human ancestor commemoration. To demonstrate this effect, we programmed a group of 150 Persons with these characteristics. This population size was chosen following Dunbar's research in primate social group size (Dunbar 1993), although the effects were observed at a range of larger and smaller group sizes. A single population was chosen for presentation here, rather than an average across many populations, in order to be able to discuss specific Persons from that community. Averaging a large number of runs causes the unique characteristics of ancestor commemoration (e.g., individual apical ancestors commemorated by the living group) to disappear, since different individuals are commemorated by each different run. The population described below is typical of numerous other runs of the simulation. Details are provided at the end of this section confirming the repeatability of this pattern, and discussing the results of several parametric studies that help establish the range of values under which these conditions hold.

3.2

Figures 1 and 2 show a snapshot of the PersonModels held by all living Persons in this community at the end of ten generations. The graphs illustrate a number of details about what members of the currently living generation believe about each other, and what they believe about their predecessors. Figures 1 and 2 are a matched pair, showing two views of the same population.

3.3

Figure 1 shows the average dominance of all the PersonModels held by all living Persons (i.e., their "thoughts" about the dominance of other Persons). This dominance value is high if the population tends to share the opinion that the Person in question is, or was, a dominant member of their community. The dominance value is low if that Person is a submissive member of the community. The chart shows the community's opinion (i.e., average of all PersonModels) of both living Persons, shown as black dots, and deceased Persons, shown as hollow dots.

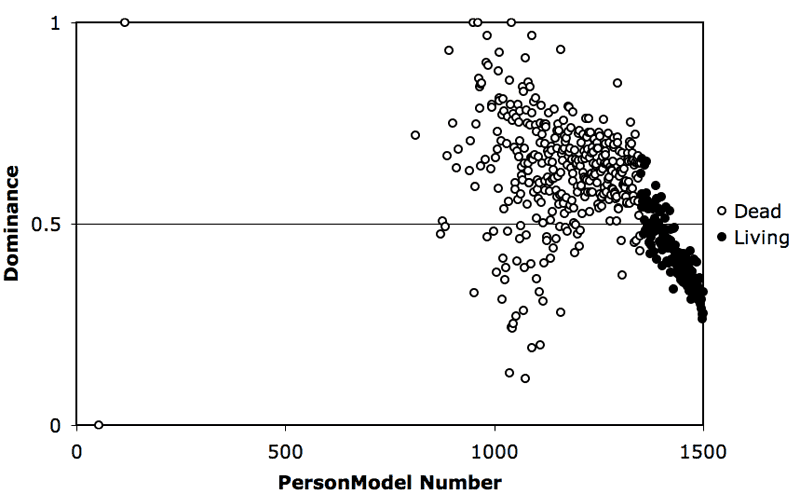
Figure 1. Community's average opinion of the dominance of all individuals that have ever lived, from newborns (at right) to long dead ancestors (at left). Black dots signify currently living agents, while hollow dots are deceased agents.

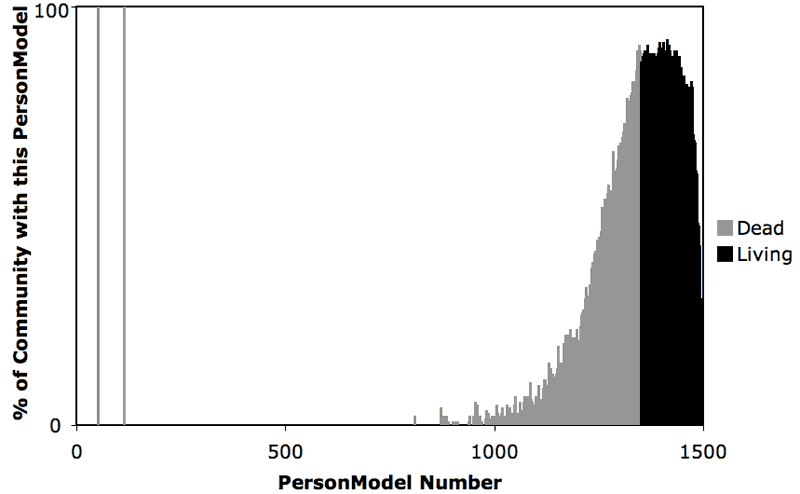
Figure 2. Percentage of living community that knows about a given individual (either through direct interaction or indirect communication), from newborns (at right) to long dead ancestors (at left). Black bars signify living agents, while gray bars signify deceased agents.

3.4

Figure 2 shows the percentage of the living population that holds a PersonModel for (and therefore has "heard of") each given Person that has ever existed. If the entire living population has a PersonModel attached to a certain Person's identity, that Person's value on this chart is 100. If no living Person has a PersonModel for that identity, that Person's value is 0.

3.5

Both of these charts show a snapshot of the population's history, as recorded in the memories of the community members. It may be easiest to think about the PersonModel's number as showing how long ago the associated Person died. So, for example, the PersonModel shown at 116 (the hollow dot near the top left of the chart) died a very long time ago, whereas the one shown at 1500 (the black dot near the bottom right) was just born. If this graph were animated, the dots would move slowly from right to left as time proceeded.

3.6

The following paragraphs provide a detailed analysis of this particular snapshot in time, of a group of 150 living agents, who are living in a community that has been in existence for ten generations. In this community, the agents had a 10% chance of initiating an interaction at each timestep, and a 100% chance of telling someone about a Relationship. The range of viable values for these parameters is described at the end of this section.

3.7

At the far right of Figure 1, from PersonModels 1500-1350, we can see that the dominance of Persons tends to increase as they get older. Shortly after birth, they tend to have a dominance of around 0.31, which gradually increases to an average of approximately 0.57 by the time of death. There is significant variability within these values, with agents exhibiting values as low as 0.26, and as high as 0.66. Nevertheless, there is a clear positive slope to the change in dominance over time. This slope is due primarily to the age effect, in which Persons have lower dominance during a brief period at the beginning of their lives, but continues to rise steadily even after Persons have reached the age of adulthood when dominance is no longer limited.

3.8

The corresponding section of Figure 2 shows that the percentage of the community that knows of the Person increases rapidly for the first portion of their life. This number increases in two ways - first, through Persons having direct dominance interactions with the Person in question, and second, through hearing communication acts involving that Person. As the Person begins to be known by a larger percentage of the population, the number of people who have yet to encounter this individual drops, and the rate of growth slows. By the time of death, most (~87%) of the living members of the community have either met or heard about that Person.

3.9

During the first half-generation after the death of a Person, the dominance of the Person tends to increase, as seen in PersonModels 1275-1350 of Figure 1. This increase occurs because most living Persons still have first-hand Relationships with the deceased Person and, since the Persons remaining alive tended to have been submissive to their elders due to the age effect, most of the Persons' communication acts confirm that the deceased was dominant. The percentage of the population that knows about a given Person drops off steadily during this period, as seen across PersonModels 1200-1275 in Figure 2.

3.10

During the second half-generation after the death of a Person, the number of Persons who have first-hand experience with the deceased is now below 50% of the total population. During this time, we see a shift in the prevailing force acting in Figure 1. Prior to this time, the actual dominance of the Person was the most important force in determining that Person's perceived dominance among other community members. During this period, as seen in PersonModels 1275-1200, we begin to see a polarizing force begin to prevail over the upward trend. While the few remaining Persons who had direct interactions with the deceased still provide reports of that agent's dominance, the positive feedback mechanism of the dominance relationship system begins to make small differences become larger.

3.11

During this period (PersonModels 1275-1200) in Figure 2, we see that the number of Persons who have heard of a Person continues to drop off. However, it does not drop off linearly. Rather it forms a rough approximation of an exponential curve, as some individuals continue to hear about these Persons via word of mouth. Through this mechanism, PersonModels may be passed from generation to generation, preserving the memory of deceased predecessors.

3.12

After all Persons who ever had a first-hand Relationship with a Person have died, Persons know of that Person's name and dominance only through communication acts from their social partners. During this time, seen in Figure 1 from PersonModels 1200-700, the average dominance of the PersonModels becomes polarized, with certain individuals becoming even more highly dominant through the positive feedback of the communicated Relationships, and others gradually becoming more submissive as they are juxtaposed with their dominant contemporaries. This polarization occurs because all Relationships must involve two PersonModels, and therefore with each telling, the dominance of one individual and the submissiveness of another are simultaneously reinforced.

3.13

During this same time period, as seen in Figure 2 from PersonModels 1200-700, the percentage of the population that knows about a given PersonModel continues to fall. While the PersonModels of a few individuals continue to be passed on by word of mouth, most PersonModels fall completely out of the community's memory, never to be remembered. Once there is no living Person who holds a Relationship involving a particular deceased Person, that deceased Person can never be reintroduced into the community's memory. (In a community with written language, this reintroduction could happen. The communities described here represent purely oral cultures.)

3.14

Nearly all Persons who have been dead for several generations fall out of the collective memory of the community, as seen in both figures from PersonModels 700-200. Two particular Persons (116 and 53) from the first generation, however, live on in the communication acts of their community long after their death. The Relationships between these long dead ancestors have been told to the currently living generation by their immediate ancestors, who were told it by their ancestors, and so on. The Relationship between PersonModels 116 and 53 is known by every member of the community, despite eight generations having passed since those Persons died. This Relationship has been communicated from generation to generation, and the positive feedback mechanism of the dominance relationships has caused this Relationship to become more and more polarized with each telling, with PersonModel 116 having average dominance of 1.0 (the highest possible value) and PersonModel 53 having average dominance of 0.0 (the lowest possible value). Both of these values are known by 100% of the community.

3.15

The Relationship between this pair of well-remembered apical ancestors is passed on from generation to generation, to the exclusion of interim ancestors, because it is the Relationship in which the living Persons are most confident. This confidence is one of the criteria that causes a Relationship to be passed on in their interactions with other members of their community. This effect is not unique to this particular run (although the specific remembering of PersonModels 116 and 53 is unique to this run). In most runs of this simulation, there is a pair of individuals in the first generation of the community whose relationship becomes commemorated very strongly, to the point where it is known by all or nearly all members of the community within several generations.

3.16

This cultural transmission of a Relationship among apical ancestors is predicated on acts of inter-Personal communication. If communication is disabled for a period of time at the beginning of the simulation (for example, to avoid the impact of initial conditions), the apical ancestors arise from among the first generation after communication is activated. A continuous chain of communicating descendents is necessary for commemoration to occur.

3.17

Persons in this community were programmed to communicate their most confident Relationship 80% of the time, the most recent Relationships 15% of the time, and random Relationships the remaining 5% of the time. In runs where Persons communicate only the single most dominant Relationship that they hold, the chart usually lacks any of the intermediate ancestors, and features only a single pair of apical ancestors that the community commemorates. In runs with a higher degree of randomness or recency in the Relationships that are shared, there are more interim ancestors, although one pair from the eldest generation still often dominates. These constants produced data that was sufficiently clear to show the ancestor generation effect, while presenting enough of several other characteristics for them to be addressed in the above discussion. The range of viable values for these parameters is described below.

3.18

Through these processes, members of each successive generation engage in acts of communication that preserve the memory of the identities of the oldest ancestors to which the living group is linked by a chain of communication.

Parametric Studies

3.19

One hundred runs of the simulation were conducted using the same settings described above. In all hundred of them, there were precisely two individuals in the first 152^[1] born for whom members of the living generation had memories. Each of these individuals was known by every member of their communities. In each run, one of the two known ancestors had a dominance of 1.0, and the other had dominance of 0.0. The run described above is typical of this group.

3.20

The ancestor commemoration phenomenon occurs within a range of parameters. To test the range of viable values, we first varied the frequency with which Persons interacted directly with each other and communicated relationships to each other. We found that with a direct interaction rate of 5% (i.e., a Person directly interacted with a social partner during 5% of its update cycles), ancestor commemoration arose when communication occurred at a rate of 55% or more. With a direct interaction rate of 10% or 20%, ancestor commemoration arose when communication occurred with a frequency of greater than 60% and 60% respectively. These results suggest that ancestor commemoration occurs in populations in which communication acts are significantly more frequent than direct interactions.

3.21

To examine another set of parameters, we ran populations similar to the configuration described in depth above, but with a range of degrees to which Persons communicated their most confident relationships vs. their most recent relationships. We found that ancestor commemoration occurred if at least 40% of the communication acts conveyed the most confident relationship rather than the most recent. These results suggest that this phenomenon is able to tolerate a relatively wide range of communication style and content.

3.22

We also ran this simulation at a variety of population sizes. We found evidence for ancestor commemoration in populations of 5, 15, 150, and 500 Persons. These results suggest that ancestor commemoration is robust across a range of community sizes.

3.23

We also implemented a version of the simulation that used an even simpler relationship mechanism, in which each Person simply stored a confidence value for each social partner it ever encountered (either via direct interaction or via communication from another Person). Ancestor commemoration occurred in this case as well. The critical element in the relationship mechanism appears to be a positive feedback system, by which PersonModels that are well known in generation n become even more well known in generation n +1.

3.24

While the simulation presented here does not have nearly the complexity of actual human ancestor commemoration, it nevertheless demonstrates that the core elements of this human behavioural pattern may have come about due to the interactions among relationships, communication and life/death cycles. Beyond this simple version, additional complexity could be layered on top of this framework to explore other facets of ancestor commemoration and related phenomena. The key conceptual benefit of this simulation is to demonstrate that it is not necessary for ancestor commemoration to be transmitted via complex/unique pathways. Rather, a combination of several simpler phenomena results in ancestor commemoration arising spontaneously.

Reciprocity

4.1

The above simulation demonstrates a mechanism by which ancestor commemoration may have been introduced in human societies. However, it does not speak to the mechanism by which such a behavioural pattern might be sustained by that community, rather than, for example, being "selected out" by some negative selection pressure. In order for a behavioural pattern to become pervasive, it needs not only to have an opportunity to arise, but it also needs to confer some benefit on the individuals enacting it, or at least not cause a significant impediment to their survival.

4.2

To demonstrate a potential mechanism by which ancestor commemoration could have been reinforced and perpetuated within communities, we implemented a simple cooperation system based on reciprocal altruism (Trivers 1971). Reciprocal altruism is a behavioural pattern that can lead to enhanced survival, for example via food sharing (Wilkinson 1984). Reciprocity and reputations have previously been studied using agent-based models, e.g., Younger (2004); the cooperation system used here uses a model of reciprocity based on a simple social distance calculation, rather than on individual reputations.

4.3

In this system, each living Person cooperates with another living Person at each time step, choosing some amount of "social capital" to contribute toward that partner. The amount of the contribution, C, is deducted from the cooperator's social capital, and (B * C) is added to the partner's social capital, where B is the benefit of cooperation. The value of B must be greater than 1 in order for cooperation to be better than non cooperation. In this simulation, we set B = 1.5, which means that overall it was 50% better for the community for individuals to cooperate than not to cooperate. However, in the absence of reciprocity, cooperation does not benefit the individual making the initial cooperative act.

4.4

The amount of social capital, measured in arbitrary "social capital units" (SCUs), contributed by an individual is based on the inverse of the social distance that the cooperator calculates toward the partner. This value simulates the expected reciprocity that had been exhibited in the past, or that would be exhibited in the future, by that partner. This social distance value is based on the degree of correlation between the rankings of the identities of the top several PersonModels that the cooperator has direct Relationships with, and the top several PersonModels that the cooperator knows that the partner has relationships with. So, for example, if Person A's closest social partner is the same as Person B's closest social partner, that would demonstrate that A and B have a small social distance between them. In this system, we used the top 10 relationships to calculate social distance. For each of the Person's top 10 social relationships, the difference between the rankings of that partner is added to the social distance value, up to a maximum of 10 per partner. For example, if two partners have exactly the same top ten partners, their social distance will be 0, and they will make the maximum contribution to the other Person each tick. If, on the other hand, there is no overlap between their ten partners, the social distance between them will be the maximum amount, and the contribution to each cooperation act will therefore be 0. We chose this distance model, rather than a more complex one involving kinship or other factors, because we wanted to keep the model as simple as possible. While it is likely necessary to include kinship and many other factors to develop a simulation that seeks to approach the complexity of human ancestor commemoration, we seek here to demonstrate that such factors may not be necessary for the basic elements of such behaviour to arise.

4.5

Figure 3 shows the difference between the increase in social capital in a community with Relationships only among living Persons (shown in red) and remembered Relationships among both living and dead individuals (shown in blue). Relationships with long-dead ancestors that are held by all members of the community help to reduce social distance, and therefore lead to increased reciprocity and increased average social capital. In particular, the fact that in this population all or nearly all community members are confident in their knowledge of the relationship between their two apical ancestors (PersonModels 116 and 53 from Figures 1 and 2 above) makes it very likely that at least two PersonModels will be shared across any pair of social partners.

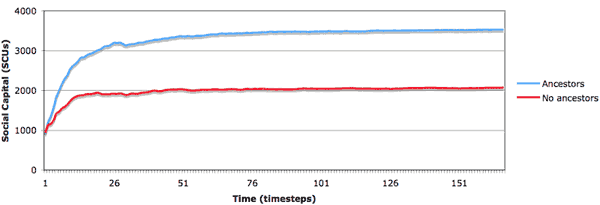
Figure 3. Reciprocity enables the average social capital to be higher in communities that perform ancestor veneration than in communities who communicate only Relationships involving living Persons

4.7

Through the process described above, reciprocity enables the average social capital to be higher in communities that perform ancestor commemoration than in communities who communicate only Relationships involving living Persons. This positive effect could be sufficient to overcome the energetic cost or other potential disadvantages that might accompany the behavioural pattern of ancestor commemoration.

4.8

Although the reduction of social distance, and ensuing increase in reciprocity, could provide a survival benefit that would enable ancestor commemoration to become established in a community, it bears reiterating that this process is not necessary for ancestor commemoration to occur. In fact, during this research, once we had implemented dominance, communication, and cycles of life and death, ancestor commemoration arose spontaneously, and we then had to write additional code in order to disable it. Ancestor commemoration may not simply be made possible by these existing human abilities; it may be made inevitable by them.

Discussion

5.1

Anthropologists have argued that ancestor worship is universal across human cultures (Steadman, Palmer and Tilley 1996). From the ghosts of the Romans to the ancestral spirits of the North American Iroquois and Australian Arunta peoples, various forms of this phenomenon occur across many cultures. Steadman et al. offer that "[r]eligious rituals that focused on ancestors could strengthen kinship ties and the traditions on which they depend" (p. 73). Kinship ties are important to the survival of many human and non-human groups; strengthening them via the commemoration of ancestors could provide a significant survival advantage.

5.2

It is difficult to draw connections between the results of a simulation of this kind and the operation of real human societies; the complex causes of human behaviour make it nearly impossible to assert claims of causality with much certainty. Therefore, we are reluctant to claim that the above mechanism is the definitive cause of human ancestor commemoration, or to try to draw too clear parallels between this simulation and human cultures. Nevertheless, the simulation described here does seek to provide a simple mechanism by which this widespread phenomenon may have arisen. The law of parsimony would support a very simple explanation for a human universal; this work is part of an effort to find simple mechanisms for humanity's complex behaviour.

5.3

There are many aspects of human ancestor commemoration that this project does not capture. It does not include many of the effects of kinship, such as the nested nature of families, clans, and larger groupings. The communication model is greatly impoverished, missing the subtlety with which people exchange social information. Many cultures engage in extensive rituals and ceremonies around their ancestors, the grandeur of which is missing from this numerical simulation. Nevertheless, this work may serve as a starting point for more complex examinations of this area.

Future Work

6.1

This computational model of ancestor commemoration may be useful as a platform for exploring various mechanisms and attributes of ancestor commemoration and related phenomena. For example, this system could be used to test different computational models of cultural transmission. Specific research questions in this area could include: What are the characteristics of relationship transmission that would be optimal for preserving the commemoration of apical ancestors? If agents have preferences for interacting with certain social partners, based on proximity, kinship, or other factors, would ancestor commemoration occur differently? What characteristics match most closely to various human cultures? How does written language impact this kind of cultural transmission? Results from these studies could then inform further research about ancestor commemoration in the real world using the predictions of those models.

6.2

This system could also be used to test the optimality of various different parameters of ancestor commemoration through which to reduce social distance and thereby encourage reciprocity. For example, if each member of a community can only know 150 individuals well (as Dunbar's research might suggest (Dunbar 1993)), is it better to know 150 living people, 150 ancestors, or some blend of the two? Is there a way for people to know generalizations about groups of people, such as archetypes, that can help us form more relationships? People in the real world often appear to know more than 150 people; how do ancestors, television characters, and other non-living personalities factor into the relationships that we form?

6.3

Finally, this simulation could serve as a platform for examining a wide array of more complex social phenomena related to ancestor commemoration. What happens when more complex emotional models, more complex perceptual systems, or more complex learning mechanisms are layered onto this system? Is the behaviour of the agents still plausible if they are embodied in animated virtual characters (or robots), or does it change significantly? Can ancestor commemoration be used as a starting point for further explorations of more complex social systems such as religions?

Conclusion

7.1

The simulation presented in this paper offers evidence in support of a proximate model by which human ancestor commemoration may have arisen. While the system described here does not have the full complexity of this suite of behaviours found in human civilizations, it does demonstrate that a number of core elements of ancestor commemoration appear to arise from the interactions among dominance relationships, communication, and life/death cycles. In addition, this paper offers a functional example of ancestor commemoration reducing social distance, and thereby enhancing reciprocity and providing a significant survival advantage. This paper therefore suggests not only how ancestor commemoration may have arisen, but also why it may have been perpetuated within human cultures.

7.2

This computational model of ancestor commemoration may be useful as a platform for exploring various mechanisms and attributes of ancestor commemoration and related phenomena. In doing so, it may be able to provide some insight into the workings of the human brain, and our apparently complex behaviour.

Notes

¹ It is significant that the commemorated ancestors in the parametric studies are found among the first 152 individuals, rather than in the first 150, which would be precisely the first generation. In a few of the runs, one of the commemorated ancestors was among the first few born after the founding community was created.

References

BAINBRIDGE, W (2006) God from the Machine: Artificial Intelligence Models of Religious Cognition. AltaMira Press.

BARRETT, L, Henzi, S, Weingrill, T, Lycett, J, and Hill, R (2000) Female baboons do not raise the stakes but they give as good as they get. Animal Behaviour, 59, pp. 763-770.

BROTHERS, L (1997) Friday's Footprint: How Society Shapes the Human Mind. Oxford: Oxford University Press.

COHEN, M, Riolo, R, and Axelrod, R (1999) The Emergence of Social Organization in the Prisoner's Dilemma: How Context-Preservation and Other Factors Promote Cooperation.

DE VRIES, H (1998) Finding a dominance order most consistent with a linear hierarchy: a new procedure and review. Animal Behaviour, 55, pp. 827-843.

DUNBAR, R (1993) Coevolution of neocortical size, group size and language in humans. Behavioral and Brain Sciences, 16(4), pp. 681-735.

ENGH, A, Esch, L, Smale, L, and Holekamp, K (2000) Mechanisms of maternal rank 'inheritance' in the spotted hyaena, Crocuta crocuta. Animal Behaviour, 60, pp. 323-332.

HARCOURT, A, and de Waal, F (1992) Coalitions and Alliances in Humans and other Animals. Oxford: Oxford University Press.

HAUSER, M (1998) The Evolution of Communication. Cambridge, MA: MIT Press.

LI, L (2000) Ancestor worship: an archaeological investigation of ritual activities in Neolithic north China. Journal of East Asian Archaeology, 2(1), pp. 129-164. doi: 10.1163/156852300509826.

LUCERO, L. (2007) The Politics of Ritual. Current Anthropology 44(4). http://www.journals.uchicago.edu/doi/full/10.1086/375870.

MCANANY, P (2000) Living with the Ancestors: Kinship and Kingship in Ancient Maya Society. University of Texas Press.

MECH, L (1999) Alpha status, dominance, and division of labor in wolf packs. Canadian Journal of Zoology, 77, pp. 1196-1203.

MEHRABIAN, A, and Russell, J (1974) An Approach to Environmental Psychology. Cambridge, MA: MIT Press.

PEREIRA, M (1995) Development and social dominance among group-living primates. American Journal of Primatology, 37(2), pp. 143-175.

REYNOLDS, C (1987) Flocks, Herds and Schools: A Distributed Behavioral Model. In Proceedings of ACM SIGGRAPH 87, pp. 25-34.

SIMS, K (1994) Evolving virtual creatures. In Proceedings of the 21st annual conference on Computer graphics and interactive techniques, pp. 15-22. ACM.

STEADMAN, L, Palmer, C, and Tilley, C (1996) The Universality of Ancestor Worship. Ethnology, 35(1), pp. 63-76.

TOMLINSON, W (2002) Synthetic Social Relationships for Computational Entities. Massachusetts Institute of Technology, Ph.D. dissertation, Media Arts & Sciences.

TRIVERS, R (1971) The evolution of reciprocal altruism. Quarterly Review of Biology, 46, pp. 35-57.

UPAL, M (2005) Simulating the Emergence of New Religious Movements. Journal of Artificial Societies and Social Simulation 8(1). https://www.jasss.org/8/1/6.html.

WILKINSON, G (1984) Reciprocal food sharing in the vampire bat. Nature, 308(5955), 181-184. doi: 10.1038/308181a0.

WRANGHAM, R, and Peterson, D (1996) Demonic Males. Boston: Houghton Mifflin.

YOUNGER, S (2004) The Effect of Communicating Normative Reputation on the Benefits of Resource Sharing in Simple Societies. Journal of Artificial Societies and Social Simulation 7(1). https://www.jasss.org/7/1/5.html.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2009]