Luca Arciero, Claudia Biancotti, Leandro D'Aurizio and Claudio Impenna (2009)
Exploring Agent-Based Methods for the Analysis of Payment Systems: A Crisis Model for StarLogo TNG
Journal of Artificial Societies and Social Simulation
vol. 12, no. 1 2
<https://www.jasss.org/12/1/2.html>
For information about citing this article, click here
Received: 10-Mar-2008 Accepted: 12-Jun-2008 Published: 31-Jan-2009
 Abstract
Abstract|
|
| Figure 1. Basic functioning of an RTGS environment |
|
|
| Figure 2. The simulated world before and after the critical event (The simulated world is depicted one second before (left) and 140 seconds after (right) a critical event hitting the circled agent. In the "after" scenario, enough time has elapsed since the disruption to allow all banks to exclude the inactive bank from the flow of payment requests, represented by colored spheres moving on the terrain.) |
| Table 1: Main scenario (€ millions) | ||||
| Agent number | Average payments settled daily | Largea payments settled (% of the total) | Average end-of-day liquidity | Average end-of-day collateral |
| 1 | 18,384 | 3.0 | 5,302 | 2,648 |
| 2 | 22,669 | 6.6 | 3,583 | 3,947 |
| 3 | 13,718 | 3.1 | 4,780 | 2,766 |
| 4 | 18,451 | 8.8 | 2,211 | 850 |
| 5 | 43,339 | 7.5 | 439 | 10,119 |
| Total | 116,562 | 5.0 | 16,315 | 20,329 |
|
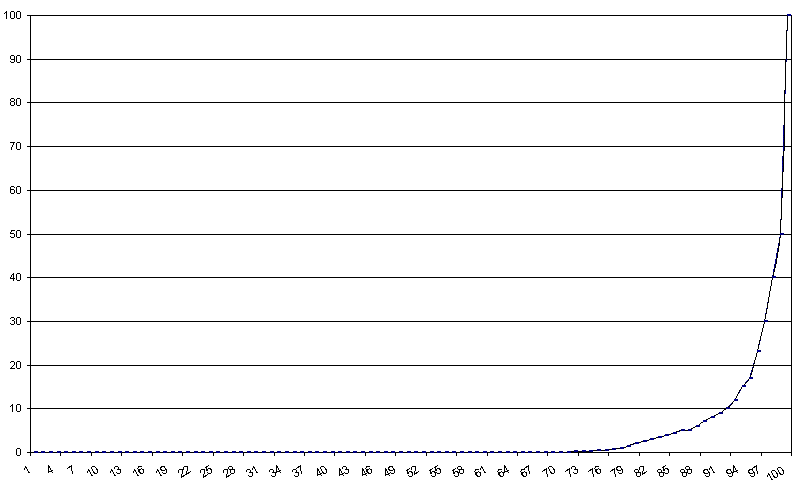
| Figure 3. Concentration curve for payments submitted by the five superbanks |
with payments larger than the 95 th percentile accounting for 85 per cent of the total amount exchanged and those above the 99 th percentile alone accounting for 50 per cent. The average payment (2.9 million euros) is therefore scarcely representative of the data mass, and such a high concentration makes kernel estimates of the underlying density function very unreliable. The relevant feature of the payment distribution is therefore that it is formed by a great mass of payments of relatively small values and an isolated cluster of huge ones; also that tends to be evenly spread among participants.
|
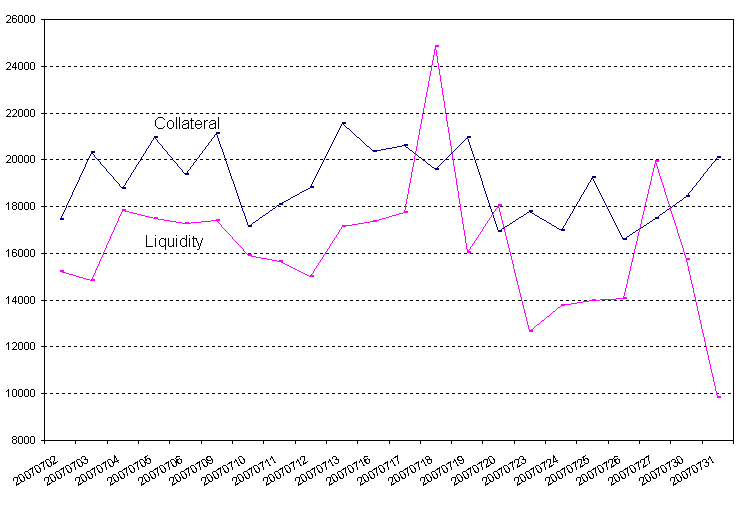
| Figure 4. Total daily amounts of collateral and liquidity (€ millions) |
This could be explained by the fact that cash is also held to meet Eurosystem reserve requirements. Finally, the time series of daily payments is not correlated with either collateral or cash flow, which chimes with the fact that the vast majority of payments is settled through liquidity obtained in the course of the same day.
|
|
| Total liquidity (€ millions) |
|
|
| Average expected liquidity (€ millions) |
|
|
| Number of lending operations |
|
|
| Number of delays |
|
|
| Total losses (€ millions) |
| Figure 5. Time patterns of the relevant variables during the simulation (disruptive event indicated by the vertical line) |
2 A comprehensive description of the design and activity of RTGS systems in most industrialized countries can be found in Bank for International Settlements (2005).
3 The alternative settlement mode to RTGS is the deferred net settlement (DNS) model, in which only net positions among banks are settled on their accounts at the central bank, usually once a day in the late afternoon. This system requires banks to hold less intraday liquidity, but exposes the payment system to higher risks of financial distress, since banks extend intraday credit to their debtors until the net settlement phase is successfully completed. A default by a bank unable to fund its net debit position could trigger a domino effect within the system.
4 Beside this strand of studies based on a simulation approach, some authors have analyzed the effects of disruptive events from an econometric perspective. Among others, McAndrews and Potter (2002) use a panel approach to estimate how US banks participating in the US RTGS system Fedwire changed their strategy in term of payment submission during the 9/11 crisis. Payment systems can also be represented as a complex network, with banks as nodes and mutual liabilities/claims defining the arches; this kind of modeling is static, in the sense that the time dimension is not directly taken into account. Network theory has been exploited to study the main features of real interrelations among Austrian banks (Boss et al. 2004), making it possible to understand the system's level of concentration, i.e. whether few banks are responsible for the bulk of the links. The consequences of catastrophic events are simply modeled by removing a specific node and measuring the performances of the rest of the network.
5 Available for download at http://education.mit.edu/starlogo-tng/.
6 Though not game-theoretically founded, this rule satisfactorily reflects the fact that banks schedule a large share of outgoing payments according to intraday deadlines (cut-offs). These cut-offs can be agreed with customers, who initiate payments, or with the receiving bank, when the payment arises from interbank trades; see for example the guidelines of the Euro Banking Federation for money market-related payments. Alternatively, they might derive directly from the institutional setting, as in the case of payments related to monetary policy operations.
7 Our representation of the money market is partial. First of all, there are no prices, which equates to assuming that the overnight interest rate on the market is constant throughout the day, and equal for all pairs of counterparties. Empirical evidence points in a different direction, highlighting how the price of funding decreases during the day (Furfine 2001; Baglioni and Monticini 2007), how banks discriminate among counterparties (Iori et al.2008; Furfine 2003), and how the cost of overnight funding might depend, among other factors, on the perceived creditworthiness of each participant (Nobili and Picillo 2008). We also overlook the existence of repo markets as an alternative to unsecured funding, in spite of their ever-increasing importance. These aspects have to be taken onboard in any model that aims at being operationally relevant. In the case of the exercise presented here, however, we merely aim at giving a macro-level sketch of how interbank transactions might be instrumental in the transmission of external shocks to settlement activity in the short run. The very introduction of a money market innovates with respect to previous agent-based models; for the time being, we do not focus on interest rate dynamics.
8 Notably, the 2001 BIS Core Principles for Systemically Important Payment Systems and the consequent framework of the European System of Central Banks.
9 The five agents do not include non-banks, i.e. the central bank, central securities depositories and other clearing agents, as well as banks not directly participating in BI-REL, but using EU-RTGS systems linked to it.
10 Some tests on standard systems have shown that the current version of StarLogo TNG cannot handle the real-life number of banks. While the simulation still runs if there are 20 banks, the informational gain does not appear to be substantial enough to offset the losses in terms of speed and stability of the simulation.
11 The BI-REL system is, however, quite concentrated; two superbanks, for example, correspond to actual single banking groups, with a high level of internal coordination in the payment system.
12 Broadly speaking, the "type of payment" attribute indicates whether a transaction is initiated by a bank customer or stems from the bank's own activity in the financial market.
13 The results presented here refer to a single "frozen" run that should be taken as representative of the typical behavior of the system, since it was quite similar to many other runs we did not keep. At the time of writing, the StarLogo TNG platform did not allow for automatic averaging of the results of multiple runs, and did not track the changes in random seeds over the course of a single simulation sessions or over different sessions. The features for the preservation of results were in an experimental phase, and hence not entirely stable.
14 Note that this result is a consequence of the joint absence from the model of money market prices and general trust levels. Should these variables be included, a disruptive event might well result in a contraction of money markets, along the lines of what happened during the subprime crisis.
J. ARNOLD, M. L. Bech, W. E. Beyeler, R. J. Glass and K. Soramäki, 2006, "The topology of interbank payment flows", Federal Reserve Bank of New York, Staff Report 243.
BANK for International Settlements, 2005, "New developments in large-value payment systems", Committee on Payment and Settlement Systems.
A. BAGLIONI and A. Monticini, 2007, "The intraday price of money: evidence from the e-MID market", mimeo, available from http://www.ssrn.com.
M. BECH and R. Garratt, 2003, "The intraday liquidity management game", Journal of Economic Theory, 109: 198-219.
P. BEDFORD, S. Millard and J. Yang, 2005, "Analysing the impact of operational incidents in large-value payment systems: a simulation approach", in H. Leinonen (ed.), Liquidity, risks and speed in payments and settlement systems - a simulation approach, Bank of Finland Studies, E:31.
M. BOSS, H. Elsinger, M. Summer and S. Thurner, 2004, "Network topology of the interbank market", Quantitative Finance, 4: 677-684.
G. FIORETTI, 2005, "Financial fragility in a basic agent-based model", mimeo.
C. FURFINE, 2001, "Banks as monitors of other banks: evidence from the overnight federal funds market", Journal of Business, 74: 33-57.
C. FURFINE, 2003, When is Inter-Transaction Time Informative?, Federal Reserve Bank of Chicago Working Paper No. 2003-04.
M. GALBIATI and K. Soramäki, 2007, "A competitive multi-agent model of interbank payment systems", mimeo.
M. GLASER and P. Haene, "Simulation of participant-level operational disruption in Swiss Interbank Clearing", 2007, presentation given at the 5th simulator workshop in Helsinki, http://www.bof.fi/en/rahoitusmarkkinat/kehityshankkeet/BoF-PSS2/seminar07.htm
R. HEIJIMANS, 2007, "Stress simulations: a Dutch case", presentation given at the 5th simulator workshop in Helsinki, http://www.bof.fi/en/rahoitusmarkkinat/kehityshankkeet/BoF-PSS2/seminar07.htm.
M. HELLQVIST and J. Koskinen, 2005, "Stress testing securities clearing and settlement systems using simulations", in Leinonen, H. (ed.), Liquidity, risks and speed in payments and settlement systems - a simulation approach, Bank of Finland Studies, E:31
G. IORI, G. De Masi, O. Precup, G. Gabbi and G. Caldarelli, 2008, "A Network Analysis of the Italian Overnight Money Market", Journal of Economic Dynamics and control, 32: 2008.
A. LUBLY and E. Tanai, 2007, "Operational disruption and the Hungarian RTGS system VIBER", presentation given at the 5th simulator workshop in Helsinki, http://www.bof.fi/en/rahoitusmarkkinat/kehityshankkeet/BoF-PSS2/seminar07.html.
J. MCANDREWS and S. M. Potter, 2002, "Liquidity effects of the events of September 11, 2001", FRBNY Economic Policy Review, 59-79, November.
A. NOBILI and C. Picillo, 2008, "Cost of funding in the money market and banks' creditworthiness: evidence from e-MID", mimeo, Bank of Italy.
© Copyright Journal of Artificial Societies and Social Simulation, [2009]