Errors and Artefacts in Agent-Based Modelling
Journal
of Artificial Societies and Social Simulation vol. 12, no. 1 1
<https://www.jasss.org/12/1/1.html>
For information about citing this article, click here
Received: 13-Feb-2008 Accepted: 12-Oct-2008 Published: 31-Jan-2009
 Abstract
Abstract"You should assume that, no matter how carefully you have designed and built your simulation, it will contain bugs (code that does something different to what you wanted and expected)." (Gilbert 2007, p. 38).
"Achieving internal validity is harder than it might seem. The problem is knowing whether an unexpected result is a reflection of a mistake in the programming, or a surprising consequence of the model itself. […] As is often the case, confirming that the model was correctly programmed was substantially more work than programming the model in the first place." (Axelrod 1997b)
"Indeed, the 'robustness' of macrostructures to perturbations in individual agent performance […] is often a property of agent-based-models and exacerbates the problem of detecting 'bugs'. " (Axtell and Epstein 1994, p. 31)
|
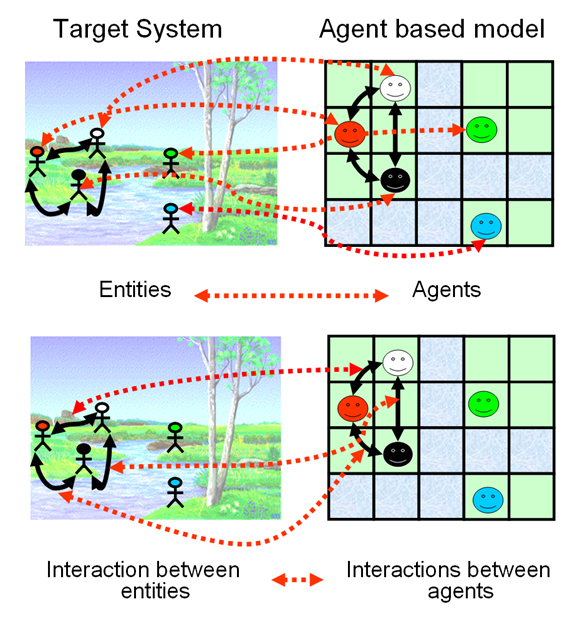
| Figure 1. In agent-based modelling the entities of the system are represented explicit and individually in the model. The limits of the entities in the target system correspond to the limits of the agents in the model, and the interactions between entities correspond to the interactions of the agents in the model (Edmonds 2001). |
|
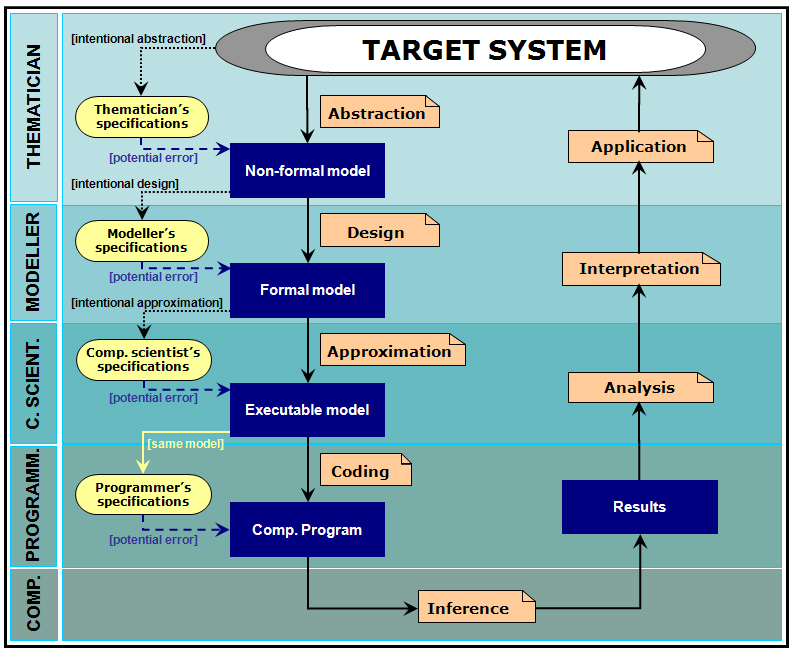
| Figure 2. Different stages in the process of designing, implementing and using and agent-based model. |
"An ontology is defined by Gruber (1993) as "a formal, explicit specification of a shared conceptualisation". Fensel (2001) elaborates: ontologies are formal in that they are machine readable; explicit in that all required concepts are described; shared in that they represent an agreement among some community [...] and conceptualisations in that an ontology is an abstraction of reality." (Polhill and Gotts 2006, p. 51)
2 By “mathematically intractable” we mean that applying deductive inference to the mathematically formalised model, given the current state of development of mathematics, does not provide a solution or clear insight into the behaviour of the model, so there is a need to resort to techniques such as simulation or numerical approximations in order to study the input-output relationship that characterises the model.
3 The reader can see an interesting comparative analysis between agent-based and equation-based modelling in Parunak et al. (1998).
4 Note that the thematician faces a similar problem when building his non-formal model. There are potentially an infinite number of models for one single target system.
5 Each individual member of this set can be understood as a different model or, alternatively, as a different parameterisation of one single -more general- model that would itself define the whole set.
6 There are some interesting attempts with INGENIAS (Pavón and Gómez-Sanz 2003) to use modelling and visual languages as programming languages rather than merely as design languages (Sansores and Pavón 2005; Sansores , Pavón and Gómez-Sanz 2006). These efforts are aimed at automatically generating several implementations of one single executable model (in various different simulation platforms).
7 See a complete epistemic review of the validation problem in Kleindorfer et al. (1998) and discussion about the specific domain of agent-based modelling in Windrum et al (2007) and Moss (2008).
8 If we accept, as Edmonds and Hales (2005) propose, that a computational simulation is a theoretical experiment, then our definition of the concept of accessory assumption could be assimilated by analogy to a particular case of auxiliary assumption as defined in the context of the Duhem-Quine thesis (Windrum, Fagiolo and Moneta 2007). Notwithstanding, in order to be considered an artefact, an assumption not only needs the condition of auxiliary hypothesis but also the condition of significant assumption.
9 This finding does not refute some of the most important conclusions of the model.
ARTHUR W B, Holland J H, LeBaron B, Palmer R and Tayler P (1997) Asset Pricing under Endogenous Expectations in an Artificial Stock Market. In Arthur W B, Durlauf S, and Lane D (Eds.) The Economy as an Evolving Complex System II: 15-44. Reading, MA: Addison-Wesley Longman.
AXELROD R M (1986) An Evolutionary Approach to Norms. American Political Science Review, 80(4), pp. 1095-1111.
AXELROD R M (1997a) The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution, 41(2), pp. 203-226.
AXELROD R M (1997b) Advancing the Art of Simulation in the Social Sciences. In Conte R, Hegselmann R, and Terna P (Eds.) Simulating Social Phenomena, Lecture Notes in Economics and Mathematical Systems 456: 21-40. Berlin: Springer-Verlag.
AXTELL R L (2000) Why Agents? On the Varied Motivations for Agent Computing in the Social Sciences. In Macal C M and Sallach D (Eds.) Proceedings of the Workshop on Agent Simulation: Applications, Models, and Tools: 3-24. Argonne, IL: Argonne National Laboratory.
AXTELL R L and Epstein J M (1994) Agent-based Modeling: Understanding Our Creations. The Bulletin of the Santa Fe Institute, Winter 1994, pp. 28-32.
BIGBEE T, Cioffi-Revilla C and Luke S (2007) Replication of Sugarscape using MASON. In Terano T, Kita H, Deguchi H, and Kijima K (Eds.) Agent-Based Approaches in Economic and Social Complex Systems IV: 183-190. Springer Japan.
BONABEAU E (2002) Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences of the United States of America, 99(2), pp. 7280-7287.
BOX G E P and Draper N R (1987) Empirical model-building and response surfaces. New York: Wiley.
CARON-LORMIER G, Humphry R W, Bohan D A, Hawes C and Thorbek P (2008) Asynchronous and synchronous updating in individual-based models. Ecological Modelling, 212(3-4), pp. 522-527.
CASTELLANO C, Marsili M and Vespignani A (2000) Nonequilibrium phase transition in a model for social influence. Physical Review Letters, 85(16), pp. 3536-3539.
CHALMERS A F (1999) What is this thing called science? Indianapolis: Hackett Pub.
CHRISTLEY S, Xiang X and Madey G (2004) Ontology for agent-based modeling and simulation. In Macal C M, Sallach D, and North M J (Eds.) Proceedings of the Agent 2004 Conference on Social Dynamics: Interaction, Reflexivity and Emergence: Chicago, IL: Argonne National Laboratory and The University of Chicago. http://www.agent2005.anl.gov/Agent2004.pdf.
CIOFFI-REVILLA C (2002) Invariance and universality in social agent-based simulations. Proceedings of the National Academy of Sciences of the United States of America, 99(3), pp. 7314-7316.
CUTLAND, N (1980) Computability: An Introduction to Recursive Function Theory. Cambridge University Press.
DROGOUL A, Vanbergue D and Meurisse T (2003) Multi-Agent Based Simulation: Where are the Agents? In Sichman J S, Bousquet F, and Davidsson P (Eds.) Proceedings of MABS 2002 Multi-Agent-Based Simulation, Lecture Notes in Computer Science 2581: 1-15. Bologna, Italy: Springer-Verlag.
EDMONDS B (2000) The Purpose and Place of Formal Systems in the Development of Science, CPM Report 00-75, MMU, UK. http://cfpm.org/cpmrep75.html.
EDMONDS B (2001) The Use of Models - making MABS actually work. In Moss S and Davidsson P (Eds.) Multi-Agent-Based Simulation, Lecture Notes in Artificial Intelligence 1979: 15-32. Berlin: Springer-Verlag.
EDMONDS B (2005) Simulation and Complexity - how they can relate. In Feldmann V and Mühlfeld K (Eds.) Virtual Worlds of Precision - computer-based simulations in the sciences and social sciences: 5-32. Münster, Germany: Lit-Verlag.
EDMONDS B and Hales D (2003) Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation, 6(4) https://www.jasss.org/6/4/11.html.
EDMONDS B and Hales D (2005) Computational Simulation as Theoretical Experiment. Journal of Mathematical Sociology, 29, pp. 1-24.
EDWARDS M, Huet S, Goreaud F and Deffuant G (2003) Comparing an individual-based model of behaviour diffusion with its mean field aggregate approximation. Journal of Artificial Societies and Social Simulation, 6(4) https://www.jasss.org/6/4/9.html.
EHRENTREICH N (2002) The Santa Fe Artificial Stock Market Re-Examined - Suggested Corrections. Economics Working Paper Archive at WUSTL. http://econwpa.wustl.edu:80/eps/comp/papers/0209/0209001.pdf.
EHRENTREICH N (2006) Technical trading in the Santa Fe Institute Artificial Stock Market revisited. Journal of Economic Behavior & Organization, 61(4), pp. 599-616.
EPSTEIN J M (1999) Agent-based computational models and generative social science. Complexity, 4(5), pp. 41-60.
EPSTEIN J M and Axtell R L (1996) Growing Artificial Societies. Social Science From the Bottom Up. Cambridge, MA: Brookings Institution Press-MIT Press.
FENSEL D (2001) Ontologies: A Silver Bullet for Knowledge Management and Electronic Commerce. Berlin: Springer.
FLACHE A and Hegselmann R (2001) Do Irregular Grids make a Difference? Relaxing the Spatial Regularity Assumption in Cellular Models of Social Dynamics. Journal of Artificial Societies and Social Simulation, 4(4) https://www.jasss.org/4/4/6.html.
FLACHE A and Macy M W (2002) Stochastic Collusion and the Power Law of Learning. Journal of Conflict Resolution, 46(5), pp. 629-653
GALAN J M and Izquierdo L R (2005) Appearances Can Be Deceiving: Lessons Learned Re-Implementing Axelrod's 'Evolutionary Approach to Norms'. Journal of Artificial Societies and Social Simulation, 8(3) 2 https://www.jasss.org/8/3/2.html.
GILBERT N (2007) Agent-Based Models. Quantitative Applications in the Social Sciences. London: SAGE Publications.
GILBERT N and Terna P (2000) How to build and use agent-based models in social science. Mind and Society, 1(1), pp. 57-72.
GILBERT N and Troitzsch K G (1999) Simulation for the social scientist. Buckingham, UK: Open University Press.
HAMMOND R A and Axelrod R M (2006a) Evolution of contingent altruism when cooperation is expensive. Theoretical Population Biology, 69(3), pp. 333-338.
HAMMOND R A and Axelrod R M (2006b) The Evolution of Ethnocentrism. Journal of Conflict Resolution, 50(6), pp. 926-936.
GOTTS N M, Polhill J G and Adam W J (2003) Simulation and Analysis in Agent-Based Modelling of Land Use Change. Online proceedings of the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21 September 2003. http://www.uni-koblenz.de/~kgt/ESSA/ESSA1/proceedings.htm.
GRUBER T R (1993) A translation approach to portable ontology specifications. Knowledge Acquisition, 5(2), pp. 199-220.
HARE M and Deadman P (2004) Further towards a taxonomy of agent-based simulation models in environmental management. Mathematics and Computers in Simulation, 64(1), pp. 25-40.
HEYWOOD J G (1990) The Navier-Stokes equations. Theory and numerical methods. Proceedings of a conference held at Oberwolfach, FRG, Sept. 18-24, 1988. Lecture Notes in Mathematics. Berlin: Springer-Verlag.
HUET S, Edwards M and Deffuant G (2007) Taking into Account the Variations of Neighbourhood Sizes in the Mean-Field Approximation of the Threshold Model on a Random Network. Journal of Artificial Societies and Social Simulation, 10(1) 10 https://www.jasss.org/10/1/10.html.
IZQUIERDO L R, Izquierdo, S S, Galán, J M and Santos, J I (2009) Techniques to Understand Computer Simulations: Markov Chain Analysis. Journal of Artificial Societies and Social Simulation, 12(1) 6 https://www.jasss.org/12/1/6.html.
IZQUIERDO S S, Izquierdo, L R and Gotts N M (2008) Reinforcement learning dynamics in social dilemmas. Journal of Artificial Societies and Social Simulation, 11(2) 1 https://www.jasss.org/11/2/1.html.
IZQUIERDO L R, Izquierdo S S, Gotts N M and Polhill J G (2007) Transient and Asymptotic Dynamics of Reinforcement Learning in Games. Games and Economic Behavior, 61(2), pp. 259-276. http://dx.doi.org/10.1016/j.geb.2007.01.005.
IZQUIERDO L R and Polhill J G (2006) Is your model susceptible to floating point errors? Journal of Artificial Societies and Social Simulation, 9(4) 4 https://www.jasss.org/9/4/4.html.
IZQUIERDO S S and Izquierdo L R (2006) On the Structural Robustness of Evolutionary Models of Cooperation. In Corchado E, Yin H, Botti V J, and Fyfe C (Eds.) Intelligent Data Engineering and Automated Learning - IDEAL 2006. Lecture Notes in Computer Science 4224: 172-182. Berlin Heidelberg: Springer.
IZQUIERDO S S and Izquierdo L R (2007) The Impact on Market Efficiency of Quality Uncertainty without Asymmetric Information. Journal of Business Research, 60(8), pp. 858-867. http://dx.doi.org/10.1016/j.jbusres.2007.02.010.
KLEIJNEN J P C (1995) Verification and validation of simulation models. European Journal of Operational Research, 82(1), pp. 145-162.
KLEINDORFER G B, O'Neill L and Ganeshan R (1998) Validation in simulation: Various positions in the philosophy of science. Management Science, 44(8), pp. 1087-1099.
KLEMM K, Eguíluz V M, Toral R and San Miguel M (2003a) Role of dimensionality in Axelrod's model for the dissemination of culture. Physica A, 327, pp. 1-5.
KLEMM K, Eguiluz V M, Toral R and Miguel M S (2003b) Global culture: A noise-induced transition in finite systems. Physical Review E, 67(4).
KLEMM K, Eguiluz V M, Toral R and San Miguel M (2003c) Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E, 67(2).
KLEMM K, Eguiluz V M, Toral R and San Miguel M (2005) Globalization, polarization and cultural drift. Journal of Economic Dynamics & Control, 29(1-2), pp. 321-334.
KLUVER J and Stoica C (2003) Simulations of group dynamics with different models. Journal of Artificial Societies and Social Simulation, 6(4) https://www.jasss.org/6/4/8.html.
LEBARON B, Arthur W B and Palmer R (1999) Time series properties of an artificial stock market. Journal of Economic Dynamics & Control, 23(9-10), pp. 1487-1516.
LEOMBRUNI R and Richiardi M (2005) Why are economists sceptical about agent-based simulations? Physica A, 355, pp. 103-109.
MABROUK N, Deffuant G and Lobry C (2007) Confronting macro, meso and micro scale modelling of bacteria dynamics. M2M 2007: Third International Model-to-Model Workshop, Marseille, France, 15-16 March 2007. http://m2m2007.macaulay.ac.uk/M2M2007-Mabrouk.pdf.
MACY M W and Flache A (2002) Learning Dynamics in Social Dilemmas. Proceedings of the National Academy of Sciences of the United States of America, 99(3), pp. 7229-7236.
MILLER J H and Page S E (2004) The standing ovation problem. Complexity, 9(5), pp. 8-16.
MOSS S (2008) Alternative Approaches to the Empirical Validation of Agent-Based Models. Journal of Artificial Societies and Social Simulation, 11(1) 5 https://www.jasss.org/11/1/5.html.
MOSS S and Edmonds B (2005) Sociology and Simulation: - Statistical and Qualitative Cross-Validation, American Journal of Sociology, 110(4), pp. 1095-1131.
MOSS S, Edmonds B and Wallis S (1997) Validation and Verification of Computational Models with Multiple Cognitive Agents. Centre for Policy Modelling Report, No.: 97-25 http://cfpm.org/cpmrep25.html.
PARUNAK H V D, Savit R and Riolo R L (1998) Agent-based modeling vs. equation-based modeling: A case study and users' guide. In Sichman J S, Conte R, and Gilbert N (Eds.) Multi-Agent Systems and Agent-Based Simulation, Lecture Notes in Artificial Intelligence 1534: 10-25. Berlin, Germany: Springer-Verlag.
PAVÓN J and Gómez-Sanz J (2003) Agent Oriented Software Engineering with INGENIAS. In Marik V, Müller J, and Pechoucek M (Eds.) Multi-Agent Systems and Applications III, 3rd International Central and Eastern European Conference on Multi-Agent Systems, CEEMAS 2003. Lecture Notes in Artificial Intelligence 2691: 394-403. Berlin Heidelberg: Springer-Verlag.
PIGNOTTI E, Edwards P, Preece A, Polhill J G and Gotts N M (2005) Semantic support for computational land-use modelling. 5th International Symposium on Cluster Computing and the Grid (CCGRID 2005): 840-847. Piscataway, NJ: IEEE Press.
POLHILL J G and Gotts N M (2006) A new approach to modelling frameworks. Proceedings of the First World Congress on Social Simulation: 50-57. Kyoto.
POLHILL J G and Izquierdo L R (2005) Lessons learned from converting the artificial stock market to interval arithmetic. Journal of Artificial Societies and Social Simulation, 8(2) https://www.jasss.org/8/2/2.html.
POLHILL J G, Izquierdo L R and Gotts N M (2006) What every agent-based modeller should know about floating point arithmetic. Environmental Modelling & Software, 21(3), pp. 283-309.
POLHILL J G, Izquierdo L R and Gotts N M (2005) The ghost in the model (and other effects of floating point arithmetic). Journal of Artificial Societies and Social Simulation, 8(1) https://www.jasss.org/8/1/5.html.
POLHILL J G, Pignotti E, Gotts N M, Edwards P and Preece A (2007) A Semantic Grid Service for Experimentation with an Agent-Based Model of Land-Use Change. Journal of Artificial Societies and Social Simulation, 10(2) 2 https://www.jasss.org/10/2/2.html.
RICHIARDI M, Leombruni R, Saam N J and Sonnessa M (2006) A Common Protocol for Agent-Based Social Simulation. Journal of Artificial Societies and Social Simulation, 9(1) 15 https://www.jasss.org/9/1/15.html.
RIOLO R L, Cohen M D and Axelrod R M (2001) Evolution of cooperation without reciprocity. Nature, 411, pp. 441-443.
SAKODA J M (1971) The Checkerboard Model of Social Interaction. Journal of Mathematical Sociology, 1(1), pp. 119-132.
SALVI R (2002) The Navier-Stokes equations. Theory and numerical methods. Lecture Notes in Pure and Applied Mathematics. New York, NY: Marcel Dekker.
SANSORES C and Pavón J (2005) Agent-based simulation replication: A model driven architecture approach. In Gelbukh A F, de Albornoz A, and Terashima-Marín H (Eds.) MICAI 2005: Advances in Artificial Intelligence, 4th Mexican International Conference on Artificial Intelligence, Monterrey, Mexico, November 14-18, 2005, Proceedings. Lecture Notes in Computer Science 3789: 244-253. Berlin Heidelberg: Springer.
SANSORES C, Pavón J and Gómez-Sanz J (2006) Visual modeling for complex agent-based simulation systems. In Sichman J S and Antunes L (Eds.) Multi-Agent-Based Simulation VI, International Workshop, MABS 2005, Utrecht, The Netherlands, July 25, 2005, Revised and Invited Papers. Lecture Notes in Computer Science 3891: 174-189. Berlin Heidelberg: Springer.
SARGENT R G (2003) Verification and Validation of Simulation Models. In Chick S, Sánchez P J, Ferrin D, and Morrice D J (Eds.) Proceedings of the 2003 Winter Simulation Conference: 37-48. Piscataway, NJ: IEEE.
SCHELLING T C (1978) Micromotives and macrobehavior. New York: Norton.
SCHELLING T C (1971) Dynamic Models of Segregation. Journal of Mathematical Sociology, 1(1), pp. 147-186.
SCHÖNFISCH B and De Roos A (1999) Synchronous and asynchronous updating in cellular automata. BioSystems, 51(3), pp. 123-143.
STANISLAW H (1986) Tests of computer simulation validity. What do they measure? Simulation and Games 17, pp. 173-191.
TAKADAMA K, Suematsu Y L, Sugimoto N, Nawa N E and Shimohara K (2003) Cross-element validation in multiagent-based simulation: Switching learning mechanisms in agents. Journal of Artificial Societies and Social Simulation, 6(4) https://www.jasss.org/6/4/6.html.
TAYLOR A J (1983) The Verification of Dynamic Simulation Models. Journal of the Operational Research Society, 34(3), pp. 233-242.
VILÀ X (2008) A Model-To-Model Analysis of Bertrand Competition. Journal of Artificial Societies and Social Simulation, 11(2) 11 https://www.jasss.org/11/2/11.html.
WILENSKY U and Rand W (2007) Making Models Match: Replicating an Agent-Based Model. Journal of Artificial Societies and Social Simulation, 10(4) 2 https://www.jasss.org/10/4/2.html.
WINDRUM P, Fagiolo G and Moneta A (2007) Empirical Validation of Agent-Based Models: Alternatives and Prospects. Journal of Artificial Societies and Social Simulation, 10(2) https://www.jasss.org/10/2/8.html.
XU J, Gao Y and Madey G (2003) A Docking Experiment: Swarm and Repast for Social Network Modeling. Seventh Annual Swarm Researchers Meeting (Swarm2003): Notre Dame, IN.
Return to
Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]