André C. R. Martins (2008)

Replication in the Deception and Convergence of Opinions Problem

Journal of Artificial Societies and Social Simulation vol. 11, no. 4 8
<https://www.jasss.org/11/4/8.html>

For information about citing this article, click here

Received: 19-Jan-2008    Accepted: 27-Sep-2008    Published: 31-Oct-2008

Abstract

Reported results of experiments are usually trustworthy, but some of them might be obtained from errors or deceptive behavior. When an agent only read articles about experimental results and use the articles to update his subjective opinions about different theories, the existence of deception can have severe consequences. An earlier attempt to solve that problem suggested that reading replicated results would solve the problems associated with the existence of deception. In this paper, we show that result is not a general case and, for experiments subject to statistical uncertainty, the solution is simply wrong. The analysis of the effect of replicated experiments is corrected here by introducing a differentiation between honest and dishonest mistakes. We observe that, although replication does solve the problem of no convergence, under some circumstances, it is not enough for achieving a reasonable amount of certainty for a realistic number of read reports of experiments.

Keywords:

Replication, Deception, Rational Agents, Epistemology, Opinion Dynamics

Introduction

1.1

Reproducibility of results is considered one of the main basis of the scientific process. It is important in order to ensure that reported results are not a consequence of errors neither of some deceptive behavior from the authors. Of course, not every experiment is completely replicable, at least not exactly in the same way as the original reported experiments (Gilles 2006). But some way to corroborate the results is expected to exist and the community should pay attention to attempts to recreate new results obtained by its members.

1.2

Despite that, it is not very common to see reports of replicated results. Professionals of different areas seem to assign different importance to the replication of results (Chase 1971). In Marketing, per example, there is evidence that far less replications of reported results are published than it would be reasonable and scientifically healthy to expect (Hubbard and Armstrong 1994,Evanschitzky et al 2007). This same observation can be especially worrying when repeated in health related areas, where treatments are often prescribed based on non-replicated results (Ioannidis 2005). Currently, in order to deal with this problem, a number of journals have started sections dedicated to replication of results. In Psychology, there is even a whole journal dedicated to experiments that failed to give the expected result, replicated or not, the Journal of Articles in Support of the Null Hypothesis ( http://www.jasnh.com/), and an associated repository for replication failures, the Index of Null Effects and Replication Failures ( http://www.jasnh.com/m9.htm).

1.3

Analyzing the problem of how agents who only get information about an area from reading about it, Martins (2005) proposed a model, based on an idea from Jaynes (2003), for an agent who reads the reported results of experiments. Based on that information, the agent tries to choose between two competing theories, A and B, where A is the best description of the world (a fact that the agent is not aware of). The agent started with a prior opinion about the amount of errors and deception in the area of the research and, at first, it assigned equal probabilities to both theories. This idealized agent of the model represents anyone who obtains information from others who tell the agent if the world seems to support A or B. That is, the agent can be a scientist learning about experiments she doesn't perform herself; or a student learning about his specialization; or anyone outside the academic world who must trust reports to make up his mind. That is, medical doctors, politicians, or anyone who wants to run a business, to name just a few examples. Of course, in particular cases, there might be special circumstances that should be taken into account and that the model ignores. Since the objective is to study the general case, this is a problem left for possible future works. In the original article, convergence towards the best description was studied and it was observed that, for a certain amount of prior deception, there were circumstances where the agent would never achieve certainty about the best theory, even if it were able to read an infinite number of papers.

1.4

Palmer (2006) replicated Martins results and proposed a solution to that disturbing problem, by dividing the erroneous results as two types, honest mistakes and real deceptions. He assumed that once an honest attempt was made and it supported the correct theory, A, as the best one, every replication of the initial honest experiment would provide the same result. This alteration of the model allowed the agents to reach certainty. After reading enough articles, the agent believed that theory A was the correct one with almost certainty. This result was obtained assuming that agents obtained their information only from experiments that had replicated results. From a practical point of view, however, the recommendation of using only replicated articles might not be feasible in many areas. As pointed above, in some areas, such experiments might be hard to find. Palmer results seem to give more strength to the argument that we need more replications performed, in order to trust the results we see in the literature.

1.5

However, the supposition that honest replications of honest successful experiments will always favor A is not justifiable, in most cases. It is certainly wrong when the uncertainty in the initial experiment was due to statistical errors, as per example, in the case of two theories that predict close results that are hard to discern from the available data, or in areas where predictions are so uncertain that data may sometime support, due to statistical error, the worst theory. Palmer supposition might be correct in a different type of problems. If you want to write an algorithm for some task, once you get the algorithm right and publish how it is done, people should be able to use it with a much smaller chance of error than the initial development. But the argument simply fails when applied to most scientific problems.

1.6

On the other hand, Palmer's ideas of reading only replicated experiments and introducing honest mistakes in the description of the problem have merits. Treated properly, they can be used in order to get more realistic results than those of the original paper (Martins 2005), at least, for areas where experiments are routinely replicated. In this paper, this problem will be investigated and both types of errors, honest mistakes and real deceptions, will be modeled. Since a correct experiment will not be followed by a mistake (but it can give a different result, due to statistical error), the non-identifiability of the parameters in Martins' model is solved and inference can be obtained about the probability that each theory is correct. However, although certainty can always be achieved in the limit of infinite articles, deception is still observed as a serious problem. Depending on the circumstances, after a realistic number of readings, the agent will still be in doubt about the best choice.

1.7

Before we go on, a few comments are in order. First of all, the real phenomena are much more complex than the treatment given here. Therefore, the results that follow are to be understood as an approximation to the problem of gaining knowledge about the world when one depends only on the accounts of others. New layers of complexity in the reasoning of the agents can always be introduced and that can change the results presented here. The aim of this paper is to study a model for the effects of eventual deceptive behavior on the part of some of the authors and the consequence of that to the certainty one can have about theories in a general case.

1.8

This problem is a version of a typical epistemological problem. While the most accepted reliable sources of knowledge are perception, memory, consciousness and reason (see, per example, Audi 2002, for a more complete account of the problem of sources of knowledge), reading about the works of others might be better classified as learning from testimony. That means that it doesn't fit into the four initial categories, but actually belong to a category that is usually considered untrustworthy. The reason we actually trust reported results is that they are believed to be subject to a series of controls, from peer-reviewing to future replication of the results. However, despite that, there is evidence that some of the reported results are due to misconduct (Titus et al. 2008) and that makes it important to investigate possible consequences of that misconduct.

Replicating Articles

Readers

2.1

Assume there are two theories, A and B, and each agent must decide which one of them is the best description of the world. Without any loss of generality, we can pick A as the correct answer, but the agents are not aware of that. There are experiments that scientists can perform to decide about the correctness of the theories. For simplification, we will ignore the details of the experiments and assume that the agents can calculate the likelihoods of different experimental results directly from the theory. Let S be the event that an experiment will support A (~S means it will support B). Let a and b be the likelihoods a=P(S|A) and b=P(~S|B). That is, a is the chance an experiment will support A, if A were true, and b is the chance an experiment will support B, if B were true^[1]. It is reasonable to assume that both a and b are larger than 0.5 (the experiment should be more likely to confirm a correct theory than not, especially when there are only two competing alternatives), but they might be just a little larger than 0.5. That would happen for theories with similar predictions or problems where the measurements have a lot of uncertainty. One should notice that this description does not prevent the falseability of a theory. As one theory becomes more likely to be true, the other becomes less likely and, therefore, it is falsified, although in a probabilistic sense.

2.2

Following Martins (2005), an agent assigns an average probability p=P(A) to the possibility that A is better and will read reports of experiments in order to update p. Since either one or the other theory is correct, p is actually the average value of a random variable that assumes only 0 or 1 as possible values. The agent is aware that there might be errors and deception in the reports. Therefore, the agent also has prior continuous opinions about the proportion e of articles that are errors, and the proportion d of those errors that support A. Notice that, at this point, no distinction is made about what kind of error is committed. The error can be an experiment done the wrong way, faulty calculations, or some kind of scientific misconduct, such as fabrication of data or any other. The probability given by e is simply the probability that the report has some kind of problem that invalidates its conclusions. Since we don't know if that kind of error will favor A or B more, d is used to measure the chance it will favor A.

2.3

Given the parameters, the agent assigns a probability to the event S that a given article will support A given by

P(S|p,e,d,a,b)=ed+(1-e)[pa+(1-p)(1-b)]

(1)

2.4

Both continuous variables e and d have priors associated with them and the easier way to model that is to use Beta functions. Under those circumstances, Martins (2005) shows that above a certain level of prior average belief about e and for small a and b, the agent might never achieve certainty. The problem is related to the fact that the inference the agent obtains from the reports is about P(S) and not about p=P(A). The variables p, e and d are non-identifiable, in the Bayesian sense, and, therefore, prior information survives even after an infinite amount of data.

Replications

2.5

Assume now, following Palmer (2006), that the agent knows that result and is analyzing a problem where both theories make similar claims about the world (per example, a=b=0.6). In order to avoid the consequences of reading articles with no confirmation of the reported results, the agent decides to read only about experiments that were replicated. By replication, in this paper, it is meant that someone else has repeated the experiment described in the article as well as possible. This is an important point, since a different experiment for the same theories could lead to new sources of error that we will not model bellow. The problem now becomes what influence the first result should have on the chances of the second result. Complete independence would mean that a replicated result is just another independent experiment and add nothing more than a second, independent experiment would. Palmer, on the other hand, suggested that, whenever an article were not a deception and confirmed the correct theory, A, all honest replications should also return A as answer.

2.6

Using this supposition, Palmer obtained curves relating the final opinion of the agent to the proportion of articles that support opinion A. Those curves were clear step functions. If the agent read about 2,000 experiments, his posterior changed abruptly at an observed proportion of 50% of articles supporting A. If most articles supported B, the agent believed in B with almost certainty (p=0); if most articles supported A, A was believed with almost certainty (p=1).

2.7

But Palmer proposal goes too far on the direction of dependence between results, as discussed above. Experiments based on stochastic events will not turn out the same way again just because the first scientist was an honest person and was lucky to obtain the correct answer. In order to correct Palmer's result, but still use his insight, we need to introduce the concept of an honest mistake in the problem. That is, we will still assign a probability e that each paper is an error (intentional or honest, e has the same meaning as in the original model). From those errors, a proportion h is due to honest mistakes, while the rest, 1-h, are real deceitful reports. Notice that honest mistakes are those made by a researcher who wants to find the truth, but fails to perform the experiment as well as he should. Therefore, we will assume that those experiments are as likely to favor one theory as the other. The deceitful reports, on the other hand, correspond to cases where the author does not care about truth, only about proving himself right. Therefore, he will always support one specific theory and we should estimate the proportion d of dishonest people that supports A. In other words, from the total number of original experiments, e(1-h) are the result of true deception. Since we are assuming that honest mistakes do not favor A or B (both results are equally like), and that d now measures the proportion of deceitful reports that support A, Equation 1 becomes, for one non-replicated article,

P(S|p,e,d,a,b)=e[0.5h+(1-h)d]+(1-e)[pa+(1-p)(1-b)]

(2)

2.8

Prior opinions are now needed for h as well. The advantage of this approach is that, when the initial experiment was not a mistake (that happens with chance 1-e), the replication will have a smaller chance of error, since honest mistakes will not happen during the replication stage. That is, the chance of error in the replication is now limited to the probability associated with true deceptions, e(1-h). Honest scientists trying to replicate a deceitful result might still make mistakes, since there is no reason to believe that the reported experiment would be free of errors. Also, statistical effects will still exist and are represented by a and b. When an honest experiment is subject to statistical chances, there is still a chance that, even if it is done perfectly well, bad luck might cause it to support the wrong theory. This is important, because this is the main difference of the approach presented here, when compared to Palmer's paper.

2.9

Opening the tree to describe the problem is a little tedious, but it is straightforward work. At the end, instead of representing the probability of one simple case, there are four different likelihoods and only one of them is dependent of the other three. Calling R the event that the replication support A, we have the likelihoods associated to SR, ~SR, S~R, and ~S~R given by

P(SR)= e{[e(0.5h+(1-h)d)+(1-e)(pa+(1-p)(1-b))] [0.5h+(1-h)d]} +(1-e){[pa+(1-p)(1-b)][e(1-h)d+(1-e(1-h))(pa+(1-p)(1-b))]} P(S~R)= e{[e(0.5h+(1-h)d)+(1-e)(p(1-a)+(1-p)b)] [0.5h+(1-h)(1-d)]} +(1-e){[ pa+(1-p)(1-b)][e(1-h)(1-d)+(1-e(1-h))(p(1-a)+(1-p)b)]} P(~SR)= e{[e(0.5h+(1-h)(1-d))+(1-e)(pa+(1-p)(1-b))] [0.5h+(1-h)d]} +(1-e){[ p(1-a)+(1-p)b][e(1-h)d+(1-e(1-h))(pa+(1-p)(1-b))]} and P(~S~R)= e{[e(0.5h+(1-h)(1-d))+(1-e)(p(1-a)+(1-p)b)] [0.5h+(1-h)(1-d)]} +(1-e){[ p(1-a)+(1-p)b][e(1-h)(1-d)+(1-e(1-h))(p(1-a)+(1-p)b)]}

(3)

2.10

As a consequence, the final observed proportion of original articles supporting A, o(S) will be different from the proportion of replications supporting A, o(R). One can actually show that o(R)>o(S), except for a few pathological cases when they are equal (per example, when every existing article is deceitful). This happens because o(R) and o(S) are the same except when the initial article was a correct experiment. If that is the case, honest scientists will not make honest mistakes during the replication. Since in an honest mistake, there was a 50% chance of supporting A and in a correct experiment, the chance is a>50%, the chance that a replicated result will support the correct theory is larger than the chance associated with the initial experiment.

2.11

This effect is the real origin of the difference introduced by replications. The final effect on the agent beliefs is that the agent can decide which theory is better by noticing which one is bigger, o(R) or o(S). The agent doesn't need to be aware of that, simple updating from one article at a time will produce that effect. However, it is not too hard to see that, if o(R) and o(S) are different but close, the number of articles and replications an agent would have to read in order to achieve certainty might be impossibly large. But it is certainly smaller than infinite now.

2.12

Despite being larger, o(R) can not have any value, regardless of o(S), since it is calculated from the same parameters. This means that o(R)-o(S) will be a little larger than zero, but, in general, not much larger. Per example, for a=b=0.6, the only way o(S) can be 0.95 is if e and d are large enough and h must be small. Since not many papers are honest, the effect of replication will be small (actually, it can be shown that o(R) will not be even as large as 0.951).

2.13

Replication will have an effect when the agent can be sure that o(R)-o(S) is different from zero. Since we have independent draws based on the proportions o(R) and o(S), we can estimate the error associated to each measure as a function of the number of read articles by the sample distribution for proportions. This can help us estimate the sample size needed so that the error is comparable to o(R)-o(S) and we have, approximately

n = 4o(S)(1-o(S)) / [o(R)-o(S)]2

(4)

where it was assumed, for the numerator that o(R) and o(S) were very close and that o(S)(1-o(S)) was basically the same as o(R)(1-o(R)).

Simulations

2.14

The problem described in the previous Subsection was implemented in FORTRAN code (download it here). In order to obtain faster convergence to average results, a variation of the latin-hypercube algorithm was implemented. The continuous variables were divided into sectors and in each random draw, a value was chosen inside each sector, successively. The code simulates one agent who reads t pairs of papers, where a pair consists of an original experiment and its replication. The results each article reports were obtained by picking values of o(S) and o(R) that are compatible with Equation 3, respecting the fact that, for a given o(S), there is only a range of possible values for o(R).

2.15

Since no analytic solution was found to the inference problem based on the likelihoods in Equation 3, the simulation was performed by a discretization of the continuous variables. The values of e, d, and h were modeled in intervals of 2%. This can introduce errors in the observed posterior averages, but, in general, the few simulations that were run with a finer discretization showed no important difference in the results.

Analyses of the Results

3.1

Simulations were performed for different values of a and b as well as for different numbers of pairs of articles read by the agent. In order to study the effect of reading more articles, the simulations were performed for different proportions of experiments that support A, o(S), and values of o(R) were obtained that were as far as possible from o(S), in order to allow replication to have a stronger effect. In all simulations presented here, the prior average for e was chosen as 0.2.

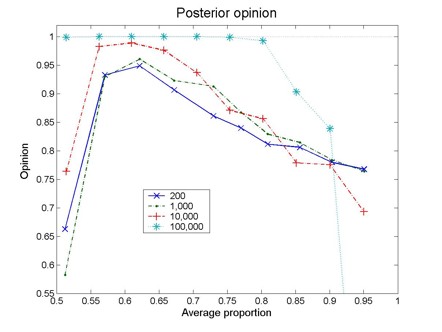
Figure 1. Posterior opinion as a function of the average proportion, 0.5(o(S)+o(R)). Each curve corresponds to a different number of pairs of articles (original experiment and replication). The results correspond to a=b=0.6. For 200 and 1,000 pairs, the results correspond to averages over 20 different realizations

3.2

Figure 1 shows the case where a=b=0.6. The x axis shows the average between 0.5(o(S)+o(R)) used in the simulations and the points were chosen so that o(S) changed by 0.05 from 0.5 to 0.95. Only one realization of 100,000 pairs was performed because the errors in this case were assumed to be much smaller. The first thing to notice is that even for 10,000 pairs of articles, the observed curve is not a step function, but a smooth curve. The step behavior is somehow recovered if the agent reads about 100,000 pairs of articles, although a sharp drop is observed for o(S)=0.95. This drop was observed also in a second run of the same problem and is probably due to the fact that, since o(S) and o(R) are very close in this region, the rounding errors, due to the discretization, can become a serious problem. Notice also that, from Equation 4, in order to measure the difference between o(S)=0.95 and o(R)= 0.9508 (values used in the simulation), a sample of about 300,000 would have been necessary.

3.3

Replication seems to solve the problem observed in Martins (2005), since the agent will eventually converge to the correct opinion with certainty. But we can see that, if, at first, the agent believes there is a reasonably high amount of deception (20%) and if the tests are not too significant, it can take too long for the convergence to occur.

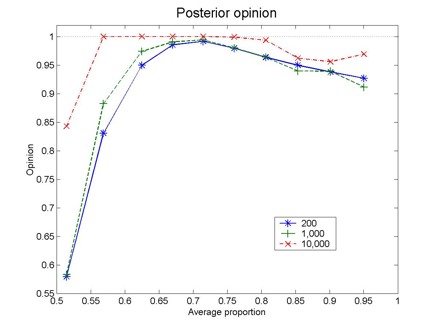
Figure 2. Posterior opinion as a function of the average proportion, 0.5(o(S)+o(R)). Each curve corresponds to a different number of pairs of articles (original experiment and replication). These results were obtained with a=b=0.7

3.4

In order to test the effect of the power the experiments have to discriminate between the two theories, the simulations in Figure 1 were repeated, this time with a=b=0.7. The results can be observed in Figure 2. As expected, the consequences of deception are less severe, but they can still be observed. The curve tends to a step function earlier, but even after 1,000 pair of articles it is still clearly not there, in contrast with Palmer's result. One does not have to read close to 100,000 results to be certain, though. This suggests that replication can be a powerful tool to deal with errors and deceptions, but the picture is not nearly as optimistic as that presented by Palmer.

3.5

In order to investigate what happens when an agent won't spend an excessive time reading about experiments and replications, simulations were also performed for different values of a=b, assuming the agent always reads 200 pairs of results, a large, but not impossible number. The results are shown in Figure 3.

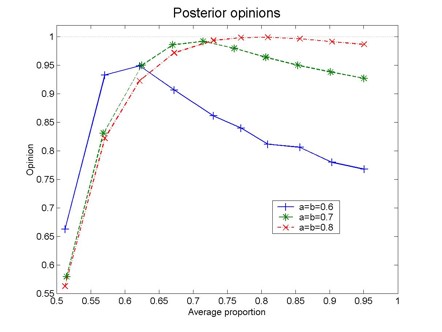
Figure 3. Posterior opinion as a function of the average proportion, 0.5(o(S)+o(R)), for different values of a and b. The results correspond to 200 pairs of articles (original experiment and replication) and are averages over 20 different realizations

3.6

Notice that, for a=b=0.7 and a=b=0.8, the curves go close to 1 for an observed proportion of experiments close to the values of a and b (where it is possible that no errors are happening). This means that a situation when everyone is honest and correct will not cause much damage and certainty can be achieved after reading a reasonable number of articles. The same is not true for a=b=0.6 where certainty goes up to 0.95 at best. That is much better than the results where no replication was introduced, but one can still notice the damage caused by the possibility of a high amount of erroneous work.

Conclusions

4.1

One possible criticism about the relevance of this paper is that Science, in time, tends to correct itself. Wrong results shouldn't survive the test of time, since, sooner or later, people will perform new tests and realize they were wrong. And they will correct themselves. This argument sounds reasonably solid to most of us but, before we can really trust it, it must be tested, just like every other conclusion. Thus, this work aims to test how solid Science might be when faced with the problem of deceptive behavior. Had the simulations shown that, whatever the case, the agents get close to certainty fast enough, those simulations would serve as evidence that the above argument is correct. Indeed, depending on a and b, certainty is very easily reachable. For theories that make distinct predictions, a and b will be large and, therefore, it seems that our faith in the fast self-correcting aspects of Science is well justified. This result had already been observed in the original model (Martins 2005) and it is still valid here.

4.2

However, the original model showed that there was a worrisome region, when a and b got closer to 0.5, that is, when models made predictions that were similar (or with large statistical errors). Notice that when our models of the world are vague and incapable of making precise predictions, we are in that region. And, when that happens, deception could be a very serious problem. Originally, it seemed there were circumstances where this problem could actually completely prevent any agent from reaching certainty. Palmer (2006) introduced the idea of reading only about replicated experiments, as a strategy to correct that problem. His analysis seemed to show that this strategy would solve the problem completely, but it failed at addressing the cases where experiments could go wrong due to statistical errors.

4.3

Here, we have observed that replication does buy us a way out of the deception problem, but, as we have seen, its price is not so low as previously thought. Eventually, the system converges to certainty about the most common result, but the rate of convergence is highly dependent of the situation. If someone wants to get close to certainty, this can require one to read many more articles than it would seem reasonable. Figure 2 shows clearly that, sometimes, even 1,000 articles might not be enough. In circumstances where the competing theories make very different claims and the experiments can easily discriminate between them, the existence of error or deception is not something that should worry any scientist too much. This case seems to be a better description of the current state of natural sciences.

4.4

Where disputing ideas can't make precise predictions, making it hard for experiments to differentiate between those ideas, replication still helps, but much less than defended by Palmer. The slow convergence might make certainty out of reach of any real agent with limited time to read about experiments. One should notice that if an area is not capable of making exact predictions, that means that there is a lot of uncertainty on the outcome of any experiment, even assuming one theory is correct. That corresponds to values of a and b dangerously close to 0.5. The Humanities seem to be such a case. The results show that it might be important to know which case your area is in, before becoming too certain about a theory you haven't tested yourself.

4.5

Of course, calculating a and b from theories is not possible in most of the cases in Humanities, since, most of the time, there are no probabilistic theories from where exact values can be estimated. This, however, does not affect the argument presented here, since all that is really required is that each agent estimate those likelihoods somehow. This estimation doesn't need to be actually performed in any conscious way. Notice that it makes sense to consider this as a description of the way we update our opinions, even when there are no mathematical theories involved. We see the data, somehow evaluate which theory explains it better, and then, we change our minds accordingly. Although we are certainly not born as statisticians, experiments have shown that we reason in a way that is, at least, similar to a Bayesian induction (Martins 2006;Tenenbaum 2007).

4.6

Therefore, it shouldn't come as a surprise that there are old issues that are still debated and, about which, no certainty seems to be achieved in the scientific community. This makes reports like those of Hubbard and Armstrong (1994), Evanschitzky et al (2007), or Ioannidis (2005), where too little replication was observed, even more worrisome. Without the limited but important help from replication, even the slow convergence should disappear and no certainty would be achieved at all. In the cases where replication doesn't help in a fast way, it still seems to be our only path to avoid the problems described in the original model. It might be very slow sometimes, but it will make us move in the correct direction, eventually. However, since it might be a slow process, deception can cause a lot of damage in the sense of wasted resources. And this indicates that the scientific community should worry about misconduct, probably much more than it currently does.

Notes

¹ One simple way to understand the likelihoods is in a typical inference problem. Assume that inference on the average value of a random variable is required and that it is known that the average is one of only two values, x and y, where x is valid if A is true, and y is the right value when B is. In this case, if one observes a sample of values, the likelihood is given by the probabilities those values will be observed for each scenario. Per example, assume that A and B are different species of a plant that look the same, except for the size of their leaves. You know that species A leaves are, in average, about 10cm wide while species B leaves are about 14cm. The width of the leaves of both species follows a Normal distribution with a standard deviation of 2cm. Therefore, you decide that, if you observe a leave larger than 12 cm, it is probably from plant B; if it is smaller, plant A is more likely. Here, the parameter a will mean the chance that one leave from A will actually have less than 12cm, while b is the probability that a leave of plant A will be larger than 12cm. Notice that you decide in favor of the most likely explanation, but some uncertainty will remain. Of course, for full scientific theories, a and b might be very hard to estimate. This problem will be discussed later. It is interesting to notice that, since the aim of this work is to reflect subjective beliefs, a and b might also be altered by psychological reasons, to reflect the fact that agents tend to change their opinion less than they should.

References

AUDI, R. (2002), The Sources of Knowledge, in Moser, P. K., The Oxford Handbook of Epistemology (Oxford: Oxford University Press).

CHASE, J.E. (1971), Normative criteria for scientific publications, American Sociologist, 5, 262-265.

EVANSCHITZKY, H., Baumgarth, C., Hubbard, R., and Armstrong, J. S. (2007) Replication Research in Marketing Revisited: A Note on a Disturbing Trend, Journal of Business Research, 60, 411-415.

GILES, J. (2006) The Trouble with Replication. Nature, 442, 344 - 347.

HUBBARD, R., and Armstrong, J. S. (1994) Replications and Extensions in Marketing — Rarely Published But Quite Contrary, International Journal of Research in Marketing, 11, 233-248

JAYNES, E.T. (2003) Probability Theory: The Logic of Science (Cambridge: Cambridge University Press).

IOANNIDIS, J. P. A. (2005) Contradicted and initially stronger effects in highly cited clinical research. Journal of the American Medical Association, 294, 218-228.

MARTINS, A. C. R. (2005) Deception and Convergence of Opinions, Journal of Artificial Societies and Social Simulations, vol. 8 (2) 3 https://www.jasss.org/8/2/3.html.

MARTINS, A. C. R. (2006) Probabilistic Biases as Bayesian Inference. Judgment And Decision Making, 1, 108-117.

PALMER, V. (2006) Deception and Convergence of Opinions Part 2: the Effects of Reproducibility, Journal of Artificial Societies and Social Simulations, 9 (1) 14 https://www.jasss.org/9/1/14.html.

TENENBAUM, J. B., Kemp, C. and Shafto, P. (2007) Theory-based Bayesian models of inductive reasoning, in Feeney, A. and Heit, E., Inductive reasoning, Cambridge, Cambridge University Press.

TITUS, S. L., Wells, J. A., and Rhoades, L. J. (2008) Repairing research integrity, Nature, 453, 980-982.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2008]