D. Scott Bennett (2008)

Governments, Civilians, and the Evolution of Insurgency: Modeling the Early Dynamics of Insurgencies

Journal of Artificial Societies and Social Simulation vol. 11, no. 4 7
<https://www.jasss.org/11/4/7.html>

For information about citing this article, click here

Received: 15-Jan-2008    Accepted: 22-Jul-2008    Published: 31-Oct-2008

Abstract

This paper models the early dynamics of insurgency using an agent-based computer simulation of civilians, insurgents, and soldiers. In the simulation, insurgents choose to attack government forces, which then strike back. Such government counterattacks may result in the capture or killing of insurgents, may make nearby civilians afraid to become insurgents, but may also increase the anger of surrounding civilians if there is significant collateral damage. If civilians become angry enough, they become new insurgents. I simulate the dynamics of these interactions, focusing on the effectiveness of government forces at capturing insurgents vs. their accuracy in avoiding collateral damage. The simulations suggest that accuracy (avoidance of collateral damage) is more important for the long-term defeat of insurgency than is effectiveness at capturing insurgents in any given counterattack. There also may be a critical 'tipping point' for accuracy below which the length of insurgencies increases dramatically. The dynamics of how insurgencies grow or decline in response to various combinations of government accuracy and effectiveness illustrate the tradeoffs faced by governments in dealing with the early stages of an insurgency.

Keywords:

Agent Based Models, Insurgency, Dynamics, Civil War

Introduction

1.1

The ongoing involvement of the United States in Iraq suggests a continuing need to understand the dynamics of insurgency, and especially how insurgencies become sustained. Insurgency^[1] is not a new phenomenon, but given the important geopolitical positions of the United States, Iraq, and its neighbors, the current conflict has brought home the salience of violent intrastate conflicts between governments and opposing forces. Historical evidence suggests that once insurgencies become well-established and conflict between insurgents and state governments becomes protracted, resolving the conflict takes many years and is often quite bloody. And in most such cases, governments have great difficulty prevailing militarily in the conflict. Military historians seeking lessons for fighting successful counterinsurgency campaigns have relatively few cases to draw on, particularly the British experience in Malaya during the 1950s, and U.S. experiences in the Philippines at the beginning of the 20th century. Insurgents in other cases have been able to defeat existing governments or force 3rd parties to leave (e.g. Vietnam, Algeria), or sometimes manage to bring down a government but then find it much more difficult to take over governing than to fight against a government, leading to further conflict (e.g. Afghanistan). But history also shows that many nascent insurgencies actually fail quickly, with only a few managing to become so well-established. For example, Bapat's (2005) data on 129 insurgencies since 1955 finds that while the mean duration of an insurgency is 7 years, the median is 4 years, and a quarter of insurgencies are defeated in less than 1 year. In their early stages, insurgencies are in fact quite vulnerable, and insurgencies at this stage can be (and often are) defeated. We rarely see discussion of such insurgencies because they are short, do not have time to attract media attention, and do not cause the destruction that brings attention to insurgencies in the first place. But these short-lived insurgencies are actually quite important as a contrast to the very long insurgencies we typically think about. It is important to know what leads some insurgencies to become well established, and others to fail.

1.2

This paper focuses on understanding the dynamics of the early stages of insurgency, and in particular how government military actions against insurgents may backfire. Insurgent military actions and government responses can be critical in affecting whether an insurgency manages to become established. The paper focuses on how civilians, the majority of whom are initially undecided about supporting insurgents, respond to government activity against known insurgents. To explore government/insurgent/civilian interactions, I develop and present a baseline agent-based simulation model that illustrates the effects of government responses to insurgent attacks. In this paper I do not examine the tactics used in locating and defeating particular insurgent groups in particular countries, or on the particular grievances that lead insurgents to gain the support of the population, but instead focus on the likely consequences of actions taken against insurgents across settings, and the tradeoffs among those actions. The baseline model can be easily extended in further work, but offers useful insights even on its own.

1.3

Specifically, by focusing on typical tradeoffs faced by governments in fighting a nascent insurgency, this paper develops a model that can be used to explore several critical questions about insurgency:

• Is it effective to use big sticks with a high probability of capturing or killing insurgents, even at the risk of civilian casualties?
• When it comes to defeating insurgency, what is the tradeoff between increasing accuracy (avoiding civilian casualties) and effectiveness (capturing insurgents), if there is one?
• What kind of interactive dynamics can we generate from simple rules of government/civilian interaction?
• Can the current conventional wisdom that it is important for government forces to be precise in counter-insurgency operations be easily reproduced in a simulated environment? How accurate is this conventional wisdom, and does it seem to hold under most circumstances, or only some?

1.4

The importance of evaluating varying approaches to dealing with insurgency, and concerns with the risks of heavy-handed (big stick) approaches, are evident in the current literature on counterinsurgency warfare (COIN). Nagl (2005: 26-27) contrasts two approaches to fighting unconventional war, one which emphasizes sticks, attrition warfare, and the direct use of military force against guerrillas/insurgents, and the second of which emphasizes concern for the population and their support for insurgent. He labels the first a "direct approach," noting that it considers winning in unconventional warfare as similar to winning in conventional warfare, where it is only necessary to defeat the enemy's armed forces in order to defeat the enemy. He labels the second an "indirect approach;" this approach "recognizes that it is essential also to attack the support of the people for the insurgents." In contrasting the success of the approaches, Nagl quotes the British military counterinsurgency field manual that concludes "the record of success for attrition in COIN operations is generally a poor one... The wider consequences of this approach, seen both in South Vietnam and elsewhere, will often be an upward spiral of civilian alienation" (2005:26). The much-heralded new version of the U.S. Army Counterinsurgency Field Manual (released in late 2006) discusses the risks inherent in using military force as a counterinsurgency tool, although only as one point among many. It notes that "COIN is 'war amongst the people.' Combat operations must therefore be executed with an appropriate level of restraint to minimize or avoid injuring innocent people. Not only is there a moral basis for the use of restraint or measured force; there are practical reasons as well. Needlessly harming innocents can turn the populace against the COIN effort." (United States Department of the Army 2007 p. 167.)

1.5

Although the U.S. military has a clear "indirect approach" to counterinsurgency warfare in its new doctrine, there are many cases (both historical and recent) where states have taken actions fitting with Nagl's "direct approach," and Nagl (2005) discusses extensively military resistance to the indirect approach. In the introduction to the University of Chicago edition of the new US Army/Marine Corps Counterinsurgency Field Manual (United States Department of the Army 2007:xxiv), Sewell points to some U.S. tactics in Vietnam such as free-fire zones and carpet bombing, or Russia's overall approach to fighting Chechen rebels, as fitting an approach focused solely on insurgent fighters. O'Neill (2005: 174-175) notes violent, excessive, and counterproductive government reactions to insurgencies in Peru, Sri Lanka, and Afghanistan. And despite stated U.S. doctrine (and in fact leading to an emphasis on new counterinsurgency training), even U.S. military actions in Iraq have fit this model. Writing in 2004, Record and Terrill (2004: 27) note that "U.S. forces have relied heavily on 'sticks' in Sunni Arab strongholds... [T]hose forces have conducted numerous raids into potentially hostile areas with the aim of arresting suspected insurgents, finding documents of intelligence value, [and] seizing illegal weapons and explosives... Raids can, however, alienate innocent people swept up in them or offended by the terrifying surprise intrusion of foreign troops in private family settings. The employment of attack aircraft as a weapon of counterinsurgency in Iraq certainly risks the kind of overkill impeded U.S. pacification efforts in South Vietnam." Hendrickson and Tucker (2005: 14) further point out how common practice by U.S. forces "had the effect of increasing hostility toward them in the broader population. Insurgents setting off roadside bombs sometimes attacked U.S. forces responding to the disaster, so U.S. forces frequently adopted the tactic of spraying fire rather indiscriminately once they were attacked - an expedient that did not endear them to the local population."

1.6

The simulation model presented here allows an exploration of some of the issues associated with fighting insurgency, and in particular at fighting with an emphasis on the "direct approach" vs. an emphasis concerned with surrounding civilians. In some cases, a heavy hand may work to defeat an insurgency. In others, it may backfire. But when? How significant are the consequences of targeting insurgents militarily even at the risk of injuring civilians? The simulation explores this by modeling how accuracy (avoiding collateral damage) and effectiveness (being able to capture or kill targeted insurgents in any given military action) interact and drive either the spread of, or decline of, a nascent insurgency. Previewing the results that emerge from the simulation, the model suggests that accuracy is more important for the long-term defeat of insurgency than is effectiveness of any given counterattack on insurgents. When action against insurgents results in many injuries and an increase in population anger, governments do the work of insurgents for them, and make successful prosecution of a counterinsurgency campaign more difficult. Even if relatively less effective at any particular time, a counterinsurgency campaign that is accurate enough to avoid high civilian damage tends to lead to shorter insurgencies than a campaign characterized by high effectiveness but low accuracy. In addition, the model suggests that there may be a quite narrow critical range for accuracy, where only a slight decrease in accuracy yields a dramatic non-linear increase in insurgency duration. The model suggests something like a "tipping point" or point of no return in terms of accuracy when it comes to defeating insurgency. These dynamics emerge even in a simple simulation devoid of overlapping aspects of insurgency that are sometimes discussed as critical features, such as insurgent recruitment techniques, media, ethnicity, religion, or politics.

1.7

While focusing on government responses to insurgent attacks, the model here builds on several "stylized facts" about insurgency that are generally accepted in the literature on insurgency (e.g.Bapat 2005, Fearon and Laitin 2003, Galula 2006, Metz and Millen 2004, Manwaring 2004,Nagl 2005). The core assumption of the model is that the actions of insurgents and governments take place against a backdrop of a large, initially uncommitted middle in a country (the audience). Insurgencies develop and become sustained not because insurgents defeat government forces in large-scale conventional military battles, but because they manage to win enough support ("hearts and minds") among a population for the insurgents to hide, receive support, recruit new members, and conduct continuing guerrilla-type operations against governments over a long period. In fact, government military forces rarely lose outright to insurgent military forces, and certainly not quickly. Rather, the political aspect of insurgency, popular support for insurgents and against a government, and the withdrawal of government forces from particular regions or government concessions is the norm, rather than direct military overthrow of the government. With this in mind, the simulations here concentrate on the purposive acts of insurgents and government forces while treating civilians as an audience which solely reacts to the actions of those insurgents and soldiers.

1.8

The model also assumes that, as in reality, insurgencies are very weak relative to the government at their early stages. Insurgencies start at a great disadvantage relative to government authority when it comes to strength, influence, and support, and are almost always vulnerable to concerted government efforts against them. This contributes to the need in insurgencies to act in secret and develop a non-hierarchical network of distributed cells that are not subject to "decapitation." As Metz and Millen ( 2004:5) note, "Starting an insurgency is easy. A dozen or so dedicated radicals with access to munitions and explosives can do it. Building an effective insurgency, though, is difficult. History suggests that it requires a specific set of conditions... When facing a determined regime with an understanding of counterinsurgency and the resources to undertake it, all of these conditions must be present for any degree of success by the insurgents." One of the challenges to an insurgent movement is thus how to increase its visibility and public support without exposing itself too much and making itself vulnerable. Insurgents choose from a variety of tactics, both peaceful and violent (for some discussion and examples, see e.g., Wimberley 1997, Galula 2006,O'Neill 2005). Peaceful tactics include peaceful recruitment, for instance by holding meetings, making public speeches, publishing literature, or providing services that the government does not or cannot. Violent tactics (bombings, assassination, direct military attack) may seek to demonstrate a government's inability to stop the insurgency, or to gain public visibility. But in fact, violence may be consciously planned not so much to have a direct effect on government forces or structures as to generate a disproportionate government response that does the work of the insurgents for them. Hendrickson and Tucker (2005: 14) actually argue that this is one dynamic of the U.S. engagement in Iraq, suggesting that "[p]erhaps the key advantage enjoyed by the insurgents was the capability of putting U.S. forces in situations where the military response would further antagonize the population and make any contact with them a source of profound danger." The model takes as a final stylized fact that such provocation is a common feature of insurgency.

1.9

Popular literature and press accounts discuss many other influences on the course of insurgencies, including the availability of outside sponsorship, the availability of weapons, the effect of media coverage on public opinion, networks of cells and social linkages, and the effect of religious or ethnic differences on the course of internal conflict. While different insurgencies certainly vary on these characteristics, scholars have questioned whether any of these descriptive features of conflicts are really critical to the development of insurgency. That is, while outside sponsorship may help certain insurgencies develop, it is not a necessary condition for insurgency (some insurgencies have outside support, but others do not). Similarly, while electronic media or social networks may spread word of insurgent attacks more rapidly than print or word-of-mouth, insurgencies have certainly developed in the absence of media. Indeed, rigorous academic analysis has even questioned whether internal conflicts are more likely (or evolve differently) in ethnically or religiously mixed societies versus homogenous ones (e.g.Fearon and Laitin 2003). The model developed here abstracts away from these specifics, placing the focus specifically on fundamental individual attitudes, violent insurgent acts, and government responses, If the simulation developed here cannot replicate any patterns that look like insurgent behavior, then we might conclude that we must add one or more additional features to the model. But, previewing some of the patterns emerging from the simulation, the simulation actually yields patterns that look like a real spread of insurgency without social networks, media, religion, and so on. In fact, the essentials of the model here could potentially be applicable to other situations where representatives of a central authority are engaged in repeated fighting or confrontation with members of a population with grievances, for instance in circumstances of police facing rioters, or tribal groups resisting centrally-imposed government policies. The model would seem to most closely parallel situations in which authorities have force at their disposal which may result in injury/insult/anger among targeted citizens, and where those resisting authority may engage in attacks intending to provoke such responses. While the nuances of specific situations will always differ, the central dynamics of many situations may be quite similar.

1.10

Several agent-based simulations have dealt with related issues of rebellion and internal warfare within countries, although various studies use the labels of "civil war" or "guerrilla war" along with "insurgency." The governments of many countries are interested in whether, and how, agent-based models may be applied to better understand such conflictual situations as well (in the United States, for example, the Military Operations Research Society devoted a 2005 workshop to the topic of "Agent-Based Models and Other Analytic Tools in Support of Stability Operations" (Military Operations Research Society 2006)). One of many general and descriptive introductory papers that discusses some of the uses and risks of agent-based models in studying military/regional threats is Louie and Carley (2007); some recent examples of models of internal conflict/insurgency include Bhavnani et al. (2008), Cederman (2006), Chaturvedi et al. (2005), Doran (2005), and Epstein et al. (2001). Relevant to the social structure modeled here, Cui and Potok (2007) explore a model showing that unified leadership and strategic planning among insurgent groups are not necessary for insurgents to obtain their objectives. Models specifically focusing on citizen loyalties toward an insurgency/rebellion or the state include Warren (2006), Wheeler (2005), Ruby et al. (2005), and Findley and Young (2007). The typical approach used in all of these models is to model (roughly, and with significant variation) a cost-benefit calculation on the part of civilians in a region. Depending on attitudes toward and benefits received from governments and civilians, civilians may provide intelligence to peacekeepers (Wheeler 2005) or align to varying degrees with insurgents or the government (Ruby et al. 2005,Findley and Young 2007). Of these models, Findley and Young's model is the closest in "flavor" to the model developed here. Findley and Young contrast a "costs" strategy for combating insurgency (which attempts to deter insurgents by inflicting high costs on them) to a "hearts and minds" strategy (which attempts to keep civilians aligned with the government by providing benefits, even though some government-provided benefits might be diverted to insurgents). This leads to a necessary balance for counterinsurgents (governments) between providing benefits and imposing costs to neutralize insurgents and possible recruits.

1.11

None of these models focus specifically on the dynamics of the possibly counterproductive effects of actions targeting insurgents. But it is widely accepted in studies of terrorism, insurgency, and guerrilla warfare that insurgents and guerrilla fighters pay close attention to media, publicity, and perceptions of their (and government's) activities. Insurgents/guerrillas are quick to (attempt to) take advantage of government activities that hurt civilians. Especially in an age of ready-access to media, it is easy for governments to hurt themselves (hence the importance of events like the publicized photos of degrading treatment of prisoners in Abu Ghraib prison in Iraq which help the insurgent cause). Given that targeting insurgents is not a sure thing, if governments are to be effective at fighting insurgents, an effort to understand the dynamics of productive and counter-productive action vs. insurgents is warranted. This simulation is developed to focus specifically on the positive and risky aspects of government actions vs. insurgents, and to do so in a narrow fashion.

1.12

In Axelrod's (2004:13) terms, the model here uses "light" agents, that is, a model in which the agents have relatively few individual characteristics. It also keeps a specific focus on a very limited number of dynamics and features of the simulated system. We could contrast this model to a model with "heavy" agents in which each agent might be endowed with a particular ethnicity, religion, amount of weaponry, job status, political party, a network of contacts, and so on. We could similarly model actual terrain, social networks, media activities, psychological processes, and so on in a heavy, or complex, model. Several of the models previously cited (e.g.Doran 2005, Chaturvedi et al. 2005,Bhavnani et al. 2008) have developed models with many agent characteristics and/or many interactive processes included. For many purposes, such as identifying particular likely conflict locations in some country, or attempting to develop models that practitioners could use "on the ground" to predict the results of particular actions, a working and well-calibrated heavy model could be quite useful. However, the additional features and interactions of complex models may also make them difficult to understand, visualize, or extract the particular dynamics we are interested in. Each additional factor modeled adds to the complexity of the simulation, to the size of the parameter space, and to the number of assumptions that must be made about parameter values to make useful runs of the model. Large models may run the risk that fundamental patterns will become lost as the parameter space for evaluation grows, and the effect of other assumed parameters becomes large, possibly concealing the possible dynamics of interest. Scholars have recognized this problem, of course; for instance, Doran (2005: 6) indicates this challenge with the Iruba model, noting that "such models contain a wide range of adjustable parameters and also many model components that can be structured in alternative ways... Which parameter values and which structural alternatives should be used are impossible to determine with any confidence even for a specific ongoing conflict." He continues with valuable discussions of different responses to this problem, one of which is to work with more abstract and simplified models that focus on one component of a process (an alternative is to develop a generic "all possibilities included" model). In this light, Axelrod (2004:12-14) compares a variety of modeling approaches, and suggests that different types of models (where "types" may be agent-based vs. equation-based or econometric models, or agent-based models with different levels of detail) may have different strengths. Within agent-based models, he suggests that light agents are relatively good for heuristic value and for transparency, which heavy agents are relatively good for incorporating substantial amounts of subject matter expertise. He notes in particular that complicated models (which can be understood only with more difficulty) run the risk of being dismissed if their conclusions run counter to the beliefs of a viewer. Here, I have chosen to keep the model simple and clean with a light-agent formulation in order to be able to more-fully explore and understand the dynamics developing within the simulation. The benefit of this approach is that the dynamics and focus of the simulation are clear; the cost is that the model omits a variety of features of the world to gain this more stylized representation.

Simulation Overview

2.1

The simulation assumes two core types of agents: civilians, and soldiers. Soldiers represent the government, or potentially troops of a supporting (or occupying) power. No distinction for simulation purposes is made between government soldiers and international soldiers; all soldiers are taken as representatives of a group to which the insurgents are opposed.^[2] Civilians represent the mass of a population. Individual civilians are characterized by a degree of anger at the government, a degree of fear of the government, and a propensity to use violence under the right circumstances. An insurgent is a civilian who is willing to engage in violence against the government, and specifically against a nearby soldier. Insurgents in turn may be potential or latent insurgents who are willing to engage in violence, or active insurgents who have actually done so.

2.2

The main agent transition in the model is that ordinary civilians may turn into insurgents under the right circumstances. The transition decision rule for the civilian agents is that if a civilian is more angry than afraid, and if the civilian's anger passes a threshold propensity to use violence, then this civilian becomes a latent insurgent. This is a civilian who is angry enough, and is not so afraid of the government, that they will attack a government target (a soldier) if given the opportunity. Some civilians with a low violence threshold will be willing to attack a soldier with little provocation (low anger). But if they have a high enough threshold (suggesting a pacific nature), then even a very high level of anger will not lead to such an attack. If a latent insurgent is within a defined range of a soldier and is given an opportunity, then this latent insurgent will conduct an attack and become an active insurgent. The first dynamic of the simulation results from the transition of ordinary civilians to latent insurgents to active insurgents.

2.3

The second dynamic of the simulation emerges from responses to insurgent attacks. Attacking exposes latent insurgents. After any attack, soldiers can respond to the attack by targeting the insurgent with a counterattack of their own. The intent of such counterattacks is to remove (capture or kill) the insurgent so that the insurgent is unable to make further attacks. Such counterattacks (or similarly, raids to capture known insurgents) may also deter civilians from becoming insurgents by increasing their level of fear. It is the government's goal to remove all of the insurgents from the world, thereby defeating the insurgency.

2.4

Three relevant and well-known stylized facts about violent government targeting of insurgents or guerrillas are critical during the response stage, and make the model more than simply insurgent attacks followed by insurgent removal. First, even effective militaries are not always able to capture or kill the insurgents that they pursue, meaning that insurgents often remain even after government counterattacks. The ability of soldiers to capture or kill a targeted insurgent is parameterized by the soldier's level of effectiveness. Second, we know that regardless of whether they manage to capture or kill a particular targeted insurgent, militaries sometimes - perhaps often - inflict significant "collateral damage" when they engage in anti-insurgent activity. The most salient form of collateral damage is the accidental death of civilians that occur as a result of mistaken shootings or bombings, but collateral damage can also occur in the form of injury, property damage, or even personal insult if innocent civilians are perceived to be mistreated during searches or pursuit of an insurgent. The probability that a soldier's counterattack inflicts collateral damage is parameterized by the soldier's level of accuracy. Third, we know that civilians are made angry by widespread deaths among the civilian population and perceived mistreatment of civilians. This increase in anger at the government occurs at the same time that civilian fear of the government may increase in response to violent government actions.

2.5

Each of these stylized facts can be modeled in a world of individual agents. The first fact, that militaries cannot always capture or kill a particular insurgent, is captured in an effectiveness parameter in the model. The fact of collateral damage that increases both the anger and fear of civilians is captured through a parameter for soldier accuracy (accuracy decreases the probability of collateral damage), a rate at which civilian fear increases after a nearby insurgent is targeted, and a rate at which civilian anger increases when other nearby civilians are hurt by collateral damage. With these features in place, the dynamic that results is one where an insurgent attack triggers a response that might remove insurgents, but also runs the risk of creating more potential insurgents. The relative risk of these occurrences, and the variety of interesting dynamics that can result from the model, emerge from the combinations of values on these critical parameters that influence the course of insurgencies.

2.6

The course of the simulation is that in each time tick of the simulation, one insurgent (latent or already active) is randomly selected to attack a soldier in range of the insurgent. Following this attack, the soldier responds with a counterattack. With probability equal to effectiveness, the insurgent is removed from the simulation. Then, with probability equal to1-accuracy, each civilian in the neighborhood surrounding the insurgent is injured (representing collateral damage). The level of fear of each injured civilian in the neighborhood is increased, and the level of anger of each injured civilian is increased by an amount proportional to the total number of civilians injured. If anger and fear levels change appropriately, either latent insurgents in the neighborhood may "fall out" of the insurgency and become "regular" civilians, or non-insurgents may become latent insurgents. In combination with the (possible) removal of the initial insurgent, this may lead to a net increase or decrease in the total number of latent insurgents. The simulation continues until all of the insurgents in range of a soldier that could be targeted are removed from the simulation, or the simulation hits a tick cutoff (indicating a self-sustaining insurgency, which is typically quite obvious well before the cutoffs used in the simulations).

2.7

In this simulation, individual soldier agents do not "die" in the initial attack by insurgents (they might in a different type of agent based model, such as a predator-prey model). Rather, as soldiers represent parts of an established government, any soldier actually killed is assumed to be replaced immediately. The attacking insurgent can die (be removed from the simulation), however. This structure captures the known, critical feature of early insurgencies confronting governments that they are at a significant disadvantage militarily. National governments are well-established, bureaucratized institutions with large resources (e.g. an organized military) relative to insurgents. Insurgencies begin with small numbers of members/supporters, who are typically unable to stand up in an open fight with government military forces. Since individual insurgents can be captured or killed by government forces and lack the infrastructure or defenses to resist for very long in sustained confrontation, insurgencies are always militarily vulnerable early on. By contrast, governments typically cannot be substantially hurt at early stages of an insurgency. Soldiers can be replaced, and minor damage can be repaired. Early on, insurgencies may very much be a nuisance rather than a major threat. This combination of relative strength and the ability to affect the other actor is reflected in the simulation with soldiers who are not removed from the simulation when attacked, but insurgents who are. This leads to the termination of the simulation only when all of the insurgents are removed or the simulation continues long enough. At the early stages of insurgencies being modeled here, a termination because of government defeat is not realistic.^[3]

2.8

The simulation was programmed in Java using the RePast 3.1 simulation libraries. RePast handles many standard agent-based simulation functions with ease, such as drawing and displaying maps and displays, keeping track of agents and their status, and recording the history of multiple simulation runs. Code was developed for the soldier and civilian agents, to specify the agents' decision rules, and to specify the sequence of actions. A single iteration of the model can take from a few seconds (if the insurgency ends with 50 to 100 ticks), or a few minutes (if the insurgency becomes self-sustaining).

Simulation Details

Agents

3.1

The model has two types of agents, soldiers, and civilians.

3.2

Soldiers: Soldiers have no individual characteristics apart from a physical location. All soldiers share two global parameters, their level of effectiveness (the probability that they capture or kill an insurgent after that insurgent attacks), and their level of accuracy (the probability that they avoid collateral damage to civilians near the insurgent). By default there are 100 soldiers placed in the simulation space.

3.3

Civilians: Civilians have three individual characteristics, namely anger at the government (which increases their likelihood of attacking a soldier and becoming an active insurgent), fear of the government (which suppresses their likelihood of attacking a soldier), and a violence threshold. Each can range between 0 and 1. For anger, a 0 indicates that a civilian is not at all angry at the government, while a 1 indicates maximum anger. For fear, a 0 indicates that a civilian is not at all fearful of a government response to any action (such as an attack) that the civilian takes against the government, while a 1 indicates maximum fear. For the violence threshold, a 0 indicates that an individual has a low threshold to commit violence, and would use violence under many (or all) circumstances. A 1 on the violence threshold indicates a high threshold, and that the individual will be very reluctant to turn to violence, regardless of how angry they might be. To be a latent insurgent (one who is willing to undertake an insurgent attack against a soldier), a civilian's level of anger must be greater than both the civilian's fear level and violence threshold. By default, there are 500 civilians placed in the simulation space.

3.4

Each civilian in the simulation has individual values for their anger, fear, and violence threshold. Initial values for individual agents are drawn from a truncated normal distribution with mean and standard deviations set at values listed in Table 1; the distributions are shown graphically in Figure 1. The distributions are truncated in that all values must fall between 0 and 1 (if a draw is less than 0, 0 is assigned; if a draw is greater than 1, 1 is assigned). Initially, the default population is significantly more fearful than it is angry (mean fear=0.5, mean anger=0.25, with standard deviations equal to half of the mean), and with a higher violence threshold than the mean anger level. The result of this combination is that only a small percentage of civilians initially meet the criteria for becoming latent insurgents.

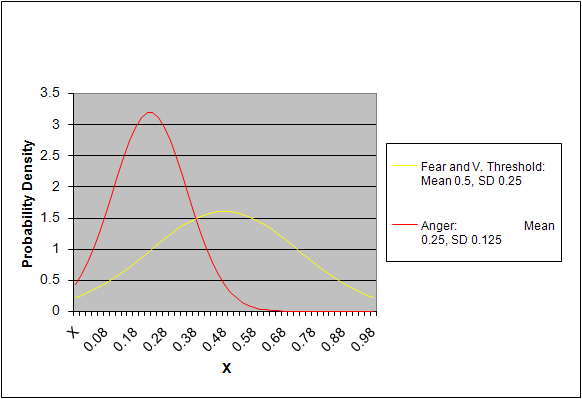
Table 1: Mean and Standard Deviation of Population Initial Anger, Fear, and Violence Threshold Distributions
	Mean	Standard Deviation
Anger	0.25	0.125
Fear	0.5	0.25
Violence Threshold	0.5	0.25

Figure 1. Default Probability Distributions of Fear, Anger, and Violence Threshold

Space

3.5

The space in the model is simulated by a 2-dimensional grid of rectangular cells. The space has edge boundaries (it is not a torus), and agents interact only with their neighbors, where neighbors are defined as all actors within a specified Moore distance (3 cells by default). This represents the typical geography of a conflictual region - actors typically act within the confines of a defined region, such as a city, a country, or perhaps a small region that goes outside the boundaries of one state. By default, the grid is 50 x 50 cells. Each soldier or civilian in the simulation occupies one grid cell, and only one agent can occupy any cell location.

3.6

It is easily possible to modify the simulation to use a toroidal representation. Using a torus for the actor space would allow actors to interact across the boundaries, that is, actors at the visual top of the space would also touch actors at the bottom of the space, and actors on the visual right of the space touch actors on the left of the space. However, while a torus might be appropriate for a space envisioned as a globe, a bounded grid corresponding to a limited geographic region seems appropriate for modeling insurgency, where geography and the presence of other bounding actors (e.g. other states) place real limits on the scope of interaction. In terms of its effect on the simulation, shifting to a torus typically leads the simulation to run somewhat longer until insurgency is eliminated (if it is a run with parameters that lead to termination in a finite time at all). This is because latent insurgents at the border of the space have potential interactions with more other actors (those at the opposite side of the grid space).

Display

3.7

Agents and soldiers are displayed in the space using different colors and shapes. Soldier agents are represented by blue squares; when they are attacked, the square is outlined in red for a fixed number of iterations for visualization purposes. Civilian agents may be green, yellow, orange, or red. Green civilians are those where their anger level is less than their level of fear and their violence threshold. Intuitively, these are civilians about whom the government does not need to (immediately) worry; they are not at risk of carrying out an insurgent attack. Civilians are displayed in yellow if their anger is greater than their fear, but does not cross their violence threshold. Civilians are also displayed in yellow if their anger is greater than their violence threshold, but their fear level is greater than their anger. Intuitively, these are civilians about whom the government should worry, as they are "halfway" to becoming insurgents. Civilians are orange if their anger is greater than their fear and their anger is greater than their violence threshold, but they have not yet carried out an attack against a soldier. These civilians are considered latent insurgents - they would attack given an opportunity, but simply haven't had the opportunity yet. Finally, civilians are displayed in red if they meet the anger, fear, and violence threshold conditions to be a latent insurgent, and have actually carried out an attack. These agents are active insurgents.

Agent Actions

3.8

Agents undertake one of two actions in the model. First, civilians may attack a soldier target. They do so only if they are latent or active insurgents (that is, they have anger greater than fear, and anger greater than violence threshold), and if they are within range of a soldier. The range is determined by a global parameter for interaction range, and is set by default to a range of 3 grid cells (in a typical 50 x 50 grid).

3.9

An insurgent attack in turn generates a second action, a soldier counterattack against the attacking insurgent. Intuitively, a counterattack is an attempt by the government to capture or kill an insurgent who has conducted an attack vs. a soldier. The probability that a soldier will counterattack in response to an insurgent attack is governed by a global parameter for sensitivity, which in the current simulation is always set to 1.0 (that is, soldiers always respond to attacks).^[4]

Action Effects

3.10

An attack on a soldier has the effect of transforming an insurgent from a latent insurgent to an active insurgent. In practice, the distinction is largely for display purposes; active insurgents (those who have carried out attacks) are represented in red on the simulation display, while latent insurgents are orange.

3.11

A counterattack on an insurgent has effects both on the insurgent who attacked and on neighboring civilians. First, a counterattack has a probability of removing the insurgent from the simulation (in the real world, capturing or killing the insurgent). The probability of removing the insurgent is determined by the soldier's effectiveness value, currently equal for all soldiers. With p= effectiveness, the attacking insurgent is removed from the simulation. Second, a counterattack may injure^[5] civilians near the site of the counterattack, which is the location of the initial insurgent who attacked. Each civilian within a range specified by the interaction range parameter may be injured. Injury to each civilian occurs with p=(1-accuracy), where accuracy is a parameter which is currently equal for all soldiers.

3.12

When civilians are injured by a soldier's response, they experience an increase in both fear, and anger.^[6] In the simulations reported, civilians shift their fear 10% of the way toward 1.0 from their current level of fear when they are injured (this increase is parameterized in the model). That is,

Fear t+1 = Feart + 0.10*(1-Feart).

(1)

3.13

For example, a civilian with 0 fear would see an increase to 0.10 when they are injured; a civilian with 0.50 fear would see an increase to 0.55. The increase in fear each time a civilian is injured is thus decreasing as civilians become more fearful. The functional form of this fear response is in part designed to restrict the parameter to between 0 and 1. In addition, though, the "diminishing return" in fearfulness that results from government action reflects real-world habituation. Over time, it typically takes more and more extreme actions to evoke the same response in human beings. This is one reason that terrorists must seek new, different, and larger ("splashier") actions to gain attention - human beings can become accustomed to nearly any given level of violence or news, and their reactions lessen when seeing subsequent, similar acts.

3.14

The function of increasing anger follows a different form. We expect civilians to become more angry when soldier responses are indiscriminate and injure more civilians. Thus anger is modeled as increasing at a rate proportional to the number of individuals injured in a counterattack. In the reported simulations, civilians experience an increase in anger equal to 5% of the distance to an anger level of 1.0 per civilian injured in a counterattack (this increase is parameterized in the model), to a maximum anger of 1.0. That is,

Anger t+1 = Angert + 0.05*(Number of Civilians Hurt)*(1-Angert)

(2)

If

Anger t+1 > 1.0, Anger t+1=1.0

(3)

For example, if a counterattack injures 5 civilians, then an injured civilian will increase its anger 25% of the way toward the maximum possible anger (1.0).

3.15

Counterattacks by soldiers can only remove insurgents. Civilians are not killed or removed from the simulation when hurt in a counterattack, and remain for possible recruitment by insurgents, or further injury, in later rounds. This assumption fits with the image of a region of insurgency with many civilians, but fewer insurgents who potentially could all be killed or captured. Initially there is no replacement of insurgents removed from the population (this is changed in the model expansion discussed later).

Model Parameters and Default Values

3.16

Table 2 shows the model's parameters, the range allowable for each parameter, and the default values programmed in the simulation (and used in the demonstration scenarios unless otherwise noted).

Table 2: Summary of Key Model Parameters
Parameter	Scope	Definition	Range	Default Value
Space Size	Global	Dimensions of map grid	1+	50
Interaction Range	Global	Size of neighborhood for insurgents looking to attack, and for range for collateral damage to civilians	1 to size of map	3
Effectiveness	Global / All Soldiers	Probability of removing an insurgent during a soldier's counterattack	0.0 to 1.0	0.8*
Accuracy	Global / All Soldiers	1-accuracy equals the probability of injuring any civilian within interaction range during a soldier's counterattack	0.0 to 1.0	0.8*
Sensitivity	Global / All Soldiers	Probability of a soldier responding to an attack. Always 1.0 for this simulation (included for later expansion)	1.0	1.0
Initial Anger	Individual / Each Civilian	Level of this civilian's initial anger at the government	0.0 to 1.0	Normally distributed, mean 0.25, std. dev. 0.125.
Initial Fear	Individual / Each Civilian	Level of this civilian's initial fear of government response to insurgent act	0.0 to 1.0	Normally distributed, mean 0.5, std. dev. 0.25.
Violence Threshold	Individual / Each Civilian	Level that anger must pass for civilian to be willing to engage in violent insurgency	0.0 to 1.0	Normally distributed, mean 0.5, std. dev. 0.25.
Anger Increment per Injury	Global	Amount per injured civilian that anger increases in each civilian injured by a soldier counterattack	0+	0.05
Fear Increment	Global	Amount that fear increases in each civilian injured by a soldier counterattack	0+	0.10

* This is one of the key parameters systematically varied in the simulations

Simulation Sequence

3.17

The sequence of events in the simulation is as follows:

1. Model initialized. Soldiers and civilians are distributed randomly around the hypothetical landscape. Individual civilian agent anger, fear, violence thresholds are generated from distributions. Civilians with appropriate levels of anger, fear are set as "latent" insurgents. Display is updated.
2. One latent or active insurgent is selected at random. If within range of a soldier, the insurgent attacks that soldier, and is designated an active insurgent. If multiple soldiers are in range, one is selected at random. Display is updated to show attack and activation of insurgent.
3. The soldier counterattacks.
   1. With probability=effectiveness, the insurgent is captured/killed by the counterattack. In expanded versions of the simulation, a replacement civilian is randomly placed in the space to replace the removed insurgent.
   2. With probability=(1-accuracy), each nearby civilian (within interaction range) is hurt by the counterattack. If a civilian is hurt, his/her anger and fear increase following formulas above, and using the total number of civilians hurt.
   3. Display updated as needed to remove attacking insurgent and change civilian display colors.
4. Simulation ends if a) no latent insurgents remain, b) latent insurgents remain, but none are within interaction range of any soldier, or c) simulation hits fixed tick count (set at 2000 or 5000 in various runs).
5. Repeat from step 2.

Basic Runs

4.1

I illustrate the dynamics of the simulation and its display output by showing a series of one individual run each for three scenarios with selected combinations of accuracy and effectiveness. I then turn to a more general assessment of multiple runs over the full range of combinations of accuracy and effectiveness.

Initial Scenario: high accuracy (0.8), high effectiveness (0.8)

4.2

A single initial run of the model illustrates the typical dynamics of a possible insurgency that begins but is quickly defeated by the government. In this initial run, accuracy = 0.8, and effectiveness = 0.8 (seed was set to 37). Figure 2 shows two depictions of the state of the model after 10 iterations. The left-hand-side map ("World Display") shows the simulated world. As noted, blue squares are soldiers, while circles are civilians of varying anger levels. Soldiers with red squares around them have been attacked in the first 10 ticks. Most civilians are green or yellow - they are not angry enough to join the young insurgency. A few circles are orange, showing latent insurgents that will attack in future ticks. Even less circles are red, showing active insurgents who have carried out an attack on a soldier and not been removed in the ensuing counterattack.

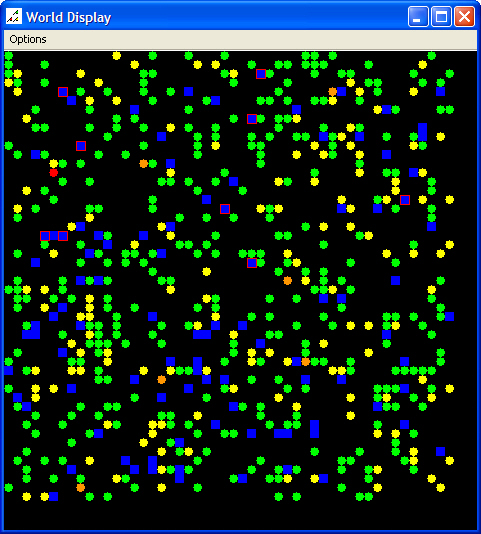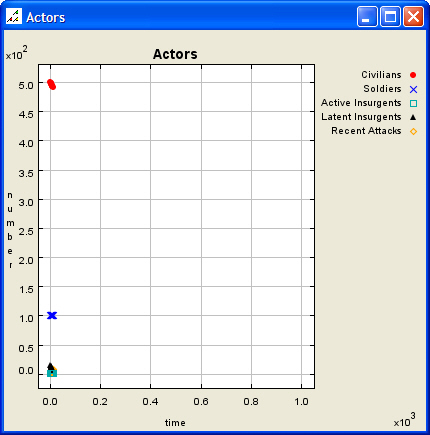
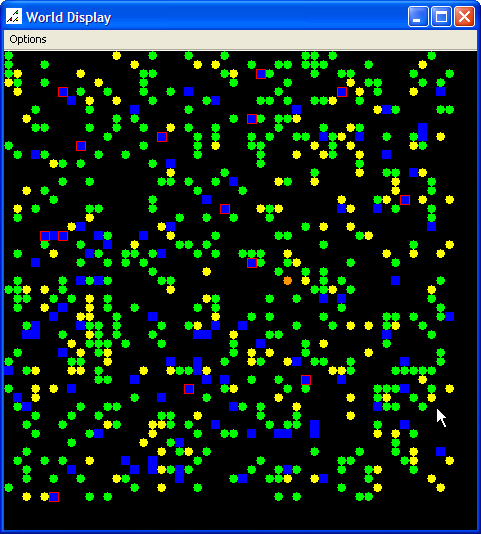
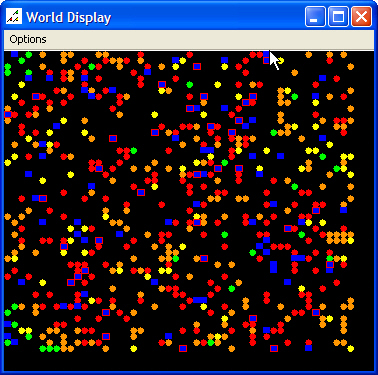
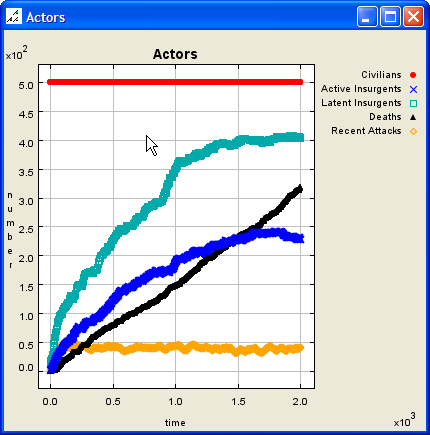
Figure 2. Initial Scenario Map and Data Graph

4.3

The right-hand-side graph shows a count of the number of civilians, soldiers, and insurgents over time, together with a count of the number of attacks that have occurred within the past 50 ticks. An initial population of 500 civilians is shown which starts to drop as soldiers target and remove insurgents during counterattacks. To better see the dynamics of insurgents, a blow up of the lower part of the "Actors" display is displayed in Figure 3.

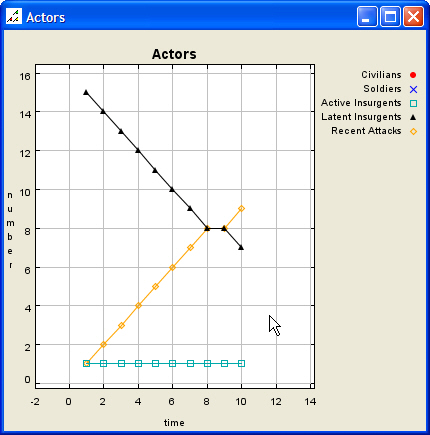
Figure 3. Initial Scenario Data Graph, Expanded

4.4

Initially, there are 16 latent insurgents in this particular simulation (the graph starts at tick 1, actually after one insurgent has attacked and been removed by a counterattack). They begin to carry out attacks on soldiers (most often, one attack occurs per tick, increasing the cumulative number of attacks represented by the yellow line). After each attack, the targeted soldier counterattacks, and with an effectiveness of 0.8 the attacking insurgent is then removed in most cases. This leads to a drop in the number of latent insurgents (black line), and a flat level of active insurgents (turquoise line; insurgents are nearly always removed, so they do not remain active long).

4.5

In this particular run, the simulation ended after 22 ticks when no more insurgents were in range of any soldier. The final world and a blow up of the "Actors" display are shown in Figure 4.

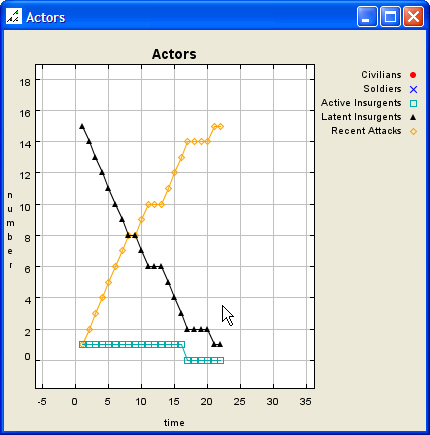
Figure 4. Initial Scenario Map and Data Graph, After Termination

4.6

At the end of the simulation, no active and only one latent insurgent remains (turquoise and black graph lines). The sum of recent attacks peaks at 15 attacks, after each of the insurgents in range of a soldier has attacked. One latent insurgent remains at the end of the simulation (this insurgent is out of range of any soldier and so cannot attack or be attacked).

4.7

This initial simulation shows a situation of a typical abortive insurgency, where insurgents are quickly removed once they reveal themselves by attacking. The quick end to the insurgency occurs because insurgents are being removed at a rate of 80% each time they attack, and nearby civilians are not being hurt very much (only 20% of the time). The insurgency does not spread widely beyond the initial latent insurgents (a few new insurgents are created; the flat spots on the "Actors" graph are situations where either insurgents were not successfully removed by counterattack, or where new insurgents were created, but these are not very many).

4.8

What does it take to get a growing insurgency? The simulation reveals that the key is for effectiveness and accuracy to drop to lower levels. But with current parameterizations, they must drop to a surprisingly low level on both effectiveness and accuracy. First, I show typical graphs of runs with lower effectiveness and accuracy levels, and then present a full summary of repeated runs.

Scenario 2: High effectiveness (0.8), low accuracy (0.2, high collateral damage)

4.9

An individual run of a second scenario (effectiveness 0.8, accuracy 0.2, seed 1) begins to reveal a more dangerous pattern that we might expect in certain violent situations where governments can become their own worst enemy. In this scenario, whose termination state is displayed in Figure 5, soldiers are still effective at removing insurgents (removing them with p=0.8 in any counterattack). But this comes in this simulation at the cost of great injury to surrounding civilians (injuring each civilian in the surrounding neighborhood with p=0.8). With these values, the length of time until the insurgency is defeated is substantially longer than previously (about 250 ticks in the sample run shown). In these results I also show the number of deaths that result as insurgents (who are also members of the civilian population) are killed. Looking at the world map and examining the number of deaths in the graph, we can see that the simulation terminates (and the insurgency is defeated here) only at the cost of about 125 civilian (insurgent) deaths. We might see this scenario as an "iron hand" scenario where indiscriminate violence is used to defeat an insurgency. This strategy works, but over a long time, and with a cost of many civilians removed. This follows from the key feature of the insurgency to note in this case. Because of inaccuracy in counterattacks, at early stages of this scenario the number of latent insurgents grows very rapidly. Initially, many more civilians are being "converted" to insurgency than are being removed. When accuracy is high (scenario 1), no new insurgents were ever created. With lower accuracy, they are. The higher number of deaths in this scenario results from the higher number of insurgents being created, who must then be targeted and removed.

4.10

We can also observe in this run the emergence of geography in the simulation. A large swath of the lower-right-hand quadrant of the world map is empty of civilians at the end of this run. The dynamics here are that insurgents were slightly more concentrated initially of the lower-right quadrant of the map (as a result of random distribution). As they conducted attacks on soldiers, and soldiers responded, more civilians in this region became angry, and became latent and eventually active insurgents. The scenario ends essentially only when everyone in the "insurgent region" is dead.

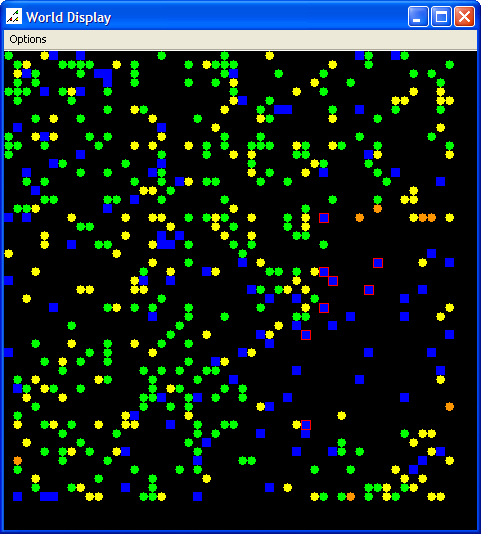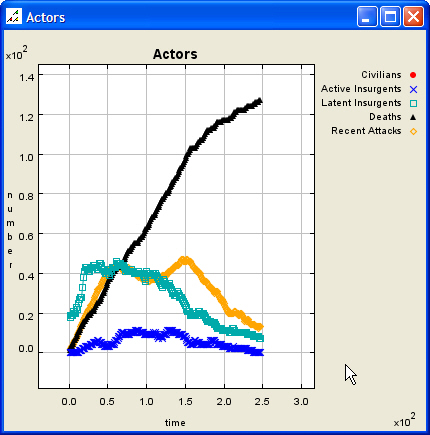
Figure 5. High Effectiveness, Low Accuracy Scenario, After Termination

Scenario 3: Low effectiveness (0.2), low accuracy (0.2)

4.11

The circumstance of low effectiveness and low accuracy might be seen as the nightmare scenario for most governments. In this case, soldiers are not effective at capturing insurgents, and they also cause widespread injury when they counterattack. Such circumstances might fit the case of fighting an urban counterinsurgency campaign, where insurgents have many places to hide, and where non-insurgent civilians are densely packed. The results of an illustrative run of this simulation fit the fear of governments - that an insurgency might spread to the entire population - and it might be defeated only with extreme, and long-lasting, measures. The simulation run depicted in Figure 6 [seed=8382] has been artificially terminated at 2000 ticks. Here, even after 2000 iterations, there are still many insurgents, and a continuing level of attacks against government soldiers. Over this long period, deaths continued to climb (the graph includes a line for the civilian population to show that over half of the fixed population were killed in soldier counterattacks during this typical run). Although a pocket of content civilians remain, after 2000 ticks, most of the population is either dead, or latent insurgents. [In fact, if this simulation is run further, many of these content civilians become insurgents too, and the simulation ends after 4598 ticks, with a remaining civilian population of 125.]

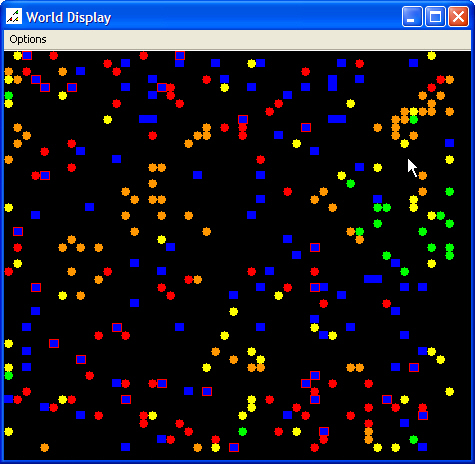
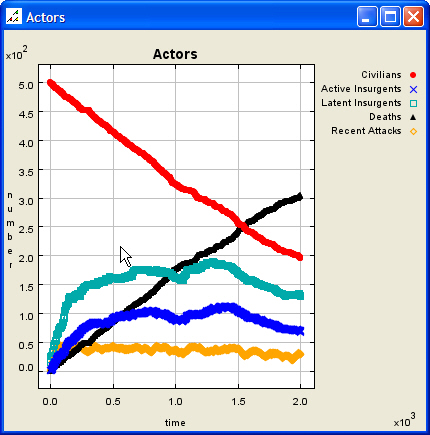
Figure 6. Low Effectiveness, Low Accuracy Scenario, After Termination

Other scenarios

4.12

Exploration of the simulation continued with a sequential review of individual runs of various combinations of effectiveness and accuracy (high effectiveness (0.8) plus moderate accuracy (0.5); moderate effectiveness (0.5) plus high accuracy (0.8); low effectiveness (0.2) plus high accuracy (0.8); moderate effectiveness (0.5) plus moderate accuracy (0.5)). For example, the combination of lower levels of effectiveness with high accuracy allows an examination of the circumstance of soldiers who accurate (avoiding civilian injury) but simply less able to capture insurgents. This combination allows active insurgents to "live" longer, and carry out more attacks; despite the better level of accuracy, this time might allow more insurgents to be created. In fact, the pattern with high accuracy and medium effectiveness is similar to the pattern resulting from medium effectiveness and high accuracy, with scenarios typically resulting in the end of insurgencies after a moderate period of time. When effectiveness falls too much, however (to 0.2 during exploratory simulations), then the circumstance reappears in which only a high number of deaths defeats an insurgency. Runs with low effectiveness and high accuracy closely resemble those with high effectiveness but low accuracy, at least in general form, with moderate insurgency lengths. Interestingly, though, a combination of moderate levels of accuracy and effectiveness does not lead to the same high-death-resolution scenarios as do cases with an extreme on either effectiveness or accuracy. Apparently, at least one of the parameters must be very low if an insurgency is to flourish and last hundreds of iterations.

Results of Repeated Simulations

5.1

The above graphs and figures give a feel for what is happening under various scenarios. To gain a full understanding of the interactive effects of effectiveness and accuracy on insurgency, I ran 25 simulations for each combination of soldier effectiveness from 0.1 to 1.0 and accuracy from 0.0 to 1.0 at increments of 0.1 (2750 runs total, each with a different random seed). An effectiveness level of 0.0 is excluded because in that circumstance counterattacks never remove any insurgent and the simulation continues indefinitely. The durations of each insurgency under each condition (meaning time until the insurgency is defeated, or a termination point of 5000 ticks is reached) were then averaged by condition. Figure 7 shows the average ending time for the simulations run with each combination of accuracy and effectiveness.^[7]

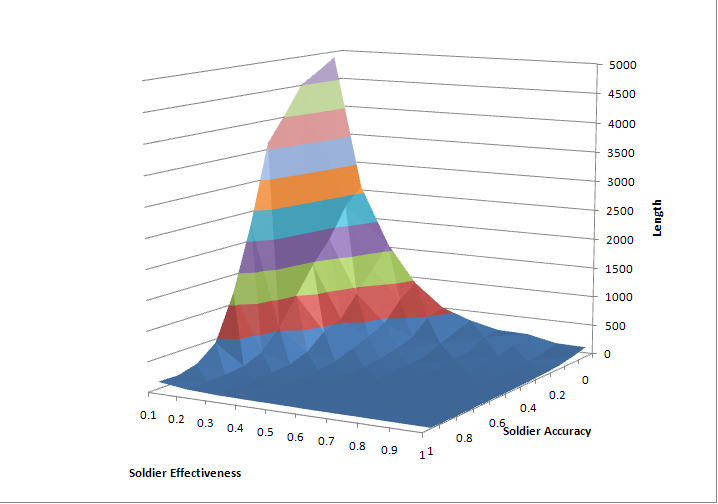
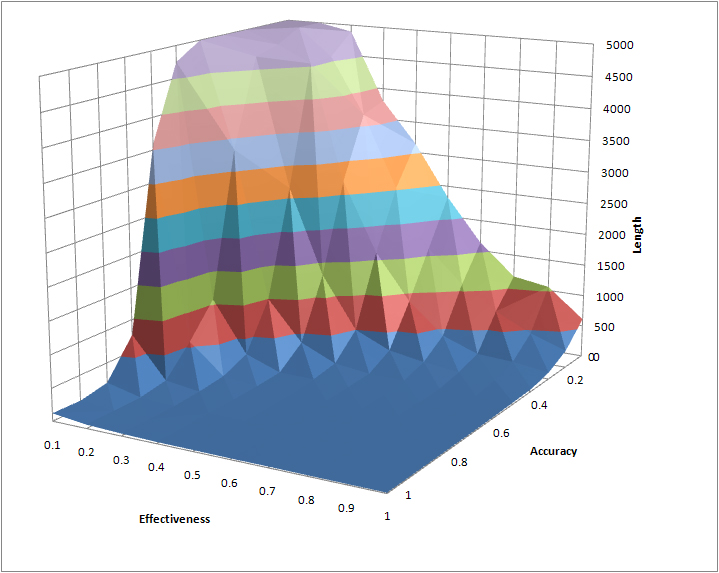
Figure 7. Average Time to Simulation Termination, Varying Accuracy and Effectiveness, 25 Runs per Combination

5.2

In most combinations of accuracy and effectiveness, insurgencies end relatively quickly (less than 500 ticks). And if one parameter is maintained at a high value (high effectiveness, or high accuracy), then even if the other parameter is low (bad conditions), insurgencies are still defeated. It seems to require both low accuracy and low effectiveness to get a long insurgency; when both are at low levels, the time until the end of the simulation (on average) is much higher, indicating a protracted insurgency.

5.3

Critically, however, it appears that the average length of simulation/average length of insurgency is more sensitive to drops in accuracy than to drops in effectiveness. That is, for any scenario apart from the highest levels of effectiveness and accuracy, a drop in accuracy leads to a greater increase in the length of insurgency than a comparable drop in effectiveness from that same point. For example, if accuracy=0.1, it takes a drop in effectiveness to 0.5 to lead to an insurgency of (average) length 500. But if effectiveness=0.1, it only takes a drop to accuracy=0.7 to lead to a 500-tick insurgency. The relationship is that with low effectiveness, what happens is that it takes longer (on average) to kill or capture any given insurgent, but low numbers of new insurgents are created. In contrast, with low accuracy, new insurgents are created at a high enough rate with each counterattack that net removal of insurgents does not occur (or takes much longer). In addition, the simulation appears to show a slightly steeper initial slope in changing accuracy (length increases faster for a unit change in accuracy when accuracy is higher) than effectiveness. But this effect is slight and not entirely clear (it will become clearer in subsequent simulations using replacement, discussed below).

Sensitivity Checks

5.4

Several variations on the default values of non-central parameters were explored to determine whether the core result - that the simulation is more sensitive to changes in accuracy than effectiveness - would change.

• Increasing population size: The initial scenarios run (and those presented above) all assumed a population of 500 spread over the 2500 grid cells of the map. When population size is increased, insurgency spreads more rapidly, and it takes longer for insurgencies to be defeated. The cause of this effect is partly direct, because it takes more time on average to defeat the larger number of insurgents that is present in a larger population, given the random distributions of agent attributes. But increasing the population actually has a more dramatic effect that operates through population density. With a higher population density, each counterattack injures more civilians (for any analysis with accuracy < 1.0), pushing more individuals toward insurgency. In fact, since anger increases in proportion to the number of civilians injured in each counterattack, there is a triple whammy: more civilians means more injuries, and more injuries mean that more individual civilians increase their anger by a greater amount. This emergent effect of population density was initially unanticipated.
• Varying initial anger, fear, violence threshold: when the population starts angrier, less fearful, or with a lower violence threshold, it takes on average a bit longer to defeat an insurgency at any levels of effectiveness and accuracy. This is because in these circumstances, there is simply a larger number of latent insurgents from the start.
• Varying soldier to civilian ratio: has little effect on results or pattern. When soldiers are scarce, the simulations end more often with remaining latent insurgents, as they are out of range of any soldier. Otherwise, since the simulation is sequential, it takes similar time on average for soldiers to be attacked and insurgents removed.
• Increasing interaction range: the presence of a larger interaction range leads to faster increases in the number of latent insurgents and a longer time to the end of insurgency. This is largely because for any level of accuracy < 1.0, a larger neighborhood means more injuries (on average) and more new insurgents potentially created with each counterattack. With a larger interaction range, scenarios are also less likely to end with some remaining insurgents, as insurgents are more likely to be in range of some soldier to carry out an attack and receive a response. Most dramatically, with a large enough interaction range, many scenarios end only with a near decimation of the population. With large interaction range (e.g. 6 rather than 3, and with any accuracy level of 0.7 or less), nearly all civilians eventually become latent insurgents, with the simulation ending only after the long time it takes for each to be killed. In the real world, an increased interaction range might reflect any of a few interesting things. In terms of insurgent attack, it would reflect an increased range of operations for individual insurgents. In terms of soldier counterattack, it might reflect more destructive capability (injury occurs in a more widespread range). It might also reflect the influence of media that spread word of the results of counterattacks more widely. With this last interpretation, we see why some analysts might be concerned with how media can exacerbate an insurgency (more "injuries" perceived when media spreads word of actual injuries. At the same time, though, insurgency can (and does) develop even in situations of low interaction range (e.g. where contact is only direct or where word of mouth might constitute the dominant communication method).
• Varying rules for increasing anger and fear in response to soldier counterattacks: Two model parameters govern how much individuals' anger and fear increase in response to soldiers. The default simulation values are to increase fear by 10% per counterattack, and anger by 5% per civilian injury. Lowering the anger increment per injury leads to a faster resolution of insurgency, as civilians are angered less by each counterattack, and fewer new insurgents are created. In contrast, increasing the anger increment per injury leads to a faster increase in the number of latent insurgents for any level of accuracy < 1. The simulation then ends only after a larger number of (insurgent) deaths. But even with higher anger increments (e.g. 0.1, 0.2), in scenarios with relatively high accuracy and effectiveness (e.g. 0.8), insurgencies are still defeated quickly. At moderate levels of accuracy and effectiveness (e.g. both at 0.5), insurgencies are dramatically longer with higher anger increments. Lowering the fear increment while keeping the anger increment constant leads to slightly longer simulations. But if accuracy is low enough, then even a greater fear increment that deters more civilians doesn't help. When many people are injured, the anger increase still overcomes a greater fear increment. More generally, the emergent pattern that reductions in accuracy have greater effects on insurgency duration than reductions in effectiveness holds across a wide range of values and ratios of these parameters when they were varied between 0.01 and 0.20. Similarly, the pattern that there is a narrow critical range of accuracy which is not evident in effectiveness (which emerges clearly when adding replacement, and is discussed further below) is evident even given substantial variation on these values.

5.5

These analyses both make sense individually, and overall still show the main emergent patterns concerning accuracy vs. effectiveness tradeoffs.

Extension: Adding Replacement

6.1

None of the initial simulations resulted in a critical scenario that leaders fear, a truly self-sustaining insurgency. In fact, a run that never ends could not emerge from the initial program, because eventually (with any effectiveness level > 0) all insurgents could be removed from the simulation (a scenario ending in this way could be the result of killing nearly every civilian in the simulated world). In reality, even brutal repressions of the most violent insurgencies do not typically achieve that level of destruction of the population. Although it might be possible to fully simulate a world with millions of agents, only thousands of whom are insurgents, and thus achieve a result close to the reality of self-sustaining insurgency, this is unnecessary. Instead, I turn now to the simulated replacement of killed insurgents with new civilians. Allowing replacement results in a simulated world closer to a reality in which new individuals may move into areas where people have moved out (or been removed), and where there are always (in practice) more potential insurgents to replace those who have been killed. One of the ways in which the end of insurgency was achieved in the first set of models was through the complete depopulation of certain regions. In some extreme cases, this might occur in the real world, perhaps with forced migration or mass killings in a specific region. But in most circumstances, especially at the early stages of insurgency, civilians vastly outnumber insurgents, and migration and (over the longer- term) birth/maturing can introduce new civilians around a country. We might speculate that if population density cannot be reduced to the complete level of depopulation of some of the initial simulations, the dynamics of insurgency and counterinsurgency might change.

6.2

In this second wave of simulations that adds replacement into the model, a new civilian is added to the world each time a civilian (insurgent) is removed. This maintains a constant population. New civilians are placed at a random location on the map. New civilians are unlikely to be exactly like the insurgents they replace, and so I run two variants in generating their individual characteristics. The anger, fear, and violence threshold of each replacement individual are initially generated from the same distributions as described initially. In some runs, these agent characteristics are left unmodified. In other runs these individual values are modified by the neighborhood into which these individuals are "born." Specifically, in runs with "neighborhood influence," the final characteristics of each individual are an average of their inherent random draws and the average of the other civilians in their neighborhood.

6.3

The most obvious change in the results of these simulations is that insurgencies can indeed continue indefinitely, sometimes with nearly all of the population mobilized as insurgents against the government. With replacement, there is always a new pool of individuals who may become insurgents. Figure 8 shows the state of the world after 2000 model ticks in a low effectiveness, low accuracy scenario (effectiveness 0.2, accuracy 0.2, seed 47, with replacement, without neighborhood influence). Comparing to the model with the same parameters but no replacement (Figure 6), there is a much larger number of latent (and active) insurgents; this results from the placement of new individuals who in turn become angry in response to injuries. Since individuals are replaced, the overall population remains at 500 individuals. The simulation here does not move toward termination through the elimination of insurgents, as soldiers are simply too ineffective to remove insurgents, and a pool of new civilians reacts to each attempt.

Figure 8. Scenario with Replacement, No Neighborhood Influence

6.4

Changing the characteristics of new agents to partly reflect the attributes of surrounding neighbors changes the simulation only slightly. The effect of averaging new random individual characteristics with neighbors has the effect on average of increasing the anger and fear levels of the new individuals (because existing agents can only become more angry and afraid than their initial draws; this increase is transferred to new agents). What this does to the simulated world is that the number of latent insurgents increases faster and on average reaches a slightly higher level than the simulation without neighborhood influence (several simulations were run to t=5000 to verify this stability). Overall, this modification to the basic routines seems to have little effect on the key accuracy/effectiveness dynamics of the simulation. However, the simulation is a closer reflection to a reality in which insurgencies are not likely to be defeated by mass killing, with the resulting pattern resembling what we think of as ongoing insurgency.

Repeated Simulations with Replacement

7.1

As previously, I ran 25 simulations each for all combinations of accuracy and effectiveness values at 0.1 intervals. The times to end of the simulations were then averaged. Figure 9 shows the average ending time of the simulation across the 25 combinations at each combination given replacement but without the influence of existing neighbors on the new agents. Figure 10 shows the average ending time of the simulation across the 25 combinations at each combination given replacement and with neighborhood influence.

Figure 9. Time to Simulation Termination, Varying Accuracy and Effectiveness, Simulations with Replacement and No Neighborhood Influence, Average of 25 Runs per Combination

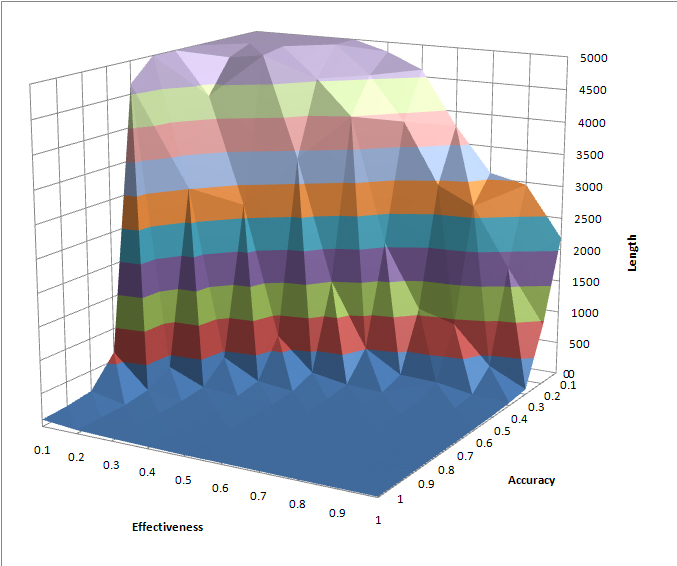
Figure 10. Time to Simulation Termination, Varying Accuracy and Effectiveness, Simulations with Replacement and Neighborhood Influence, Average of 25 Runs per Combination

7.2

In contrast to the graph in Figure 7, the number of scenarios that become long insurgencies is higher in Figure 9, and even higher in 10. That is, the range of problematic combinations of accuracy and effectiveness is greater when we simulate a population with replacement than without. This makes sense, as in this case the population cannot simply be "removed" to create a government victory. In addition, when new citizens are created, some will start as latent insurgents, and all are vulnerable to injury and possible movement toward supporting the insurgency. When relatively more civilians are present (relative to the prior scenarios where the number of civilians was dropping), more injury also results in larger anger increases in everyone within an affected neighborhood. And finally, since anger generally increases in these scenarios, the circumstance where new agents are influenced by other existing agents (new agents receive a boost to their anger and fear from others in their neighborhood) leads to the most long insurgencies.

7.3

Also in contrast to the prior results, these scenarios suggest that even very high effectiveness may be inadequate to counter the negative effects of low accuracy. Even when effectiveness is 1.0, if accuracy is below about 0.25, the length until the defeat of an insurgency jumps dramatically in comparison to the simulations without replacement. By contrast, even if effectiveness is low, there is some high enough level of accuracy that will lead to very short insurgencies.

7.4

These simulations show that there seems to be a narrow critical range of accuracy values over which the length of insurgencies jumps up very quickly. If accuracy is above this value, then insurgencies are relatively short. But once this critical threshold is passed and accuracy falls below it, there is a dramatic and non-linear increase in insurgency duration. For example, in the graph showing the simulations with replacement and neighborhood influence (Figure 10), if effectiveness is held to 0.1 (for illustration), then we see a small increase in average length when accuracy decreases from 0.8 to 0.7, but a much larger increase when accuracy changes from 0.7 to 0.6. Anywhere below this level of accuracy (again, at this particular effectiveness level), the insurgency is self-sustaining (the surface is actually not flat in length, but is infinitely high; the flatness is due to the artificial cutoff of the simulation at 5000 iterations). This sharp "tipping point" does not seem to exist with effectiveness, where the increase in insurgency length as effectiveness decreases is slower (and close to linear at many levels of accuracy), regardless of the level of accuracy.

7.5

Overall, these simulations with replacement continue to suggest the dominance of accuracy over effectiveness as the major influence on the length of insurgency. These simulations may represent a closer parallel to real-world circumstances than the initial version without replacement. They continue to suggest that accuracy should be a critical area of focus.

Implications

8.1

The apparent sensitivity of the model to accuracy over effectiveness has important real-world implications. First, suppose a military could invest in getting new weapons or modifying training techniques so that either 1) counterattacks are more accurate (imposing lower collateral damage), or 2) counterattacks increase their effectiveness (keeping the same collateral damage, but increasing their kill/capture rate). Or consider the tradeoff in a scenario where effectiveness could be increased but only at a cost to accuracy. The simulations suggest that in the long-run, the benefit of keeping the number of new insurgents down by maintaining or increasing accuracy outweighs the short-term cost of missing the capture of some insurgents. When action against insurgents results in many injuries and an increase in population anger, governments do the work of insurgents for them, and make successful prosecution of a counterinsurgency campaign more difficult.

8.2

A second implication relating the importance of accuracy to national context emerges from the initially unanticipated effect of population density. As discussed, increasing the population has important effects that operate through population density; with a higher population density, each counterattack injures more civilians, pushing more individuals toward insurgency at a greater rate. Situations of high population density magnify the effects of inaccurate targeting. Unfortunately, situations of high population density (e.g. urban environments) may also endogenously decrease the ability to be accurate. That is, with high-precision weapons, it may be possible to distinguish a single target insurgent under conditions where possible individual targets are visible and spread out. But in a crowd, or large building, it may be both harder to spot or locate an individual target, and easier for any counterattack with given technical accuracy (e.g., likely injury radius from a bomb) to injure multiple civilians. Density may thus not be exogenous to accuracy, and the resulting effects of counterattacks; it causes a double-whammy of both decreasing accuracy rates and magnifying the negative effects of any inaccuracy.

8.3

A third implication involves the possible existence of a narrow critical range or tipping point of accuracy. If indeed there is a narrow range where small decreases in accuracy can lead to major increases in the length of insurgency, it suggests even more that militaries must be cautious about accuracy. There is bound to be a degree of uncertainty about how accurate military forces are. Given an inability to know precisely where a state is, and indeed where the tipping point is (since the specific values of 0.2, 0.3, 0.4, etc. are representations for simulation purposes), if a state happens to have accuracy levels close to critical, then it could only take a tiny slippage in accuracy at any time to lead to major negative results. And because of the rapid deterioration that accompanies accuracy levels below "OK," trial and error to discover what accuracy level is good enough may be disastrous. By contrast, any small decrease in effectiveness yields a smaller change in outcomes; it is possible that slippage here could be caught and corrected before matters become too much worse.

8.4

Finally, a critical question of interest may be what values correctly characterize levels of accuracy and effectiveness in real conflicts? With specific operationalizations, accuracy and effectiveness rates could in principle be calculated from real data. For instance, we might narrowly operationalize accuracy as the percentage of neighboring civilians to a target point that are physically injured in any government/military action. We could then track injuries after any government action, whether through media sources, hospital records, or government documents. Similarly, if we take effectiveness as the percentage of attempts to capture or kill insurgents that are successful, we know that the military tracks military operations and keeps track of insurgents captured. The proportion of successes per operation is a direct measure of effectiveness. The full range of such information is unavailable to academic analysts (it is likely classified), but taking the case of the U.S. involvement in Iraq, for instance, and simply reading accounts in U.S. news media, we may be able to give a ballpark estimate. For instance, when we read accounts of the capture of wanted insurgents in Iraq, it is not uncommon for the news article to note that several prior attempts to capture the individual had been made, with explanations for prior failures typically including the suspect "narrowly escaping" a prior search, or the suspect being tipped off. We could also consider as examples the search for Saddam Hussein which took months, or for Osama Bin Laden which continues. Do the available data suggest a 0.2 effectiveness rate, or a 0.4 (for example)? We cannot estimate a figure that accurately, but it seems that the reality is far from 0.8. We can also look at news reports of civilian injury, where we frequently see reference to events where 5, 10, 20, or more nearby civilians were injured or killed in an attack, even attacks using precision-guided weapons. Is accuracy such that 80% of surrounding civilians avoid injury? The rate here is unclear, because we do not have data about the number of total civilians around targeted locations, but it seems unlikely that the accuracy rate is this high, either. If real-world values are below 50% on each of these parameters in some case, this puts the simulation world into an area where extended insurgencies could indeed be the result primarily of government actions.

Conclusions

9.1

This paper has developed a simulation of the dynamics of early insurgent attack and soldier/government response that demonstrates the tradeoffs between accuracy and precision in fighting an insurgency. The simulation started with minimal assumptions about agent interactions, including the deterrent effects of military actions vs. the effects on anger, building on what we observe of military acts that target single or small groups of individuals in many cases, and recognizing that that collateral damage affects many individuals. The simulation was purposefully designed to include "light" agents with few characteristics in order to keep the focus on clear dynamics rather than multiple distributions of individual parameters and interactions of different characteristics. The key questions were then how accuracy and effectiveness would interact in leading to long or short insurgencies. Even with a simple model, interesting and critical dynamics about the interaction of governments, insurgents, and civilians emerge from the simulation. The results suggesting that accuracy is critical to the long-term defeat of an insurgency, and that there may be a "tipping point" in accuracy, appear quite robust to changes in surrounding conditions such as the size of neighborhood and the relative magnitude of increases in fear and anger.

9.2

The conclusions parallel and demonstrate the logic of recent literature that suggests new approaches to counterinsurgency strategy. At the same time, the model results themselves do not represent facts. Rather, they may be seen as suggesting hypotheses about real-world relationships. If enough features of real-world dynamics and government-insurgent interactions parallel the model, we should find similar relationships if we conducted broad empirical testing. In particular, we should find that situations where nascent insurgencies were confronted with a counterinsurgency strategy that focused on accuracy in avoiding civilian damage should result in shorter insurgencies (or a higher probability of defeat) when compared to situations where accuracy was ignored, or an emphasis was placed on capturing insurgents regardless of civilian casualties. Many individual cases seem to validate the pattern emerging from the model, but do not represent a comprehensive and large-n test. If one were able to obtain cross-sectional time-series data on the training and doctrine of military forces, one could use data on insurgencies (for instance, that fromBapat 2005) to more systematically test the relationship. Such data is not currently available, and a thorough test remains for future work.

9.3

Given the large literature on insurgency and terrorism in the social science literature, it is useful to conclude by pointing out some of the supposed "critical attributes" of insurgencies that are not present in this model, which nevertheless generates ongoing insurgencies:

• There is no active recruitment by insurgents, no safe houses, no defensible terrain.
• There is no media that distorts or widely broadcasts the results of government responses to insurgent attacks, or broadcasts an insurgent message. Instead, opinions are changed only by direct contact/presence in a neighborhood directly affected by a counterattack.
• There is no central insurgent leadership, or formal network of insurgents. Rather, dynamics are driven solely by individual soldier agents, response, and by negative reactions to those responses at a very local level.
• There is no identity to any agent, such as ethnicity, political party, or religious affiliation. The generic anger/grievance, and generic deterrent effect of fear, allow this simulation to be viewed as "content free" in the sense of not attributing particular motives to any agent, but instead allowing a variety of real-world content to be attached.

9.4

Depending on the interests and intuitions of the researcher, these or other features could be added to the base simulation. For instance, if we expected attacks to differentially effect members of different ethnic groups, we might want to add ethnicity or religion (it would not be useful to add it only as an abstract characteristic unless it had some differential effect on rules of behavior or interaction). If transmission mechanisms were seen as particularly critical to an observer, agent movement or social networks which transmit information or anger could be added. As with ethnicity or religion, such networks would need to be added in a way that differentiated among actors and future behavior somehow. If networks simply transmit information more widely, then they would have effects similar to increasing the agents' interaction range, or if they just transmitted information to particular other non-adjacent regions of the simulated world, then the pattern of insurgency spread would be different but there would be no anticipated effect on the net length of insurgencies under different conditions. Recruitment is currently being added to the model (Bennett 2008a) as an extension to allow exploration of other strategies that could be employed by insurgents or government representatives. Another extension in progress is adding learning to the simulation to judge whether, when, and how much a "bump" to accuracy or effectiveness can decrease the length of an insurgency (Bennett 2008b). Rather than add all features of the real world to the simulation at once, those extensions follow the path of gradually relaxing the "keep it simple" approach of this initial version.

9.5

The simulation here shows that insurgencies can spread solely in response to government actions in response to insurgents, and reveals the risks and dilemmas that governments face when engaging in counterinsurgency. The real world features trade-offs between effectiveness and accuracy when pursuing insurgents; a "heavy hand" more likely to capture insurgents is also likely to inflict more collateral damage, while an approach that privileges the avoidance of civilian harm is likely less effective (in the short run) at capturing targeted individuals. The simulation suggests it is critical to recognize the serious risks of inflicting unintended harm on others as an important step to making difficult circumstances of confronting an insurgency even worse. Careful attention to tradeoffs between accuracy and effectiveness, and on the importance of accuracy, may help to minimize unintended cycles of violence.

Acknowledgements

I would like to thank the participants in the international relations reading group at the Pennsylvania State University, Ahmer Tarrar, Lars-Erik Cederman, Idean Salehyan, Nils Weidmann, and the participants in the ETH speaker series for helpful comments. The simulation was programmed in Java using the RePast 3.1 simulation libraries in a Windows XP environment. The final version of the simulation used here is v 1.2. Code for the simulation, as well as auxiliary material, is available on the author's website at http://www.personal.psu.edu/dsb10/.

Notes

¹ A variety of specific definitions of insurgency exist in the literature. We generally think of insurgency as an internal military and political struggle by a group to replace a given government with one more to the insurgents' liking. One useful and more comprehensive definition is that insurgency is “a struggle between a nonruling group and the ruling authorities in which the nonruling group consciously uses political resources (e.g., organizational expertise, propaganda, and demonstrations) and violence to destroy, reformulate, or sustain the basis of legitimacy of one or more aspects of politics” (O'Neill 2005: 15). Insurgency may be closely related to more general social movements (which are typically seen as nonviolent) and to civil war (once an insurgency reaches some critical mass of armed force, violence reaches a high level, and insurgents control a significant amount of territory, we may call it a civil war [see Small and Singer 1982). Critical components of the definition include the use of violence in seeking to obtain political change, and the fact that the insurgent group is largely internal to a political system (state), unlike the circumstances in conventional interstate warfare. This does not exclude the possible influence of outside actors, of course.

² It is generally accepted that it is easier to motivate civilians to oppose occupying forces or a government seen as a puppet rather than a legitimate indigenous government and its forces (e.g. Metz and Millen 2004). In the model developed here, the difference in these situations is easily captured by increasing the baseline level of anger among civilians (discussed below), and so differences will be explored in the sensitivity analysis. This higher level of anger at an occupying or puppet government would not require changes to the dynamics of the model, however.

³ A different model could be developed to focus on the dynamics of final national government defeat by insurgents. That model would likely be quite different, with quite different dynamics of government defeat at play. This later stage of an insurgency, specifically after it reaches the point of being self-sustaining, is not the focus of the model here.

⁴ The simulation parameterizes this probability of response to allow future exploration of a possible optimal response strategy for a government dealing with insurgents that might include only partial or occasional responses to attacks.

⁵ While it is easiest to think of “injury” as literal injury (injured civilians) in the case of collateral damage in conflict situations, in other circumstances the “injury” that civilians react to could be property damage, individual disruption (being forced from homes, searched), or neighborhood disruption (setup of checkpoints, vehicle searches). All of these actions might inflame anger at the soldiers undertaking the actions.

⁶ In the versions of the simulation presented here, only the fear and anger of those civilians actually injured in a counterattack are updated. In a variant, everyone in the neighborhood (that is, within the “interaction range” of the targeted insurgent) has their fear and anger updated. The main effects of the simulation and the effectiveness/accuracy relationships are not substantially affected by this change.

⁷ In every combination, the standard deviation of length over the 25 runs is smaller than the mean, typically between 25% and 50% of the mean length. The s.d. is typically smaller in runs at the “edges” of the space, that is, where accuracy or effectiveness are close to 0 or 1. There is thus a good bit of variation within the runs, but not enough to conceal a clear trend in the mean. More runs do not appreciably change the shape of the figures displayed here. The author's website includes a spreadsheet listing the mean and standard deviation of the 25 runs at each combination of accuracy and effectiveness, and computing 75% and 89% bounds for the mean based on the Chebyshev inequality.

References

AXELROD, Robert (2004) Comparing Modeling Methodologies. Manuscript, March 18, 2004. Available online at http://www-personal.umich.edu/~axe/.

BAPAT, Navin (2005) Insurgency and the Opening of Peace Processes. Journal of Peace Research 42: 699-717.

BENNETT, D. Scott (2008a) Recruiting Your Way to Victory: Varying Strategies in Insurgent/Counterinsurgent Warfare. Paper presented at the annual meeting of the Midwest Political Science Association, Chicago, IL, April 5, 2008.

BENNETT, D. Scott (2008b) Being Your Own Worst Enemy, and Learning to Win: A Model of Government Learning in Responding to Insurgency. Manuscript.

BHAVNANI, Ravi, Dan Miodownik, and Jonas Nart (2008) REsCape: An Agent-Based Framework for Modeling Resources, Ethnicity, and Conflict. Journal of Artificial Societies and Social Simulation (11: 27). https://www.jasss.org/11/2/7.html.

CEDERMAN, Lars-Erik (2006) Articulating the Geo-Cultural Logic of Nationalist Insurgency. In Kalyvas, Stathis, and Iain Shapiro, eds., Order, Conflict, and Violence. Cambridge: Cambridge University Press.

CHATURVEDI, A. R., D. Dolk, R Chaturvedi, M. Mulpuri, D. Lengacher, S. Mellema, P. Poddar, C. Foong, and B. Armstrong (2005) Understanding Insurgency by Using Agent-Based Computational Experimentation: Case Study of Indonesia." Proceedings of the Agent 2005 Conference on Generative Social Processes, Models, and Mechanisms.

CUI, Xiaohui, and Thomas E. Potok (2007) A Particle Swarm Social Model for Multi-Agent Based Insurgency Warfare Simulation. Software Engineering Research, Management & Applications, 2007: 177-183.

DORAN, Jim (2005) Iruba: An Agent-Based Model of the Guerrilla War Process. In Klaus Troitzsch, ed. Representing Social Reality: Pre-Proceedings of the Third Conference of the European Social Simulation Association, Koblenz, September 5-9, 2005. Germany: Verlag Dietmar Fölbach, pp. 198-205.

EPSTEIN, Joshua M., John D. Steinbruner, Miles T. Parker (2001) Modeling Civil Violence: An Agent-Based Computational Approach. Center on Social and Economic Dynamics, Brookings Institution, Working Paper No. 20, January 2001.

FEARON, James D. and David D. Laitin (2003) Ethnicity, Insurgency, and Civil War. American Political Science Review 97:75-90.

FINDLEY, Michael G., and Joseph K. Young (2007) Fighting Fire with Fire? How (Not) to Neutralize an Insurgency. Civil Wars 9(4): 378-401.

GALULA, David (2006) Counterinsurgency Warfare: Theory and Practice. Westport, CT: Praeger Security International. Originally published 1964.

HENDRICKSON, David C., and Robert W. Tucker (2005) Revisions in Need of Revising: What Went Wrong in the Iraq War. Carlisle, PA: Strategic Studies Institute of the U.S. Army War College.

LOUIE, Marcus A., and Kathleen M. Carley (2007) The Role of Dynamic-Network Multi-Agent Models of Socio-Political Systems in Policy. Manuscript.

MANWARING, Max (2004) Shadows of Things Past and Images of the Future: Lessons for the Insurgencies in our Midst. Carlisle, PA: Strategic Studies Institute of the U.S. Army War College.

METZ, Steven, and Raymond Millen (2004) Insurgency and Counterinsurgency in the 21st Century. Carlisle, PA: Strategic Studies Institute of the U.S. Army War College.

MILITARY Operations Research Society (2006) MORS Workshop Report: Agent-Based Models and Other Analytic Tools in Support of Stability Operations. Unclassified Research Report for MORS Workshop, October 25-27, 2005.

NAGL, John A (2005) Learning to Eat Soup with a Knife: Counterinsurgency Lessons from Malaya and Vietnam. Chicago: Chicago.

O'NEILL, Bard E(2005) Insurgency & Terrorism. Washington: Potomac Books.

RECORD, Jeffrey, and W. Andrew Terrill (2004) Iraq and Vietnam: Differences, Similarities, and Insights. Carlisle, PA: Strategic Studies Institute of the U.S. Army War College.

RUBY, Keven, David L. Sallach, Charles M. Macal, Veena S. Mellarkod, Alexander Wendt (2005) Occupation Dynamics: Contesting Hearts and Minds. Proceedings of the North American Association for Computational Social and Organizational Science, June 26-28, 2005.

SMALL, Melvin, and J. David Singer (1982) Resort to Arms: International and Civil Wars, 1816-1980. Beverly Hills, Calif.: Sage Publications.

UNITED STATES DEPARTMENT OF THE ARMY (2007) The U.S. Army/Marine Corps Counterinsurgency Field Manual. Chicago: University of Chicago.

WARREN, T. Camber (2006) Communication, Coordination, and Conflict: An Agent-Based Model of Loyalty Fragmentation. Paper presented at the Annual Meeting of the American Political Science Association, August 31-September 3, 2006.

WHEELER, Scott (2005) It Pays to Be Popular: a Study of Civilian Assistance and Guerilla Warfare. Journal of Artificial Societies and Social Simulation 8(4) https://www.jasss.org/8/4/9.html.

WIMBERLEY, Scott (1997) Special Forces Guerrilla Warfare Manual. Boulder: Paladin Press.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2008]