Gokhan Ozertan and Baris Cevik (2008)
Pricing Strategies and Protection of Digital Products Under Presence of Piracy: A Welfare Analysis
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 1
<https://www.jasss.org/11/4/1.html>
For information about citing this article, click here
Received: 29-Nov-2005 Accepted: 14-Jul-2008 Published: 31-Oct-2008
 Abstract
Abstract
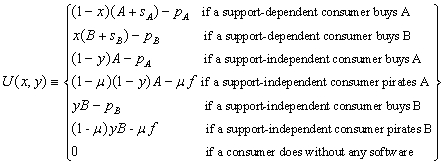
|
(1) |
| ΠA = pADA-(A'-A)2/2-(sA'-sA)2/2-C(μ), | (2) |
and
| ΠB = pBDB-(B'-B)2/2-(sB'-sB)2/2-C(μ), | (3) |
where A, B, sA, sB are the initial quality levels of software and support packs of A and B, respectively. Now, we can get the profit functions by substituting the relevant demand functions into (2) and (3).
| SW = CSA+CSB+ΠA+ΠB+μf. | (4) |
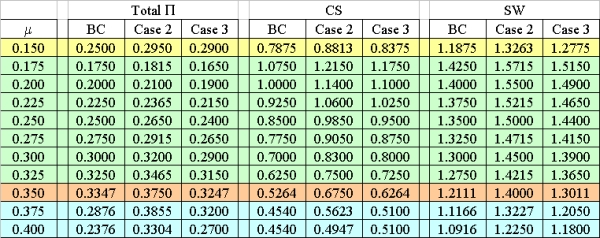
Proposition 1. In the symmetric set-up of the "Benchmark Case," profits are maximized at monitoring rates corresponding to price levels close to monopoly (Region 3), whereas consumers' surplus and social welfare are maximized at monitoring rates corresponding to competitive price levels (Region 2). Firms prefer either low monitoring-high price, or high monitoring-high price combinations, since deviations from monitoring rates of Region 1 first decrease and only then increase profits. From a social welfare maximizing point of view, by deviating from monitoring rates of Region 1 to those of Region 2 at μ = 0.250 consumers' surplus and social welfare can be increased without decreasing profits.
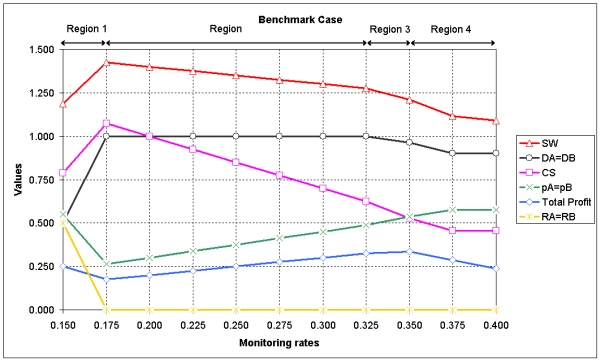
|
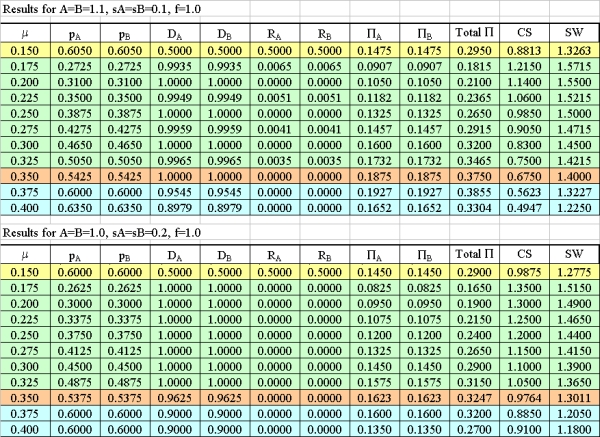
| Figure 1. Values that model variables take depending on the monitoring rates selected: A = 1.1, B = 1.0, sA = sB = 0.1, f = 1.0 |
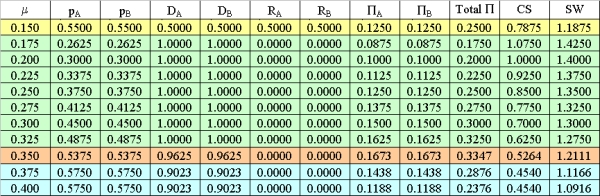
|
| Table 1. Numerical example results for A = B = 1.0, sA = sB = 0.1, f = 1.0 |
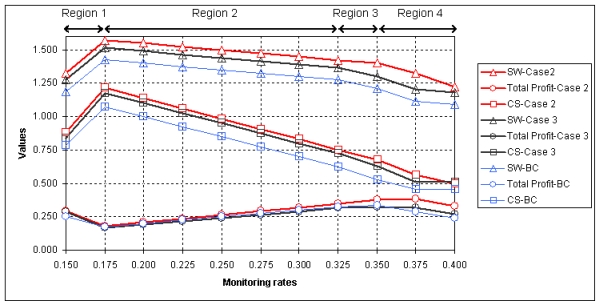
Proposition 2. When both firms offer software with better quality, compared with the BC, profits, consumers' surplus and social welfare increase at all monitoring levels. The improvement in quality also affects prices charged which are higher than those of the BC across all monitoring levels. Some users pirate both software products at monitoring levels corresponding to competitive prices of Region 2.
|
| Table 2. Changes in model parameters after improvements in software (Case 2) and support pack (Case 3): Comparison with the Benchmark Case values |
|
| Figure 2. Values of total profits, consumers' surplus, and social welfare in Case 2 (A = B = 1.1) and Case 3 (sA = sB = 0.2): Comparison with the Benchmark Case (BC) values |
Proposition 3. When both firms increase qualities of support packs they produce, compared with the BC, improvement in quality is not reflected in prices except in Regions 1 and 4. There are increases and decreases in profits at different monitoring levels, but consumers' surplus and social welfare both increase at all monitoring rates with no piracy occurring.
2The computer code is available from the authors upon request.
| yAW = (A-pA)/A. | (A.1) |
By using the individual rationality constraint, (1-μ)(1-y)A-μf ≥ 0, we can derive the location of the marginal user yA'W who is indifferent between pirating A and doing without as
| yA'W = 1-μf/((1-μ )A). | (A.2) |
Suppose that yA'W < yAW. Then, from (A.1) and (A.2) we can derive that
| 1-μf/((1-μ )A) < (A-pA)/A, which is equal to μf/(1-μ) > pA. | (A.3) |
For some support-independent users to pirate software A, we need to have (1-μ)A-μf ≥ A-pA > 0 (y is dropped here, but this does not affect the calculations). And once this equation is solved, we get
| pA ≥ μ(A+f). | (A.4) |
When we combine (A.3) and (A.4) we obtain
| μf/(1-μ ) > pA ≥ μ(A+f). | (A.5) |
And this implies that
| μf/(1-μ ) > μ (A+f). | (A.6) |
This contradicts our assumption about (1-μ)A-μf ≥ 0. Hence, no support independent user pirates software A if yA'W < yAW.
| Case.A) yB'W < yBW < yAW | Case.F) yB'W < yAW < yA'W < yBW |
| Case.A1) yA'W < yB'W < yBW < yAW | Case.G) yAW < yB'W < yBW < yA'W |
| Case.A2) yB'W < yA'W < yBW < yAW | Case.H) yB'W < yAW < yBW < yA'W |
| Case.A3) yB'W < yBW < yA'W < yAW | Case.I) yB'W < yBW < yAW < yA'W |
| Case.B) yBW < yAW | Case.J) yAW < yA'W < yBW |
| Case.B1) yA'W < yBW < yB'W < yAW | Case.J1) yAW < yA'W < yBW < yB'W |
| Case.B2) yA'W < yBW < yAW < yB'W | Case.K) yAW < yBW < yA'W |
| Case.B3) yBW < yA'W < yB'W < yAW | Case.K1) yAW < yBW < yB'W < yA'W |
| Case.B4) yBW < yB'W < yA'W < yAW | Case.K2) yAW < yBW < yA'W < yB'W |
| Case.B5) yBW < yA'W < yAW < yB'W | Case.L) yAW < yB'W < yBW |
| Case.C) yBW < yAW < yA'W | Case.L1) yA'W < yAW < yB'W < yBW |
| Case.C1) yBW < yB'W < yAW < yA'W | Case.M) yB'W < yAW < yBW |
| Case.C2) yBW < yAW < yB'W < yA'W | Case.M1) yA'W < yB'W < yAW < yBW |
| Case.C3) yBW < yAW < yA'W < yB'W | Case.M2) yB'W < yA'W < yAW < yBW |
| Case.D) yAW < yA'W < yB'W < yBW | Case.N) yAW < yBW |
| Case.E) yAW < yB'W < yA'W < yBW | Case.N1) yA'W < yAW < yBW < yB'W |
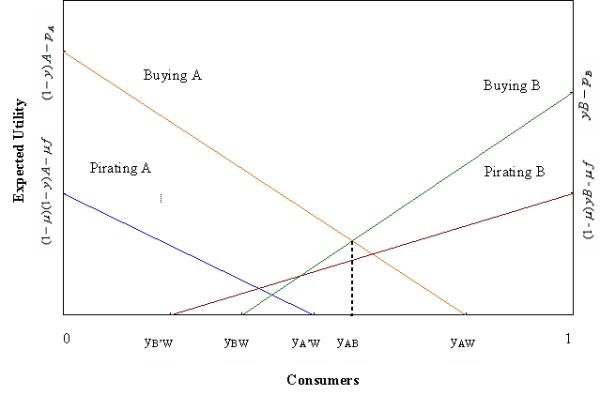
|
| Figure A.1. Expected Utility curves for Case A3 |
In Figure A.1, we observe that at every point up to yAW, buying A brings strictly more expected benefit than pirating A. Therefore, in this subcase, no support-independent user will pirate software package A. In order to find the demand functions, we trace the utility curves from zero to 1 and pick up the utility curve that brings more net expected benefit than the others. Starting from zero up to yAB, buying A brings the highest benefit, since its utility curve lies above all of the remaining utility curves. From yAB to 1, buying B brings the highest benefit, since its utility curve lies above all of the other utility curves. Thus, in this subcase, support-independent users buy either software package A or software package B, and they never pirate. This implies that with no piracy we have RA = RB = 0. Support-independent users' demands for original software packages are given as DASI = yAB = (A+pB-pA)/(A+B) and DBSI = 1-yAB = (B-pB+pA)/(A+B). Support-dependent users' demand for original software packages are given as DASD = (A-pA+pB+sA)/(A+sA+B+sB), and DBSD = (B-pB+pA+sB)/(A+sA+B+sB). After adding up these values we obtain the demand functions for both products. Profits are calculated based on equations (2) and (3). For users who pirate software, consumers' surplus is defined to be the expected benefit of pirating. We define CSA as the total surplus of users buying and pirating software package A and calculate it as
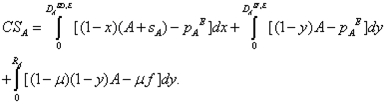
|
(A.7) |
Since we have RA = 0 for this case, we end up with
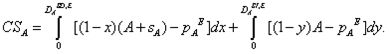
|
(A.8) |
A similar calculation is done for CSB. Finally, SW for this subcase is calculated using (4).
|
| Table A.1. Numerical example results for A = B = 1.1, sA = sB = 0.1, f = 1.0 and A = B = 1.0, sA = sB = 0.2, f = 1.0 |
BAE S. H. and Choi, J. P. (2006) "A Model of Piracy," Information Economics and Policy, 18, pp.303-320.
BANERJEE D. S. (2006) "Lobbying and commercial software piracy", European Journal of Political Economy, 22, pp.139-155.
BELLEFLAMME P. and Picard P. M. (2007) "Piracy and Competition", Journal of Economics & Management Strategy, 16, pp.351-383.
BSA (2007a) "Fourth Annual BSA and IDC Global Software Piracy Study" http://w3.bsa.org/globalstudy/.
BSA (2007b) "BSA Conducts Record Global Anti-Piracy Enforcement Action: International Media Company Learns the Cost of Unlicensed Software" http://www.bsa.org/country/News%20and%20Events/News%20Archives/en/2007/en-09182007-globalsettlement.aspx.
CHEN, Y. and Png, I. (2003) "Information goods pricing and copyright enforcement: welfare analysis", Information Systems Research, 14, pp.107-123.
CONNER K.R. and Rumelt R. P. (1991) "Software piracy: an analysis of protection strategies", Management Science, 37, pp.125-39.
GAYER A. and Shy O. (2005) "Copyright Enforcement in the Digital Era", CESifo Economic Studies, 51, pp.477-489.
GOPAL R. D. and Sanders G. L. (1997) "Preventive and Deterrent Controls for Software Piracy", Journal of Management Information Systems, 13, pp.29-48.
JOHNSON W. R. (1985) "The Economics of Copying", Journal of Political Economy, 93, pp.158-174.
LAU E. K. (2007) "Interaction Effects in Software Piracy", Business Ethics: A European Review, 16, pp.34-47.
LIU L. P. and Fang W.C. (2003) "Ethical Decision-Making, Religious Beliefs and Software Piracy", Asia Pacific Management Review, 8, pp.185-200.
PEITZ M. and Waelbroeck P. (2006) "Piracy of digital products: A critical review of the theoretical literature", Information Economics and Policy, 18, pp.449-476.
POLINSKY A. M. and Shavell S. (2000) "The Economic Theory of Public Enforcement of Law", Journal of Economic Literature, XXXVIII, pp.45-76.
SHY O. and Thisse J.F. (1999) "A strategic approach to software protection", Journal of Economics & Management Strategy, 8, pp.163-190.
SUNDARARAJAN A. (2004) "Managing digital piracy: Pricing and protection", Information Systems Research, 15, pp.287-308.
TRADE-RELATED ASPECTS OF INTELLECTUAL PROPERTY RIGHTS (TRIPS) AGREEMENT. (1994) Agreement on the Trade-Related Aspects of Intellectual Property Rights. Annex 1C of the Uruguay Round of General Agreement on Trade and Tariffs (GATT), signed in June 1994 in Marakesh.
YOON, K. (2002) "The optimal level of copyright protection", Information Economics and Policy, 14, pp.327-348.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]