Gero Schwenk and Torsten Reimer (2008)
Simple Heuristics in Complex Networks: Models of Social Influence
Journal of Artificial Societies and Social Simulation
vol. 11, no. 3 4
<https://www.jasss.org/11/3/4.html>
For information about citing this article, click here
Received: 14-Sep-2007 Accepted: 22-Mar-2008 Published: 30-Jun-2008
 Abstract
Abstract|
|
We call this rule the " Contact All " or ALL rule. According to the second rule, agents contact only those neighbors who have at least the same (or a higher) status value wjas the agents themselves.
|
|
We call this rule the " Higher Equal " or HE rule. Its inclusion is based on observations in research on collective choice, which indicate that group members who have high levels of expertise or status are, at times, more influential in the group decision process than members who have low levels (e.g., Bonner, Baumann, Lehn, Pierce, & Wheeler 2006). Both rules include the searching agent himself/herself as an information source.
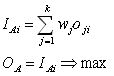
|
IAi designates the inference of agent A made on a specific alternative i. This inference IAi is computed in two steps. Firstly, the available opinion oji of neighbor j on alternative i is weighted with the latter neighbor's status wj. Secondly, all k neighbors' weighted opinions wjoji are summed up. Agent A chooses the inference IAi with maximal value as her preference OA.
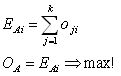
|
|
|
|
|
As can be seen in Table 1, we have considered all possible combinations of contact and decision rules. The FTL -rule is listed only once, because it makes no difference whether the leader (by definition, the member with the highest status) is selected from amongst all neighbors or only from amongst the subset of higher status neighbors.
| Table 1: Contact and Decision Rules Considered | |
| Contact Rule | Decision Rule |
| HE (Higher Equal) | UWM (Unit Weight Model) |
| HE (Higher Equal) | WADD (Weighted Additive Model) |
| HE (Higher Equal) | MIN (Minimalist) |
| HE (Higher Equal) | FTL (Follow the Leader) |
| ALL (All Neighbors) | UWM (Unit Weight Model) |
| ALL (All Neighbors) | WADD (Weighted Additive Model) |
| ALL (All Neighbors) | MIN (Minimalist) |
|
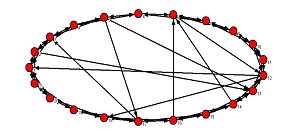
| Figure 1. Small world network ( n =21, k =2, pr =0.1). The network has been created by introducing shortcut ties to a regular ring network, where every node is connected to two neighbors on each side |
| Table 2: Employed Variations of the Small-World Model ( n =21, k =2). | |
| Rewiring Probability | Network Characteristic |
| pr=0 | Cyclic Regular, high clustering |
| pr=0.1 | Small-world |
| pr=1 | Random regular, no clustering |
|
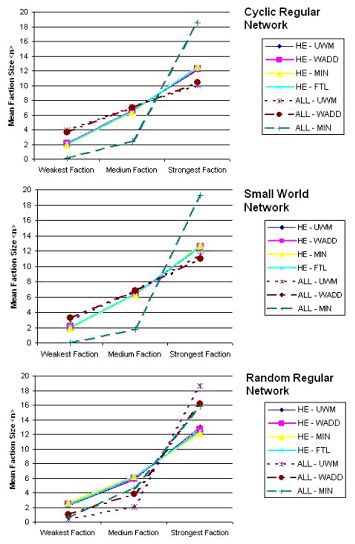
| Figure 2. Mean faction sizes over networks with decreasing clustering. Results were sorted according to the size of the faction in an individual simulation run, regardless of the actual choice-alternative favored. A majority is reached at eleven. |
Different patterns of faction sizes were observed for strategies containing an HE- or ALL contact rule. As expected, the decrease of network clustering generally led to smaller sizes of minority factions.
|
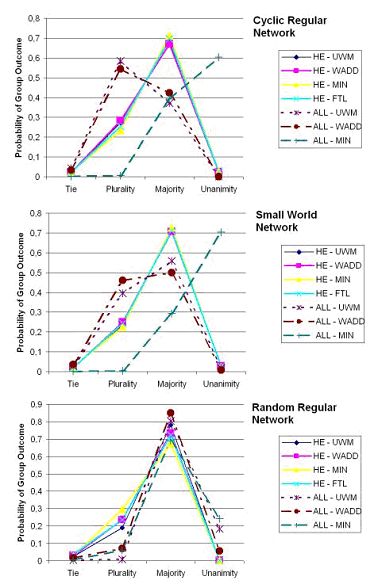
| Figure 3. Group level outcomes over networks with decreasing clustering. |
|
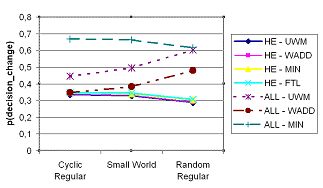
| Figure 4. Probability of decision change of high status members over networks with decreasing clustering (cyclic regular, small world, random regular). |
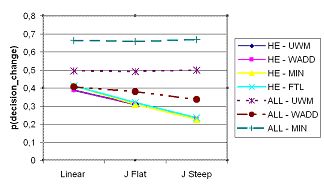 |
| Figure 5. Probability of decision change in high status members in a small world network over status distributions of increasing steepness. |
|
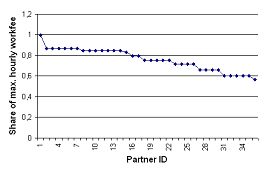
| Figure 6. Status distribution of partners in an empirical network. Partners are numbered according to seniority. |
|
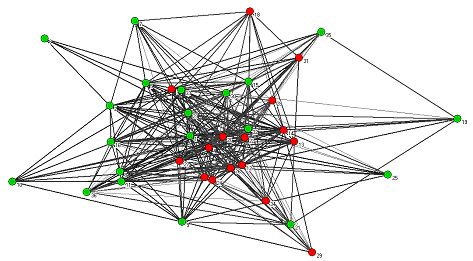
| Figure 7. Empirical influence network. Highly connected partners are located in the center of the network. Dark and wide arrows represent high status relations. Green nodes represent an "as - is" and red nodes a "less flexible" policy opinion. Partners are numbered according to their seniority. |
|
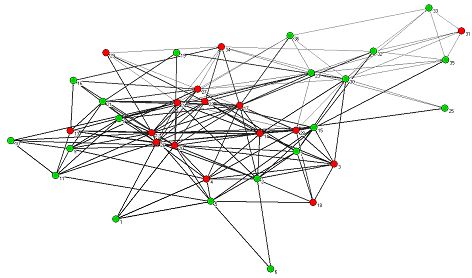
| Figure 8. HE - relevant subnet of the empirical influence network: highly connected partners are located in the center of the network. Dark and wide arrows represent high status relations. Green nodes represent an "as - is" and red nodes a "less flexible" policy opinion. Partners are numbered according to their seniority. |
| Table 3: Preference distributions for the considered strategies in the network. The two possible preferences were "keep case assignment as it is" and "organize case assignment less flexible via a central authority." As can bee seen, the final distributions of opinions depart considerably from the initial distributions. | |||
| Strategy | n(as-is) | n(less flexible) | Equilibrium cycle |
| HE - UWM | 34 | 2 | 7 |
| HE - WADD | 34 | 2 | 5 |
| HE - MIN | Majority | Minority | Fluctuating |
| HE - FTL | 26 | 10 | 3 |
| ALL - UWM | 36 | 0 | 4 |
| ALL - WADD | 36 | 0 | 4 |
| ALL - MIN | 36 (p=0.77) | 36 (p=0.23) | Mean=17.8 |
| Initial distribution | 20 | 16 | -- |
2 Originally, we employed both high and low valued linear status distributions. As expected, both induced exactly the same process behavior.
BONNER, B, Baumann, M, Lehn, A, Pierce, D, and Wheeler E. (2006). 'Modeling collective choice: Decision-making on complex intellective tasks.' European Journal of Social Psychology, 36, 617-633.
CARLEY, K, Prietula, M and Lin, Z. (1998). 'Design Versus Cognition: The interaction of agent cognition and organizational design on organizational performance.' Journal of Artificial Societies and Social Simulation, 1(3), https://www.jasss.org/1/3/4.html.
CSERMELY, P (2006). Weak links: Stabilizers of complex systems from proteins to social networks. Berlin, Springer-Verlag.
DAVIS, J (1973). 'Group decision and social interaction: A theory of social decision schemes.' Psychological Review, 80, 97-125.
FESTINGER, L, Schachter, S and Back, K. (1950). Social pressures in informal groups. New York: Harper and Row.
FRENCH, J (1956). 'A formal theory of social power.' Psychological Review , 63(3),181-194.
FRIEDKIN, N (1998). A structural theory of social influence. MA: Cambridge University Press.
GIGERENZER, G, Todd, P, and the ABC Research Group (1999). Simple heuristics that make us smart. New York: Oxford University Press.
GUIMERA, R, Uzzi, B, Spiro, J and Amaral L (2007) 'Team assembly mechanisms determine collaboration network structure and team performance.' Science, 308, 697-702
HASTIE, R and Kameda, T (2005). 'The robust beauty of majority rules in group decisions'. Psychological Review, 112, 494-508.
KEARNS, M., Suri, S and Monfort N (2006) 'An experimental study on the coloring problem on human subject networks,' Science, 313, 824-827
KERR, N and Tindale, R (2004). 'Group performance and decision making.' Annual Review of Psychology, 55, 623-655.
LATANÉ, B (1981). 'The psychology of social impact.' American Psychologist, 36, 343-356.
LATANÉ, B (1996). 'Dynamic social impact: The creation of culture by communication.' Journal of Communication, 46, 13-25.
LATANÉ, B and L'Herrou, T (1996). 'Spatial clustering in the conformity game: Dynamic social impact in electronic groups.' Journal of Personality and Social Psychology, 70 (6), 1218-1230.
LAZEGA, E (2001). The collegial phenomenon: The social mechanisms of cooperation among peers in a corporate law partnership. England: Oxford University Press.
LITTLEPAGE, G, Schmidt, G, Whisler, E and Frost A. (1995). 'An input-process-output analysis of influence and performance in problem.' Journal of Personality and Social Psychology, 69 (5), 877-889
MASON, A, Conrey, F and Smith, E (2007). 'Situating social influence processes: Dynamic, multidirectional flows of influence within social networks.' Personality and Social Psychology Review, 11, 279-300.
MASUDA, N and Konno, N (2006). 'The VIP-club phenomenon: emergence of elites and masterminds in social networks.' Social Networks, 28, 297-309
NEWMAN, M. (2003). 'The structure and function of complex networks.' SIAM Review, 45(2), 167-256.
REIMER, T and Hoffrage, U (in press). 'Combining simple heuristics by a majority rule: The ecological rationality of simple heuristics in a group context.' In Todd, P, Gigerenzer, G and the ABC Research Group (Eds.), Ecological rationality: Intelligence in the world. New York: Oxford University Press.
REIMER, T and Hoffrage, U (2006). 'The ecological rationality of simple group heuristics: Effects of group member strategies on decision accuracy.' Theory and Decision, 60, 403-438.
REIMER, T and Hoffrage, U (2005). 'Can simple group heuristics detect hidden profiles in randomly generated environments?' Swiss Journal of Psychology, 64, 21-37.
REIMER, T and Katsikopoulos, K (2004). 'The use of recognition in group decision-making' Cognitive Science, 28, 1009-1029
SCHWENK, G and Reimer, T (2007). 'Social influence and bounded rationality: Heuristic decision making in complex networks.' In D.S. McNamara, D and Trafton, G (Eds.), Proceedings of the twenty-ninth annual conference of the cognitive science society (1479 - 1484). NJ: Lawrence Erlbaum Associates.
SEELEY, T, (2001). 'Decision making in superorganisms. How collective wisdom arises from the poorly informed masses.' In Gigerenzer, G and Selten, R (Eds.), Bounded rationality. The adaptive toolbox. Cambridge MA: MIT Press.
SORKIN, R, West, R, and Robinson, D. (1998). 'Group performance depends on the majority rule.' Psychological Science, 9, 456-463.
SUN, R (Editor) (2006). Cognition and multi agent interaction: from cognitive modeling to social simulation. New York: Cambridge University Press
SUN, R and Naveh, I (2004). 'Simulating organizational decision-making using a cognitively realistic agent model.' Journal of Artificial Societies and Social Simulation, 7(3), https://www.jasss.org/7/3/5.html
TURNER, J (1996). Social influence. Buckingham, England: Open University Press.
WASSERMAN, S and Faust, K (1994). Social network analysis. Methods and applications. MA: Cambridge University Press.
WATTS, D (1999). 'Networks, dynamics, and the small-world phenomenon.' American Journal of Sociology, 105, 493-527.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]