Dara Curran and Colm O'Riordan (2007)
Cultural Learning in a Dynamic Environment: an Analysis of Both Fitness and Diversity in Populations of Neural Network Agents
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 3
<https://www.jasss.org/10/4/3.html>
For information about citing this article, click here
Received: 14-Aug-2006 Accepted: 17-Sep-2007 Published: 31-Oct-2007
 Abstract
AbstractThis paper examines the effects of cultural learning on the evolutionary process of a population of neural networks. In particular, the paper examines the genotypic and phenotypic diversity of a population as well as its fitness. Using these measurements, it is possible to examine the effects of cultural learning on the population's genetic makeup. Furthermore, the paper examines whether cultural learning provides a more robust learning mechanism in the face of environmental changes.
Three benchmark tasks have been chosen as the evolutionary task for the population: the bit-parity problem, the game of tic-tac-toe and the game of connect-four. Experiments are conducted with populations employing evolutionary learning alone and populations combining evolutionary and cultural learning in an environment that changes dramatically.
 Related Work
Related Work Model
Model

|
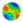
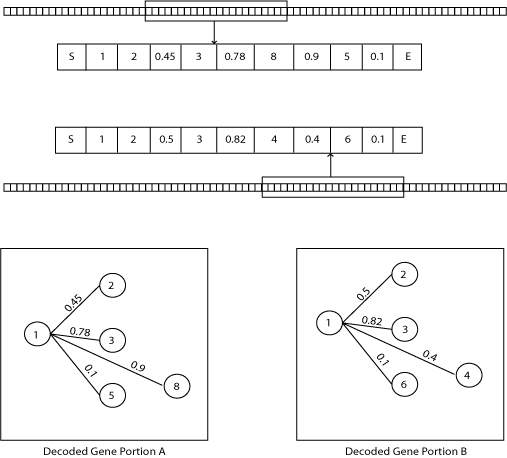
| Figure 1. Neural Network Encoding Example |
|
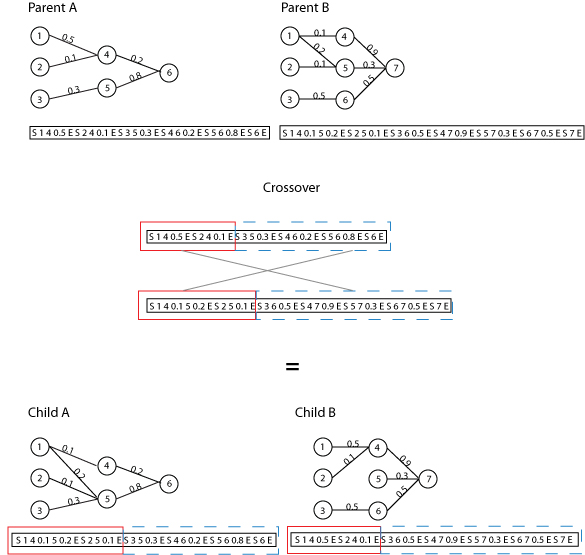
| Figure 2. Sample crossover |
|
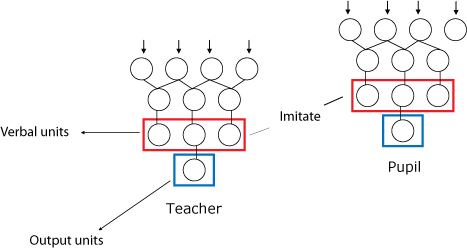
| Figure 3. Agent Communication Architecture |
|
| Figure 4. Genotypic diversity measure |
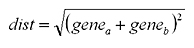
|
(1) |
The distance measures for each pair of portions is averaged together to give a diversity measure for the two full length chromosomes.
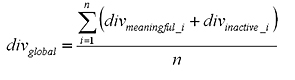
|
(2) |
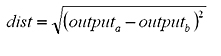
|
(3) |
 Experimental Results
Experimental Results
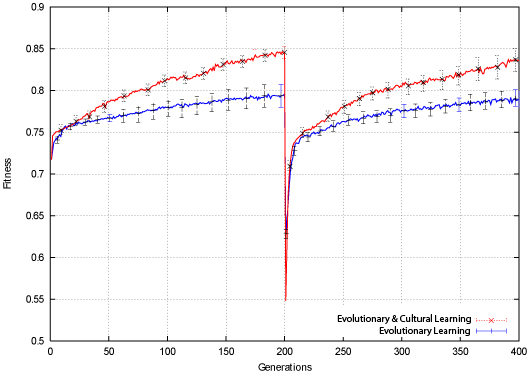
|
| Figure 5. Bit-Parity Population Fitness |
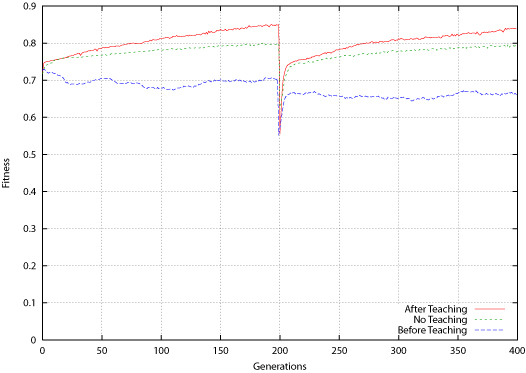
|
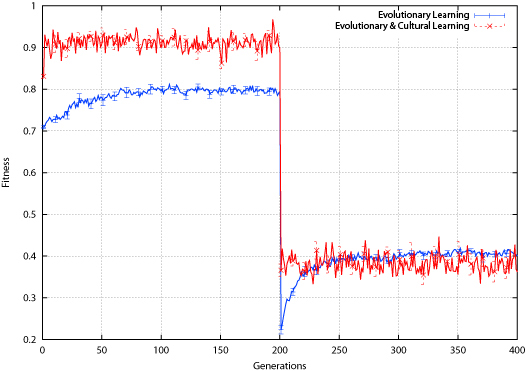
| Figure 6. Bit-Parity Average Fitness for Population Before and After Teaching |
|
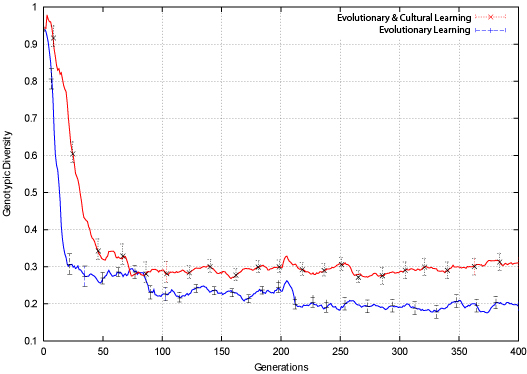
| Figure 7. Bit-Parity Genotypic Diversity |
|
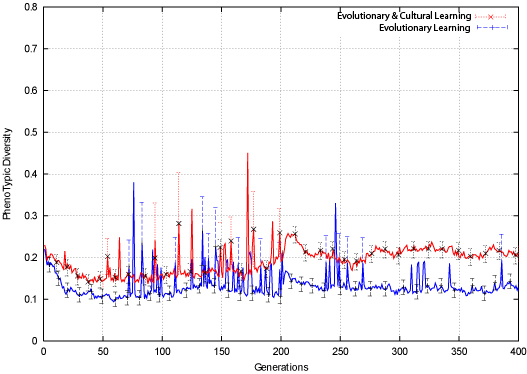
| Figure 8. Bit-Parity Phenotypic Diversity |
|
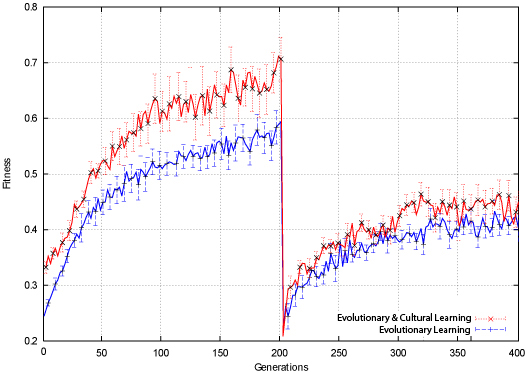
| Figure 9. Tic-Tac-Toe Average Fitness |
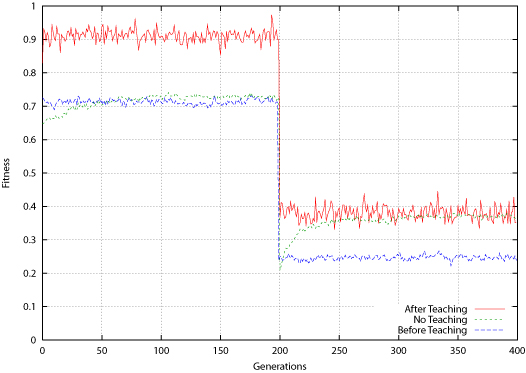
|
| Figure 10. Tic-Tac-Toe Average Fitness for Population Before and After Teaching |
|
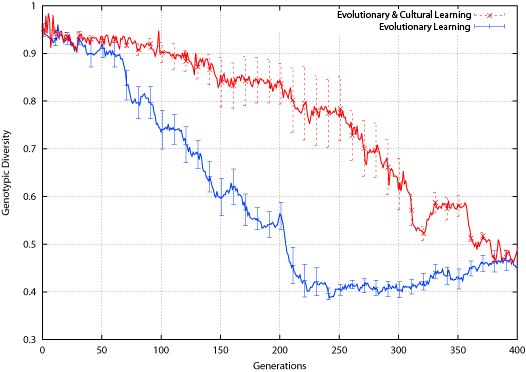
| Figure 11. Tic-Tac-Toe Genotypic Diversity |
The effect of the environment change is different for the two populations: the population employing evolutionary learning alone shows a slight drop in phenotypic diversity around the environment change, while the cultural learning population shows a slight rise. Again, this is different than what was found in the bit-parity experiment, where both populations showed a slight rise in phenotypic diversity around the environment change.
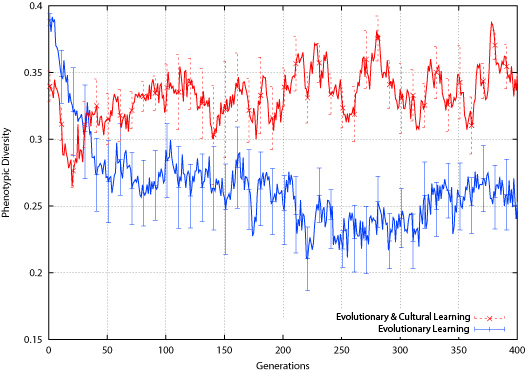
|
| Figure 12. Tic-Tac-Toe Phenotypic Diversity |
|
| Figure 13. Connect-4 Average Fitness |
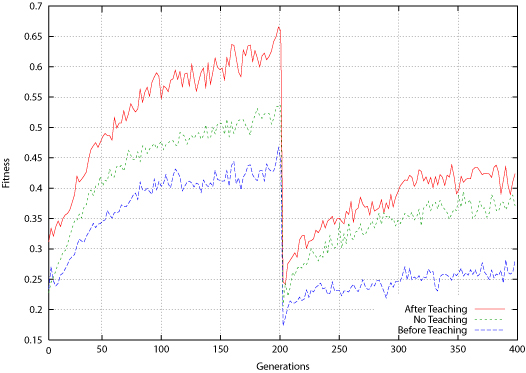
|
| Figure 14. Connect-4 Average Fitness for Population Before and After Teaching |
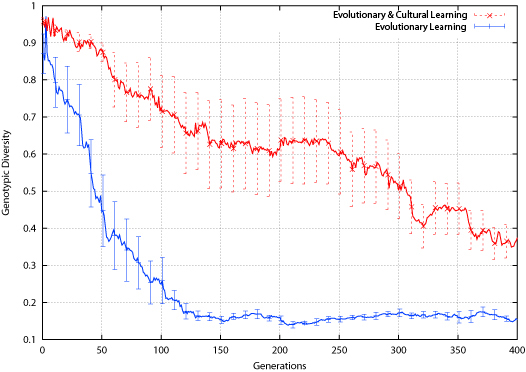
|
| Figure 15. Connect-4 Genotypic Diversity |
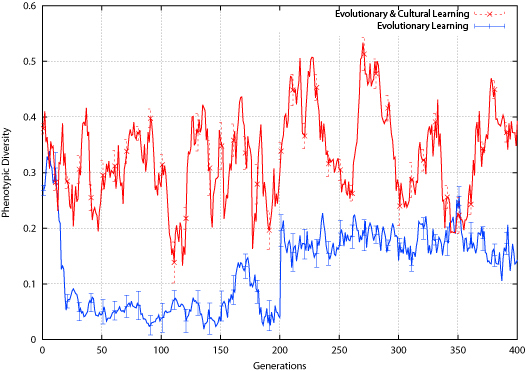
|
| Figure 16. Connect-4 Phenotypic Diversity |
 Discussion
Discussion Conclusion
ConclusionThe first author would also like to acknowledge the support of the Irish Research Council for Science, Engineering and Technology.
BATALI, J. (1998) 'Computational simulations of the emergence of grammar', Approaches to the evolution of language: Social and cognitive bases, Cambridge: Cambridge University Press.
BELEW, R. K. (1990) 'Evolution, learning and culture: Computational metaphors for adaptive algorithms', Complex Systems, Vol. 4, pp. 11-49.
BELEW, R. K., McInerney, J., & Schraudolph, N. N. (1992) 'Evolving networks: Using the genetic algorithm with connectionist learning', Proceedings of Artificial life II. pp. 511-547. Redwood City, CA: Addison-Wesley.
BEST, M. L. (1999) 'How culture can guide evolution: An inquiry into gene/meme enhancement and opposition', Adaptive Behavior, Vol. 7(3/4), pp. 289-306.
BOOKER, L. B. (1982) 'Intelligent behavior as an adaptation to the task environment', Unpublished doctoral dissertation, The University of Michigan.
BOOKER, L. B. (1985) 'Improving the performance of genetic algorithms in classifier systems', Proceedings of the international conference on genetic algorithms and their applications, pp. 80-92. Pittsburgh, PA.
BORENSTEIN, E., & Ruppin, E. (2003) 'Enhancing autonomous agents evolution with learning by imitation', Interdisciplinary Journal of Artificial Intelligence and the Simulation of Behaviour, Vol. 1(4), pp. 335-348.
BOYD, R., & Richerson, P. (1985) Culture and the evolutionary process. University of Chicago Press.
BRIGHTON, H., & Kirby, S. (2001) 'The survival of the smallest: Stability conditions for the cultural evolution of compositional language', In Proceedings of ECAL'01, pp. 592-601, Springer-Verlag.
CANGELOSI, A. (1999) 'Evolution of communication using combination of grounded symbols in populations of neural networks', Proceedings of IJCNN99 international joint conference on neural networks, Vol. 6, pp. 4365-4368, Washington, DC: IEEEPress.
CAVALLI-SFORZA, L. L. (1981). Cultural transmission and evolution, a quantitative approach, Princeton University Press.
CLIFF, D., & Miller, G. F. (1995). 'Tracking the red queen: Measurements of adaptive progress in co-evolutionary simulations', Proceedings of the Third European Conference on Artificial Life (ECAL 1995), p. 200-218, Springer.
COLLINS, R. J., & Jefferson, D. R. (1991) 'Selection in massively parallel genetic algorithms'. Proceedings of the Fourth International Conference on Genetic Algorithms, pp. 249-256.
CURRAN, D., & O'Riordan, C. (2003) 'On the design of an artificial life simulator', Proceedings of the seventh international conference on knowledge-based intelligent information & engineering systems (KES 2003), pp. 549-555, University of Oxford, United Kingdom.
CURRAN, D., & O'Riordan, C. (2004) 'A comparison of population learning and cultural learning in artificial life societies'. Proceedings of ninth international conference on the simulation and synthesis of living systems (ALIFE9).
CURRAN, D., & O'Riordan, C. (2005) 'Applying cultural learning to sequential decision task problems', Proceedings of the 16th Irish artificial intelligence and cognitive science conference (AICS 2005).
CURRAN, D., & O'Riordan, C. (2006a) 'The Effects of Cultural Learning in Populations of Neural Networks', Artificial Life, Vol. 13(1), pp. 45-67.
CURRAN, D., & O'Riordan, C. (2006b) 'Increasing population diversity through cultural learning', Adaptive Behavior, Vol. 14(4), pp. 315-338.
DARWIN, C. (1859) The origin of species: By means of natural selection or the preservation of favoured races in the struggle for life. Bantam Classics.
DAVIDOR, Y. (1991) 'A naturally occurring niche and species phenomenon: The model and first results', Proceedings of ICGA, pp. 257-263, San Diego, CA, USA: Morgan Kaufmann.
DE JONG, E. D. (1999) 'Analyzing the evolution of communication from a dynamical systems perspective', Proceedings of the European conference on artificial life (ECAL 1999), pp. 689-693.
DE JONG, K. A. (1975) 'Analysis of behavior of a class of genetic adaptive systems', Unpublished doctoral dissertation, The University of Michigan.
DEB, K., & Goldberg, D. E. (1989) 'An investigation of niche and species formation in genetic function optimization', Proceedings of the third international conference on genetic algorithms, pp. 42-50, San Francisco, CA,USA: Morgan Kaufmann Publishers Inc.
DENARO, D., & Parisi, D. (1996) 'Cultural evolution in a population of neural networks', Proceedings of the 8th italian workshop on neural nets, pp. 100-111.
FLOREANO, D., & Mondada, F. (1996) 'Evolution of plastic neurocontrollers for situated agents', From Animals to Animats IV: Proceedings of the Fourth International Conference on Simulation of Adaptive Behavior, Vol. 4.
GOLDBERG, D. E., & Richardson, J. (1987) 'Genetic algorithms with sharing for multimodal function optimization', Proceedings of the second international conference on genetic algorithms on genetic algorithms and their application, pp. 41-49, Mahwah, NJ, USA: Lawrence Erlbaum Associates, Inc.
GREFENSTETTE, J. J. (1992) 'Genetic algorithms for dynamic environments', Parallel problem solving from nature 2, pp. 137-144.
GRUAU, F. (1994) 'Neural network synthesis using cellular encoding and the genetic algorithm', Unpublished doctoral dissertation, Centre d'etude nucleaire de Grenoble, Ecole Normale Superieure de Lyon, France.
GUSFIELD, D. (1997) Algorithms on strings, trees and sequences: computer science and computational biology, Cambridge Univ. Press. (Gusfield)
HILLIS, W. D. (1990) 'Co-evolving parasites improve simulated evolution as an optimization procedure', Proceedings of the ninth annual international conference of the center for nonlinear studies on self-organizing, collective, and cooperative phenomena in natural and artificial computing networks on emergent computation, pp. 228-234. Amsterdam, The Netherlands, The Netherlands: North-Holland Publishing Co.
HOLLAND, J. H. (1975) Adaptation in Natural and Artificial Systems, University of Michigan Press
HUTCHINS, E., & Hazlehurst, B. (1991) 'Learning in the cultural process', Proceedings of Artificial life II, pp. 689-706, Cambridge, MA: MIT Press.
HUTCHINS, E., & Hazlehurst, B. (1995) 'How to invent a lexicon: The development of shared symbols in interaction', Artificial societies: The computer simulation of social life, pp. 157-189, London: UCL Press.
KIRBY, S., & Hurford, J. (1997) 'Learning, culture and evolution in the origin of linguistic constraints', ECA 19'97, pp. 493-502, MIT Press.
KITANO, H. (1990) 'Designing neural networks using genetic algorithm with graph generation system', Complex Systems, Vol. 4, pp. 461-476.
KOLEN, J. F., & Pollack, J. B. (1991) 'Back propagation is sensitive to initial conditions', Advances in Neural Information Processing Systems, 3, pp. 860-867.
KOZA, J. R., & Rice, J. P. (1991) 'Genetic generation of both the weights and architecture for a neural network', International joint conference on neural networks, IJCNN-91, Vol. 2, pp. 397-404), Seattle, WA: IEEEComputer Society Press.
MAHFOUD, S. W. (1995a) 'A comparison of parallel and sequential niching methods', Proceedings of the sixth international conference on genetic algorithms, pp. 136-143.
MAHFOUD, S. W. (1995b) 'Niching methods for genetic algorithms', Unpublished doctoral dissertation, University of Illinois.
MANDISCHER, M. (1993) 'Representation and evolution of neural networks', Artificial neural nets and genetic algorithms proceedings of the international conference at Innsbruck, Austria, pp. 643-649. Wien and New York: Springer.
MCQUESTEN, P. H. (2002) 'Cultural enhancement of neuroevolution', Unpublished doctoral dissertation, University of Texas, Austin.
MENCZER, F. (1994) 'Changing latent energy environments: A case for the evolution of plasticity', Technical report cs94-336.
MILLER, G. F., Todd, P. M., & Hedge, S. U. (1989), 'Designing neural networks using genetic algorithms', Proceedings of the third international conference on genetic algorithms and their applications, pp. 379-384.
MORIARTY, D. E., & Miikkulainen, R. (1995) 'Discovering complex othello strategies through evolutionary neural networks', Connection Science, Vol. 7(3-4), pp. 195-209.
MORRISON, R. W. (2004) Designing Evolutionary Algorithms for Dynamic Environments, Springer.
MUHLENBEIN, H. (1989) 'Parallel genetic algorithms, population genetics and combinatorial optimization'. Proceedings of the third international conference on genetic algorithms, pp. 416-421, San Francisco, CA, USA Morgan Kaufmann Publishers Inc.
NOLFI, S., & Parisi, D. (1993) 'Self-selection of input stimuli for improving performance', Neural networks in robotics, pp. 403-418,. Kluwer.
NOLFI, S., & Parisi, D. (1994) 'Desired answers do not correspond to good teaching inputs in ecological neural networks', Neural processing letters, Vol. 1(2), p. 1-4.
NOLFI, S., & Parisi, D. (1996) 'Learning to adapt to changing environments in evolving neural networks', Adaptive Behavior, Vol. 5(1), pp. 75-97.
NOLFI, S., Parisi, D., & Elman, J. L. (1994) 'Learning and evolution in neural networks', Adaptive Behavior, 3(1), pp. 5-28.
OLIPHANT, M., & Batali, J. (1997) 'Learning and the emergence of coordinated communication', The newsletter of the Center for Research in Language, Vol. 11(1).
O'REILLY, U. M. (1997) 'Using a distance metric on genetic programs to understand genetic operators'. IEEE international conference on systems, man, and cybernetics, Vol. 5, pp. 4092-4097.
PUJOL, J. C. F., & Poli, R. (1998) 'Efficient evolution of asymmetric recurrent neural networks using a two-dimensional representation', Proceedings of the first European workshop on genetic programming (EUROGP) , pp. 130-141.
ROSCA, J. P. (1995) 'Entropy-driven adaptive representation', Proceedings of the workshop on genetic programming: From theory to real-world applications, pp. 23-32.
SASAKI, T., & Tokoro, M. (1997), 'Adaptation toward changing environments: Why Darwinian in nature?', Fourth European conference on artificial life, pp. 145-153, Cambridge, MA: MIT Press.
SAUNDERS, G. M., & Pollack, J. B. (1994) 'The evolution of communication in adaptive agents', Technical Report of the Department of Computer and Information Science, The Ohio State University.
SPIESSENS, P., & Manderick, B. (1991) 'A massively parallel genetic algorithm: Implementation and first analysis', Proceedings of the 4th International Conference on Genetic Algorithms, pp. 279-287. San Diego, CA, USA: Morgan Kaufmann.
SUTTON, R. S. (1986) 'Two problems with back-propagation and other steepest-descent learning procedures for Networks', Proceedings of the 8th annual conference of the cognitive science society, pp. 823-831.
TROJANOWSKI, K., & Michalewicz, Z. (1999) 'Evolutionary algorithms for non-stationary environments', Proceedings of 8th workshop: Intelligent information systems, pp. 229-240, Watson, J., & Wiles, J. (2002) 'The rise and fall of learning: A neural network model of the genetic assimilation of acquired traits', Proceedings of the 2002 congress on evolutionary computation (CEC 2002), pp. 600-605.
WHITE, D. W. (1994) 'Gannet: A genetic algorithm for searching topology and weight spaces in neural network design', Unpublished doctoral dissertation, University of Maryland College Park.
YANCO, H., & Stein, L. (1993) 'An adaptive communication protocol for cooperating mobile robots'. From Animals to Animats 2: Proceedings of the second international conference on simulation of adaptive behavior, pp. 478-485, Cambridge MA: MIT Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]